Introduction

Shape memory alloy (SMA) polycrystals are metallic materials that can be deformed far beyond the elastic deformation limit up to several percents of strain and yet recover the original shape upon unloading or unloading and heating. The material can accommodate and recover large strains due to the martensitic phase transformation. In NiTi-based SMA, transformation between the parent phase—austenite—and the product phase—martensite—under tensile stress tends to localize so that martensite band fronts (MBFs) form and propagate along the sample leaving the material with modified dimensions and microstructure (phase) behind. Since this is similar to the localization of plastic deformation observed in certain steels and alloys [1], it has been called in the literature Lüders-like deformation. Nevertheless, there are several specific features of the localized deformation in NiTi alloys different from that in steels related to the different natures of the process (e.g., [2, 3]). Microstructural aspects of the localization phenomenon, e.g., interaction of phases and their compatibility at internal interfaces or internal strain and stress inhomogeneities, are complex and not fully understood yet (cf. [4, 5]), even though the phenomenon has been thoroughly experimentally investigated in the last two decades, e.g., [6,7,8,9,10,11]. Localization occurs only in NiTi alloys with a suitable texture and only in particular loading modes and deformation rates [12], and it is a critical issue for fatigue [13]. Naturally, this motivates further investigation of the phenomenon particularly in commercially successful NiTi wires [14,15,16].

Recently, we have analyzed MBF in a stretched superelastic NiTi wire by the three-dimensional X-ray diffraction method (3D-XRD) on grain by grain level and used it for reconstruction of mesoscopic phase and stress fields in the wire [17]. This also motivated development of an enhanced constitutive model, which could be employed in a complementary finite element (FE) analysis of the MBF. As claimed in [12, 18], localization of deformation in NiTi is not merely a geometric effect, but strain-softening material constitutive response beyond the transformation yield limit plays a key role. In the pioneering studies, e.g., [6, 19], the authors used a simple J2-elastoplasticity model with strain softening to study localization in NiTi samples deformed in pure tension, and they were able to capture some basic features. Based on experiments on laminates, Hallai and Kyriakides [20] refined the original constitutive law to obtain a smooth uniaxial stress–strain response. Duval [21] utilized nonlocal gradient approach to incorporate localization into a two-dimensional superelastic reduction of a rather advanced SMA constitutive model [22]; this was further refined for any thermomechanical loadings by Armattoe et al. [23]. Examples of other conventional SMA models modified for strain softening can be found in [24,25,26].

In this study, we present further details on the extension of our earlier three-dimensional NiTi constitutive model developed in [17] to capture the strain localization phenomenon. The core model features an elaborated form of the dissipation function (directly related to “yield functions”) and takes into account some phenomena specific to textured NiTi SMA which makes it particularly suitable for simulations of experimental observations of localization in this alloy. The extension consists mainly in the introduction of strain softening into the constitutive law and correct (mesh-independent) numerical implementation into FE software via the so-called nonlocal integral averaging technique. To illustrate viability of the solution, we perform an FE simulation mimicking tensile loading of a NiTi wire utilizing experiment-adjusted material parameters and specific numerical treatment of the ensuing boundary value problem. Although the experimental motivation is also summarized, much more details on this aspect of our study can be found elsewhere [17].

Experimental Motivation

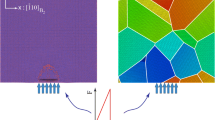
The shape of the MBF propagating in tensioned NiTi wire and internal stress surrounding it (Fig. 1) were for the first time experimentally reconstructed by three-dimensional X-ray diffraction technique in our related study [17]. The experiment was performed at the European Synchrotron Research Facility (Grenoble, France) on a superelastic NiTi wire (Ti–50.8 at.% Ni, Fort Wayne Metals) with diameter 0.1 mm which was heat treated by a short electric current pulse to reach desired microstructure with eliminated R-phase. The sample was mounted on a load frame, stretched to create an MBF and the length of the wire was fixed. The load frame was rotated around the axis parallel to the wire axis with increments Δω = 0.3°, and multispot 2D diffraction patterns (contain reflections from suitably oriented grains within the illuminated cross section of the wire) were recorded on a 2D detector (Fig. 1a). By moving the sample position with 4 μm steps in the vertical direction and repeating the ω-rotation, 50 “layers” were scanned within the probed length of the wire of 200 μm so that complete “austenitic neighborhood” of MBF was scanned. Each spot bears partial information on the position, structure, orientation and elastic deformation of the crystal lattice within one of the polycrystal grains. The already transformed martensite grains were not analyzed for grain resolved information since diffraction from martensite phase was not as spotty as required for the 3D-XRD method; the obtained experimental dataset contained 15,000 austenitic grains (Fig. 1c).

Fig. 1
figure 1

Schematic sketch of the experiment. Superelastic NiTi wire was stretched till the mid of the transformation plateau, and the wire segment containing the martensite band front was probed by a monochromatic beam of highly energetic photons using the 3D-XRD method (a). Grain microstructures, nose-cone shapes of the front as well as strain and stress tensors in 15,000 austenite grains were reconstructed (b, c). See [17] for further details

Full size image

Components of the elastic strain tensor and the stress tensor for each of these grains were calculated based on refined unit cell parameters and tensor of elastic constants of the austenite lattice. In addition, grain resolved stress components weighted by the grain size were averaged over equivolumetric cells and interpolated to reconstruct the macroscopic internal stress field in austenite phase in front of the MBF with stress resolution of 20 MPa and spatial resolution of about 1 μm. This allowed to quantify strong internal stress gradients and elevated shear stresses developing at the edge of the nose-cone-shaped macroscopic phase interface (Fig. 1b) which forms the core of the propagating MBF. Whereas the macroscopic nominal tensile stress needed for the propagation (“plateau stress”) was about 420 MPa, the averaged mean equivalent stress at the phase interface reached almost 590 MPa. This contradicts the assumption that the martensitic transformation in NiTi wire takes place under stresses close to nominal tensile stress and motivates the particular adjustment of parameters related to the strain softening in our constitutive model.

Modeling

The original (local) rate-independent constitutive model has been formulated within the continuum mechanics framework in [27], and its FE implementation has been validated in [15, 28]. Two internal variables (volume fraction of martensite, ξ, mean transformation strain, εtr) allow capturing microstructural effects on the macroscopic level of description via the enhanced dissipation function [29]. A parameterized constraint on the latter variable assures that the tension–compression asymmetry and the (texture-induced) transformation strain anisotropy of NiTi wire are captured. A particular form of the free energy couples the influence of strain and temperature on the phase transformation. Let us also note that the elastic deformation is phase dependent, whereas plastic deformation due to dislocation slip is neglected (cf. e.g., [30]). Analogous to similar approaches in the literature [23,24,25], a substantial material softening (i.e., stress needed for the further promotion of the transformation decreases with the increasing strain) is incorporated; our own-developed original regularizing–hardening term of the free energy rhard is expressed as follows:

$$r^{\text{hard}} (\xi ,\varepsilon^{\text{tr}} ) = k\xi \frac{{\left\langle {\varepsilon^{\text{tr}} } \right\rangle^{2} }}{{\left( {1 - \left\langle {\varepsilon^{\text{tr}} } \right\rangle } \right)^{2} }}\left( {E_{0}^{\text{int}} + E_{1}^{\text{int}} \exp ( - \beta \xi )} \right),$$
(1)

where 〈εtr〉 denotes a particular convex function of transformation strain defined in [27], k denotes the maximum transformation strain in pure tension, E int0 is a hardening coefficient, whereas E int1 and β are material parameters adjusting the extent of softening during phase transformation. Figure 2a illustrates the proposed constitutive law on a superelastic loading loop. The nominal stress–strain relation in uniaxial loading (of a single material point) exemplifies the reversible phase transformation with pronounced hysteresis, strain softening, and different elasticities of phases. The energy term (1) makes the material mechanically unstable during the phase transformation; unfortunately, this implies loss of ellipticity of governing equations (in statics), which has severe negative consequences: the ensuing mathematical formulation (boundary value problem) becomes ill-posed; thus, numerical simulations (e.g., FE analysis) may exhibit sensitivity on the size of finite elements and the mesh structure. To recover regularity of such constitutive models, researchers have proposed various generalized continuum formulations in the literature [31]. Introduction of an additional nonlocal counterpart to the internal dissipative variable(s) [32, 33] is one suitable tool for regularization leading to two closely related, often employed methods [34]. In the nonlocal gradient approach, the local and corresponding nonlocal variables are linked via an additional partial differential equation; in the nonlocal integral approach, these variables are linked via an integral relation, and the nonlocal variable in a material point is defined as a weighted spatial integral average of the local one. We have applied the integral approach and introduced a nonlocal counterpart to the volume fraction of martensite, denoted ξN, which has substituted the local variable ξ in the exponential term on the right-hand side of Eq. (1); hence, rhard depends both on the local and nonlocal volume fractions of martensite. The integral relation takes the form

Fig. 2
figure 2

Superelastic stress–strain response and internal stress in NiTi wire deformed in tension simulated by FE-implemented SMA model adapted for strain softening in tension (a, dash line). Macroscopic dependence of nominal stress on relative elongation computed in FE simulation (a, solid line) exhibits both nucleation overpeaks and propagation plateaux; Maxwell stress for the loading (a, dotted line) is far below the plateau stress. Computed (left halves) distributions of von Mises equivalent stress (b, color range 300–600 MPa) and axial stress component (c, color range 200–600 MPa) correspond to their macroscopic averaged experimental counterparts (right halves) (Color figure online)

Full size image
$$\xi_{\text{N}} (x) = \int_{\varOmega } {\xi (y)\omega_{\rm d} (x,y)} {\text{d}}y,$$
(2)

for any x within the set of material points constituting the sample Ω. The integration kernel ωd (x, y) is chosen as the normalized Gaussian radial function with the center in x and the standard deviation d. Combined experimental and theoretical research by Ball et al. [35] suggests that when emerging from a mechanically stabilized martensitic single crystal, austenite tends to nucleate predominantly close to specific locations on the surface of the sample determined by its geometry. Inspired by that study, we suggest to complete the above definition of nonlocal martensite by a formal assignment of the value of ξ: for any point y in the space outside the body Ω, let us define ξ(y): = 1 − ξ(x), independently for each material point x appearing in Eq. (2) (Table 1).

Table 1 The set of material parameters used in the simulation
Full size table

The complete constitutive model was implemented into FE software Abaqus FEA. Our previously developed UMAT subroutine (see [29] for details) has been modified in the regularization energy term introduced in Eq. (1) and complemented by a newly developed subroutine UEXTERNALDB. The latter subroutine is activated after each increment in order to update the values of the nonlocal variable. To this end, a virtual meshing of the computational domain Ω and a (relevant part of) surrounding space is performed so that nodes of the virtual mesh coincide with those of the axisymmetric mesh (described below), and values of the nonlocal volume fraction are regularly updated according to Eq. (2). However, to reduce computation costs, we implement the following numerical simplifications in the present study: (i) the integration kernel has a limited spatial coverage, i.e., a finite number of neighboring virtual elements are accounted for; (ii) in each time increment, ξN is computed based on values of internal variables obtained in the previous converged increment; and (iii) ξ is set equal to one outside the computation domain for the whole simulation (any time increment).

The experimental setup introduced in “Experimental Motivation” was modeled as a simple mechanical problem: the axial tension of a straight homogenous NiTi SMA wire segment at a constant temperature. We assumed that the radial symmetry is preserved and employed the axisymmetric setting in Abaqus. 20 elements per radius r = 50 μm and 200 per length l0 = 500 μm arranged in a rectangular domain composed a uniform structured mesh of 4000 quadrilateral (square) 4-node elements with centroid integration (CAX4R). Both the radial displacement of nodes on the symmetry axis and the axial displacement of nodes at the lower end of the computation domain were fixed. At the upper end of the domain, axial displacement was uniformly and gradually increased beyond 10% of the total length of the wire and then decreased back to no strain condition. To initiate the nonlocal events (shearband formation), we have taken advantage of the temperature dependence of critical (transformation-triggering) stress in SMA: the otherwise spatially constant temperature field of 20 °C was decreased by 5 °C in all nodes at the fixed end, so that forward phase transformation initiated there and propagated along the wire segment toward the other end; similarly, temperature at the other end was increased by 5 °C for controlled initialization of the reverse transformation. By this way, we avoid introducing artificial geometric imperfections into the mesh common in the literature (e.g., [36]). Let us note that the whole domain was in pure austenite initially. Values of material parameters used in the simulation are summarized in Tab. 1. They reflect the experimentally observed superelastic stress–strain behavior of the wire and are comparable to sets used in [27, 37]. Let us note that parameters related to the extended regularization term, E int0 , E int1 , and β were adjusted so that simulated stress gradients quantitatively reflect the experimental observations (Fig. 2b).

Discussion

The simulated relation between nominal stress (force per reference cross section) and relative elongation of the wire is also shown in Fig. 2a. The incipient nucleation event manifested as a stress peak is followed by a flat stress plateau corresponding to the propagation of the MBF along the wire. The stress drop at the end of the plateau relates to the annihilation of the band front on the upper end of the computational domain. Similar behavior is observed during the unloading. Figure 2b, c presents distributions of von Mises equivalent stress and axial stress close to MBF, respectively. For easier comparison, the left half of each figure presents experimental results whereas the right one the simulation with the same color scale used. The dashed line denotes the conical MBF as determined from last distinguishable austenitic grains in the experiment (grains below the line were already at least partially in the martensitic state; hence, they could not be resolved by the present technique). Simulation counterparts show the distributions also in the martensitic region. Presented figures correspond to a snapshot when the relative elongation of the wire reaches about 5% in loading, but the whole simulation shows identical distributions around the MBF for any state on the loading plateau as the stable MBF propagates along the wire. In both distributions, stress state in austenite far from the MBF is homogenous whereas distinct and severe stress gradients develop close to MBF and, according to simulation, also in martensite far from the front (Fig. 2b, c). In austenite, the simulation results perfectly match the experimental data: the equivalent stress reaches maximum on and close to the whole MBF cone and minimum in the central region just above, whereas the axial stress is maximized on the wire surface close to the MBF and minimized in the central region on the conical MBF. The redistribution of stress close to the MBF is a direct consequence of the strain softening, although it is also influenced by the isochoric nature of the martensitic transformation leading to the reduced wire diameter of martensitic band below the MBF. Moreover, owing to different stress conditions the material is exposed to, during the transformation process, in the middle and on the periphery of the radial cross section of the wire, different transformation strains develop in the respective regions when the MBF passes through. This conversely results in increased values of both axial and equivalent stresses on and close to the surface of the wire in the martensitic region behind the MBF as seen in the simulation. Let us note that similar basic features of the equivalent stress distribution have been earlier obtained in numerical results by Iadacola and Shaw [19], and they could contribute to better understanding of the recently observed cross-sectional strain heterogeneity [38].

Let us also note that the loading plateau stress in FE simulation 2A is above the so-called Maxwell stress obtained from the strain-softening response via energy balance condition known as Maxwell construction or “equal area rule” (see [39] for an application in SMA). This is consistent with recent systematic observations of localized deformation superelastic NiTi strips loaded at various temperatures by Xiao et al. [40]—the Maxwell stress evaluated in their experiments always underestimated the real plateau stress. This indicates an increase of energy during real loading compared with “idealized” situation represented by the Maxwell construction. The additional energy might be attributed to the heterogeneous strain state in martensite behind the MBF, which is just related to significant stress redistribution when the front passes a material point (see also [41]); yet, this inference remains to be verified by more detailed studies in future.

Conclusions

We have briefly reviewed the recent progress of our research into the localized behavior of NiTi which was initiated in the mid-2000s. We focused on the synergic experimental-modeling approach employing the 3D XRD method and a NiTi-tailored constitutive model used to investigate strain and stress fields in the vicinity of the MBF in a stretched NiTi wire. Experimental results confirmed that complex heterogeneous stress fields are induced in austenite prior to the front, and simulation revealed inhomogeneous transformation strain behind it. The latter fact may provide a clue for understanding the deviation of the plateau stress from the Maxwell stress. This study and our very recent study [42] show that the localization phenomena can be and must be incorporated into existing SMA models if correct and reliable predictions of NiTi mechanical response are required.