Abstract
Constitutive models are necessary to design shape memory alloy (SMA) components at nano- and micro-scales in NEMS and MEMS. The behavior of small-scale SMA structures deviates from that of the bulk material. Unfortunately, this response cannot be modeled using conventional constitutive models which lack an intrinsic length scale. At small scales, size effects are often observed along with large gradients in the stress or strain. Therefore, a gradient-based thermodynamically consistent constitutive framework is established. Generalized surface and body forces are assumed to contribute to the free energy as work conjugates to the martensite volume fraction, transformation strain tensor, and their spatial gradients. The rates of evolution of these variables are obtained by invoking the principal of maximum dissipation after assuming a transformation surface, which is a differential equation in space. This approach is compared to the theories that use a configurational force (microforce) balance law. The developed constitutive model includes energetic and dissipative length scales that can be calibrated experimentally. Boundary value problems, including pure bending of SMA beams and simple torsion of SMA cylindrical bars, are solved to demonstrate the capabilities of this model. These problems contain the differential equation for the transformation surface as well as the equilibrium equation and are solved analytically and numerically. The simplest version of the model, containing only the additional gradient of martensite volume fraction, predicts a response with greater transformation hardening for smaller structures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Shape memory alloys (SMAs) have recently been used as high-performance actuators in micro-electro-mechanical systems (MEMS) in the form of thin films/beams including micropumps [1], microvalves [2], microgrippers [3], and microactuators [4]. Also, compared to bulk SMAs, thin films can be thermally activated at a higher frequency due to the larger exposed free surfaces. The elastic and inelastic response of materials changes as their size approaches the micron/nanometer region where fluctuations in the microstructural and physical features of the material cannot be resolved by smearing their effect through averaging and homogenization. Such an experimentally observed size-dependent behavior can be modeled using continuum mechanics without resort to cost-prohibitive molecular/atomistic frameworks by using nonlocal or gradient continuum theories. Higher gradients of stress or strain usually occur in smaller sizes. For example, for the same maximum strain on the outer layer, beams with smaller thicknesses undergo higher gradients of strain, motivating the use of higher-order models containing gradient terms for modeling their behavior. Toward this end, the objective for this communication is to develop a thermodynamically consistent gradient-based nonlocal constitutive model for shape memory alloys with the capability of capturing the size effect.
A size effect generally occurs when a characteristic length in the loading, boundary conditions, or geometry of the sample (such as the size of the stress concentration region, curvature of bending, or thickness of the sample) is of the same order of magnitude as a microstructural length scale in the material (such as grain size, size of the dislocation loop in metals, or martensitic twin variants in shape memory alloys). In that case, the heterogeneities in the microstructure of the specimen and hence the local state of the material become significant and cannot be averaged out to produce a larger scale [5]. Size effect has been observed for elastic properties [6–8] as well as inelastic response of materials, such as in dislocation plasticity [9–11].
SMAs are not an exception in this regard because the properties characterizing their unique behavior, i.e., the critical stresses to start and finish the forward and reverse transformations as well as the transformation dissipation and hysteresis, have been shown to depend on the size of the specimen.
The size effect was observed in microcrystalline SMA particles in nontransformable solid matrix, and also in free-standing nano/micro-sized SMA powders. Experimental results demonstrated that by decreasing the size of the SMA particle or powder, the martensitic transformation was fully or partially suppressed [12, 13].
Furthermore, the compressive stress–strain response of SMA micro/nanopillars was shown to depend on the diameter. An increase in the critical stresses to start the austenite to martensite transformation and also in the stress–strain hysteresis was seen when the diameter of the pillars was less than one micron [14–18]. This phenomenon was also observed in SMA wires where the critical stresses for the start of martensite and austenite transformations were reported to increase for diameters below 100 μm [19].
SMA thin films with thicknesses in the micron scale, deposited commonly on glass or silicon substrates, showed reduced transformation temperatures compared to that of the bulk SMA, and in some cases the martensitic transformation was impeded for thicknesses below 100 nm [20–23].
It was also shown through experiments and numerical modeling that martensitic transformation diminishes with decreasing grain size in SMA samples with nano-sized grains, and there exists a critical grain size below which transformation is inhibited [24–29].
It is possible to account for such high-resolution internal microstructural features explicitly by considering the spatial variation of the material properties in a lower scale (for example, using an FEA model including detailed microstructural features or an atomistic/molecular modeling approach). However, this strategy requires much computational resources. The nonlocal models, either differential or integral, introduce one or more length scales in their formulation that can represent the lower scale features in an average sense in the continuum scale.
The standard continuum theories predict a singular state of stress at the tip of a crack or center of a dislocation core. Nonlocal theories of elasticity can eliminate these singularities [30–32]. In addition, standard continuum theories have difficulty predicting size dependence in the elastic torsional or flexural response of certain materials [6, 7, 33–35, 8]. Furthermore, the elastoplastic response of micron and submicron-sized specimens feature an increased plastic hardening with decreasing size. This effect was modeled using both implicit and explicit strain gradient plasticity models [36, 37]. Plastic size effects include nano-scale indentation depth dependence for hardness of several metals [38], thickness dependence in nondimensional moment-curvature response of Ni thin films [39], and size-dependent yield stress in torsional response of micron-sized Cu wires [9]. The standard plasticity models, due to the lack of intrinsic material length scales, cannot capture such an observed size effect featuring a stronger response as the size of the structure reduces [10].
Nonlocal integral plasticity models are a generalization of the classical plasticity models that include nonlocal measures of the plastic strain, defined via a weighted volume integral over the domain, in their yield function [40, 41]. Strongly nonlocal implicit gradient plasticity models [42] also include an integral nonlocal variable in their constitutive equations. However, the nonlocal variable (such as damage or the accumulated plastic strain) can be obtained via solution of a Helmholtz-type differential equation over the material body with Neumann boundary conditions applied on the external boundary (and not on the evolving elastic-plastic boundary) and solved in a coupled fashion with the equilibrium equation [43]. In contrast, weakly nonlocal constitutive models [42] for inelastic material behavior directly include the spatial gradients of the state variables (hence also called explicit gradient models) that capture the effect of an infinitesimally small neighborhood around a material point. This can be the higher gradients of the displacement field (or the gradients of total strain) [44] or can be exclusive to the gradients of the internal variables such as the accumulated plastic strain [45–47] or the martensite volume fraction (MVF) [48, 49]. Explicit gradient models were shown to be more effective in capturing the strengthening as a result of reducing the specimen size, while nonlocal implicit models proved to be more efficient in regularizing the problem of strain localization in materials with softening behavior [50]. Gudmundson et al. [51] presented a thermodynamic framework that can be used to derive many of the existing strain gradient plasticity models. A generalized principle of virtual power was assumed that considers the contributions from elastic strains, plastic strains, and the plastic strain gradients along with their respective work conjugates of Cauchy stress, microstress, and moment stress. The principle of virtual power led to the balance equations and corresponding standard and nonstandard boundary conditions with respect to the force and moment force tractions. The balance law regarding microstresses is often denoted as the microforce balance after Gurtin [52]. The microforce balance acts as a generalized flow rule in this context. The rates of the plastic strain and the plastic strain gradient were obtained based on satisfaction of the second law of thermodynamics through derivatives of a yield function. The yield function was defined based on generalized stress and plastic strain measures that accommodated three different intrinsic material length scales. Connections between this theory and strain gradient theories of Aifantis [53–55], and Fleck and Hutchinson [36, 47], were also demonstrated.
Phenomenological modeling of SMAs using internal variables has been under development for the past two decades [56]. The SMA phenomenological models are similar to rate-independent dislocation-based plasticity models. The nonlocal continuum models motivated by the experimentally observed SMA behavior, such as the size effect or transformation front localization, are also similar to the nonlocal plasticity models [57, 58, 48].
Duval et al. [58] provided the nonlocal extension of an existing phenomenological SMA constitutive model [59]. This nonlocal implicit gradient model was inspired by the work of Engelen et al. [43]. In addition to the conventional internal variable of martensite volume fraction (MVF) f, the integral average of it over the domain was also considered as the nonlocal MVF, \(\bar{f}\). Similar to the implicit gradient plasticity models, \(\bar{f}\) was obtained from an additional PDE with a Neumann-type boundary condition on the domain boundary ensuring the equality of local and nonlocal MVF averaged over the entire domain. The nonlocal model was implemented in the finite element software package ABAQUS through the user element (UEL) feature. The experimentally observed softening behavior (stress peak of nucleation and subsequent stress plateau for propagation) in the SMAs was captured by gradually decreasing the critical force for martensitic transformation through the nonlocal MVF resulting in lower stresses required for propagation of martensite compared to its nucleation. Therefore, the nonlocal model performed as a localization limiter improving the otherwise pathological behaviors of the local models. The nucleation and propagation of martensite transformation front in tensile loading of an SMA plate with a hole were simulated with results showing the dependence of the localization width and the stress peak of nucleation on the intrinsic length scale introduced in the model through the nonlocal variable.
Another nonlocal implicit gradient SMA model was presented by Badnava et al. [57]. The model was based on a 3D extension of Brinson’s SMA model [60] and was intended to capture the unstable softening and localization behavior of SMAs upon nucleation and propagation of martensite transformation. The effectiveness of the model as a localization limiter was demonstrated through FEA simulation of SMA structures after implementation in ABAQUS UEL.
The explicit gradient-based SMA model of Qiao et al. [48] was inspired by the strain gradient plasticity work of Gurtin and Anand [61]. This isothermal one-dimensional model was intended to capture the size-dependent superelastic response of SMA micro/nanopillars under compression tests. The Helmholtz free energy for the material contained the gradient of MVF through which an energetic length scale was introduced. Through the use of a generalized form for the principle of virtual power, stress equilibrium equation and a balance equation regarding the microstresses (conjugates to the martensite volume fraction and its spatial gradient) along with their corresponding boundary conditions were obtained. Constitutive relations were assumed for the microstresses such that the microforce balance played the role of the transformation partial differential equation giving the rate of MVF. The variational form of this equation was implemented in a 1D finite element framework to simulate size effect in the response of Cu-Al-Ni SMA micropillars under compression.
In the work by Sun and He [62], a multiscale continuum phenomenological strain gradient model was developed to study the effect of grain size in the response of polycrystalline SMA specimens. The model was based on a nonlocal nonconvex strain energy function. The characteristic length scales introduced were the specimen size L, grain size l, and the intrinsic material length scale ℓ related to the width of austenite–martensite interface. The results demonstrated that the energy dissipation during phase transformation is governed by the ratios of \(\frac{L}{l}\) and \(\frac{l}{\ell }\). The martensitic transformation, hence dissipation, was diminished in the case of an SMA with large grains close to the size of the specimen (denoting a single crystal behavior) and also in the case where the grains were of the order of nanometer in size close to the intrinsic length scale (denoting the transformation inhibition observed in ultrafine-grain SMAs).
In the current work, a gradient-based thermodynamically consistent constitutive model is developed for the response of SMAs at small scales. It is assumed that generalized surface and body forces contribute to the free energy as work conjugates to the MVF, transformation strain tensor, and their spatial gradients. The rates of evolution of these variables are obtained by invoking the maximum dissipation postulate. The generalized transformation surface is a differential equation for the spatial distribution of the thermodynamic forces, whereas in conventional constitutive theories, the transformation surface is an algebraic equation. The connection between this model and the theories that use a configurational force (microforce) balance law is established by showing the latter to be a specific case of a generalized transformation surface.
Using such a framework, gradient-based constitutive models are developed that include energetic and dissipative length scales which can be calibrated experimentally. These models are simplified for 1D. Example boundary value problems are solved analytically and, where impossible, numerically for pure bending of SMA beams and simple torsion of SMA cylindrical bars. The simplest gradient-based SMA constitutive model, containing only the additional gradient of MVF, can capture the size effect in the response of these structures by demonstrating an increased hardening for smaller sizes.
Gradient-Based SMA Constitutive Modeling
In this section, a thermodynamically consistent gradient-based model for SMAs is developed. A treatment based on generalized principles of continuum mechanics is given in the Appendix “Fundamentals” section; however, the internal variable approach is used herein. The development begins by specifying the Gibbs free energy, G. The strain and entropy are shown to be the derivatives of the Gibbs free energy with respect to stress and temperature. A dissipation potential is formulated to obtain (rate-independent) evolution equations for the internal variables.
To begin, the dependent and independent state variables are introduced:
The independent state variables include the Cauchy stress σ, the absolute temperature T, and a set of internal variables Υ with ɛ tr, the tensor for transformation strain, and ξ, the volume fraction of martensite phase in the SMA. Also included are the spatial gradients of the MVF and the transformation strain tensor up to orders n and m. It is assumed, henceforth, that m = n. The dependent variables are ɛ the infinitesimal strain (we assume infinitesimal strains), q the heat flux vector, s the specific entropy, and G the specific Gibbs free energy.
Referring to the inequality in Eq. (90) and the development in the Appendix “Fundamentals” section, the Clausius–Plank inequality becomes
Assuming that all the constitutive variables and their rates are independent, the Clausius–Plank inequality (and hence the second law of thermodynamics as mentioned in the Appendix “Constitutive Equations” subsection) is satisfied given the following constitutive equations:
Therefore, the dissipation is
where \({\dot{\textbf{Y}}}\) denotes the set of generalized thermodynamic fluxes with corresponding thermodynamic forces, Γ, given by
That is
It is common to consider the martensitic transformation a volume-preserving process such that tr(ɛ tr) = 0. Therefore, the hydrostatic part of the generalized stress, \({{\mathbf{\varsigma }}^{\text{D}}}\), does not contribute to the dissipation. Hence, only its deviatoric part will be considered for determining the evolution of the internal variables:
It is assumed that a transformation surface defines the region for the thermoelastic state of the material in the space of the generalized forces and that any admissible state of the material must satisfy the condition imposed by
For the rate-independent response considered here, the fluxes are associated with the forces through derivatives of a transformation potential [63]. One approach uses the principle of maximum dissipation (PMD) such that the fluxes will be normal to the transformation surface. Normality of the fluxes in the space of the generalized forces and also convexity of the transformation surface are the results of the PMD. According to PMD, the transformation state of the SMA material, belonging to the set of admissible states, is the one that maximizes the dissipation D tr or
This is a minimization programming which is solved using the method of Lagrange multipliers, further described in the Appendix “Fundamentals” section and Eqs. (98)–(101) including the corresponding Kuhn–Tucker conditions. As a result, the rates of the internal variables can be found from
Hence, the response is associative in the space of generalized thermodynamic forces.
Next we assume a form for the transformation surface Φ(Γ). For Φ to be a general anisotropic convex function of \({\acute{\mathbf{\varsigma }}}^{\text{D}}\), π, \({\bar{\mathbf{\pi }}}^{1} , \ldots ,{\bar{\mathbf{\pi }}}^{n}\), and \({\varvec{\uptau}}^{1} , \ldots ,{\varvec{\uptau}}^{n}\) satisfying the second law of thermodynamics for forward and reverse martensitic transformations, it is sufficient to have
where various φ are homogeneous of degree 1, convex functions of their respective variables. A general quadratic form is commonly assumed such that
with no summation over k. Here, notice that if \({\bar{\mathbf{\pi }}}^{k}\) or \({\varvec{\uptau}}^{k} \in {\mathcal{T}}^{m}\) then \({\varvec{\Xi}}^{{II_{k} }}\) or \({\varvec{\Xi}}^{{III_{k} }} \in {\mathcal{T}}^{m}\) and \({\varvec{\Lambda}}^{{II_{k} }}\) or \({\varvec{\Lambda}}^{{III_{k} }} \in {\mathcal{T}}^{2m}\). The tensors Λ and Ξ can be assigned the symmetry necessary to achieve the directional dependence of the yield surface and flow observed in the response of the SMA. Y is a constant that is equal to one-half of the amount of energy dissipation in a full transformation path.
The surface ϕ given by Eq. (11) can result in multiple forms of differential equations. For example, consider \({\bar{\mathbf{\pi }}}^{1} = - \rho \frac{\partial G}{\partial \nabla \xi } = a\nabla \xi\) and \({\bar{\mathbf{\pi }}}^{2} = - \rho \frac{\partial G}{{\partial \nabla^{2} \xi }} = b\nabla^{2} \xi\) which can be part of an isotropic SMA constitutive model including ξ, ∇ξ, and ∇2 ξ as internal variables. Hence, one can have first and second-order differential terms, including the Laplacian ξ ,ii , within the definition of the partial differential equation for the transformation surface:
It is possible to eliminate λ from Eq. (10) such that the rate of evolution of the internal variables will be proportional to \({\dot{\xi }}\) since \({\dot{\xi }} = \lambda \frac{\partial \Phi }{\partial \pi } = \lambda\). This implies that \({\dot{\xi }}\) plays the role of the plastic multiplier as in the analysis of dissipation surfaces and flow in plasticity. \({\dot{\xi }}\) can, furthermore, be determined using the consistency condition.
According to the Kuhn–Tucker condition (iii), while \({\dot{\xi }} = \lambda \ne 0 \to \Phi = 0\), thus the consistency condition during forward or reverse transformation (fwd/rev) can be obtained considering the transformation surface in Eq. (11):
which leads to the following for the evolution of the martensite volume fraction:
Once the evolution of internal variables is given by the derivatives of the transformation surface as in Eq. (10), the dissipation due to martensitic transformation can be obtained as follows:
in which Euler’s homogeneous function theorem is used as ϕ(Γ) is continuously differentiable and homogeneous of degree one. The satisfaction of the second law of thermodynamics is guaranteed through Eq. (17), which requires careful attention. First, the rates of internal variables ξ and ∇k ξ and also ɛ tr and ∇k ɛ tr are not independent because they are related by a spatial gradient. This imposes the following restrictions on the transformation surface:
The first one of these constraints is trivially satisfied in light of \({\dot{\xi }} = \lambda\) and (10). A discussion about such restrictions on the transformation surface can also be found in [64]. Second, as observed in Eq. (17), the dissipation does not explicitly depend on the rate of the gradient of MVF and transformation strain. This is a consequence of the specific form assumed for the transformation surface, Eq. (11), and also the rates of ξ and ∇ξ as well as ɛ tr and ∇ɛ tr. However, the inhomogeneous distributions of the martensitic volume fraction and the transformation strain in the body contribute to the dissipation by changing the evolution of ξ as a result of their influence on the transformation surface.
The Most General Anisotropic 3rd Degree SMA Gradient Model
In this section, an anisotropic gradient-based constitutive model for SMAs is presented, with Y considered as the following list of internal variables:
The derivation of the constitutive response follows the procedure used from the beginning of this section, so only the key equations will be discussed in this section. The form for the Gibbs free energy
is commonly selected to be a polynomial in terms of the variables considered to determine the state of the material. The polynomial function can be truncated depending on the level of coupling desired between the variables and on the physical phenomena as well as the material symmetry sought to be captured [65, 66]. The reference state, \({\mathcal{X}}_{0}\), for the free energy is
Taylor’s expansion with respect to this reference state results in a polynomial form for the free energy function
The most general anisotropic as well as isotropic forms for Gibbs free energy of Eq. (20) is provided in the Appendix “The Most General Anisotropic/Isotropic Gibbs Free Energy for the Gradient-Based SMA Constitutive Model” section.
The constitutive variables and generalized forces are similarly given by Eqs. (3) and (6). The response of the SMA in this section is assumed to be isotropic so that in Eq. (13), the tensors Ξ, being of odd rank, vanish and the tensors Λ can be rewritten in terms of the fundamental isotropic tensors
The six constants ℓ d can be regarded as dissipative length scales. Hence, the forward and reverse transformation surfaces will be
The Simplified SMA Gradient Model Including ∇ξ and ∇ɛ tr
In this section, a simplified version of the general isotropic SMA model introduced in the previous section is considered. The free energy is decomposed into local and nonlocal parts with no coupling between the local state variables and the nonlocal internal state variable. For the nonlocal part of the free energy, only three quadratic terms including ξ i and ɛ tr ij,k are retained. The Gibbs free energy, given to its most general form in Eq. (119), is simplified to
The local and nonlocal parts are given as follows:
The tensor S(ξ) is the phase-dependent isotropic fourth-order compliance tensor defined linearly (rule of mixtures) with respect to the compliance of the austenite S A and martensite S M phases. α(ξ) is the phase-dependent effective coefficient of thermal expansion. The material parameters c, s 0, and u 0 are the effective specific heat, effective specific entropy at a reference state, and the effective specific internal energy at the reference state, respectively. They also follow a rule of mixtures with respect to their corresponding values for austenite and martensite phases, i.e.,
The function f(ξ) is the hardening function attributable to the obstacles inhibiting the propagation of the transformation phase front. f(ξ) can take various forms, from linear to smooth hardening, as discussed in [67] and [68]. The energetic length scales ℓ1 to ℓ3 are introduced here with their corresponding constant coefficients a 1 to a 3 (with dimensions of energy per volume).
The constitutive variables and thermodynamic forces can be determined using Eqs. (3), (6), and the free energy given in Eq. (27):
Also, the transformation surfaces in Eq. (23) are simplified to
which can be rewritten by substituting for the generalized forces determined in (29):
In (31), \(\acute{\sigma }_{ij}\) are the components of the deviatoric stress and the newly introduced dissipative length scales, \(\ell_{{{\text{d}}_{1} }}\) and \(\ell_{{{\text{d}}_{2} }}\), are assumed to be positive. Thus, this model has three nonlocal constants in the Gibbs free energy and two in the transformation surface.
The rates of the internal variables are given by
In order to further investigate the contribution from the gradient of transformation, the model is reduced for a one-dimensional problem where only a single component of stress (σ 11) is nonzero. In this case, it is possible to analytically integrate the equation for evolution of transformation strain, (32), such that \(\varepsilon_{11}^{\text{tr}} = H\xi ,\;\varepsilon_{22}^{\text{tr}} = - \frac{1}{2}H\xi ,\;\varepsilon_{33}^{\text{tr}} = - \frac{1}{2}H\xi\). Hence, the surfaces for forward and reverse transformations become
where
This shows that the 1D transformation surface, as a result of the nonlocal terms, is a first-order differential equation and the nonlocal material constants can be grouped in a nonlocal parameter, \({\mathcal{M}}\). Specifically, because the transformation strain evolves proportional to the MVF, adding the variable ∇ɛ tr results in additional restrictions and constants without changing the form of the transformation surface that must be finally solved in conjunction with the equilibrium equation. Therefore, ∇ɛ tr will be excluded from the next simplified SMA gradient model and the focus will be on the coupling of ∇ξ with other state variables.
The Simplified SMA Gradient Model Including Only Terms with ∇ξ
The general isotropic SMA model introduced in “The Most General Anisotropic 3rd-Degree SMA Gradient Model” section is simplified in this section to include the terms with ∇ξ but not ∇ɛ tr. The resulting Gibbs free energy cannot be decomposed into two additive parts as before because the cubic terms provide coupling between the local and nonlocal state variables:
Six energetic length scales are introduced in this model that attribute to the coupling between ∇ξ and the other state variables.Footnote 1 The material constants a 1, a 4, and a 5 have dimensions of energy per volume, while a 3 has dimension of energy per volume per temperature and a 2 and a 6 are dimensionless. Because they originate from the same tensorial constant, there exists a relation between the constants coupling σ and ∇ξ, i.e., a 2ℓ 22 = 2a 6ℓ 26 . The local material constants of Eq. (35) follow a similar linear rule of mixtures as listed in Eq. (28).
The constitutive variables and thermodynamic forces can be determined via (3) and (6) using the free energy given in Eq. (35):
The transformation surfaces, Φ(Γ), are slightly modified for the forward and reverse processes:
which can be rewritten by substituting for the generalized forces determined in Eq. (36). Notice that the deviatoric part of the generalized stress tensor conjugate to transformation strain is \({\acute{\mathbf{\varsigma }}}^{\text{D}} = {\mathbf{\varsigma }}^{\text{D}} - \frac{1}{3}{\text{tr}}({\mathbf{\varsigma }}^{\text{D}} )\) and the constant H is the maximum achievable transformation strain. Therefore, \(\tilde{\varphi }\) is a Mises-type transformation surface; ℓ d is the dissipative length scale that has different values during the forward or reverse transformations, hence ℓ fwd d and ℓ rev d .
The energetic and dissipative intrinsic length scales, ℓ1 to ℓ6 plus ℓd, are combined in the nonlocal parameter \({\mathcal{M}}_{i}\). \({\mathcal{M}}_{i}\) has dimensions of length× energy/volume. Appearing in the transformation surfaces, \({\mathcal{M}}_{i}\) are given by (no summation on i)
It will be shown later that such nonlocal parameters appear in the differential equation for the transformation surface as part of the analysis of SMA structures.
The rates of the internal variables can thus be obtained as
in which
The rate of MVF is determined using the consistency condition, \(\dot{\Phi } = 0\) or (16), repeated here:
in which we have
and
Thus, the evolution of MVF, Eq. (41), is affected by the heterogeneity in its distribution coupled with the temperature as well as the stress tensor.
To complete the modeling section, it is necessary to introduce the hardening function, f(ξ). A linear form is chosen for f(ξ) with the relevant material constants b M, b A, μ 1, and μ 2:
In addition, a smooth hardening function can be introduced that results in a continuous transition between the linear elastic and transforming regimes, for example in a uniaxial stress–strain loading plot. Its differentiated form is given by [68]
where n 1 to n 4 and b 1 to b 3 are constants.
One-Dimensional Analysis of SMA Structures
The gradient-based SMA constitutive model introduced in “The Simplified SMA Gradient Model Including Only Terms with ∇ξ ” section is reduced to consider the case when only one component of stress is nonzero. The proposed model is then used to investigate the response of SMA wires and thin films which are commonly encountered in microactuators. Extension of an SMA homogenous prismatic bar is analytically investigated to demonstrate that the gradient-based model recovers the results of a conventional SMA model in the case of a uniform deformation. In addition, the torsion of SMA wires is studied in which the variation of stress, and hence the martensitic volume fraction, over the diameter of the wire demonstrates the size-dependent features of the gradient-based model. The response of an SMA thin film is also analytically modeled for forward transformation as a beam under pure bending. The loading–unloading response of the SMA beam under pure bending, including the forward and reverse transformations, is numerically modeled.
Extension of SMA Prismatic Bars
The purpose of this section is to show that the proposed nonlocal model yields a local response if the material undergoes a homogeneous deformation. A prismatic bar is assumed to undergo a uniaxial isothermal loading at a temperature above the austenite finish temperature, A f . The bar is isothermally loaded from austenite so that the transformation to martensite occurs. The schematic for the 1D boundary value problem, considering the symmetry (at the left end) and boundary conditions, is shown in Fig. 1. It is assumed that the state of the bar, including the MVF, is symmetric about the left end.
The kinematic and equilibrium equations, along with the equation for decomposition of strain, (36a), result in the following:
The stress does not vary through the length of the bar. The equation for transformation surface, after simplifying Eq. (37) and considering linear hardening for the transformation, can be rewritten as follows:
Upon satisfying the symmetry boundary condition, \(\tfrac{{{\text{d}}\xi }}{{{\text{d}}x}}|_{x = 0}\) at the left end, the nonlocal contribution due to the derivative of ξ vanishes. Therefore, MVF depends only on the stress with a constant homogeneous distribution along the bar:
A similar analysis for the reverse transformation results in
This solution will be used in the Appendix “Experimental Measurement of the SMA Material Properties” section in order to relate the typical experimentally observed SMA properties to the material constants of the developed constitutive model.
Simple Torsion of an SMA Bar
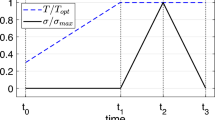
The solution for the torsion of an SMA bar using the nonlocal model of “The Simplified SMA Gradient Model Including Only Terms with ∇ξ ” section is obtained in this section. It is assumed that the bar has a circular cross section representing a wire with a diameter of D. An opposite and equal torque T is applied to the ends of the wire (Fig. 2). Also, it is assumed that the wire is initially in a fully austenitic state at a temperature above A f.
The twist per unit length of the circular bar is denoted by Θ, a constant. This problem is axisymmetric, and it is assumed that the radii on the cross section remain straight. The shear strain in the plane perpendicular to the axis is, therefore, given by
The state of stress in the SMA bar, satisfying the boundary conditions for end moments and traction-free side, is considered to be
Therefore, the equilibrium equations reduce to
which are all satisfied in the case of \(\sigma_{\theta z} = \hat{\sigma }_{\theta z} (r)\). This implies that \(\xi = \hat{\xi }(r)\). Also, for the regions in the material undergoing elastic loading σ θz = GrΘ where \(G = \frac{E}{2(1 + \nu )}\).
The relation for total strain, according to the model of “The Simplified SMA Gradient Model Including Only Terms with ∇ξ ” section, is given in Eq. (36a). For this problem, after considering that the MVF changes only with the radial coordinate, the θz component of strain tensor can be written as
The generalized stress tensor, \({{\mathbf{\varsigma }}^{\text{D}}}\), conjugate to transformation strain can be determined by simplifying Eq. (36) which finally leads to
In this sense then
which means, after Eq. (39a), the rate of transformation strain can be given by
or in terms of components,
For this simple torsion problem, in addition to transformation shear strains, the SMA gradient model results in transformation strain in normal directions as well. Therefore, by the initiation and propagation of transformation in the bar, the cross section may undergo swelling or warping. This point can be used for identification and calibration of the nonlocal parameter a 5ℓ 25 as discussed in the results section. Equation (36d) reduces to
The generalized force \({\bar{\mathbf{\pi }}}\) in component form can be given by
The last two components vanish in light of the relations given for the rate of transformation strain components, Eq. (57c). Hence after Eq. (37) and with ℓ d = ℓ fwdd = ℓ revd ,
It is reasonable to assume that σ θz ≥ 0 and \(\frac{\partial \xi }{\partial r} \ge 0\), after which the forward transformation surface becomes
The boundary conditions required to solve this differential equation are determined by considering the interface between the elastic and transforming regions in the circular bar. The forward transformation begins at the outer surface, while the inner core is still loading elastically. The schematic for the distribution of MVF in this case is shown in Fig. 2 where \({\varrho }\) denotes the radial position of the interface. Hence,
due to the zeroth- and first-order continuity of ξ(r). Equations (61) and (62) enable one to find \({\varrho }\).
For the reverse transformation,
Similarly, the boundary conditions for (63) are the continuity of ξ(x) and \(\frac{{{\text{d}}\xi (r)}}{{{\text{d}}r}}\) across the interface, \(x = {\acute{\varrho }}\), where the transition form the reverse transformation to elastic unloading takes place.
For this problem, the differential equations for the transformation surfaces, Eqs. (61) or (63), must be solved in a coupled fashion with the equations for the rate of transformation strain, (57), and the equation for the decomposition of strain, (53), in order to find the distribution of ξ(r) and σ θz (r).
Ultimately, it is possible to find the relation between the twist per length in the bar Θ, as the loading parameter, and the applied torque:
The complexity of the problem here prohibits one from obtaining a closed-form solution. Therefore, such system of differential equations was solved numerically using the finite difference method. The following nondimensional parameters are, notably, introduced for the purpose of results.
The nondimensional torque, T *, and nondimensional angle of twist per length, Θ *, are obtained by considering the critical torque to start the transformation at the surface of the circular SMA bar, T fwds , and the corresponding critical angle of twist per length, Θ fwds . The critical shear stress to start forward transformation is given via \(\tau_{\text{s}}^{\text{fwd}} = \frac{{\sigma_{\text{s}}^{\text{fwd}} }}{\sqrt 3 }\).
In the next section, pure bending of an SMA beam is considered with its solution for when only one of the length scales, a 1ℓ 21 , is nonzero.
Pure Bending of an SMA Beam
The deflection of SMA thin film actuators is investigated in this section. For simplicity, all of the nonlocal length scales in the nonlocal SMA constitutive model except a 1 ℓ 21 are considered to vanish. It will be shown that even in this simplified version, the SMA gradient model is capable of capturing the size effect in the response.
It is considered that a slender prismatic SMA beam (with a width of W and thickness of 2 h) undergoes a state of pure bending (Fig. 3) such that the Euler–Bernoulli assumptions hold, i.e., the planar sections remain planar and perpendicular to the neutral axis and rotate with reasonably small slopes. Hence,
where κ is the curvature of bending deformation. We assume that the only nonzero component of stress is the normal stress on the cross section, σ x . In addition to that, the decomposition of strain in the axial x direction using the SMA gradient-based model results in
First, the start of forward transformation on the outermost layers of the beam under loading is investigated to find an analytical nondimensional response. The state of the beam including stress, strain, and martensitic volume fraction reduces to a one-dimensional problem with variation along the thickness of the beam or y direction; \(\sigma_{x} (y),\quad {\mkern 1mu} \varepsilon_{x} (y),{\mkern 1mu} \quad \xi (y)\). The normal stress in the x direction is the only nonzero component of the stress tensor. The deformation is isothermal at a temperature above A f, thus the loading begins, while the beam is entirely in an austenite state. The loading causes the transformation to martensite to begin at the outer layers and propagate towards the neutral axis. The interface between transforming outer layers and the elastic austenitic inner layers of the beam is denoted by r on the y-axis, ξ(y = r) = 0. Because the stress state is 1D, the forward transformation equation for the SMA gradient-based model becomes
in which a linear hardening function is used. Also, \({\mathcal{M}}_{1}^{\text{fwd/rev}} \equiv \frac{{a_{1} \ell_{1}^{2} }}{{\ell_{\text{d}} }}\), after the definition given in Eq. (38). Considering the symmetry about the neural axis, only the top portion of the beam is studied hence σ x ≥ 0 and, therefore, \(\tfrac{{{\text{d}}\xi }}{{{\text{d}}y}} \ge 0\). The material constants in the above equation can be collected together to reach
with the newly introduced constants of forward transformation with linear hardening (Table 2),
Equation (69) is a differential equation that requires a boundary condition for its solution. Obviously, the condition at the boundary of the elastic-transforming regions or, ξ(r) = 0, must be satisfied. But this relation gives the constant of integration for (69) as a function of r which is still an unknown parameter of loading. Implicit in the analysis of the nonlocal constitutive model developed here is the fact that the forward or reverse transformation front entails a smooth transition from the elastic to the transforming region, i.e., all the state variables, including ∇ξ(X), must be continuous across the interface. In a polycrystalline SMA sample, the transformation front progresses by the martensitic transformation first occurring in the grains with favorable crystalline direction to the stress direction and then gradually transitioning to the elastic behavior in the transformed regions. This can be simulated by having a smooth scalar field variable, ξ. Thus, at the elastic-transforming boundary interface,
Satisfaction of the boundary conditions in (71) gives a relation for both the constant of integration in the ODE of (69) and the location of the elastic-transforming boundary r with respect to the current curvature, κ, as the loading parameter. The transition to the fully martensitic region is not smooth in terms of ξ, i.e., ∇ξ will not be continuous across the transformation finish front.
Interestingly, using (71) in the equation for forward transformation surface (69) results in
The loading here is proportional, so it is possible to directly integrate the rate of evolution of transformation strains
to obtain
In order to attain a closed-form solution, the difference in the elastic modulus of austenite and martensite is ignored, i.e., E = E M = E A which means A = 0.
The differential equation in Eq. (69) (with A = 0) is linear first order with a general solution given by
which after applying the boundary condition in Eq. (71) and replacing ζ yields
The first term on the R.H.S. of the above equation pertains to the local part of the model and gives a bilinear distribution in ξ, while the second term is the exponential contribution from the nonlocal part. The moment, M, applied to the beam section corresponding to the current curvature, κ, can be readily calculated from
Using Eqs. (74) and (76) in the integration of (77) results in
which is the equation of moment-curvature in a nondimensional form for pure bending of an SMA beam.
The nondimensional parameters introduced in (78) are now defined. The nondimensional moment, M *, and nondimensional curvature are obtained based on a normalization using the critical moment and curvature to start the forward transformation, M fwds and κ fwds :
In addition, \({\mathcal{M}}^{\text{fwd*}}\) can be defined as the nondimensional form of the nonlocal parameter as well as the nondimensional hardening, β
It is also helpful to write down the local nondimensional response of the SMA beam
Comparing Eqs. (78) and (81) reveals the size effect in the response for pure bending of SMA beams. The first term on the R.H.S of both equations pertains to the elastic portion of the SMA behavior, i.e., M * = κ *. This portion is size-independent because the nonlocality is only considered for the inelastic part of the response. Nonetheless, the remainder of Eq. (81) is also size-independent, because there is no effect from the thickness of the beam in the hardening parameter β. Therefore, the moment-curvature response using the conventional local model cannot capture the size effect in pure bending of SMAs because it can be fully normalized with respect to the thickness h. The response according to the nonlocal constitutive model, on the other hand, is able to capture the size effect, due to the nondimensional nonlocal parameter \({\mathcal{M}}_{1}^{\text{fwd*}}\) which depends on the thickness; \({\mathcal{M}}_{1}^{\text{fwd*}} = \frac{1}{{EH^{2} }}\frac{{{\mathcal{M}}^{\text{fwd}} }}{h}\). Hence by changing \({\mathcal{M}}_{1}^{\text{fwd*}}\) either through \({\mathcal{M}}_{1}^{\text{fwd}}\) or h, the moment-curvature response of the beam changes.
The analysis of the reverse transformation can be performed by following similar steps. Upon unloading, the reverse transformation first begins where its corresponding differential equation is first satisfied:
It can be shown that the reverse transformation begins at the outer layer and propagates towards the neutral axis with progression of unloading. The interface between the region of reverse transformation and the region where unloading takes place elastically is denoted by r′. The reverse transformation finishes when r′ reaches r. Although extremely lengthy, it is possible to develop a closed-form analytical response for unloading step as well. Equation (82) can be integrated considering the continuity of ξ and \(\frac{{{\text{d}}\xi (y)}}{{{\text{d}}y}}\) at y = r′.
However, a numerical algorithm was developed to solve both of the ODEs in (69) and (82) for forward and reverse transformations using the finite difference method. The thickness of the beam was discretized through which the differential equations were integrated using a forward Euler method. The imposed curvature was considered as the loading parameter, and having solved for the MVF at each discretization point, the stress was found using the decomposition of strain in Eq. (67) and integrated over the thickness, Eq. (77), to obtain the corresponding moment. The results of this analysis are presented in the next section.
Results and Discussions
The modeling results developed in the previous section for pure bending and simple torsion of the SMA structures are now presented. Where nondimensional numbers could not be realized, the material constants listed in Table 1 are used for the local part of the SMA constitutive model. They are selected from the properties of a typical shape memory alloy.
It is noted that the nonlocal model in “The Simplified SMA Gradient Model Including Only Terms with ∇ξ ” section contains six energetic length scales. The analysis for simple torsion included all, whereas only one was considered for the pure bending analysis.
The effect of the nonlocal parameter \({\mathcal{M}}_{1}^{\text{fwd/rev}} = \frac{{a_{1} \ell_{1}^{2} }}{{\ell_{\text{d}}^{\text{fwd/rev}} }}\) [with the units of (mm MPa)] on the pure bending of the SMA beam is investigated. It is assumed that \({\mathcal{M}}_{1} = {\mathcal{M}}_{1}^{\text{fwd}} = {\mathcal{M}}_{1}^{\text{rev}}\). For an SMA beam with W = 1 (mm), the plot of the nondimensional moment vs. curvature is illustrated in Fig. 4.
The case of \({\mathcal{M}}_{1}^{*} = 0\) pertains to the local conventional model. Inclusion of the nonlocal effect in the model results in a macroscopic hardening effect. More energy is dissipated due to the existence of the nonlocal term and therefore more flexural work is required to achieve a given curvature. This plot can act as the characterization point for the nonlocal parameter. Given a fixed thickness and known tensile SMA properties, it is possible to determine the value of the nonlocal parameter by calibrating the nondimensional flexural response of an SMA sample.
Figure 5 shows the variation in the distribution of MVF for this SMA beam under a curvature of κ* = 3.3 during loading and that of κ* = 1.6 during unloading. Through the nonlocal model, the inelastic energy generated contributes both to the martensitic transformation and also its gradient. The higher the nonlocal effect, the lower the total amount of transformation. Note that the conventional local model \(({\mathcal{M}}_{1}^{*} = 0)\) results in a linear distribution of ξ, as expected from the linear choice for the hardening function. Also, note that the SMA gradient model does not capture the size effect in the elastic regime.
The model used for the pure bending analysis included only one nonlocal parameter, \({\mathcal{M}}_{1}\). That corresponds to considering only the quadratic terms in the free energy for the gradient of MVF and showed the capability in capturing the size effect.
The SMA nonlocal model, in general, has 6 parameters coupling the gradient of MVF with the rest of the state variables, Eq. (35). In what follows, the effect of coupling between the two internal variables is investigated. As shown in Eq. (35), the nonlocal energetic length scale, a 5 ℓ 25 with dimensions of [mm2 MPa], acts as the coupling term between the gradient of MVF and the transformation strain tensor. The significance of this coupling appears when the solution for simple torsion of an SMA bar is considered.
According to (35), axial, circumferential, and radial transformation strains are generated under simple torsion in addition to the common shear term for the transformation strain. Here then we assume \({\mathcal{M}}_{5} = {\mathcal{M}}_{5}^{\text{fwd}} = {\mathcal{M}}_{5}^{\text{rev}}\) where \({\mathcal{M}}_{5}^{\text{fwd/rev}} = \frac{{a_{5} \ell_{5}^{2} }}{{\ell_{\text{d}}^{\text{fwd/rev}} }}\).
Figures 6 and 7 show the response of an SMA bar with a diameter D = 1 mm under pure torsion. The only nonzero nonlocal parameter here is \({\mathcal{M}}_{5},\) and according to Fig. 6a, the nonlocal torque–twist response is close to the local one. The distribution of the martensite volume fraction across the diameter, however, varies by changing the nonlocal parameter. This can be clarified by referring to Fig. 7a, where the shear transformation strain is plotted, in which the local and nonlocal responses also differ insignificantly. According to the equation for the transformation surface, Eq. (61), and what has been observed so far, the nonlocal effect tends to inhibit the transformation as plotted in Fig. 6b. But this will not affect the evolution of the shear transformation strain, as shown in Eq. (57), where a decrease in the MVF is counteracted by a larger nonlocal parameter. On the other hand, the nonlocal parameter gives rise to transformation strains in the radial, hoop, and axial directions, Eq. (57) and Fig. 7b. Therefore, a pure torsion experiment cannot be used to calibrate such a nonlocal parameter unless the experimentalist obtains the distribution of MVF or measures the axial/radial transformation strain, if any.
The ability of the proposed nonlocal model to capture the size effect in the bending response of SMA thin films as well as simple torsion of SMA bars was demonstrated. Beams of various thicknesses from the same SMA show different responses. As the thickness of the SMA beam increases, its response becomes closer to the results of the local model. This is supported by the fact that by moving away from the small scale, the transformation behavior becomes independent of the size and can be nondimensionalized based on the mode and complexity of the deformation. SMA beams of smaller thickness, according to Fig. 4, show a hardening effect demonstrating the experimentally established “smaller is stronger.”
Conclusions
The response of SMA structures with submicron dimensions deviate from that of the bulk material. Conventional constitutive models, due to lack of intrinsic length scales, cannot capture such an experimentally observed size effect.
In the current work, a thermodynamically consistent constitutive model for the behavior of SMAs is developed that includes additional internal variables for the spatial gradients of martensite volume fraction and the transformation strain. The gradient-based constitutive model includes various energetic and dissipative length scales that can be calibrated experimentally. The length scales contribute to additional hardening in the structural SMA response.
A boundary value problem, defined by such model, contains the differential equation for the transformation surface including the gradients of internal variables as well as the equilibrium equation. The boundary value problems are solved analytically and, where impossible, numerically for simple extension of an SMA bar, pure bending of an SMA beam, and simple torsion of an SMA cylindrical bar. The gradient model attains to the results of a conventional SMA model in the case of a homogeneous problem. Unlike pure bending of a beam, the solution to simple torsion of an SMA bar featured a coupling between the gradient of MVF and transformation strain that resulted in transformation strains in normal directions in addition to transformation shear strains. Moreover, for structures that include gradients of stress, the most simplified version of the nonlocal SMA constitutive model, containing only one nonlocal parameter, can capture the size effect demonstrating a stronger response for smaller sizes.
Notes
Notice that the nonlocal length scales here are independent of the ones in Eq. (27).
It is assumed here that if \({\textbf{Y}}_{i} \in {\mathcal{T}}^{m}\), the space of mth-rank tensors, then \({\varvec{\upmu}}_{i}^{s} \in {\mathcal{T}}^{m + 1}\) and \({\varvec{\upmu}}_{i}^{b} \in {\mathcal{T}}^{m}\).
References
Benard WL, Kahn H, Heuer AH, Huff MA (1998) Thin-film shape-memory alloy actuated micropumps. J Microelectromech Syst 7(2):245–251
Kahn H, Huff MA, Heuer AH (1998) The TiNi shape-memory alloy and its applications for MEMS. J Micromech Microeng 8(3):213
Fu YQ, Luo JK, Ong SE, Zhang S, Flewitt AJ, Milne WI (2008) A shape memory microcage of TiNi/DLC films for biological applications. J Micromech Microeng 18(3):035026
Shin DD, Lee DG, Mohanchandra KP, Carman GP (2006) Thin film NiTi microthermostat array. Sens Actuators, A 130:37–41
Arzt E (1998) Size effects in materials due to microstructural and dimensional constraints: a comparative review. Acta Mater 46(16):5611–5626
Bazant ZP, Planas J (1997) Fracture and size effect in concrete and other quasibrittle materials. New directions in civil engineering. Taylor & Francis, London
Chen CQ, Shi Y, Zhang YS, Zhu J, Yan YJ (2006) Size dependence of young’s modulus in ZnO nanowires. Phys Rev Lett 96:075505
Yang F (2004) Size-dependent effective modulus of elastic composite materials: spherical nanocavities at dilute concentrations. J Appl Phys 95(7):3516–3520
Fleck NA, Muller GM, Ashby MF, Hutchinson JW (1994) Strain gradient plasticity: theory and experiment. Acta Metall Mater 42(2):475–487
Hutchinson JW (2000) Plasticity at the micron scale. Int J Solids Struct 37(1):225–238
Morrison JLM (1939) The yield of mild steel with particular reference to the effect of size of specimen. Proc Inst Mech Eng 142(1):193–223
Frommen C, Wilde G, Rösner H (2004) Wet-chemical synthesis and martensitic phase transformation of Au–Cd nanoparticles with near-equiatomic composition. J Alloy Compd 377(1–2):232–242
Glezer AM, Blinova EN, Pozdnyakov VA, Shelyakov AV (2003) Martensite transformation in nanoparticles and nanomaterials. J Nanopart Res 5(5–6):551–560
Frick CP, Orso S, Arzt E (2007) Loss of pseudoelasticity in nickel–titanium sub-micron compression pillars. Acta Mater 55(11):3845–3855
San Juan J, Nó ML (2013) Superelasticity and shape memory at nano-scale: size effects on the martensitic transformation. J Alloy Compd 577(Supplement 1):S25–S29
Norfleet DM, Sarosi PM, Manchiraju S, Wagner MF, Uchic MD, Anderson PM, Mills MJ (2009) Transformation-induced plasticity during pseudoelastic deformation in Ni–Ti microcrystals. Acta Mater 57(12):3549–3561
Ozdemir N, Karaman I, Mara NA, Chumlyakov YI, Karaca HE (2012) Size effects in the superelastic response of Ni54Fe19Ga27 shape memory alloy pillars with a two stage martensitic transformation. Acta Mater 60(16):5670
San Juan J, Nó ML, Schuh CA (2009) Nanoscale shape-memory alloys for ultrahigh mechanical damping. Nat Nanotechnol 4(7):415–419
Chen Y, Schuh CA (2011) Size effects in shape memory alloy microwires. Acta Mater 59(2):537–553
Babanly MB, Lobodyuk VA, Matveeva NM (1993) Size effect in martensite transformation in TiNiCu alloys. Fiz Met Metalloved 75(5):89–95
Busch JD, Johnson AD, Lee CH, Stevenson DA (1990) Shape-memory properties in Ni-Ti sputter-deposited film. J Appl Phys 68(12):6224–6228
Ishida A, Sato M (2003) Thickness effect on shape memory behavior of Ti-50.0at.%Ni thin film. Acta Mater 51(18):5571–5578
Wan D, Komvopoulos K (2005) Thickness effect on thermally induced phase transformations in sputtered titanium-nickel shape-memory films. J Mater Res 20:1606–1612
Guimarães JRC (2007) Excess driving force to initiate martensite transformation in fine-grained austenite. Scr Mater 57(3):237–239
Kim Y, Cho G, Hur S, Jeong S, Nam T (2006) Nanocrystallization of a Ti–50.0Ni(at.%) alloy by cold working and stress/strain behavior. Mater Sci Eng, A 438–440:531–535
Kockar B, Karaman I, Kim JI, Chumlyakov YI, Sharp J, Yu CJ (2008) Thermomechanical cyclic response of an ultrafine-grained NiTi shape memory alloy. Acta Mater 56(14):3630–3646
Malygin GA (2008) Nanoscopic size effects on martensitic transformations in shape memory alloys. Phys Solid State 50(8):1538–1543
Waitz T, Antretter T, Fischer FD, Simha NK, Karnthaler HP (2007) Size effects on the martensitic phase transformation of NiTi nanograins. J Mech Phys Solids 55(2):419–444
Waitz T, Kazykhanov V, Karnthaler HP (2004) Martensitic phase transformations in nanocrystalline NiTi studied by {TEM}. Acta Mater 52(1):137–147
Eringen AC (1978) Line crack subject to shear. Int J Fract 14(4):367–379
Eringen AC (1983) On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl Phys 54(9):4703–4710
Lazar M, Maugin GA (2005) Nonsingular stress and strain fields of dislocations and disclinations in first strain gradient elasticity. Int J Eng Sci 43(13–14):1157–1184
Choi K, Kuhn JL, Ciarelli MJ, Goldstein SA (1990) The elastic moduli of human subchondral, trabecular, and cortical bone tissue and the size-dependency of cortical bone modulus. J Biomech 23(11):1103–1113
Kakunai S, Masaki J, Kuroda R, Iwata K, Nagata R (1985) Measurement of apparent young’s modulus in the bending of cantilever beam by heterodyne holographic interferometry. Exp Mech 25(4):408–412
Lakes RS (1986) Experimental microelasticity of two porous solids. Int J Solids Struct 22(1):55–63
Fleck NA, Hutchinson JW (1997) Strain gradient plasticity. Adv Appl Mech 33:295–361
Jirasek M (2004) Nonlocal theories in continuum mechanics. Acta Polytech 44(5–6):16–34
McElhaney KW, Vlassak JJ, Nix WD (1998) Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. J Mater Res 13:1300–1306
Stölken JS, Evans AG (1998) A microbend test method for measuring the plasticity length scale. Acta Mater 46(14):5109–5115
Bazant ZP, Jirásek M (2002) Nonlocal integral formulations of plasticity and damage: survey of progress. J Eng Mech 128(11):1119–1149
Borino G, Fuschi P, Polizzotto C (1999) A thermodynamic approach to nonlocal plasticity and related variational principles. J Appl Mech 66(4):952–963
Jirasek M, Bazant ZP (2002) Inelastic analysis of structures. Wiley, New York
Engelen RAB, Geers MGD, Baaijens F (2003) Nonlocal implicit gradient-enhanced elasto-plasticity for the modelling of softening behaviour. Int J Plast 19(4):403–433
Fleck NA, Hutchinson JW (1993) A phenomenological theory for strain gradient effects in plasticity. J Mech Phys Solids 41(12):1825–1857
Aifantis EC (1984) On the microstructural origin of certain inelastic models. J Eng Mater Technol 106(4):326–330
Aifantis EC (1999) Strain gradient interpretation of size effects. Int J Fract 95(1–4):299–314
Fleck NA, Hutchinson JW (2001) A reformulation of strain gradient plasticity. J Mech Phys Solids 49(10):2245–2271
Qiao L, Rimoli JJ, Chen Y, Schuh CA, Radovitzky R (2011) Nonlocal superelastic model of size-dependent hardening and dissipation in single crystal Cu-Al-Ni shape memory alloys. Phys Rev Lett 106(8):085504
M Tabesh, JG Boyd, DC Lagoudas (2014) Modeling size effect in the SMA response: a gradient theory. In: Proceedings of SPIE, vol 9058, pp 905803–905803–11
Engelen R, Fleck NA, Peerlings RHJ, Geers M (2006) An evaluation of higher-order plasticity theories for predicting size effects and localisation. Int J Solids Struct 43(7):1857–1877
Gudmundson P (2004) A unified treatment of strain gradient plasticity. J Mech Phys Solids 52(6):1379–1406
Gurtin ME (1996) Generalized Ginzburg-Landau and Cahn-Hilliard equations based on a microforce balance. Phys D 92(3):178–192
Aifantis EC (2003) Update on a class of gradient theories. Mech Mater 35(3):259–280
Aifantis EC (2011) On the gradient approach—relation to Eringen’s nonlocal theory. Int J Eng Sci 49(12):1367–1377
Mühlhaus HB, Aifantis EC (1991) A variational principle for gradient plasticity. Int J Solids Struct 28(7):845–857
Lagoudas DC (ed) (2008) Shape memory alloys: modeling and engineering applications. Springer, New York
Badnava H, Kadkhodaei M, Mashayekhi M (2014) A non-local implicit gradient-enhanced model for unstable behaviors of pseudoelastic shape memory alloys in tensile loading. Int J Solids Struct 51(23):4015–4025
Duval A, Haboussi M, Zineb TB (2011) Modelling of localization and propagation of phase transformation in superelastic SMA by a gradient nonlocal approach. Int J Solids Struct 48(13):1879–1893
Peultier B, Zineb TB, Patoor E (2006) Macroscopic constitutive law of shape memory alloy thermomechanical behaviour. Application to structure computation by FEM. Mech Mater 38(5):510–524
Brinson LC (1993) One-dimensional constitutive behavior of shape memory alloys: thermomechanical derivation with non-constant material functions and redefined martensite internal variable. J Intell Mater Syst Struct 4(2):229–242
Gurtin ME, Anand L (2005) A theory of strain-gradient plasticity for isotropic, plastically irrotational materials. Part I: small deformations. J Mech Phys Solids 53(7):1624–1649
Sun QP, He YJ (2008) A multiscale continuum model of the grain-size dependence of the stress hysteresis in shape memory alloy polycrystals. Int J Solids Struct 45(13):3868–3896
Lubliner J (2008) Plasticity theory. Courier Dover Publications, New York
Santaoja K (2004) Gradient theory from the thermomechanics point of view. Eng Fract Mech 71(4):557–566
Boehler JP (1987) Representations for isotropic and anisotropic non-polynomial tensor functions. In: Boehler JP (ed) Applications of tensor functions in solid mechanics. International Centre for Mechanical Sciences, vol 292. Springer, Vienna, pp 31–53
Spencer AJM (1987) Isotropic polynomial invariants and tensor functions. In: Boehler JP (ed) Applications of tensor functions in solid mechanics. International Centre for Mechanical Sciences, vol 292. Springer, Vienna, pp 141–169
Lagoudas DC, Bo Z, Qidwai MA (1996) A unified thermodynamic constitutive model for SMA and finite element analysis of active metal matrix composites. Mech Compos Mater Struct 3(2):153–179
Lagoudas DC, Hartl D, Chemisky Y, Machado L, Popov P (2012) Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys. Int J Plast 32:155–183
Gurtin ME (1982) An introduction to continuum mechanics. Academic Press, New York
Maugin GA (1999) The thermomechanics of nonlinear irreversible behaviors. World Scientific, Singapore
Rivlin RS (1997) On the principles of equipresence and unification. In: Barenblatt GI, Joseph DD (eds) Collected papers of RS Rivlin. Springer, Berlin, pp 1425–1426
Gurtin ME, Anand L (2009) Thermodynamics applied to gradient theories involving the accumulated plastic strain: the theories of Aifantis and Fleck and Hutchinson and their generalization. J Mech Phys Solids 57(3):405–421
Lele SP, Anand L (2008) A small-deformation strain-gradient theory for isotropic viscoplastic materials. Philos Mag 88(30–32):3655–3689
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
Fundamentals
The independent state variables, assumed in the development of the strain gradient constitutive model, include the stress \({\varvec{\upsigma}}\), the absolute temperature \(T\), and a set of generalized state variables \({\textbf{Y}}\) related to the microstructure of the material. The definition of \({\textbf{Y}}\) as the set of internal variables or internal degrees of freedom is discussed later in this section. The dependent state variables that change in response to the changes in the independent state variables are assumed to be
The response function ɛ is the infinitesimal strain, q is the heat flux vector, s is the specific entropy, G is the specific Gibbs free energy, and μ s and μ b are the generalized forces conjugate to Y through surface and body action, respectively. The specific Gibbs free energy can be related to the specific internal energy, u, through the Legendre transformation.
Tensors of any arbitrary rank can constitute the set of generalized state variables Y = {Y 1, Y 2, Y 3, …} and their corresponding generalized forces μ s = {μ s1 , μ s2 , μ s3 , …} and μ b = {μ b1 , μ b2 , μ b3 , …}.Footnote 2 The variables Y i are related to the mechanisms of microstructural rearrangement; for example, plastic deformation due to the movement of dislocations, twinning of crystals, or slip of grain boundaries or transformation strain due to the stress/temperature-induced martensitic transformation. For the current study of an SMA gradient theory, the martensitic transformation is considered as the mechanism of microstructural changes. Therefore, Y includes the MVF, ξ, and its spatial gradients, ∇ξ, …, ∇p ξ, as well as the martensitic transformation strain tensor, ɛ tr, and its spatial gradients, ∇ɛ tr, …, ∇q ɛ tr. We assume here that the Y i are independent, but later we will see that some Y i are related by the evolution equations.
The conventional conservation laws of continuum mechanics as for the principle of conservation of mass, linear momentum, and angular momentum as well as the second law of thermodynamics in the form of the Clausius–Duhem inequality are considered [69]. The localization procedure, in going from the integral to the PDE form, assumes a continuous and smooth function for all of the fields integrated.
Generalized Principle of Conservation of Energy
The first law of thermodynamics states that the rate of change of kinetic and internal energy for a continuum body is equal to the rate at which external mechanical work is exerted on that body as well as external heat added to it. The external work is performed partly due to the contact and body forces. In its generalized form herein, it is assumed that the generalized state variables are capable of performing work through generalized surface and body forces. No physical justification is given here. However, one can argue that since the generalized state variables contribute to the internal energy, they must do external work in the balance of energy:
where \(\frac{D}{Dt}\) and \((\cdot) \)denote the material (or Lagrangian) time derivative, V is the volume of the body with mass density ρ, and \({{\textbf{v}}} = \dot{\mathbf{u}}\) being the velocity of the material point. Also, b is the body force per unit volume, t is the surface traction, and σ is the symmetric Cauchy stress tensor which is related to the surface traction operating on a surface with a unit normal n through σn = t. In addition, r is the body heat source, and μ s i and μ b i are the generalized surface and body forces, respectively. Equation (85) can be localized using the equilibrium equation, \(\nabla \cdot {\varvec{\upsigma}} + {\mathbf{b}} = \rho {\dot{\text{v}}}\), and the divergence theorem to get the local form of the generalized principle of conservation of energy,
For the special case of \({\textbf{Y}} \equiv \{ \xi ,{\mkern 1mu} {\varvec{\upvarepsilon}}^{\text{tr}} ,{\mkern 1mu} \nabla \xi ,{\mkern 1mu} \nabla {\varvec{\upvarepsilon}}^{\text{tr}} \}\), \({\varvec{\upmu}}^{s} \equiv \{ {\varvec{\upmu}}_{1}^{s} ,{\mkern 1mu} {\varvec{\upmu}}_{2}^{s} ,{\mkern 1mu} {\varvec{\upmu}}_{3}^{s} ,{\mkern 1mu} {\varvec{\upmu}}_{4}^{s} \}\), and \({\varvec{\upmu}}^{b} \equiv \{ \mu_{1}^{b} ,{\mkern 1mu} {\varvec{\upmu}}_{2}^{b} ,{\mkern 1mu} {\varvec{\upmu}}_{3}^{b} ,{\mkern 1mu} {\varvec{\upmu}}_{4}^{b} \}\), the local form of the generalized principle of conservation of energy will be
Constitutive Equations
External thermodynamic state variables perform work on the surface of the body. Internal thermodynamic state variables (ISV), on the other hand, are identifiable and measurable, but cannot be linked to any external force variable. Therefore, ISVs do not perform work, i.e., they do not appear in the mechanical work in the first law of thermodynamics [70]. The constitutive equations give relationships between the dependent state variables at time t and the independent external state variables and the ISVs. These state equations must be accompanied by evolution laws for the internal variables.
The generalized state variables, Y, contribute to the internal energy through their surface and body work conjugates. According to the aforementioned definition, therefore, Y i are not internal state variables. They are rather the internal degrees of freedom related to the microstructure. In order to derive the constitutive equations, it is assumed that all the material points in the continuum body at any time, t, go through thermodynamic processes that obey the 2nd law of thermodynamics. Using the Legendre transform for G, it is possible to combine the first and second laws of thermodynamics in their local form to obtain
This can be reduced to the Clausius–Plank inequality assuming the Fourier’s law of conduction.
Thus, by assigning surface work to generalized state variables, Y, the gradients ∇Y appear in the rate of energy dissipation.
If the set of generalized variables, Y, used in Eq. (87) are considered, we will have
The inequality (90) is satisfied by considering the following constitutive equations:
where D, the dissipation rate, is given by
Whether internal degrees of freedom or internal state variables, the above equations must be augmented by evolution equations for the state variables \({\dot{\textbf{Y}}} = \left\{ {{\dot{\textbf{Y}}}_{i} } \right\}\), as well as constitutive equations for μ s = {μ s i } and μ b = {μ b i }. In any case, it is possible to use the concept of generalized thermodynamic forces, Γ, and fluxes, \({\dot{\mathbf{\varPi }}}\). In relation to Eq. (89), after including (91)a and b, one can write
For the case of SMA response, by redefining the variables in Eq. (92), we will have
A common method to achieve a rate-independent response is to define a threshold for Γ at which the dissipative mechanism activates. This can be done by assuming the existence of a convex set K such that
No dissipation occurs if Γ is inside K. Equation (95) is known as Hill–Mandel’s principle of maximum dissipation. A hypersurface
can be defined in the space of generalized forces that define the convex boundary of the convex set K. In the case of dislocation plasticity, Φ = 0 is the yield surface. Φ can also be associated with the dissipation potential the result of which is the normality in the space of generalized forces. To that end, the state of generalized variables is considered to be the one that maximizes the dissipation, D, or
It is shown that the problem in (97) is equivalent to finding the minimum of a Lagrangian, L,
so that
on the condition that the following Kuhn–Tucker conditions are satisfied:
Therefore, the rates of the generalized fluxes can be found via
demonstrating the associativity of the response in the space of generalized forces. The existence of the time derivative on both sides does not imply a rate-dependent response because it can be viewed as differentiation with respect to a loading parameter.
The rate of the Lagrange multiplier can be determined from the consistency condition:
It is customary for ϕ(Γ) to be assumed a homogeneous function of degree k. In that case the dissipation, (94) satisfying the second law of thermodynamics, can be obtained from
in which Euler’s homogeneous function theorem is used. The connection between the general constitutive model developed in this section and the higher-order theories that use a microscopic force balance or microforce balance law is shown in “Connection with the Gradient Theories Based on the Microforce Balance Law” section.
Reformulation of the Gradient Theory with Internal Variables
The approach of thermodynamics with internal variables is chosen to capture the microstructural changes in an SMA due to the martensitic phase transformation. According to the discussion in “Constitutive Equations” section, the internal variables, by definition, cannot perform work through surface or body forces. The internal variable theory is recovered by setting the generalized forces μ s and μ b to zero such as in Eq. (89), resulting in
Thus with \({\textbf{Y}} \equiv \{ \xi ,{\mkern 1mu} {\varvec{\upvarepsilon}}^{\text{tr}} ,{\mkern 1mu} \nabla \xi ,{\mkern 1mu} \nabla {\varvec{\upvarepsilon}}^{\text{tr}} \}\), Eq. (92) reduces to
It is acknowledged that the equivalence of “nonexistence” versus “being present with zero value” is a point of controversy [71]. Nonetheless, the final outcome is equivalent for the purpose of the current constitutive formulation.
Connection with the Gradient Theories Based on the Microforce Balance Law
Several gradient-based theories of plasticity postulate an additional balance law that incorporates the configurational or microscopic forces associated with the effective or accumulated plastic strain [72, 73]. This microscopic force balance or microforce balance law [52] can be obtained from a generalized form of the principle of virtual power, in which it is assumed that microtractions act as work conjugates to the generalized variable of the accumulated plastic strain and contribute to the external power. Also, it is assumed that the accumulated plastic strain and its spatial gradient contribute to the internal power.
As an example, Eq. (3.9) from Gurtin and Anand [72] is rewritten here
Following Gurtin and Anand’s notation, the scalar microstress π is the power conjugate to the accumulated plastic strain \(\dot{\gamma }^{\text{p}} = \left\| {{\dot{\mathbf{E}}}^{\text{p}} } \right\|\), ξ a vector microstress conjugate to \(\nabla \dot{\gamma }^{\text{p}}\), and χ(n) is the surface microtraction. It is then assumed that \({\mathcal{W}}_{\text{int}} = {\mathcal{W}}_{\text{ext}}\) for any arbitrary subregion P of the body and for any consistent virtual velocities \({\mathcal{V}} = \left( {{\dot{\mathbf{u}}},{\dot{\mathbf{E}}}^{\text{el}} ,\dot{\gamma }^{\text{p}} } \right)\).
The generalized principle of virtual power results in the conventional and microforce balance laws
as well as standard traction and microtraction boundary conditions
where τ is the (Von Mises) equivalent stress. Furthermore, the dissipation inequality as given in Eq. (6.13) of [72] is
where \(\psi = \hat{\psi }\left( {{\mathbf{E}}^{\text{el}} ,{\mkern 1mu} \gamma^{\text{p}} ,{\mkern 1mu} \nabla \gamma^{\text{p}} } \right)\) is the Helmholtz free energy. Replacing π and ξ in the microforce balance (107) yields
which is Eq. (6.15) in [72]. Equation (109), together with constitutive equations for π dis and ξ dis, acts as the flow rule for the gradient plasticity theory. It will now be shown that (109) can be obtained following the general model established in “Constitutive Equations” section. This, however, will be performed for the shape memory response by replacing the accumulated plastic strain with the MVF. To that end, it is assumed that the generalized variables are
where μ s1 is the surface power conjugate to ξ and μ b1 and μ b3 are, respectively, the body power conjugates to ξ and ∇ξ in the generalized first law of thermodynamics (86). The dissipation in Eq. (92) reduces to
Hence, the list of generalized forces and fluxes is as follows:
Constitutive assumptions are now considered for the generalized forces and fluxes. First, it is assumed that Γ 3 ≡ 0 such that
In addition, the transformation surface in Eq. (96) is considered to have the form
or
Now, if the form of the Gibbs free energy is such that
then
equivalent to the microforce balance in Eq. (109) augmented with the constitutive relations π dis ≡ Y − μ b1 and ξ dis ≡ −μ b3 .
The Most General Anisotropic/Isotropic Gibbs Free Energy for the Gradient-Based SMA Constitutive Model
The form for the Gibbs free energy of Eq. (20) is given in this appendix. The most general anisotropic Gibbs free energy with a polynomial form including terms up to 3rd degree is
The free energy includes all possible couplings between the state variables with their corresponding tensorial material constants. The tensorial material constants are the derivatives of the free energy calculated at the reference state leading to the major and minor symmetries.
The Gibbs free energy for the case of isotropic materials can be obtained by rewriting the constant tensors included in Eq. (118) in terms of their isotropic invariants. That is,
In this equation, the notation for the scalar constants is chosen based on their corresponding tensor. The rank-8 tensors, as listed, are not expanded due to the prohibitively large number, 91, of scalar constants involved. Four conditions are taken into account for the coefficient tensorial material constants in order to derive Eq. (119) from Eq. (118) as follows: (1) isotropy, (2) major symmetry as a result of interchangeability in differentiation of G with respect to state variables, (3) minor symmetry as a result of symmetry in σ, ɛ tr, and ∇ɛ tr, and (4) tr(ɛ tr) = 0 due to the volume-preserving assumption for the transformation strain.
Experimental Measurement of the SMA Material Properties
An attempt is made herein to relate the material constants of the constitutive model in “The Simplified SMA Gradient Model Including Only Terms with ∇ξ ” section to the typical experimentally observed properties of shape memory alloys. For that, the solution to uniaxial loading of an SMA bar is considered (“Extension of SMA Prismatic Bars” section). The typical pseudoelastic response of SMAs, based on Eqs. (48) and (49), is shown in Fig. 8. σ fwds and σ fwdf are the stresses to start and finish the forward transformation to martensite at the current temperature and σ revs and σ revf are the stresses to start and finish the reverse transformation to austenite, respectively.
The material constants used in the model can be found based on the following critical transformation start and finish conditions for a stress-free heating and cooling path:
-
1.
At the start of forward transformation, T = M s, ξ = 0,
-
2.
At the end of forward transformation, T = M f, ξ = 1,
-
3.
At the start of reverse transformation, T = A s , ξ = 1,
-
4.
At the end of reverse transformation, T = A f , ξ = 0.
-
5.
The Gibbs free energy and thus the hardening function, f(ξ), must be continuous, i.e., f(ξ = 1)|fwd = f(ξ = 1)|rev. The form of f is given in Eq. (44) for the linear hardening rule. Notice that this condition for ξ = 0 is trivially satisfied. For the smooth hardening function, \(\frac{\partial f(\xi )}{\partial \xi }\) is explicitly given in Eq. (45). Hence, the continuity condition can be written in the integral form as \(\int_{0}^{1} {\frac{{\partial f^{\text{fwd}} (\xi )}}{\partial \xi }} {\mkern 1mu} {\text{d}}\xi = \int_{0}^{1} {\frac{{\partial f^{\text{rev}} (\xi )}}{\partial \xi }} {\mkern 1mu} {\text{d}}\xi\).
-
6.
By taking the differential of (48) and (49) and letting dξ to vanish, it is possible to recover the slopes of the transformation regions on the stress–temperature phase diagram at a specific stress (for here the calibration stress σ = σ *). This leads to a relation for ρΔs 0 based on the forward and reverse transformation slopes, \(C_{M} \equiv \tfrac{{{\text{d}}\sigma }}{{{\text{d}}T}}|_{{\sigma = \sigma^{*} }}^{\text{fwd}}\) and \(C_{A} \equiv \tfrac{{{\text{d}}\sigma }}{{{\text{d}}T}}|_{{\sigma = \sigma^{*} }}^{\text{rev}}\).
The results of the conditions listed above are summarized in Table 2 for the linear hardening and in Table 3 for the smooth hardening rules.
The SMA model in this form cannot capture a response with different Clausius–Clapeyron slopes, as per the last equation shown in Tables 2 or 3, hence C A = C M.
In addition,
To derive the relations in (120), the difference between the elastic moduli of austenite and martensite is ignored.
The nonlocal model developed in “The Simplified SMA Gradient Model Including Only Terms with ∇ξ ” section introduces six energetic and two dissipative length scales in addition to the SMA material constants already being used in the classical local Boyd–Lagoudas SMA model [56]. A simplified version of the model considering only the three independent length scales ℓ 1, ℓ fwdd , and ℓ revd was used to study the behavior of SMA beams with various thicknesses. Based on the nonlocal constants, two parameters \({\mathcal{M}}_{1}^{\text{fwd}}\) and \({\mathcal{M}}_{2}^{\text{rev}}\) can be identified in the transformation differential equation. The material constants used in nonlocal modeling for SMAs are given in Table 4. The dissipative length scales, ℓ fwdd and ℓ revd , are excluded from this table since they do not independently appear in the solution of the SMA structures studied. This is because the solutions of the transformation surfaces, e.g., Eq. (68), rather than the rate forms are considered for those one-dimensional problems.
The relation between the local material parameters expressed in the course of model development and the more common SMA properties listed in Table 4 was established in this section using the problem of isothermal uniaxial stretching of an SMA bar (“Extension of SMA Prismatic Bars” section). Solution to this problem showed that the nonlocal model reduces to the original local SMA model for the cases in which there are no spatial gradients of the MVF.
Therefore, calibration of the nonlocal parameters, e.g., \({\mathcal{M}}_{1}^{\text{fwd}}\) and \({\mathcal{M}}_{1}^{\text{rev}}\) for the case of “Pure Bending of an SMA Beam” section, must be performed using specially designed experiments which provide spatial gradients. To this end, bending of SMA beams with various thicknesses was discussed in the results section. Also torsion of SMA thin wires with various diameters, or compression of tapered SMA pillars with different diameters are promising for nonlocal material parameter calibration purposes. To the best knowledge of the authors, there are no experimental results published for bending of SMA thin films with different thicknesses, although this has been done for the case of dislocation plasticity using aluminum foils [39]. Experimental observations for compression of SMA micropillars, on the other hand, are available and can be used for calibration of the current SMA gradient model.
Rights and permissions
About this article
Cite this article
Tabesh, M., Boyd, J. & Lagoudas, D. A Gradient-Based Constitutive Model for Shape Memory Alloys. Shap. Mem. Superelasticity 3, 84–108 (2017). https://doi.org/10.1007/s40830-017-0100-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40830-017-0100-9