Introduction

Shape memory alloys possess unique properties which are referred to as the pseudo-elastic (or austenitic) and the pseudo-plastic (or martensitic) material behavior. In contrast to other metallic materials, shape memory alloys are able to undergo a martensitic phase transformation not only during thermal loading but also during mechanical loading. The macroscopic effects of this evolution of microstructure are strains up to 8% which are reversible (for the austenitic behavior) or vanish after moderate heating and cooling of the material (for the martensitic behavior) (see, e.g., [1,2,3]). This characteristic makes shape memory alloys rather unique for metallic materials and allow for various applications such as medical devices, automotive, and aviation among which the medical sector is probably the most important one. A prominent example of industrial construction parts made of shape memory alloys are stents which allow for a healing of congested blood vessels without use of bypass surgeries.

Although the properties of shape memory alloys offer a huge variety of applications, the thermomechanically coupled material behavior, which influences also manufacturing, complicates a prediction of the functionality of the final construction part under realistic boundary conditions. Modern modeling techniques along with numerical simulations support this complex engineering process in a time- and cost-efficient way. There are several material models for shape memory alloys available, e.g., [4,5,6,7,8,9,10,11] to mention just a few. For the material model proposed in [12,13,14] it could be demonstrated in [15] that all model parameters can be expressed in terms of energetic quantities which allowed for a prediction of the mechanical material behavior while being calibrated solely on thermal experiments. This model property gives rise to the valid expectation that the numerical experiments are realistic and close to testing results also for arbitrarily complex construction parts. To be applicable also to further problems in which plastic deformations are present, the material model is expanded now by plastic effects including non-linear isotropic hardening.

Several works on the inclusion of plastic defects into the modeling of shape memory alloys already exist. For instance, Wang and coauthors presented in [16] a micromechanically motivated material model which includes also effects of pretexture. They simulated the pretexture by varying crystal orientation in each finite element. Although yielding interesting results, they only presented results for the austenitic (= pseudo-elastic) case and no thermal loading case. Furthermore, the varying orientation for each finite element complicates the application of the model to industrially relevant problems. Another energy-based formulation was presented by Hartl and Lagoudas in [17] which was implemented into Abaqus to perform sophisticated simulations and compare them to experimental results with convincing agreement (see also the preceding model in [18]). This model was also limited to the pseudo-elastic case. Lu and Weng presented one of the first self-consistent models for shape memory alloys including plastic effects in 1998, see [19]. Again, no pseudo-plastic (= martensitic) material behavior could be captured by this model. A model which accounts on the irrecoverable strains due to cyclic loading was presented by Yu and coauthors in [20]. They investigate the modeling of the effect of an evolving shape of the hysteresis for cyclic loadings. Due to the formation of dislocations during phase transformation, local stress peaks stabilize the martensite phase which favors the phase transition in the next loading step. This interesting and important effect, however, is beyond the scope of this contribution. Here, we focus on the plastic deformation which is present after stresses reach a critical value when following the elastic branch after the stress plateau in a stress/strain diagram. Waimann et al. expanded the original model on which the current contribution is based on in [21] to model the cyclic behavior of shape memory alloys.

The evolution of plastic deformations is not only an interesting “side information.” In contrast, it is known that plastic deformations stabilize the martensitic phase which, in turn, has a remarkable influence on the macroscopic behavior of construction parts. Thus, we begin with the theoretical derivation of the material model including non-linear isotropic hardening. Afterwards, we present several application examples, starting with tensile tests at various temperatures, proceeding with a plate with notch, and ending with a thermomechanically coupled simulation of a stent including large deformations and contact boundary conditions. We close our work with conclusions and an outlook.

Material Model

The model roots back to the one presented in [12]. The principal idea of the model is the introduction of a set of internal variables, volume fractions for the individual crystallographic phases, and Euler angles for the parameterization of the martensite strain orientation that describes the load-dependent microstructural state in shape memory alloys. The model was further condensed in [13]. Here, a scheme for easy model calibration based on stress/strain diagrams was also given (see also [14]). The entire model was formulated solely in energetic quantities, i.e., in terms of the Helmholtz free energy \(\Psi\) and a dissipation function \(\mathcal {D}\) which accounts for the dissipative character of phase transformations. It turned out that this energy-based formulation provides a rather universal character: experimental digital scattering calorimetry (DSC) measurements allow for the estimation of the latent heat and deductively of the caloric part of the Helmholtz free energy. Theoretical investigation of the model equations showed that the caloric part of the Helmholtz free energy and the dissipation function are linked. In the end, this allowed for a complete model calibration based on DSC measurements. Subsequent comparison of numerical prediction of the mechanical behavior, i.e., force/displacement diagrams, to their experimental counterparts revealed an extraordinary good agreement without further model fitting or comparable. This energy-based model was thus considered to possessing a rather universal applicability, see [15]. In this contribution, we start from this model and expand it to account for irreversible deformations including effects of non-linear isotropic harding.

For the model derivation, the principle of the minimum of the dissipation potential is employed. This principle results as a special case from the Hamilton principle (see [22, 23]), for absent gradients of internal variables. It is generally formulated as

$$\begin{aligned} \mathcal {L}:= \dot{\Psi }+ \mathcal {D}+ \mathrm {cons} \rightarrow \underset{\dot{\varvec{\upsilon }}}{\text {stat}} \end{aligned},$$
(1)

with the rate of the Helmholtz free energy \(\dot{\Psi }\), the dissipation function \(\mathcal {D}\) , and model specific constraints \(\mathrm {cons}\). The Lagrange function \(\mathcal {L}\) is evaluated at its stationary point with respect to the rate of the generalized internal variable \({\dot{\varvec{\upsilon }}}\). If gradients of the internal variable are included, the more general form of the Hamilton principle has to be used. An example for this case was presented in [24] for evolutionary topology optimization.

Following [12, 13], two quantities are used as internal variables which describe the microstructural state: on the one hand, volume fractions for the crystallographic phase austenite and variants of martensite are introduced, all collected in the vector \(\varvec{\lambda }\) with \(\lambda _0\) indicating the austenite phase and \(\lambda _i\), \(0<i\le n\) for the ith martensitic phase (n indicates the maximum number of martensitic phases considered). On the other hand, industrial shape memory alloys are polycrystals for the vast majority of applications. Since the polycrystalline material behavior differs significantly from the single crystal, the orientation distribution function of martensite strain has to be taken into account. To this end, a dynamic evolution of the orientation distribution function has been proposed in [12]. It has been proven beneficial to introduce Euler angles \(\varvec{\alpha }= \{\varphi ,\nu ,\omega \}\) which serve also as internal variables. This modeling approach is now expanded by irreversible deformation effects. The irreversible deformations are considered in terms of plastic strains \(\varvec{\varepsilon }_\mathrm {p}\) while the hardening behavior is described in terms of a hardening variable \(\alpha _\mathrm {h}\). The set of internal variables is consequently extended, i.e., \(\varvec{\upsilon }=\{\varvec{\lambda },\varvec{\alpha },\varvec{\varepsilon }_\mathrm {p},\alpha _\mathrm {h}\}\).

For the application of the minimum of the dissipation potential, it is necessary to define the Helmholtz free energy, the dissipation function, and the constraints. There are no constraints to be considered for the Euler angles. On the other hand, the volume fractions have to fulfill mass conservation which is put into formula by

$$\begin{aligned} \sum _{i=0}^n \lambda _i = 1 \qquad \Leftrightarrow \qquad \sum _{i=0}^n \dot{\lambda }_i = 0 \end{aligned}.$$
(2)

Furthermore, only non-negative values for the volume fractions can be interpreted physically, meaning

$$\begin{aligned} \lambda _i \ge 0 \quad \forall i \end{aligned}.$$
(3)

There is one constraint for the plastic strains, precisely the evolution of plastic strains is volume-preserving, i.e., the plastic strains are traceless, yielding

$$\begin{aligned} \sum _{j=1}^3 \varepsilon _{\text {p},jj} = 0 \qquad \Leftrightarrow \qquad \sum _{j=1}^3 \dot{\varepsilon }_{\text {p},jj} = 0 \end{aligned}.$$
(4)

The last constraint effects the hardening variable \(\alpha _\mathrm {h}\). The physical process that causes the macroscopic hardening phenomenon is the evolution of dislocations, termed \(\bar{\rho }\). Without modeling their evolution in detail, it may be assumed that there exist a proportional relation between the evolution of dislocations and the hardening variable. Additionally, the plastic strains also describe effects caused by dislocations in a “condensed” way. It is thus convenient to postulate \({\dot{\bar{\rho }}}\propto {\dot{\alpha }}_\mathrm {h}\ge |{\dot{\varvec{\varepsilon }}}_\mathrm {p}| \Leftrightarrow -{\dot{\alpha }}_\mathrm {h}+|{\dot{\varvec{\varepsilon }}}_\mathrm {p}|\le 0\) which is ensured by the Kuhn–Tucker parameter \(\gamma _2\), defined by

$$\begin{aligned} \gamma _2 = {\left\{ \begin{array}{ll} \bar{\gamma }_2 &{} : -{\dot{\alpha }}_\mathrm {h}+|{\dot{\varvec{\varepsilon }}}_\text {p}| >0 \\ 0 &{} :\text { else} \end{array}\right. } \end{aligned}$$
(5)

For the inclusion of all constraints, Kuhn–Tucker [\(\varvec{\gamma }\) for Eq. (3) and \(\gamma _2\) for the constraint in Eq. (5)] and Lagrange [\(\beta _\text {T}\) for Eq. (2) and \(\beta _\text {P}\) for Eq. (4)] parameters are used, respectively,

$$\begin{aligned} \mathcal {L}= \dot{\Psi }+ \mathcal {D}+ \beta _\text {T} \sum _{i=0}^3 \dot{\lambda }_i - \varvec{\gamma }\cdot \dot{\varvec{\lambda }} + \beta _\text {P} \sum _{j=1}^3 \dot{\varepsilon }_{\text {p},jj}+ \gamma _2 (-{\dot{\alpha }}_\mathrm {h}+ |\dot{\varvec{\varepsilon }}_\text {p}|) \rightarrow \min _{{\dot{\varvec{\lambda }}},{\dot{\varvec{\alpha }}},{\dot{\varvec{\varepsilon }}}_\mathrm {p},{\dot{\alpha }}_\mathrm {h}} \end{aligned}.$$
(6)

The dissipation function \(\mathcal {D}\) has to be chosen in a way that the resulting evolution equation is of the desired type, e.g., rate-independent, rate-dependent (= viscous), or elasto-viscoplastic. The evolution of the plastic strains is assumed to evolve in a rate-independent fashion which demands a contribution of the rate of the plastic strains to the dissipation function which is homogeneous of order one. The evolution of the Euler angles is assumed to be rate-dependent for sake of simplicity, whereas the evolution of volume fractions is assumed to evolve in an elasto-viscoplastic manner (see [13]). This results in

$$\begin{aligned} \mathcal {D}= & {} r_1 |{\dot{\varvec{\lambda }}}| + \frac{r_2}{2} |{\dot{\varvec{\lambda }}}|^2 + \frac{r_\alpha }{2} ||\varvec{\Omega }||^2 + r_\mathrm {p}|{\dot{\varvec{\varepsilon }}}_\mathrm {p}| \nonumber \\= & {} r_1 |{\dot{\varvec{\lambda }}}| + \frac{r_2}{2} |{\dot{\varvec{\lambda }}}|^2 + \frac{r_\alpha }{2} \left( {\dot{\varphi }}^2+\dot{\nu }^2+2{\dot{\varphi }}{\dot{\omega }} \, \cos \nu + {\dot{\omega }}^2\right) + r_\mathrm {p}|{\dot{\varvec{\varepsilon }}}_\mathrm {p}| \end{aligned}$$
(7)

with the skew-symmetric matrix of angular velocities \(\varvec{\Omega }\) and dissipation parameters \(r_1,r_2,r_\alpha ,r_\mathrm {p}\).

Finally, the Helmholtz energy has to be specified. For each crystallographic phase, it is assumed to be quadratic in the elastic strains and to be contributed by caloric effects. This yields

$$\begin{aligned} \bar{\Psi }_i = \frac{1}{2} \left( \varvec{\varepsilon }_i - \varvec{Q}^T\cdot \varvec{\eta }_i\cdot \varvec{Q}- \varvec{\varepsilon }_\mathrm {p}\right) : \mathbb {E}_i : \left( \varvec{\varepsilon }_i - \varvec{Q}^T\cdot \varvec{\eta }_i\cdot \varvec{Q}- \varvec{\varepsilon }_\mathrm {p}\right) + c_i(\theta ) \end{aligned}.$$
(8)

Here, \(\varvec{\varepsilon }_i\) denotes the total strain in the respective phase. The quantity \(\varvec{\eta }_i\) is the transformation strain, \(\varvec{Q}=\varvec{Q}(\varvec{\alpha })\) is the rotation matrix, \(\varvec{\varepsilon }_\mathrm {p}\) is the plastic strain (which is constant for the entire material point but evolves during loading), \(\mathbb {E}_i\) is the stiffness tensor, and \(c_i(\theta )\) is the temperature-dependent caloric energy. The energy for each phase is homogenized via relaxation, meaning

$$\begin{aligned} \bar{\Psi }= \inf _{\varvec{\varepsilon }_i} \left\{ \left. \sum _{i=0}^n \lambda _i \bar{\Psi }_i \ \right| \ \sum _{i=0}^n \lambda _i\varvec{\varepsilon }_i = \varvec{\varepsilon }\right\} \end{aligned}.$$
(9)

Skipping the detailed calculation and just presenting the result gives

$$\bar{\Psi } = \frac{1}{2}\left( {\varepsilon - Q^{T} \cdot \bar{\eta } \cdot Q \cdot - {\text{ }}\varepsilon _{{\text{p}}} } \right):{\mathbb{\bar{E}}}\left( {{\text{ }}\varepsilon - {\text{ }}Q^{T} \cdot \bar{\eta } \cdot Q - {\text{ }}\varepsilon _{{\text{p}}} } \right) + \bar{c}(\theta )$$
(10)

with the effective quantities

$$\bar{\eta } = \sum\limits_{{i = 0}}^{n} {\lambda _{i} } \eta _{i} \;,\qquad {\mathbb{\bar{E}}} = \left[ {\sum\limits_{{i = 0}}^{n} {\lambda _{i} } {\mathbb{E}}_{i}^{{ - 1}} } \right]^{{ - 1}} ,\qquad \;\bar{c}(\theta ) = \sum\limits_{{i = 0}}^{n} {\lambda _{i} } c_{i} (\theta )$$
(11)

More details can be found in [12, 13]. The total Helmholtz free energy consists of \(\bar{\Psi }\) and a hardening contribution, termed \(\Psi _\mathrm {h}\):

$$\begin{aligned} \Psi = \bar{\Psi }+ \Psi _\mathrm {h} \end{aligned}.$$
(12)

Inserting the relaxed energy \(\Psi\), see Eq. (10), and the dissipation function according to Eq. (7), into the principle of the minimum of the dissipation potential in Eq. (6) yields the stationarity conditions

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial \dot{\lambda }_i}&= 0 =&-p_{\text {T},i} + r_1 \frac{\dot{\lambda }_i}{|{\dot{\varvec{\lambda }}}|} + r_2 \dot{\lambda }_i + \beta _{\text {T}} - \gamma \end{aligned}$$
(13)
$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {\dot{\varvec{\alpha }}}}&= \varvec{0} =&-\varvec{p}_\alpha +r_\alpha \mathrm {obj}_{\text {I}}\ {\dot{\varvec{\alpha }}} \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {\dot{\varvec{\varepsilon }}}_\mathrm {p}}&= \varvec{0} =&- \varvec{p}_{\text {P}} + r_\mathrm {p}\frac{{\dot{\varvec{\varepsilon }}}_\mathrm {p}}{|{\dot{\varvec{\varepsilon }}}_\mathrm {p}|} + \beta _{\text {P}} \varvec{I}+ \gamma _2 \frac{{\dot{\varvec{\varepsilon }}}_\mathrm {p}}{|{\dot{\varvec{\varepsilon }}}_\mathrm {p}|}\end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial \dot{\alpha }_\mathrm {h}}&= 0 =&-p_\mathrm {h} - \gamma _2 \end{aligned}.$$
(16)

Here, the driving forces for the volume fractions \(p_{\text {T,i}} := -\partial \Psi /\partial \lambda _i\), the Euler angles \(\varvec{p}_\alpha := -\partial \Psi /\partial \varvec{\alpha }\), the plastic strains \(\varvec{p}_{\text {P}} := -\partial \Psi /\partial \varvec{\varepsilon }_\mathrm {p}\), and the hardening variable \(p_\mathrm {h}:=-\partial \Psi /\partial \alpha _\mathrm {h}\) have been introduced. The inverse objectivity operator is defined as

$$\begin{aligned} \mathrm {obj}_{\text {I}} \varvec{g}= \mathrm {obj}_{\text {I}} \left( \begin{matrix} g_1 \\ g_2 \\ g_3 \end{matrix} \right) := \left( \begin{matrix} g_1 - g_3 \cos \vartheta \\ g_2 \\ g_3 - g_1 \cos \vartheta \end{matrix}\right) \end{aligned}.$$
(17)

Equation (13) can be transformed to the evolution equation for the phases

$$\begin{aligned} {\dot{\varvec{\lambda }}} = \frac{1}{r_2} \left[ |\mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}| - r_1 \right] _+ \frac{\mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}}{|\mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}|} \end{aligned}$$
(18)

with \([x]_+:= (x +|x|)/2\) and the active deviator \(\mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}} := \varvec{p}_\lambda - \varvec{I}_n \frac{1}{n_\mathcal {A}} \sum _{j\in \mathcal {A}} p_{\text {T},j}\) where the active set \(\mathcal {A}=\left\{ i |\lambda _i\not =0\right\} \cup \{i|\lambda _i=0 \wedge \dot{\lambda }_i>0 \}\) has been defined. The quantity \(n_\mathcal {A}\) is the number of active phases and \(\varvec{I}_n\) is the one-vector of length \(n\). For more details, we refer to [13]. For an improved numerical treatment, an adaptive viscosity \(r_2\) is chosen according to

$$\begin{aligned} r_2 = -|\mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}|^{-2} \left[ \mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}\cdot \frac{\partial \mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}}{\partial \varvec{\lambda }}\cdot \mathrm {dev}_\mathcal {A}\varvec{p}_{\text {T}}\right] ^{-1} \end{aligned}.$$
(19)

The evolution equation for the Euler angles can be derived from Eq. (14) as

$$\begin{aligned} {\dot{\varvec{\alpha }}} = \frac{1}{\sqrt{2}r_\alpha (1-\cos ^2\vartheta )} \mathrm {obj} \ \varvec{p}_\alpha \end{aligned}$$
(20)

with the objectivity operator

$$\begin{aligned} \mathrm {obj} \ \varvec{g}= \mathrm {obj} \left( \begin{matrix} g_1 \\ g_2 \\ g_3 \end{matrix} \right) := \left( \begin{matrix} g_1 - g_3 \cos \vartheta \\ g_2 (1- \cos ^2\vartheta ) \\ g_3 - g_1 \cos \vartheta \end{matrix}\right) \end{aligned}.$$
(21)

It remains to calculate the evolution equation for the plastic strains from Eq. (15). First, summation of all components with identical indices gives

$$\begin{aligned} - \mathrm {tr} \ \varvec{p}_{\text {P}} + 3 \beta _{\text {P}} = 0 \qquad \Leftrightarrow \qquad \beta _{\text {P}} = \frac{1}{3} \mathrm {tr} \ \varvec{p}_{\text {P}} \end{aligned},$$
(22)

where the constraint according to Eq. (4) has been employed. Hence, Eq. (15) transforms to

$$\begin{aligned} \dot{\varvec{\varepsilon }}_{\text {p}} = \frac{|\dot{\varvec{\varepsilon }}_{\text {p}}|}{r_\mathrm {p}+\gamma _2} \left[ \varvec{\sigma }- \frac{1}{3} \varvec{I}:\varvec{\sigma }\right] = \frac{|\dot{\varvec{\varepsilon }}_{\text {p}}|}{r_\mathrm {p}+\gamma _2} \mathrm {dev}\varvec{\sigma }{\; := \rho _\mathrm {p} \, \mathrm {dev}\varvec{\sigma }} \end{aligned}$$
(23)

with the stress deviator \(\mathrm {dev}\varvec{\sigma }\). The (positive) pre-factor \(\rho _\mathrm {p} := |{\dot{\varvec{\varepsilon }}}_\mathrm {p}|/(r_\mathrm {p}+\gamma _2)\ge 0\) is identified as consistency parameter and a Legendre transform of the dissipation function with respect to \({\dot{\varvec{\varepsilon }}}_\mathrm {p}\) results in the associated yield function

$$\begin{aligned} \Phi := |\mathrm {dev}\varvec{\sigma }| - (r_\mathrm {p}+\gamma _2) \overset{!}{\le }0 \end{aligned}$$
(24)

and the Karush–Kuhn–Tucker conditions \(\rho _\mathrm {p}\ge 0\), \(\Phi \le 0\), \(\rho _\mathrm {p} \Phi =0\), see e.g., [25]. Still, the evolution of \({\dot{\alpha }}_\mathrm {h}\) as well as the Lagrange parameter \(\gamma _2\) need to be specified. To this end, let us evaluate Eq. (16) resulting in

$$\begin{aligned} \gamma _2 = \frac{\partial \Psi }{\partial \alpha _\mathrm {h}} \end{aligned}.$$
(25)

Furthermore, we assume that the maximum plastic strains possible evolve for a given rate of the dislocations (\({\dot{\alpha }}_\mathrm {h}=|{\dot{\varvec{\varepsilon }}}_\mathrm {p}|\)) yielding

$$\begin{aligned} {\dot{\alpha }}_\mathrm {h}= \rho _\mathrm {p} \left( r_\mathrm {p}+\frac{\partial \Psi }{\partial \alpha _\mathrm {h}} \right) \end{aligned}.$$
(26)

For the hardening energy \(\Psi _\mathrm {h}\) we propose the following approach

$$\begin{aligned} \Psi _\mathrm {h} = \frac{1}{2} k_1 \alpha _\mathrm {h}^2 + \frac{1}{\beta } \left( \alpha _\mathrm {h}\left( k_1-k_0\right) + \frac{k_0-k_1}{\beta } e^{-\beta \alpha _\mathrm {h}} \right) \end{aligned}$$
(27)

with the initial and end slope of the hardening curve, \(k_0\) and \(k_1\), respectively, and the exponential parameter \(\beta\) which controls the transition from \(k_0\) to \(k_1\). The yield function including hardening thus reads (with \(r_\mathrm {p}\) being the initial deviator norm of the yield stress)

$$\begin{aligned} \Phi = |\mathrm {dev}\varvec{\sigma }| - \left( r_\mathrm {p}+k_1 \alpha _\mathrm {h}+ \frac{1}{\beta } (k_1-k_0)\left( e^{-\beta \alpha _\mathrm {h}}-1\right) \right) \end{aligned}.$$
(28)

The material parameters which control the plastic behavior of the material, that are \(k_0\), \(k_1\), \(\beta\), and \(r_\mathrm {p}\), are presented here as temperature-independent quantities. This, however, does not limit the generality of the model: all parameters may be replaced by temperature-dependent functions. In this contribution, in which the approach is presented for the first time, we use temperature-independent values in Sect. 4.

From the evolution equation for the plastic strains in Eq. (23), it can be seen that \(\varvec{\varepsilon }_\text {p}\) evolve in the direction of the stress deviator (which is of usual fashion for plasticity). Since the transformation strain depends on the current orientation, given in terms of the Euler angles \(\varvec{\alpha }\), the very same holds true for the stresses. Thus, the plastic strains evolve not only dependent on the direction of the (local) load direction but also dependent on the current martensite strain orientation.

Algorithmic Implementation

The material model consists of four differential equations which describe the evolution of the four internal variables \(\varvec{\lambda }\), \(\varvec{\alpha }\), \(\varvec{\varepsilon }_\mathrm {p}\), and \(\alpha _\mathrm {h}\). For the solution of such (coupled) systems of differential equations, there exists various strategies for finding an approximate solution. We perform for each variable a “consistent linearization” from a broken Taylor expansion, meaning

$$\begin{aligned} \varvec{\xi }^{n+1} \approx \varvec{\xi }^n+\left. \frac{\partial \varvec{\xi }}{\partial t}\right| ^n \Delta t \end{aligned},$$
(29)

where \(n+1\) denotes the current and n the previous time (= load) step. The quantity \(\varvec{\xi }\) is one of the time-dependent variables to be calculated. The derivative \(\partial \varvec{\xi }/\partial t\) is nothing but the rate of the respective variable. It holds for each evolution equation \({\dot{\varvec{\xi }}}\approx \Delta \varvec{\xi }/\Delta t\). The second term in Eq. (29) hence becomes \(\Delta t \partial \varvec{\xi }/\partial t|^n \approx \Delta \varvec{\xi }^n\). Thus, we update according to the following (explicit) scheme

$$\begin{aligned} \varvec{\lambda }^{n+1}= & {} \varvec{\lambda }^n + \Delta \varvec{\lambda }^n, \quad \varvec{\varepsilon }_\mathrm {p}^{n+1} = \varvec{\varepsilon }_\mathrm {p}^n + \Delta \varvec{\varepsilon }_\mathrm {p}^n \nonumber \\ \varvec{\alpha }^{n+1}= & {} \varvec{\alpha }^n + \Delta \varvec{\alpha }^n, \quad \alpha _\mathrm {h}^{n+1} = \alpha _\mathrm {h}^n + \Delta {\alpha }_\mathrm {h}^n \nonumber \; .\end{aligned}$$

The increments \(\Delta \varvec{\xi }^n\) are given by the evolution equations and the superscript n indicates that they are evaluated for the current time step \(n+1\) using the (given and fixed) values from the previous time step n. Furthermore, we perform same linearization for the stresses and apply an operator split for the stresses in terms of the Euler angles: for each time step, we fix the Euler angles for the computation of the stresses, i.e., \(\varvec{\sigma }=\varvec{\sigma }(\varvec{\varepsilon },\varvec{\lambda },\varvec{\varepsilon }_\mathrm {p})\), and update \(\varvec{\alpha }\) independently. The rate of the stresses is thus given (in Voigt notation) by

$$\begin{aligned} {\dot{\varvec{\sigma }}} = \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }}\cdot \frac{\partial \varvec{\varepsilon }}{\partial t} + \frac{\partial \varvec{\sigma }}{\partial \varvec{\lambda }}\cdot \frac{\partial \varvec{\lambda }}{\partial t} + \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }_\mathrm {p}}\cdot \frac{\partial \varvec{\varepsilon }_\mathrm {p}}{\partial t} \end{aligned},$$
(30)

such that the linearization according to Eq. (29) yields

$$\begin{aligned} \varvec{\sigma }^{n+1} = \varvec{\sigma }^n + \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }}\right| ^n \cdot \Delta \varvec{\varepsilon }^n + \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\lambda }}\right| ^n\cdot \Delta \varvec{\lambda }^n+\left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }_\mathrm {p}}\right| ^n\cdot \Delta \varvec{\varepsilon }_\mathrm {p}^n \end{aligned}.$$
(31)

The individual derivatives of the stress read (see also [14])

$$\begin{aligned}&\left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }}\right| ^n = {\bar{\mathbb {E}}}|^n, \qquad \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }_\mathrm {p}}\right| ^n = -{\bar{\mathbb {E}}}|^n , \\&\left. \frac{\partial \varvec{\sigma }}{\partial \lambda _i}\right| ^n = \left. -\frac{\partial p_{\text {T},i}}{\partial \varvec{\varepsilon }}\right| ^n = - \left[ \left( \varvec{Q}^T\cdot \varvec{\eta }_i \cdot \varvec{Q}+ \mathbb {E}_i^{-1}:\varvec{\sigma }\right) : {\bar{\mathbb {E}}} \right] ^n \end{aligned}.$$

The computation of the tangent, which is necessary for a finite element implementation, is due to the consistent linearization very simple. For instance, the Abaqus tangent is defined as

$$\begin{aligned} \varvec{C}:= \frac{\partial \Delta \varvec{\sigma }}{\partial \Delta \varvec{\varepsilon }} \overset{(31)}{=} \left. \frac{\partial \varvec{\sigma }}{\partial \varvec{\varepsilon }}\right| ^n = {\bar{\mathbb {E}}}|^n \end{aligned}.$$
(32)

This implementation follows an explicit Euler procedure which possesses the drawback of being numerically unstable for large time steps. We therefore limit the times steps to 1% of the maximum load (which holds true for mechanical and thermal loads). As can be seen in the numerical results, we obtain very smooth and stable solutions with an exceptionally good convergence behavior although we employ an explicit update. Therefore, we consider this procedure to be more beneficial for complex problems than an implicit update scheme, for instance, which renders to be very complex for the current material model due to the complicated constraint for the volume fractions \(\varvec{\lambda }\): the active set may be regarded as a non-differentiable function whose derivative is still necessary for an implicit procedure. Details on a different numerical implementation of the original model can be found in [14].

Numerical Results

For all simulations, we used the set of parameters given in Table 1 of which the parameters of the original model are taken from the calibration presented in [13, 14]. We present results for different boundary value problems: we start with a simple tensile test for a first understanding of the model results. Afterwards, we proceed with a plate with notch which shows the stabilizing effects of irreversible strains on the martensite phase. Finally, we present a result for a stent which is crimped in a first loading step at –10 \(^{\circ }\)C in a martensitic configuration, heated later to body temperature of 37 \(^{\circ }\)C, and finally deployed at the very same temperature. The material model is implemented both into FEAP and Abaqus and shows in both finite element programs a fast convergence behavior by also being extremely stable.

Table 1 Material parameters
Full size table

Tensile Tests

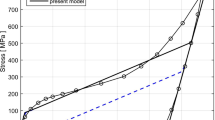
In anticipation of the temperatures investigated for the stent simulation, we present tensile tests for –10, 20, and 37 °C for loading and unloading to zero strains. They are given in Fig. 1.

Fig. 1
figure 1

From left to right tensile tests for –10, 20, and 37 °C

Full size image

The material model describes the temperature-dependent behavior without further modifications in an accurate way: at low temperatures (–10 °C), the martensitic behavior is present with a pseudo-plastic stress/strain response exhibiting the typical negative stress during unloading. At high temperatures (37 °C), the austenitic behavior is present, whereas at a temperature close to the A\({}_\text {f}\) temperature (20 °C) still the austenitic behavior is present but with a stress close to zero during unloading. All results show the clear plastic response at high strains yielding a non-linear transition into a second stress plateau which is caused by the evolution of plastic deformations. This effect is also visible during unloading: whereas a pure austenitic (= pseudo-elastic) behavior would yield zero stresses for zero strains after unloading, the evolution of plastic strains causes well-known eigen-stresses which appear as negative stress values even for the pseudo-elastic behavior. A clear indicator for a reduction of the plastic strains is the negative stress plateau at 37 °C.

Plate with Notch

As a more sophisticated example, we present simulation results for a plate with notch under tension in vertical direction at 37 °C. The notch will not evolve in a dynamic way so that no crack propagation is investigated. One finite element is chosen in thickness direction. The total number of tri-linear elements is 720 with 1526 nodes. The global material reaction is given in terms of a force/displacement diagram shown in Fig. 2. It can be seen that during phase transformation and evolution of plastic strains, a distinct change in the slope of the curve is present. This, however, does not form a perfect plateau due to the localized microstructural evolution. After unloading, a small permanent deformation remains. This is well in agreement to the distribution of plastic strains, shown in Fig. 3.

Fig. 2
figure 2

Plate with notch: force/displacement diagram

Full size image

At the tip of the notch, stress peaks are present which trigger an evolution of plastic deformations. They exhibit a dog bone shape at maximum load (left hand side) and decrease slightly during the process of unloading.

Fig. 3
figure 3

Plate with notch: distribution of the norm of the plastic strain \(|\varvec{\varepsilon }_\mathrm {p}|\) at maximum load (left) and at unloading (right). Zoomed plot

Full size image

This evolution of plastic strains has a strong impact on the phase transformation, depicted in Fig. 4. The distribution of the austenite phase differs at maximum load slightly from the one in [13] which was simulated while neglecting plastic deformations. Furthermore, this example demonstrates the fundamental influence of plastic strains on the phase composition: after unloading, plastic strains stabilize the martensitic phase such that the reverse transformation from martensite to austenite remains incomplete.

Fig. 4
figure 4

Plate with notch: distribution of the austenite phase \(\lambda _0\) at maximum load (left) and at unloading (right)

Full size image

In contrast, the amount of austenite remains at zero percent at the tip of the notch.

Stent

The last example presented here is the simulation of a stent which is modeled by one strut discretized using approximately 150,000 nodes. The results are mirrored later to display the total stent. The simulation is performed with the commercial software Abaqus in which a fully non-linear geometrical treatment is employed. The initial temperature is set to be –10 °C implying the martensitic configuration. Contact boundary conditions are applied for the crimping. After fully crimped, the contact boundary conditions are fixed and the temperature is increased to a typical body temperature of 37 °C. Afterwards, the stent is deployed expanding to a configuration without prescribed boundary conditions. The complete picture is given in Fig. 5.

Fig. 5
figure 5

Stent: distribution of one martensitic phase. From left to right: initial state at –10 °C; crimped configuration at –10 °C; after heating in crimped position at 37 °C; deployed configuration at 37 °C

Full size image

Due to geometrical reasons, phase transformation is most prominent during crimping at the edges of the stent. During heating, parts of the stent remain in the martensitic configuration, enforced by mechanical stresses. Other parts with lower mechanical stress states transform temperature-driven to the austenitic configuration such that the amount of martensite reduces to zero percent in these areas. When the stent is deployed, the material transforms completely to the austenitic configuration which is the stable one at 37 °C.

Fig. 6
figure 6

Stent: distribution of the logarithmic principal strain. From left to right: initial state at –10 °C; crimped configuration at –10 °C; after heating in crimped position at 37 °C; deployed configuration at 37 °C

Full size image

The impact of plastic deformations is in this example of minor importance (see Fig. 6, right hand side). However, for a stronger compression rate or other alloy compositions, for which the model parameters have to be updated after calibration, the effect of plasticity might be much more pronounced.

Conclusions and Outlook

We presented the expansion of an energy-based material model for shape memory alloys by plastic effects including non-linear isotropic hardening. The model was derived from the Hamilton principle and calibrated based on previous publications. Tensile tests at various temperatures provided an insight to the general behavior of the material model. A plate with notch under tension served as an example for the interaction of plastic deformations and phase transformations which are of particular interest for construction parts with stress localizations due to geometric reasons. A real-life simulation was presented as final example by simulating a stent under both mechanical and thermal loads. This simulation was performed using a commercial finite element environment (Abaqus). Contact boundary conditions and a non-linear deformation measure were applied. The very satisfactory convergence behavior indicates the capability of this material model to provide realistic simulation results also for industrially relevant problems including non-linearities and a huge number of unknowns (finite elements / nodes). Future investigations could aim at the cyclic behavior of shape memory alloys.