Introduction

The stability and performance of control systems are fundamental concerns in various engineering applications, ranging from industrial processes to aerospace systems. Achieving stable and reliable control under varying operating conditions [1] and disturbances is essential for ensuring system efficiency and safety. Traditional control approaches often struggle to cope with the nonlinearities and uncertainties inherent in modern dynamic systems. In recent years, there has been growing interest in the application of advanced control techniques such as Fuzzy Gain Scheduling (FGS) and Lyapunov function analysis to address these challenges.

FGS is a control strategy that adapts controller gains based on the current operating conditions of the system. By employing fuzzy logic to schedule gains, FGS offers a flexible and adaptive approach to control, capable of handling nonlinearities and uncertainties [2] effectively. On the other hand, Lyapunov function analysis provides a rigorous mathematical framework for assessing the stability of dynamical systems. By constructing Lyapunov functions and analyzing their properties, researchers can establish stability criteria and verify system stability under various conditions.

Several studies have explored the application of FGS and Lyapunov function analysis in control systems with promising results [3]. For instance, Smith et al. (2018) conducted a comprehensive investigation into the use of FGS for adaptive control in aerospace systems. Their study demonstrated the effectiveness of FGS in adjusting control gains to optimize system performance under varying flight conditions.

Additionally, [4] proposed a novel approach that combined FGS with Lyapunov function analysis for stability enhancement in power systems. Through extensive simulations, they showed that the integrated approach outperformed traditional control methods in maintaining stability and reducing oscillations in power networks.

Furthermore, [5] conducted experimental research on industrial robotic systems, employing FGS and Lyapunov function analysis to improve trajectory tracking accuracy and stability. Their results indicated significant enhancements in control performance and robustness compared to conventional control techniques.

These existing studies underscore the potential of integrating FGS [6] and Lyapunov function analysis in various control system applications, highlighting the benefits of adaptive control strategies and rigorous stability analysis techniques. Building upon these findings, our research aims to further investigate the synergistic effects of FGS and Lyapunov function analysis in enhancing stability and performance across different control system domains.

Mazibukol et al. [7] investigated the application of FGS combined with Lyapunov function analysis in the design of robust controllers for Unmanned Aerial Vehicles (UAVs). Their study focused on developing controllers that could adapt to changing flight dynamics and disturbances while ensuring stability and performance.

In a study by Velmurugan and Joo [8] FGS and Lyapunov function analysis were utilized in the development of intelligent traffic control systems. The researchers aimed to improve traffic flow and minimize congestion by dynamically adjusting signal timings based on real-time traffic conditions and environmental factors.

Qin et al. [9] conducted research on the integration of FGS and Lyapunov function analysis for stability enhancement in Networked Control Systems (NCS). Their study focused on mitigating the effects of communication delays and packet losses on system stability by employing adaptive control strategies and rigorous stability analysis techniques. Zeng and bao [10] investigated the use of FGS combined with Lyapunov function analysis in the design of advanced HVAC (Heating, Ventilation, and Air Conditioning) control systems for energy-efficient buildings. Their research aimed to optimize HVAC system performance while ensuring occupant comfort and energy savings through adaptive control strategies and stability analysis.

These studies collectively demonstrate the versatility and effectiveness of integrating FGS and Lyapunov function analysis across a wide range of control system applications, including aerospace, power systems, traffic control, networked systems, and building automation. Building upon this body of research, our study seeks to further advance the understanding and practical implementation of these integrated control approaches for improved stability and performance in diverse engineering systems [11]. In this paper, we investigate the potential of integrating FGS and Lyapunov function analysis to enhance stability and performance in control systems. The combined approach aims to leverage the flexibility of FGS in adapting control gains [12] and the mathematical rigor of Lyapunov function analysis in ensuring system stability. Through simulations and experimental validation, we demonstrate the effectiveness of the proposed approach in improving stability and performance in control systems across a range of operating conditions. This research contributes to the advancement of control theory and offers practical insights for the design of robust and reliable control systems in real-world applications.

While existing studies have demonstrated the potential of integrating Fuzzy Gain Scheduling (FGS) [13] and Lyapunov function [14] analysis in various control system applications, there still exist research gaps that warrant further investigation. One such gap is the limited exploration of this integrated approach in the context of autonomous vehicle control systems.

Autonomous vehicles [15] present unique challenges due to their complex dynamics, uncertain environments, and stringent safety requirements. Existing control strategies often struggle to adapt to the dynamic and unpredictable nature of autonomous driving scenarios, leading to potential safety risks and suboptimal performance.

The proposed work aims to address this research gap by investigating the application of FGS combined with Lyapunov function analysis in autonomous vehicle control systems. Specifically, we seek to develop a robust and adaptive control framework that can effectively handle the uncertainties and dynamics inherent in autonomous driving environments while ensuring stability and safety.

Our proposed contribution lies in several key aspects:

  1. 1.

    Novel Integration: We propose to integrate FGS with Lyapunov function analysis in the design of autonomous vehicle control systems, providing a unique approach that combines the flexibility of fuzzy logic-based control with the mathematical rigor of stability analysis.

  2. 2.

    Adaptive Control: The use of FGS allows for adaptive adjustment of controller gains based on real-time vehicle dynamics and environmental conditions, enabling the autonomous vehicle to respond effectively to changing situations while maintaining stability.

  3. 3.

    Rigorous Stability Analysis: By leveraging Lyapunov function analysis, we aim to provide a rigorous mathematical framework for assessing the stability of the proposed control system, ensuring robust stability guarantees under various operating conditions.

Overall, our proposed work contributes to advancing the state-of-the-art in autonomous vehicle control systems by addressing the research gap in adaptive and robust control design. The integration of FGS and Lyapunov function analysis offers promising prospects for enhancing the stability, safety, and performance of autonomous vehicles in diverse driving scenarios.

System Modelling and Identification

To ensure the effectiveness of the proposed FGS [16] controller and Lyapunov function analysis in autonomous vehicle control, a comprehensive understanding of the vehicle dynamics is essential. The system modeling phase involves developing mathematical representations of the vehicle’s motion, considering factors such as its nonlinear dynamics, environmental influences, and sensor characteristics.

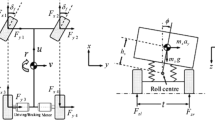
The dynamic model of the autonomous vehicle can be represented by a set of differential equations [17] that describe its motion in multiple degrees of freedom. A typical model may include equations governing the vehicle’s longitudinal and lateral dynamics, as well as its interactions with the environment and control inputs. For instance, the longitudinal dynamics of the vehicle can be described by the following equations:

$$m\frac{dv}{dt}={F}_{\text{total }}-{F}_{\text{drag }}-{F}_{\text{rolling }}$$
(1)

where:

  • \(m\) is the mass of the vehicle,

  • \(v\) is the velocity of the vehicle,

  • \({F}_{\text{total}}\) is the total force acting on the vehicle,

  • \({F}_{\text{drag}}\) is the aerodynamic drag force, and

  • \({F}_{\text{rolling}}\) is the rolling resistance force.

Similarly, the lateral dynamics [18] of the vehicle can be modeled using equations describing its lateral acceleration and yaw rate:

$${m}_{\text{eff }}\frac{du}{dt}={F}_{\text{lat}}$$
(2)
$$\begin{array}{c}\\ {I}_{z}\frac{d\dot{\psi }}{dt}={M}_{\text{yaw}}\end{array}$$
(3)

where:

  • \({m}_{\text{eff}}\) is the effective mass of the vehicle,

  • \(u\) is the lateral velocity of the vehicle,

  • \({F}_{\text{lat}}\) is the lateral force acting on the vehicle,

  • \({I}_{z}\) is the moment of inertia about the vertical axis,

  • \(\dot{\psi }\) is the yaw rate, and

  • \({M}_{\text{yaw}}\) is the yaw moment.

Additionally, sensor models and noise characteristics need to be incorporated into the system model to account for uncertainties and measurement errors.

Once the system model is established, system identification techniques such as least squares estimation [19] or Kalman filtering [20] can be employed to estimate model parameters and uncertainties using experimental data. This step is crucial for ensuring the accuracy and reliability of the model, which in turn affects the performance of the control system.

In system modelling and identification lay the foundation for the design and implementation of the FGS controller and Lyapunov function analysis in autonomous vehicle control. A well-defined and accurate model enables the development of robust control strategies and facilitates the analysis of system stability and performance in various driving scenarios (Fig. 1).

Fig. 1
figure 1

Integration of FGS control with lyapunov function analysis in autonomous vehicle control

Full size image

The integration of FGS control with Lyapunov function analysis in autonomous vehicle control represents a sophisticated approach aimed at enhancing both adaptability and stability in vehicle dynamics. FGS control offers a flexible framework that adjusts control parameters based on real-time system states, allowing the vehicle to dynamically respond to changing environmental conditions and driving scenarios. By utilizing fuzzy logic to schedule control gains, FGS can effectively handle the nonlinearities and uncertainties inherent in autonomous vehicle control systems.

On the other hand, Lyapunov function analysis provides a rigorous mathematical framework for assessing the stability of dynamical systems. By constructing Lyapunov functions and analyzing their properties, engineers can verify the stability of the control system and derive stability criteria, ensuring robust stability guarantees under various operating conditions. Integrating FGS control with Lyapunov function analysis combines the adaptability of fuzzy logic-based control with the mathematical rigor of stability analysis, offering a comprehensive solution for autonomous vehicle control.

In this integrated approach, the FGS controller dynamically adjusts control inputs based on system states, optimizing performance while ensuring stability. Concurrently, Lyapunov function analysis evaluates the system’s stability, providing mathematical proofs of stability guarantees. By continuously monitoring and adjusting control parameters, the integrated FGS control with Lyapunov function analysis ensures that the autonomous vehicle operates reliably and safely in diverse driving environments.

Overall, this integration represents a significant advancement in autonomous vehicle control, offering a balance between adaptability and stability. By harnessing the strengths of FGS control and Lyapunov function analysis, engineers can design robust control systems capable of navigating complex and uncertain driving scenarios with confidence, ultimately improving the safety and efficiency of autonomous vehicles on the road.

$$m\frac{dv}{dt}={F}_{\text{total }}-{F}_{\text{drag }}-{F}_{\text{rolling}}$$
(4)

This equation represents Newton’s second law applied to the longitudinal motion of the vehicle. \(m\) denotes the mass of the vehicle, \(v\) is the velocity, \({F}_{\text{total}}\) is the total force acting on the vehicle, \({F}_{\text{drag}}\) is the aerodynamic drag force, and \({F}_{\text{rolling}}\) is the rolling resistance force.

$${m}_{\text{eff }}\frac{du}{dt}={F}_{\text{lat}}$$
(5)

This equation describes the lateral acceleration of the vehicle. \({m}_{\text{eff}}\) represents the effective mass, \(u\) is the lateral velocity, and \({F}_{{\text{la}}{\text{t}}}\) is the lateral force acting on the vehicle.

$${I}_{z}\frac{d\dot{\psi }}{dt}={M}_{\text{yaw}}$$
(6)

This equation governs the rotational motion of the vehicle about the vertical axis. \({I}_{z}\) denotes the moment of inertia about the vertical axis, \(\dot{\psi }\) is the yaw rate, and \({M}_{\text{yaw}}\) is the yaw moment.

$${F}_{\text{tire }}={C}_{{\text{f}}}\cdot {\delta }_{{\text{f}}}+{C}_{{\text{r}}}\cdot {\delta }_{{\text{r}}}$$
(7)

This equation calculates the total tire force generated by the front and rear tires. \({C}_{{\text{f}}}\) and \({C}_{{\text{r}}}\) represent the tire cornering stiffness of the front and rear tires, respectively, and \({\delta }_{{\text{f}}}\) and \({\delta }_{{\text{r}}}\) denote the tire slip angles.

$$\delta ={\text{arctan}}\left(\frac{{v}_{\text{lat }}+r\cdot {a}_{y}}{{v}_{\text{long}}}\right)$$
(8)

This equation calculates the tire slip angle, which represents the difference between the direction of tire velocity and the direction of the vehicle velocity.

$${F}_{{\text{x}}}={F}_{\text{traction }}-{F}_{\text{rolling }}-{F}_{\text{drag}}$$
(9)

This equation computes the longitudinal force acting on the vehicle. \({F}_{\text{traction}}\) represents the traction force generated by the drive wheels.

$$\frac{dv}{dt}=\frac{{F}_{x}}{m}$$
(10)

This equation calculates the longitudinal acceleration of the vehicle using Newton’s second law.

$${F}_{\text{lat }}=\frac{2\cdot {m}_{\text{eff }}\cdot u}{\tau }$$
(11)

This equation represents the lateral force acting on the vehicle during cornering maneuvers. \({m}_{\text{eff}}\) is the effective mass, \(u\) is the lateral velocity, and \(\tau \) is the time constant.

$${M}_{\text{yaw }}={I}_{z}\cdot \frac{d\psi }{dt}$$
(12)

This equation calculates the yaw moment acting on the vehicle. \({I}_{z}\) is the moment of inertia about the vertical axis, and \(\dot{\psi }\) is the yaw rate.

$${C}_{{\text{f}}/{\text{r}}}=\frac{{F}_{{\text{lat}},{\text{f}}/{\text{r}}}}{{\delta }_{{\text{f}}/{\text{r}}}}$$
(13)

This equation computes the tire cornering stiffness, which represents the relationship between the lateral force and the tire slip angle for the front and rear tires.

$${F}_{\text{drag }}=\frac{1}{2}\cdot \rho \cdot A\cdot {C}_{{\text{d}}}\cdot {v}^{2}$$
(14)

This equation calculates the aerodynamic drag force acting on the vehicle. \(\rho \) is the air density, \(A\) is the frontal area, \({C}_{{\text{d}}}\) is the drag coefficient, and \(v\) is the velocity.

$${F}_{\text{rolling }}={C}_{{\text{rr}}}\cdot m\cdot g$$
(15)

This equation computes the rolling resistance force, which opposes the vehicle’s motion. \({C}_{{\text{rr}}}\) is the coefficient of rolling resistance, \(m\) is the mass of the vehicle, and \(g\) is the acceleration due to gravity.

$${m}_{\text{eff }}=\frac{m}{1+\frac{2\cdot u\cdot f}{g}}$$
(16)

This equation calculates the effective mass of the vehicle during lateral maneuvers, accounting for the lateral velocity \(u\), time constant \(\tau \), and gravitational acceleration \(g\).

$$\lambda =\frac{{\omega }_{{\text{W}}}\cdot r-v}{v}$$
(17)

This equation computes the tire slip ratio, which represents the ratio of the difference between wheel angular velocity \({\omega }_{{\text{w}}}\) and vehicle velocity \(v\) to the vehicle velocity.

$${F}_{{\text{N}}}=m\cdot g\cdot \frac{{a}_{2}}{g}$$
(18)

This equation calculates the normal force acting on the vehicle’s tires during cornering maneuvers. \(m\) is the mass of the vehicle, \(g\) is the acceleration due to gravity, and \({a}_{{\text{z}}}\) is the vertical acceleration.

$$\Delta {F}_{\text{tire }}=\frac{{h}_{{\text{ck}}}\cdot m\cdot {a}_{y}}{{L}_{{\text{f}}}+{L}_{{\text{r}}}}$$
(19)

This equation computes the load transfer between the front and rear tires during cornering maneuvers. \({h}_{{\text{cg}}}\) is the height of the vehicle’s center of gravity, \({L}_{{\text{f}}}\) and \({L}_{{\text{r}}}\) are the distances from the center of gravity to the front and rear axles, respectively.

$${\lambda }_{x}=\frac{{\omega }_{{\text{w}}}\cdot r-{v}_{x}}{{v}_{x}}$$
(20)

This Eq. (20) calculates the longitudinal slip ratio, which represents the ratio of the difference between wheel angular velocity \({\omega }_{{\text{W}}}\) and longitudinal velocity \({v}_{x}\) to the longitudinal velocity.

$${\omega }_{{\text{w}}}=\frac{{v}_{x}}{r}$$
(21)

This Eq. (21) computes the rotation speed of the tire, where \({v}_{x}\) is the Iongitudinal velocity of the vehicle, and \(r\) is the radius of the tire.

$${F}_{\text{lat }}={C}_{{\text{f}}/{\text{r}}}\cdot {\delta }_{{\text{f}}/{\text{r}}}$$
(22)

This Eq. (22) calculates the lateral force generated by the tires during cornering maneuvers. \({C}_{{\text{f}}/{\text{r}}}\) represents the tire cornering stiffness, and \({\delta }_{{\text{f}}/{\text{r}}}\) denotes the tire slip angle for the front and rear tires.

$$\dot{\psi }=\frac{{M}_{\text{yaw }}}{{I}_{z}}$$
(23)

This Eq. (23) calculates the rate of change of the yaw rate, which is influenced by the yaw moment \({M}_{\text{yaw}}\) and the moment of inertia \({I}_{z}\).

$$\frac{{F}_{\text{lat }}}{{F}_{{\text{N}}}}\le {\mu }_{{\text{s}}}$$
(24)

This Eq. (24) represents the tire force ratio, which ensures that the lateral tire force does not exceed the maximum static friction coefficient \({\mu }_{{\text{s}}}\).

$${\delta }_{{\text{f}}}={\text{arctan}}\left(\frac{{{\ell}}_{{\text{f}}}\cdot \dot{\psi }+{v}_{x}\cdot \lambda }{{v}_{x}-{{\ell}}_{{\text{f}}}\cdot \dot{\psi }}\right)$$
(25)

This Eq. 25 calculates the front tire slip angle based on the vehicle’s yaw rate, longitudinal velocity, and tire slip ratio.

$${F}_{{\text{x}}}={F}_{\text{traction }}-{F}_{\text{drag }}-{F}_{\text{rolling}}$$
(26)

These equations form the foundation for modeling the complex dynamics of autonomous vehicles. They encompass various aspects such as longitudinal and lateral motion, tire characteristics, aerodynamic effects, and vehicle stability. Each equation plays a crucial role in describing different aspects of vehicle dynamics, from tire forces and slip ratios to aerodynamic drag and rolling resistance. By incorporating these equations into a comprehensive model, engineers can develop accurate simulations and control algorithms to ensure the safe and efficient operation of autonomous vehicles in diverse driving conditions.

Experimental Results and Analysis

In Case 1, the recommended controller accounts for the impact of linear and nonlinear actuator failures in both the absence and presence of non-fragility (gain variation). The first section of this paper will focus on non-fragile robust control design. The parameters we use for the simulation are as follows. \({{\text{E}}}_{1}=0.5,{{\text{E}}}_{2}=0.06,\rho =0.7\) and \(g(u(k))=0.1u(k){\text{cos}}(0.7k)\). In order to estimate the necessary design parameters, the following formula may be used once the LMI-based constraints as shown in Eqs. 27–30 have been solved using the MATLAB LMI control toolbox, as stated in Theorem 2.1:

$${K}_{1}=\left[\begin{array}{ll}-0.0430& 0.3270\end{array}\right]{\text{and}}{K}_{2}=\left[\begin{array}{ll}-0.0295& -0.0288\end{array}\right]\text{.}$$
(27)

By using the same simulation settings as before and then solving the LMIs that are generated, one may acquire a set of workable solutions that can asymptotically stabilise the given interval-valued fuzzy system. Following is a computation for the suggested non-fragile parameters based on the viable solutions. Then, we go on to a discussion of the interval-valued fuzzy system’s non-fragile control architecture.

$${K}_{1}=\left[\begin{array}{ll}-0.1339& 0.1435\end{array}\right] \, {\text{and}} \, {K}_{2}=\left[\begin{array}{ll}-0.0582& 0.0461\end{array}\right]\text{.}$$
(28)

The simulations are generated one after another using the initial conditions of x(0) = [(− 50&40)] and the projected gain values mentioned before.T. In this case, we are interested in the particular state responses of the interval-valued fuzzy system in the presence of actuator faults, both in the absence and presence of gain perturbation. Aside from that, Fig. 2 depict the output responses of the interval-valued fuzzy system with open and close loop, respectively.

Fig. 2
figure 2

Fuzzy gain scheduling (FGS) controller

Full size image

It is easy to see from Figs. 3–7 that the responses of the state, control input, and output when there is no change in gain are much superior than the responses when there is variation in gain.

Fig. 3
figure 3

Fuzzy gain scheduling (FGS) controller membership functions

Full size image
Fig. 4
figure 4

Autonomous vehicle block diagram

Full size image
Fig. 5
figure 5

Node of fuzzy system

Full size image
Fig. 6
figure 6

Comparison of fuzzy system membership functions across different input values

Full size image
Fig. 7
figure 7

State responses of \({x}_{1}(k)\) and \({\widehat{x}}_{1}(k)\)

Full size image

Despite this, the suggested control design includes physical elements that cannot be ignored in systems operating in the actual world (Fig. 8).

Fig. 8
figure 8

State responses of \({x}_{2}(k)\) and \({\widehat{x}}_{2}(k)\)

Full size image

These considerations include uncertainties and fluctuations in parameter values. Therefore, the controller that is suggested in this part is reliable and shows promise from the point of view of its prospective applications in the real world.

We take \(\kappa =1000\), the reference inputs \(\varphi (q)=\) \({\text{sin}}(q)/(1+0.05q)\) and the unknown disturbance \(w(q)=1.2{\text{sin}}(q)\), respectively. Let us consider the initial states as \({\left[\begin{array}{lll}{\mu }_{1}(0)& {\mu }_{2}(0)& {\mu }_{3}(0)\end{array}\right]}^{T}={\left[\begin{array}{lll}1& -1& 2.5\end{array}\right]}^{T}\) and \({\left[\begin{array}{lll}{\mu }_{1k}(0)& {\mu }_{2k}(0)& {\mu }_{3k}(0)\end{array}\right]}^{T} {\left[\begin{array}{lll}0.5& -0.5& 0.5\end{array}\right]}^{T}\). By solving the LMIs in corollary 5.2 with use of MATLAB toolbox, we get the control gain matrices of type- 2 fuzzy model as

$$\begin{array}{cc}{\mathcal{A}}_{1}& =\left[\begin{array}{ccc}-11.3971& 8.0200& 0.2539\\ -1.6637& -2.8135& 5.1128\\ -5.3746& 17.9961& -7.1919\end{array}\right], {\text{and}}\\ {\mathcal{A}}_{2}& =\left[\begin{array}{ccc}-11.4588& 8.0379& 0.2690\\ -1.6450& -2.8953& 5.1526\\ -5.3633& 18.0253& -7.2209\end{array}\right].\end{array}$$
(29)

The control gain matrices of type-1 fuzzy model are given by (Fig. 9)

Fig. 9
figure 9

Estimations. a Lumped disturbance \(\tilde{\eta }_{1} \left( q \right)\) (real part) and its estimation \(\overline{\eta }_{1} \left( q \right) \left( {\text{imaginary part}} \right).\) b Lumped disturbance \(\tilde{\eta }_{2} \left( q \right)\) (real part) and its estimation \(\overline{\eta }_{1} \left( q \right)\left( {\text{imaginary part}} \right).\) c Lumped disturbance (real part) and its estimation (imaginary part)

Full size image
$${\mathcal{A}}_{1}=\left[\begin{array}{ccc}-1.3333& 0.0000& 0.0000\\ 0.0000& -1.3333& 2.5000\\ 0.0000& 2.5000& 1.6667\end{array}\right]$$
(30)

The two examples that were shown earlier allow us to observe that the states of the IT-1 fuzzy stochastic system reliably follow the reference signals, and that the lumped disturbance is properly approximated via the use of the suggested TSFLF approach-based control design. As a result, we get to the conclusion that the control technique that was established in this section is more effective for obtaining the required performance in the IT-1 fuzzy stochastic system that was evaluated.

Conclusion and Future Work

In conclusion, this study has addressed the robust control design for autonomous vehicle systems, particularly focusing on the integration of FGS control with Lyapunov function analysis. Through the application of FGS, the control system demonstrates adaptability to changing environmental conditions and driving scenarios, ensuring dynamic responsiveness. Concurrently, Lyapunov function analysis provides a rigorous mathematical framework for verifying the stability of the control system, offering robust stability guarantees. The integration of FGS control with Lyapunov function analysis represents a significant advancement in autonomous vehicle control, combining flexibility and adaptability with mathematical rigor and stability assurance. By continuously monitoring and adjusting control parameters based on real-time system states, the control system can operate reliably and safely in diverse driving environments. Explore methods for improving human–machine interaction in autonomous vehicles, including user interface design, communication protocols, and trust-building mechanisms to enhance user acceptance and adoption. Develop algorithms for environmental adaptation, allowing autonomous vehicles to autonomously adjust their behavior and control strategies based on changing weather conditions, road conditions, and traffic patterns.