1 Introduction

Nowadays, fears of environmental pollution and high fuel prices are the interest of researchers in alternative energy sources. These fears led to the development of hybrid electric vehicles (HEVs) with the benefits of electric traction engines in terms of providing rapid acceleration and internal combustion engines in terms of good work at fixed speeds. This technology leads to a reduction in fuel consumption and gas emissions from vehicle exhausts [1].

With the recent focus by many vehicle manufacturers on hybrid vehicles, the stability and handling of these vehicles have become an exciting research area. When the tires reach their physical limit of adhesion, the vehicle may move in a different direction than intended when turning [2]. Although the antilock braking system (ABS) can avoid wheel locking during braking and the traction control system (TCS) can avoid steering wheel spin during acceleration, they cannot actively control the directional movement of the vehicle. Hence, the critical need to enhance the vehicle’s stability and handling performance [3, 4]. Therefore, the primary motivation of this paper lies in enhancing the lateral stability of HEVs during cornering. The direct yaw control (DYC) system is therefore built to track the intended vehicle yaw rate, which limits the vehicle sideslip angle. The DYC system produces corrective yaw moment by differential braking between the left and right tires [5].

Utilizing this hydraulic braking technology has the significant drawback of impairing longitudinal dynamics and reducing longitudinal vehicle velocity. Since it is easy to control both the driving and braking torque of an electric motor, this type of vehicle has two electric motors built into the rear wheels. The two motors on each side of the vehicle produce opposite forces, which creates the corrective yaw moment, which makes the vehicle stable by controlling the torque of each motor separately [6, 7].

There is a great deal of literature covering vehicle yaw stability control. Model predictive control [8], sliding mode control [9], adaptive control [10], optimal control [11], robust control [12]. The desired yaw moment was calculated using all of them. Kang et al. [13] developed a driving control algorithm for a four-wheel drive electric vehicle with two independent controllers of braking and torque of the front and rear drive motors to enhance vehicle handling. In [14], Mashadi and Majidi devised a multilayer sliding mode controller that integrates the active front steering (AFS) and DYC systems to generate the final braking torque via two electric motors in the rear wheels based on the corrective steering angle and yaw moment. Feng et al. [15] proposed a multilayer hierarchical approach for improving the stability of vehicles during corners by employing four-wheel differential braking. The upper-level control tracks the desired vehicle motion based on the sliding mode control theory by calculating the desired yaw moment and longitudinal forces. At the lower layer, operator commands are distributed optimally. Kazemi et al. [16, 17] used the yaw rate error and its derivative to get the required yaw moment. Their research uses a neural network to produce the standard yaw rate. Additionally, they suggested a fuzzy control technique in which the slip ratio error and its derivative serve as fuzzy slip controller inputs to protect the tire from saturation.

The fuzzy control method is based on human expertise, is simple to design and implement, and has outstanding control performance due to its structure, low computational complexity, and simplicity. Additionally, fuzzy logic control (FLC) can benefit uncertain nonlinear systems [18]. Therefore, fuzzy control is a powerful technology that can be applied to various applications, such as the operation and control of electric power systems [19], robotics [20, 21], gyroscopes [22, 23], industrial process control [24, 25], and image processing [26]. This type of control has recently attracted the attention of researchers and designers in the field of vehicle control, and several studies on fuzzy control devices for vehicle stability control have been published in the scientific literature related to vehicle systems. Boada et al. [27] used a fuzzy control strategy to improve a vehicle’s lateral stability in different road conditions. There are two levels to the proposed control structure. A corrective yaw moment is designed through the upper control layer, converted into braking torque, and distributed to the front wheels in the lower control layer. Zhang et al. [28] applied an adaptive fuzzy-PID control to obtain the corrective yaw moment. Although the fuzzy-PID controller is self-tuned, its response to input steering angle changes has not been robust, resulting in significant yaw rate and sideslip angle oscillations. Li et al. [29] used PID and fuzzy logic methods for the DYC system. All control strategies were designed using the 2-DOF vehicle, which is so far from the actual vehicle model that the reference steering angle tracking was inaccurate. Furthermore, only the J-turn maneuver with a constant tire-road friction coefficient has been considered in this research to evaluate the proposed control strategy. Haiying et al. [30] applied the fuzzy logic algorithm for the DYC system to improve vehicle stability in a straight line under the crosswind. The DYC system developed in this article can reduce yaw rate amplitude and enhance the vehicle’s straight-line stability. However, the driver’s velocity control is the key to enhancing the vehicle’s safety in crosswinds. Bayar et al. [31] used the fuzzy controller in order to generate the yaw moment to improve lateral vehicle stability for hybrid electric vehicles that use axle electric motors.

Recently, advanced types of fuzzy controllers have been used in vehicle stability due to the development of fuzzy controllers. In [32], using non-stationary fuzzy sets, Mohammadzadeh and Taghavifar presented a novel non-singleton fuzzy system designed to enhance the estimation performance of conventional fuzzy systems and reduce the computational expense of type 2 fuzzy systems. Under a wide range of operating conditions and external disturbances, the proposed control strategy has been demonstrated to be effective for autonomous vehicles to follow paths, despite the inability to restrict control signals. A fuzzy control method for lateral dynamic stabilization of autonomous electric vehicle systems based on adaptive event-triggered dynamic output feedback interval type-2 (IT-2 T-S) is presented in [33], which takes into account nonlinear tire dynamics and changes in longitudinal velocity over time. Tian et al. [34] developed a novel type 3 fuzzy controller that is not based on the mathematical model of autonomous road vehicles (ARV) but is optimized online by adaptation rules. Type 3 FLSs with online adaptation rules have been proposed to handle uncertainties and estimation errors estimated by the suggested adaptation laws. Adaptive supervisors compensate for these uncertainties. The results show that the ARV tracks the desired trajectory with an acceptable lateral displacement and that the proposed controller resists changing longitudinal velocity. Taghieh et al. [35] proposed robust control laws based on a type 3 fuzzy logic system (IT3FLS) to analyze the path tracking control (PFC) problem of an underactive surface vehicle (USV). Predictive compensations were used to address the main limitations of the single fuzzy controller regarding the approximation ability of the uncertainties and external perturbations of the complex nonlinear USV. The results showed the proposed control strategy’s effectiveness in solving the PFC problem and improving USV trajectory tracking performance in the presence of more complex unknown dynamic models and external perturbations.

On the other hand, despite the FLC structure’s simplicity, human experiments cannot synthesize the optimal FLC. Due to their exceptional ability to address optimization problems in various applications, heuristic-inspired algorithms have garnered significant attention over the past several decades. Many fuzzy controller optimization methods have been applied in the literature, such as particle swarm optimization (PSO) [36], genetic algorithm (GA) [37], bat algorithm [38], ant algorithm [39], and cuckoo search (CS) [40]. However, recent studies have shown that (COA) is potentially more efficient than other algorithms in solving fuzzy controller parameter optimization problems [41].

Following a review of the literature on FLC parameter optimization using the COA algorithm, some work will be described briefly. Einan et al. [42] proposed a novel intelligent method for active power controllers in isolated networks using a combination of fuzzy controller and cuckoo optimization algorithm (COA) techniques to overcome the phenomenon of drooping under varying weather conditions. The optimized coefficients in this paper include fuzzy controller input–output gains. However, optimizing the fuzzy controller’s membership functions was not considered. Gabriel et al. [43] presented an optimization procedure based on the CS algorithm for optimizing the FLC’s membership function and the rule base for a nonlinear magnetic levitation system. However, this paper did not notice optimizing the fuzzy controller input–output gains. In [44], a multi-robot 3D mooring force (MFFC) (pulse, sway, and yaw) system was developed to dampen the motion of the moored ship. The COA optimizes the MFFC output factor to reduce the driving force difference between different robot actuators caused by the line distribution of mooring robots along the quay. However, optimizing the fuzzy controller’s membership functions was not considered. In [45], presented a comparative performance analysis of three popular metaheuristic algorithms; particle swarm optimization (PSO), BAT algorithm, and cuckoo search (CS), which are applied to control a quadrotor system’s attitude by optimizing the distribution of the singleton output membership functions. However, this paper did not consider the optimization of input Membership Functions and Input and output gains of the controller.

Based on a review of the presented literature, which showed different applications of vehicle stability control, no studies were found on cuckoo-based optimal fuzzy control of hybrid electric vehicle stability to reduce the effect of parameter changes. This paper aims to use the new methodology for FLC parameter optimization using COA, including the membership functions and the input–output gains of the fuzzy controller, to tackle the problem of unknown changes in lateral vehicle dynamics during single lane-change and J-turn maneuvers at high speeds.

The proposed control system consists of a two-layer structure. The corrective yaw moment is obtained in the upper layer by cuckoo-based optimal fuzzy control to track the desired vehicle’s yaw rate and sideslip angle and maintain the sideslip angle at a smaller value than required. In the lower layer, the yaw moment is directly turned into the braking torque of the two electric motors built into the rear wheels. A distribution algorithm applies the braking torque to the rear wheels to produce the yaw moment required for stability. Additionally, the controller was tested in several situations where the vehicle’s mass, the moment of inertia, the tire stiffness, and the road-tire friction coefficient were altered as uncertainties to produce robust control over the changes in these parameters.

The main contribution of this study is outlined in the following points:

  • Various studies applying the cuckoo algorithm to optimize fuzzy control parameters have been shown. However, no studies have been found to optimize both fuzzy controller membership functions and their input–output gains to generate the yaw moment control for the lateral stability of hybrid electric vehicles.

  • Tire forces do not occur instantly due to a specific slip ratio but take time to build up when a force is applied to a tire. At high speeds and critical maneuvers, such as avoiding obstacles or hard braking, delays in transmitting forces to the tires can result in vehicle control loss. For simplicity, most control research ignores this delay. While this paper uses a typical dynamical model to express this delay by applying a first-order delay to the lateral forces.

  • Most previous studies considered parametric uncertainties in vehicle parameters such as total mass, moment of inertia, and tire stiffness. Whereas in this research, the road tire friction coefficient and those parameters were included in the vehicle model as uncertainties to evaluate the performance of the COA in improving vehicle stability in uncertainties.

Finally, the rest of the paper is organized as follows: Sect. 2 presents the vehicle dynamics model to support the development of this research. Section 3 presents the hierarchical control structure. The simulation results and discussion are discussed in Sect. 4. Finally, the conclusion is presented in Sect. 5.

2 Vehicle dynamics model

This section uses two vehicle models: a nonlinear 8-DOF vehicle to design the optimal fuzzy controller and for results simulation and a 2-DOF model to generate the desired yaw rate and sideslip angle.

2.1 8-DOF vehicle model

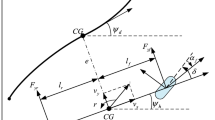
Figure 1 depicts the general architecture of a nonlinear 8-DOF vehicle model with two additional electric motors implanted in free-rolling rear wheels. The longitudinal velocity \(u\), the lateral velocity \(v\), the yaw rate \(r\), and the roll rate \(\dot{\varnothing }\), according to Fig. 1, can be described as follows [27, 46].

$$ m\dot{u} = mvr + F_{{x1}} + F_{{x2}} + F_{{x3}} + F_{{x4}} - F_{{{\text{aero}}}} $$
(1)
$$ m\dot{v} = - mur - m_{{\text{s}}} h_{{\text{s}}} \ddot{\emptyset } + F_{{y1}} + F_{{y2}} + F_{{y3}} + F_{{y4}} $$
(2)
$$ I_{{zz}} \dot{r} = I_{{xz_{{\text{s}}} }} \ddot{\emptyset } + l_{{\text{f}}} \left( {F_{{y1}} + F_{{y2}} } \right) - l_{\rm r} \left( {F_{{y3}} + F_{{y4}} } \right) + M_{z} $$
(3)
$$ I_{{xx_{\rm s} }} \ddot{\emptyset } = - m_{{\text{s}}} h_{{\text{s}}} \dot{v} + I_{{xz_{{\text{s}}} }} \dot{r} - m_{{\text{s}}} h_{{\text{s}}} ur + m_{{\text{s}}} gh_{{\text{s}}} \sin \emptyset - K_{\emptyset } \emptyset - C_{\emptyset } \dot{\emptyset } $$
(4)

\({M}_{z}\) is the direct yaw moment and can be defined as

$${M}_{z}=\frac{T}{2}\left[\left({F}_{x1}+{F}_{x3}\right)-({F}_{x2}+{F}_{x4})\right]$$
(5)

The rotational speed of each wheel (\({\omega }_{1},{\omega }_{2},{\omega }_{3},{\omega }_{4}\)) can be modeled from Fig. 2.

$$ I_{{\text{w}}} \dot{\omega }_{i} = - R_{{\text{w}}} F_{{ti}} + T_{{bi}} \;{\text{with}}\;i = 1, \ldots ,4. $$
(6)

\({F}_{xi}\) and \({F}_{yi}\) are the longitudinal and lateral forces of tires in the vehicle fixed, respectively. \({F}_{\rm aero}\) Indicate the aerodynamic drag forces are by [46, 47]:

$$ F_{{{\text{aero}}}} = 0.5\rho _{{\text{a}}} C_{{\text{d}}} A_{{\text{f}}} u^{2} $$
(7)
Fig. 1
figure 1

8-DoF vehicle dynamics model [48]

Full size image
Fig. 2
figure 2

Diagram of wheel-free

Full size image

Table 1 lists the parameters used in the simulation and equations for vehicle dynamics.

Table 1 Vehicle and electric motor parameters [14, 27, 46]
Full size table

Also, \(\varnothing\) is the roll angle of the vehicle, \({T}_{bi}\) are Four-wheel braking torque.

Tire forces are transferred from a fixed coordinate system of the tires to a fixed coordinate system of the vehicle according to the following equations:

$$ F_{{xi}} = F_{{ti}} \cos \delta _{i} - F_{{si}} \sin \delta _{i} \;{\text{with}}\;i = 1, \ldots ,4 $$
(8)
$$ F_{{yi}} = F_{{ti}} \sin \delta _{i} + F_{{si}} \cos \delta _{i} \;{\text{with}}\;i = 1, \ldots ,4 $$
(9)

where \(\delta\) is the vehicle’s steering angle, and \({F}_{\rm t}\) and \({F}_{\rm s}\) are the traction forces and the lateral forces of the tire in the wheel fixed coordinate system, respectively.

We have made the following assumptions in this paper:

  • For simplicity, the moment of inertia for roll and yaw is ignored.

  • The rear steering angles are considered to be zero.

  • The front and rear steering angles are impacted by the rolling motion of the vehicle body owing to suspension kinematics [47].

$${\delta }_{1 }={\delta }_{2 }={\delta }_{sw}+{K}_{\rm rsf}.{\varnothing}$$
(10)
$${\delta }_{3 }={\delta }_{4 }={K}_{\rm rsr }.\varnothing$$
(11)

where \({\delta }_{\rm sw }\) is the steering angle of the handwheel.

2.2 Tire model

Different tire models, like the Dugoff, Magic Formula, and Brush models, can be used to explain how tires behave. As tires’ longitudinal and lateral forces are directly related to the road factor [5, 49], the Dugoff model was chosen to simulate the nonlinear tire system.

The following equations give the lateral and longitudinal tires generated by the Dugoff model:

$$\begin{aligned} {F}_{{{s}}_{i}}&=\frac{{C}_{{\upalpha }}\text{tan}\left({\alpha }_{i}\right)}{1-{{\uplambda }}_{i}}f\left({{s}}_{i}\right) i=1,\dots ,4\\{F}_{ti}&=\frac{{C}_{{\uplambda }}{{\uplambda }}_{i}}{1-{{\uplambda }}_{i}}f\left({{s}}_{i}\right) i=1,\dots ,4 \end{aligned}$$
(12)

Where

$$ f\left( {{{s}}_{i} } \right) = \left\{ {\begin{array}{*{20}l} {{{s}}_{i} \left( {2 - {{s}}_{i} } \right),} & {{{s}}_{i} < 1} \\ {1,} & {{{s}}_{i} \ge 1} \\ \end{array} } \right.\quad i = 1, \ldots ,4 $$
(13)

And

$${{s}}_{i}=\frac{\mu {F}_{zi}\left(1-{\varepsilon }_{\rm r}u \sqrt{{{\lambda }}_{i}^{2}+{\text{tan}}^{2}\left({\alpha }_{i}\right)}\right)}{2\sqrt{{C}_{{\uplambda }}^{2}{{\uplambda }}_{i}^{2}+{C}_{\alpha }^{2}{\tan}^{2}\left({\alpha }_{i}\right)}}\left(1-{{\uplambda }}_{i}\right) i=1,\dots ,4$$
(14)

\({{\lambda }}_{i}\) and \({\alpha }_{i}\) are the longitudinal slip ratio and slip angle of the tire road, respectively, given by the following relations [14, 50]:

$$ \lambda _{i} = \left\{ {\begin{array}{*{20}l} { - 1 + \frac{{R_{\rm w} \omega _{i} }}{{v_{{xwi}} }},} & {R_{\rm w} \omega _{i} < v_{{xwi}} } \\ {1 - \frac{{v_{{xwi}} }}{{R_{\rm w} \omega _{i} }},} & {R_{\rm w} \omega _{i} \ge v_{{xwi}} } \\ \end{array} } \right.\quad {\text{with}}\quad i = 1, \ldots ,4 $$
(15)
$${\alpha }_{i}={\delta }_{i}-{\tan}^{-1}\left(\left(v+{d}_{i}r)/(u-0.5{ \left(-1\right)}^{i} Tr\right)\right) i=1,\dots ,4 {d}_{i}=\left\{\begin{array}{c}{l}_{\rm f} i=1, 2\\ {l}_{\rm r }i={3,4}\end{array}\right.$$
(16)

The following equations give the longitudinal velocity of the wheels’ center \({ v}_{xwi}\):

$$ v_{{xwi}} = \left( {u - 0.5\left( { - 1} \right)^{i} Tr} \right)\cos \delta _{i} + \left( {v + d_{i} r} \right)\sin \delta _{i} \;i = 1, \ldots ,4 $$
(17)

\({F}_{z}\) is the normal load of each tire given by the following equations:

$${F}_{zi}=\frac{mg{l}_{\rm r}}{2 L}-\frac{m{a}_{x}h}{2 L}-{\left(-1\right)}^{i}{K}_{\rm rsf}\left(\frac{m{a}_{y}h}{T}-\frac{{m}_{\rm s}g{h}_{\rm s}}{T}\text{sin}{\varnothing}\right) i=1, 2$$
(18)
$${F}_{zi}=\frac{mg{l}_{f}}{2 L}+\frac{m{a}_{x}h}{2 L}-{\left(-1\right)}^{i}\left(1-{K}_{\rm rsf}\right)\left(\frac{m{a}_{y}h}{T}-\frac{{m}_{\rm s}g{h}_{\rm s}}{T}\text{sin}{\varnothing}\right) i=3, 4$$
(19)

Additionally, \({a}_{y}\) represents the vehicle’s lateral acceleration, while \(l\) represents the vehicle’s longitudinal wheelbase.

Tire force lag also plays a significant role in the lateral vehicle dynamics during high-acceleration maneuvers, so it was also applied as a first-order delay [14, 51].

$$ \tau \dot{F}_{{{\text{rms}}}} + F_{{\text{s}}} = F_{{{\text{s}}_{{{\text{ss}}}} }} $$
(20)

The lateral tire force \( F_{{{\text{rms}}_{{{\text{ss}}}} }} \) in the steady state during the time constant τ is given as

$$ \tau = {\text{RL}}_{y} /u $$
(21)

Motors embedded in the rear wheels produce the corrective yaw moment by controlling their braking or driving forces. Considering the reduction gear ratio \(n\) between the wheel and rotor of the electric motor embedded in the rear wheels, the rotating dynamic of the rear wheels and the rotor is derived as follows [14, 52]:

$$ I_{{{\text{eq}}}} \dot{\omega }_{i} = nT_{\rm e} - B_{{{\text{eq}}}} \omega _{i} - T_{{Li}} \;{\text{with}}\;i = 3,4 $$
(22)

In this equation, a motor’s electromagnetic torque is called \({ T}_{\rm e}\). \({I}_{\rm eq}\) is an equivalent moment of inertia, \({B}_{\rm eq}\) is the equivalent damping factor, and \({T}_{\rm L}\) is the equivalent load torque of wheel and rotor, which can be found in the following formulas:

$${I}_{\rm eq}={I}_{\rm w}+{n}^{2}{I}_{\rm m}$$
(23)
$${B}_{\rm eq}={n}^{2}{B}_{\rm m}$$
(24)
$${T}_{Li}={R}_{\rm w}{F}_{ti}$$
(25)

\({I}_{\rm m}\) and \({B}_{\rm m}\) are the rotating inertia of the motor and the damping coefficient, respectively.

2.3 Reference model

The 2-DoF vehicle model is used in this paper to calculate yaw rate and sideslip angle references. Figure 3 shows a 2-DOF vehicle model that includes lateral and yaw motions where small letters \((f,r)\) indicate the positions of the front and rear wheels. The proposed hierarchical controller will track the desired yaw rate. Furthermore, the desired sideslip angle will be nearly zero.

Fig. 3
figure 3

Framework of linear 2-DOF vehicle model

Full size image

The following formulas can be used to determine the vehicle’s desired yaw rate and sideslip angle [5, 50]:

$${r}_{\rm ss}=\frac{u}{l+{K}_{\rm US}{u}^{2}}{\delta }_{\rm f}$$
(26)
$${\beta }_{\rm ss}=\frac{1}{l+{K}_{\rm US}{u}^{2}}\left({l}_{\rm r}-\frac{{l}_{\rm f}}{l}\frac{m}{2{C}_{{\upalpha }r}}{u}^{2}\right){\delta }_{\rm f}$$
(27)

KUS is called the vehicle’s understeer coefficient given by Eq. (28):

$${K}_{\rm US}=\frac{m\left(b{C}_{{\upalpha }r}-a{C}_{{\upalpha }f}\right)}{2 {l C}_{{\upalpha }f}{C}_{{\upalpha }r}}$$
(28)

Along with the tire force, it is essential to know that the desired yaw rate and lateral slip angle cannot be reached if the tire force exceeds the tire’s physical adhesion limit. Equations (29) and (30) give the upper limits for the rate of yaw and the lateral slip angle.

$${r}_{\rm d}=0.85\frac{\mu g}{u}$$
(29)
$$ \beta _{\rm d} = {\text{arctan}}\left( {0.02\;\upmu g} \right) $$
(30)

The optimal fuzzy controller is designed to maintain a sideslip angle equal to or less than the desired value while tracking the desired yaw rate.

3 Proposed controller design

The proposed control system comprises two layers, an upper layer, and a lower layer. Based on the desired yaw rate \(\left({r}_{\rm d}\right)\) and sideslip \(\left({\beta }_{\rm d}\right)\) obtained from the 2-DoF vehicle model, the appropriate yaw moment (\({M}_{z}\)) in the upper layer is determined based on the optimal fuzzy controller. The lower layer applies the vehicle’s braking force distribution algorithm based on the upper layer’s control input. Figure 4 shows the hierarchical control system proposed.

Fig. 4
figure 4

Proposed vehicle control method structure

Full size image

3.1 High-layer controller design

In this section, due to the nonlinearity of the vehicle, fuzzy control technology was used to ensure the vehicle’s stability by tracking the yaw rate and maintaining the slip angle in the stability area. The cuckoo-based fuzzy controller produces the external yaw moment as a control input according to the difference between the reference and the measured yaw rate, the reference sideslip angle, and the observed sideslip angle.

The yaw rate and sideslip angle are signals sent to the control system. The gyroscope measures the yaw rate directly, unlike the sideslip angle, which must be measured using GPS or optical sensors, which is too expensive for typical vehicles. Since the lateral slip angle cannot be measured directly, it is estimated by a nonlinear observer [53].

3.1.1 Fuzzy controller

The fuzzy logic controller aims to increase lateral stability by tracking the desired yaw rate and decreasing the sideslip angle. Therefore, two error variables are applied to the upper-layer controller to generate the corrective yaw moment as an output of this level.

The Mamdani fuzzy controller generally consists of four major components, fuzzification, rule base, inference engine, and defuzzification [54], as shown in Fig. 5:

Fig. 5
figure 5

Fuzzy logic controller structure

Full size image

Inputs and outputs:

For the DYC controller, the first input of FLC is yaw rate error \(({e}_{\rm r}=r-{r}_{\rm d})\), which represents the error between the desired and actual yaw rate. The second input of the FLC is the sideslip angle error \(({e}_{\beta }=\beta -{\beta }_{\rm d})\), which represents the error between the desired and actual sideslip angle. The corrective yaw moment \({M}_{z}\) is defined as the controller output.

Fuzzification:

The fuzzification interface interprets and compares inputs with rule bases based on their modification. Input and output values are converted into membership variables and linguistic variables. There are five membership functions for each of the two input variables, including NB (negative big), NS (negative small), ZE (zero), PS (positive small), and PB (positive big). There are seven membership functions for the output variables, including NB (negative large), NM (negative middle), NS (negative small), ZE (zero), PS (positive small), PM (positive middle), and PB (positive large). Figure 2 shows fuzzy membership functions.

Inference engine:

The inference engine determines what input should be provided to the plant based on which control rules are appropriate at the time. The rule bases in Table 2 are introduced based on expert knowledge and extensive simulations.

Table 2 Fuzzy rules
Full size table

The fuzzy rule base is composed of the following fuzzy IF-THEN rules [55]:

IF \({\varvec{e}}_{\varvec{r}}\) is (A) and \({\varvec{e}}_{\varvec{\beta }}\) is (B) THEN \({\varvec{M}}_{\varvec{z}}\) is (C)

Where (A, B) are fuzzy sets in the input domains, and C is the output domain’s fuzzy set (Fig. 6).

Fig. 6
figure 6

The membership functions of the fuzzy controller for: a first input (\({e}_{\beta }\)), b second input (\({e}_{\rm r}\)), c output (\({M}_{Z}\))

Full size image

Defuzzification:

The defuzzification interfaces convert conclusions reached by the inference engine into inputs for the plant. In this paper, the center-of-area method was used for defuzzification.

3.1.2 Optimization

Fuzzy controller design generally depends on user information related to system performance understudies, such as the type and number of membership functions, fuzzy rules, or the number and type of inputs. It often takes a long time to determine the fuzzy control parameters and evaluate their quality, requiring many experiments. One of the most effective ways to find the most convenient control parameters, including membership function parameters, rules parameters, etc., is to use optimization algorithms.

Remark

An evolution-based algorithm can sometimes move in the direction of instability if used in an online control system. Supposing the algorithm is designed within the range of controller parameters (input–output gain values and membership functions). In that case, the algorithm will not lead to instability in the system. Thus, the algorithm can find the optimal answer within the range of controller parameter changes.

A fuzzy control approach based on an improved optimization algorithm, namely COA, is applied in this paper to achieve the maximum improvement in lateral vehicle stability at the upper level of the proposed control strategy.

How the Cuckoo Optimization Algorithm works.

COA is a novel evolutionary optimization algorithm based on cuckoo lifestyles. These birds have a special lifestyle in terms of egg-laying and breeding. As a result, the Cuckoo Optimization Algorithm aims to utilize these special characteristics for solving optimization problems. COA begins its calculations with initial birds and their eggs. Each initial cuckoo aims to survive in society, and this is the main point of inspiration for COA. According to some predefined factors, each environment has a profit value. Each cuckoo has to move toward a better environment to live and let its eggs breed. In this process, some cuckoos or eggs will be destroyed, and at each step, the number of cuckoos in the total population decreases. This procedure continues until there is only one society where all cuckoos live [56].

Figure 7 shows the COA flowchart. This algorithm starts with an initial cuckoo population. This population lays eggs in the hosts’ nests. The eggs that are similar to the hosts may survive and grow. Others get detected by the host and killed. Depending on how many cuckoos stay in an area, it may be possible to determine whether that area is suitable for cuckoo conservation. Currently, COA is optimizing the position of the nest to ensure that more eggs survive and can find the appropriate habitat.

Fig. 7
figure 7

Flowchart of cuckoo optimization algorithm [56]

Full size image

This algorithm maximizes profit by determining the number of eggs each cuckoo can lay, variable limits (\( {\text{Var}}_{{\min }} \) and\( {\text{Var}}_{{\max }} \)), and an “Egg Laying Radius” (ELR) for each of them as follows:

$$ {\text{ELR}} = r \times \frac{{{\text{Number}}\;{\text{of}}\;{\text{current}}\;{\text{cuckoo}}^{\prime } {\text{seggs}}}}{{{\text{Total}}\;{\text{Equation}}\;{\text{Number}}\;{\text{of}}\;{\text{eggs}}}} \times \left( {{\text{Var}}_{{{\text{max}}}} - {\text{Var}}_{{{\text{min}}}} } \right) $$
(31)

The maximum ELR can be changed by adjusting the integer parameter г.

For grouping the cuckoos, the optimization process uses K-means clustering. In this case, the cuckoos will move as much as possible toward the best habitat by calculating the mean profit value and identifying the best habitat with maximum profit. Cuckoos do not fly to their destination habitat when moving toward a goal point. They only fly part of the way a percentage of the distance \(\left(\zeta \%\right)\) with deviation\(\theta\), as shown in Fig. 8. The parameters \(\zeta\) and \(\theta\) are defined as follows for each cuckoo:

$$\zeta \sim {{U}}\left( {0,1} \right)$$
(32)
$$\theta \sim {{U}}\left( { - \Omega ,\Omega } \right)$$
(33)

where \(\zeta \sim {{U}}\left( {0,1} \right)\) means a random number between 0 and 1, and \({\Omega }\) is a parameter constraining deviations from goal habitats. For convergence, \({\Omega }\) of \(\pi /6 (\text{rad})\) is sufficient.

Fig. 8
figure 8

Cuckoo migration toward the target

Full size image

3.1.3 Cuckoo-based optimal fuzzy DYC Controller

The main objective of this section is to reduce the vehicle path error, which includes minimizing the error in tracking both the yaw and sideslip angle between the actual and desired values. So, the objective function to evaluate the optimality of the decision variables in the process of COA is considered as the following:

$$ {\text{Objective}}\;{\text{Function}} = 0.5\int _{0}^{\infty } e_{\rm r} \left( t \right)^{2} {\text{d}}t + 0.5\int _{0}^{\infty } e_{\beta } \left( t \right)^{2} {\text{d}}t $$
(34)

The control system has a fuzzy controller at the upper layer that must be optimized to improve lateral vehicle stability. The optimization operation includes the following:

  1. (1)

    The membership functions of the fuzzy controller. These membership functions are defined as triangular membership functions, which are characterized by a triangular shape with a peak at the center and linear slopes on either side. The left and right values determine the triangle’s width, while the peak value determines its height. Optimizing the membership function involves automatically finding the optimal values of its parameters to achieve the desired output behavior.

  2. (2)

    The controller’s input–output gains: Input–output scaling gains can significantly affect fuzzy system performance regarding response speed and stability as follows:

    • Increased input scaling gains may narrow the membership function; the system may become unstable and oscillate around the desired output value. In contrast, if the input scaling gains are decreased, the membership function may widen; the system may not be able to respond rapidly to changes in the input or may not converge to the desired output value.

    • Increased output scaling gains will result in more significant crisp output values produced by the system for the same fuzzy output values, which could cause the system to become unstable and oscillate around the desired output value. On the other hand, if the output scaling gains are decreased, the crisp output values produced by the system will be smaller for the same fuzzy output values; the system may be too slow to respond to changes in the input or may not converge to the desired output value at all.

During the initialization phase, the CS algorithm initializes a random sample of search space solutions. The solution’s dimension and the population’s extent must be specified.

The dimension of the solution \({N}_{\rm Var}\) is determined by the overall number of optimization parameters. The FLC devised in Sect. 3.1.1 relates these parameters to mapping the MF and the input–output gains. Here, inputs (yaw rate and sideslip angle errors) consist of five fuzzy sets, whereas the output (control signal) consists of nine. Due to the symmetry of the membership functions depicted in Figs. 9 and 10, the proposed optimization algorithm should be used to determine the optimal values of 24 decision variables, including three input and output gain decision variables, for optimal fuzzy control. The length of the population is fixed as a value of \({N}_{\rm Pop}\)=30. The initial random population is expressed as a \({N}_{\rm Pop}\times {N}_{\rm Var}\) matrix in which each row represents a candidate dimension solution.

After completing the creation of the matrix, the process of randomly generating new membership functions and values for the input and output gains begins, where 3 to 5 solutions are generated, and these values are used as max and min limits to devote the solution to each iteration (100 iterations in this research).

In an optimization algorithm with an upper bound of \( {\text{Var}}_{{{\text{max}}}} \) and a lower bound of \( {\text{Var}}_{{{\text{min}}}} \) for the variables [0.1, 0.9], the solutions are generated within the ELR (Eq. 31), which is proportional to the solution generation radius factor of ELR (\(r = 5\)).

When the set of generated solutions is placed in the new environment, it cannot recognize which set it should belong to. To solve this problem, cuckoos are grouped with the K-means clustering method (k = 5 seems sufficient). After the solution groups are formed, the average error value of the objective function (Eq. 34) is calculated. The minimum value of (Eq. 34) then determines the target group, so the best habitat for that group is the new home of the migratory cuckoo. In this research, the movement parameters of each cuckoo toward the target point were experimentally determined as: \(\zeta =5\) and \( \theta = \pi /6\;({\text{rad}}) \).

Fig. 9
figure 9

Upper-level control diagram

Full size image
Fig. 10
figure 10

a Membership functions for two inputs, b membership functions for the output

Full size image

4 Simulation results and discussion

A simulation of the 8-DoF vehicle model and the proposed control system is conducted using MATLAB/Simulink software. This simulation evaluates the effectiveness of the control strategy proposed in this paper for improving the stability and performance of the vehicle based on DYC. Several parameters are associated with the vehicle model for the controlling system, including COA, which are listed in Tables 1 and 3.Therefore, there are two different maneuvers (Single lane-change and J-turn), as shown in Fig. 11. The vehicle parameter uncertainties can be considered as + 10% in the vehicle mass, + 15% in the moment of inertia, and − 15% in the tire stiffness. Simulation results include yaw rate, sideslip angle, braking torque, and corrective yaw moment. This paper considers the ratio between the angles turned by the steering wheel and the road wheel to be 20.

Table 3 COA parameters
Full size table
Fig. 11
figure 11

Wheel steering angle, a change-line maneuver, b J-turn maneuver

Full size image

4.1 Dry road single lane-change maneuver

In this maneuver, the vehicle runs on a dry road at 30 m/s with \(\mu = 0.9\). The robustness and effectiveness of the proposed controller with input steering angle change for this maneuver are verified by comparing the performance of the optimized fuzzy controller with the fuzzy controller presented in [27].

Figure 12 shows the yaw rate and slip angle effects on the vehicle’s response. In an uncontrolled vehicle, the yaw rate and sideslip angles are greater than the desired values, resulting in instability. The performances of the optimal and non-optimal controllers are almost the same. Still, the optimal controller provides better yaw tracking with the slip angle remaining less than the desired value. Figure 13a, b also depicts the corrective yaw moment the optimal fuzzy controller produces and transforms into the required braking torque to achieve vehicle stability.

Fig. 12
figure 12

Response of the vehicle to single lane-change maneuver on dry road \((\mu = 0.9)\) a yaw rate \( ({\text{rad/s}}) \) b sideslip angle\( ({\text{deg}}) \)

Full size image
Fig. 13
figure 13

An evaluation of the corrective yaw moment and braking torques on a dry road (\(\mu = 0.9)\)by considering single lane-change maneuver

Full size image

According to Fig. 14, an optimal fuzzy controller can produce good tracking performance by spending less corrective yaw moment \({M}_{z}\) than a non-optimal fuzzy controller. Figure 15a, b shows the braking torques of the two control strategies (for the left and right rear wheels according to this paper and for the left and right front wheels applied in [27]), where it appears that the braking torque produced by the optimal controller is less than the braking torque produced by the non-optimal controller but with a longer application time during tracing.

Fig. 14
figure 14

An evaluation of the corrective yaw moment \({M}_{z}\) for optimal and non-optimal fuzzy controllers on a dry road \((\mu = 0.9)\) by considering single lane-change maneuver

Full size image
Fig. 15
figure 15

Comparison of braking torques for the single lane-change maneuver on the dry road \((\mu = 0.9)\): a left braking torque \( ({\text{N}}\;{\text{m}}) \), b right braking torque \( ({\text{N}}\;{\text{m}}) \)

Full size image

4.2 J-turn maneuver on rainy road

The vital point in this scenario is that as the coefficient of friction between the tires and the road decreases, the possibility of vehicle instability increases. Thus, the effectiveness of the control system becomes evident. Therefore, the robustness and effectiveness of the proposed controller with input steering angle changes are validated by testing the vehicle on a rainy road with \(\mu = 0.5\) at a longitudinal velocity of 20 m/s.

Figure 16a, b shows the yaw rate and slip angle tracking performance for two cases: the uncontrolled vehicle and the vehicle controlled with a fuzzy control strategy and a non-optimal fuzzy control strategy. Figure 16a displays the failure of the non-optimal fuzzy control system to track the reference yaw rate by exceeding the sliding angle value by the desired value, as shown in Fig. 16b. Thus, the vehicle deviates from the required path. While the optimal fuzzy control strategy offers the ability to track the reference yaw rate and keep the slip angle smaller than the desired value despite the increase in overshoot before reaching stability. Thus, the optimal fuzzy control system improves vehicle stability and is robust under different road conditions compared to the non-optimum fuzzy control system. Figure 17a, b shows the left and right brake torques generated by the corrective yaw moment \({M}_{z}\) using the proposed optimal fuzzy control strategy.

Fig. 16
figure 16

Response of the vehicle to J-turn maneuver on rainy road (µ = 0.5) a yaw rate \( ({\text{rad/s}}) \) b sideslip angle \( (\deg ) \)

Full size image
Fig. 17
figure 17

An evaluation of braking torques and the corrective yaw moment \({M}_{z}\) \( ({\text{N}}\;{\text{m}}) \) using the optimal fuzzy controller for\((\mu =0.5\)): a Rear-left braking torque \( ({\text{N}}\;{\text{m}}) \), b Rear-right braking torque \( ({\text{N}}\;{\text{m}}) \)

Full size image

4.3 Single lane-change maneuver on split-\(\varvec{\mu }\) road

This scenario involves the vehicle moving on a split-\(\mu\) road at a longitudinal speed of \(20\) m/s with a friction coefficient of 0.8 on the left side and 0.5 on the right side during the test period.

Figure 18a, b shows the effect of the yaw rate and slip angle on the vehicle’s response when moving on a split-\(\mu\) road in two cases: the uncontrolled vehicle and the vehicle controlled by the optimal fuzzy control strategy. With an uncontrolled vehicle, we find an unexpected deviation in the yaw rate and a significant increase in the slip angle due to changes in the tire-road friction coefficient \(\mu\). In contrast, the optimal fuzzy controller can produce good tracking performance for the reference yaw rate and keep the slip angle smaller than the desired value despite the presence of some overshoot by generating a corrective yaw moment \({ M}_{z}\), which is transformed into the braking torque of the left and right rear wheels, as shown in Fig. 19a, b.

Fig. 18
figure 18

Response of the vehicle to single lane-change maneuver on a split-\(\mu\) road (a) yaw rate \( ({\text{rad/s}}) \) (b) sideslip angle\( (\deg ) \)

Full size image
Fig. 19
figure 19

An evaluation of braking torques and the corrective yaw moment \({M}_{z}\) \( ({\text{N}}\;{\text{m}}) \) using the optimal fuzzy controller for a split-\(\mu\) road: a Rear-left braking torque \( ({\text{N}}\;{\text{m}}) \), b Rear-right braking torque \( ({\text{N}}\;{\text{m}}) \)

Full size image

5 Conclusion

This paper presents an optimized fuzzy controller by COA applied to HEVs to improve vehicle stability during critical driving. The proposed control structure consists of two layers. The main objective of the upper layer is to generate an accurate external yaw moment based on the optimization of the membership functions and the input–output weights of the fuzzy controller to tackle the problem of unknown changes in lateral vehicle dynamics during single lane-change and J-turn maneuvers at high speeds. The lower layer applies the braking torques to the left or right rear wheels depending on the corrective yaw moment obtained from the upper layer.

The proposed method’s efficacy was evaluated with computer simulations on MATLAB by simulating three scenarios in various road conditions using a nonlinear 8-DOF vehicle model with parameter uncertainties to ensure the robustness of the proposed control strategy against changes in road conditions. The simulation results compared the suggested optimized fuzzy controller’s efficiency to a fuzzy controller’s in [27] for dry road single lane-change and rainy road J-turn maneuvers. The results showed that the proposed control system tracked the desired yaw rate and kept the sideslip angle equal to or smaller than the desired value with fewer control efforts. The most important disadvantages of the proposed algorithm are computational complexity, premature convergence, and stagnation, which can be considered in future studies.