Introduction

Fractional differential equations (FDEs) appeared in the modeling and treatment of some real phenomena in several fields such as biology, chemistry, physics, fluid mechanics, epidemiology, viscoelasticity, finance and engineering and other areas of science were presented in [1,2,3,4,5]. The emergence of FDEs is due to the fact that the non-local nature of fractional derivative operators can be used as a distinct mathematical tool to more accurately describe dynamic systems involving memory effects [6,7,8,9,10]. The growing interest in applications involving FDEs makes it necessary to expand, develop and improve stable and robust analytical and numerical methods for solving such models. For instance, some methods such as variational iteration method [11, 12], homotopy analysis method [13, 14], Adomain decomposition method [15, 16], Laplace transform method [17, 18] and predictor corrector method [19, 20] have been developed to solve FDEs where the fractional derivative is taken in the sense of Caputo defined below. In the literature, many definitions of fractional derivatives have been proposed as most of them are based on definitions of fractional integrals such as

$$\begin{aligned}&\textit{Riemann-Liouville}: \quad \quad I^{\alpha }_{a^{+}}f(x)=\frac{1}{\Gamma (\alpha )}\int _{a}^{x} (x-\tau )^{\alpha -1} f(\tau )d\tau ,\;x> a, \end{aligned}$$
(1)
$$\begin{aligned}&\textit{Hadamard}: \quad \quad I^{\alpha }_{a^{+}}f(x)=\frac{1}{\Gamma (\alpha )}\int _{a}^{x} \left( \log \frac{x}{\tau }\right) ^{\alpha -1} f(\tau ) \displaystyle \frac{d\tau }{\tau },\quad \quad \;x> a,\quad \quad \end{aligned}$$
(2)
$$\begin{aligned}&\textit{Katugampola}: \quad I^{\alpha ,\rho }_{a^{+}}f(x)=\frac{\rho ^{1-\alpha }}{\Gamma (\alpha )}\int _{a}^{x} \tau ^{\rho -1}(x^{\rho }-\tau ^{\rho })^{\alpha -1} f(\tau )d\tau ,\quad x>a,\quad \;\rho >0,\nonumber \\ \end{aligned}$$
(3)

where \(\alpha >0\) and \(a\ge 0\). Depending on the Riemann–Liouville definition, which is one of the most studied, the Riemann–Liouville and Caputo fractional derivatives of order \(\alpha >0\) are defined as

$$\begin{aligned} ^{R}D^{\alpha }_{a^{+}}f(x)= & {} D^{n} I^{n-\alpha }_{a^{+}}f(x)=\frac{1}{\Gamma (n-\alpha )} \frac{d^{n}}{dx^{n}}\int _{a}^{x}(x-\tau )^{n-\alpha -1} f(\tau )d\tau ,\quad \quad x>a, \end{aligned}$$
(4)
$$\begin{aligned} ^{C}D^{\alpha }_{a^{+}}f(x)= & {} I^{n-\alpha }_{a^{+}}D^{n}f(x)=\frac{1}{\Gamma (n-\alpha )} \int _{a}^{x}(x-\tau )^{n-\alpha -1} f^{(n)}(\tau ) d\tau ,\quad \quad x>a, \end{aligned}$$
(5)

respectively, such that \(a\ge 0\), \(n-1<\alpha \le n\) and \(n\in I\!\!N\). As an extension of the Riemann–Liouville fractional integral, Osler [21] highlighted a useful generalization of the fractional integral of a function f with respect to the function h as

$$\begin{aligned} I^{\alpha ,h}_{a^{+}}f(x)= \displaystyle \frac{1}{\Gamma ({\alpha })} \int _{a}^{x}h'(\tau )(h(x)-h(\tau ))^{\alpha -1}f(\tau )d\tau ,\quad \quad x>a, \end{aligned}$$
(6)

where \(\alpha >0\). In case of \(h(x) = x\), \(h(x)=\log x\) and \(h(x)=x^{\rho }/\rho \), the generalized fractional integral operator given in Eq. (6) reduces to the Riemann–Liouville, Hadamard and Katugampola fractional integral operators given in Eqs. (1), (2) and (3), respectively. Furthermore, if \(\alpha ,\;\beta >0\) and \(\gamma >-1\) the generalized fractional integral given in (6) satisfies the following properties

$$\begin{aligned} I^{\alpha ,h}_{a^{+}}I^{\beta ,h}_{a^{+}}f(x)= & {} I^{\alpha +\beta ,h}_{a^{+}}f(x), \end{aligned}$$
(7)
$$\begin{aligned} I^{\alpha , h}_{a^{+}}\big ( h(x)-h(a)\big )^{\gamma }= & {} \frac{\Gamma (\gamma +1)}{\Gamma (\gamma +\alpha +1)}\big ( h(x)-h(a)\big )^{\gamma +\alpha }. \end{aligned}$$
(8)

According to the generalization given in Eq. (6), the generalized Riemann–Liouville-type and the Caputo-type fractional derivatives of order \(\alpha >0\) are identified as

$$\begin{aligned} \;^{R}D^{\alpha , h}_{a^{+}}f(x)= & {} \displaystyle \frac{1}{\Gamma (n-\alpha )}\left( \frac{1}{h'(x)} \frac{d}{dx}\right) ^{n}\int _{a}^{x}h'(\tau )(h(x)-h(\tau ))^{n-\alpha -1}f(\tau )d\tau ,\quad \quad x>a, \end{aligned}$$
(9)
$$\begin{aligned} \;^{C}D^{\alpha , h}_{a^{+}}f(x)= & {} \displaystyle \frac{1}{\Gamma (n-\alpha )} \int _{a}^{x}h'(\tau )(h(x)-h(\tau ))^{n-\alpha -1}\left( \frac{1}{h'(\tau )} \frac{d}{d\tau }\right) ^{n}f(\tau )d\tau ,\quad \quad x>a, \end{aligned}$$
(10)

respectively, where \(n-1<\alpha \le n\) and \(n\in I\!\!N\). In case of \(h(x)=x\), the fractional operators (9) and (10) reduces to (4) and (5), respectively. Therefore, the Riemann–Liouville and Caputo fractional derivative operators with respect to the function h given in Eqs. (9) and (10) can be considered as generalizations of the fractional derivative operators given in Eqs. (4) and (5). This topic has been a source of inspiration to researchers due to its importance and use in many fields including physics, control theory of dynamical systems etc. [18, 22,23,24,25].

On the other hand, the Adomain decomposition method (ADM), introduced by Adomain in 1980 [26], has received great interest due to its rapid convergence [27, 28] and ease of use to provide analytical solutions for various functional equation types in many engineering and physical applications. This method has some merits over other methods; It gives analytical series solutions without using linearity or perturbation, in addition, it transforms a non-linear functional equation into a series of linear equations that can be solved straightforwardly and directly. Some numerical comparisons between the ADM and other methods are presented in [29,30,31], while improved versions and modifications of the ADM can be found in [32,33,34]. Moreover, the method has been modified to handle non-linear differential equations of fractional order, where the fractional derivative is taken in the sense of Caputo [15, 16, 33, 35,36,37,38].

In [20], a novel predictor-corrector algorithm was developed for providing numerical approximate solutions to IVPs involving generalized Caputo-type (G-C) fractional derivatives. According to our knowledge, analytical solutions for IVPs including G-C fractional derivatives have not been presented yet. Therefore, motivated by the recent developments of mathematical models that include G-C fractional derivatives and the challenging issues to solve such models, a modification of the ADM has been proposed in this paper to solve nonlinear IVPs containing the studied fractional derivatives. The main objective of the current paper is to construct analytical fractional power series solutions of the studied models. In addition, to demonstrate the effectiveness and efficiency of the used modified scheme in obtaining approximate solutions, numerical comparisons are made with a predictor-corrector method by means of some illustrative examples.

This paper is organized as follows. Definitions, notations, and properties of G-C fractional operators are introduced in section 2. In section 3, approximate analytical solutions of IVPs involving FDEs with the studied G-C fractional derivatives are derived by a modified scheme of Adomain decomposition method. Next, some test problems of the studied models using some special cases of the function h, are examined in section 4 to show the merits of the proposed scheme. Numerical comparisons between the proposed scheme and a predictor-corrector method are made. Finally, some concluding remarks are made in section 5.

Preliminaries

This section recalls some definitions, characteristics and properties of the G-C fractional derivative operator identified in Eq. (10). In real-life problems, the Caputo fractional derivative has been widely used in modelling many functional differential problems in science and engineering because it has many features similar to those of ordinary derivatives. The initial conditions for IVPs involving Caputo derivatives can be expressed in terms of the initial values of integer order derivatives [39, 40]. Therefore, several Caputo-type fractional derivatives have been introduced and studied. For example, the Caputo–Hadamard fractional derivative of order \(\alpha >0\) is defined as [41]

$$\begin{aligned} \;^{CH}D^{\alpha }_{a^{+}}f(x)=\displaystyle \frac{1}{\Gamma (n-\alpha )}\displaystyle \int ^{x}_{a} \left( \log \displaystyle \frac{x}{\tau }\right) ^{n-\alpha -1}\left( \tau \frac{d}{d\tau }\right) ^{n}f(\tau )\displaystyle \frac{d\tau }{\tau },\quad \quad x>a, \end{aligned}$$
(11)

and the Caputo–Katugampola fractional derivative of order \(\alpha >0\) is introduced as [25]

$$\begin{aligned} \;^{C}D^{\alpha ,\rho }_{a^{+}}f(x)=\displaystyle \frac{\rho ^{\alpha -n+1}}{\Gamma (n-\alpha )} \displaystyle \int ^{x}_{a}\tau ^{\rho -1}\left( x^{\rho }-\tau ^{\rho }\right) ^{n-\alpha -1}\left( \tau ^{1-\rho }\frac{d}{d\tau }\right) ^{n}f(\tau )d\tau , \quad \quad x>a,\nonumber \\ \end{aligned}$$
(12)

where \(\rho >0\), \(a\ge 0\), \(n-1<\alpha \le n\) and \(n\in I\!\!N\). Now, using the generalization given in Eq. (6), we introduce an alternative characterization of the G-C fractional derivative given in Eq. (10). Let h be any strictly increasing function on [a, b] which has a continuous derivative on (a, b) such that \(h'(x)\ne 0\) on [a, b]. The G-C fractional derivative of f with respect to the function h of order \(\alpha \), \(n-1<\alpha \le n\) and \(n\in I\!\!N\), is defined as [24]

$$\begin{aligned} \;^{C}D^{\alpha , h}_{a^{+}}f(x)=I^{n-\alpha ,h}_{a^{+}}\left( \frac{1}{h'(x)} \frac{d}{dx}\right) ^{n}f(x),\quad \quad a<x<b. \end{aligned}$$
(13)

Let \(h\in C^{n}[a,b]\) such that \(h'(x)>0\) on [a, b]. Define the space of functions \(AC^{n}_{h}[a,b]\) as

$$\begin{aligned} AC^{n}_{h}[a,b]=\left\{ f:[a,b]\longrightarrow I\!R \,and \;\left( \frac{1}{h'(t)}\frac{d}{dt}\right) ^{n-1}f \in AC[a,b] \right\} , \end{aligned}$$
(14)

where AC[a, b] is the space of absolutely continuous functions on [a, b].

Remark 1

If \(f\in AC^{n}_{h}[a,b]\) and \(n-1<\alpha \le n\), then the G-C fractional derivative of f with respect to the function h exist almost everywhere on [a, b] [18].

Remark 2

Let \(f\in C^{n+m}[a,b]\), such that \(n,\;m\in I\!\!N \), and \(n-1<\alpha \le n\). Then [24]

$$\begin{aligned} ^{C}D^{\alpha , h}_{a^{+}}\left( \frac{1}{h'(x)}\frac{d}{dx}\right) ^{m}f(x)=\;^{C}D^{\alpha +m, h}_{a^{+}}f(x),\quad \quad n-1<\alpha \le n. \end{aligned}$$
(15)

Remark 3

Let \(\alpha >0\) and \(f\in C^{1}[a,b]\). Then [24]

$$\begin{aligned} ^{C}D^{\alpha , h}_{a^{+}}\;I^{\alpha , h}_{a^{+}}f(x)=f(x). \end{aligned}$$
(16)

Theorem 1

The relationship between the G-C fractional derivative and the generalized fractional integral with respect to function h, where \(f\in C^{n}[a,b]\) and \(n-1<\alpha \le n\), is given by [24]

$$\begin{aligned} I^{\alpha ,h}_{a+}\;^{C}D_{a+}^{\alpha ,h}f(x)=f(x)-\sum _{j=0}^{n-1}\frac{1}{j!} \big (h(x)-h(a)\big )^{j}\left[ \left( \frac{1}{h'(t)}\frac{d}{dt}\right) ^{j}f(t)\right] _{t=a},\quad a<x<b. \nonumber \\ \end{aligned}$$
(17)

Remark 4

In particular, if \(0<\alpha \le 1\), we get

$$\begin{aligned} I^{\alpha ,h}_{a+}\;^{C}D_{a+}^{\alpha ,h}f(x)=f(x)-f(a). \end{aligned}$$
(18)

Theorem 2

The relationship between the generalized Riemann–Liouville-type and the G-C fractional derivatives of order \(\alpha >0\), with \(f\in C^{n}[a,b]\) and \(n-1<\alpha \le n\), is given by [24]

$$\begin{aligned} ^{C}D_{a+}^{\alpha ,h}f(x)= & {} \;^{R}D^{\alpha ,h}_{a+}\left\{ f(x)-\sum _{j=0}^{n-1}\frac{1}{j!} \big (h(x)-h(a)\big )^{j}\left[ \left( \frac{1}{h'(t)}\frac{d}{dt}\right) ^{j}f(t)\right] _{t=a}\right\} ,\nonumber \\&\qquad a<x<b. \end{aligned}$$
(19)

Theorem 3

Let \(g^{\beta }(x)=(h(x)-h(a))^{\beta }\) and \(\beta >n-1\). Then, for \(\alpha >0\), [24]

$$\begin{aligned} ^{C}D^{\alpha , h}_{a^{+}}g^{\beta }(x)=\frac{\Gamma (\beta +1)}{\Gamma (\beta -\alpha +1)} g^{\beta -\alpha }(x),\quad \quad x>a. \end{aligned}$$
(20)

In the case of \(n>m\), where \(n,\; m \in I\!\!N\), we have

$$\begin{aligned} ^{C}D^{\alpha , h}_{a^{+}}g^{m}(x)=0. \end{aligned}$$
(21)

Theorem 4

Suppose there exists some \(p\in I\!\!N\) with \(\alpha \), \(\beta >0\) and \(\beta \), \(\alpha +\beta \in [p-1, p]\). Then, for \(f\in C^{p}[a,b]\), we have [24]

$$\begin{aligned} ^{C}D^{\alpha , h}_{a^{+}}\;^{C}D^{\beta , h}_{a^{+}}f(x)= \;^{C}D^{\alpha +\beta ,h} _{a^{+}}f(x). \end{aligned}$$
(22)

The Adomain Decomposition Method

The ADM has been successfully implemented in handling IVPs of functional equation types including nonlinear ODEs and PDEs for both integer and fractional orders. This section proposes a modified scheme of the ADM as an effective tool for producing approximate analytical solutions to IVPs that include nonlinear Caputo-type fractional differential equations. The principle of the proposed scheme is to express the solution as an infinite series of function components where the components are given by fractional powers of \(\left( h(x)-h(a)\right) \). Here, the goal is to find approximate analytical solution for the IVP

$$\begin{aligned} \left\{ \begin{array}{lll} ^{C}D_{a+}^{\alpha ,h}y(x)+\mathcal {R}(y(x))+\mathcal {N}(y(x)) &{} = &{} g(x),\quad \quad a<x<b,\\ \;\quad y^{(k)}(a) &{} = &{} y_{0}^{k},\quad \quad k=0,1,...,n-1, \end{array} \right. \end{aligned}$$
(23)

where \(n-1<\alpha \le n\), \(n\in I\!\!N\), \(\;^{C}D_{a+}^{\alpha ,h}\) is the G-C fractional derivative operator given in Eq. (13), \(\mathcal {R}\) is a linear operator, \(\mathcal {N}\) represents a nonlinear operator and g is the source function. Suppose h is any strictly increasing function on [a, b] and has a continuous derivative on (a, b) such that \(h'(x)\ne 0\) on [a, b] and let \(y \in C^{n}[a,b]\). At first, for \(a<x<b\) the IVP (23) is equivalent, in view of Theorem 1, to the integral equation

$$\begin{aligned}&y(x)+I^{\alpha ,h}_{a+}\mathcal {R}(y(x))+I^{\alpha ,h}_{a+}\mathcal {N}(y(x))\nonumber \\&\quad =I^{\alpha ,h}_{a+}g(x)+\sum _{j=0}^{n-1}\frac{1}{j!} \big (h(x)-h(a)\big )^{j}\left[ \left( \frac{1}{h'(t)}\frac{d}{dt}\right) ^{j}y(t)\right] _{t=a}. \end{aligned}$$
(24)

The modified scheme suggests the solution y(x) be decomposed by the series

$$\begin{aligned} y(x)=\displaystyle \sum _{j=0}^{\infty }y_{j}(x), \end{aligned}$$
(25)

and the nonlinear term \(\mathcal {N}(y)\) be expressed as

$$\begin{aligned} \mathcal {N}(y(x))=\displaystyle \sum _{j=0}^{\infty }A_{j}(x), \end{aligned}$$
(26)

where the Adomian polynomials \(A_{j}(x)\) can be evaluated using the relation [42]

$$\begin{aligned} A_{j}(x)=\displaystyle \frac{1}{j!}\left[ \displaystyle \frac{d^{j}}{d\lambda ^{j}} \mathcal {N}\left( \displaystyle \sum _{i=0}^{\infty } \lambda ^{i}y_{i}(x) \right) \right] _{\lambda =0},\quad \quad j\ge 0. \end{aligned}$$
(27)

Inserting the series given in Eqs. (25) and (26) into the integral Eq. (24), we get

$$\begin{aligned} \displaystyle \sum _{j=0}^{\infty }y_{j}(x)= & {} y_{0}^{0}+ \displaystyle \frac{h(x)-h(a)}{h'(a)}y_{0}^{1}+...+\frac{1}{(n-1)!} \big (h(x)-h(a)\big )^{n-1} \left[ \left( \displaystyle \frac{1}{h'(t)}\displaystyle \frac{d}{dt}\right) ^{n-1}y(t)\right] _{t=a}\nonumber \\&+I^{\alpha ,h}_{a+}\left( g(x)\right) -I^{\alpha ,h}_{a+}\left( \mathcal {R}\left( \displaystyle \sum _{j=0}^{\infty }y_{j}(x)\right) \right) -I^{\alpha ,h}_{a+}\left( \displaystyle \sum _{j=0}^{\infty }A_{j}(x)\right) . \end{aligned}$$
(28)

Consequently, The modified scheme produces the series solution \(y(x)=\sum _{j=0}^{\infty }y_{j}(x)\), where the term function \(y_{j}(x)\), \(j = 0, 1, \cdots \), can be obtained recursively by using the formula

$$\begin{aligned} \left\{ \begin{array}{lll} y_{0}(x)&{}=&{}\displaystyle \sum _{j=0}^{n-1}\frac{1}{j!} \big (h(x)-h(a)\big )^{j}\left[ \left( \displaystyle \frac{1}{h'(t)}\displaystyle \frac{d}{dt}\right) ^{j}y(t)\right] _{t=a}+I^{\alpha ,h}_{a+}\left( g(x)\right) ,\\ y_{j+1}(x)&{}=&{}-I^{\alpha ,h}_{a+}\left( \mathcal {R}\left( y_{j}(x)\right) \right) -I^{\alpha ,h}_{a+}\left( A_{j}(x)\right) ,\quad \quad \quad \quad \quad \quad \quad j\ge 0, \end{array} \right. \end{aligned}$$
(29)

where \(A_{j}(x)\) is determined using Eq. (27). Clearly, if our decomposition series \(\sum _{j=0}^{\infty }y_{j}(x)\) converges and if we apply the G-C fractional derivative operator to Eq. (28), using Remark 3 and Theorem 3, we get

$$\begin{aligned} ^{C}D_{a+}^{\alpha ,h}\sum _{j=0}^{\infty }y_{j}(x)= g(x)-\mathcal {R}\left( \displaystyle \sum _{j=0}^{\infty }y_{j}(x)\right) -\displaystyle \sum _{j=0}^{\infty }A_{j}(x). \end{aligned}$$
(30)

Therefore, since \(\sum _{j=0}^{\infty }A_{j}(x)=\mathcal {N}\left( \sum _{i=0}^{\infty } y_{i}(x)\right) \), \(y(x)=\sum _{j=0}^{\infty }y_{j}(x)\) is exactly a solution of the IVP (23). The convergence of the ADM has been discussed by Cherruault in [28, 43].

Remark 5

Let \(f(x)=\sum _{j=0}^{n-1}\frac{1}{j!} \big (h(x)-h(a)\big )^{j}\left[ \left( \frac{1}{h'(t)}\frac{d}{dt}\right) ^{j}y(t)\right] _{t=a}+I^{\alpha ,h}_{a+}\left( g(x)\right) \). In order to facilitate the calculations, the presented approach can be improved by dividing the function f by a series of infinite components [44]. In this case, assume that the function f can be represented by the series \(f(x)=\sum _{j=0}^{\infty }f_{j}(x)\). Then, the series solution \(y(x)=\sum _{j=0}^{\infty }y_{j}(x)\) to the IVP (23) can be obtained where the term function \(y_{j}(x)\), \(j = 0, 1, \cdots \), satisfies the formula

$$\begin{aligned} \left\{ \begin{array}{lll} y_{0}(x)&{}=&{}f_{0}(x),\\ y_{1}(x)&{}=&{}f_{1}(x)-I^{\alpha ,h}_{a+}\left( \mathcal {R}\left( y_{0}(x)\right) \right) -I^{\alpha ,h}_{a+}\left( A_{0}(x)\right) ,\\ y_{j+1}(x)&{}=&{}f_{j+1}(x)-I^{\alpha ,h}_{a+}\left( \mathcal {R}\left( y_{j}(x)\right) \right) -I^{\alpha ,h}_{a+}\left( A_{j}(x)\right) ,\quad \quad j\ge 1. \end{array} \right. \end{aligned}$$
(31)

For application purposes, we may truncate the infinite series \( \sum _{j=0}^{\infty }y_{j}(x)\) at the N-th term and use the resulting partial sum \(\sum _{j=0}^{N-1}y_{j}(x)\), where \(N\in I\!\!N\), as an approximation to the solution y(x).

Applications

This section derives analytical approximate solutions to IVPs involving FDEs with the studied G-C fractional derivatives. In this regard, the modified scheme presented in the previous section is implemented to provide approximate solutions for the studied models using some special cases of the function h, where the function h is assumed to be any strictly increasing function on [a, b] which has a continuous derivative on (a, b) such that \(h'(x)\ne 0\) on [a, b]. Numerical comparisons were made between the proposed scheme and the universal predictor-corrector (P-C) method, introduced in [20], using the Mathematica software package. The universal P-C algorithm has proven to be an efficient, stable and accurate tool in providing approximate numerical solutions for the studied IVPs. Numerical simulation of the studied models was carried out to show the influence of the considered derivative parameters on their dynamics.

Example 1

First, we consider the fractional IVP

$$\begin{aligned} \left\{ \begin{array}{lll} \;^{C}D^{\alpha ,h}_{0+}y(x)&{}=&{}2\,y(x)-y^{2}(x)+1,\quad \quad 0<\alpha \le 1,\quad \quad 0< x \le 1, \\ \quad y(0)&{}=&{}0, \end{array}\right. \end{aligned}$$
(32)

where \(\;^{C}D_{0+}^{\alpha ,h}\) is the G-C fractional derivative operator of order \(\alpha \). The exact solution of (32), when \(h(x)=x\) and \(\alpha =1\), is given as follows [45]

$$\begin{aligned} y(x)=1+\sqrt{2}\,\tanh \left[ \sqrt{2}\,x+\frac{1}{2}\log \left( \frac{\sqrt{2}-1}{\sqrt{2}+1}\right) \right] . \end{aligned}$$
(33)

Applying the integral operator \(I^{\alpha ,h}_{0+}\) to both sides of Eq. (32), using Theorem 1 and the relation (8), we obtain

$$\begin{aligned} y(x)=I^{\alpha ,h}_{0+}(2\,y(x))-I^{\alpha ,h}_{0+}(y^{2}(x))+\displaystyle \frac{(h(x)-h(0))^{\alpha }}{\Gamma (\alpha +1)}. \end{aligned}$$
(34)

Our modified scheme suggests the series solution \(y(x)=\sum _{j=0}^{\infty }y_{j}(x)\), such that the nonlinear term \(\mathcal {N}(y)=y^{2}\) be expressed as \(y^{2}(x)=\sum _{j=0}^{\infty }A_{j}(x)\), where the component function \(y_{j}(x)\), \(j = 0, 1, \cdots \), can be obtained recursively by using the formula

$$\begin{aligned} \left\{ \begin{array}{lll} y_{0}(x)&{}=&{}\displaystyle \frac{(h(x)-h(0))^{\alpha }}{\Gamma (\alpha +1)},\\ y_{j+1}(x)&{}=&{}I^{\alpha ,h}_{0+}(2 \,y_{j}(x)-A_{j}(x)),\quad \quad j\ge 0, \end{array} \right. \end{aligned}$$
(35)

and

$$\begin{aligned} A_{j}(x)=\displaystyle \frac{1}{j!}\left[ \displaystyle \frac{d^{j}}{d\lambda ^{j}} \left( \displaystyle \sum _{i=0}^{\infty } \lambda ^{i}y_{i}(x) \right) ^{2}\right] _{\lambda =0},\quad \quad j\ge 0. \end{aligned}$$
(36)

The Adomain polynomials \(A_{j}\), \(j=0,1,\cdots \), can be calculated as

$$\begin{aligned} \left\{ \begin{array}{lll} A_{0}=y^{2}_{0},\\ A_{1}=2\, y_{0}y_{1},\\ A_{2}=2\, y_{0}y_{2}+y^{2}_{1},\\ A_{3}=2\, y_{0}y_{3}+2\, y_{1}y_{2},\\ A_{4}=2\, y_{0}y_{4}+2\, y_{1}y_{3}+y^{2}_{2},\\ \quad \,\,\,\, \vdots \end{array} \right. \end{aligned}$$
(37)

Therefore, utilizing the recurrence relation (35), we get the series solution

$$\begin{aligned} y(x)=\displaystyle \sum _{j=1}^{\infty }c_{j}\left( h(x)-h(0)\right) ^{j\alpha }, \end{aligned}$$
(38)

where

$$\begin{aligned} \begin{array}{lll} c_{1}&{}=&{}\displaystyle \frac{1}{\Gamma (\alpha +1)}, \\ c_{2}&{}=&{}\displaystyle \frac{2}{\Gamma (2\alpha + 1)},\\ c_{3}&{}=&{}\displaystyle \frac{-\Gamma (2\alpha + 1)+4\,\Gamma (2\alpha + 1)^{2}}{\Gamma (\alpha + 1)^{2}\Gamma (3\alpha + 1)},\\ c_{4}&{}=&{}\displaystyle \frac{-2\,\Gamma (2\alpha + 1)^{2}-4\,\Gamma (3\alpha + 1)\Gamma (\alpha +1)}{\Gamma (\alpha + 1)^{2}\Gamma (2\alpha + 1)\Gamma (4\alpha + 1)},\\ c_{5}&{}=&{}\displaystyle \frac{2\,\Gamma (2\alpha + 1)\Gamma (4\alpha + 1)}{\Gamma (\alpha + 1)^{3}\Gamma (3\alpha + 1)\Gamma (5\alpha + 1)},\\ &{}\vdots &{} \end{array} \end{aligned}$$
(39)

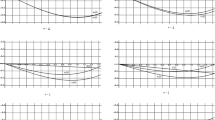
In Tables 1, 2 and 3, we show approximate solutions produced using our modified scheme of the ADM (\(y_{ADM}\)) when \(N=10\) and the approximate solutions produced using the universal P-C method (\(y_{P-C}\)) to the IVP (32), for some value of \(\alpha \) and \(\rho \), with three cases of the function h (\(h(x)=x^{\rho }\), \(h(x)=\exp (\rho x)\) and \(h(x)=\log (\rho x+1)\)). Furthermore, the solution behavior of the fractional model given in the IVP (32) regarding the different cases of the function h against the variable x is described in Figs. 1 and 2. Figure 1 pictures approximate solutions produced using our modified scheme when \(N=10\), the approximate solutions produced using the universal P-C method and the exact solution, where \(h(x)=x\). Figure 2 pictures approximate solutions produced using our modified scheme when \(N=10\) and the approximate solutions produced using the universal P-C method, where \(h(x)=\exp (\rho x)\) and \(h(x)=\log (\rho x +1)\). In Fig. 3, we draw the absolute error of the approximate solutions obtained using our modified scheme when \(h(x)=x\) and \(\alpha =1\).

Table 1 Numerical solutions to the IVP (32) for some values of \(\alpha \) and \(\rho \) with \(h(x)=x^{\rho }\)
Full size table
Table 2 Numerical solutions to the IVP (32) for some values of \(\alpha \) and \(\rho \) with \(h(x)=\exp (\rho x)\)
Full size table
Table 3 Numerical solutions to the IVP (32) for some values of \(\alpha \) and \(\rho \) with \(h(x)=\log (\rho x+1)\)
Full size table
Fig. 1
figure 1

Plots of approximate solutions and exact solution for the IVP (32) when \(\alpha =1\) and \(\rho =1\): Exact solution (black line); Modified scheme of ADM (blue line); Universal P-C method (red line)

Full size image
Fig. 2
figure 2

Plots of approximate solutions for the IVP (32) when \(\alpha =1\) and \(\rho =1\): Modified scheme of ADM (blue line); Universal P-C method (red line)

Full size image
Fig. 3
figure 3

Plots of absolute error for the IVP (32) when \(\alpha =1\) and \(\rho =1\)

Full size image

From the numerical results displayed in Tables 1, 2 and 3 and Figs. 1, 2 and 3, we can notice that the approximate solutions produced using our modified scheme of ADM are highly compatible with those obtained using the universal P-C method. Certainly, the accuracy of our scheme can be improved by adding more terms to the truncated series approximate solutions.

Example 2

Next, we consider the fractional IVP

$$\begin{aligned} \left\{ \begin{array}{lll} \;^{C}D^{\alpha ,h}_{0+}y(x)&{}=&{}-\gamma y(x)-\mu y^{3}(x),\quad \quad 1<\alpha \le 2,\quad \quad x>0, \\ \quad y(0)&{}=&{}\displaystyle \frac{1}{2},\\ \quad y'(0)&{}=&{}0, \end{array}\right. \end{aligned}$$
(40)

where \(\gamma ,\; \mu \in I\!\!R\) and \(\;^{C}D_{0+}^{\alpha ,h}\) is the G-C fractional derivative operator of order \(\alpha \). Applying the integral operator \(I^{\alpha ,h}_{0+}\) to both sides of Eq. (40), using Theorem 1, we obtain

$$\begin{aligned} y(x)=\displaystyle \frac{1}{2}-I^{\alpha ,h}_{0+}\left( \gamma y(x)+\mu y^{3}(x)\right) . \end{aligned}$$
(41)

Our modified scheme suggests the series solution \(y(x)=\sum _{j=0}^{\infty }y_{j}(x)\), such that the nonlinear term \(\mathcal {N}(y)=y^{3}\) be expressed as \(y^{3}(x)=\sum _{j=0}^{\infty }B_{j}(x)\), where the component function \(y_{j}(x)\), \(j = 0, 1, \cdots \), can be obtained recursively by using the formula

$$\begin{aligned} \left\{ \begin{array}{lll} y_{0}(x)=\displaystyle \frac{1}{2},\\ y_{j+1}(x)=-I^{\alpha ,h}_{0+}\left( \gamma y_{j}(x)+\mu B_{j}(x)\right) ,\quad \quad j\ge 0, \end{array} \right. \end{aligned}$$
(42)

and

$$\begin{aligned} B_{j}(x)=\displaystyle \frac{1}{j!}\left[ \displaystyle \frac{d^{j}}{d\lambda ^{j}} \left( \displaystyle \sum _{i=0}^{\infty } \lambda ^{i}y_{i}(x) \right) ^{3}\right] _{\lambda =0},\quad \quad j\ge 0. \end{aligned}$$
(43)

In Tables 4, 5 and 6, we exhibit approximate solutions produced using our modified scheme of ADM (\(y_{ADM}\)) when \(N=10\) and the approximate solutions produced using the universal P-C method (\(y_{P-C}\)) to the IVP (40), for some value of \(\alpha \) and \(\rho \), with three cases of the function h (\(h(x)=x^{\rho }\), \(h(x)=\exp (\rho x)\) and \(h(x)=\log (\rho x+1)\)), where \(\gamma =2\) and \(\mu =1\). Furthermore, the solution behavior of the fractional model given in the IVP (40) regarding the different cases of the function h against the variable x is described in Fig. 4. Figure 4 pictures approximate solutions produced using our modified scheme when \(N=10\) and the approximate solutions produced using the universal P-C method, where \(h(x)=x^{\rho }\), \(h(x)=\exp (\rho x)\) and \(h(x)=\log (\rho x+1)\), when \(\alpha =2\), \(\rho =1\), \(\gamma =2\) and \(\mu =1\).

Table 4 Numerical solutions to the IVP (40) for some values of \(\alpha \) and \(\rho \) with \(h(x)=x^{\rho }\)
Full size table
Table 5 Numerical solutions to the IVP (40) for some values of \(\alpha \) and \(\rho \) with \(h(x)=\exp (\rho x)\)
Full size table
Table 6 Numerical solutions to the IVP (40) for some values of \(\alpha \) and \(\rho \) with \(h(x)=\log (\rho x+1)\)
Full size table
Fig. 4
figure 4

Plots of approximate solutions for the IVP (40) when \(\alpha =2\) and \(\rho =1\): Modified scheme of ADM (blue line); Universal P-C method (red line)

Full size image

Clearly, from the numerical results displayed in Tables 4, 5 and 6 and Fig. 4, we can deduce that the approximate solutions produced using our modified scheme of ADM are in high agreement with those obtained using the universal P-C method. The accuracy of the approximate solutions provided using our scheme can be improved when N becomes large.

Example 3

Finally, we consider the fractional IVP

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\;^{C}D^{\alpha ,h}_{0+}u(x,t)=\displaystyle \frac{\partial ^z}{\partial x^{2}}u(x,t)+a\,u(x,t)-b\,u^{2}(x,t) ,\quad \quad 0<\alpha \le 1,\quad \quad t>0, \\ &{}\;\;\;\;\;u(x,0)=\displaystyle \frac{1}{\left( \sqrt{\frac{b}{a}}+\exp \left( \sqrt{\frac{a}{6}}x\right) \right) ^{2}}, \end{array}\right. \end{aligned}$$
(44)

where \(a,b>0\) and \(\;^{C}D_{0+}^{\alpha ,h}\) is the G-C fractional derivative operator with respect to the variable t of order \(\alpha \). The exact solution of the IVP (44), when \(h(t)=t\) and \(\alpha =1\), is given by [46]

$$\begin{aligned} u(x,t)=\displaystyle \frac{1}{\left( \sqrt{\frac{b}{a}}+\exp \left( \sqrt{\frac{a}{6}}x - \frac{5 a}{6} t \right) \right) ^{2}}. \end{aligned}$$
(45)

Applying the integral operator \(I^{\alpha ,h}_{0+}\) with respect to the variable t to both sides of Eq. (44), using Theorem 1, we obtain

$$\begin{aligned} u(x,t)=\displaystyle \frac{1}{\left( \sqrt{\frac{b}{a}}+\exp \left( \sqrt{\frac{a}{6}}x\right) \right) ^{2}}+I^{\alpha ,h}_{0+}\left( \displaystyle \frac{\partial ^z}{\partial x^{2}}u(x,t)+a\,u(x,t)-b\,u^{2}(x,t)\right) . \end{aligned}$$
(46)

Our modified scheme suggests the series solution \(u(x,t)=\sum _{j=0}^{\infty }u_{j}(x,t)\), such that the nonlinear term \(\mathcal {N}(u)=u^{2}\) be expressed as \(u^{2}(x,t)=\sum _{j=0}^{\infty }C_{j}(x,t)\), where the component function \(u_{j}(x,t)\), \(j = 0, 1, \cdots \), can be obtained recursively by using the formula

$$\begin{aligned} \left\{ \begin{array}{lll} u_{0}(x,t)=\displaystyle \frac{1}{\left( \sqrt{\frac{b}{a}}+\exp \left( \sqrt{\frac{a}{6}}x\right) \right) ^{2}},\\ u_{j+1}(x,t)=I^{\alpha ,h}_{0+}\left( \displaystyle \frac{\partial ^z}{\partial x^{2}}u_{j}(x,t)+a\,u_{j}(x,t)-b \,C_{j}(x,t)\right) ,\quad \quad j\ge 0, \end{array} \right. \end{aligned}$$
(47)

and

$$\begin{aligned} C_{j}(x,t)=\displaystyle \frac{1}{j!}\left[ \displaystyle \frac{d^{j}}{d\lambda ^{j}} \left( \displaystyle \sum _{i=0}^{\infty } \lambda ^{i}u_{i}(x,t) \right) ^{2}\right] _{\lambda =0},\quad \quad j\ge 0. \end{aligned}$$
(48)

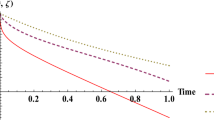
Here, to examine the accuracy of the suggested algorithm, we evaluated approximate solutions of the fractional model given in the IVP (44) in the case of fixation of the space variable x. In Tables 7, 8, 9 and 10, we show approximate solutions produced using our modified scheme of ADM (\(y_{ADM}\)) when \(N=10\) and \(x=1\) to the IVP (44), for some value of \(\alpha \), \(\rho \), a and b with three cases of the function h (\(h(t)=t^{\rho }\), \(h(t)=\exp (\rho t)\) and \(h(t)=\log (\rho t+1)\)). Figure 5 pictures approximate solutions produced using our modified scheme when \(x=1\) and \(N=10\) against the exact solution of the IVP (44) where \(\alpha =1\) and \(\rho =1\) for some values of a and b. In Fig. 6, we draw the absolute error of the approximate solutions obtained using our modified scheme when \(h(t)=t\) and \(\alpha =1\), where \(x=1\).

Table 7 Numerical solutions to the IVP (44) for some values of \(\alpha \) and \(\rho \), when \(a =1.25\) and \(b=2.75\), with \(h(t)=t^{\rho }\) and \(x=1\)
Full size table
Table 8 Numerical solutions to the IVP (44) for some values of \(\alpha \) and \(\rho \), when \(a =1.25\) and \(b=2.75\), with \(h(t)=\exp (\rho t)\) and \(x=1\)
Full size table
Table 9 Numerical solutions to the IVP (44) for some values of \(\alpha \) and \(\rho \), when \(a =1.25\) and \(b=2.75\), with \(h(t)=\log (\rho t +1)\) and \(x=1\)
Full size table
Table 10 Numerical solutions to the IVP (44) for some values of \(\alpha \) and \(\rho \), when \(a =3\) and \(b=8\), with \(h(t)=t^{\rho }\) and \(x=1\)
Full size table
Fig. 5
figure 5

Plots of approximate solutions and exact solution for the IVP (44) when \(h(t)=t\) and \(\alpha =1\), where \(x=1\): Exact solution (black line); Modified scheme of ADM (blue line)

Full size image
Fig. 6
figure 6

Plots of absolute error for the IVP (44) when \(h(t)=t\) and \(\alpha =1\), where \(x=1\)

Full size image

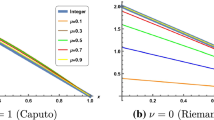
Clearly, from the numerical results displayed in Tables 7 and 10 and Figs. 5 and 6, where the exact solution is known, we can observe that the approximate solutions produced using our modified scheme of ADM are very close to the exact solution. Figs. 7 and 8 show the solution behavior of the fractional model given in the IVP (44) regarding the different cases of the function h against the variable t when \(x=1\). They picture approximate solutions produced using our modified scheme of ADM when \(N=10\) for some values of \(\alpha \), \(\rho \), a and b.

Fig. 7
figure 7

Plots of modified scheme of ADM approximate solutions for the IVP (44) when \(a=1.25\) and \(b=2.75\), where \(x=1\): \(\alpha =0.95\), \(\rho =0.75\) (black); \(\alpha =0.925\), \(\rho =0.8\) (blue); \(\alpha =0.9\), \(\rho =0.85\) (red); \(\alpha =0.8\), \(\rho =0.9\) (green)

Full size image
Fig. 8
figure 8

Plots of modified scheme of ADM approximate solutions for the IVP (44) when \(a=3\) and \(b=8\), where \(x=1\): \(\alpha =0.95\), \(\rho =0.75\) (black); \(\alpha =0.925\), \(\rho =0.8\) (blue); \(\alpha =0.9\), \(\rho =0.85\) (red); \(\alpha =0.8\), \(\rho =0.9\) (green)

Full size image

Conclusion

In this work, a modified scheme of the ADM has been developed for the treatment of IVPs involving FDEs with the studied G-C fractional derivatives. We have employed some special cases of the function h for the numerical simulation task. There are some concluding remarks to be discussed here. Firstly, the proposed scheme has been successfully implemented to provide approximate analytical solutions to the considered fractional models. Secondly, the results of the discussed test problems confirm that the approximate solutions produced by the proposed scheme of ADM are close to the exact solution in the integer-order case when \(h(x)=x\) and are highly compatible with those obtained using the universal P-C method in the other cases. Thirdly, it is believed that the proposed scheme of the ADM can be further implemented in exhibiting approximate analytical solutions for several models involving the studied G-C fractional derivatives.