1 Introduction

In recent years many complex physical problems employ fractional integral as it can describe the cumulation of some quantity better than the regular integral. It is hard to deny that, in some cases, the fractional derivative is accurate and effective over the integer order. For example, in problems involving Newtonian fluids and viscoelastic fluids in the study of emulsion plastics, signal processing, control and dynamical systems, electrochemistry of corrosion, etc., the role of the fractional derivative is extensive.

Research articles based on various methods of solving fractional order developed strongly. Solving non-linear differential equations has always fascinated researchers. While considering the different techniques involved in solving the differential equation, Adomian [1] introduced the decomposition method for solving various differential equations, especially for the differential equation that emerged in stochastic problems. Numerous research articles are available in past history and recent times that deal with the Adomian decomposition method (ADM), including the recent article by Zeiden et al. [35]. Homotopy perturbation method (HPM) which is merger between homotopy method and perturbation method was initially given by He [12]. His contribution to homotopy perturbation is extensive, including his recent work with El-Dib [13]. Wu and Lee [30] gave another tool to study the fractional order system on the modified Riemann–Liouville derivative using the variational iteration method (VIM).

The solution of fractional order differential equations is studied by many researchers and has several applications in real-time problems. Iyiola and Zaman [17] applied fractional order to solve cancer model, Yang et al. [34] studied one-dimensional fractional order heat equation, Shah et al. [25] analyzed time-fractional diffusion equation through numerical approach and so on. Other methods of solving fractional order differential equations include the finite element method by Zeng et al. [36], differential transform method by Secor [24] to find the analytic solution of fractional heat and wave-like equations, natural decomposition method by Rawashdeh [23] and Khan et al. [19]. Laplace transform is widely used for solving fractional differential equations. In literature, the He-Laplace method is used when coupled with the homotopy perturbation method. Moreover, the Laplace transform makes the variational iteration method much more straightforward. Many analytical solutions for various mathematical models of the chemical process involve Laplace transform technique. Few articles that describe the application of the Laplace transform in chemical engineering are available in the literature, for example, the work of Kolev and Linden [21] to find the solution of the partial differential equation describing time-dependent two, three-dimensional transport phenomena. The result of Ahmed and Batin [2] to investigate the effects of conduction-radiation and porosity of the porous medium on a laminar convective heat transfer flow utilized Laplace transform method to solve the boundary layer equations analytically. Using Laplace iteration method, Yan [33] worked on solving Fokker-Plank equation. The work of Srivastava and his collaborators on applications of fractional order equations in real-life problems [26,27,28] can be referred for interested readers, and more exciting works involving other fractional derivatives can be found in [3, 9, 16, 18, 32].

In this regard, other than the solution of the differential equation with the Liouville–Caputo derivative, solutions of differential equations with other derivative orders are discussed in significantly fewer numbers. He’s fractional derivative and two-scale derivatives are some of the well-known fractional derivatives used in the fractal vibration model, which can eliminate the drawback of traditional theories. A detailed analysis of such results is available in [10, 11, 14]. In particular, the numerical and analytic analysis of the Hilfer fractional derivative, which is studied in this paper, is new in this direction. The results are helpful in learning the analogy between Liouville–Caputo and Riemann–Liouville’s order differential equation. Hilfer fractional derivative was given by Hilfer [15] when he wanted a generalized Riemann–Liouville derivative for the glass-forming differential system. Research based on the Hilfer fractional order started to rise after the proof of the existence of solution of Cauchy problem with Hilfer fractional derivative given by Furati et al. [6] and by Gu and Trujillo [8].

This paper is devoted mainly to applying the modified Laplace iterative transform method on various dimensional fractional systems with Hilfer fractional derivative. The observations show different characteristic behavior when the type of Hilfer fractional derivative shuttles between Liouville–Caputo and Riemann–Liouville derivative order. The paper is arranged so that Sect. 2 contains the preliminary definitions required for further sections. Section 3 holds the procedure that is applied in the differential equations. Section 4 is the application part of the derived method. This section deals with both graphical and numerical evaluation. The conclusion thus acquired is written in detail in Sect. 5.

2 Preliminaries

The corresponding Riemann–Liouville fractional derivative operators \(^{RL}D^{\mu }_{a+}\) and \(^{RL}D^{\mu }_{a-}\) are given by [22]

$$\begin{aligned} \left( {}^{RL}I^{\mu }_{a+}g\right) (t)=\dfrac{1}{\Gamma (\mu )}\int ^{t}_{a}(t-s)^{\mu -1}g(s)ds, \left( t>a; {\mathfrak {R}}(\mu )>0\right) ,\\ \left( {}^{RL}I^{\mu }_{a-}g\right) (t)=\dfrac{1}{\Gamma (\mu )}\int ^{a}_{t}(s-t)^{\mu -1}g(s)ds, \left( t<a; {\mathfrak {R}}(\mu )>0\right) , \end{aligned}$$

and

$$\begin{aligned} \left( ^{RL}D^{\mu }_{a\pm }\right) g(t)=\left( \pm \dfrac{d}{dt}\right) ^{n}\left( I^{n-\mu }_{a\pm }g\right) (t),\left( {\mathfrak {R}}(\mu )\ge 0; n=[{\mathfrak {R}}(\mu )]+1\right) . \end{aligned}$$

Definition 2.1

[8] The Hilfer fractional derivative of order \(0< \mu <1\) and type \(0\le \nu \le 1\) of function g(t) is defined by

$$\begin{aligned} \left( D^{\mu ,\nu }_{a\pm }g\right) (t)=\left( I_{a\pm }^{\nu (1-\mu )}D\big (I_{a\pm }^{(1-\nu )(1-\mu )}g\big )\right) (t), \end{aligned}$$
(2.1)

where \(D:=\dfrac{d}{dt}\). The above given generalization (2.1) reduces to the classical Riemann–Liouville fractional derivative for a particular case when \(\nu =0\). And when \(\nu =1\), the definition (2.1) reduces to classical Liouville–Caputo derivative. The Liouville–Caputo derivative is generally defined as follows:

Definition 2.2

[22] The Liouville–Caputo derivative of order \(\mu >0\) for a function \(g:[0,\infty )\rightarrow {\mathbb {R}}\) is defined by

$$\begin{aligned} ^{C}D^{\mu }_{t}g(t)=\dfrac{1}{\Gamma (n-\mu )}\int ^{t}_{0}(t-s)^{n-\mu -1}g^{(n)}(s)ds, t>0,n-1< \mu <n, \end{aligned}$$

where \(\Gamma (\cdot )\) is the (Euler’s) Gamma function.

Definition 2.3

[20] The Mittag–Leffler function with one parameter \(\alpha\) and two parameters \(\alpha\) and \(\beta\) are given respectively by

$$\begin{aligned} E_{\alpha }(z)=\sum _{k=0}^{\infty }\dfrac{z^{k}}{\Gamma (\alpha k+1)} \text{ and }E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }\dfrac{z^{k}}{\Gamma (\alpha k+\beta )} \end{aligned}$$
(2.2)

where \(z, \alpha , \beta \in {\mathfrak {C}}\) , \(\Re (\alpha )>0\) and for \(\beta =1\), it is clear that \(E_{\alpha }(z)=E_{\alpha ,1}(z)\).

Definition 2.4

(see, [29, p. 798]) The Laplace transform of Hilfer derivative is given by

$$\begin{aligned} {\mathcal {L}}[D_{t}^{\mu ,\nu }g(t)]=s^{\mu }{\mathcal {L}}[g(t)]-\sum _{i=0}^{m-1}s^{m(1-\nu )+\mu \nu -i-1}\left( {}^{RL}I_{0+}^{(1-\nu )(m-\mu )-i}g\right) (0^{+}), \end{aligned}$$
(2.3)

where \(\left( {}^{RL}I_{0+}^{(1-\nu )(m-\mu )-i}g\right) (0^{+})\) is the Riemann–Liouville fractional integral.

3 Laplace iterative method for Hilfer fractional derivative

A new iterative method using \(\rho\)-Laplace transform was given by Bhangale et al. [4]. This chapter considers the same procedure for \(\rho =1\), and Hilfer fractional derivative is employed instead of the Liouville–Caputo generalized fractional derivative. It is to be noted that, Daftardar-Gejji and Jafari in [5] gave this basic iterative procedure, where they discussed the fractional diffusion-wave equation. As given by Bhangale et al. [4], any functional equation can be written as

$$\begin{aligned} u=g+L(u)+N(u), \end{aligned}$$
(3.1)

where g is the given function, L(u) is the linear function of u and N(u) is the nonlinear function of u. The solution is given by the series

$$\begin{aligned} u=\displaystyle \sum _{k=0}^{\infty }u_{k}=u_{0}+u_{1}+u_{2}+u_{3}+\cdots . \end{aligned}$$
(3.2)

General linear and nonlinear terms in equation (3.1) separately can be written as

$$\begin{aligned} L(u)=&\sum _{k=0}^{\infty }L(u_{k}),\end{aligned}$$
(3.3)
$$\begin{aligned} N(u)=&N(u_{0})+\sum _{k=0}^{\infty }\left[ N\bigg (\sum _{l=0}^{k}u_{l}\bigg )-N\bigg (\sum _{l=0}^{k-1}u_{l}\bigg )\right] . \end{aligned}$$
(3.4)

From equations (3.2), (3.3) and (3.4), it can be seen that (3.1) is equivalent to

$$\begin{aligned} u=\displaystyle \sum _{k=0}^{\infty }u_{k}=g+\sum _{k=0}^{\infty }L(u_{k})+N(u_{0})+\sum _{k=1}^{\infty }\left[ N\bigg (\sum _{l=0}^{k}u_{l}\bigg )-N\bigg (\sum _{l=0}^{k-1}u_{l}\bigg )\right] . \end{aligned}$$
(3.5)

The terms in the above series can be written as,

$$\begin{aligned} u_{0}=&g,u_{1}\,=\,L(u_{0})+N(u_{0}),\\ u_{n+1}\,=\,&L(u_{n})+\left[ N\bigg (\sum _{k=0}^{n}u_{k}\bigg )-N\bigg (\sum _{l=0}^{n-1}u_{k}\bigg )\right] ,n=1,2,\ldots \end{aligned}$$

A general nonlinear Hilfer fractional initial value problem can be defined as

$$\begin{aligned} D^{\mu ,\nu }_{0+}u(x,t)+Nu(x,t)\,=\,g(x,t), 0<\mu <1, 0\le \nu \le 1, \end{aligned}$$
(3.6)

with the initial condition \(I_{0+}^{(1-\mu )(1-\nu )}u(x,0)\). Applying the Laplace transform for Hilfer fractional derivative defined in (2.3) on each terms of the equation (3.6), gives

$$\begin{aligned} s^{\mu }{\bar{u}}(x,s)-s^{\nu (\mu -1)}[I_{0+}^{(1-\mu )(1-\nu )}u(x,0)]={\mathcal {L}}[g(x,t)]-{\mathcal {L}}[Nu(x,t)]. \end{aligned}$$

Simplification of the above equation reduces to

$$\begin{aligned} {\bar{u}}(x,s)=\dfrac{[I_{0+}^{(1-\mu )(1-\nu )}u(x,0)]}{s^{\lambda }}+\dfrac{{\mathcal {L}}[g(x,t)]}{s^{\mu }}-\dfrac{{\mathcal {L}}[N(u(x,t))]}{s^{\mu }}. \end{aligned}$$
(3.7)

By taking the inverse Laplace transform on both sides of equation (3.7), the following equation is obtained.

$$\begin{aligned} u(x,t)=&\dfrac{t^{\lambda -1}}{\Gamma (\lambda )}[I_{0+}^{(1-\mu )(1-\nu )}u(x,0)]+{\mathcal {L}}^{-1}\big [s^{-\mu }{\mathcal {L}}[g(x,t)]\big ]+{\mathcal {L}}^{-1}\big [s^{-\mu } {\mathcal {L}}[N(u(x,t))]\big ]. \end{aligned}$$

The other terms L(u) and N(u) can be estimated by comparing with (3.3) and (3.4), respectively. The terms of the new iterative method applied in the Hilfer fractional differential equation are summarized below.

$$\begin{aligned} g=\dfrac{t^{\lambda -1}}{\Gamma (\lambda )}[I_{0+}^{(1-\mu )(1-\nu )}&u(x,0)],L(u)={\mathcal {L}}^{-1}\big [s^{-\mu }{\mathcal {L}}[g(x,t)]\big ],\nonumber \\ N(u)&={\mathcal {L}}^{-1}\big [s^{-\mu }{\mathcal {L}}[N(u(x,t))]\big ],\nonumber \\ \sum _{k=0}^{\infty }u_{k}&=g+L\left( \sum _{k=0}^{\infty }u_{k}\right) +N\left( \sum _{k=0}^{\infty }u_{k}\right) . \end{aligned}$$
(3.8)

The above mentioned procedure is simple and the error is minimum.

4 Applications

The above-mentioned iterative method can be applied to linear and nonlinear fractional differential equations to obtain an iterative solution that reduces to the exact solution in closed form. The value \(\nu\) can be altered to switch between the Liouville–Caputo and the Riemann–Liouville fractional order differential equations.

Example 1

Consider the one-dimensional linear Hilfer fractional heat equation:

$$\begin{aligned} \left\{ \begin{array}{ll} D^{\mu ,\nu }_{0+}u(x,t)=u_{xx},0<\mu <1,0 \le \nu \le 1,t\ge 0,\\ I_{0+}^{(1-\mu )(1-\nu )}u(x,0)=2-1.5x+\sin (\pi x),0\le x\le 1. \end{array} \right. \end{aligned}$$
(4.1)

Taking the Laplace transform on each terms of the given heat equation (4.1), we get

$$\begin{aligned} s^{\mu }{\bar{u}}(x,s)-s^{\nu (\mu -1)}I_{0+}^{(1-\mu )(1-\nu )}u(x,0)={\mathcal {L}}[u_{xx}]. \end{aligned}$$

Using the initial conditions given in problem (4.1), the above equation reduces to

$$\begin{aligned} s^{\mu }&{\bar{u}}(x,s)=\left( s^{\nu (\mu -1)}(2-1.5x+\sin (\pi x))\right) +{\mathcal {L}}[u_{xx}]\\ \Longrightarrow&{\bar{u}}(x,s)=\dfrac{\left( 2-1.5x+\sin (\pi x)\right) }{s^{\lambda }}+\dfrac{{\mathcal {L}}[u_{xx}]}{s^{\mu }}. \end{aligned}$$

Applying the inverse Laplace transform of each term in the above equation gives

$$\begin{aligned} u(x,t)={\mathcal {L}}^{-1}\Big [\dfrac{\left( 2-1.5x+\sin (\pi x)\right) }{s^{\lambda }}\Big ]+{\mathcal {L}}^{-1}\Big [\dfrac{{\mathcal {L}}[u_{xx}]}{s^{\mu }}\Big ]. \end{aligned}$$

Using the Laplace iterative method (3.8), the recursive terms of the solution are given by

$$\begin{aligned} g={\mathcal {L}}^{-1}\Big [\dfrac{\left( 2-1.5x+\sin (\pi x)\right) }{s^{\lambda }}\Big ],L(u)={\mathcal {L}}^{-1}\Big [\dfrac{{\mathcal {L}}[u_{xx}]}{s^{\mu }}\Big ]. \end{aligned}$$

Accordingly, a few terms in the series are obtained as follows

$$\begin{aligned} u_{0}=&\,\dfrac{t^{\lambda -1}}{\Gamma (\lambda )}(2-1.5x+\sin (\pi x)),\\ u_{1}=&\, L(u_{0})={\mathcal {L}}^{-1}\Big [\dfrac{{\mathcal {L}}[t^{\lambda -1}(-\pi ^{2})\sin (\pi x)]}{s^{\mu }\Gamma (\lambda )}\Big ]=-\pi ^{2}\sin (\pi x){\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu +\lambda }}\Big ],\\ u_{1}=&\,\dfrac{-\pi ^{2}\sin (\pi x) (t)^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )}. \end{aligned}$$

The successive terms of the solution are obtained in a similar way

$$\begin{aligned} u_{2}= L(u_{1})={\mathcal {L}}^{-1}\Big [\dfrac{{\mathcal {L}}[t^{\mu +\lambda -1}(\pi ^{4})\sin (\pi x)]}{s^{\mu }\Gamma (\lambda )}\Big ]=\dfrac{\pi ^{4}\sin (\pi x) (t)^{2\mu +\lambda -1}}{\Gamma (2\mu +\lambda )}. \end{aligned}$$

The series solution can thus be written as

$$\begin{aligned} u(x,t)=&\,u_{0}+u_{1}+u_{2}+\cdots \\ \Longrightarrow u(x,t)=&\,\dfrac{t^{\lambda -1}}{\Gamma (\lambda )}\big (2-1.5x+\sin (\pi x)\big )+\dfrac{(-\pi ^{2})\sin (\pi x) (t)^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )}\\&\quad +\dfrac{\pi ^{4}\sin (\pi x) (t)^{2\mu +\lambda -1}}{\Gamma (2\mu +\lambda )}+\cdots \end{aligned}$$

With the help of Definition 2.2, the series form of solution for the Hilfer fractional one-dimensional heat equation (4.1) is derived as

$$\begin{aligned} u(x,t)=\sin (\pi x)t^{\lambda -1}E_{\mu ,\lambda }(-\pi ^{2}t^{\mu })+\dfrac{2t^{\lambda -1}}{\Gamma (\lambda )}-\dfrac{1.5 x t^{\lambda -1}}{\Gamma (\lambda )}. \end{aligned}$$
(4.2)

The derived solution reduces to the exact solution \(u(x,t)=\sin (\pi x)e^{-\pi ^{2}t}+2-1.5x\) in closed form when \(\mu =1\). A detailed analysis of the solution, for various values of \(0<\mu <1\) with \(\nu =0\) and \(\nu =1\) is discussed below.

Fig. 1
figure 1

Analytical solution for different values of \(\mu\) and \(t=0.5\) in Example 1

Full size image
Fig. 2
figure 2

3D plot when \(\mu =0.9\)

Full size image

Observation 1

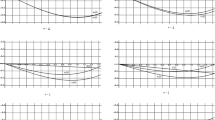
From Fig. 1a, it is clear that the iterated solution for the case \(\nu =1\), and for nearly all values of \(0<\mu <1\), is proximate to the exact solution. When \(\nu =0\) and \(0<\mu <1\), the derived solution reduces to a fractional-order system with the Riemann–Liouville derivative. From Fig. 1b, it can be observed that the trajectory of the derived solution with \(\nu =0\) is not very close to the trajectory of the exact solution except for the higher values of \(\nu\). The 3D plot in Fig. 2 represents the comparative display of the exact solution and the derived solution for various values of \(\nu\) and \(\mu =0.9\). As the value of \(\nu\) increases from 0 to 1, the solution of the fractional-order system (4.1) approaches the exact solution faster and closer.

Fig. 3
figure 3

Error analysis of Example 1 for \(t=0.5\)

Full size image

Observation 2

Figure 3 exhibits the variation between the derived solution and the exact solution for two values, \(\mu =0.9\) and \(\mu =0.1\), with three different values of \(\nu\). It can be noticed that the deviation of the fractional order from the integer order attains zero when \(\mu =0.9\) or \(\mu =0.1\) with \(\nu =1\). The variation is still minimum for the case \(\nu =0.5\) and \(\mu =0.9\). To conclude, the deviation is maximum for lower values of \(\nu\), lower values of \(\mu\), and lower values of x.

Example 2

Consider the one-dimensional linear time fractional heat-like model with Hilfer derivative for \(1<\mu <2\) [3]:

$$\begin{aligned} D^{\mu ,\nu }_{0+}u(x,t)-\dfrac{x^{2}}{2}u_{xx}=0, 1<\mu<2, 0 \le \nu \le 1, 0<t<1, \end{aligned}$$
(4.3)

with initial conditions,

$$\begin{aligned} I_{0+}^{(1-\mu )(1-\nu )}u(x,0)=x,I_{0+}^{(1-\mu )(2-\nu )-1}u(x,0)=x^{2},-1<x<1. \end{aligned}$$
(4.4)

Applying the Laplace transform on each term of the heat equation and using Eq. (2.3), gives

$$\begin{aligned} s^{\mu }{\bar{u}}(x,s)=&\,s^{\nu (\mu -2)+1}I_{0+}^{(1-\mu )(2-\nu )}u(x,0)+ s^{\nu (\mu -2)}I_{0+}^{(1-\mu )(2-\nu )-1}u(x,0)+\dfrac{x^{2}}{2}{\mathcal {L}}[u_{xx}]. \end{aligned}$$

Now, on substituting the initial conditions given in the problem (4.4) in the above equation, it is found that

$$\begin{aligned} {\bar{u}}(x,s)=\dfrac{x}{s^{\lambda +\nu -1}}+\dfrac{x^{2}}{s^{\lambda +\nu }}+\dfrac{x^{2}}{2}\dfrac{1}{s^{\mu }}{\mathcal {L}}[u_{xx}]. \end{aligned}$$

Taking the inverse Laplace transform of the above equation, gives

$$\begin{aligned} u(x,t)=\dfrac{xt^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+\dfrac{x^{2}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}+ \dfrac{x^{2}}{2}{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu }}{\mathcal {L}}[u_{xx}]\Big ]. \end{aligned}$$

Using the derived Laplace iterative method (3.8), the recursive terms of series solution are obtained as

$$\begin{aligned} g=\dfrac{xt^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+\dfrac{x^{2}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )},L(u)=\dfrac{x^{2}}{2}{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu }}{\mathcal {L}}{(u_{xx})}\Big ]. \end{aligned}$$

The other few terms in the series can be calculated as follows:

$$\begin{aligned} u_{0}=&\,\dfrac{xt^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+\dfrac{x^{2}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )},\\ u_{1}=&\,L(u_{0})=\dfrac{x^{2}}{2}{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{2t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}\Big ]\Bigg ] =x^{2}{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu +\nu +\lambda }}\Big ],\\ \Longrightarrow u_{1}=&\,\dfrac{x^{2}t^{\mu +\lambda +\nu -1}}{\Gamma (\mu +\lambda +\nu )}. \end{aligned}$$

The successive terms of the series solution are obtained in the following similar way.

$$\begin{aligned} u_{2}= L(u_{1})={\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{x^{2}t^{\mu +\lambda +\nu -1}}{\Gamma (\mu +\lambda +\nu )}\Big ]\Bigg ]= \dfrac{x^{2}t^{2\mu +\lambda +\nu -1}}{\Gamma (2\mu +\lambda +\nu )}. \end{aligned}$$

The solution in series form can thus, be written as

$$\begin{aligned} u(x,t)=&\,u_{0}+u_{1}+u_{2}+\cdots \\ \Longrightarrow u(x,t)=&\,\dfrac{xt^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+\dfrac{x^{2}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )} +\dfrac{x^{2}t^{\mu +\lambda +\nu -1}}{\Gamma (\mu +\lambda +\nu )} +\dfrac{x^{2}t^{2\mu +\lambda +\nu -1}}{\Gamma (2\mu +\lambda +\nu )}+\cdots . \end{aligned}$$

Using Definition 2.2, the solution of the Hilfer fractional one dimensional heat equation (4.3) reduces to

$$\begin{aligned} u(x,t)=\dfrac{xt^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+x^{2}t^{\lambda +\nu -1}E_{\mu ,\lambda +\nu }(t^{\mu }). \end{aligned}$$
(4.5)

It can observed that the derived solution converges to the exact solution \(x+x^{2}\sinh t\) in a closed form. Further analysis of the trajectory of the iterated solution when \(1<\mu <2\) with \(\nu =0\) and \(\nu =1\) is given separately.

Fig. 4
figure 4

Plot of Example 2 for \(t=0.5\)

Full size image

Observation 3

Figure 4 clearly illustrates the trajectory of the fractional-order solution and the exact solution for the case \(\nu =0\) and \(\nu =1\). The difference of the fractional order from the integer value is minimum for positive values of x. The plot in Fig. 4a clearly explains that the derived solution for the Liouville–Caputo order traces the exact solution path very closely.

Fig. 5
figure 5

Deviation when \(-1<x<1\) in Example 2

Full size image

Observation 4

Figure 5 sketches the error difference between the series solution and the exact solution for two different values of \(\mu\) with three values of \(\nu\) of the integral. At this point, it is essential to mention the fact that the plot given by Khan et al. [19] has some constraints. Even though their graph is for \(0<\mu \le 1\), the hypothesis of their result is given for \(1<\mu \le 2\). Hence their plot requires a different analysis.

Example 3

Consider the two-dimensional Hilfer fractional wave equation:

$$\begin{aligned} D^{\mu ,\nu }_{0+}u(x,y,t)=\dfrac{y^{2}}{2}u_{yy}+\dfrac{x^{2}}{2}u_{xx}, 0<\mu <1, 0 \le \nu \le 1, 0 \le t\le 1, \end{aligned}$$
(4.6)

with initial conditions,

$$\begin{aligned} I_{0+}^{(1-\mu )(1-\nu )}u(x,y,0)=y^{2}. \end{aligned}$$
(4.7)

Taking the Laplace transform (2.3) on both sides of the given wave equation (4.6), gives

$$\begin{aligned} s^{\mu }{\bar{u}}(x,y,t)=&\,s^{\nu (\mu -1)}[I_{0+}^{(1-\mu )(1-\nu )}u(x,y,0)]+{\mathcal {L}}\Big [\dfrac{y^{2}}{2}u_{yy}\Big ]+{\mathcal {L}}\Big [\dfrac{x^{2}}{2}u_{xx}\Big ]. \end{aligned}$$

Substituting the initial condition given in (4.7) in the above equation leads to

$$\begin{aligned} {\bar{u}}(x,y,t)=\dfrac{y^{2}}{s^{\lambda }}+\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{y^{2}}{2}u_{xx}\Big ] +\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{x^{2}}{2}u_{yy}\Big ]. \end{aligned}$$

The inverse Laplace transform is applied to each term to get the series solution. This means,

$$\begin{aligned} u(x,y,t)=\dfrac{y^{2}t^{\lambda -1}}{\Gamma (\lambda )}+{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{y^{2}}{2}u_{xx}\Big ]\Bigg ] +{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{x^{2}}{2}u_{yy}\Big ]\Bigg ]. \end{aligned}$$

From the iterative method, the general following recursive term can be found as

$$\begin{aligned} u_{0}=\dfrac{y^{2}t^{\lambda -1}}{\Gamma (\lambda )}, L(u)={\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{y^{2}}{2}u_{xx}\Big ]\Bigg ] +{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{x^{2}}{2}u_{yy}\Big ]\Bigg ]. \end{aligned}$$

Few iterative terms are obtained as follows:

$$\begin{aligned} u_{1}&=L(u_{0})=\dfrac{x^{2}t^{\lambda -1}}{\Gamma (\lambda )}{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu +\lambda }}\Big ]=x^{2}\dfrac{t^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )},\\ u_{2}&=L(u_{1})=y^{2}\dfrac{t^{2\mu +\lambda -1}}{\Gamma (2\mu +\lambda )},\cdots . \end{aligned}$$

The series solution is given by

$$\begin{aligned} u(x,y,t)=&\,u_{0}+u_{1}+u_{2}+\cdots \\ \Longrightarrow u(x,y,t)=&\, x^{2}t^{\lambda -1}\Bigg (\dfrac{t^{\mu }}{\Gamma (\mu +\lambda )}+\dfrac{t^{3\mu }}{\Gamma (3\mu +\lambda )}+\dfrac{t^{5\mu }}{\Gamma (5\mu +\lambda )}+\cdots \Bigg )\\&\quad + y^{2}t^{\lambda -1}\Bigg (\dfrac{1}{\Gamma (\lambda )}+\dfrac{t^{\mu }}{\Gamma (2\mu +\lambda )}+\dfrac{t^{4\mu }}{\Gamma (4\mu +\lambda )}+\cdots \Bigg ). \end{aligned}$$

Using Definition 2.2, the solution obtained is given by

$$\begin{aligned} u(x,y,t)=x^{2}t^{\mu +\lambda -1}E_{2\mu ,\mu +\lambda }(t^{2\mu })+y^{2}t^{\lambda -1}E_{2\mu ,\lambda }(t^{2\mu }). \end{aligned}$$
(4.8)

The exact solution in closed form of this wave equation is given by

$$\begin{aligned} u(x,y,t)=x^{2}\sinh t+y^{2}\cosh t. \end{aligned}$$

The iterated solution reduces to the exact solution when \(\mu =1\). For the values \(0<\mu <1\), the table explains that the difference between the fractional-order solution and the exact solution is very minimum for various fractional order and type.

Observation 5

Table 1 displays the difference between the fractional-order solution and the exact solution for various values of \(\mu\) with \(\nu =0\). The error difference in the last column is calculated between the values of the iterated solution when \(\mu =0.9\) and the exact solution. These values are calculated for \(t=0.5\) and for various values of x and y. It can be observed that the difference is minimum for the lower values of x and y. Table 2 displays the difference between the iterated solution and the exact solution for various values of \(\mu\) with \(\nu =1\). Similar to the previous table, the deviation between the values of the derived solution and the exact solution is minimum when \(\mu =0.9\).

Observation 6

Figure 6a explains the error when \(0\le x,y \le 1\) and \(t=0.5\), for various values of order and type of the derivative. From Figs. 6b,  7a and  7b, we can observe that for \(0\le x,y \le 1\), the trajectory of the fractional-order solution almost coincides with the trajectory of the exact solution when \(\mu =0.9\) and \(0\le \nu \le 1\). For the lower values of the fractional order, there is a considerable deviation between the trajectory of the fractional-order solution and the exact solution.

Example 4

Consider the two-dimensional non-linear Hilfer fractional wave equation:

$$\begin{aligned} D^{\mu ,\nu }_{0+}u(x,t)=\dfrac{\partial ^{2}u}{\partial x \partial y}(u_{xx})-\dfrac{\partial ^{2}u}{\partial x \partial y}(xyu_{xx}u_{yy})-u, 1<\mu <2,0\le \nu \le 1 \end{aligned}$$
(4.9)

with initial conditions,

$$\begin{aligned} I_{0+}^{(1-\mu )(1-\nu )}u(x,0)=e^{xy},I_{0+}^{(1-\mu )(2-\nu )-1}u(x,0)=e^{xy},0\le x,y \le 1. \end{aligned}$$
(4.10)

Taking the Laplace transform on both sides of the given wave equation (4.9) gives

$$\begin{aligned} s^{\mu }{\bar{u}}(x,s)&=s^{\nu (\mu -2)+1}I_{0+}^{(1-\mu )(2-\nu )}u(x,0) + s^{\nu (\mu -2)}I_{0+}^{(1-\mu )(2-\nu )-1}u(x,0)\\&\quad +{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x \partial y}(u_{xx})-\dfrac{\partial ^{2}u}{\partial x \partial y}(xyu_{xx}u_{yy})-u\Big ]. \end{aligned}$$

Substituting the initial conditions given in (4.10) in the above equation, yields

$$\begin{aligned} {\bar{u}}(x,s)=\dfrac{e^{xy}}{s^{\lambda +\nu -1}}+\dfrac{e^{xy}}{s^{\lambda +\nu }}+\dfrac{1}{s^{\mu }}{\mathcal {L}}\Bigg [\dfrac{\partial ^{2}u}{\partial x \partial y}(u_{xx})-\dfrac{\partial ^{2}u}{\partial x \partial y}(xyu_{xx}u_{yy})-u\Bigg ]. \end{aligned}$$

Taking the inverse Laplace transform of each term in the above equation leads to

$$\begin{aligned} u(x,t)&={\mathcal {L}}^{-1}\Big [\dfrac{e^{xy}}{s^{\lambda +\nu -1}}+\dfrac{e^{xy}}{s^{\lambda +\nu }}\Big ]+{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu }}{\mathcal {L}}[-u]\Big ]\\&\quad +{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x \partial y}(u_{xx})-\dfrac{\partial ^{2}u}{\partial x \partial y}(xyu_{xx}u_{yy})\Big ]\Bigg ]. \end{aligned}$$

Using the derived Laplace transform method (3.8), the terms are separated as follows:

$$\begin{aligned} g=\dfrac{e^{xy}t^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+\dfrac{e^{xy}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}, L(u)={\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu }}{\mathcal {L}}[-u]\Big ]\\ N(u)={\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x \partial y}(u_{xx})-\dfrac{\partial ^{2}u}{\partial x \partial y}(xyu_{xx}u_{yy})\Big ]\Bigg ]. \end{aligned}$$

Accordingly, the iterative terms are obtained as below,

$$\begin{aligned} u_{0}=&\,\dfrac{e^{xy}t^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}+\dfrac{e^{xy}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )},\\ u_{1}=&\,L(u_{0})+N(u_{0}). \end{aligned}$$

Here,

$$\begin{aligned} L(u_{0})=&\,{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu }}{\mathcal {L}}[u_{0}]\Big ]={\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{e^{xy}t^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)} +\dfrac{e^{xy}t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}\Big ]\Bigg ],\\ L(u_{0})=&\,e^{xy}{\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu +\lambda +\nu -1}}+\dfrac{1}{s^{\mu +\lambda +\nu }}\Big ],\\ \Longrightarrow L(u_{0})=&\,e^{xy}\left[ \dfrac{t^{\mu +\lambda +\nu -2}}{\Gamma (\mu +\lambda +\nu -1)}+\dfrac{t^{\mu +\lambda +\nu -1}}{\Gamma (\mu +\lambda +\nu )}\right] , \end{aligned}$$

and

$$\begin{aligned} N(u_{0})=&\,{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial ^{2}}{\partial x \partial y}\Big [x^{2}y^{2}e^{2xy}\Big (\dfrac{t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}+\dfrac{t^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}\Big )^{2}\Big ]\\&\quad -\dfrac{\partial ^{2}}{\partial x\partial y}\Big [x^{2}y^{2}e^{2xy}\Big (\dfrac{t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}+\dfrac{t^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}\Big )^{2}\Big ]\Big ] \Bigg ]=0. \end{aligned}$$

Hence,

$$\begin{aligned} u_{1}=-e^{xy}\left[ \dfrac{t^{\mu +\lambda +\nu -2}}{\Gamma (\mu +\lambda +\nu -1)}+\dfrac{t^{\mu +\lambda +\nu -1}}{\Gamma (\mu +\lambda +\nu )}\right] . \end{aligned}$$

Using the given iterative procedure, it can be found that \(u_{2}=L(u_{1})+N(u_{0}+u_{1})-N(u_{0})\), where

$$\begin{aligned} L(u_{1})=e^{xy}\left[ \dfrac{t^{2\mu +\lambda +\nu -2}}{\Gamma (2\mu +\lambda +\nu -1)}+\dfrac{t^{2\mu +\lambda +\nu -1}}{\Gamma (2\mu +\lambda +\nu )}\right] ,N(u_{0}+u_{1})=0,N(u_{0})=0. \end{aligned}$$

As a result, the series is written as:

$$\begin{aligned} u(x,t)=&\,u_{0}+u_{1}+u_{2}+\cdots \\ \Longrightarrow u(x,t)=&\,e^{xy}\left[ \dfrac{t^{\lambda +\nu -1}}{\Gamma (\lambda +\nu )}-\dfrac{t^{\mu +\lambda +\nu -1}}{\Gamma (\mu +\lambda +\nu )} +\dfrac{t^{2\mu +\lambda +\nu -1}}{\Gamma (2\mu +\lambda +\nu )}-\cdots \right] \\&\quad +e^{xy}\left[ \dfrac{t^{\lambda +\nu -2}}{\Gamma (\lambda +\nu -1)}-\dfrac{t^{\mu +\lambda +\nu -2}}{\Gamma (\mu +\lambda +\nu -1)}+ \dfrac{t^{2\mu +\lambda +\nu -2}}{\Gamma (2\mu +\lambda +\nu -1)}-\cdots \right] \end{aligned}$$

The series solution is thus, given by

$$\begin{aligned} u(x,t)=e^{xy}t^{\lambda +\nu -1}E_{\mu ,\lambda +\nu }(-t^{\mu })+e^{xy}t^{\lambda +\nu -2}E_{\mu ,\lambda +\nu -1}(-t^{\mu }). \end{aligned}$$
(4.11)

The exact solution of the two dimensional wave equation in closed form is given by \(u(x,t)=e^{xy}(\sin t+ \cos t).\) The exact solution is reduced from the fractional-order solution when \(\mu =2\).

Observation 7

Tables 3 and 4 gives the data clearly on how the derived solution deviates from the exact solution when \(\nu =1\) and \(\nu =0\) for various values of \(\mu\), respectively. The error difference is calculated between the values of the iterated solution when \(\mu =0.9\) and the exact solution. Further, Fig. 8 gives an overall view of the error for various values of \(\nu\) when \(\mu =1.9\). The error plot clearly shows that the fractional-order solution with the Liouville–Caputo derivative converges close to the integer solution.

Example 5

Consider the Fokker-Plank time fractional nonlinear equation with Hilfer fractional derivative

$$\begin{aligned} D^{\mu ,\nu }_{0+}u(x,t)=-\dfrac{\partial }{\partial x}\Bigg (\dfrac{3u^{2}}{x}-\dfrac{xu}{3}\Bigg )+\dfrac{\partial ^{2}}{\partial x^{2}}(u^{2}), 0<\mu <1,0\le \nu \le 1, \end{aligned}$$
(4.12)

with initial conditions,

$$\begin{aligned} I_{0+}^{(1-\mu )(1-\nu )}u(x,0)=x^{2}, 0\le x \le 1,0<t<1. \end{aligned}$$
(4.13)

Taking the Laplace transform for each term of the given wave equation (4.12) and applying the initial conditions given in (4.13), gives

$$\begin{aligned} s^{\mu }{\bar{u}}(x,s)=&\,s^{\nu (\mu -1)}I_{0+}^{(1-\mu )(1-\nu )}u(x,0)+{\mathcal {L}}\Big [\dfrac{\partial }{\partial x}\Big (\dfrac{xu}{3}\Big )\Big ]+{\mathcal {L}}\Big [\dfrac{\partial ^{2}}{\partial x^{2}}(u^{2})-\dfrac{\partial }{\partial x}\Big (\dfrac{3u^{2}}{x}\Big )\Big ],\\ \Longrightarrow {\bar{u}}(x,s)=&\,\dfrac{x^{2}}{s^{\lambda }}+\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial }{\partial x}\Big (\dfrac{xu}{3}\Big )\Big ]+\dfrac{1}{s^{\mu }} {\mathcal {L}}\Big [\dfrac{\partial ^{2}}{\partial x^{2}}(u^{2})-\dfrac{\partial }{\partial x}\Big (\dfrac{3u^{2}}{x}\Big )\Big ]. \end{aligned}$$

Taking the inverse Laplace transform on both sides of the above equation leads to

$$\begin{aligned} u(x,t)=\,{\mathcal {L}}^{-1}\Big [\dfrac{x^{2}}{s^{\lambda }}\Big ]+{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial }{\partial x}\Big (\dfrac{xu}{3}\Big )\Big ] +\dfrac{1}{s^{\mu }} {\mathcal {L}}\Big [\dfrac{\partial ^{2}}{\partial x^{2}}(u^{2})-\dfrac{\partial }{\partial x}\Big (\dfrac{3u^{2}}{x}\Big )\Big ]\Bigg ]. \end{aligned}$$

Comparing with the iterative procedure (3.8), u(x, t) can be written as,

$$\begin{aligned} u(x,t)=\dfrac{x^{2}t^{\lambda -1}}{\Gamma (\lambda )}+L(u)+N(u). \end{aligned}$$

Here,

$$\begin{aligned} u_{0}=\dfrac{x^{2}t^{\lambda -1}}{\Gamma (\lambda )},u_{1}=L(u_{0})+N(u_{0}). \end{aligned}$$

The successive iterative terms \(L(u_{0})\) and \(N(u_{0})\) are calculated as below.

$$\begin{aligned} L(u_{0})=&\,{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial }{\partial x}\Big (\dfrac{x^{3}t^{\lambda -1}}{\Gamma (\lambda )}\Big )\Big ]\Bigg ]=\dfrac{x^{2}t^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )},\\ N(u_{0})=&\,{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial ^{2}}{\partial x^{2}}\Big (\dfrac{x^{4}t^{2\lambda -2}}{(\Gamma (\lambda ))^{2}}\Big )\Big ]\Bigg ] -{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial }{\partial x}\Big (\dfrac{3x^{4}t^{2\lambda -2}}{(\Gamma (\lambda ))^{2}}\Big )\Big ]\Bigg ],\\ =&\,{\mathcal {L}}^{-1}\Big [\dfrac{12x^{2}}{s^{\mu }(\Gamma (\lambda ))^{2}}{\mathcal {L}}[t^{2\lambda -2}]\Big ]- {\mathcal {L}}^{-1}\Big [\dfrac{12x^{2}}{s^{\mu }(\Gamma (\lambda ))^{2}}{\mathcal {L}}[t^{2\lambda -2}]\Big ]=0,\\ \Longrightarrow u_{1}=&\,\dfrac{x^{2}t^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )}. \end{aligned}$$

The next term according to the iterative method (3.5) is given by \(u_{2}=L(u_{1})+N(u_{0}+u_{1})-N(u_{0})\). It can be obtained that \(N(u_{0}+u_{1})=0\). Substituting these values in the series solution, yields

$$\begin{aligned} u(x,t)=&\,u_{0}+u_{1}+u_{2}+\cdots , \nonumber \\ u(x,t)=&\,\dfrac{x^{2}t^{\lambda -1}}{\Gamma (\lambda )}+\dfrac{x^{2}t^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )}+\dfrac{x^{2}t^{2\mu +\lambda -1}}{\Gamma (2\mu +\lambda )}+\cdots , \nonumber \\ =&\, x^{2}t^{\lambda -1}\left[ \dfrac{1}{\Gamma (\lambda )}+\dfrac{t^{\mu }}{\Gamma (\mu +\lambda )}+\dfrac{t^{2\mu }}{\Gamma (2\mu +\lambda )}+\cdots \right] , \nonumber \\ \Longrightarrow u(x,t)=&\,x^{2}t^{\lambda -1}E_{\mu ,\lambda }(t^{\mu }). \end{aligned}$$
(4.14)

The exact solution in closed form of the given differential system (4.12) is given by,

$$\begin{aligned} u(x,t)=x^{2}e^{t}. \end{aligned}$$

Figure 9 is the trajectory of the fractional-order solution for various values of \(\mu\) with respect to the cases \(\nu =0\) and \(\nu =1\). In both cases, it is clear that as the value of \(\mu\) increases, the series solution approaches the exact solution.

Table 1 Error difference between the closest value of \(\mu\) in the analytic solution with the exact solution when \(\nu =0\)
Full size table
Table 2 Error difference between the closest value of \(\mu\) in the analytic solution with the exact solution when \(\nu =1\)
Full size table
Fig. 6
figure 6

Error analysis of Example 3 for \(0\le x,y \le 1\)

Full size image
Fig. 7
figure 7

Error analysis of Example 3 for \(0 \le x,y \le 1\)

Full size image
Table 3 Error difference between the closest value of \(\mu\) in the analytic solution with the exact solution when \(\nu =1\) of Example 4
Full size table
Table 4 Error difference between the closest value of \(\mu\) in the analytic solution with the exact solution when \(\nu =0\) of Example 4
Full size table
Fig. 8
figure 8

Error plot of the solution for \(0<t<1\) of Example 4

Full size image
Fig. 9
figure 9

Riemann–Liouville order and the Liouville–Caputo order in Example 5

Full size image
Table 5 Error difference between the closest value of \(\mu\) in the analytic solution with the exact solution when \(\nu =0\) of Example 5
Full size table

Observation 8

A more detailed analysis in terms of values are given in Tables 5 and  6 . The tabulated values in Table 5 shows the error analysis with \(t=0.5\), for \(\mu =0\). The error is minimum for values of \(x<0.5\). Table 6 shows the error with \(t=0.5\), for \(\mu =1\). It can be seen that the error is minimum for values of \(x<0.7\). For higher order values, the solution trajectories with Riemann–Liouville and Liouville–Caputo derivatives trace a similar path to the integer order solution.

Table 6 Error difference between the closest value of \(\mu\) in the analytic solution with the exact solution when \(\nu =1\) of Example 5
Full size table

Example 6

Consider three-dimensional Hilfer fractional-order diffusion equation:

$$\begin{aligned} D^{\mu ,\nu }_{0+}u(x,y,z,t)=\dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}}+\dfrac{\partial ^{2}u}{\partial z^{2}}, 0<\mu<1,0\le \nu \le 1, 0<t<1, \end{aligned}$$
(4.15)

with initial conditions,

$$\begin{aligned} I_{0+}^{(1-\mu )(1-\nu )}u(x,y,0)=\sin x\,\sin y\,\sin z , 0\le x,y,z \le 10. \end{aligned}$$
(4.16)

Taking the Laplace transform on both sides of the given wave equation (4.15) using the formula given by (2.3) gives

$$\begin{aligned} s^{\mu }{\bar{u}}(x,y,z,t)-s^{\nu (1-\mu )}I_{0+}^{(1-\mu )(1-\nu )}[u(x,y,z,0)]={\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}}+\dfrac{\partial ^{2}u}{\partial z^{2}}\Big ]. \end{aligned}$$

Substituting the initial conditions given in (4.16) in the above equation reduces to

$$\begin{aligned} s^{\mu }{\bar{u}}(x,s)&=\left( s^{\nu (1-\mu )}(\sin x\,\sin y\,\sin z )\right) +{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}}+\dfrac{\partial ^{2}u}{\partial z^{2}}\Big ],\\ \Longrightarrow {\bar{u}}(x,s)&=\dfrac{\sin x\,\sin y\,\sin z }{s^{\lambda }}+s^{-\mu }{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}}+\dfrac{\partial ^{2}u}{\partial z^{2}}\Big ]. \end{aligned}$$

Taking the inverse Laplace inverse transform leads to

$$\begin{aligned} u(x,y,z,t)={\mathcal {L}}^{-1}\Big [\dfrac{\sin x\,\sin y\,\sin z }{s^{\lambda }}\Big ]+{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}}+\dfrac{\partial ^{2}u}{\partial z^{2}}\Big ]\Bigg ]. \end{aligned}$$

Comparing with the iterative method (3.8), \(u_{0}\) and L(u) are given by,

$$\begin{aligned} u_{0}(x,y,z,t)&=\sin x\,\sin y\,\sin z \, \dfrac{t^{\lambda -1}}{\Gamma (\lambda )},\\ L(u)=&\,{\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}}\Big [\dfrac{\partial ^{2}u}{\partial x^{2}}+\dfrac{\partial ^{2}u}{\partial y^{2}}+\dfrac{\partial ^{2}u}{\partial z^{2}}\Big ]\Bigg ]. \end{aligned}$$

The successive terms of the series solution are as follows:

$$\begin{aligned} u_{1}=&\,L(u_{0})={\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}} \Big [-3\sin x\,\sin y\,\sin z \,\dfrac{t^{\lambda -1}}{\Gamma (\lambda )}\Big ]\Bigg ],\\ =&\, -3 \sin x\,\sin y\,\sin z {\mathcal {L}}^{-1}\Big [\dfrac{1}{s^{\mu +\lambda }}\Big ] = -3\sin x\,\sin y\,\sin z \, \dfrac{t^{\mu +\lambda }}{\Gamma (\mu +\lambda )},\\ u_{2}=&L(u_{1})={\mathcal {L}}^{-1}\Bigg [\dfrac{1}{s^{\mu }}{\mathcal {L}} \Big [9\sin x\,\sin y\,\sin z \,\dfrac{t^{\mu +\lambda -1}}{\Gamma (\mu +\lambda )}\Big ]\Bigg ], \\ =&\, 9 \sin x\,\sin y\,\sin z \, \dfrac{t^{\mu +\lambda -1}}{\Gamma (2\mu +\lambda )}. \end{aligned}$$

The series solution is written as,

$$\begin{aligned} u(x,t,z,t)=&\,u_{0}+u_{1}+u_{2}+\cdots ,\\ \Longrightarrow u(x,y,z,t)=&\,\sin x\,\sin y\,\sin z \,\dfrac{t^{\lambda -1}}{\Gamma (\lambda )}-3\sin x\,\sin y\,\sin z \, \dfrac{t^{\mu +\lambda }}{\Gamma (\mu +\lambda )}\\ +&9 \sin x\,\sin y\,\sin z \,\dfrac{t^{\mu +\lambda -1}}{\Gamma (2\mu +\lambda )} -\cdots . \end{aligned}$$

The solution is thus given by

$$\begin{aligned} u(x,y,z,t)=\sin x\,\sin y\,\sin z \, t^{\lambda -1}[E_{\mu ,\lambda }(-3t^{\mu })], \end{aligned}$$
(4.17)

and the exact solution in closed form is given by

$$\begin{aligned} u(x,y,z,t)=e^{-3t}\sin x\,\sin y\,\sin z . \end{aligned}$$

Observation 9

It can be observed that the fractional-order solution (4.17) does not explicitly depend on the value of \(\nu\). Hence, it can be concluded that for \(\mu =1\) the series solution reduces to exact solution irrespective of \(\nu =0\) or \(\nu =1\). Thus the solution trajectory of the integer order and fractional-order with the Riemann–Liouville derivative and Liouville–Caputo derivative traces a close path.

Fig. 10
figure 10

Error analysis of Example 6 for \(x=y=z=5\), \(0<t<1\)

Full size image
Fig. 11
figure 11

Error analysis of Example 6 for \(x=y=z=5\) for \(0<t<1\)

Full size image

Observation 10

From the error plot in Fig. 10a, it is clear that for \(\nu =0\), the error difference converges to zero for \(t\rightarrowtail 1\). The error plot in Figs. 10b and  11a shows that the error value increases as the value of the type \(\nu\) of the derivative increases. Figure 11b gives a consolidate image of error variation. While analyzing Fig. 10a, it is evident that the solution of the differential equation with the Riemann–Liouville derivative is close to the exact solution than with the Liouville–Caputo order solution, as \(t\rightarrowtail 1\).

5 Conclusion

Analytic solution of fractional differential equation reduced to closed-form to the exact solution with order \(0<\mu <1\) and type \(0 \le \nu \le 1\) is studied in this paper. Examples of one-dimensional, two-dimensional, and three-dimensional systems that generate different differential models in chemistry are discussed with appropriate initial conditions. The solution of differential equations with Hilfer fractional derivative with numerical and graphical comparison has not been studied. Mathematica 12.2 has been utilized for the graphical representations. It can be noticed that the observations vary from example to example. For some examples, the trajectory of the solution of the differential equation with the Riemann–Liouville fractional derivative traces a relatively close path to the integer-order trajectory. In some examples, the trajectory of the solution of the differential equation with Liouville–Caputo order traces a close path. There are also examples where the solution trajectory of the differential equation is similar with little difference compared to the solution trajectory of the differential equation with integer order. These results will give rise to studying the fractional-order system from a different view with a more profound analysis. An immediate open problem that can be explored is the analysis of the Hilfer fractional derivative involving the Sumudu transform. For recent results on Sumudu transform, the article by Gao et al. [7] can be referred to.