Abstract
In this paper, we broaden the utilization of a beautiful computational scheme, residual power series method (RPSM), to attain the fractional power series solutions of nonhomogeneous and homogeneous nonlinear time-fractional systems of partial differential equations. This paper considers the fractional derivatives of Caputo-type. The approximate solutions of given systems of equations are calculated through the utilization of the provided initial conditions. This iterative scheme generates the fast convergent series solutions with conveniently determinable components. The implementation of this numerical scheme clearly exhibits its effectiveness, reliability and easiness regarding the procedure of the solution, as well as its better approximation. The repercussions of the fractional order of Caputo derivatives on solutions are depicted through graphical presentations for various particular cases.
Similar content being viewed by others
1 Introduction
Physical phenomena of the miscellaneous fields of engineering and science can be modelled very appropriately by utilizing fractional partial differential equations (FPDEs). Presently the theory of fractional calculus is equipped with fantastic tools to describe the dynamical behaviour, and memory related characteristics of scientific systems and processes. Various authors have used fractional differential equations (FDEs) in the modelling and analysis of scientific phenomena in different fields of knowledge [1–3]. Presently the theory of fractional calculus has been widely utilized in various fields and it is growing very fast in developing models due to its relation with memory and fractals which are abundant in real physical systems. Fractional order modelling minimizes the inaccuracy that arises from the ignorance of significant real parameters. It permits a greater degree of freedom in the model compared to an integer-order system. FDEs are equipped with magnificent techniques for the characterization of hereditary and memory characteristics which are simply ignored by the integer order system. In addition, they are also suitable in modelling the behaviour of real systems and also relevant in the investigation of dynamical systems. FDEs are also appropriate in case of modelling of systems with longer-range interactivity both in time and space. Fractional order systems are normally associated to the systems of memory which allows the incorporation of several types of information. The stability region increases in case of a fractional order system as compared to its integer order framework. Fractional calculus also provides non-local fractional derivative operators and numerical results with high accuracy. In addition, fractional order systems ultimately converge to the integer-order systems.
The non-local property of the fractional operator is the most advantageous feature in this context. The theory of fractional calculus develops many generalizations with respect to non-local characteristics of fractional operators, enhanced degree of freedom, maximum utilization of information, and these characteristics only occur in the case of fractional order systems and not of integer-order systems. The numerical schemes provided by fractional calculus originate the deeper understanding of complex systems and reduce the computational work regarding the solution procedure. Accurate analytical solutions are not found easily in the case of FDEs. Thus in the last two decades, many iterative schemes such as Adomian decomposition method (ADM) [4–6], Variational iteration method (VIM) [7–10], Homotopy perturbation method (HPM) [11, 12], Homotopy perturbation transform method (HPTM), residual power series method (RPSM), etc., have been developed to determine the numerical solutions of several classes of fractional ordinary differential equations (ODEs) and partial differential equations (PDEs).
During the last decade, FDEs have gained popularity due to their extensive usefulness and relevance regarding the investigation of behaviour of real physical models. In the recent years, many authors have tried to solve various types of PDEs in different fields and obtained numerical solutions by using different approximation techniques. Some authors have acquired exact solutions of time-fractional PDEs by employing latest iterative technique [13]. Ceser et al. [14] have used a differential transform scheme to handle the system of FPDEs. In 2013, Neamaty et al. [15] utilized an iterative Laplace transform scheme and wavelet operational method, respectively, to handle a system of FPDEs. Babolian et al. [16] have used the combination of ADM and Spectral scheme to acquire the solution of FPDEs. In addition, the exact solutions of FPDEs by using the sub-equation method have been derived by Bekir et al. [17]. Wang et al. [18] have applied a fractional modified sub-equation scheme, and Gupta et al. [19] have employed Laplace transform to solve a system of FPDEs. Very recently a variety of FPDEs have been analysed by using Laplace VIM and Laplace ADM [20], modified HPM [21], HPM [22]. Neamaty et al. [23] have tried variational homotopy perturbation iteration method (VHPIM) and Zayed et al. [24] have utilized complex transformation for nonlinear FPDEs arising in mathematical physics.
Additionally, Singh et al. [25] have presented the analysis of coupled fractional Burger’s equations by employing a homotopy technique. In 2017, FPDEs have been handled by using Muntz–Legendre polynomial approach [26], fractional complex differential transform scheme [27], and two-dimensional Laplace transform [28]. Recently the FPDEs with Caputo–Fabrizio fractional operator have been investigated through HPTM by Gomez-Aguilar et al. [29]. Singla et al. [30] have derived solutions of Nizhnik–Novikov–Veselov (NNV) system, Burger system and Navier–Stokes equations by using a generalized Lie symmetry approach. Generalized solitary wave solutions for fractional Klein–Gordon equation have been derived by an exp-function scheme [31]. In 2018, FPDEs were analysed by a B-spline polynomial approach [32] and hybrid Laplace transform technique [33]. Wang et al. [34] have gained solutions for FPDEs with proportional delay with iterative RPSM and HATM schemes.
Recently a bunch of new mathematical models have been studied by some authors with various singular and non-singular fractional derivative operators. Baleanu et al. [35] have handled the fractional Lagrangian and fractional Hamilton’s equations of the movement of a particle in a round-shaped cavity with fractional derivative in Caputo sense and with Mittag-Leffler kernel. Recently some researchers have studied new mathematical models with fractional derivative operators related to the field of medical science and diseases. Baleanu et al. [36] have studied a newly generated fractional model for a tumor-immune surveillance with singular and non-singular derivative operators. In 2019, Jajarmi et al. [37] investigated a mathematical model of dengue fever outbreak based on FDEs. In this sequence, a new fractional mathematical model of diabetes and tuberculosis co-existence with a Mittag-Leffler non-singular derivative operator has also been analysed by Jajarmi et al. [38].
Over a decade ago, Baleanu et al. [39] derived the Lagrangians with linear velocities with RL fractional derivatives. Recently Baleanu and his co-workers have contributed to the classical and fractional study of physical systems with different types of fractional derivative operators. Baleanu et al. [40] have explored unusual characteristics of a physical model in the form of fractional Euler–Lagrange equations elucidating the motion of a capacitor microphone within non-singular derivative. Investigation of new features of a fractional model of spring pendulum and two coupled pendulums have been also carried out by Baleanu et al. [41, 42]. Some time ago a group of authors studied the fractional optimal control problems by using certain approximation schemes. Mohammadi et al. [43] presented a numerical scheme based on hybrid Chelyshkov functions (HCFs) to handle a class of fractional optimal control problems (FOCPs). In this sequence, a new approximation approach has been utilized to investigate the nonlinear FOCPs by Jajarmi et al. [44].
This paper presents the execution of RPSM to compute the fractional power series (FPS) solutions of nonhomogeneous and homogeneous nonlinear systems of FPDEs arising in physical sciences as given below:
Problem 1
Solve the nonhomogeneous nonlinear fractional system
subject to initial conditions
Problem 2
Solve the homogeneous nonlinear fractional system
subject to the initial conditions
where \(0 < \alpha \le 1\) signifies the order of fractional time derivative.
Various definitions have been established for a fractional derivative. But this paper deals with a fractional derivative of Caputo type because it handles initial value problems (IVPs) in a very efficient way. The RPSM beautifully handles the systems of nonlinear ODEs and PDEs and computes the analytical solutions in a Taylor series form. It was first proposed and utilized by O.A. Arqub [45] to investigate the fuzzy differential equations so as to evaluate the coefficients of a power series solution. In addition, RPSM has been also applied to Lane–Emden equation, composite and non-composite DEs, regular IVP and fractional order boundary value problems (BVPs) [46–49]. Many authors have used RPSM to solve the problems of diverse streams of science and engineering [50–55].
Recently, Kumar et al. [56–58] have presented the analysis of the fractional exothermic reactions model, the fractional vibration equation and new fractional SIRS-SI malaria disease model with a variety of fractional operators with different kinds of kernel. Very recently a new investigation of Drinfeld–Sokolov–Wilson (DSW) equation was carried out by Bhatter et al. [59]. Singh et al. [60] have explored the new features of fractional Biswas–Milovic model with Mittag-Leffler kernel. In 2019, fractional Black–Scholes equations have been studied via RPSM by Dubey et al. [61].
The suggested nonhomogeneous and homogeneous systems of nonlinear fractional PDEs with Caputo derivatives, to the best of our knowledge, have not been handled utilizing RPSM in the available literature, yet. The main reason to choose the RPSM for application is that it effectively produces the approximate analytical solution of FDEs in the power series form with high accuracy and fast convergence. The primary purpose of the present work is to analyse the given systems of fractional PDEs with Caputo time derivatives through RPSM. The present work derives the fractional power series (FPS) solutions of the above-mentioned systems of FPDEs and further investigates the variations of numerical results obtained in a series form regarding time and several values of fractional parameter α through the two-dimensional and three-dimensional graphs.
There are various methods in the available literature that have been used to handle the above mentioned systems of FPDEs. Many researchers like Jafari et al. [62, 63]; Wazwaz [64]; Aminikhah et al. [65] and Koçak et al. [66] have successfully utilized a variety of schemes to handle these systems of nonlinear fractional PDEs. But the RPSM has never been used to handle these systems of FDEs. The novelty of the present paper lies in the smooth implementation of RPSM to the systems of nonlinear PDEs arising in physical sciences, along with depiction of variation of numerical results regarding various values of fractional parameter α. The other novel factor in the proposed work is the handling of the set of nonlinear PDEs with Caputo fractional derivative (CFD). However, Riemann–Liouville (RL) fractional integral and derivative operators have been used significantly in the derivation of other fractional integral and derivative operators. But various problems of applied nature require conveniently suitable format of fractional derivatives, for instance, the Caputo derivative which delivers easy to deal with initial conditions having clear elucidation for the FDEs. This fact promotes the CFD as a more appropriate operator in comparison to the Riemann–Liouville definition regarding the application. However, it is noteworthy that the Caputo derivative demands the possibility of evaluation of the nth derivative of a function which makes its scope broader than its RL substitute. But a large class of mathematical functions that appear in applications satisfy this requirement.
This paper significantly presents the implementation of the RPSM to the systems of PDEs of nonlinear nature with Caputo fractional derivatives. This recently generated iterative scheme provides the solutions in analytical Taylor series form for the systems of ODEs and PDEs of both linear and nonlinear type. This semi-analytic technique actually utilizes the generalized Taylor series expansion accompanying the residual error function to build up the solution in a form of FPS expansion for a class of nonlinear FDEs without incorporating any additional restrictions. Utilizing the idea of residual error, a numerical solution is achieved straightforwardly in the form of truncated series. The primary benefit of this technique over the others is that it is directly applicable to the stated system with a proper pick of an initial guess approximation and it also lessens the complications originating in calculation of intricate terms. The remaining part of the manuscript is structured as follows: Sect. 2 describes the elemental concepts and formulae connected to the field of fractional calculus and theorems of fractional power series. Section 3 presents the fundamental procedure of RPSM. In Sects. 4 and 5, we present the application of RPSM to Problems 1 and 2, respectively, and related graphs are also presented there. Section 6 provides the numerical results and discussion. Finally, Sect. 7 records the concluding remarks.
2 Preliminaries and notations
This part formally presents some essential definitions related to the stream of the fractional calculus and some fundamental theorems related to the FPS expansion as follows:
Definition 2.1
([67])
The fractional integral operator of order \(\mu\ (\mu \ge 0)\) of \(g ( y )\) of Riemann–Liouville (RL) type is defined as
Definition 2.2
([67])
The fractional derivative of \(g(y), y > 0\), in the RL sense is defined as
Definition 2.3
([67])
The β-order fractional derivative operator of Caputo type for the function \(g(y), y > 0\), is formulated as
where \(D^{\kappa } \) signifies the κ-order Newtonian derivative.
The following expressions hold true in the context of Caputo derivative:
Definition 2.4
([68])
The fractional derivative of order \(\alpha > 0\) in the Caputo sense is stated as
Definition 2.5
([69])
The Mittag-Leffler function \({E}_{\sigma } ( \zeta )\) with \(\sigma > 0\) is defined as
Definition 2.6
An FPS expansion about the point \(\zeta = \zeta _{0}\) is represented as
Theorem 2.1
Let the FPS representation for the function ℘ at \(\zeta = \zeta _{0}\)be of the form \(\wp ( \zeta ) = \sum_{\ell = 0}^{\infty } c_{\ell } ( \zeta - \zeta _{0} )^{\ell \gamma }, \zeta _{0} \le \zeta < \zeta _{0} + \Re \), where ℜ signifies the radius of convergence.
If \(D^{\ell \gamma } \wp ( \zeta ), \ell = 0, 1, 2, 3,\ldots\)are continuous on the interval \(( \zeta _{0}, \zeta _{0} + \Re )\), the multipliers \(c_{\ell } \)are provided by the expression \(c_{\ell } = \frac{D^{\ell \gamma } \wp ( \zeta _{0} )}{ \varGamma ( 1 + \ell \gamma )}, \ell = 0,1, 2,\ldots\)where \(D^{\ell \gamma } = D^{\gamma } D^{\gamma }\cdots D^{\gamma }\) (ℓtimes).
Definition 2.7
A multiple FPS expansion about the point \(\zeta = \zeta _{0}\) for the function ℘ is expressed in the form \(\sum_{\ell = 0}^{\infty } \wp _{\ell } ( z ) ( \zeta - \zeta _{0} )^{\ell \gamma } \). Here ζ signifies a variable and \(\wp _{\ell } ( z )\) are the coefficients of the expansion series.
Theorem 2.2
Let the multiple FPS expansion at \(\xi = \xi _{0}\)for the function \(\vartheta ( z,\zeta )\)be of the form \(\vartheta ( z,\zeta ) = \sum_{\ell = 0} ^{\infty } \wp _{\ell } ( z ) ( \zeta - \zeta _{0} ) ^{k\alpha }, z \in I, \zeta _{0} \le \zeta < \zeta _{0} + \Re, 0 \le \ell - 1 < \gamma \le \ell, \zeta \ge \zeta _{0}\).
If \(D_{\zeta }^{\ell \gamma } \vartheta ( z,\zeta ), \ell = 0, 1, 2, 3,\ldots\)are continuous on the interval \(I \times ( \zeta _{0}, \zeta _{0} + \Re )\)then the coefficients \(\wp _{ \ell } \)are determined as \(\wp _{\ell } ( z ) = \frac{D _{\zeta }^{\ell \gamma } \vartheta ( z,\zeta _{0} )}{ \varGamma ( 1 + \ell \gamma )}, \ell = 0, 1, 2,\ldots\) .
Therefore the FPS expansion of \(\vartheta ( z,\zeta )\)at \(\zeta _{0}\)will be of the form
which is actually the formula of a generalized Taylor series.
The classical Taylor series for \(\gamma = 1\) is produced as
Corollary 2.1
Let \(\vartheta ( z, \omega, \zeta )\) have a multiple FPS representation about the point \(\zeta = \zeta _{0}\) of the form
If \(D_{\zeta }^{\ell \gamma } \vartheta ( z,\omega,\zeta ), \ell = 0, 1, 2, 3,\ldots\)are continuous on \(I \times I \times ( \zeta _{0}, \zeta _{0} + \Re )\)then \(\wp _{\ell } ( z,\omega ) = \frac{D_{\zeta }^{\ell \gamma } \vartheta ( z,\omega,\zeta _{0} )}{\varGamma ( 1 + \ell \gamma )}, \ell = 0, 1, 2,\ldots\) .
3 RPSM: fundamental procedure
In this section, the basic procedure of residual power series (RPS) algorithm is provided.
For the purpose of illustration of fundamental procedure of RPSM for fractional order PDEs, the ensuing fractional PDE is taken which is about to be mentioned here:
subject to the conditions:
where \(D_{\zeta }^{\lambda \gamma } = \frac{\partial ^{\lambda \gamma }}{\partial \zeta ^{\lambda \gamma }} \) specifies the fractional derivative in Caputo sense; \(F [ \vartheta ]\) and \(E [ \vartheta ]\) characterize the nonlinear and linear operators in ϑ and \(H ( \vartheta,\zeta )\) denotes a continuous function.
As stated by RPS algorithm, the solution of equations (3.1)–(3.2) can be expressed as an FPS expansion about the point \(\zeta = 0\). Now it is assumed that the solution of the above mentioned PDE acquires the series expansion form as
Therefore, the approximate analytical solution for equations (3.1) and (3.2) in the shape of an infinite FPS is provided by the RPS algorithm. In this sequence, the ℓth truncated series of \(w ( \vartheta ,\zeta )\), i.e. \(w_{\ell } ( \vartheta,\zeta )\) is defined as
Clearly, the initial condition (3.2) is satisfied by \(w ( \vartheta,\zeta )\) thus from equation (3.3), the following algebraic expression is obtained:
From equation (3.4), the initial guess approximation of \(w ( \vartheta,\zeta )\) may be expressed as
Now the expansion series of equation (3.4) can be rewritten as
Now to compute the values of multipliers \(h_{\lambda } ( \vartheta ), \lambda = 1, 2, 3,\ldots,\ell \) in the series expansion of \(w_{\ell } ( \vartheta,\zeta )\) in equation (3.7), the residual function is expressed as
and the ℓth residual function, \(\operatorname{Re} s_{w,\ell } \) is expressed in the following form:
Clearly,
In fact, this leads to \(D_{\zeta }^{ ( \ell - 1 )\gamma } \operatorname{Re} s_{\ell } ( \vartheta,\zeta _{0} ) = 0, \ell = \overline{1,\infty } \) as the CFD of a constant is zero. Now the fractional derivatives \(D_{\zeta }^{ ( \ell - 1 )\gamma } \) of \(\operatorname{Re} s ( \vartheta,\zeta )\) and \(\operatorname{Re} s_{\ell } ( \vartheta,\zeta )\) coincide at \(\zeta = 0\) for each \(\ell = \overline{1,\infty }\).
To determine the coefficients \(h_{\lambda } ( \vartheta ), \lambda = 1, 2, 3,\ldots\ell \), the ℓth truncated series of \(w ( \vartheta,\zeta )\), i.e. \(w_{\ell } ( \vartheta ,\zeta )\) is putted into the ℓth residual function \(\operatorname{Re} s_{w,\ell } (\vartheta,\zeta )\) and in sequence the fractional derivative \(D_{\zeta }^{ ( \ell - 1 )\gamma } \) is operated on \(\operatorname{Re} s_{\ell } ( \vartheta,\zeta )\), \(\ell = \overline{1,\infty } \) at \(\zeta = 0\). Now the acquired algebraic equation can be solved to compute the required coefficients, i.e. there is a requirement to solve the ensuing algebraic equation provided as
Thus all the desired coefficients of multiple FPS of equations (3.1) and (3.2) can be easily calculated by endorsing the above-mentioned procedure.
4 Application of RPSM for Problem 1
The given nonhomogeneous system of nonlinear FPDEs is
subject to the conditions:
The RPS algorithm assumes the solutions for the above system of equations (1.1) as an FPS expansion about \(\zeta = 0\) as
Obviously, \(u ( \vartheta,\zeta )\) and \(v ( \vartheta,\zeta )\) satisfy the initial conditions and thus the initial conditions can be expressed as
Hence the initial guess approximations of \(u ( \vartheta,\zeta )\) and \(v ( \vartheta,\zeta )\) are obtained as
Thus equations (4.1) and (4.2) can be written as
Let the kth truncated series of \(u ( \vartheta,\zeta )\) and \(v ( \vartheta,\zeta )\) expressed in equations (4.7) and (4.8) be
Now the residual functions \(\operatorname{Re} s_{u} ( \vartheta ,\zeta )\) and \(\operatorname{Re} s_{v} ( \vartheta, \zeta )\) for system (1.1) are defined as
Therefore the kth residual functions are given as
To find the first unknown coefficients \(\varphi _{1} ( \vartheta )\) and \(\phi _{1} ( \vartheta )\), putting \(k = 1\) in equations (4.13) and (4.14) yields
where
Therefore, equations (4.15) and (4.16) reduce to
Now the above-mentioned residual functions at point \(\zeta = 0\) are given by
Now equation (3.10) suggests that
Using the system of equations (4.19), equations (4.17) and (4.18) reduce to the following expressions:
Solving the system of equations (4.20), we get
Therefore, the first RPS approximate solutions are
To compute the second unknown coefficients \(\varphi _{2} ( \vartheta )\) and \(\phi _{2} ( \vartheta )\), putting \(k = 2\) in equations (4.13) and (4.14), we get
where
Therefore
Now
Now the above-mentioned residual functions at point \(\zeta = 0\) are given by
Now equation (3.10) suggests that
Using the system of equations (4.27), equations (4.25) and (4.26) reduce to the following expressions:
Solving the system of equations (4.28), we get
Therefore, the second RPS approximate solutions are
To compute the third unknown coefficients \(\varphi _{3} ( \vartheta )\) and \(\phi _{3} ( \vartheta )\), putting \(k = 3\) in equations (4.13) and (4.14), we get
where
Now
Now the above-mentioned residual functions at point \(\zeta = 0\) are given by
Now equation (3.10) suggests that
Using the system of equations (4.34), equations (4.32) and (4.33) reduce to
After solving and simplifying the above-mentioned pair of equations, the values of \(\varphi _{3}(\vartheta )\) and \(\phi _{3}(\vartheta )\) can be written as
Therefore, the third RPS approximate solutions are
The remaining coefficients of \(u_{n}(\vartheta )\) and \(v_{n} ( \vartheta )\), for \(n \ge 4\) can be computed in the same fashion and therefore the series solutions are fully determined. Finally, the solutions of time-fractional system (1.1) are presented in the series form as
5 Application of RPSM for Problem 2
The given homogeneous nonlinear system of FPDEs is
subject to the conditions:
The RPS algorithm assumes the following set of solutions for the above system of equations (1.2) as an FPS expansion about \(\zeta = 0\) as
Clearly, \(u ( \vartheta,\eta,\zeta )\), \(v ( \vartheta ,\eta,\zeta )\) and \(w ( \vartheta,\eta,\zeta )\) satisfy the initial conditions which can be written as
Hence the initial guess approximations of \(u ( \vartheta,\eta, \zeta )\), \(v ( \vartheta,\eta,\zeta )\) and \(w ( \vartheta,\eta,\zeta )\) are obtained as
Hence
Let the kth truncated series of \(u ( \vartheta,\eta,\zeta )\), \(v ( \vartheta,\eta,\zeta )\) and \(w ( \vartheta,\eta, \zeta )\) be
Now the residual functions \(\operatorname{Re} s_{u} ( \vartheta ,\eta,\zeta )\), \(\operatorname{Re} s_{v} ( \vartheta, \eta,\zeta )\) and \(\operatorname{Re} s_{w} ( \vartheta, \eta,\zeta )\) for the equations of system (5.5) are defined as
Therefore the kth residual functions are defined as
Now the first unknown coefficients \(\varphi _{1} ( \vartheta, \eta ), \phi _{1} ( \vartheta,\eta )\) and \(\psi _{1} ( \vartheta,\eta )\) can be determined by putting \(k = 1\) in the system of equations (5.7):
where
Thus
Now the above-mentioned residual functions at the point \(\zeta = 0\) are
From equation (3.10), it is deduced that
Therefore, system (5.9) reduces to
Solving the system of equations (5.10), we obtain
Therefore, the first RPS approximate solutions are
To find the second unknown coefficients \(\varphi _{2} ( \vartheta ,\eta ), \phi _{2} ( \vartheta,\eta )\) and \(\psi _{2} ( \vartheta,\eta )\), putting \(k = 2\) in system of equations (5.7) yields
where
From equation (3.10), it is deduced that
Simplifying the system of equations (5.13), we get
Solving the system of equations (5.14) provides
Therefore, the second RPS approximate solutions are
To find the third unknown coefficients \(\varphi _{3} ( \vartheta, \eta ), \phi _{3} ( \vartheta,\eta )\) and \(\psi _{3} ( \vartheta,\eta )\), putting \(k = 3\) in the system of equations (5.7), we get
where
Now Eq. (3.10) suggests that
Simplifying and solving system (5.17), we get
Therefore, the third RPS approximate solutions are
Continuing in a similar manner, the remaining coefficients of \(u_{n}(\vartheta,\eta,\zeta ), v_{n}(\vartheta,\eta,\zeta )\) and \(w_{n}(\vartheta,\eta,\zeta ), n \ge 4\) can be computed, and consequently the solutions in series form are fully acquired.
Now the final solutions of time-fractional homogeneous system (1.2) can be expressed as
where \(E_{\alpha } (\cdot )\) signifies the Mittag-Leffler function of the first kind.
6 Numerical results and discussion
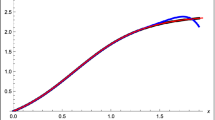
In this section, the numerical values of the functions \(u ( \vartheta,\zeta ), v (\vartheta,\zeta ), u ( \vartheta ,\eta,\zeta ), v (\vartheta,\eta,\zeta )\), and \(w (\vartheta ,\eta,\zeta )\) are computed for various values of fractional parameter \(\alpha = \frac{1}{3}, \frac{2}{3}\) and classical motion \(\alpha = 1\). Figures 1–8 illustrate Problem 1, and Figs. 9–20 represent Problem 2. Figures 1 and 2 graphically show the two-dimensional variations of \(u ( \vartheta,\zeta )\), \(v (\vartheta, \zeta )\) with respect to ϑ and time ζ for \(\vartheta = 1\). Figures 3, 5 and 7 graphically describe the three-dimensional variations of \(u ( \vartheta,\zeta )\) in respect of ϑ and ζ. Clearly, \(u ( \vartheta, \zeta )\) decreases with increasing time ζ and decreasing α, whereas Figs. 4, 6 and 8 show that \(v (\vartheta, \zeta )\) increases with increasing time ζ and decreasing α. Figure 9 depicts that \(u ( \vartheta,\eta,\zeta )\) decreases with increasing time ζ and decreasing α for \(\vartheta = 1\). It is also observed from Figs. 10 and 11 that \(v (\vartheta,\eta,\zeta )\) and \(w (\vartheta,\eta, \zeta )\) increase with increasing ζ and decreasing α for \(\vartheta = 1\). Figures 12–20 graphically portray the three-dimensional representation of variations of \(u ( \vartheta ,\eta,\zeta )\), \(v (\vartheta,\eta,\zeta )\) and \(w (\vartheta ,\eta,\zeta )\) with respect to ϑ and ζ for the value \(\eta = 0.4\). This study undoubtedly deduces that the achieved approximate analytical solutions continuously depend on the fractional parameter α. Two- and three-dimensional graphical demonstrations ensure the high accuracy of the generated results using RPSM by involving four iterations only. Nevertheless, the numerical results can be generated more precisely by computing additional iterative terms.
The approximate analytical solutions and numerical results of the given sets of PDEs obtained via RPSM are in good correspondence with the results obtained via HAM [63], VIM [64], Laplace transform new homotopy perturbation method (LTNHPM) [65], and three-dimensional transform method [72]. The other methods and RPSM yield accurate solutions, but RPSM is simpler compared to other methods. The most significant feature of the RPS algorithm is that it solves a chain of single variable linear equations to compute the required coefficients of a power series solution which makes the solution procedure very easy and straightforward in comparison to other semi-analytical techniques.
7 Concluding remarks
This article extends the implementation of an iterative scheme based on the RPS algorithm to acquire approximate solutions for a nonlinear time-fractional nonhomogeneous and homogeneous systems of PDEs. The repercussions of the fractional order of Caputo time derivatives on the numerical solutions are well depicted through graphical representations for various specific cases. The study authenticates that RPSM supplies accurate numerical solutions without any restrictive assumptions on nonlinear PDEs. This technique has a clear advantage over other techniques in the sense that it yields approximate solutions of the problems by utilizing the contextual choice of an initial guess approximation. This technique delivers rapidly convergent series and also minimizes the complications that arise in the evaluation procedure of certain intricate terms. This paper beautifully checks the applicability strength and potency of RPSM to generate numerical solutions of a system of FPDEs. The stated systems of nonlinear FPDEs in this manuscript can also be investigated by the accurate discretization method which was earlier applied by Hajipour et al. [73] to one-, two-, and three-dimensional highly nonlinear Bratu-type problems. In this discretization method, nonlinear equations are discretized via a fourth-order nonstandard computational finite difference formula, and finally the given problem is reduced to the solution of a highly nonlinear algebraic system. In addition, the semi-implicit finite difference weighted essentially non-oscillatory (WENO) scheme of the sixth order utilized by Hajipour et al. [74] to solve the nonlinear heat equation can also be tried to investigate the described systems of FPDEs in this manuscript. These numerical schemes probably can provide new insights regarding application to FPDEs and further new conclusions in the future.
References
Ross, B.: A brief history and exposition of the fundamental theory of fractional calculus. In: Ross, B. (ed.) The Fractional Calculus and Its Applications, pp. 1–36. Springer, Berlin (1975)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equation. Wiley, New York (1993)
Momani, S., Shawagfeh, N.T.: Decomposition method for solving fractional Riccati differential equations. Appl. Math. Comput. 182(2), 1083–1092 (2006)
Gejji, V.D., Jafari, H.: Solving a multi-order fractional differential equation. Appl. Math. Comput. 189(1), 541–548 (2007)
Wang, Q.: Numerical solutions for fractional KdV–Burgers equation by Adomian decomposition method. Appl. Math. Comput. 182(2), 1048–1055 (2006)
Inc, M.: The approximate and exact solutions of the space and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 345(1), 476–484 (2008)
Yang, X.J., Baleanu, D., Khan, Y., Mohyud-Din, S.T.: Local fractional variational iteration method for differential and wave equations on Cantor sets. Rom. J. Phys. 59(1–2), 36–48 (2014)
Baleanu, D., Machado, J.A.T., Cattani, C., Baleanu, M.C., Yang, X.J.: Local fractional variational iteration and decomposition methods for wave equation on Cantor sets within local fractional operators. Abstr. Appl. Anal. 2014, Article ID 535048 (2014). https://doi.org/10.1155/2014/535048
Yang, X.J., Baleanu, D.: Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci. 17(2), 625–628 (2013)
Odibat, Z., Momani, S.: Modified homotopy perturbation method: application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 36(1), 167–174 (2008)
Hosseinnia, S., Ranjbar, A., Momani, S.: Using an enhanced homotopy perturbation method in fractional differential equations via deforming the linear part. Comput. Math. Appl. 56(12), 3138–3149 (2008)
Dhaigude, C.D., Nikam, V.R.: Solution of fractional partial differential equations using iterative method. Fract. Calc. Appl. Anal. 15(4), 684–699 (2012)
Secer, A., Akinlar, M.A., Cevikel, A.: Efficient solutions of systems of fractional partial differential equations by the differential transform method. Adv. Differ. Equ. 2013, 188 (2012)
Neamaty, A., Agheli, B., Darzi, R.: Solving fractional partial differential equation by using wavelet operational method. J. Math. Comput. Sci. 7, 230–240 (2013)
Babolian, E., Vahidi, A.R., Shoja, A.: An efficient method for nonlinear fractional differential equations: combination of the Adomian decomposition method and spectral method. Indian J. Pure Appl. Math. 45(6), 1017–1028 (2014)
Bekir, A., Aksoy, E., Cevikel, A.C.: Exact solutions of nonlinear time fractional partial differential equations by sub-equation method. Math. Methods Appl. Sci. 38(13), 2779–2784 (2014)
Wang, G.W., Xu, T.Z.: The modified fractional sub-equation method and its applications to nonlinear fractional partial differential equations. Rom. J. Phys. 59(7–8), 636–645 (2014)
Gupta, S., Kumar, D., Singh, J.: Numerical study for systems of fractional differential equations via Laplace transform. J. Egypt. Math. Soc. 23(2), 256–262 (2015)
Ahmed, H.F., Bahgat, M.S.M., Zaki, M.: Numerical approaches to system of fractional partial differential equations. J. Egypt. Math. Soc. 25(2), 141–150 (2017)
Karbalaie, A., Montazer, M.M., Muhammed, H.H.: New approach to find the exact solution of fractional partial differential equation. WSEAS Trans. Math. 11(10), 908–917 (2012)
Aminikah, H., Malekzadeh, N., Rezazadeh, H.: A novel effective approach for solving fractional nonlinear PDEs. Int. Sch. Res. Not. 2014, Article ID 647492 (2014)
Neamaty, A., Agheli, B., Darzi, R.: Variational iteration method and He’s polynomials for time fractional partial differential equations. Prog. Fract. Differ. Appl. 1(1), 47–55 (2015)
Zayed, E.M.E., Amer, Y.A., Shohib, R.M.A.: The fractional complex transformation for nonlinear fractional partial differential equations in the mathematical physics. J. Assoc. Arab Univ. Basic Appl. Sci. 19(1), 59–69 (2016)
Singh, J., Kumar, D., Swroop, R.: Numerical solution of time and space fractional coupled Burger’s equations via homotopy algorithm. Alex. Eng. J. 55(2), 1753–1763 (2016)
Aghashahi, M., Gandomani, M.R.: Numerical solution of fractional differential equation system using the Müntz–Legendre polynomials. Int. J. Pure Appl. Math. 115(3), 467–475 (2017)
Özkan, O.: Approximate analytical solutions of systems of fractional partial differential equations. Karaelmas Fen ve Müh. Derg. 7(1), 63–67 (2017)
Aghili, A., Masomi, M.R.: Solving systems of fractional partial differential equations via two dimensional Laplace transforms. Int. J. Res.-Granthaalayah. 5(12), 406–420 (2017)
Gómez-Aguilar, J.F., Yépez-Martínez, H., Torres-Jiménez, J., Córdova-Fraga, T., Escobar-Jiménez, R.F., et al.: Homotopy perturbation transform method for nonlinear differential equations involving to fractional operator with exponential kernel. Adv. Differ. Equ. 2017, 68 (2017)
Singla, K., Gupta, R.K.: Generalized Lie symmetry approach for fractional order systems of differential equations. J. Math. Phys. 58, 061501 (2017)
Hassan, Q.M.U., Mohyud-Din, S.T.: On an efficient technique to solve nonlinear fractional order partial differential equations. Int. J. Nonlinear Sci. 19(1), 3–8 (2015)
Jafari, H., Tajadodi, H.: New method for solving a class of fractional partial differential equations with applications. Therm. Sci. 22(1), S277–S286 (2018)
Jacobs, B.A., Harley, C.: Application of nonlinear time fractional partial differential equations to image processing via hybrid Laplace transform method. J. Math. 2018, Article ID 8924547 (2018)
Wang, L., Wu, Y., Ren, Y., et al.: Two analytical methods for fractional partial differential equations with proportional delay. Int. J. Appl. Math. 49(1), 1–6 (2019)
Baleanu, D., Asad, J.H., Jajarmi, A.: New aspects of the motion of a particle in a circular cavity. Proc. Rom. Acad. Ser. A 19(2), 361–367 (2018)
Baleanu, D., Jajarmi, A., Sajjadi, S.S., Mozyrska, D.: A new fractional model and optimal control of a tumor-immune surveillance with non-singular derivative operator. Chaos, Interdiscip. J. Nonlinear Sci. 29(8), 083127 (2019)
Jajarmi, A., Arshad, S., Baleanu, D.: A new fractional modelling and control strategy for the outbreak of dengue fever. Phys. A, Stat. Mech. Appl. 535, 122524 (2019)
Jajarmi, A., Ghanbari, B., Baleanu, D.: A new and efficient numerical method for the fractional modelling and optimal control of diabetes and tuberculosis co-existence. Chaos, Interdiscip. J. Nonlinear Sci. 29(9), 093111 (2019)
Baleanu, D., Avkar, T.: Lagrangians with linear velocities within Riemann–Liouville fractional derivatives. Nuovo Cimento B 119(1), 73–79 (2004)
Baleanu, D., Sajjadi, S.S., Jajarmi, A., Asad, J.H.: New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur. Phys. J. Plus 134(4), 181 (2019)
Baleanu, D., Asad, J.H., Jajarmi, A.: The fractional model of spring pendulum: new features within different kernels. Proc. Rom. Acad. Ser. A 19(3), 447–454 (2018)
Baleanu, D., Jajarmi, A., Asad, J.H.: Classical and fractional aspects of two coupled pendulums. Rom. Rep. Phys. 71(1), 13 (2019)
Mohammadi, F., Moradi, L., Baleanu, D., Jajarmi, A.: A hybrid functions numerical scheme for fractional optimal control problems: application to non-analytic dynamical systems. J. Vib. Control 24(21), 5030–5043 (2018)
Jajarmi, A., Hajipour, M., Mohammadzadeh, E., Baleanu, D.: A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J. Franklin Inst. 335(9), 3938–3967 (2018)
Arqub, O.A.: Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 5(1), 31–52 (2013)
Arqub, O.A., El-Ajou, A., Al-Zhour, Z., Momani, S.: Multiple solutions of nonlinear boundary value problems of fractional order: a new analytic iterative technique. Entropy 16, 471–493 (2014)
El-Ajou, A., Arqub, O.A., Momani, S., et al.: A novel expansion iterative method for solving linear partial differential equations of fractional order. Appl. Math. Comput. 257, 119–133 (2015)
Arqub, O.A., El-Ajou, A., Bataineh, A., Hashim, I.: A representation of the exact solution of generalized Lane–Emden equations using a new analytical method. Abstr. Appl. Anal. 2013, Article ID 378593 (2013)
Arqub, O.A., Abo-Hammour, Z., Al-Badarneh, R., Momani, S.: A reliable analytical method for solving higher-order initial value problems. Discrete Dyn. Nat. Soc. 2013, Article ID 673829 (2013)
Kumar, A., Kumar, S.: Residual power series method for fractional Burger type equations. Nonlinear Eng. 5(4), 235–244 (2016)
Komashynska, I., Al-Smadi, M., Ateiwi, A., et al.: Approximate analytical solution by residual power series method for system of Fredholm integral. Appl. Math. Inf. Sci. 10(3), 975–985 (2016)
Xu, F., Gao, Y., Yang, X., et al.: Construction of fractional power series solutions to fractional Boussinesq equations using residual power series method. Math. Probl. Eng. 2016, Article ID 5492535 (2013)
Arafa, A., Elmahdy, G.: Application of residual power series method to fractional coupled physical equations arising in fluid flow. Int. J. Difference Equ. 2018, Article ID7692849 (2018)
Zhang, Y., Kumar, A., Kumar, S., Baleanu, D., et al.: Residual power series method for time-fractional Schrodinger equations. J. Nonlinear Sci. Appl. 9(11), 5821–5829 (2016)
Al Qurashi, M.M., Korpinar, Z., Baleanu, D., et al.: A new iterative algorithm on the time-fractional Fisher equation: residual power series method. Adv. Mech. Eng. 9(9), 1–8 (2017)
Kumar, D., Singh, J., Tanwar, K., Baleanu, D.: A new fractional exothermic reactions model having constant heat source in porous media with power, exponential and Mittag-Leffler laws. Int. J. Heat Mass Transf. 138, 1222–1227 (2019)
Kumar, D., Singh, J., Baleanu, D.: On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math. Methods Appl. Sci. (2019). https://doi.org/10.1002/mma.5903
Kumar, D., Singh, J., Al Qurashi, M., Baleanu, D.: A new fractional SIRS-SI malaria disease model with application of vaccines, anti-malarial drugs, and spraying. Adv. Differ. Equ. 2019, 278 (2019)
Bhatter, S., Mathur, A., Kumar, D., Singh, J.: A new analysis of fractional Drinfeld–Sokolov–Wilson model with exponential memory. Phys. A, Stat. Mech. Appl. 537, 122578 (2020)
Singh, J., Kumar, D., Baleanu, D.: New aspects of fractional Biswas–Milovic model with Mittag-Leffler law. Math. Model. Nat. Phenom. 14(3), 303 (2019)
Dubey, V.P., Kumar, R., Kumar, D.: A reliable treatment of residual power series method for time-fractional Black–Scholes European option pricing equations. Phys. A, Stat. Mech. Appl. 533, 122040 (2019)
Jafari, H., Nazari, M., Baleanu, D., Khalique, C.M.: A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 66(5), 838–843 (2013)
Jafari, H., Seifi, S.: Solving system of nonlinear fractional partial differential equations by homotopy analysis method. Commun. Nonlinear Sci. Numer. Simul. 14, 1962–1969 (2009)
Wazwaz, A.M.: The variational iteration method for solving linear and nonlinear systems of PDEs. Comput. Math. Appl. 54, 895–902 (2007)
Aminikah, H., Sheikhani, A.H.R., Rezazadeh, H.: Exact and numerical solutions of linear and non-linear systems of fractional partial differential equations. J. Math. Model. 2(1), 22–40 (2014)
Koçak, H., Yildirim, A.: An efficient new iterative method for finding exact solutions of nonlinear time-fractional partial differential equations. Nonlinear Anal., Model. Control 16(4), 403–414 (2011)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)
Caputo, M.: Linear models of dissipation whose Q is almost frequency independent. Part II. J. Roy Astrol. Soc. 13, 529–539 (1967)
Mittag-Leffler, G.: Sur La Nouvelle Fonction E(x). C. R. Math. Acad. Sci. 137, 554–558 (1903)
El-Ajou, A., Arqub, O.A., Al Zhour, Z., Momani, S.: New results on fractional power series: theories and applications. Entropy 15, 5305–5323 (2013)
El-Ajou, A., Arqub, O.A., Momani, S.: Approximate analytical solution of the nonlinear fractional KdV–Burgers equation: a new iterative algorithm. J. Comput. Phys. 293, 81–95 (2015)
Kurulay, M., Ibrahimoğlu, B.A., Bayram, M.: Solving a system of nonlinear fractional partial differential equations using three dimensional transform method. Int. J. Phys. Sci. 5(6), 906–912 (2010)
Hajipour, M., Jajarmi, A., Baleanu, D.: On the accurate discretization of a highly nonlinear boundary value problem. Numer. Algorithms 79(3), 679–695 (2018)
Hajipour, M., Jajarmi, A., Malek, A., Baleanu, D.: Positivity-preserving sixth-order implicit finite difference weighted essentially non-oscillatory scheme for the nonlinear heat equation. Appl. Math. Comput. 325, 146–158 (2018)
Acknowledgements
Not applicable.
Availability of data and materials
Not applicable.
Funding
No specific funding received for this work.
Author information
Authors and Affiliations
Contributions
Problem statement and formulation done by VPD and RJ; problem solved by DK; results computed by IK; results discussed by JS. All authors equally contributed in making the first draft and revision. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dubey, V.P., Kumar, R., Kumar, D. et al. An efficient computational scheme for nonlinear time fractional systems of partial differential equations arising in physical sciences. Adv Differ Equ 2020, 46 (2020). https://doi.org/10.1186/s13662-020-2505-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-2505-6