Applications of Fractional Reduced Differential Transform Method for Solving the Generalized Fractional-order Fitzhugh–Nagumo Equation

Abstract

In the current study, we establish a fractional reduced differential transform method, which is successfully applied to obtain the analytical approximate solutions of the nonlinear generalized fractional-order Fitzhugh–Nagumo equation. Also, we considered three different cases of generalized fractional-order Fitzhugh–Nagumo equation for different values of $\alpha$. The fractional derivative is considered in the context of the Caputo derivative. The obtained results show that the proposed technique is efficient, and convenient to implement fractional-order differential equations. We compared the approximate solutions and the exact solutions of the partial fractional differential equations for integer order. The approximate solutions are rapidly convergences of the exact solutions and also, this method reduced numerical calculation.

Introduction

Anomalous phenomena in mathematics are nonlinear and it has paramount importance in applied physics, mathematics, biology, mechanics, and so on. Therefore, explicit solutions to the nonlinear equations are of fundamental significance to preserve the actual physical distinctiveness of the problem and described process can be understood deeply. To solve such equations, Semi-analytical method such as the Fractional Reduced Differential Transform Method (FRDTM) is used. The FRDTM has no specific requirements for nonlinear operators, discretization, linearization, transformation or perturbation. The fractional Reduced Differential Transform Method (FRDTM) is a strong and efficient method, which can be widely used to handle linear and nonlinear models due to the flexibility of applications, convenience and accuracy of obtained results.

The generalized Fitzhugh–Nagumo equation is fractionalized into fractional-order and defined as [4, 12]

$$\begin{aligned} \dfrac{\partial ^{\alpha } \theta }{\partial t^{\alpha } } =\dfrac{\partial ^{2} \theta }{\partial x^{2} } -\theta ^{3} +\left( 1+\beta \right) \theta ^{2} -\beta \theta , \,\,\, where, \,\, 0<\alpha \le 1 \end{aligned}$$

(1)

having the exact solution as follows [4]

$$\begin{aligned} \theta \left( x,t\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x+\left( 1-2\beta \right) t}{4} \right) \end{aligned}$$

(2)

Eq. 1 is an important nonlinear reaction-diffusion equation and frequently used to represent the spread of nerve impulses [5]; moreover, used in mathematical biology, the area of population genetics, and circuit theory as a mathematical model [2]. Therefore, in this paper, the FRDTM is applied to find the closed-form solution of the fractional-order non-linear Fitzhugh–Nagumo equation (when $\beta = 1$) [12, 16], Newell–Whitehead equation (when $\beta = -1$) [4, 12] and Fisher’s equation (when $\beta = 0$) [3, 17].

Zhengab and Shen [18] investigated the effect of diffusion on pattern formation in FitzHugh–Nagumo model and also they discussed the dynamics of the conduction of electrical impulses along a nerve fiber, and reveal how the dynamics of ion conduction is affected by diffusion. Prakash and Kaur [12] studied the fractional model of Fitzhugh–Nagumo equation arising in the transmission of nerve impulses with a reliable computationally effective numerical scheme, which was compilation of homotopy perturbation method with Laplace transform approach. Agbavon and Appadu [1] constructed four versions of nonstandard finite difference schemes in order to solve the FitzHugh–Nagumo equation with specified initial and boundary conditions. Khan [9] studied the partial differential equation of Fitzhugh–Nagumo equation which is modified by the appropriate wave transforms into a dimensionless nonlinear ordinary differential equation and solved by using a semi-inverse variational method.

Many researchers and scientists are solving such equations using different techniques. Keskin and Oturanc [7, 8] solved linear and nonlinear wave equations using the RDTM, and they showed the accuracy and the effectiveness of the proposed method. Moreover, Keskin and Oturanc showed that the number of iterations it takes to get an approximate solution is less than the one used by the DTM and other well-known methods in the field. Singh and Kumar [15] obtained the solution of time-fractional order multi-dimensional Navier–Stokes equation by adopting a semi-analytical scheme, FRDTM. Singh and Gupta [14] obtained the analytical solutions of space-time fractional hyperbolic-like equations with two reliable methods, New Integral Projected Differential Transform Method (NIPDTM) and FRDTM. Moreover, they compared both the methods and concluded that FRDTM solutions are easy to compute without using any transformation as compared to NIPDTM. Mukhtar et. al [11] used FRDTM for Solving Different Types of Nonlinear Fractional Burgers’ Equations in one, two coupled, and three dimensions and compared their results with the exact solutions.

The paper is organized as follows. In Sect. 2, we define definitions and preliminary concepts of fractional derivatives. In Sect. 3 we describe the fractional reduced differential transform method (FRDTM). In Sect. 4, we examine the generalized Fitzhugh-Nagumo equation for different values of $\beta$ with the described method introduced in Sect. 3. Finally, conclusion and advantages are given in Sect. 5.

Definitions and Preliminary Concepts

In this section, we discuss some necessary definitions and properties of the fractional calculus theory.

Definition 2.1

The fractional derivative $\left( {{D^\alpha }} \right)$ of $f\left( x \right)$ in the Caputo’s sense is defined as [10]:

$$\begin{aligned} {D^\alpha }f\left( t \right) = \dfrac{1}{{\varGamma \left( {n - \alpha } \right) }}\int _0^1 {\left( {t - \xi } \right) } {f^{\left( n \right) }}\left( \xi \right) \,d\xi , \text {for} n - 1 < \alpha \leqslant n,\,\,\,n \in N. \end{aligned}$$

(3)

Definition 2.2

For $\alpha > 0$ the Caputo fractional derivative of order $D_t^\alpha {t^r} = \dfrac{{\varGamma \left( {r + 1} \right) }}{{\varGamma \left( {r - \alpha + 1} \right) }}{t^{r\, - \,\alpha }},\,r > 0$ on the whole space, denoted by ${}^cD_ + ^\alpha$, is defined by [6]:

$$\begin{aligned} {}^cD_ + ^\alpha f\left( x \right) = \dfrac{1}{{\varGamma \left( {n - \alpha } \right) }}\int _{ - \infty }^x {{{\left( {x - \xi } \right) }^{n - \alpha - 1}}{D^n}f\left( \xi \right) \,\,d\xi } . \end{aligned}$$

(4)

Property: Some useful formula and important property of the modified Riemann – Liouville derivative is as follows [13]:

$$\begin{aligned} D_t^\alpha {t^r} = \dfrac{{\varGamma \left( {r + 1} \right) }}{{\varGamma \left( {r - \alpha + 1} \right) }}{t^{r\, - \,\alpha }},\,r > 0. \end{aligned}$$

(5)

Overview of Fractional Reduce Differential Transform Method

Consider a function $\theta \left( {x,t} \right)$, which is analytical, and it is the function of t and x. Now $\theta \left( {x,t} \right)$ is multiplication of two individual variable functions, expressed as $\theta \left( {x,t} \right) = \xi \left( x \right) \cdot \psi \left( t \right)$. So, the function can be denoted as

$$\begin{aligned} \theta \left( {x,t} \right) = \left( {\sum \limits _{i = 0}^\infty {\zeta \left( i \right) {x^i}} } \right) \left( {\sum \limits _{j = 0}^\infty {\varPsi \left( j \right) {t^j}} } \right) = \sum \limits _{k = 0}^\infty {{\varTheta _k}\left( x \right) {t^k}}. \end{aligned}$$

(6)

Definition 3.1

The t-dimensional spectrum function, for the analytic and continuously differentiable function $\theta \left( {x,t} \right)$ with respect to x and t in the domain, is given by

$$\begin{aligned} {W_k}\left( x \right) = \dfrac{1}{{\varGamma \left( {\alpha k + 1} \right) }}{\left[ {\dfrac{{{\partial ^{\alpha k}}}}{{\partial {t^{\alpha k}}}}\theta \left( {x,t} \right) } \right] _{t = {t_0}}}. \end{aligned}$$

(7)

Where a parameter $\alpha$ describes the order of time-functional derivative.

Throughout this paper, $\theta \left( {x,t} \right)$ represents the original function and ${\varTheta _k}\left( x \right)$ represents the reduced transformed function. The differential inverse transform of ${\varTheta _k}\left( x \right)$ is given by

$$\begin{aligned} \theta \left( {x,t} \right) = \sum \limits _{k = 0}^\infty {{\varTheta _k}\left( x \right) {{\left( {t - {t_0}} \right) }^{\alpha k}}}. \end{aligned}$$

(8)

Combining equations (7) and (8), we obtain

$$\begin{aligned} {\varTheta _k}\left( x \right) = \sum \limits _{k = 0}^\infty {\dfrac{1}{{\varGamma \left( {\alpha k + 1} \right) }}{{\left[ {\dfrac{{{\partial ^{\alpha k}}}}{{\partial {t^{\alpha k}}}}\theta \left( {x,t} \right) } \right] }_{t = {t_0}}}{{\left( {t - {t_0}} \right) }^{\alpha k}}}. \end{aligned}$$

(9)

When ${t_0} = 0$, equation (9) becomes

$$\begin{aligned} \theta \left( {x,t} \right) = \sum \limits _{k = 0}^\infty {\dfrac{1}{{\varGamma \left( {\alpha k + 1} \right) }}{{\left[ {\dfrac{{{\partial ^{\alpha k}}}}{{\partial {t^{\alpha k}}}}\theta \left( {x,t} \right) } \right] }_{t = 0}}{t^{\alpha k}}}. \end{aligned}$$

(10)

Some properties of reduced differential transformation method are [7, 8] as shown in Table 1.

Table 1 Properties of Reduce Differential Transform Method

Applications of Fractional Reduced Differential Transform Method

In this section, we apply the FRDTM to three numerical examples like Fitzhugh–Nagumo equation, Newell–Whitehead equation, and Fisher’s equation which are different cases of generalized Fitzhugh–Nagumo equation for different $\beta$ values. Also, we compare our approximate solutions results to the exact solutions followed by the discussion (2).

Case 1: If $\beta =1$, then Eq. (1) is called fractional-order Fitzhugh–Nagumo equation and it is defined as [12, 16]

$$\begin{aligned} \dfrac{\partial ^{\alpha } \theta }{\partial t^{\alpha } } =\dfrac{\partial ^{2} \theta }{\partial x^{2} } -\theta ^{3} +2\theta ^{2} -\theta , \,\,\, where, \,\,\, 0<\alpha \le 1 \end{aligned}$$

(11)

with initial condition

$$\begin{aligned} \theta \left( x,t\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) \end{aligned}$$

(12)

According to the FRDTM and properties of Table 1, the derivatives of Eq. (11) becomes

$$\begin{aligned} \begin{array}{l} {\dfrac{\varGamma \left( \alpha \left( k+1\right) +1\right) }{\varGamma \left( k\alpha +1\right) } \varTheta _{k+1} \left( x\right) =\dfrac{\partial ^{2} }{\partial x^{2} } \varTheta _{k} \left( x\right) -\sum \limits _{i=0}^{k}\sum \limits _{j=0}^{i}\varTheta _{j} \, \left( x\right) \varTheta _{i-j} \left( x\right) \, \varTheta _{k-i} \left( x\right) } \\ {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, +2\sum \limits _{i=0}^{k}\varTheta _{i} \left( x\right) \, \varTheta _{k-i} \left( x\right) -\varTheta _{k} \left( x\right) } \end{array} \end{aligned}$$

(13)

or

$$\begin{aligned} \varTheta _{k+1} \left( x\right) =\dfrac{\varGamma \left( k\alpha +1\right) }{\varGamma \left( \alpha \left( k+1\right) +1\right) } \left[ \begin{array}{l} {\dfrac{\partial ^{2} }{\partial x^{2} } \varTheta _{k} \left( x\right) -\sum \limits _{i=0}^{k}\sum \limits _{j=0}^{i}\varTheta _{j} \, \left( x\right) \varTheta _{i-j} \left( x\right) \, \varTheta _{k-i} \left( x\right) } \\ {\, +2\sum \limits _{i=0}^{k}\varTheta _{i} \left( x\right) \, \varTheta _{k-i} \left( x\right) -\varTheta _{k} \left( x\right) } \end{array}\right] \nonumber \\ \end{aligned}$$

(14)

From the initial conditions Eq. (12), we write

$$\begin{aligned} \varTheta _{0} \left( x\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) \end{aligned}$$

(15)

Putting Eq. (15) into Eq. (14), we can obtain

$$\begin{aligned} \begin{array}{l} {\varTheta _{1} \left( x\right) =-\dfrac{1}{8} \dfrac{1}{\varGamma \left( \alpha +1\right) \cosh ^{2} \left( \dfrac{\sqrt{2} x}{4} \right) } } \\ {\varTheta _{2} \left( x\right) =-\dfrac{1}{16} \dfrac{\sinh \left( \dfrac{\sqrt{2} x}{4} \right) }{\varGamma \left( 2\alpha +1\right) \cosh ^{3} \left( \dfrac{\sqrt{2} x}{4} \right) } } \\ {\, \, \, \, \, \vdots } \end{array} \end{aligned}$$

(16)

and so on.

So, an approximation solution as follows

$$\begin{aligned} \begin{array}{l} {{\mathop {\theta }\limits ^{\frown }}_{n} \left( x,t\right) =\sum \limits _{k=0}^{n}\varTheta _{k} \left( x\right) t^{k\alpha } } \\ {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, =\, \dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) -\dfrac{1}{8} \dfrac{t^{\alpha }}{\varGamma \left( \alpha +1\right) \cosh ^{2} \left( \dfrac{\sqrt{2} x}{4} \right) } -\dfrac{1}{16} \dfrac{\sinh \left( \dfrac{\sqrt{2} x}{4} \right) t^{2\alpha } }{\varGamma \left( 2\alpha +1\right) \cosh ^{3} \left( \dfrac{\sqrt{2} x}{4} \right) } +\cdots } \end{array}\nonumber \\ \end{aligned}$$

(17)

Eq. (17) is the approximate solution of the fractional-order nonlinear Fitzhugh–Nagumo equation.

Fig. 1

Comparison between FRDTM and Exact Solution of Fitzhugh–Nagumo equation

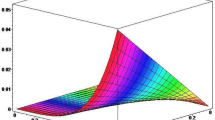
Fig. 1 shows the graphical comparison between FRDTM and Exact Solution of Fitzhugh–Nagumo equation for different values of t. The absolute error between FRDTM and exact solutions at the surface is shown in Fig. 2. Figure 3 shows the graphical representation for $\theta \left( x,t\right)$ of Fitzhugh–Nagumo equation for different fractional order values $\alpha =0.25, 0.50, 0.75$ and $t=0.2, 0.8.$ Moreover, it shows the solution increases with increasing $\alpha$ values.

Fig. 2

Surface of $\theta _{Abs.Error} =\left| \mathrm{Exact}\, \, \mathrm{-}\, \, \mathrm{FRDTM}\right| \,$for Fitzhugh–Nagumo equation

Table 3 shows numerical values for $\theta \left( x,t\right)$ of Fitzhugh–Nagumo equation for fractional order values $\alpha =0.25, 0.50, 0.75$ as well as integer order $\alpha =1.$ Furthermore, it shows the comparison between the solutions obtained using FRDTM and the exact solutions at different values of x and t. The solution of FRDTM has minor error when compared to the exact solution. When $\alpha$ values approaches to 1, the values close to exact solution; also, the FRDTM solutions converge to the exact solutions for integer order $\alpha =1.$

Fig. 3

Graphical representation for $\theta \left( x,t\right)$ of Fitzhugh–Nagumo equation for different fractional values $\alpha =0.25, 0.50, 0.75$ and $t=0.2, 0.8.$

Table 2 Numerical values for $\theta \left( x,t\right)$ of Fitzhugh–Nagumo equation for different fractional values $\alpha =0.25, 0.50, 0.75$ and compared with the exact solution when $\alpha =1$

Case 2: If $\left( \beta =-1\right)$, then Eq. (1) is called fractional-order Newell–Whitehead equation and it is defined as [4, 12]

$$\begin{aligned} \dfrac{\partial ^{\alpha } \theta }{\partial t^{\alpha } } =\dfrac{\partial ^{2} \theta }{\partial x^{2} } -\theta ^{3} +\theta , \,\, where, \,\, 0<\alpha \le 1 \end{aligned}$$

(18)

with initial condition

$$\begin{aligned} \theta \left( x,0\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) \end{aligned}$$

(19)

According to the FRDTM and properties of Table 1, the derivatives of Eq. (18) becomes

$$\begin{aligned} \dfrac{\varGamma \left( \alpha \left( k+1\right) +1\right) }{\varGamma \left( k\alpha +1\right) } \varTheta _{k+1} \left( x\right) =\dfrac{\partial ^{2} }{\partial x^{2} } \varTheta _{k} \left( x\right) -\sum \limits _{i=0}^{k}\sum \limits _{j=0}^{i}\varTheta _{j} \, \left( x\right) \varTheta _{i-j} \left( x\right) \, \varTheta _{k-i} \left( x\right) \, +\varTheta _{k} \left( x\right) \nonumber \\ \end{aligned}$$

(20)

or

$$\begin{aligned} \varTheta _{k+1} \left( x\right) =\dfrac{\varGamma \left( k\alpha +1\right) }{\varGamma \left( \alpha \left( k+1\right) +1\right) } \left[ \dfrac{\partial ^{2} }{\partial x^{2} } \varTheta _{k} \left( x\right) -\sum \limits _{i=0}^{k}\sum \limits _{j=0}^{i}\varTheta _{j} \, \left( x\right) \varTheta _{i-j} \left( x\right) \, \varTheta _{k-i} \left( x\right) +\varTheta _{k} \left( x\right) \right] \nonumber \\ \end{aligned}$$

(21)

From the initial conditions Eq. (19), we write

$$\begin{aligned} \varTheta _{0} \left( x\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) \end{aligned}$$

(22)

Putting Eq. (22) into Eq. (21), we can obtain

$$\begin{aligned} \begin{array}{l} {\varTheta _{1} \left( x\right) =\dfrac{3}{8} \dfrac{1}{\varGamma \left( \alpha +1\right) \cosh ^{2} \left( \dfrac{\sqrt{2} x}{4} \right) } } \\ {\varTheta _{2} \left( x\right) =-\dfrac{9}{16} \dfrac{\sinh \left( \dfrac{\sqrt{2} x}{4} \right) }{\varGamma \left( 2\alpha +1\right) \cosh ^{3} \left( \dfrac{\sqrt{2} x}{4} \right) } } \\ {\, \, \, \, \, \, \vdots } \end{array} \end{aligned}$$

(23)

and so on. So, an approximation solution as follows

$$\begin{aligned} \begin{array}{l} {{\mathop {\theta }\limits ^{\frown }}_{n} \left( x,t\right) =\sum \limits _{k=0}^{n}\varTheta _{k} \left( x\right) t^{k\alpha } } \\ {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, =\, \dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) +\dfrac{3}{8} \dfrac{t^{\alpha }}{\varGamma \left( \alpha +1\right) \cosh ^{2} \left( \dfrac{\sqrt{2} x}{4} \right) } -\dfrac{9}{16} \dfrac{\sinh \left( \dfrac{\sqrt{2} x}{4} \right) t^{2\alpha } }{\varGamma \left( 2\alpha +1\right) \cosh ^{3} \left( \dfrac{\sqrt{2} x}{4} \right) } +\cdots } \end{array}\nonumber \\ \end{aligned}$$

(24)

Eq. (24) is the approximate solution of the fractional-order Newell–Whitehead equation.

Fig. 4

Comparision between FRDTM and Exact Solution of Newell–Whitehead equation

Figure 4 shows the comparison between FRDTM and Exact Solution for Newell–Whitehead equation for different values of t. Figure 5 shows the absolute error between FRDTM and exact solutions at the surface. Figure 6 shows the graphical representation for $\theta \left( x,t\right)$ of Fitzhugh–Nagumo equation for different fractional order values $\alpha =0.25, 0.50, 0.75$ and $t=0.2, 0.8.$ Moreover, it shows the solution decreases with increasing $\alpha$ values.

Fig. 5

Surface of $\theta _{Abs.Error} =\left| \mathrm{Exact}\, \, \mathrm{-}\, \, \mathrm{FRDTM}\right|$for Newell–Whitehead equation

Fig. 6

Graphical representation for $\theta \left( x,t\right)$ of Newell–Whitehead equation for different fractional values $\alpha =0.25, 0.50, 0.75$ and $t=0.2, 0.8.$

Table 3 Numerical values for $\theta \left( x,t\right)$ of Newell–Whitehead equation for different fractional values $\alpha =0.25, 0.50, 0.75$ and compared with the exact solution when $\alpha =1.$

Table 3 shows the numerical values for $\theta \left( x,t\right)$of fractional order Newell–Whitehead equation obtained using FRDTM for different fractional-order values $\alpha =0.25,\, 0.5\, \, and\, \, 0.75.$ Moreover, A comparison between the computed solutions using FRDTM and the exact solutions at different values of x and t are shown. By observing the absolute error, it can be concluded that there is an excellent agreement between FRDTM and the numerical results for integer order $\alpha =1.$

Case 3: If $\left( \beta =0\right)$, then Eq. (1) is called fractional-order Fisher’s equation and it is defined as [3, 17]

$$\begin{aligned} \dfrac{\partial ^{\alpha } \theta }{\partial t^{\alpha } } =\dfrac{\partial ^{2} \theta }{\partial x^{2} } -\theta ^{3} +\theta ^{2}, \,\, where, \,\, 0<\alpha \le 1 \end{aligned}$$

(25)

with initial condition

$$\begin{aligned} \theta \left( x,0\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) \end{aligned}$$

(26)

According to the FRDTM and properties of Table 1, the derivatives of Eq. (25) becomes

$$\begin{aligned} \begin{array}{l} {\dfrac{\varGamma \left( \alpha \left( k+1\right) +1\right) }{\varGamma \left( k\alpha +1\right) } \varTheta _{k+1} \left( x\right) =\dfrac{\partial ^{2} }{\partial x^{2} } \varTheta _{k} \left( x\right) -\sum \limits _{i=0}^{k}\sum \limits _{j=0}^{i}\varTheta _{j} \, \left( x\right) \varTheta _{i-j} \left( x\right) \, \varTheta _{k-i} \left( x\right) } \\ {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, +\sum \limits _{i=0}^{k}\varTheta _{i} \left( x\right) \, \varTheta _{k-i} \left( x\right) } \end{array} \end{aligned}$$

(27)

or

$$\begin{aligned} \varTheta _{k+1} \left( x\right) =\dfrac{\varGamma \left( k\alpha +1\right) }{\varGamma \left( \alpha \left( k+1\right) +1\right) } \left[ \begin{array}{l} {\dfrac{\partial ^{2} }{\partial x^{2} } \varTheta _{k} \left( x\right) -\sum \limits _{i=0}^{k}\sum \limits _{j=0}^{i}\varTheta _{j} \, \left( x\right) \varTheta _{i-j} \left( x\right) \, \varTheta _{k-i} \left( x\right) } \\ {\, +\sum \limits _{i=0}^{k}\varTheta _{i} \left( x\right) \, \varTheta _{k-i} \left( x\right) } \end{array}\right] \end{aligned}$$

(28)

From the initial conditions Eq. (26), we write

$$\begin{aligned} \varTheta _{0} \left( x\right) =\dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) \end{aligned}$$

(29)

Putting Eq. (29) into Eq. (28), we can obtain

$$\begin{aligned} \begin{array}{l} {\varTheta _{1} \left( x\right) =\dfrac{1}{8} \dfrac{1}{\varGamma \left( \alpha +1\right) \cosh ^{2} \left( \dfrac{\sqrt{2} x}{4} \right) } } \\ {\varTheta _{2} \left( x\right) =-\dfrac{1}{16} \dfrac{\sinh \left( \dfrac{\sqrt{2} x}{4} \right) }{\varGamma \left( 2\alpha +1\right) \cosh ^{3} \left( \dfrac{\sqrt{2} x}{4} \right) } } \\ {\, \, \, \, \vdots } \end{array} \end{aligned}$$

(30)

and so on.

So, an approximation solution as follows

$$\begin{aligned} \begin{array}{l} {{\mathop {\theta }\limits ^{\frown }}_{n} \left( x,t\right) =\sum \limits _{k=0}^{n}\varTheta _{k} \left( x\right) t^{k\alpha } } \\ {\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, =\, \dfrac{1}{2} +\dfrac{1}{2} \tanh \left( \dfrac{\sqrt{2} x}{4} \right) +\dfrac{1}{8} \dfrac{t^{\alpha }}{\varGamma \left( \alpha +1\right) \cosh ^{2} \left( \dfrac{\sqrt{2} x}{4} \right) } -\dfrac{1}{16} \dfrac{\sinh \left( \dfrac{\sqrt{2} x}{4} \right) t^{2\alpha } }{\varGamma \left( 2\alpha +1\right) \cosh ^{3} \left( \dfrac{\sqrt{2} x}{4} \right) } +\cdots } \end{array}\nonumber \\ \end{aligned}$$

(31)

Eq. (31) is the approximate solution of the fractional-order nonlinear Fisher’s equation.

Fig. 7

Comparision between FRDTM and Exact Solution of Fisher’s equation

Fig. 8

Surface of $\theta _{Abs.Error} =\left| \mathrm{Exact}\, \, \mathrm{-}\, \, \mathrm{FRDTM}\right|$for Fisher’s equation

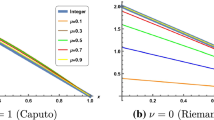
Figure 7 shows the comparison between FRDTM and Exact Solution for Fisher’s equation for different values of t. Figure 8 shows the absolute error between FRDTM and exact solutions at the surface. Figure 9 shows the graphical representation for $\theta \left( x,t\right)$ of Fisher’s equation for different fractional order values $\alpha =0.25, 0.50, 0.75$ and $t=0.2, 0.8.$ Moreover, it shows the solution decreases with increasing $\alpha$ values.

Fig. 9

Graphical representation for $\theta \left( x,t\right)$ of Newell–Whitehead equation for different fractional values $\alpha =0.25, 0.50, 0.75$ and $t=0.2, 0.8.$

Table 4 Numerical values for $\theta \left( {x,t} \right)$ of Fisher’s equation for different fractional values $\alpha = 0.25, 0.50, 0.75$ and compared with the exact solution when $\alpha = 1$

Table 4 shows the numerical values for $\theta \left( {x,t} \right)$ of fractional order Fisher’s equation obtained using FRDTM for different fractional-order values $\alpha = 0.25, 0.5$ and 0.75. The results shows that, when fractional order $\alpha$ value increases, the solution decreases. Moreover, a comparison made between the solutions obtained using FRDTM and the exact solutions at different values of x and t. By observing the absolute error, it can be concluded that there is an excellent agreement between FRDTM and the numerical results for integer-order $\alpha =1$. Dehghan et al. [4] solved the generalized Fitzhugh-Nagumo equation using ADM, HPM and, VIM. Besides, it is found that the solution obtained using FRDTM is the same as compared to ADM, HPM and, VIM for $\alpha =1$.

Conclusion

In this paper, FRDTM has been implemented in three cases of the generalized fractional-order Fitzhugh-Nagumo equation to study the effectiveness and accurateness of the proposed method. It is found that FRDTM solutions are in excellent agreement with the available exact solution. This shows that FRDTM is an effective, efficient and powerful mathematical tool, which is easily applied in finding out the approximate analytic solutions for a wide range of real-world problems arising in engineering and applied sciences.