1 Introduction

Fractional differential equations involving fractional derivatives are generalizations of classical differential equations and widely used in chemical, physical and engineering sciences. Fractional partial differential equations (FPDEs) are very efficiently to characterize many important physical and engineering events [1,2,3,4,5,6]. To find solutions of FPDEs is very challenging procedure in which we need to use hard mathematical solutions methods. It is well-known that to get exact solutions of FPDEs in terms of composite elementary functions in a simple way is not so easy, hence for the such solutions we need to use effective, reliable numerical algorithms. It has been shown that fractional differential equations have important role to model various problems from many different disciplines. Also, this method can provide more useful results for physical and engineering problems than models just including integer derivatives. Therefore, fractional differential equations widely studied among researchers from many different disciplines such as in [7,8,9,10,11,12,13].

It is well-known that series expansions are very important sources to evaluate functions, integrals, derivatives etc. Based on this fact, we focus on obtaining series expansion to obtain approximate solutions of FPDEs. Although computer based numerical algorithms which don’t use series expansion solutions are proposed after the development of automatic methods for formula manipulation, solutions including series expansion again becomes popular among the researchers. DTM proposed by Zhou [14] is also a based series expansion method that can be applied Ordinary Differential Equations (ODEs), Partial Differential Equations(PDEs) and FPDEs. The method provides an iterative procedure to get the spectrum of analytic solutions. It has been proven that the technique is an efficient mathematical tool for solving various kinds of problems [14,15,16,17].

In recent years, many hybrid methods combining the Laplace transform method with Adomian decomposition method (ADM) [10], homotopy analysis method (HAM) [11], variational iteration method (VIM) [12, 13] are presented to solve FPDE. Using the same spirit, the aim of this study is to propose a new method combining Laplace transform method with DTM to obtain approximate solutions of FPDEs.

The main idea of the presented new method in the current study is to convert Fractional Partial Differential Equations (FPDEs) into Ordinary Differential Equations (ODEs) by using Laplace Transformation Method. After this transformation, we are in a position to solve obtained ODEs via DTM which is a very effective tool to solve for such equations. Basics of the used method during transformations and the applications of the method can be seen in coming sections.

Nowadays, fractional boundary value problems (FBVPs) appears more and more frequently in different research fields and engineering applications. To solve the FBVPs accurately and efficiently is considered a very important issue. Fractional boundary value problems (FBVPs) have been solved by various methods such as finite sine transform technique and separation of variables methods. One of the advantage of the presented study we utilize a new iterative method for solving the FBVPs with mixed boundary conditions. To best advantage of this study no such work has been made to combine Laplace transform and DTM to solve FBVPs. Another, the basic motivation of this work is to overcome of a deficiency of generalized DTM [17]. Because; generalized DTM can be used to solve FPDEs with accuracy approximation, which is acceptable for a small interval, because boundary conditions are satisfied via the method, and the remaining unsatisfied conditions play no roles in the final results. The aim of the using Laplace transform is to overcome the deficiency that is mainly caused by the unsatisfied conditions

This paper is organized as follows: in Sect. 2, we introduce the basics knowledge of fractional calculus and Laplace transformation. In Sect. 3, we introduce the key points of standard Differential Transform Method. In Sect. 4, we introduce Fractional Laplace Differential Transform method. In Sect. 5, we introduce convergence analysis and error estimation of DTM. Additionally, the method is applied to different problems in Sect. 6. Finally, a brief conclusion is given in Sect. 7.

2 Basic definitions and preliminaries

In this section, we mention the following basic definitions and properties of the fractional calculus theory and Laplace transform which will be used in this paper:

Definition 1.1

A real function f(t), \(t>0\) is said to be in the space \(C_{\mu }\), \(\mu \in \mathfrak {R}\), if there exists a real number \(p>\mu\), such that \(f(t)=t^{p}f_{1}(t)\) where \(f_{1}(t)\in C(0,\infty ),~\)and it is said to be in the space \(C_{n}\) iff \(\ f^{(n)}\in C_{\mu },n\in {\mathbb {N}} .\)

Definition 1.2

The left sided Riemann–Liouville fractional integral of order \(\mu \ge 0,\) of a function \(f\in C_{\alpha }\), \(\alpha \ge -1\) is defined [18] as,

$$\begin{aligned} I^{\mu }f(t)=\left\{ \begin{array}{cc} \frac{1}{\Gamma (\mu)}\int _{0}^{t}(t-\tau )^{\mu -1}f(\tau )d\tau ,& \quad ~\mu>0,\,t>0 \\ f(t),& \quad \mu =0 \end{array},\right. \end{aligned}$$

where \(\Gamma (.)\)is Gamma function.

Definition 1.3

The left sided Caputo fractional derivative of \(\ f,f\in C_{-1}^{m},m\in {\mathbb {N}} \cup \left\{ 0\right\} ,~\)is defined by Podlubny [19] and Samko et al. [20] as

$$\begin{aligned} D_{*}^{\mu }f(t)=\frac{\partial ^{\mu }f(t)}{\partial t^{\mu }}=\left\{ \begin{array}{cc} I^{m-\mu }\left[ \frac{\partial ^{m}f(t)}{\partial t^{m}}\right] ,&{} \quad m-1<\mu <m,m\in {\mathbb {N}}, \\ \frac{\partial ^{m}f(t)}{\partial t^{m}},&{} \quad \mu =m. \end{array} \right. \end{aligned}$$

Definition 1.4

The Laplace transform of f(t) in\(\left[ 0,\infty \right)\) is defined as

$$\begin{aligned} F(s)=L\left[ f(t)\right] =\int _{0}^{\infty }e^{-st}f(t)dt \end{aligned}$$

where s is real or complex number.

Definition 1.5

The Laplace transform \(L\left[ f(t)\right] ~\)of the Riemann–Liouville fractional integral is defined [21] as

$$\begin{aligned} L\left[ I_{t}^{\alpha }f(t)\right] =s^{-\alpha }F(s). \end{aligned}$$

Definition 1.6

The Laplace transform \(L\left[ f(t)\right] ~\)of the Caputo fractional derivative is defined [21] as

$$\begin{aligned} L\left[ D_{t}^{n\alpha }f(t)\right] =s^{n\alpha }F(s)-\sum _{k=0}^{n-1}s^{(n\alpha -k-1)}f^{(k)}(0),\ \ \ \ \ n-1<\alpha \leqslant n. \end{aligned}$$

Definition 1.7

The Mittag-Leffler function \(E_{\alpha }\) with \(\alpha >0~\) is defined by following series representation, valid in the whole complex plane [22]:

$$\begin{aligned} E_{\alpha }(t)=\sum _{n=0}^{\infty }\frac{t^{n}}{\Gamma (n\alpha +1)},\alpha >0,~t\in C. \end{aligned}$$

3 Differential transform method (DTM)

The basic definitions and fundamental operations of the differential transform method (DTM) are defined in [14,15,16,17] as follows:

The differential transform of k-th derivative of a given univariate function u(x) which is analytic and continuously differentiable in the domain of interest is defined as

$$\begin{aligned} U(k)=\frac{1}{k!}\left[ \frac{d^{k}u(x)}{dx^{k}}\right] _{x=x_{0}} \end{aligned}$$
(1)

where U(k) is the transformed function of u(x). Also, the relevant differential inverse transform for function U(k) is defined as

$$\begin{aligned} u(x)=\sum _{k=0}^{\infty }\left\{ U(k)(x-x_{0})^{k}\right\} . \end{aligned}$$
(2)

Combining Eqs. (1) and (2), we get

$$\begin{aligned} u(x)=\sum _{k=0}^{\infty }\frac{1}{k!}\left[ \frac{d^{k}u(x)}{dx^{k}}\right] _{x=x_{0}}(x-x_{0})^{k} \end{aligned}$$
(3)

which implies that the concept of differential transform is derived from Taylor series expansion, but the method does not used to evaluate the derivatives symbolically. Some basic operations of the one-dimensional differential transform are listed in Table 1. Proofs of the given operations in Table 1 can be extracted from [14,15,16,17].

Table 1 Some operations of the dimensional differential transformation
Full size table

4 Basic idea of the new fractional laplace differential transform method (FLDTM)

In order to illustrate the solution procedure of the fractional laplace differential transform method for the FPDEs, we consider the following general nonlinear FPDE:

$$\begin{aligned} D_{t}^{\alpha }u(x,t)+R[x]u(x,t)+N[x]u(x,t)=f(x,t),\ \ t\in {\mathbb {R}} _{0}^{+}, x\in {\mathbb {R}},\ 0<\alpha \leqslant 1 \end{aligned}$$
(4)

where \(\ D_{{}}^{\alpha }=\frac{\partial ^{\alpha }\ }{\partial t^{\alpha }}\) and \(R[x],\ N[x]\) corresponds to linear, nonlinear operator in x, respectively while f (x, t) is a continuous function. For simplicity, we disregard all boundary and initial conditions of Eq. (4). They can be used in similar procedure. Let’s start with to apply the laplace transformation on both sides of Eq. (4) with respect to t. Thus, we get:

$$\begin{aligned} L\left[ D_{t}^{\alpha }u(x,t)\right] +L\left[ R[x]u(x,t)+N[x]u(x,t)\right] =L \left[ f(x,t)\right] . \end{aligned}$$

Now, by using Definition 1.6, we obtain the following ordinary differential equation which can be solved via DTM.

$$\begin{aligned} D{\overline{u}}(x,s)+N{\overline{u}}(x,s)=q(x,s) \end{aligned}$$
(5)

where \({\overline{u}}(x,s)=L\left[ u(x,t)\right]\). Here, \(D=\frac{d\ }{dx}+ \frac{d\ ^{2}}{dx^{2}}+\cdots +\frac{d\ ^{n}}{dx^{n}},n\in {\mathbb {N}} ,\) is a linear operator\(,\ N\) is a nonlinear operator, and q (x, s) is a known analytical function.

Then, applying DTM to both sides of the Eq. (5) yields to the following recursive system:

$$\begin{aligned} A(k)U(k+n)+F(k)=Q(k) \end{aligned}$$
(6)

where \(A(k)\) is the coefficient of \(U(k+n)\) which is differential transform of \(D{\overline{u}}(x,s).\)F(k),Q(k) are the transformations of \(N{\overline{u}}(x,s),q(x,s)\), respectively. As mentioned before, for the sake of simplicity, we ignore initial and boundary conditions. Naturally, if the equation representing the system (4) is transformed into Eq. (6), we have to transform also the initial and boundary conditions given (4) into new forms that will be used to represent in Eq. (6). This will give us U (k), \(k=0,1,\ldots ,n-1\). By using U(k), \(k=0,1,\ldots ,n-1\)and Eq. (6), we can iteratively obtain \(U(k),k=n,n+1,n+2,\ldots\). Here, it must be noted that U(k)  values are the components of the spectrum of \({\overline{u}}(x,s)\). Finally, we get approximate solution of the Eq. (5) in the following form:

$$\begin{aligned} {\overline{u}}(x,s)=\sum \limits _{k=0}^{\infty }U(k)x^{k}. \end{aligned}$$
(7)

Taking the inverse Laplace transform with respect to \(s\) from both sides of Eq. (7), we get \(u(x,t)\) which is the solution of Eq. (4).

Instead of Eq. (4), let us consider the system

$$\begin{aligned} D_{t}^{\alpha _{i}}u_{i}(x,t)=A_{i}\left( u_{1}(x,t),\ldots ,u_{n}(x,t)\right) { ,\ \ m}_{i}-1\le \alpha _{i}\le m_{i}, \quad i=1,2,\ldots ,n,\ \ m_{i}\in {\mathbb {N}} \end{aligned}$$
(8)

where \(A_{i}\) are nonlinear operators and \(u_{i}(x,t)\) are unknown functions of fractional partial differential equations (FPDEs). Taking Laplace transform on both sides of Eq. (8), we obtain

$$\begin{aligned} L\left[ D_{t}^{\alpha _{i}}u_{i}(x,t)\right] =L\left[ A_{i}\left( u_{1}(x,t),\ldots ,u_{n}(x,t)\right) \right], \quad i=1,2,\ldots,n. \end{aligned}$$

In view of Definition 1.6. and initial conditions, we obtain the system (9) in below of ordinary differential equations which can be solved via DTM.

$$\begin{aligned} s^{\alpha _{i}}L\left[ u_{i}(x,t)\right] -\sum \limits _{k=0}^{m_{i}-1}s^{ \alpha _{i}-k-1}u_{i}^{(k)}(x,0)=L\left[ A_{i}\left( u_{1}(x,t),\ldots ,u_{n}(x,t)\right) \right], \quad i=1,2,\ldots,n \end{aligned}$$
(9)

after this modification, rest of the solution can be obtained by above same analog.

5 Convergence analysis and error estimation of DTM

Recently, Odibat et al. [23] proved the sufficient condition for convergence of generalized differential transform method and estimate the maximum absolute truncated error of the fractional power series. In case of \(\alpha =1\) the generalized differential transform method reduces to the classical differential transform method.

In this section, convergence and error estimation of differential transform method which is \(\alpha =1\) case in Odibat et al. [23] is given for the convenience of the reader. The convergence of differential transform method can be obtained by following a similar argument in Odibat et al. [23]. Moreover based on sufficient condition for convergence, an error estimation of the solutions can be also obtained with the same analog with Odibat et al. [23].

As we mention before in Sect. 3, the main steps of the differential transform method are the following. First, we apply the differential transform Eq. (1) to the given problem, and then the result is a recurrence relation. Second, solving this relation and using the differential inverse transform Eq. (2), we can obtain the solution of the problem as \(u(x)=\sum _{k=0}^{\infty }U(k)(x-x_{0})^{k}\), where U(k) is the differential transform of u(x).

The fundamental operations of the differential transform method consists in obtaining power series expansion for the solutions of non-linear models containing derivatives about the initial time \(x_{0}\),

$$\begin{aligned} u(x)=\sum _{k=0}^{\infty }a_{k}(x-x_{0})^{k},\ \ \ \ \ \ \ x\,\epsilon\, I, \end{aligned}$$
(10)

where \(I=(x_{0},x_{0}+r),r>0.\) Now, we are ready to give the convergence results.

Theorem 4.1

Let\(\phi _{k}(x)=a_{k}(x-x_{0})^{k}\), then the series solution\(\sum _{k=0}^{\infty }\phi _{k}(x)\), defined in Eq. (10), converges if\(\exists 0<\gamma <1\) such that \(\parallel \phi _{k+1}(x)\parallel \le \gamma \parallel \phi _{k}(x)\parallel ,\forall k\ge k_{0}\), for some \(k_{0}\in {\mathbb {N}}\).

Now we will give the proof of Theorem 4.1.

Proof

Let \((C[I],\parallel .\parallel )\) the Banach space of all continuous functions on  I  with the norm \(\parallel f(x)\parallel =max_{x\in I}|f(x)|\). Let \(\left\{ S_{n}\right\} _{n=0}^{\infty }~\) be the sequence of partial sums

$$\begin{aligned} S_{n}=\phi _{0}(x)+\phi _{1}(x)+\cdots +\phi _{n}(x), \end{aligned}$$

where \(\phi _{k}(x)=a_{k}(x-x_{0})^{k}\). We know that every Cauchy sequence is convergent in Banach space. So if we were able to prove that \(\left\{ S_{n}\right\} _{n=0}^{\infty }\) is a Cauchy sequence in this Banach space then it’s complete the proof. For this purpose, consider

$$\begin{aligned} \parallel S_{n+1}-S_{n}\parallel =\parallel \phi _{n+1}(x)\parallel \le \gamma \parallel \phi _{n}(x)\parallel \le \cdots \le \gamma ^{n-k_{0}+1}\parallel \phi _{k_{0}}(x)\parallel =\gamma ^{n-k_{0}+1}~max_{x\in I}|\phi _{k_{0}}(x)|. \end{aligned}$$

For every \(n,m\in {\mathbb {N}}, n\ge m>k_{0},\) we have

$$\begin{aligned} \parallel S_{n}-S_{m}\parallel & = \parallel \sum _{j=m}^{n-1}(S_{j+1}-S_{j})\parallel \le \sum _{j=m}^{n-1}\parallel (S_{j+1}-S_{j})\parallel \end{aligned}$$
(11)
$$\begin{aligned}\le & {} \sum _{j=m}^{n-1}\gamma ^{j-k_{0}+1}~max_{x\in I}|\phi _{k_{0}}(x)|= \frac{1-\gamma ^{n-m}}{1-\gamma }\gamma ^{m-k_{0}+1}~max_{x\in I}|\phi _{k_{0}}(x)| \end{aligned}$$
(12)

and because \(0<\gamma <1\), we obtain

$$\begin{aligned} \lim _{n,m\rightarrow \infty }\parallel S_{n}-S_{m}\parallel =0. \end{aligned}$$

Therefore, \(\left\{ S_{n}\right\} _{n=0}^{\infty }~\) is a Cauchy sequence in the Banach space \((C[I],\parallel .\parallel )\), so it is convergent.

Now we will prove the error estimation of the DTM.

Simply, using the fact that \(\parallel \phi _{k}(x)\parallel =|a_{k}|max_{x\in I}(x-x_{0})^{k}\), the sufficient condition for convergence in Theorem 4.1 can be replaced by the following condition

$$\begin{aligned} \lim _{k\rightarrow \infty }|\frac{a_{k+1}}{a_{k}}|.max_{x\in I}(x-x_{0})<1. \end{aligned}$$

Consequently, the series solution \(u(x)=\sum _{k=0}^{\infty }a_{k}(x-x_{0})^{k}\), where \(x\in I\), converges if \(~\lim _{k\rightarrow \infty }|\frac{a_{k+1}}{a_{k}}|<1/max_{x\in I}(x-x_{0})\). If the series \(\sum _{k=0}^{\infty }a_{k}(x-x_{0})^{k}\) converges, and then the function \(u(x)\) is said to be analytic function at \(x_{0}\) [24].

Theorem 4.2

Assume that the series solution\(\sum _{k=0}^{\infty }\phi _{k}(x)\), where\(\phi _{k}(x)=a_{k}(x-x_{0})^{k}\), converges to the solutionu(x). If the truncated series \(\sum _{k=0}^{m}\phi _{k}(x)\) is used as an approximation to the solutionu(x), and then the maximum absolute truncated error is estimated as

$$\begin{aligned} \parallel u(x)-\sum _{k=0}^{m}\phi _{k}(x)\parallel ~\le \frac{1}{1-\gamma } \gamma ^{m-m_{0}+1}~max_{x\in I}|a_{m_{0}}(x-x_{0})^{m_{0}}|, \end{aligned}$$
(13)

for any\(m_{0}\ge 0\), where \(a_{m_{0}}\ne 0.\)

Proof

From Theorem 4.1, following inequality Eq. (12), we have

$$\begin{aligned} \parallel S_{n}-S_{m}\parallel ~\le \frac{1-\gamma ^{n-m}}{1-\gamma }\gamma ^{m-m_{0}+1}~max_{x\in I}|a_{m_{0}}(x-x_{0})^{m_{0}}| \end{aligned}$$
(14)

with \(n\ge m\ge m_{0}~\) for any \(m_{0}\ge 0\), where \(a_{m_{0}}\ne 0\). Since \(0<\gamma <1\), we have \(\left( 1-\gamma ^{n-m}\right) <1\), and so, the inequality (14) can be reduced to

$$\begin{aligned} \parallel S_{n}-S_{m}\parallel ~\le \frac{1}{1-\gamma }\gamma ^{m-m_{0}+1}~max_{x\in I}|a_{m_{0}}(x-x_{0})^{m_{0}}|, \end{aligned}$$

Clearly, when \(n\rightarrow \infty ,S_{n}\rightarrow u(x)\). Hence, inequality () is obtained. This completes the proof of Theorem 4.2.

As a conclusion, Theorem 4.1 states that the power series solution, given in Eq. (), converges to an exact solution under the condition that \(\exists 0<\gamma <1\) such that \(\parallel \phi _{k+1}(x)\parallel \le \gamma \parallel \phi _{k}(x)\parallel ,\forall k\ge k_{0}\), for some \(k_{0}\in {\mathbb {N}}\). In other words, if we define, for every \(~i\ge k_{0}\), the parameters,

$$\begin{aligned} \gamma _{i+1}=\left\{ \begin{array}{cc} \frac{\parallel \phi _{i+1}(x)\parallel }{\parallel \phi _{i}(x)\parallel } ,&{} \quad \parallel \phi _{i}(x)\parallel \ne 0 \\ 0,&{} \quad \parallel \phi _{i}(x)\parallel =0 \end{array} \right. \end{aligned}$$

\(i\in {\mathbb {N}} \cup \{0\}\) where \(\parallel \phi _{i}(x)\parallel =max_{x\in I}|a_{i}(x-x_{0})^{i}|\), then the series solution \(\sum _{k=0}^{\infty }\phi _{k}(x)\) converges to an exact solution, u(x), when \(0\le \gamma _{i}<1,\forall i\ge k_{0}\).

Moreover, as we state in Theorem 4.2, the maximum absolute truncation error is estimated to be \(\parallel u(x)-\sum _{k=0}^{m}\phi _{k}(x)\parallel \le \frac{1}{1-\beta }\beta ^{m-m_{0}+1}~max_{x\in I}|a_{m_{0}}(x-x_{0})^{m_{0}}|\), where \(\beta =max\{\gamma _{i},i=m_{0}+1,m_{0}+2,\ldots ,m+1\}\).

6 Results and discussion

In this section, the applicability of the algorithm will be demostrated by using some examples. All the results are calculated by using the software Maple.

Example 5.1

We consider the following homogeneous time fractional partial differential equation

$$\begin{aligned} \frac{\partial ^{\alpha }u\left( x,t\right) \ }{\partial t^{\alpha }}=\frac{ \partial ^{2}u\left( x,t\right) \ }{\partial x^{2}}+\frac{\partial u\left( x,t\right) }{\partial x}+u\left( x,t\right) \ ,\ \ \ \ \ \ \ \ \ \ \ t\ge 0,\ 0<\alpha \leqslant 1 \end{aligned}$$
(15)

subject to the initial and boundary conditions

$$\begin{aligned} u(x,0)=e^{-x},u(0,t)=E_{\alpha }(t^{\alpha }),u_{x}(0,t)=-E_{\alpha }(t^{\alpha }). \end{aligned}$$
(16)

As above, we use the notation \({\overline{u}}(x,s)=L\left[ u(x,t)\right]\) for the Laplace transform of \(u.\) Operating the Laplace transform on both sides in Eq. (15) with respect to t and after using the differentiation property of Laplace transform for fractional derivative, we obtain

$$\begin{aligned} s^{\alpha }L\left[ u(x,t)\right] -s^{\alpha -1}u(x,0)=L\left[ u_{xx}+u_{x}+u\right] . \end{aligned}$$

Application of the proposed method summarized above gives

$$\begin{aligned}&\frac{d^{2}{\overline{u}}\ }{dx^{2}}+\frac{d\ {\overline{u}}}{dx}+(1-s^{\alpha }) {\overline{u}}=-s^{\alpha -1}e^{-x} \end{aligned}$$
(17)
$$\begin{aligned}&{\overline{u}}\ (0,s)=\frac{s^{\alpha }}{s(s^{\alpha }-1)},\ \ \ \frac{d\ {\overline{u}}}{dx}(0,s)=\frac{-s^{\alpha }}{s(s^{\alpha }-1)}. \end{aligned}$$
(18)

This is a constant coefficient second order ODE. To solve above problem (17)–(18) by means of DTM, the recurrence equation can easily be constructed as follows

$$\begin{aligned} U(k+2) &= \frac{-1}{(k+1)(k+2)}\left[ (k+1)U(k+1)+(1-s^{\alpha })U(k)+s^{\alpha -1}\frac{(-1)^{k}}{k!}\right] \end{aligned}$$
(19)
$$\begin{aligned} U(0) & = \frac{s^{\alpha }}{s(s^{\alpha }-1)},\ \ U(1)=\frac{-s^{\alpha }}{ s(s^{\alpha }-1)}. \end{aligned}$$
(20)

Components of the spectrum of \({\overline{u}}\), U(k), can be calculated by utilizing the recurrence relation (19) and the transformed initial conditions (20). From the inverse transform of DTM given by Eq. (2) and via Eq. (3), we get the approximate solution of the problem (17)–(18) in series form

$$\begin{aligned} {\overline{u}}(x,s) =\frac{s^{\alpha }}{s(s^{\alpha }-1)}\left( 1-x+\frac{1}{ 2!}x^{2}-\frac{1}{3!}x^{3}+\cdots \right) . \end{aligned}$$
(21)

Taking the inverse Laplace transform on both sides of Eq. (21) with respect to s, we have

$$\begin{aligned} {\small u(x,t)} =L^{-1}\left[ {\overline{u}}(x,s)\right] =E_{\alpha }(t^{\alpha }) \left( 1-x+\frac{1}{2!}x^{2}-\frac{1}{3!}x^{3}+\cdots \right) . \end{aligned}$$
(22)

If \(\alpha =1/2\), then we get \({\small u(x,t)}=E_{1/2}(\sqrt{t} )\sum \limits _{k=0}^{\infty }\frac{(-1)^{k}x^{k}}{k!}\) which is in complete agreement with [25].

As a special case when \(\alpha =1\) in Eq. (22), we reproduce the solution of the problem (15)–(16) as follows:

$$\begin{aligned} {\small u(x,t)}\small = e^{t}\left( 1-x+\frac{1}{2!}x^{2}-\frac{1}{3!}x^{3}+\cdots \right) . \end{aligned}$$
(23)

So, the exact solution of Eqs. (15) and (16) in a closed form of elementary function will be \(u\left( x,t\right) =e^{-x+t}\). As we see, the proposed hybrid technique provides a closed form approximation for this problem. The convergence and the accuracy of the solution series in (23) when it is truncated at level \(n~\epsilon\)\({\mathbb {N}}\) are analyzed by calculation the absolute errors \(E_{n}\) which is defined as follows: \(E_{n}=\mid u_{exact}(x,t)-u_{n}(x,t)\mid ~\) where \(\ u_{i}(t,x)=\sum \nolimits _{k=0}^{i}\sum \nolimits _{h=0}^{i}U(k,h)t^{k}x^{h}, \ i \epsilon \ {\mathbb {N}}\) and \(\ u_{exact}(x,t)\) denotes the exact solution of the equation.

Figure 1 shows the error \(E_{4}\) of approximate solutions at \(\alpha =1\). We can say that \(E_{n}\) is decreasing by n. So convergence of the method is promising in numerically. For theoretical convergence further analysis is required.

Fig. 1
figure 1

\(E_{4}=|u_{exact}-u_{4}(x,t)|\) for \(\alpha =1\)

Full size image

Example 5.2

In this example, we consider the time fractional partial differential equation [26] of the form

$$\begin{aligned} \frac{\partial ^{\alpha }u\left( x,t\right) \ }{\partial t^{\alpha }}=\frac{ \partial ^{2}u\left( x,t\right) \ }{\partial x^{2}}+\frac{\partial \ }{ \partial x}(xu\left( x,t\right) ) \end{aligned}$$
(24)

subject to the initial and boundary conditions

$$\begin{aligned} u(x,0)=1,u(0,t)=E_{\alpha }(t^{\alpha }),u_{x}(0,t)=0 \end{aligned}$$
(25)

where \(\ t>0,\ {x\in {\mathbb {R}} },\ 0<\alpha \le 1~\). As the previous application, applying Laplace transform first on both sides of Eq. (24) with respect to t gives

$$\begin{aligned} L\left[ D_{t}^{\alpha }u(x,t)\right] =L\left[ u_{xx}+(xu)_{x}\right] . \end{aligned}$$

Using the method described in Sect. 4, as we have employed in Example 5.1, the recurrence equation can be ready constructed as follows

$$\begin{aligned}&\frac{d^{2}{\overline{u}}\ }{dx^{2}}+\frac{d\ }{dx}(x{\overline{u}}\ )-s^{\alpha }{\overline{u}}=-s^{\alpha -1}, \\&{\overline{u}}\ (0,s)=\frac{s^{\alpha }}{s(s^{\alpha }-1)},\ \ \ {\overline{u}}\ _{x}(0,s)=0. \end{aligned}$$

Then,

$$\begin{aligned} U(k+2) & = \frac{-1}{(k+1)(k+2)}\left[ (1-s^{\alpha })U(k)+(k+1){\sum\limits_{r=0}^{k}\delta (r-1)U(k+1-r)+\delta (k)}s^{\alpha -1}\right] , \end{aligned}$$
(26)
$$\begin{aligned} U(0) & = \frac{s^{\alpha }}{s(s^{\alpha }-1)},\ \ U(1)=0. \end{aligned}$$
(27)

Components of the spectrum of \({\overline{u}}\), U(k) , can be calculated by utilizing the recurrence relation (26) and the transformed initial condition (27).

The inverse transform of DTM given by Eq. (2) and via Eq. (3) results in

$$\begin{aligned} {\overline{u}}(x,s)=\frac{1}{s^{1-\alpha }(s^{\alpha }-1)}. \end{aligned}$$
(28)

Applying the inverse Laplace transform on both sides of Eq. (28) with respect to s, the FLDTM solution of Eqs. (24) and (25) can be constructed as follows:

$$\begin{aligned} {\small u(x,t)}=L^{-1}\left[ {\overline{u}}(x,s)\right] ={\small L} ^{-1}\left[ \frac{1}{s^{1-\alpha }(s^{\alpha }-1)}\right] =E_{\alpha }(t^{\alpha }) \end{aligned}$$

which is precisely the exact solution. As a special case when \(\alpha =1\), the FLDTM solution of the problem (24)–(25) has the general pattern form which is coinciding with the exact solution in terms of elementary function

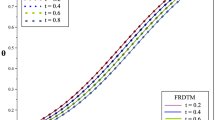
$$\begin{aligned} {\small u(x,t)}=e^{t}. \end{aligned}$$

The proposed solution of the problem (24)–(25) obtained by FLDTM at any x level for \(\alpha =1.0,\alpha =0.75,\alpha =0.50\) and \(\alpha =0.25\) can be seen in Fig. 2.

Fig. 2
figure 2

2D graphical representation for the solution of the problem (24)–(25) for different values of \(\alpha\)

Full size image

Example 5.3

Consider the following nonlinear time-fractional partial differential equation in the following form

$$\begin{aligned} \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}+\frac{1}{2}\frac{\partial }{\partial x}\left( u\right) ^{2}-u(1-u)=0 \end{aligned}$$

with the initial and boundary conditions

$$\begin{aligned} u(x,0)=e^{-x},u(0,t)=E_{\alpha }(t^{\alpha }),u_{x}(0,t)=-E_{\alpha }(t^{\alpha }) \end{aligned}$$

where \(\ t>0,\ {x\in {\mathbb {R}} },\ 0<\alpha \le 1~\) [27]. Using the method described in Sect. 4, similar to previous examples, we obtain the following solution:

$$\begin{aligned} {\small u(x,t)}=E_{\alpha }(t^{\alpha })\sum _{k=0}^{\infty }\frac{ (-1)^{k}x^{k}}{k!}. \end{aligned}$$

Example 5.4

In this example, we illustrate the applicability of FLDTM for solving system of fractional partial differential equations. Consider the following system of linear fractional partial differential equations

$$\begin{aligned} \left\{ \begin{array}{c} \frac{\partial ^{\alpha }u}{\partial t^{\alpha }}-\frac{\partial v}{\partial x}+v+u=0, \\ \frac{\partial ^{\alpha }v}{\partial t^{\alpha }}-\frac{\partial u}{\partial x}+v+u=0, \end{array} \right. \end{aligned}$$
(29)

subject to

$$\begin{aligned} u(x,0)=\sinh (x),v(x,0)=\cosh (x),u(0,t)=\sinh (-\alpha t),v(0,t)=\cosh (-\alpha t) \end{aligned}$$
(30)

where \(\ t>0,\ {x\in {\mathbb {R}} },\ 0<\alpha \le 1\). Using the method, as we have employed in previous examples, setting \(\alpha =1,\) we obtain

$$\begin{aligned} {\small u(x,t)}=\sinh (x-t),v{\small (x,t)=\cosh }(x-t) \end{aligned}$$
(31)

which gives us the exact solution of (29)–(30).

7 Conclusion

In this paper, we proposed a new method called fractional Laplace differential transform method which combines Laplace transformation method and Differential Transform Method. The idea of the method is to convert Fractional Partial Differential Equations by Fractional Laplace Differential Transform Method into ordinary differential equations and then, to solve ordinary differential equations by using Differential Transform Method. The proposed method is successfully applied to different equations. From the obtained results, it is show that the fractional Laplace differential transform method yields very accurate approximate solutions by using only a few iterations. The main superiority of the proposed method is the simplicity of computing the coefficients of series expansion by using only algebraic calculus in the fractional case. However, other analytic methods such as Adomian decomposition method, Homotopy analysis method and Variational iteration method need the integration and differentiation operators which are difficult to use in this case. Thus, it can be concluded that Fractional Laplace Differential Transform Method can be applied a wide class of fractional partial differential equations arising in various fields of science and engineering.