Introduction

Now a days, there are several computational models for microscopic and macroscopic systems. The membranes create the main components in acoustics and the music such as the components of microphones, speakers and the related devices [1]. To investigate the design of hearing aids, the knowledge of large membrane vibration [2] is vital. The vibration of membranes plays a major role in analysis of wave mechanics in two dimensions and wave propagation, bio-engineering etc. In bio-engineering, several human tissues are anticipated as the membranes. The vibrational features of eardrum is valuable to understand the hearing. The equation of vibration is used to designate the vibration of membranes [3].

The integer order vibration equation [4] is,

$$ \frac{1}{{{\text{c}}^{2} }}\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial t^{2} }} = {\text{~}}\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + \frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}};{\text{~~r}} \ge 0,{\text{t~}} \ge 0, $$
(1)

with initial settings:

$$ {\text{w}}\left( {{\text{r}},0} \right) = \varphi \left( {\text{r}} \right),\frac{{\partial w(r,0)}}{{\partial t}} = {\text{c}}\xi \left( {\text{r}} \right),{\text{~~}}0 \le {\text{r}} \le 1,{\text{~}}0 \le {\text{~t}} \le 1. $$
(2)

where \(w\left(r,t\right)\) signifies probability density function [5] of particle at time \(\mathrm{t}\) at position \(\mathrm{r}.\) Also, c is wave velocity of vibrations.

Fractional order derivatives describe hereditary and the memory related properties of various real-life processes and materials [6]. The analysis of fractional differential equations (FDE) [7,8,9,10,11] in mathematical physics, vibration, signal processing, visco-elasticity, chemical engineering [12], seismic wave propagation [13], modelling of diseases [14, 15] etc. is a growing field of interest for the researchers. In the literature, there exist operational matrix method [3], decomposition method [4], homotopy perturbation scheme (HPM) [5], variational iteration scheme [16] etc. to solve the vibration equation. The homotopy analysis method (HAM) offers a simple mode to confirm convergence of the solution [17,18,19]. HAM was first introduced by Liao [20] for solving the differential equations. The HPM was first introduced by Ji-huan He [21, 22]. It is a united form of perturbation method and the homotopy in topology. It has been applied [23, 24] to solve problems in various fields. But these methods have some limitations such as massive computation with more time consumption [25]. So, they necessitate to be linked with a transform operator.

The hybrid methods using integral transforms [26, 27] are useful to get a solution of nonlinear FDE. Homotopy analysis transform method (HATM) is a united form of the HAM and Laplace’s transformation. In [1, 28], the researchers used the HATM to solve fractional vibration equation. The homotopy perturbation Laplace transform method (HPTM) is also a collective form of HPM and Laplace’s transformation. In [28], Goyal et al. found the solution to the coupled FDE using HPTM. The reliability of scheme is also vital than modeling dimensions of equations [29, 30].

The Sumudu transform [31, 32, 32] has an interesting advantage of the ‘unity’ feature over the Laplace transform which could arise with expediency when we develop the solutions of FDE. It leads combinations into the permutations hence it is suitable for the discrete systems. The function along with its Sumudu transform has identical Taylor coefficients other than factor n. Watugala [33, 34] proposed the Sumudu transform. Asiru [35] proved its properties.

Singh et al. [36] proposed the homotopy perturbation Sumudu transform method (HPSTM) which is a graceful merger of the HPM, He polynomials and the Sumudu transform. It is largely due to the works of Saberi-Nadjafi and Ghorbani [37]. Unlike HPM, the HPSTM is uniformly valid for both small, large parameters and variables [38]. The benefit of HPSTM is its power of embracing two robust computational schemes for tackling an FDE. This approach can reduce the computation work and time as compared to existing schemes simultaneously preserving the efficiency of results. HPSTM has already been applied for solving heat like equations [39], fractional coupled Burger’s equations [40], MHD viscous flow [41], fractional energy balance equation [42], Keller-Segel equation [43], etc.

Our aim is to investigate the fractional model of vibration Eq. (1) and to get its solution by applying the HPSTM. Our paper is presented in the following manner. In Sect. 1, there is introduction. In Sect. 2, the basic results of derivative in Liouville-Caputo sense, the Sumudu transform and its properties are provided. In Sect. 3, the mathematical model of time dependent vibration equation is discussed along with its necessity and our motivation in finding its possible solution. In Sect. 4, the idea of HPSTM is given. In Sect. 5, its implementation on fractional vibration equation is shown with the convergence analysis. In Sect. 6, the numerical experiments by taking several initial conditions are conducted. In Sect. 7, the numerical results are discussed using figures and tables while in Sect. 8, we summarize the conclusion.

Preliminaries

Definition 2.1

[44] A real function \(h\left(\chi \right),\chi >0\) is called in space.

a. \({\text{~}}C_{\zeta } ,{\text{~}}\zeta \in \mathbb{R}\) if there exists a real number q (> \(\zeta \)), such that \(h\left( \chi \right) = \chi ^{q} h_{1} \left( \chi \right),{\text{~}}h_{1} \left( \chi \right) \in C[0,\infty )\).

Clearly, \( C_{\varsigma } \subset C_{\gamma } \) if \(\gamma \le \zeta \).

b. \(C_{\zeta }^{m} ,{\text{~}}m \in \mathbb{N} \cup \left\{ 0 \right\} \) if \({h}^{(m)}\in {C}_{\zeta .}\)

Definition 2.2

[44,45,46] If \(\varphi \left( \eta \right) \in L_{1} \left( {a,b} \right),{\text{~}}L_{1} \left( {a,b} \right)\) is a set of all integrable functions in \(\left(a,b\right),\) then, Liouville-Caputo derivative of fractional order \(\alpha >0\) is defined as:

$$ ^{{LC}} D_{{a + }}^{\alpha } \phi (\eta ) = \frac{1}{{\Gamma (n - \alpha )}}\int_{a}^{\eta } {(\eta - \varsigma )^{{(n - \alpha - 1)}} } D_{\varsigma }^{n} \phi \;(\varsigma )d\varsigma ,\;(n - 1{ < }\alpha { \leqq }{\text{n}};\;{\text{n}} \in {\text{N}}), $$

where, \(D_{\eta }^{n} : = \frac{{d^{n} }}{{d\eta ^{n} }}{\text{~~}}\left( {n \in \mathbb{N}_{0} : = \mathbb{N} \cup \left\{ 0 \right\}} \right). \)

Definition 2.3

[44,45,46] Liouville-Caputo \(\alpha \)-order derivative (\(\alpha >0)\) on space \(\mathbb{R} = ( - \infty ,{\text{~}}\infty )\) is:

$$ ^{{LC}} D_{{ - \infty + }}^{\alpha } \varphi \left( \zeta \right) = \frac{1}{{\Gamma \left( {{\text{n}} - \alpha } \right)}}\int_{{ - \infty }}^{\zeta } {\left( {\zeta - \varsigma } \right)^{{n - \alpha - 1}} } D_{\varsigma }^{n} \varphi \left( \varsigma \right){\text{d}}\varsigma ,\;(n - 1{ < }\alpha{ \leqq }n;n \in \mathbb{N}). $$

a. [46]\( I_{t}^{\zeta } h\left( {x,t} \right) = \frac{1}{{\Gamma \zeta }}\mathop \int \limits_{0}^{t} \left( {t - s} \right)^{{\zeta - 1}} h\left( {x,s} \right)ds;{\text{~}}\zeta ,t > 0\)

b. [46] \(D_{\tau }^{\upsilon } V(x,\tau ) = I_{\tau }^{{m - \upsilon }} \frac{{\partial ^{m} V(x,\tau )}}{{\partial \tau ^{m} }},m - 1 < \upsilon \le m.\)

c. [46] \({D}_{t}^{\zeta }{I}_{t}^{\zeta }h\left(t\right)=h\left(t\right)\)\( ,~m - 1{ < }\zeta \le m,~m \in \mathbb{N}. \)

d. [46] \( I_{t}^{\zeta } D_{t}^{\zeta } h\left( t \right) = h\left( t \right) - {\text{~}}\sum\limits_{{k = 1}}^{{m - 1}} {h^{{(k)}} } (0^{ + } )\frac{{t^{k} }}{{k!}}\),\(m-1<\zeta \le m,m\in \mathbb{N}.\)

e. [46] \( I^{\beta } t^{\alpha } = {\text{~}}\frac{{\Gamma \left( {\alpha + 1} \right)}}{{\Gamma \left( {\beta + \alpha + 1} \right)}}t^{{\beta + \alpha }}\)

f. [46] \(D_{t}^{\beta } t^{\alpha } = \frac{{\Gamma \left( {\alpha + 1} \right)}}{{\Gamma \left( {\alpha + 1 - \beta } \right)}}t^{{\alpha - \beta }}\)

Definition 2.4

[47] Sumudu transform over a set of functions.

$$ {\text{Q}} = \{ {\text{h}}({\text{p}})|\exists {\text{N}},~p_{{1,}} p_{2} {\text{ > }},\left| {{\text{h}}\left( {\text{p}} \right)} \right|{ < }{\text{Ne}}^{{\frac{{\left| {\text{p}} \right|}}{{{\text{p}}_{{{\text{j}}~}} }}}} {\text{if}}~{\text{p}} \in \left( {{\text{ - 1}}} \right)^{{\text{j}}} \times \left[ {{\text{0}},\infty } \right)\} , $$

is defined as:

$$ {\text{S}}[{\text{h}}({\text{p}})] = \mathop {\mathop \int \limits^{\infty } }\limits_{0} {\text{h}}\left( {{\text{wp}}} \right){\text{e}}^{{ - {\text{p}}}} {\text{dp}},{\text{~w}} \in \left( { - {\text{p}}_{1} ,{\text{~p}}_{2} } \right). $$

Definition 2.5

[47] The Sumudu transform for the arbitrary order Liouville-Caputo derivative is: \( {\text{S}}\left[ {{\text{D}}_{{\text{t}}}^{\beta } \omega \left( {\text{t}} \right)} \right] = {\text{p}}^{{ - \beta }} {\text{S}}\left[ {\omega \left( {\text{t}} \right)} \right] - \sum\limits_{{{\text{k}} = 0}}^{{{\text{m}} - 1}} {{\text{s}}^{{\left( { - \beta + {\text{k}}} \right)}} } \omega ^{{({\text{k}})}} \left( {0 + } \right),\;{\text{m}} - 1{ < }\beta \le {\text{m}}.\)

Mathematical Model of Time Dependent Vibration Equation of Fractional Order

In computational models for macroscopic and microscopic systems [48,49,50,51,52,53,54,55,56,57], several physical quantities are related with past so to know their physical models well by inducting the memory effects, fractional order models of such systems gain more importance [3]. FDE accomplish such systems with the memory effect. The non-local property is actually the key use of working with an FDE in a model. It indicates that the future state is also dependent on past states. Thus, the models having fractional order derivatives follow the reality. The integer order model suggested in [4] was found unable to possess memory effect in vibrational motion, so to contain these effects, the model of integer order is generalized to the fractional order model by transforming derivative of integer order to that of fractional order \(\mathrm{\alpha }\) in Liouville-Caputo sense where \(1<\mathrm{\alpha }\le 2.\) Liouville-Caputo derivative is suitable for the differentiable functions. It allows the conditions to include in modeling a problem.

The differential equation of arbitrary order [1, 5, 6, 16] for vibration model is given as,

$$ \frac{1}{{c^{2} }}\frac{{\partial ^{\alpha } w\left( {r,t} \right)}}{{\partial t^{\alpha } }} = ~\frac{{\partial ^{2} w\left( {r,t} \right)}}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial w\left( {r,t} \right)}}{{\partial r}},~~1 < ~\alpha ~ \le 2. $$
(3)

The response expression has a parameter which states arbitrary order of the derivative. It can be altered to get diverse responses [6]. For \(\mathrm{\alpha }=2,\) Eq. (3) becomes Eq. (1). Equation (3) depicts particle motion with memory in time. The time dependent derivative proposes modulation of memory. The vibrational motion gets affected by the memory in time that scripts the aptness of fractional modeling for the system. Thus, a comprehensive study of Eq. (3) to find its possible solution is important. It motivated us to solve this equation by a reliable analytical scheme HPSTM.

Basic Idea of the HPSTM

Take a general arbitrary order non-linear non-homogeneous partial differential equation:

$$\frac{{d}^{\alpha }u(x,t)}{{dt}^{\alpha }}+Ru\left(x,t\right)+Nu\left(x,t\right)=h\left(x,t\right),$$
(4)
$$u\left(x,0\right)=g\left(x\right),$$
(5)

where \(\frac{{d}^{\alpha }}{{dt}^{\alpha }}\) is fractional Liouville-Caputo derivative. \(R\) is linear while \(N\) is non-linear differential operator. \(h\left(x,t\right)\) is a source term.

Taking Sumudu transform on sides of Eq. (4), we get,

$$ S\left[ {\frac{{d^{\alpha } u\left( {x,t} \right)}}{{dt^{\alpha } }}} \right] + S[Ru\left( {x,t} \right)] + S[Nu\left( {x,t} \right)] = S[h\left( {x,t} \right)] $$
(6)

Using property of Sumudu transform in [32], we get,

$$S\left[u\left(x,t\right)\right]=g\left(x\right)+{q}^{\alpha }S\left[h\left(x,t\right)\right]-{q}^{\alpha }S\left[Ru\left(x,t\right)+Nu\left(x,t\right)\right],$$
(7)

Taking inverse transform on Eq. (7),

$$u\left(x,t\right)=F\left(x,t\right)-{S}^{-1}{[q}^{\alpha }S\{Ru\left(x,t\right)+Nu\left(x,t\right)\}],$$
(8)

where, \(F\left(x,t\right)\) arise from initial condition and source term.

Now, applying the HPM,

$$u\left(x,t\right)=\sum _{m=0}^{\infty }{p}^{m}{u}_{m}\left(x,t\right).$$
(9)

The nonlinear term is stated as,

$$Nu\left(x,t\right)=\sum _{m=0}^{\infty }{p}^{m}{H}_{m}\left(u\left(x,t\right)\right).$$
(10)

He’s polynomials, \({H}_{m}\left(u\left(x,t\right)\right)\) are,

$$ H_{n} \left( {u_{0} ,u_{1} ,u_{2} , \ldots ,u_{n} } \right) = \frac{1}{{n!}}\frac{{\partial ^{n} }}{{\partial p^{n} }}\left[N\left( {\sum\limits_{{m = 0}}^{\infty } {p^{m} } u_{m} (x,t)} \right)\right]_{{p = 0}} ,~n = {\text{0}},{\text{1}},2, \ldots$$
(11)

Substituting Eq. (9) and (10) in Eq. (8),

$$ \sum\limits_{{m = 0}}^{\infty } {p^{m} } u_{m} (x,t) = F\left( {x,t} \right) - p\left[ {S^{{ - 1}} \left\{ {q^{\alpha } S\left[ {R\sum\limits_{{m = 0}}^{\infty } {p^{m} } u_{m} \left( {x,t} \right) + \sum\limits_{{m = 0}}^{\infty } {p^{m} } H_{m} (u\left( {x,t} \right))} \right]} \right\}} \right], $$
(12)

This is a pairing of Sumudu transform and the HPM with He polynomials.

Comparing the coefficients of alike powers of \(p,\)

$$ \left. \begin{gathered} p^{0} :u_{0} \left( {x,t} \right) = F~\left( {x,t} \right), \hfill \\ p^{1} :u_{1} \left( {x,t} \right) = - S^{{ - 1}} \left[ {q^{\alpha } S\left\{ {Ru_{0} \left( {x,t} \right) + H_{0} \left( {u\left( {x,t} \right)} \right)} \right\}} \right], \hfill \\ p^{2} :u_{2} \left( {x,t} \right) = - S^{{ - 1}} \left[ {q^{\alpha } S\left\{ {Ru_{1} \left( {x,t} \right) + H_{1} \left( {u\left( {x,t} \right)} \right)} \right\}} \right], \hfill \\ p^{3} :u_{3} \left( {x,t} \right) = - S^{{ - 1}} \left[ {q^{\alpha } S\left\{ {Ru_{2} \left( {x,t} \right) + H_{2} \left( {u\left( {x,t} \right)} \right)} \right\}} \right], \hfill \\ \end{gathered} \right\} $$
(13)

Persisting with this trend, the rest components \({u}_{m}\left(x,t\right);m\ge 4\) can be computed.

Finally, the solution \(u\left(x,t\right)\) is determined as:

$$u\left(x,t\right)=\underset{N\to \infty }{\mathrm{lim}}\sum _{m=0}^{N}{u}_{m}(x,t)$$
(14)

Implementation of HPSTM on Vibration Equation of Fractional Order

Take the fractional order vibration model discussed in Sect. 3 as,

\(\frac{1}{{{\text{c}}^{2} }}\frac{{\partial ^{\alpha } \omega \left( {{\text{r}},{\text{t}}} \right)}}{{\partial t^{\alpha } }} = {\text{~}}\frac{{\partial ^{2} \omega \left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + \frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}},{\text{~~}}1{ < }\alpha {\text{~}} \le 2,{\text{~}} \) (2)

Applying Sumudu transform, we attain,

$$ {\text{S}}\left[ {{\text{w}}\left( {{\text{r}},{\text{t}}} \right)} \right] - {\text{q}}^{\alpha } \sum\limits_{{{\text{k}} = 0}}^{{{\text{n}} - 1}} {\frac{{{\text{w}}^{{\left( {\text{k}} \right)}} \left( {{\text{r}},{\text{~~}}0} \right)}}{{{\text{s}}^{{\left( {\alpha - {\text{k}}} \right)}} }}} - {\text{q}}^{\alpha } \left[ {{\text{S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right] = 0. $$
(15)

Taking inverse Sumudu transform,

$$ {\text{w}}\left( {{\text{r}},{\text{t}}} \right) = {\text{F}}\left( {{\text{r}},{\text{t}}} \right) + {\text{S}}^{{ - 1}} \left[ {{\text{q}}^{\alpha } {\text{~S}}\left[ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right]} \right], $$
(16)

Using HPM and He’s polynomials as discussed in Sect. 4, we get,

$$ \sum\limits_{{{\text{n}} = 0}}^{\infty } {{\text{p}}^{{\text{n}}} } {\text{w}}_{{\text{n}}} ({\text{r}},{\text{t}}) = {\text{F}}\left( {{\text{r}},{\text{t}}} \right) + {\text{p}}\left( {{\text{S}}^{{ - 1}} \left[ {{\text{q}}^{\alpha } {\text{~S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right]} \right) $$
(17)

Equating the coefficients of alike powers of \(p\),

$$ \begin{gathered} {\text{p}}^{0} :~{\text{w}}_{0} \left( {{\text{r}},~{\text{t}}} \right) = {\text{F}}\left( {{\text{r}},~{\text{t}}} \right), \hfill \\ {\text{p}}^{1} :~{\text{w}}_{1} \left( {{\text{r}},~{\text{t}}} \right) = {\text{S}}^{{ - 1}} \left[ {{\text{q}}^{\alpha } {\text{S}}\left[ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w_{0} \left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w_{0} \left( {r,t} \right)}}{{\partial r}}} \right)} \right]} \right], \hfill \\ {\text{p}}^{2} :~{\text{w}}_{2} \left( {{\text{r}},~{\text{t}}} \right) = {\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } {\text{S}}\left[ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w_{1} \left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w_{1} \left( {r,t} \right)}}{{\partial r}}} \right)} \right]} \right], \hfill \\ {\text{and}}\;{\text{ similarly}}, \hfill \\ {\text{p}}^{{\text{n}}} :~{\text{w}}_{{\text{n}}} \left( {{\text{r}},~{\text{t}}} \right) = {\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } {\text{S}}\left[ {{\text{c}}^{2} \left\{ {\frac{{\partial ^{2} w_{{n - 1}} \left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w_{{n - 1}} \left( {r,t} \right)}}{{\partial r}}} \right\}} \right]} \right], \hfill \\ \end{gathered} $$
(18)

Solution is presented by the series as

$$w\left(r,t\right)=\underset{N\to \infty }{\mathrm{lim}}\sum _{m=0}^{N}{w}_{m}(r,t)$$
(19)

The focus is on convergence of the HPSTM applied to Eq. (3) in Sect. 3. Sufficient conditions for convergence are provided. The series in Eq. (19) is generally convergent but some suggestions by Ji-huan He [21] are illustrated to get the rate of convergence on nonlinear operator.

  • (1) Second derivative of \(N(w)\) should be smaller as parameter can be relatively large, i.e.\(p\to 1.\)

  • (2) Norm of \({L}^{-1}\frac{\partial N}{\partial w}\) must be less than 1 for the series to be convergent.

Theorem

[58]. Let X and Y be Banach spaces. Let \(T:X\to Y\) be a contraction nonlinear mapping, that is \(\forall {\text{ ~}}\rho ,\mathop \rho \limits^{\sim} \in X;\)

$$ \left\| {T\left( \rho \right)} \right. - \left. {T\left( {\mathop \rho \limits^{\sim} } \right)} \right\| \le \chi \left\| \rho \right. - \left. {\mathop \rho \limits^{\sim} } \right\|,~0{ < }\chi {\text{ }}{ < }1, $$

that by Banach fixed point theorem, have fixed point u, i.e.,\(T\left(u\right)=u.\)

The sequence formed by HPM is,

\({W}_{n}=T\left({W}_{n-1}\right),\) \(W_{{n - 1}} = \sum\limits_{{i = 0}}^{{n - 1}} {u_{i} } ,{\text{~}}n = {\text{1}},{\text{2}},3, \ldots \) and,

Suppose \({W}_{0}={w}_{0}={u}_{0}\in {B}_{r}\left(u\right)\) where \(B_{r} \left( u \right) = \{ u^{*} \in X{\text{~}}|\left\| {u^{*} } \right. - \left. u \right\|\} { < }r, \) then,

$$ (i)\;\left\| {W_{n} } \right. - \left. u \right\| \le \chi ^{n} \left\| {w_{0} } \right. - \left. u \right\|,\;\left( {ii} \right)W_{n} \in B_{r} \left( u \right),\;\left( {iii} \right)\mathop {\lim }\limits_{{n \to \infty }} W_{n} = u. $$

Numerical Experiments

Here, the applicability of the HPSTM is illustrated via some examples.

Test Example 1. Consider the fractional vibration equation,

$$ \frac{1}{{{\text{c}}^{2} }}\frac{{\partial ^{\alpha } w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial t^{\alpha } }} = ~\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + \frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}},~~1{ < }\alpha ~ \le 2, $$

with initial condition,\( {\text{w}}_{0} ({\text{r}},{\text{t}}) = {\text{r}}^{2} + {\text{c~t~r}}.\)

Taking Sumudu transform of above equation, we get

$$ {\text{S}}\left[ {{\text{w}}\left( {{\text{r}},{\text{t}}} \right)} \right] = \frac{{{\text{r}}^{2} + {\text{c~t~r}}}}{{\text{u}}}{\text{~}} + {\text{u}}^{\alpha } {\text{S}}\left[ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right], $$
(20)

Now, by taking inverse Sumudu transform, we get,

$$ {\text{w}}\left( {{\text{r}},{\text{t}}} \right) = {\text{r}}^{2} + {\text{c~t~r}} + {\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } {\text{~S}}\{ {\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)\} } \right], $$
(21)

Applying the HPM on Eq. (21),

$$ \sum\limits_{{{\text{n}} = 0}}^{\infty } {{\text{p}}^{{\text{n}}} } {\text{w}}_{{\text{n}}} ({\text{r}},{\text{t}}) = {\text{r}}^{2} + {\text{c}}~{\text{t}}~{\text{r}} + {\text{p}}\left( {{\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } ~{\text{S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right]} \right), $$
(22)

Equating the coefficients of alike powers of \(p\),

$$ {\text{p}}^{0} :{\text{w}}_{0} \left( {{\text{r}},{\text{t}}} \right) = {\text{~r}}^{2} + {\text{c~t~r}}, $$
$$ {\text{p}}^{1} :{\text{w}}_{1} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{{\text{~c}}^{2} {\text{~~t}}^{\alpha } {\text{~}}\left( {{\text{c~t}} + 4{\text{~r~}}\left( {1 + \alpha } \right)} \right)}}{{{\text{~r~}}\Gamma \left( {2 + \alpha } \right)}}, $$
$$ {\text{p}}^{2} :{\text{w}}_{2} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{{\text{~c}}^{5} {\text{~~t}}^{{1 + 2{\text{~}}\alpha }} {\text{~}}}}{{{\text{~r}}^{3} {\text{~}}\Gamma \left( {2 + 2\alpha } \right)}}, $$
$$ {\text{p}}^{3} :{\text{w}}_{3} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{9{\text{~c}}^{7} {\text{~~t}}^{{1 + 3{\text{~}}\alpha }} {\text{~}}}}{{{\text{~r}}^{5} {\text{~}}\Gamma \left( {2 + 3\alpha } \right)}}, $$

and, so on. Hence, subsequent iterations \({\text{w}}_{{{\text{m~}}}} (r,t),{\text{~}}m \ge 4\) can be found.

Thus, the series solution is obtained as given by Eq. (19) as:

$$w\left(r,t\right)=\underset{N\to \infty }{\mathrm{lim}}\sum _{m=0}^{N}{w}_{m}\left(r,t\right).$$

Test Example 2. Consider the equation,

$$ \frac{{\partial ^{\alpha } w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial t^{\alpha } }} = {\text{c}}^{2} \left(~\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + \frac{1}{{\text{r}}}\frac{{\partial w\left( {r,t} \right)}}{{\partial r}}\right),~~1{ < }\alpha ~ \le 2, $$

with initial condition, \( {\text{w}}_{0} ({\text{r}},{\text{t}}) = {\text{r}} + {\text{c~t~r}}. \)

Taking Sumudu transform of above equation, we get

$$ {\text{S}}\left[ {{\text{w}}\left( {{\text{r}},{\text{t}}} \right)} \right] = \frac{{{\text{r}} + {\text{c~t~r}}}}{{\text{u}}} + {\text{u}}^{\alpha } {\text{S}}\left[ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right] $$
(23)

Taking the inverse transform,

$$ {\text{w}}\left( {{\text{r}},{\text{t}}} \right) = {\text{r}} + {\text{c}}~{\text{t}}~{\text{r}} + {\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } ~{\text{S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right] $$
(24)

Applying the HPM on Eq. (24),

$$ \sum\limits_{{{\text{n}} = 0}}^{\infty } {{\text{p}}^{{\text{n}}} } {\text{w}}_{{\text{n}}} ({\text{r}},{\text{t}}) = ~{\text{r}} + {\text{c}}~{\text{t}}~{\text{r}} + {\text{p}}\left( {{\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } ~{\text{S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right]} \right) $$
(25)

Equating the coefficients of alike powers of \(p\),

$$ {\text{p}}^{0} :{\text{w}}_{0} \left( {{\text{r}},{\text{t}}} \right) = {\text{~r}} + {\text{c~t~r}}, $$
$$ {\text{p}}^{1} :{\text{w}}_{1} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{{\text{~c}}^{2} {\text{~~t}}^{\alpha } {\text{~}}(1 + {\text{c~t~}} + {\text{~}}\alpha )}}{{{\text{~r~}}\Gamma \left( {2 + \alpha } \right)}} $$
$$ {\text{p}}^{2} :{\text{w}}_{2} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{{\text{~c}}^{2} {\text{~~t}}^{{2{\text{~}}\alpha }} {\text{~}}(1 + {\text{c~t~}} + 2{\text{~}}\alpha )}}{{{\text{~r}}^{3} {\text{~}}\Gamma \left( {2{\text{~}} + {\text{~}}2\alpha } \right)}}, $$
$$ {\text{p}}^{3} :{\text{w}}_{3} \left( {{\text{r}},{\text{t}}} \right) = \frac{{9{\text{~c}}^{6} {\text{~~t}}^{{3{\text{~}}\alpha }} {\text{~}}\left( {1 + {\text{c~t~}} + {\text{~}}3{\text{~}}\alpha } \right)}}{{{\text{~r}}^{5} {\text{~}}\Gamma \left( {2{\text{~}} + {\text{~}}3{\text{~}}\alpha } \right)}}, $$

and, so on. Hence, subsequent iterations \( {\text{w}}_{{{\text{m~}}}} (r,t),{\text{~}}m \ge 4 \) can be found.

Thus, the series solution is obtained as:

$$w\left(r,t\right)=\underset{N\to \infty }{\mathrm{lim}}\sum _{m=0}^{N}{w}_{m}\left(r,t\right).$$

Test Example 3. Consider the equation,

$$ \frac{{\partial ^{\alpha } w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial t^{\alpha } }} = ~c^{2} \left( {~\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + \frac{1}{\rm r}\frac{{\partial w\left( {r,t} \right)}}{{\partial r}}} \right),~~1 < ~\alpha ~ \le 2, $$

with initial condition, \( {\text{w}}_{0} ({\text{r}},{\text{t}}) = \sqrt {\text{r}} + {\text{~}}\frac{{{\text{c~t}}}}{{\sqrt {\text{r}} }} \).

Taking Sumudu transform of above equation, we get

$$ {\text{S}}\left[ {{\text{w}}\left( {{\text{r}},{\text{t}}} \right)} \right] = \frac{{(\sqrt {\text{r}} + {\text{~}}\frac{{{\text{c~t}}}}{{\sqrt {\text{r}} }})}}{{\text{u}}}{\text{~}} + {\text{u}}^{\alpha } {\text{S}}\left[ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + {\text{~}}\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right] $$
(26)

Taking inverse transform,

$$ {\text{w}}\left( {{\text{r}},{\text{t}}} \right) = \sqrt {\text{r}} + ~\frac{{{\text{c}}~{\text{t}}}}{{\sqrt {\text{r}} }} + {\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } ~{\text{S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right] $$
(27)

Applying the HPM on Eq. (27),

$$ \sum\limits_{{{\text{n}} = 0}}^{\infty } {{\text{p}}^{{\text{n}}} } {\text{w}}_{{\text{n}}} ({\text{r}},{\text{t}}) = \sqrt {\text{r}} + ~\frac{{{\text{c}}~{\text{t}}}}{{\sqrt {\text{r}} }} + {\text{p}}\left( {{\text{S}}^{{ - 1}} \left[ {{\text{u}}^{\alpha } ~{\text{S}}\left\{ {{\text{c}}^{2} \left( {\frac{{\partial ^{2} w\left( {{\text{r}},{\text{t}}} \right)}}{{\partial r^{2} }} + ~\frac{1}{{\text{r}}}\frac{{\partial w(r,t)}}{{\partial r}}} \right)} \right\}} \right]} \right) $$
(28)

Equating coefficients of alike powers of \(p\),

$$ {\text{p}}^{0} :{\text{w}}_{0} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\sqrt {\text{r}} + {\text{~}}\frac{{{\text{c~t}}}}{{\sqrt {\text{r}} }}{\text{~}}, $$
$$ {\text{p}}^{1} :{\text{w}}_{1} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{{\text{~c}}^{2} {\text{~~t}}^{\alpha } {\text{~}}({\text{r~}} + {\text{~c~t~}} + {\text{~r~}}\alpha )}}{{4{\text{~r}}^{{5/2}} {\text{~}}\Gamma \left( {2 + \alpha } \right)}}, $$
$$ {\text{p}}^{2} :{\text{w}}_{2} \left( {{\text{r}},{\text{t}}} \right) = {\text{~}}\frac{{{\text{~c}}^{4} {\text{~~t}}^{{2{\text{~}}\alpha }} {\text{~}}\{ 25{\text{~c~t~}} + {\text{~}}9{\text{~r~}}(1 + 2{\text{~}}\alpha )\} }}{{16{\text{~r}}^{{9/2}} {\text{~}}\Gamma \left( {2{\text{~}} + {\text{~}}2{\text{~}}\alpha } \right)}}, $$
$$ {\text{p}}^{3} :{\text{w}}_{3} \left( {{\text{r}},{\text{t}}} \right) = \frac{{9{\text{~c}}^{6} {\text{~~t}}^{{3{\text{~}}\alpha }} \left\{ {225{\text{~c~t}} + 49{\text{~r~}}\left( {1 + 3{\text{~}}\alpha } \right)} \right\}}}{{64{\text{~r}}^{{\frac{{13}}{2}}} {\text{~}}\Gamma \left( {2{\text{~}} + {\text{~}}3{\text{~}}\alpha } \right)}}, $$

and, so on. Hence, subsequent iterations \( {\text{w}}_{{{\text{m~}}}} (r,t),{\text{~}}m \ge 4 \) can be found.

The series solution is obtained as:

$$w\left(r,t\right)=\underset{N\to \infty }{\mathrm{lim}}\sum _{m=0}^{N}{w}_{m}(r,t)$$

Numerical Results and Discussion

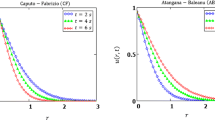
Figures 1a–c depict the behavior of HPSTM solution \(w(r,t)\) of Eq. (3) at the order \(\alpha =2\) of the derivative for Examples 1, 2 and 3 respectively. They have been drawn for \(\alpha =2\) to show the nature of the unknown solution of the vibration model. Figure 2a–c describe the behavior of solution \(w(r,t)\) with time t for distinct values of wave velocity \(c\) of vibrations at \(\alpha =2\) in Examples 1, 2 and 3 respectively. Figure 3a–c illustrate the behavior of solution \(w(r,t)\) with time \(t\) for the fractional order \( \alpha = 1.7,{\text{~}}1.8,{\text{~}}1.9{\text{~}}\;{\text{and~}}\;2 \) in Examples 1, 2 and 3 respectively. They reveal that probability density function \(w(r,t)\) of the particle increases with increase in time t but decreases if order \(\alpha \) of the derivative increases. This is in total agreement with the point discussed in Sect. 3. Figure 4 shows the comparison of solution by HPSTM and methods in [1, 3,4,5,6, 16] at \(\alpha =1.5\) for Example 1. Figure 5 illustrates the comparison of solution by HPSTM and methods in [1, 5] at \(\alpha =1.5\) for Example 2. Figure 6 depicts the comparison of solution by HPSTM and methods in [3, 4] at \( c = 0.1{\text{~}}\;{\text{and~}}\;\alpha = 2 \) for Example 3. Figure 7a–c depict the absolute error between consecutive approximations at \(\alpha =1.5\) in Examples 1, 2 and 3 respectively which clearly indicates that the gained solutions are convergent. Also, the tabular comparison of results with published work is shown in Tables 1, 2 and 3 at distinct values of arbitrary order \(\alpha \). So, the solution by the HPSTM at different grid points is in a good pact. The Tables 4, 5 and 6 confirm that the error between successive approximations is negligible and becomes zero as the number of iterations are increased. Hence, we conclude that the HPSTM also works for those models of fractional order that do not possess an exact solution.

Fig. 1
figure 1

Behaviour of solution \(w\left(r,t\right)\) at \(\alpha =2\) by HPSTM for (a) Example 1 (b) Example 2 (c) Example 3

Full size image
Fig. 2
figure 2

Behaviour of solution \(w(r,t)\) Vs. t by HPSTM for distinct ‘c’ at \(\alpha =2\) in (a) Example 1 (b) Example 2 (c) Example 3

Full size image
Fig. 3
figure 3

Behavior of solution \(w(r,t)\) Vs. t by HPSTM for distinct values of \(\alpha \) n (a) Example 1 (b) Example 2 (c) Example 3

Full size image
Fig. 4
figure 4

Comparison of solution by HPSTM and methods in [1, 3,4,5,6, 16] at \(\alpha =1.5\) for Example 1

Full size image
Fig. 5
figure 5

Comparison of solution by HPSTM and methods in [1, 5] at \(\alpha =1.5\) for Example 2

Full size image
Fig. 6
figure 6

Comparison of solution by HPSTM and methods in [3, 4] at \(c=.1,\alpha =2\) for Example 3

Full size image
Fig. 7
figure 7

Error between consecutive approximations at \(\alpha =1.5\) for (a) Example 1 (b) Example 2 (c) Example 3

Full size image
Table 1 Comparison of results in example 1, \(\varphi \left(r\right)={r}^{2},\xi \left(r\right)=r\) at \(c=0.1\) at \( \alpha = 1.5{\text{~}}\;{\text{and}}\;{\text{~}}2 \)
Full size table
Table 2 Comparison of results in Example 2 at \(c=5,r=6,\) at \(\mathrm{\alpha }\) = 1.5 and 2
Full size table
Table 3 Comparison of the results in Example 3 at \(c=0.1,\mathrm{\alpha }=2\)
Full size table
Table 4 Absolute error between successive iterations, when exact solution is unknown, at \(c=0.1\) for distinct values of order α in Example 1
Full size table
Table 5 Absolute error between successive iterations, when exact solution is unknown, at \(c=0.1\) at distinct values of order α in Example 2
Full size table
Table 6 Absolute error between successive iterations, when exact solution is unknown, at \(c=0.1\) at distinct values of order α in Example 3
Full size table

Conclusion

In this pioneer work, the HPSTM is efficaciously used to inspect the time fractional vibration equation. The outcomes disclose that the derived results are trustworthy and the obtained solution is convergent. The numerical simulations endorse the high accuracy of our results as compared to those obtained by other schemes in published work so far. This scheme is capable of lessening the time and the size of computation. It is easier to use for both small as well as large parameters. The obtained solutions are bounded and positive. It is exciting to observe that the HPM works efficiently when coupled with Sumudu transform due to its ‘unity’ feature. Also, the non-linear term can easily be handled via the Sumudu transform. It is heartening to note that HPSTM also work competently when the exact solution is not known. Hence, this scheme is highly effective, accurate, systematic, logical and attractive. It can be useful to study and find solutions of a wide range of fractional order mathematical models of physical, biological and social importance.