1 Introduction

First references to the fractional-order derivatives were made in the seventeenth century. In the last few decades, fractional calculus has developed as a prospective tool in potential theory, control theory, fluid dynamic traffic, viscoelasticity, electromagnetic theory, neurophysiology, bioengineering, electric technology, plasma physics, mathematical economy, etc. Normally, we deal with the real-world processes of fractional order. Heat diffusion into a semi-infinite solid in which heat flow is half-derivative of temperature is one of its examples. Mass–energy equation of Einstein is gained with conjecture of absolute smooth space–time, but the space–time is congenitally discontinuous if it inclines to quantum scale. For discontinuous space–time, fractal theory is used to explain numerous phenomenon [1,2,3,4,5]. The cocoon’s heat-proof property cannot be divulged by advanced calculus. If cocoon wall is supposed to be a continuous medium, then we cannot explain why the temperature change on its inner surface, is very slow, irrespective of environmental temperature [6]. Time becomes discontinuous in microphysics, i.e., fractal kinetics takes place on a very small timescale [7]. Fractional differential equations (FDEs) [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23] govern the systems with memory.

Bloch equations are a set of first-order macroscopic differential equations that describe the magnetization behavior under the magnetic fields and relaxation. Bloch, in 1946, introduced them and used for describing NMR. They are also used in electron spin resonance spectroscopies and MRI. Relaxation of spin system is described phenomenologically by them, that features the rate of change of magnetization M of the spin system. In NMR spectroscopy and imaging, the key idea is solving the Bloch equations for combinations of gradient magnetic fields and applied static radio frequency. Bloch equations [24,25,26,27] are

$$ \begin{aligned} & \frac{{{\text{d}}M_{x} \left( t \right)}}{{{\text{d}}t}} = \omega_{0} M_{y} \left( t \right) - \frac{{M_{x} \left( t \right)}}{{T_{2} }}, \\ & \frac{{{\text{d}}M_{y} \left( t \right)}}{{{\text{d}}t}} = - \omega_{0} M_{x} \left( t \right) - \frac{{M_{y} \left( t \right)}}{{T_{2} }}, \\ & \frac{{{\text{d}}M_{z} \left( t \right)}}{{{\text{d}}t}} = \frac{{M_{0} - M_{z} \left( t \right)}}{{T_{1} }}, \\ \end{aligned} $$
(1)

with initial settings Mx(0) = 0 = Mz(0), My(0) = 100.

Here, Mx(t), My(t) and Mz(t) are the system magnetization. ω0 = 2πf0 is frequency of resonance, \( B_{0} = \frac{{\omega_{0} }}{\gamma } \) is static magnetic field in z-component, M0 is equilibrium magnetization while T1, T2 are the spin–lattice and spin–spin relaxation times, respectively. The exact solution to Eq. (1) is,

$$ \begin{aligned} & M_{x} \left( t \right) = e^{{ - t/T_{2} }} \left( {M_{x} \left( 0 \right)\cos w_{0} t + M_{y} \left( 0 \right)\sin w_{0} t } \right), \\ & M_{y} \left( t \right) = e^{{ - t/T_{2} }} \left( {M_{y} \left( 0 \right)\cos w_{0} t - M_{x} \left( 0 \right)\sin w_{0} t } \right), \\ & M_{z} \left( t \right) = M_{z} \left( 0 \right)e^{{ - t/T_{1} }} M_{0} \left( {1 - e^{{ - t/T_{1} }} } \right). \\ \end{aligned} $$
(2)

To study the heterogeneity, complex structure and memory effects in relaxation process, Eq. (1) is generalized to fractional Bloch equations [28] by extending integer derivative to Caputo’s fractional derivative. The benefit of having FDEs in physical models is their non-local property. The fractional derivative is non-local, while the derivative of integer order is local. It indicates that the upcoming physical system state is also dependent on all of its historical states other than its present state. Hence fractional models are more realistic. The fractional Bloch equations are:

$$ \left. {\begin{array}{*{20}l} {D_{t}^{\alpha } M_{x} \left( t \right) = \omega_{0} M_{y} \left( t \right) - \frac{{M_{x} \left( t \right)}}{{T_{2} }},} \hfill \\ {D_{t}^{\beta } M_{y} \left( t \right) = - \omega_{0} M_{x} \left( t \right) - \frac{{M_{y} \left( t \right)}}{{T_{2} }},} \hfill \\ {D_{t}^{\gamma } M_{z} \left( t \right) = \frac{{M_{0} - M_{z} \left( t \right)}}{{T_{1} }},} \hfill \\ \end{array} } \right\};\quad 0 < \alpha ,\beta ,\gamma \le 1 $$
(3)

subject to the conditions Mx(0) = 0 = Mz(0), My(0) = 100. Total order of system is (α, β, γ).

Mx, My, Mz are sufficiently differentiable functions. Parameters ω0, T1, T2 possess units of s−α that keep a steady set of units for magnetization.

Time-fractional equations depict particle motion with memory in time. Space-fractional derivatives take place for heavy-tailed variations. They refer to the particle motion that explains variation in flow field over the complete system. The fraction in time derivative suggests the modulation of memory of the system. It is apparent that magnetization behavior and relaxation of the spin system are influenced by memory. This fact marks fractional modeling suitable for such systems. So, the study of time-fractional Bloch model given by Eq. (3) is very important.

The physical sense of Eq. (3) goes back to the basic formulation of fractional-order Schrödinger’s equation in quantum mechanics. It is obvious that the fractional-order derivative is highly reliant on initial conditions therefore a proper fractional derivative must be selected for handling them. Initial state of system in NMR is detailed by magnetization components so they need to be visibly recognized. Stability of these equations is already examined and proved in [29]. The mathematical model of Eq. (3) is solved by homotopy perturbation method (HPM) [30], predictor–corrector method [31], operational matrix method [32], implicit alternating direction method [33], Galerkin finite element method [34], and fractional variational iteration method (FVIM) [35], etc. This model has not yet been studied by the q-HATM.

Physically, it is reasonable to have fractional-order derivative of a constant equal to zero. However, for Caputo fractional operator [36], \( {}_{a}^{C} D_{t}^{\alpha } c = 0 \), c is a constant. One of its great advantages is that it permits traditional boundary and initial conditions to be involved in formulation of the problem. Now, consider the following IVP involving Caputo’s operator:

$$ D^{\alpha } y\left( t \right) - \lambda y\left( t \right) = 0,\quad t > 0,\quad n - 1 < \alpha < n;\quad y^{k} \left( 0 \right) = b_{k} ,\quad k = 0, \ldots ,n - 1, $$

Here, usual initial conditions in terms of derivatives of integer order are used. These conditions have obvious physical explanation as an initial position y(a) at point a, initial velocity y′(a), initial acceleration y″(a), and so on. To compute Caputo’s fractional derivative of a function, existence of its nth-order derivative is required. Luckily, most functions that appear in applications fulfill this prerequisite. Caputo’s fractional derivative is defined for differentiable functions only, and we have taken Mx(t), My(t) and Mz(t) as sufficiently differentiable functions in this paper.

Most nonlinear FDEs do not possess exact solutions so some numerical techniques are required for their approximate numerical solution. The reliability of solution schemes is also a very important aspect than modeling the dimensions of equations [37, 38]. The q-homotopy analysis method (q-HAM) is an improvement of parameter q ∈ [0, 1] in HAM [39] to \( q \in \left[ {0, \frac{1}{n}} \right] \), n ≥ 1. The presence of \( \left( {\frac{1}{n}} \right)^{m} \) in the solution provides faster convergence than HAM. It is obvious that linking of method with a transform [40,41,42] escapes time consuming concerns and requires less CPU time to examine numerical solutions to nonlinear problems. The q-HATM [43,44,45] is an elegant union of q-HAM and transform of Laplace. Its advantage is its potential of assimilating strong computational methodologies for probing FDEs. It gives a simpler way to control convergence region of the series solution in a large allowable domain by proper selection of ħ. It offers more acceptable results for the same grid point and the order of series solution. The validity of solution in convergent region is witnessed by ħ and n-curves. The q-HATM has the qualities that it does not need discretization, linearization, perturbations or any restrictive assumptions, reduces mathematical calculations significantly, promises large convergence region, offers non-local effect, and is free from computing complicated polynomials, integrations, and physical parameters.

The objective of this paper is to attain the numerical solution of Eq. (3) using the q-HATM and compare results with other existing techniques and the exact solution. This paper is structured in the following manner. Section 1 is introduction. In Sect. 2, a brief review of preliminary descriptions of Caputo fractional derivative and some other results helpful for learning FDEs are given. In Sect. 3, the basic plan of the q-HATM is shown. In Sect. 4, the q-HATM is implemented on an example to find the numerical solution. Section 5 deals with discussion of gained results using table and figures. In Sect. 6, we recapitulate outcomes and draw inferences.

2 Preliminaries

Definition 2.1

Consider a real function h(χ), χ > 0. It is called in

  1. a.

    space \( C_{\zeta } , \zeta \in R \) if ∋ a real number b (> ζ), s.t. h(χ) = χbh1(χ), \( h_{1} \in C\left[ {0,\infty } \right) \). It is clear that \( C_{\zeta } \subset C_{\gamma } \) if γ ≤ ζ.

  2. b.

    space \( C_{\zeta }^{m} , m \in {\mathbb{N}} \cup \left\{ 0 \right\} \) if \( h^{\left( m \right)} \in C_{\zeta } \).

Definition 2.2

Caputo fractional derivative [36] of h(t), \( h \in C_{ - 1}^{m} , m \in {\mathbb{N}} \cup \left\{ 0 \right\} \) is

$$ D_{t}^{\beta } h\left( t \right) = \left\{ {\begin{array}{*{20}l} {\left[ {I^{m - \beta } h^{\left( m \right)} \left( t \right)} \right],} \hfill & {m - 1 < \beta < m,\quad m \in N,} \hfill \\ {\frac{{{\text{d}}^{m} }}{{{\text{d}}t^{m} }}h\left( t \right),} \hfill & {\beta = m.} \hfill \\ \end{array} } \right. $$
  1. a.
    $$ I_{t}^{\zeta } h\left( {x,t} \right) = \frac{1}{\varGamma \zeta }\int_{0}^{t} {\left( {t - s} \right)^{\zeta - 1} h\left( {x,s} \right){\text{d}}s} \,\, \zeta ,t > 0. $$
  2. b.
    $$ D_{\tau }^{\nu } V\left( {x,\tau } \right) = I_{\tau }^{m - \nu } \frac{{\partial^{m} V\left( {x,\tau } \right)}}{{\partial t^{m} }},\quad m - 1 < \nu \le m. $$
  3. c.
    $$ D_{t}^{\zeta } I_{t}^{\zeta } h\left( t \right) = h\left( t \right),\quad m - 1 < \zeta \le m,\quad m \in {\mathbb{N}}. $$
  4. d.
    $$ I_{t}^{\zeta } D_{t}^{\zeta } h\left( t \right) = h\left( t \right) - \mathop \sum \limits_{1}^{m - 1} h^{k} \left( {0 + } \right)\frac{{t^{k} }}{k!},\quad m - 1 < \zeta \le m, , m \in {\mathbb{N}}. $$
  5. e.
    $$ I^{v} t^{\zeta } = \frac{{\varGamma \left( {\zeta + 1} \right)}}{{\varGamma \left( {v + \zeta + 1} \right)}}t^{v + \zeta } . $$

Definition 2.3

Laplace transform of Caputo’s fractional-order derivative [36] is

$$ L\left[ {D^{\alpha } g\left( t \right)} \right] = p^{\alpha } F\left( p \right) - \mathop \sum \limits_{k = 0}^{n - 1} p^{\alpha - k - 1} g^{\left( k \right)} \left( 0 \right), \quad n - 1 < \alpha \le n. $$

3 Analysis of the q-HATM for time-fractional Bloch equations

Ponder over a nonlinear fractional nonhomogeneous PDE:

$$ \left. {\begin{array}{*{20}l} {D_{t}^{\alpha } M_{x} \left( t \right) + R_{1} M_{x} \left( t \right) + N_{1} M_{x} \left( t \right) = g_{1} \left( t \right)} \hfill \\ {D_{t}^{\beta } M_{y} \left( t \right) + R_{2} M_{y} \left( t \right) + N_{2} M_{y} \left( t \right) = g_{2} \left( t \right)} \hfill \\ {D_{t}^{\gamma } M_{z} \left( t \right) + R_{3} M_{z} \left( t \right) + N_{3} M_{z} \left( t \right) = g_{3} \left( t \right)} \hfill \\ \end{array} } \right\};\quad \ell - 1 < \alpha , \beta , \gamma \le \ell , $$
(4)

where \( D_{t}^{\alpha } ,D_{t}^{\beta } , D_{t}^{\gamma } \) are Caputo fractional operators of orders α, β, and γ, respectively. R1, R2, R3 and N1, N2, N3 are linear and nonlinear differential operators, respectively. g1(t), g2(t), and g3(t) are the source terms. Mx(t), My(t), and Mz(t) are the sufficiently differentiable functions.

Applying transform of Laplace on each side of Eq. (4) and then simplifying, we acquire

$$ \begin{aligned} L\left[ {M_{x} \left( t \right)} \right] - \frac{1}{{p^{\alpha } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\alpha - k - 1} M_{x}^{k} \left( {t,0} \right) + \frac{1}{{p^{\alpha } }}\{ L[R_{1} M_{x} \left( t \right) + N_{1} M_{x} \left( t \right) - g_{1} \left( t \right)]\} = 0, \hfill \\ L\left[ {M_{y} \left( t \right)} \right] - \frac{1}{{p^{\beta } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\beta - k - 1} M_{y}^{k} \left( {t,0} \right) + \frac{1}{{p^{\beta } }}\{ L[R_{2} M_{y} \left( t \right) + N_{2} M_{y} \left( t \right) - g_{2} \left( t \right)]\} = 0, \hfill \\ L\left[ {M_{z} \left( t \right)} \right] - \frac{1}{{p^{\gamma } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\gamma - k - 1} M_{z}^{k} \left( {t,0} \right) + \frac{1}{{p^{\gamma } }}\{ L[R_{3} M_{z} \left( t \right) + N_{3} M_{z} \left( t \right) - g_{3} \left( t \right)]\} = 0. \hfill \\ \end{aligned} $$
(5)

The nonlinear operators are formulated as

$$ \begin{aligned} & N\left[ {\varphi_{1} \left( {t;q} \right)} \right] = L\left[ {\varphi_{1} \left( {t;q} \right)} \right] - \frac{1}{{p^{\alpha } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\alpha - k - 1} \varphi_{1}^{k} \left( {t,q} \right)\left( {0^{ + } } \right) \\ & \quad + \frac{1}{{p^{\alpha } }}\{ L[R_{1} \varphi_{1} \left( {t;q} \right) + N_{1} \varphi_{1} \left( {t;q} \right)]\} - \frac{1}{{p^{\alpha } }}\left\{ {L\left[ {g_{1} \left( t \right)} \right]} \right\}, \\ & N\left[ {\varphi_{2} \left( {t;q} \right)} \right] = L\left[ {\varphi_{2} \left( {t;q} \right)} \right] - \frac{1}{{p^{\beta } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\beta - k - 1} \varphi_{2}^{k} \left( {t,q} \right)\left( {0^{ + } } \right) \\ & \quad + \frac{1}{{p^{\beta } }}\{ L[R_{2} \varphi_{2} \left( {t;q} \right) + N_{2} \varphi_{2} \left( {t;q} \right)]\} - \frac{1}{{p^{\beta } }}\left\{ {L\left[ {g_{2} \left( t \right)} \right]} \right\}, \\ & N\left[ {\varphi_{3} \left( {t;q} \right)} \right] = L\left[ {\varphi_{3} \left( {t;q} \right)} \right] - \frac{1}{{p^{\gamma } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\gamma - k - 1} \varphi_{3}^{k} \left( {t,q} \right)\left( {0^{ + } } \right) \\ & \quad + \frac{1}{{p^{\gamma } }}\{ L[R_{3} \varphi_{3} \left( {t;q} \right) + N_{3} \varphi_{3} \left( {t;q} \right)]\} - \frac{1}{{p^{\gamma } }}\left\{ {L\left[ {g_{3} \left( t \right)} \right]} \right\}. \\ \end{aligned} $$
(6)

Here \( q \in \left[ {0, \frac{1}{n}} \right] \) is embedding parameter. φi(t; q); i = 1, 2, 3 are real-valued functions.

Now, we build the homotopy as:

$$ \begin{aligned} & \left( {1 - nq} \right) L\left[ {\varphi_{1} - M_{x0} \left( t \right)} \right] = \hbar q HN\left[ {\varphi_{1} } \right], \\ & \left( {1 - nq} \right) L\left[ {\varphi_{2} - M_{y0} \left( t \right)} \right] = \hbar q HN\left[ {\varphi_{2} } \right], \\ & \left( {1 - nq} \right) L\left[ {\varphi_{3} - M_{z0} \left( t \right)} \right] = \hbar q HN\left[ {\varphi_{3} } \right], \\ \end{aligned} $$
(7)

Here, L is the Laplace transformation operator, n ≥ 1. H(t) ≠ 0 is an auxiliary function. ħ ≠ 0 is an auxiliary parameter. Mx0(t), My0(t) and Mz0(t) are the initial approximations. φi(t; q); i = 1, 2, 3 are unknown functions. For q = 0 and \( q = \frac{1}{n} \), the subsequent results hold:

$$ \begin{aligned} & \varphi_{1} \left( {t;0} \right) = M_{x0} \left( t \right), \varphi_{2} \left( {t;0} \right) = M_{y0} \left( t \right), \varphi_{3} \left( {t;0} \right) = M_{z0} \left( t \right), \\ & \varphi_{1} \left( {t;\frac{1}{n}} \right) = M_{x} \left( t \right), \varphi_{2} \left( {t;\frac{1}{n}} \right) = M_{y} \left( t \right), \varphi_{3} \left( {t;\frac{1}{n}} \right) = M_{z} \left( t \right). \\ \end{aligned} $$

Consequently, as q grows from 0 to \( \frac{1}{n} \), n ≥ 1, φi(t; q), i = 1, 2, 3 swift from initial approximation Mx0(t), My0(t), Mz0(t) to solutions Mx(t), My(t), and Mz(t), respectively.

Applying Taylor’s theorem on φi(t; q), i = 1, 2, 3 to expand it about q in series form, we find

$$ \begin{aligned} & \varphi_{1} = M_{x0} \left( t \right) + \mathop \sum \limits_{m = 1}^{\infty } M_{xm} \left( t \right)q^{m} , \\ & \varphi_{2} = M_{y0} \left( t \right) + \mathop \sum \limits_{m = 1}^{\infty } M_{ym} \left( t \right)q^{m} , \\ & \varphi_{3} = M_{z0} \left( t \right) + \mathop \sum \limits_{m = 1}^{\infty } M_{zm} \left( t \right)q^{m} , \\ \end{aligned} $$
(8)

where

$$ \begin{aligned} & M_{xm} \left( t \right) = \frac{1}{m!} \left. {\frac{{\partial^{m} \varphi_{1} }}{{\partial q^{m} }}} \right|_{q = 0,} \\ & M_{ym} \left( t \right) = \frac{1}{m!} \left. {\frac{{\partial^{m} \varphi_{2} }}{{\partial q^{m} }}} \right|_{q = 0,} \\ & M_{zm} \left( t \right) = \frac{1}{m!} \left. {\frac{{\partial^{m} \varphi_{3} }}{{\partial q^{m} }}} \right|_{q = 0.} \\ \end{aligned} $$
(9)

For suitable selection of auxiliary linear operator, Mx0(t), My0(t), Mz0(t), ħ, n, H, the series (8) converges at \( q = \frac{1}{n} \) and we get,

$$ \begin{aligned} & M_{x } \left( t \right) = M_{x0} \left( t \right) + \mathop \sum \limits_{m = 1}^{\infty } M_{xm} \left( t \right) \left( {\frac{1}{n}} \right)^{m} , \\ & M_{y } \left( t \right) = M_{y0} \left( t \right) + \mathop \sum \limits_{m = 1}^{\infty } M_{ym} \left( t \right)\left( {\frac{1}{n}} \right)^{m} , \\ & M_{z} \left( t \right) = M_{z0} \left( t \right) + \mathop \sum \limits_{m = 1}^{\infty } M_{zm} \left( t \right)\left( {\frac{1}{n}} \right)^{m} , \\ \end{aligned} $$
(10)

Express vectors as

$$ \vec{M}_{xm} = \left\{ {M_{x0} \left( t \right), M_{x1} \left( t \right), \ldots ,M_{xm} \left( t \right)} \right\}. $$
(11)

Differentiating Eq. (7) m-times w.r.t. ‘q’, then dividing by m! and finally taking q = 0, we develop the ensuing mth-order deformation Eq.:

$$ \begin{aligned} & L\left[ {M_{xm} \left( t \right) - k_{m} M_{xm - 1 } \left( t \right)} \right] = \hbar H\,{{\ae }}_{m} \left( {\vec{M}_{xm - 1} } \right), \\ & L\left[ {M_{ym} \left( t \right) - k_{m} M_{ym - 1 } \left( t \right)} \right] = \hbar H\,{{\ae }}_{m} \left( {\vec{M}_{ym - 1} } \right), \\ & L\left[ {M_{zm} \left( t \right) - k_{m} M_{zm - 1 } \left( t \right)} \right] = \hbar H\,{{\ae }}_{m} \left( {\vec{M}_{zm - 1} } \right). \\ \end{aligned} $$
(12)

Taking inverse transform:

$$ \begin{aligned} & M_{xm} = k_{m} M_{xm - 1 } + \hbar L^{ - 1} \left[ {H\,{{\ae }}_{m} \left( {\vec{M}_{xm - 1} } \right)} \right], \\ & M_{ym} = k_{m} M_{ym - 1 } + \hbar L^{ - 1} \left[ {H\,{{\ae }}_{m} \left( {\vec{M}_{ym - 1} } \right)} \right], \\ & M_{zm} = k_{m} M_{zm - 1 } + \hbar L^{ - 1} \left[ {H\,{{\ae }}_{m} \left( {\vec{M}_{zm - 1} } \right)} \right]. \\ \end{aligned} $$
(13)

In Eq. (13), we express \( {{\ae }}_{m} \left( {\vec{M}_{ \xi m - 1} } \right) \) in a new manner as:

$$ {{\ae }}_{m} \left( {\vec{M}_{\xi m - 1} } \right) = L M_{\xi m - 1 } \left( t \right) - \left( {1 - \frac{{k_{m} }}{n}} \right)\left( {\frac{1}{{p^{\alpha } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\alpha - k - 1} M_{\xi }^{k} \left( {t,0} \right) + \frac{1}{{p^{\alpha } }}L\left[ {g_{1} \left( t \right)} \right]} \right) + \frac{1}{{p^{\alpha } }}L[R_{1} M_{\xi m - 1} \left( t \right) + P_{m - 1} ], $$
(14)

and km is presented as

$$ k_{m} = \left\{ {\begin{array}{*{20}l} {0, } \hfill & {m \le 1,} \hfill \\ {n,} \hfill & {m > 1.} \hfill \\ \end{array} } \right. $$
(15)

In Eq. (14), Pm is homotopy polynomial [46, 47] expressed as:

$$ P_{ m} = \frac{1}{m!} \left[ {\frac{{\partial^{m} \phi \left( {t;q} \right)}}{{\partial q^{m} }}} \right]|_{q = 0} , $$
(16)

and

$$ \phi = \phi_{0} + q \phi_{1} + q^{2} \phi_{2} + \cdots . $$
(17)

Employing the results of Eq. (14) in Eq. (13), we get

$$ \begin{aligned} M_{\xi m} \left( t \right) & = \left( {k_{m} + \hbar } \right)M_{\xi m - 1 } \left( t \right) - \hbar \left( {1 - \frac{{k_{m} }}{n}} \right)L^{ - 1} \left( {\frac{1}{{p^{\alpha } }}\mathop \sum \limits_{k = 0}^{\ell - 1} p^{\alpha - k - 1} M_{\xi }^{k} \left( {t,0} \right) + \frac{1}{{p^{\alpha } }}L\left[ {g_{1} \left( t \right)} \right]} \right) \\ & \quad + \, \hbar L^{ - 1} \left[ {\frac{1}{{p^{\alpha } }}L[R_{1} M_{\xi m - 1} \left( t \right) + P_{m - 1} ]} \right]. \\ \end{aligned} $$
(18)

Hence from Eq. (18), the components Mxm(t), Mym(t) and Mzm(t) for m ≥ 1 can be computed. The q-HATM solution is presented in subsequent form

$$ \begin{aligned} & M_{x } \left( t \right) = \mathop \sum \limits_{m = 0}^{\infty } M_{xm} \left( t \right) \left( {\frac{1}{n}} \right)^{m} , \\ & M_{y } \left( t \right) = \mathop \sum \limits_{m = 0}^{\infty } M_{ym} \left( t \right) \left( {\frac{1}{n}} \right)^{m} , \\ & M_{z } \left( t \right) = \mathop \sum \limits_{m = 0}^{\infty } M_{zm} \left( t \right) \left( {\frac{1}{n}} \right)^{m} . \\ \end{aligned} $$
(19)

We mention that in the q-HATM, we have freedom to fix the initial approximation, ħ, H and n. For n = 1 in Eq. (10), it reduces to HAM. The ħ plays a vital role in controlling the convergence region and rate. The valid convergence region for ħ is horizontal segment of each ħ-curve. The value of ħ is chosen corresponding to arbitrary n(n ≥ 1) from the range of convergence. We can see from ħ-curves that convergence range is directly proportional to n. The ħ- and n-curves show the validity of q-HATM for infinitely many acceptable solutions. The middle point of ħ-curve interval, i.e., ħ = −n is an appropriate choice. For n = 1, ħ = −1 is the proper choice to get the optimum solution.

Theorem

[43] If ∃a constant 0 < β < 1 s.t.\( \left| {\left| {\omega_{m + 1} \left( t \right)} \right|} \right| \le \beta \left| {\left| { \omega_{m} \left( t \right)} \right|} \right| \) ∀ m and if truncated series\( \sum\nolimits_{m = 0}^{r} {\omega_{ m} \left( t \right) \left( {\frac{1}{n}} \right)^{m} } \)is used as an approximate solution ω(t), then max. absolute truncation error is found as

$$ \left| {\left| { \omega \left( t \right) - \sum\limits_{m = 0}^{r} {\omega_{ m} \left( t \right)} \left( {\frac{1}{n}} \right)^{m} } \right|} \right| \le \frac{{\beta^{r + 1} }}{{n^{r} \left( {n - \beta } \right)}}\left| {\left| {\omega_{0} \left( t \right)} \right|} \right|. $$

4 Numerical example

By using initial conditions, we may initialize with Mx0 = 0, My0 = 100 and Mz0 = 0 and applying Laplace transform to Eq. (3), we get

$$ \begin{aligned} & L\left[ {M_{x} } \right] + \frac{1}{{p^{\alpha } }} L\left[ { - \omega_{0} M_{y} + \frac{{M_{x} }}{{T_{2} }}} \right] = 0, \\ & L\left[ {M_{y} } \right] - \frac{100}{p} + \frac{1}{{p^{\beta } }}L\left[ {\omega_{0} M_{x} + \frac{{M_{y} }}{{T_{2} }}} \right] = 0, \\ & L\left[ {M_{z} } \right] + \frac{1}{{p^{\gamma } }}L\left[ { - \frac{{M_{0} - M_{z} }}{{T_{1} }}} \right] = 0. \\ \end{aligned} $$
(20)

We state the nonlinear operators as:

$$ \begin{aligned} & N\left[ {\varphi_{1} } \right] = L\left[ {\varphi_{1} } \right] + \frac{1}{{p^{\alpha } }} L\left[ { - \omega_{0} \varphi_{2} + \frac{{\varphi_{1} }}{{T_{2} }}} \right], \\ & N\left[ {\varphi_{2} } \right] = L\left[ {\varphi_{2} } \right] - \left( {1 - \frac{{k_{m} }}{n}} \right)\frac{100}{p} + \frac{1}{{p^{\beta } }} L\left[ {\omega_{0} \varphi_{1} + \frac{{\varphi_{2} }}{{T_{2} }}} \right], \\ & N\left[ {\varphi_{3} } \right] = L\left[ {\varphi_{3} } \right] + \frac{1}{{p^{\gamma } }} L\left[ { - \frac{{M_{0} - \varphi_{3} }}{{T_{1} }}} \right], \\ \end{aligned} $$
(21)

and thus \( {{\ae }}_{m} \left( {M_{xm - 1} } \right),\,{{\ae }}_{m} \left( {M_{ym - 1} } \right)\,{\text{and}}\,{{\ae }}_{m} \left( {M_{zm - 1} } \right) \) are represented as:

$$ \begin{aligned} & {{\ae }}_{m} \left( {M_{x m - 1} } \right) = L \left[ {M_{xm - 1 } \left( t \right)} \right] + \frac{1}{{p^{\alpha } }} L\left[ { - \omega_{0} M_{ym - 1} + \frac{{M_{xm - 1} }}{{T_{2} }}} \right], \\ & {{\ae }}_{m} \left( {M_{ym - 1} } \right) = L \left[ {M_{ym - 1 } \left( t \right)} \right] - \left( {1 - \frac{{k_{m} }}{n}} \right)\frac{100}{p} + \frac{1}{{p^{\beta } }} L\left[ {\omega_{0} M_{xm - 1} + \frac{{M_{ym - 1} }}{{T_{2} }}} \right], \\ & {{\ae }}_{m} \left( {M_{zm - 1} } \right) = L \left[ {M_{zm - 1 } \left( t \right)} \right] + \frac{1}{{p^{\gamma } }} L\left[ { - \frac{{M_{0} - M_{zm - 1} }}{{T_{1} }}} \right]. \\ \end{aligned} $$
(22)

Now, taking initial approximation Mx0 = 0, My0 = 100, Mz0 = 0, and scheme (13), we find following approximations q-HATM solution:

$$ \begin{aligned} & M_{x1 } = - \frac{{100 \omega_{0} \hbar t^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}},M_{y1 } = \frac{100 \hbar t^{\beta} }{{T_{2} \varGamma \left( {1 + \beta } \right)}},M_{z1 } = - \frac{{M_{0} \hbar t^{\gamma } }}{{T_{1} \varGamma \left( {1 + \gamma } \right)}}, \\ & M_{x2 } = - \frac{{100 \omega_{0} \hbar n t^{\alpha } }}{{ \varGamma \left( {1 + \alpha } \right)}} - \frac{{100 \omega_{0} \hbar^{2} t^{\alpha } }}{{ \varGamma \left( {1 + \alpha } \right)}} - \frac{{100 \omega_{0 } \hbar^{2} t^{2\alpha } }}{{T_{2} \varGamma \left( {1 + 2\alpha } \right)}} - \frac{{100 \omega_{0} \hbar^{2} t^{\alpha + \beta } }}{{T_{2} \varGamma \left( {1 + \alpha + \beta } \right)}}, \\ & M_{y2 } = \frac{{100 \hbar n t^{\beta } }}{{T_{2} \varGamma \left( {1 + \beta } \right)}} + \frac{{100\hbar^{2} t^{\beta } }}{{T_{2} \varGamma \left( {1 + \beta } \right)}} - \frac{{100 \omega_{0}^{2} \hbar^{2} t^{\alpha + \beta } }}{{ \varGamma \left( {1 + \alpha + \beta } \right)}} + \frac{{100 \hbar^{2} t^{2\beta } }}{{T_{2}^{2} \varGamma \left( {1 + 2\beta } \right)}}, \\ & M_{z2 } = - \frac{{M_{0} \hbar n t^{\gamma } }}{{T_{1} \varGamma \left( {1 + \gamma } \right)}} - \frac{{\hbar \left( {1 + \hbar } \right)M_{0} t^{\gamma } }}{{T_{1} \varGamma \left( {1 + \gamma } \right)}} - \frac{{M_{0} \hbar^{2} t^{2\gamma } }}{{T_{1}^{2} \varGamma \left( {1 + 2\gamma } \right)}}. \\ \end{aligned} $$

Persisting this way, we can compute rest components of Mxm, Mym, and Mzm, m > 1 of the q-HATM solution. Then, solution can be written as:

$$ \begin{aligned} & M_{x } \left( t \right) = \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{m = 0}^{N} M_{xm} \left( t \right) \left( {\frac{1}{n}} \right)^{m} , \\ & M_{y } \left( t \right) = \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{m = 0}^{N} M_{ym} \left( t \right) \left( {\frac{1}{n}} \right)^{m} , \\ & M_{z } \left( t \right) = \mathop {\lim }\limits_{N \to \infty } \mathop \sum \limits_{m = 0}^{N} M_{ym} \left( t \right) \left( {\frac{1}{n}} \right)^{m} . \\ \end{aligned} $$
(23)

5 Results and discussion

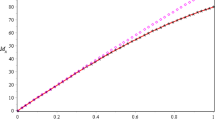
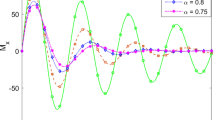
We performed the numerical simulations for fractional Bloch Eq. (3) for various values of t, α, β and γ. Table 1 depicts the comparison of values of Mx(t), My(t) and Mz(t) at α = 1; t = 0.1, 0.3, 0.5, 0.7, and 0.9 found by the q-HATM with exact solution and those from existing methods. The numerical results show that the q-HATM performs very well for the solution of Eq. (3) among others existing methods, even when it is applied with a lower order approximate solution. However, its accuracy can be improved using higher order approximate solutions. Figures 1, 2, 3 depict the behavior of numerical solutions Mx(t), My(t) and Mz(t) vs. t at ħ = − 1, n = 1, α = β = γ = 1, as well as its comparison with the exact solution obtained by the q-HATM. It is clear from Figs. 1, 2, 3 that the approximate solutions Mx(t), My(t) and Mz(t) of Eq. (3) gained by using the q-HATM is in complete agreement with the exact solution. The numerical results for different specific cases of α, β, γ, ħ and n are presented in Figs. 4, 5 and 6. They exhibit the behavior of solutions for diverse Brownian motions α = 0.5, 0.75; β = 0.5, 0.75; γ = 0.5, 0.75 and the standard motion α = β = γ = 1, at ħ = − 1, n = 1. From Figs. 4 and 6, it is clear that Mx(t) and Mz(t) increases with increase in time t for diverse values of α = γ = 0.5, 0.75 and converges to the exact solution at α = γ = 1, while in Fig. 5, My(t) decreases with increase in time t for diverse values of β = 0.5, 0.75 but again converges to the exact solution at β = 1. In Figs. 7, 8, 9, 10, 11, 12, 13, 14, and 15, different values of convergence control parameter ħ are selected to curtail residual errors for Mx(t), My(t) and Mz(t) respectively. From Figs. 7, 8, 9, 10, 11, 12, 13, 14, and 15, it can also be observed that convergence range depends positively on value of n. Figures 16, 17, and 18 display n-curves for distinct order of fractional derivative.

Table 1 Comparison of approximate solution by existing and proposed methods with the exact solution
Full size table
Fig. 1
figure 1

Comparison of exact and approximate solutions for Mx(t) at n = 1 and ħ = − 1

Full size image
Fig. 2
figure 2

Comparison of exact and approximate solutions for My(t) at n = 1 and ħ = − 1

Full size image
Fig. 3
figure 3

Comparison of exact and approximate solutions for Mz(t) at n = 1 and ħ = − 1

Full size image
Fig. 4
figure 4

Plot of Mx(t) (n = 1 and ħ = − 1) solution for different value of α

Full size image
Fig. 5
figure 5

Plot of My(t) (n = 1 and ħ = − 1) solution for different value of β

Full size image
Fig. 6
figure 6

Plot of Mz(t) (n = 1 and ħ = − 1) solution for different value of γ

Full size image
Fig. 7
figure 7

ħ-curves drawn for Mx(t) solution when t = 0.01, n = 1 for various values of α

Full size image
Fig. 8
figure 8

ħ-curves drawn for Mx(t) solution when t = 0.01, n = 2 for various values of α

Full size image
Fig. 9
figure 9

ħ-curves drawn for Mx(t) solution when t = 0.01, n = 3 for various values of α

Full size image
Fig. 10
figure 10

ħ-curves drawn for My(t) solution when t = 0.01, n = 1 for various values of β

Full size image
Fig. 11
figure 11

ħ-curves drawn for My(t) solution when t = 0.01, n = 2 for various values of β

Full size image
Fig. 12
figure 12

ħ-curves drawn for My(t) solution when t = 0.01, n = 3 for various values of β

Full size image
Fig. 13
figure 13

ħ-curves drawn for Mz(t) solution when t = 0.01, n = 1 for various values of γ

Full size image
Fig. 14
figure 14

ħ-curves drawn for Mz(t) solution when t = 0.01, n = 2 for various values of γ

Full size image
Fig. 15
figure 15

ħ-curves drawn for Mz(t) solution when t = 0.01, n = 3 for various values of γ

Full size image
Fig. 16
figure 16

n-curves drawn for Mx(t) solution when t = 0.01, ħ = − 1 for various values of α

Full size image
Fig. 17
figure 17

n-curves drawn for My(t) solution when t = 0.01, ħ = − 1 for various values of β

Full size image
Fig. 18
figure 18

n-curves drawn for Mz(t) solution when t = 0.01, ħ = − 1 for various values of γ

Full size image

6 Conclusions

In this article, the q-HATM is successfully applied to solve fractional model of Bloch equations. It is clearly seen from illustrative example that the q-HATM is easy to implement and powerful numerical method to find an approximate solution than from the existing methods. It must be noted that the q-HATM is used directly without using perturbation, linearization, Adomian polynomials, or other restrictive assumptions. The results of fractional-order Bloch Eq. (3) by the q-HATM are closer to the exact solution in comparison with the other existing techniques. Hence, the q-HATM is more efficient, convenient, and easier than other existing methods.