1 Introduction

Fractional Calculus (FC) is a branch of mathematics that deals with derivatives and integrals to arbitrary orders (real or complex orders). It generalises the concepts of classical calculus, which deals with integer-order derivatives and integrals, to the case of fractional-order derivatives and integrals. In fractional calculus, the notion of a derivative is extended to derivatives of non-integer order, such as 0.5, 1.7 or \(-2.3\). This leads to the introduction of new mathematical objects and concepts, such as fractional derivatives (FD), fractional integrals and fractional differential equations (FDEs). FC has a wide range of applications in fields, such as physics, engineering and finance, where it is used to model complex phenomena that cannot be described by classical calculus. For example, in physics, FC has been used to describe anomalous diffusion, viscoelasticity and memory effects. In engineering, it has been used to model control systems, electrical circuits and signal processing. While FC is a relatively new area of mathematics, it has been rapidly growing in recent years and has received increasing attention from the research community. This is due to its ability to provide new insights and solutions to problems in a variety of fields and its potential for further development and application in the future [1, 2]. An FDE is a type of mathematical equation that involves derivatives of fractional order. In contrast to classical differential equations, which involve derivatives of integer order, FDEs involve derivatives of non-integer order, such as 0.5, 1.7 or \(-2.3\). FDs are often defined using the Riemann–Liouville or Caputo–Fabrizio fractional derivative (CFFD). These operators provide a way to generalise the notion of differentiation to fractional order and they have a number of interesting properties and applications in areas, such as physics, engineering and finance. Solving FDEs can be challenging, as FD introduces new complexities and difficulties compared to integer-order derivatives. Numerical methods, such as finite difference or spectral methods and analytical methods, such as Laplace transforms, can be used to find approximate or exact solutions to FDEs, depending on the specific problem and desired level of accuracy [3,4,5,6]. Researchers have been studying semi-analytical solutions using nonlinear fractional partial differential equations (NFPDEs) in recent years. There are numerous established techniques for solving NFPDEs, such as tanh function method [7], Poisson random measures [8],  He’s variational iteration method [9], bifurcation     theory     analysis    [10],     Caputo–Fabrizio operator [11], Riemann–Liouville [12],  FHPTM [13], extension of natural transform method [14], residual power series method [15], q-homotopy analysis transform method [16], the fractional natural decomposition method [17], the new iterative method [18], the Sumudu transform method [19], the sine-Gordon expansion method [20,21,22], the bvp4c method [23], the new travelling wave solutions [24], the Chebyshev wavelet method [25], the Atangana Baleanu–Caputo derivative [26], the instability modulation [27], Sumudu transform [28], the fixed point theorem [29], the pseudospectral collocation method [30]. Some novel properties, as well as numerical approximations of these new operators are discussed, along with some real-world applications [31, 32], the nonlinear least-squares fitting method [33], the conformable derivatives [34], the fractional Adams Bashforth method [35]. In both physical and mathematical studies of capillary and nonlinear dispersive gravity waves, the Emden–Fowler equation has gained significant importance [36]. The Laplace transform [37], the Caputo fractional derivatives [38], the Riccati substitution [39], the rational sine–cosine and rational sinh–cosh methods [40], the extended rational sine–cosine and sinh–cosh techniques [41], the incomplete global GMERR algorithm [42], the operational method [43], the extended sinh-Gordon equation expansion method [44], the new extension algebraic method [45], the Chebyshev spectral collocation method [46] and many others are available [47,48,49,50,51,52,53]. In this paper, the Kuramoto–Sivashinsky equation is a partial differential equation that describes the behaviour of nonlinear waves in a variety of physical systems, including fluid dynamics, combustion and crystal growth. The equation was first derived by Yoshiki Kuramoto and Grigory Sivashinsky in the late 1970s and has been used to study the behaviour of a wide range of phenomena, including pattern formation, turbulence and chaotic dynamics.

The equation is given by [16]

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0D_t^\alpha \;\phi + \phi \phi _{x}+ \beta \phi _{xx}+\tau \phi _{xxx}+ \theta \phi _{xxxx}=0, \nonumber \\{} & {} 0<\alpha \le 1 \end{aligned}$$
(1)

with the initial condition

$$\begin{aligned} \phi (x,0)= h(x) \end{aligned}$$
(2)

with the boundary condition \(\phi (l,t)=\psi _1(x),~ \phi (m,t)=\psi _2(x), \phi _x(x,t)\!=\!\phi _x(m,t) \,\textrm{and}\, \phi _{xx}(l,t)=\phi _{xx}(m,t)=0.\) Here \(\tau ,~ \delta \) and \(\theta \)  are constants, \(h(x), \psi _1(x)\,\textrm{and}\, \psi _2(x)\) are known functions. The equation has a wide range of interesting behaviours, including the formation of complex patterns, such as spirals and spatiotemporal chaos. These patterns are the result of the interplay between the nonlinear term \((\phi \phi _{x})\) and the linear damping term \((\beta \phi _{xx})\) in the equation. The coefficient \( \phi _{xxxx}\) represents an additional nonlinear term that can lead to further complexity in the behaviour of the system. The Kuramoto–Sivashinsky equation has had a significant impact on our understanding of nonlinear dynamics and chaotic behaviour and continues to be an active area of research. Its versatility and broad applicability make it a valuable tool for researchers in different fields and its simplicity makes it accessible to students and researchers alike. Overall, the Kuramoto–Sivashinsky equation is a testament to the power of mathematical models to shed light on complex physical phenomena and advance our understanding of the world around us.

The dynamics behaviour of the Kuramoto–Sivashinsky equation can exhibit a wide range of complex and interesting phenomena, including

  • Chaos: The Kuramoto–Sivashinsky equation is one of the early examples of a partial differential equation that exhibits chaotic behaviour. The chaotic dynamics observed in the solutions make it an interesting model for studying turbulence and pattern formation in fluid systems.

  • Pattern formation: The equation is well known for its ability to produce a variety of pattern formations, such as rolls, stripes and spirals. These patterns arise from the interplay between nonlinear convection and diffusion.

  • Travelling waves: The equation supports travelling wave solutions, where the height of the interface moves in one direction without changing shape. These solutions are important for understanding the propagation of flame fronts and other types of fronts in physical systems.

  • Turbulence: The equation is also used to study turbulence, a complex and chaotic flow behaviour that occurs in many physical systems, including fluid dynamics, combustion and atmospheric science.

  • Stability: The equation can also exhibit stable solutions, where the height of the interface remains constant over time. However, these solutions are often destabilised by small perturbations, leading to more complex dynamic behaviours.

The rich variety of dynamic behaviours displayed by the Kuramoto–Sivashinsky equation makes it an important model for understanding complex physical systems and has led to its widespread use in a variety of fields, including combustion, fluid mechanics, material science and nonlinear dynamics.

This paper is divided to six sections as follows: Definitions of fractional derivatives are discussed in §2, the fractional homotopy perturbation method via CFFD is discussed in §3 and in §4 the semi-analytical solution of the fractional-order Kuramoto–Sivashinsky equation is presented with four examples that show the efficiency of the methods. The result and discussion are given in §5. Finally, §6 concludes the present work.

2 Preliminaries

Here, we will discuss some basic definitions and characteristics of the theory of fractional calculus.

Definition 1

The Caputo derivative is defined for \(\alpha \ge 0\) and \(n\in N\cup {0}\) as follows [13]:

$$\begin{aligned} ^{\textrm{C}}_0D_t^\alpha \phi (t)= \frac{1}{\Gamma (n-\alpha )}\int _{0}^{t}(t-\xi )\frac{\textrm{d}^n}{\textrm{d}t^n}h(\xi )\textrm{d}\xi , \end{aligned}$$
(3)

where \(^{\textrm{C}}_0D_t^\alpha \;\) is a Caputo derivative with respect to t.

Definition 2

Let \(\phi \) be a function \(\phi \in H^1(a_1,b_1),~ b_1>0,~ 0<\alpha <1.\) Define as Caputo–Fabrizio derivative [13]

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0D_t^\alpha \phi (t)=\frac{M(\alpha )}{1-\alpha )}\int _{0}^{t}\exp \bigg [-\frac{\alpha (1-\xi )}{1-\alpha }\bigg ] \phi '(\xi )\textrm{d}\xi ,\quad \nonumber \\{} & {} t\ge 0,~0<\alpha <1. \end{aligned}$$
(4)

Definition 3

The Caputo–Fabrizio fractional integral operator of order \( 0<\alpha <1\) is given as [13]

$$\begin{aligned} ^{\textrm{CF}}_0D_t^\alpha \;\phi (t)= & {} \frac{2(1-\alpha )}{M(\alpha )(2-\alpha )}\phi (t)\nonumber \\{} & {} + \frac{2\alpha }{M(\alpha )(2-\alpha )} \int _{0}^{t} \phi (\xi )\textrm{d}\xi ,~t\ge 0, \end{aligned}$$
(5)

where \(^{\textrm{CF}}_0D_t^\alpha \phi (t)=0,\) if \(\phi \) is a constant function.

Definition 4

For \( 0<\alpha <1\) and \(m\in N\) define as CFD [13]

$$\begin{aligned} \begin{aligned}&{\mathscr {L}}\left[ ^{\textrm{CF}}_0D_t^{(m+\alpha )}u(t)\right] (s)\\&\quad = \frac{1}{1-\alpha } {\mathscr {L}}[u^{m+1}(t)] {\mathscr {L}}\left[ \exp \left( \frac{-\alpha }{(1-\alpha )}t\right) \right] \\&\quad = \frac{s^{m+1} {\mathscr {L}}[u(t)]{-} s^m u(0){-}s^{m-1}u'(0)\cdots {-} u^m (0) }{s{+}\alpha (1{-}s)} \end{aligned} \end{aligned}$$
(6)

In particular, we have

$$\begin{aligned}{} & {} {\mathscr {L}} \left[ ^{\textrm{CF}}_0D_t^{(m+\alpha )}u(t)\right] (s)=\frac{s {\mathscr {L}}(u(t))}{s+ \alpha (1-s)},\\{} & {} m=0, \\{} & {} {\mathscr {L}}\left[ ^{\textrm{CF}}_0D_t^{(m+\alpha )}\;u(t)\right] (s)= \frac{s^2 {\mathscr {L}}(u(t)){-} su(o){-}u'(0)}{s{+} \alpha (1{-}s)},\\{} & {} m=1. \end{aligned}$$

3 Methodology

Let us consider the following nonlinear partial differential equations (NPDEs) along with the Caputo–Fabrizio fractional derivative:

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0D^{m+\alpha }_t \phi (x,t) + \beta \phi (x,t) + \varphi \phi (x,t) = k(x,t),~~~~ \nonumber \\{} & {} n-1< \alpha +m \le n, \end{aligned}$$
(7)

for the initial conditions

$$\begin{aligned} \frac{\partial ^k \phi (x,0)}{\partial t^k} = f_k(x), ~~~~ k= 0,1,2, \ldots , n-1. \end{aligned}$$
(8)

When we apply the Laplace transform’s derivative rule to eqs (7)–(8), we get

$$\begin{aligned}{} & {} {\mathscr {L}}[\phi (x,t)]= \Theta (x,s) - \left( \frac{s+ \alpha (1- s)}{s^{n+1}} \right) \nonumber \\{} & {} \times {\mathscr {L}} [\beta \phi (x,t) + \varphi \phi (x,t)]. \end{aligned}$$
(9)

Here

$$\begin{aligned} \Theta (x,s)= & {} \frac{1}{s^{m+1}}[s^m f_0(x){+} s^{m-1}f_1(x){+} \cdots {+} f_m(x)]\nonumber \\{} & {} + \frac{s+ \alpha (1-s)}{s^{n+1}} \tilde{k}(x,s). \end{aligned}$$
(10)

Applying inverse Laplace transform on both sides of eq. (9), we have

$$\begin{aligned} \phi (x,t)= & {} \Theta (x,s) - {\mathscr {L}}^{-1} \bigg [\left( \frac{s+ \alpha (1-s)}{s^{n+1}} \right) \nonumber \\{} & {} \times {\mathscr {L}}[\beta \phi (x,t) + \varphi \phi (x,t)]\bigg ], \end{aligned}$$
(11)

as a result of an infinite series

$$\begin{aligned} \phi (x,t) = \sum _{m=0}^{\infty } z^m \phi _m(x,t) \end{aligned}$$
(12)

and the nonlinear term is decomposable like

$$\begin{aligned} \varphi \phi (x,t) = \sum _{m=0}^{\infty } z^m H_m(x,t). \end{aligned}$$
(13)

\(H_m(x,t)\) are He’s polynomials that can be evaluated using the following formula [31]:

$$\begin{aligned}{} & {} H_m(\phi _0, \phi _1, \phi _2, \ldots ,\phi _n) \,{=}\,\frac{1}{n!}\frac{\partial ^m}{\partial z^m}\left[ \left( \sum _{m{=}0}^{\infty } p^i \phi _i \right) \right] _{z{=}0}, \nonumber \\{} & {} m = 0,1,2, \ldots . \end{aligned}$$
(14)

We substitute (12) and (13) into (15), to get

$$\begin{aligned}{} & {} \sum _{m=0}^{\infty } \phi _m(x,t)= \Theta (x,s)- z {\mathscr {L}}^{-1} \bigg [\left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \nonumber \\{} & {} \times \mathscr {L} \bigg [\beta \sum _{m=0}^{\infty }z^m \phi _m(x,t) + \sum _{n=0}^{\infty }z^m H_m \bigg ] \bigg ]. \end{aligned}$$
(15)

The following approximations are obtained by equating the terms with similar powers in z in eq. (15):

$$\begin{aligned}&z^0: \phi _0(x,t) = \Theta (x,s) \\&z^1: \phi _1(x,t) = - {\mathscr {L}}^{-1}\times \bigg [\left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \\&\quad \times {\mathscr {L}} [\beta \phi _0(x,t) + H_0 (u) ] \bigg ] \\&z^2: \phi _2(x,t) = -{\mathscr {L}}^{-1}\times \bigg [\left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \\&\quad \times {\mathscr {L}} [\beta \phi _1(x,t) + H_1 (u) ] \bigg ] \\&z^3: \phi _3(x,t) = -{\mathscr {L}}^{-1}\bigg [\left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \\&\quad \times {\mathscr {L}} [\beta \phi _2(x,t) + H_2 (u) ] \bigg ] \\&\vdots \\&z^{m+1}: \phi _{m+1}(x,t) = -{\mathscr {L}}^{-1}\bigg [\left( \frac{s+ \alpha (1-s)}{s^{m+1}} \right) \\&\quad \times {\mathscr {L}} [\beta u_{m+1}(x,t) + H_{m+1} (\phi ) ] \bigg ]. \end{aligned}$$

In the same manner, one can evaluate other elements of \(\phi _{m+1}(x,t)\) and then find series solution.

We approximate numerical solution \(\phi (x,t)\) as

$$\begin{aligned} \phi (x,t) = \sum _{m=0}^{\infty } \phi _m(x,t). \end{aligned}$$
(16)

Equation (16) represents a series solution, which converges very fast.

Fig. 1
figure 1

(a) The results of the FHPTM for fractional-order KSE with the first initial condition (eq. (18)) for \(~\alpha = 0.25,~ 0.5, 0.75\) and 1 and (b) 3D graphs of exact solution for Example 1.

Full size image
Fig. 2
figure 2

For the fractional-order KSE with the first initial condition (eq. (18)) of eq. (1), FHPTM result for \(\phi (x,t)\) when (a) \(\alpha = 0.25,\) (b) \(\alpha = 0.50\), (c) \(\alpha = 0.75\) and (d) \(\alpha = 1\).

Full size image

4 Numerical examples

In this section, we apply the FHPTM method along with CFFD to nonlinear Kuramoto–Sivashinsky equations (KSEs) of fractional order with the known exact solution.

Example 1

Consider the following nonlinear fractional Kuramoto–Sivashinsky equation (1) for \(\tau =-1,~ \delta = 0,~ \theta = 1\) [16]:

$$\begin{aligned} ^{\textrm{CF}}_0D_t^\alpha \;\phi + \phi \phi _{x}- \phi _{xx} + \phi _{xxxx}=0, ~~~~~ 0<\alpha \le 1. \end{aligned}$$
(17)

Then the initial conditions

$$\begin{aligned} \phi (x,0)= \frac{\beta +\tanh ^3[k(x-\lambda )]- 45 \tanh [k(x-\lambda )] }{19\sqrt{19}} \end{aligned}$$
(18)

and the boundary conditions

$$\begin{aligned} \phi (l,t)= \phi (m,t)= 0, \end{aligned}$$
(19)

where k and  \(\lambda \) are arbitrary constants. Taking the Laplace transform on both sides of eq. (17), we get

$$\begin{aligned}&{\mathscr {L}}[\phi (x,t)]\nonumber \\&\quad = \frac{1}{s}\frac{\beta +\tanh ^3[k(x-\lambda )]- 45 \tanh [k(x-\lambda )] }{19\sqrt{19}} \nonumber \\&\qquad - \left( \frac{s+ \alpha (1-s)}{s} \right) {\mathscr {L}}\left[ \phi \phi _{x}- \phi _{xx} + \phi _{xxxx} \right] .\nonumber \\ \end{aligned}$$
(20)

Applying the inverse Laplace transform for eq.  (20)

$$\begin{aligned}{} & {} \phi (x,t)=\frac{\beta +\tanh ^3[k(x-\lambda )]- 45 \tanh [k(x-\lambda )] }{19\sqrt{19}}\nonumber \\{} & {} \quad {-}{\mathscr {L}}^{-1}\left[ \left( \frac{s{+} \alpha (1-s)}{s} \right) {{L}}\left[ \phi \phi _{x}- \phi _{xx} {+} \phi _{xxxx} \right] \right] .\nonumber \\ \end{aligned}$$
(21)

Now, we apply the FHPTM

$$\begin{aligned}{} & {} \sum _{m=0}^{\infty } \phi _m(x,t){=} \frac{\beta {+}\tanh ^3[k(x-\lambda )]{-} 45 \tanh [k(x-\lambda )] }{19\sqrt{19}}\nonumber \\{} & {} \quad - z{\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) {\mathscr {L}}\left[ \sum _{m=0}^{\infty }z^m H_m(\phi )\right. \right. \nonumber \\{} & {} \quad -\bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xx}\nonumber \\{} & {} \quad \left. \left. + \bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xxxx} \right] \right] . \end{aligned}$$
(22)

Here

$$\begin{aligned} \sum _{m=0}^{\infty } z^m H_m(u)= \phi _0 (\phi _0)_x. \end{aligned}$$

The first few components of a homotopy polynomial are written as

$$\begin{aligned} H_0(\phi )= & {} \, \phi _0 (\phi _0)_x\nonumber \\ H_1(\phi )= & {} \, \frac{\partial }{\partial z}[(\phi _0 + z \phi _1) (\phi _0 + z \phi _1)_x]_{z=0}\nonumber \\= & {} \,\phi _0 (\phi _1)_x+ \phi _1 (\phi _0)_x\nonumber \\ H_2(\phi )= & {} \, \frac{1}{2}\frac{\partial ^2}{\partial z^2}[(\phi _0 + z \phi _1 +z^2 \phi _2)\nonumber \\{} & {} \times (\phi _0 + z \phi _1+ z^2 \phi _2)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _2)_x+ \phi _1 (\phi _1)_x + \phi _2 (\phi _0)_x\nonumber \\{} & {} \cdots . \end{aligned}$$
(23)

The result of comparing the coefficients of similar powers of z is

$$\begin{aligned} \phi _0(x,t)= \frac{\beta +\tanh ^3[k(x-\lambda )]- 45 \tanh [k(x-\lambda )] }{19\sqrt{19}}. \end{aligned}$$
(24)

By carrying on in this manner, we obtain the final element of the iteration formulas. Consequently, the approximate answer is

$$\begin{aligned} \phi (x,t) = \sum _{m=0}^{\infty } \phi _m(x,t). \end{aligned}$$
(25)
Fig. 3
figure 3

(a) The results of the FHPTM for the fractional-order KSE with the second initial condition (eq. (27)) for \(\alpha = 0.25,\) 0.5,  0.75 and 1 and (b) 3D graphs of exact solution for Example 2.

Full size image
Fig. 4
figure 4

For the fractional-order KSE with the second initial condition (eq. (27)) of eq. (1), FHPTM result for \(\phi (x,t)\) when (a) \(\alpha = 0.25\), (b) \(\alpha = 0.50\), (c) \(\alpha = 0.75\) and (d) \(\alpha = 1\).

Full size image

Example 2

Consider the following nonlinear fractional Kuramoto–Sivashinsky eq. (1) for \(\tau = 1,~ \delta = 0,~ \theta = 1\) [16]:

$$\begin{aligned} ^{\textrm{CF}}_0D_t^\alpha \;\phi + \phi \phi _{x}+ \phi _{xx} + \phi _{xxxx}=0, ~~~~~ 0<\alpha \le 1. \end{aligned}$$
(26)

Then the initial conditions

$$\begin{aligned} \phi (x,0)= & {} \beta + \frac{15}{19}\sqrt{\frac{11}{19}}\left( -9 \tanh [k(x-\lambda )]\right. \nonumber \\{} & {} \left. + 11 \tanh ^3[k(x-\lambda )]\right) , \end{aligned}$$
(27)

where k and \(\lambda \) are suitably chosen constants. Taking the Laplace transform on both sides of eq. (26), we get

$$\begin{aligned}&{\mathscr {L}}[\phi (x,t)]=\beta + \frac{15}{19}\sqrt{\frac{11}{19}}\nonumber \\&\quad \times \left( -9\tanh [k(x-\lambda )]+ 11 \tanh ^3[k(x-\lambda )]\right) \nonumber \\&\quad - \left( \frac{s+ \alpha (1-s)}{s} \right) {\mathscr {L}}\left[ \phi \phi _{x}+ \phi _{xx} + \phi _{xxxx} \right] . \end{aligned}$$
(28)

Applying the inverse Laplace transform for eq. (28)

$$\begin{aligned}{} & {} \phi (x,t)=\beta + \frac{15}{19}\sqrt{\frac{11}{19}}\left( -9\tanh [k(x-\lambda )]\right. \nonumber \\{} & {} \left. \qquad + 11 \tanh ^3[k(x-\lambda )]\right) \nonumber \\{} & {} - {\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) {\mathscr {L}}\left[ \phi \phi _{x}+ \phi _{xx} + \phi _{xxxx} \right] \right] \nonumber \\ \end{aligned}$$
(29)

Now, we apply the FHPTM

$$\begin{aligned}{} & {} \sum _{m=0}^{\infty } \phi _m(x,t)= \beta \nonumber \\{} & {} \quad + \frac{15}{19} \sqrt{\frac{11}{19}}\left( -9\tanh [k(x\!-\!\lambda )]\!+\! 11 \tanh ^3[k(x\!-\!\lambda )]\right) \nonumber \\{} & {} \quad - z{\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \nonumber \\{} & {} \quad \times {\mathscr {L}}\left[ \sum _{m=0}^{\infty }z^m H_m(\phi )-\bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xx}\right. \nonumber \\{} & {} \left. \left. + \bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xxxx} \right] \right] , \end{aligned}$$
(30)

where

$$\begin{aligned} \sum _{m=0}^{\infty } z^m H_m(u)= \phi _0 (\phi _0)_x. \end{aligned}$$

The first few components of a homotopy polynomial are written as

$$\begin{aligned} H_0(\phi )= & {} \,\phi _0 (\phi _0)_x\nonumber \\ H_1(\phi )= & {} \, \frac{\partial }{\partial z}[(\phi _0 + z \phi _1) (\phi _0 + z \phi _1)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _1)_x+ \phi _1 (\phi _0)_x\nonumber \\ H_2(\phi )= & {} \, \frac{1}{2}\frac{\partial ^2}{\partial z^2}[(\phi _0 + z \phi _1 +z^2 \phi _2)\nonumber \\{} & {} \quad \times (\phi _0 + z \phi _1+ z^2 \phi _2)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _2)_x+ \phi _1 (\phi _1)_x + \phi _2 (\phi _0)_x\nonumber \\{} & {} \cdots . \end{aligned}$$
(31)

The result of comparing the coefficients of similar powers of z is

$$\begin{aligned}{} & {} \phi _0(x,t)= \beta + \frac{15}{19}\sqrt{\frac{11}{19}}\nonumber \\{} & {} \times \left( -9\tanh [k(x-\lambda )] + 11 \tanh ^3[k(x-\lambda )]\right) . \end{aligned}$$
(32)

By carrying on in this manner, we obtain the final element of the iteration formulas. Consequently, the approximate answer is

$$\begin{aligned} \phi (x,t) = \sum _{m=0}^{\infty } \phi _m(x,t). \end{aligned}$$
(33)
Fig. 5
figure 5

(a) The results of the FHPTM for fractional-order KSE with the third initial condition (eq. (35)) for \(\alpha = 0.25,\) 0.5, 0.75 and 1 and (b) 3D graphs of exact solution for Example 3.

Full size image
Fig. 6
figure 6

For the fractional-order KSE with the second initial condition (eq. (35)) of eq. (1), FHPTM result for \(\phi (x,t)\) when (a) \(\alpha = 0.25\), (b) \(\alpha = 0.50\), (c) \(\alpha = 0.75\) and (d) \(\alpha = 1\).

Full size image

Example 3

Consider the following nonlinear fractional Kuramoto–Sivashinsky equation (1) for \(\tau = 1,~ \delta = 4,~ \theta = 1\) [16]:

$$\begin{aligned}{} & {} ^{\textrm{CF}}_0D_t^\alpha \;\phi + \phi \phi _{x}+ \phi _{xx} + 4\phi _{xxx}+ \phi _{xxxx}=0, \nonumber \\{} & {} \quad 0<\alpha \le 1. \end{aligned}$$
(34)

Then the initial conditions

$$\begin{aligned} \phi (x,0)= & {} \beta + 9-15 \left( \tanh [k(x-\lambda )]\right. \nonumber \\{} & {} \left. +\! \tanh ^2[k(x\!-\!\lambda )] \!-\!\tanh ^3[k(x\!-\!\lambda )]\right) , \end{aligned}$$
(35)

where k and \(\lambda \) are arbitrary constants. Taking the Laplace transform on both sides of eq. (34), we get

$$\begin{aligned} L [\phi (x,t)]= & {} \beta + 9-15 \left( \tanh [k(x-\lambda )]\right. \nonumber \\{} & {} \left. + \tanh ^2[k(x-\lambda )]-\tanh ^3[k(x-\lambda )] \right) \nonumber \\{} & {} - \left( \frac{s+ \alpha (1-s)}{s} \right) \nonumber \\{} & {} \times \,L \left[ \phi \phi _{x}+ \phi _{xx} + 4\phi _{xxx}+ \phi _{xxxx} \right] . \end{aligned}$$
(36)

Applying the inverse Laplace transform for eq. (36)

$$\begin{aligned} \phi (x,t)= & {} \beta + 9-15 \big (\tanh [k(x-\lambda )]\nonumber \\{} & {} \quad +\,\tanh ^2[k(x-\lambda )]-\tanh ^3[k(x-\lambda )] \big )\nonumber \\{} & {} \quad - {\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s}\right) \right. \nonumber \\{} & {} \quad \times \left. {\mathscr {L}}\left[ \phi \phi _{x}+ \phi _{xx} + 4\phi _{xxx}+ \phi _{xxxx} \right] \right] .\nonumber \\ \end{aligned}$$
(37)

Now, we apply the FHPTM

$$\begin{aligned}{} & {} \sum _{m=0}^{\infty } \phi _m(x,t)= \beta + 9-15 \big (\tanh [k(x-\lambda )]\nonumber \\{} & {} \quad + \tanh ^2[k(x-\lambda )]-\tanh ^3[k(x-\lambda )] \big ) \nonumber \\{} & {} \quad - z {\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \nonumber \\{} & {} \quad \times {\mathscr {L}}\left[ \sum _{m=0}^{\infty }z^m H_m(\phi )-\bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xx} \right. \nonumber \\{} & {} \quad + 4\bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xxx}\nonumber \\{} & {} \quad \left. \left. + \bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xxxx}\right] \right] , \end{aligned}$$
(38)

where

$$\begin{aligned} \sum _{m=0}^{\infty } z^m H_m(u)= \phi _0 (\phi _0)_x. \end{aligned}$$

For example, the first few components of He’s polynomials are given by

$$\begin{aligned} \! H_0(\phi )= & {} \, \phi _0 (\phi _0)_x\nonumber \\ \! H_1(\phi )= & {} \, \frac{\partial }{\partial z}[(\phi _0 + z \phi _1) (\phi _0 + z \phi _1)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _1)_x+ \phi _1 (\phi _0)_x\nonumber \\ \! H_2(\phi )= & {} \, \frac{1}{2}\frac{\partial ^2}{\partial z^2}[(\phi _0 + z \phi _1 +z^2 \phi _2)\\{} & {} \times (\phi _0 + z \phi _1+ z^2 \phi _2)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _2)_x+ \phi _1 (\phi _1)_x + \phi _2 (\phi _0)_x\nonumber \\{} & {} \, \cdots .\nonumber \end{aligned}$$
(39)

When the coefficients of the same powers of z are compared, we get

$$\begin{aligned} \phi _0(x,t)= & {} \beta + 9-15 \big (\tanh [k(x-\lambda )]\nonumber \\{} & {} +\tanh ^2[k(x-\lambda )]-\tanh ^3[k(x-\lambda )] \big ).\nonumber \\ \end{aligned}$$
(40)

By carrying on in this manner, we obtain the final element of the iteration formulas. Consequently, the approximate answer is

$$\begin{aligned} \phi (x,t) = \sum _{m=0}^{\infty } \phi _m(x,t). \end{aligned}$$
(41)

Example 4

Consider the following nonlinear fractional Kuramoto–Sivashinsky eq. (1) for \(\tau = 1,~ \delta = 0,~ \theta = 1\) [16]:

$$\begin{aligned} ^{\textrm{CF}}_0D_t^\alpha \;\phi + \phi \phi _{x}+ \phi _{xx} + \phi _{xxxx}=0, ~~~~~ 0<\alpha \le 1\qquad \end{aligned}$$
(42)

then the initial conditions

$$\begin{aligned} \phi (x,0)= \textrm{e}^{-x^2}. \end{aligned}$$
(43)

Taking the Laplace transform on both sides of eq. (42), we get

$$\begin{aligned} \begin{aligned} {\mathscr {L}}[\phi (x,t)]&= \textrm{e}^{-x^2} - \left( \frac{s+ \alpha (1-s)}{s} \right) \\&\times {\mathscr {L}}\left[ \phi \phi _{x}+ \phi _{xx} + \phi _{xxxx} \right] . \end{aligned} \end{aligned}$$
(44)

Applying the inverse Laplace transform for eq. (44)

$$\begin{aligned} \phi (x,t)= & {} \textrm{e}^{-x^2} - {\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) \right. \nonumber \\{} & {} \quad \times \left. {\mathscr {L}}\left[ \phi \phi _{x}+ \phi _{xx} + \phi _{xxxx} \right] \right] . \end{aligned}$$
(45)

Now, we apply the FHPTM

$$\begin{aligned}{} & {} \!\! \sum _{m=0}^{\infty } \phi _m(x,t)= \textrm{e}^{-x^2} \nonumber \\{} & {} \quad - z{\mathscr {L}}^{-1}\left[ \left( \frac{s+ \alpha (1-s)}{s} \right) {\mathscr {L}}\left[ \sum _{m=0}^{\infty }z^m H_m(\phi )\right. \right. \nonumber \\{} & {} \quad -\bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xx}\nonumber \\{} & {} \quad \left. \left. + \bigg (\sum _{m=0}^{\infty }z^m \phi _m(x,t)\bigg )_{xxxx} \right] \right] , \end{aligned}$$
(46)

where

$$\begin{aligned} \sum _{m=0}^{\infty } z^m H_m(x,t)= \phi _0 (\phi _0)_x. \end{aligned}$$

For example, the first few components of He’s polynomials are given by

$$\begin{aligned} H_0(\phi )= & {} \, \phi _0 (\phi _0)_x\nonumber \\ H_1(\phi )= & {} \, \frac{\partial }{\partial z}[(\phi _0 + z \phi _1) (\phi _0 + z \phi _1)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _1)_x+ \phi _1 (\phi _0)_x\nonumber \\ H_2(\phi )= & {} \, \frac{1}{2}\frac{\partial ^2}{\partial z^2}[(\phi _0 + z \phi _1 +z^2 \phi _2)\nonumber \\{} & {} \times (\phi _0 + z \phi _1+ z^2 \phi _2)_x]_{z=0}\nonumber \\= & {} \, \phi _0 (\phi _2)_x+ \phi _1 (\phi _1)_x + \phi _2 (\phi _0)_x\nonumber \\{} & {} \cdots . \end{aligned}$$
(47)

When we compare the coefficients of different powers of z,  we get

$$\begin{aligned} \phi _0(x,t)= \textrm{e}^{-x^2} . \end{aligned}$$
(48)

By carrying on in this manner, we obtain the final element of the iteration formulas. Consequently, the approximate answer is

$$\begin{aligned} \phi (x, t) = \sum _{m=0}^{\infty } \phi _m(x, t). \end{aligned}$$
(49)
Fig. 7
figure 7

The results of the FHPTM for fractional-order KSE with the fourth initial condition (eq. (43)) for \(\alpha = 0.25\), 0.5, 0.75 and 1.

Full size image
Fig. 8
figure 8

For the fractional-order KSE with the second initial condition (eq. (43)) of eq. (1), FHPTM result for \(\phi (x,t)\) when (a) \(\alpha = 0.25\), (b) \(\alpha = 0.50\), (c) \(\alpha = 0.75\) and (d) \(\alpha = 1\).

Full size image

5 Results and discussion

In this section, the dynamics of the semi-analytical solutions of the fractional-order Kuramoto–Sivashinsky equation (1) are presented. We precisely determine the values of arbitrary constants and parameters to characterise the behaviour of the reported solutions. By utilising the FHPTM on the fractional-order Kuramoto–Sivashinsky equation we attain different sets of the well-known and standard semi-analytical solutions, such as the solitary wave solutions, hyperbolic function, tangent hyperbolic function with a suitable choice of arbitrary constants and parameters under the acceptable range by using the symbolic computation tool Mathematica. Here, the fractional-order Kuramoto–Sivashinsky equation is represented graphically with appropriate parametric values as follows:

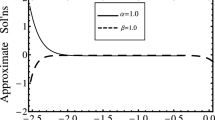
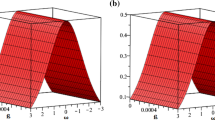
Figure 1a displays the 2D plot for solution representing a wave profile for different values of parameters and fractional order \(\alpha \) where \(\alpha = 0.25,~ 0.50,~ 0.75,~ 1,\beta = 5,~ k={1}/{2 \sqrt{19}} \) and \(x=1,~0\le t\le 10\). Figure 1b  displays the 3D graph of the exact solutions \(\phi (x, t)\) when \(\beta = 5,~k={1}/{2 \sqrt{19}}\) and \(-1\le x\le 1,~ 0\le t\le 1\). Figures 2a–2d show the 3D plot of the semi-analytical solutions for different values of parameters and fractional order \(\alpha \). Figure 3a shows the 2D plot for the solution representing a wave profile for different values of parameters and fractional order \(\alpha \) where \(\alpha = 0.25,~ 0.50,~ 0.75,~ 1,~ \beta = 5,~ k= 0.5\sqrt{{11}/{19}} \) and \(x=1,~~0\le t\le 10\). Figure 3b displays the 3D analysis of the exact solutions \(\phi (x, t)\) with parametric values \(\beta = 5,~k= 0.5\sqrt{{11}/{19}}\) and \(-1\le x\le 1,~ 0\le t\le 1\). Figures 4a–4d show the 3D plot of the semi-analytical solutions for different values of parameters and fractional order \(\alpha \). Figure 5a shows the 2D plot for the solution representing a wave profile for different values of parameters and fractional order \(\alpha \) where \(\alpha = 0.25,~ 0.50,~ 0.75,~ 1,~ \beta = 3,~ k= 0.5 \) and \(x=1,~~0\le t\le 1\). Figure 5b displays the 3D graph of the exact solutions \(\phi (x, t)\) with parametric values \(\beta = 5,~k= 0.5\) and \(-1\le x\le 1,~ 0\le t\le 1\). Figures 6a–6d show the 3D plot of the semi-analytical solutions for different values of parameters and fractional order \(\alpha \). Figure 7 shows the 2D plot for the solution representing a wave profile for different values of parameters and fractional order \(\alpha \) where \(\alpha = 0.25,~ 0.50,~ 0.75,~ 1 \) and \(x=1,~~0\le t\le 1\). Figures 8a–8d show the 3D plot of the semi-analytical solutions for different values of parameters and fractional order \(\alpha \).

In the present work, FHPTM covers a wide range of semi-analytic solutions of fractional-order Kuramoto–Sivashinsky equation, which were not described earlier in the literature. The obtained solutions exhibit richer dynamical behaviour due to the presence of arbitrary parameters. With respect to the time and space variables, the dynamic behaviour of the provided solutions is explained by the appropriate selection of arbitrary parameters and range space.

6 Conclusion and applications

In this paper, we apply the fractional homotopy perturbation transform method (FHPTM) to deliver an effective semi-analytical technique for determining fractional-order Kuramoto–Sivashinsky equations. The technique combines the Laplace transform with the Caputo–Fabrizio fractional derivative (CFFD) of order \(\alpha \) where \(\alpha \in (0, 1]\). We can discover the classical solution to the above models’ four alternative initial circumstances. We found some new semi-analytical solutions of the fractional-order KSEs. The KS equation is known to exhibit various bifurcation phenomena, where the behaviour of solutions changes qualitatively as parameters such as  \(\beta , k\) and \(\lambda \) are varied. In certain parameter regimes, the KS equation supports soliton solutions. Solitons are stable, localised wave packets that can propagate through the system without changing their shape. The KSE serves as a fundamental model for exploring the intricate dynamics of spatially extended systems. Its rich behaviour, including pattern formation, turbulence and chaos, makes it a valuable tool for researchers studying nonlinear phenomena in physics and engineering.

The KSE has a number of applications in various fields, including:

  • Combustion: The equation has been used to study the behaviour of flame fronts in combustion processes, including combustion-generated turbulence and the formation of cellular patterns in flames.

  • Fluid mechanics: The equation is used to study the dynamics of fluid interfaces, including the formation of turbulence in shear flows and the evolution of thin liquid films.

  • Material science: The equation has been used to study the behaviour of solid–liquid interfaces in the growth of dendritic structures and the formation of patterns in phase-separation processes.

  • Nonlinear dynamics: The equation is important for understanding the basic principles of pattern formation, turbulence and chaos and is used in the study of nonlinear dynamics and chaotic systems.

  • Numerical methods: In addition, the equation is used to test and develop numerical methods for solving partial differential equations, such as finite difference and spectral methods.

These applications highlight the versatility and broad applicability of the KSE, which has proven to be a valuable tool for studying a wide range of complex phenomena.