Introduction

The study of non-linear PDEs exhibit a great variety of non-linear phenomena, arise in various fields such as astrophysics, fluid mechanics, plasma physics, condensed matter physics, solid-state physics, etc. Therefore, finding analytical (exact) or numerical solutions for the system of non-linear PDEs related to the physical phenomena in fluid physics and general relativity, etc., are of great importance for the physical insight. Various model equations have been solved by the numerical methods such as, Sedov [1] and Carrus et al. [2] obtained the numerical solutions for adiabatic flow in a gravitating gas, independently. The self-similarity solution for the propagation of shock wave in the presence or absence of gravitational effects with radiation heat flux and heat conduction was obtained by Vishwakarma and Singh [3]. The similarity solution for flow behind a magnetogasdynamics (MGD) shock wave in a gravitating gas driven by a moving piston was discussed in [4]. The propagation of MGD shock wave in a self-gravitating gas in the case of exponential law shock path have been studied in [5, 6].

In general, determining the exact solution of non-linear equations especially the system of non-linear PDEs is a very difficult task, and only in some appropriate cases, one can get the solution explicitly [7, 8]. Moreover, the study of propagation of shallow-water waves and optical fibers, nonlinear and super-nonlinear traveling waves, solitons, shock waves, etc., have experienced over the past decades. Ivanova [9] has been determined all classes of solutions using Lie symmetry analysis of 2-D Burgers equation with variable-coefficient. The obtained solution can be employed for modeling the formation and decay of non-planar shock waves.

In the literature, there are different methods for studying and finding the solutions of linear or non-linear PDEs, but only in precise cases, it is possible to find the solutions. Lie group theoretic method, developed by Sophus Lie pioneered, one of the systematic methods for obtaining the class of solutions for systems of non-linear PDEs. The application of Lie group theoretic method, for study non-linear models, is one of the effective methods that answer the difficult problem developed in the past few years described in the papers [10,11,12,13,14]. Lie symmetry analysis is used to obtain a similarity variable and transformation of the flow variables, that converted the set of PDEs into ODEs, which are generally non-linear. There are some particular cases, in which we have to solve these ODEs. However, in most of the cases, the differential equations are solved by numerical methods.

Donato [15] has studied the similarity analysis and non-linear wave propagation. In [15] author has reduced a quasi linear hyperbolic systems of PDEs in conservative form into autonomous form using the stretching group of transformation under suitable conditions. Torrisi [16] has obtained the similarity solutions for wave propagation in polytropic gas. In [16] the Lie group analysis is used to reduce the governing equations in autonomous form and the exact solution of the ZND (Zel’dovic, Von Newmann, Doering) model for detonation wave has been also obtained. Donato and Oliveri [17] have reduced the set of equations like Eqs. (1)–(5) of our considered problem under the suitable conditions to autonomous form using Lie group analysis and by introducing canonical variables and obtained the exact solutions of axis-symmetric magnetohydrodynamic (MHD) equations. Using substitution principles and Lie group analysis Oliveri and Speciale [18, 19] have applied the different approach to study the unsteady equations of ideal gas and ideal magnetogasdynamic equations.

Bira and Sekhar [20] obtained the exact solutions of the isentropic magnetogasdynamic problem using Lie group analysis. The exact similarity solution using the product solution of progressive wave (Mc Vittie [21]), for MHD shock wave in a non-ideal gas with radiation pressure, radiation energy and radiation heat flux under the gravitational field in spherical geometry was discussed in [22]. Recently, Liu and Zhang [23] have been obtained the exact solutions using group theoretic method for coupled four systems of non-linear PDEs which have many real-life applications. In real physical problems, they have presented the point symmetries of the system and based on the system reductions exact solutions are discussed in detail. They have reduced exact solutions in terms of the power series forms (using power series method) and the infinite-dimensional vector field. Some other important works related to group theoretic method can be found in [24,25,26].

In all of the works, mentioned above, the exact as well as numerical solutions using the group symmetric analysis for the propagation of shock wave with axial magnetic field in a self-gravitating medium has not been studied as known to us, whereas the given model has various applications in many areas as, astrophysics, space science, plasma physics, nuclear physics, etc. The solutions might be a significant role in the study of \(\gamma \)- ray burst, the central part of star-burst galaxies, solar winds, cloud-cloud collisions, supernova explosions, etc.

The main objective of this study is, to obtain the exact solutions as well as numerical solution using the Lie group analysis for 1-D unsteady cylindrical shock wave propagation in a self-gravitating ideal gas, subject to the axial magnetic field. Lie group analysis is used for constructing the similarity variables and similarity transformations for the flow variables which convert the set of PDEs into ODEs with the unknown function of the similarity variable. The exact solutions are obtained in three particular cases and numerical solutions in two cases. The set of PDEs are reduced into set of ODEs and these ODEs can be solved numerically. The cases with exponential law and power law shock paths, in which numerical solutions are possible. This is the main advantage of group theoretic method that we can obtained the numerical solutions in more number of cases, whereas the method of dimensionality provides the numerical solution in only one case. In our works, the numerical solution for shock wave propagation in a cylindrical geometry with shock path varying as power law are worked out in detail using forth order Runge-Kutta method. The effect of physical parameters such as, gravitational parameter, magnetic field strength and adiabatic index on the shock strength and on the flow-fields are discussed. Solutions of gravitating and non-gravitating cases are also compared with each other.

Model Equations

The model equations for 1-D, unsteady cylindrical symmetric flow of a self-gravitating gas in which an axial magnetic field is permeated can be expressed as [3,4,5, 27]

$$\begin{aligned}&\dfrac{\partial \rho }{\partial t} + \dfrac{\partial (u\rho )}{\partial r} = -\dfrac{\rho u }{ r}, \end{aligned}$$
(1)
$$\begin{aligned}&\dfrac{\partial u}{\partial t} + u \dfrac{\partial u}{\partial r} +\dfrac{1}{\rho }\left[ \mu h \dfrac{\partial h}{\partial r} + \dfrac{\partial p}{\partial r}\right] = - \dfrac{Gm}{r}, \end{aligned}$$
(2)
$$\begin{aligned}&\dfrac{\partial p}{\partial t} + u \dfrac{\partial p}{\partial r} + \dfrac{\gamma p}{r}\dfrac{\partial (u r)}{\partial r} = 0, \end{aligned}$$
(3)
$$\begin{aligned}&\dfrac{\partial h}{\partial t} +\dfrac{\partial (uh) }{\partial r} = -\dfrac{u h }{ r}, \end{aligned}$$
(4)
$$\begin{aligned}&\dfrac{\partial m}{\partial r} -2\pi \rho r=0, \end{aligned}$$
(5)

where r is space coordinate and t is time coordinate; \( \rho \) the density, p the pressure, u the velocity, h the axial magnetic field, m the mass and \(\mu \) the magnetic permeability.

The equation of state for perfect gas is taken to be

$$\begin{aligned} p= R \rho T \quad and \quad e_m = \frac{p}{\rho (\gamma -1)}, \end{aligned}$$
(6)

where (\( e_m\)) is internal energy per unit mass; R is the universal gas constant and T is temperature.

Let us consider that the position of shock wave is \(r= R(t)\), propagating with the speed \(V = \dfrac{dR}{dt}\) into a medium described as

$$\begin{aligned} u= 0, \quad \rho = \rho _{1}(r), \quad p = p_{1}(r) , \quad h= h_{1}(r), \quad m = m_{1}(r), \end{aligned}$$
(7)

here the subscript ‘1’ refers the condition just in front of the shock.

The jump conditions, across the shock front at the MGD shock wave are derived by taking laws of conservation of momentum, mass and energy [4, 6], namely,

$$\begin{aligned}&\rho _{1} V = \rho _{2} (V - u_{2}), \nonumber \\&h_{1}V = h_{2} (V- u_{2}), \nonumber \\&p_{1} + \dfrac{1}{2} \mu h_{1}^{2} + \rho _{1} V^{2} = p_{2} + \dfrac{1}{2} \mu h_{2}^{2} + \rho _{2} (V - u_{2})^{2}, \nonumber \\&e_{m_{1}} + \dfrac{p_{1}}{\rho _{1}}+ \dfrac{1}{2} V^{2} + \dfrac{\mu h_{1}^{2}}{\rho _{1}} = e_{m_{2}} + \dfrac{p_{2}}{\rho _{2}}+ \dfrac{1}{2} (V - u_{2})^{2} + \dfrac{\mu h_{2}^{2}}{\rho _{2}},\nonumber \\&m_{1} = m_{2}, \end{aligned}$$
(8)

where the subscript ‘2’ represents the conditions just behind the shock front.

If, the shock wave is strong, then \(p\approx 0,\; e_{m_{1}}\approx 0\). From Eq. (8), shock conditions reduced to conditions for strong shock as

$$\begin{aligned} \rho _{2}&= \dfrac{\rho _{1}}{\beta }, \nonumber \\ u_{2}&= (1 - \beta )V, \nonumber \\ p_{2}&= \left[ (1 - \beta ) + \frac{M_{a}^{-2}}{2} \left( 1 - \dfrac{1}{\beta ^{2}} \right) \right] \rho _{1} V^{2}, \nonumber \\ h_{2}&= \dfrac{h_{1}}{\beta },\nonumber \\ m_{2}&= m_{1}, \end{aligned}$$
(9)

where \( M_{a} = \left( \dfrac{\rho _{1} V^{2}}{\mu h_{1}^{2}}\right) ^{\frac{1}{2}} \) is the Alfven-Mach number.

The expression of density ratio \(\beta \) \((0<\beta < 1)\) is derived by solving the equation given below

$$\begin{aligned} \beta ^{2} -\dfrac{\beta }{(\gamma +1)} \left[ \gamma \left( \dfrac{1}{M_{a}^{2}} +1\right) - 1 \right] + \left( \dfrac{\gamma - 2}{\gamma +1}\right) \dfrac{1}{M_{a}^{2}} = 0. \end{aligned}$$
(10)

Similarity Analysis

To find the similarity solution, Let, consider one parameter group under which the set of Eqs. (1)–(5) are invariant (see [11, 13]):

$$\begin{aligned} \left. \begin{aligned} {\tilde{r}} = r+ \epsilon \chi +O(\epsilon ^{2}), \quad {\tilde{t}}&= t+ \epsilon \psi +O(\epsilon ^{2}), \quad {\tilde{\rho }} = \rho + \epsilon \Omega +O(\epsilon ^{2}), \quad {\tilde{u}} = u+ \epsilon U +O(\epsilon ^{2}), \\ {\tilde{p}}= p + \epsilon P+O(\epsilon ^{2}),\quad {\tilde{m}}&= m+ \epsilon F+O(\epsilon ^{2}),\quad {\tilde{h}}= h + \epsilon \Pi +O(\epsilon ^{2}), \end{aligned}\right. \end{aligned}$$
(11)

where the generators \(\psi , \chi ,\; \;U, \;\Omega , \; \Pi , \; F \) and P are the function of \(r,\; t,\; u,\;\rho , \; h,\; m\) and p resp. The entity \(\epsilon \) is a small parameter. If, it is possible to find such a group permits us to reduce the number of independent variables in the problem by one, thereby the set of PDEs (1)–(5) transformed into a set of ODEs. Now, consider \(r_1 =t,\; r_2=r,\; v_1 =\rho ,\; v_2= u,\; v_3 =p,\; v_4=h, \;v_5= m\) and \(p_j^i=\partial {v_i}/\partial {r_j}\), where \(i= 1 \;to\; 5 \) and \(j = 1,2\). Using summation convention, the set of Eqs. (1)–(5) can be written as

$$\begin{aligned} H_k(r_j, \; v_i, \; p_{j}^{i})=0 \quad ( k=1\; to\; 5), \end{aligned}$$

under the group of transformation (11) the system given above is conformally invariant, if there exist constants \(\sigma _{ks}\;( s,\;k= 1 \;to\; 5)\) s. t. for all smooth surfaces, \(v_i=v_i(r_j)\), we have

$$\begin{aligned} \mathcal {L}H_k=\sigma _{ks}H_s, \end{aligned}$$
(12)

where the Lie derivative \(\mathcal {L}\) is defined as

$$\begin{aligned} \mathcal {L} = \xi _{r}^{j}\dfrac{\partial }{\partial {r_j}} + \xi _{v}^{i}\dfrac{\partial }{\partial {v_i}}+ \xi _{p_{j}}^{i}\dfrac{\partial }{\partial {p_{j}^{i}}}, \end{aligned}$$
(13)

with \( \xi _{r}^{1}= \psi \), \( \xi _{r}^{2} = \chi \), \( \xi _{v}^{1}= \Omega \), \(\xi _{v}^{2}= U \), \(\xi _{v}^{3}= P\), \( \xi _{v}^{4}= \Pi \), \(\xi _{v}^{5}= F \) and the generators of the derivative transformations is given by

$$\begin{aligned} \xi _{p_{j}}^{i}= \dfrac{\partial \xi _{v}^{i}}{\partial {r_j}} + \dfrac{\partial \xi _{v}^{i}}{\partial {v_k}}p_{j}^{k} - \dfrac{\partial \xi _{r}^{l}}{\partial {r_j}}p_{l}^{i} - \dfrac{\partial \xi _{r}^{l}}{\partial {v_n}}p_{l}^{i}\;p_{j}^{n} \quad (n= 1\; to \; 5, \; l= 1,2 ), \end{aligned}$$
(14)

Using Eq. (13) in Eq. (12), we have

$$\begin{aligned} \dfrac{\partial H_{k}}{\partial {r_j}}\xi _{r}^{j} + \dfrac{\partial H_{k}}{\partial {v_i}}\xi _{v}^{i} + \dfrac{\partial H_{k}}{\partial {p_j^{i}}}\xi _{p_{j}}^{i}= \sigma _{ks}H_s \quad ( k= 1,\; 2,..., 5 \quad and \quad s= 1,\; 2,..., 5). \end{aligned}$$
(15)

Substitution of \(\xi _{p_j}^{i}\) from Eq. (14) into the Eq. (15) gives a polynomial in \(p_{j}^{i}\). Equating the coefficients of \(p_{j}^{i}\) and \(p_{j}^{i}p_{l}^{k}\) both sides give the linear first-order system of PDEs in term of generators. The obtained equations, is the set of over-determining equations of the invariance group which can be solved to get the invariance group (11). If the above procedure is implemented for Eqs. (1)–(5), yield the set of over-determining equations. We find the generators of the group transformations by solving the obtained set of over-determining equations:

$$\begin{aligned}&\psi = b+at, \quad \chi = (2a+\sigma _{22})r , \quad \Omega = -2a\rho , \quad U = (a+\sigma _{22})u, \nonumber \\&P= 2\sigma _{22}p, \quad \Pi = \sigma _{22}h, \quad F = 2(\sigma _{22}+a)m, \end{aligned}$$
(16)

where \(\sigma _{22}\), a and b are arbitrary constants.

The Eq. (16) for infinitesimal generators admits a 3-dimensional Lie algebra with the following generators:

$$\begin{aligned}&Z_{1}= 2r\dfrac{\partial }{\partial r}+ t\dfrac{\partial }{\partial t} -2\rho \dfrac{\partial }{\partial \rho } +u\dfrac{\partial }{\partial u}+ 2m\dfrac{\partial }{\partial m}, \quad Z_2= r\dfrac{\partial }{\partial r} +u\dfrac{\partial }{\partial u}+2p\dfrac{\partial }{\partial p}+h\dfrac{\partial }{\partial h} + 2m\dfrac{\partial }{\partial m},\nonumber \\&Z_3= \dfrac{\partial }{\partial t}. \end{aligned}$$
(17)

Symmetries and the Optimal System

In this section, we investigated the optimal system of equations of motion with the aid of the method as discussed in [28, 29]. The commutation relations of Lie algebra determined by \(Z_\alpha ,\; \alpha = 1,\; 2,\; 3\) are depicted in Table 1. It is obvious that \(Z_\alpha \) is closed under the Lie bracket.

Table 1 Commutator Table
Full size table

where the entry \(\alpha \) is used for row and \(\tau \) are coloum. Therefore, we have

$$\begin{aligned} {[}Z_\alpha ,\;Z_\tau ]= Z_{\alpha }Z_{\tau }-Z_{\tau } Z_{\alpha }. \end{aligned}$$
(18)

Furthermore, we can compute the adjoint representations of the vector fields. With the help of the Lie series, we constructed adjoint representation in Table 2 as given below

$$\begin{aligned} Ad \exp (\epsilon _\alpha Z_\alpha )Z_\tau = Z_\tau -\epsilon _\alpha [Z_\alpha ,\;Z_\tau ] +\dfrac{\epsilon _{\alpha }^2}{2}[Z_\alpha ,\;[Z_\alpha ,\;Z_\tau ]], \end{aligned}$$
(19)

where \(\epsilon _\alpha \) is arbitrary constant and \(\alpha ,\;\tau =1,\;2,\;3\).

Table 2 Adjoint Table
Full size table

By using the Table 2 as given above, we obtain the adjoint matrix A by applying the adjoint actions of \(Z_1\), \(Z_2\) and \(Z_3\) to general element Z which is given as

$$\begin{aligned} Z= a_{1}Z_1 +a_{2}Z_2 +a_{3}Z_3, \end{aligned}$$
(20)

where \(a_1=a,\; a_2=\sigma _{22},\; a_3=b \).

$$\begin{aligned}&Ad \exp (\epsilon _1 Z_1)(a_{1}Z_1 +a_{2}Z_2 +a_{3}Z_3)\nonumber \\&\quad = a_{1} Ad \exp (\epsilon _1 Z_1)Z_1 +a_{2} Ad \exp (\epsilon _1 Z_1)Z_2 +a_{3} Ad \exp (\epsilon _1 Z_1)Z_3\nonumber \\&\quad = a_{1}Z_{1}+a_{2}Z_{2} +e^{\epsilon _{1}} Z_3\nonumber \\&\quad =(a_1,\;a_2,\;a_3) \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0\\ 0&{}0&{}e^{\epsilon _1} \end{array} \right) \left( \begin{array}{c} Z_1 \\ Z_2 \\ Z_3\end{array} \right) . \end{aligned}$$
(21)

The above equation is written as

$$\begin{aligned} Ad \exp (\epsilon _1 Z_1)(a_{1}Z_1 +a_{2}Z_2 +a_{3}Z_3)&= (a_1,\;a_2,\;a_3)A_{1}( Z_1,\; Z_2,\; Z_3 )^T, \end{aligned}$$
(22)

superscript T denotes the transpose of matrix.

$$\begin{aligned}&\text{ where }\quad A_1= \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0\\ 0&{}0&{}e^{\epsilon _1} \end{array} \right) . \end{aligned}$$
(23)
$$\begin{aligned}&Ad \exp (\epsilon _2 Z_2)(a_{1}Z_1 +a_{2}Z_2 +a_{3}Z_3) \nonumber \\&\quad = a_{1} Ad \exp (\epsilon _2 Z_2)Z_1 +a_{2} Ad \exp (\epsilon _2 Z_2)Z_2 +a_{3} Ad \exp (\epsilon _2 Z_2)Z_3\nonumber \\&\quad = a_{1}Z_{1}+a_{2}Z_{2} +e^{\epsilon _{1}} Z_3\nonumber \\&\quad =(a_1,\;a_2,\;a_3) \left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0\\ 0&{}0&{}1 \end{array} \right) \left( \begin{array}{c} Z_1 \\ Z_2 \\ Z_3\end{array} \right) , \end{aligned}$$
(24)
$$\begin{aligned}&\text{ where }\quad A_2 =\left( \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0\\ 0&{}0&{}1 \end{array} \right) . \end{aligned}$$
(25)
$$\begin{aligned}&Ad \exp (\epsilon _3 Z_3)(a_{1}Z_1 +a_{2}Z_2 +a_{3}Z_3) \nonumber \\&\quad = a_{1} Ad \exp (\epsilon _3 Z_3)Z_1 +a_{2} Ad \exp (\epsilon _1 Z_1)Z_2 +a_{3} Ad \exp (\epsilon _1 Z_1)Z_3\nonumber \\&a_{1}(Z_{1}-\epsilon _{3}Z_3)+a_{2}Z_{2} +e^{\epsilon _{1}} Z_3\nonumber \\&\quad =(a_1,\;a_2,\;a_3) \left( \begin{array}{ccc} 1 &{} 0 &{} -\epsilon _{3} \\ 0 &{} 1 &{} 0\\ 0&{}0&{}1 \end{array} \right) \left( \begin{array}{c} Z_1 \\ Z_2 \\ Z_3\end{array} \right) , \end{aligned}$$
(26)
$$\begin{aligned}&\text{ where }\quad A_3 = \left( \begin{array}{ccc} 1 &{} 0 &{} -\epsilon _{3} \\ 0 &{} 1 &{} 0\\ 0&{}0&{}1 \end{array} \right) . \end{aligned}$$
(27)

Thus, by using Eqs. (23), (25) and (27), we obtain the general adjoint transformation matrix A as

$$\begin{aligned} A= A_1A_2A_3 = \left( \begin{array}{ccc} 1 &{} 0 &{} -\epsilon _{3} \\ 0 &{} 1 &{} 0\\ 0&{}0&{}e^{\epsilon _{1}} \end{array} \right) . \end{aligned}$$
(28)

To obtain the optimal system ( see [28] ) , we have

$$\begin{aligned} \dfrac{1}{a}A (\alpha _1,\; \alpha _{2},\;\alpha _{3})^{T}&= (\beta _1,\; \beta _{2},\;\beta _{3})^{T}\nonumber \\&\text{ or }\nonumber \\ \dfrac{1}{a}\left( \begin{array}{c} \alpha _{1}-\epsilon _{3}\alpha _3 \\ \alpha _2 \\ e^{\epsilon _1}\alpha _{3}\end{array} \right)&= \left( \begin{array}{c} \beta _1 \\ \beta _2 \\ \beta _3\end{array} \right) , \end{aligned}$$
(29)

where \(a\ne 0\), \(\beta = (\beta _1,\; \beta _{2},\;\beta _{3}) \rightarrow (a_1,\; a_{2},\;a_{3})\).

Now, using Eq. (29), one can start to construct the optimal system, we have the following different cases:

  • Case (i) when \(\alpha _1 \ne 0,\; \alpha _2=0,\; \alpha _3=0\), then by choosing \(\alpha _1= a\), we obtain the \(\beta = (1,\;0,\;0)\). Therefore, the generator is \(W_1= Z_1\).

  • Case (ii) when \(\alpha _2 \ne 0,\; \alpha _1=0,\; \alpha _3=0\), then choosing \(\alpha _2= a\), we find the \(\beta = (0,\;1,\;0)\). Therefore, the generator is \(W_2= Z_2\).

  • Case (iii) when \(\alpha _3 \ne 0,\; \alpha _1=0,\; \alpha _2=0\), by choosing \(\epsilon _1= \log \dfrac{aa_{3}}{\alpha _3},\; \epsilon _3=-\frac{aa_{1}}{\alpha _3}\), we find the \(\beta = (a_1,\;0,\;a_3)\). Therefore, the generator is \(W_3= a_1 Z_1+a_3 Z_3\).

  • Case (iv) when \(\alpha _1 \ne 0,\; \alpha _2\ne 0,\; \alpha _3=0\), by choosing \(\alpha _1= aa_{1},\; \alpha =aa_{2}\), we find the \(\beta = (a_1,\;a_2,\;0)\). Therefore, the generator is \(W_4= a_1 Z_1+a_2 Z_2\).

  • Case (v) when \(\alpha _1 \ne 0,\; \alpha _2 = 0,\; \alpha _3 \ne 0\), by choosing \(\epsilon _1= \log \dfrac{a}{\alpha _3},\; \epsilon _3=\frac{\alpha _1}{\alpha _3}\), we find the \(\beta = (0,\;0,\;1)\). Therefore, the generator is \(W_5= Z_3\).

  • Case (vi) when \(\alpha _1 =0,\; \alpha _2 \ne 0,\; \alpha _3 \ne 0\), by choosing \(\epsilon _1= \log \dfrac{aa_{3}}{\alpha _3},\; \epsilon _3=\frac{aa_{1}}{\alpha _3}, \alpha _2=aa_{2}\), we find the \(\beta = (a_1,\;a_2,\;a_3)\). Therefore, the generator is \(W_6= a_1 Z_1+ a_2 Z_2+a_3 Z_3\).

  • Case (vii) when \(\beta _1 =0\), by choosing \(\alpha _1=\epsilon _3\alpha _3,\;\epsilon _1= \log \dfrac{aa_{3}}{\alpha _3},\; \alpha _2=aa_{2}\), we find the \(\beta = (0,\;a_{2},\;a_{3})\). Therefore, the generator is \(W_7= a_2 Z_2+a_3 Z_3\).

Collecting all the representatives from seven cases given above, We have the seven optimal classes as follow \(W_1= Z_1,\;W_2= Z_2,\;W_3= a_1 Z_1+a_3 Z_3,\;W_4= a_1 Z_1+a_2 Z_2,\;W_5= Z_3,\; W_6= a_1 Z_1+ a_2 Z_2+a_3 Z_3,\;W_7= a_2 Z_2+a_3 Z_3\). Out of seven optimal classes \(W_4\), \( W_6\) are same and \(W_1\), \( W_3\) are same because the optimal classes \(W_6\) and \( W_3\),reduces the optimal classes \(W_4\) and \(W_1\) by using translation property respectively. Therefore, the five optimal classes \(W_1, \; W_2,\; W_4,\; W_5\) and \(W_7\) are obtained. The similarity solutions corresponding to the five optimal classes are discussed below:

Similarity Solutions

In order to construct the solution for the system of Eqs (1)–(5), we derive similarity variable and the corresponding the transformation for the flow variables, by which the set of PDEs (1)–(5), are converted into the set of ODEs. Hence, by solving the obtained ODEs, we can predict the shock strength for the shock wave propagation and the nature of flow variables corresponding to different shock path (power law shock path and exponential law shock path). In the present article, we have study the all possible solutions in the following different cases:

\( \mathbf{Case}\;I :\) when infinitesimal generator is \(W_1= \langle Z_1\rangle = \langle 2r\dfrac{\partial }{\partial r}+ t\dfrac{\partial }{\partial t} -2\rho \dfrac{\partial }{\partial \rho } +u\dfrac{\partial }{\partial u}+ 2m\dfrac{\partial }{\partial m}\rangle \) or \(W_3= <a_1 Z_1+a_3 Z_3>= \langle 2ar\dfrac{\partial }{\partial r}+ (at+b)\dfrac{\partial }{\partial t} -2a\rho \dfrac{\partial }{\partial \rho } +au\dfrac{\partial }{\partial u}+ 2am\dfrac{\partial }{\partial m}\rangle \), then by using the shifting property in \(W_3\) for r and t defined by \({\tilde{r}}=r,\;{\tilde{t}}=t +b/a\), does not alter the system of Eqs. (1)–(5). Therefore, \(W_3\) is rewritten in new variables \({\tilde{r}}\) and \({\tilde{t}}\), we obtain \(aW_1\) after dropping the tilde sign.

Therefore, the characteristic equation associated with \(W_3\) or \(W_1\) is

$$\begin{aligned} \dfrac{dt}{2r}= \dfrac{dr}{t}= \dfrac{d\rho }{-2\rho }= \dfrac{du}{u}= \dfrac{dp}{0}= \dfrac{dh}{0}= \dfrac{dm}{2m}. \end{aligned}$$
(30)

Integration of Eq. (30), gives the similarity variable and the dependent variables as

$$\begin{aligned}&\eta = \dfrac{r}{t^{2}}, \quad \rho = t^{-2}\Omega ^{*}(\eta ), \quad u = U^{*}(\eta )t, \quad p = P^{*}(\eta ),\quad h = \Pi ^{*}(\eta ), \quad m = t^{2}F^{*}(\eta ). \end{aligned}$$
(31)

Substitution of Eq. (31) into the PDEs (1)–(5), gives the set of ODEs after dropping the asterisk sign becomes:

$$\begin{aligned}&(U - 2\eta ) \Omega ^{'} -2\Omega + \Omega U^{'}+ \dfrac{\Omega U}{\eta } = 0 , \end{aligned}$$
(32)
$$\begin{aligned}&U + (U - 2 \eta )U^{'} + \dfrac{1}{\Omega } P^{'} + \dfrac{\mu \Pi }{\Omega } \Pi ^{'} + \dfrac{G \;F }{\eta } = 0 , \end{aligned}$$
(33)
$$\begin{aligned}&(U - 2 \eta ) P^{'} + \gamma P U^{'}+ \dfrac{\gamma P U}{\eta } = 0 , \end{aligned}$$
(34)
$$\begin{aligned}&(U - 2 \eta ) \Pi ^{'} + \Pi U^{'}+ \dfrac{\Pi U}{\eta } = 0, \end{aligned}$$
(35)
$$\begin{aligned}&F ^{'} - 2\pi \eta \Omega = 0, \end{aligned}$$
(36)

where prime represents the differentiation w.r.t. eta (\(\eta \)).

By solving the above Eqs. (32)–(36) for \(\gamma =2\), we obtained the solution as given below

$$\begin{aligned}&\Omega = c_1, \quad U = \eta , \quad P= c_{2} \eta ^{4}, \quad \Pi = c_{3} \eta ^{2}, \quad \textit{when}\quad G=0\quad and \quad 2c_{2}+\mu c_{3}^{2}= 0, \end{aligned}$$
(37)

where \(c_{1}, \; c_{2},\; c_{3} \) are constants of integration.

Now using Eq. (31) in equation (37) we obtain the solution of Eqs. (1)–(5) respectively, as follow:

$$\begin{aligned}&\rho =c_{1}t^{-2}, \quad u= \dfrac{r}{t}, \quad p = c_{2}\dfrac{r^{4}}{t^{8}}, \quad h= c_{3}\dfrac{r^{2}}{t^{4}}, \quad \textit{when} \quad G=0\quad and \quad 2c_{2}+\mu c_{3}^{2}= 0. \end{aligned}$$
(38)

\(\mathbf{Case}\;II :\) when infinesimal generator is \(W_5=Z_3=\dfrac{\partial }{\partial t}\), therefore, the similarity variable and the flow variables are obtained as

$$\begin{aligned}&\eta = r, u = U^{*}(\eta ), \quad p = P^{*}(\eta ), \quad h = \Pi ^{*}(\eta ), .\quad \rho = \Omega ^{*}(\eta ),\quad m =F ^{*}(\eta ). \end{aligned}$$
(39)

Substitution of Eq. (39) into the Eqs. (1)–(5), gives the following set of ODEs after dropping the asterisk sign:

$$\begin{aligned}&U \Omega ^{'} + \Omega U^{'}+ \dfrac{\Omega U}{\eta } = 0 , \end{aligned}$$
(40)
$$\begin{aligned}&U U^{'} + \dfrac{1}{\Omega } P^{'} + \dfrac{\mu \Pi }{\Omega } \Pi ^{'} + \dfrac{G \;F }{\eta } = 0 , \end{aligned}$$
(41)
$$\begin{aligned}&U P^{'} + \gamma PU^{'}+ \dfrac{\gamma PU}{\eta } = 0 , \end{aligned}$$
(42)
$$\begin{aligned}&U \Pi ^{'} + \Pi U^{'}+\dfrac{\Pi U}{\eta } = 0, \end{aligned}$$
(43)
$$\begin{aligned}&F ^{'} - 2\pi \eta \Omega = 0. \end{aligned}$$
(44)

By solving the above Eqs. (40)–(44) for \(\gamma =2\) and \(G=0\), we obtained the solution as follow

$$\begin{aligned} \quad&\Omega = \dfrac{c_{4}}{\eta }, \quad U =c_{5}, \quad P= \dfrac{c_{6}}{\eta ^{2}}, \quad \Pi = \dfrac{c_{7}}{\eta }, \end{aligned}$$
(45)

where \(c_{4}\), \(c_{5}\), \(c_{6}\) and \(c_{7}\) are constants of integration with the relation \(2c_{6}+\mu c_{7}^{2}= 0\).

The solution of Eqs. (1)–(5) are obtained using Eqs. (39) and (45), given below:

$$\begin{aligned} \rho = \dfrac{c_{4}}{r}, \quad u= c_{5}, \quad p = \dfrac{c_{6}}{r^{2}}, \quad h= \dfrac{c_{7}}{r},\quad when \quad G=0 \quad and \quad 2c_{6}+\mu c_{7}^{2}= 0. \end{aligned}$$
(46)

\(\mathbf{Case}\;III :\) when infinitesimal generator is \( W_6 = a_1 Z_1+a_2Z_2+a_3Z_3\) or \( W_4 = a_1 Z_1+a_2Z_2\), then the dependent variables are obtained as given below

$$\begin{aligned}&\rho = t^{-2}\Omega ^{*}(\eta ),\quad u = t^{\delta -1}U^{*}(\eta ), \quad p = t^{2(\delta -2)}P^{*}(\eta ),\nonumber \\&h = t^{\delta -2}\Pi ^{*}(\eta ),\quad m = t^{2(\delta -1)}F ^{*}(\eta ), \end{aligned}$$
(47)

where \( \delta = \dfrac{(\sigma _{22}+2a)}{a}\) and the function \(\Omega ^{*}, \; U^{*},\; P^{*},\; \Pi ^{*} \) and \(F ^{*}\) depend only on the similarity variable \(\eta \) given by

$$\begin{aligned} \eta =\dfrac{r}{B t ^{\delta }}. \end{aligned}$$
(48)

where B is a dimensional constant.

The Eqs. (1)–(5), convert the following set of ODEs using Eq. (47), which on dropping the asterisk sign becomes:

$$\begin{aligned}&-2\Omega +(U - \delta \eta )\Omega ^{'} + \Omega U^{'}+ \dfrac{\Omega U}{\eta } = 0 , \end{aligned}$$
(49)
$$\begin{aligned}&(U -\delta \eta )U^{'} +(\delta -1)U + \dfrac{1}{\Omega } P^{'} + \dfrac{\mu \; \Pi }{\Omega } \Pi ^{'} + \dfrac{G\;F }{\eta } = 0 , \end{aligned}$$
(50)
$$\begin{aligned}&2(\delta -2)P + (U - \delta \eta ) P^{'} + \gamma P U^{'}+ \dfrac{\gamma P U}{\eta } = 0 , \end{aligned}$$
(51)
$$\begin{aligned}&(\delta -2) \Pi + (U - \delta \eta ) \Pi ^{'} + \Pi U^{'} + \dfrac{U \Pi }{\eta } = 0, \end{aligned}$$
(52)
$$\begin{aligned}&F ^{'} - 2\pi \eta \Omega = 0, \end{aligned}$$
(53)

The solution of set of Eqs. (1)–(5) are obtained by solving the above set of Eqs. (49)–(53) for \(G=0\) and \(\gamma =2\) and using Eq. (47), we have

$$\begin{aligned}&\rho = \dfrac{c_{8}}{t^2}, .\quad u= \dfrac{r}{t}, \quad p = c_{9}r^{\left( \dfrac{2\delta }{\delta -1}\right) }t^{\left( 2\dfrac{3\delta -2}{1-\delta }\right) }, \quad h= c_{10}r^{\left( \dfrac{\delta }{\delta -1}\right) }t^{\left( \dfrac{3\delta -2}{1-\delta }\right) }. \end{aligned}$$
(54)

Where \(\delta \ne 1\); \(c_{8}\), \(c_{9}\) and \(c_{10}\) are constants of integration and \(c_{9}\) and \(c_{10}\) are satisfy the relation \(2c_{9}+\mu c_{10}^{2}= 0\).

In all cases (I-III) the exact feasible solution of Eqs. (1)–(5) are possible only in non-gravitating case. Therefore, we discuss numerical solutions in non-gravitating and gravitating cases.

Let \(\eta = 1\) be the shock front position, thus, the shock path R(t) and the shock velocity V are given by

$$\begin{aligned} R = Bt ^{\delta }, \quad V= \dfrac{dR}{dt} = \delta B t ^{\delta -1}. \end{aligned}$$
(55)

The shock conditions at \(\eta = 1\), are given below

$$\begin{aligned}&\rho \vert _{\eta =1} =\Omega ^{*}(1) t^{-2},\quad u\vert _{\eta =1} =t^{\delta -1} U^{*}(1),\quad p \vert _{\eta =1}= P^{*}(1)t^{2(\delta -2)},\nonumber \\&h\vert _{\eta =1} = t^{\delta -2} \Pi ^{*}(1),\quad m \vert _{\eta =1}= F ^{*}(1)t^{2(\delta -1)}. \end{aligned}$$
(56)

In view of Eq. (7), suggest the following form of flow variables just in front of the shock are

$$\begin{aligned} \rho _{1}= \rho ^{*}R^{\theta },\quad h_{1} = h^{*}R^{\lambda }, \quad m_{1} = \dfrac{2\pi \rho ^{*}}{(\theta +2)}R^{(\theta +2)}, \end{aligned}$$
(57)

where \(h^{*},\; \rho ^{*}\) are dimensional constants and \(\lambda , \; \theta \) are arbitrary constants.

From Eqs. (55) and (57), we obtain

$$\begin{aligned} M_{a}^{2} = \dfrac{\rho _{1}V^{2}}{\mu h_{1}^{2}} = \dfrac{\rho ^{*}\delta ^{2}B^{(\theta +2-2\lambda \delta )}}{\mu h^{*{2}}}t^{\delta \theta +2(\delta -1)-2\delta \lambda }, \end{aligned}$$
(58)

For existence of similarity solutions the \(M_{a}^{2}\) should be constant, therefore,

$$\begin{aligned} \theta \delta +2( \delta -1)= 2\lambda \delta . \end{aligned}$$
(59)

In view of invariance of jump condition (9), the condition on \(\Omega ^{*}, \; U^{*},\; P^{*},\; F^{*} \) and \(\Pi ^{*}\) at \(\eta = 1\), are obtained from Eqs. (55)–(58) are

$$\begin{aligned}&\Omega ^{*}(1)= \dfrac{B^{\theta } \rho ^{*}}{\beta }, U^{*}(1)= \delta (\beta -1) B,\nonumber \\&P^{*}(1)= \left[ \frac{M_{a}^{-2}}{2} \left( 1 - \dfrac{1}{\beta ^{2}} \right) + (1 - \beta ) \right] \rho ^{*} \delta ^{2}B^{\theta +2},\nonumber \\&\Pi ^{*}(1)= \dfrac{1}{\beta M_{a}}\left( \dfrac{\rho ^{*}\delta ^{2}B^{\theta +2}}{\mu }\right) ^{1/2},\quad F ^{*}(1)= \dfrac{2\pi \rho ^{*}{B}^{\theta +2}}{(\theta +2)}. \end{aligned}$$
(60)

where \( \delta \;\theta +2=0\) is required to derive the similarity solution.

Using Eqs. (55), (57) and (58), Eq. (47) can be rewritten as

$$\begin{aligned} \rho = \rho _{1} {\widehat{\Omega }}(\eta ), \quad u = V {\widehat{U}}(\eta ), \quad p = \rho _{1} V^{2} {\widehat{P}}(\eta ), \quad h \sqrt{\mu } = \sqrt{\rho _{1}} V {\widehat{\Pi }}(\eta ), \quad m= m_{1}{\widehat{F}}(\eta ), \end{aligned}$$
(61)

where

$$\begin{aligned}&{\widehat{\Omega }}(\eta )= \dfrac{\Omega ^{*}}{\rho ^{*}{B}^{\theta }}(\eta ),\quad {\widehat{U}}(\eta )= \dfrac{1}{B\delta }U^{*}(\eta ),\quad {\widehat{P}}(\eta )= \dfrac{1}{\delta ^{2} \rho ^{*}B^{\theta +2}}P^{*}(\eta ), \nonumber \\&{\widehat{\Pi }}(\eta )= \dfrac{\Pi ^{*}(\eta )}{B \delta }\left( \dfrac{\mu }{\rho ^{*}B^{\theta }}\right) ^{1/2}, \quad {\widehat{F}}(\eta )= \dfrac{(\theta +2) F ^{*}(\eta )}{2\pi \rho ^{*}{B}^{\theta +2}}. \end{aligned}$$
(62)

The set of Eqs. (1)–(5) are changed into ODEs using Eq. (61), which on dropping the hat sign becomes:

$$\begin{aligned}&\theta \Omega +(U - \eta )\Omega ^{'} + \Omega U^{'}+ \dfrac{\Omega U}{\eta } = 0 , \end{aligned}$$
(63)
$$\begin{aligned}&(U - \eta )U^{'} + \dfrac{(\delta -1)}{\delta }U+ \dfrac{P^{'}}{\Omega } + \dfrac{ \Pi \; \Pi ^{'}}{\Omega } + \dfrac{g\;F}{\eta \delta ^{2}(\theta +2)} = 0 , \end{aligned}$$
(64)
$$\begin{aligned}&\left( \theta + \dfrac{2(\delta -1)}{\delta }\right) P + (U - \eta ) P^{'} + \gamma P U^{'}+ \dfrac{\gamma PU}{\eta } = 0 , \end{aligned}$$
(65)
$$\begin{aligned}&\left( \dfrac{(\delta -1)+}{\delta }+ \dfrac{\theta }{2} \right) \Pi + (U - \eta ) \Pi ^{'} + \Pi U^{'} + \dfrac{\Pi U}{\eta } = 0, \end{aligned}$$
(66)
$$\begin{aligned}&F ^{'} - (\theta +2)\eta \Omega = 0, \end{aligned}$$
(67)

where \(g= 2\pi \rho ^{*}G B^{\theta }\) is taken as the gravitational parameter.

The shock jump conditions are obtained using Eqs. (60) and (62) which becomes after dropping the hat sign

$$\begin{aligned}&\Omega (1)= \dfrac{1}{\beta },\quad U(1)= (1- \beta ),\nonumber \\&P(1)= \left[ \frac{1}{2M_{a}^{2}} \left( 1 - \dfrac{1}{\beta ^{2}} \right) +(1 - \beta ) \right] ,\nonumber \\&\Pi (1)= \dfrac{1}{M_{a}\;\beta },\quad F(1)= 1. \end{aligned}$$
(68)

The flow variables are normalized with their respective values at the shock, as

$$\begin{aligned} \dfrac{\rho }{\rho _2} = \dfrac{\Omega (\eta )}{\Omega (1)}, \quad \dfrac{u}{u_2} = \dfrac{U(\eta )}{U(1)},\quad \dfrac{h}{h_2} = \dfrac{\Pi (\eta )}{\Pi (1)}, \quad \dfrac{p}{p_2} = \dfrac{P(\eta )}{P(1)}, \quad \dfrac{m}{m_2} = \dfrac{F(\eta )}{F(1)}. \end{aligned}$$
(69)

The numerical solution of Eqs. (63)–(68) with boundary conditions (68) are obtained in Sect. 6 and results are shown in Figs. 1a–e and  2.

\(\mathbf{Case}\;IV :\) when the infinitesimal generator is \(W_7= a_2Z_2+a_3Z_3\) then the dependent variables and similarity variable are obtained in the form given below

$$\begin{aligned} u = e^{\delta t}U^{*}(\eta ), \quad \rho = \Omega ^{*}(\eta ), \quad h = e^{\delta t}\Pi ^{*}(\eta ), \quad p = e^{2\delta t}P^{*}(\eta ), \quad m = e^{2\delta t}F ^{*}(\eta ), \quad \eta =\dfrac{ r }{Ae^{\delta t}}, \end{aligned}$$
(70)

where \(\delta = \dfrac{\sigma _{22}}{b}\); A is the dimensional constant.

The shock path R(t) and the shock velocity V in this case are

$$\begin{aligned} R(t)= Ae^{\delta t}, \quad V = \delta R, \end{aligned}$$
(71)

Therefore, flow variables just in front the shock are taken in the form

$$\begin{aligned} \rho _{1}= \rho ^{*}e^{\theta t},\quad h_{1}= h^{*}e^{\lambda t}, \quad m_{1}= \dfrac{2\pi A^{2} \delta \rho ^{*}}{(\theta +2\delta )} e^{(\theta +2\delta )t}. \end{aligned}$$
(72)

For existence of solutions, \(M_{a}\) should be constant, therefore,

$$\begin{aligned} \theta +2 \delta = 2\lambda . \end{aligned}$$
(73)

The shock jump conditions at \(\eta = 1\) are obtained using Eqs. (70)–(73) as

$$\begin{aligned}&\Omega ^{*}(1)= \dfrac{\rho ^{*}}{\beta },\quad U^{*}(1)= \delta (1- \beta ) A,\nonumber \\&P^{*}(1)= \rho ^{*}A^{2}\delta ^{2}\left[ \frac{1}{2M_{a}^{2}} \left( 1 - \dfrac{1}{\beta ^{2}} \right) + (1 - \beta )\right] ,\nonumber \\&\Pi ^{*}(1)= \dfrac{1}{\beta }\left( \dfrac{\rho ^{*}\delta ^{2}A^{2}}{\mu M_{a}^{2}}\right) ^{1/2},\quad F ^{*}(1)= \dfrac{2\pi A^{2}\delta \rho ^{*}}{(\theta +2\delta )}, \end{aligned}$$
(74)

with \(\theta =0\).

From Eqs. (70)–(72), the transformations are in the form

$$\begin{aligned} \rho = \rho _{1} {\widehat{\Omega }}(\eta ), \quad u = V {\widehat{U}}(\eta ), \quad p = \rho _{1} V^{2} {\widehat{P}}(\eta ), \quad h \sqrt{\mu } = \sqrt{\rho _{1}} V {\widehat{\Pi }}(\eta ), \quad m= m_{1}{\widehat{F}}(\eta ), \end{aligned}$$
(75)

where

$$\begin{aligned}&{\widehat{\Omega }}(\eta )= \dfrac{1}{\rho ^{*}}\Omega ^{*}(\eta ), \quad {\widehat{U}}(\eta )= \dfrac{1}{\delta A}U^{*}(\eta ), \quad {\widehat{P}}(\eta )= \dfrac{1}{\delta ^{2} \rho ^{*}A^{2}}P^{*}(\eta ), \nonumber \\&{\widehat{\Pi }}(\eta )= \dfrac{\sqrt{\mu }\Pi ^{*}(\eta )}{\delta A \sqrt{\rho ^{*}}}, \quad {\widehat{F}}(\eta )= \dfrac{ (\theta +2\delta ) F ^{*}(\eta )}{2\pi A^{2}\delta \rho ^{*}}. \end{aligned}$$
(76)

Using Eq. (75), the fundamental equations of motion (1)–(5) are converted into the set of ODEs, after dropping the hat sign becomes:

$$\begin{aligned}&(U - \eta )\Omega ^{'} + \Omega U^{'} + \dfrac{\Omega U}{\eta } = 0, \end{aligned}$$
(77)
$$\begin{aligned}&(U - \eta )U^{'} + U + \dfrac{P^{'}}{\Omega } + \dfrac{ \Pi \Pi ^{'}}{\Omega } + \dfrac{g_{1} F }{\eta \delta ^{2}} = 0, \end{aligned}$$
(78)
$$\begin{aligned}&2 P + (U - \eta ) P^{'} + \gamma PU^{'}+ \dfrac{\gamma PU}{\eta } = 0, \end{aligned}$$
(79)
$$\begin{aligned}&(U - \eta ) \Pi ^{'}+ \Pi + U^{'}\Pi + \dfrac{U \Pi }{\eta } = 0, \end{aligned}$$
(80)
$$\begin{aligned}&F ^{'} - 2\delta \eta \Omega = 0, \end{aligned}$$
(81)

where \(g_{1}= \pi \rho ^{\star }G\) is considered as the gravitational parameter.

In this case, we are not able to obtain the feasible exact solution for any value of \(\gamma \); whereas the numerical solution exist for any value of \(\gamma \). Thus, in the present case, set of ODEs (77)–(81), under the jump conditions (68) can be solved numerically to discuss the behavior of the flow variables.

\(\mathbf{Case}\;V :\) when the infinitesimal generator is \(W_2= Z_2=r\dfrac{\partial }{\partial r} +u\dfrac{\partial }{\partial u}+2p\dfrac{\partial }{\partial p}+h\dfrac{\partial }{\partial h} + 2m\dfrac{\partial }{\partial m}\), then, the similarity variable and the flow variables are obtained as

$$\begin{aligned} \eta = t, \quad \rho = \Omega ^{*}(\eta ),\quad u = rU^{*}(\eta ),\qquad h = r\Pi ^{*}(\eta ),\quad p = P^{*}(\eta )r^{2},.\quad m = r^{2}F^{*}(\eta ). \end{aligned}$$
(82)

Using Eq. (82), the set of PDEs (1)–(5), are converted into set of ODEs, after dropping the asterisk sign become:

$$\begin{aligned}&\Omega ^{'}+ \Omega U = 0 , \end{aligned}$$
(83)
$$\begin{aligned}&U^{'} + G\;F = 0 , \end{aligned}$$
(84)
$$\begin{aligned}&P^{'} + \gamma PU = 0 , \end{aligned}$$
(85)
$$\begin{aligned}&\Pi ^{'} + \dfrac{U \Pi }{\eta } = 0, \end{aligned}$$
(86)
$$\begin{aligned}&F - \pi \Omega = 0. \end{aligned}$$
(87)

In this case, we are not able to obtain the feasible exact solution for any value of \(\gamma \). Also, numerical solution does not exist using similarity method.

The exact solutions for non-gravitating gas are obtained in cases \(\textit{I-III}\) and presented in Eqs. (38), (46) and (54). The pressure is negative in all three cases because the constants appearing in the obtained solution for pressure should be negative for existence of exact solution. Physically the negative pressure (repulsive action) is generally used in the context of dark energy, cosmology in astrophysics and astronomy which represents an unknown form of energy that affects the universe on the largest scales. Also, dark energy is distributed uniformly in space and cosmological constant of dark energy is non-zero. The simplest clarification for dark energy is that it is a vacuum energy or cosmological constant that occurs in space throughout the whole Universe. The vacuum energy is related to the quantum vacuum (see [30]). The class of solutions in general relativity of importance for astrophysics and cosmology was studied by Wesson [31]. He has shown that when the pressure in expanding ideal fluid solutions has to be negative, the mass increases in general. It has become popular to apply as a model for particle production in the early Universe. The effects of negative pressure in compact objects, which have an equation of state that shows negative pressure at the core of the object (see [32]). Also, the self-similar solutions with negative pressure and violating the strong energy condition were discussed by Carr and Coley [33], which can be applicable in the early Universe. Thus, our obtained exact solution may be applicable in the early Universe and dark energy.

Results and Discussion

To discuss behavior of the flow variable and the strength of shock wave in case \(\mathbf{III} \). The Eqs. (63)–(67), are integrated numerically under the shock conditions (68), using \(4^{th}\) order Runga-Kutta method between shock front \((\eta = 1)\) and position of the inner contact surface \(\eta = \eta _p\). The entire computation work has been carried out by using Mathematica software. The numerical calculations are performed by taking the values of the physical parameters \(\gamma = \dfrac{4}{3},\; \dfrac{5}{3}\); \(g= 0,\; 1,\; 10\); \(M_{a}^{-2}= 0,\; 0.05, \; 0.1\) and \(\theta =-1\). We have taken \(\gamma = \dfrac{4}{3}\) for relativistic gases and \(\gamma = \dfrac{5}{3}\) for fully ionized gas, which are applicable to interstellar medium. These values of adiabatic index \(\gamma = \dfrac{4}{3}\) and \( \dfrac{5}{3}\) are taken the most general range of values which are seen in real stars. The effects of magnetic field on the flow variables behind the shock front are significant when \((1/M_{a}^{2})\ge 0.01\) (see [34]). Thus, the values of \(1/ M_{a}^{2}\) are chosen for calculation as given above. The value \(g=0\), \(M_{a}^{-2}=0\) refers to the non-gravitating and non-magnetic case.

Tables 3 and 4 depict the variation of the inner contact surface position and density ratio across the shock front. Table 3 for various values of g and \(M_{a}^{-2}\) for \(\gamma = \dfrac{5}{3}\); \(\theta =-1\); and Table 4 for various values of \(\gamma \) and \(M_{a}^{-2}\) with \(g=10\), respectively.

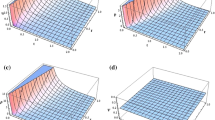
The variation of reduced velocity \( \dfrac{u}{u_2}\), reduced density \(\dfrac{\rho }{\rho _2}\), reduced axial magnetic field \(\dfrac{h}{h_2}\), reduced pressure \(\dfrac{p}{p{_2}}\) and reduced mass \(\dfrac{m}{m_2}\) for \(M_{a}^{-2}= 0, \; 0.05,\; 0.1\); \(g= 0,\; 1,\; 10\) with \(\theta = -1\) and \(\gamma = \dfrac{5}{3}\) are shown in Fig. 1a–e. The Fig. 2 exhibits the dispersal of flow variables reduced velocity \( \dfrac{u}{u_2}\), reduced pressure \( \dfrac{p}{p_2}, \), density \(\dfrac{\rho }{\rho _2}\) and reduced mass \(\dfrac{m}{m_2}\) for \(\gamma =\dfrac{4}{3},\; \dfrac{5}{3}\); \(M_{a}^{-2}= 0, \; 0.05\), \(\theta = -1\) with \(g=10\).

Figure 1a–e shown that the reduced mass \(\dfrac{m}{m_2}\) decreases; whereas the reduced velocity \(\dfrac{u}{u_2}\), density \(\dfrac{\rho }{\rho _2}\), pressure \(\dfrac{p}{p_2}\) and axial magnetic field \(\dfrac{h}{h_2}\) increase as we move inward to the inner contact surface from the shock front.

Fig. 1
figure 1figure 1

Dispersal of flow variables behind the shock wave for \(\gamma =\dfrac{5}{3}\) with \(\theta =-1\): (a) velocity \(\dfrac{u}{u_{2}}\), (b) density \(\dfrac{\rho }{\rho _{2}}\), (c) axial magnetic field \(\dfrac{h}{h_{2}}\), (d) pressure \( \dfrac{p}{p_{2}}\), (e) mass \(\dfrac{m}{m_{2}}\), 1. \( g = 0 \) \(M_{a}^{-2} = 0 \); 2. \( g = 1 \), \(M_{a}^{-2} = 0 \);3. \( g = 10 \), \(M_{a}^{-2} = 0 \) ; 4. \( g = 0 \), \(M_{a}^{-2} = .05 \);5. \( g = 1 \), \(M_{a}^{-2} = .05 \);6. \( g = 10 \) , \(M_{a}^{-2} = .05 \); 7. \( g = 0 \), \(M_{a}^{-2} = .1 \);8. \( g = 1 \), \(M_{a}^{-2} = .1 \); 9. \( g = 10 \), \(M_{a}^{-2} = .1 \)

Full size image

Effects of an Increase in the Value of the Magnetic Field Strength \(M_{a}^{-2}\)

By increasing the value of the magnetic field strength, the distance between shock front and inner contact surface and the value of \(\beta \) increases, that is the strength of shock wave decreases (see Tables 3 and 4). The flow variables \(\dfrac{m}{m_2}\) and \(\dfrac{u}{u_2}\) increase; but the flow variables \(\dfrac{\rho }{\rho _2}\), \(\dfrac{h}{h_2}\) and \(\dfrac{p}{p_2}\) decrease (see Fig. 1a–e).

Effects of an Increase in g

There is a reduction in the distance between the shock front and inner contact surface, when the value of gravitational parameter g is increased, that is to rise in the shock strength (see Table 3). The flow variable \(\dfrac{m}{m_2}\) decreases; whereas the flow variables \(\dfrac{h}{h_2}\), \(\dfrac{p}{p_2}\), \(\dfrac{u}{u_2}\) and \(\dfrac{\rho }{\rho _2}\) increase (see Fig. 1a–e).

Effects of an Increase in the Value of Adiabatic Index \(\gamma \)

With an increase in the value of adiabatic index, the distance between the inner contact surface and shock front increases, i.e. the shock strength decreases an increase in the value of \(\gamma \) (see Table 4). The flow variables \(\dfrac{u}{u_2}\), \(\dfrac{p}{p_2}\) and \(\dfrac{m}{m_2}\) increase; whereas the flow variables \(\dfrac{h}{h_2}\) and \(\dfrac{\rho }{\rho _2}\) decrease with an increase in \(\gamma \) (see Fig. 2).

Table 3 The position of inner contact surface and the density ratio across the shock front for various values of g and \( M_{a}^{-2} \) for \(\gamma =5/3\) and \(\theta =-1\)
Full size table
Table 4 The position of inner contact surface and the density ratio across the shock front for various values of \( M_{a}^{-2} \) and \( \gamma \) for \(\theta =-1\) and \(g=10\)
Full size table
Fig. 2
figure 2

Dispersal of flow variables behind the shock wave for \(\gamma =\dfrac{4}{3}, \gamma =\dfrac{5}{3}\); \(M_{a}^{-2} = 0,\; 0.05\); and \( g = 10 \) with \(\theta =-1\): 1. density \(\dfrac{\rho }{\rho _{2}}\), 2. velocity \(\dfrac{u}{u_{2}}\), 3. pressure \( \dfrac{p}{p_{2}}\), 4. axial magnetic field \(\dfrac{h}{h_{2}}\),5. mass \(\dfrac{m}{m_{2}}\)

Full size image

Conclusions

In summary, we have used Lie group theoretic method to derive all classes of solutions of the model Eqs. (1)–(5), that describe an unsteady flow of a cylindrical shock wave with axial magnetic field in a self-gravitating medium.

The magnetic field has an important role in the formation and evolution of molecular cloud, supernova explosion, synchrotron radiation from supernova remnants, galactic winds, etc. Also, we considered that the self-gravitating gas, the consideration of gravitational effect plays a fundamental role in constructing a quantitative description of equilibrium and motion of gas masses that form a star. The consideration of the formation process of astrophysical objects, (for example - stars and galaxies) the most important factor is self-gravity (Ghanbari and Abbassi [35]). To find a theoretical explanation for nova and supernova flare-ups, it is always useful to obtain solutions of the equations for unsteady gas motion with gravitational effect taken into consideration. These may be considered as the models reflecting the essential features of the actual phenomenon of stellar flare-ups (see Sedov [1]).

The group theoretic method is applied to the governing equations, yields the over-determined equations and solving these over determined equations, we obtain the infinitesimal group of generators. An optimal system is obtained to construct the similarity variables and transformations for the flow variables. Using the transformations for the variables the set of PDEs is transformed into the ODEs. All class of solutions corresponding to the set of ODEs in possible cases are obtained. These solutions may have various applications in physics and engineering. The obtained exact solutions are important in the sense that solutions may be used to check the validity of the numerical solution of a system of PDEs for studying wave propagation phenomenon using similarity method. The present work is related to the explosion problem which can be used to represent many physical phenomena involving non-linear hyperbolic PDEs. The shock waves in conducting ideal gas may be important for description of shock wave in explosion in the ionosphere and supernova explosions. Out of the five different possible cases in which the considered problem have similarity solutions, we are able to obtain feasible exact solution only in three cases and numerical solutions in the cases of exponential law and power law shock paths. In the present works we have discussed the numerical solution in the case of power law shock path. Similarly, we can obtained the numerical solution for the exponential law shock path. In case V, neither exact nor numerical solution exist for any value of \(\gamma \). We conclude as follows, from Table 3 and 4 and Fig. 1a–e and 2:

  1. 1.

    The strength of shock wave decreases with an increase in the value of the magnetic field strength and adiabatic exponent; but it increases with an increase in the value of gravitational parameter.

  2. 2.

    The mass decreases; whereas the density, magnetic field, velocity and pressure increase in \(g=0\) and \(g\ne 0\) as we approach to inner contact surface from shock front.

  3. 3.

    The flow variables pressure, density, velocity and magnetic field increase; whereas mass decreases with a rise in the value of gravitational parameter.

  4. 4.

    The increase in the value of \(M_{a}^{-2}\) and g have adverse effect on the pressure, density, mass, magnetic field and similar effect on the velocity.

  5. 5.

    The profile of the mass, velocity and pressure increase; whereas the density and magnetic field decrease with an increase in \(\gamma \). The \(M_{a}^{-2}\) and \(\gamma \) have similar effect on velocity, magnetic field, mass and density.

  6. 6.

    The increase in the value of g and \(\gamma \) have similar effect on the velocity, pressure and adverse effect on the magnetic field, mass and density.