1 Introduction

The study of cylindrical shock wave in the presence of magnetic field has many applications. Some of the applications include explosion of long thin wire, experiments on pinch effect, to a few axially symmetric hypersonic problems such as the shock envelope trailing fast meteor or missile, etc (see [1]). Other potential applications can be found in astrophysics in connection with shock waves in interstellar gas clouds. The gravitational force has significant effect on many astrophysical problems (see [2]). A qualitative behavior of the gaseous mass may be examined with the aid of the equations of motion and equilibrium considering gravitational forces (see [3, 4]).

The expanded Lie group of transformations is commonly used to study the continuous symmetry in mathematics, mechanics and theoretical physics. The complex problems of the physical systems can be simplified to solvable mathematical equations with the help of transformation. The theory of Lie group of transformations and its applications in various fields for working out problems of real world can be found in the works presented in Hydon [5], Bluman and Cole [6], Bluman and Kumei [7], Stephani [8], Ibragimov [9], Olver [10], Ovsiannikov [11] and in Logan and Perez [12]. Zedan [13] has obtained class of exact solutions using Lie group analysis for one-dimensional motion of a gas under monochromatic radiation. Till now, research has been emphasized on the alternative problem of categorizing all initial or boundary conditions that are consistent with symmetries of a particular differential equation. Solvable initial-value problems (IVPs) for evolution equations with two independent variables can be classified as of Basarab and Zhdanov [14]. Some IVPs can be solved by means of solving a simpler IVP, for linear (or linearizable) partial differential equations (PDEs) (see [15]).

In the case when radiation heat transfer effects are present implicitly, the presumption of flow to be isothermal is physically realistic. On the propagation of shock, the temperature behind it increases and grows to very high value. By radiation there is intense transfer of energy. This process leads to the approach of temperature gradient to zero, which means that the dependent temperature behind the shock front becomes uniform and the flow becomes isothermal [16,17,18,19,20]. Lerche [21, 22] developed mathematical theory for one-dimensional isothermal blast waves under the influence of magnetic field. Purohit [23] and Singh and Vishwakarma [24] have studied homothermal flows behind a spherical shock wave in a self-gravitating gas. For self-gravitating hydrodynamic problems in 3D, Truelove et al. [25] have presented a new code for numerical solution. The numerical study for the simplest case of the interaction between a spherical cloud and shock was presented by Klein et al. [26]. In their work, shock is steady and planar, far from the cloud. Also, magnetic fields and gravitational forces are not taken into account. The interaction procedure of supernova strong shock wave and interstellar molecular cloud was studied by Rybakin et al. [27] in three dimensions by numerical simulation.

The similarity solution in the context of formation of blast wave by very intense explosion can be found in the works of Taylor [28, 29]. Sedov [30] developed similarity solution in the context of shock wave propagation. It is very difficult to obtain solution of system of quasilinear hyperbolic PDEs without approximations. Hence, the attempt is to find self-similar solutions in which solution exists along similarity curves and along these curves the system of equations converts to a system of ODEs. There are two type of self-similar solutions. In the first type, the similarity exponent is decided either by dimensional considerations or by the conservation laws, whereas in the second type, the similarity exponent is determined by integrating the ODEs for the reduced functions (see [31]).

To the best of authors’ knowledge, the problem of cylindrical shock for isothermal flow under the influence of axial magnetic field in a self-gravitating gas using Lie group of transformations has not been studied. Also, similarity solutions for a magnetogasdynamic shock in a self-gravitating gas under isothermal flow condition using the approach of Sedov [30] were obtained in Nath and Sinha [32]. In the present work, we have considered axial magnetic field while in Nath and Sinha [32] they have taken azimuthal magnetic field, and we have used Lie group of transformations to obtain the solutions. Using Lie group of transformation method, we are able to obtain similarity solutions in two cases. In the first case, we obtain the similarity solution with power law shock path which is similar to the solution obtained by Nath and Sinha [32], and in the second case, we have similarity solutions with exponential law shock path. Thus, our solution is more general than the solution obtained in Nath and Sinha [32]. The effects of varying the values of Alfven-Mach number, gravitational parameter, ambient density variation index and ambient magnetic field variation index on the flow variables are studied for the cases of power law shock path and exponential law shock path. It is found that the flow variables magnetic field, mass and velocity decreases; however, density (pressure) increase and decrease after attaining a maximum value for power law shock path. In the case of exponential law shock path, it is obtained that reduced density and fluid velocity increase; however, mass decreases and magnetic field increases slightly and then decreases after attaining a maximum. The increase in value of Alfven-Mach number leads to an increase in the density ratio which infers to the decrease in shock strength.

2 Equations of motion and boundary conditions

We pursue for the solution of magnetogasdynamic cylindrical shock in a perfectly conducting ideal gas across which the magnetic field is axial (i.e., normal to the flow). The gas is taken to be self-gravitating and the flow is considered to be isothermal. Viscosity, thermal conductivity and electrical resistivity are not considered in the present problem. The fundamental equations are thus incorporating the statements of conservation of mass, momentum, magnetic field equation, mass in the cylinder and the isothermal flow condition. The gas ahead of the shock is considered to be at rest. Also the shock is assumed to be driven out by an inner expanding surface which could physically be the surface of the stellar corona or the diaphragm containing a very high pressure gas or the condensed explosive.

Thus, the fundamental equations of motion are given as (see [4, 18,19,20,21,22, 32])

$$\begin{aligned}&\dfrac{\partial \rho }{\partial t} + u \dfrac{\partial \rho }{\partial r} + \rho \dfrac{\partial u}{\partial r} + \dfrac{ u \rho }{r} = 0, \end{aligned}$$
(1)
$$\begin{aligned}&\dfrac{\partial u}{\partial t} + u \dfrac{\partial u}{\partial r} + \dfrac{1}{\rho } \left[ \dfrac{\partial p}{\partial r} + \mu h \dfrac{\partial h}{\partial r} \right] +\dfrac{G m}{r} =0, \end{aligned}$$
(2)
$$\begin{aligned}&\dfrac{\partial h}{\partial t} + u \dfrac{\partial h}{\partial r} + h \dfrac{\partial u}{\partial r}+\dfrac{h u}{r} = 0, \end{aligned}$$
(3)
$$\begin{aligned}&\dfrac{\partial m}{\partial r}=2 \pi \rho r,\end{aligned}$$
(4)
$$\begin{aligned}&\dfrac{\partial T}{\partial r}=0, \end{aligned}$$
(5)

where \(\rho \) denotes the density, u the fluid velocity, p the pressure, G the gravitational constant, h the axial magnetic field, \(\mu \) is the magnetic permeability, m the mass for cylinder of unit length and radius r, t and r denote independent time and space coordinates and T is the temperature.

The equation of state along with internal energy is given as

$$\begin{aligned} p=R \rho T; \quad e_{m}=\dfrac{p}{(\gamma -1) \rho }, \end{aligned}$$
(6)

where R is the universal gas constant, \(e_{m}\) is the internal energy per unit mass and \(\gamma \) is the adiabatic exponent.

A strong cylindrical shock wave is assumed to be propagating outwards from the axis of symmetry in the undisturbed ideal gas with variable density, variable axial magnetic field and zero radial fluid velocity. The law of variation of ambient density and magnetic field are considered according to different cases of shock path obtained, as in Eqs. (29) and (45). Since shock is strong, \(p_{1}\approx 0\) and \(e_{m1}\approx 0\).

For strong shock, the Rankine–Hugoniot jump conditions across the shock front are given as (see [32, 33])

$$\begin{aligned}&u_{2}=(1-\beta )C, \rho _{2}=\dfrac{\rho _{1}}{\beta },\quad h_{2}=\dfrac{h_{1}}{\beta }, \quad p_{2}=L \rho _{1} C^{2},\quad m_{2}=m_{1}, \end{aligned}$$
(7)

where (\(F_{2}-F_{1}\)) is presumed to be negligible in comparison with the product of \(p_{2}\) and C for strong shock (see [4, 16, 20]), F is the radiation heat flux; \(L=\left[ (1-\beta )+\dfrac{M_{A}^{-2}}{2}\left( 1-\dfrac{1}{\beta ^{2}}\right) \right] \), C is the shock velocity and, ‘1’ and ‘2’ denote the conditions just ahead and behind the shock. The density ratio \(\beta \) (\(0<\beta <1\)) across the shock front is given by the quadratic equation

$$\begin{aligned} \beta ^{2} (\gamma +1)-\beta \left[ \gamma (1+M_{A}^{-2})-1\right] +(\gamma -2)M_{A}^{-2}=0, \end{aligned}$$
(8)

where \(M_{A}\) is the Alfven-Mach number defined as \(M_{A}=\sqrt{\dfrac{\rho _{1} C^{2}}{ \mu h_{1}^{2}}}\).

Equations (5) and (6) together give the relation

$$\begin{aligned} \dfrac{p}{p_{2}}=\dfrac{\rho }{\rho _{2}}. \end{aligned}$$
(9)

3 Similarity analysis

For the similarity reduction of equations of motion (1)–(5), the Lie group of transformations method is used. We can write a one-parameter infinitesimal group of transformations as

$$\begin{aligned}&r^{*}=r+ \epsilon \chi (\rho , u, p, h, m, r, t),\quad t^{*}=t+ \epsilon \tau (\rho , u, p, h, m, r, t),\nonumber \\&\rho ^{*}=\rho + \epsilon D (\rho , u, p, h, m, r, t),\quad u^{*}=u+ \epsilon U (\rho , u, p, h, m, r, t),\nonumber \\&p^{*}=p+ \epsilon P (\rho , u, p, h, m, r, t),\quad h^{*}=h+ \epsilon H (\rho , u, p, h, m, r, t),\nonumber \\&m^{*}=m+ \epsilon M (\rho , u, p, h, m, r, t), \end{aligned}$$
(10)

where \(\chi \), \(\tau \), D, U, P, H, M are the infinitesimal generators and \(\epsilon \) is very small quantity such that its second and higher power terms can be neglected. The system (1)-(5) along with the shock conditions (7) remains invariant under the above group of transformation (10).

Introducing the notations for time coordinate t, space coordinate r and flow variables \(\rho \), u, p, h and m as

$$\begin{aligned} x_{1}=t,\quad x_{2}=r,\quad u_{1}=\rho ,\quad u_{2}=u,\quad u_{3}=p, \quad u_{4}=h,\quad u_{5}=m, \end{aligned}$$
(11)

and

$$\begin{aligned} p_{j}^{i}=\dfrac{\partial u_{i}}{\partial x_{j}}, \end{aligned}$$
(12)

where \(j=1,2\) and \(i=1,2,3,4,5\). Equations (1)–(5) can be written in the form

$$\begin{aligned} F_{q}(x_{j}, u_{i},p_{j}^{i})=0, q=1,2,3,4,5. \end{aligned}$$
(13)

Using (13), the system of Eqs. (1)–(5) are said to be invariant under Lie group of transformations (10) if they satisfy

$$\begin{aligned} K F_{q}=\lambda _{q r}F_{r}, \end{aligned}$$
(14)

where \(r=1,2,3,4,5\) and \(K=\zeta _{x}^{j} \dfrac{\partial }{\partial x_{j}}+\zeta _{u}^{i} \dfrac{\partial }{\partial u_{i}}+\zeta _{pj}^{i} \dfrac{\partial }{\partial p_{j}^{i}}\),

and

$$\begin{aligned} \zeta _{x}^{1}=\tau ,\quad \zeta _{x}^{2}=\chi ,\quad \zeta _{u}^{1}=D,\quad \zeta _{u}^{2}=U,\quad \zeta _{u}^{3}=P, \quad \zeta _{u}^{4}=H, \quad \zeta _{u}^{5}=M. \end{aligned}$$
(15)

\(\zeta _{pj}^{i}\) is given as

$$\begin{aligned} \zeta _{pj}^{i}=\dfrac{\partial \zeta _{u}^{i}}{\partial x_{j}}+\dfrac{\partial \zeta _{u}^{i}}{\partial u_{k}}p_{j}^{k}-\dfrac{\partial \zeta _{x}^{l}}{\partial x_{j}}p_{l}^{i}-\dfrac{\partial \zeta _{x}^{l}}{\partial u_{n}}p_{l}^{i}p_{j}^{n}, \end{aligned}$$
(16)

where \(k=1,2,3,4,5\); \(l=1,2\); \(n=1,2,3,4,5\).

From Eqs. (1) and (14), the determining equations are obtained as

$$\begin{aligned}&\dfrac{\partial D}{\partial \rho }-\dfrac{\partial \tau }{\partial t}-u\dfrac{\partial \tau }{\partial r}=\lambda _{11}, \quad u \dfrac{\partial D}{\partial m}+ \rho \dfrac{\partial U}{\partial m} =\lambda _{14}, \dfrac{\partial D}{\partial m}=0,\nonumber \\&\dfrac{\partial D}{\partial u}-\rho \dfrac{\partial \tau }{\partial r}=\lambda _{12}, \quad D+u \dfrac{\partial D}{\partial u}+\rho \dfrac{\partial U}{\partial u}-\rho \dfrac{\partial \chi }{\partial r}=\lambda _{11} \rho + \lambda _{12} u+\lambda _{13} h,\nonumber \\&\dfrac{\partial D}{\partial p}=0, \quad u\dfrac{\partial D}{\partial p}+\rho \dfrac{\partial U}{\partial p}=\lambda _{12}\dfrac{1}{\rho }+\lambda _{15}, \dfrac{\partial D}{\partial h}=\lambda _{13},\nonumber \\&u\dfrac{\partial D}{\partial h}+\rho \dfrac{\partial U}{\partial h}=\dfrac{\mu h}{\rho }\lambda _{12}+u \lambda _{13}, \quad \dfrac{\partial \tau }{\partial \rho }=0, \quad -\dfrac{\partial \tau }{\partial u}=0,\nonumber \\&U-\dfrac{\partial \chi }{\partial t}+u\dfrac{\partial D}{\partial \rho }-u\dfrac{\partial \chi }{\partial r}+\rho \dfrac{\partial U}{\partial \rho }=u \lambda _{11}-\dfrac{p}{\rho } \lambda _{15},\nonumber \\&\dfrac{ D u}{r}-\dfrac{ u \rho }{r^{2}}\chi +\dfrac{\rho U}{r}+\dfrac{\partial D}{\partial t} +u \dfrac{\partial D}{\partial r}+\rho \dfrac{\partial U}{\partial r}=\dfrac{ u \rho }{r} \lambda _{11}+\dfrac{G m}{r} \lambda _{12}+\dfrac{ h u}{r} \lambda _{13}-2 \pi r \rho \lambda _{14}. \end{aligned}$$
(17)

From Eqs. (2) and (14), the determining equations are obtained as

$$\begin{aligned}&\dfrac{\partial U}{\partial u}-\dfrac{\partial \tau }{\partial t}-u\dfrac{\partial \tau }{\partial r}=\lambda _{22},\quad u\dfrac{\partial U}{\partial \rho }+\dfrac{1}{\rho }\dfrac{\partial P}{\partial \rho }+\dfrac{\mu h}{\rho }\dfrac{\partial H}{\partial \rho }=u \lambda _{21}-\dfrac{p}{\rho }\lambda _{25},\nonumber \\&\dfrac{\partial U}{\partial \rho }=\lambda _{21}, U-\dfrac{\partial \chi }{\partial t}+u \dfrac{\partial U}{\partial u}-u \dfrac{\partial \chi }{\partial r}+\dfrac{1}{\rho }\dfrac{\partial P}{\partial u}+\dfrac{\mu h}{\rho }\dfrac{\partial H}{\partial u}=\rho \lambda _{21}+u \lambda _{22}+h \lambda _{23},\nonumber \\&\dfrac{\partial U}{\partial p}-\dfrac{1}{\rho }\dfrac{\partial \tau }{\partial r}=0, \quad -\dfrac{D}{\rho ^{2}}+u\dfrac{\partial U}{\partial p}+\dfrac{1}{\rho }\dfrac{\partial P}{\partial p}-\dfrac{1}{\rho }\dfrac{\partial \chi }{\partial r}+\dfrac{\mu h}{\rho }\dfrac{\partial H}{\partial p}=\dfrac{\lambda _{22}}{\rho }+\lambda _{25},\nonumber \\&\dfrac{\mu H}{\rho }-\dfrac{D}{\rho ^{2}}\mu h+u \dfrac{\partial U}{\partial h}+\dfrac{1}{\rho }\dfrac{\partial P}{\partial h}+\dfrac{\mu h}{\rho } \dfrac{\partial H}{\partial h}-\dfrac{\mu h}{\rho }\dfrac{\partial \chi }{\partial r}=\lambda _{22}\dfrac{\mu h}{\rho }+\lambda _{23}u,\nonumber \\&\dfrac{\partial U}{\partial h}-\dfrac{\mu h}{\rho }\dfrac{\partial \tau }{\partial r}=\lambda _{23}, \quad u \dfrac{\partial U}{\partial m}+\dfrac{1}{\rho }\dfrac{\partial P}{\partial m}+\dfrac{\mu h}{\rho }\dfrac{\partial H}{\partial m}=\lambda _{24}, \quad \dfrac{\partial U}{\partial m}=0,\nonumber \\&\dfrac{G m}{ r}-\chi \dfrac{G m}{r^{2}}+\dfrac{\partial U}{\partial t}+u \dfrac{\partial U}{\partial r}+\dfrac{1}{\rho }\dfrac{\partial P}{\partial r}+\dfrac{\mu h}{\rho }\dfrac{\partial H}{\partial r}=\dfrac{ u \rho }{r}\lambda _{21}+\dfrac{G m}{r}\lambda _{22}+\dfrac{h u}{r} \lambda _{23}-2 \pi \rho r \lambda _{24}. \end{aligned}$$
(18)

From Eqs. (3) and (14), the determining equations are obtained as

$$\begin{aligned}&\dfrac{\partial H}{\partial \rho }=\lambda _{31}, h\dfrac{\partial U}{\partial \rho }+u \dfrac{\partial H}{\partial \rho }=u \lambda _{31}-\dfrac{p}{\rho } \lambda _{35},\nonumber \\&\dfrac{\partial H}{\partial u}-h \dfrac{\partial \tau }{\partial r}=\lambda _{32}, \quad H+h \dfrac{\partial U}{\partial u}-h \dfrac{\partial \chi }{\partial r}+u \dfrac{\partial H}{\partial u}=\rho \lambda _{31}+u \lambda _{32}+h \lambda _{33},\nonumber \\&\dfrac{\partial H}{\partial p}=0,\quad h \dfrac{\partial U}{\partial p}+u \dfrac{\partial H}{\partial p}=\dfrac{1}{\rho }\lambda _{32}+\lambda _{35},\nonumber \\&\dfrac{\partial H}{\partial h}-\dfrac{\partial \tau }{\partial t}-u\dfrac{\partial \tau }{\partial r}=\lambda _{33}, \quad h \dfrac{\partial U}{\partial m}+u \dfrac{\partial H}{\partial m}=\lambda _{34},\nonumber \\&U-\dfrac{\partial \chi }{\partial t}+h\dfrac{\partial U}{\partial h}+u\dfrac{\partial H}{\partial h}-u\dfrac{\partial \chi }{\partial r}=\dfrac{\mu h}{\rho }\lambda _{32}+ u \lambda _{33},\nonumber \\&\dfrac{U h}{r}-\chi \dfrac{h u}{r^{2}}+\dfrac{H u}{r} +\dfrac{\partial H}{\partial t}+h\dfrac{\partial U}{\partial r}+u\dfrac{\partial H}{\partial r}=\dfrac{u \rho }{r}\lambda _{31}+ \dfrac{G m}{r} \lambda _{32}+\dfrac{h u}{r} \lambda _{33}-2 \pi r \rho \lambda _{34}. \end{aligned}$$
(19)

From Eqs. (4) and (14), the determining equations are obtained as

$$\begin{aligned}&\dfrac{\partial M}{\partial \rho }=u \lambda _{41}-\dfrac{p}{\rho } \lambda _{45}, \quad \dfrac{\partial M}{\partial u}=\rho \lambda _{41}+u \lambda _{42}+h \lambda _{43},\nonumber \\&\dfrac{\partial M}{\partial p}=\dfrac{1}{\rho } \lambda _{42}+\lambda _{45}, \quad \dfrac{\partial M}{\partial h}=\dfrac{\mu h}{\rho } \lambda _{42}+u \lambda _{43}, \quad \dfrac{\partial M}{\partial m}-\dfrac{\partial \chi }{\partial r}=\lambda _{44},\nonumber \\&\dfrac{\partial M}{\partial r}-2 \pi \rho \chi -2 \pi r D =\dfrac{u \rho }{r}\lambda _{41}+\dfrac{G m}{r} \lambda _{42}+\dfrac{h u}{r} \lambda _{43}- 2 \pi \rho r \lambda _{44}. \end{aligned}$$
(20)

From Eqs. (5) and (14), the determining equations are obtained as

$$\begin{aligned}&\dfrac{p}{\rho }\dfrac{\partial \tau }{\partial r}=\lambda _{51}, \quad \dfrac{D p}{\rho ^{2}}-\dfrac{P}{\rho }-\dfrac{p}{\rho } \dfrac{\partial D}{\partial \rho } +\dfrac{p}{\rho }\dfrac{\partial \chi }{\partial r}+\dfrac{\partial P}{\partial \rho }=u \lambda _{51}-\dfrac{p}{\rho } \lambda _{55},\nonumber \\&\lambda _{52}=0, \quad -\dfrac{p}{\rho }\dfrac{\partial D}{\partial u}+\dfrac{\partial P}{\partial u}=\rho \lambda _{51}+u \lambda _{52}+ h \lambda _{53},\nonumber \\&\dfrac{\partial \tau }{\partial r}=0, \quad -\dfrac{p}{\rho } \dfrac{\partial D}{\partial p}+\dfrac{\partial P}{\partial p}-\dfrac{\partial \chi }{\partial r}=\dfrac{1}{\rho } \lambda _{52}+\lambda _{55},\nonumber \\&\lambda _{53}=0,\quad -\dfrac{p}{\rho } \dfrac{\partial D}{\partial h}+\dfrac{\partial P}{\partial h}=\dfrac{\mu h}{\rho } \lambda _{52}+u \lambda _{53},\nonumber \\&\dfrac{\partial P}{\partial m}-\dfrac{p}{\rho } \dfrac{\partial D}{\partial m}=\lambda _{54}, \quad -\dfrac{p}{\rho } \dfrac{\partial D}{\partial r}+\dfrac{\partial P}{\partial r}=\dfrac{u \rho }{r} \lambda _{51}+\dfrac{G m}{r} \lambda _{52}+\dfrac{h u}{r} \lambda _{53}-2 \pi \rho r \lambda _{54}. \end{aligned}$$
(21)

On solving the set of Eqs. (17), (18), (19), (20) and (21) of the determining equations, the infinitesimal generators are obtained as follows:

$$\begin{aligned}&\tau =\alpha t+c, \quad \chi =(\lambda _{22}+2 \alpha )r, \quad U=(\lambda _{22}+ \alpha )u, \quad D=(\lambda _{11}+ \alpha ) \rho ,\nonumber \\&P=(2 \lambda _{22})p,\quad H=\lambda _{22}h, \quad M=2 (\lambda _{22}+ \alpha ) m, \end{aligned}$$
(22)

where \(\alpha \) and c are constants.

4 Similarity solutions

Taking into consideration the constants arising in the expressions of infinitesimal generators in Eq. (22), different cases of solutions can be obtained which are discussed below:

Case (i): When \(\alpha \ne 0\) and \(\lambda _{22}+2\alpha \ne 0\)

The new variables \({\overline{r}}\) and \({\overline{t}}\) are defined as:

$$\begin{aligned} {\overline{r}}=r, \quad {\overline{t}}=t+\dfrac{c}{\alpha }. \end{aligned}$$
(23)

We find that the set of Eqs. (13)–(22) remain invariant under the transformation (23). Using (22) and (23), the new set of infinitesimals for this case in terms of \({\overline{r}}\) and \({\overline{t}}\) after suppressing the bar sign is given as:

$$\begin{aligned}&\tau =\alpha t, \quad \chi =(\lambda _{22}+2\alpha )r, \quad D=(\lambda _{11}+\alpha ) \rho ,\quad U=(\lambda _{22}+\alpha )u, \nonumber \\&P=(2 \lambda _{22})p, \quad H=\lambda _{22}h, \quad M=2 (\lambda _{22}+ \alpha ) m. \end{aligned}$$
(24)

The invariant surface conditions for the infinitesimal generators (24) are given as

$$\begin{aligned}&\tau \rho _{t}+\chi \rho _{r}=D, \quad \tau u_{t}+\chi u_{r}=U,\quad \nonumber \\&\tau p_{t}+\chi p_{r}=P,\quad \tau h_{t}+\chi h_{r}=H, \quad \tau m_{t}+\chi m_{r}=M. \end{aligned}$$
(25)

Using (24) in (25), and after integration, we obtain

$$\begin{aligned}&\rho =t^{\dfrac{(\lambda _{11}+\alpha )}{\alpha }} D^{*}(x), \quad u=t^{\dfrac{(\lambda _{22}+\alpha )}{a}} U^{*}(x), \quad p=t^{\dfrac{2\lambda _{22}}{\alpha }} P^{*}(x), \nonumber \\&h=t^{\dfrac{\lambda _{22}}{\alpha }} H^{*}(x), \quad m=t^{\dfrac{2 (\lambda _{22}+ \alpha )}{\alpha }} M^{*}(x), \end{aligned}$$
(26)

where \(\delta =\dfrac{\lambda _{22}+2\alpha }{\alpha }\) and similarity variable x is obtained as

$$\begin{aligned} x=\dfrac{r}{At^{\delta }}, \end{aligned}$$
(27)

where A is a dimensional constant.

Shock path and shock velocity are obtained as

$$\begin{aligned} R(t)=At^{\delta },\quad C=\dfrac{dR}{dt}=A\delta t^{\delta -1}. \end{aligned}$$
(28)

The flow variables just ahead of the shock front are characterized as

$$\begin{aligned} \rho _{1}=\rho ^{*} R^{\phi }, h_{1}=h^{*} R^{-\theta }, m_{1}=m^{*} R^{\phi +2}, \end{aligned}$$
(29)

where \(\rho ^{*}\), \(\phi \), \(h^{*}\), \(\theta \) are constants and \(m^{*}=\dfrac{2 \pi \rho ^{*}}{(\phi +2)}\). The necessary condition for \(M_{A}\) to be a constant is

$$\begin{aligned} \phi \delta +2 \delta -2+2 \theta \delta =0. \end{aligned}$$
(30)

At the shock, i.e., at \(x=1\), using (26) the flow variables are given as

$$\begin{aligned}&\rho \mid _{x=1}=t^{\dfrac{(\lambda _{11}+\alpha )}{\alpha }} D^{*}(1), \quad u\mid _{x=1}=t^{\dfrac{(\lambda _{22}+\alpha )}{\alpha }} U^{*}(1),\quad p\mid _{x=1}=t^{\dfrac{2\lambda _{22}}{\alpha }} P^{*}(1),\nonumber \\&h\mid _{x=1}=t^{\dfrac{\lambda _{22}}{\alpha }} H^{*}(1),\quad m\mid _{x=1}=t^{\dfrac{2 (\lambda _{22}+ \alpha )}{\alpha }} M^{*}(1). \end{aligned}$$
(31)

Using (7), (29) and (31), the boundary conditions for the infinitesimal generators are obtained as follows

$$\begin{aligned}&D^{*}(1)=\dfrac{\rho ^{*} A^{\phi }}{\beta }, \quad U^{*}(1)= (1-\beta ) A \delta , \quad P^{*}(1)=L \rho ^{*} \delta ^{2} A^{\phi +2}, \nonumber \\&H^{*}(1)=\dfrac{\delta A^{(\phi +2)/2} \sqrt{\rho ^{*}}}{\sqrt{\mu }M_{A} \beta }, \quad M^{*}(1)=m^{*} A^{\phi +2}, \end{aligned}$$
(32)

where \(\phi =\dfrac{\lambda _{11}+\alpha }{\lambda _{22}+2\alpha }.\)

Using (26) and (29), the flow variables are obtained in the form

$$\begin{aligned}&\rho = \rho _{1} {\overline{D}}(x), \quad u=C {\overline{U}}(x), \quad p=\rho _{1} C^{2}{\overline{P}}(x),\quad \sqrt{\mu } h=\rho _{1}^{1/2} C {\overline{H}}(x), \quad m=m_{1} {\overline{M}}(x), \end{aligned}$$
(33)

where \({\overline{D}}=\dfrac{D^{*}}{\rho ^{*} A^{\phi }}\), \({\overline{U}}=\dfrac{U^{*}}{\delta A}\), \({\overline{P}}=\dfrac{P^{*}}{\rho ^{*} A^{\phi +2} \delta ^{2}}\), \({\overline{H}}=\dfrac{H^{*}\sqrt{\mu }}{\delta A^{(\phi +2)/2} \sqrt{\rho ^{*}}}\), \({\overline{M}}=\dfrac{M^{*}}{m^{*} A^{\phi +2}}\).

The set of Eqs. (1)–(4), using (33) and after suppressing the bar sign are transformed as

$$\begin{aligned}&\phi D +(U-x)D^{'}+D U^{'}+ \dfrac{D U}{x}=0, \end{aligned}$$
(34)
$$\begin{aligned}&\dfrac{(\delta -1)}{\delta }U D +(U-x) U^{'} D + P^{'}+ H H^{'}+\dfrac{G_{0} M D}{\delta ^{2} x}=0, \end{aligned}$$
(35)
$$\begin{aligned}&\dfrac{1}{2}\phi H +\dfrac{(\delta -1)}{\delta }H+(U-x) H^{'}+H U^{'}+ \dfrac{H U}{x}=0,\end{aligned}$$
(36)
$$\begin{aligned}&M^{'}=(\phi +2) x D, \end{aligned}$$
(37)

where \(G_{0}=G m^{*}\) is the gravitational parameter, \(\delta =\dfrac{-2}{\phi }\) and \((\prime )\) represents differentiation w.r.t. x. Using Eq. (7) and similarity transformations (33) in (9), we obtain a relation between P(x) and D(x) as

$$\begin{aligned} P(x)=L \beta D(x). \end{aligned}$$
(38)

The set of ODEs (34)–(37) are solved numerically. The boundary conditions obtained from (32) using (33) after suppressing the bar sign are obtained as

$$\begin{aligned}&D(1)=\dfrac{1}{\beta }, \quad U(1)= (1-\beta ), \quad P(1)=L, \quad H(1)=\dfrac{1}{M_{A} \beta }, \quad M(1)=1. \end{aligned}$$
(39)

Normalizing the flow variables \(\rho , u, p, h\) and m, we get

$$\begin{aligned} \dfrac{\rho }{\rho _{2}}=\dfrac{D(x)}{D(1)},\quad \dfrac{u}{u_{2}}=\dfrac{U(x)}{U(1)},\quad \dfrac{p}{p_{2}}=\dfrac{P(x)}{P(1)},\quad \dfrac{h}{h_{2}}=\dfrac{H(x)}{H(1)}, \quad \dfrac{m}{m_{2}}=\dfrac{M(x)}{M(1)}. \end{aligned}$$
(40)

Case (ii): When \(\alpha =0\), \(\lambda _{22}\ne 0\) and \(c\ne 0\)

From (22), the infinitesimal generators for the present case are obtained as

$$\begin{aligned}&\tau =c, \quad \chi =\lambda _{22} r, \quad D=\lambda _{11} \rho , \quad U=\lambda _{22} u,\nonumber \\&P=(2 \lambda _{22}) p, \quad H=\lambda _{22} h,\quad M=2 \lambda _{22}m. \end{aligned}$$
(41)

The invariant surface conditions in this case is same as (25) in case (i). Using (25) and (41) on integration, we obtain

$$\begin{aligned}&\rho =exp\left( \dfrac{\lambda _{11}t}{c}\right) D^{*}(x), \quad u=exp(\delta t) U^{*}(x),\quad p=exp (2 \delta t) P^{*}(x), \nonumber \\&h=exp ( \delta t ) H^{*}(x),\quad m=exp(2 \delta t ) M^{*}(x), \end{aligned}$$
(42)

where \(\delta =\dfrac{\lambda _{22}}{c}\) and similarity variable x is obtained as

$$\begin{aligned} x= \dfrac{r}{A e^{\delta t}}. \end{aligned}$$
(43)

Shock path and shock velocity are obtained as

$$\begin{aligned} R(t)=A e^{\delta t}, C=\dfrac{dR}{dt}=A \delta e^{\delta t}. \end{aligned}$$
(44)

As the shock path and shock velocity vary according to the exponential law, given by Eq. (44). Thus, to obtain the similarity solutions we need to consider the flow variables just ahead of the shock front varying according to the exponential law such as,

$$\begin{aligned} \rho _{0}=\rho ^{*} exp(\phi t), \quad h_{0}=h^{*} exp(-\theta t). \end{aligned}$$
(45)

From (42), the flow variables at the shock, i.e., at \(x=1\) are given as

$$\begin{aligned}&\rho \mid _{x=1}=exp\left( \dfrac{\lambda _{11}t}{c}\right) D^{*}(1), \quad u\mid _{x=1}=exp(\delta t) U^{*}(1),\quad p\mid _{x=1}=exp(2 \delta t) P^{*}(1), \nonumber \\&h\mid _{x=1}=exp( \delta t) H^{*}(1),\quad m\mid _{x=1}=exp(2 \delta t) M^{*}(1). \end{aligned}$$
(46)

The boundary conditions for infinitesimal generators are as given by (32), with \(\phi =\dfrac{\lambda _{11}}{\lambda _{22}}\). For the existence of similarity solution in this case, the density needs to be necessarily constant. Using (42) and (45), we obtain the flow variables in the form

$$\begin{aligned}&\rho = \rho _{1} {\overline{D}}(x), \quad u=C {\overline{U}}(x), \quad p=\rho _{1} C^{2}{\overline{P}}(x),\quad \sqrt{\mu }h=\rho _{1}^{1/2} C {\overline{H}}(x), \quad m=m_{1} {\overline{M}}(x), \end{aligned}$$
(47)

where \({\overline{D}}=\dfrac{D^{*}}{\rho ^{*} A^{\phi }}\), \({\overline{U}}=\dfrac{U^{*}}{ A\delta }\), \({\overline{P}}=\dfrac{P^{*}}{\rho ^{*} \delta ^{2} A^{\phi +2}}\), \({\overline{H}}=\dfrac{\sqrt{\mu }H^{*}}{\delta A^{(\phi +2)/2} \sqrt{\rho ^{*}}}\), \({\overline{M}}=\dfrac{M^{*}}{m^{*} A^{\phi +2}}\).

The condition for \(M_{A}\) to be a constant in the present case is

$$\begin{aligned} \delta =-\theta . \end{aligned}$$
(48)

Using (47) the set of Eqs. (1)–(4), after suppressing the bar sign is transformed as

$$\begin{aligned}&(U-x)D^{'}+D U^{'}+ \dfrac{ D U}{x}=0, \end{aligned}$$
(49)
$$\begin{aligned}&U D +(U-x) U^{'} D + P^{'}+ H H^{'}+\dfrac{G_{0} M D}{\delta ^{2} x}=0, \end{aligned}$$
(50)
$$\begin{aligned}&H+(U-x) H^{'}+H U^{'}+\dfrac{HU}{x}=0,\end{aligned}$$
(51)
$$\begin{aligned}&M^{'}=2 x D, \end{aligned}$$
(52)

where \((\prime )\) represents differentiation w.r.t. x. The relation between P(x) and D(x) will be same as given by (38). The system of Eqs. (49)–(52) can be integrated numerically using (38), boundary conditions (39) and the value of \(\delta \) from equation (48).

Case (iii): When \(\alpha =0\) and \(\lambda _{22}=0\). In this case, the similarity variable is not obtained as a combination of the space coordinate and the time coordinate; thus, the similarity solutions cannot be obtained.

Case (iv): When \(\alpha \ne 0\) and \(\lambda _{22}=0\). In this case, the boundary conditions obtained for the flow variables are not independent of the time coordinate; thus, the similarity solutions cannot be obtained.

5 Results and discussion

Using Lie group of transformation method, similarity solutions in two cases are obtained. In Case (i), we obtain the similarity solution with power law shock path which is similar to the solution obtained by Nath and Sinha [32]; in Case (ii), we obtain similarity solutions with exponential law shock path. The set of Eqs. (34)–(37) for power law shock path, i.e., Case (i) and Eqs. (49)–(52) for exponential law shock path, i.e., Case (ii), using relation (38) and the boundary conditions (39) are integrated numerically for the distribution of flow variables density D, magnetic field H, mass M and fluid velocity U between the shock front and the inner expanding surface by the Runge-Kutta method of fourth order using the software Mathematica. For numerical integration in Case (i), the values of flow parameters are taken to be: \(M_{A}^{-2}=0.02, 0.03\); \(\phi =-1.8, -1.85\) and \(G_{0}=0.1, 0.15\). For Case (ii), the values of flow parameters are taken to be: \(M_{A}^{-2}=0.02, 0.06\); \(\theta =-0.4, -0.8\) and \(G_{0}=0.1, 0.2\). The influence of magnetic field on the flow behind the shock is noteworthy when \(M_{A}^{-2}\ge 0.01\) (Rosenau and Frankenthal [34]); thus, in the present problem values of \(M_{A}^{-2}\) are taken to be 0.02, 0.03 and 0.06. The value of adiabatic exponent \(\gamma \) is taken to be as 5/3 in both the cases. For fully ionized gas \(\gamma =5/3\), which is significant to the interstellar medium and it is the most general value seen in real stars.

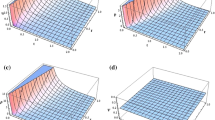
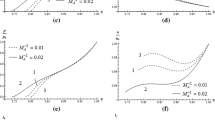
The values of density ratio \(\beta \) and position of inner expanding surface are obtained in Table 1 by considering different values of \(M_{A}^{-2}\), \(\phi \), \(G_{0}\) and \(\gamma =5/3\) for Case (i). Table 2 exhibits the values of density ratio \(\beta \) and position of inner expanding surface for different values of \(M_{A}^{-2}\), \(\theta \), \(G_{0}\) and \(\gamma =5/3\) for Case (ii). From Tables 1 and 2 it is obtained that with increase in value of Alfven-Mach number, the density ratio increases, i.e., the shock strength decreases which can also be inferred by the increase in distance between the shock front and the inner expanding surface with increase in \(M_{A}^{-2}\). Also with increase in \(G_{0}\), the distance of the shock front from the inner expanding surface increases, i.e., the shock strength decreases in the case of power law shock path. But in the case of exponential law shock path, the distance of the shock front from the inner expanding surface decreases with increase in \(G_{0}\), i.e., the shock strength increases. The dispersal of reduced flow variables density (pressure), magnetic field, mass and fluid velocity for Case (i) for different values of flow parameters \(M_{A}^{-2}\), \(\phi \) and \(G_{0}\) are illustrated through Fig. 1a–d. And the dispersal of reduced flow variables density (pressure), magnetic field, mass and fluid velocity for Case (ii) with different values of flow parameters \(M_{A}^{-2}\), \(\theta \) and \(G_{0}\) are illustrated through Fig. 2a–d. It is obtained from Fig. 1, i.e., for Case (i) that reduced magnetic field, reduced mass and reduced fluid velocity decrease, whereas the reduced density ( reduced pressure) increase and decrease after attaining a maximum. From Fig. 2, i.e., for Case (ii), it is obtained that reduced density and fluid velocity increase; however, mass decreases and magnetic field increases slightly and the then decreases after attaining a maximum.

Table 1 Values of \(\beta \) and position of inner expanding surface for different values of \(M_{A}^{-2}\), \(\phi \) and \(G_{0}\) with \(\gamma =5/3\) for power law shock path
Full size table
Table 2 Values of \(\beta \) and position of inner expanding surface for different values of \(M_{A}^{-2}\), \(\theta \) and \(G_{0}\) with \(\gamma =5/3\) for exponential law shock path
Full size table

5.1 Effects of increase in strength of ambient magnetic field on the flow variables and shock strength are

With increase in the strength of magnetic field, i.e., the increase in value of \(M_{A}^{-2}\), the density ratio \(\beta \) increases, i.e., the shock strength decreases for both Cases (i) and (ii). Also the distance of the shock front from the inner expanding surface increases (see Table 1 and Table 2). For power law shock path (Case (i)), the reduced density (pressure), reduced magnetic field and reduced fluid velocity increase with increase in \(M_{A}^{-2}\) (see Fig. 1a, b, d) but the mass decreases near the inner expanding surface (see Fig. 1c). For exponential law shock path (case (ii)), reduced mass and fluid velocity increase (see Fig. 2c, d); however, magnetic field increases in general (see Fig. 2b). Reduced density decreases near shock but increases as the inner expanding surface is approached in general (see Fig. 2a).

5.2 Effects of increase in values of ambient density variation index \(\phi \) on the flow variables

With increase in ambient density variation index \(\phi \), the reduced density (pressure), reduced magnetic field and reduced fluid velocity increase (see Fig. 1a, b, d); however, the reduced mass decreases (see Fig. 1c).

5.3 Effects of increase in values of \(G_{0}\) on the flow variables and shock strength

For power law shock path (Case (i)), with increase in the value of gravitational parameter \(G_{0}\), the distance of the shock front from the inner expanding surface increases (see Table 1) which infers to the decrease in shock strength. Whereas in case of exponential law shock path (Case (ii)), the gravitational parameter has reverse effect on shock strength as that of the Case (i). For Case (i), the reduced density (pressure), reduced magnetic field and reduced fluid velocity increase (see Fig. 1a, b, d); however, reduced mass decreases with increase in \(G_{0}\) (see Fig. 1c). For Case (ii), reduced density increases in general and fluid velocity increases (see Fig. 2a, d); however, mass decreases (see Fig. 2c). Reduced magnetic field increases near shock but decreases as the inner expanding surface is approached (see Fig. 2b).

5.4 Effects of increase in values of ambient magnetic field variation index \(\theta \) on the flow variables

Reduced density and fluid velocity increase (see Fig. 2a, d) however, mass decreases (see Fig. 2c) with increase in \(\theta \). Reduced magnetic field increases near shock but decreases as the inner expanding surface is approached (see Fig. 2b).

Fig. 1
figure 1

Dispersal of the flow variables in the region behind the shock front with \(\gamma =5/3\) for power law shock path (Case (i)). a Reduced density \((\rho /\rho _{2})\) (= reduced pressure \(p/ p_{2}\)); b reduced magnetic field \((h/h_{2})\); c reduced mass \((m/m_{2})\); d reduced velocity \((u/u_{2})\): 1.\(M_{A}^{-2}=0.02, \phi =-1.8, G_{0}=0.1\); 2. \(M_{A}^{-2}=0.02, \phi =-1.8, G_{0}=0.15\); 3. \(M_{A}^{-2}=0.02, \phi =-1.85, G_{0}=0.1\); 4. \(M_{A}^{-2}=0.02, \phi =-1.85, G_{0}=0.15\); 5. \(M_{A}^{-2}=0.03, \phi =-1.8, G_{0}=0.1\); 6. \(M_{A}^{-2}=0.03, \phi =-1.8, G_{0}=0.15\); 7.\(M_{A}^{-2}=0.03, \phi =-1.85, G_{0}=0.1\); 8.\(M_{A}^{-2}=0.03, \phi =-1.85, G_{0}=0.15\)

Full size image
Fig. 2
figure 2

Dispersal of the flow variables in the region behind the shock front with \(\gamma =5/3\) for exponential law shock path (Case (ii)). a Reduced density \((\rho /\rho _{2})\) (= reduced pressure \(p/ p_{2}\)); b reduced magnetic field \((h/h_{2})\); c reduced mass \((m/m_{2})\); d reduced velocity \((u/u_{2})\): 1.\(M_{A}^{-2}=0.02, \theta =-0.4, G_{0}=0.1\); 2. \(M_{A}^{-2}=0.02, \theta =-0.4, G_{0}=0.2\); 3. \(M_{A}^{-2}=0.02, \theta =-0.8, G_{0}=0.1\); 4. \(M_{A}^{-2}=0.02, \theta =-0.8, G_{0}=0.2\); 5. \(M_{A}^{-2}=0.06, \theta =-0.4, G_{0}=0.1\); 6. \(M_{A}^{-2}=0.06, \theta =-0.4, G_{0}=0.2\); 7.\(M_{A}^{-2}=0.06, \theta =-0.8, G_{0}=0.1\); 8.\(M_{A}^{-2}=0.06, \theta =-0.8, G_{0}=0.2\)

Full size image

6 Conclusions

Propagation of cylindrical shock wave in a self-gravitating perfect gas in the presence of axial magnetic field under isothermal flow condition using Lie group of transformation method is investigated. Numerical solutions for both the cases of power law shock path and exponential law shock path are obtained. This study can have potential applications like analysis of data from exploding wire experiments and axially symmetric hypersonic flow problems associated with meteors or re-entry vehicles (see [35, 36]). From the present study, the following can be concluded:

  1. (i)

    The increase in value of Alfven-Mach number leads to an increase in the density ratio across the shock, which infers to the decrease in shock strength for both the cases of power law and exponential law shock path.

  2. (ii)

    In case of power law shock path, with increase in \(G_{0}\), the distance of the shock front from the inner expanding surface increases, i.e., the shock strength decreases; however, increase in value of \(G_{0}\) in case of exponential law shock path has reverse effect on shock strength as that of \(G_{0}\) in case of power law shock path.

  3. (iii)

    The reduced fluid velocity, density (pressure) and magnetic field increase with an increase in the strength of ambient magnetic field in case of power law shock path. Increase in values of gravitational parameter has similar effects on reduced density (pressure), magnetic field and fluid velocity as that of ambient magnetic field on these flow variables.

  4. (iv)

    In case of exponential law shock path, the increase in \(G_{0}\) or \(\theta \) has similar effects on flow variables reduced mass and fluid velocity.

  5. (v)

    It is found that the flow variables reduced magnetic field, reduced mass and reduced velocity decrease; however, reduced density (pressure) increase and decrease after attaining a maximum value as we move from the shock front to the inner expanding surface for case of power law shock path. In case of exponential law shock path, it is obtained that reduced density and fluid velocity increase; however, mass decreases and magnetic field increases slightly and the then decreases after attaining a maximum.