Abstract
In this study, we propose and analyze a new mathematical model formulated by partial differential equations in order to better understand the mechanisms and dynamics of hepatitis B virus (HBV) infection in vivo. The proposed model incorporates the intracellular HBV DNA-containing capsids, spatial diffusion in both capsids and viruses, and adaptive immune response exerted by cytotoxic T lymphocytes and antibodies. Further, the infection process is modeled by a general incidence function that includes many cases existing in the literature. We first show the global existence, uniqueness, positivity and boundedness of solutions. The global stability and instability of equilibria are established by means of Lyapunov’s direct and indirect methods. Finally, numerical simulations are presented to illustrate the dynamical behaviors of the model and to support the theoretical results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Recently, modeling the dynamics of HBV infection with capsids has attracted interest of many researchers. In 2015, Manna and Chakrabarty [1] improved the model of Murray et al. [2] by proposing two models. The first model was formulated by four ordinary differential equations (ODEs) and the second one by delay differential equations (DDEs) in order to describe the time delay between the process of infection of cells and the production of new virions. In 2017, they extended the second DDE model by considering another delay in the production of matured capsids [3]. Guo et al. [4] considered a third delay in the production of matured viruses and they proposed PDE model with general incidence rate and spatial diffusion only in the viruses. The spatial mobility of both capsids and viruses is considered in [5, 6]. In 2018, Manna [7] extended the model presented in [5] by taking into account the role of cytotoxic T lymphocyte (CTL) immune response in HBV infection. Another model with CTL immune response and nonlinear incidence was proposed by Xu and Geng [8]. This last model is a generalization of both ODE and DDE models with bilinear incidence introduced in [9].
For HBV infection, immune responses of the host individual acts as a significant defense mechanism against the infection progression by diminishing the viral load and clearing the infected hepatocytes [10, 11]. Generally, the effective immune response against HBV infection in an infected host individual comprises of the combination of innate and adaptive immunity of the host [12]. Innate immunity actually takes part in very early stage of the infection process to regulate the infection spread and activates adaptive immune response [12]. The adaptive immunity consists of a complex web of effector cells, namely, antibody B cells and CTLs [12]. As a consequence of adaptive immune response, the reinfection process slows down due to the neutralization of free virus particles by B cells and clearance of infected hepatocytes by CTLs through cytolytic and non-cytolytic mechanisms [12]. Therefore, incorporation of adaptive immunity in the modeling approach and their analysis seems to be very important in order to get valuable insights of the complex dynamical behaviors of the HBV infection process. But the above mentioned models for HBV infection and their analysis did not incorporate the effect of the adaptive immunity in the modeling approach. Also to the best of our knowledge, there does not exist any work in literature which incorporates both capsid and adaptive immunity for the modeling of HBV infection process in vivo.
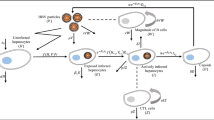
The above discussions provide us strong motivation to study an HBV infection model incorporating both capsid and adaptive immunity. Thus, we propose the following reaction-diffusion system for HBV infection in vivo:
where H(x, t), I(x, t), D(x, t), V(x, t), W(x, t) and Z(x, t) denote the densities of uninfected hepatocytes, infected hepatocytes, HBV DNA-containing capsids, virions, antibodies and CTL cells at position x and time t, respectively. Uninfected hepatocytes are produced at rate s, die at rate \(\mu H\) and become infected by the virions at rate f(H, I, V)V. The parameter \(\delta \) is the death rate of infected hepatocytes and capsids. However, \(\sigma \) and \(\widetilde{\sigma }\) are the death rates of CTL cells and antibodies, respectively. The parameters a, \(\beta \) and c are, respectively, the production rate of capsids from infected hepatocytes, the rate at which the capsids are transmitted to blood in order to get converted into virions, and the clearance rate of virions. Infected hepatocytes are killed by CTL cells at rate pIZ while virions are neutralized by antibodies at rate \(\widetilde{p}VW\). Antibodies develop in response to virions at rate \(\widetilde{q}VW\), and CTL cells expand in response to viral antigens derived from infected hepatocytes at rate qIZ. Further, the first delay parameter \(\tau _{1}\) denotes the time needed for infected hepatocytes to produce capsids after viral entry and the factor \(e^{-\alpha _{1}\tau _{1}}\) accounts for the probability of surviving from time \(t-\tau _{1}\) to time t, where \(\alpha _{1}\) is the death rate for infected but not yet virus-producing cells. The second delay parameter \(\tau _{2}\) represents the time spent in the production of matured intracellular HBV DNA-containing capsids which in turn contributes to the production of virions. The probability of survival of immature capsids is given by \(e^{-\alpha _{2}\tau _{2}}\) and the average life time of an immature capsid is given by \(\frac{1}{\alpha _{2}}\). The third delay parameter \(\tau _{3}\) denotes the time necessary for the newly produced capsids to become virions and the factor \(e^{-\alpha _{3}\tau _{3}}\) accounts for the probability of surviving from time \(t-\tau _{3}\) to time t, where \(\frac{1}{\alpha _{3}}\) is the average life time of an immature virion. Finally, \(\triangle \) is the Laplacian operator, and \(d_{D}\) and \(d_{V}\) are the diffusion coefficients of capsids and virions, respectively.
As it has been considered in [13, 14], we assume that the general incidence function f(H, I, V) is continuously differentiable in the interior of \(\mathbb {R}^{3}_{+}\) and satisfies the following assumptions:
- (\(A_{1}\)):
-
\(f(0,I,V)=0\), for all \(I\ge 0\) and \( V\ge 0\);
- (\(A_{2}\)):
-
f(H, I, V) is a strictly monotone increasing function with respect to H, for any fixed \(I\ge 0\) and \( V\ge 0\);
- (\(A_{3}\)):
-
f(H, I, V) is a monotone decreasing function with respect to I and V, i.e, \(\frac{\partial f}{\partial I}(H,I,V)\le 0\) and \(\frac{\partial f}{\partial V}(H,I,V)\le 0\) for all \(H\ge 0\), \(I\ge 0\) and \(V\ge 0\).
The above assumptions are biologically reasonable and consistent with the reality. For more details on the biological meanings of these three assumptions, we refer the reader to the works [15, 16]. In addition, the general incidence function f(H, I, V) includes many forms such as the bilinear incidence which was used recently in [7], the saturation incidence presented in [17], the standard incidence function used in [18], the Beddington-DeAngelis functional response proposed in [19, 20] and used in [21], the Crowley-Martin functional response introduced in [22] and used in [23], and the Hattaf-Yousfi functional response [24] which was recently used in [25, 26].
The reaction-diffusion system (1) is subjected to the following initial conditions
and the following zero-flux boundary conditions
where \(\tau =\max \{\tau _{1},\tau _{2},\tau _{3}\}\), \(\Omega \) is a bounded domain in \(\mathbb {R}^{n}\) with smooth boundary \(\partial \Omega \), and \(\displaystyle \frac{\partial }{\partial \nu }\) denotes the outward normal derivative on \(\partial \Omega \). Biologically speaking, the zero-flux boundary conditions mean that the capsids and virions do not have any movement across the boundary \(\partial \Omega \).
The main purpose of this study is to investigate about the global dynamical behaviors of the proposed generalized delayed reaction-diffusion model of HBV infection. We organize the rest of this paper as follows. In “Well-posedness and equilibria” section, we establish the well-posedness of the model and the threshold parameters for the existence of equilibria. “Stability analysis” section is devoted for the stability analysis of five equilibria. In “Numerical simulations” section, we present some numerical simulations to support the analytical results and to further illustrate the dynamical behaviors of the model. Finally, some biological and mathematical conclusions are given in the last section.
Well-Posedness and Equilibria
In this section, we prove the existence, uniqueness, non-negativity and boundedness of solutions of the proposed problem (1)–(3) as they represent the densities of hepatocytes, capsids, virions, antibodies and CTL cells. Furthermore, we define five threshold parameters for the existence of equilibria.
Let \(\mathcal {X}=C(\overline{\Omega },\mathbb {R}^{6})\) be the Banach space of continuous functions from \(\overline{\Omega }\) to \(\mathbb {R}^{6}\), and \(\mathcal {C}=C([-\tau ,0],\mathcal {X})\) be the Banach space of continuous functions from \([-\tau ,0]\) to \(\mathcal {X}\) equipped with the usual supremum norm. For convenience, we identify an element \(\varphi \in \mathcal {C}\) as a function from \(\overline{\Omega }\times [-\tau ,0]\) to \(\mathbb {R}^{6}\) defined by \(\varphi (x,\theta )=\varphi (\theta )(x)\). For any continuous function \(\omega (.)\) : \([-\tau ,b)\rightarrow \mathcal {X}\) for \(b>0\), we define \(\omega _{t}\in \mathcal {C}\) by \(\omega _{t}(\theta )=\omega (t+\theta )\), \(\theta \in [-\tau ,0]\).
Theorem 1
For any given initial condition \(\phi \in \mathcal {C}\) satisfying (2), there exists a unique solution of the problem (1)–(3) defined on \([0,+\infty )\) and this solution remains non-negative and bounded for all \(t\ge 0\).
Proof
For any \(\phi =(\phi _{1},\phi _{2},\phi _{3},\phi _{4},\phi _{5},\phi _{6})^{T}\in \mathcal {C}\) and \(x\in \overline{\Omega }\), we define \(F=(F_{1},F_{2},F_{3},F_{4},F_{5},F_{6}) : \mathcal {C}\rightarrow \mathcal {X}\) by
Then the system (1)–(3) can be rewritten as the following abstract functional differential equation:
where \(\omega =(H,I,D,V,W,Z)^{T}\), \(\phi =(\phi _{1},\phi _{2},\phi _{3},\phi _{4},\phi _{5},\phi _{6})^{T}\) and \(A\omega =(0,0,d_{D}\Delta D,d_{V}\Delta V,0,0)^{T}\). Obviously, we observe that F is locally Lipschitz in \(\mathcal {C}\). It follows from [27,28,29,30,31] that there exists a unique local solution of system (4) on \([0,T_{max})\), where \(T_{max}\) is the maximal existence time for solution of (4).
Clearly, \(\mathbf 0 =(0,0,0,0,0,0)\) is a lower-solution of the problem (1)–(3) and hence, we have \(H(x,t)\ge 0\), \(I(x,t)\ge 0\), \(D(x,t)\ge 0\), \(V(x,t)\ge 0\), \(W(x,t)\ge 0\) and \(Z(x,t)\ge 0\).
Now, it remains to prove the boundedness of solutions. For this purpose, let us assume
Thus, we have
where \(\gamma =\min \{\mu ,\delta ,\sigma \}\) and it is obvious that \(0<e^{-\alpha _{1}\tau _{1}}<1\). Hence, we obtain
This shows that H, I and Z are bounded. Now, using the bound for I and the system (1)–(3), we notice that D satisfies the following system:
where \(M_{1}=\max \left\{ \frac{s}{\gamma },\max _{x\in \overline{\Omega }}\{e^{-\alpha _{1}\tau _{1}}\phi _{1}(x,-\tau _{1})+\phi _{2}(x,0)+ \frac{p}{q}\phi _{6}(x,0)\}\right\} \).
Let \(\widetilde{D}(t)\) be a solution to the following ODE:
Thus, we have \(\widetilde{D}(t)\le \max \left\{ \frac{aM_{1}e^{-\alpha _{2}\tau _{2}}}{\beta +\delta },\max _{x\in \overline{\Omega }}\phi _{3}(x,0)\right\} \) for all \(t\in [0,T_{max})\). Now using the comparison principle [32], we can conclude that \(D(x,t)\le \widetilde{D}(t)\). Therefore, we obtain
Now, using the bound for D and the system (1)–(3), we observe that V satisfies the following system:
where \(M_{2}=\max \left\{ \frac{aM_{1}e^{-\alpha _{2}\tau _{2}}}{\beta +\delta },\max _{x\in \overline{\Omega }}\phi _{3}(x,0)\right\} \). Let \(\widetilde{V}(t)\) and \(\widetilde{W}(t)\) be the solution of the following system of ODEs:
Let us assume \(T_{1}(t)=\widetilde{V}(t)+\frac{\widetilde{p}}{\widetilde{q}}\widetilde{W}(t)\). Then, we obtain
where \(\gamma _{1}=\min \{c,\widetilde{\sigma }\}\). Hence, we have
Again using the comparison principle [32], we conclude that \(V(x,t)+\frac{\widetilde{p}}{\widetilde{q}}W(x,t)\le M_{3}\) for all \((x,t)\in \overline{\Omega }\times [0,T_{max})\). This implies that V and W are bounded.
The above analysis confirms the boundedness of H(x, t), I(x, t), D(x, t), V(x, t), W(x, t) and Z(x, t) on \(\overline{\Omega }\times [0,T_{max})\) and further from the standard theory of semi-linear parabolic PDEs we have \(T_{max}=+\infty \) [33]. This completes the proof. \(\square \)
Now, we discuss about all the biologically feasible spatially homogeneous equilibria for our proposed model (1). Any spatially homogeneous equilibrium point \(E=(\widehat{H},\widehat{I},\widehat{D},\widehat{V},\widehat{W},\widehat{Z})\) of the model (1) satisfies the following system of algebraic equations:
Clearly from the above system of equations (5), we can notice that \(E_{0}=(H_{0},0,0,0,0,0)\) represents a unique infection-free equilibrium for the model (1) with \(H_{0}=\frac{s}{\mu }\) and it exists always. The basic reproduction number of the model (1) is given by
and it represents the average number of freshly infected hepatocytes from one infected hepatocyte when the infection sets off.
Let us first consider \(\widehat{W}=0\) and \(\widehat{Z}=0\) and then we have the following equation
with \(\widehat{I}=\frac{s-\mu \widehat{H}}{\delta }e^{-\alpha _{1}\tau _{1}}\) and \(\widehat{V}=\frac{a\beta (s-\mu \widehat{H})}{c\delta (\beta +\delta )}e^{-\alpha _{1}\tau _{1}-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}}\). Since \(\widehat{I}\) represents the number of infected hepatocytes, we need to have \(\widehat{I}\ge 0\) and this condition leads to \(\widehat{H}\le \frac{s}{\mu }\). Now, we define a function \(G_{1}\) on the closed interval \([0,s/\mu ]\) as follows
Then, we have
and
It can be easily observed that \(G_{1}(s/\mu )>1\) if \(R_{0}>1\). From the hypotheses \((A_{2}){-}(A_{3})\) on the general incidence function f(H, I, V), we obtain \(G_{1}'(H)>0\) and this implies that \(G_{1}\) is a strictly increasing function of H. Therefore, for \(R_{0}>1\) we have a unique immune-free equilibrium \(E_{1}=(H_{1},I_{1},D_{1},V_{1},0,0)\), where \(H_{1}\in (0,s/\mu )\), \(I_{1}=\frac{(s-\mu H_{1})}{\delta e^{\alpha _{1}\tau _{1}}}\), \(D_{1}=\frac{a(s-\mu H_{1})}{\delta (\beta +\delta )e^{\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}}}\) and \(V_{1}=\frac{a\beta (s-\mu H_{1})}{c\delta (\beta +\delta )e^{\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}}\).
Now, let us assume that \(\widehat{W}\ne 0\) and \(\widehat{Z}=0\), and in this case, we find \(\widehat{V}=\frac{\widetilde{\sigma }}{\widetilde{q}}\). Then, from the first two equations of the system (5), we obtain
Again, since \(\widehat{W}\) represents the number of antibody immune cells, we need to have \(\widehat{W}\ge 0\), i.e., \(\widehat{W}=\frac{a\beta \widetilde{q}(s-\mu \widehat{H})}{\delta (\beta +\delta )\widetilde{p}\widetilde{\sigma }} e^{-\alpha _{1}\tau _{1}-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}}-\frac{c}{\widetilde{p}}\ge 0\). This criterion leads to \(\widehat{H}\le \frac{s}{\mu }-\frac{c\delta (\beta +\delta )\widetilde{\sigma }}{a\beta \mu \widetilde{q}} e^{\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}\). Let us consider
Then, we have \(G_{2}(0)=-\frac{s\widetilde{\sigma }}{\widetilde{q}}<0\) and \(G_{2}'(H)=\frac{\partial f}{\partial H}- \frac{\mu }{\delta }e^{-\alpha _{1}\tau _{1}}\frac{\partial f}{\partial I}+\frac{\mu \widetilde{q}}{\widetilde{\sigma }}\). Now, using the hypotheses \((A_{2}){-}(A_{3})\) on the general incidence function f(H, I, V), we have \(G_{2}'(H)>0\) and this implies that \(G_{2}\) is also a strictly increasing function of H. Now, we define antibody immune response reproduction number as
which denotes the average number of antibody immune cells activated by virus in case of successful HBV infection and CTL immune response is yet to be established [34]. Here, \(\widetilde{q}\) is the activation rate of antibody immune response, \(\frac{1}{\widetilde{\sigma }}\) represents the average life span of antibody immune cells and \(V_{1}\) denotes the number of viruses at the immune-free equilibrium \(E_{1}\).
Note that when \(R_{1}>1\), then \(V_{1}>\frac{\widetilde{\sigma }}{\widetilde{q}}\) and \(H_{1}<\frac{s}{\mu }- \frac{c\delta (\beta +\delta )\widetilde{\sigma }}{a\beta \mu \widetilde{q}}e^{\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}\) and we have
Therefore, the model (1) admits a unique infection equilibrium with only antibody immune response \(E_{2}=(H_{2},I_{2},D_{2},V_{2},W_{2},0)\), where \(H_{2}\in \left( 0,\frac{s}{\mu }-\frac{c\delta (\beta +\delta )\widetilde{\sigma }}{a\beta \mu \widetilde{q}} e^{\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}\right) \), \(I_{2}=\frac{s-\mu H_{2}}{\delta }e^{-\alpha _{1}\tau _{1}}\), \(D_{2}=\frac{aI_{2}}{\beta +\delta }e^{-\alpha _{2}\tau _{2}}\), \(V_{2}=\frac{\widetilde{\sigma }}{\widetilde{q}}\) and \(W_{2}=\frac{a\beta \widetilde{q}(s-\mu H_{2})}{\delta (\beta +\delta )\widetilde{p}\widetilde{\sigma }} e^{-\alpha _{1}\tau _{1}-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}}-\frac{c}{\widetilde{p}}\), provided \(R_{1}>1\).
Now, we consider the case when \(\widehat{W}=0\) and \(\widehat{Z}\ne 0\), and then we find \(\widehat{I}=\frac{\sigma }{q}\), \(\widehat{D}=\frac{a\sigma }{q(\beta +\delta )}e^{-\alpha _{2}\tau _{2}}\) and \(\widehat{V}=\frac{a\beta \sigma }{cq(\beta +\delta )}e^{-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}}\). From the first equation of the system (5), we obtain
From the second equation of the system (5), we get \(\widehat{Z}=\frac{q}{p\sigma }(s-\mu \widehat{H})e^{-\alpha _{1}\tau _{1}}-\frac{\delta }{p}\) and this leads to \(\widehat{H}\le \frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\) since \(\widehat{Z}\) denotes the number of CTL cells. Let us denote
Then, we obtain \(G_{3}(0)=-\frac{csq(\beta +\delta )}{a\beta \sigma }e^{\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}<0\) and \(G_{3}'(H)=\frac{\partial f}{\partial H}+\frac{cq\mu (\beta +\delta )}{a\beta \sigma }e^{\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}\). Then using the hypothesis \((A_{2})\) on the general incidence function f(H, I, V), we conclude that \(G_{3}\) is a strictly increasing function of H as \(G_{3}'(H)>0\). Now, we define CTL immune response reproduction number as
which represents the average number of CTL immune cells activated by infected hepatocytes in case of successful HBV infection and antibody immune response is yet to be established [34]. Here, q is the activation rate of CTL immune response, \(\frac{1}{\sigma }\) represents the average life span of CTL immune cells and \(I_{1}\) denotes the number of infected hepatocytes at the immune-free equilibrium \(E_{1}\).
Note that when \(R_{2}>1\), then \(I_{1}>\frac{\sigma }{q}\) and \(H_{1}<\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\), and we have
Therefore, the model (1) admits a unique infection equilibrium with only CTL immune response \(E_{3}=(H_{3},I_{3},D_{3},V_{3},0,Z_{3})\), where \(H_{3}\in \left( 0,\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\right) \), \(I_{3}=\frac{\sigma }{q}\), \(D_{3}=\frac{a\sigma }{q(\beta +\delta )}e^{-\alpha _{2}\tau _{2}}\), \(V_{3}=\frac{a\beta \sigma }{cq(\beta +\delta )}e^{-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}}\) and \(Z_{3}=\frac{q(s-\mu H_{3})}{p\sigma }e^{-\alpha _{1}\tau _{1}}\frac{\delta }{p}\), provided \(R_{2}>1\).
Now, we consider \(\widehat{W}\ne 0\) and \(\widehat{Z}\ne 0\), and then we have \(\widehat{I}=\frac{\sigma }{q}\), \(\widehat{V}=\frac{\widetilde{\sigma }}{\widetilde{q}}\) and \(\widehat{D}=\frac{a\sigma }{q(\beta +\delta )}e^{-\alpha _{2}\tau _{2}}\). From the first equation of the system (5), we get
From the second equation of the system (5), we obtain \(\widehat{Z}=\frac{q(s-\mu \widehat{H})}{p\sigma }e^{-\alpha _{1}\tau _{1}}-\frac{\delta }{p}\) and this leads to \(\widehat{H}\le \frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\) as we need to have \(\widehat{Z}\ge 0\). Let us define
Then, we have \(G_{4}(0)=-\frac{s\widetilde{q}}{\widetilde{\sigma }}<0\) and \(G_{4}'(H)=\frac{\partial f}{\partial H}+\frac{\widetilde{q}\mu }{\widetilde{\sigma }}>0\) using the hypothesis \((A_{2})\). Here, we define competitive CTL immune response reproduction number as
which represents the average number of CTL immune cells activated by infected hepatocytes when the antibody immune response has already been established [34]. So if \(R_{3}>1\), then we have \(I_{2}>\frac{\sigma }{q}\), \(H_{2}<\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\) and
Therefore, there exists a unique \(H_{4}\in \left( 0,\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\right) \) such that \(G_{4}(H_{4})=0\). Now, we define competitive antibody immune response reproduction number as
which denotes the average number of antibody immune cells activated by viruses when CTL immune response has already been established [34]. From the fourth equation of the system (5), we obtain \(W_{4}=\frac{a\widetilde{q}\beta \sigma }{\widetilde{p}q\widetilde{\sigma }(\beta +\delta )}e^{-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}} -\frac{c}{\widetilde{p}}=\frac{c}{\widetilde{p}}(R_{4}-1)\).
Therefore, the model (1) admits a unique infection equilibrium with both the antibody and CTL immune responses (i.e., in presence of adaptive immune responses) \(E_{4}=(H_{4},I_{4},D_{4},V_{4},W_{4},Z_{4})\), where \(H_{4}\in \left( 0,\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\right) \), \(I_{4}=\frac{\sigma }{q}\), \(D_{4}=\frac{a\sigma }{q(\beta +\delta )}e^{-\alpha _{2}\tau _{2}}\), \(V_{4}=\frac{\widetilde{\sigma }}{\widetilde{q}}\), \(W_{4}=\frac{c}{\widetilde{p}}(R_{4}-1)\) and \(Z_{4}=\frac{q(s-\mu H_{4})}{p\sigma }e^{-\alpha _{1}\tau _{1}}-\frac{\delta }{p}\), provided \(R_{3}>1\) and \(R_{4}>1\).
Summarizing the above discussions, we get the following theorem.
Theorem 2
If \(R_{0}\le 1\), the model (1) has a unique infection-free equilibrium \(E_{0}=(H_{0},0,0,0,0,0)\) with \(H_{0}=\frac{s}{\mu }\). If \(R_{0}>1\), the model (1) has additional four equilibria along with the equilibrium \(E_{0}\). For \(R_{0}>1\),
-
(i)
there always exists a unique immune-free equilibrium \(E_{1}=(H_{1},I_{1},D_{1},V_{1},0,0)\), where \(H_{1}\in (0,s/\mu )\) and \(I_{1},D_{1},V_{1}>0\);
-
(ii)
there exists a unique infection equilibrium with only antibody immune response \(E_{2}=(H_{2},I_{2},D_{2},V_{2},W_{2},0)\), where \(H_{2}\in \left( 0,\frac{s}{\mu }-\frac{c\delta (\beta +\delta )\widetilde{\sigma }}{a\beta \mu \widetilde{q}} e^{\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3}}\right) \) and \(I_{2},D_{2},V_{2},W_{2}>0\) when \(R_{1}>1\);
-
(iii)
there exists a unique infection equilibrium with only CTL immune response \(E_{3}=(H_{3},I_{3},D_{3},V_{3},0,Z_{3})\), where \(H_{3}\in \left( 0,\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\right) \) and \(I_{3},D_{3},V_{3},Z_{3}>0\) when \(R_{2}>1\);
-
(iv)
there exists a unique infection equilibrium with adaptive immune response \(E_{4}=(H_{4},I_{4},D_{4},V_{4},W_{4},Z_{4})\), where \(H_{4}\in \left( 0,\frac{s}{\mu }-\frac{\delta \sigma }{q\mu }e^{\alpha _{1}\tau _{1}}\right) \) and \(I_{4},D_{4},V_{4},W_{4},Z_{4}>0\) when \(R_{1}>1\), \(R_{2}>1\), \(R_{3}>1\) and \(R_{4}>1\).
Stability Analysis
In this section, we investigate the stability properties of all five possible equilibria of the delayed spatiotemporal system (1)–(3). We study the stability properties through the linearization technique and constructing Lyapunov functions. Now, we will present some useful notations before proceeding further. Let \(0=\lambda _{1}<\lambda _{2}<\cdots<\lambda _{n}<\cdots \) be the eigenvalues of the operator \(-\Delta \) on \(\Omega \) in presence of the homogeneous Neumann boundary conditions and \(\mathcal {F}(\lambda _{i})\) be the eigenfunction space corresponding to the eigenvalue \(\lambda _{i}\) in \(C^{1}(\Omega )\). Let \(\{\varphi _{ij} : j=1,2, \ldots , \dim \mathcal {F}(\lambda _{i})\}\) denotes an orthonormal basis of \(\mathcal {F}(\lambda _{i})\), \(\mathbb {X}=[C^{1}(\Omega )]^{6}\) and \(\mathbb {X}_{ij}=\{d\varphi _{ij} : d\in \mathbb {R}^{6}\}\). Then we have
Let \(E_{*}=(H_{*},I_{*},D_{*},V_{*},W_{*},Z_{*})\) be an arbitrary spatially homogeneous equilibrium of the system (1)–(3) and assume the following perturbations about the components of the equilibrium \(E_{*}\):
Linearizing the model (1) about \(E_{*}\), we obtain the following linearized system:
where
Note that the partial derivatives \(\frac{\partial f}{\partial H}\), \(\frac{\partial f}{\partial I}\) and \(\frac{\partial f}{\partial V}\) in the matrices \(\mathfrak {J}_{1}\) and \(\mathfrak {J}_{2}\) are evaluated at the equilibrium \(E_{*}\). We define \(\mathcal {L}U=\mathcal {D}\Delta U+\mathfrak {J}_{1}U(x,t)+\mathfrak {J}_{2}U(x,t-\tau _{1})+\mathfrak {J}_{3}U(x,t-\tau _{2})+\mathfrak {J}_{4}U(x,t-\tau _{3})\). Now, \(\mathbb {X}_{i}\) is invariant under the operator \(\mathcal {L}\) for each \(i\ge 1\), \(\xi \) is an eigenvalue of \(\mathcal {L}\) if and only if it is a root of the equation \(\det (-\lambda _{i}\mathcal {D}+\mathfrak {J}_{1}+\mathfrak {J}_{2}e^{-\xi \tau _{1}}+\mathfrak {J}_{3}e^{-\xi \tau _{2}}+ \mathfrak {J}_{4}e^{-\xi \tau _{3}}-\xi \mathbb {I}_{6})=0\) for some \(i\ge 1\) and in this case, there exists an eigenvector in \(\mathbb {X}_{i}\).
Theorem 3
The infection-free equilibrium \(E_{0}\) is globally asymptotically stable if \(R_{0}\le 1\) and it becomes unstable if \(R_{0}>1\).
Proof
Let us define a Lyapunov function \(L_{0}(t)\) as follows:
where \(H_{0}=\frac{s}{\mu }\). We denote \(\psi (x,t)=\psi \) and \(\psi (x,t-\tau _{i})=\psi _{\tau _{i}}\) for \(i=1,2,3\) and \(\psi \in \{H,I,D,V,W,Z\}\) for the sake of notational simplicity. Taking the derivative of \(L_{0}\) with respect to time t along the solution trajectories of the system (1)–(3), we obtain
Now, using the zero-flux boundary conditions (3) and the divergence theorem, we obtain
Thus, we eventually have
Further, from the hypothesis \((A_{2})\) on the general incidence function we know that f(H, I, V) is a strictly increasing function with respect to H and this eventually gives rise to the following inequality:
Hence, we have \(\frac{dL_{0}}{dt}\le 0\) if \(R_{0}\le 1\) and \(\frac{dL_{0}}{dt}=0\) holds if and only if \(H=H_{0}=\frac{s}{\mu }\), \(I=0\), \(D=0\), \(V=0\), \(W=0\) and \(Z=0\). This indicates that the singleton set \(\{E_{0}\}=\{(\frac{s}{\mu },0,0,0,0,0)\}\) is the largest invariant set in \(\{(H,I,D,V,W,Z)\in \mathbb {R}_{+}^{6}|\frac{dL_{0}}{dt}=0\}\). Therefore, it follows from LaSalle invariance principle [35] that the infection-free equilibrium \(E_{0}\) is globally asymptotically stable whenever \(R_{0}\le 1\).
Now, it remains to investigate the stability property of the infection-free equilibrium \(E_{0}\) when \(R_{0}>1\). Through some simple computations, we arrive at the following characteristic equation at the infection-free equilibrium \(E_{0}\):
Easily from the above Eq. (11), we can observe that \(\xi =-\mu (<0)\), \(\xi =-\widetilde{\sigma }(<0)\) and \(\xi =-\sigma (<0)\) represent three roots of the characteristic equation (11). The remaining roots of the Eq. (11) are obtained by solving the equation \(g_{i}(\xi )=0\), where
Now, since \(\lambda _{1}=0\), we have \(g_{1}(0)=c\delta (\beta +\delta )-a\beta f(H_{0},0,0)e^{-(\alpha _{1}\tau _{1}+\alpha _{2}\tau _{2}+\alpha _{3}\tau _{3})}=c\delta (\beta +\delta )(1-R_{0})\) and for \(R_{0}>1\), we obtain \(g_{1}(0)<0\). Also, we have \(\lim _{\xi \rightarrow +\infty }g_{i}(\xi )=+\infty \). Therefore, there exists a real positive root \(\xi ^{*}\) of \(g_{1}(\xi )=0\) and this in turn implies that the infection-free equilibrium \(E_{0}\) is unstable whenever \(R_{0}>1\). This completes the proof. \(\square \)
Before presenting the remaining analytical results, we introduce the function \(\mathbb {G}(u)=u-1-\ln u\) for \(u>0\). Note that \(\mathbb {G}(u)=0\) if and only if \(u=1\). Further, we introduce the following hypothesis:

where \(I_{i}\) and \(V_{i}\) denote the infected hepatocyte and virus components of the equilibrium \(E_{i}\) for \(i=1,2,3,4\).
Theorem 4
Let us assume that the hypothesis \((A_{4})\) and the inequality \(R_{0}>1\) hold. Then the immune-free equilibrium \(E_{1}\) is globally asymptotically stable if \(R_{1}\le 1\) and \(R_{2}\le 1\). It becomes unstable if \(R_{1}>1\) or \(R_{2}>1\).
Proof
Let us define a Lyapunov function \(L_{1}(t)\) as follows:
where \(H_{1}\), \(I_{1}\), \(D_{1}\) and \(V_{1}\) denote the uninfected hepatocyte, infected hepatocyte, capsid and virus components of the immune-free equilibrium \(E_{1}\), respectively. Taking the derivative of \(L_{1}\) with respect to time t along the solution trajectories of the system (1)–(3), we obtain
Now, again using the zero-flux boundary conditions (3) and the divergence theorem, we obtain
and
This leads to
Further, from the hypothesis \((A_{2})\) on the general incidence function we know that f(H, I, V) is a strictly increasing function with respect to H and this eventually gives rise to the following inequality:
Hence, using the hypothesis \((A_{4})\) we obtain \(\frac{dL_{1}}{dt}\le 0\) if \(R_{1}\le 1\) and \(R_{2}\le 1\). Also, we have \(\frac{dL_{1}}{dt}=0\) holds if and only if \(H=H_{1}\), \(I=I_{1}\), \(D=D_{1}\), \(V=V_{1}\), \(W=0\) and \(Z=0\). This indicates that the singleton set \(\{E_{1}\}=\{(H_{1},I_{1},D_{1},V_{1},0,0)\}\) is the largest invariant set in \(\{(H,I,D,V,W,Z)\in \mathbb {R}_{+}^{6}|\frac{dL_{1}}{dt}=0\}\). Therefore, it follows from LaSalle invariance principle [35] that the immune-free equilibrium \(E_{1}\) is globally asymptotically stable whenever \(R_{1}\le 1\) and \(R_{2}\le 1\).
Now, it remains to investigate the stability property of the immune-free equilibrium \(E_{1}\) when any one of \(R_{1}\) and \(R_{2}\) becomes greater than unity. Through some simple computations, we arrive at the following characteristic equation at the immune-free equilibrium \(E_{1}\):
where

From the above Eq. (12), we can easily notice that \(\xi _{1}=\widetilde{q}V_{1}-\widetilde{\sigma }\) and \(\xi _{2}=qI_{1}-\sigma \) represent two roots of the characteristic equation (12). So, if \(R_{1}=\frac{\widetilde{q}}{\widetilde{\sigma }}V_{1}>1\) then we have \(\xi _{1}>0\) and if \(R_{2}=\frac{q}{\sigma }I_{1}>1\) then we have \(\xi _{2}>0\). This indicates that if any one of \(R_{1}\) and \(R_{2}\) is greater than unity then there exists a real positive root of the characteristic equation (12). Therefore, the immune-free equilibrium \(E_{1}\) is unstable whenever \(R_{1}>1\) or \(R_{2}>1\). This completes the proof. \(\square \)
Theorem 5
Let us assume that the hypothesis \((A_{4})\) and the inequalities \(R_{0}>1\) and \(R_{1}>1\) hold. Then the infection equilibrium with only antibody immune response \(E_{2}\) is globally asymptotically stable if \(R_{3}\le 1\) and it becomes unstable if \(R_{3}>1\).
Proof
Let us define a Lyapunov function \(L_{2}(t)\) as follows:
where \(H_{2}\), \(I_{2}\), \(D_{2}\), \(V_{2}\) and \(W_{2}\) denote the uninfected hepatocyte, infected hepatocyte, capsid, virus and antibody components of the infection equilibrium with only antibody immune response \(E_{2}\), respectively. Taking the derivative of \(L_{2}\) with respect to time t along the solution trajectories of the system (1)–(3), we obtain
Further, from the hypothesis \((A_{2})\) on the general incidence function we know that f(H, I, V) is a strictly increasing function with respect to H and this eventually gives rise to the following inequality:
Hence, using the hypothesis \((A_{4})\) we obtain \(\frac{dL_{2}}{dt}\le 0\) if \(R_{3}\le 1\). Also, we have \(\frac{dL_{2}}{dt}=0\) holds if and only if \(H=H_{2}\), \(I=I_{2}\), \(D=D_{2}\), \(V=V_{2}\), \(W=W_{2}\) and \(Z=0\). This indicates that the singleton set \(\{E_{2}\}=\{(H_{2},I_{2},D_{2},V_{2},W_{2},0)\}\) is the largest invariant set in \(\{(H,I,D,V,W,Z)\in \mathbb {R}_{+}^{6}|\frac{dL_{2}}{dt}=0\}\). Therefore, it follows from LaSalle invariance principle [35] that the infection equilibrium with only antibody immune response \(E_{2}\) is globally asymptotically stable whenever \(R_{3}\le 1\).
Now, it remains to investigate the stability property of the infection equilibrium with only antibody immune response \(E_{2}\) when \(R_{3}\) becomes greater than unity. Through some simple computations, we arrive at the following characteristic equation at the equilibrium \(E_{2}\):
where
From the above Eq. (13), we can easily notice that \(\xi =qI_{2}-\sigma \) represents a root of the characteristic equation (13). So, if \(R_{3}=\frac{q}{\sigma }I_{2}>1\) then we have \(\xi >0\). This indicates that if \(R_{3}\) is greater than unity then there exists a real positive root of the characteristic equation (13). Therefore, the infection equilibrium with only antibody immune response \(E_{2}\) is unstable whenever \(R_{3}>1\). This completes the proof. \(\square \)
Theorem 6
Let us assume that the hypothesis \((A_{4})\) and the inequalities \(R_{0}>1\) and \(R_{2}>1\) hold. Then the infection equilibrium with only CTL immune response \(E_{3}\) is globally asymptotically stable if \(R_{4}\le 1\) and it becomes unstable if \(R_{4}>1\).
Proof
Let us define a Lyapunov function \(L_{3}(t)\) as follows:
where \(H_{3}\), \(I_{3}\), \(D_{3}\), \(V_{3}\) and \(Z_{3}\) denote the uninfected hepatocyte, infected hepatocyte, capsid, virus and CTL cell components of the infection equilibrium with only CTL immune response \(E_{3}\), respectively. Taking the derivative of \(L_{3}\) with respect to time t along the solution trajectories of the system (1)–(3), we obtain
Further, from the hypothesis \((A_{2})\) on the general incidence function we know that f(H, I, V) is a strictly increasing function with respect to H and this eventually gives rise to the following inequality:
Hence, using the hypothesis \((A_{4})\) we obtain \(\frac{dL_{3}}{dt}\le 0\) if \(R_{4}\le 1\). Also, we have \(\frac{dL_{3}}{dt}=0\) holds if and only if \(H=H_{3}\), \(I=I_{3}\), \(D=D_{3}\), \(V=V_{3}\), \(W=0\) and \(Z=Z_{3}\). This indicates that the singleton set \(\{E_{3}\}=\{(H_{3},I_{3},D_{3},V_{3},0,Z_{3})\}\) is the largest invariant set in \(\{(H,I,D,V,W,Z)\in \mathbb {R}_{+}^{6}|\frac{dL_{3}}{dt}=0\}\). Therefore, it follows from LaSalle invariance principle [35] that the infection equilibrium with only CTL immune response \(E_{3}\) is globally asymptotically stable whenever \(R_{4}\le 1\).
Now, it remains to investigate the stability property of the infection equilibrium with only CTL immune response \(E_{3}\) when \(R_{4}\) becomes greater than unity. Through some simple computations, we arrive at the following characteristic equation at the equilibrium \(E_{3}\):
where
From the above Eq. (14), we can easily notice that \(\xi =\widetilde{q}V_{3}-\widetilde{\sigma }\) represents a root of the characteristic equation (14). So, if \(R_{4}=\frac{\widetilde{q}}{\widetilde{\sigma }}V_{3}>1\) then we have \(\xi >0\). This indicates that if \(R_{4}\) is greater than unity then there exists a real positive root of the characteristic equation (14). Therefore, the infection equilibrium with only CTL immune response \(E_{3}\) is unstable whenever \(R_{4}>1\). This completes the proof. \(\square \)
Theorem 7
Let us assume that the hypothesis \((A_{4})\) holds. Then the infection equilibrium with adaptive immune response \(E_{4}\) is globally asymptotically stable whenever it exists (that is, when \(R_{0}>1\), \(R_{1}>1\), \(R_{2}>1\), \(R_{3}>1\) and \(R_{4}>1\)).
Proof
Let us define a Lyapunov function \(L_{4}(t)\) as follows:
where \(H_{4}\), \(I_{4}\), \(D_{4}\), \(V_{4}\), \(W_{4}\) and \(Z_{4}\) denote the corresponding components of the infection equilibrium with adaptive immune response \(E_{4}\), respectively. Taking the derivative of \(L_{4}\) with respect to time t along the solution trajectories of the system (1)–(3), we obtain
Hence, using the hypotheses \((A_{2})\) and \((A_{4})\) we obtain \(\frac{dL_{4}}{dt}\le 0\). Also, we have \(\frac{dL_{4}}{dt}=0\) holds if and only if \(H=H_{4}\), \(I=I_{4}\), \(D=D_{4}\), \(V=V_{4}\), \(W=W_{4}\) and \(Z=Z_{4}\). This indicates that the singleton set \(\{E_{4}\}=\{(H_{4},I_{4},D_{4},V_{4},W_{4},Z_{4})\}\) is the largest invariant set in \(\{(H,I,D,V,W,Z)\in \mathbb {R}_{+}^{6}|\frac{dL_{4}}{dt}=0\}\). Therefore, it follows from LaSalle invariance principle [35] that the infection equilibrium with adaptive immune response \(E_{4}\) is globally asymptotically stable whenever it exists, that is, when \(R_{0}>1\), \(R_{1}>1\), \(R_{2}>1\), \(R_{3}>1\) and \(R_{4}>1\). This completes the proof. \(\square \)
Numerical Simulations
In this section, we present a particular example for our generalized model by incorporating a specific functional response term in place of the general incidence function f(H, I, V) and provide several numerical illustrations of it in order to corroborate the obtained theoretical results. For this purpose, we consider the incidence function \(f(H,I,V)=\frac{kH}{H+V}\) [36, 37]. Then the generalized model (1) gets transformed into the following delayed reaction-diffusion system:
subjected to the non-negative initial conditions (2) and the zero-flux boundary conditions (3).
We can easily observe that the considered specific form of incidence function indeed satisfies the hypotheses (\(A_{1}\))–(\(A_{3}\)). The infection-free equilibrium for the model (15) is given by \(E_{0}=(\frac{s}{\mu },0,0,0,0,0)\) and the basic reproduction number is given by \(R_{0}=\frac{a\beta k}{c\delta (\beta +\delta )}e^{-\alpha _{1}\tau _{1}-\alpha _{2}\tau _{2}-\alpha _{3}\tau _{3}}\). When \(R_{0}>1\), we can obtain remaining four equilibria numerically for suitable parameter values and also we can numerically compute other reproduction numbers, such as \(R_{1}\), \(R_{2}\), \(R_{3}\) and \(R_{4}\). Therefore, we can directly apply the theoretical results obtained earlier for this specific model (15). For the simplicity of numerical illustrations of the obtained theoretical results, we consider one-dimensional bounded spatial domain \(\Omega =[0,50]\). For all numerical simulations, we consider the spatial step size as \(\Delta x=1\), temporal step size as \(\Delta t=0.1\) and diffusion coefficients as \(d_{D}=d_{V}=0.1\). All the numerical results have been obtained for the time delays \(\tau _{1}=1\), \(\tau _{2}=2\) and \(\tau _{3}=5\). All other hypothetical parameter values for each situation are mentioned in the caption of the corresponding figure. Figure 1 validates the result demonstrated in Theorem 3 and shows that the solution trajectories approach towards the infection-free equilibrium \(E_{0}=(1000,0,0,0,0,0)\). We observe that the solution trajectories tend towards the immune-free equilibrium \(E_{1}=(12.17,184.53,293.94,52.41,0,0)\) in Fig. 2, which is actually the situation shown in Theorem 4. Then Fig. 3 supports the statement of Theorem 5 and demonstrates that the corresponding solution trajectories eventually approach the infection equilibrium with only antibody immune response \(E_{2}=(998.33,0.31,0.496,0.017,54.54,0)\). Further, Theorem 6 is supported by the Fig. 4 where the solution trajectories tend towards the infection equilibrium with only CTL immune response \(E_{3}=(992.89,0.25,0.398,0.071,0,1.14)\). Finally, the last figure (i.e., Fig. 5) exhibits the asymptotic stability of the infection equilibrium with adaptive immune response \(E_{4}=(998.33,0.25,0.398,0.017,4.13,0.065)\), which is actually the case exhibited by Theorem 7.
Spatiotemporal dynamics of the model (15) when \(R_{0}=0.531<1\). The parameter values are: \(s=10.0\), \(\mu =0.01\), \(k=0.1\), \(\delta =0.053\), \(a=1.5\), \(\beta =0.87\), \(c=3.8\), \(p=0.2\), \(q=0.2\), \(\sigma =0.05\), \(\widetilde{p}=0.3\), \(\widetilde{q}=0.3\), \(\widetilde{\sigma }=0.05\), \(\alpha _{1}=0.01\), \(\alpha _{2}=0.01\), \(\alpha _{3}=0.05\), \(\tau _{1}=1\), \(\tau _{2}=2\) and \(\tau _{3}=5\)
Spatiotemporal dynamics of the model (15) when \(R_{0}=5.306>1\), \(R_{1}=0.314<1\) and \(R_{2}=0.738<1\). The parameter values are: \(s=10.0\), \(\mu =0.01\), \(k=1.0\), \(\delta =0.053\), \(a=1.5\), \(\beta =0.87\), \(c=3.8\), \(p=0.002\), \(q=0.002\), \(\sigma =0.5\), \(\widetilde{p}=0.003\), \(\widetilde{q}=0.003\), \(\widetilde{\sigma }=0.5\), \(\alpha _{1}=0.01\), \(\alpha _{2}=0.01\), \(\alpha _{3}=0.05\), \(\tau _{1}=1\), \(\tau _{2}=2\) and \(\tau _{3}=5\)
Spatiotemporal dynamics of the model (15) when \(R_{0}=5.306>1\), \(R_{1}=3144.7>1\), \(R_{2}=369.1>1\) and \(R_{3}=0.623<1\). The parameter values are: \(s=10.0\), \(\mu =0.01\), \(k=1.0\), \(\delta =0.053\), \(a=1.5\), \(\beta =0.87\), \(c=3.8\), \(p=0.2\), \(q=0.1\), \(\sigma =0.05\), \(\widetilde{p}=0.3\), \(\widetilde{q}=0.3\), \(\widetilde{\sigma }=0.005\), \(\alpha _{1}=0.01\), \(\alpha _{2}=0.01\), \(\alpha _{3}=0.05\), \(\tau _{1}=1\), \(\tau _{2}=2\) and \(\tau _{3}=5\)
Spatiotemporal dynamics of the model (15) when \(R_{0}=5.306>1\), \(R_{1}=314.47>1\), \(R_{2}=738.11>1\) and \(R_{4}=0.372<1\). The parameter values are: \(s=10.0\), \(\mu =0.01\), \(k=1.0\), \(\delta =0.053\), \(a=1.5\), \(\beta =0.87\), \(c=3.8\), \(p=0.2\), \(q=0.2\), \(\sigma =0.05\), \(\widetilde{p}=0.3\), \(\widetilde{q}=0.3\), \(\widetilde{\sigma }=0.05\), \(\alpha _{1}=0.01\), \(\alpha _{2}=0.01\), \(\alpha _{3}=0.05\), \(\tau _{1}=1\), \(\tau _{2}=2\) and \(\tau _{3}=5\)
Spatiotemporal dynamics of the model (15) when \(R_{0}=5.306>1\), \(R_{1}=3144.7>1\), \(R_{2}=738.11>1\), \(R_{3}=1.24>1\) and \(R_{4}=4.26>1\). The parameter values are: \(s=10.0\), \(\mu =0.01\), \(k=1.0\), \(\delta =0.053\), \(a=1.5\), \(\beta =0.87\), \(c=3.8\), \(p=0.2\), \(q=0.2\), \(\sigma =0.05\), \(\widetilde{p}=0.3\), \(\widetilde{q}=0.3\), \(\widetilde{\sigma }=0.005\), \(\alpha _{1}=0.01\), \(\alpha _{2}=0.01\), \(\alpha _{3}=0.05\), \(\tau _{1}=1\), \(\tau _{2}=2\) and \(\tau _{3}=5\)
Conclusion
In this paper, we have proposed and investigated a reaction-diffusion HBV infection model with capsids, three delays, adaptive immunity and general incidence rate that includes the classical bilinear incidence rate, the Beddington-DeAngelis functional response, the Crowley-Martin functional response and the Hattaf-Yousfi functional response. We have derived five threshold parameters in order to fully characterize the dynamical behaviors of model. These parameters are the basic reproduction number \(R_{0}\), the antibody immune response reproduction number \(R_{1}\), the CTL immune response reproduction number \(R_{2}\), the competitive CTL immune response reproduction number \(R_{3}\), and the competitive antibody immune response reproduction number \(R_{4}\). More concretely, when \(R_{0}\le 1\), the infection-free equilibrium is globally asymptotically stable which biologically indicates that the HBV is cleared and the infection dies out. When \(R_{0}>1\), the infection-free equilibrium becomes unstable and four infection steady states are appeared which are: (1) the immune-free equilibrium is globally asymptotically stable if \(R_{1}\le 1\) and \(R_{2}\le 1\) and it becomes unstable if \(R_{1}>1\) or \(R_{2}>1\); (2) the infection equilibrium with only antibody immune response exists if \(R_{1}>1\), it is globally asymptotically stable if \(R_{3}\le 1\) and becomes unstable if \(R_{3}>1\); (3) the infection equilibrium with only CTL immune response exists if \(R_{2}>1\), it is globally asymptotically stable if \(R_{4}\le 1\) and becomes unstable if \(R_{4}>1\); (4) the infection equilibrium with both antibody and CTL immune responses is globally asymptotically stable whenever it exists. It follows from these results that the activation of one or both arms of adaptive immunity is unable to eradicate the virus from the liver. In addition, the proposed model and the results obtained in this paper extend and improve the ODE, DDE and PDE models and the corresponding results presented in [1, 3,4,5,6,7,8,9].
Recently, there has been growing interest among researchers to model biological phenomena in fractional calculus setup as these models can eventually predict more realistic information about the complex dynamical behaviors [38, 39]. Therefore, an immediate future direction will be to study our model in fractional calculus setup. Another interesting relevant future study will be to adopt off-line nonlinear model predictive control (NMPC) approach in our present model [40]. Further, we want to study the effect of discretization on the dynamical behavior of our model as in [41,42,43]. We will carry out these interesting research prospects in our subsequent future studies.
References
Manna, K., Chakrabarty, S.P.: Chronic hepatitis B infection and HBV DNA-containing capsids: modeling and analysis. Commun. Nonlinear Sci. Numer. Simul. 22, 383–395 (2015)
Murray, J.M., Purcell, R.H., Wieland, S.F.: The half-life of hepatitis B virions. Hepatology 44, 1117–1121 (2006)
Manna, K., Chakrabarty, S.P.: Global stability of one and two discrete delay models for chronic hepatitis B infection with HBV DNA-containing capsids. Comput. Appl. Math. 36, 525–536 (2017)
Guo, T., Liu, H., Xu, C., Yan, F.: Global stability of a diffusive and delayed HBV infection model with HBV DNA-containing capsids and general incidence rate. Discrete Contin. Dyn. Syst. B 23(10), 4223–4242 (2018)
Manna, K.: Dynamics of a diffusion-driven HBV infection model with capsids and time delay. Int. J. Biomath. 10(5), 1750062 (2017). (18 pages)
Geng, Y., Xu, J., Hou, J.: Discretization and dynamic consistency of a delayed and diffusive viral infection model. Appl. Math. Comput. 316, 282–295 (2018)
Manna, K.: Dynamics of a delayed diffusive HBV infection model with capsids and CTL immune response. Int. J. Appl. Comput. Math. 4(5), 116 (2018)
Xu, J., Geng, Y.: Dynamic consistent NSFD scheme for a delayed viral infection model with immune response and nonlinear incidence. Discrete Dyn. Nat. Soc. 2017, 1–12 (2017)
Manna, K.: Global properties of a HBV infection model with HBV DNA-containing capsids and CTL immune response. Int. J. Appl. Comput. Math. 3, 2323–2338 (2017)
Ciupe, S.M., Ribeiro, R.M., Nelson, P.W., Perelson, A.S.: Modeling the mechanisms of acute hepatitis B virus infection. J. Theor. Biol. 247, 23–35 (2007)
Vierling, J.M.: The immunology of hepatitis B. Clin. Liver Dis. 11, 727–759 (2007)
Bertoletti, A., Gehring, A.J.: The immune response during hepatitis B virus infection. J. Gen. Virol. 87, 1439–1449 (2006)
Hattaf, K., Yousfi, N., Tridane, A.: Mathematical analysis of a virus dynamics model with general incidence rate and cure rate. Nonlinear Anal. Real World Appl. 13, 1866–1872 (2012)
Hattaf, K., Yousfi, N.: A generalized HBV model with diffusion and two delays. Comput. Math. Appl. 69, 31–40 (2015)
Hattaf, K., Yousfi, N.: A numerical method for a delayed viral infection model with general incidence rate. J. King Saud Univ. Sci. 28(4), 368–374 (2016)
Wang, X.-Y., Hattaf, K., Huo, H.-F., Xiang, H.: Stability analysis of a delayed social epidemics model with general contact rate and its optimal control. J. Ind. Manag. Optim. 12(4), 1267–1285 (2016)
Xu, R., Ma, Z.E.: An HBV model with diffusion and time delay. J. Theoret. Biol. 257, 499–509 (2009)
Chan Chí, N., Ávila Vales, E., García Almeida, G.: Analysis of a HBV model with diffusion and time delay. J. Appl. Math. 2012, 1–25 (2012)
Beddington, J.R.: Mutual interference between parasites or predators and its effect on searching effciency. J. Anim. Ecol. 44, 331–340 (1975)
DeAngelis, D.L., Goldstein, R.A., O’Neill, R.V.: A model for trophic interaction. Ecology 56(4), 881–892 (1975)
Yang, Y., Xu, Y.: Global stability of a diffusive and delayed virus dynamics model with Beddington-DeAngelis incidence function and CTL immune response. Comput. Math. Appl. 71, 922–930 (2016)
Crowley, P.H., Martin, E.K.: Functional responses and interference within and between year classes of a dragonfly population. J. N. Am. Benthol. Soc. 8, 211–221 (1989)
Kang, C., Miao, H., Chen, X., Xu, J., Huang, D.: Global stability of a diffusive and delayed virus dynamics model with Crowle-Martin incidence function and CTL immune response. Adv. Differ. Equ. (2017). https://doi.org/10.1186/s13662-017-1332-x
Hattaf, K., Yousfi, N.: A class of delayed viral infection models with general incidence rate and adaptive immune response. Int. J. Dyn. Control 4, 254–265 (2016)
Riad, D., Hattaf, K., Yousfi, N.: Dynamics of capital-labour model with Hattaf-Yousfi functional response. Br. J. Math. Comput. Sci. 18(5), 1–7 (2016)
Mahrouf, M., Hattaf, K., Yousfi, N.: Dynamics of a stochastic viral infection model with immune response. Math. Model. Nat. Phenom. 12(5), 15–32 (2017)
Travis, C.C., Webb, G.F.: Existence and stability for partial functional differential equations. Trans. Am. Math. Soc. 200, 395–418 (1974)
Fitzgibbon, W.E.: Semilinear functional differential equations in Banach space. J. Differ. Equ. 29, 1–14 (1978)
Martin, R.H., Smith, H.L.: Abstract functional-differential equations and reaction-diffusion systems. Trans. Am. Math. Soc. 321, 1–44 (1990)
Martin, R.H., Smith, H.L.: Reaction-diffusion systems with time delays: monotonicity, invariance, comparison and convergence. J. reine Angew. Math. 413, 1–35 (1991)
Wu, J.: Theory and Applications of Partial Functional Differential Equations. Springer, New York (1996)
Protter, M.H., Weinberger, H.F.: Maximum Principles in Differential Equations. Prentice Hall, Englewood Cliffs (1967)
Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Mathematics, vol. 840. Springer, New York (1981)
Miao, H., Teng, Z., Abdurahman, X., Li, Z.: Global stability of a diffusive and delayed virus infection model with general incidence function and adaptive immune response. Comput. Appl. Math. 37, 3780–3805 (2018)
Hale, J.K., Verduyn Lunel, S.M.: Introduction to Functional Differential Equations. Springer, New York (1993)
Zhuo, X.: Analysis of a HBV infection model with non-cytolytic cure process. In: IEEE 6th International Conference on Systems Biology, pp. 148–151 (2012)
Sun, Q., Min, L.: Dynamics analysis and simulation of a modified HIV infection model with a saturated infection rate. Comput. Math. Methods Med. 2014, Article ID 145162 (2014)
Jajarmi, A., Baleanu, D.: A new fractional analysis on the interaction of HIV with CD\(4^{+}\) T-cells. Chaos Solitons Fractals 113, 221–229 (2018)
Hajipour, M., Jajarmi, A., Baleanu, D., Sun, H.G.: On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 69, 119–133 (2019)
Sajjadi, S.S., Pariz, N., Karimpour, A., Jajarmi, A.: An off-line NMPC strategy for continuous-time nonlinear systems using an extended modal series method. Nonlinear Dyn. 78(4), 2651–2674 (2014)
Hattaf, K., Lashari, A.A., El Boukari, B., Yousfi, N.: Effect of discretization on dynamical behavior in an epidemiological model. Differ. Equ. Dyn. Syst. 23(4), 403–413 (2015)
Manna, K.: A non-standard finite difference scheme for a diffusive HBV infection model with capsids and time delay. J. Differ. Equ. Appl. 23, 1901–1911 (2017)
Hattaf, K., Yousfi, N.: A numerical method for delayed partial differential equations describing infectious diseases. Comput. Math. Appl. 72, 2741–2750 (2016)
Acknowledgements
The authors convey their gratitude to the learned reviewer for his/her valuable suggestions and comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Manna, K., Hattaf, K. Spatiotemporal Dynamics of a Generalized HBV Infection Model with Capsids and Adaptive Immunity. Int. J. Appl. Comput. Math 5, 65 (2019). https://doi.org/10.1007/s40819-019-0651-x
Published:
DOI: https://doi.org/10.1007/s40819-019-0651-x