Introduction

Hepatitis B virus (HBV) infection which is a hepatic condition resulting from infection of the hepatocytes (or the liver cells), is a disease of critical concern for public health at a global level [1]. The prognosis of HBV infection is typically acute or chronic in nature. The chronic cases can potentially have severe long term implications such as liver cirrhosis and hepatocellular carcinoma (HCC) [2]. The fairly complex process of HBV replication has been discussed in detail by Rebeiro et al. [2] and Lewin et al. [3]. About 2 billion individuals are believed to be infected with HBV at some point in their life span resulting in about 350 million chronically infected and carriers of the virus [4]. The chronic infection leads to an estimated annual casualty of 1 million [4] which makes HBV infection a subject of serious research.

The study of virus dynamics models using mathematical techniques is useful in understanding the viral infections such as human immunodeficiency virus (HIV), hepatitis C virus (HCV) and HBV infections etc. Nowak et al. [5] introduced the basic virus infection model which has been widely used by researchers in the studies of virus infection dynamics. Several mathematical models and their qualitative analysis for HBV infection can be found in [6–9]. Since biological processes are not instantaneous in nature, there are some intracellular time delays involved in these processes. While the above mentioned models did not account for delays, some delay induced HBV infection models and analysis of their dynamical behaviors can be found in [10–12]. Nowak and Bangham [13] extended the basic virus infection model by incorporating the cytotoxic T lymphocytes (CTLs) immune responses for HIV, HBV, human T cell leukemia virus-1 (HTLV-1) infections. Some other HBV infection models with CTL immune responses and their analysis can be found in [4, 14, 15].

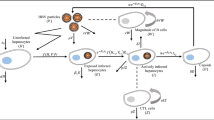
In a recent article, Manna and Chakrabarty [16] presented and analyzed a HBV infection model with HBV DNA-containing capsids. Their model involved four populations such as uninfected hepatocytes (H), infected hepatocytes (I), capsids (D) and virions (V). The model presented in [16] is as follows:

$$\begin{aligned} \frac{{ dH}(t)}{{ dt}}= & {} s-{\mu }H(t)-{ kH}(t)V(t),\nonumber \\ \frac{{ dI}(t)}{{ dt}}= & {} { kH}(t)V(t)-{\delta }I(t),\nonumber \\ \frac{{ dD}(t)}{{ dt}}= & {} { aI}(t)-(\beta +\delta )D(t),\nonumber \\ \frac{{ dV}(t)}{{ dt}}= & {} {\beta }D(t)-cV(t), \end{aligned}$$
(1)

where s represents the constant production rate, \(\mu \) is the natural death rate of uninfected hepatocytes and k is the conversion rate of the uninfected hepatocytes to infected ones. \(\delta \) is the death rate of infected hepatocytes and capsids with a being the production rate of capsids from infected hepatocytes. Capsids lead to viral replication at the rate \(\beta \) accompanied by the natural death of the virions at a rate of c. It is assumed that \(\mu \le \delta \) which is a reasonable assumption because otherwise that would lead to a low chance of patient survival [16]. The CTL immune response which was not a part of the model (1) has been included in this work and then investigated for global dynamical behavior.

The organization of this paper is as follows. In the next section, we present the model with CTL immune responses and establish some of the basic properties. In section “Global Analysis”, the global asymptotic stability of the steady states are established. In section “Delay Model”, we incorporate two discrete delays in the model and present some of the basic results. In section “Global Analysis of the Delay Model”, we present the global properties for the delay model. In the subsequent section, we present illustrative numerical simulations to validate the theoretical results. Finally, section ”Conclusion” concludes the results obtained.

Mathematical Model

In this section, we propose a modified HBV infection model by incorporating CTL immune responses in the model (1). Here, Z(t) represents the number of CTL cells at time t. We propose the following modified model:

$$\begin{aligned} \frac{{ dH}(t)}{{ dt}}= & {} s-{\mu }H(t)-{ kH}(t)V(t),\nonumber \\ \frac{{ dI}(t)}{{ dt}}= & {} { kH}(t)V(t)-{\delta }I(t)-{ pI}(t)Z(t),\nonumber \\ \frac{{ dD}(t)}{{ dt}}= & {} { aI}(t)-(\beta +\delta )D(t),\nonumber \\ \frac{{ dV}(t)}{{ dt}}= & {} {\beta }D(t)-{ cV}(t),\nonumber \\ \frac{{ dZ}(t)}{{ dt}}= & {} { qI}(t)Z(t)-{\sigma }Z(t), \end{aligned}$$
(2)

with the initial conditions \(H(0)>0\), \(I(0)>0\), \(D(0)>0\), \(V(0)>0\) and \(Z(0)>0\). The infected hepatocytes are removed by CTLs at the rate p while q denotes the CTL responsiveness and \(\sigma \) represents decay rate for CTLs in absence of stimulation. It can be shown that the solutions of the model (2) with positive initial conditions will remain positive. Now, we prove the boundedness of the solutions of the model (2) for \(t\ge 0\). For this purpose, let us define a new variable \(T(t)=H(t)+I(t)+\frac{p}{q}Z(t)\). Then, from the first two and last equations of (2), we have

$$\begin{aligned} \frac{{ dT}(t)}{{ dt}}= & {} s-{\mu }H(t)-{\delta }I(t)-\frac{p\sigma }{q}Z(t)\\\le & {} s-\mu _{1}T(t), \end{aligned}$$

where \(\mu \le \delta \) and \(\mu _{1}=\min \{\mu ,\sigma \}\). Therefore, we have \(\limsup \nolimits _{t\rightarrow \infty } T(t)\le \frac{s}{\mu _{1}}\) and in a similar manner, we can obtain \(\limsup \nolimits _{t\rightarrow \infty } D(t)\le \frac{as}{\mu _{1} (\beta + \delta )}\) and \(\limsup \limits _{t\rightarrow \infty } V(t)\le \frac{a\beta s}{c\mu _{1} (\beta + \delta )}\). Hence, all solutions of the model (2) are bounded. For our model (2), the basic reproduction number of the virus is introduced as \(R_{0}=\frac{a\beta sk}{c\delta \mu (\beta +\delta )}\) and the immune response reproduction number is introduced as \(R_{{ CTL}}=\frac{a\beta skq}{\delta \{cq\mu (\beta +\delta )+a\beta \sigma k\}}\). Here, \(R_{0}\) represents the average number of the newly infected hepatocytes generated from one infected hepatocyte at the beginning of the infectious process in absence of a CTL immune response and \(R_{{ CTL}}\) represents reproduction number in presence of CTL immune response. Also, it can be shown that \(R_{{ CTL}}<R_{0}\) is always true. The model (2) has three steady states:

  1. 1.

    The disease-free steady state, \(E_{0}=\left( H_{0},I_{0},D_{0},V_{0},Z_{0}\right) =\left( \frac{s}{\mu },0,0,0,0\right) \).

  2. 2.

    The immune-free steady state, \(E_{1}=\left( H_{1},I_{1},D_{1},V_{1},Z_{1}\right) \), where \(H_{1}=\frac{c\delta (\beta +\delta )}{a\beta k}\), \(V_{1}=\left[ \frac{a\beta s}{c\delta (\beta +\delta )}-\frac{\mu }{k} \right] \), \(D_{1}=\left[ \frac{c}{\beta }\right] V_{1}\), \(I_{1}=\left[ \frac{\beta +\delta }{a}\right] D_{1}\) and \(Z_{1}=0\). The immune-free steady state, \(E_{1}\), exists provided the basic reproduction number \(R_{0}>1\).

  3. 3.

    The endemic steady state, \(E^{*}=\left( H^{*},I^{*},D^{*},V^{*},Z^{*}\right) \), where \(H^{*}=\frac{scq(\beta +\delta )}{cq\mu (\beta +\delta )+a\beta \sigma k}\), \(I^{*}=\frac{\sigma }{q}\), \(D^{*}=\frac{a}{(\beta +\delta )}I^{*}\), \(V^{*}=\frac{\beta }{c}D^{*}\), \(Z^{*}=\frac{\delta }{p}\left[ \frac{a\beta skq}{\delta \{cq\mu (\beta +\delta )+a\beta \sigma k\}}-1\right] \). The endemic steady state, \(E^{*}\), exists provided the immune response reproduction number \(R_{{ CTL}}>1\).

Global Analysis

In this section, the global asymptotic stability of the three steady states is studied through the method of Lyapunov function construction. For this purpose, we present some useful inequalities [17–19]. Here we consider the function \(G(x)=x-1-\ln x\) for \(x>0\). Note that \(G(x)\ge 0, \forall x\) and that \(G(x)=0\) if and only if \(x=1\). Let \(x_{1},x_{2},\dots ,x_{n}\) be positive real numbers. Then

$$\begin{aligned} 1-x_{i}+\ln x_{i}=-G(x_{i})\le 0, \quad \forall i=1:n. \end{aligned}$$
(3)

Taking summation of (3) over \(i=1:n\), we get

$$\begin{aligned} n-\sum _{i=1}^{n} x_{i}+\ln \left( \prod _{i=1}^{n} x_{i}\right) \le 0. \end{aligned}$$
(4)

For \(x_{i}=\frac{p_{i}}{q_{i}}\) where \(p_{i}>0, q_{i}>0\) for \(i=1:n\), it follows that

$$\begin{aligned} n-\sum _{i=1}^{n} \frac{p_{i}}{q_{i}}+\ln \left( \prod _{i=1}^{n} \frac{p_{i}}{q_{i}}\right) \le 0. \end{aligned}$$
(5)

If \(p_{1}p_{2}\dots p_{n}=q_{1}q_{2}\dots q_{n}\), then \(\prod _{i=1}^{n} \frac{p_{i}}{q_{i}}=1\) and we have

$$\begin{aligned} n-\sum _{i=1}^{n}\frac{p_{i}}{q_{i}}\le 0. \end{aligned}$$
(6)

Theorem 1

The disease-free steady state \(E_{0}\) is globally asymptotically stable if \(R_{0}\le 1\).

Proof

We define a Lyapunov function \(L_{1}\) as follows:

$$\begin{aligned} L_{1}(t)= H_{0}G\left( \frac{H}{H_{0}}\right) +I(t)+\frac{\delta }{a}D(t)+ \frac{\delta (\beta +\delta )}{a\beta }V(t)+\frac{p}{q}Z(t). \end{aligned}$$

Taking the derivative of \(L_{1}\) along the solutions of the model (2), we obtain

$$\begin{aligned} \frac{{ dL}_{1}}{{ dt}}= & {} \left( 1-\frac{H_{0}}{H}\right) \frac{{ dH}}{{ dt}}+ \frac{{ dI}}{{ dt}}+\frac{\delta }{a}\frac{{ dD}}{{ dt}} +\frac{\delta (\beta +\delta )}{a\beta }\frac{{ dV}}{{ dt}}+ \frac{p}{q}\frac{{ dZ}}{{ dt}}\\= & {} \left( 1-\frac{H_{0}}{H}\right) [s-\mu H-{ kHV}]+[{ kHV}- \delta I-{ pIZ}]+\frac{\delta }{a}[{ aI}-(\beta +\delta )D]\\&+\,\frac{\delta (\beta +\delta )}{a\beta }[\beta D-{ cV}]+ \frac{p}{q}[{ qIZ}-\sigma Z]\\= & {} s\left[ 2-\frac{H}{H_{0}}-\frac{H_{0}}{H}\right] +\left[ { kH}_{0}- \frac{c\delta (\beta +\delta )}{a\beta }\right] V -\frac{p\sigma }{q}Z\\= & {} s\left[ 2-\frac{H}{H_{0}}-\frac{H_{0}}{H}\right] +\frac{c\delta (\beta +\delta )}{a\beta }[R_{0}-1]V-\frac{p\sigma }{q}Z\\= & {} -\frac{s}{{ HH}_{0}}(H-H_{0})^{2}+\frac{c\delta (\beta +\delta ) }{a\beta }[R_{0}-1]V-\frac{p\sigma }{q}Z. \end{aligned}$$

Therefore, \(\frac{{ dL}_{1}}{{ dt}}\le 0\) if \(R_{0}\le 1\). Assume that M is the largest invariant set in \(\{(H,I,D,V,Z)|\frac{{ dL}_{1}}{{ dt}}=0\}\). Note that \(\frac{{ dL}_{1}}{{ dt}}=0\) if and only if \(H=H_{0}=\frac{s}{\mu }\), \(I=0\), \(D=0\), \(V=0\) and \(Z=0\). Hence, \(M=\{E_{0}\}=\{(\frac{s}{\mu },0,0,0,0)\}\). Thus, by the Lyapunov-LaSalle invariance principle [14, 16, 18], \(E_{0}\) is globally asymptotically stable if \(R_{0}\le 1\). \(\square \)

Theorem 2

The immune-free steady state \(E_{1}\) is globally asymptotically stable if \(R_{{ CTL}}\le 1<R_{0}\).

Proof

We define a Lyapunov function \(L_{2}\) as follows:

$$\begin{aligned} L_{2}(t)= H_{1}G\left( \frac{H}{H_{1}}\right) +I_{1}G\left( \frac{I}{I_{1}}\right) + \frac{\delta }{a}D_{1}G\left( \frac{D}{D_{1}}\right) +\frac{\delta (\beta +\delta )}{a\beta }V_{1}G\left( \frac{V}{V_{1}}\right) +\frac{p}{q}Z(t). \end{aligned}$$

Taking the derivative of \(L_{2}\) along the solutions of the model (2), we obtain

$$\begin{aligned} \frac{{ dL}_{2}}{{ dt}}= & {} \left( 1-\frac{H_{1}}{H}\right) \frac{{ dH}}{{ dt}}+ \left( 1-\frac{I_{1}}{I}\right) \frac{{ dI}}{{ dt}}+ \frac{\delta }{a}\left( 1-\frac{D_{1}}{D}\right) \frac{{ dD}}{{ dt}}\\&+\,\frac{\delta (\beta +\delta )}{a\beta }\left( 1-\frac{V_{1}}{V} \right) \frac{{ dV}}{{ dt}}+\frac{p}{q}\frac{{ dZ}}{{ dt}}\\= & {} \left( 1-\frac{H_{1}}{H}\right) [s-\mu H-{ kHV}]+ \left( 1-\frac{I_{1}}{I}\right) [{ kHV}-\delta I-{ pIZ}]\\&+\,\frac{\delta }{a}\left( 1-\frac{D_{1}}{D}\right) [{ aI}- (\beta +\delta )D]+\frac{\delta (\beta +\delta )}{a\beta } \left( 1-\frac{V_{1}}{V}\right) [\beta D-{ cV}]\\&+\,\frac{p}{q}[{ qIZ}-\sigma Z]\\= & {} \mu H_{1}\left[ 2-\frac{H}{H_{1}}-\frac{H_{1}}{H}\right] +\delta I_{1}\left[ 4-\frac{H_{1}}{H}-\frac{{ HI}_{1}V}{H_{1}{} { IV}_{1}}- \frac{{ ID}_{1}}{I_{1}D}-\frac{{ DV}_{1}}{D_{1}V}\right] \\&-\,\left( 1-\frac{I_{1}}{I}\right) { pIZ}+\frac{p}{q}[{ qIZ}-\sigma Z]\\= & {} \mu H_{1}\left[ 2-\frac{H}{H_{1}}-\frac{H_{1}}{H}\right] +\delta I_{1}\left[ 4-\frac{H_{1}}{H}-\frac{{ HI}_{1}V}{H_{1}{} { IV}_{1}}- \frac{{ ID}_{1}}{I_{1}D}-\frac{{ DV}_{1}}{D_{1}V}\right] \\&+\,\frac{{ ps}}{\delta R_{{ CTL}}}[R_{{ CTL}}-1]Z\\= & {} -\,\frac{\mu }{H}(H-H_{1})^{2}+\delta I_{1}\left[ 4-\frac{H_{1}}{H}- \frac{{ HI}_{1}V}{H_{1}{} { IV}_{1}}-\frac{{ ID}_{1}}{I_{1}D}- \frac{{ DV}_{1}}{D_{1}V}\right] \\&+\,\frac{{ ps}}{\delta R_{{ CTL}}}[R_{{ CTL}}-1]Z \end{aligned}$$

Taking \(p_{1}=H_{1},p_{2}={ HI}_{1}V,p_{3}={ ID}_{1},p_{4}={ DV}_{1}, q_{1}=H,q_{2}=H_{1}{} { IV}_{1},q_{3}=I_{1}D,q_{4}=D_{1}V\) and using the inequality (6) for \(n=4\), we obtain

$$\begin{aligned} 4-\frac{H_{1}}{H}-\frac{{ HI}_{1}V}{H_{1}{} { IV}_{1}}- \frac{{ ID}_{1}}{I_{1}D}-\frac{{ DV}_{1}}{D_{1}V}\le 0. \end{aligned}$$

Therefore, \(\frac{{ dL}_{2}}{{ dt}}\le 0\) if \(R_{{ CTL}}\le 1\). Assume that M is the largest invariant set in \(\{(H,I,D,V,Z)|\frac{{ dL}_{2}}{{ dt}}=0\}\). Note that \(\frac{{ dL}_{2}}{{ dt}}=0\) if and only if \(H=H_{1}\), \(I=I_{1}\), \(D=D_{1}\), \(V=V_{1}\) and \(Z=Z_{1}=0\). Hence, \(M=\{E_{1}\}\). Since \(E_{1}\) exists whenever \(R_{0}>1\), then by the Lyapunov-LaSalle invariance principle [14, 16, 18], \(E_{1}\) is globally asymptotically stable if \(R_{{ CTL}}\le 1<R_{0}\). \(\square \)

Theorem 3

The endemic steady state \(E^{*}\) is globally asymptotically stable if \(R_{{ CTL}}>1\).

Proof

We define a Lyapunov function \(L_{3}\) as follows:

$$\begin{aligned} L_{3}(t)= & {} H^{*}G\left( \frac{H}{H^{*}}\right) +I^{*}G\left( \frac{I}{I^{*}}\right) +\frac{(\delta +{ pZ}^{*})}{a}D^{*}G\left( \frac{D}{D^{*}}\right) \\&+\,\frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta }V^{*} G\left( \frac{V}{V^{*}}\right) +\frac{p}{q}Z^{*}G\left( \frac{Z}{Z^{*}}\right) . \end{aligned}$$

Taking the derivative of \(L_{3}\) along the solutions of the model (2), we obtain

$$\begin{aligned} \frac{{ dL}_{3}}{{ dt}}= & {} \left( 1-\frac{H^{*}}{H}\right) \frac{{ dH}}{{ dt}}+\left( 1-\frac{I^{*}}{I}\right) \frac{{ dI}}{{ dt}}+ \frac{(\delta +{ pZ}^{*})}{a}\left( 1-\frac{D^{*}}{D}\right) \frac{{ dD}}{{ dt}}\\&+\, \frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta }\left( 1-\frac{V^{*}}{V}\right) \frac{{ dV}}{{ dt}}+ \frac{p}{q}\left( 1-\frac{Z^{*}}{Z}\right) \frac{{ dZ}}{{ dt}}\\= & {} \left( 1-\frac{H^{*}}{H}\right) [s-\mu H-{ kHV}]+ \left( 1-\frac{I^{*}}{I}\right) [{ kHV}-\delta I-{ pIZ}]\\&+\, \frac{(\delta +{ pZ}^{*})}{a}\left( 1-\frac{D^{*}}{D}\right) [{ aI}-(\beta +\delta )D]+ \frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta }\left( 1-\frac{V^{*}}{V}\right) \\&[\beta D-{ cV}]+\frac{p}{q}\left( 1-\frac{Z^{*}}{Z}\right) [{ qIZ}-\sigma Z]\\= & {} -\frac{\mu }{H}(H-H^{*})^{2}+(\delta I^{*}+{ pI}^{*}Z^{*}) \left[ 4-\frac{H^{*}}{H}-\frac{{ HI}^{*}V}{H^{*}{} { IV}^{*}}- \frac{{ ID}^{*}}{I^{*}D}-\frac{{ DV}^{*}}{D^{*}V}\right] \\&+\,({ kH}^{*}V^{*}-\delta I^{*}-{ pI}^{*}Z^{*})\frac{V}{V^{*}}. \end{aligned}$$

Since \({ kH}^{*}V^{*}=\delta I^{*}+{ pI}^{*}Z^{*}\), we have

$$\begin{aligned} \frac{{ dL}_{3}}{{ dt}}= & {} -\frac{\mu }{H}(H-H^{*})^{2}+(\delta I^{*}+{ pI}^{*}Z^{*})\left[ 4-\frac{H^{*}}{H}- \frac{{ HI}^{*}V}{H^{*}{} { IV}^{*}}-\frac{{ ID}^{*}}{I^{*}D}- \frac{{ DV}^{*}}{D^{*}V}\right] . \end{aligned}$$

Now, taking \(p_{1}=H^{*},p_{2}={ HI}^{*}V,p_{3}={ ID}^{*},p_{4}={ DV}^{*}, q_{1}=H,q_{2}=H^{*}{} { IV}^{*},q_{3}=I^{*}D,q_{4}=D^{*}V\) and using the inequality (6) for \(n=4\), we obtain

$$\begin{aligned} 4-\frac{H^{*}}{H}-\frac{{ HI}^{*}V}{H^{*}{} { IV}^{*}}- \frac{{ ID}^{*}}{I^{*}D}-\frac{{ DV}^{*}}{D^{*}V}\le 0. \end{aligned}$$

Therefore, \(\frac{{ dL}_{3}}{{ dt}}\le 0\). Assume that M is the largest invariant set in \(\{(H,I,D,V,Z)| \frac{{ dL}_{3}}{{ dt}}=0\}\). Note that \(\frac{{ dL}_{3}}{{ dt}}=0\) if and only if \(H=H^{*}\), \(I=I^{*}\), \(D=D^{*}\), \(V=V^{*}\) and \(Z=Z^{*}\). Hence, \(M=\{E^{*}\}\). Since \(E^{*}\) exists whenever \(R_{{ CTL}}>1\), then by the Lyapunov-LaSalle invariance principle [14, 16, 18], \(E^{*}\) is globally asymptotically stable if \(R_{{ CTL}}>1\). \(\square \)

Delay Model

In this section, we include two discrete delays in the model (2) and discuss the basic properties such as positivity and boundedness of the solutions. In two recent articles by Manna and Chakrabarty [16, 18], one intracellular delay was incorporated in the production of productively infected hepatocytes from the uninfected ones for HBV infection model. Also, another delay in the production of matured intracellular HBV DNA-containing capsids which in turn contributes to the production of virions was taken into account in [18]. Taking into account these two delays, we propose the following model with two intracellular delays:

$$\begin{aligned} \frac{{ dH}(t)}{dt}= & {} s-\mu H(t)-{ kH}(t)V(t),\nonumber \\ \frac{{ dI}(t)}{dt}= & {} { kH}(t-\tau _{1})V(t-\tau _{1})-\delta I(t)-pI(t)Z(t),\nonumber \\ \frac{{ dD}(t)}{dt}= & {} aI(t-\tau _{2})-(\beta +\delta )D(t),\nonumber \\ \frac{{ dV}(t)}{dt}= & {} \beta D(t)-cV(t),\nonumber \\ \frac{{ dZ}(t)}{dt}= & {} { qI}(t)Z(t)-\sigma Z(t), \end{aligned}$$
(7)

where \(\tau _{1}\) represents the delay in the production of productively infected hepatocytes and \(\tau _{2}\) represents the delay in the production of capsids. The initial conditions of the model (7) are given by \(H(\theta )>0\), \(I(\theta )>0\), \(D(\theta )>0\), \(V(\theta )>0\) and \(Z(\theta )>0\) for \(\theta \in [-\rho ,0]\), where \(\rho =\max \{\tau _{1},\tau _{2}\}\). It can be shown that the solutions of the model (7) with positive initial conditions will remain positive. For proving the boundedness of the solutions of the model (7), let us define a new variable

$$\begin{aligned} T_{1}(t)= H(t)+I(t+\tau _{1})+\frac{\delta }{2a}D(t+\tau _{1}+\tau _{2})+\frac{\delta }{2a}V(t+\tau _{1}+\tau _{2})+\frac{p}{q}Z(t+\tau _{1}). \end{aligned}$$

Then, using the equations of (7), we get

$$\begin{aligned} \frac{dT_{1}(t)}{dt}= & {} s-\mu H(t)-\frac{\delta }{2}I(t+\tau _{1})-\frac{\delta ^{2}}{2a}D(t+\tau _{1}+\tau _{2})\\&-\,\frac{c\delta }{2a}V(t+\tau _{1}+\tau _{2})-\frac{p\sigma }{q}Z(t+\tau _{1})\\\le & {} s-\mu _{2}T_{1}(t), \end{aligned}$$

where \(\mu \le \delta \) and \(\mu _{2}=\min \{\mu ,\frac{\delta }{2},c,\sigma \}\). Therefore, we have \(\limsup \nolimits _{t\rightarrow \infty } T_{1}(t)\le \frac{s}{\mu _{2}}\). Hence, all solutions of the model (7) are bounded for sufficiently large t. The model (7) has the same three steady states as the non-delay model (2), namely, the disease-free steady state \(E_{0}=\left( H_{0},I_{0},D_{0},V_{0},Z_{0}\right) =\left( \frac{s}{\mu },0,0,0,0\right) \), the immune-free steady state \(E_{1}=\left( H_{1},I_{1},D_{1},V_{1},Z_{1}\right) \) which exists whenever \(R_{0}>1\) and the endemic steady state \(E^{*}=\left( H^{*},I^{*},D^{*},V^{*},Z^{*}\right) \) which exists whenever \(R_{{ CTL}}>1\).

Global Analysis of the Delay Model

In this section, we study the global asymptotic stability for the delay model (7).

Theorem 4

The disease-free steady state \(E_{0}\) is globally asymptotically stable for any delay \(\tau _{1}>0,~\tau _{2}>0\) if \(R_{0}\le 1\).

Proof

We define a Lyapunov function \(L_{4}\) as follows:

$$\begin{aligned} L_{4}(t)= & {} H_{0}G\left( \frac{H}{H_{0}}\right) +I(t)+\frac{\delta }{a}D(t)+ \frac{\delta (\beta +\delta )}{a\beta }V(t)+\frac{p}{q}Z(t)\\&+\,k\int _{t-\tau _{1}}^{t}H(\xi )V(\xi )d\xi +\delta \int _{t-\tau _{2}}^{t}I(\xi )d\xi . \end{aligned}$$

Taking the derivative of \(L_{4}\) along the solutions of the model (7), we obtain

$$\begin{aligned} \frac{{ dL}_{4}}{{ dt}}= & {} \left( 1-\frac{H_{0}}{H}\right) \frac{{ dH}}{{ dt}}+\frac{{ dI}}{{ dt}} +\frac{\delta }{a}\frac{{ dD}}{{ dt}} +\frac{\delta (\beta +\delta )}{a\beta }\frac{{ dV}}{{ dt}}+ \frac{p}{q}\frac{{ dZ}}{{ dt}}\\&+\, k[{ HV}-H(t-\tau _{1})V(t-\tau _{1})]+\delta [I-I(t-\tau _{2})]\\= & {} \left( 1-\frac{H_{0}}{H}\right) [s-\mu H-{ kHV}] +[{ kH}(t-\tau _{1})V(t-\tau _{1})-\delta I-{ pIZ}]\\&+\, \frac{\delta }{a}[{ aI}(t-\tau _{2})-(\beta +\delta )D]+ \frac{\delta (\beta +\delta )}{a\beta }[\beta D-{ cV}]+ \frac{p}{q}[{ qIZ}-\sigma Z]\\&+\,k[{ HV}-H(t-\tau _{1})V(t-\tau _{1})]+\delta [I-I(t-\tau _{2})]\\= & {} s\left[ 2-\frac{H}{H_{0}}-\frac{H_{0}}{H}\right] + \frac{c\delta (\beta +\delta )}{a\beta }[R_{0}-1]V-\frac{p\sigma }{q}Z\\= & {} -\frac{s}{{ HH}_{0}}(H-H_{0})^{2}+\frac{c\delta (\beta +\delta ) }{a\beta }[R_{0}-1]V-\frac{p\sigma }{q}Z. \end{aligned}$$

Therefore, \(\frac{{ dL}_{4}}{{ dt}}\le 0\) if \(R_{0}\le 1\). Assume that M is the largest invariant set in \(\{(H,I,D,V,Z)|\frac{{ dL}_{4}}{{ dt}}=0\}\). Note that \(\frac{{ dL}_{4}}{{ dt}}=0\) if and only if \(H=H_{0}=\frac{s}{\mu }\), \(I=0\), \(D=0\), \(V=0\) and \(Z=0\). Hence, \(M=\{E_{0}\}=\{(\frac{s}{\mu },0,0,0,0)\}\). Thus, by the Lyapunov-LaSalle invariance principle [14, 16, 18], \(E_{0}\) is globally asymptotically stable if \(R_{0}\le 1\). \(\square \)

Theorem 5

The immune-free steady state \(E_{1}\) is globally asymptotically stable for any delay \(\tau _{1}>0,~\tau _{2}>0\) if \(R_{{ CTL}}\le 1<R_{0}\).

Proof

We define a Lyapunov function \(L_{5}\) as follows:

$$\begin{aligned} L_{5}(t)= & {} H_{1}G\left( \frac{H}{H_{1}}\right) +I_{1}G\left( \frac{I}{I_{1}}\right) + \frac{\delta }{a}D_{1}G\left( \frac{D}{D_{1}}\right) +\frac{\delta (\beta +\delta )}{a\beta }V_{1}G\left( \frac{V}{V_{1}}\right) +\frac{p}{q}Z(t)\\&+\,kH_{1}V_{1}\int _{t-\tau _{1}}^{t}G\left( \frac{H(\xi )V(\xi )}{H_{1}V_{1}}\right) d\xi +\delta I_{1}\int _{t-\tau _{2}}^{t}G\left( \frac{I(\xi )}{I_{1}}\right) d\xi \\= & {} L_{5}^{1}+L_{5}^{2}+L_{5}^{3}, \end{aligned}$$

where

$$\begin{aligned} L_{5}^{1}= & {} H_{1}G\left( \frac{H}{H_{1}}\right) +I_{1}G\left( \frac{I}{I_{1}}\right) + \frac{\delta }{a}D_{1}G\left( \frac{D}{D_{1}}\right) +\frac{\delta (\beta +\delta )}{a\beta }V_{1}G\left( \frac{V}{V_{1}}\right) +\frac{p}{q}Z(t),\\ L_{5}^{2}= & {} { kH}_{1}V_{1}\int _{t-\tau _{1}}^{t}G\left( \frac{H(\xi )V(\xi )}{H_{1}V_{1}}\right) d\xi ,\\ L_{5}^{3}= & {} \delta I_{1}\int _{t-\tau _{2}}^{t}G\left( \frac{I(\xi )}{I_{1}}\right) d\xi . \end{aligned}$$

Taking the derivative of \(L_{5}^{1}\) along the solutions of the model (7), we obtain

$$\begin{aligned} \frac{{ dL}_{5}^{1}}{{ dt}}= & {} \left( 1-\frac{H_{1}}{H}\right) \frac{{ dH}}{{ dt}}+ \left( 1-\frac{I_{1}}{I}\right) \frac{{ dI}}{{ dt}}+ \frac{\delta }{a}\left( 1-\frac{D_{1}}{D}\right) \frac{{ dD}}{{ dt}}\\&+\,\frac{\delta (\beta +\delta )}{a\beta }\left( 1-\frac{V_{1}}{V} \right) \frac{{ dV}}{{ dt}}+\frac{p}{q}\frac{{ dZ}}{{ dt}}\\= & {} \left( 1-\frac{H_{1}}{H}\right) [s-\mu H-{ kHV}]+ \left( 1-\frac{I_{1}}{I}\right) [{ kH}(t-\tau _{1})V(t-\tau _{1})\\&-\,\delta I-{ pIZ}]+\frac{\delta }{a}\left( 1-\frac{D_{1}}{D} \right) [{ aI}(t-\tau _{2})-(\beta +\delta )D]\\&+\,\frac{\delta (\beta +\delta )}{a\beta }\left( 1- \frac{V_{1}}{V}\right) [\beta D-{ cV}] +\frac{p}{q}[{ qIZ}-\sigma Z]\\= & {} \left( 1-\frac{H_{1}}{H}\right) [s-\mu H-{ kHV}]+ \left( 1-\frac{I_{1}}{I}\right) [{ kHV}-\delta I-{ pIZ}]\\&+\, \frac{\delta }{a}\left( 1-\frac{D_{1}}{D}\right) [{ aI}-(\beta +\delta )D]+ \frac{\delta (\beta +\delta )}{a\beta } \left( 1-\frac{V_{1}}{V}\right) [\beta D-{ cV}]\\&+\,\frac{p}{q}[{ qIZ}-\sigma Z]+k\left( 1-\frac{I_{1}}{I}\right) [H(t-\tau _{1})V(t-\tau _{1})-{ HV}]\\&+\,\delta \left( 1-\frac{D_{1}}{D}\right) [I(t-\tau _{2})-I]\\= & {} \mu H_{1}\left[ 2-\frac{H}{H_{1}}-\frac{H_{1}}{H}\right] + \delta I_{1}\left[ 4-\frac{H_{1}}{H}-\frac{{ HI}_{1}V}{H_{1}{} { IV}_{1}}- \frac{{ ID}_{1}}{I_{1}D}-\frac{{ DV}_{1}}{D_{1}V}\right] \\&+\,\frac{{ ps}}{\delta R_{{ CTL}}}[R_{{ CTL}}-1]Z+ k\left( 1-\frac{I_{1}}{I}\right) [H(t-\tau _{1})V(t-\tau _{1})-{ HV}]\\&+\,\delta \left( 1-\frac{D_{1}}{D}\right) [I(t-\tau _{2})-I]\\= & {} \mu H_{1}\left[ 2-\frac{H}{H_{1}}-\frac{H_{1}}{H}\right] + \delta I_{1}\left[ 4-\frac{H_{1}}{H}-\frac{H(t-\tau _{1})I_{1} V(t-\tau _{1})}{H_{1}{} { IV}_{1}}-\frac{I(t-\tau _{2})D_{1}}{I_{1}D} \right. \\&\left. -\,\frac{{ DV}_{1}}{D_{1}V}\right] +\frac{{ ps}}{\delta R_{{ CTL}}}[R_{{ CTL}}-1]Z+{ kH}_{1}V_{1} \left[ \frac{H(t-\tau _{1})V(t-\tau _{1})}{H_{1}V_{1}}-\frac{{ HV}}{H_{1}V_{1}}\right] \\&+\,\delta I_{1}\left[ \frac{I(t-\tau _{2})}{I_{1}}-\frac{I}{I_{1}}\right] \\= & {} -\frac{\mu }{H}(H-H_{1})^{2}+\delta I_{1}\left[ 4-\frac{H_{1}}{H}-\frac{H(t-\tau _{1})I_{1}V(t-\tau _{1})}{H_{1}{} { IV}_{1}}-\frac{I(t-\tau _{2})D_{1}}{I_{1}D}\right. \\&\left. -\frac{{ DV}_{1}}{D_{1}V}\right] +\frac{{ ps}}{\delta R_{{ CTL}}}[R_{{ CTL}}-1]Z+{ kH}_{1}V_{1}\left[ \frac{H(t-\tau _{1})V(t-\tau _{1})}{H_{1}V_{1}}-\frac{{ HV}}{H_{1}V_{1}}\right] \\&+\,\delta I_{1}\left[ \frac{I(t-\tau _{2})}{I_{1}}-\frac{I}{I_{1}}\right] . \end{aligned}$$

Also,

$$\begin{aligned} \frac{{ dL}_{5}^{2}}{{ dt}}= & {} { kH}_{1}V_{1}\left[ \frac{{ HV}}{H_{1}V_{1}}-\frac{H(t-\tau _{1}) V(t-\tau _{1})}{H_{1}V_{1}}+\ln \frac{H(t-\tau _{1})V(t-\tau _{1})}{{ HV}}\right] ,\\ \frac{{ dL}_{5}^{3}}{{ dt}}= & {} \delta I_{1}\left[ \frac{I}{I_{1}}-\frac{I(t-\tau _{2})}{I_{1}}+ \ln \frac{I(t-\tau _{2})}{I}\right] . \end{aligned}$$

Therefore, the derivative of \(L_{5}\) along the solutions of the model (7) is

$$\begin{aligned} \frac{{ dL}_{5}}{{ dt}}= & {} \frac{{ dL}_{5}^{1}}{{ dt}}+ \frac{{ dL}_{5}^{2}}{{ dt}}+\frac{{ dL}_{5}^{3}}{{ dt}}\\= & {} -\frac{\mu }{H}(H-H_{1})^{2}+\delta I_{1}\left[ 4- \frac{H_{1}}{H}-\frac{H(t-\tau _{1})I_{1}V(t-\tau _{1})}{H_{1}{} { IV}_{1}}- \frac{I(t-\tau _{2})D_{1}}{I_{1}D}\right. \\&\left. -\,\frac{{ DV}_{1}}{D_{1}V}+\ln \frac{H(t-\tau _{1})V(t-\tau _{1}) I(t-\tau _{2})}{{ HVI}}\right] +\frac{ps}{\delta R_{{ CTL}}}[R_{{ CTL}}-1]Z. \end{aligned}$$

Taking \(p_{1}=H_{1},p_{2}=H(t-\tau _{1})I_{1}V(t-\tau _{1}),p_{3}=I(t-\tau _{2}) D_{1},p_{4}={ DV}_{1},q_{1}=H,q_{2}=H_{1}{} { IV}_{1},q_{3}=I_{1}D,q_{4}=D_{1}V\) and using the inequality (5) for \(n=4\), we obtain

$$\begin{aligned}&4-\frac{H_{1}}{H}-\frac{H(t-\tau _{1})I_{1}V(t-\tau _{1})}{H_{1}{} { IV}_{1}}-\frac{I(t-\tau _{2})D_{1}}{I_{1}D}-\frac{{ DV}_{1}}{D_{1}V}\nonumber \\&\quad +\ln \frac{H(t-\tau _{1})V(t-\tau _{1})I(t-\tau _{2})}{{ HVI}}\le 0. \end{aligned}$$

Therefore, \(\frac{{ dL}_{5}}{{ dt}}\le 0\) if \(R_{{ CTL}}\le 1\). Assume that M is the largest invariant set in \(\{(H,I,D,V,Z)|\frac{{ dL}_{5}}{{ dt}}=0\}\). Note that \(\frac{{ dL}_{5}}{{ dt}}=0\) if and only if \(H=H_{1}\), \(I=I_{1}\), \(D=D_{1}\), \(V=V_{1}\) and \(Z=Z_{1}=0\). Hence, \(M=\{E_{1}\}\). Since \(E_{1}\) exists whenever \(R_{0}>1\), then by the Lyapunov-LaSalle invariance principle [14, 16, 18], \(E_{1}\) is globally asymptotically stable if \(R_{{ CTL}}\le 1<R_{0}\). \(\square \)

Theorem 6

The endemic steady state \(E^{*}\) is globally asymptotically stable for any delay \(\tau _{1}>0,~\tau _{2}>0\) if \(R_{{ CTL}}>1\).

Proof

We define a Lyapunov function \(L_{6}\) as follows:

$$\begin{aligned} L_{6}(t)= & {} H^{*}G\left( \frac{H}{H^{*}}\right) +I^{*}G\left( \frac{I}{I^{*}}\right) \nonumber \\&+\,\frac{(\delta +{ pZ}^{*})}{a}D^{*}G\left( \frac{D}{D^{*}}\right) +\frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta }V^{*} G\left( \frac{V}{V^{*}}\right) \\&+\,\frac{p}{q}Z^{*}G\left( \frac{Z}{Z^{*}}\right) + kH^{*}V^{*}\int _{t-\tau _{1}}^{t}G \left( \frac{H(\xi )V(\xi )}{H^{*}V^{*}}\right) d\xi \nonumber \\&+\,(\delta I^{*}+{ pI}^{*}Z^{*})\int _{t-\tau _{2}}^{t} G\left( \frac{I(\xi )}{I^{*}}\right) d\xi \\= & {} L_{6}^{1}+L_{6}^{2}+L_{6}^{3}, \end{aligned}$$

where

$$\begin{aligned} L_{6}^{1}= & {} H^{*}G\left( \frac{H}{H^{*}}\right) +I^{*}G\left( \frac{I}{I^{*}}\right) +\frac{(\delta +{ pZ}^{*})}{a}D^{*}G\left( \frac{D}{D^{*}}\right) \nonumber \\&+\,\frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta }V^{*} G\left( \frac{V}{V^{*}}\right) +\frac{p}{q}Z^{*}G\left( \frac{Z}{Z^{*}}\right) ,\\ L_{6}^{2}= & {} { kH}^{*}V^{*}\int _{t-\tau _{1}}^{t}G\left( \frac{H(\xi )V(\xi )}{H^{*}V^{*}}\right) d\xi ,\\ L_{6}^{3}= & {} (\delta I^{*}+{ pI}^{*}Z^{*})\int _{t-\tau _{2}}^{t}G\left( \frac{I(\xi )}{I^{*}}\right) d\xi . \end{aligned}$$
Fig. 1
figure 1

Dynamics of the model (2) when \(R_{0}\le 1\) with three different initial conditions IC1, IC2, IC3

Full size image
Fig. 2
figure 2

Dynamics of the model (2) when \(R_{{ CTL}}>1\) with three different initial conditions \({ IC}1,{ IC}2,{ IC}3\)

Full size image

Taking the derivative of \(L_{6}^{1}\) along the solutions of the model (7), we obtain

$$\begin{aligned} \frac{{ dL}_{6}^{1}}{{ dt}}= & {} \left( 1-\frac{H^{*}}{H}\right) \frac{{ dH}}{{ dt}}+\left( 1-\frac{I^{*}}{I}\right) \frac{{ dI}}{{ dt}}+ \frac{(\delta +{ pZ}^{*})}{a}\left( 1-\frac{D^{*}}{D}\right) \frac{{ dD}}{{ dt}}\\&+\, \frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta }\left( 1-\frac{V^{*}}{V}\right) \frac{{ dV}}{{ dt}}+ \frac{p}{q}\left( 1-\frac{Z^{*}}{Z}\right) \frac{{ dZ}}{{ dt}}\\= & {} \left( 1-\frac{H^{*}}{H}\right) [s-\mu H-{ kHV}]+ \left( 1-\frac{I^{*}}{I}\right) [{ kH}(t-\tau _{1})V(t-\tau _{1})\\&-\delta I-{ pIZ}]+ \frac{(\delta +{ pZ}^{*})}{a}\left( 1-\frac{D^{*}}{D}\right) [{ aI}(t-\tau _{2})-(\beta +\delta )D]\\&+\, \frac{(\delta +{ pZ}^{*})(\beta +\delta )}{a\beta } \left( 1-\frac{V^{*}}{V}\right) [\beta D-{ cV}]+ \frac{p}{q}\left( 1-\frac{Z^{*}}{Z}\right) [{ qIZ}-\sigma Z]\\= & {} -\frac{\mu }{H}(H-H^{*})^{2}+(\delta I^{*}+{ pI}^{*}Z^{*}) \left[ 4-\frac{H^{*}}{H}-\frac{H(t-\tau _{1})I^{*}V(t-\tau _{1})}{H^{*}{} { IV}^{*}}\right. \\&\left. -\,\frac{I(t-\tau _{2})D^{*}}{I^{*}D}-\frac{{ DV}^{*}}{D^{*}V}\right] + { kH}^{*}V^{*}\left[ \frac{H(t-\tau _{1})V(t-\tau _{1})}{H^{*}V^{*}}- \frac{{ HV}}{H^{*}V^{*}}\right] \\&+\,(\delta I^{*}+{ pI}^{*}Z^{*})\left[ \frac{I(t-\tau _{2})}{I^{*}}- \frac{I}{I^{*}}\right] . \end{aligned}$$

Also,

$$\begin{aligned} \frac{{ dL}_{6}^{2}}{{ dt}}= & {} { kH}^{*}V^{*}\left[ \frac{{ HV}}{H^{*}V^{*}}-\frac{H(t-\tau _{1}) V(t-\tau _{1})}{H^{*}V^{*}}+ \ln \frac{H(t-\tau _{1})V(t-\tau _{1})}{{ HV}}\right] ,\\ \frac{{ dL}_{6}^{3}}{{ dt}}= & {} (\delta I^{*}+{ pI}^{*}Z^{*})\left[ \frac{I}{I^{*}}-\frac{I(t-\tau _{2})}{I^{*}}+\ln \frac{I(t-\tau _{2})}{I}\right] . \end{aligned}$$

Therefore, the derivative of \(L_{6}\) along the solutions of the model (7) is

$$\begin{aligned} \frac{{ dL}_{6}}{{ dt}}= & {} \frac{{ dL}_{6}^{1}}{{ dt}}+ \frac{{ dL}_{6}^{2}}{{ dt}}+\frac{{ dL}_{6}^{3}}{{ dt}}\\= & {} -\frac{\mu }{H}(H-H^{*})^{2}+(\delta I^{*}+{ pI}^{*}Z^{*}) \left[ 4-\frac{H^{*}}{H}-\frac{H(t-\tau _{1})I^{*}V(t-\tau _{1})}{H^{*}{} { IV}^{*}}\right. \\&\left. -\,\frac{I(t-\tau _{2})D^{*}}{I^{*}D}-\frac{DV^{*}}{D^{*}V}+\ln \frac{H(t-\tau _{1})V(t-\tau _{1})I(t-\tau _{2})}{{ HVI}}\right] . \end{aligned}$$

Taking \(p_{1}=H^{*},p_{2}=H(t-\tau _{1})I^{*}V(t-\tau _{1}),p_{3}=I(t-\tau _{2})D^{*},p_{4}={ DV}^{*},q_{1}=H, q_{2}=H^{*}{} { IV}^{*},q_{3}=I^{*}D,q_{4}=D^{*}V\) and using the inequality (5) for \(n=4\), we obtain

$$\begin{aligned}&4-\frac{H^{*}}{H}-\frac{H(t-\tau _{1})I^{*}V(t-\tau _{1})}{H^{*}{} { IV}^{*}}-\frac{I(t-\tau _{2})D^{*}}{I^{*}D}-\frac{{ DV}^{*}}{D^{*}V}\nonumber \\&\quad +\ln \frac{H(t-\tau _{1})V(t-\tau _{1})I(t-\tau _{2})}{{ HVI}}\le 0. \end{aligned}$$

Therefore, \(\frac{{ dL}_{6}}{{ dt}}\le 0\). Assume that M is the largest invariant set in \(\{(H,I,D,V,Z)| \frac{{ dL}_{6}}{{ dt}}=0\}\). Note that \(\frac{{ dL}_{6}}{{ dt}}=0\) if and only if \(H=H^{*}\), \(I=I^{*}\), \(D=D^{*}\), \(V=V^{*}\) and \(Z=Z^{*}\). Hence, \(M=\{E^{*}\}\). Since \(E^{*}\) exists whenever \(R_{{ CTL}}>1\), then by the Lyapunov-LaSalle invariance principle [14, 16, 18], \(E^{*}\) is globally asymptotically stable if \(R_{{ CTL}}>1\). \(\square \)

Fig. 3
figure 3

Dynamics of the model (7) when \(R_{0}\le 1\) with four sets of delays \((\tau _{1},\tau _{2})=\{(5,5),(5,30),(30,5),(30,30)\}=\{{ DS}1,{ DS}2,{ DS}3,{ DS}4\}\) in days respectively

Full size image
Fig. 4
figure 4

Dynamics of the model (7) when \(R_{{ CTL}}>1\) with four sets of delays \((\tau _{1},\tau _{2})=\{(5,5),(5,30),(30,5),(30,30)\}=\{{ DS}1,{ DS}2,{ DS}3,{ DS}4\}\) in days respectively

Full size image

Numerical Simulation

In this section, we illustrate the theoretical results through numerical simulations. We first consider the parameter values \(s=2.6\times 10^{7}, \mu =0.01, k=3\times 10^{-13}, \delta =0.053, p=0.95, a=150, \beta =0.87, c=3.8, q=0.12\) and \(\sigma =0.05\). Here, the values of p, q and \(\sigma \) are taken from [4] while other parameter values are chosen from [16, 18]. For this set of parameter values, we have \(R_{0}<1\). For the case \(R_{{ CTL}}>1\), we consider \(k=1.67\times 10^{-12}\) [16, 18] while other parameter values are same as before. For these two cases, we have considered three different initial conditions. For the first case (i.e., \(R_{0}<1\)), numerical simulation was observed for a period of 400 days. From Fig. 1, it can be seen that the solutions eventually approach the disease-free steady state (\(E_{0}\)) and it supports our theoretical result in this case. For the second case (i.e., \(R_{{ CTL}}>1\)), numerical simulation was observed for a period of 5000 days. In this case, the solutions eventually approach the endemic steady state (\(E^{*}\)) which is illustrated in Fig. 2. It can be seen from Fig. 2 that oscillations of the solutions are decreasing and if we run the simulation for a longer period of time the solutions eventually converge to \(E^{*}\). A set of feasible (clinically valid) parameter values for the case \(R_{{ CTL}}\le 1<R_{0}\) was not available in the literature for our model, and consequently the numerical illustration for this case is omitted.

For the delay model, we consider the above two sets of parameter values, one initial condition and four sets of time delays (in days), namely, \((\tau _{1},\tau _{2})=\{(5,5),(5,30),(30,5),(30,30)\}\). Figure 3 illustrates numerical simulation of the model (7) when \(R_{0}<1\). In this case, the simulation is carried out for a period of 1000 days and it is evident from Fig. 3 that the delays and their lengths do not affect the global asymptotic stability of \(E_{0}\). For the case \(R_{{ CTL}}>1\), the simulation is observed for a period of 5000 days and it can be observed that the solutions converge to \(E^{*}\) (from Fig. 4). From Figs. 2 and 4, interestingly it can be seen that the solution trajectories of the model with two delays converge to the endemic steady state much faster than the solutions of the model without any delay.

Conclusion

In this paper, a modified HBV infection model with intracellular HBV DNA-containing capsids and CTL immune responses has been studied. This model admits three steady states, namely, disease-free steady state (\(E_{0}\)), immune-free steady state (\(E_{1}\)) and endemic steady state (\(E^{*}\)). The global properties of these three steady states have been analyzed by constructing suitable Lyapunov functions and using the Lyapunov-LaSalle invariance principle. The results have been obtained in terms of the basic reproduction number (\(R_{0}\)) and the immune response reproduction number (\(R_{{ CTL}}\)). It is shown that \(E_{0}\) is globally asymptotically stable whenever \(R_{0}\le 1\), \(E_{1}\) is globally asymptotically stable whenever \(R_{{ CTL}}\le 1<R_{0}\) and \(E^{*}\) is globally asymptotically stable whenever \(R_{{ CTL}}>1\).

Further, we have incorporated two delays in the model where one delay is for the production of productively infected hepatocytes from the uninfected ones and another delay is for the production of matured capsids. These two delays have been included in the model to see if these delays can result in any periodic oscillation and Hopf bifurcation. But, the results show that inclusion of these delays does not cause periodic oscillations and Hopf bifurcations and the global dynamics of the delay model is unaltered as in the case for non-delay model.