1 Introduction

In the past few decades, backstepping-based adaptive control has become one of the most popular design methods to deal with nonlinear systems and has obtained many very meaningful results [1, 2]. To give a few examples, with the help of the backstepping-based adaptive neural network technique, [3] solves the asymptotic tracking control problem of high-order fully actuated systems. Based on the research in Zhao et al. [3], a fuzzy state observer is introduced for nonstrict nonlinear systems in [4] to address the unmeasurable state problem and the algebraic loop problem. Since the backstepping method requires repeated differentiation of the virtual controller, the above literatures [3, 4] inevitably have the phenomenon of “complexity explosion” as the order of the system increases. To solve this problem, dynamic surface control technology is used in Wang et al. [5] to successfully reduce the complexity of n-order nonstrict feedback system in the controller design process. In Singh et al. [6], flight path angle of the aircraft is controlled asymptotically for a class of nonstrict feedback system by employing robust backstepping dynamic surface control. Further [7] combines the adaptive dynamic surface method with the gain suppressing inequality technique to solve the predefined tracking control problem of stochastic systems. Although the adaptive dynamic surface control method has a certain degree of robustness to resist external uncertainties, unfortunately, it cannot solve the system dynamics caused by the actuator failure.

In practical engineering, due to the complexity of the working environment and the limitation of the material itself, the actuator will inevitably fail. The existence of faults can seriously damage the system performance and cause adverse effects on economy. Therefore, designing a reasonable fault-tolerant control scheme to reduce the impact of faults on the system meets the needs of social development. In terms of practical applications, for the supersonic tailless aircraft subject to actuator faults, [8] develops a fault-tolerant scheme based on reconfiguration control allocation. Nevertheless, for the spacecraft attitude control system with actuator faults, [9] presents a fault-tolerant scheme based on iterative learning observer. In addition, compared with the active fault-tolerant control used in Cong et al. [8, 9], the passive fault-tolerant control scheme is adopted in Shi et al. [10] for the three-phase machine system, which speeds up system response. In terms of theoretical research, for polynomial fuzzy systems with linear actuator faults, [11] develops a polynomial adaptive fuzzy observer to estimate actuator faults. However, for high-order nonlinear system with non-affine nonlinear faults, [12] constructs a new adaptive fuzzy fault-tolerant controller based on the high-order fully actuated systems theory. Considering that multi-agent systems are vulnerable to malicious attacks during communication, [13] proposes an adaptive collaborative fault-tolerant control scheme based on distributed sliding mode observer. The above literatures only focus on the steady-state performance of the system. In fact, the convergence rate is also an important factor affecting the industrial production. Therefore, it is necessary to develop a control scheme that considers both stability and convergence rate.

The fixed-time control can take into account both the steady-state performance and the convergence rate of the system. Compared with the finite-time control, it gets rid of the dependence on the initial conditions. In recent years, fixed-time control has received great attention and has been applied in many fields, such as aerospace field [14, 15], robotics field [16, 17], automotive field [14, 18, 19] studies the fixed-time attitude tracking control problem of spacecraft with prescribed performance, and designs a prescribed performance tracking controller based on disturbance observer. [15] further considers the impact of actuator failures on spacecraft based on the findings of [14]. Zhou et al. [16] designed a neural network fixed-time slide mode trajectory controller to adjust the desired angular positions of rigid-flexible coupled robotic mechanisms for the rigid-flexible coupled robotic mechanisms with large beam deflections. To guarantee the transient and steady-state performance of uncertain robotic manipulators within fixed time, an approximate continuous fixed-time terminal sliding mode control with prescribed performance is developed in Sai et al. [17]. Jia et al. [18, 19] studied the adaptive fixed-time control problem of active suspension systems with actuator faults and active suspension systems with time-varying displacement constraints, respectively.

Based on the above paper’s inspiration, this paper mainly studies the adaptive fuzzy fixed-time fault-tolerant control problem for nonstrict feedback nonlinear systems with non-affine faults. Based on the dynamic surface technique, an adaptive fuzzy fixed-time fault-tolerant controller is constructed. The controller can ensure that the tracking error converges to the small neighborhood near the origin regardless of whether the fault exists. The main contributions are as follows:

  1. (1)

    For nonlinear systems with actuator failures, an adaptive fuzzy passive fault-tolerant control scheme based on fixed time is proposed. Compared with the active fault-tolerant control scheme in Sha et al. [20], the passive fault-tolerant control strategy proposed is simpler and the response speed is faster. More to the point, the combination of passive fault-tolerant control and fixed-time stability theory ensures the stability and tracking accuracy of the system while retaining the original advantages of passive fault-tolerance.

  2. (2)

    Non-affine nonlinear faults causing actuator failure are considered. Different from linear faults in Yang et al. [21, 22], non-affine nonlinear faults are more common in industry. By giving the upper bound of the undivided term composed by the unknown function and the unknown fault function, using the approximation characteristics of fuzzy logic systems (FLSs), the fault-tolerant control problem considered in this paper is reduced to dealing with the unknown bounding function problem.

  3. (3)

    In this paper, a more representative nonlinear system with nonstrict feedback structure is considered and the approximation performance of fuzzy logic is used to deal with the nonlinear functions containing all state variables in the system. In addition, the introduction of dynamic surface control technology not only solves the problem of “complexity explosion” in Ha et al. [23], but also avoid the calculation of partial derivatives.

The rest of this paper is organized as follows. Section 2 gives the preliminaries, which are used in the design of the fixed-time fault-tolerant tracking controller. The control strategy and stability analysis are completed in Sect. 3. Section 4 uses two simulations as examples to verify the effectiveness of the proposed scheme. In the end, the conclusion is given in detail in Sect. 5.

2 Problem Statement and Preliminaries

In order to meet the design requirements of the fault-tolerant tracking controller, a nonlinear system model is given, which has nonstrict feedback form and non-affine fault term.

$$\begin{aligned} {\left\{ \begin{array}{l} \dot{x}_1=x_2+{{f}_{1}}(x)\\ \qquad \qquad \vdots \\ \dot{x}_i=x_{i+1}+{{f}_{i}}(x)\\ \qquad \qquad \vdots \\ \dot{x}_n=u+{{f}_{n}}(x)+\zeta (t-T_0)\tau (x,u)\\ y={{x}_{1}} \end{array} \right. } \end{aligned},$$
(1)

where \(x=[x_1,x_2,\ldots,x_n]\in \mathfrak {R}^n\), \(u\in \mathfrak {R}\), and \(y\in \mathfrak {R}\) stand for the state vector, input, and output of system (1), respectively. Given a desired tracking signal \(y_r\), system output y can track desired output \(y_r\) well under the action of the developed fault-tolerant tracking controller, and the tracking error is denoted as e and \(e=y-y_r\). \({{f}_{i}}(x)\) denotes the smooth nonlinear function, which is unknown in this paper. Some unknown changes may occur due to existing faults in the system, represented by \(\tau (x,u)\), where \(\tau (x,u)\in \mathfrak {R}\). \(\zeta (t-T_0)\) refers to the homologous time profile of the fault that occurs at some unknown time \(T_0\) and can be described by the following two cases:

Case 1: If \(t<T_0\) is satisfied, \(\zeta (t-T_0)\) can be written as

$$\begin{aligned} \zeta (t-T_0)=0 \end{aligned}.$$
(2)

Case 2: If \(t\geqslant {T_0}\) is satisfied, \(\zeta (t-T_0)\) can be written as

$$\begin{aligned} \zeta (t-T_0)=1-e^{-\varrho (t-T_0)} \end{aligned},$$
(3)

where \(\varrho\) is a non-negative constant that represents the corresponding evolution rate caused by unknown faults.

This paper employs the passive fault-tolerant control scheme based on fixed-time to offset the effects and changes of system non-dynamics caused by faults. Non-affine nonlinear faults involving system state and controller output are considered. When the value of \(\varrho\) is relatively small, the fault type of the system is an incipient fault. On the contrary, when the value of \(\varrho\) is pretty large, the fault type of the system is an abrupt fault. The passive fault-tolerant control scheme does not require the fault identification and isolation unit, but only evaluates the fault level by designing the corresponding adaptive law. The adaptive law feeds the evaluation results back to the fault-tolerant controller. Then, under the action of fault-tolerant controller, the effects and changes of system non-dynamics caused by faults are weakened.

The following two assumptions are given, which are essential to solving such problems in order to successfully design the controller for a plant with non-affine faults.

Assumption 1

In system (1), the reference signal \(y_r(t)\) and its corresponding first-order time derivative \(\dot{y}_r(t)\) and second-order time derivative \(\ddot{y}_r(t)\) are all bounded and known.

Assumption 2

Given an unknown non-negative function \(\bar{h}(x,u)\), such that it satisfies the following equation:

$$\begin{aligned} \mid {f}_{n}(x)+\zeta (t-T_0)\tau (x,u)\mid \leqslant \bar{h}(x,u) \end{aligned}$$
(4)

Remark 1

Assumption 1 only restricts \(y_r(t)\), \(\dot{y}_r(t)\), and \(\ddot{y}_r(t)\), but does not astrict the remaining n-order time derivatives, where n is an integer greater than 2. The strict constraints on the previous reference signals \(y_r(t)\) are relaxed and the computational complexity is reduced. Assumption 2 treats the term \({f}_{n}(x)\) and the term \(\zeta (t-T_0)\tau (x,u)\) as a whole, called h(x, u). Meanwhile, h(x, u) satisfies the condition \(\mid {h}(x,u)\mid \leqslant \bar{h}(x,u)\). The ultimate purpose of Assumption 1 and Assumption 2 is to simplify the calculation process and reduce the computational complexity. For similar assumptions, see [24,25,26] for detail.

In order to successfully complete the design task of the fault-tolerant tracking controller, some related Lemmas are introduced.

Lemma 1

(Young’s inequality [27]) For \(\forall (x,y)\in \mathfrak {R}^2\), the following inequality holds:

$$\begin{aligned} xy\leqslant \frac{\vartheta ^m}{m}\mid x\mid ^m+\frac{1}{n\vartheta ^n}\mid y\mid ^n, \end{aligned}$$
(5)

where \(\vartheta >0\), \(m>1\), \(n>1\). At the same time, in order for (5) to hold, m and n must also satisfy \((m-1)(n-1)=1\).

Lemma 2

[28] Consider \(f_l>0\), the following inequalities hold:

$$\begin{aligned} \bigg (\sum \limits _{l=1}^{n}{f_l}\bigg )^{p} \leqslant {\sum \limits _{l=1}^{n}{{f_l}^p}} \leqslant {n^{1-p}}\bigg (\sum \limits _{l=1}^{n}{f_l}\bigg )^{p}, \end{aligned}$$
(6)
$$\begin{aligned} {n^{1-q}}\bigg (\sum \limits _{l=1}^{n}{f_l}\bigg )^{q} \leqslant {\sum \limits _{l=1}^{n}{{f_l}^q}} \leqslant \bigg (\sum \limits _{l=1}^{n}{f_l}\bigg )^{q}, \end{aligned}$$
(7)

where \(0<p\leqslant 1\), \(q\geqslant 1\).

Lemma 3

[29] Suppose V(x) satisfies the following conditions: (1) V(x) is a positive definite function; (2) \(\dot{V}(x)\) is a negative definite function. If any solution x(t) of the plant (1) satisfies \(\dot{V}(x)\leqslant -sV^\kappa (x)-tV^\iota (x)\), then the system (1) is globally stable in fixed-time, and the setting-time T of the plant (1) is \(T\leqslant {T}_\text {max}=1/(s(1-\kappa ))+1/(t(\iota -1))\). If x(t) satisfies \(\dot{V}(x)\leqslant -sV^\kappa (x)-tV^\iota (x)+W\), then the system (1) is practically stable in fixed-time, and the setting-time T is \(T\leqslant {T}_\text {max}=1/(s\eta (1-\kappa ))+1/(t\eta (\iota -1))\). In the above inequality, s, t, \(\kappa\), \(\iota\), \(\eta\), and W all denote constants, and satisfy \(s>0\), \(t>0\), \(0<\kappa <1\), \(\iota >1\), \(0<\eta <1\), and \(W>0\), respectively.

Proof See [30,31,32] for the proof of Lemma 3.

In this paper, the approximation performance of FLSs is needed to deal with unknown nonlinear functions f in the plant (1), and then be applied to dynamic surface control technique to design the desired controller. FLSs can be divided into four parts: knowledge base, fuzzifier, fuzzy inference engine, and defuzzifier. The knowledge base of FLSs is composed of a set of If-Then rules, as follows:

\(\Upsilon ^k\): If \(\chi ^k_1\) is \(\Psi _1\) and \(\chi ^k_2\) is \(\Psi _2\) and... and \(\chi ^k_n\) is \(\Psi _n\),then y is \(\Phi ^k\), \(k=1, 2,\ldots,n\). Here, \(\chi =[\chi _1, \chi _2,\ldots, \chi _n]^T\) represents the input vector of FLSs, y refers to the output of FLSs. \(\mu \Psi ^k_i(\chi _i)\) and \(\mu \Phi ^i(\chi _i)\) are defined on fuzzy sets \(\Psi ^k_i\) and \(\Phi ^i\), respectively. \(\mu \Psi ^k_i(\chi _i)\) and \(\mu \Phi ^i(\chi _i)\) are called membership functions. N denotes the number of rules. Therefore, the output expression of FLSs can be written in the following form:

$$\begin{aligned} y(\chi )=\frac{\sum \nolimits _{k=1}^{N}{\vartheta _k \prod \nolimits _{i=1}^{n}\mu \Psi ^k_i(\chi _i)}}{\sum \nolimits _{k=1}^{N}\bigg ({\prod \nolimits _{i=1}^{n} \mu \Phi ^i(\chi _i)}\bigg )}, \end{aligned}$$
(8)

where \(\vartheta _k=\text {max}\ y\in \mu \Phi ^k(y)\), \(\varpi =[\vartheta _1, \vartheta _2,\ldots, \vartheta _N]^T=[\varpi _1, \varpi _2,\ldots,\varpi _N]^T\). The basis functions are defined as

$$\begin{aligned} \varphi _k(\chi )=\frac{{\prod \nolimits _{i=1}^{n}\mu \Psi ^k_i(\chi _i)}}{\sum \nolimits _{k=1}^{N} \bigg ({\prod \nolimits _{i=1}^{n}\mu \Phi ^i(\chi )}\bigg )}. \end{aligned}$$
(9)

Let \(\varphi (\chi )=[\varphi _1(\chi ), \varphi _2(\chi ),\ldots, \varphi _N(\chi )]\), one can get

$$\begin{aligned} y(\chi )=\varpi ^T\varphi (\chi ). \end{aligned}$$
(10)

Lemma 4

[33] Suppose there exists an unknown nonlinear function f that is smooth and defined on the complete set \(\Pi\). FLSs can be expressed in the following form:

$$\begin{aligned} \sup \limits _{\chi \in \Pi }\mid f(\chi )-\varpi ^{*T}\varphi (\chi )\mid \leqslant \epsilon \end{aligned},$$
(11)

where \(\varpi ^{*T}\) stands for the ideal weight vector, \(\epsilon\) is the approximation error, which is a constant and satisfies \(\epsilon >0\). It is worth noting that the smaller \(\epsilon\) is, the higher the approximation accuracy of FLSs is.

The unknown nonlinear function \(f_i(\chi ), i=1, 2,\ldots, n\) is expressed as the following form according to the content of Lemma 4.

$$\begin{aligned} f_i(\chi \mid \varpi )=\varpi _i^T\varphi (\chi ) \end{aligned}.$$
(12)

Then the ideal weight vector \(\varpi ^*\) and approximation error \(\epsilon\) can be expressed as

$$\begin{aligned} \varpi _i^*&=\arg \min \limits _{\varpi _i\in \Pi _i}\{\sup \limits _{\chi _i\in \Pi _i}\mid f_i(\chi \mid \varpi _i)-f_i(\chi )\mid \} \end{aligned}.$$
(13)
$$\begin{aligned} \epsilon _i&=f_i(\chi )-f_i(\chi \mid \varpi _i^*) \end{aligned},$$
(14)

\(\varpi ^*\), \(\hat{\varpi }\) , and \(\tilde{\varpi }\) are defined as the corresponding ideal weight vector, estimation vector, and estimation error, respectively. Meanwhile, the relationship among the three is \(\tilde{\varpi }=\varpi ^*-\hat{\varpi }\).

3 Control Strategy and Stability Analysis

In this section, the design work of the controller is executed. The paper uses dynamic surface technique to construct the controller, with its coordinate transformation as follows: \(e_1=y-y_r\), \(e_i=x_i-\omega _i\), \(\eta _i=\omega _i-\alpha _{i-1}\), \(i=2,\ldots, n\). Different from the backstepping method, the dynamic surface method employed in this paper uses \(\omega _i\) instead of \(\dot{\alpha }_{i-1}\) in each step so that simple algebraic operations replaced the original complex differential operations, simplifying the derivation process of the controller.

3.1 Control Strategy

Step 1: According to the above coordinate transformations and the plant (1), we can get the following formula:

$$\begin{aligned} \dot{e}_1=e_2+\eta _2+\alpha _1+f_1(x)-\dot{y}_r \end{aligned}.$$
(15)

Since \(f_1(x)\) is an unknown nonlinear function, it can be approximated by FLSs. According to formulas (12), (14), and \(\tilde{\varpi }_1=\varpi ^*_1-\hat{\varpi }_1\), we can get \(f_1(x)=\epsilon _1+\tilde{\varpi }_1^T\varphi _1(x)+\hat{\varpi }_1^T\varphi _1(x)\). Therefore, (15) can be rewritten as

$$\begin{aligned} \dot{e}_1=e_2+\eta _2+\alpha _1+\epsilon _1+\tilde{\varpi }_1^T\varphi _1(x) +\hat{\varpi }_1^T\varphi _1(x)-\dot{y}_r \end{aligned}.$$
(16)

Considering the Lyapunov function \(V_1=\frac{1}{2}e_1^2+\frac{1}{2r_1}\tilde{\varpi }_1^T\tilde{\varpi }_1\), its time derivative can be obtained

$$\begin{aligned} \dot{V}_1&=e_1(e_2+\eta _2+\alpha _1+\epsilon _1 +\tilde{\varpi }_1^T\varphi _1(x)\nonumber \\&\quad +\hat{\varpi }_1^T\varphi _1(x)-\dot{y}_r) -\frac{1}{r_1}\tilde{\varpi }_1^T\dot{\hat{\varpi }}_1 \end{aligned}.$$
(17)

Using Young’s inequality to deal with terms \(e_1\eta _2\) and \(e_1\epsilon _1\), the time derivative \(\dot{V}_1\) of \(V_1\) can be rewritten

$$\begin{aligned} \dot{V}_1&\leqslant {e_1}(-A_{2,1}e_1^{2q-1}+A_{2,1}e_1^{2q-1}\nonumber \\&\quad +e_1+e_2+\alpha _1-\dot{y}_r+\hat{\varpi }_1^T\varphi _1(x))\nonumber \\&\quad +\frac{1}{2}\eta _2^2+\frac{1}{2}\epsilon _1^2 +\tilde{\varpi }_1^T(-\frac{1}{r_1}\dot{\hat{\varpi }}_1+e_1\varphi _1(x)) \end{aligned}.$$
(18)

At this point, the virtual controller \(\alpha _1\) and the adaptive law \(\dot{\hat{\varpi }}_1\) are deduced

$$\begin{aligned} \alpha _1&=-A_{1,1}e_1^{2p-1}-A_{2,1}e_1^{2q-1} -\hat{\varpi }_1^T\varphi _1(x)-e_1+\dot{y}_r \end{aligned},$$
(19)
$$\begin{aligned} \dot{\hat{\varpi }}_1&=r_1e_1\varphi _1(x)-R_1\hat{\varpi }_1 \end{aligned},$$
(20)

where \(A_{1,1}\), \(A_{2,1}\), p, q, \(R_1\) , and \(r_1\) are all design parameters that simultaneously satisfy \(A_{1,1}, A_{2,1}, R_1, r_1 >0\), \(0<p<1\), \(q>1\).

By inserting the virtual controller \(\alpha _1\) and the adaptive law \(\dot{\hat{\varpi }}_1\) into (18), the final form of \(\dot{V}_1\) can be written as

$$\begin{aligned}{} & {} \dot{V}_1\leqslant {e_1}e_2-A_{1,1}e_1^{2p}-A_{2,1}e_1^{2q} +\frac{R_1}{r_1}\tilde{\varpi }_1^T\hat{\varpi }_1\nonumber \\{} & {} \quad +\frac{1}{2}\epsilon _1^2+\frac{1}{2}\eta _2^2 \end{aligned}.$$
(21)

In order to avoid the “complex explosion” problem, a first-order linear filter of the following form is introduced

$$\begin{aligned} \delta _2\dot{\omega }_2+\omega _2=\alpha _1 \end{aligned},$$
(22)

where \(\omega _2(0)=\alpha _1(0)\) and \(\delta _2>0\) is constant.

Substituting \(\eta _2=\omega _2-\alpha _1\) into (22), \(\dot{\omega }_2=-\frac{\eta _2}{\delta _2}\) can be obtained after simplifying. Due to \(\dot{\eta }_2=\dot{\omega }_2-\dot{\alpha }_1\), one can deduce

$$\begin{aligned} \dot{\eta }_2=-\frac{\eta _2}{\delta _2}+Q_2 \end{aligned},$$
(23)

where \(Q_2=-\dot{\alpha }_1=(2p-1)A_{1,1}e_1^{2p-2}+(2q-1)A_{2,1}e_1^{2q -2}+\dot{e}_1-\ddot{y}_r+\dot{\hat{\varpi }}_1^T\varphi _1(x_1) +\hat{\varpi }_1^T\frac{\partial \varphi _1(x_1)}{\partial {x_1}}\dot{x}_1,\).

Remark 2

The traditional backstepping method requires repeated differentiation of the virtual controller at each step, therefore, as the system order increases, the computational workload will grow exponentially. It is shown that when the system order is greater than 3, the actual controller structure will be extremely complex in the backstepping recursive process [34, 35]. The dynamic surface technique introduces a first-order filter based on the traditional backstepping method to replace the first-order derivative of the virtual controller so that simple algebraic operations replaced the original complex differential operations. When the system order is relatively low, the complexity of the two methods is not obvious. With the increase of the order, the advantage of dynamic surface technique in reducing the computation redundancy becomes more obvious. Swaroop et al. [36] give a more detailed comparison of the two methods.

Step i (\(2\leqslant {i}\leqslant {n-1}\)): According to the coordinate transformation of the i-th step and system (1), the following equation can be obtained:

$$\begin{aligned} \dot{e}_i=e_{i+1}+\eta _{i+1}+\alpha _i+\epsilon _i+\tilde{\varpi }_i^T \varphi _i(x)+\hat{\varpi }_i^T\varphi _i(x)-\dot{\omega }_i \end{aligned},$$
(24)

where \(\epsilon _i>0\) is the approximation error of FLSs.

Choose the Lyapunov function candidate with \(r_i>0\)

$$\begin{aligned} V_i=V_{i-1}+\frac{1}{2}e_i^2+\frac{1}{2}\eta _i^2 +\frac{1}{2r_i}\tilde{\varpi }_i^T\tilde{\varpi }_i \end{aligned}.$$
(25)

It follows from (24) and (25) that

$$\begin{aligned} \dot{V}_i=&\dot{V}_{i-1}+e_i(e_{i+1}+\eta _{i+1}+\alpha _i +\epsilon _i-\dot{\omega }_i+\tilde{\varpi }_i^T\varphi _i(x)\nonumber \\&\quad +\hat{\varpi }_i^T\varphi _i(x))+\eta _i(-\frac{\eta _i}{\delta _i}+Q_i) -\frac{1}{r_i}\tilde{\varpi }_i^T\dot{\hat{\varpi }}_i \end{aligned}.$$
(26)

According to Lemma 1, the following inequalities hold

$$\begin{aligned} e_i\eta _{i+1}&\leqslant \frac{1}{2}e_i^2+\frac{1}{2}\eta _{i+1}^2 \end{aligned},$$
(27)
$$\begin{aligned} e_i\epsilon _i&\leqslant \frac{1}{2}e_i^2+\frac{1}{2}\epsilon _i^2 \end{aligned},$$
(28)
$$\begin{aligned} \eta _iQ_i&\leqslant \frac{1}{2k}\eta _i^2Q_i^2+\frac{1}{2}k \end{aligned},$$
(29)

where \(k>0\).

Substituting (27), (28), and (29) into (26) produces

$$\begin{aligned} \dot{V}_i&=\dot{V}_{i-1}-e_{i-1}e_i-\frac{1}{2}\eta _i^2 +e_i(e_{i-1}+e_{i+1}\nonumber \\&\quad+\alpha _i-\dot{\omega }_i+e_i+\hat{\varpi }_i^T\varphi _i(x))\nonumber \\&\quad-\eta _i^2(\frac{1}{\delta _i}-\frac{1}{2k}Q_i^2-\frac{1}{2}) +\frac{1}{2}\epsilon _i^2+\frac{1}{2}k\nonumber \\&\quad+\frac{1}{2}\eta _{i+1}^2 +\tilde{\varpi }_i^T(-\frac{1}{r_i} \dot{\hat{\varpi }}_i+e_i\varphi _i(x)) \end{aligned}.$$
(30)

Therefore, the virtual controller \(\alpha _i\) and the adaptive law \(\dot{\hat{\varpi }}_i\) are constructed

$$\begin{aligned} \alpha _i&=-A_{1,i}e_i^{2p-1}-A_{2,i}e_i^{2q-1} -\hat{\varpi }_i^T\varphi _i(x)-e_{i-1}-e_i+\dot{\omega }_i \end{aligned},$$
(31)
$$\begin{aligned} \dot{\hat{\varpi }}_i&=r_ie_i\varphi _i(x)-R_i\hat{\varpi }_i \end{aligned},$$
(32)

where \(A_{1,i}\) and \(A_{2,i}\) are design parameters that simultaneously satisfy \(A_{1,i}>0\), \(A_{2,i}>0\).

Substituting the above two equations into (30), \(\dot{V}_i\) can be written as

$$\begin{aligned} \dot{V}_i&\leqslant {e_i}{e_{i+1}}-\sum _{j=1}^{i}A_{1,j}e_j^{2p} -\sum _{j=1}^{i}A_{2,j}e_j^{2q}-\sum _{j=2}^{i} \eta _j^2\Big(\frac{1}{\delta _j}-\frac{1}{2k}Q_j^2\nonumber \\&\quad -\frac{1}{2}\Big)+\sum _{j=1}^{i}\frac{1}{2}\epsilon _j+\sum _{j=1}^{i}\frac{R_j}{r_j} \tilde{\varpi }_j^T\hat{\varpi }_j+\frac{1}{2}\eta _{i+1}^2+\frac{i-1}{2}k \end{aligned}.$$
(33)

Construct the filter according to the method in step 1

$$\begin{aligned} \delta _{i+1}\dot{\omega }_{i+1}+\omega _{i+1}=\alpha _i \end{aligned},$$
(34)

where \(\omega _{i+1}(0)=\alpha _i(0)\) and \(\delta _{i+1}>0\) is constant.

Substituting \(\eta _{i+1}=\omega _{i+1}-\alpha _i\) into (34), \(\dot{\omega }_{i+1}=-\frac{\eta _{i+1}}{\delta _{i+1}}\) can be obtained after simplifying. Due to \(\dot{\eta }_{i+1}=\dot{\omega }_{i+1}-\dot{\alpha }_i\), one can deduce

$$\begin{aligned} \dot{\eta }_{i+1}=-\frac{\eta _{i+1}}{\delta _{i+1}}+Q_{i+1} \end{aligned},$$
(35)

where \(Q_{i+1}=-\dot{\alpha }_i=(2p-1)A_{1,i}e_i^{2p-2}+(2q-1) A_{2,i}e_i^{2q-2}+\dot{e}_{i-1}+\dot{e}_i+\dot{\hat{\varpi }}_i^T \varphi _i(x_i)+\hat{\varpi }_i^T\frac{\partial \varphi _i(x_i)}{\partial {x_i}}\dot{x}_i+\frac{\eta _i}{\delta _i}\).

Step n: In the light of coordinate transformations and nonlinear system (1), \(\dot{e}_n\) can be written as

$$\begin{aligned} \dot{e}_n=u+f_n(x)+\zeta (t-T_0)\tau (x,u)-\dot{\omega }_n \end{aligned}.$$
(36)

Define the following augmented Lyapunov function with \(r_n>0\) as

$$\begin{aligned} V_n=V_{n-1}+\frac{1}{2}e_n^2+\frac{1}{2}\eta _n^2 +\frac{1}{2r_n}\tilde{\varpi }_n^T\tilde{\varpi }_n \end{aligned}.$$
(37)

Combining (36) and (37) gets the time derivative \(\dot{V}_n\) of \(V_n\)

$$\begin{aligned} \dot{V}_n&=\dot{V}_{n-1}+e_n(u+f_n(x)+\zeta (t-T_0)\tau (x,u)\nonumber \\&\quad-\dot{\omega }_n)+\eta _n(-\frac{\eta _n}{\delta _n}+Q_n) -\frac{1}{r_n}\tilde{\varpi }_n^T\dot{\hat{\varpi }}_n \end{aligned}.$$
(38)

According to (38), \(\zeta (t-T_0)\tau (x,u)\) is the failure encountered by the system, \(\tau (x,u)\) represents the non-affine nonlinear fault function involving system state and controller output and \(\zeta (t-T_0)\) refers to the homologous time profile of the fault that occurs at some unknown time. In order to improve the fault-tolerance of the system and ensure the normal operation of the system, it is necessary to use the idea of fault-tolerance to design the controller and the adaptive law. The noteworthy point is that this paper is based on the idea of passive fault-tolerance, the adaptive law is designed to replace the fault detection and isolation module. The adaptive law evaluates the fault level and feeds the evaluation results back to the fault-tolerant controller. Then, under the action of fault-tolerant controller, the effects and changes of system non-dynamics caused by faults are weakened.

In order to design an adaptive law and a controller with fault-tolerance, the following processes are required.

Consider \(f_n(x)\) and \(\zeta (t-T_0)\tau (x,u)\) as a whole, and use the knowledge of Assumption 2 to deal with the faults, that is

$$\begin{aligned} e_n(f_n(x)+\zeta (t-T_0)\tau (x,u))\leqslant \mid {e_n}\mid \mid \bar{h}(x,u)\mid \end{aligned}.$$
(39)

The final result is obtained by using Young’s inequality

$$\begin{aligned} \mid {e_n}\mid \mid \bar{h}(x,u)\mid \leqslant \frac{1}{2b} e_n^2\bar{h}^2(x,u)+\frac{1}{2}b \end{aligned}.$$
(40)

Let \(h(x,u)=\frac{1}{2b}e_n\bar{h}^2(x,u)\), and use FLSs to process h(x, u), the following inequality holds

$$\begin{aligned} \mid {e_n}\mid \mid \bar{h}(x,u)\mid&\leqslant {e_n}h(x,u) +\frac{1}{2}b\nonumber \\&\leqslant {e_n}(\epsilon _n+\tilde{\varpi }_n^T\varphi _n(x) +\hat{\varpi }_n^T\varphi _n(x))+\frac{1}{2}b \end{aligned},$$
(41)

where \(b>0\) and \(\epsilon _n>0\) are the design parameter and the approximation error of FLSs.

At this point, fault handling is complete.

Using Young’s inequality deals with the term \(e_n\epsilon _n\) and the term \(\eta _nQ_n\)

$$\begin{aligned} e_n\epsilon _n&\leqslant \frac{1}{2}e_n^2 +\frac{1}{2}\epsilon _n^2 \end{aligned},$$
(42)
$$\begin{aligned} \eta _nQ_n&\leqslant \frac{1}{2k}\eta _n^2Q_n^2 +\frac{1}{2}k \end{aligned}.$$
(43)

Substituting (39), (41), (42), and (43) into (38), the following inequality is derived:

$$\begin{aligned} \dot{V}_n&\leqslant \dot{V}_{n-1}-e_{n-1}e_n-\frac{1}{2}\eta _n^2 +e_n(u+\hat{\varpi }_n^T\varphi _n(x)+\frac{1}{2}e_n\nonumber \\&\quad -e_{n-1}-\dot{\omega }_n)-\eta _n^2(\frac{1}{\delta _n} -\frac{1}{2k}Q_n^2-\frac{1}{2}) +\frac{1}{2}\epsilon _n^2+\frac{1}{2}k\nonumber \\&\quad +\frac{1}{2}b+\tilde{\varpi }_n^T( -\frac{1}{r_n}\dot{\hat{\varpi }}_n+e_n\varphi _n(x)) \end{aligned}.$$
(44)

So the required actual controller u and adaptive law \(\dot{\hat{\varpi }}_n\) are obtained

$$\begin{aligned} u&=-A_{1,n}e_n^{2p-1}-A_{2,n}e_n^{2q-1}-\hat{\varpi }_n^T\varphi _n(x) -e_{n-1}-\frac{1}{2}e_n+\dot{\omega }_n \end{aligned},$$
(45)
$$\begin{aligned} \dot{\hat{\varpi }}_n&=r_ne_n\varphi _n(x)-R_n\hat{\varpi }_n \end{aligned},$$
(46)

where \(A_{1,n}\) and \(A_{2,n}\) are design parameters that simultaneously satisfy \(A_{1,n}>0\), \(A_{2,n}>0\).

Substituting (45) and (46) into (44), \(\dot{V}_n\) can be rewritten as

$$\begin{aligned} \dot{V}_n&\leqslant -\sum _{j=1}^{n}A_{1,j}e_j^{2p} -\sum _{j=1}^{n}A_{2,j}e_j^{2q}+\sum _{j=1}^{n}\frac{1}{2}\epsilon _j\nonumber \\&\quad +\sum _{j=1}^{n}\frac{R_j}{r_j}\tilde{\varpi }_j^T\hat{\varpi }_j\nonumber \\&\quad -\sum _{j=2}^{n}\eta _j^2\Big(\frac{1}{\delta _j} -\frac{1}{2k}Q_j^2-\frac{1}{2}\Big)+\frac{n-1}{2}k+\frac{1}{2}b \end{aligned}.$$
(47)

Based on the above discussions, the block diagram of the design procedure for the proposed controller is shown in Fig. 1.

Fig. 1
figure 1

The block diagram of the design procedure for the proposed controller

Full size image

Remark 3

The most significant parts of fault-tolerant control policies in this paper are the design of the fixed-time fault-tolerant controller. The non-affine nonlinear faults involving system state and controller output are transformed into compound nonlinear function which can be approximated by fuzzy logic systems. Based on the dynamic surface technique and Lyapunov fixed-time stability criterion, the adaptive fuzzy fixed-time controller and the adaptive law are designed, where the adaptive law is used to estimate the fault level and feed the results back to the fault-tolerant controller, which performs control actions to weaken the influence of faults on the system.

3.2 Stability Analysis

According to the design process in Part 3.1, the following theorem is summarized.

Theorem 1

Consider the uncertain nonlinear plant (1) subjected to actuator faults that belong to the non-affine fault type. The dynamic surface control technique combined with the backstepping method avoids the repeated derivation of the virtual controller \(\alpha _i\), where \(i=1,2,\ldots,n-1\). Under Assumptions \(1-2\), the fault-tolerant controller (45), with the intermediate virtual controllers (19), (31), and adaptive laws (20), (32), and (46) guarantee that all the signals in the closed-loop system are semi-globally uniformly ultimately bounded in probability. The output y of the control system can track the desired signal \(y_r\) with a high enough accuracy.

The proof of Theorem 1 is as follows.

Proof To make the above control scheme meet the fixed-time stability condition of Lemma 3, we need to do the following processing for (47).

First of all, the term \(\sum _{j=1}^{n}\frac{R_j}{r_j}\tilde{\varpi }_j^T\hat{\varpi }_j\) is handled. According to \(\tilde{\varpi }=\varpi ^*-\hat{\varpi }\) and Young’s inequality, \(\tilde{\varpi }^T\hat{\varpi }=\tilde{\varpi }^T(\varpi ^*-\tilde{\varpi })\) is deduced, and then the following inequality holds

$$\begin{aligned} \sum _{j=1}^{n}\frac{R_j}{r_j}\tilde{\varpi }_j^T\hat{\varpi }_j \leqslant \sum _{j=1}^{n}\frac{R_j}{2r_j}\varpi _j^{*T}\varpi _j^* -\sum _{j=1}^{n}\frac{R_j}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j \end{aligned}.$$
(48)

Replacing the term \(\sum _{j=1}^{n}\frac{R_j}{r_j}\tilde{\varpi }_j^T\hat{\varpi }_j\) in (47) with (48) has

$$\begin{aligned} \dot{V}_n\leqslant&-\sum _{j=1}^{n}A_{1,j}e_j^{2p} -\sum _{j=1}^{n}A_{2,j}e_j^{2q}-\sum _{j=1}^{n}\nonumber \\&\frac{R_j}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j +\frac{n-1}{2}k+\frac{1}{2}b\nonumber \\&-\sum _{j=2}^{n}\eta _j^2\Big(\frac{1}{\delta _j} -\frac{1}{2k}Q_j^2 -\frac{1}{2}\Big)\nonumber \\&+\sum _{j=1}^{n}\frac{R_j}{2r_j}\varpi _j^{*T} \varpi _j^*+\sum _{j=1}^{n}\frac{1}{2}\epsilon _j \end{aligned}.$$
(49)

Let \(a=\min \{A_{1,1},\ldots,A_{1,n}, A_{2,1},\ldots,A_{2,n}, \frac{1}{\delta _2}-\frac{Q_2^2}{2k}-\frac{1}{2},\ldots, \frac{1}{\delta _n}-\frac{Q_n^2}{2k}-\frac{1}{2}, \frac{R_1}{2},\ldots,\frac{R_n}{2}\},\) and \(W_1=\sum _{j=1}^{n}\frac{R_j}{2r_j}\varpi _j^{*T}\varpi _j^* +\sum _{j=1}^{n}\frac{1}{2}\epsilon _j+\frac{n-1}{2}k+\frac{1}{2}b\), the inequality (49) can be simplified into the following form

$$\begin{aligned} \dot{V}_n&\leqslant -a\sum _{j=1}^{n}e_j^{2p}-a\sum _{j=1}^{n}e_j^{2q}\nonumber \\&\quad -a\sum _{j=2}^{n}\eta _j^2-a\sum _{j=1}^{n} \frac{1}{r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j+W_1 \end{aligned}.$$
(50)

Second, use Lemma 2 to deal with terms \(a\sum _{j=1}^{n}e_j^{2p}\) and \(a\sum _{j=1}^{n}e_j^{2q}\)

$$\begin{aligned} a\sum _{j=1}^{n}e_j^{2p}&=2^p a\sum _{j=1}^{n}\bigg (\frac{e_j^2}{2}\bigg )^p \geqslant 2^p{a}\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}\bigg )^p \end{aligned},$$
(51)
$$\begin{aligned} a\sum _{j=1}^{n}e_j^{2q}&=2^q a\sum _{j=1}^{n}\bigg (\frac{e_j^2}{2}\bigg )^q \geqslant 2^pn^{1-q}{a}\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}\bigg )^q \end{aligned}.$$
(52)

Substituting (51) and (52) into (50) gives

$$\begin{aligned} \dot{V}_n\leqslant&-2^p{a}\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}\bigg )^p -2^pn^{1-q}{a}\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}\bigg )^q\nonumber \\&-a\bigg (\sum _{j=2}^{n} \frac{1}{2}\eta _j^2\bigg )^p -a\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q\nonumber \\&-a\bigg (\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^p\nonumber \\&-a\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^q +a\bigg (\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^p\nonumber \\&+a\bigg (\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\bigg )^p+a\sum _{j=2}^{n} \bigg (\frac{1}{2}\eta _j^2\bigg )^q-a\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\nonumber \\&+a\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^q\nonumber \\&-a\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j \nonumber \\&-a\sum _{j=2}^{n}\frac{1}{2}\eta _j^2-a\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j+W_1 \end{aligned}.$$
(53)

In the light of Young’s Inequality, one get \(\bigg (\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\bigg )^p\leqslant (1-p)p^ {(\frac{p}{1-p})}+\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\) and \(\bigg (\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg ) ^p\leqslant (1-p)p^{(\frac{p}{1-p})}+\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j\).

Therefore, (53) can be rewritten as

$$\begin{aligned} \dot{V}_n\leqslant&-c\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}\bigg )^p -c\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}\bigg )^q\nonumber \\&-c\bigg (\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\bigg )^p -c\bigg (\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^p\nonumber \\&-c\bigg (\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^q\nonumber \\&-c\bigg (\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\bigg )^q +c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\nonumber \\&+c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^q -c\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j+W_2 \end{aligned},$$
(54)

where \(c=\min \{2^pa, 2^qn^{1-q}a, a\}\) and \(W_2=2(1-p)p^{(\frac{p}{1-p})}+W_1\).

If the conditions \(q>1\) is met, it can be divided into four situations to discuss.

Case 1: If \(\tilde{\varpi }_j^T\tilde{\varpi }_j<2r_j\) and \(\eta _j^2<2\), the following inequality holds

$$\begin{aligned} c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T \tilde{\varpi }_j\bigg )^q-c\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j&<0 \end{aligned},$$
(55)
$$\begin{aligned} c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2&<0 \end{aligned}.$$
(56)

At this point, combining Lemma 2, (56) can be rewritten as

$$\begin{aligned} \dot{V}_n\leqslant&-3^{1-q}c\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2} +\sum _{j=2}^{n}\frac{1}{2}\eta _j^2+\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^q\nonumber \\&-c\bigg (\sum _{j=1}^{n}\frac{e_j^2}{2}+\sum _{j=2}^{n}\frac{1}{2} \eta _j^2+\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j\bigg )^p+W_2\nonumber \\ \leqslant&-CV_n^p-SV_n^q+W_2 \end{aligned}.$$
(57)

Case 2: If \(\tilde{\varpi }_j^T\tilde{\varpi }_j<2r_j\) and \(\eta _j^2>2\), the following inequality holds

$$\begin{aligned} c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T \tilde{\varpi }_j\bigg )^q-c\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j&<0 \end{aligned},$$
(58)
$$\begin{aligned} c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2&>0 \end{aligned}.$$
(59)

At this point, (56) can be rewritten as

$$\begin{aligned} \dot{V}_n\leqslant -CV_n^p-SV_n^q+W_3 \end{aligned}.$$
(60)

Case 3: If \(\tilde{\varpi }_j^T\tilde{\varpi }_j>2r_j\) and \(\eta _j^2<2\), the following inequality holds

$$\begin{aligned} c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T \tilde{\varpi }_j\bigg )^q-c\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j&>0 \end{aligned}.$$
(61)
$$\begin{aligned} c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2&<0 \end{aligned}.$$
(62)

In the same way,

$$\begin{aligned} \dot{V}_n\leqslant -CV_n^p-SV_n^q+W_4 \end{aligned}.$$
(63)

Case 4: If \(\tilde{\varpi }_j^T\tilde{\varpi }_j>2r_j\) and \(\eta _j^2>2\), the following inequality holds

$$\begin{aligned} c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T \tilde{\varpi }_j\bigg )^q-c\sum _{j=1}^{n}\frac{1}{2r_j} \tilde{\varpi }_j^T\tilde{\varpi }_j&>0 \end{aligned},$$
(64)
$$\begin{aligned} c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2&>0 \end{aligned}.$$
(65)

Similarly,

$$\begin{aligned} \dot{V}_n\leqslant -CV_n^p-SV_n^q+W_5 \end{aligned},$$
(66)

where \(C=c\), \(S=3^{1-q}c\), \(W_3=W_2+c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\), \(W_4=W_2+c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T \tilde{\varpi }_j\bigg )^q-c\sum _{j=1}^{n} \frac{1}{2r_j}\tilde{\varpi }_j^T\tilde{\varpi }_j\), and \(W_5=W_2+c\sum _{j=1}^{n}\bigg (\frac{1}{2r_j}\tilde{\varpi }_j^T \tilde{\varpi }_j\bigg )^q-c\sum _{j=1}^{n}\frac{1}{2r_j}\tilde{\varpi }_j^ T\tilde{\varpi }_j+c\sum _{j=2}^{n}\bigg (\frac{1}{2}\eta _j^2\bigg )^q -c\sum _{j=2}^{n}\frac{1}{2}\eta _j^2\).

Therefore, based on the above analysis, it is clear that the proposed control scheme satisfies Lemma 3 and Theorem 1 holds.

Remark 4

The control performance of the system depends on many design parameters. It can be seen from the stability analysis that the parameters \(A_{1,i}\), \(A_{2,i}\), \(r_i\), and \(R_i\) can adjust the convergence error and convergence accuracy at the same time. By selecting larger \(A_{2,i}\), smaller \(R_i\) as well as appropriate \(A_{1,i}\), \(r_i\), the convergence speed can be improved and the final error can be reduced. In addition, the exponents p and q determine the boundary of the convergence time and influence the convergence accuracy. Choosing suitable exponents can reduce the convergence time and improve the convergence accuracy.

4 Simulation Studies

Two simulation examples are used to verify the effectiveness of the above designed fault-tolerant control scheme.

Example 1

(Numerical Simulation): Consider the following second-order nonstrict nonlinear systems with non-affine faults

$$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2} + {f_1}(x)}\\ {{{\dot x}_2} = u + {f_2}(x) + \zeta (t - {T_0})\tau (x,u)}\\ {y = {x_1}} \end{array}} \right.,$$
(67)

where \(f_1(x)=0\), \(f_2(x)=x_2sin(x_1)e^{-(1+2x_1x_2)}\). We assume that the ideal reference signal is \(y_r=0.5sin(t)\). The approximation error of the system is \(e=y-y_r\). In this paper, we consider two types of faults: incipient fault and abrupt fault. From formulas (2) and (3), it can be seen that \(\zeta (t-T_0)=0, (T_0<10)\) and \(\zeta (t-T_0)=1-e^{-\varrho (t-T_0)}, (T_0\geqslant 10)\), where \(T_0\) is the time of the fault occurred. If \(\varrho\) is a bounded constant (this simulation assumes \(\varrho =23\)), the fault considered is an incipient fault. If \(\varrho\) approaches infinity, the fault considered is abrupt fault. The fault function is defined as \(\tau (x,u)=5(x_1x_2+sin(u))+10\).

In the simulation study, fuzzy if-then rules are chosen as follows:

\(\Upsilon ^1\): if \(x_1^1\) is \(\Psi _1^1\) and \(x_2^1\) is \(\Psi _2^1\), then y is \(\Phi ^1\);

\(\Upsilon ^2\): if \(x_1^2\) is \(\Psi _1^2\) and \(x_2^2\) is \(\Psi _2^2\), then y is \(\Phi ^2\);

\(\Upsilon ^3\): if \(x_1^3\) is \(\Psi _1^3\) and \(x_2^3\) is \(\Psi _2^3\), then y is \(\Phi ^3\);

\(\Upsilon ^4\): if \(x_1^4\) is \(\Psi _1^4\) and \(x_2^4\) is \(\Psi _2^4\), then y is \(\Phi ^4\);

\(\Upsilon ^5\): if \(x_1^5\) is \(\Psi _1^5\) and \(x_2^5\) is \(\Psi _2^5\), then y is \(\Phi ^5\);

where fuzzy sets are chosen as \(\Psi _1^1=(NL)\), \(\Psi _2^1=(NL)\), \(\Psi _1^2=(NS)\), \(\Psi _2^2=(NS)\), \(\Psi _1^3=(ZE)\), \(\Psi _2^3=(ZE)\), \(\Psi _1^4=(PS)\), \(\Psi _2^4=(PS)\), \(\Psi _1^5=(PL)\), \(\Psi _2^5=(PL)\), which are defined over the interval \([-2, 2]\) for variables \(x_1^k\) and \(x_2^k\), respectively. NL, NS, ZE, PS and PL denote negative large, negative small, zero, positive small, positive large, respectively. Their center points are selected as \(-2\), \(-1\), 0, 1, 2, respectively. The fuzzy membership functions for each fuzzy set are chosen as Gaussian-shaped membership functions, and they are given as follows:

$$\begin{aligned} \mu \Psi _i^k(x_i^k)&=\text {exp} \bigg [-\frac{(x_i^k+3-k)^2}{4^2}\bigg ]\qquad i=1,2\quad k=1,2,3,4,5. \end{aligned}$$
(68)

According to the controller design flow in Sect. 3, the fixed-time fault-tolerant controllers and adaptive laws designed for the second-order system (67) are shown below.

$$\begin{aligned} \alpha _1&=-A_{1,1}e_1^{2p-1}-A_{2,1}e_1^{2q-1} -\frac{1}{2}e_1+\dot{y}_r, \end{aligned}$$
(69)
$$\begin{aligned} u&=-A_{1,2}e_2^{2p-1}-A_{2,2}e_2^{2q-1} -\frac{1}{2}e_2-e_1-\hat{\varpi }_2^T\varphi _2(x_2)+\dot{\omega }, \end{aligned}$$
(70)
$$\begin{aligned} \dot{\hat{\theta }}_1&=0 \end{aligned},$$
(71)
$$\begin{aligned} \dot{\hat{\theta }}_2&=r_2e_2\varphi _2(x_2)-R_2\hat{\varpi }_2 \end{aligned}.$$
(72)
Fig. 2
figure 2

a Comparison trajectories of \(x_1\) and \(x_2\) under incipient fault, b comparison trajectories of y and \(y_r\) under incipient fault, c comparison trajectories of \(e_1\) under incipient fault, d Comparison trajectories of u under incipient fault

Full size image

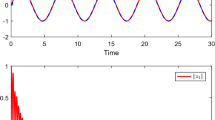
In order to make the simulation results more convincing, we compare the adaptive fuzzy fixed-time fault-tolerant controller proposed in this paper with the adaptive fuzzy finite-time fault-tolerant controller under the condition that the considered system and related parameters are consistent. The relevant parameters are chosen as \(A_{1,1}=1\), \(A_{2,1}=50\), \(A_{1,2}=30\), \(A_{2,2}=100\), \(p=0.9\), \(q=1.5\), \(r_2=2\), \(R_2=0.5\), \(\delta _2=0.01\). We choose 0.3 and \(-0.1\) as the initial conditions of state variables \(x_1\) and \(x_2\). The initial value \(\hat{\theta }(0)\) of \(\hat{\theta }\) is set to \([0,0,0,0,0]^T\). The above parameter values are used whether the system suffers from the incipient fault or the abrupt fault. The simulation results are presented in Figs. 2 and 3. Figure 2 shows the simulation comparison results of the two scheme when the system suffers from the incipient fault. Figure 2a is the state variable trajectories of the system under the control of the two schemes. The tracking errors of the system are shown in Fig. 2b. Figure 2c and d displays the output trajectories of the system and the waveforms of the controller under two schemes, respectively. Figure 3 shows the simulation comparing results of the two scheme when the system suffers from the abrupt fault. Correspondingly, Fig. 3a–d represents the state variable trajectories, tracking error trajectories, system output trajectories, and controller waveforms for the considered system under the control of the two schemes, respectively.

Fig. 3
figure 3

a Comparison trajectories of \(x_1\) and \(x_2\) under abrupt fault, b comparison trajectories of y and \(y_r\) under abrupt fault, c comparison trajectories of \(e_1\) under abrupt fault, d comparison trajectories of u under abrupt fault

Full size image

From Figs. 2 and 3, it is clear that the fixed-time fault-tolerant control scheme proposed in this paper is superior to the finite-time fault-tolerant control scheme both in terms of convergence speed and control accuracy. When the fault does not occur, the difference is not significant in tracking accuracy between the fixed-time fault-tolerant control scheme and the finite-time fault-tolerant control scheme. When the fault occurs, the tracking accuracy of the system under the fixed-time fault-tolerant control scheme decreases but still meets the requirements of the system. However, the tracking accuracy of the system under the finite-time fault-tolerant control scheme shows the phenomenon of divergence as time increased.

Example 2

(Model Simulation): With reference to the robotic manipulator system proposed in Wang et al. [37], we verify the control effect of the control strategy proposed above. The dynamic equation of the robotic manipulator system is shown as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}D\ddot{q}+B\dot{q}+Mgl\sin (q)=\tau \\ &{}M_m\dot{\tau }+H_m\tau =u-K_m\dot{q} \end{array} \right. } \end{aligned},$$
(73)

where the physical significance of q, \(\dot{q}\) and \(\ddot{q}\) are the angle, angular velocity and angular acceleration of the link, respectively. The rotation inertia of the servo motor, the mass of the link, the gravitational acceleration, and the damping coefficient are represented by the letters D, M, g, and B, respectively. l is the length from the axis of joint to the mass center. \(\tau\) denotes the torque produced by the motor, u is the voltage applied to the motor or control input. \(M_m\), \(H_m\), and \(K_m\) refer to the armature inductance, the armature resistance, and the back electromotive force coefficient, respectively. According to [37], the values of the above physical parameters are given, that is, \(D=1\) Kg \(\text {m}^2\), \(B=1\) N/(m/s), \(Mgl=1\), \(M_m=0.1H\), \(H_m=1\Omega\), \(K_m=0.2Nm/A\). The purpose of this simulation is to make the moving trajectory of the robotic manipulator track the given reference trajectory in fixed-time under the control of the designed controller and control the tracking error within a small neighborhood near the origin. The given reference trajectory is \(y_r=0.5\text {sin}(t)\).

In view of the system studied in this paper, we introduce the non-affine nonlinear fault into the third-order nonlinear system, so (73) can be rewritten as

$$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {x_2}}\\ {{{\dot x}_2} = {x_3} - {x_2} - \sin ({x_1})}\\ {{{\dot x}_3} = 10u - 2{x_2} - 10{x_3} + \zeta (t - {T_0})\tau (x,u)}\\ {y = {x_1}} \end{array}} \right.$$
(74)

where \(x_1=q\), \(x_2=\dot{q}\), \(x_3=\ddot{q}\), \(\zeta (t-T_0)\tau (x,u)\) is the fault item.

According to (2) and (3), we select the fault time \(T_0=10s\). At the same time, if the fault type is incipient fault, \(\varrho =8\) is selected, and if the fault type is abrupt fault, \(\varrho =+\infty\) is selected. The non-affine nonlinear fault function is uniformly constructed as \(\tau =x_1x_2x_3+sin(u)+5\).

For the target system (74), the actual controller and adaptive law are obtained as follows referring to the design process in Sect. 3.1.

$$\begin{aligned} u&=-A_{1,3}e_3^{2p-1}-A_{2,3}e_3^{2q-1}-\frac{1}{2}e_3 -e_2-\hat{\varpi }_3^T\varphi _3+\dot{\omega } \end{aligned},$$
(75)
$$\begin{aligned} \dot{\hat{\theta }}_3&=r_3e_3\varphi _3-R_3\hat{\varpi }_3 \end{aligned}.$$
(76)

In the simulation, the same initial conditions are used, i.e., \(x(0)=[0.3, -0.2, 1]\). For the controlled system with incipient fault, the relevant design parameters are selected as \(A_{1,1}=0.5\), \(A_{2,1}=1\), \(A_{1,2}=0.5\), \(A_{2,2}=1\), \(A_{1,3}=1\), \(A_{2,3}=20\), \(p=0.99\), \(q=1.01\), \(r_2=2\), \(r_3=2\), \(R_2=1\), \(R_3=0.8\). Similarly, for the controlled system with abrupt fault, the relevant design parameters are selected as \(A_{1,1}=0.05\), \(A_{2,1}=1\), \(A_{1,2}=1\), \(A_{2,2}=1\), \(A_{1,3}=1\), \(A_{2,3}=20\), \(p=0.85\), \(q=1.3\), \(r_2=2\), \(r_3=2\), \(R_2=1\), \(R_3=0.6\). The simulation results are shown in Fig. 4. Specifically, Fig. 4a shows the trajectory of the angle, angular velocity, and angular acceleration of the robotic manipulator system with time. Figure 4b shows the tracking error of the robotic manipulator system with the incipient fault and the abrupt fault. Figure 4c is the tracking of the actual output of the system to the given reference output under the schemes proposed, corresponding to Fig. 4b. Figure 4d shows the controller response waveform when the system is subjected to the abrupt fault and the incipient fault under the scheme proposed in this paper.

Fig. 4
figure 4

a Trajectories of \(x_1\), \(x_2\), and \(x_3\), b Trajectories of \(e_1\), c Trajectories of y and \(y_r\), d Trajectories of u

Full size image

In order to further verify the effectiveness of the proposed scheme, the fixed-time fault-tolerant controller based on adaptive fuzzy constructed in this paper is compared with the fuzzy-free PID controller, where PID controller parameters for the robotic manipulator system with the incipient fault are selected as \(K_p=2\), \(K_i=0.23\), \(K_d=0.6\) and PID controller parameters for the robotic manipulator system with the abrupt fault are selected as \(K_p=2.6\), \(K_i=0.47\), \(K_d=0.55\). The comparison results are shown in Fig. 5. Top: comparison results of the system under incipient fault, and Bottom: comparison results of the system under abrupt fault. Specifically, Fig. 5a shows the tracking error under the proposed scheme and the tracking error under the fuzzy-free PID control scheme. Obviously, the scheme proposed in this paper can well ensure the convergence of tracking error, even if the system starts to suffer the impact of actuator fault in the 10s, the tracking performance is not significantly affected. However, since the fuzzy-free PID controller is too sensitive to the parameters, the tracking accuracy will drift obviously and diverge with the increase of time after being disturbed by the actuator fault. Figure 5b shows the tracking of the actual output of the system to the given reference output under the two schemes.

Fig. 5
figure 5

a Trajectories of \(e_1\), b Trajectories of y and \(y_r\)

Full size image

According to the simulation results of Example 1 and Example 2, we can easily get the following conclusions:

  1. (1)

    All the variables involved are bounded;

  2. (2)

    The proposed fixed-time fault-tolerant control scheme is less affected by faults, which not only ensures the semi-global practical fixed-time stability of the system but also makes the tracking error converge to a small neighborhood near the origin.

5 Conclusion

This paper solves the fixed-time fault-tolerant control problem for nonstrict feedback nonlinear systems with actuator faults by using dynamic surface control technique, adaptive fuzzy technique, and fixed-time stability theory. The fusion of fixed-time control and fault-tolerant control maintains the stability of the controlled system when the actuator fault occurs. The complexity explosion caused by the traditional backstepping method is also mitigated by the introduction of a first-order filter. Meanwhile, the unknown drift term in the system and the non-dynamic effects and changes caused by faults are offset by the application of adaptive fuzzy technique. Finally, the effectiveness of the proposed controller is verified by two simulations. In view of the pursuit of the optimal system performance index while completing the specified tasks and reducing costs in actual production, exploring the optimal control scheme in the sense of fixed-time will be our next research plan.