1 Introduction

In recent decades, many researchers have been focusing on adaptive control techniques using fuzzy logic systems (FLS) for various classes of nonlinear systems [1,2,3,4,5,6]. The stability analysis of the aforementioned works is performed using Lyapunov technique, where the tracking errors are shown to converge only to a small residual set due to approximation errors. For the actual practical control plants, actuator failures occurring seem unavoidable individually or simultaneously, which may drive the control plants to a catastrophic accident or even destroy the stability during operation [7, 8], for which security, accuracy, performance constraints, and fault tolerant remain the key points in the designed controllers. Hence, the research on how to design fault-tolerant control schemes that lead systems to keep the desired performances and operate in the best conditions with enhanced safety and reliability, even if actuators are normal or faulty, is of great interest [9,10,11,12,13,14].

Fault-tolerant control (FTC) is grouped into passive and active techniques. Promptly, the passive fault-tolerant control (PFTC) technique is withdrawn from the newest control approaches and replaced by active fault-tolerant control (AFTC) techniques due to the fixed control laws and predefined faults description [15, 16]. Active fault-tolerant control is based on fault detection using a module called fault detection and diagnosis (FDD); therefore, the fault will be isolated and estimated to recognize the controller [17,18,19]. Many techniques have been investigated widely in AFTC area; in the midst of these works, adaptive fuzzy control is the upper hand, due to the guaranteed transient and steady-state performances, and the capability of tackling the unknown uncertainties. Moreover, adaptive fuzzy control allows the online update of the controller without the help of an explicit FDI module [20,21,22,23,24,25,26,27].

Recent years have witnessed several adaptive control approaches for many classes of nonlinear systems [28], e.g., strict-feedback [29], output-feedback systems [30, 31], pure-feedback systems [32], and so on. This technique is based essentially on universal approximators such as fuzzy logic system (FLS) and neural networks (NN) when the plant model is uncertain or too complex which makes the designing of a suitable controller very hard [33,34,35]. Plenty of works have focused on \(H_{\infty }\) technique to ensure the attenuation of the tracking error to a certain given level [36, 37]; a reliable adaptive \(H_{\infty }\) static output-feedback control against Markovian jumping sensor failures is carried out in [36]; a fault detection filter is proposed for stochastic parameter varying Markovian jump systems [37]. In [38], an overview of model-free adaptive control schemes, using dynamic linearization, for an unknown nonlinear plant was proposed. Based on the Razumikhin lemma and a dynamic signal, an adaptive neural network-based fault-tolerant control is synthesized to deal only with unmodeled dynamics and only lock-in-place and loss of effectiveness faults [39]. Initial value compensation leaning data-driven ILC was investigated and applied on a batch reactor and fed-batch ethanol fermentation [40]. A novel linear descriptor reduced-order observer for Markovian jump systems has been proposed in [41] with decoupling technology to allow the direct estimation of state and sensor faults. However, only loss of accuracy faults kind is considered. An enhanced result to deal with simultaneous actuator and sensor loss of accuracy faults has been developed in [42] using a new descriptor reduced-order sliding mode observer for Markovian jump systems. In [43], adaptive fault-tolerant control is applied on a flexible spacecraft with state-dependent actuator failures using simple linear sets of system states and errors combination. In [44], the authors presented an active fault-tolerant control using neural networks combined with sliding mode and \(H_{2}\) performance index, applied on a spacecraft system under actuator faults (only loss of effectiveness type). In [45], authors presented an adaptive fuzzy actuator failure compensation control for strict-feedback nonlinear systems taking into account both of loss of effectiveness and lock-in-place actuator faults. In [46], the authors proposed a dynamic surface-based control approach using Nussbaum-type function for attitude stabilization of a spacecraft under actuator saturation. In [47], an approximation-based active FTC using the backstepping approach for MIMO uncertain nonlinear systems is synthesized, where four scenarios of velocity sensor faults (drift, loss of accuracy, bias, and loss of effectiveness) are considered. In [48], authors have investigated an adaptive observer based on backstepping approach with time-varying sensor failures. Only, few works have been carried out on the case of four scenarios of sensor and actuator failures (drift, loss of accuracy, bias, and loss of effectiveness) for nonlinear systems. Authors in [49] have investigated an adaptive fuzzy fault-tolerant control scheme for a class of nonlinear systems with simultaneous actuator and sensor failures. A combination method based on fuzzy systems (FSs) and backstepping approach allowed the online estimation of the adaptive parameters and guaranteed the boundedness of all signals in the closed-loop system. In [50], an active fault-tolerant control scheme has been developed for a class of MIMO nonlinear systems with sensor failures based on dynamic surface control (DSC). In [51,52,53], authors have presented an active fault-tolerant tracking scheme with only the attitude measurement of a spacecraft subjected to one or two kinds of actuator failures. Active fault-tolerant control for a class of nonlinear systems with nonlinear actuator faults with only loss of effectiveness and loss of accuracy has been studied in [54].

In general, the control gain sign (CGS) which is also commonly called in the literature as the control direction sign is required to be known a priori during the design stage. Moreover, in the practical areas, there are plenty of nonlinear systems with unknown control gain sign (CGS). Owing to the fact that one cannot determine the direction along which the controller operates, that is why the issue of designing a successful adaptive control scheme without a priori knowledge of CGS is receiving increasing attention. Nussbaum-type functions have been effectively developed for single linear systems [55]. Few results for nonlinear systems are achieved using the grouping of the unknown control coefficients with linear transformation technique as in [56]. Later, researchers have focused on incorporating Nussbaum gain in various adaptive control schemes for various classes of nonlinear systems [57,58,59,60,61,62,63]. In [57], a Nussbaum-type function is employed to tackle the issue of the unknown control direction of strict-feedback systems class with input quantization using a high-gain fuzzy state observer, combined with backstepping technique. In [58], the same Nussbaum-type function and the mean value theorem are used to develop an adaptive fault-tolerant control for pure-feedback nonlinear systems with sensor failures. In [59] and the references therein, an adaptive controller based on fuzzy systems is developed for a class of feedback linearizable uncertain MIMO nonlinear systems with prescribed performances and unknown control gain sign. To avoid Nussbaum-type functions, authors in [60] assumed that the control gain sign is considered as an unknown constant parameter which is updated online via an appropriate adaptation law. In [61], a fuzzy backstepping approach based on adaptive fault-tolerant control is synthesized taking into account actuator faults and unknown control gain sign. The advantage of this method resides in the number of adaptive parameters which is less than the order on the same system. A robust Nussbaum-type function has been developed in [62] for a class of nonlinear systems with input nonlinearities, unknown control gain sign, and external disturbances that are addressed simultaneously and applied on a MIMO Robotic System. In [63], a region-dependent segmentation analysis technique is coupled with Nussbaum-type function to circumvent the issues of the unknown control gain sign and sensor faults for a class of nonlinear systems.

Motivated by the aforementioned papers, the presented work focuses on adaptive fuzzy fault-tolerant tracking control (AFFTTC) for a class of unknown MIMO nonlinear systems subjected to nonlinear state-dependent actuator failures, external disturbances, and unknown control directions. The developed control law is an adaptive fuzzy controller with a robust control term, which is equipped with Nussbaum-type function to allow a fast approximation and resolve the unknown control directions issue. The stability of the proposed control scheme is carried out using Lyapunov theory. In contrast to the aforementioned works, the main contributions of the presented work are sixfold:

  1. 1.

    Unlike in Refs. [51,52,53], where authors required data about the actuator faults models, in the proposed controller any data about the actuator faults models are required in the design stage; therefore, the proposed controller deals automatically with unknown actuator faults.

  2. 2.

    Unlike in Refs. [35, 39, 41, 44, 45, 51,52,53,54, 58], where just a few kinds actuator faults are considered which impressively confines the applicability of these AFTC techniques, in the proposed control scheme four kinds of state-dependent actuator faults are considered with bias, drift, loss of effectiveness, and loss of accuracy.

  3. 3.

    Unlike in Refs. [47, 48, 50, 61], where restrictive assumptions on external disturbances are imposed. In Ref [48]., the disturbance is described as an exogenous neutral stable system, while in Refs. [47, 50] it is modeled based on time-varying free models with derivable bounds, and in Ref. [61] authors assumed that disturbances are bounded with nonnegative smooth functions. In our scheme, only the disturbance boundedness condition is needed without additional information.

  4. 4.

    Contrary to Refs. [17,18,19, 41], where the approaches are based on fault detection and isolation (FDI) module to locate faults before handling them, in the proposed scheme, the FDI is completely avoided thanks to the ability of the developed controller to deal online with the occurring faults, which makes it fast and accurate control scheme without any time wasting.

  5. 5.

    In Refs. [47, 48, 50], authors assumed that the control gain is a known nonlinear function and as a simple constant in Refs. [44, 54]; however, in the proposed approach, it is considered as a general unknown nonlinear function to cover many practical systems such as an inverted pendulum, an induction motor drive, a single-link robot arm, a mass-spring-damper system, a flexible spacecraft, a quadrotor.

  6. 6.

    Contrary to Refs. [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33, 43,44,45,46,47,48,49,50], where the sign of the control gain (CGSs) is assumed to be known a priori, which is a restrictive condition on the developed control schemes, and therefore limits its applicability; in the proposed approach, the control gain sign is considered completely unknown, which make our approach more general with less restrictive conditions on the controlled plant.

The emphasis of this work is summarized as follows: Sect. 2 introduces the system description and problem formulation. In Sect. 3, the developed control scheme is presented with the stability proof. Numerical simulation on two-inverted pendulum is given in Sect. 4. Finally, a recap of the proposed technique is presented in Sect. 5.

2 Plant model and control objective

2.1 Problem formulation

Consider a class of unknown MIMO nonlinear systems described by the following \(q\) subsystems, where the dynamic is described by the following equations as in [43, 47, 49, 50]:

$$\mathop \sum \limits_{i} :\left\{ {\begin{array}{*{20}c} {\dot{x}_{i,1} = x_{i,2} } \\ {\dot{x}_{i,2} = x_{i,3} } \\ { \vdots } \\ {\dot{x}_{i,j} = f_{i} \left( x \right) + g_{i} \left( x \right)u_{i} + d_{i} \left( t \right), i = 1,2, \ldots , q; j = 1, 2, \ldots , n_{i} } \\ {y_{i} = x_{i,1} } \\ \end{array} } \right.$$
(1)

where \(x = \left[ {x_{1,1} ,x_{1,2} , \ldots , x_{{1,n_{1} }} , \ldots ,x_{q,1} ,x_{q,2} , \ldots ,x_{{q,n_{q} }} } \right]^{\text{T}} \epsilon {\Re }^{n}\) is the state vector, \(n_{i}\) is the order of the ith subsystem with \(n = \mathop \sum \nolimits_{i = 1}^{q} n_{i}\); \(u = \left[ {u_{1} , \ldots ,u_{q} } \right]^{\text{T}} \in {\Re }^{q}\) is the system input vector; \(d\left( t \right) = \left[ {d_{1} \left( t \right),d_{2} \left( t \right), \ldots ., d_{q} \left( t \right)} \right]^{\text{T}} \epsilon {\Re }^{q}\) denotes the external disturbances vector; \(y_{i} \in {\Re }^{p}\) is the output vector; \(f_{i}\) and \(g_{i} , i = 1,2, \ldots ,q\) are unknown smooth nonlinear functions.

The system model described in Eq. (1) is free from actuator faults (healthy case). However, real systems may be subjected to actuator faults at any moment during its operation, so that it is important to point out how to design a suitable control strategy that is capable to drive the system outputs \(y_{i} \left( t \right)\) to track promptly and accurately the desired trajectory \(y_{di} \left( t \right)\) and deal automatically with the unknown dynamics, actuator faults and keep the desired performances.

In this work, an adaptive fuzzy fault-tolerant tracking control (AFFTTC) is developed with unknown system dynamics, disturbances, and three additives (drift, loss of accuracy, and bias) and one multiplicative (loss of effectiveness) actuator faults as in [47, 49, 50]. Table 1 describes the aforementioned faults.

Table 1 Actuator faults
Full size table

2.2 Actuator fault models

The faults considered in Table 1 are time-varying models taking into account time-varying bias, drift, loss of accuracy, and loss of effectiveness. To expand our approach to deal with state-dependent nonlinear actuator faults as in [43], Table 2 shows the new integrated faults.

Table 2 Expanded actuator faults
Full size table

Using the aforementioned definitions described in Table 2, one can write the faulty actuator as

$$u_{i}^{f} \left( t \right) = \rho_{i} \left( {x,t} \right)u_{i} \left( t \right) + \bar{u}_{i} \left( {x,t} \right)$$
(2)

and replacing Eq. (2) into Eq. (1) we get

$$\mathop \sum \limits_{i} :\left\{ {\begin{array}{*{20}c} {\dot{x}_{i,1} = x_{i,2} } \\ {\dot{x}_{i,2} = x_{i,3} } \\ { \vdots } \\ {\dot{x}_{i,j} = f_{i} \left( x \right) + g_{i} \left( {\rho_{i} \left( {x,t} \right)u_{i} \left( t \right) + \bar{u}_{i} \left( {x,t} \right) } \right) + d_{i} \left( t \right), i = 1,2, \ldots ., q; j = 1, 2, \ldots , n_{i} } \\ {y_{i} = x_{i,1} } \\ \end{array} } \right.$$
(3)

Then

$$\mathop \sum \limits_{i} :\left\{ {\begin{array}{*{20}c} {\dot{x}_{i,1} = x_{i,2} } \\ {\dot{x}_{i,2} = x_{i,3} } \\ { \vdots } \\ {\dot{x}_{i,j} = f_{i} \left( x \right) + g_{i} (\left( {\rho_{i} \left( {x,t} \right) - 1} \right)u_{i} \left( t \right) + \bar{u}_{i} \left( {x,t} \right) + u_{i} \left( t \right)) + d_{i} \left( t \right), i = 1,2, \ldots , q; j = 1, 2, \ldots , n_{i} } \\ {y_{i} = x_{i,1} } \\ \end{array} } \right.$$
(4)

and finally, we get,

$$\mathop \sum \limits_{i} :\left\{ {\begin{array}{*{20}c} {\dot{x}_{i,1} = x_{i,2} } \\ {\dot{x}_{i,2} = x_{i,3} } \\ { \vdots } \\ {\dot{x}_{i,j} = f_{i} \left( x \right) + g_{i} u_{i} \left( t \right) + g_{i} (\left( {\rho_{i} \left( {x,t} \right) - 1} \right)u_{i} \left( t \right) + \bar{u}_{i} \left( {x,t} \right)) + d_{i} \left( t \right), i = 1,2, \ldots , q; j = 1, 2, \ldots , n_{i} } \\ {y_{i} = x_{i,1} } \\ \end{array} } \right.$$
(5)

Let define \(f_{ai} \left( {x,u} \right) = g_{i} (\left( {\rho_{i} \left( {x,t} \right) - 1} \right)u_{i} + \bar{u}_{i} \left( {x,t} \right))\), one can find

$$\mathop \sum \limits_{i} :\left\{ {\begin{array}{*{20}c} {\dot{x}_{i,1} = x_{i,2} } \\ {\dot{x}_{i,2} = x_{i,3} } \\ { \vdots } \\ {\dot{x}_{i,j} = f_{i} \left( x \right) + g_{i} u_{i} \left( t \right) + f_{ai} \left( {x,u} \right) + d_{i} \left( t \right), i = 1,2, \ldots , q; j = 1, 2, \ldots , n_{i} } \\ {y_{i} = x_{i,1} } \\ \end{array} } \right.$$
(6)

Remark 1

It is worth noting that the newly defined function \(f_{ai} \left( {x,u} \right)\) represents the actuator failure taking into account all the kinds mentioned in Table 2. Moreover, the model of the considered faults is introduced directly in the dynamic equations of the system and the dynamic is changed according to the above development (Eqs. 3–6), while in [43,44,45], the faults model is introduced directly as an additional function, except in (see Refs. [47, 49, 50]).

Over this paper, the following assumptions are made:

Assumption 1

The desired trajectory \(y_{di} \,\epsilon\, \Re^{q}\) and its time derivatives \(\dot{y}_{di} , \ddot{y}_{di}\) are supposed to be known, smooth, and bounded.

Assumption 2

The control gains \(g_{i} \left( x \right)\) and the CGSs are unknown with \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{g}_{i} \le g_{i} \left( x \right) \le \bar{g}_{i}\), where \(\bar{g}_{i}\) and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{g}_{i}\) are unknown positive constants.

Assumption 3

The external disturbances are considered bounded as \(\left| {d_{i} } \right| \le d_{0i}\) with \(d_{0i}\) are unknown positive constants, \(d_{0i} > 0.\)

Remark 2

In this paper, the tracking trajectories with their derivatives are assumed to be known (assumption 1) as in [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60]. Assumption 2 is introduced to guarantee the controllability of studied system Eq. (6). Assumption 3 reasonably indicates that the disturbance must be bounded, which can be commonly found in many papers ([41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63] and so on).

First, it is assumed that the nonlinear functions given by \(f_{i} \left( x \right)\), \(g_{i} \left( x \right)\) and \(f_{ai} \left( {x,u} \right)\) are unknown and also the control gain signs (CGSs) are unknown. Therefore, it is not easy to design a suitable control law which allows the system outputs \(y_{i} \left( t \right)\) to track promptly and accurately a given certain desired trajectories \(y_{di} \left( t \right)\) and ensure the boundedness of all signals in the closed-loop system. For this situation, we propose a control strategy based on a combination between fuzzy logic systems (FLSs) and Nussbaum-type function (NTF) to approximate the nonlinearities and tackle the issue of the unknown control gain signs.

2.3 Fuzzy logic systems

Fuzzy logic systems (FLSs) are capable of approximating any real continuous function over a compact set with an arbitrary precision [64]. Let define \(x = \left[ {x_{1} , \ldots ,x_{n} } \right]^{\text{T}}\) be the input of the fuzzy system (FS) and \(y\) is considered as an output. For each input \(x_{i}\) is associated \(m_{i}\) fuzzy sets \(F_{i}^{j}\) in \(X_{i}\) its universe of discourse, as for \(x_{i} \in X_{i}\) there is at least one degree of membership given by \(\mu_{{F_{i}^{j} }} \left( {x_{i} } \right) \ne 0\) where \(i = 1,2, \ldots ,n\) and \(j = 1,2, \ldots ,m_{i}\). The rules base of the (FS) has \(N = \mathop \prod \nolimits_{i = 1}^{n} m_{i}\) fuzzy rules taking the following form:

$$R_{k} :{\text{if}}\,x_{1} \,{\text{is}}\, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{F}_{1}^{k} \,{\text{and}} \ldots {\text{and}}\,x_{n} \,{\text{is}}\, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{F}_{n}^{k} \,{\text{Then}}\,y = f_{k} \left( x \right), k = 1, \ldots ,N$$

where \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{F}_{i}^{k} \in \left\{ {F_{i}^{1} , \ldots ,F_{i}^{{m_{i} }} } \right\}\) are linguistic values and \(f_{k} \left( x \right)\) is a numerical function of the output variable. In general, \(f_{k} \left( x \right)\) is a polynomial function dependent on input variables. In the case when \(f_{k} \left( x \right)\) is a polynomial of zero order, it takes the form as \(f_{k} \left( x \right) = a^{k}\), which is commonly called Takagi–Sugeno zero order (TSZ-O). Throughout this paper (TSZ-O) will be used. Each rule has a numerical conclusion, and the output of the (FS) is tacking out by calculating a weighted average as shown below:

$$y\left( x \right) = w^{\text{T}} \left( x \right)\theta$$
(7)

where

  • \(\theta = \left[ {a^{1} \ldots a^{ N} } \right]\): Conclusion values.

  • \(w\left( x \right) = \left[ {w_{1} \left( x \right) \ldots w_{N} \left( x \right)} \right]^{T} ,\)

$$w_{N} \left( x \right) = \frac{{\mu_{k} \left( x \right)}}{{\mathop \sum \nolimits_{j = 1}^{N} \mu_{j} \left( x \right)}},\quad k = 1, \ldots ,N$$
(8)

with \(\mu_{k} \left( x \right) = \mathop \prod \nolimits_{i = 1}^{n} \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{F}_{i}^{k} }} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{F}_{i}^{k} \in \left\{ {F_{i}^{1} , \ldots ,F_{i}^{{m_{i} }} } \right\}\), weight of fuzzy rules.

2.4 Nussbaum-type function and some lemmas

Any continuous function \(N\left( s \right):{\mathbb{R}} \to {\mathbb{R}}\) is cited a Nussbaum-type function if the following properties are achieved:

$$\left\{ {\begin{array}{*{20}l} {\mathop {\lim }\limits_{v \to + \infty } \,{ \sup }\left( {\frac{1}{v}\mathop \int \limits_{0}^{v} N\left( \tau \right){\text{d}}\tau } \right) = + \infty } \hfill \\ {\mathop {\lim }\limits_{v \to + \infty } \,{ \inf }\left( {\frac{1}{v}\mathop \int \limits_{0}^{v} N\left( \tau \right){\text{d}}\tau } \right) = - \infty } \hfill \\ \end{array} } \right.$$
(9)

For example, the continuous functions \(\tau \to e^{{\tau^{2} }} { \cos }\left( {\left( {\frac{\pi }{2}} \right)\tau } \right)\) and \(\tau \to \tau^{2} { \cos }\left( \tau \right)\) are Nussbaum-type functions. In this paper, the even Nussbaum function \(\tau^{2} { \cos }\left( \tau \right)\) is used.

Lemma 1

[65] \(V\left( . \right)\) and \(\tau \left( . \right)\) are smooth functions defined on \(\left[ {0,t_{f} } \right)\) with \(V\left( t \right) \ge 0,\forall t \in \left[ {0,t_{f} } \right);N\left( . \right)\) is an even smooth Nussbaum-type function. If the following inequality holds for \(\forall t \in \left[ {0,t_{f} } \right)\): \(V\left( t \right) \le c_{0} + \mathop \int \nolimits_{0}^{t} \left( {g\left( \zeta \right)N\left( {\tau \left( \zeta \right)} \right) + c_{1} } \right)\dot{\tau }\left( \zeta \right){\text{d}}\zeta\) where \(g\left( t \right)\) is piecewise continuous time function which takes values in the unknown closed interval \(I = \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{g} , \bar{g}} \right]\) with \(0 \notin I; c_{1}\) is any positive number and \(c_{0}\) represents some suitable constant, then \(V\left( . \right)\), \(\tau \left( . \right)\) and \(\mathop \int \nolimits_{0}^{t} \left( {g\left( \zeta \right)N\left( {\tau \left( \zeta \right)} \right) + c_{1} } \right)\dot{\tau }\left( \zeta \right){\text{d}}\zeta\) are bounded on \(\left[ {0,t_{f} } \right)\).

3 Adaptive fuzzy control

The main objective of the proposed scheme is to design an adaptive fuzzy fault-tolerant tracking control laws \(u_{i} \left( t \right)\) to ensure that the system outputs \(y_{i} \left( t \right)\) track as possible the desired trajectories \(y_{di} \left( t \right)\) and guarantee the stability of the closed-loop system and the convergence of the tracking errors to the origin in the presence of unknown nonlinearities, actuator faults, external disturbances, and unknown control directions.

Remark 3

It is important to point out that authors in [50] and some references therein introduced a first-order filter to improve the approximation because they are based on an ordinary approximation which complicates the control law with many design parameters. In the proposed approach, fuzzy systems can give us a prompt and accurate approximation according to Ref. [64]. Moreover, Nussbaum-type function will enhance the robustness of the closed-loop system and resolve the problem of unknown CGSs.

The nonlinear functions and the unknown actuator faults can be approximated, over a compact set \(\varOmega_{x}\), using fuzzy systems (FSs) as described in Eq. (7) as follows

$$\left\{ {\begin{array}{*{20}l} {f_{i} \left( x \right) = \hat{f}_{i} \left( {x,\theta_{{f_{i} }}^{*} } \right) + \varepsilon_{{f_{i} }} \left( x \right) } \hfill \\ {g_{i} \left( x \right) = \hat{g}_{i} \left( {x,\theta_{{g_{i} }}^{*} } \right) + \varepsilon_{{g_{i} }} \left( x \right) } \hfill \\ {f_{ai} \left( {x,u} \right) = \hat{f}_{ai} \left( {x,u,\theta_{{f_{ai} }}^{*} } \right) + \varepsilon_{{f_{ai} }} \left( {x,u} \right) } \hfill \\ \end{array} } \right.$$
(10)

where \(\varepsilon_{fi} \left( x \right)\), \(\varepsilon_{gi} \left( x \right)\), and \(\varepsilon_{{f_{ai} }} \left( x \right)\) are the fuzzy approximation errors; \(\theta_{{f_{i} }}^{*}\) \(\theta_{{g_{i} }}^{*}\) and \(\theta_{{f_{ai} }}^{*}\), are, respectively, the optimal parameters minimizing the approximation errors \(\varepsilon_{{f_{i} }} \left( x \right)\), \(\varepsilon_{{g_{i} }} \left( x \right)\), and \(\varepsilon_{{f_{ai} }} \left( x \right)\).

$$\left\{ {\begin{array}{*{20}l} {\theta_{{f_{i} }}^{*} = \arg \mathop {\hbox{min} }\limits_{{\theta_{{f_{i} }} }} \left\{ {\mathop {\sup }\limits_{x} \left| {\begin{array}{*{20}c} {f_{i} \left( x \right) - } \\ {\hat{f}_{i} \left( {x,\theta_{{f_{i} }} } \right)} \\ \end{array} } \right|} \right\} } \hfill \\ {\theta_{{g_{i} }}^{*} = \arg \mathop {\hbox{min} }\limits_{{\theta_{{g_{i} }} }} \left\{ {\mathop {\sup }\limits_{x} \left| {\begin{array}{*{20}c} {g_{i} \left( x \right) - } \\ {\hat{g}_{i} \left( {x,\theta_{{g_{i} }} } \right)} \\ \end{array} } \right|} \right\} } \hfill \\ {\theta_{{f_{ai} }}^{*} = \arg \mathop {\hbox{min} }\limits_{{\theta_{{f_{ai} }} }} \left\{ {\mathop {\sup }\limits_{x} \left| {\begin{array}{*{20}c} {f_{ai} \left( {x,u} \right) - } \\ {\hat{f}_{ai} \left( {x,u,\theta_{{f_{ai} }} } \right)} \\ \end{array} } \right|} \right\}} \hfill \\ \end{array} } \right.$$
(11)

The optimal parameters given by \(\theta_{{f_{i} }}^{*}\), \(\theta_{{g_{i} }}^{*}\), and \(\theta_{{f_{ai} }}^{*}\) are unknown constants given only for theoretical development in the stability stage, and their values are also not needed to design the proposed control laws. So, we can write:

$$\left\{ {\begin{array}{*{20}l} {f_{i} \left( x \right) - \hat{f}_{i} \left( {x,\theta_{{f_{i} }} } \right) = w_{{f_{i} }}^{\text{T}} \left( x \right)\tilde{\theta }_{{f_{i} }} + \varepsilon_{{f_{i} }} \left( x \right) } \hfill \\ {g_{i} \left( x \right) - \hat{g}_{i} \left( {x,\theta_{{g_{i} }} } \right) = w_{{g_{i} }}^{\text{T}} \left( x \right)\tilde{\theta }_{{g_{i} }} + \varepsilon_{{g_{i} }} \left( x \right) } \hfill \\ {f_{ai} \left( {x,u} \right) - \hat{f}_{ai} \left( {x,u,\theta_{{f_{ai} }} } \right) = w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} + \varepsilon_{{f_{ai} }} \left( {x,u} \right)} \hfill \\ \end{array} } \right.$$
(12)

where \(\tilde{\theta }_{{f_{i} }} = \theta_{{f_{i} }}^{*} - \theta_{{f_{i} }}\), \(\tilde{\theta }_{{g_{i} }} = \theta_{{g_{i} }}^{*} - \theta_{{g_{i} }}\), and \(\tilde{\theta }_{{f_{ai} }} = \theta_{{f_{ai} }}^{*} - \theta_{{f_{ai} }}\) are the parameter estimation errors.

Assumption 4

Fuzzy approximation errors are bounded for all \(x \,\epsilon \,\varOmega_{x}\) as

$$\left| {\varepsilon_{fi} \left( x \right)} \right| \le \bar{\varepsilon }_{fi} ,\left| {\varepsilon_{gi} \left( x \right)} \right| \le \bar{\varepsilon }_{gi} \quad {\text{and}}\quad \left| {\varepsilon_{{f_{ai} }} \left( {x,u} \right)} \right| \le \bar{\varepsilon }_{{f_{ai} }} .$$

where \(\bar{\varepsilon }_{fi} ,\bar{\varepsilon }_{gi} ,\bar{\varepsilon }_{{f_{ai} }}\) are unknown positive constants that will be designed later.

Remark 4

Assumption 4 is reasonable since we assumed that fuzzy systems have universal approximation property [64]. Furthermore, this assumption will ensure the boundedness of the approximation errors [49, 60].

Based on the above approximations, the following adaptive control law is proposed:

$$u_{i} = u_{ic} + u_{ir}$$
(13)

The proposed adaptive control law is a combination of adaptive fuzzy systems (AFSs) and Nussbaum-type function (NTF). The first term \(u_{ic}\) is introduced to circumvent the unknown nonlinear systems, unknown actuator faults, and control gain signs, while the second is a robust term inserted to deal with disturbances and approximation errors.

The adaptive term will take the following form

$$u_{ic} = \frac{{\hat{g}_{i} \left( x \right)}}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}}\left( { - \hat{f}_{i} \left( x \right) - \hat{f}_{ai} \left( {x,u} \right) + y_{di}^{\left( n \right)} + k^{T} e_{i} + \alpha \hat{g}_{i} \left( {x,\theta } \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right)$$
(14)

where \(\varepsilon_{0} :\) is a very small positive constant and \(G_{i} = e_{i}^{\text{T}} P_{i} B\).

Remark 5

The proposed term \(\frac{{\hat{g}_{i} \left( x \right)}}{{\hat{g}^{2}_{i} \left( x \right) + \varepsilon_{0} }}\) in Eq. (14) is introduced to ensure that the proposed adaptive controller term is well defined even when \(\hat{g}_{i} \left( x \right)\) tends to zero, for which the term \(\hat{g}_{i}^{ - 1} \left( x \right)\) is replaced by \(\frac{{\hat{g}_{i} \left( x \right)}}{{\hat{g}^{2}_{i} \left( x \right) + \varepsilon_{0} }}\) and can be considered as the Levenberg–Marquardt regularized inverse for a scalar function [49].

The robust controller term will take the following form:

$$u_{ir} = u_{rbi} N_{i} \left( {\tau_{i} } \right)$$
(15)

where

$$u_{rbi} = \frac{{\left| {e_{i}^{\text{T}} P_{i} B} \right|\varphi_{i} - \delta_{i}^{2} }}{{e_{i}^{T} P_{i} B}}$$
(16)

Nussbaum-type function is described as follows:

$$N_{i} \left( {\tau_{i} } \right) = \tau_{i}^{2} \cos \left( {\tau_{i} } \right)$$
(17)
$$\varphi_{i} = \hat{\varepsilon }_{ui} + \hat{\varepsilon }_{gi} \left| {u_{ic} - \alpha_{i} N_{i} \left( {\tau_{i} } \right)G_{i} } \right| + \left| {\bar{u}_{i0} } \right|$$
(18)

where \(\varphi_{i}\) is considered as a function of the approximation errors due to the use of fuzzy logic systems.

The intermediate adaptive control law will take the following form:

$$\bar{u}_{i0} = \frac{{\varepsilon_{0} }}{{\varepsilon_{0} + \hat{g}^{2}_{i} \left( x \right)}}\left( { - \hat{f}_{i} \left( x \right) - \hat{f}_{ai} \left( {x,u} \right) + y_{di}^{\left( n \right)} + k^{T} e_{i} + \alpha \hat{g}_{i} \left( {x,\theta } \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right)$$
(19)

\(\hat{\varepsilon }_{ui} ,\hat{\varepsilon }_{gi}\) are the estimates of the following unknown parameters:

$$\bar{\varepsilon }_{ui} = \bar{\varepsilon }_{fi} + d_{0i} + \bar{\varepsilon }_{{f_{ai} }} \quad {\text{and}}\quad \bar{\varepsilon }_{gi}$$

where \(\bar{\varepsilon }_{ui}\) is an unknown parameter depending on the upper bound of the system and the external disturbances, and \(\bar{\varepsilon }_{gi}\) is an unknown parameter depending on the upper bound of the control gain function.

Let us define the following adaptive parameters as:

$$\dot{\theta }_{fi} = - \gamma w_{fi} \left( x \right)e_{i}^{\text{T}} P_{i} B$$
(20)
$$\dot{\theta }_{fai} = - \gamma w_{fai} \left( x \right)e_{i}^{\text{T}} P_{i} B$$
(21)
$$\dot{\theta }_{gi} = - \gamma w_{gi} \left( x \right)e_{i}^{\text{T}} P_{i} B \left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right)$$
(22)
$$\dot{\hat{\varepsilon }}_{fu} = \gamma_{\varepsilon } \left| {e_{i}^{\text{T}} P_{i} B } \right|$$
(23)
$$\dot{\hat{\varepsilon }}_{g} = \gamma_{\varepsilon } \left| {e_{i}^{\text{T}} P_{i} B } \right|\left| {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right|$$
(24)
$$\dot{\tau }_{i} = e_{i}^{\text{T}} P_{i} B u_{rbi} + \alpha e_{i}^{\text{T}} P_{i} B ^{2}$$
(25)
$$\dot{\delta }_{i} = - \sigma_{n} \delta_{i}$$
(26)

where

$$\gamma > 0,\gamma_{\varepsilon } > 0,\sigma_{n} > 0, \delta_{i} \left( 0 \right) > 0$$

Remark 6

Authors in [47,48,49,50, 52, 54] assume that the time derivative of the considered actuator faults must be bounded, which is a restrictive condition and limits the applicability of the designed controller. In this paper, this assumption is avoided and no longer needed in controller analysis or design.

The proposed control approach is recapped in Fig. 1, and the following theorem discloses the stability of the closed-loop system.

Fig. 1
figure 1

Schematic of the proposed control strategy (AFFTTC)

Full size image

Theorem 1

For the considered system in Eq. (6) with satisfied Assumptions (1–4), the proposed AFFTTC in Eq. (13) with the adaptive term Eq. (14), robust term Eq. (15), and the adaptation laws Eqs. (20–26) ensure the boundedness of all signals in the closed-loop system and the convergence of the tracking errors to the origin.

Proof

To achieve the control objective, a novel AFFTTC scheme will be synthesized for the system in Eq. (6) with the following steps.

Consider the tracking errors as follows:

$$e_{i} = y_{di} - y_{i}$$
(27)

The \(n\) time derivative of the tracking error is given below

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - y_{i}^{\left( n \right)}$$
(27a)

Using Eq. (6), one can find

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - f_{i} \left( x \right) - g_{i} \left( x \right)u_{i} - f_{ai} \left( {x,u} \right) - d_{i}$$
(28)

by adding and subtracting \(\hat{f}_{i} \left( x \right), \hat{f}_{ai} \left( {x,u} \right)\) and \(\hat{g}_{i} \left( x \right)u_{ic}\), Eq. (28) will be in the following form

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - f_{i} \left( x \right) + \hat{f}_{i} \left( x \right) - g_{i} \left( x \right)u_{ic} + \hat{g}_{i} \left( x \right)u_{ic} - \hat{g}_{i} \left( x \right)u_{ic} - \hat{f}_{i} \left( x \right) - g_{i} \left( x \right)u_{ir} - f_{ai} \left( {x,u} \right) - d_{i} + \hat{f}_{ai} \left( {x,u} \right) - \hat{f}_{ai} \left( {x,u} \right)$$
(29)

Based on some mathematical manipulations, one can get

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - \left( {f_{i} \left( x \right) - \hat{f}_{i} \left( x \right)} \right) - \left( {f_{ai} \left( {x,u} \right) - \hat{f}_{ai} \left( {x,u} \right)} \right){-}\left( {g_{i} \left( x \right) - \hat{g}_{i} \left( x \right)} \right)u_{ic} - \hat{g}_{i} \left( x \right)u_{ic} - \hat{f}_{i} \left( x \right) - g_{i} \left( x \right)u_{ir} - \hat{f}_{ai} \left( {x,u} \right) - d_{i}$$
(30)

Replacing Eq. (12) into Eq. (30) one can find

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - w_{{f_{i} }}^{T} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} u_{ic} - \varepsilon_{gi} \left( x \right)u_{ic} - \hat{g}_{i} \left( x \right)u_{ic} - \hat{f}_{i} \left( x \right) - g_{i} \left( x \right)u_{ir} - \hat{f}_{ai} \left( {x,u} \right) - d_{i}$$
(31)

Replacing Eq. (13) into Eq. (31) one can write

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - w_{{f_{i} }}^{\text{T}} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} u_{ic} - \varepsilon_{gi} \left( x \right)u_{ic} - \hat{g}_{i} \left( x \right)\left[ {\frac{{\hat{g}_{i} \left( x \right)}}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}}\left( { - \hat{f}_{i} \left( x \right) - \hat{f}_{ai} \left( {x,u} \right) + y_{di}^{\left( n \right)} + k_{i}^{\text{T}} e_{i} + \alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right)} \right] - \hat{f}_{i} \left( x \right) - g_{i} \left( x \right)u_{ir} - \hat{f}_{ai} \left( {x,u} \right) - d_{i}$$
(32)

Adding and subtracting \(k_{i}^{\text{T}} e_{i}\) and \(\alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i}\) then

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - w_{{f_{i} }}^{\text{T}} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} u_{ic} - \varepsilon_{gi} \left( x \right)u_{ic} + \frac{{\hat{g}_{i}^{2} \left( x \right)\hat{f}_{i} \left( x \right)}}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}} + \frac{{\hat{g}_{i}^{2} \left( x \right)\hat{f}_{ai} \left( {x,u} \right)}}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}} - \frac{{\hat{g}_{i}^{2} \left( x \right)y_{di}^{\left( n \right)} }}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}} - \frac{{\hat{g}_{i}^{2} \left( x \right)k^{\text{T}} e_{i} }}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}} - \frac{{\hat{g}_{i}^{2} \left( x \right)\left( {\alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right)}}{{\varepsilon_{0} + \hat{g}_{i}^{2} \left( x \right)}} - \hat{f}_{i} \left( x \right) - g_{i} \left( x \right)u_{ir} - \hat{f}_{ai} \left( {x,u} \right) - d_{i} + k_{i}^{\text{T}} e_{i} - k_{i}^{\text{T}} e_{i} + \alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} - \alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i}$$
(33)

Using Eq. (19), one can find the following result

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - w_{{f_{i} }}^{T} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} u_{ic} - \varepsilon_{gi} \left( x \right)u_{ic} + \bar{u}_{i0} - g_{i} \left( x \right)u_{ir} - d_{i} - k_{i}^{\text{T}} e_{i} - \alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i}$$
(34)

Adding and subtracting \(\alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i}\), Eq. (34) leads to

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - w_{{f_{i} }}^{T} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} u_{ic} - \varepsilon_{gi} \left( x \right)u_{ic} + \bar{u}_{i0} - g_{i} \left( x \right)u_{ir} - d_{i} - k_{i}^{\text{T}} e_{i} - \alpha \hat{g}_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} + \alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} - \alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i}$$
(35)

Based on some manipulations, one can write

$$e_{i}^{\left( n \right)} = y_{di}^{\left( n \right)} - w_{{f_{i} }}^{\text{T}} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} \left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) - \varepsilon_{gi} \left( x \right)\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) + \bar{u}_{i0} - g_{i} \left( x \right)u_{ir} - d_{i} - k_{i}^{\text{T}} e_{i} - \alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i}$$
(36)

At this stage, we can write the dynamic of the errors as follows:

$$\dot{e}_{i} \left( t \right) = A_{i} e_{i} \left( t \right) + B\left[ {y_{di}^{\left( n \right)} - w_{{f_{i} }}^{T} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} \left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) - \varepsilon_{gi} \left( x \right)\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) + \bar{u}_{i0} - g_{i} \left( x \right)u_{ir} - d_{i} - \alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right]$$
(37)

where

$$A_{i} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ { - k_{{n_{i} }} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 1 \\ 0 \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ { - k_{{\left( {n - 1} \right)_{i} }} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 1 \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ \cdots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ \cdots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots \\ \cdots \\ {\begin{array}{*{20}c} \ddots \\ \cdots \\ \ldots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} \vdots \\ 0 \\ \cdots \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 0 \\ {\begin{array}{*{20}c} \vdots \\ 1 \\ { - k_{{1_{i} }} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} 0 \\ \vdots \\ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \right]$$

Until \(\left( {\left| {sI - A_{i} } \right|} \right) = s^{\left( n \right)} + k_{{1_{i} }} s^{{\left( {n - 1} \right)}} + \ldots + k_{{n_{i} }}\) is stable \(\left( {A_{i} \,{\text{stable}}} \right)\), we know that there exists a symmetric positive definite matrix \(P_{i} \left( {n, n} \right)\) that satisfies the following Lyapunov equation:

$$A_{i}^{\text{T}} P_{i} + P_{i} A_{i}^{\text{T}} = - Q_{i}$$
(38)

where \(Q_{i}\) are symmetric positive definite matrix of arbitrary dimensions \((n \times n\)).

Then, the augmented Lyapunov-like equation is described by

$$V = \frac{1}{2}\mathop \sum \limits_{i = 1}^{q} \left( {e_{i}^{T} P_{i} e_{i} } \right)^{2} + \frac{1}{\gamma }\tilde{\theta }^{\text{T}}_{fi} \tilde{\theta }_{fi} + \frac{1}{\gamma }\tilde{\theta }^{\text{T}}_{{f_{ai} }} \tilde{\theta }_{{f_{ai} }} + \frac{1}{\gamma }\tilde{\theta }^{\text{T}}_{gi} \tilde{\theta }_{gi} + \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }^{2}_{ui} + \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }^{2}_{gi} + \frac{1}{{\sigma_{n} }}\delta_{i}^{2}$$
(39)

where

$$\gamma , \gamma_{\varepsilon } , \sigma_{n} > 0,\tilde{\varepsilon }_{ui} = \bar{\varepsilon }_{ui} - \hat{\varepsilon }_{ui} ,\tilde{\varepsilon }_{gi} = \bar{\varepsilon }_{gi} - \hat{\varepsilon }_{gi}$$

The time derivative of the augmented Lyapunov-like equation is described as follows

$$\dot{V} = \mathop \sum \limits_{i = 1}^{q} \frac{1}{2}\left( {\dot{e}_{i}^{\text{T}} P_{i} e_{i} } \right) + \frac{1}{2}\left( {e_{i}^{\text{T}} P_{i} \dot{e}_{i} } \right) - \frac{1}{\gamma }\tilde{\theta }_{fi}^{\text{T}} \dot{\theta }_{fi} - \frac{1}{\gamma }\tilde{\theta }_{fai}^{\text{T}} \dot{\theta }_{fai} - \frac{1}{\gamma }\tilde{\theta }_{gi}^{\text{T}} \dot{\theta }_{gi} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{ui} \dot{\hat{\varepsilon }}_{ui} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{gi} \dot{\hat{\varepsilon }}_{gi} + \frac{1}{{\sigma_{n} }}\dot{\delta }_{i} \delta_{i}$$
(40)

Replacing Eq. (36) into Eq. (40), one can find

$$\dot{V} = \sum\limits_{i = 1}^{q} {\frac{1}{2}e_{i}^{\text{T}} \left( {A_{i}^{\text{T}} P_{i} + P_{i} A_{i}^{\text{T}} } \right)e_{i} + e_{i}^{\text{T}} P_{i} B} \left[ { y_{di}^{\left( n \right)} - w_{{f_{i} }}^{T} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} \left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) - \varepsilon_{gi} \left( x \right)\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) + \bar{u}_{i0} - g_{i} \left( x \right)u_{ir} - d_{i} - \alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right] - \frac{1}{\gamma }\tilde{\theta }_{fi}^{\text{T}} \dot{\theta }_{fi} - \frac{1}{\gamma }\tilde{\theta }_{fai}^{\text{T}} \dot{\theta }_{fai} - \frac{1}{\gamma }\tilde{\theta }_{gi}^{\text{T}} \dot{\theta }_{gi} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{ui} \dot{\hat{\varepsilon }}_{ui} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{gi} \dot{\hat{\varepsilon }}_{gi} + \frac{1}{{\sigma_{n} }}\dot{\delta }_{i} \delta_{i}$$
(41)

From Eq. (37) one can obtain

Remark 7

To give the best perceivability and demonstrate the adequacy of the proposed control technique contrasted with other related works, a comparison is made in Table 3.

$$\dot{V} = \sum\limits_{i = 1}^{q} { - \frac{1}{2}e_{i}^{\text{T}} Qe_{i} + e_{i}^{\text{T}} P_{i} B\left[ { y_{di}^{\left( n \right)} - w_{{f_{i} }}^{\text{T}} \left( x \right)\tilde{\theta }_{{f_{i} }} - \varepsilon_{{f_{i} }} \left( x \right) - w_{{f_{ai} }}^{\text{T}} \left( {x,u} \right)\tilde{\theta }_{{f_{ai} }} - \varepsilon_{{f_{ai} }} \left( {x,u} \right) - w_{gi}^{\text{T}} \left( x \right)\tilde{\theta }_{gi} \left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) - \varepsilon_{gi} \left( x \right)\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right) + \bar{u}_{i0} - g_{i} \left( x \right)u_{ir} - d_{i} - \alpha g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} } \right] - \frac{1}{\gamma }\tilde{\theta }_{fi}^{\text{T}} \dot{\theta }_{fi} - \frac{1}{\gamma }\tilde{\theta }_{fai}^{\text{T}} \dot{\theta }_{fai} - \frac{1}{\gamma }\tilde{\theta }_{gi}^{\text{T}} \dot{\theta }_{gi} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{ui} \dot{\hat{\varepsilon }}_{ui} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{gi} \dot{\hat{\varepsilon }}_{gi} + \frac{1}{{\sigma_{n} }}\dot{\delta }_{i} \delta_{i} }$$
(42)

which can be rearranged as follows

$$\dot{V} = \mathop \sum \limits_{i = 1}^{q} - \frac{1}{2}e_{i}^{\text{T}} Qe_{i} - \alpha e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} + \dot{V}_{1} + \dot{V}_{2}$$
(43)

where

$$\dot{V}_{1} = \mathop \sum \limits_{i = 1}^{q} - \tilde{\theta }_{fi}^{\text{T}} \left( {\frac{1}{\gamma }\dot{\theta }_{fi} + w_{fi} \left( x \right)e_{i}^{\text{T}} P_{i} B} \right) - \tilde{\theta }_{fai}^{T} \left( {\frac{1}{\gamma }\dot{\theta }_{fai} + w_{fai} \left( {x,u} \right)e_{i}^{\text{T}} P_{i} B} \right) - \tilde{\theta }_{gi}^{T} \left( {\frac{1}{\gamma }\dot{\theta }_{gi} + e_{i}^{\text{T}} P_{i} Bw_{gi} \left( x \right)\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right)} \right)$$
(44)
Table 3 Comparative study
Full size table

Using Eqs. (20–22), Eq. (44) can be simplified to

$$\dot{V}_{1} = 0$$
(45)
$$\dot{V}_{2} = \mathop \sum \limits_{i = 1}^{q} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} - e_{i}^{\text{T}} P_{i} Bg_{i} \varepsilon_{f} \left( x \right) - e_{i}^{\text{T}} P_{i} Bg_{i} \varepsilon_{{f_{ai} }} \left( {x,u} \right) - e_{i}^{\text{T}} P_{i} Bg_{i} \varepsilon_{g} \left( x \right)(u_{c} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} ) - e_{i}^{\text{T}} P_{i} Bd_{i} + e_{i}^{\text{T}} P_{i} B\bar{u}_{i0} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{ui} \dot{\hat{\varepsilon }}_{ui} - \frac{1}{{\gamma_{\varepsilon } }}\tilde{\varepsilon }_{gi} \dot{\hat{\varepsilon }}_{gi} + \frac{1}{{\sigma_{n} }}\dot{\delta }_{i} \delta_{i}$$
(46)

using Assumptions (3, 4), \(\dot{V}_{2}\) can be upper bounded by:

$$\dot{V}_{2} \le \sum\limits_{i = 1}^{q} { - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} + \left| {e_{i}^{\text{T}} P_{i} B\bar{u}_{i0} } \right| + \left| {e_{i}^{\text{T}} P_{i} B} \right|\bar{\varepsilon }_{fai} + \left| {e_{i}^{\text{T}} P_{i} B} \right|\bar{\varepsilon }_{fi} + \left| {e_{i}^{\text{T}} P_{i} B} \right|d_{i} } + \left| {e_{i}^{\text{T}} P_{i} B\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right)} \right|\bar{\varepsilon }_{gi} - \frac{1}{{\gamma_{\varepsilon } }}\left( {\bar{\varepsilon }_{fui} - \hat{\varepsilon }_{fui} } \right)\dot{\hat{\varepsilon }}_{fui} - \frac{1}{{\gamma_{\varepsilon } }}\left( {\bar{\varepsilon }_{gi} - \hat{\varepsilon }_{gi} } \right)\dot{\hat{\varepsilon }}_{gi} + \frac{1}{{\sigma_{n} }}\dot{\delta }_{i} \delta_{i}$$
(47)

Using the fact that \(\bar{\varepsilon }_{ui} = \bar{\varepsilon }_{fi} + d_{0i} + \bar{\varepsilon }_{{f_{ai} }}\), one can find

$$\dot{V}_{2} \le \mathop \sum \limits_{i = 1}^{q} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} + \left| {e_{i}^{\text{T}} P_{i} B\bar{u}_{i0} } \right| + \left| {e_{i}^{\text{T}} P_{i} B} \right|\bar{\varepsilon }_{fui} + \left| {e_{i}^{\text{T}} P_{i} B\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right)} \right|\bar{\varepsilon }_{gi} - \frac{1}{{\gamma_{\varepsilon } }}\left( {\bar{\varepsilon }_{fui} - \hat{\varepsilon }_{fui} } \right)\dot{\hat{\varepsilon }}_{fui} - \frac{1}{{\gamma_{\varepsilon } }}\left( {\bar{\varepsilon }_{gi} - \hat{\varepsilon }_{gi} } \right)\dot{\hat{\varepsilon }}_{gi} + \frac{1}{{\sigma_{n} }}\dot{\delta }_{i} \delta_{i}$$
(48)

Substituting Eqs. (23, 24, 26) into Eq. (48) one can rewrite

$$\dot{V}_{2} \le \mathop \sum \limits_{i = 1}^{q} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} + \left| {e_{i}^{\text{T}} P_{i} B\bar{u}_{i0} } \right| + \left| {e_{i}^{\text{T}} P_{i} B} \right|\hat{\varepsilon }_{fui} + \left| {e_{i}^{\text{T}} P_{i} B\left( {u_{ic} - \alpha N_{i} \left( {\tau_{i} } \right)G_{i} } \right)} \right|\hat{\varepsilon }_{gi} - \delta_{i}^{2}$$
(49)

using Eq. (18), Eq. (49) can be simplified to

$$\dot{V}_{2} \le \mathop \sum \limits_{i = 1}^{q} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} + \left| {e_{i}^{\text{T}} P_{i} B} \right|\varphi_{i} - \delta_{i}^{2}$$
(50)

Adding and subtracting \(e_{i}^{\text{T}} P_{i} Bu_{rbi}\), Eq. (50) becomes

$$\dot{V}_{2} \le \mathop \sum \limits_{i = 1}^{q} - e_{i}^{T} P_{i} Bg_{i} \left( x \right)u_{ir} + \left| {e_{i}^{\text{T}} P_{i} B} \right|\varphi_{i} - \delta_{i}^{2} + e_{i}^{\text{T}} P_{i} Bu_{rbi} - e_{i}^{\text{T}} P_{i} Bu_{rbi}$$
(51)

Using Eq. (16) one obtains

$$\dot{V}_{2} \le \mathop \sum \limits_{i = 1}^{q} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} + e_{i}^{\text{T}} P_{i} Bu_{rbi}$$
(52)

Substituting the results obtained in Eqs. (45, 52), \(\dot{V}\) can be bounded as

$$\dot{V} \le \mathop \sum \limits_{i = 1}^{q} - \frac{1}{2}e_{i}^{\text{T}} Qe_{i} - \alpha e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)u_{ir} + e_{i}^{\text{T}} P_{i} Bu_{rbi}$$
(53)

From Eq. (15), one can obtain

$$\dot{V} \le \mathop \sum \limits_{i = 1}^{q} - \frac{1}{2}e_{i}^{\text{T}} Qe_{i} - \alpha e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)G_{i} - e_{i}^{\text{T}} P_{i} Bg_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)u_{rbi} + e_{i}^{\text{T}} P_{i} Bu_{rbi}$$
(54)

Using the fact that \(G_{i} = e_{i}^{\text{T}} P_{i} B\), thus, \(\dot{V}\) can be rewritten as

$$\dot{V} \le \mathop \sum \limits_{i = 1}^{q} - \frac{1}{2}e_{i}^{T} Qe_{i} - g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)\left( {\alpha e_{i}^{\text{T}} P_{i} B^{2} + e_{i}^{\text{T}} P_{i} Bu_{rbi} } \right) + e_{i}^{\text{T}} P_{i} Bu_{rbi}$$
(55)

Adding and subtracting \(\alpha e_{i}^{\text{T}} P_{i} B^{2} ,\dot{V}\) can be rewritten as

$$\dot{V} \le \mathop \sum \limits_{i = 1}^{q} - \frac{1}{2}e_{i}^{\text{T}} Qe_{i} - g_{i} \left( x \right)N_{i} \left( {\tau_{i} } \right)\left( {\alpha e_{i}^{\text{T}} P_{i} B^{2} + e_{i}^{\text{T}} P_{i} Bu_{rbi} } \right) + e_{i}^{\text{T}} P_{i} Bu_{rbi} + \alpha e_{i}^{\text{T}} P_{i} B^{2} - \alpha e_{i}^{\text{T}} P_{i} B^{2}$$
(56)

Substituting Eq. (25)

$$\dot{V} \le \mathop \sum \limits_{i = 1}^{q} - \frac{1}{2}e_{i}^{\text{T}} Qe_{i} - \left( {\alpha e_{i}^{\text{T}} P_{i} B^{2} } \right) - g_{i} \left( x \right)\dot{\tau }_{i} N_{i} \left( {\tau_{i} } \right) + \dot{\tau }_{i}$$
(57)

where \(\alpha > 0\)

we can obtain the following inequality

$$V\left( t \right) - V\left( 0 \right) \le \mathop \int \limits_{0}^{t} - \left( {g_{i} \left( v \right)N_{i} \left( v \right) + 1} \right)\dot{\tau }_{i} \left( v \right) {\text{d}}v$$
(58)

Equation (57) can be simplified to

$$V\left( t \right) \le V\left( 0 \right) + \mathop \int \limits_{0}^{t} - \left( {g_{i} \left( v \right)N_{i} \left( v \right) + 1} \right)\dot{\tau }_{i} \left( v \right) {\text{d}}v$$
(59)

Using Lemma 1, we can conclude from Eq. (59) the boundedness of:

  • \(V\left( t \right)\), \(N_{i} \left( {\tau_{i} } \right)\)

  • \(\mathop \int \limits_{0}^{t} - \left( {g_{i} \left( v \right)N_{i} \left( v \right) + 1} \right)\dot{\tau }_{i} \left( v \right){\text{d}}v, t\epsilon \left[ {0,t_{f} } \right).\)

According to [66, 67], since no finite time escape phenomenon may happen, then \(t_{f} \to \infty\) (Table 4).

Table 4 Performance comparison
Full size table

Therefore, \(\tilde{\theta }_{fi} \left( t \right)\), \(\tilde{\theta }_{fai} \left( t \right), e_{i} \left( t \right)\), \(\tilde{\theta }_{gi} \left( t \right)\), \(\hat{\varepsilon }_{f} \left( t \right)\), \(\hat{\varepsilon }_{g} \left( t \right)\), \(\delta_{i} \left( t \right)\), \(x\left( t \right)\), and \(u_{i} \left( t \right)\) are bounded, as an intermediate result \(e_{i} \left( t \right)\) is square integrable and \(\dot{e}_{i} \left( t \right)\) is bounded. Moreover, by invoking Barbalat’s lemma, we can conclude the asymptotic convergence of \(e_{i} \left( t \right)\).

4 Simulation results

To outline the effectiveness and benefits of the recommended AFFTTC, we consider the control issue of two-inverted pendulums associated with a spring as appeared in Fig. 2. Every pendulum might be actuated by a torque input \(u_{i} \left( t \right)\) generated by a servomotor at its base. Let \(\left( {x_{1,1} ,x_{2,1} } \right) = \left( {\theta_{1} ,\theta_{2} } \right)\) be the angular positions of the pendulums from vertical and \(\left( {x_{1,2} ,x_{2,2} } \right) = \left( {\dot{\theta }_{1} ,\dot{\theta }_{2} } \right)\) their angular velocities, respectively. The mathematical equations of the two-inverted pendulums are given by [50, 67, 68]:

Fig. 2
figure 2

Two-inverted pendulums configuration

Full size image
$$\left\{ {\begin{array}{*{20}c} {\dot{x}_{1,1} = x_{1,2} } \\ {\dot{x}_{1,2} = \left( {\frac{{m_{1} gr}}{{j_{1} }} - \frac{{kr^{2} }}{{j_{1} }}} \right)\sin \left( {x_{1,1} } \right) + \frac{kr}{{2j_{1} }}\left( {l - b} \right) + \frac{{kr^{2} }}{{4j_{1} }}\sin \left( {x_{2,1} } \right) + \frac{1}{{j_{1} }}u_{1} \left( t \right) + d_{{\dot{1}}} \left( t \right)} \\ {\dot{x}_{2,1} = x_{2,2} } \\ {\dot{x}_{2,2} = \left( {\frac{{m_{2} gr}}{{j_{2} }} - \frac{{kr^{2} }}{{j_{2} }}} \right)\sin \left( {x_{2,1} } \right) + \frac{kr}{{2j_{2} }}\left( {l - b} \right) + \frac{{kr^{2} }}{{4j_{2} }}\sin \left( {x_{1,1} } \right) + \frac{1}{{j_{2} }}u_{2} \left( t \right) + d_{2} \left( t \right)} \\ \end{array} } \right.$$
(60)

where \(m_{1} , m_{2}\) are the pendulum end masses; \(j_{1} , j_{2}\) the moments of inertia; \(k\) the spring constant of the connecting spring; \(r\) the pendulum height; \(l\) the length of the spring; \(b\) the distance between the pendulum hinges; \(g\) the gravitational acceleration.

In this simulation, the objective is to force the angular positions \(y = \left[ { \theta_{1} , \theta_{2} } \right]^{\text{T}}\) to track accurately the desired trajectories \(y_{d} = \left[ { \theta_{1d} , \theta_{2d} } \right]^{\text{T}}\) under the simultaneous occurrence of four types of state-dependent actuator faults and external disturbances.

The desired trajectories are selected as sinusoidal signals having the following equation:

$$y_{d} = \left[ {\sin \left( t \right), \sin \left( t \right)} \right]^{\text{T}}$$
(61)

Disturbances are given by \(d = \left[ {\sin \left( {\pi t} \right), 0.5 + \cos \left( {2\pi t} \right)} \right]^{\text{T}}\)

Remark 8

Contrasted to the works in the same area, we can easily see that the proposed desired trajectories having a maximum amplitude of \(1\;{\text{rad}}\), while it is only limited to 0.1 rad (see Ref. [57]) and it is around 0.5 rad at maximum in Refs. [44, 47, 48]. Expanding the amplitude of the desired trajectories makes it more challenging for testing the capacity of the proposed scheme controllers. Moreover, in our paper, the proposed control scheme is based on an online fuzzy logic system (FLS) and Nussbaum-type function, which allows selecting these challenging trajectories.

Within this simulation, fifteen fuzzy systems on the form of Eq. (13) are introduced to approximate the unknown functions \(\left( {f_{i} \left( x \right), g_{i} \left( x \right), f_{ai} \left( {x,u} \right)} \right)\). The input variables of the used fuzzy systems are selected as \(\left( {x_{1,1} ,x_{1,2} , x_{2,1} ,x_{2,2} } \right)\) for \(f_{i} \left( x \right), g_{i} \left( x \right)\) and \(\left( {x_{1,1} ,x_{1,2} , x_{2,1} ,u_{i} } \right)\) for \(f_{ai} \left( {x, u} \right)\). For each input variable, we have defined five Gaussian membership functions with centers \(C_{i} = \left[ { - 3.5, - 1.5, 0, 1.5, 3.5} \right]\) and a variance equal to \(\sigma = 1.6\).

$$\mu_{{F_{i}^{1} }} \left( {x_{i} } \right) = \exp \left\{ { - \frac{1}{2}\left( {\frac{{x_{i} - C_{i} }}{\sigma }} \right)^{2} } \right\},\quad i = 1:4$$

The system initial condition is

$$x\left( 0 \right) = \left[ {\frac{\pi }{6},0,\frac{\pi }{6},0} \right]$$

The synthesis parameters of our controller, adaption laws, and the physical parameters of the two-inverted pendulums are selected in Tables 5 and 6, respectively.

Table 5 Controller parameters
Full size table
Table 6 Two-inverted pendulums physical parameters
Full size table

Within this simulation, a white Gaussian noise (WGN) with centers \(C_{i} = \left[ { 0, 1.5} \right]\) and a variance equal to \(\sigma = 1.2\), is applied on both angular positions and angular velocities. Three simulation cases are given below to give a reliable test of the proposed control scheme with many scenarios.

The first simulation case is executed without any faults (free from actuator failures), and only disturbances are included.

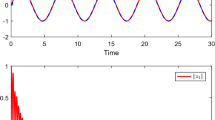
In Fig. 3a, b, we can easily see the perfect tracking performances between the desired trajectories \(\left( {y_{d1} , y_{d2} } \right)\) and the angular positions \(\left( {\theta_{1} , \theta_{2} } \right)\), while Fig. 3e, f depicts the tracking errors. Figure 3c, d shows the angular velocities. The control inputs of the two-inverted pendulums \((u_{1} , u_{2} )\) are depicted in Fig. 3g, h.

Fig. 3
figure 3

Evolution of the two-inverted pendulums without any faults. a, b Trajectories tracking of angular positions: actual (blue lines); desired (red lines); e, f tracking error signal; c, d trajectories tracking of angular velocity: actual (red lines); desired (blue lines); g, h control input signals (colour figure online)

Full size image

In the second simulation case, time-varying actuator faults (bias, drift, loss of accuracy, loss of effectiveness) are applied at the same time on the control inputs \((u_{1} , u_{2} )\) at \(T_{f} \ge 5\;{\text{s}}\).

The faults models are described in Table 7. In Fig. 4a, b, we can easily see the perfect tracking performances between the desired trajectories \(\left( {y_{d1} , y_{d2} } \right)\) and the angular positions \(\left( {\theta_{1} , \theta_{2} } \right)\) even in the presence of the aforementioned faults, while Fig. 4e, f depicts the tracking errors. Figure 4c, d shows the angular velocities. The control inputs of the two-inverted pendulums \((u_{1} , u_{2} )\) are depicted in Fig. 4g, h.

Table 7 Time-varying actuator faults
Full size table
Fig. 4
figure 4

Evolution of the two-inverted pendulums with time-varying actuator faults. a, b Trajectories tracking of angular positions: actual (blue lines); desired (red lines); e, f tracking error signal; c, d trajectories tracking of angular velocity: actual (red lines); desired (blue lines); g, h control input signals (colour figure online)

Full size image

Remark 9

In the works given in [41,42,43,44, 46, 47, 50], authors consider faults for only a short period of time during the simulation stage, and also a few kinds of faults are applied at the same time. However, in the contrary, in our simulation four kinds (see Table 1) of time-varying actuator faults (bias, drift, loss of accuracy, loss of effectiveness) are applied at the same time on the control inputs \((u_{1} , u_{2} )\) at \(T_{f} \ge 5\;{\text{s}}\), which allow us to ensure the desired performances (tracking and stability) during the whole simulation period (see the performances comparative in Table 4).

In the last case, the simulation study is carried out with time-varying and state-dependent actuator faults (see Table 2) at \(T_{f} \ge 5\;{\text{s}}\).

The form of the considered actuator faults is depicted in (see Table 8). In Fig. 5a, b, we can easily see the perfect tracking performances between the desired trajectories \(\left( {y_{d1} , y_{d2} } \right)\) and the angular positions \(\left( {\theta_{1} , \theta_{2} } \right)\) even in the presence of the aforementioned faults, while Fig. 5e, f depicts the tracking errors. Figure 5c, d shows the angular velocities. The control inputs of the two-inverted pendulums \((u_{1} , u_{2} )\) are depicted in Fig. 5g, h.

Table 8 Time-varying and state-dependent actuator faults
Full size table
Fig. 5
figure 5

Evolution of the two-inverted pendulums with time-varying actuator faults. a, b Trajectories tracking of angular positions: actual (blue lines); desired (red lines); e, f tracking error signal; c, d trajectories tracking of angular velocity: actual (red lines); desired (blue lines); g, h control input signals (colour figure online)

Full size image

4.1 Results analysis and comments

It is shown that the control scheme proposed in this paper leads to a good transient performance against faults, and tracking errors converge to zero exponentially in different cases.

  • The first case is faults free and only disturbances are presented. One can see that the system’s outputs follow the desired trajectories with small tracking errors and smooth control inputs signals without any peak phenomenon (see Fig. 3).

  • In the second case, we added time-varying actuator faults (see Table 7) with a time-profile starting at \(T_{f} \ge 5\;{\text{s}}\). One can see the deviation of the angular positions corresponding to the first and the second pendulums. Furthermore, at time instant 6 s, i.e., just after 1 s from the fault’s occurrence, the proposed control laws reacted in order to circumvent these faults and recover the angular positions tracking within short transient time (see Fig. 4).

  • In the last case, state-dependent actuator faults are considered (see Table 8) with a time-profile starting at \(T_{f} \ge 5\;{\text{s}}\). This kind of faults is a little hard to handle due to either the variation of the system’s state and the time progression. Only 1.5 s from the faults’ occurrence, we can see in Fig. 5 the rapid recovering of the angular positions tracking corresponding to the first and the second pendulums in the expense of nonsmooth control signals with peaking phenomena.

5 Conclusion

In the present paper, an active fault-tolerant control problem was addressed for a class of MIMO nonlinear systems under actuator faults, unknown system dynamics, and external disturbances. Based on a combination between fuzzy logic systems (FLSs) and Nussbaum-type function, the developed control scheme can circumvent the problem of nonlinearities and cope with the problem of the control gain signs (CGSs). The proposed controller is updated online, which allows avoiding fault detection and isolation module (FDI), and can, automatically, deal with both faulty and healthy cases. The stability is studied by using Lyapunov technique and Barbalat’s lemma, to guarantee the global stability of the system and conclude the asymptotic convergence of the tracking errors. A comparative study in the theoretical stage was performed, and a simulation example applied on two-inverted pendulums was performed to test the effectiveness and the accuracy of the proposed method.