Output Feedback Adaptive Fuzzy Control for Uncertain Fractional-Order Nonlinear Switched System with Output Quantization

Abstract

In this paper, a novel adaptive fuzzy controller is developed for the uncertain fractional-order switched nonlinear systems whose output is quantized by a class of sector-bounded quantizers. Since the states are not completely measurable, an observer with quantized output signal is designed to estimate the unknown system states. Meanwhile, based on the fractional Lyapunov stability criterion, the Lyapunov function with sum functions and the virtual control function with hyperbolic tangent functions are designed. Besides, in order to improve the approximation accuracy of the unknown nonlinear functions generated by fractional differential, the prediction errors and auxiliary variables of series-parallel estimation model are introduced in backstepping procedures. The simulation results show that the control scheme ensures that all the signals of the considered system remain semi-globally uniformly ultimately bounded, and the tracking error converges to a small neighborhood of the origin regardless of arbitrary switching.

1 Introduction

Since the end of the twentieth century, fractional calculus is no longer a strange mathematical theory. With the deepening of people’s understanding of nonlinear systems and genetic effect, the limitation of traditional mathematical model based on integral calculus is increasingly obvious. Taking the actual power system as an example, there are often many diffusion phenomena in the motor and transformer, such as skin effect, eddy current loss, heat loss, etc. For these systems, the modeling method of integer-order systems often ignores these slow diffusion effects. Therefore, the fractional system model is more suitable to describe these real physical systems with genetic and long memory effects. There are many researches on fractional-order systems [1,2,3]. At the same time, hybrid systems can describe various problems in the real world more accurately and reasonably. Switched system is one of the most important hybrid systems, which consists of several subsystems and one switching rule. Because of its broad representativeness, it has become one of the focus of control workers. At present, there are a lot of research results on switched system [4,5,6,7]. Meanwhile, adaptive control [8] has been widely studied. An adaptive neural network feedback control scheme for nonlinear switched pulse systems with a permissible switched strategy was proposed in [9].

Quantization can be regarded as the mapping of continuous signals to discrete finite sets [10,11,12]. It has important theoretical and practical significance in modern engineering and has attracted extensive attention in recent years. For the system with information quantization, its continuous control input, state variable and control output are quantized by quantizer, which leads to inevitable quantization error. Therefore, the effect of quantization error on the performance of the closed-loop system, especially on the stability of the system, needs to be studied carefully and clearly. [13] developed a hysteresis quantizer for the first time, which avoids the oscillation caused by the logarithmic quantizer and extends the conclusions from uncertain linear systems to uncertain nonlinear systems. The problem of adaptive quantization feedback control of SISO strict-feedback uncertain nonlinear systems with hysteresis quantization input was studied in [14].

Aiming at the uncertainty of nonlinear system, intelligent control [15,16,17] based on fuzzy logic systems (FLSs) and neural network (NN) has been widely studied. The universal approximation property of fuzzy logic can provide theoretical basis for modeling nonlinear systems and analyzing the unknown properties of complex systems. In the cause of approximating the unknown dynamics of the system, an adaptive control scheme was proposed in [18], which directly adjusts the ideal weight vector estimation of the switch. When the backstepping method is applied to nonlinear system, the derivative process of virtual control will cause the expansion of item number, so the dynamic surface control (DSC) method is adopted, which cannot only eliminate the expansion of differential terms, make the controller and parameter design simple, but also reduce the number of input variables of neural network and fuzzy system. [19] used DSC method, the disturbance observer adaptive control of nonlinear transport model with external disturbance was proposed.

It is well known that backstepping design has become a major controller construction method for nonlinear system control [20,21,22,23]. Many advantages of backstepping design have been widely recognized, such as adaptive controller design, global stabilization controller design and robustness. At present, most of the results of the backstepping design method are aimed at the traditional integer-order nonlinear system, and there are few applications in the fractional-order nonlinear system control [24,25,26]. Therefore, how to design an adaptive backstepping controller for triangular fractional-order nonlinear system based on fractional-order Lyapunov stability criterion is still a problem to be solved. It is worth noting that, because the fractional derivative of quadratic function is very complex, most existing backstepping control methods of integer-order nonlinear system cannot be directly extended to fractional-order nonlinear system. In [27], for the uncertain fractional-order nonlinear systems with triangular structure, an adaptive backstepping controller based on a certain transformation and integral-order Lyapunov method was designed. For a class of fractional-order nonlinear systems, [28] constructed a class of adaptive backstepping controller. However, for fractional-order nonlinear switched systems with unknown state variables, there is no control scheme can solve the system stability problem with measurement signal error caused by output quantization. Hence, on the basis of the existing results, it is urgent to design a new controller to make the fractional-order nonlinear switching system with output quantization stable and have good tracking performance.

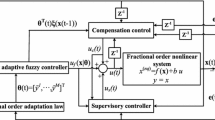
Motivated by the above observations, in this paper, an adaptive fuzzy controller is developed for the uncertain fractional-order switched nonlinear systems with quantized output, where the quantizers contain the hysteresis, logarithmic and uniform quantizer. The unmeasured state is obtained by using the switched fuzzy state observer. By introducing the delta function, one can use the previous estimated values as original value of the parameters at the switching instants. The contributions of this paper can be summarized as follows: (1) For uncertain fractional-order nonlinear systems, an adaptive fuzzy backstepping recursive algorithm is proposed. The convergence of the algorithm is analyzed by fractional Lyapunov method. (2) By constructing the prediction errors and auxiliary variables based on the serial-parallel estimation model, a compound learning method is proposed to update fuzzy membership functions and improve approximate accuracy, which can dynamically show the working process of intelligent approximation. (3) Based on different subsystems and switched adaptive laws, switched filters are designed to reduce the conservativeness of the adaptive controllers, and all the signals are bounded under arbitrary switching.

The content of this paper is as follows: Sect. 2 puts forward some preliminary ideas and briefly describes the existing problems. A fuzzy switched observer is designed in Sect. 3. In Sect. 4, the adaptive control scheme is proposed. Section 5 gives the stability analysis of the design scheme. The simulation results in Sect. 6 represent the effectiveness of the scheme, followed by conclusions in Sect. 7.

2 Preliminaries and Problem Formulation

2.1 Preliminaries

Consider the following SISO fractional-order nonlinear switched system:

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&{\mathcal {D}}^\alpha _t x_i=x_{i+1}+f_{i,\delta (t)}({\underline{x}}_i)+d_{i,\delta (t)}(t),\quad 1\le i<n\\&{\mathcal {D}}^\alpha _t x_n=u_\delta (t)+f_{n,\delta (t)}({\underline{x}}_n)+d_{n,\delta (t)}(t),\\&y=x_1 \end{aligned} \right. \end{aligned} \end{aligned}$$

(1)

where $\alpha \in (0,1]$ and ${\underline{x}}_i=[x_1,x_2,...,x_i]^\text{T},i=1,2,...,n$ is the state vector, $y\in R$ is the output of the system. $\delta (t)\rightarrow {\mathbb {N}}=\{1,2,...r\}$ is the switching signal. $\delta (t)=k\in {\mathbb {N}}$ indicates the kth subsystem in the implementation. $f_{i,\delta (t)}(x_{1},...,x_{i})$ is an unknown smooth function representing the uncertainty of the system. $u_k$ denotes the switched input signal.

2.2 Fuzzy Logic Systems

Because of the uncertainty of the considered system, the fuzzy logic system is introduced. Construct a fuzzy logic system (FLS) in the form of If-Then rules:

$R^{q}$: If $x_{1}$ is $F^{q}_{1}$ and $x_{2}$ is $F^{q}_{2}$ and ...and $x_{n}$ is $F^{q}_{n}$, then y is $B^{q},q=1,2,\ldots ,\iota$, where $x=[x_1,\ldots ,x_n]^\text{T}$ is the fuzzy logic system input, y is the fuzzy logic system output, fuzzy sets $F^{q}_i$ and $B^{q}$, associated with the fuzzy functions $\mu _{F^q_i}(x_i)$ and $\mu _{B^q}(y)$, respectively. $\iota$ is the rules number. Through singleton function, the FLS can be formulated as

$$\begin{aligned} y(x(t)) = \frac{\sum ^\iota _{q=1} {\overline{y}}_q\prod ^q_{i=1}\mu _{F^q_i}(x_i)}{\sum ^\iota _{q=1}(\prod ^n_{i=1}\mu _{F^q_i}(x_i))}, \end{aligned}$$

(2)

where ${\overline{y}}_{q} = \max _{y\in R}\mu _{B^q}(y)$.

Let $\varphi _q = \frac{\prod ^n_{i=1}\mu _{F^q_i}(x_i)}{\sum ^\iota _{q=1}(\prod ^n_{i=1}\mu _{F^q_i}(x_i))}$, and denote $\theta =[ {\overline{y}}_1,{\overline{y}}_2, \cdots ,{\overline{y}}_\iota ]^\text{T}=[\theta _1,\theta _2,\cdots ,\theta _\iota ]^{\text{T}}$ and $\varphi ^\text{T}(x)=[\varphi _1(x),...,\varphi _\iota (x)]$, then FLS can be rewritten as $y(x)=\theta ^\text{T}\varphi (x).$

Lemma 1

[29] Letf(x) be a continuous function defined on a compact set${\varOmega }$. Then for any constant$\nu$, there exists an FLS such as

$$\begin{aligned} \underset{x\in {\varOmega }}{sup}|f(x)-\theta ^\text{T}\varphi (x)|\le \nu \end{aligned}$$

(3)

By Lemma 1, FLSs are general approximators, which can approximate any smooth function on a compact set, so the nonlinear terms can be approximated as

$$\begin{aligned} f_i(\underline{x}_i)={\theta ^*}^\text {T}_i\phi _i(\underline{x}_i)+\nu _i,\quad 1\le i\le n \end{aligned}$$

(4)

To facilitate the further analysis, the system (1) is rewritten as

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&{\mathcal {D}}^\alpha _t x_i=x_{i+1}+{\theta ^*}^\text {T}_{i,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)+{\varDelta } f_{i,\delta (t)}+\varepsilon _{i,\delta (t)}\\&{\mathcal {D}}^\alpha _t x_n=u_\delta (t)+{\theta ^*}^\text {T}_{n,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)+{\varDelta } f_{n,\delta (t)}+\varepsilon _{n,\delta (t)}(t) \end{aligned} \right. \end{aligned} \end{aligned}$$

(5)

where $\varepsilon _{i,\delta (t)}=\nu _{i,\delta (t)}+d_{i,\delta (t)}(t),i=1,2,\ldots ,n-1$, ${\varDelta } f_{i,\delta (t)} =f_{i,\delta (t)}({\underline{x}}_i)-f_{i,\delta (t)}(\hat{{\underline{x}}}_i)$, $\hat{{\underline{x}}}_i$ stands for the estimate of $\underline{x}_i$ and $\hat{{\underline{x}}}_i= ({\hat{x}}_1,{\hat{x}}_2,\ldots ,{\hat{x}}_i)^\text{T}$. $\nu _{i,\delta (t)}=f_{i,\delta (t)}({\hat{x}}_i)- {\theta ^*}^\text {T}_{i,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)$ satisfies that $\vert \nu _{i,\delta (t)}\vert \le \nu ^*_{i,\delta (t)}$, and for given $\delta (t)=k$, $\nu ^*_{i,\delta (t)}$ is an unknown positive constant.

Assumption 1

$d_{i,\delta (t)}$ satisfies that $\vert d_{i,\delta (t)}\vert \le d^*_{i,\delta (t)}$, and for given $\delta (t)=k$, $d^*_{i,\delta (t)}$ is an unknown positive constant.

Assumption 2

Assume that the unknown function $f_i(\cdot )$ satisfies the global Lipschitz condition. That is, there exist some known constants $m_i$ such that $\vert f_i({\underline{x}}_i)-f_i(\hat{{\underline{x}}}_i)\vert \le m_i\Vert {\underline{x}}_i-\hat{{\underline{x}}}_i\Vert$, where $i=1,2,...,n$. $\Vert \cdot \Vert$ represents the 2-norm of a vector.

2.3 Quantizer

With the application and development of network control system, quantitative control has become an effective way to solve control system problems. The commonly used quantizer include logarithmic quantizer, uniform quantizer and hysteresis quantizer. They are defined as follows

2.3.1 Uniform Quantizer

The form of uniform quantizer is as follows

$$\begin{aligned} \begin{aligned} q(u)= \left\{ \begin{aligned}&u_isign(u),\quad u_i-\frac{l}{2}<\vert u\vert \le u_i+\frac{l}{2}\\&0,\quad \quad \quad \quad \quad \vert u\vert \le u_0 \end{aligned} \right. \end{aligned} \end{aligned}$$

(6)

where $u_0>0$ and $u_1=u_0+\frac{l}{2}$, $u_i=u_{i-1}+l$, l stands for quantization interval.

2.3.2 Logarithmic Quantizer

The form of logarithmic quantizer is as follows

$$\begin{aligned} \begin{aligned} q(u)= \left\{ \begin{aligned}&u_isign(u),\quad \frac{u_i}{1+\sigma }<\vert u\vert \le \frac{u_i}{1-\sigma }\\&0,\quad \quad \quad \quad \quad \vert u\vert \le \frac{\eta }{1+\sigma } \end{aligned} \right. \end{aligned} \end{aligned}$$

(7)

where $u_i=\rho ^{1-i}\eta$ and $\rho =\frac{1-\sigma }{1+\sigma }$ and $q(u)\in U=\{0,\pm u_i\}$.

2.3.3 Hysteresis Quantizer

The form of hysteresis quantizer is as follows

$$\begin{aligned} \begin{aligned} q(u)= \left\{ \begin{aligned}&u_isign(u), \quad \quad \quad \frac{u_i}{1+\sigma }<\vert u\vert \le u_i,\dot{u}<0, \\&\quad \quad \quad \quad \quad \quad \quad \ \, {\text{or}}, u_i<\vert u\vert \le \frac{u_i}{1-\sigma },\dot{u}>0\\&u_i(1+\sigma )sign(u), u_i<\vert u\vert \le \frac{u_i}{{1-\sigma }},\dot{u}<0,\\&\quad \quad \quad \quad \quad \quad \quad \ \, {\text{or}}, \frac{u_i}{1+\sigma }<\vert u\vert \le u_i,\dot{u}>0 \\&0, \quad \quad \quad \quad \quad \quad \quad 0<\vert u\vert \le \frac{\eta }{1+\sigma },\dot{u}<0,\\&\quad \quad \quad \quad \quad \quad \quad \ \,{\text{or}},\frac{\eta }{1+\sigma }\le u\le \eta ,\dot{u}>0\\&q(u(t^-)),\quad \quad \quad \quad \dot{u}=0 \end{aligned} \right. \end{aligned} \end{aligned}$$

(8)

where $u_i=\rho ^{1-i}\eta$ and $\rho =\frac{1-\sigma }{1+\sigma }$ and $q(u)\in U = \{0,\pm u_i, \pm u_i (1+\sigma )\}$.

2.3.4 Quantization Error

For the practical system, the quantization error will affect the stability of the system. So quantification is important but challenging. The difference between the quantized result and the value before quantification is called quantization error. The quantization error satisfies

$$\begin{aligned} \begin{aligned} \vert q(u)-u\vert \le \sigma \vert u\vert +(1-\sigma )d=\sigma \vert u\vert +\eta \end{aligned} \end{aligned}$$

(9)

where $0<\sigma <1$ and d are known parameters of quantizer. Therefore, the output quantification error considered in this paper is in the following form: $\vert q(y)-y\vert \le \sigma \vert y\vert +(1-\sigma )d=\sigma \vert y\vert +\eta$.

Remark 1

Different from uniform quantizer, there are unequal quantization levels in hysteresis and logarithmic quantizers, which are easy to implement and also reduce the average rate. Having different quantized values but the same coarseness, two logarithmic quantizers can compose a hysteresis quantizer. Besides, chattering by the additional quantization levels can be avoided by employing hysteresis quantizer [30].

2.4 Fractional Calculus and Related Lemmas

This section introduces several important lemmas of fractional calculus.

The form of fractional-order integration is as follows:

$$\begin{aligned} {\mathcal {I}}^\alpha _t f(t)=\frac{1}{{\varGamma }(\alpha )} \int _{t_0}^t(t-\tau )^{\alpha -1}f(\tau )\text {d}\tau \end{aligned}$$

(10)

where ${\varGamma }(\alpha )=\int _{0}^\infty \tau ^{\alpha -1}e^{-\tau }d\tau$ is the gamma function. The form of the $\alpha$th Caputo fractional derivative is as follows

$$\begin{aligned} {\mathcal {D}}^\alpha _t f(t)=\frac{1}{{\varGamma }(n-\alpha )} \int _{t_0}^t(t-\tau )^{n-\alpha -1}f^{(n)}(\tau )\text {d}\tau \end{aligned}$$

(11)

where $n-1<\alpha \le n$. The Mittag-Leffler function with two parameters $\alpha$ and $\gamma$ is defined as

$$\begin{aligned} E_{\alpha ,\gamma }(t)=\sum _{i=0}^\infty \frac{t^i}{{\varGamma }(i\alpha +\gamma )}, \alpha >0,\quad E_1(t)=e^t \end{aligned}$$

(12)

Its Laplace transform can be written as

$$\begin{aligned} {\mathcal {L}}\{t^{\gamma -1}E_{\alpha ,\gamma }(-at^\alpha )\}=\frac{s^{\alpha -\gamma }}{s^\alpha +a} \end{aligned}$$

(13)

Lemma 2

[31] Let$x(t)\in R^n$be a vector of differentiable function. Then,${\mathcal {D}}^\alpha _t (x^\text {T}(t)x(t))\le 2x^\text {T}(t){\mathcal {D}}^\alpha _t (x(t))$holds for any time instant$t\ge t_0$and$\alpha \in (0,1]$.

Lemma 3

[32] Let$x(t)\in R^n$be a vector of differentiable function. Then, the following relationship${\mathcal {D}}^\alpha _t (x^\text {T}(t)P x(t))\le 2x^\text {T}(t)P{\mathcal {D}}^\alpha _t (x(t))$holds for any time instant$t\ge t_0$and$\alpha \in (0,1]$, wherePis a constant, square, symmetric, and positive-definite matrix.

Lemma 4

[33] For a real number$\alpha$satisfying$0<\alpha <2$, a real numberpsatisfying$\frac{\pi \alpha }{2}<p<\min \{\pi ,\pi \alpha \}$and a complex numberq, the following formula applies to all integers$n\ge 1$

$$\begin{aligned} E_{\alpha ,q}(t)=-\sum ^n_{j=1}\frac{1}{{\varGamma }(q-\alpha j)t^j}+o\left( \frac{1}{\vert t\vert ^{n+1}}\right) \end{aligned}$$

(14)

when $\vert t\vert \rightarrow \infty$, $p\le \vert \arg (t)\vert \le \pi$.

Lemma 5

[33] For a real number$\alpha$satisfying$0<\alpha < 2$and an arbitrary real numberq, if there exists a positive constantpand$\frac{\pi \alpha }{2}<p\le \min \{\pi ,\pi \alpha \}$, then one has

$$\begin{aligned} \vert E_{\alpha ,q}(t)\vert \le \frac{C}{1+\vert t\vert } \end{aligned}$$

(15)

where$C>0$, $p\le \vert \arg (t)\vert \le \pi$and$\vert t\vert \ge 0$.

3 Adaptive State Observer Design

Noting that all states $x_1,\ldots ,x_n$ in system (1) are not completely measurable for feedback design. Therefore, a state observer should be established to estimate the states. The state observer is designed as follows

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&{\mathcal {D}}^\alpha _t {\hat{x}}_i={\hat{x}}_{i+1}+{\theta }^\text {T}_{i,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)+l_{i,\delta (t)}(q(y)-{\hat{x}}_1) \\&{\mathcal {D}}^\alpha _t {\hat{x}}_n=u_{\delta (t)}+{\theta }^\text {T}_{n,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)+l_{n,\delta (t)}(q(y)-{\hat{x}}_1) \end{aligned} \right. \end{aligned} \end{aligned}$$

(16)

Construct observer error as $e=x-{\hat{x}}$. Then, from (1), (5) and (16), the observer error equation is expressed as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t e&=A_{\delta (t)}e+{\Delta } F_{\delta (t)}+\sum _{i=1}^nB_i{\widetilde{\theta }}^\text {T}_{i,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)\\&\quad +\,L_{\delta (t)}(x_1-q(y))+\varepsilon _{\delta (t)} \end{aligned} \end{aligned}$$

(17)

where ${\widetilde{\theta }}^\text {T}_{i,\delta (t)}={\theta ^*}^\text {T}_{i,\delta (t)}-\theta ^\text {T}_{i,\delta (t)}$, and ${\varDelta } F_{\delta (t)}=({\varDelta } f_{1, \delta (t)}, {\varDelta } f_{2, \delta (t)},\ldots ,{\varDelta } f_{n, \delta (t)})^\text{T}$, $B_i=(0,\ldots ,0,1,0,\ldots ,0)^\text{T}$,

$$\begin{aligned} {A_{\delta }}=\left( \begin{matrix} {-l_{1,\delta (t)} }&{} 1 &{} 0 &{} \cdots &{} 0\\ {-l_{2,\delta (t)}} &{} 0 &{} 1 &{}\cdots &{} 0\\ \vdots &{}\vdots &{}\vdots &{} \ddots &{}\vdots \\ { -l_{n-1,\delta (t)}} &{} 0 &{} 0 &{} \cdots &{} 1\\ { -l_{n,\delta (t)}} &{} 0 &{} 0 &{} \cdots &{} 0\\ \end{matrix}\right) , {L_{\delta }}=\left( \begin{matrix} {-l_{1,\delta (t)}} \\ {-l_{2,\delta (t)}}\\ \vdots \\ {-l_{n-1,\delta (t)}} \\ {-l_{n,\delta (t)}} \\ \end{matrix}\right) . \end{aligned}$$

The coefficient $l_{i,\delta (t)}$ is chosen such that for any given $Q^\text {T}_{\delta (t)}=Q_{\delta (t)}>0$, there exists a common positive-definite matrix P, such that

$$\begin{aligned} A^\text {T}_{\delta (t)}P+PA_{\delta (t)}=-Q_{\delta (t)} \end{aligned}$$

(18)

On the basis of the fuzzy state observer (16), a series-parallel estimation model similar to [34] is designed

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&{\mathcal {D}}^\alpha _t {\hat{\hat{x}}}_i={\hat{x}}_{i+1}+{\theta }^\text {T}_{i,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)+{\varLambda }_{i,\delta (t)}(q(y)-{\hat{x}}_1)\\&{\mathcal {D}}^\alpha _t {\hat{\hat{x}}}_n=u_{\delta (t)}+{\theta }^\text {T}_{n,\delta (t)}\phi _{i,\delta (t)}(\hat{{\underline{x}}}_i)+{\varLambda }_{n,\delta (t)}(q(y)-{\hat{x}}_1) \end{aligned} \right. \end{aligned} \end{aligned}$$

(19)

where ${\varLambda }_{i,\delta (t)},i=1,2,\ldots n-1$ is a designed constants. The prediction error $\zeta _i$ is defined as $\zeta _i={\hat{x}}_i-\hat{{\hat{x}}}_i$, then, one can obtain

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\alpha _t \zeta _i=L_{i,\delta (t)}(q(y)-{\hat{x}}_1)-{\varLambda }_{n,\delta (t)}(q(y)-{\hat{x}}_1) \end{aligned} \end{aligned}$$

(20)

which will be used later.

Choose the common Lyapunov candidate $V_0$ as

$$\begin{aligned} V_0=e^\text {T}Pe \end{aligned}$$

(21)

For the kth activated subsystem, the time derivative of $V_0$ is computed by using (17) and Lemma 3 as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_0&\le -e^\text {T}Q_ke+2e^\text {T}P[{\varDelta } F_{k}+\sum _{i=1}^nB_i{\widetilde{\theta }}^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)\\&\quad +\,{L_{k}}(x_1-q(y))+\varepsilon _k] \end{aligned} \end{aligned}$$

(22)

By Youngs inequality and $0<\phi ^\text {T}_{i,k}(\cdot )\phi _{i,k}(\cdot )\le 1$, it follows that

$$\begin{aligned} \begin{aligned}&2e^\text {T}P\sum _{i=1}^nB_i{\widetilde{\theta }}^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)\le n\Vert e\Vert ^2+\Vert P\Vert ^2\sum _{i=1}^n{\widetilde{\theta }}^\text {T}_{i,k}{\widetilde{\theta }}_{i,k} \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned} \begin{aligned} 2e^\text {T}P[{\varDelta } F_{k}+\varepsilon _k]&\le \left( 2+\Vert P\Vert ^2\sum _{i=1}^nm^2_{i,k}\right) \Vert e\Vert ^2\\&\quad +\Vert P\Vert ^2\Vert \varepsilon ^*_k\Vert ^2 \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned} \begin{aligned} 2e^\text {T}PL_k(x_1-q(y))\le&\Vert P\Vert ^2\Vert L\Vert ^2+(2\Vert P\Vert \Vert L_k\Vert \sigma +\sigma ^2{\hat{x}}_1\\&+\Vert P\Vert ^2\Vert L_k\Vert ^2 )\Vert e\Vert ^2+\eta ^2 \end{aligned} \end{aligned}$$

(25)

where $\varepsilon ^*_k=(\varepsilon ^*_{1,k},\varepsilon ^*_{2,k},\ldots ,\varepsilon ^*_{n,k})^\text{T}$ and $\varepsilon ^*_{i,k}=\nu ^*_{i,k}+d^*_{i,k}$ is an unknown constant.

Then, the time derivative of $V_0$ along the solution of (23)–(25) is computed as

$$\begin{aligned} {\mathcal {D}}^\alpha _t V_0\le -\lambda _0\Vert e\Vert ^2+\Vert P\Vert ^2\sum _{i=1}^n{\widetilde{\theta }}^\text {T}_{i,k}{\widetilde{\theta }}_{i,k}+M_0 \end{aligned}$$

(26)

where $\lambda _0=\lambda _{\text {min}}(Q)-n-2-\Vert P\Vert ^2\sum _{i=1}^nm^2_{i,k}-2\Vert P\Vert \Vert L_k\Vert \sigma +\sigma ^2{\hat{x}}_1-\Vert P\Vert ^2+\Vert L_k\Vert ^2$ and $M_0=\Vert P\Vert ^2\Vert \varepsilon ^*_k\Vert ^2+\eta ^2+\Vert P\Vert ^2\Vert L_k\Vert ^2$.

4 Switched Adaptive Output Feedback Controller Design

To overcome the explosion of complex problems caused by repeated differentiation of the virtual control, the following changes of coordinates are designed as

$$\begin{aligned}&z_1={\hat{x}}_1,\quad z_i={\hat{x}}_i-{\hat{x}}_{ic},\quad i=2,3,\ldots ,n \end{aligned}$$

(27)

where ${\hat{x}}_{ic}$ can be obtained by the virtual control ${\hat{x}}_{id}$ through the filter with a switched positive constant $\omega _{i,k}$, as follows

$$\begin{aligned} \omega _{i,k}{\mathcal {D}}^\alpha {\hat{x}}_{ic}+{\hat{x}}_{ic}&={\hat{x}}_{id} \end{aligned}$$

(28)

$$\begin{aligned} {\hat{x}}_{ic}(t_0)&={\hat{x}}_{id}(t_0) \end{aligned}$$

(29)

Let the definition of $\chi _i$ be the compensated tracking error

$$\begin{aligned} \chi _i=z_i-v_i,\quad i=1,2,\ldots ,n \end{aligned}$$

(30)

where $v_i$ are the subsidiary variables to be designed. Then, the design process of the controller is as follows

Step 1: According to (16), the Caputo fractional derivative of $z_1$ is

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t z_1&={\hat{x}}_2+\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)+l_{1,k}(q(y)-{\hat{x}}_1) \end{aligned} \end{aligned}$$

(31)

Consider the Lyapunov function candidate as

$$\begin{aligned} \begin{aligned} V_1=V_0+\frac{1}{2}\chi ^2_1+\frac{1}{2}\zeta ^2_1+\sum _{l=1}^r\frac{1}{2 \varpi _1}{\widetilde{\theta }}^\text {T}_{1,l}{\widetilde{\theta }}_{1,l} \end{aligned} \end{aligned}$$

(32)

where $\varpi _1$ is a positive constant. From (20), (30), (31) and Lemma 2, it follows that

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_1&={\mathcal {D}}^\alpha _t V_0+\chi _1[{\mathcal {D}}^\alpha _t z_1-{\mathcal {D}}^\alpha _t v_1]+\zeta _1{\mathcal {D}}^\alpha _t\zeta _1\\&\quad -\sum _{l=1}^r\frac{1}{\varpi _1}{\widetilde{\theta }}^\text {T}_{1,l}{\mathcal {D}}^\alpha _t\theta _{1,l}\\&=\chi _1[{\hat{x}}_2+\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)+l_{1,k}(q(y)-{\hat{x}}_1)-{\mathcal {D}}^\alpha _t v_1]\\&\quad +{\mathcal {D}}^\alpha _t V_0+\zeta _1{\mathcal {D}}^\alpha _t\zeta _1-\sum _{l=1}^r\frac{1}{\varpi _1}{\widetilde{\theta }}^\text {T}_{1,l}{\mathcal {D}}^\alpha _t\theta _{1,l}\\&=\chi _1[z_2+{\hat{x}}_{2c}-{\hat{x}}_{2d}+\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)+l_{1,k}e_1\\&\quad +\,l_{1,k}(q(y)-x_1)-{\mathcal {D}}^\alpha _t v_1-{\widetilde{\theta }}^\text {T}_{1,l}\phi _{1,l}({\hat{x}}_1)+{\hat{x}}_{2d}]\\&\quad +\,{\mathcal {D}}^\alpha _t V_0+\zeta _1[l_{1,k}(q(y)-x_1)-l_{1,k}e_1-{\varLambda }_{1,k}\zeta _1]\\&\quad -\sum _{l=1}^r\frac{1}{\varpi _1}{\widetilde{\theta }}^\text {T}_{1,l}{\mathcal {D}}^\alpha _t\theta _{1,l}+\chi _1{\widetilde{\theta }}^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1) \end{aligned} \end{aligned}$$

(33)

By using Youngs inequality, the fact $0<\phi ^\text {T}_{i,k}\phi _{i,k}<1$ and the fact $\vert x\vert \le x \tanh (x/\varrho )+\beta \varrho$ with $\beta =0.2785$ and $\varrho$ is a positive constant, one has

$$\begin{aligned} \begin{aligned}&\chi _1\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)\le \sum _{k=1}^r\vert \chi _1\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)\vert \\&\quad \le \chi _1\sum _{k=1}^r\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)\tanh \left( \frac{\chi _1\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)}{\tau _{1,k}}\right) +\sum _{k=1}^r\beta \tau _{1,k} \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned} \begin{aligned}&\chi _1l_{1,k}e_1\le \sum _{k=1}^r\vert \chi _1l_{1,k}e_1\vert \\&\quad \le \chi _1\sum _{k=1}^rl_{1,k}e_1\tanh \left( \frac{\chi _1l_{1,k}e_1}{\nu _{1,k}}\right) +\sum _{k=1}^r\beta \nu _{1,k} \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned} \begin{aligned}&\chi _1l_{1,k}(q(y)-x_1)\le \vert \chi _1l_{1,k}\vert (\sigma e_1+\sigma {\hat{x}}_1+\eta )\\&\quad \le \frac{3}{2}\chi ^2_1+\frac{1}{2}\sigma ^2l^2_{1,k}\Vert e\Vert ^2+\frac{1}{2}l^2_{1,k}\sigma ^2{\hat{x}}^2_1+\frac{1}{2}\eta ^2l^2_{1,k} \end{aligned} \end{aligned}$$

(36)

$$\begin{aligned} \begin{aligned}&\zeta _1l_{1,k}(q(y)-x_1)\\&\quad \le \frac{3}{2}\zeta ^2_1+\frac{1}{2}\sigma ^2l^2_{1,k}\Vert e\Vert ^2+\frac{1}{2}l^2_{1,k}\sigma ^2{\hat{x}}^2_1+\frac{1}{2}\eta ^2l^2_{1,k} \end{aligned} \end{aligned}$$

(37)

$$\begin{aligned}&\zeta _1l_{1,k}e_1\le \frac{\zeta ^2_1}{2}+\frac{1}{2}l^2_{1,k}\Vert e\Vert ^2 \end{aligned}$$

(38)

$$\begin{aligned}&\chi _1{\widetilde{\theta }}^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)\le \frac{1}{2}\chi ^2_1+\frac{1}{2}{\widetilde{\theta }}^\text {T}_{1,k}{\widetilde{\theta }}_{1,k} \end{aligned}$$

(39)

where $\tau _{1,k}$ and $\nu _{1,k}$ are positive constants.

The virtual control ${\hat{x}}_{2d}$, the time fractional derivative of $v_1$ and the corresponding update law are as follows

$$\begin{aligned} \begin{aligned} {\hat{x}}_{2d}&=-\sum _{k=1}^r\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)\tanh \left( \frac{\chi _1\theta ^\text {T}_{1,k}\phi _{1,k}({\hat{x}}_1)}{\tau _{l,k}}\right) \\&\quad -c_1z_1-\sum _{k=1}^rl_{1,k}e_1\tanh \left( \frac{\chi _1l_{1,k}e_1}{\nu _{l,k}}\right) \end{aligned} \end{aligned}$$

(40)

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\alpha _t v_1=-c_1v_1+v_2+{\hat{x}}_{2c}-{\hat{x}}_{2d} \end{aligned} \end{aligned}$$

(41)

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\alpha _t\theta _{1,l}=\xi _{1,l}[\chi _1\varpi _1\phi _{1,l}({\hat{x}}_1)-\mu _1\theta _{1,l}] \end{aligned} \end{aligned}$$

(42)

where $\xi _{1,l}$ is a delta function defined as

$$\begin{aligned} \begin{aligned}\xi _{1,l}= \left\{ \begin{aligned} 1,\quad k=l\\ 0,\quad k\ne l \end{aligned} \right. \end{aligned} \end{aligned}$$

(43)

Substituting (40)–(43) into (33) results in

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_1&\le -\lambda _1\Vert e\Vert ^2-(c_1-2)\chi ^2_1+\chi _1\chi _2\\&\quad +\frac{1}{2}{\widetilde{\theta }}^\text {T}_{1,k}{\widetilde{\theta }}_{1,k}+\left( \frac{1}{2}-{\varLambda }_{1,k}\right) \zeta ^2\\&\quad +\,\Vert P\Vert ^2\sum _{i=1}^n{\widetilde{\theta }}^\text {T}_{i,k}{\widetilde{\theta }}_{i,k}+\frac{\mu _1}{\varpi _1}{\widetilde{\theta }}^\text {T}_{1,k}\theta _{1,k}+M_1 \end{aligned} \end{aligned}$$

(44)

where $\lambda _1=\lambda _0-\sigma ^2 l^2_{1,k}-\frac{1}{2}l^2_{1,k}$ and $M_1=M_0+l^2_{1,k}\sigma ^2{\hat{x}}^2_1+\eta ^2l^2_{1,k}+\sum _{k=1}^r\beta \tau _{1,k}+\sum _{k=1}^r\beta \nu _{1,k}$.

Step i: According to (27), one can obtain $z_i= {\hat{x}}_i-{\hat{x}}_{ic}$. By using (16), the derivative of $z_i$ can be expressed as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t z_i&={\mathcal {D}}^\alpha _t {\hat{x}}_i-{\mathcal {D}}^\alpha _t{\hat{x}}_{ic}={\hat{x}}_{i+1}+\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)\\&\quad +\,l_{i,k}(q(y)-{\hat{x}}_1)-{\mathcal {D}}^\alpha _t{\hat{x}}_{ic} \end{aligned} \end{aligned}$$

(45)

Consider the Lyapunov function candidate as

$$\begin{aligned} \begin{aligned} V_i=V_{i-1}+\frac{1}{2}\chi ^2_{i}+\frac{1}{2}\zeta ^2_i+\sum _{l=1}^r\frac{1}{2\varpi _i}{\widetilde{\theta }}^\text {T}_{i,l}{\widetilde{\theta }}_{i,l} \end{aligned} \end{aligned}$$

(46)

where $\varpi _i$ is a positive constant. From (20), (44) and Lemma 2, it follows that

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_i&={\mathcal {D}}^\alpha _t V_{i-1}+\chi _i[{\mathcal {D}}^\alpha _t z_i-{\mathcal {D}}^\alpha _t v_i]+\zeta _i{\mathcal {D}}^\alpha _t\zeta _i\\&\quad -\sum _{l=1}^r\frac{1}{\varpi _i}{\widetilde{\theta }}^\text {T}_{i,l}{\mathcal {D}}^\alpha _t\theta _{i,l}\\&={\mathcal {D}}^\alpha _t V_{i-1}+\chi _i[{\hat{x}}_{i+1}+\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)+l_{i,k}(q(y)-{\hat{x}}_1)\\&\quad -{\mathcal {D}}^\alpha _t{\hat{x}}_{ic}-{\mathcal {D}}^\alpha _t v_i]+\zeta _i{\mathcal {D}}^\alpha _t\zeta _i-\sum _{l=1}^r\frac{1}{\varpi _i}{\widetilde{\theta }}^\text {T}_{i,l}{\mathcal {D}}^\alpha _t\theta _{i,l}\\&={\mathcal {D}}^\alpha _t V_{i-1}+\chi _i[z_{i+1}+{\hat{x}}_{(i+1)c}-{\hat{x}}_{(i+1)d}\\&\quad +\,\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)+l_{i,k}e_1+l_{i,k}(q(y)-x_1)\\&\quad -{\mathcal {D}}^\alpha _t{\hat{x}}_{ic}-{\mathcal {D}}^\alpha _t v_i-{\widetilde{\theta }}^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)+{\hat{x}}_{(i+1)d}]\\&\quad +\zeta _i[l_{i,k}(q(y)-x_1)-l_{i,k}e_1-{\varLambda }_{i,k}\zeta _i]\\&\quad -\sum _{l=1}^r\frac{1}{\varpi _i}{\widetilde{\theta }}^\text {T}_{i,l}{\mathcal {D}}^\alpha _t\theta _{i,l}+\chi _i{\widetilde{\theta }}^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i) \end{aligned} \end{aligned}$$

(47)

Similar to (34)–(39), one has

$$\begin{aligned} \begin{aligned}&\chi _i\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)\le \sum _{k=1}^r\vert \chi _i\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)\vert \\&\quad \le \chi _i\sum _{k=1}^r\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)\tanh \left( \frac{\chi _i\theta ^\text {T}_{i,k}\phi _{i,k}(\hat{{\underline{x}}}_i)}{\tau _{i,k}}\right) +\sum _{k=1}^r\beta \tau _{i,k} \end{aligned} \end{aligned}$$

(48)

$$\begin{aligned} \begin{aligned}&\chi _il_{i,k}e_1\le \sum _{k=1}^r\vert \chi _il_{i,k}e_1\vert \\&\quad \le \chi _i\sum _{k=1}^rl_{i,k}e_1\tanh \left( \frac{\chi _il_{i,k}e_1}{\nu _{i,k}}\right) +\sum _{k=1}^r\beta \nu _{i,k} \end{aligned} \end{aligned}$$

(49)

$$\begin{aligned} \begin{aligned}&(\chi _i+\zeta _i)l_{i,k}(q(y)-x_1)\\&\quad \le \frac{3}{2}\chi ^2_i+\frac{3}{2}\zeta ^2_i+\sigma ^2l^2_{i,k}\Vert e\Vert ^2+l^2_{i,k}\sigma ^2{\hat{x}}^2_1+\eta ^2l^2_{i,k} \end{aligned} \end{aligned}$$

(50)

$$\begin{aligned} \begin{aligned}&\zeta _il_{i,k}e_1\le \frac{\zeta ^2_i}{2}+\frac{1}{2}l^2_{i,k}\Vert e\Vert ^2 \end{aligned} \end{aligned}$$

(51)

$$\begin{aligned} \begin{aligned}&\chi _i{\widetilde{\theta }}^\text {T}_{i,k}\phi _{i,k}({\hat{x}}_1)\le \frac{1}{2}\chi ^2_i+\frac{1}{2}{\widetilde{\theta }}^\text {T}_{i,k}{\widetilde{\theta }}_{i,k} \end{aligned} \end{aligned}$$

(52)

where $\tau _{i,k}$ and $\nu _{i,k}$ are positive constants.

The virtual control ${\hat{x}}_{(i+1)d}$, the time fractional derivative of $v_{i}$ and the corresponding update law are as follows

$$\begin{aligned} \begin{aligned} {\hat{x}}_{(i+1)d}&=-\,c_iz_i-\sum _{k=1}^r\theta ^\text {T}_{i,k}\phi _{i,k}({\hat{x}}_1)\tanh \left( \frac{\chi _i\theta ^\text {T}_{i,k}\phi _{1,k}({\hat{x}}_1)}{\tau _{i,k}}\right) \\&\quad -\,z_{i-1}-\sum _{k=1}^rl_{i,k}e_1\tanh \left( \frac{\chi _il_{i,k}e_1}{\nu _{i,k}}\right) +{\mathcal {D}}^\alpha _t{\hat{x}}_{ic} \end{aligned} \end{aligned}$$

(53)

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\alpha _t v_i=-\,c_iv_i-v_{i-1}+v_{i+1}+{\hat{x}}_{(i+1)c}-{\hat{x}}_{(i+1)d} \end{aligned} \end{aligned}$$

(54)

$$\begin{aligned} \begin{aligned}&{\mathcal {D}}^\alpha _t\theta _{i,l}=\xi _{i,l}[\chi _i\varpi _i\phi _{i,l}(\hat{{\underline{x}}}_i)-\mu _i\theta _{i,l}] \end{aligned} \end{aligned}$$

(55)

where $\xi _{i,l}$ is a delta function defined as

$$\begin{aligned} \begin{aligned}\xi _{i,l}= \left\{ \begin{aligned} 1,\quad k=l\\ 0,\quad k\ne l \end{aligned} \right. \end{aligned} \end{aligned}$$

(56)

Substituting (53)–(56) into (47) results in

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_i&\le -\lambda _i\Vert e\Vert ^2-\sum ^i_{j=1}(c_j-2)\chi ^2_j+\chi _i\chi _{i+1}\\&\quad +\sum ^i_{j=1}\left( \frac{1}{2}-{\varLambda }_{j,k}\right) \zeta ^2_j+\frac{1}{2}\sum _{j=1}^i{\widetilde{\theta }}^\text {T}_{j,k}{\widetilde{\theta }}_{j,k}\\&\quad +\Vert P\Vert ^2\sum _{i=1}^n{\widetilde{\theta }}^\text {T}_{i,k}{\widetilde{\theta }}_{i,k}+\sum ^i_{j=1}\frac{\mu _j}{\varpi _j}{\widetilde{\theta }}^\text {T}_{j,k}\theta _{j,k}+M_i \end{aligned} \end{aligned}$$

(57)

where $\lambda _i=\lambda _{i-1}-\sigma ^2 l^2_{i,k}-\frac{1}{2}l^2_{i,k}$ and $M_i=M_{i-1}+l^2_{i,k}\sigma ^2{\hat{x}}^2_1+\eta ^2l^2_{i,k}+\sum _{k=1}^r\beta \tau _{i,k}+\sum _{k=1}^r\beta \nu _{i,k}$.

Step n: According to (27), one can obtain $z_n= {\hat{x}}_n-{\hat{x}}_{nc}$. By using (16), the derivative of $z_n$ can be expressed as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t z_n&={\mathcal {D}}^\alpha _t {\hat{x}}_n-{\mathcal {D}}^\alpha _t{\hat{x}}_{nc}\\&=u_k+\theta ^\text {T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_n)+l_{n,k}(q(y)-{\hat{x}}_1)-{\mathcal {D}}^\alpha _t{\hat{x}}_{nc} \end{aligned} \end{aligned}$$

(58)

Consider the Lyapunov function candidate as

$$\begin{aligned} \begin{aligned} V_n=V_{n-1}+\frac{1}{2}\chi ^2_{n}+\frac{1}{2}\zeta ^2_{n}+\sum _{l=1}^r\frac{1}{2\varpi _n}{\widetilde{\theta }}^\text {T}_{n,l}{\widetilde{\theta }}_{n,l} \end{aligned} \end{aligned}$$

(59)

where $\varpi _n$ is a positive constant. From (20), (58) and Lemma 2, it follows that

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_n&={\mathcal {D}}^\alpha _t V_{n-1}+\chi _n[{\mathcal {D}}^\alpha _t z_n-{\mathcal {D}}^\alpha _t v_n]+\zeta _n{\mathcal {D}}^\alpha _t\zeta _n\\&\quad -\sum _{l=1}^r\frac{1}{\varpi _n}{\widetilde{\theta }}^\text {T}_{n,l}{\mathcal {D}}^\alpha _t\theta _{n,l}\\&={\mathcal {D}}^\alpha _t V_{n-1}+\chi _n[u_k+\theta ^\text {T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_n)+l_{n,k}(q(y)-{\hat{x}}_1)\\&\quad -\,{\mathcal {D}}^\alpha _t{\hat{x}}_{nc}-{\mathcal {D}}^\alpha _t v_n]+\zeta _n{\mathcal {D}}^\alpha _t\zeta _n-\sum _{l=1}^r\frac{1}{\varpi _1}{\widetilde{\theta }}^\text {T}_{1,l}{\mathcal {D}}^\alpha _t\theta _{1,l}\\&={\mathcal {D}}^\alpha _t V_{n-1}+\chi _i[u_k+\theta ^\text {T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_n)+l_{n,k}e_1\\&\quad +\,l_{n,k}(q(y)-x_1)-{\mathcal {D}}^\alpha _t{\hat{x}}_{nc}-{\mathcal {D}}^\alpha _t v_n-{\widetilde{\theta }}^\text {T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_n)]\\&\quad +\,\zeta _n[l_{n,k}(q(y)-x_1)-l_{n,k}e_1-{\varLambda }_{n,k}\zeta _n]\\&\quad -\sum _{k=1}^r\frac{1}{\varpi _n}{\widetilde{\theta }}^\text {T}_{n,k}{\mathcal {D}}^\alpha _t\theta _{n,k}+\chi _n{\widetilde{\theta }}^\text {T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_n) \end{aligned} \end{aligned}$$

(60)

Similar to (50)–(52), one has

$$\begin{aligned} \begin{aligned}&(\chi _n+\zeta _n)l_{n,k}(q(y)-x_1)\\&\quad \le \frac{3}{2}\chi ^2_n+\frac{3}{2}\zeta ^2_n+\sigma ^2l^2_{n,k}\Vert e\Vert ^2+l^2_{n,k}\sigma ^2{\hat{x}}^2_1+\eta ^2l^2_{n,k} \end{aligned} \end{aligned}$$

(61)

$$\begin{aligned} \begin{aligned}&\zeta _nl_{n,k}e_1\le \frac{\zeta ^2_n}{2}+\frac{1}{2}l^2_{n,k}\Vert e\Vert ^2 \end{aligned} \end{aligned}$$

(62)

$$\begin{aligned} \begin{aligned}&\chi _n{\widetilde{\theta }}^\text {T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_1)\le \frac{1}{2}\chi ^2_n+\frac{1}{2}{\widetilde{\theta }}^\text {T}_{n,k}{\widetilde{\theta }}_{n,k} \end{aligned} \end{aligned}$$

(63)

The control $u_k$, the time Caputo fractional derivative of $v_{n}$ and the corresponding update law are as follows

$$\begin{aligned}&u_k=-c_nz_n-z_{n-1}-\theta ^\text{T}_{n,k}\phi _{n,k}(\hat{{\underline{x}}}_n)-l_{n,k}e_1 \end{aligned}$$

(64)

$$\begin{aligned}&{\mathcal {D}}^\alpha _t v_n=-c_iv_n+v_{n-1} \end{aligned}$$

(65)

$$\begin{aligned}&{\mathcal {D}}^\alpha _t\theta _{n,k}=\xi _{n,k}[\chi _n\varpi _n\phi _{n,k}(\hat{{\underline{x}}}_n)-\mu _n\theta _{n,k}] \end{aligned}$$

(66)

where $\xi _{n,l}$ is a delta function defined as

$$\begin{aligned} \begin{aligned}\xi _{n,l}= \left\{ \begin{aligned} 1,\quad k=l\\ 0,\quad k\ne l \end{aligned} \right. \end{aligned} \end{aligned}$$

(67)

Substituting (64)–(67) into (60) results in

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V_n&\le -\lambda _n\Vert e\Vert ^2-\sum ^n_{i=1}(c_i-2)\chi ^2_i+\sum ^n_{i=1}\left( \frac{1}{2}-{\varLambda }_{i,k}\right) \zeta ^2_i\\&\quad +\left( \frac{1}{2}-\frac{\mu _i}{\varpi _i}+\Vert P\Vert ^2\right) \sum _{i=1}^n{\widetilde{\theta }}^\text{T}_{i,k}{\widetilde{\theta }}_{i,k}+M_n \end{aligned} \end{aligned}$$

(68)

where $\lambda _n=\lambda _{n-1}-\sigma ^2 l^2_{n,k}-\frac{1}{2}l^2_{n,k}$, $M_n=M_{n-1}+l^2_{n,k}\sigma ^2{\hat{x}}^2_1+\eta ^2l^2_{n,k}+\frac{1}{2}\sum ^n_{i=1}\frac{\mu _i}{\varpi _i}{\theta ^*}^\text {T}_{i,k}\theta ^*_{i,k}$ and inequality ${\widetilde{\theta }}^\text {T}_{i,k}\theta _{i,k}\le -\frac{1}{2}{\widetilde{\theta }}^\text {T}_{i,k}{\widetilde{\theta }}_{i,k}+\frac{1}{2}\widetilde{\theta ^*}^\text {T}_{i,k}{\widetilde{\theta }}^*_{i,k}$ is used.

Define $V=V_n$, $a=\min _{k}\{\lambda _n/\lambda _{\max }(P),c_i-2,1-\frac{\mu _i}{\varpi _i}+2\Vert P\Vert ^2,1-2{\varLambda }_{i,k},i=1,2,\ldots ,n\}$, $c=\max _k\{\Vert P\Vert ^2\Vert \varepsilon ^*_k \Vert ^2 +\eta ^2+\Vert P\Vert ^2\Vert L_k\Vert ^2+\sum _{i=1}^n\sigma ^2{\hat{x}}^2_1l^2_{i,k}+\sum _{i=1}^n\eta ^2 l^2_{i,k}+\frac{1}{2}\sum ^n_{i=1} \frac{\mu _i}{\varpi _i}{\theta ^*}^\text {T}_{i,k}\theta ^*_{i,k},i=1,2,\ldots ,n\}$ and $V^k_{\theta }=\frac{1}{2}\sum _{l\ne k\in N}{\widetilde{\theta }}^\text {T}_{i,l}{\widetilde{\theta }}_{i,l}$. Then, (66) can be further written as

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V\le -a(V-V^k_{\theta })+c \end{aligned} \end{aligned}.$$

(69)

Remark 2

It is hard to design common Lyapunov functions as well as common virtual control functions for the existence of switched adaptive parameters. From (32), (46), (59), (40) and (53) it can be observed that by using the sum function and hyperbolic tangent function, the Lyapunov function and common virtual control functions are successfully designed and ensure their continuity.

Remark 3

Repeated differentiations of virtual control functions can lead to complexity explosion, so the filters are introduced to solve this problem. The filters with switched parameters have been designed in this paper, which can reduce the conversation of common control scheme.

Remark 4

The backstepping control method of a class of fractional-order nonlinear system is also proposed in paper [35]. It applies the stability analysis of integer-order lyapunov method to the known fractional-order system. However, in this paper, the system model may be completely unknown. In addition, the fractional-order adaptive law is proposed to analyze the stability by using the stability criterion.

5 Stability analysis

Theorem 1

Under Assumptions 1–2, considering the fractional-order switched nonlinear system (1) with output quantization. The filters (28), the control laws (64) and the adaptive laws, (42), (55) and (66) are designed. By adjusting the design parameters properly, the closed-loop signals are uniformly and bounded, and all error variables can be arbitrarily small.

Proof

According to (69), it is obtained that

$$\begin{aligned} \begin{aligned} {\mathcal {D}}^\alpha _t V+m(t)=-aV(t)+c \end{aligned} \end{aligned}$$

(70)

where $m(t)\ge 0$. The Laplace transform of (70) is equal to

$$\begin{aligned} \begin{aligned} V(s)=\frac{s^{\alpha -1}}{s^{\alpha }+c}V(0)+\frac{c}{s(s^\alpha +c)}-\frac{M(s)}{s^\alpha +c} \end{aligned} \end{aligned}$$

(71)

where V(s) and M(s) are the Laplace transforms of V(t) and m(s), respectively. By formula (13), one gets

$$\begin{aligned} \begin{aligned} V(t)&=V(0)E_{\alpha ,1}(-at^\alpha )+ct^\alpha E_{\alpha ,1+\alpha }(-at^\alpha )\\&\quad -\,m(t)*t^{-1}E_{\alpha ,0}(-at^\alpha ) \end{aligned} \end{aligned}$$

(72)

where $*$ shows the location of the convolution operator. Noticing that m(t) and $t^{-1}E_{\alpha ,0}(-at^\alpha )$ are nonnegative functions, then one can obtain

$$\begin{aligned} \begin{aligned} \vert V(t)\vert =\vert V(0)\vert E_{\alpha ,1}(-at^\alpha )+at^\alpha E_{\alpha ,1+\alpha }(-at^\alpha ) \end{aligned} \end{aligned}$$

(73)

Noting that $\arg (-at^\alpha )=-\pi$, $\vert -at^\alpha \vert \ne 0$ for all $t\ne 0$ and $\alpha \in (0,1]$ and Lemma 5, there’s a positive constant C such that

$$\begin{aligned} \begin{aligned} \vert E_{\alpha ,1}(-at^\alpha ) \vert \le \frac{C}{1+at^\alpha } \end{aligned} \end{aligned}$$

(74)

Then, one gets

$$\begin{aligned} \begin{aligned} \lim _{t\rightarrow \infty }\vert V(0)\vert E_{\alpha ,1}(-at^\alpha )=0 \end{aligned} \end{aligned}$$

(75)

Therefore, for each $\iota$, there exists a constant $t_1>0$ such that $t>t_1$, which means that

$$\begin{aligned} \begin{aligned} \vert V(0)\vert E_{\alpha ,1}(-at^\alpha )<\frac{\iota }{3} \end{aligned} \end{aligned}$$

(76)

At the same time, through Lemma 4, it is obtained that

$$\begin{aligned} \begin{aligned} E_{\alpha ,1+\alpha }(-at^\alpha )=\frac{1}{{\varGamma }(1)at^\alpha }+o\left( \frac{1}{\vert at^\alpha \vert ^{1+1}}\right) \end{aligned} \end{aligned}$$

(77)

From (77), for each $\iota >0$, there is a positive constant $t_2$, which makes

$$\begin{aligned} \begin{aligned} ct^\alpha E_{\alpha ,1+\alpha }(-at^\alpha )\le \frac{c}{a}+\frac{\iota }{3} \end{aligned} \end{aligned}$$

(78)

For all $t>t_2$. One can adjust the parameters to satisfy $\frac{c}{a}<\frac{\iota }{3}$, therefore, one gets

$$\begin{aligned} \begin{aligned} \vert V(t)\vert <\iota \end{aligned} \end{aligned}$$

(79)

Through (79), it is shown that $x_i$, $z_i$, $v_i$, $\chi _i$ and $\theta _i,k$ are semi-globally uniformly ultimately bounded and $\chi _i<\sqrt{2\iota }$.

Remark 5

In this paper, the integer-order non-strict system is extended to fractional-order systems. By designing fractional-order control and the related adaptive law, the fractional-order stability criterion of the system is established. The fractional-order stability criterion is established.

Remark 6

Through (78) and (79), one knows that the final limit of tracking error depends on a, c. It is clear that the decrease of $\iota$ can be achieved through decreasing c or increasing a. Therefore, one can properly adjust the design parameters to decrease the tracking error.

Remark 7

Neural network control [36, 37] and fuzzy logic control [38] have many same characteristics. They can control a process individually or in combination. Compared with neural network control, the advantage of fuzzy logic system design is fast and simple. Once people determine the fuzzy variables and fuzzy sets according to experience, the model of fuzzy logic control system can be completed in a short time. Neural network scheme can be designed as similar performance control, but it needs huge amount of fast computing power. Because the fuzzy criteria depend too much on the subjective factors of human beings, it is a very worthy choice to combine them to form the fuzzy neural network system, which is also the future work of this paper.

6 Simulation Example

In this section, a fractional-order gyroscope is simulated to prove the validity of our main results.

$$\begin{aligned} \begin{aligned} \left\{ \begin{aligned}&{\mathcal {D}}^\alpha _t x_1=x_2\\&{\mathcal {D}}^\alpha _t x_2=-p_{\delta (t)}(t)x_1-b_{1,\delta (t)}x_1-b_{2,\delta (t)}x^3_2\\&\quad \quad \quad \ \, +q_{\delta (t)}(t)x^3_1+u_{\delta (t)}+d(t)_{\delta (t)}\\ \end{aligned} \right. \end{aligned} \end{aligned}$$

(80)

where $\delta (t)\in \{1,2\}$, $p_{\delta }(t)=\frac{m^2_\delta }{4}-f_\delta \sin (wt)$, $q_{\delta }(t)=\frac{m^2_\delta }{12}-\frac{d}{6}-\frac{f_\delta \sin (wt)}{6}$, $m^2_1=100$, $m^2_2=50$, $d_1=1$, $d_2=1$, $w=25$, $f_1=35.5$, $f_2=45.5$. $b_{1,1}=2$$b_{1,2}=1$, $b_{2,1}=2$, $b_{2,2}=1$. The additive disturbance is $d_1(t)=0.05\sin (25t)$ and $d_2(t)=0.03\cos (25t)$.

Choosing fuzzy membership functions as

$$\begin{aligned} \mu _{F^l_{i,1}}({{x}}_i)&=\exp \left[ -\frac{({{x}}_i-0.2+l)^2}{4}\right] ,i=1,2,l=1,2,3,4,5.\\ \mu _{F^l_{i,2}}({{x}}_i)&=\exp \left[ -\frac{({{x}}_i-0.5+l)^2}{4}\right] ,i=1,2,l=1,2,3,4,5.\\ \end{aligned}$$

Defining fuzzy basis functions as

$$\begin{aligned}&\varphi _{1l,k}(x_1)=\frac{\mu _{F^l_{1,k}}}{{\varSigma }^5_{j=1}\mu _{F^j_{1,k}}},\nonumber \\&\varphi _{2l,k}( {\underline{x}}_2)=\frac{\mu _{F^l_{i,k}}...\mu _{F^l_{i,k}}}{{\varSigma }^5_{k=1}\mu _{F^l_{i,k}}...\mu _{F^l_{i,k}}}. \end{aligned}$$

(81)

where $l=1,2,3,4,5$ and $k=1,2$.

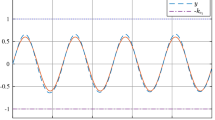
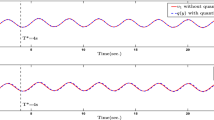
The initial state of system is $x(0)=[0.01, 0.01]^\text {T}$, and the fractional order be $\alpha =0.9$. The control gains for the controller are selected as $c_1=c_2=5$, $\varpi _1=10$, $\varpi _2=5$, $\mu _1=\mu _2=1$, $\eta =0.0002$ and $\sigma =0.5$. By solving the LMI. one can obtain $L_1=[17.0116, 39.5777]^\text{T}$ and $L_2=[16.9416, 41.2860]^\text{T}$. The simulation results are given in Figs. 1, 2, 3, 4, 5, 6, 7. The trajectory of the state variable $x_1$, the observation value ${\hat{x}}_1$ and the quantization output q(y) are shown in Fig. 1. The quantization error varies with the fluctuation of the output signal and they are positively correlated. However, when the output signal increases, the tracking error can still converge to the small neighborhood of the origin, which means that the quantization error can be compensated successfully. Fig. 2 expresses the trajectories of $x_2$ and ${\hat{x}}_2$. Fig. 3 shows the error trajectories. As one can see, the tracking errors converge on the small neighborhood of the origin. The trajectories of the tracking errors $z_i$ and the auxiliary variables $v_i$ are shown in Figs. 4 and 5. The control signal u is plotted in Fig. 6. Figure 7 shows the demonstration of switching signal. The simulation results show that the control scheme has good tracking performance and high reliability.

Fig. 1

The trajectories of $x_1$, ${\hat{x}}_1$ and q(y)

Fig. 2

The trajectories of $x_2$ and ${\hat{x}}_2$

Fig. 3

Observation errors $e_1$ and $e_2$

Fig. 4

The trajectories of $z_1$ and $z_2$

Fig. 5

The trajectories of $v_1$ and $v_2$

Fig. 6

The trajectory of control u

Fig. 7

Switching signal

7 Conclusion

For a class of uncertain fractional-order nonlinear switched systems, an observer-based adaptive output feedback tracking control scheme has been proposed under the framework of adaptive backstepping control technology. At the same time, the output quantization of the system has been also considered in the control scheme. In order to obtain a good approximation of the system uncertainty, the serial-parallel estimation model has been added to backstepping procedure. In addition, an effective switched fractional-order filter has been designed by DSC technology to overcome the problem of “explosion of complexity”. The simulation results show that the controller designed in this paper ensures that all signals of the closed-loop system are bounded when switching occurs, and the tracking error converges to a small neighborhood of the origin.