1 Introduction

Multiple attribute decision making (MADM) is one of meaningful and significant behaviors which selects optimal alternative from several candidates with respect to finite attributes according to evaluation information given by decision makers (DMs). It has been widely focused and largely applied in the various fields, such as the determination of importance ratings of customer requirements [1], assessment of the renewable energies [2], evaluation of water conservancy project [3], research and development (R&D) project selection [4], investment projects’ selection for company [5], selection of intelligent medical hospital [6] and so on. Since the complexity of decision making and fuzziness of human thinking, one of the challenges in MADM problems is to correctly depict DMs’ evaluation. As an extension of hesitant fuzzy sets (HFSs), hesitant fuzzy linguistic term sets (HFLSs) were introduced by Rodriguez et al. [7] to quantitatively express experts’ judgement with two or more linguistic terms in case of hesitancy when DMs evaluate in decision making. Although HFLSs are powerful, they merely consider different importances/occurance probabilities/preference degrees for all possible linguistic variables. To mitigate this issue, Pang et al. [8] proposed probabilistic linguistic term sets (PLTSs), which can simultaneously present the hesitancy and preference degree of DMs, to reflect evaluators’ opinions with several linguistic terms and corresponding probabilistic distributions. Then, scholars have turned to research MADM problems with probabilistic linguistic preference information called probabilistic linguistic MADM (PLMADM) problems [9,10,11,12,13,14,15,16].

In the PLMADM process, the aggregation of evaluation information is an essential step, and aggregation operators have been investigated increasingly. Most classical and popular aggregation operators are probabilistic linguistic arithmetic averaging (PLA) operator and probabilistic linguistic geometric (PLGeo) operator developed by Pang et al. [8]. A strict assumption of these two operators is that attributes are seemed as independent when using PLA or/and PLGeo operators. However, attributes in the real applications are interrelated but not independent. Some researchers then focus on aggregation operators which are able to capture the interrelationship among input arguments in PLMADM problems. Probabilistic linguistic geometric Bonferroni mean (PLGeoBM) operator [17] and probabilistic linguistic Heronian mean (PLHM) operator [18] have been gradually developed to consider interrelationship between arbitrary two input arguments. Besides, Liu and Li [19] designed probabilistic linguistic geometric Maclaurin symmetric mean (PLGeoMSM) operator to capture correlation among any three arguments. However, there may exist many situations in which multi-input arguments instead of three or two arguments interrelate with each other in PLMADM problems. Hence, it is urgent to introduce more feasible and general operators to capture interrelationships among any number of input arguments. Dual Muirhead mean (DMM) operator is just the suitable one which enables to consider the interrelationships of multi-input arguments by a parameter vector and is a generalization of some existing aggregation operators, such as averaging operator, geometric operator, geometric BM operator, geometric MSM operator, etc. At present, DMM operators have been populated and extended in the light of several fuzzy sets, such as hesitant fuzzy sets [20], Pythagorean fuzzy sets [21], interval-valued probabilistic hesitant fuzzy sets [22], q-rung orthopair fuzzy sets [23], T-spherical fuzzy sets [24], etc. With the strength of generalization and flexibility, therefore, DMM operators were improved in this paper to fuse probabilistic linguistic preference information.

The information aggregated through above operators usually was utilized to determine the final decision making for DMs with the aid of MADM approaches. VIKORFootnote 1 method, proposed by Opricovic [25], is one of effective ways to solve MADM problems especially with incompatible and noncommensurable information [26]. VIKOR mainly concentrates on ranking and selecting from a collection of candidates in the presence of conflicting criterion. It also maximizes the majority’s group utility as well as minimizes the individual regret for minority so as to offer DMs a compromised solution [27,28,29,30]. Owing to its features and superiority, we introduce VIKOR method based on PLTSs and design a powerful decision-making approach to address PLMADM problems.

Based on above analysis, it is necessary and valuable to investigate relative theory of PLTS since it can genuinely depict psychology of evaluators in MADM process. Besides, DMM operators offer a quite flexible function to aggregate evaluations and solve MADM problems more appropriately, and VIKOR method can address conflicts among attributes as well as give a compromised solution. Therefore, it is extremely worth processing PLMADM problems by extending DMM operators to the probabilistic linguistic environment and exploring a decision-making approach based on VIKOR method. The innovations of this paper are summarized as follows:

  1. 1.

    DMM operators are introduced and improved in this paper to capture interrelationships among any number of multi-input arguments in PLMADM problems;

  2. 2.

    We define two novel aggregation operators based on DMM operators, i.e., probabilistic linguistic DMM (PLDMM) operator and probabilistic linguistic weighted DMM (PLWDMM), and further investigate their corresponding propositions, theorems as well as properties;

  3. 3.

    A powerful decision-making approach based on PLWDMM operator and VIKOR has been designed to address complex PLMADM problems.

The rest of the paper is organized as follows. Section 2 briefly reviews the relevant studies. Aggregation operators (i.e., PLDMM and PLWDMM), and their corresponding definitions, propositions, theorems as well as properties are developed in Sect. 3. A novel decision-making approach based on PLWDMM aggregation operator and VIKOR is designed to solve a complex PLMADM problem in Sect. 4. In Sect. 5, an illustrative example is provided to explain the validity and feasibility of the proposed decision-making method. Finally, Sect. 6 concludes the paper and elaborates on future studies.

2 Preliminaries

In this section, we briefly review some basic concepts, including probabilistic linguistic term sets (PLTSs), Muirhead mean (MM), and dual Muirhead mean (DMM).

2.1 Probabilistic Linguistic Term Sets (PLTSs)

Probabilistic linguistic term set (PLTS) is a kind of useful extension of hesitant fuzzy linguistic term set (HFLTS), which considers the multiple preference information and their corresponding occurrence probabilities simultaneously. In the following, we introduce some concepts of PLTSs, relative operation and comparison laws.

Definition 1

[8] Let \(S=\left\{ S_{t}|t=-\tau ,\dots ,-1,0,1,\dots ,\tau \right\}\) be a linguistic term set. Then, a PLTS is defined as

$$\begin{aligned} \begin{aligned} L(P)=&\left\{ L^{(k)}\left( P^{(k)}\right) \big |L^{(k)}\in S, r^{(k)}\in t, P^{(k)}\ge 0,\right. \\&\left. k=1,2,\dots ,\#L(P),\sum _{k=1}^{\#L(P)}P^{(k)}\leqslant 1\right\} , \end{aligned} \end{aligned}$$
(1)

where \(L^{(k)} \left( P^{(k)} \right)\) is the linguistic term \(L^{(k)}\) associated with probability \(P^{(k)}\), \(r^{(k)}\) is the subscript of \(L^{(k)}\) and \(\#L(P)\) is the number of all linguistic terms in L(P).

To facilitate the information fusion as well as maintain the consistency, Gou and Xu [31] and Bai et al. [32] have developed the equivalent transformation functions of L(P) as follows.

Definition 2

[31, 32] Let \(S=\left\{ S_{t}|t=-\tau ,\dots ,-1,0,1,\right.\)  \(\left. \dots ,\tau \right\}\) be a linguistic term set. L(P) is a PLTS. Then, equivalent transformation function of L(P) is given as

$$\begin{aligned} \begin{aligned} g:[-\tau ,\tau ]\rightarrow [0,1], g\left( L(P)\right)&=\left\{ g\left( L^{(k)}\left( P^{(k)}\right) \right) \right. \\&\left. \left[ \frac{r^{(k)}}{2\tau }+\frac{1}{2}\right] \left( P^{(k)}\right) \bigg |r^{(k)}\in [-\tau ,\tau ]\right\} \\&=L_\gamma (P). \end{aligned} \end{aligned}$$
(2)
$$\begin{aligned} \begin{aligned} g^{-1}:[0,1] \rightarrow [-\tau ,\tau ],g^{-1}\left( L_\gamma (P)\right)&=\left\{ g^{-1}\left( L_{\gamma ^{(k)}}\left( P^{(k)}\right) \right) \right. \\&\left. S_{(2\gamma -1)\tau }\left( P^{(k)}\right) \bigg |\gamma \in [0,1]\right\} \\&=L(P). \end{aligned} \end{aligned}$$
(3)

Definition 3

[31, 32] Let \(S=\left\{ S_{t}|t=-\tau ,\dots ,-1,0,1,\right.\)  \(\left. \dots ,\tau \right\}\) be a linguistic term set. \(\lambda\) be a positive real number. L(P), \(L_{1}(P_{1})\) and \(L_{2}(P_{2})\) be three PLTSs, which satisfy the following operation laws:

  1. (i)

    \(\begin{aligned} \begin{aligned}&L_1(P_{1})\oplus L_2(P_{2})\\&=g^{-1}\left( \bigcup _{\eta _1^{(i)}\in g(L_1),\eta _2^{(j)}\in g(L_2)}\left\{ \left( \eta _1^{(i)}+\eta _2^{(j)}-\eta _1^{(i)}\eta _2^{(j)}\right) \left( P_1^{(i)}P_2^{(j)}\right) \right\} \right) ,\\&i=1,2,\dots ,\#L_1(P_{1}),j=1,2,\dots ,\#L_2(P_{2}); \end{aligned} \end{aligned}\)

  2. (ii)

    \(\begin{aligned} \begin{aligned}&L_1(P_{1})\otimes L_2(P_{2})\\ =\,&g^{-1}\left( \bigcup _{\eta _1^{(i)}\in g(L_1),\eta _2^{(j)}\in g(L_2)}\left\{ \left( \eta _1^{(i)}\eta _2^{(j)}\right) \left( P_1^{(i)}P_2^{(j)}\right) \right\} \right) ,\\&i=1,2,\dots ,\#L_1(P_{1}),j=1,2,\dots ,\#L_2(P_{2}); \end{aligned} \end{aligned}\)

  3. (iii)

    \(\begin{aligned} \begin{aligned} \lambda L(P)=\,&g^{-1}\left( \bigcup _{\eta ^{(k)}\in g(L)}\left\{ \left( 1-\left( 1-\eta ^{(k)}\right) ^\lambda \right) \left( P^{(k)}\right) \right\} \right) ,\\&k=1,2,\dots ,\#L(P); \end{aligned} \end{aligned}\)

  4. (iv)

    \(\begin{aligned} \begin{aligned} \left( L(P)\right) ^\lambda =\,&g^{-1}\left( \bigcup _{\eta ^{(k)}\in g(L)}\left\{ \left( \eta ^{(k)}\right) ^\lambda \left( P^{(k)}\right) \right\} \right) ,\\&k=1,2,\dots ,\#L(P). \end{aligned} \end{aligned}\)

For the PLTS, it cannot be compared when the numbers of linguistic terms are unequal. Pang et al. [8] has defined normalization of PLTSs as follows.

Definition 4

[8] Let \(L_1(P)=\left\{ L_1^{(k)}\left( P_1^{(k)}\right) \big |k=1,2,\dots ,\right.\) \(\left. \#L_1(P)\right\}\) and \(L_2(P)=\left\{ L_2^{(k)}\left( P_2^{(k)}\right) \big |k=1,\dots ,\#L_2(P)\right\}\) be arbitrary two PLTSs, \(\#L_1(P)\) and \(\#L_2(P)\) are their relative numbers of linguistic terms, separately. Generally, \(\#L_1(P)\ne \#L_2(P)\). Therefore, we add \(\#L_1(P)-\#L_2(P)\) linguistic terms to \(L_2(P)\) if \(\#L_1(P)>\#L_2(P)\) so as to unify the numbers of linguistic terms in \(L_1(P)\) and \(L_2(P)\). The added linguistic terms are the smallest ones in \(L_2(P)\) following by zero probabilities.

The score function and deviation degree have proposed by Pang et al. [8] to help DMs compare arbitrary two PLTSs.

Definition 5

[8] Let \(L(P)=\left\{ L^{(k)}\left( P^{(k)}\right) \big |k=1,2,\dots ,\right.\) \(\left. \#L(P)\right\}\) be a PLTS, and \(r^{(k)}\) be the subscript of linguistic term \(L^{(k)}\). Then, the score of L(P) is defined as

$$\begin{aligned} E\left( L(P)\right) =S_{\tilde{\alpha }}, \end{aligned}$$
(4)

where \({\widetilde{\alpha }}=\left. {\sum _{k=1}^{\#L(P)}{r^{(k)}\left( P^{(k)}\right) }}\bigg /{\sum _{k=1}^{\#L(P)}P^{(k)}}\right.\), and the deviation degree of L (P) is

$$\begin{aligned} \sigma \left( L(P)\right) =\left. \left( \sum _{k=1}^{\#L(P)}\left( P^{(k)}\left( r^{(k)}-\tilde{\alpha }\right) \right) ^{2}\right) ^{1/2}\bigg /{\sum _{k=1}^{\#L(P)}P^{(k)}}\right. {.} \end{aligned}$$
(5)

A preorder for PLTSs can be constructed through the score and deviation degree formulas. Let \(L_{1}(P_{1})\) and \(L_{2}(P_{2})\) are arbitrary two PLTSs, and the detailed comparison laws are denoted as follows [8]:

  1. 1.

    if \(E(L_1(P_{1}))> E(L_2(P_{2}))\), then \(L_1(P_{1}) > L_2(P_{2})\);

  2. 2.

    if \(E(L_1(P_{1}))< E(L_2(P_{2}))\), then \(L_1(P_{1}) < L_2(P_{2})\);

  3. 3.

    if \(E(L_1(P_{1})) = E(L_2(P_{2}))\), then

    1. a.

      if \({\sigma \left( L_1(P_{1})\right) }> {\sigma \left( L_2(P_{2})\right) }\), then \(L_1(P_{1})< L_2(P_{2});\)

    2. b.

      if \({\sigma \left( L_1(P_{1})\right) }< {\sigma \left( L_2(P_{2})\right) }\), then \(L_1(P_{1})> L_2(P_{2});\)

    3. c.

      if \({\sigma \left( L_1(P_{1})\right) }={\sigma \left( L_2(P_{2})\right) }\), then \(L_1(P_{1})\sim L_2(P_{2}).\)

Pang et al. [8] also designed Euclidean distance measure between any two PLTSs. The detailed definition is presented as follows.

Definition 6

[8] Let \(L_1(P)=\left\{ L_1^{(k)}\left( P_1^{(k)}\right) \big |k=1,2,\dots ,\right.\) \(\left. \#L_1(P)\right\}\) and \(L_2(P)=\left\{ L_2^{(k)}\left( P_2^{(k)}\right) \big |k=1,\dots ,\#L_2(P)\right\}\) be arbitrary two PLTSs, the Euclidean distance measure between \(L_1(P_1)\) and \(L_2(P_2)\) is described as:

$$\begin{aligned} d\left( L_1(P_1),L_2(P_2)\right) =\sqrt{\frac{\sum _{k=1}^{\#L_1(P_1)}\left( r_1^{(k)}P_1^{(k)}-r_2^{(k)}P_2^{(k)}\right) ^2}{\#L_1(P_1)}}, \end{aligned}$$
(6)

where \(\#L_1(P_1)=\#L_2(P_2)\). \(r_1^{(k)}\) and \(r_2^{(k)}\) are separately subscripts of \(L_1^{(k)}\) and \(L_2^{(k)}\).

2.2 Muirhead Mean (MM)

Since the superiority of capturing the interrelationship among multi-input arguments, the MM operator is regarded as an available aggregation method. The definition of MM is presented as follows.

Definition 7

[33] Let \(a_{j} (j=1,2,\dots ,n)\) be a collection of real numbers, \(P=(p_1,p_2,\dots ,p_n)\in R^n\) be a parameter vector which denotes the risk appetite values, then MM is given as

$$\begin{aligned} MM^{P}(a_1,a_2,\dots ,a_n)=\left( \frac{1}{n!}\sum _{\vartheta \in S_{n}}\prod _{j=1}^{n}a_{\vartheta (j)}^{p_j}\right) ^{\frac{1}{\sum _{j=1}^{n}{p_j}}}, \end{aligned}$$
(7)

where \(\vartheta (j)(j=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\), and \(S_n\) is the set of all possible permutations of \((1,2,\dots ,n)\).

2.3 Dual Muirhead Mean (DMM)

Definition 8

[34, 35] Let \(a_{j} (j=1,2,\dots ,n)\) be a collection of real numbers, \(P=(p_1,p_2,\dots ,p_n)\in R^n\) be a parameter vector which denotes the risk appetite values, then DMM is given as

$$\begin{aligned} DMM^{P}(a_1,a_2,\dots ,a_n)=\frac{1}{\sum _{j=1}^{n}{p_j}}\left( \prod _{\vartheta \in S_{n}}\sum _{j=1}^{n}\left( p_{j}a_{\vartheta (j)} \right) \right) ^{\frac{1}{n!}}, \end{aligned}$$
(8)

where \(\vartheta (j)(j=1,2,\dots ,n)\) be any permutation of \((1,2,\dots,n),\)

and \(S_n\) is the set of all possible permutations of \((1,2,\dots ,n)\).

3 Probabilistic Linguistic Dual Muirhead Mean Operators

We extend the traditional DMM operator to appropriate the probabilistic linguistic preference environment. Aggregation operators, i.e., PLDMM operator and PLWDMM operator, and their corresponding definitions, propositions, theorems as well as properties are explored detailedly as follows.

3.1 Probabilistic Linguistic Dual Muirhead Mean (PLDMM) Operator

Definition 9

Let \(L_i(P_i)\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\)  \((i=1,2,\dots ,n)\) be n PLTSs, \(P=(p_1,p_2,\dots ,p_n)\) \(\in R^n\) be a parameter vector denoting the risk appetite values. Then, we define PLDMM operator as

$$\begin{aligned} \begin{aligned}&PLDMM^P(L_1(P_1),\dots ,L_i(P_i),\dots ,L_n(P_n))\\ =&{\frac{1}{\sum _{i=1}^{n}p_i}}\left( \otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_i\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \right) \right) ^{\frac{1}{n!}}, \end{aligned} \end{aligned}$$
(9)

where \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\), and \(S_n\) is the set of all possible permutations of \((1,2,\dots ,n)\).

We can obtain some outcomes from Definition 9 by means of operation laws of PLTSs.

Proposition 1

Suppose \(L_i(P_i)=\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots ,\)  \(\#L_i(P_i)\}(i=1,2,\dots ,n)\) be n PLTSs, \(p_i(i=1,2,\dots ,n)\) is arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \\&=g^{-1}\left( \bigcup _{\eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) } \left\{ \left( 1-\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \left( P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(10)

Proof

With the aid of operation law (iii) depicted in Definition 3, it is easy to demonstrate the Proposition 1 always holds. \(\square\)

Proposition 2

Suppose \(L_i(P_i)=\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots ,\)  \(\#L_i(P_i)\}(i=1,2,\dots ,n)\) be n PLTSs, \(p_i(i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&\oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \left( \prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(11)

Proof

In the light of the result of Proposition 1 and the operation law (i) of Definition 3, we can compute

$$\begin{aligned} \begin{aligned}&p_{1}\left( L_{\vartheta (1)}\left( P_{\vartheta (1)}\right) \right) \oplus p_{2}\left( L_{\vartheta (2)}\left( P_{\vartheta (2)}\right) \right) \\ =\,&g^{-1}\left( \bigcup _{\eta _{\vartheta (1)}^{(k)}\in g\left( L_{\vartheta (1)}\right) }\left\{ \left( 1-\left( 1-\eta _{\vartheta (1)}^{(k)}\right) ^{p_1}\right) \left( P_{\vartheta (1)}^{(k)}\right) \right\} \right) \\&\oplus g^{-1}\left( \bigcup _{\eta _{\vartheta (2)}^{(k)}\in g\left( L_{\vartheta (2)}\right) } \left\{ \left( 1-\left( 1-\eta _{\vartheta (2)}^{(k)}\right) ^{p_2}\right) \left( P_{\vartheta (2)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\eta _{\vartheta (1)}^{(k)}\in g\left( L_{\vartheta (1)}\right) ,\eta _{\vartheta (2)}^{(k)}\in g\left( L_{\vartheta (2)}\right) }\right. \\&\left. \left\{ \left( 1-\left( 1-\eta _{\vartheta (1)}^{(k)}\right) ^{p_1}\left( 1-\eta _{\vartheta (2)}^{(k)}\right) ^{p_2}\right) \left( P_{\vartheta (1)}^{(k)}P_{\vartheta (2)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1, 2 \end{array}}\left\{ \left( 1-\prod _{i=1}^2\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \left( \prod _{i=1}^{2}P_{\vartheta (i)}^{(k)}\right) \right\} \right) \end{aligned} \end{aligned}$$

then we have

$$\begin{aligned} \begin{aligned}&\oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \left( \prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$

Hence, we complete the proof of Proposition 2. \(\square\)

Proposition 3

Suppose \(L_i(P_i)=\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots ,\)  \(\#L_i(P_i)\}(i=1,2,\dots ,n)\) be n PLTSs, \(p_i(i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&\otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(12)

Proof

From the operation law (ii) in Definition 3 and Proposition 2, we can compute

$$\begin{aligned} \begin{aligned}&\left( \oplus _{i=1}^{n}p_{i}\left( L_{1(i)}\left( P_{1(i)}\right) \right) \right) \otimes \left( \oplus _{i=1}^{n}p_{i}\left( L_{2(i)}\left( P_{2(i)}\right) \right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{1(i)}^{(k)}\in g\left( L_{1(i)}\right) \\ i=1,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^n\left( 1-\eta _{1(i)}^{(k)}\right) ^{p_i}\right) \left( \prod _{i=1}^{n}P_{1(i)}^{(k)}\right) \right\} \right) \\&\otimes g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{2(i)}^{(k)}\in g\left( L_{2(i)}\right) \\ i=1,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^n\left( 1-\eta _{2(i)}^{(k)}\right) ^{p_i}\right) \left( \prod _{i=1}^{n}P_{2(i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{1(i)}^{(k)}\in g\left( L_{1(i)}\right) , \eta _{2(i)}^{(k)}\in g\left( L_{2(i)}\right) \\ i=1,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( 1-\prod _{i=1}^n\left( 1-\eta _{1(i)}^{(k)}\right) ^{p_i}\right) \left( 1-\prod _{i=1}^n\left( 1-\eta _{2(i)}^{(k)}\right) ^{p_i}\right) \left( \prod _{i=1}^{n}P_{1(i)}^{(k)}\prod _{i=1}^{n}P_{2(i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ \vartheta =1,2; i=1,\dots ,n \end{array}}\left\{ \left( \prod _{\vartheta =1}^{2}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) \left( \prod _{\vartheta =1}^{2}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) \end{aligned} \end{aligned}$$

and we get

$$\begin{aligned} \begin{aligned}&\otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \right) \\&=g^{-1}\left( \ !\bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(13)

Therefore, the statement of Proposition 3 holds. \(\square\)

Proposition 4

Suppose \(L_i(P_i)=\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots ,\)  \(\#L_i(P_i)\}(i=1,2,\dots ,n)\) be n PLTSs, \(p_i(i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&\left( \otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \right) \right) ^{\frac{1}{n!}}\\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(14)

Proof

In accordance with the result of Proposition 3 and operation law (iv) in Definition 3, it is easy to prove Proposition 4 always holds. \(\square\)

Theorem 1

Suppose \(L_i(P_i)=\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots ,\)  \(\#L_i(P_i)\}(i=1,2,\dots ,n)\) be n PLTSs, \(p_i(i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then, aggregated result by Definition 9 is shown as

$$\begin{aligned} \begin{aligned}&PLDMM^P(L_1(P_1),\dots ,L_i(P_i),\dots ,L_n(P_n))\\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( 1-\left( 1-\left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\right) ^{\frac{1}{\sum _{i=1}^{n}p_i}}\right) \right. \right. \\&\left. \left. \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(15)

Proof

According to the outcomes of Proposition 4, Definition 9 and operation law (iii) described in Definition 3, we have

$$\begin{aligned} \begin{aligned}&PLDMM^P(L_1(P_1),\dots ,L_i(P_i),\dots ,L_n(P_n))\\ =&{\frac{1}{\sum _{i=1}^{n}p_i}}\left( \otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_i\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) \right) \right) ^{\frac{1}{n!}}\\ =&{\frac{1}{\sum _{i=1}^{n}p_i}}g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( 1-\left( 1-\left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^n\left( 1-\eta _{\vartheta (i)}^{(k)}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\right) ^{\frac{1}{\sum _{i=1}^{n}p_i}}\right) \right. \right. \\&\left. \left. \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$

\(\square\)

So, we complete the proof of Theorem 1.

Next, we begin to investigate properties of PLDMM operator and deduce four corollaries.

Corollary 1

(Monotonity). Let \(L(P)_a=\left\{ L_1(P_1)_a,\dots ,\right.\) \(\left. L_n(P_n)_a\right\}\) and \(L(P)_b=\left\{ L_1(P_1)_b,\dots ,L_n(P_n)_b\right\}\) be arbitrary two PLTSs, \(P=(p_1,p_2,\dots ,p_n)\in R^n\) be a parameter vector denoting the risk appetite values. For \(\eta _{\vartheta a(i)}^{(k)}\in g(L_{\vartheta a(i)})\), \(\eta _{\vartheta b(i)}^{(k)}\in g(L_{\vartheta b(i)})\), if \(\eta _{\vartheta a(i)}^{(k)}\leqslant \eta _{\vartheta b(i)}^{(k)}\) and \(P_{\vartheta a(i)}^{(k)}\leqslant P_{\vartheta b(i)}^{(k)}\), then we have

$$\begin{aligned}\begin{aligned} PLDMM^P&\left( L_1(P_1)_a,\dots ,L_n(P_n)_a\right) \\&\leqslant PLDMM^P\left( L_1(P_1)_b,\dots ,L_n(P_n)_b\right) . \end{aligned}\end{aligned}$$

Corollary 2

(Idempotency). If \(L_i{P_i}=L(P)=\left\{ L^{(k)}\left( P^{(k)}\right)\right.\)

\(\big |L^{(k)}\in S, r^{(k)}\in t, P^{(k)}\ge 0, k=1,2,\dots ,\#L(P),\) \(\left. \sum _{k=1}^{\#L(P)}P^{(k)}\leqslant 1\right\}\) for all \(i=1,2,\dots ,n\), then we have

$$\begin{aligned} PLDMM^P\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) =L(P). \end{aligned}$$

Corollary 3

(Commutativity). If \(L_i^{'}(P_i^{'})\) be any permutation of \(L_i(P)_i(i=1,2,\dots ,n)\), then we have the relationship:

$$\begin{aligned} \begin{aligned} PLDMM^P&\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\&=PLDMM^P\left( L_1^{'}(P_1^{'}),L_2^{'}(P_2^{'}),\dots ,L_n^{'}(P_n^{'})\right) . \end{aligned} \end{aligned}$$

Corollary 4

(Boundness). Let \(L(P)^{-}=min(L_1(P_1),\)

\(L_2(P_2),\dots ,L_n(P_n))\) and \(L(P)^{+}=max(L_1(P_1),L_2(P_2),\)

\(\dots ,L_n(P_n))\), then we have

$$\begin{aligned} \begin{aligned} PLDMM^P&\left( L(P)^{-},L(P)^{-},\dots ,L(P)^{-}\right) \\&\leqslant PLDMM^P\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\&\leqslant PLDMM^P\left( L(P)^{+},L(P)^{+},\dots ,L(P)^{+}\right) \end{aligned} \end{aligned}$$

In the following, we further explore five special cases of PLDMM operator in accordance with different values of parameter vector P.

Case 1

If parameter vector is \(P=(1,0,\dots ,0)\), then PLDMM operator will reduce to probabilistic linguistic geometric (PLGeo) operator, which is denoted as

$$\begin{aligned} \begin{aligned}&PLDMM^{(1,0,\dots ,0)}\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\ =&\left( \bigotimes _{i=1}^{n}\left( L_i(P_i)\right) \right) ^{\frac{1}{n}}\\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{(i)}^{(k)}\in g\left( L_{(i)}\right) \\ i=1,2,\dots ,n \end{array}} \left\{ \left( \prod _{i=1}^{n}\eta _{(i)}^{(k)}\right) ^{\frac{1}{n}} \left( \prod _{i=1}^{n}P_{(i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(16)

Case 2

If parameter vector is \(P=(\lambda ,0,\dots ,0)\), then PLDMM operator will reduce to probabilistic linguistic generalized geometric (PLGGeo) operator, which is presented as

$$\begin{aligned} \begin{aligned}&PLDMM^{(\lambda ,0,\dots ,0)}\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\ =&\frac{1}{\lambda }\left( \bigotimes _{i=1}^{n}\lambda \left( L_i(P_i)\right) \right) ^{\frac{1}{n}}\\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{(i)}^{(k)}\in g\left( L_{(i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( 1-\left( 1-\left( \prod _{i=1}^{n}\left( 1-\left( 1-\eta _{(i)}^{(k)}\right) ^{\lambda }\right) \right) ^{\frac{1}{n}}\right) ^{\frac{1}{\lambda }}\right) \left( \prod _{i=1}^{n} P_{(i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(17)

Case 3

If parameter vector is \(P=(1,1,0,\dots ,0)\), then PLDMM operator will reduce to probabilistic linguistic geometric Bonferroni mean (PLGeoBM) operator, which is displayed as

$$\begin{aligned} \begin{aligned}&PLDMM^{(1,1,0,\dots ,0)}\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\ =&\frac{1}{2}\left( \bigotimes _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^{n}\left( L_i(P_i)\oplus L_j(P_j)\right) \right) ^{\frac{1}{n(n-1)}}\\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{(i)}^{(k)}\in g\left( L_{(i)},\eta _{(j)}^{(k)}\in g\left( L_{(j)}\right) \right) \\ i,j=1,2,\dots ,n\\ i\ne j \end{array}}\right. \\&\left\{ \left( 1-\left( 1-\left( \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^{n}\left( 1-\left( 1-\eta _{(i)}^{(k)}\right) \left( 1-\eta _{(j)}^{(k)}\right) \right) \right) ^{\frac{1}{n(n-1)}}\right) ^{\frac{1}{2}}\right) \right. \\&\left. \left. \left( \prod _{\begin{array}{c} i,j=1\\ i\ne j \end{array}}^{n}P_{(i)}^{(k)}P_{(j)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(18)

Case 4

If parameter vector is \(P=(\overbrace{1,1,\dots ,1}^{m},\overbrace{0,\dots ,0}^{n-m})\), then PLDMM operator will reduce to probabilistic linguistic geometric Maclaurin Symmetric mean (PLGeoMSM) operator, that is,

$$\begin{aligned} \begin{aligned}&PLDMM^{(\overbrace{1,1,\dots ,1}^{m},\overbrace{0,\dots ,0}^{n-m})}\left( L_1(P_1),\dots ,L_n(P_n)\right) \\ =&\frac{1}{m}\left( \otimes _{1\leqslant i_1< \cdots<i_m \leqslant n}\oplus _{j=1}^{m}\left( L_{i_j}(P_{i_j})\right) \right) ^{\frac{1}{C_n^{m}}}\\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{(i)}^{(k)}\in g\left( L_{(i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left\{ \left( 1-\left( 1-\left( \prod _{1\leqslant i_1< \cdots<i_m \leqslant n}\left( 1-\prod _{j=1}^{m} \left( 1-\eta _{({i_j})}^{(k)}\right) \right) \right) ^{\frac{1}{C_n^{m}}}\right) ^{\frac{1}{m}}\right) \right. \\&\left. \left. \left( \prod _{1\leqslant i_1< \cdots <i_m \leqslant n}\prod _{j=1}^{m}P_{i_j}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(19)

Case 5

If parameter vector is \(P=(1,1,\dots ,1)\) or \(P= (\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})\), then PLDMM operator will reduce to probabilistic linguistic arithmetic averaging (PLA) operator, namely

$$\begin{aligned} \begin{aligned}&PLDMM^{(1,1,\dots ,1)}\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\ =&\frac{1}{n}\left( \oplus _{i=1}^{n}\left( L_i(P_i)\right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{(i)}^{(k)}\in g\left( L_{(i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\left( \prod _{i=1}^{n}\left( 1-\eta _{(i)}^{(k)}\right) \right) ^{\frac{1}{n}}\right) \left( \prod _{i=1}^{n}P_{(i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned} \begin{aligned}&PLDMM^{(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})}\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\ =&\oplus _{i=1}^{n}\left( \frac{1}{n}\left( L_i(P_i)\right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{(i)}^{(k)}\in g\left( L_{(i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\left( \prod _{i=1}^{n}\left( 1-\eta _{(i)}^{(k)}\right) \right) ^{\frac{1}{n}}\right) \left( \prod _{i=1}^{n}P_{(i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(21)

3.2 Probabilistic Linguistic Weighted Dual Muirhead Mean (PLWDMM) Operator

With the consideration of importance of aggregated multi-input arguments, we further define PLWDMM operator in this section.

Definition 10

Let \(L_i{(P_i)}\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\) \((i=1,\dots ,n)\) be n PLTSs, \(P=(p_1,\dots ,p_n)\in R^n\) be a parameter vector denoting the risk appetite values. Suppose that \(\omega _i\) be the weight of input argument \(L_i(P_i)\) such that \(\omega _i\in [0,1]\) and \(\sum _{i=1}^{n}\omega _i=1\). Then, PLWDMM operator is described as

$$\begin{aligned} \begin{aligned}&PLWDMM^P(L_1(P_1),\dots ,L_i(P_i),\dots ,L_n(P_n))\\ =&{\frac{1}{\sum _{i=1}^{n}p_i}}\left( \otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_i\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\right) \right) ^{\frac{1}{n!}}, \end{aligned} \end{aligned}$$
(22)

where \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots,n),\)

and \(S_n\) is the set of all possible permutations of \((1,2,\dots ,n)\).

Based on the Definition 10 and operation laws depicted in Definition 3, we can get the following propositions.

Proposition 5

Suppose \(L_i{(P_i)}\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\) \((i=1,2,\dots ,n)\) be n PLTSs, \(p_i (i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\\&=g^{-1}\left( \bigcup _{\eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) }\left\{ \left( 1-\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \left( P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(23)

Proof

In the light of the result of Proposition 1 and operation law (iv) in Definition 3, we have

$$\begin{aligned} \begin{aligned}&p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\\ =&p_{i}g^{-1}\left( \bigcup _{\eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) } \left\{ \left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\left( P_{\vartheta (i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) }\left\{ \left( 1-\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \left( P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$

So, the statement of Proposition 5 holds. \(\square\)

Proposition 6

Suppose \(L_i{(P_i)}\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\) \((i=1,2,\dots ,n)\) be n PLTSs, \(p_i (i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&\oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\\&=g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_{i}}\right) \left( \prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(24)

Proof

According to outcome of Proposition 5 and operation law (i) in Definition 3, we have

$$\begin{aligned} \begin{aligned}&p_{1}\left( L_{\vartheta (1)}\left( P_{\vartheta (1)}\right) \right) ^{n\omega _{\vartheta (1)}}\oplus p_{2}\left( L_{\vartheta (2)}\left( P_{\vartheta (2)}\right) \right) ^{n\omega _{\vartheta (2)}}\\ =\,&g^{-1}\left( \bigcup _{\eta _{\vartheta (1)}^{(k)}\in g\left( L_{\vartheta (1)}\right) }\left\{ \left( 1-\left( 1-\left( \eta _{\vartheta (1)}^{(k)}\right) ^{n\omega _{\vartheta (1)}}\right) ^{p_1}\right) \left( P_{\vartheta (1)}^{(k)}\right) \right\} \right) \\&\oplus g^{-1}\left( \bigcup _{\eta _{\vartheta (2)}^{(k)}\in g\left( L_{\vartheta (2)}\right) }\left\{ \left( 1-\left( 1-\left( \eta _{\vartheta (2)}^{(k)}\right) ^{n\omega _{\vartheta (2)}}\right) ^{p_2}\right) \left( P_{\vartheta (2)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\eta _{\vartheta (1)}^{(k)}\in g\left( L_{\vartheta (1)}\right) ,\eta _{\vartheta (2)}^{(k)}\in g\left( L_{\vartheta (2)}\right) }\right. \\&\left. \left\{ \left( 1-\left( 1-\left( \eta _{\vartheta (1)}^{(k)}\right) ^{n\omega _{\vartheta (1)}}\right) ^{p_{1}}\left( 1-\left( \eta _{\vartheta (2)}^{(k)}\right) ^{n\omega _{\vartheta (2)}}\right) ^{p_{2}}\right) \left( P_{\vartheta (1)}^{(k)}P_{\vartheta (2)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2 \end{array}}\left\{ \left( 1-\prod _{i=1}^{2}\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_{i}}\right) \left( \prod _{i=1}^{2}P_{\vartheta (i)}^{(k)}\right) \right\} \right) \end{aligned} \end{aligned}$$

and we can get

$$\begin{aligned} \begin{aligned}&\oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\\&=g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_{i}}\right) \left( \prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$

Hence, we finish the proof of Proposition 6. \(\square\)

Proposition 7

Suppose \(L_i{(P_i)}\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\) \((i=1,2,\dots ,n)\) be n PLTSs, \(p_i (i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&\otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\right) \\&=g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^{n}\left( 1- \left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(25)

Proof

With the aid of result of Proposition 6 and operation law (ii) in Definition 3, we have

$$\begin{aligned} \begin{aligned}&\left( \oplus _{i=1}^{n}p_{i}\left( L_{1(i)}\left( P_{1(i)}\right) \right) ^{n\omega _{1(i)}}\right) \otimes \left( \oplus _{i=1}^{n}p_{i}\left( L_{2(i)}\left( P_{2(i)}\right) \right) ^{n\omega _{2(i)}}\right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{1(i)}^{(k)}\in g\left( L_{1(i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{1(i)}^{(k)}\right) ^{n\omega _{1(i)}}\right) ^{p_{i}}\right) \left( \prod _{i=1}^{n}P_{1(i)}^{(k)}\right) \right\} \right) \\&\otimes g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{2(i)}^{(k)}\in g\left( L_{2(i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{2(i)}^{(k)}\right) ^{n\omega _{2(i)}}\right) ^{p_{i}}\right) \left( \prod _{i=1}^{n}P_{2(i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{1(i)}^{(k)}\in g\left( L_{1(i)}\right) ,\eta _{2(i)}^{(k)}\in g\left( L_{2(i)}\right) \\ i=1,2,\dots ,n \end{array}}\left\{ \left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{1(i)}^{(k)}\right) ^{n\omega _{1(i)}}\right) ^{p_{i}}\right) \right. \right. \\&\left. \left. \left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{2(i)}^{(k)}\right) ^{n\omega _{2(i)}}\right) ^{p_{i}}\right) \left( \prod _{i=1}^{n}P_{1(i)}^{(k)}\prod _{i=1}^{n}P_{2(i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ \vartheta =1,2;i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta =1}^{2}\left( 1-\prod _{i=1}^{n}\left( 1- \left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) \left( \prod _{\vartheta =1}^{2}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) \end{aligned} \end{aligned}$$

then

$$\begin{aligned} \begin{aligned}&\otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^{n}\left( 1- \left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$

Therefore, Proposition 7 always holds. \(\square\)

Proposition 8

Suppose \(L_i{(P_i)}\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\) \((i=1,2,\dots ,n)\) be n PLTSs, \(p_i (i=1,2,\dots ,n)\) is an arbitrary nonnegative number, which denotes the risk appetite value. \(\vartheta (i)(i=1,2,\dots ,n)\) be any permutation of \((1,2,\dots ,n)\). Then we have

$$\begin{aligned} \begin{aligned}&\left( \otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\right) \right) ^{\frac{1}{n!}}\\&=g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^{n}\left( 1- \left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$
(26)

Proof

It is not difficult to demonstrate Proposition 8 through the outcome of Proposition 7 and operation law (iv) presented in Definition 3. \(\square\)

Theorem 2

Suppose \(L_i{(P_i)}\!=\!\{L_i^{(k)}P_i^{(k)}\big |k=1,2,\dots,\#L_i(P_i)\}\) \((i=1,2,\dots ,n)\) be n PLTSs, \(P=(p_1,\dots ,p_n)\in R^n\) be a parameter vector denoting the risk appetite values, \(\omega _i\) be the weight of input argument \(L_i(P_i)\) with \(\omega _i \in [0,1]\) and \(\sum _{i=1}^{n}\omega _i=1\). Then aggregated result by Definition 10 is shown as

$$\begin{aligned} \begin{aligned}&PLWDMM^P(L_1(P_1),\dots ,L_i(P_i),\dots ,L_n(P_n))\\&=g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left\{ \left( 1-\left( 1-\left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\right) ^{\frac{1}{\sum _{i=1}^{n}p_i}}\right) \right. \\&\left. \left. \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned}\end{aligned}$$
(27)

Proof

Based on Theorem 1, Propositions 5–8 and operation laws of PLTSs described in Definition 3, we have

$$\begin{aligned} \begin{aligned}&PLWDMM^P(L_1(P_1),\dots ,L_i(P_i),\dots ,L_n(P_n))\\ =&{\frac{1}{\sum _{i=1}^{n}p_i}}\left( \otimes _{\vartheta \in S_n}\left( \oplus _{i=1}^{n}p_{i}\left( L_{\vartheta (i)}\left( P_{\vartheta (i)}\right) \right) ^{n\omega _{\vartheta (i)}}\right) \right) ^{\frac{1}{n!}}\\ =&{\frac{1}{\sum _{i=1}^{n}p_i}}g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left. \left\{ \left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^{n}\left( 1- \left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (i)}^{(k)}\in g\left( L_{\vartheta (i)}\right) \\ i=1,2,\dots ,n \end{array}}\right. \\&\left\{ \left( 1-\left( 1-\left( \prod _{\vartheta \in S_n}\left( 1-\prod _{i=1}^{n}\left( 1-\left( \eta _{\vartheta (i)}^{(k)}\right) ^{n\omega _{\vartheta (i)}}\right) ^{p_i}\right) \right) ^{\frac{1}{n!}}\right) ^{\frac{1}{\sum _{i=1}^{n}p_i}}\right) \right. \\&\left. \left. \left( \prod _{\vartheta \in S_n}\prod _{i=1}^{n}P_{\vartheta (i)}^{(k)}\right) \right\} \right) . \end{aligned} \end{aligned}$$

\(\square\)

Thus, we complete the proof of Theorem 2.

Likewise, we further explore desirable properties for PLWDMM operator and give four corollaries.

Corollary 5

(Monotonity). Let \(L(P)_a=\left\{ L_1(P_1)_a,\dots ,\right.\) \(\left. L_n(P_n)_a\right\}\) and \(L(P)_b=\left\{ L_1(P_1)_b,\dots ,L_n(P_n)_b\right\}\) be arbitrary two PLTSs, \(P=(p_1,p_2,\dots ,p_n)\in R^n\) be a parameter vector denoting the risk appetite values. For \(\eta _{\vartheta a(i)}^{(k)}\in g(L_{\vartheta a(i)})\), \(\eta _{\vartheta b(i)}^{(k)}\in g(L_{\vartheta b(i)})\), if \(\eta _{\vartheta a(i)}^{(k)}\leqslant \eta _{\vartheta b(i)}^{(k)}\) and \(P_{\vartheta a(i)}^{(k)}\leqslant P_{\vartheta b(i)}^{(k)}\), then we have

$$\begin{aligned} \begin{aligned} PLWDMM^P&\left( L_1(P_1)_a,\dots ,L_n(P_n)_a\right) \\&\leqslant PLWDMM^P\left( L_1(P_1)_b,\dots ,L_n(P_n)_b\right) . \end{aligned} \end{aligned}$$

Corollary 6

(Idempotency). If \(L_i{P_i}\!=\!L(P)\!=\!\left\{ L^{(k)}\left( P^{(k)}\right) \right.\)

\(\big |L^{(k)}\in S, r^{(k)}\in t, P^{(k)}\ge 0, k=1,2,\dots ,\#L(P),\) \(\left. \sum _{k=1}^{\#L(P)}P^{(k)}\leqslant 1\right\}\) for all \(i=1,2,\dots ,n\), then we have

$$\begin{aligned} PLWDMM^P\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) =L(P). \end{aligned}$$

Corollary 7

(Commutativity). If \(L_i^{'}(P_i^{'})\) be any permutation of \(L_i(P)_i(i=1,2,\dots ,n)\), then we have the relationship:

$$\begin{aligned} \begin{aligned} PLWDMM^P&\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\&=PLWDMM^P\left( L_1^{'}(P_1^{'}),L_2^{'}(P_2^{'}),\dots ,L_n^{'}(P_n^{'})\right) . \end{aligned} \end{aligned}$$

Corollary 8

(Boundness). Let \(L(P)^{-}=min(L_1(P_1),\)

\(L_2(P_2),\dots ,L_n(P_n))\) and \(L(P)^{+}=max(L_1(P_1),L_2(P_2),\)

\(\dots ,L_n(P_n))\), then we have

$$\begin{aligned} \begin{aligned} PLWDMM^P&\left( L(P)^{-},L(P)^{-},\dots ,L(P)^{-}\right) \\&\leqslant PLWDMM^P\left( L_1(P_1),L_2(P_2),\dots ,L_n(P_n)\right) \\&\leqslant PLWDMM^P\left( L(P)^{+},L(P)^{+},\dots ,L(P)^{+}\right. \end{aligned} \end{aligned}$$

If \(\omega =(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})\), then PLWDMM operator is reduced to PLDMM operator. Therefore, PLDMM operator is regarded as a special case of PLWDMM operator. According to Theorems 1 and 2, it is clear that PLWDMM operator being an effective extension of PLDMM operator is more appropriate to capture the interrelationship and importance of multi-input arguments in the PLMADM problems.

4 A Novel Decision-Making Approach to PLMADM Based on PLWDMM Operator and VIKOR

In this section, we investigate a novel method in accordance with PLWDMM aggregation operator and VIKOR to handle complicated PLMADM problems.

4.1 Problem Description

For a PLMADM problem, DMs are required to pick out the optimal or best alternative from several candidates with regard to finite attributes. Therefore, alternatives and attributes should be decided first. Let \(A=\left\{ a_1,\dots ,a_i,\dots ,a_m\right\}\) be a discrete collection of m alternatives, \(C=\left\{ c_1,\dots ,c_j,\dots ,c_n\right\}\) be a finite set of n attributes, and weight sector of attributes is given as \(\omega =\left( \omega _1,\dots ,\omega _j,\dots ,\omega _n\right) ^{T}\) such that \(\sum _{j=1}^{n}{\omega _j}=1\) and \(\omega _j \in [0,1]\). Suppose that \(DM=\left\{ dm_1,\dots ,dm_q,\dots ,dm_e\right\}\) be a set of DMs with relative weights \(\lambda =\left( \lambda _1,\dots ,\lambda _q,\dots ,\lambda _e\right) ^{T}\). Similarly, for \(q=1,2,\dots ,e\), \(\lambda _q\) satisfies \(\sum _{q=1}^{e}{\lambda _q}=1\) and \(\lambda _q \in [0,1]\). According to linguistic scale \(S=\left\{ S_{t}|t=-\tau ,\dots ,-1,0,1,\dots ,\tau \right\}\), each DM is invited to choose suitable linguistic terms in set S and display corresponding possible probability/preference degree when providing his/her evaluation information on each alternative with respect to attributes. Let \(D^{q}=\left( r_{ij}^{q}\right) _{m\times n}\) be alternatives–attributes probabilistic linguistic evaluation matrix given by decision maker \(dm_{q} (q=1,2,\dots ,e)\). The matrix \(D^{q}\) can be written as follows:

$$\begin{aligned} D^{q}= \left( \begin{array}{cccccc} r_{11}^q &{} r_{12}^q &{} \cdots &{} r_{1j}^q &{} \cdots &{} r_{1n}^q\\ r_{21}^q &{} r_{22}^q &{} \cdots &{} r_{2j}^q &{} \cdots &{} r_{2n}^q\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ r_{i1}^q &{} r_{i2}^q &{} \cdots &{} r_{ij}^q &{} \cdots &{} r_{in}^q\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ r_{m1}^q &{} r_{m2}^q &{} \cdots &{} r_{mj}^q &{} \cdots &{} r_{mn}^q \end{array} \right) . \end{aligned}$$

where for all \(i=1,2,\dots ,m; j=1,2,\dots ,n\), \(r_{ij}^{q}=L_{ij}^{q}\left( P_{ij}^{q}\right)\) presents probabilistic linguistic evaluation information provided by decision maker \(dm_{q}\) over alternative \(a_i\) about attribute \(c_j\).

4.2 Decision Procedures for PLMADM Based on PLWDMM Operator and VIKOR

DMs are invited one by one to offer their real evaluation on alternatives regarding to different attributes. Then e alternatives–attributes probabilistic linguistic evaluation matrices are successfully constructed. In the light of PLWDMM operator, collective result of alternative \(a_i\) with respect to attribute \(c_j\) is fused by means of formulas (22) and (27) for all \(i=1,2,\dots ,m; j=1,2,\dots ,n\). The outcome is denoted as

$$\begin{aligned} \begin{aligned} r_{ij} =&L_{ij}(P_{ij})=PLWDMM^{P} (r_{ij}^{1},\dots ,r_{ij}^{q},\dots ,r_{ij}^{e})\\ =&PLWDMM^{P}\left( L_{ij}^{1}\left( P_{ij}^{1}\right) ,\dots ,L_{ij}^{q}\left( P_{ij}^{q}\right) ,\dots ,L_{ij}^{e}\left( P_{ij}^{e}\right) \right) \\ =\,&g^{-1}\left( \bigcup _{\begin{array}{c} \eta _{\vartheta (q)}^{(k)}\in g\left( L_{\vartheta (q)}^{q}\right) \\ q=1,2,\dots ,e \end{array}}\right. \\&\left\{ \left( 1-\left( 1-\left( \prod _{\vartheta \in S_e}\left( 1-\prod _{q=1}^{e}\left( 1-\left( \eta _{\vartheta (q)}^{(k)}\right) ^{e\lambda _{\vartheta (q)}}\right) ^{p_q}\right) \right) ^{\frac{1}{e!}}\right) ^{\frac{1}{\sum _{q=1}^{e}p_q}}\right) \right. \\&\left. \left. \left( \prod _{\vartheta \in S_e}\prod _{q=1}^{e}P_{\vartheta (q)}^{(k)}\right) \right\} \right) , \end{aligned} \end{aligned}$$
(28)

where \(\vartheta (q)(q=1,2,\dots ,e)\) be any permutation of \((1,2,\dots,e),\)

and \(S_e\) is the set of all possible permutations of \((1,2,\dots ,e)\).

Similarly, we can obtain other aggregated information. Then alternatives–attributes group evaluation matrix denoted as \(D=\left( r_{ij}\right) _{m\times n}\) is built and depicted as follows:

$$\begin{aligned} D= \left( \begin{array}{cccccc} r_{11} &{} r_{12} &{} \cdots &{} r_{1j} &{} \cdots &{} r_{1n}\\ r_{21} &{} r_{22} &{} \cdots &{} r_{2j} &{} \cdots &{} r_{2n}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ r_{i1} &{} r_{i2} &{} \cdots &{} r_{ij} &{} \cdots &{} r_{in}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ r_{m1} &{} r_{m2} &{} \cdots &{} r_{mj} &{} \cdots &{} r_{mn} \end{array} \right) , \end{aligned}$$

where for all \(i=1,2,\dots ,m; j=1,2,\dots ,n\), \(r_{ij}=L_{ij}\left( P_{ij}\right)\) presents group probabilistic linguistic evaluation information on alternative \(a_i\) regarding to attribute \(c_j\).

According to Definition 4, group evaluation matrix D can be normalized as \({\bar{D}}\), in which the numbers of linguistic terms in all evaluation information are identical.

Next, we further use VIKOR method to solve PLMA-DM problem described in Sect. 4.1. First of all, we need to find the positive ideal solutions and negative ideal solutions according to matrix \({\bar{D}}\). Let \(R^{+}\!=\!(r_1^{+},\dots,r_j^{+},\dots ,r_n^{+})\)

and \(R^{-}=(r_1^{-},\dots ,r_j^{-},\dots ,r_n^{-})\) be positive and negative ideal solutions, respectively. \(r_j^{+}\) and \(r_j^{-}\) separately denote the best and the worst solutions on attribute \(c_j\), which are computed by formulas (29) and (30):

$$\begin{aligned} r_j^{+}={\bar{L}}_{j}\left( {\bar{P}}_{j}\right) ^{+}=\left\{ \left( {\bar{L}}_{j}^{(1)}\right) ^{+},\dots ,\left( {\bar{L}}_{j}^{(k)}\right) ^{+},\dots ,\left( {\bar{L}}_{j}^{(\#{\bar{L}}_{ij}(P))}\right) ^{+}\right\} , \end{aligned}$$
(29)

where \(\left( {\bar{L}}_{j}^{(k)}\right) ^{+}=S_{\begin{array}{c} max\\ 1\leqslant i \leqslant m \end{array}\left\{ r_{ij}^{(k)}P_{ij}^{(k)}\right\} }\), \(\#{\bar{L}}_{ij}(P)\) presents number of linguistic terms in \({\bar{L}}_{ij}(P)\). For all \(i=1,\dots ,m;\)  \(j=1,\dots ,n\), \(r_{ij}^{(k)}\) is the subscript of the linguistic term \({\bar{L}}_{ij}^{(k)}\) and \(P_{ij}^{(k)}\) be corresponding possible probability or preference degree of linguistic term \({\bar{L}}_{ij}^{(k)}\).

$$\begin{aligned} r_j^{-}={\bar{L}}_{j}\left( {\bar{P}}_{j}\right) ^{-}=\left\{ \left( {\bar{L}}_{j}^{(1)}\right) ^{-},\dots ,\left( {\bar{L}}_{j}^{(k)}\right) ^{-},\dots ,\left( {\bar{L}}_{j}^{(\#{\bar{L}}_{ij}(P))}\right) ^{-}\right\} , \end{aligned}$$
(30)

where \(\left( {\bar{L}}_{j}^{(k)}\right) ^{-}=S_{\begin{array}{c} min\\ 1\leqslant i \leqslant m \end{array}\left\{ r_{ij}^{(k)}P_{ij}^{(k)}\right\} }\), \(\#{\bar{L}}_{ij}(P)\) presents number of linguistic terms in \({\bar{L}}_{ij}(P)\). For all \(i=1,\dots ,m;\)  \(j=1,\dots ,n\), \(r_{ij}^{(k)}\) is the subscript of the linguistic term \({\bar{L}}_{ij}^{(k)}\) and \(P_{ij}^{(k)}\) be corresponding possible probability or preference degree of linguistic term \({\bar{L}}_{ij}^{(k)}\).

For each alternative \(a_i\), we then compute group utility \(S_i\) and individual regret \(R_i\) based on the positive ideal solutions and negative ideal solutions.

The group utility \(S_i\) is given by

$$\begin{aligned} S_i=\sum _{j=1}^{n}\omega _j\frac{d\left( r_j^{+},r_{ij}\right) }{d\left( r_j^{+},r_j^{-}\right) }. \end{aligned}$$
(31)

The individual regret \(R_i\) can be calculated by

$$\begin{aligned} R_i=\begin{array}{c} max\\ 1\leqslant j\leqslant n \end{array}\omega _j\frac{d\left( r_j^{+},r_{ij}\right) }{d\left( r_j^{+},r_j^{-}\right) }, \end{aligned}$$
(32)

where \(\omega _j\) be the weight of attribute \(c_j\), \(d\left( r_j^{+},r_{ij}\right)\) presents the distance between \(r_j^{+}\) and \(r_{ij}\). Distance measure of PLTSs is cited from [8] depicted in Definition 6.

Now, we calculate total utility \(Q_i\) for every alternative \(a_i\) by the following formula:

$$\begin{aligned} Q_i=\mu {\frac{S_i-S^{+}}{S^{-}-S^{+}}}+(1-\mu ){\frac{R_i-R^{+}}{R^{-}-R^{+}}}, \end{aligned}$$
(33)

where \(S^{+}=\begin{array}{c} min\\ i \end{array}S_i\), \(S^{-}=\begin{array}{c} max\\ i \end{array}S_i\),  \(R^{+}=\begin{array}{c} min\\ i \end{array}R_i\), \(R^{-}=\begin{array}{c} max\\ i \end{array}R_i\). Parameter \(\mu (\mu \in [0,1])\) denotes weight of maximum group utility, and \(1-\mu\) is the weight of individual regret. In general, \(\mu\) is equal to 0.5 [26, 29, 36].

According to values of \(S_i,R_i,Q_i\), three ranking results for all alternatives in ascending orders are obtained.

Assumed that \(A^{(1)},A^{(2)},\dots ,A^{(m)}\) be a increasing ranking based on values of \(Q_i(i=1,2,\dots ,m)\). \(A^{(1)}\) is a promising solution if satisfying the following two constraints:

  1. (i)

    Acceptable advantage: \(Q\left( A^{(2)}\right) -Q\left( A^{(1)}\right) \ge \frac{1}{m-1}\);

  2. (ii)

    Acceptable stability: alternative \(A^{(1)}\) also be in first position by \(S_i\) or/and \(R_i\).

However, these two conditions sometimes cannot be met simultaneously, then compromised solutions have been developed as follows:

If constraint (ii) is not satisfied, then \(A^{(1)}\) and \(A^{(2)}\) are regarded as compromised solutions. If constraint (i) is not met, then \(A^{(1)},A^{(2)},\dots ,A^{(M)}\) are considered as compromised solutions, in which value of M is obtained by \(Q\left( A^{(M)}\right) -Q\left( A^{(1)}\right) < \frac{1}{m-1}\) for maximum M.

4.3 The Algorithm for PLMADM Based on PLWDMM Operator and VIKOR

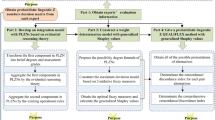
Based on the above-detailed decision procedures, we further summarize our proposed decision-making approach described in Fig. 1 and put forward a powerful algorithm for dealing with complex PLMADM problems through PLWDMM operator and VIKOR method. The algorithm for PLMADM is depicted as follows:

Fig. 1
figure 1

Framework of our proposed decision-making approach to PLMADM

Full size image
  1. Step 1:

    Identify alternatives set \(A=\{a_1,\dots ,a_i,\dots ,a_m\}\), attributes set \(C=\{c_1,\dots ,c_j,\dots ,c_n\}\) and DMs set \(DM=\{dm_1,\dots ,dm_q,\dots ,dm_e\}\). Given that weight vectors of attributes and DMs are denoted as \(\omega =\left( \omega _1,\dots ,\omega _j,\dots ,\omega _n\right) ^{T}\) and \(\lambda =\left( \lambda _1,\dots ,\lambda _q,\dots ,\lambda _e\right) ^{T}\), respectively. Each evaluator is invited to choose linguistic term in set \(S=\left\{ S_{t}|t=-\tau ,\dots ,-1,0,1,\dots ,\tau \right\}\) and express relative possible probability/preference degree when evaluating each candidate with regard to attributes;

  2. Step 2:

    Construct e alternatives–attributes probabilistic linguistic evaluation matrices;

  3. Step 3:

    Fuse collective result of alternative \(a_i\) with respect to attribute \(c_j\) by means of formula (28), and obtain the alternatives–attributes group evaluation matrix \(D=\left( r_{ij}\right) _{m\times n} \left( i=1,2,\dots ,m;\right.\)  \(\left. j=1,2,\dots ,n\right)\);

  4. Step 4:

    Acquire normalized group evaluation matrix \({\bar{D}}\) according to Definition 4;

  5. Step 5:

    Find the positive ideal solutions \(R^{+}=(r_1^{+},\dots ,r_j^{+},\) \(\dots ,r_n^{+})\) and negative ideal solutions \(R^{-}=(r_1^{-},\dots ,\) \(r_j^{-},\dots ,r_n^{-})\) with the aid of formulas (29) and (30);

  6. Step 6:

    Compute group utility \(S_i\) and individual regret \(R_i\) by formulas (31) and (32) for each alternative \(a_i\);

  7. Step 7:

    Calculate total utility \(Q_i\) for every alternative \(a_i\) in the light of formulas (6) and (33);

  8. Step 8:

    Obtain three ranking results for all candidates in ascending orders according to values of \(S_i,R_i,\) \(Q_i\);

  9. Step 9:

    Determine the compromised solution: assumed that \(A^{(1)},A^{(2)},\dots ,A^{(m)}\) be an increasing ranking based on values of \(Q_i (i=1,2,\dots ,m)\). If \(A^{(1)}\) meets constraints of acceptable advantage and acceptable stability, then \(A^{(1)}\) is a promising solution; If only constraint of acceptable advantage is satisfied, then \(A^{(1)}\) and \(A^{(2)}\) are regarded as compromised solutions. If only condition of acceptable stability is met, then \(A^{(1)},A^{(2)},\dots ,A^{(M)}\) are considered as compromised solutions, in which value of M is obtained by \(Q\left( A^{(M)}\right) -Q\left( A^{(1)}\right) <\frac{1}{m-1}\) for maximum M.

5 Illustrative Example

In the following, we further demonstrate the practicality and feasibility of the proposed decision-making approach by a practical example adapted from Liang et al. [17].

Owing to severe ceaselessly environment pollution in China and finite medical resources, some domestic hospitals have to be assessed to seek the optimal one, especially their personalized healthcare systems. Suppose that three DMs \(DM=\{dm_1,dm_2,dm_3\}\) with the weight vector \(\lambda =(0.3,0.3,0.4)^T\) are invited to evaluate four hospitals \(a_i (i=1,2,3,4)\) according to three attributes. They are (1) the environmental factor of medical and health service \((c_1)\); (2) personalized diagnosis and treatment optimization \((c_2)\); (3) social resource allocation optimization under the pattern of wisdom medical and health services \((c_3)\). The weights of attributes are given as \(\omega =(0.2,0.1,0.7)^T\). And the original decision matrices expressed in the form of PLTSs are integrated and presented in Table 1.

Table 1 The integrated decision matrix provided by all DMs
Full size table

5.1 The Proposed Decision-Making Approach for the Example

According to the designed decision-making approach described in Sect. 4, we first aggregate the probabilistic linguistic evaluation information presented in Table 1. The collective result for every candidate \(a_i\) with respect to attribute \(c_j (i=1,2,3,4;j=1,2,3)\) can be acquired in the light of PLWDMM aggregation operator depicted in the formula (28) when parameter vector is given as \(P=(1,1,1)\). The obtained group evaluation matrix D is presented in Table 2. Based on Definition 4, we normalize group evaluation matrix D and get the normalized group evaluation matrix.

Table 2 The group evaluation matrix D
Full size table

Based on the normalized group evaluation matrix as well as formulas (29) and (30), we then find the positive ideal solutions \(R^{+}=(\{S_3,S_{0.306},S_{0.1728},S_{0.0708}\},\) \(\{S_{1.005},S_{0.875},S_{0.2625},S_{0.213}\},\{S_3,S_{0.072},S_0,S_0\})\) and negative ideal solutions

\(R^{-}=(\{S_{0.36},S_0,S_0,S_0\},\{S_{0.03},\) \(S_0,S_0,S_0\},\{S_{0.012},S_0,S_{-0.114},S_{-0.116}\})\). We further calculate group utility \(S_i\), individual regret \(R_i\) and total utility \(Q_i\) for each alternative \(a_i (i=1,2,3,4)\) with the aid of formulas (31–33). The calculation and ranking results for all candidates are integrated and shown in Table 3.

Table 3 The calculation and ranking results for all alternatives
Full size table

From two constraints of VIKOR method and results shown in Table 3, it is clear that alternative \(a_2\) is the best in the ranking lists of S and R. However, \(Q(A^{(2)})-Q(A^{(1)})=0.14<1/(4-1)\approx 0.33\). It implies that constraint (i) is not met. We then deduce the following relationship: \(Q(A^{(3)})-Q(A^{(1)})=0.6>1/(4-1)\approx 0.33\). Hence, the alternative hospitals \(a_2\) and \(a_3\) are the compromised solutions.

5.2 The Effect of Risk Appetite Parameter on Ranking Result

In Sect. 5.1, we have taken the relationships parameter vector \(P=(1,1,1)\). Obviously, P can also take other values with different risk appetites. Generally, if DM is risk-seeking, then parameter vector is defined as \(P=(1,1,0,\dots ,0)\) or/and \(P=(\overbrace{1,\dots ,1}^{m},\overbrace{0,\dots ,0}^{n-m})\) in PLWDMM operator; on the contrary, if DM prefers to risk-averse, parameter vector is given as \(P=(1,0,\dots ,0)\) or \(P=(\lambda ,0,\dots ,0)\); if DM is risk-neutral, parameter vector is denoted as \(P=(1,1,\dots ,1)\) or \(P=(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})\). For discussing the effect of parameter vector P on the ranking list, several values of P are introduced to analyze the ranking results which are depicted in Table 4.

Table 4 The ranking results for different values of parameter vector P
Full size table

As shown in Table 4, we find that three kinds of ranking results are almost the same and are in accordance with the ranking \(a_2>a_3>a_4>a_1\) except the ranking result from Q derived when parameter vector is given as \(P=(2,0,0)\). When \(P=(2,0,0)\) presents the risk appetite values of DMs, we can compute \(Q(A^{(2)})-Q(A^{(1)})=0<0.33\) and \(Q(A^{(3)})-Q(A^{(1)})=1>0.33\). Based on the two constraints of VIKOR method, we deduce alternative hospitals \(a_2\) and \(a_3\) are the compromised solutions which are exactly consistent with the outcomes from other values of parameter vector P. Therefore, a meaningful conclusion is summarized as follows: the compromised solutions (i.e., \(a_2\) and \(a_3\)) determined by PLWDMM operator and VIKOR are totally unchanged in this example although the parameter vector P changes. This interesting phenomenon can also illustrate the proposed decision-making approach has wonderful robust property.

5.3 Further Discussions

To further signify the superiorities and strength of proposed decision-making approach in handling MADM problems under probabilistic linguistic preference environment, we further compare the proposed method with other existing approaches in this section.

5.3.1 Comparison with Method from Pang et al.

[8]

Based on the MADM with PLTSs, Pang et al. [8] fused evaluation information by PLWA operator and utilized TOPSIS method to deal with PLMADM problems. As mentioned in Sect. 3.1, PLDMM operator will become PLA operator as long as parameter vector is \(P=(1,1,\dots ,1)\) or \(P=(1/n,1/n,\dots ,1/n)\). To reduce the differences and enhance the comparability; therefore, PLWDMM operator with parameter vector \(P=(1,1,1)\) or \(P=(1/n,1/n,1/n)\) is used to compare the proposed approach and method from Pang et al. [8]. The decision results of these two techniques are presented in Table 5.

Table 5 The ranking results derived by proposed method and method from Pang et al. [8]
Full size table

Table 5 shows that ranking results are remaining the same in spite of derived from different decision-making methods. It implies the outcome acquired by designed decision-making approach is reasonable and proposed technique is feasible. In the following, we analyze some characteristics of different aggregation operators which are listed in Table 6. According to the result of Table 6, we find that being a special case of PLWDMM, PLWA operator has two limitations when aggregating evaluations: (1) input arguments are regarded as independent when fusing information by PLWA operator; (2) PLWA operator does not consider interrelationships of input arguments in PLMADM problems. However, PLWDMM aggregation operator not only takes these interrelationships into account but also is a generalization of most existing operators (including PLWA operator). Hence, our proposed PLWDMM operator is more flexible and general than PLWA operator to fuse input arguments in PLMADM problems. Besides, though ideal solutions are involved both in TOPSIS technique and VIKOR method, VIKOR is more suitable to handle sophisticated MADM problems especially with conflicted attributes. Therefore, proposed approach is totally superior than method from Pang et al. [8] in dealing with PLMADM problems.

Table 6 The characteristics of three aggregation operators
Full size table

5.3.2 Comparison with Method from Liang et al.

[17]

Similarly, Liang et al. [17] proposed the PLWGeoBM operator to aggregate information and employed GRA to solve PLMADM problems. Since PLWDMM operator with parameter vector \(P=(1,1,0,\dots ,0)\) is equivalent to PLWGeoBM with parameters \(p=q=1\), we use PLWDMM operator with \(P=(1,1,0)\) and VIKOR to compare with method from Liang et al. [17]. And the decision results determined by proposed approach and method from Liang et al. [17] are shown in Table 7.

Table 7 The ranking results determined by proposed method and method from Liang et al. [17]
Full size table

From results of Table 7, we know that ranking result from proposed approach is in accordance with the result from Liang et al. [17], which not only further demonstrates the rational of outcome obtained from proposed approach but also explains the available of designed decision-making approach. Although PLWGeoBM being a special case of PLWDMM operator involves the interrelationship of two input arguments according to the result of Table 6, it cannot capture these interrelationships among three or multiple input arguments and lacks of the ability to make decision-making approach flexible. On the contrary, PLWDMM operator can accurately analyze interrelationships of multi-input arguments and make the designed decision-making method flexible. In real situation, input arguments in PLMADM problems are interrelated even multiple; therefore, PLWDMM operator plays better at dealing with multi-input arguments in PLMADM problems. Compared with GRA, VIKOR can provide DMs with compromised solutions in the situation where criterion are conflicted. So, it also proves that proposed approach is better at addressing complex PLMADM problems than method in Liang et al. [17].

Based on above analysis, the desirable advantages of our proposed method are concluded as follows: (1) it not only contains probabilistic linguistic preference information, but also fully captures the interrelationships among multi-input arguments; (2) it is flexible with the aid of parameter vector and is fulfilled with robust property. (3) Our proposed method offers DMs an effective way to get compromised solutions under PLP environment. Thus, our proposed method is more appropriate to deal with complicated PLMADM problems.

6 Conclusion

With the consideration of interrelationships among multi-input arguments, we extend the traditional DMM operator into probabilistic linguistic preference surroundings. In this paper, we separately define PLDMM and PLWDMM aggregation operators which have the characteristics of generalization, flexibility and robust property. For sophisticated PLMADM problems, we investigate a new extension of the VIKOR method and design a corresponding decision-making approach in the light of PLWDMM operator. Introduction of DMM operator not only contributes to expand the application of PLTSs and propose relative aggregation operators but also conduces to develop a novel technique based on improved PLWDMM operator and VIKOR method to solve PLMADM problems. Our designed decision-making approach can also be powerful in addressing other operational research problems, such as supplier selection, performance evaluation for enterprises, assessment of project quality, etc. Future work will further focus on exploring new generalized operators and decision-making methods to handle complex PLMADM problems.