Probabilistic Linguistic Z Number Decision-Making Method for Multiple Attribute Group Decision-Making Problems with Heterogeneous Relationships and Incomplete Probability Information

Abstract

Probabilistic linguistic Z number (PLZN) is considered as an effective information representation model. It not only describes the decision-making information, but also demonstrates its reliability. To handle the increasing problems of complexity and uncertainty in real-life, PLZN is widely used to indicate qualitative information. In this paper, a novel decision-making method with PLZNs is proposed, focusing on multiple attribute group decision-making (MAGDM) problems with fewer alternatives and more interacted attributes in PLZN environment. Firstly, all basic theories of PLZNs are shown, where the possibility degree of PLZNs is defined. Then, an integration model based on evidential reasoning theory is constructed to aggregate numerous PLZNs, which fully considers the incomplete probability distributions in PLZNs. The mathematical programming model with the generalized Shapley function is introduced to determinate the important degrees of attributes and reflect the interactive characteristics among them. In addition, the probabilistic linguistic Z QUALIFLEX (PLZ-QUALIFLEX) method with the generalized Shapley function is proposed to rank small numbers of alternatives with respect to large numbers of attributes with heterogeneous relationships. Lastly, after demonstrating the rationalities and superiorities of the proposed method, it is applied to solve some numerical cases, in which is compared with other methods.

1 Introduction

With the rapid development in society and economy, real-world decision-making problems show a continuous dynamic change where uncertainty and fuzziness appear [7, 12, 17]. To model such uncertainty, incompleteness, or hesitation, qualitative linguistic information is chosen to express decision makers’ perspectives instead of the specific crisp numbers. Up to now, many scholars have made concrete and thoroughly researches, which elaborate richer linguistic information presentation models to express greater amount of decision makers’ preferences or opinions under uncertain environment [6, 8, 10, 13, 14, 20, 24]. Zadeh [29,30,31] first proposed the discrete linguistic terms to express decision makers’ opinion, which lays a foundation for further researches on linguistic information presentation models. However, often single linguistic terms are limited or cannot present decision makers’ personal opinion completely. Rodriguez et al. [13] used several linguistic terms to express decision makers’ opinion and proposed hesitant fuzzy linguistic term set. Based on this, Pang et al. [10] proposed probabilistic linguistic term set (PLTS) which not only use several linguistic terms to express decision maker’ opinion but also use probability information to express his/her different sentiment degree implied in opinion. Although PLTS can present the decision-making information more realistically than the existing linguistic information presentation models, the reliability of decision-making information described by PLTS has not been taken into account or reflected. In the existing research literature, it can be found that linguistic Z number (LZN) not only describes decision-making information itself but also considers the reliability of decision-making information [20]. Taking the advantages of both PLTS and LZN, Wang et al. [22] introduced the probabilistic linguistic Z number (PLZN) which utilizes PLTS to model restriction measure of decision-making information and uses the linguistic term to describe reliability measure. PLZN, as the combination of PLTS and LZN, models the evaluations of decision makers more accurately and avoids the distortion and loss of original information effectively. Due to the superiorities of PLZN in modeling evaluation information under the complicated decision-making environment, it can be widely applied in increasingly complex decision-making problems, especially in MAGDM problems with high ambiguity and uncertainty. Therefore, this paper focuses on the MAGDM problems under probabilistic linguistic Z numbers (PLZNs) context.

In group decision-making process, several decision makers give evaluation information depending on their background of knowledge. How to integrate much information given by different decision makers is one of the crucial topics. The most widely used integration models are the wider variety of information aggregation operators [19, 20, 24]. However, information aggregation operators are limited or do not process evaluation information with incompleteness, which either neglects the incompleteness or compensate the incompleteness by other information directly. Certainly, there are always other integration tools which realize the effective fusion of evaluation information with incompleteness [12, 26]. Among these tools, evidential reasoning method has a significant advantage in processing incompleteness, which is a probabilistic inference rule that is suitable for handling conflicts in information and allows judgmental weighting on evidence sources [26,27,28]. Similar to PLTS, there also exist incomplete probability distributions in PLZN. Therefore, this paper constructs an integration model with PLZNs based on evidential reasoning method, which can improves the perspicacity and rationality of decision-making process. Based on the proposed integration model, the MAGDM problems under PLZNs context can be degenerated into MADM problems with PLZNs.

It is well-known that the decision-making result must be measured by means of multiple attributes, and the weights of attributes play a very important role in decision-making process. In recent years, scholars have put forward various kinds of weight determination models [10, 11, 18]. However, most of these models are constructed on the assumption that all attributes are independent. In real-life, there are heterogeneous relationships among attributes. For example, in evaluation of urban disaster emergency response ability, the abilities of hazards identification and disaster forecast can affect the emergency command ability. It is necessary to construct a weight determination model to capture the heterogeneous relationships among attributes while determining the weights of attributes. Fuzzy measure is an effective tool in modeling the interactions between attributes, which has been analyzed and utilized in many fields [5, 16]. Then, the generalized Shapley functions based on various fuzzy measures are proposed successively, which are more comprehensive to reflect the interactive characteristics among attributes [9]. Hence, this paper proposes a weight determination model based on generalized Shapley function to determinate the weights of attributes with heterogeneous relationships. In addition to the determination of weights, the construction of decision-making method is a critical part of the decision-making process. Several decision-making methods have been developed to accomplish the evaluation assignment of alternatives, that can be split into two categories, i.e., the utility value-based decision-making methods [10, 19, 25] and the outranking theory-based decision-making methods [7, 11, 22]. However, the outranking theory-based decision-making methods stand out because they consider the incomparability and indifference, which better fits the realistic situations. Among the various outranking theory-based decision-making methods, the most widely used one comes out to be the QUALIFLEX method [1, 3, 4]. The most distinctive advantage of the QUALIFLEX method is the correct treatment of cardinal and ordinal information, which is adept at handling decision-making problems where the number of attributes is greatly exceed the number of alternatives. Since it better fits the realistic situations, this paper construct an improved PLZN decision-making method based on QUALIFLEX method. Moreover, the various interactions among attributes need to be considered as well in the proposed method. Therefore, this paper proposed an appropriate decision-making method with PLZNs based on QUALIFLEX method and generalized Shapley function.

Integrating the above three parts, this paper describes a resolution framework for the PLZNs MAGDM problems where the number of attributes markedly outnumber the alternatives and these attributes are not independent. The major contributions and novelties of this paper include the following:

• (1) An PLZNs integration model based on evidential reasoning theory is constructed to aggregate PLZNs from different experts, which can process PLZNs more effectively with incomplete probability distributions.

• (2) A mathematical programming model with PLZNs based on generalized Shapley function is designed to determinate the important degree of attributes and reflect the interactive characteristics among attributes.

• (3) A PLZ-QUALIFLEX method with generalized Shapley function is proposed to determinate the optimal ranking result of multiple alternatives, which is adept at ranking a limited of alternatives with respect to large numbers of attributes with heterogeneous relationships.

• (4) A MAGDM method based on the PLZNs integration model and the PLZ-QUALIFLEX method is offered to overcome the deficiency of these existing methods and to deal with numerical example. Both the rationality and superiority of the proposed method are illustrated by some examples.

The remaining portion of the paper is organized as below. Section II reviews some basic theories related to PLZNs, evidential reasoning theory and generalized Shapley function. Section III describes the resolution framework for MAGDM problem with PLZNS, including the description of the MAGDM problems with PLZNs and the resolution framework with PLZNs. Section IV introduces three parts of MAGDM method, i.e., the integration model based on evidential reasoning theory, the PLZNs mathematical programming model and the PLZ-QUALIFLEX method with generalized Shapley function. In Section V, several numerical examples are utilized to demonstrate the reasonability and validity of the proposed method. Section VI concludes the whole paper.

2 Preliminary

To facilitate a better understanding of the whole paper, this section introduces some basic theories related to PLZNs, providing theoretical basis for the subsequent part of this study.

2.1 Probabilistic Linguistic Z Number

Definition 1

[22] Suppose $Y$ is a universe of discourse,$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\ldots,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{\tau } } \right\}$ and $\Im = \left\{ {\varsigma_{0} ,\varsigma_{1} ,\ldots,\varsigma_{t} } \right\}$ are any two finite and completely ordered linguistic term sets with odd cardinality. Then, a PLZN on $Y$ can be given as follows:

$$z = \left\{ {\left( {y,A_{z} \left( y \right),B_{z} \left( y \right)} \right)|y \in Y} \right\},$$

where $A_{z} \left( y \right) = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {p_{i} } \right)|i = 0,1,\ldots,\tau ,\sum\nolimits_{i = 0}^{\tau } {p_{i} \le 1} } \right\}$ is a PLTS, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \in \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}$ and $p_{i}$ is the probability distribution of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$, $B_{z} \left( y \right) \in \Im$. $A_{z} \left( y \right)$ means a fuzzy restriction on the values that $Y$ can take, and $B_{z} \left( y \right)$ is a reliability of $A_{z} \left( y \right)$. Note that the linguistic term sets are usually different, and they are the descriptions of different linguistic information and their special meaning. When there is a specific element $\alpha$ in $Y$, the PLZN is described as $z_{\alpha } = \left( {A_{z} \left( \alpha \right),B_{z} \left( \alpha \right)} \right)$.

PLZN is the generalized forms of many linguistic information representation models. (1) If there is only one linguistic term $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$ in the first component $A_{z} \left( y \right)$ and its probability distribution is equal to 1, PLZN is degenerated into linguistic Z number; (2) If the probability distributions of all possible linguistic terms $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$ in the first component $A_{z} \left( y \right)$ are equal and the sum of probability distributions is equal to 1, PLZN is degenerated into generalized Z number with only one linguistic term in the second component $B_{z} \left( y \right)$, and can be further reduced to uncertain linguistic Z number.

Definition 2

[22] Let $z_{\alpha } = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {p_{i}^{\alpha } } \right)|i = 0,1,\ldots,\tau ,\sum\nolimits_{i = 0}^{\tau } {p_{i}^{\alpha } \le 1} } \right\},\varsigma_{{k_{\alpha } }}^{{}} } \right)$ and $z_{\beta } = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {p_{i}^{\beta } } \right)|i = 0,1,\ldots,\tau ,\sum\nolimits_{i = 0}^{\tau } {p_{i}^{\beta } \le 1} } \right\},\varsigma_{{k_{\beta } }}^{{}} } \right)$ be any two PLZNs. The operation of PLZNs is given as follows:

$$\lambda_{1} z_{\alpha } \oplus \lambda_{2} z_{\beta } = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {\lambda_{1} p_{i}^{\alpha } + \lambda_{2} p_{i}^{\beta } } \right)|i = 0,1,\ldots,\tau } \right\},} \right.g^{ - 1} \left( {\lambda_{1} g\left( {\varsigma_{{k_{\alpha } }}^{{}} } \right) + \lambda_{2} g\left( {\varsigma_{{k_{\beta } }}^{{}} } \right)} \right)$$

(1)

where $\lambda_{1} + \lambda_{2} = 1$,$g\left( \cdot \right)$ is the linguistic scale function in [21] and $g^{ - 1} \left( \cdot \right)$ is the inverse of $g\left( \cdot \right).$

Definition 3

[22] Suppose $z_{\alpha } = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {p_{i}^{\alpha } } \right)|i = 0,1,\ldots,\tau ,\sum\nolimits_{i = 0}^{\tau } {p_{i}^{\alpha } \le 1} } \right\},\varsigma_{{k_{\alpha } }}^{{}} } \right)$ is a PLZN, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}^{{}} \in \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}$ and $\varsigma_{{k_{\alpha } }}^{{}} \in \Im$. The expectation function of $z_{\alpha }$ and deviation function of $z_{\alpha }$ are shown as follows:

$$E\left( {z_{\alpha } } \right) = {{\sum\limits_{i = 0}^{\tau } {f\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} } \right) \cdot } p_{i}^{\alpha } \cdot g\left( {\varsigma_{{k_{\alpha } }}^{{}} } \right)} \mathord{\left/ {\vphantom {{\sum\limits_{i = 0}^{\tau } {f\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} } \right) \cdot } p_{i}^{\alpha } \cdot g\left( {\varsigma_{{k_{\alpha } }}^{{}} } \right)} {\sum\limits_{i = 0}^{\tau } {p_{i}^{\alpha } } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{i = 0}^{\tau } {p_{i}^{\alpha } } }}$$

(2)

$$\sigma \left( {z_{\alpha } } \right) = {{\left( {\left( {\sum\limits_{i =0}^{\tau } {f\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} } \right) \cdot } p_{i}^{\alpha } \cdot g\left( {\varsigma_{{k_{\alpha } }}^{{}} } \right) - E\left( {Z_{\alpha } } \right)} \right)} \right)^{1/2} } \mathord{\left/ {\vphantom {{\left( {\left( {\sum\limits_{i = 0}^{\tau } {f\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} } \right) \cdot } p_{i}^{\alpha } \cdot g\left( {\varsigma_{{k_{\alpha } }}^{{}} } \right) - E\left( {Z_{\alpha } } \right)} \right)} \right)^{1/2} } {\sum\limits_{i = 0}^{\tau } {p_{i}^{\alpha } } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{i = 0}^{\tau } {p_{i}^{\alpha } } }}$$

(3)

where $f\left( \cdot \right)$ and $g\left( \cdot \right)$ are linguistic scale functions in [21],$E\left( {z_{\alpha } } \right)$ is the expectation value of PLZN $z_{\alpha }$, and $\sigma \left( {z_{\alpha } } \right)$ is the deviation value of PLZN $z_{\alpha }$.

Definition 4

[22] Suppose $z_{\alpha }$ and $z_{\beta }$ are any two PLZNs, the comparison method is shown as follows:

• (1) If $E\left( {z_{\alpha } } \right) > E\left( {z_{\beta } } \right)$, then $z_{\alpha } \succ z_{\beta }$;

• (2) If $E\left( {z_{\alpha } } \right) = E\left( {z_{\beta } } \right)$, then.

  • (i) If $\sigma \left( {z_{\alpha } } \right) > \sigma \left( {z_{\beta } } \right)$, then $z_{\alpha } \prec z_{\beta }$;

  • (ii) If $\sigma \left( {z_{\alpha } } \right) = \sigma \left( {z_{\beta } } \right)$, then $z_{\alpha } \sim z_{\beta }$.

Definition 5

Let $z_{1} = \left( {A_{1} ,B_{1} } \right)$ and $z_{2} = \left( {A_{2} ,B_{2} } \right)$ be any two PLZNs, where $A_{1} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}^{{}} \left( {p_{i}^{1} } \right)|i = 0,1,\ldots,\tau ,\sum\nolimits_{i = 0}^{\tau } {p_{i}^{1} \le 1} } \right\}$,$B_{1} = \varsigma_{{k_{1} }}^{{}}$ and $A_{2} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} \left( {p_{f}^{2} } \right)|f = 0,1,\ldots,\tau ,\sum\nolimits_{f = 0}^{\tau } {p_{f}^{2} \le 1} } \right\}$,$B_{2} = \varsigma_{{k_{2} }}^{{}}$. The possibility degree of PLZNs is defined as follows.

$$P\left( {z_{1} \ge z_{2} } \right) = \theta P\left( {A_{1} \ge A_{2} } \right) + \left( {1 - \theta } \right)P\left( {B_{1} \ge B_{2} } \right)$$

(4)

where the parameter $\theta$ lies in [0,1], and it represents the attention of an expert paid to the first component of the PLZNs. The parameter $0 \le \theta < 0.5$ means that the expert thinks that the reliability of the information is more important than the information itself; When the parameter $\theta = 0.5$, the expert thinks the reliability of an information is as important as the information itself; When the parameter $0.5 < \theta \le 1$, the expert pays more attention to the information itself.

The possibility degree $P\left( {A_{1} \ge A_{2} } \right)$ of the first components in PLZNs is shown as in [4]:

$$P\left( {A_{1} \ge A_{2} } \right) = \frac{{H_{1} }}{{H_{1} + H_{2} }}\left( {1 - \sum\limits_{i = 0;f = 0}^{\tau } {R\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \right)} } \right) + \sum\limits_{i = 0;f = 0}^{\tau } {\frac{1}{2}R\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \right)}$$

(5)

$$H_{\kappa } = \left\{ {\begin{array}{*{20}c} {\frac{1}{{\# A_{1} \# A_{2} }}\sum\limits_{{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \right) \in I_{k} }} {\left| {i - f} \right|p_{i} p_{f} ,I_{\kappa } \ne \emptyset } } \\ {0,\;\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad I_{\kappa } = \emptyset } \\ \end{array} } \right.,k = 1,2$$

(6)

$$R\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \right) = \left\{ {\begin{array}{*{20}c} {p_{i} p_{f} ,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \\ {0,\;\quad \,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \ne \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \\ \end{array} } \right.$$

(7)

$$I_{1} = \left\{ {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \right)|i - f > 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}^{{}} \left( {p_{i}^{1} } \right) \in A_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f}^{{}} \left( {p_{f}^{2} } \right) \in A_{2} } \right\}$$

(8)

$$I_{2} = \left\{ {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f} } \right)|i - f < 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}^{{}} \left( {p_{i}^{1} } \right) \in A_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{f}^{{}} \left( {p_{f}^{2} } \right) \in A_{2} } \right\}$$

(9)

where $\# A_{1}$ is the number of linguistic terms with probability distribution greater than 0 in $A_{1}$, and $\# A_{2}$ is the number of linguistic terms with probability distribution greater than 0 in $A_{2}$.

The possibility degree $P\left( {B_{1} \ge B_{2} } \right)$ of the second components in PLZNs is shown as:

The linguistic terms $\varsigma_{{k_{1} }}^{{}}$ and $\varsigma_{{k_{2} }}^{{}}$ in $\Im = \left\{ {\varsigma_{0} ,\varsigma_{1} ,\ldots,\varsigma_{t} } \right\}$ can be transformed into triangular fuzzy numbers $T_{1} = \left( {T_{{l_{1} }} ,T_{{m_{1} }} ,T_{{u_{1} }} } \right)$ and $T_{2} = \left( {T_{{l_{2} }} ,T_{{m_{2} }} ,T_{{u_{2} }} } \right)$. On the basis of the possibility degree of TFNs [11],

$$P\left( {B_{1} \ge B_{2} } \right) = \int_{0}^{1} {P^{\mu } \left( {T_{1} \ge T_{2} } \right)d\mu } = \int_{0}^{1} {\max \left\{ {1 - \max \left\{ {\frac{{\left( {T_{{u_{2} }} - \mu } \right) - \left( {T_{{l_{1} }} + \mu } \right)}}{{\left[ {\left( {T_{{u_{2} }} - \mu } \right) - \left( {T_{{l_{2} }} + \mu } \right)} \right] + \left[ {\left( {T_{{u_{1} }} - \mu } \right) - \left( {T_{{l_{1} }} + \mu } \right)} \right]}}} \right\},0} \right\}d\mu }$$

(10)

Definition 6

Suppose $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\ldots,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{\tau } } \right\}$ and $\Im = \left\{ {\varsigma_{0} ,\varsigma_{1} ,\ldots,\varsigma_{t} } \right\}$ are any two linguistic term sets, $z_{1}$ and $z_{2}$ are any two PLZNs, then.

• (1) If $P\left( {z_{1} \ge z_{2} } \right) = 1$, then $z_{1}$ is absolutely superior to $z_{2}$, i.e., $z_{1} \succ_{s} z_{2}$;

• (2) If $0.5 < P\left( {z_{1} \ge z_{2} } \right) < 1$, then $z_{1}$ is superior to $z_{2}$ with the possibility degree of $P\left( {z_{1} \ge z_{2} } \right)$, i.e., $z_{1} \succ_{P} z_{2}$;

• (3) If $P\left( {z_{1} \ge z_{2} } \right) = 0.5$, then $z_{1}$ is indifferent with $z_{2}$, i.e., $z_{1} \sim z_{2}$.

Example 1

There are two PLZNs $z_{1} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} \left( {0.149} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.189} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.089} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.467} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.107} \right)} \right\},\varsigma_{3} } \right)$ and $z_{2} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} \left( {0.249} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.176} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.154} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.224} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.197} \right)} \right\},\varsigma_{2} } \right)$ from the linguistic term sets $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{0} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{6} } \right\}$ and $\Im = \left\{ {\varsigma_{0} ,\varsigma_{1} ,\varsigma_{2} ,\varsigma_{3} ,\varsigma_{4} } \right\}$. In accordance with the Eq. (4)–Eq. (10), the possibility degree of $P\left( {z_{1} \ge z_{2} } \right)$ can be obtained as follows:

$$I_{1} = \left\{ {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} } \right)} \right\}$$

$$I_{2} = \left\{ {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} } \right),\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} } \right)} \right\}$$

$$H_{1} = 0.029,H_{2} = 0.034$$

$$P\left( {A_{1} \ge A_{2} } \right) = \frac{0.029}{{0.029 + 0.034}}\left( {1 - 0.027 - 0.082 - 0.014 - 0.042 - 0.029} \right) + \frac{1}{2}\left( {0.027 + 0.082 + 0.014 + 0.042 + 0.029} \right) = 0.465.$$

Because the linguistic term $\varsigma_{3}$ is equivalent to triangular fuzzy number $\left( {0.25,0.5,0.75} \right)$ and $\varsigma_{2}$ is equivalent to triangular fuzzy number $\left( {0,0.25,0.5} \right)$, the possibility degree of $P\left( {B_{1} \ge B_{2} } \right)$ can be calculated as follows:

$$P\left( {B_{1} \ge B_{2} } \right) = \frac{0.75}{{0.5 + 0.5}} + \frac{0.25}{{0.5 + 0.5}}\ln \left( {\frac{0.25}{{0.25 + 0.25}}} \right) = 0.577$$

So, the possibility degree of $P\left( {z_{1} \ge z_{2} } \right)$ can be obtained (Suppose $\theta = 0.5$)

$$P\left( {z_{1} \ge z_{2} } \right) = 0.5 \times 0.465 + 0.5 \times 0.577 = 0.521$$

Property 1

Suppose $z_{1}$ and $z_{2}$ are any two PLZNs. The possibility degree of $z_{1}$ and $z_{2}$ satisfies the following properties:

• (1) $0 \le P\left( {z_{1} \ge z_{2} } \right) \le 1$;

• (2) $P\left( {z_{1} \ge z_{2} } \right) + P\left( {z_{2} \ge z_{1} } \right) = 1$;

• (3) $P\left( {z_{1} \ge z_{2} } \right) = P\left( {z_{2} \ge z_{1} } \right) = 0.5$, if and only if $z_{1} \sim z_{2}$;

• (4) If $P\left( {z_{1} \ge z_{2} } \right) \ge 0.5,P\left( {z_{2} \ge z_{3} } \right) \ge 0.5,{\kern 1pt}$ then $P\left( {z_{1} \ge z_{3} } \right) \ge 0.5{\kern 1pt}$.

2.2 Evidential Reasoning Theory

Definition 7

[2, 15] Let $\Theta = \left\{ {\aleph_{1} ,\aleph_{2} ,\ldots,\aleph_{N} } \right\}$ be a frame of discernment. A mass function is mapping $\tilde{m}:R\left( \Theta \right) \to \left[ {0,1} \right]$, which is also called a basic probability assignment, satisfying.

$\tilde{m}\left( \emptyset \right) = 0$ and $\sum\nolimits_{D \subseteq \Theta } {\tilde{m}\left( D \right)} = 1$, where $\emptyset$ is an empty set, $D$ is any subset of $\Theta$, $R\left( \Theta \right)$ is the power set of $\Theta$, consisted of all subsets of $\Theta$, i.e., $R\left( \Theta \right) = \left\{ {\emptyset ,\left\{ {\aleph_{1} } \right\},\ldots,\left\{ {\aleph_{N} } \right\},\left\{ {\aleph_{1} \cup \aleph_{2} } \right\},\ldots,\left\{ {\aleph_{1} \cup \aleph_{N} } \right\},\ldots,\Theta } \right\}$. $\tilde{m}\left( D \right)$ is the belief degree assigned to $D$, which represents how strongly the evidence supports $D$. $\tilde{m}\left( \Theta \right)$ is the belief degree of ignorance. If $\tilde{m}\left( D \right) > 0$, then $D$ is called a focal element, and all focal elements make up the body of evidence $\tilde{m}$.

Definition 8

[15] Suppose $F_{1}$ and $F_{2}$ are any two pieces of evidence. The mass functions for two items are $\tilde{m}_{1}$ and $\tilde{m}_{2}$. The D-S rule of evidence fusion is shown:

$$\tilde{m}\left( D \right) = \left( {\tilde{m}_{1} \oplus \tilde{m}_{2} } \right)\left( D \right) = \frac{{\sum\limits_{G,H \subset \Theta ,G \cap H = D} {\tilde{m}_{1} \left( G \right)} \tilde{m}_{2} \left( H \right)}}{{1 - \sum\limits_{G \cap H = \emptyset } {\tilde{m}_{1} \left( G \right)} \tilde{m}_{2} \left( H \right)}}$$

(11)

2.3 Fuzzy Mmeasure and Generalized Shapley Function

Definition 9

[5] Let $g$ be the 2-additive fuzzy measure on $N = \left\{ {r_{1} ,r_{2} ,\ldots,r_{n} } \right\}$, given any $R \subseteq N$ with $\# R \ge 2$, then

$$g\left( R \right) = \sum\limits_{{\left\{ {r_{\alpha } ,r_{\beta } } \right\} \subseteq R}} {g\left( {\left\{ {r_{\alpha } ,r_{\beta } } \right\}} \right) - \left( {\# R - 2} \right)} \sum\limits_{{r_{\alpha } \in R}} {g\left( {\left\{ {r_{\alpha } } \right\}} \right)} .$$

(12)

where $\# R$ is the number of elements in $R$. To acquire 2-additive fuzzy measure, it is only needed that $n\left( {n + 1} \right)/2$ coefficients $g\left( {\left\{ {r_{\alpha } } \right\}} \right)$ and $g\left( {\left\{ {r_{\alpha } ,r_{\beta } } \right\}} \right)$ are determined.

Theorem 1

[5] Suppose $g$ is a 2-additive fuzzy measure on $N = \left\{ {r_{1} ,r_{2} ,\ldots,r_{n} } \right\}$, if and only if there are coefficients $g\left( {\left\{ {r_{\alpha } } \right\}} \right)$ and $g\left( {\left\{ {r_{\alpha } ,r_{\beta } } \right\}} \right)$ for $\forall r_{\alpha } \in N,\forall r_{\beta } \in N$, which meets the following conditions:

• (1) $g\left( {\left\{ {r_{\alpha } } \right\}} \right) \ge 0,r_{\alpha } \in N$;

• (2) $\sum\nolimits_{{\left\{ {r_{\alpha } ,r_{\beta } } \right\} \subseteq N}} {g\left( {\left\{ {r_{\alpha } ,r_{\beta } } \right\}} \right) - \left( {\# N - 2} \right)} \sum\nolimits_{{r_{\alpha } \in R}} {g\left( {\left\{ {r_{\alpha } } \right\}} \right)} = 1$;

• (3) $\sum\nolimits_{{\left\{ {r_{\alpha } } \right\} \subseteq Q\backslash \left\{ {r_{\beta } } \right\}}} {\left( {g\left( {\left\{ {r_{\alpha } ,r_{\beta } } \right\}} \right) - g\left( {\left\{ {r_{\alpha } } \right\}} \right)} \right)} \ge \left( {\# Q - 2} \right)g\left( {\left\{ {r_{\beta } } \right\}} \right),\forall Q \subseteq N,r_{\beta } \in Q,with\# Q \ge, 2$ where $\# Q$ and $\# N$ are the cardinalities of $Q$ and $N$, respectively, and $Q\backslash \left\{ {r_{\beta } } \right\}$ is the difference set between $Q$ and $\left\{ {r_{\beta } } \right\}$.

Theorem 2

[9] Suppose $g$ is the 2-additive fuzzy measure on $N = \left\{ {r_{1} ,r_{2} ,\ldots,r_{n} } \right\}$. The generalized Shapley function is shown as follows:

$$\phi_{R} \left( {g,N} \right) = \sum\limits_{{\left\{ {r_{\alpha } ,r_{\beta } } \right\} \subseteq R}} {g\left( {r_{\alpha } ,r_{\beta } } \right)} + \frac{1}{2}\sum\limits_{{r_{\alpha } \in R,r_{\beta } \in N\backslash R}}^{{}} {\left( {g\left( {r_{\alpha } ,r_{\beta } } \right) - \# Rg\left( {r_{\beta } } \right)} \right) - } \frac{\# N + \# R - 4}{2}\sum\limits_{{r_{\alpha } \in R}}^{{}} {g\left( {r_{\alpha } } \right)}$$

(13)

where $\# R$ and $\# N$ are the cardinalities of $R$ and $N$, respectively. If there is only one element in $R$, i.e., $\left\{ {r_{\alpha } } \right\} = R \subseteq N$, then the generalized Shapley function is degenerated into the Shapley function with 2-additive fuzzy measure:

$$\phi_{{\left\{ {r_{\alpha } } \right\}}} \left( {g,N} \right) = \frac{3 - \# N}{2}g\left( {r_{\alpha } } \right) + \frac{1}{2}\sum\limits_{{r_{\beta } \in N\backslash \left\{ {r_{\alpha } } \right\}}}^{{}} {\left( {g\left( {r_{\alpha } ,r_{\beta } } \right) - g\left( {r_{\beta } } \right)} \right)} ,\forall r_{\alpha } \in N.$$

(14)

Theorem 3

[9] Suppose $g$ is the 2-additive fuzzy measure on $N = \left\{ {r_{1} ,r_{2} ,\ldots,r_{n} } \right\}$, and $\phi$ is the generalized Shapley function with 2-additive fuzzy measure $g$. Then,

$$\phi_{{R \cup \left\{ {r_{\sigma } } \right\}}} \left( {g,N} \right) - \phi_{R} \left( {g,N} \right) = \phi_{{\left\{ {r_{\sigma } } \right\}}} \left( {g,N} \right),\forall r_{\sigma } \in N,\forall R \subseteq N,r_{\sigma } \notin R.$$

(15)

3 Framework for MAGDM Problem with Incomplete Probabilities and Heterogeneous Correlations

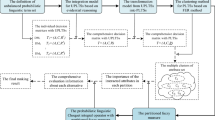
This section describes a MAGDM problem where lots of interacted attributes are utilized to rank a limited number of alternatives and the incomplete information exist in experts’ consciousness. The specific resolution framework which is used to analyze and solve such MAGDM problem is displayed as follows.

3.1 Description of the MAGDM Problem with PLZNS

Due to the increasing complexity of decision-making environment, the PLZNs are utilized to present decision-making information about alternatives in the attribute set. The following notations describe the MAGDM problems with PLZNs.

• (1) Let $X = \left\{ {X_{1} ,X_{2} ,\ldots,X_{m} } \right\}$ be the set of $m$ alternatives, where $X_{l} \left( {l = 1,2,\ldots,m} \right)$ is the lth alternative. The $m$ alternatives are the evaluation of objects, which can be regarded as the urban disaster emergency response capability of m cities in this paper.

• (2) Let $C = \left\{ {C_{1} ,C_{2} ,\ldots,C_{n} } \right\}$ be the set of $n$ attributes, where $C_{j} \left( {j = 1,2,\ldots,n} \right)$ is the jth attribute and $n$ is more than $m$. The $n$ attributes are the appraisal standards, in concrete that the ability of hazards identification, the ability of disaster forecast, the emergency command ability, the emergency resource reserve ability, the medical rescue ability, the ability of post-disaster reconstruction, the rescue coordination ability, the disaster assessment and decision-making ability.

• (3) Let $W = \left( {w_{1} ,w_{2} ,\ldots,w_{n} } \right)$ be the vector of weight on the attribute set, where $w_{j} \left( {j = 1,2,\ldots,n} \right)$ is the weight of attribute $C_{j}$, such that $0 \le w_{j} \le 1$ and $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1.$ This paper assumes that the weights in attribute set are incompletely unknown.

• (4) Let $D = \left\{ {D_{1} ,D_{2} ,\ldots,D_{d} } \right\}$ be the set of $d$ experts, where $D_{e} \left( {e = 1,2,\ldots,d} \right)$ is the eth expert. The $d$ experts are the scholars engaged in the research of crisis management in Colleges and universities and the staff of municipal government emergency office in this paper.

• (5) Let $\omega = \left( {\omega_{1} ,\omega_{2} ,\ldots,\omega_{d} } \right)$ be the vector of weight on the expert set, where $\omega_{e} \left( {e = 1,2,\ldots,d} \right)$ is the weight of expert $D_{e}$, such that $0 \le \omega_{e} \le 1$ and $\sum\nolimits_{e = 1}^{d} {\omega_{e} } = 1$. The weight $\omega_{e}$ represents the importance of expert $D_{e}$, which dependents on the expert’ vocational accomplishment and the standard of knowledge.

• (6) Let $Z^{e} = \left[ {z_{lj}^{e} } \right]_{m \times n}$ be the probabilistic linguistic Z number decision matrix, where $z_{lj}^{e}$ is the evaluation information of the alternative $X_{l}$ with respect to the attribute $C_{j}$ given by expert $D_{e}$. This evaluation information is shown in the form of PLZN, in which exist incomplete probability distributions of linguistic terms in the first component.

3.2 Resolution Framework for the MAGDM Problem with PLZNs

In accordance with the characteristic existed in MAGDM problem, a resolution framework is constructed to solve the above problem (shown in Fig. 1), which can be divided into the following parts:

Fig. 1

The framework of MAGDM method for probabilistic term Z number sets

3.3 Part 1: Obtain Experts’ Evaluation Information

According to their own cognitive context of experts, respectively, each expert gives his/her evaluation information $z_{lj}^{e}$, which contains two components: the first component showing in the form of PLTS describes his/her true feeling about the alternative $X_{l}$ with respect to the attribute $A_{j}$; the second component shows his/her reliability of the presentation of personal feeling. The evaluation information given by all experts about alternatives in the attribute set are collected to form probabilistic linguistic Z number decision matrix.

3.4 Part 2: Develop an Integration Model with PLZNs Based on Evidential Reasoning Theory

In view of the incomplete probability distributions in first component of PLNZ, an integration model based on evidential reasoning theory is proposed to aggregate PLZNs from different experts. In consideration of the effect of evidential reasoning theory in handling incomplete uncertainty, the proposed integration model can be applied more widely in obtaining the comprehensive evaluation information of alternatives in attribute set.

3.5 Part 3: Construct a Weight Determination Model with Generalized Shapley Function

Given that the attribute weight is incompletely unknown and there are heterogeneous relationships among attributes, a weight determination model with generalized Shapley function is developed to calculate the importance of each attribute. The model is constructed on the theory that an attribute with smaller difference on evaluation values among alternatives displays less importance, while an attribute with larger difference on evaluation values among alternatives shows greater importance. In this model, the generalized Shapley values are utilized to represent the importance of attributes.

3.6 Part 4: Give a probabilistic linguistic Z QUALIFLEX method with generalized Shapley function

Considering that the number of attributes is more than the number of alternatives, this part develops an extended probabilistic linguistic Z QUALIFLEX method. Meanwhile, in view of the heterogeneous relationships among attributes, the generalized Shapley function is incorporated into the probabilistic linguistic Z QUALIFLEX method, thus providing a probabilistic linguistic Z QUALIFLEX method with generalized Shapley function. The proposed method is constructed on the pairwise comparison of alternatives with respect to each attribute among all possible permutations of alternatives.

4 MAGDM Method with Heterogeneous Correlations Among Attributes

4.1 The Integration Model Based on Evidential Reasoning Theory

In accordance with the PLZN with the first component displaying in the form of PLTS and the second component showing the form of linguistic term, we utilize the evidential theory to aggregate the first component $A_{lj}^{e} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {p_{{i,_{lj}^{e} }} } \right)|i = 0,1,\ldots,\tau ,\sum\nolimits_{i = 0}^{\tau } {p_{{i,_{lj}^{e} }} \le 1} } \right\}$ in PLZNs $z_{lj}^{e} = \left( {A_{lj}^{e} ,B_{lj}^{e} } \right)$. The probability distribution $p_{{i,_{lj}^{e} }}$ of linguistic term $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$ can be regarded as belief degree $p_{{i,_{lj}^{e} }}$ given to an assessment grade $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$. And then we can get the basic probability assignment by multiplying the belief degree $p_{{i,_{lj}^{e} }}$ by the weight $w_{e}$ using the following formula.

• (1) Obtain the weighted basic probability assignment

  $$\tilde{m}_{i} \left( {A_{lj}^{e} } \right) = w_{e} p_{{i,_{lj}^{e} }} ,{\kern 1pt} \;i = 0,1,\ldots,\tau ;e = 1,2,\ldots,d;l = 1,2,\ldots,m;j = 1,2,\ldots,n$$

  (16)
  $$\tilde{m}_{S} \left( {A_{lj}^{e} } \right) = 1 - \sum\limits_{i = 0}^{\tau } {w_{e} p_{{i,_{lj}^{e} }} }$$

  (17)

• (2) Determinate the combined basic probability assignment $\tilde{n}_{i} \left( {A_{lj}^{{\left( {\sigma + 1} \right)}} } \right)$ from the expert subset $\left\{ {D_{1} ,D_{2} ,\ldots,D_{\sigma + 1} } \right\}$ $\left( {\sigma = 1,2,\ldots,d - 1} \right)$ experts and the remaining combined probability assignment $\tilde{n}_{S} \left( {A_{lj}^{{\left( {\sigma + 1} \right)}} } \right)$

  $$\tilde{n}_{i} \left( {A_{lj}^{{\left( {\sigma + 1} \right)}} } \right) = \frac{{\tilde{n}_{i} \left( {A_{lj}^{\left( \sigma \right)} } \right) \cdot \tilde{m}_{i} \left( {A_{lj}^{\sigma + 1} } \right) + \tilde{n}_{i} \left( {A_{lj}^{\left( \sigma \right)} } \right) \cdot \tilde{m}_{S} \left( {A_{lj}^{\sigma + 1} } \right) + \tilde{n}_{S} \left( {A_{lj}^{\left( \sigma \right)} } \right) \cdot \tilde{m}_{i} \left( {A_{lj}^{\sigma + 1} } \right)}}{{1 - \sum\limits_{i = 0}^{\tau } {\sum\limits_{f = 0;f \ne i}^{\tau } {\tilde{n}_{i} \left( {A_{lj}^{\left( \sigma \right)} } \right) \cdot \tilde{m}_{f} \left( {A_{lj}^{\sigma + 1} } \right)} } }}$$

  (18)
  $$\tilde{n}_{S} \left( {A_{lj}^{{\left( {\sigma + 1} \right)}} } \right) = \frac{{\tilde{n}_{S} \left( {A_{lj}^{\left( \sigma \right)} } \right) \cdot \tilde{m}_{S} \left( {A_{lj}^{\sigma + 1} } \right)}}{{1 - \sum\limits_{i = 0}^{\tau } {\sum\limits_{f = 0;f \ne i}^{\tau } {\tilde{n}_{i} \left( {A_{lj}^{\left( \sigma \right)} } \right) \cdot \tilde{m}_{f} \left( {A_{lj}^{\sigma + 1} } \right)} } }}$$

  (19)

  where $\tilde{n}_{i} \left( {A_{lj}^{{o\left( {\sigma + 1} \right)}} } \right)$ denotes the combined basic probability assignment of the assessment grade $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$ from the expert subset $\left\{ {D_{1} ,D_{2} ,\ldots,D_{\sigma + 1} } \right\}$ about the alternative $X_{l}$ under the attribute $C_{j}$; $\tilde{n}_{S} \left( {A_{lj}^{{o\left( {\sigma + 1} \right)}} } \right)$ denotes the combined basic probability assignment that is not assigned to any assessment grade.

  $$\tilde{n}_{i} \left( {A_{lj}^{\left( 1 \right)} } \right) = \tilde{m}_{i} \left( {A_{lj}^{1} } \right),\tilde{n}_{S} \left( {A_{lj}^{\left( 1 \right)} } \right) = \tilde{m}_{S} \left( {A_{lj}^{1} } \right)$$

  (20)

• (3) Calculate the comprehensive basic probability assignment of the assessment grade $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$ from all experts

  $$\tilde{p}_{S} \left( {A_{lj} } \right) = \sum\limits_{e = 1}^{d} {w_{e} } \left( {1 - \sum\limits_{i = 0}^{\tau } {p_{{i,_{lj}^{e} }} } } \right)$$

  (21)
  $$\tilde{p}_{i} \left( {A_{lj} } \right) = \left( {1 - \tilde{p}_{S} \left( {A_{lj} } \right)} \right)\frac{{\tilde{n}_{i} \left( {A_{lj}^{\left( d \right)} } \right)}}{{1 - \tilde{n}_{S} \left( {A_{lj}^{\left( d \right)} } \right)}}$$

  (22)

  where $\tilde{p}_{i} \left( {A_{lj} } \right)$ means the comprehensive basic probability assignment of linguistic term $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i}$, and $\tilde{p}_{S} \left( {A_{lj} } \right)$ means the unknown probability assigned to $A_{lj}$, which satisfies $\sum\nolimits_{i = 0}^{\tau } {\tilde{p}_{i} \left( {A_{lj} } \right) + \tilde{p}_{S} \left( {A_{lj} } \right)} = 1$.

Therefore, the aggregated result of the first component in PLZN is shown as $A_{lj} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{i} \left( {\tilde{p}_{i} \left( {A_{lj} } \right)} \right)|i = 0,1,\ldots,\tau ;\sum\nolimits_{i = 0}^{\tau } {\tilde{p}_{i} \left( {A_{lj} } \right) = 1} } \right\}$.

According to the operational rule of PLZNs in [22], the aggregated result of the second component $B_{lj}^{e} = \varsigma_{{k,_{lj}^{e} }}$ in PLZNs is

$$B_{lj} = \mathop \oplus \limits_{e = 1}^{d} w_{e} B_{lj}^{e} = g^{ - 1} \left( {\sum\limits_{e = 1}^{d} {w_{e} \cdot g\left( {\varsigma_{{k_{{_{lj}^{e} }} }}^{{}} } \right)} } \right)$$

(23)

Through the analysis, we can obtain the aggregated result $z_{lj} = \left( {A_{lj} ,B_{lj} } \right)$ from all experts about alternative $A_{l}$ with respect to attribute $C_{j}$.

4.2 The PLZNs Mathematical Programing Model

We measure the weighted possibility degree which the alternative $X_{l}$ is not inferior to other alternatives $X_{h} \left( {h \ne l} \right)$ with respect to attribute $C_{j}$.

$$P_{lj} = \sum\limits_{f = 1;f \ne l}^{m} {\left( {\varphi_{{C_{j} }} \left( {g,C} \right) \cdot P\left( {z_{lj} \ge z_{fj} } \right)} \right)}^{2}$$

(24)

where $P\left( {z_{lj} \ge z_{fj} } \right)$$l = 1,2,\ldots,m;j = 1,2,\ldots,n$ is obtained by Eq. (4).

We measure the total weighted square possibility degree $P_{j}$ which all alternatives superior to the others with respect to attribute $C_{j}$ is determined as:

$$P_{j} = \sum\limits_{l = 1}^{m} {P_{lj} } = \sum\limits_{l = 1}^{m} {\sum\limits_{f = 1;f \ne l}^{m} {\left( {\varphi_{{C_{j} }} \left( {g,C} \right) \cdot P\left( {z_{lj} \ge z_{fj} } \right)} \right)^{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} } }$$

(25)

Finally, based on these analyses, it is reasonable to determine the attribute weight vector, which makes the total weighted square possibility degree $P_{j}$ maximized. Hence, a programming model is established:

$$Max\,P = \sum\limits_{j = 1}^{n} {\sum\limits_{l = 1}^{m} {\sum\limits_{f = 1;f \ne l}^{m} {\left( {\varphi_{{C_{j} }} \left( {g,C} \right) \cdot P\left( {z_{lj} \ge z_{fj} } \right)} \right)^{2} } } }$$

$$\left\{ {\begin{array}{*{20}c} {\varphi_{{C_{j} }} \left( {g,C} \right) = \frac{3 - n}{2}g\left( {C_{j} } \right) + \frac{1}{2}\sum\limits_{{C_{\eta } \in C\backslash C_{j} }} {\left( {g\left( {C_{j} ,C_{\eta } } \right) - g\left( {C_{\eta } } \right)} \right)} } \\ {g\left( \phi \right) = 0,g\left( C \right) = 1\quad \quad \quad \quad \quad \quad \;\;\quad \quad \quad \quad \quad \quad \;\;\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {g\left( Q \right) \le g\left( R \right),\forall Q,R \subseteq C,Q \subseteq R\quad \quad \quad \quad \quad \quad \quad \;\;\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {g\left( {C_{j} } \right) \in H_{{C_{j} }} \quad \quad \quad \quad \quad \quad \quad \;\;\quad \quad \quad \quad \quad \quad \quad \quad \;\;\quad } \\ \end{array} } \right.$$

(26)

where $P\left( {z_{lj} \ge z_{fj} } \right)$ is the possibility degree that $z_{lj}$ is better than $z_{fj}$.

4.3 The PLZ-QUALIFLEX Method with the Generalized Shapley Values

QUALIFELX method is one of the well-known outranking methods, which correctly treat the cardinal and ordinal information. We extend the classical QUALIFLEX method to probabilistic linguistic Z number environment. Due to the heterogeneous relationships among attributes, the generalized Shapley values of attributes are combined with the extension of QUALIFLEX in PLZNs context. Based on this, PLZ-QUALIFLEX method with generalized Shapley values is constructed as:

(1) Obtain all of the possible permutations of alternatives.

Based on $m$ alternatives, we can obtain $m!$ permutations of $m$ alternatives. Let ${\mathbb{R}}_{r}$ be the rth permutation as: ${\mathbb{R}}_{r} = \left( {\ldots,X_{\varepsilon } ,X_{\upsilon } } \right),r = 1,2,\ldots,m!$, where $X_{\varepsilon } ,X_{\upsilon } \in X$ and the alternative $X_{\varepsilon }$ is ranked higher than or equal to $X_{\upsilon }$.

(2) Determinate the concordance/discordance index ${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)$ for each pair of $\left( {X_{\varepsilon } ,X_{\upsilon } } \right)$ in the permutation ${\mathbb{R}}_{r}$ under the attribute $C_{j}$.

$${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right) = P\left( {z_{\varepsilon j} \ge z_{\upsilon j} } \right) - 0.5$$

(27)

If ${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right) \in \left[ {0,0.5} \right]$, then there is concordance; If ${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right) \in \left[ {\left. { - 0.5,0} \right)} \right.$, then there is discordance.

(3) Calculate the overall concordance/discordance index ${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)$ for each pair of $\left( {X_{\varepsilon } ,X_{\upsilon } } \right)$ in the permutation ${\mathbb{R}}_{r}$.

$${\mathbb{C}}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right) = \sum\limits_{j = 1}^{n} {\left( {\varphi_{{\hat{C}_{j} }} \left( {g,C} \right) - \varphi_{{\hat{C}_{j + 1} }} \left( {g,C} \right)} \right){\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)} ,\;r = 1,2,\ldots,m!;\varepsilon ,\upsilon = 1,2,\ldots,m.$$

(28)

where $\varphi_{{\hat{C}_{\left( j \right)} }} \left( {g,C} \right)$ is the generalized Shapley value of the attribute subset $\hat{C}_{j} = \left\{ {C_{j} ,C_{j + 1} ,\ldots,C_{n} } \right\}$.

According to the theorem 3, we can know that ${\mathbb{C}}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right) = \sum\nolimits_{j = 1}^{n} {\varphi_{{C_{j} }} \left( {g,C} \right){\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)}$. So, the Eq. (28) can be degenerated into ${\mathbb{C}}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right) = \sum\nolimits_{j = 1}^{n} {\varphi_{{C_{j} }} \left( {g,C} \right){\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)}$.

(4) Obtain the comprehensive concordance/discordance index ${\mathbb{C}}^{r}$.

$${\mathbb{C}}^{r} = \sum\limits_{{X_{\varepsilon } ,X_{\upsilon } \in X}} {\sum\limits_{j = 1}^{n} {{\mathbb{C}}_{\left( j \right)}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)\left( {\varphi_{{\hat{C}_{\left( j \right)} }} \left( {g,C} \right) - \varphi_{{\hat{C}_{{\left( {j + 1} \right)}} }} \left( {g,C} \right)} \right)} }$$

(29)

(5) Determinate the optimal ranking order of alternatives.

$${\mathbb{C}}^{*} = \mathop {\max }\limits_{r = 1}^{m!} \left\{ {{\mathbb{C}}^{r} } \right\}$$

(30)

Based on the ${\mathbb{C}}^{r} ,r = 1,2,\ldots,m!$, and the final ranking order can be obtained. The larger the ${\mathbb{C}}^{r}$, the better the corresponding permutation is.

From the aforementioned procedures, it can be founded that the proposed method selects the best one from all permutations of multiple alternatives so that it is well-suited for analyzing decision-making problems where the number of attributes is greatly exceed the number of alternatives. Moreover, it utilizes the generalized Shapley values to model the interactions among attributes so that it is suitable for analyzing decision-making problems where the attributes are not independent.

5 Numerical Example

5.1 Application of the Resolution Framework

Example 2:

Along with the development of economy and the acceleration of urbanization, the economic losses and social impact caused by urban disaster begins to expand unceasingly. To improve the ability for urban disaster emergency response, it is necessary to make a scientific evaluation about the urban disaster emergency response. For evaluating the urban disaster emergency response capability of four cities $X_{1} ,X_{2} ,X_{3} ,X_{4}$, four experts $D_{1} ,D_{2} ,D_{3} ,D_{4}$ who have been engaged in emergency management for a long time evaluate the four cities separately according to the attribute set $C = \left\{ {C_{1} ,C_{2} ,\ldots,C_{8} } \right\}$. $C_{1} :$ the ability of hazards identification, $C_{2} :$ the ability of disaster forecast; $C_{3} :$ the emergency command ability; $C_{4} :$ the emergency resource reserve ability; $C_{5} :$ the medical rescue ability; $C_{6} :$ the ability of post-disaster reconstruction; $C_{7} :$ the rescue coordination ability; $C_{8} :$ the disaster assessment and decision-making ability. Generally, there exist heterogeneous relationships among attribute set, ranging from a negative synergetic interaction to a positive synergetic interaction. The four experts are equally important and they give the evaluation information about each alternative with respect to the attribute set. They select the appropriate linguistic terms from linguistic term set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S} = \left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{0} :} \right.extremely{\kern 1pt} {\kern 1pt} poor,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} :{\kern 1pt} very{\kern 1pt} poor,{\kern 1pt} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} :poor,{\kern 1pt} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} :medium,{\kern 1pt} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} :good,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} :{\kern 1pt} very{\kern 1pt} good,\left. {{\kern 1pt} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{6} :extremely{\kern 1pt} good} \right\}$ to show their performance. In view of the differences of cognition degree among experts, the reliability of their evaluation is divided into five level, i.e., $\Im = \left\{ {\varsigma_{0} :} \right.impossible,\varsigma_{1} :{\kern 1pt} doubtful,{\kern 1pt} \varsigma_{2} :fair,{\kern 1pt}$$\varsigma_{3} :acceptable,{\kern 1pt} \left. {\varsigma_{4} :credible} \right\}$. According to the evaluation information from four experts, the ranking result of four alternatives can be determined based on the resolution framework.

5.1.1 Step 1: Collect the Original Evaluation Information

Due to the hesitation and uncertainty existed in each expert’ consciousness, he/she prefers to utilize the PLTS to describe his/her true feeling about each alternative with respect to each attribute and tends to use an appropriate linguistic term to show his/her reliability. Based on the definition of PLZNs, the original evaluation information from four experts are expressed as PLZNs, shown in Tables 1, 2, 3, and 4.

Table 1 Decision matrix with PLZNs from expert D₁

Table 2 Decision matrix with PLZNs from expert D₂

Table 3 Decision matrix with PLZNs from expert D₃

Table 4 Decision matrix with PLZNs from expert D₄

5.1.2 Step 2: Obtain the Collective Evaluation Information

Because the importance of each expert is equal, the weights of experts are $\omega_{1} = 0.25,\omega_{2} = 0.25,\omega_{3} = 0.25,\omega_{4} = 0.25$. Based on the integration model shown in Sect. 4.1, the collective evaluation information can be determined, shown in Table 5.

Table 5 The collective decision matrix with PLZNs

5.1.3 Step 3: Obtain the Generalized Shapley Values of Attributes

It is assumed that these attributes are independent, and the importance of each attribute is shown below:

$g\left( {\left\{ {C_{1} } \right\}} \right) = 0.423,g\left( {\left\{ {C_{2} } \right\}} \right) = 0.049,g\left( {\left\{ {C_{3} } \right\}} \right) = 0.023,g\left( {\left\{ {C_{4} } \right\}} \right) = 0.034,g\left( {\left\{ {C_{5} } \right\}} \right) = 0.019,g\left( {\left\{ {C_{6} } \right\}} \right) = 0.036,g\left( {\left\{ {C_{7} } \right\}} \right) = 0.374,g\left( {\left\{ {C_{8} } \right\}} \right) = 0.043$.

In view of the independence between attributes, we can obtain $g\left( {\left\{ {C_{1} ,C_{2} } \right\}} \right) = g\left( {\left\{ {C_{1} } \right\}} \right) + g\left( {\left\{ {C_{2} } \right\}} \right) = 0.472.$ So, we can obtain the other 2-additive fuzzy measures, i.e.,

$$g\left( {\left\{ {C_{1} ,C_{3} } \right\}} \right) = 0.446,g\left( {\left\{ {C_{1} ,C_{4} } \right\}} \right) = 0.456,g\left( {\left\{ {C_{1} ,C_{5} } \right\}} \right) = 0.441,g\left( {\left\{ {C_{1} ,C_{6} } \right\}} \right) = 0.458,g\left( {\left\{ {C_{1} ,C_{7} } \right\}} \right) = 0.797,g\left( {\left\{ {C_{1} ,C_{8} } \right\}} \right) = 0.465,$$

$$g\left( {\left\{ {C_{2} ,C_{3} } \right\}} \right) = 0.073,g\left( {\left\{ {C_{2} ,C_{4} } \right\}} \right) = 0.083,g\left( {\left\{ {C_{2} ,C_{5} } \right\}} \right) = 0.068,g\left( {\left\{ {C_{2} ,C_{6} } \right\}} \right) = 0.085,g\left( {\left\{ {C_{2} ,C_{7} } \right\}} \right) = 0.424,g\left( {\left\{ {C_{2} ,C_{8} } \right\}} \right) = 0.092,g\left( {\left\{ {C_{3} ,C_{4} } \right\}} \right) = 0.057,g\left( {\left\{ {C_{3} ,C_{5} } \right\}} \right) = 0.042,g\left( {\left\{ {C_{3} ,C_{6} } \right\}} \right) = 0.059,g\left( {\left\{ {C_{3} ,C_{7} } \right\}} \right) = 0.397,g\left( {\left\{ {C_{3} ,C_{8} } \right\}} \right) = 0.066,g\left( {\left\{ {C_{4} ,C_{5} } \right\}} \right) = 0.052,g\left( {\left\{ {C_{4} ,C_{6} } \right\}} \right) = 0.069,g\left( {\left\{ {C_{4} ,C_{7} } \right\}} \right) = 0.408,g\left( {\left\{ {C_{4} ,C_{8} } \right\}} \right) = 0.076,g\left( {\left\{ {C_{5} ,C_{6} } \right\}} \right) = 0.054,g\left( {\left\{ {C_{5} ,C_{7} } \right\}} \right) = 0.393,g\left( {\left\{ {C_{5} ,C_{8} } \right\}} \right) = 0.061,g\left( {\left\{ {C_{6} ,C_{7} } \right\}} \right) = 0.410,$$

$$g\left( {\left\{ {C_{6} ,C_{8} } \right\}} \right) = 0.078,g\left( {\left\{ {C_{7} ,C_{8} } \right\}} \right) = 0.417.$$

In accordance with the Eq. (14), the generalized Shapley values of eight attributes can be determined, i.e.,

$$\phi \left( {\left\{ {C_{1} } \right\}} \right) = 0.423,\phi \left( {\left\{ {C_{2} } \right\}} \right) = 0.049,\phi \left( {\left\{ {C_{3} } \right\}} \right) = 0.023,\phi \left( {\left\{ {C_{4} } \right\}} \right) = 0.034,\phi \left( {\left\{ {C_{5} } \right\}} \right) = 0.019,\phi \left( {\left\{ {C_{6} } \right\}} \right) = 0.036,\phi \left( {\left\{ {C_{7} } \right\}} \right) = 0.374,\phi \left( {\left\{ {C_{8} } \right\}} \right) = 0.043.$$

5.1.4 Step 4: Determine All Possible Permutations of Alternatives

Four alternatives can form 24 permutations of alternatives, i.e.,

$${\mathbb{R}}_{1} = \left( {X_{1} ,X_{2} ,X_{3} ,X_{4} } \right),{\mathbb{R}}_{2} = \left( {X_{1} ,X_{2} ,X_{4} ,X_{3} } \right),{\mathbb{R}}_{3} = \left( {X_{1} ,X_{3} ,X_{2} ,X_{4} } \right),{\mathbb{R}}_{4} = \left( {X_{1} ,X_{3} ,X_{4} ,X_{2} } \right),{\mathbb{R}}_{5} = \left( {X_{1} ,X_{4} ,X_{2} ,X_{3} } \right),{\mathbb{R}}_{6} = \left( {X_{1} ,X_{4} ,X_{3} ,X_{2} } \right),$$

$${\mathbb{R}}_{7} = \left( {X_{2} ,X_{1} ,X_{3} ,X_{4} } \right),{\mathbb{R}}_{8} = \left( {X_{2} ,X_{1} ,X_{4} ,X_{3} } \right),{\mathbb{R}}_{9} = \left( {X_{2} ,X_{3} ,X_{1} ,X_{4} } \right),{\mathbb{R}}_{10} = \left( {X_{2} ,X_{3} ,X_{4} ,X_{1} } \right),{\mathbb{R}}_{11} = \left( {X_{2} ,X_{4} ,X_{1} ,X_{3} } \right),{\mathbb{R}}_{12} = \left( {X_{2} ,X_{4} ,X_{3} ,X_{1} } \right),$$

$${\mathbb{R}}_{13} = \left( {X_{3} ,X_{1} ,X_{2} ,X_{4} } \right),{\mathbb{R}}_{14} = \left( {X_{3} ,X_{1} ,X_{4} ,X_{2} } \right),{\mathbb{R}}_{15} = \left( {X_{3} ,X_{2} ,X_{4} ,X_{1} } \right),{\mathbb{R}}_{16} = \left( {X_{3} ,X_{2} ,X_{1} ,X_{4} } \right),{\mathbb{R}}_{17} = \left( {X_{3} ,X_{4} ,X_{1} ,X_{2} } \right),{\mathbb{R}}_{18} = \left( {X_{3} ,X_{4} ,X_{2} ,X_{1} } \right),$$

$${\mathbb{R}}_{19} = \left( {X_{4} ,X_{1} ,X_{2} ,X_{3} } \right),{\mathbb{R}}_{20} = \left( {X_{4} ,X_{1} ,X_{3} ,X_{2} } \right),{\mathbb{R}}_{21} = \left( {X_{4} ,X_{2} ,X_{1} ,X_{3} } \right),{\mathbb{R}}_{22} = \left( {X_{4} ,X_{2} ,X_{3} ,X_{1} } \right),{\mathbb{R}}_{23} = \left( {X_{4} ,X_{3} ,X_{1} ,X_{2} } \right),{\mathbb{R}}_{24} = \left( {X_{4} ,X_{3} ,X_{2} ,X_{1} } \right).$$

5.1.5 Step 5: Determinate the Concordance/Discordance Index

${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)$ (${\mathbb{C}}_{j}^{r} \left( {X_{\varepsilon } ,X_{\upsilon } } \right)$ is simplified to ${\mathbb{C}}_{j}^{r} \left( {\varepsilon ,\upsilon } \right)$).

In accordance with Eq. (28), we can obtain the concordance/discordance index, shown in Appendix A.

5.1.6 Step 6: Obtain the Comprehensive Concordance/Discordance Index

${\mathbb{C}}^{r}$

$${\mathbb{C}}^{1} = 0.0093,{\mathbb{C}}^{2} = 0.0094,{\mathbb{C}}^{3} = 0.0125,{\mathbb{C}}^{4} = 0.0174,{\mathbb{C}}^{5} = 0.0144,{\mathbb{C}}^{6} = 0.0176,{\mathbb{C}}^{7} = 0.0002,{\mathbb{C}}^{8} = 0.0003,{\mathbb{C}}^{9} = - 0.0086,$$

$${\mathbb{C}}^{10} = - 0.0176,{\mathbb{C}}^{11} = - 0.0087,{\mathbb{C}}^{12} = - 0.0174,{\mathbb{C}}^{13} = 0.0037,{\mathbb{C}}^{14} = 0.0087,{\mathbb{C}}^{15} = - 0.0144,{\mathbb{C}}^{16} = - 0.0054,{\mathbb{C}}^{17} = - 0.0003,$$

${\mathbb{C}}^{18} = - 0.0094,{\mathbb{C}}^{19} = 0.0054,{\mathbb{C}}^{20} = 0.0086,{\mathbb{C}}^{21} = - 0.0037,{\mathbb{C}}^{22} = - 0.0125,{\mathbb{C}}^{23} = - 0.0002,{\mathbb{C}}^{24} = - 0.0093$.

5.1.7 Step 7: Determinate the Optimal Ranking Result of Alternatives

By comparing the comprehensive concordance/discordance indexes, we know that ${\mathbb{C}}^{*} = {\mathbb{C}}^{5} = 0.0176$. Therefore, the ranking result is $X_{1} \succ X_{4} \succ X_{3} \succ X_{2}$.

5.2 Rationality Verification of the Proposed Method

Three test criteria are firstly given by Wang and Triantaphyllou [23] to demonstrate the rationality of MADM method. Because the MAGDM problem is a special MADM problem, three test criteria are also utilized to validate the rationality and affectivity of the proposed method. The process can now be described with more detail as follows.

Test criterion 1. As a rational decision-making method, it should not lead to changes in the optimal solution when replacing a non-optimal alternative with another non-optimal alternative. In this process, the weights remain unchanged.

The worst alternative $X_{2}$ is substituted for the non-optimal alternative $X_{2} ^{\prime}$. For simplicity, we make a simply modification to the alternative $X_{2}$ to form the alternative $X_{2} ^{\prime}$, i.e., the evaluation information of alternative $X_{2}$ with respect to the attribute $C_{1}$ from experts $D_{1} ,D_{3} ,D_{4}$ are altered to $z_{2^{\prime}1}^{1} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{1} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.6} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.2} \right)} \right\},\varsigma_{4} } \right)$, $z_{2^{\prime}1}^{3} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.5} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.1} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.2} \right)} \right\},\varsigma_{2} } \right)$, and $z_{2^{\prime}1}^{4} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.4} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.3} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.1} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.2} \right)} \right\},\varsigma_{1} } \right)$, and the evaluation information of alternative $X_{2}$ with respect to the attribute $C_{8}$ from experts $D_{1} ,D_{2}$ are altered to $z_{2^{\prime}8}^{1} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.4} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.4} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.2} \right)} \right\},\varsigma_{4} } \right)$,$z_{2^{\prime}8}^{2} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.3} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.3} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.2} \right)} \right\},\varsigma_{3} } \right)$, the evaluation information of alternative $X_{2}$ with respect to the attribute $C_{6}$ from experts $D_{1} ,D_{4}$ are altered to $z_{2^{\prime}6}^{1} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.5} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.1} \right)} \right\},\varsigma_{4} } \right)$,$z_{2^{\prime}6}^{4} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.5} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{3} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{4} \left( {0.2} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{5} \left( {0.1} \right)} \right\},\varsigma_{1} } \right)$. The remaining information is the same as that of the alternative $X_{2}$.

Utilizing the proposed method, we can obtain the comprehensive concordance/discordance index, i.e.,

$${\mathbb{C}}^{\prime 1} = - 0.010,{\mathbb{C}}^{{\prime}2} = - 0.010,{\mathbb{C}}^{{\prime}3} = 0.032,{\mathbb{C}}^{{\prime}4} = 0.073,{\mathbb{C}}^{{\prime}5} = 0.032,{\mathbb{C}}^{{\prime}6} = 0.073,{\mathbb{C}}^{{\prime}7} = - 0.055,{\mathbb{C}}^{{\prime}8} = - 0.055,{\mathbb{C}}^{{\prime}9} = - 0.064,$$

$${\mathbb{C}}^{{\prime}10} = - 0.073,{\mathbb{C}}^{{\prime}11} = - 0.064,{\mathbb{C}}^{{\prime}12} = - 0.073,{\mathbb{C}}^{{\prime}13} = 0.023,{\mathbb{C}}^{{\prime}14} = 0.064,{\mathbb{C}}^{{\prime}15} = - 0.032,{\mathbb{C}}^{{\prime}16} = - 0.023,{\mathbb{C}}^{{\prime}17} = 0.055,$$

${\mathbb{C}}^{{\prime}18} = 0.010,{\mathbb{C}}^{{\prime}19} = 0.023,{\mathbb{C}}^{{\prime}20} = 0.064,{\mathbb{C}}^{{\prime}21} = - 0.023,{\mathbb{C}}^{{\prime}22} = - 0.032,{\mathbb{C}}^{{\prime}23} = 0.055,{\mathbb{C}}^{{\prime}{24}} = 0.010$.

Therefore, we can get the optimal ranking order of alternatives, i.e., ${\mathbb{C}}^{{\prime}*} = {\mathbb{C}}^{{\prime}6} = 0.073$, the final ranking result is $X_{1} \succ X_{4} \succ X_{3} \succ X_{2^{\prime}}$. The optimal alternative is $X_{1}$ again. The proposed method is satisfied with the test criterion 1.

Test criterion 2. As an effective decision-making method, it should satisfy the transitive property.

Test criterion 3. When an original decision-making problem is broken down into several sub-problems, the same method is applied to solve these sub-problems to obtain ranking results. The integrated result of these ranking results must be consistent with the ranking result of the original decision-making problems.

According to the test criterion 2 and test criterion 3, the original MAGDM problem is split into two sub-problems. The first sub-problem consisted of three alternatives $\left\{ {X_{1} ,X_{2} ,X_{4} } \right\}$ and the second sub-problem includes three alternatives $\left\{ {X_{2} ,X_{3} ,X_{4} } \right\}$. We use the proposed method to handle with the two sub-problems, respectively, and obtain the ranking results of the sub-problems, i.e., $X_{1} \succ X_{4} \succ X_{2}$ and $X_{4} \succ X_{3} \succ X_{2}$. By integrating the ranking results of the sub-problems, we can derive the ranking result $X_{1} \succ X_{4} \succ X_{3} \succ X_{2}$, which is the same as the ranking result of the original MAGDM problem and consistent with the transitive property. Therefore, we can learn from the above analysis that the proposed method satisfies the test criterion 1 and test criterion 2.

5.3 Comparison with the Existing Methods

To further illustrate the effectiveness of the proposed method, the ranking result from the proposed method is compared with the ranking results from the existing methods [3, 22]. Because a PLTS can be reduced into a linguistic variable, a PLZN can be degenerated into a linguistic Z number. Therefore, Ding et al.’s method based on linguistic Z-number QUALIFLEX method [3] and Wang et al.’s method based on probabilistic linguistic Z-number TODIM-PROMETHEE II method [22] are select as comparators to prove its effectiveness. The ranking results from different methods are listed in Table 6.

Table 6 Ranking results from different methods in Example 2

From Table 6, we find that the ranking results from these existing methods [3, 22] are different from the ranking result from the proposed method, but the optimal alternative is the same for all three methods. The reason for Wang et al.’s method [22] and the proposed method to derive different ranking results is that the integration of PLZNs from different experts is based on the weight average operator, while the proposed method is built on the evidential reasoning theory. From the mathematical format of PLZNs, it can be found that there exist incomplete probability distributions in PLZNs. The weight average operator in Wang et al.’s method [22] ignores the influence of incomplete probability distributions in PLZNs on collective evaluation information. The incomplete probability distribution in PLZN is composed of the partial probabilities of possible linguistic terms in the first component so that it may influence the probability distributions of each linguistic term in collective evaluation information. In this point, the proposed method is better than Wang et al.’s method [3] in handling with the incomplete probability distributions in PLZNs. Moreover, another reason for the difference in ranking results is that TODIM-PROMETHEE method in Wang et al.’s method is constructed on the distance measure and the QUALIFLEX method in the proposed method is constructed on the possibility degree. Through analysis of the distance measure in Wang et al.’s method, it cannot process some special PLZNs. For example, there are two PLZNs $z_{1} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.3} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{6} \left( {0.5} \right)} \right\},\varsigma_{4} } \right)$ and $z_{2} = \left( {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{2} \left( {0.3} \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{6} \left( {0.7} \right)} \right\},\varsigma_{4} } \right)$. The distance measure between $z_{1}$ and $\tilde{z}$ is $d\left( {z_{1} } \right) = \left( {1 - \left( {\left| {{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}} - {\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}} \right| \times 0.5 + \left| {{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}} - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}} \right| \times 0.3} \right)} \right) \times {\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}} = 0.8$, and the distance measure between $z_{2}$ and $\tilde{z}$ is $d\left( {z_{2} } \right) = \left( {1 - \left( {\left| {{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}} - {\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}} \right| \times 0.7 + \left| {{\raise0.7ex\hbox{$6$} \!\mathord{\left/ {\vphantom {6 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}} - {\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 6}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$6$}}} \right| \times 0.3} \right)} \right) \times {\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 4}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$4$}} = 0.8$. From the numerical results, we can see that $d\left( {z_{1} } \right) = d\left( {z_{2} } \right)$. But, in fact, because the probability distribution of linguistic term $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{6}$ in $z_{2}$ is higher than the probability distribution of linguistic term $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{s}_{6}$ in $z_{1}$, the distance between $z_{1}$ and $\tilde{z}$ should be different from the distance between $z_{2}$ and $\tilde{z}$. And the distance measure $d\left( {z_{1} } \right)$ should be larger than the distance measure $d\left( {z_{2} } \right)$. The probabilistic linguistic Z QUALIFLEX method in the proposed method is constructed on the possibility degree formula. Based on the Eq. (4), we can obtain $P\left( {z_{1} \ge z_{2} } \right) = 0.5 \times \left( {\frac{0.15}{{\left( {0.15 + 0.21} \right)}} \times \left( {1 - 0.09 - 0.35} \right) + \frac{1}{2}\left( {0.09 + 0.35} \right)} \right) + 0.5 \times 0.5 = 0.475$ and $P\left( {z_{2} \ge z_{1} } \right) = 0.525$, which is in agreement with the actual situation that $z_{2}$ is better than $z_{1}$. At this point, the proposed method is more reasonable than Wang et al.’s method [22]. The reason for Ding et al.’s method [3] and the proposed method to derive different ranking results is that Ding et al.’s method is suitable for decision-making problems with linguistic Z-numbers, while the proposed method is suitable not only for decision-making problems with linguistic Z-numbers but also for decision-making problems with PLZNs. Because linguistic Z-number is a special case of PLZN, Ding et al.’s method [3] is applied to solve the above example which is degenerated into that with linguistic Z-numbers. The radical reason for this difference is that linguistic Z-numbers cannot cover all evaluation information shown in PLZNs. In terms of linguistic representation models, the proposed method has a wider adaptability than Ding et al.’s method [3].

Example 3

In most practical cases, there are heterogeneous relationships among attributes. Because of time pressure and lack of knowledge, the information about these attributes may be incompletely known. In view of this situation, Example 2 is adjusted to present the above situation that the attributes are interactive with the following incomplete weight information: $0.1 \le g\left( {\left\{ {C_{1} } \right\}} \right) \le 0.2,$$0.05 \le g\left( {\left\{ {C_{2} } \right\}} \right) \le 0.2,$$0.1 \le g\left( {\left\{ {C_{3} } \right\}} \right) \le 0.2,$$0.2 \le g\left( {\left\{ {C_{4} } \right\}} \right) \le 0.3,$$0.05 \le g\left( {\left\{ {C_{5} } \right\}} \right) \le 0.2,$$0.05 \le g\left( {\left\{ {C_{6} } \right\}} \right) \le 0.15,$$0.15 \le g\left( {\left\{ {C_{7} } \right\}} \right) \le 0.2,$$0.2 \le g\left( {\left\{ {C_{8} } \right\}} \right) \le 0.4$. The PLZNs decision matrices are identical to the Tables 1, 2, and 3. To better illustrate the advantages of the proposed method, Wang et al.’s method [22] and Ding et al.’s method [3] are utilized to deal with Example 3. The ranking results from these methods and the proposed method in Example 3 are shown in Table 7.

Table 7 Ranking results from different methods in Example 3

As can be seen from Table 7, the ranking results obtained by the existing methods [3, 22] are different from those of the proposed method. Especially, the optimal alternative derived by the proposed method is different from that by the existing methods. The reason for this difference is that the existing methods could not process the interactions among attributes. So, the ranking results from the existing methods cannot meet the requirement of this problem where all attributes are interacted with each other. But, the ranking result from the proposed method is reasonable because the proposed method pay attention to the interactions among attributes based on the following inequalities, i.e.,$g\left( {\left\{ {C_{1} } \right\}} \right) + g\left( {\left\{ {C_{2} } \right\}} \right) = 0.4 > g\left( {\left\{ {C_{1} ,C_{2} } \right\}} \right) = 0.333,$ $g\left( {\left\{ {C_{5} } \right\}} \right) + g\left( {\left\{ {C_{6} } \right\}} \right) = 0.35 < g\left( {\left\{ {C_{5} ,C_{6} } \right\}} \right) = 0.65$,$g\left( {\left\{ {C_{2} } \right\}} \right) + g\left( {\left\{ {C_{6} } \right\}} \right) = 0.35 = g\left( {\left\{ {C_{2} ,C_{6} } \right\}} \right) = 0.35.$ The proposed method takes the negative relationship between $C_{1}$ and $C_{2}$, the independent relationship between $C_{2}$ and $C_{6}$, and the positive relationship between $C_{5}$ and $C_{6}$. Therefore, the proposed method determinate a more realistic ranking result.

Integrating the above two examples, the proposed method has two significant superiorities compared with the existing methods. One advantage of the proposed method is that it focuses on the incomplete probability distributions in PLZNs, and considers the influence of incomplete probability distributions on the probability of each possible linguistic term in the aggregation of PLZNs. Another advantage of the proposed method is that it pays attention to heterogeneous relationships between attributes, ranging from complementariness to redundancy. Apart from the above mentioned two advantages, the proposed method has an intrinsic advantage implied in the QUALIFLEX method, which makes it more suitable for handling decision-making problems where lots of attributes are used to evaluate a limited number of alternatives.

6 Conclusions

This paper focuses on the MAGDM problem in which the number of attributes is much more than that of attributes and there exist heterogeneous relationships among attributes in the PLZNs context. And a resolution framework for this MAGDM problem is developed based on evidential reasoning theory and fuzzy measures. Three parts are involved: the information fusion process, the calculation of the attribute weights and the determination of ranking result of multiple alternatives. In the first part, the integration model based on evidential reasoning is developed to obtain the comprehensive PLZNs decision matrix, which fully considers the incomplete probabilistic distributions in PLZNs. In the second part, we give the mathematical programing model with generalized Shapley function to obtain the important degrees of attributes, which captures multiple types of interactions, such as positive synergetic interactions, negative synergetic interactions and independence. In the third part, we develop an extended PLZ-QUALIFLEX method based on the possibility degree of PLZNs to obtain the ranking result of alternatives, which takes the interrelationships between attributes into account. To make clear the superiorities and rationalities of the proposed method, two numerical examples are used for comparative analysis between the proposed method and the existing methods. From the comparison results of numerical examples, it can be found that the proposed method outperforms the existing methods. In the future research, we will research on consensus measure and research on the method for improving group consensus in probabilistic linguistic Z-number group decision-making problem. In addition, we will explore richer information representation models easy to understand to analyze decision-making problems and propose more decision-making methods [8, 14].

Appendices

Appendix A

See Table 8.

Table 8 The concordance/discordance index in Example 2

Appendix B

For the sake of easy to grasp this paper, these notations used in the proposed method are summarized in Table 9.

Table 9 The notations in proposed PLZ-QUALIFLEX method