Introduction

The measles is a respiratory virus that is very contagious and has the potential to cause serious complications, some of which might be permanent. These complications can include pneumonia, convulsions, brain damage, and even death. Measles is caused by a virus that dwells in the mucus that is found in an infected person’s nose and throat. This virus is easily spread through the air through activities such as breathing, coughing, and sneezing. When a patient with measles coughs, sneezes, or speaks, infectious droplets are released into the air (where other people can inhale them) or land on a surface, where they remain active and contagious for several hours at a time. Other people can become infected by inhaling these droplets. There is currently no specific antiviral medicine that is approved for use in the treatment of measles.

The goal of medical care is to treat complications like bacterial infections and relieve symptoms. Vitamin A may be used to treat severe measles cases in children, particularly those who are hospitalized (El Hajji and Albargi 2022; James Peter et al. 2022). Since there is no known cure for measles, the recommended management techniques for these cases center on prevention, supportive care, and the treatment of complications and secondary infections (Goodson and Seward 2015). The extremely safe MMR vaccine protects against measles in both children and adults. A single dose of the MMR vaccine is roughly 92 percent effective in preventing measles, whereas two doses are 95% effective. When the vaccination failed or the vaccine’s effects on their immunity wore off, some vaccinated people might still be vulnerable. Despite the fact that vaccination drastically decreased the global measles death rate between 2000 and 2018, by 73%. Measles is still a common disease in many impoverished nations around the world, particularly in portions of Africa and Asia (Ejima et al. 2012; Bakhtiar et al. 2020).

Numerous authors have employed mathematical models to understand how the measles spreads among various populations. For instance, authors in Bakare et al. (2012) presented a basic SEIR model without any control intervention. Authors (Tessa 2006) addressed the connection between herd immunity and mass vaccination, whereas the authors in Huang et al. (2018) model vaccine effects on measles-related deaths, the seasonality spreading element which was also taken into consideration when discussing the measles outbreak in China. To prevent a subsequent measles outbreak, the authors of Momoh et al. (2013) also take into account early testing and treatment for those who have been exposed. The authors in Musyoki et al. (2019) incorporate passive immune groups in their model, in contrast to the sources cited above, to examine the effect of this group on the measles eradication plan. The authors address the effects of the quarantine compartment in Aldila and Asrianti (2019). Additionally, they discover that a quarantine intervention can increase the efficacy of a vaccination strategy to lower the prevalence of endemic measles in the population.

Due to the occurrence of backward bifurcation, authors in Memon et al. (2020) and Peter et al. (2018) explore a vaccination model for measles transmission and discover a possibility that the fundamental reproduction number less than one does not guarantee the extinction of measles in the population and a model for the control of measles respectively. Authors in Pang et al. (2015), Adewale et al. (2016), Berhe and Makinde (2020), Ojo et al. (2022) and Pokharel et al. (2022) used the optimal control approach to find the best control for reducing disease spread by incorporating a time-dependent intervention into their models. Few authors have used fractional derivatives to explore measles transmission (Farman et al. 2018; Qureshi and Jan 2021; Qureshi 2020). Numerous researchers have developed mathematical models in recent years to understand the dynamics of measles transmission by taking into account various situations. However, none of these models examined the impact of contact rate in relation to testing and therapy rate. Our aim is to investigate different combined control parameters to predict and make recommendations for the most effective control measures that can be used to mitigate the measles burden on the populace.

Here is how the rest of the paper is laid out: Model descriptions based on population epidemiology are discussed in “Methods” section, model analysis is covered under analysis of the proposed model, next is the model fitting and parameter calibration and numerical simulations and a discussion of the findings are provided. Final, we give the conclusion with future directions

Methods

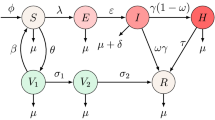
We propose a deterministic model with five compartments on the dynamics of measles in a given population based on the epidemiological status of individuals. The compartments are subdivided into the following epidemiological groups. Individuals that are prone or susceptible to measles S(t), vaccinated individuals against measles V(t), exposed individuals E(t), individuals who are infected with measles with signs and symptoms and are infectious I(t) and individuals who are infected with measles and have recovered due to natural recovery R(t). Those in this category cannot re-infect again and are not susceptible to measles again because upon recovery, the body system is permanently immune against the disease.

The rate of vaccinating the susceptible individuals is \(\sigma\). The effective contact rate between the susceptible and the infected individuals is denoted as \(\alpha\). It is assume that measles vaccine is not 100% effective, the vaccine wane at a rate \(\theta\), the recruitment rate into the susceptible population is either by immigration or birth at a rate \(\phi\), the progression rate from exposed to infected population is at a rate \(\beta\), the rate of exposed individuals who have undergone testing and therapy is \(\eta\), in most cases, infected individuals with measles naturally recovered without treatment, we represent the recovery rate as \(\gamma\), natural death rate is common to all the classes at the rate \(\mu\) while measles induced death rate is represented by \(\delta\).

The descriptions above can be illustrated by sets of non-linear differential equations in (1) while the pictorial representing the model is given in Fig. 1 and Tables 1, 2.

$$\begin{aligned} \begin{aligned} \dfrac{{\text {d}}S}{{\text {d}}t}=&\phi -\alpha SI+\theta V-(\mu +\sigma )S, \\ \dfrac{{\text {d}}V}{{\text {d}}t}=&\sigma S-(\theta +\mu )V, \\ \dfrac{{\text {d}}E}{{\text {d}}t}=&\alpha SI-(\beta +\eta +\mu )E, \\ \dfrac{{\text {d}}I}{{\text {d}}t}=&\beta E-(\mu +\delta +\gamma )I, \\ \dfrac{{\text {d}}R}{{\text {d}}t}=&\eta E+\gamma I-\mu R. \end{aligned} \end{aligned}$$
(1)
Fig. 1
figure 1

Flow chart of the proposed measles model as given in (1)

Full size image
Table 1 Description of the measles model’s variables and parameters
Full size table
Table 2 The description of parameters and their corresponding values
Full size table

Analysis of the proposed measles model

The mathematical discussion for the suggested measles model is presented in detail throughout four subsections of this current piece of work. The fundamental reproduction number is calculated using a technique called the next generation matrix approach, and the boundedness of the solution and the existence of both equilibria (disease-free and disease-endemic) have both been studied for the measles model.

Boundedness of the solution

Let the total human population be \(N=S(t)+V(t)+E(t)+I(t)+R(t)\) then

$$\begin{aligned} \frac{{\text {d}}N}{{\text {d}}t}&= \frac{{\text {d}}S}{{\text {d}}t}+\frac{{\text {d}}V}{{\text {d}}t}+\frac{{\text {d}}E}{{\text {d}}t}+\frac{{\text {d}}I}{{\text {d}}t}+\frac{{\text {d}}R}{{\text {d}}t} \nonumber \\&=\phi -\mu (S+V+E+I++R)-\delta I. \end{aligned}$$
(2)

From (2) we have,

$$\begin{aligned} \frac{{\text {d}}N}{{\text {d}}t}\le \phi -\mu N. \end{aligned}$$
(3)

Integrating both sides of (3) yields the following:

$$\begin{aligned} \int _{0}^{t}\frac{{\text {d}}N}{\phi -\mu N}\le \int _{0}^{t}dt, \end{aligned}$$
(4)
$$\begin{aligned} -\frac{1}{\mu }\ln (\phi -\mu N)\mid _{0}^{t}\le t. \end{aligned}$$
(5)

From (5), we have

$$\begin{aligned} N_t\le \frac{\phi }{\mu }-\bigg [\frac{\phi -\mu N_0}{\mu }\bigg ]e^{-\mu t}. \end{aligned}$$
(6)

Taking \(t\longrightarrow \infty\), we obtain \(N_t\le \frac{\phi }{\mu }\). This implies that the model in (1) can be studied in the feasible region as given below:

$$\begin{aligned} \Gamma =\bigg \{(S,V,E,I,R)\in R^5:N\le \frac{\phi }{\mu }\bigg \}. \end{aligned}$$
(7)

Disease-free equilibrium

The Disease-free equilibrium (DFE) \(\Omega _{DFE} = ({\tilde{S}},\ {\tilde{V}}, \ {\tilde{E}}, \ {\tilde{I}}, \ {\tilde{R}})\) is defined as the point at which there is no disease in the studied population. All infected classes will be equal to zero. Thus, the Disease-Free equilibrium satisfies

$$\begin{aligned} \Omega _{MFE}&= ({\tilde{S}},\ {\tilde{V}}, \ {\tilde{E}}, \ {\tilde{I}}, \ {\tilde{R}}) \nonumber \\&= \left( \frac{\phi (\theta +\mu )}{(\theta + \mu )(\mu +\sigma )-\theta \sigma },\frac{\phi \sigma }{(\theta + \mu )(\mu +\sigma )-\theta \sigma },0,0,0\right) . \end{aligned}$$
(8)

Measles endemic equilibrium

Let Measles Endemic Equilibrium (MEE) denoted by \(\zeta _{MEE} = (S^{*},\ V^{*}, \ E^{*}, \ I^{*}, \ R^{*})\) be defined as the point when the disease still persist in the human population. Consider the equations in system (1). Hence, the Measles Endemic equilibrium satisfies:

$$\begin{aligned} \begin{aligned} S^*=&\frac{(\beta +\eta +\mu )(\mu +\delta +\gamma )}{\beta \alpha },\\ V^*=&\frac{\sigma (\beta +\eta +\mu )(\mu +\delta +\gamma )}{\beta \alpha (\theta +\mu )},\\ E^*=&\frac{(\mu +\delta +\gamma )I^*}{\beta },\\ I^*=&\frac{\phi +\theta V^*-(\mu +\sigma )S^*}{\alpha S*},\\ R^*=&\left( \frac{\eta (\mu +\delta +\gamma )}{\beta \mu }+\frac{\gamma }{\mu }\right) I^*. \end{aligned} \end{aligned}$$
(9)

Basic reproduction number

In this section, we compute the basic reproduction number \(R_0\) using the next generation matrix method. According to the principle of next generation matrix, the basic reproduction number is the spectral radius of the next generation matrix \(FV^{-1}\) (Peter et al. 2022a, b; James Peter et al. 2022; Ojo et al. 2021; Abboubakar et al. 2022) as shown below:

$$\begin{aligned} R_{0} = \rho \Big (FV^{-1}\Big ). \end{aligned}$$
(10)

Therefore, using the Eq. (10), we split the differential equations into a new infection matrix f and transfer matrix between compartment v, and their Jacobian matrices are F and V respectfully which will be calculated at the Disease-Free Equilibrium.

$$\begin{aligned} f= & {} \begin{bmatrix} \alpha SI\\ 0 \end{bmatrix}, \quad v = \begin{bmatrix} (\beta +\eta +\mu )E &{} \\ (\mu +\delta +\gamma ) I-\beta E &{} \end{bmatrix}. \end{aligned}$$
(11)
$$\begin{aligned} F= & {} \left( \begin{array}{rr} 0 &{} \frac{\alpha {\left( \mu + \theta \right) } \phi }{{\left( \mu + \sigma \right) } {\left( \mu + \theta \right) } - \sigma \theta } \\ \\ 0 &{} 0 \end{array}\right) , \quad and \quad V =\left( \begin{array}{rr} \beta + \eta + \mu &{} 0 \\ \\ -\beta &{} \delta + \gamma + \mu \end{array}\right) \end{aligned}$$
(12)

So that,

$$\begin{aligned} V^{-1} = \left[ \begin{array}{cc} \left( \beta +\eta +\mu \right) ^{-1}&{}0 \\ {\frac{\beta }{ \left( \beta +\eta +\mu \right) \left( \mu +\delta +\gamma \right) }}&{} \left( \mu +\delta +\gamma \right) ^{-1} \end{array} \right] . \end{aligned}$$
(13)

Therefore,

$$\begin{aligned} FV^{-1} = \left[ \begin{array}{cc} {\frac{\alpha \,S_0\beta }{ \left( \beta +\eta + \mu \right) \left( \mu +\delta +\gamma \right) }}&{}{\frac{\alpha \,S_0}{ \mu +\delta +\gamma }}\\ 0&{}0\end{array} \right] . \end{aligned}$$
(14)

To obtain the spectral radius, we need to calculate the eigenvalues of \(FV^{-1}\). Therefore, simplification yields the following:

$$\begin{aligned} R_{0} = \displaystyle \frac{\alpha \beta {\left( \mu + \theta \right) } \phi }{\mu {\left( \beta + \eta + \mu \right) } {\left( \delta + \gamma + \mu \right) } {\left( \mu + \sigma + \theta \right) }}. \end{aligned}$$
(15)

Theorem 0.1

The disease-free equilibrium point is locally asymptotically stable if \(R_0<1\), and it is unstable if \(R_0>1\).

Proof

First, we calculate the Jacobian matrix of system (1) as follows:

$$\begin{aligned}&J(S,V,E,I,R) \\&\quad = \begin{bmatrix} -\alpha I-\mu -\sigma &{} \theta &{} 0 &{} -\alpha S &{} 0 \\ \sigma &{} -\theta -\mu &{} 0 &{} 0 &{} 0 \\ \alpha I &{} 0 &{} -\beta -\eta -\mu &{} \alpha S &{} 0 \\ 0 &{} 0 &{} \beta &{} -\mu -\delta -\gamma &{} 0 \\ 0 &{} 0 &{} \eta &{} \gamma &{} -\mu \end{bmatrix} . \end{aligned}$$

Then,

$$\begin{aligned}&J(\Omega _{DFE})\\&\quad = \begin{bmatrix} -\mu -\sigma &{} \theta &{} 0 &{} \frac{-\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } &{} 0 \\ \sigma &{} -\theta -\mu &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\beta -\eta -\mu &{} \frac{\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } &{} 0 \\ 0 &{} 0 &{} \beta &{} -\mu -\delta -\gamma &{} 0 \\ 0 &{} 0 &{} \eta &{} \gamma &{} -\mu \end{bmatrix} . \end{aligned}$$

The eigenvalues of \(J(\Omega _{DFE})\) can be found from \(\det (J(\Omega _{DFE})-\lambda I)=0\),

$$\begin{aligned} \begin{vmatrix} -\mu -\sigma -\lambda&\theta&0&\frac{-\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma }&0 \\ \sigma&-\theta -\mu -\lambda&0&0&0 \\ 0&0&-\beta -\eta -\mu -\lambda&\frac{\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma }&0 \\ 0&0&\beta&-\mu -\delta -\gamma -\lambda&0 \\ 0&0&\eta&\gamma&-\mu -\lambda \end{vmatrix} =0. \\ (-\mu -\lambda ) \begin{vmatrix} -\mu -\sigma -\lambda&\theta&0&\frac{-\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } \\ \sigma&-\theta -\mu -\lambda&0&0 \\ 0&0&-\beta -\eta -\mu -\lambda&\frac{\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } \\ 0&0&\beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} =0. \end{aligned}$$

We obtain the first eigenvalue as \(\lambda _1=-\mu <0\). And the characteristic equation can be calculated as follows.

$$\begin{aligned}&(-\sigma ) \begin{vmatrix} \theta&0&\frac{-\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } \\ 0&-\beta -\eta -\mu -\lambda&\frac{\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } \\ 0&\beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} \\&\quad +(-\theta -\mu -\lambda )\begin{vmatrix} -\mu -\sigma -\lambda&0&\frac{-\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } \\ 0&-\beta -\eta -\mu -\lambda&\frac{\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma }\\ 0&\beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} =0, \\&\quad \times {[}(-\sigma \theta )+(\theta +\mu +\lambda )(\mu +\sigma +\lambda )] \begin{vmatrix} -\beta -\eta -\mu -\lambda&\frac{\alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma } \\ \beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} =0, \\&\quad \times (\lambda ^2+(2\mu +\theta +\sigma )\lambda -\sigma \theta +(\theta +\mu )(\mu +\sigma ))\\&\quad \times \left[ (\beta +\eta +\mu +\lambda )(\mu +\delta +\gamma +\lambda )-\frac{\beta \alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma }\right] =0, \\&\quad \times (\lambda ^2+(2\mu +\theta +\sigma )\lambda +(\theta +\mu )(\mu +\sigma )-\sigma \theta )\\&\quad \times \left[ \lambda ^2+(\beta +\eta +\delta +\gamma +2\mu )\lambda +(\beta +\eta +\mu )(\mu +\delta +\gamma )-\frac{\beta \alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma }\right] =0. \end{aligned}$$

Consider the first term as follows:

$$\begin{aligned} \lambda ^2+(2\mu +\theta +\sigma )\lambda + (\theta +\mu )(\mu +\sigma )-\sigma \theta =0, \end{aligned}$$

in the form \(\lambda ^2+a_1\lambda + a_2 =0\), we have

$$\begin{aligned} a_1 =2\mu +\theta +\sigma >0, \end{aligned}$$

and

$$\begin{aligned} a_2 = (\theta +\mu )(\mu +\sigma )-\sigma \theta =\mu (\mu +\sigma +\theta )>0. \end{aligned}$$

These match Routh–Hurwitz criteria.

Next, consider the second term in the form \(\lambda ^2+b_1\lambda +b_2=0\), we have \(b_1=\beta +\eta +\delta +\gamma +2\mu >0\), and

$$\begin{aligned} b_2&=(\beta +\eta +\mu )(\mu +\delta +\gamma )-\frac{\beta \alpha \phi (\theta +\mu )}{(\theta +\mu )(\mu +\sigma )-\theta \sigma }, \nonumber \\&=(\beta +\eta +\mu )(\mu +\delta +\gamma )\nonumber \\&\quad \times \left[ 1-\frac{\beta \alpha \phi (\theta +\mu )}{(\beta +\eta +\mu )(\mu +\delta +\gamma )(\mu +\sigma +\theta )\mu }\right] , \nonumber \\&=(\beta +\eta +\mu )(\mu +\delta +\gamma )[1-R_0]. \end{aligned}$$
(16)

Therefore, \(b_1>0\) and \(b_2>0\) when \(R_0<1\). Hence, by Routh–Hurwitz criteria we obtain that the disease-free equilibrium point is locally asymptotically stable if \(R_0<1\) and is unstable if \(R_0>1\). This completes the proof. \(\square\)

Theorem 0.2

The disease-free equilibrium is globally asymptotically stable when \(R_0<1\).

Proof

Let the Lyapunov function be

$$\begin{aligned} L=\beta E+(\mu +\beta +\eta )I. \end{aligned}$$

The derivative of L is as follows:

$$\begin{aligned} \frac{{\text {d}}L}{{\text {d}}t}&=\beta (\alpha SI - (\beta +\eta +\mu )E) + (\mu +\beta +\eta )\nonumber \\&\quad \times (\beta E-(\mu +\delta +\gamma )I) \nonumber \\&=\beta \alpha SI - (\mu +\beta +\eta )(\mu +\delta +\gamma )I \nonumber \\&=(\mu +\beta +\eta )(\mu +\delta +\gamma )\nonumber \\&\quad \times \left[ \frac{\beta \alpha S}{(\mu +\beta +\eta )(\mu +\delta +\gamma )}-1\right] I. \end{aligned}$$
(17)

Since from the boundary condition of solutions that

$$\begin{aligned} S+V_0 \le \frac{\phi }{\mu } \end{aligned}$$

, we have

$$\begin{aligned} S&\le \frac{\phi }{\mu }-\frac{\phi \sigma }{\mu (\mu +\sigma +\theta )}=\frac{\phi (\mu +\theta )}{\mu (\mu +\sigma +\phi )}=S_0. \end{aligned}$$
(18)

Thus, \(S\le S_0\). Then, we have

$$\begin{aligned} \frac{{\text {d}}L}{{\text {d}}t}&\le (\mu +\beta +\eta )(\mu +\delta +\gamma )[\frac{\beta \alpha S_0}{(\mu +\beta +\eta )(\mu +\delta +\gamma )}-1]I \nonumber \\&=(\mu +\beta +\eta )(\mu +\delta +\gamma )[R_0-1]I. \end{aligned}$$
(19)

Thus, \(\frac{{\text {d}}L}{{\text {d}}t}=0\) when \(I=0\) and when \(R_0<1\), \(\frac{{\text {d}}L}{{\text {d}}t}<0\). Hence, the disease-free equilibrium point is globally asymptotically stable when \(R_0<1\). \(\square\)

Theorem 0.3

When \(R_0>1\), the endemic equilibrium point is locally stable if it satisfies Routh–Hurwitz criteria.

Proof

We first consider \(\det (J(S_{MEE})-\lambda I)=0\), we have

$$\begin{aligned} \begin{vmatrix} -\alpha I^*-\mu -\sigma -\lambda&\theta&0&-\alpha S^*&0 \\ \sigma&-\theta -\mu -\lambda&0&0&0 \\ \alpha I^*&0&-\beta -\eta -\mu -\lambda&\alpha S^*&0 \\ 0&0&\beta&-\mu -\delta -\gamma -\lambda&0 \\ 0&0&\eta&\gamma&-\mu -\lambda \end{vmatrix} =0. \end{aligned}$$

Similarly to the proof in Theorem 1, we obtain \(\lambda _1=-\mu <0.\) The rest of the characteristic equation can be found from

$$\begin{aligned}&\begin{vmatrix} -\alpha I^*-\mu -\sigma -\lambda&\theta&0&-\alpha S^* \\ \sigma&-\theta -\mu -\lambda&0&0 \\ \alpha I^*&0&-\beta -\eta -\mu -\lambda&\alpha S^* \\ 0&0&\beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} =0. \\&0=(-\sigma ) \begin{vmatrix} \theta&0&-\alpha S^* \\ 0&-\beta -\eta -\mu -\lambda&\alpha S^* \\ 0&\beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} \\&\qquad +(-\theta -\mu -\lambda )\\&\begin{vmatrix} -\alpha I^*-\mu -\sigma -\lambda&0&-\alpha S^* \\ \alpha I^*&-\beta -\eta -\mu -\lambda&\alpha S^* \\ 0&\beta&-\mu -\delta -\gamma -\lambda \end{vmatrix} \\&\quad =(-\sigma \theta )[(\beta +\eta +\mu +\lambda )\\&\qquad \times (\mu +\delta +\gamma +\lambda ) -\beta \alpha S^*] \\&\qquad + (-\theta -\mu -\lambda )(-\alpha I^*-\mu -\sigma -\lambda )[(\beta +\eta +\mu +\lambda )\\&\qquad \times (\mu +\delta +\gamma +\lambda )-\beta \alpha S^*]+(\theta +\mu +\lambda )\alpha I^*\beta \alpha S^* \\&\quad =(-\sigma \theta )[\lambda ^2 + (\beta +\eta +\delta +\gamma +2\mu )\lambda \\&\qquad +(\beta +\eta +\mu )(\mu +\delta +\gamma )-\beta \alpha S^*]\\&\qquad +(\theta +\mu +\lambda )(\alpha I^*+\mu +\sigma +\lambda )\\&\qquad \times [\lambda ^2+(\beta +\eta +\delta +\gamma +2\mu )\lambda + (\beta +\eta +\mu )\\&\qquad \times (\mu +\delta +\gamma )-\beta \alpha S^*]\\&\qquad +(\theta +\mu )\alpha I^*\beta \alpha S^*+\lambda (\alpha I^*\beta \alpha S^*). \end{aligned}$$

It can be written in the form \(\lambda ^4+a_1\lambda ^3+a_2\lambda ^2+a_3\lambda +a_4 = 0\), where

$$\begin{aligned} a_1&= 4\mu +\theta +\alpha I^* + \sigma +\beta +\eta +\delta +\gamma >0, \nonumber \\ a_2&= (\theta +\mu )(\alpha I^*+\mu )+\mu \sigma +(\beta +\eta +\delta +\gamma +2\mu )\nonumber \\&\quad \times (\theta +2\mu +\alpha I^*+\sigma ) \nonumber \\&\quad +[(\beta +\eta +\mu )(\mu +\delta +\gamma )-\beta \alpha S^*], \nonumber \\ a_3&= (\beta +\eta +\delta +\gamma +2\mu )[(\theta +\mu )(\alpha I^*+\mu )+\mu \sigma ]+\alpha I^*\beta \alpha S^* \nonumber \\&\quad + [(\beta +\eta +\mu )(\mu +\delta +\gamma )-\beta \alpha S^*](\theta +2\mu +\alpha I^*+\sigma ), \end{aligned}$$
(20)

and

$$\begin{aligned} a_4&= [(\beta +\eta +\mu )(\mu +\delta +\gamma )-\beta \alpha S^*]\nonumber \\&\quad \times [(\theta +\mu )(\alpha I^*+\mu )+\mu \sigma ] + (\theta +\mu )\alpha I^*\beta \alpha S^*. \end{aligned}$$
(21)

By using Routh–Hurwitz criteria, the endemic equilibrium point is locally stable if \(a_3>0\), \(a_4>0\) and \(a_1a_2a_3>a_3^2+a_1^2a_4\). \(\square\)

Theorem 0.4

The endemic equilibrium point is globally asymptotically stable when \(R_0>1\).

Proof

The following statement are obtained from equilibrium conditions which we need to use later in the proof.

$$\begin{aligned} \phi&=\alpha S^*I^* - \theta V^*+(\mu +\sigma )S^* \\ (\theta +\mu )V^*&=\sigma S^* \\ \alpha S^*I^*&= (\beta +\eta +\mu )E^* \\ \beta E^*&=(\mu +\delta +\gamma )I^*. \end{aligned}$$

Next, let the Lyapunov function be

$$\begin{aligned} L&=\int _{S^*}^{S}\left( 1-\frac{S^*}{x}\right) dx+\int _{V^*}^{V}\left( 1-\frac{V^*}{x}\right) dx \\&\quad + \int _{E^*}^{E}\left( 1-\frac{E^*}{x}\right) dx + \left( \frac{\beta +\eta +\mu }{\beta }\right) \int _{I^*}^{I}\left( 1-\frac{I^*}{x}\right) dx \end{aligned}$$

The derivative of L is

$$\begin{aligned} \frac{{\text {d}}L}{{\text {d}}t}= & {} \left( 1-\frac{S^*}{S}\right) \frac{{\text {d}}S}{{\text {d}}t}+\left( 1-\frac{V^*}{V}\right) \frac{{\text {d}}V}{{\text {d}}t} \\&\quad + \left( 1-\frac{E^*}{E}\right) \frac{{\text {d}}E}{{\text {d}}t} + \left( \frac{\beta +\eta +\mu }{\beta }\right) \left( 1-\frac{I^*}{I}\right) \frac{{\text {d}}I}{{\text {d}}t}. \end{aligned}$$

First, consider

$$\begin{aligned}&\left( 1-\frac{S^*}{S}\right) \frac{{\text {d}}S}{{\text {d}}t}=\left( 1-\frac{S^*}{S}\right) \nonumber \\&\qquad \times [\phi -\alpha SI+\theta V-(\mu +\sigma )S] \nonumber \\&\quad =\left( 1-\frac{S^*}{S}\right) [\alpha S^*I^*-\theta V^*\nonumber \\&\qquad +(\mu +\sigma )S^*-\alpha SI+\theta V-(\mu +\sigma )S] \nonumber \\&\quad =\left( 1-\frac{S^*}{S}\right) \alpha S^*I^*-\alpha SI \nonumber \\&\qquad + \alpha S^*I - \theta V^* +\frac{\theta V^*S^*}{S} + \theta V-\frac{\theta VS^*}{S} \nonumber \\&\qquad +(\mu +\sigma )S^*-\frac{(\mu +\sigma )S^{*2}}{S}-(\mu +\sigma )S\nonumber \\&\qquad +(\mu +\sigma )S^* \left( 1-\frac{V^*}{V}\right) \frac{{\text {d}}V}{{\text {d}}t} =\left( 1-\frac{V^*}{V}\right) \nonumber \\&\qquad \times [\sigma S-(\theta +\mu )V] \nonumber \\&\quad =\left( 1-\frac{V^*}{V}\right) \sigma S-(\theta +\mu )V+(\theta +\mu )V^* \nonumber \\&\quad =\left( 1-\frac{V^*}{V}\right) \sigma S-(\theta +\mu )V+\sigma S^* \nonumber \\&\quad =\sigma S - \frac{\sigma SV^*}{V}-(\theta +\mu )V+\sigma S^* \nonumber \\&\qquad \times \left( 1-\frac{E^*}{E}\right) \frac{{\text {d}}E}{{\text {d}}t}=\left( 1-\frac{E^*}{E}\right) [\alpha SI-(\beta +\eta +\mu )E] \nonumber \\&\quad =\alpha SI-\frac{\alpha SIE^*}{E}-(\beta +\eta +\mu )E +{(\beta +\eta +\mu )}E^* \nonumber \\&\quad =\alpha SI-\frac{\alpha SIE^*}{E} -(\beta +\eta +\mu )E+\alpha S^*I^*\nonumber \\&\quad \left( 1-\frac{I^*}{I}\right) \left( \frac{\beta +\eta +\mu }{\beta }\right) \frac{{\text {d}}I}{{\text {d}}t}\nonumber \\&\quad =\left( 1-\frac{I^*}{I}\right) \left( \frac{\beta +\eta +\mu }{\beta }\right) [\beta E-(\mu +\delta +\gamma )I] \nonumber \\&\quad =\left( 1-\frac{I^*}{I}\right) \left[ (\beta +\eta +\mu )E\right. \nonumber \\&\qquad \times \left. -\frac{(\beta +\eta +\mu )(\mu +\delta +\gamma )I}{\beta }\right] \nonumber \\&\quad =(\beta +\eta +\mu )E - \frac{(\beta +\eta +\mu ) (\mu +\delta +\gamma )}{\nonumber }\\&\qquad \times {\beta }I - (\beta +\eta +\mu )\frac{EI^*}{I} \nonumber \\&\qquad +(\beta +\eta +\mu )(\mu +\delta +\gamma )\frac{I^*}{\beta } \nonumber \\&\quad = (\beta +\eta +\mu )E - \frac{(\beta +\eta +\mu ) (\mu +\delta +\gamma )I}{\beta }-(\beta +\eta +\mu )\frac{EI^*}{I} \nonumber \\&\qquad +(\beta +\eta +\mu )E^* \nonumber \\&\quad =(\beta +\eta +\mu )E-\frac{\alpha S^*I^*I}{\beta E^*}\nonumber \\&\qquad \times (\mu +\delta +\gamma )-\frac{\alpha S^*I^{*2}E}{E^*I}+\alpha S^*I^*. \end{aligned}$$
(22)

Hence, we have,

$$\begin{aligned} \frac{{\text {d}}L}{{\text {d}}t}= & {} (\mu +\sigma )S^*\left[ 2-\frac{S^*}{S}-\frac{S}{S^*}\right] \\&+\alpha S^*I^*\left[ 3-\frac{S^*}{S}-\frac{I^*E}{IE^*}-\frac{E^*SI}{ES^*I^*}\right] \\&+\frac{\theta V^*S^*}{S}\left[ 1-\frac{V}{V^*}+\frac{S^2}{S^{*2}}\left( 1-\frac{V^*}{V}\right) \right] \\&+ \mu V^*\left[ 1-\frac{V}{V^*}+\frac{S}{S^*}\left( 1-\frac{V^*}{V}\right) \right] . \end{aligned}$$

Since the arithmetic mean is greater that or equal geometric mean, then

$$\begin{aligned} 2-\frac{S^*}{S}-\frac{S}{S^*}\le 0, \\ 3-\frac{S^*}{S}-\frac{I^*E}{IE^*}-\frac{E^*SI}{ES^*I^*}\le 0, \\ 1-\frac{V}{V^*}+\frac{S^2}{S^{*2}}\left( 1-\frac{V^*}{V}\right) \le 0, \end{aligned}$$

and

$$\begin{aligned} 1-\frac{V}{V^*}+\frac{S}{S^*}\left( 1-\frac{V^*}{V}\right) \le 0. \end{aligned}$$

Therefore, \(\frac{{\text {d}}L}{{\text {d}}t}\le 0\). By Lasalle’s invariance principle, the endemic equilibrium point is globally asymptotically stable when \(R_0>1\). \(\square\)

Model fitting with parameter calibration

This section provides a comprehensive breakdown of the estimation of the parameters based on the actual data that is currently available for the measles epidemic in Pakistan from January 2019 to October 2019. Because actual data sets are now readily available, it is possible to collect those biological parameters of epidemiological models that are not readily available from any source, such as demography. This presents a significant opportunity for researchers. For the mathematical model of an epidemic that is being looked at right now to be accurate, it must be checked against real medical data.

The nonlinear ordinary differential equations system needs to be simulated to the extent of getting all meaningful values of the underlying parameters while maintaining the smallest possible residuals between the predicted values of the infected class of the model and the actual cases from the available data. This simulation process keeps repeating until the maximum number of data points coincide with the simulations of the infected class of individuals.

Estimating the parameters is the most common process known as the least-squares process, wherein the residuals (errors) have to be minimized until the allowable tolerance. Although several methods are available in the literature, this one is frequently used due to its credibility and simplicity. It is. Therefore, we have also employed the method of least-squares to obtain the estimated (best fitted) values of the essential biological parameters of the proposed measles model given in (1).

It can be observed in Table 3 that the best-fitted values for some important parameters are computed with the above-stated approach. The estimates are available, but some other vital information about the parameters is also presented, including standard error, t-statistic value, p-value, and the respective confidence interval of each estimate. It may be noted that each p-value is smaller than 0.05 with \(95\%\) CI. With these values of the parameters, the basic reproduction number is determined to be \(R_0 = 2.41442\).

Moreover, Table 4 shows the calculation of vital descriptive statistical measures about the actual and predicted values from the proposed measles model. Each calculated statistical measure is in good agreement and does not deviate much from reliable information. From the mean values in both actual and simulated cases, we observe that there is good agreement in both values, thereby creating confidence in the simulations of the model and the model’s validation. Finally, it is noticed in Fig. 2 that the simulations of the infected class of the proposed measles model (1) very well approach the actual data points, which is further confirmed with the residuals plotted in Fig. 3. The symmetry among the medical data values of the simulations can be observed in the BoxWhisker chart in Fig. 4. This chart for the simulated cases is better than the box obtained with actual measles cases. The statistical analysis carried out in this section brings confidence in the reliability and the validation of the proposed measles model.

Table 3 Values of fitted biological parameters including some important statistical measures obtained via least-squares non-linear curve fitting technique
Full size table
Table 4 Some statistical measures related to actual and simulated values from the measles model in (1)
Full size table
Fig. 2
figure 2

The best curve fitting for the real measles cases and the compartment of the newly infected cases from the proposed model given in (1)

Full size image
Fig. 3
figure 3

Different kinds of residuals for the statistical analysis of the model’s simulations

Full size image
Fig. 4
figure 4

The BoxWhisker chart for each real surveillance data value and those of predicted from the proposed model (1)

Full size image

Numerical simulations with results and discussion

To further demonstrate and establish our theoretical findings, we ran additional numerical simulations here. In particular, we first examine how the most sensitive characteristics affect the reproduction number, a threshold quantity that determines the disease’s impact on a given population. We further explore the impact of these parameters on the prevalence of the infected population to better understand the regulation of measles in a specific demographic. To do this, the dynamical behaviour of the entire infected population under various scenarios of control measures will be simulated. We defined the infected population as the sum of the exposed and infected populations, so it’s important to keep that in mind. This is because, measles can spread from a person who has it to someone who is susceptible to it.

A six-stage fifth-order Runge-Kutta method was implemented on MATLAB to simulate the dynamics of the model system (1). The parameter values used are as provided in Table 2, except otherwise stated. These values were obtained from the model fitting with parameter calibration presented in Sect. 4. It is imperative to note that, because the fitted data are real data from Pakistan, the predictions based on the numerical simulation results will be more appropriate for describing the measles transmission dynamics in Pakistan.

In Fig. 5, we use a 2-D contour plot to investigate the dynamics of the reproduction number \(R_{0}\), by varying two parameters simultaneously. The reproduction number is an essential threshold which is a criterion for determining the disease’s potential to spread in a population. Epidemiologically, it measures the average number of secondary infectious cases that a single infected person can produce in a completely susceptible population. In other words, the reproduction number \(R_{0}\) given in (15) measures the average number of measles cases that a single measles infected person can generate in a population that is completely susceptible. Thus, we note that an increase in the reproduction number will upsurge the risk of measles occurrence in the populace. As a result, reducing \(R_{0}\) will be the goal of all individuals to reduce the risk or burden of measles in the population.

In Fig. 5a, we illustrate the dynamics of the reproduction number by varying the effective contact rate \(\alpha\) with respect to the testing and therapy rate of exposed individuals \(\eta\). The result shows that an increase in the testing and therapy rate of exposed individuals reduces the abundance of the reproduction number. For instance, if we fix the effective contact rate at \(\alpha = 0.06\), a testing and therapy rate at \(\eta =1.5\) will yield a reproduction number between the range of (4, 5). However, increasing the testing and therapy rate of exposed individuals to \(\eta =2.5\) will reduce the reproduction number to the range of (2, 3). From this result, we can infer that, by simultaneously reducing the effective contact rate and increasing the testing and therapy rate of exposed individuals, the reproduction number can be reduced to a minimal value. As a result, the disease burden can be mitigated. We observe a similar result in Fig. 5b. The figure shows the effect of varying the effective contact rate \(\alpha\) with respect to the recovery rate from infection \(\gamma\) on the reproduction number. Overall, the result shows that by simultaneously reducing the effective contact rate and increasing the recovery rate from infection, the reproduction number can be reduced below unity.

In Fig. 5c, we illustrate the impact of varying the progression rate of exposed to infected \(\beta\) with respect to the testing and therapy rate of exposed individuals \(\eta\) on the reproduction number. The result shows that an increase in the testing and therapy rate of exposed individuals decreases the value of the reproduction number. Similarly, reducing the progression rate of exposed individuals to an infected population will reduce the reproduction number. Thus, to reduce the measles burden in the population, it is important to increase testing and therapy for the exposed individuals to enhance their recovery. In addition, the effective contact rate must be minimized through preventive measures to reduce the transmission of measles from an infected person.

Fig. 5
figure 5

A 2-D contour plot of the reproduction number \(R_{0}\) of the measles model (1); a varying the effective contact rate \(\alpha\) with respect to the testing and therapy rate of exposed individuals \(\eta\); b varying effective contact rate \(\alpha\) with respect to the recovery rate from infection \(\gamma\); and c varying progression rate of exposed to infected \(\beta\) with respect to the testing and therapy rate of exposed individuals \(\eta\)

Full size image
Fig. 6
figure 6

Simulations of the measles model (1) with varying effects of parameters on the total infected human population; a effective contact rate \(\alpha\); b progression rate of exposed to infected \(\beta\); c testing and therapy rate for exposed individuals \(\eta\); d vaccination rate \(\sigma\); and e recovery rate from infection \(\gamma\). Parameter values used are as given in Table 2 except otherwise stated

Full size image
Fig. 7
figure 7

Simulations of the measles model (1) showing the effects of controlled parameters on the total infected human population \((E+I)\). The parameter values used are as given in Table 2 except for \(\alpha = 0.00025\), \(\beta =7.09e-6\), \(\eta = 2.54384\), \(\sigma = 0.29575\), and \(\gamma = 0.1680\)

Full size image

To investigate the effect of each parameter on mitigating the burden of measles in the populace, we simulate the impact of some parameters on the dynamics of the total infected human population \((E+I)\) in Fig. 6. Following the result from the sensitivity analysis, we regulate the baseline parameter values by reducing the effective contact rate \(\alpha\) and the progression rate from exposed to infected \(\beta\) by \(25\%\), \(50\%\), and \(75\%\) such that \(\alpha = 0.00075, 0.0005, 0.00025\) and \(\beta =2.84e-5, 2.13e-5, 1.42e-5, 7.09e-6\) respectively. Furthermore, we increase the testing and therapy rate for exposed individuals \(\eta\), vaccination rate \(\sigma\), and recovery rate from infection \(\gamma\) by \(25\%\), \(50\%\), and \(75\%\) such that \(\eta = 1.81703, 2.18043, 2.54384\), \(\sigma = 0.21125, 0.25350, 0.29575\), and \(\gamma = 0.1200, 0.1440, 0.1680\). These values were used to investigate the impact of each parameter on the total infected population.

In Fig. 6a, b, we show the outcome of the effective contact rate and the progression rate of exposed individuals to the infected population on the total infected population. The result shows that reducing the effective contact rate of measles and the progression rate of exposed humans by \(75\%\) reduces the total infected population faster. In other words, to effectively mitigate the burden of measles in the community, a need for reducing the effective contact rate through preventive measures is inevitable. Also, there must be an implementation of facilities and resources to diagnose exposed individuals early to reduce their progression to the infectious stage.

In Fig. 6c, e, we illustrate the effect of testing and therapy rate for exposed individuals \(\eta\), vaccination rate \(\sigma\), and recovery rate from infection \(\gamma\) on the total infected population. The overall result from these figures shows that an increase in \(\eta\), \(\sigma\), and \(\gamma\) will reduce the burden of measles in the population. Particularly, reducing the parameter values by \(75\%\) has a more effective impact on the total infected human population. As a result, society’s priority would be increasing the vaccination rate against measles, the recovery rate from infection through treatment or enhancement of human body immunity, and the facilitation of testing and therapy to reduce the progression of exposed individuals into the infected population. It is worth noting that even though the baseline parameters are regulated similarly to the maximum of \(75\%\), it must be noted that the dynamics of the total infected population are diverse under different parameters. For example, it is obvious in Fig. 6 that reducing the effective contact rate by \(75\%\) decreases the total infected human population faster with a higher magnitude than the others as shown in Fig. 6a. As a result of this observation, we investigate the effect of combining different control measures on the total infected population in Fig. 7. We note that we select the \(75\%\) regulated parameter values (henceforth referred to as “control”) such that \(\alpha = 0.00025\), \(\beta =7.09e-6\), \(\eta = 2.54384\), \(\sigma = 0.29575\), and \(\gamma = 0.1680\).

Our aim in simulating different combined controlled parameters is to predict and make recommendations for the most effective control measures that can be used to mitigate the measles burden on the populace. In Fig. 7a, we illustrate the impact of a single control measure \(\sigma\), double control measures \((\sigma , \eta )\), and triple control measures \((\sigma , \eta , \gamma )\), on the abundance of total infected population. In comparison to the effect of a single or double controlled parameter, the total infected population decreased faster when the three controlled parameters were used. This means that even though increasing the vaccination rate \((\sigma )\) by \(75\%\) helps in reducing disease burden, the implementation of an increase in vaccination rate, testing and therapy rate for exposed individuals, and recovery rate from infection simultaneously will aid the eradication of measles faster in the population. We see the same result in Fig. 7b, c. Overall, we can conclude that by using a combined control measure, the measles burden can be reduced more rapidly in the population compared to the use of a single control measure.

From the results presented in Fig. 7, it is worth mentioning that the combined controlled parameter \((\gamma , \eta , \alpha )\) has the greatest impact in reducing the number of the total infected population. In Fig. 7d, we simulate the dynamics of the infected population without any control and with the presence of all control measures. We defined the scenario “with all-control” as the combination of all the controlled parameters, while the scenario “without any-control” is when the parameters are in their baseline values as presented in Table 2.

Although, the cost of implementing control measures and preventive strategies can be very expensive, especially for developing countries like Pakistan, thus, it is recommended to selectively choose the most cost-effective control strategies that can be used to mitigate the disease burden on the population.

Conclusion with future directions

The measles is a very contagious and sometimes fatal illness. The number of deaths caused by measles worldwide has decreased by 73% between the years 2000 and 2018, thanks in large part to vaccination efforts. Nevertheless, the disease is still common in many developing nations, especially those in Africa and Asia. We built a deterministic mathematical model of the spread of measles to learn more about its dynamics of spread. This research finds two equilibrium points: one where the disease is absent and one where it is pervasive. To determine whether or not an equilibrium can be maintained, the basic reproduction number is used. When \(R_0<1\), the point of equilibrium where no diseases exist, the measles can be eradicated permanently. However, when \(R_0 > 1\), the endemic equilibrium point remains constant. The study’s findings imply that implementing healthcare facilities that will boost diagnosis and therapy for exposed people and the recovery rate from infection is necessary to successfully lessen the measles burden in a shorter period. Also, people should be encouraged to take steps to prevent measles from spreading in the population. For future studies, the proposed measles model would be investigated to comprehend the chaotic dynamics of the disease in the field of fractional calculus. In this connection, a few differential and integral operators, recently introduced in the literature, such as the Atangana-Baleanu and Caputo-Fabrizio, will be used. In addition, optimal control theory will assist in identifying the control measures most effective to prevent the disease from persisting for long periods within a population.