1 Introduction

Measles, also known as rubeola, is a viral infection that begins in the lungs. Despite the availability of a safe and efficient vaccination, it is still a leading cause of death globally. According to the World Health Organization, nearly 110,000 people died worldwide from measles in 2017, the majority of whom were children under the age of five [1]. Measles has an incubation period of about 8–12 days before the rash appears, followed by fever, cough, coryza, and conjunctivitis. Following these symptoms, a rash appears, which begins on the face and neck and spreads to the rest of the body [2]. The globe has had to deal with the measles pandemic on multiple occasions. Between 1988 and 1990, the United States of America experienced a measles outbreak, with over 16,000 cases and more than 70 deaths documented [3]. In 2018, Madagascar, Ukraine and Congo was hit by a measles outbreak that infected 50,000 individuals and claimed the lives of around 300 people, the majority of whom were children. Other countries like Angola, Cameroon, Kazakhstan, Chad, Nigeria, Thailand, Philippines, South Sudan, and Sudan are all experiencing the epidemics [4, 5]. According to the 2013 Nigeria Demographic and Health Survey, 25% of Nigerian children aged 12–23 months had got all recommended immunizations, whereas 42% had received measles vaccination. When compared to the Northern regions, the Southern regions had higher measles coverage (62–74%) (22–48%) [6]. The easiest way to avoid contracting measles is to be vaccinated. It’s risk-free, cost-effective, and easy to use. Young children who have not been vaccinated and pregnant women are more vulnerable to measles and its complications, which can include death. Immunity against measles provided by vaccination has been proven to last for at least 20 years and is widely considered to be life-long for most people. At 9–11 months of age, the vaccine efficacy is estimated to be 85%, increasing to 97% following a second dose given at more than 12 months [7]. Children under the age of five and adults over the age of twenty are more likely to develop issues that necessitate hospitalization. Ear infections and diarrhea are two common complications. Pneumonia and encephalitis are serious consequences. Hospitalization is required in severe instances of measles. The Centers for Disease Control and Prevention (CDC) estimates that 1 in every 4 cases of measles in the United States results in hospitalization, and 1 in 1000 cases results in death, based on historical data. With widespread measles immunization, hospitalizations for measles dropped dramatically [8,9,10]. Mathematical models have become a significant tool that many researchers have utilized to better understand the epidemiology of diseases in various populations. To gain a better insight into the disease’s transmission dynamics and control, many models have been developed and studied using various methodologies [11,12,13,14,15,16,17,18,19]. To understand the spread of measles, many scientists have employed mathematical models. Authors in [20] presented a basic SEIR model to examine the behavior of measles when no control is included in the model. The authors of [21] investigate the relationship between mass vaccination and herd immunity, whereas the authors of [22] consider the influence of vaccine on measles mortality in their model. The seasonality spreading factor was considered by the authors in [23] when discussing the transmission of measles in China. Furthermore, the authors in [24] consider early testing and therapy for those who have been exposed to measles in order to prevent subsequent outbreaks. Unlike the other references, the authors of [25] include passive immune groups in their model to investigate their impact on the measles eradication approach. The authors explain the impact of quarantine compartments in [2]. Few researchers have proposed a deterministic models by considering the transmission dynamics of the disease with double dose vaccination [5, 7]. Other related studies on the dynamics of measles can be found in [26,27,28,29]. The current study aims to examine the impact of certain prevention measures, including vaccination and contact rate, for effective measles control. Our analysis will focus on the effectiveness of the first and second vaccination doses as well as their coverage in preventing the spread of disease. Our inspiration came from a few research in the literature mentioned above that concentrated on deterministic modeling of measles; none of these studies looked at the impact of effective transmission rate, first dose vaccination rate, and second dose vaccination rate on the management of the disease. The rest of the paper is structured as follows: Sect. 2 deals with the formulation of the measles model and the model description. Section 3 deals with the equilibria and the basic reproduction number. Stability analysis and the numerical simulation are illustrated in Sects. 4 and 5, respectively, finally, the conclusion of the work is given in Sect. 6.

2 Formulation of the model

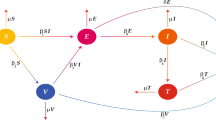
To study the dynamics of measles disease through a mathematical model approach, we divide the human population into seven classes, namely, susceptible class S(t), individual who received the first dose of the MMR vaccine \(V_{1}(t)\), individual who received the second dose of the MMR vaccine \(V_{2}(t)\), exposed class E(t), infected class I(t), hospitalized class H(t) and recovered class R(t). Recruitment into the susceptible class is either by birth or immigration at the rate \(\phi \), susceptible individuals who received the first dose of vaccine moved to vaccinated compartment at a rate \(\theta \), due to the fact that the first dose of the MMR vaccine is not very effective to protect against measles, the first dose of vaccinated individuals can still be susceptible to the disease. In this case, the first dose of vaccinated individuals moves to the susceptible class at a rate \(\beta \) and those vaccinated with the first dose took the second dose at a rate \(\sigma _1\). The second dose of vaccinated individuals moves to recovered class at a rate \(\sigma _2\), susceptible individuals become exposed to the measles at the rate \(\lambda =\alpha SI\), where \(\alpha \) is the effective contact rate, the parameter \(\varepsilon \) represents the progression rate from exposed to infected class, while \(\gamma \) is the progression rate from infected class. Most people recovered from measles naturally without medication and in some cases, complications may occur whereby about one in five individuals infected will be hospitalized due to complications [30]. We have included hospitalized compartment in our model to illustrate this. It is assume that fraction \(\omega \) recovers naturally while the rest moved to the hospitalized class. Upon treatment, individuals in the hospitalized class recovers at a rate \(\tau \), natural death rate occurs in all the compartments and it is assumed that death rate due to measles occurs only at the infected class at a rate \(\delta \). This description can be illustrated in the form of nonlinear differential equations and with the aid of schematic diagrams (see Fig. 1), our model takes the form:

Fig. 1
figure 1

Flowchart of model (1)

Full size image
$$\begin{aligned} \begin{aligned} \dfrac{\textrm{d}S}{\textrm{d}t} =&\ \phi -\alpha SI-(\theta +\mu )S+\beta V_1,\\ \dfrac{\textrm{d}V_1}{\textrm{d}t} =&\ \theta S-(\beta +\mu +\sigma _1)V_1,\\ \dfrac{\textrm{d}V_2}{\textrm{d}t} =&\ \sigma _1 V_1 -(\sigma _2+\mu )V_2,\\ \dfrac{\textrm{d}E}{\textrm{d}t} =&\ \alpha SI-(\varepsilon +\mu )E,\\ \dfrac{\textrm{d}I}{\textrm{d}t} =&\ \varepsilon E-(\mu +\delta + \gamma )I,\\ \dfrac{\textrm{d}H}{\textrm{d}t} =&\ \gamma (1-\omega ) I-(\mu +\tau )H,\\ \dfrac{\textrm{d}R}{\textrm{d}t} =&\ \gamma \omega I+\tau H+\sigma _2 V_2-\mu R, \end{aligned} \end{aligned}$$
(1)

where \(\mu \) is is the natural death rate.

In case of no disease, for the total human population N with a positive initial condition

$$\begin{aligned} (S(0),V_1(0),V_2(0),E(0),I(0),H(0),R(0)\in R^7_+, \end{aligned}$$

we have the equation

$$\begin{aligned} \dfrac{\textrm{d}N}{\textrm{d}t}= \phi -\mu N. \end{aligned}$$
(2)

Equation (2) admits a unique equilibrium \(N^*= \tfrac{\phi }{\mu }\) which is globally attractive on \(R_+\).

Table 1 Description of the models variables and parameters
Full size table

3 Equilibria and the basic reproduction number

In this section, we show that system (1) has two equlibria dependent on the value of the basic reproduction number \({\mathcal {R}}_0\): the disease-free equilibrium \(E_0\) if \({\mathcal {R}}_0 < 1\), and the endemic equilibrium \(E_1\) when \({\mathcal {R}}_0 > 1\) (Table 1).

In the absence of the disease, we obtain the disease-free equilibrium of the system (1) by equating to zero the right side of equations in system (1). Hence, the disease-free equilibrium is given by

$$\begin{aligned} \begin{aligned} E_0=&\ \left( S^*,V^*_1,V^*_2,E^*,I^*,H^*,R^*\right) \\ =&\ \left( \frac{\phi (\beta + \sigma _1 + \mu )}{\beta \mu + ( \theta + \mu ) (\sigma _1 + \mu )}, \frac{\theta \phi }{\beta \mu + (\theta + \mu ) (\sigma _1 + \mu )}, \right. \\&\left. \frac{\theta \sigma _1 \phi }{(\sigma _2 + \mu ) (\beta \mu + (\theta + \mu ) (\sigma _1 + \mu ))}, 0, 0, 0, \frac{ \sigma _{2}}{\mu }V_{2}^{*} \right) , \end{aligned} \end{aligned}$$

and always exists.

Next, we compute the basic reproduction number \({\mathcal {R}}_0\) of system (1), we follow the general approach established in [31]. Given the infectious states E, I, and H, and substituting the values of the disease-free equilibrium \(E_0\), the matrices F and V are calculated for the new infection terms and the remaining transfer terms. . The matrices F and V are given as

$$\begin{aligned} F= \begin{bmatrix} 0 &{} \alpha S^* &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix} \ \text {and} \ V= \begin{bmatrix} \varepsilon +\mu &{} 0 &{} 0 \\ -\varepsilon &{} \mu +\delta + \gamma &{} 0 \\ 0 &{} -\gamma (1- \omega ) &{} \mu +\tau \end{bmatrix}. \end{aligned}$$
(3)

The basic reproduction number, defined as the spectral radius of the matrix \(F V^{-1}\), is given by

$$\begin{aligned} {\mathcal {R}}_0= & {} \frac{\varepsilon \alpha S^*}{(\varepsilon +\mu )( \gamma + \delta +\mu )} \nonumber \\= & {} \frac{\varepsilon \alpha \phi (\beta + \sigma _1 + \mu ) }{(\varepsilon +\mu )( \gamma + \delta +\mu ) (\beta \mu + ( \theta + \mu ) (\sigma _1 + \mu ))} . \end{aligned}$$
(4)

It is easy to prove that if \({\mathcal {R}}_0 > 1\), in addition to the disease-free equilibrium point \(E_0\), system (1) also has an endemic equilibrium

$$\begin{aligned} E_1={}\left( S^{**},V^{**}_1,V^{**}_2,E^{**},I^{**},H^{**},R^{**}\right) . \end{aligned}$$

By solving the equations of the model in terms of the force of infection at steady state, we have that

$$\begin{aligned} S^{**} =&\ \frac{(\varepsilon +\mu ) (\delta + \gamma +\mu )}{\alpha \varepsilon }, \nonumber \\ V_1^{**} =&\ \frac{\theta (\varepsilon +\mu ) (\delta + \gamma +\mu )}{\alpha \varepsilon (\beta +\sigma _1+\mu )}, \nonumber \\ V_2^{**} =&\ \frac{\theta \sigma _1 (\varepsilon +\mu ) (\delta + \gamma +\mu )}{\alpha \varepsilon (\sigma _2+\mu ) (\beta +\sigma _1+\mu )}, \nonumber \\ E^{**} =&\ \frac{\phi }{\varepsilon +\mu } \left( 1-\frac{1}{{\mathcal {R}}_0}\right) , \nonumber \\ I^{**} =&\ \frac{\varepsilon \phi }{(\varepsilon +\mu ) (\delta + \gamma +\mu )} \left( 1-\frac{1}{{\mathcal {R}}_0}\right) , \nonumber \\ H^{**} =&\ \frac{ \gamma (1-\omega ) \varepsilon \phi }{(\tau +\mu ) (\varepsilon +\mu ) (\delta + \gamma +\mu )} \left( 1-\frac{1}{{\mathcal {R}}_0}\right) \nonumber \\ R^{**} =&\ \frac{\gamma \omega I^{**}+\tau H^{**}+\sigma _{2}V_{2}^{**}}{\mu } \end{aligned}$$
(5)

provided the basic reproduction number (\({\mathcal {R}}_0 \)) is greater than one. Since equation (1) is independent of the recovery population, we may concentrate our efforts on the following system:

$$\begin{aligned} \begin{aligned} \dfrac{\textrm{d}S}{\textrm{d}t} =&\ \phi -\alpha SI-(\theta +\mu )S+\beta V_1,\\ \dfrac{\textrm{d}V_1}{\textrm{d}t} =&\ \theta S-(\beta +\mu +\sigma _1)V_1,\\ \dfrac{\textrm{d}V_2}{\textrm{d}t} =&\ \sigma _1 V_1 -(\sigma _2+\mu )V_2,\\ \dfrac{\textrm{d}E}{\textrm{d}t} =&\ \alpha SI-(\varepsilon +\mu )E,\\ \dfrac{\textrm{d}I}{\textrm{d}t} =&\ \varepsilon E-(\mu +\delta + \gamma )I,\\ \dfrac{\textrm{d}H}{\textrm{d}t} =&\ \gamma (1-\omega ) I-(\mu +\tau )H,\\ \end{aligned} \end{aligned}$$
(6)

By the positivity and boundedness of the system solutions, we consider systems (1) and (6) in the positively invariant region

$$\begin{aligned}{} & {} \Omega _{1} = \big \{(S ,V_1 ,V_2,E ,I ,H,R )\in {\mathbb {R}}^7{:} \nonumber \\{} & {} S+ V_1+V_2+E +I +H+R \le \frac{\phi }{\mu }\big \}, \end{aligned}$$
(7)

and

$$\begin{aligned}{} & {} \Omega = \big \{(S ,V_1 ,V_2,E ,I ,H )\in \nonumber \\{} & {} R^6{:} \ S+ V_1+V_2+E +I +H \le \frac{\phi }{\mu }\big \}, \end{aligned}$$
(8)

respectively.

4 Stability analysis

4.1 Local stability of the equilibrium points

In this section, we show the dynamics of our model depending on the basic reproduction number. We prove the local stability of the disease-free equilibrium \(E_0\) of system (6) if the basic reproduction number \({\mathcal {R}}_0<1\), while if \({\mathcal {R}}_0>1\), then the endemic equilibrium \(E_1\) is locally asymptotically stable.

Theorem 1

The disease-free equilibrium \(E_0\) is locally asymptotically stable if \({\mathcal {R}}_0<1\), and unstable otherwise.

Proof

The Jacobian matrix of the system (6) at \(E_0\) is given by

$$\begin{aligned}{} & {} J(E_0)\\{} & {} =\left[ \begin{array}{cccccc} -\theta -\mu &{} \beta &{} 0 &{} 0 &{} -\frac{\alpha \phi (\beta +\sigma _1+\mu )}{\beta \mu +(\theta +\mu ) (\sigma _1+\mu )} &{} 0 \\ \theta &{} -\beta -\sigma _1-\mu &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \sigma _1 &{} -\sigma _2-\mu &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\varepsilon -\mu &{} \frac{\alpha \phi (\beta +\sigma _1+\mu )}{\beta \mu +(\theta +\mu ) (\sigma _1+\mu )} &{} 0 \\ 0 &{} 0 &{} 0 &{} \varepsilon &{} -\delta - \gamma -\mu &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \gamma (1-\omega ) &{} -\tau -\mu \\ \end{array} \right] . \end{aligned}$$

It is easy to verify that two of the eigenvalues of \(J(E_0)\) are \( \lambda _1= -\sigma _2-\mu <0 \) and \( \lambda _2= -\tau -\mu <0 \). The remaining four eigenvalues can be obtained from the equation

$$\begin{aligned} \left|\begin{array}{cccc} -\theta -\mu -\lambda &{} \beta &{} 0 &{} -\frac{\alpha \phi (\beta +\sigma _1+\mu )}{\beta \mu +(\theta +\mu ) (\sigma _1+\mu )} \\ \theta &{} -\beta -\sigma _1-\mu -\lambda &{} 0 &{} 0 \\ 0 &{} 0 &{} -\varepsilon -\mu -\lambda &{} \frac{\alpha \phi (\beta +\sigma _1+\mu )}{\beta \mu +(\theta +\mu ) (\sigma _1+\mu )} \\ 0 &{} 0 &{} \varepsilon &{} -\delta - \gamma -\mu -\lambda \\ \end{array} \right|=0, \end{aligned}$$

which gives the following characteristic equations:

$$\begin{aligned} 0 =&\ \lambda ^2 + (\beta +\sigma _1+2\mu +\theta ) \lambda +(\beta +\sigma _1+\mu ) (\theta +\mu )-\beta \theta , \end{aligned}$$
(9)
$$\begin{aligned} 0 =&\ \lambda ^2+ (\delta + \gamma +2\mu +\varepsilon ) \lambda +(\delta + \gamma +\mu ) (\varepsilon +\mu )\nonumber \\&- \frac{ \varepsilon \alpha \phi (\beta +\sigma _1+\mu )}{\beta \mu +(\theta +\mu ) (\sigma _1+\mu )}. \end{aligned}$$
(10)

Equation (9) has two eigenvalues \(\lambda _3\) and \(\lambda _4\) as its roots satisfying the following:

$$\begin{aligned} \begin{aligned} \lambda _3+\lambda _4 =&\ -\beta -\sigma _1-2\mu -\theta <0, \\ \lambda _3 \lambda _4 =&\ (\beta +\sigma _1+\mu ) (\theta +\mu )-\beta \theta \\ =&\ (\beta +\sigma _1+\mu ) \mu + (\sigma _1+\mu ) (\theta +\mu )>0. \end{aligned} \end{aligned}$$
(11)

Again (10) has two eigenvalues \(\lambda _5\) and \(\lambda _6\) satisfying the following:

$$\begin{aligned} \begin{aligned} \lambda _5+\lambda _6 =&\ -\delta - \gamma -2\mu -\varepsilon < 0, \\ \lambda _5 \lambda _6 =&\ (\delta + \gamma +\mu ) (\varepsilon +\mu )(1- {\mathcal {R}}_0 ). \end{aligned} \end{aligned}$$
(12)

The conditions stated in (11) and (12) imply that \(\lambda _3, \lambda _4, \lambda _5\), and \(\lambda _6\) have negative real parts when \({\mathcal {R}}_0 < 1\). Therefore, \(E_0\) is locally asymptotically stable if \({\mathcal {R}}_0 < 1\) . If \({\mathcal {R}}_0 > 1\) , at least one of \(\lambda _5\) and \(\lambda _6\) has a positive real part and \(E_0\) is unstable. \(\square \)

Theorem 2

The endemic equilibrium \(E_1\) is locally asymptotically stable if \({\mathcal {R}}_0>1\).

Proof

The Jacobian matrix of the system (6) at the endemic equilibrium \(E_1\) is

$$\begin{aligned}{} & {} J(E_1)\\{} & {} =\left[ \begin{array}{cccccc} - \alpha I^{**} -\theta -\mu &{} \beta &{} 0 &{} 0 &{} -\alpha S^{**} &{} 0 \\ \theta &{} -\beta -\sigma _1-\mu &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \sigma _1 &{} -\sigma _2-\mu &{} 0 &{} 0 &{} 0 \\ \alpha I^{**} &{} 0 &{} 0 &{} -\varepsilon -\mu &{} \alpha S^{**} &{} 0 \\ 0 &{} 0 &{} 0 &{} \varepsilon &{} - \delta - \gamma -\mu &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \gamma (1-\omega ) &{} -\tau -\mu \\ \end{array} \right] . \end{aligned}$$

The Jacobian \(J(E_1)\) has the following characteristic equation:

$$\begin{aligned} (\lambda +\mu +\sigma _2)(\lambda +\mu +\tau )(\lambda ^4 +C_3\lambda ^3 + C_2 \lambda ^2 \nonumber \\ + C_1 \lambda + C_0) = {} 0, \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{aligned} C_3=&{} \alpha I^{**}+ \beta +\delta +\varepsilon +\theta +\sigma _1+\omega \gamma +4 \mu ,\\ C_2 =&{}\alpha (\beta +\delta +\varepsilon +\sigma _1+\omega \gamma +3 \mu ) I^{**} \\&+ (\omega \gamma +\delta +\varepsilon )(\beta +\theta +\sigma _1+ 2\mu ) +3 \mu (\beta +\theta +\sigma _1)\\&+5 \mu ^2+\theta \sigma _1,\\ C_1 =&{} \alpha \left( 2 \mu (\beta +\varepsilon +\sigma _1)+ (\beta +\varepsilon \right. \\&\left. +\sigma _1+2 \mu )( \delta + \omega \gamma )+\varepsilon (\beta +\varepsilon +\sigma _1)+3 \mu ^2\right) I^{**}\\&+(\beta \mu +(\theta +\mu ) (\sigma _1+\mu )) (\delta +\varepsilon + \gamma +2 \mu ),\\ C_0 =&{} \alpha (\varepsilon +\mu ) (\beta +\sigma _1+\mu ) (\delta + \gamma +\mu )I^{**}. \end{aligned} \end{aligned}$$
(14)

From (13), \(J(E_1)\) has two negative eigenvalues are \(-\mu -\sigma _1\) and \(-\mu -\tau \). However, it is easy to verify from (14) that

$$\begin{aligned}{} & {} C_3>0,\ C_2>0,\ C_1>0,\ C_0>0 \ \text {and} \ (C_3 C_2-C_1)C_1 \\{} & {} \quad -C^2_3 C_0>0\ \text {if}\ I^{**}>0. \end{aligned}$$

According to (5), \(I^{**}>0\) if \({\mathcal {R}}_0>1\), and hence, by Routh–Hurwitz stability criterion, the endemic equilibrium \(E_1\) is locally asymptotically stable for \({\mathcal {R}}_0>1\). \(\square \)

4.2 Global stability of the equilibrium points

Irrespective of where the system (1) starts, we wish to derive condition(s) under which the system converges to the disease-free \(E_{0}\) or endemic equilibrium \(E_{1}\) points on the long run. The following theorem shows condition for the global stability of the disease-free equilibrium \(E_{0}\).

Theorem 3

The disease-free equilibrium \(E_0\) is globally stable in the feasible region \(\Omega \) if \({\mathcal {R}}_0\le 1\).

Proof

Define the Lyapunov function \({\mathcal {L}}:{\mathbb {R}}_{+}^{6}\rightarrow {\mathbb {R}}_{+}\) by

$$\begin{aligned} {\mathcal {L}}= & {} \left( S-S^{*}-S^{*}\ln \frac{S}{S^{*}}\right) \nonumber \\{} & {} +\sum \limits _{j=1}^{2}r_{j}\left( V_{j}-V_{j}^{*}-V_{j}^{*}\ln \frac{V_{j}}{V_{j}^{*}}\right) \nonumber \\{} & {} +e_{1}E+a_{1}I+b_{1}H, \end{aligned}$$
(15)

where

$$\begin{aligned} e_{1}= & {} 1, \end{aligned}$$
(16)
$$\begin{aligned} r_{1}= & {} 1, \end{aligned}$$
(17)
$$\begin{aligned} a_{1}= & {} \frac{\varepsilon +\mu }{\varepsilon }, \end{aligned}$$
(18)
$$\begin{aligned} b_{1}= & {} \left( \frac{1}{{\mathcal {R}}_{0}}-1\right) \frac{\alpha S^{*}}{(1-\omega )\gamma }, \end{aligned}$$
(19)
$$\begin{aligned} r_{2}= & {} \frac{\mu +\sigma _{1}}{\sigma _{1}}. \end{aligned}$$
(20)

It follows that

$$\begin{aligned} \begin{array}{lllll} \dfrac{\textrm{d}{\mathcal {L}}}{\textrm{d}t}&{}=&{}\phi +(\theta +\mu )S^{*}+r_{1}(\beta +\mu +\sigma _{1})V_{1}^{*}\\ &{}&{}+r_{2}(\mu +\sigma _{2})V_{2}^{*} \\ &{}&{}+\alpha (e_{1}-1)SI+(r_{1}\theta -\theta -\mu )S\\ &{}&{}+(\beta +r_{2}\sigma _{1}-r_{1}(\beta +\mu +\sigma _{1}))V_{1}\\ &{}&{}+I\left( \alpha S^{*}-a_{1}(\mu +\delta +\gamma )+b_{1}\gamma (1-\omega )\right) \\ &{}&{}+(a_{1}\varepsilon -e_{1}(\mu +\varepsilon ))E-\phi S^{*}/S-\beta S^{*} V_{1}/S\\ &{}&{}-r_{1}\theta V_{1}^{*} S/V_{1}-r_{2}(\mu +\sigma _{2})V_{2}-r_{2}\sigma _{1}V_{2}^{*}V_{1}/V_{2}\\ &{}&{}-b_{1}(\mu +\tau )H. \end{array} \end{aligned}$$
(21)

Define

$$\begin{aligned} {\bar{s}}=\frac{S}{S^{*}},\ \ {\bar{v}}_{1}=\frac{V_{1}}{V_{1}^{*}},\ \ \ {\bar{v}}_{2}=\frac{V_{2}}{V_{2}^{*}}, \end{aligned}$$
(22)

and

$$\begin{aligned} c_{1}= & {} \mu S^{*},\\ c_{2}= & {} \beta V_{1}^{*},\\ c_{3}= & {} (\mu +\sigma _{1})V_{1}^{*}=r_{2}(\mu +\sigma _{2})V_{2}^{*}. \end{aligned}$$

It follows from (21) that

$$\begin{aligned} 2c_{1}+2c_{2}+4c_{3}= & {} \phi +(\theta +\mu )S^{*}+r_{1}(\beta +\mu +\sigma _{1})V_{1}^{*}\\{} & {} +r_{2}(\mu +\sigma _{2})V_{2}^{*}, \end{aligned}$$

and

$$\begin{aligned} \begin{array}{lllll} \dfrac{\textrm{d}{\mathcal {L}}}{\textrm{d}t}&{}=&{} -c_{1}\left( {\bar{s}}+\frac{1}{{\bar{s}}}-2\right) -c_{2}\left( \frac{{\bar{v}}_{1}}{{\bar{s}}}+\frac{{\bar{s}}}{{\bar{v}}_{1}}-2\right) \\ &{}&{}-c_{3}\left( \frac{{\bar{v}}_{1}}{{\bar{v}}_{2}}+{\bar{v}}_{2}+\frac{{\bar{s}}}{{\bar{v}}_{1}}+\frac{1}{{\bar{s}}}-4\right) -b_{1}(\mu +\tau )H. \end{array} \end{aligned}$$
(23)

Using the fact that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list [32], it follows that \(\textrm{d} {\mathcal {L}}/{rm d}t\le 0\). Equality holds if \(S=S^{*}\), \(V_{k}=V_{k}^{*}\) for \(k=1,2\), \(I=E=H=0\). This implies that R converges to \(R^{*}\). Since \(E_{0}\) is the largest invariant set in the subset of \(\Omega \) where \(\textrm{d} {\mathcal {L}}/\textrm{d}t=0\), its global stability follows by the LaSalle’s Invariance Principle [33]. \(\square \)

The following theorem shows condition for the global stability of the endemic equilibrium \(E_{1}\).

Theorem 4

The endemic equilibrium \(E_1\) is globally stable in the feasible region \(\Omega _{1}\) if \({\mathcal {R}}_1> 1\).

Proof

Assume \({\mathcal {R}}_{0}>1\). Then the existence of the endemic equilibrium \(E_{1}\) given in (5) follows. Define the Lyapunov function \({\mathbb {L}}:{\mathbb {R}}_{+}^{5}\rightarrow {\mathbb {R}}_{+}\) by

$$\begin{aligned} {\mathbb {L}}= & {} \left( S-S^{**}-S^{**}\ln \frac{S}{S^{**}}\right) \nonumber \\{} & {} +\sum \limits _{j=1}^{2}{\bar{r}}_{j}\left( V_{j}-V_{j}^{*}-V_{j}^{*}\ln \frac{V_{j}}{V_{j}^{*}}\right) \nonumber \\{} & {} +{\bar{e}}_{1}\left( E-E^{**}-E^{**}\ln \frac{E}{E^{**}}\right) \end{aligned}$$
(24)
$$\begin{aligned}{} & {} +{\bar{a}}_{1}\left( I-I^{**}-I^{**}\ln \frac{I}{I^{**}}\right) , \end{aligned}$$
(25)

where

$$\begin{aligned} {\bar{e}}_{1}= & {} 1, \end{aligned}$$
(26)
$$\begin{aligned} {\bar{r}}_{1}= & {} 1, \end{aligned}$$
(27)
$$\begin{aligned} {\bar{r}}_{2}= & {} \frac{\mu +\sigma _{1}}{\sigma _{1}}, \end{aligned}$$
(28)
$$\begin{aligned} {\bar{a}}_{1}= & {} \frac{\varepsilon +\mu }{\varepsilon }. \end{aligned}$$
(29)

It follows that

$$\begin{aligned} \begin{aligned} \dfrac{\textrm{d}{\mathbb {L}}}{\textrm{d}t} =&\ \phi +(\theta +\mu )S^{**}+{\bar{r}}_{1}(\beta +\mu +\sigma _{1})V_{1}^{**}\\&+{\bar{r}}_{2} (\mu +\sigma _{2})V_{2}^{**}\\&+{\bar{e}}_{1}(\mu +\varepsilon )E^{**}+{\bar{a}}_{1}(\mu +\delta +\gamma )I^{**}\\&+\alpha ({\bar{e}}_{1}-1)SI+({\bar{r}}_{1}\theta -\theta -\mu )S\\&+(\beta +{\bar{r}}_{2} \sigma _{1}-{\bar{r}}_{1}(\beta +\mu +\sigma _{1}))V_{1}\\&+I\left( \alpha S^{**}-{\bar{a}}_{1}(\mu +\delta +\gamma )\right) +({\bar{a}}_{1} \varepsilon -{\bar{e}}_{1}(\mu +\varepsilon ))E\\&-\phi S^{**}/S-\beta S^{**} V_{1}/S\\&-{\bar{r}}_{1}\theta V_{1}^{**} S/V_{1}-{\bar{r}}_{2}(\mu +\sigma _{2})V_{2}\\&-{\bar{r}}_{2}\sigma _{1}V_{2}^{**}V_{1}/V_{2}-{\bar{e}}_{1}\alpha E^{**}SI/E-{\bar{a}}_{1}\varepsilon I^{**}E/I. \end{aligned} \end{aligned}$$
(30)

Define

$$\begin{aligned} {\hat{s}}=\frac{S}{S^{**}},\ \ {\hat{v}}_{1}=\frac{V_{1}}{V_{1}^{**}},\ \ \ {\hat{v}}_{2}=\frac{V_{2}}{V_{2}^{**}},\ \ \ {\hat{e}}=\frac{E}{E^{**}},\ \ \ {\hat{i}}=\frac{I}{I^{**}}. \end{aligned}$$

and

$$\begin{aligned} {\bar{c}}_{1}= & {} \mu S^{**}, \end{aligned}$$
(31)
$$\begin{aligned} {\bar{c}}_{2}= & {} \beta V_{1}^{**}, \end{aligned}$$
(32)
$$\begin{aligned} {\bar{c}}_{3}= & {} {\bar{r}}_{2} \sigma _{1} V_{1}^{**}={\bar{r}}_{2}(\mu +\sigma _{2})V_{2}^{**}, \end{aligned}$$
(33)
$$\begin{aligned} {\bar{c}}_{4}= & {} {\bar{e}}_{1}\alpha S^{**}I^{**}={\bar{a}}_{1}\varepsilon E^{**}. \end{aligned}$$
(34)

It follows from (30) that

$$\begin{aligned} 2{\bar{c}}_{1}+2{\bar{c}}_{2}+4{\bar{c}}_{3}+3{\bar{c}}_{4}+= & {} \phi +(\theta +\mu )S^{**}\nonumber \\ {}{} & {} +{\bar{r}}_{1}(\beta +\mu +\sigma _{1})V_{1}^{**}\nonumber \\ {}{} & {} +{\bar{r}}_{2}(\mu +\sigma _{2})V_{2}^{**}\nonumber \\ {}{} & {} +{\bar{e}}_{1}(\mu +\varepsilon )E^{**} \\{} & {} +{\bar{a}}_{1}(\mu +\delta +\gamma )I^{**},\nonumber \end{aligned}$$
(35)

and

$$\begin{aligned} \begin{aligned} \dfrac{\textrm{d}{\mathbb {L}}}{\textrm{d}t} =&\ -{\bar{c}}_{1}\left( {\hat{s}}+\frac{1}{{\hat{s}}}-2\right) \\&\quad -{\bar{c}}_{2}\left( \frac{{\hat{v}}_{1}}{{\hat{s}}}+\frac{{\hat{s}}}{{\bar{v}}_{1}}-2\right) \\&-{\bar{c}}_{3}\left( \frac{{\hat{v}}_{1}}{{\hat{v}}_{2}}+{\hat{v}}_{2}+\frac{{\hat{s}}}{{\bar{v}}_{1}}+\frac{1}{{\hat{s}}}-4\right) \\&\ -{\bar{c}}_{4}\left( \frac{{\hat{s}}{\hat{i}}}{{\hat{e}}}+\frac{{\hat{e}}}{{\hat{i}}}+\frac{1}{{\hat{s}}}-3\right) . \end{aligned} \end{aligned}$$
(36)

Using the fact that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list [32], it follows that \(\textrm{d} {\mathbb {L}}/\textrm{d}t\le 0\). Equality holds if \(S=S^{**}\), \(V_{k}=V_{k}^{**}\) for \(k=1,2\), \(I=I^{**}\), \(E=E^{**}\). This implies that H converges to \(H^{**}\) and R converges to \(R^{*}\). Since \(E_{1}\) is the largest invariant set in the subset of \(\Omega \) where \(\textrm{d} {\mathbb {L}}/\textrm{d}t=0\), its global stability follows by the LaSalle’s Invariance Principle [33]. \(\square \)

5 Numerical simulations

Fig. 2
figure 2

Time series of model (1) using parameters given by Table 2

Full size image
Fig. 3
figure 3

Time series of model (1) using parameters given by Table 2

Full size image
Fig. 4
figure 4

PRCC results for the parameters of \({\mathcal {R}}_0\)

Full size image
Fig. 5
figure 5

Contour plots for the parameters respect to \({\mathcal {R}}_0\)

Full size image
Fig. 6
figure 6

PRCC results for the parameters of \(V_1,\ V_2,\ E,\ I,\ H\), and R

Full size image

5.1 Parameter values

Some of the parameter values used in the simulation process are published parameters obtained from the literature. Those not found in the literature are estimated. Parameters based on the Nigeria data on measles for the year 2020 are obtained from [34] (Fig. 3).

Table 2 The description of parameters and values
Full size table

Using the estimated and published parameters given in Table 2, the system (1) converges to the disease-free equilibrium \(E_{0}\) irrespective of the initial condition used, and the reproduction number \({\mathcal {R}}_{0}<1\). The population receiving the first and second doses of the MMR converge to 73,083 and 84,926, respectively. The susceptible and the recovered class converge to 118,979 and 219,875,114, respectively, while the infected classes converge to zero. This analysis shows that the effect of the vaccines is significant, with the second dose of the vaccine having more effect than the first dose. The numerical simulations of these conditions are given in Fig. 2. Now, to show the influence of the interaction between the susceptible and infected classes, we increase the value of the impact of the contact rate to \(\alpha =1\times 10^{-5}\). The reproduction number increases such that \({\mathcal {R}}_{0}>1\) which means \(E_1\) becomes asymptotically stable and measles exists in the population. As the contact rate increases, the susceptible class, people who received the first dose of the MMR vaccine, people who received the second dose of the MMR vaccine, and the recovered class will decrease to 46,632, 28,644, 33,286, and 209,908,515, respectively. Measles becomes endemic which is indicated by the occurrence of exposed, infected, and hospitalized classes which, respectively, converge to 82,679, 88,706, and 55,940. Here, we can say that restricting the interaction between susceptible and infected classes play the important role in suppressing the growth rate of exposed and infected class. To learn more about the most influential parameter to the infection rate and the density for each class, the global sensitivity analysis is given in the following sub-section.

5.2 Global sensitivity analysis

To investigate the most influential parameter in model (1), the global sensitivity analysis is employed. Two biological aspects namely the basic reproduction number and the density of each class become the constraint functions of the sensitivity analysis while the ranks of the parameters are the objective function. To facilitate these works, the Partial Rank Correlation (PRCC) [35] is used for ranking along with Saltelli sampling [36, 37] to generate more than 2000 sample data around the parameter values given in Table 2. The values of \(\psi \) and \(\mu \) are fixed by considering the estimated parameters based on the data. Therefore, the parameters \(\theta \), \(\delta \), \(\gamma \), \(\sigma _1\), \(\beta \), \(\alpha \), and \(\varepsilon \) will be ranked while \(\sigma _2\), \(\omega \) and \(\tau \) are also fixed since these two parameters do not affect the value of \({\mathcal {R}}_0\). The PRCC results lie on \(-1<{\mathcal {P}}<1\) where \({\mathcal {P}}\) is set of parameter values. The most sensitive parameter given is derived using the greatest value of \(\left|{\mathcal {P}}\right|\). The sign of \({\mathcal {P}}\) indicates the relationship between the parameter with the values of the constraint functions in these cases being the reproduction number and the density of each class.

We first analyze the global sensitivity of parameters to the reproduction number \(({\mathcal {R}}_0)\) and achieved that \(\alpha \) as the effective contact rate becomes the most influential parameter with PRCC value is 0.88 as given by Fig. 4. This means that the policy-making on controlling the effective contact rate plays a major part in the existence of measles. By observing the sign of PRCC, we also know that the contact rate is directly proportional to the increase of reproduction number. The next ranks are, respectively, occupied by \(\gamma \), \(\theta \), \(\beta \), \(\sigma _1\), \(\delta \), and \(\varepsilon \), where \(\beta \) has positive relationship with \({\mathcal {R}}_0\) while others have negative relationship. This means that by increasing the movement rate from \(V_1\) to S, the reproduction number also increases. While increasing the movement rate from infected class, the first dose vaccine rate, the second dose vaccine, the measles death rate, and the progression rate from exposed to infected class, the basic reproduction number will decrease. We show all of these biological conditions in some contour plots given by Fig. 5.

Table 3 The most influential parameter for each class observes by PRCC
Full size table
Fig. 7
figure 7

Bifurcation diagram driven by \(\sigma _1\) and time-series of model (1) respect to \(V_1(t)\)

Full size image
Fig. 8
figure 8

Bifurcation diagram driven by \(\sigma _1\) and time-series of model (1) respect to \(V_2(t)\)

Full size image
Fig. 9
figure 9

Bifurcation diagram driven by \(\alpha \) and time-series of model (1) respect to E(t)

Full size image
Fig. 10
figure 10

Bifurcation diagram driven by \(\gamma \) and time-series of model (1) respect to I(t)

Full size image
Fig. 11
figure 11

Bifurcation diagram driven by \(\delta \) and time-series of model (1) respect to H(t)

Full size image
Fig. 12
figure 12

Bifurcation diagram driven by \(\theta \) and time-series of model (1) respect to R(t)

Full size image

Now, the global sensitivity analysis of parameters with respect to the density for each class is investigated. The numerical process is given as follows. We first generate random data using Saltelli sampling and compute the numerical solutions using 4th-order Runge-Kutta method. The PRCC results are given in Fig. 6. The most influential parameter is decided by observing the convergence of PRCC when time moves forward. As a result, we have the most influential parameter for each class given in Table 3. The most influential parameter for both people who received the first and second dose of the MMR vaccine (\(V_1(t)\) and \(V_2(t)\)) is given by the second dose of vaccine rate \((\sigma _1)\) (where the PRCC results are \(-0.99994\) and 0.64932), respectively. The PRCC results show that \(\sigma _1\) has negative relationship with \(V_1(t)\) and positive relationship with \(V_2(t)\) which means that by increasing the second dose vaccine rate, the number of people who only receive the first dose will decrease while those receiving the second dose will increase. For the exposed class (E(t)), the PRCC results show that the effective contact rate \((\alpha )\) becomes the most influential parameter in increasing its density. We also successfully compute the PRCC results for infected class (I(t)), hospitalized class (H(t)), and recovered class (R(t)). The sign of PRCC values indicate that movement rate from infected class and measles death rate have negative relationship with the densities of infected and hospitalized class while the first dose of vaccine rate has positive relationship with recovered class.

5.3 Bifurcations and dynamical behaviors

Based on PRCC results given in Table 3, we explore more the dynamical behaviors of model (1) by observing the change of the densities for each class when given parameters are varied. We first investigate the dynamical behaviors of model (1) when the second dose of vaccine rate \((\sigma _1)\) is varied. As a result, we have numerical simulations given in Figs. 7 and 8. The density of people who received the first and second dose of the MMR vaccine (\(V_1(t)\) and \(V_2(t)\)), respectively, decrease and increase when \(\sigma _1\) is increased which confirms the PRCC results given in Table 3. We also show that bifurcation does not exists for interval \(0.7\le \sigma _1\le 1\). Furthermore, we investigate the impact of the effective contact rate \((\alpha )\) on the density of exposed class (E(t)) by portraying the bifurcation diagram along with its time-series with respect to E(t) in Fig. 9 is the occurrence of forward bifurcation when \(\alpha \) crosses the bifurcation point \(\alpha ^*\approx 3.9\times 10^{-6}\). It is easy to compute that the value of \(\alpha ^*\) is equal to \({\mathcal {R}}_0=1\). When \(\alpha <\alpha ^*\) or \({\mathcal {R}}_0<1\). The endemic point does not exist and the disease-free point becomes asymptotically stable. When \(\alpha \) crosses \(\alpha ^*\) or \({\mathcal {R}}_0\) crosses 1, the disease-free point losses its stability while the asymptotically stable endemic point occurs in the interior via forward bifurcation. This also confirms that \(\alpha \) has positive relationship with E(t). Now, the dynamics of infected class (I(t)) are observed. The PRCC results show that they have negative relationship. This condition is confirmed by numerical simulations given in Fig. 10. The density of infected class (I(t)) decreases when \(\gamma \) increases and finally disappears when \(\gamma \) crosses \(\gamma ^*\approx 1.16\) This condition also shows the existence of forward bifurcation driven by \(\gamma \) where the bifurcation point is \(\gamma ^*\) which equal to \({\mathcal {R}}_0=1\). Next, the influence of the measles death rate \((\delta )\) on the density of hospitalized class (H(t)) is observed. Again, the endemic point disappears via forward bifurcation where the bifurcation point at \(R_0=1\) lies on \(\delta ^*=1.76\), see Fig. 11). The density of H(t) decreases as \(\delta \) goes up. Finally, Fig. 12 is given to show the positive relationship between first dose of vaccine rate \(\theta \) with recovered class (R(t)) given by the PRCC result in Fig. 6. When \(\theta \) increases, R(t) increases, which means that increasing the number of people who receive the first dose of vaccine will save more life indicated by the increase in recovered people.

6 Conclusion

A mathematical model with seven compartments has been used to study the dynamics of the measles. The basic reproduction number is determined, and the boundary of solutions established. Two equilibrium points are identified, together with their stability results. To identify the most influential parameter on the threshold quantities, we performed a global sensitivity analysis by using the Partial Rank Correlation Coefficient (PRCC). The result from this analysis informs us of the most impactful parameter that contribute most to the spread and control of the disease. This parameter is the effective transmission rate \(\alpha \). We can say that restricting the interaction between susceptible and infected classes play the important role in reducing the growth rate of exposed and infected classes. The analysis further revealed that the most influential parameter for individuals who received the first and second dose of the MMR vaccine is the second dose of vaccine rate \(\sigma _{1}\). Furthermore, the effect of the first and second vaccine dose rates was demonstrated. Increasing vaccination rates reduces the number of infected people. An increase in the second dose vaccination rate in particular, has been shown to slow the spread of measles and suppress the endemic condition. The relevance of vaccination in containing and halting the spread of the measles has also been analyzed in this study. The most effective method of containing a measles outbreak in a population is vaccination. This finding suggests that the measles outbreak is reduced when vaccination rates increase. Therefore, mass vaccination campaigns should be encouraged to vaccinate the majority of the population in order to achieve a high level of herd immunity to the disease and stop a measles outbreak. In order to address vaccination gaps and stop measles outbreaks, government and public health officials may find it helpful to use the study’s findings to develop strategic vaccination plans.