1 Introduction

The log-logistic (LL) distribution also known as Fisk distribution can be obtained from logistic distribution using logarithm transformation. It is usually treated as an alternative to the log-normal distribution. Let X be a random variable following two-parameter log-logistic distribution with probability density function given by

$$\begin{aligned} f_X(x;\alpha ,\beta )=\frac{\alpha \beta ^\alpha x^{\alpha -1}}{(x^\alpha +\beta ^\alpha )^2}, \,\,x>0, \,\alpha , \beta >0. \end{aligned}$$
(1.1)

Its cumulative distribution function is

$$\begin{aligned} F_{X}(x;\alpha ,\beta )= & {} \frac{x^\alpha }{x^\alpha +\beta ^\alpha },\,\,x>0,\, \alpha , \beta >0. \end{aligned}$$
(1.2)

We denote \(X\sim LL(\alpha , \beta )\) if X has the distribution function given by (1.2). Here, \(\alpha\) is the shape parameter and \(\beta\) is the scale parameter. The shape parameter \(\alpha\) controls the shape of the distribution. The LL distribution has several importance properties compared to many other commonly used parametric models in survival analysis. Below, we present a few.

  • The shapes of the log-logistic distribution and the log-normal distribution are similar. However, the log-logistic distribution has heavier-tails. Due to this property, it is able to cope with the outlines. Therefore, if the histogram plot of the data set provides the information that the data are actually from a right skewed distribution, then the log-logistic distribution may be used for analyzing the data. Because of this, it plays a remarkable role in modeling a wide range of bursts phenomena that occur in finance, insurance, telecommunications, meteorology, hydrology and survival analysis.

  • The log-logistic distribution has a closed-form expression of the cumulative distribution function. Thus, it is very useful for analyzing survival data with censoring. Apart from this property, the LL distribution has a non-monotone hazard function. The hazard function is monotonically decreasing when \(\alpha \le 1\) and is unimodal when \(\alpha >1\). Because of the non-monotonicity of the hazard rate of the LL distribution, it could be an appropriate model when the course of the disease is such that mortality reaches a peak after some finite period, and then slowly decreases (see [26]).

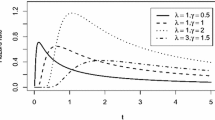
Further, the log-logistic distribution can be used as a suitable substitute for Weibull distribution. This distribution is a mixture of Gompertz as well as Gamma distributions when the mean and variance coincide and equal to one. The LL distribution can also viewed as a life testing model. It is an increasing failure rate model and also is viewed as a weighted exponential distribution. Due to several appealing properties, the LL distribution has been used in various other fields. For example, in economics, the log-logistic distribution is used as a simple model of the distribution of wealth or income (see [18]). The realized sets of precipitation and stream-flow data can be fitted well by this distribution. In this direction, we refer to Mielke et al. [34]. The LL distribution can be used in flood frequency analysis (see [3]). Shoukri et al. [40] and Ashkar and Mahdi [4] discussed goodness of fit test of the LL distribution with other distributions for fitting flood data from 114 hydrometric stations located in Canada. Figure 1 shows plots of the probability density function, reliability function and hazard rate function of the LL distribution.

Fig. 1
figure 1

Plots of the a probability density function, b reliability function and c hazard rate function of the LL distribution for some specific values of the parameters

Full size image

In this paper, we study various inferencial procedures for the estimation of the parameters and reliability characteristics of the log-logistic distribution. The study is based on the PT-II censored sample. Please refer to Aggarwala and Balakrishnan [2] for an elaborate discussion on the progressive censoring scheme. Below, we briefly discuss on the PT-II censoring scheme. Consider a test, where at the beginning we place n units. After first failure occurs, we randomly remove \(U_1\) surviving units from the test. Then, after second failure occurs, \(U_2\) surviving units are withdrawn at random. This process continues till \(m\hbox {th}\) failure occurs. Once the \(m\hbox {th}\) failure takes place, \(U_m=n-U_1-U_2-\cdots -U_{m-1}-m\) surviving units are removed from the experiment. Here, the failure times which have been observed during the experiment are denoted by \(T_{i:m:n},\,i=1,\ldots ,m\). The collection of \(T_{i:m:n}\)’s \(i=1,\ldots , m\) is known as the PT-II censored sample. For convenience, henceforth, we denote \(T_{i:m:n}\) as \(T_i,\,i=1,\ldots ,m\). That is, \(T_1=T_{1:m:n}, \ldots ,T_{m}=T_{m:m:n}\). Further, from Balakrishnan and Aggarwala [6], the joint probability density function of the random failure times \(T_1,\ldots ,T_m\) is written as

$$\begin{aligned} f_{{\underline{T}}}({\underline{t}})=\zeta \prod _{i=1}^m f_{T_i}(t_i)\left[ {\bar{F}}_{T_i}(t_i)\right] ^{U_i}, \,t_1<\ldots <t_m, \end{aligned}$$
(1.3)

where \(\zeta =n(n-U_1-1)\cdots (n-\sum _{i=1}^{m-1}(U_i+1))\). Here, \({\underline{T}}=(T_{1},\ldots ,T_{m})\) and \({\underline{t}}=(t_{1},\ldots ,t_{m})\). Note that \(f_{T_i}(t_i)\) and \({\bar{F}}_{T_i}(t_i)\) are the density and survival functions of \(T_{i}\), respectively, \(i=1,\ldots ,m\). For more details on PT-II censored scheme, we refer to Balakrishnan [5] and Balakrishnan and Cramer [7].

There have been a number of studies on estimation of parameters of the log-logistic distribution by various authors when observations are complete and censored. Here, we briefly discuss a few of the existing literature. Zhou et al. [45] studied estimation problem for log-logistic distribution based on the grouped failure data. Abbas and Tang [1] derived Bayes estimates of the parameters of LL distribution under reference and Jeffreys’ priors. He et al. [21] discussed estimation of the scale and shape parameters of a log-logistic distribution based on the simple random and rank set samples. Under the randomly censored sample, Kumar [24] studied classical and Bayes estimates for the log-logistic distribution. With respect to progressively censored sample, Kus and Kaya [25] derived maximum likelihood estimates of the unknown parameters of a LL distribution. They employed EM algorithm. Further, various inferential procedures based on PT-II censoring scheme have been introduced for some useful lifetime models. For instance, see Basak and Balakrishnan [10], Singh et al. [42], Valiollahi et al. [44] and Maiti and Kayal [30, 31] and the references contained therein. Scrolling through the literature, it is observed that based on progressive type-II censored sample, the problem of estimating parameters and reliability functions of two-parameter log-logistic distribution has not been discussed so far except partial contribution by Kus and Kaya [25]. This along with the important applications of the LL distribution motivates us to study the present problem. The reliability and hazard functions of the log-logistic distribution with distribution function (1.2) are given by

$$\begin{aligned} r(t)=\frac{\beta ^\alpha }{t^\alpha +\beta ^\alpha }\,\,\text{ and } \,\, h(t)=\frac{\alpha t^{\alpha -1}}{t^\alpha +\beta ^\alpha }, \end{aligned}$$
(1.4)

respectively, where \(t>0,\) \(\alpha >0\) and \(\beta >0\).

In the present communication, we consider point and interval estimation of \(\alpha ,\) \(\beta\), r(t) and h(t) based on the PT-II censored sample. The MLE are obtained. Since explicit expressions of the MLEs are difficult to derive, we use EM algorithm. Bayes estimates are derived under symmetric and asymmetric loss functions. In this direction, Lindley’s approximation and importance sampling methods are used. The interval estimates are constructed. Further, we obtain highest posterior density (HPD) intervals.

The paper is organized as follows. In the next section, we derive MLEs of the unknown model parameters, reliability and hazard functions. The EM algorithm has been used for the purpose of computation. In Sect. 3, we study Bayesian estimation. In particular, we consider five loss functions and obtain Bayes estimates under the assumption that the unknown parameters have independent gamma prior distributions. The explicit forms of the Bayes estimates are difficult to derive. Thus, we use Lindley’s approximation method and importance sampling method to compute Bayes estimates in Sect. 4. Section 5 deals with the computation of interval estimates. Observed Fisher information matrix is obtained. HPD credible intervals are also constructed. In Sect. 6, we consider two real data sets for the purpose of illustration of the proposed methods. In Sect. 7, we conduct a comprehensive simulation study to notice the performance of the established estimates. Finally, in Sect. 8, some concluding remarks are added.

2 Maximum Likelihood Estimation

In this section, we focus on finding maximum likelihood estimates of the unknown parameters, reliability and hazard functions for the distribution with density function given by (1.1). We assume that the random sample is PT-II censored. The log-likelihood function of \(\alpha\) and \(\beta\) is

$$\begin{aligned}&l(\alpha ,\beta |{\underline{t}})\propto m\ln \alpha + \left( m+\sum _{i=1}^m U_i\right) \alpha \ln \beta +(\alpha -1)\sum _{i=1}^m \ln t_i \nonumber \\&\quad -\sum _{i=1}^m \left( U_i+2\right) \ln (t_i^\alpha +\beta ^\alpha ). \end{aligned}$$
(2.1)

After differentiating (2.1) partially with respect to \(\alpha\) and \(\beta\), and then equating to zero, we obtain the likelihood equations of \(\alpha\) and \(\beta\) as

$$\begin{aligned} m \left( \frac{1}{\alpha }+\ln \beta \right) +\sum _{i=1}^m \ln t_i+\ln \beta \sum _{i=1}^m U_i-\sum _{i=1}^m \frac{\left( U_i+2\right) \left( \beta ^{\alpha } \ln \beta +t_i^{\alpha } \ln t_i\right) }{\beta ^{\alpha }+t_i^{\alpha }}=0 \end{aligned}$$
(2.2)

and

$$\begin{aligned} m+\sum _{i=1}^m U_i-\sum _{i=1}^m \frac{\left( U_i+2\right) \beta ^{\alpha } }{\beta ^{\alpha }+t_i^{\alpha }}=0, \end{aligned}$$
(2.3)

respectively. Now, one can get the MLEs of \(\alpha\) and \(\beta\) after solving Equations (2.2) and (2.3) simultaneously. After obtaining the MLEs of \(\alpha\) and \(\beta\), we can easily write the MLEs of r(t) and h(t). However, the explicit forms of the solutions of (2.2) and (2.3) are hard to derive. Therefore, we use EM algorithm. This is presented in the next subsection. Note that in statistical inference, it is always an important issue to see the existence and uniqueness of the MLEs. In this direction, one needs to check the conditions given by Mäkeläinen et al. [32]. Due to the complex nature of the elements of the observed Fisher information matrix, it is hard to verify the conditions. More work is required to explore this issue. To have some rough idea on it, we have depicted profile plots of the log-likelihood function of the parameters \(\alpha\) and \(\beta\) for the real data sets in Fig. 2. These graphs suggest that the desired MLEs may exist uniquely.

Fig. 2
figure 2

The profile of the log-likelihood function of \(\alpha\) and \(\beta\) for guinea pigs data (a, b) and average daily wind speeds data (c, d)

Full size image

2.1 EM Algorithm

Dempster et al. [14] proposed a general iterative approach to find the MLEs of the unknown parameters when observed and censored data are available. It is known as EM algorithm. Some merits of EM algorithm are (i) it can be applied to complex problems, (ii) log-likelihood increases at each iteration, (iii) computations are tedious but straightforward and (iv) the second and higher order derivatives are not required for calculation. The main disadvantage of this algorithm is slow convergence rate. EM algorithm has two steps, one of the E-step (expectation step) and other the M-step (maximization step). In E-step, we find the conditional expectation of the missing data given the observed data and current parameter estimates. The E-step of the EM algorithm involves computation of the pseudo-log-likelihood function. Next, M-step maximizes the likelihood function under the observed and censored data. Let the observed sample and censored data be \(T=(T_{1}, \ldots , T_{m})\) and \(Z=(Z_1,\ldots ,Z_m)\), respectively, where \(Z_j\) is a \(1\times U_j\) vector \((Z_{j1}, \ldots , Z_{jU_j})\) for \(j=1,\ldots ,m\). Note that the complete sample is a combination of the observe sample and the censored data. Then the complete sample is given by \(W=(T,Z)\). The likelihood function of complete sample (see, [36]) is given by

$$\begin{aligned} L_{C}(W;\alpha , \beta )=\prod _{j=1}^m \left[ f_T(t_{j};\alpha ,\beta ) \prod _{k=1}^{U_j} f_Z(z_{jk};\alpha ,\beta )\right] . \end{aligned}$$
(2.4)

The log-likelihood function of \(\alpha\) and \(\beta\) based on complete sample is

$$\begin{aligned} \ell_{c}(W; \alpha , \beta )= & {} n\ln (\alpha \beta ^\alpha ) +(\alpha -1)\left[ \sum _{j=1}^m \ln t_{j}+\sum _{j=1}^m\sum _{k=1}^{U_j} \ln Z_{jk}\right] \nonumber \\&-2\left[ \sum _{j=1}^m \ln (t_j^\alpha +\beta ^\alpha )+\sum _{j=1}^m\sum _{k=1}^{U_j} \ln (Z_{jk}^\alpha +\beta ^\alpha )\right] . \end{aligned}$$
(2.5)

The E-step is calculated from the conditional expectation of the log-likelihood equation of complete sample T. The condition expectation of log-likelihood function is obtained as

$$\begin{aligned} \nonumber \ell_s(W; \alpha , \beta )= & {} n\ln (\alpha \beta ^\alpha ) +(\alpha -1)\left[ \sum _{j=1}^m \ln t_{j}+\sum _{j=1}^m U_j A(t_{j}; \alpha , \beta )\right] \\&-2\left[ \sum _{j=1}^m \ln (t_j^\alpha +\beta ^\alpha )+\sum _{j=1}^m U_j B(t_{j}; \alpha , \beta )\right] . \end{aligned}$$
(2.6)

The conditional distribution of Z for given \(T=t\) is given by

$$\begin{aligned} f_{Z|T}(z_{jk}|t;\alpha , \beta )=\frac{f_Z(z_{jk}; \alpha , \beta )}{1-F_T(t_{j}; \alpha , \beta )};\,\,z_{jk}>t_{j}, \end{aligned}$$
(2.7)

where

$$\begin{aligned} A(t_{j}; \alpha , \beta )= & {} E\left[ \ln Z_{jk}|Z_{jk}>t_{j}\right] \nonumber \\= & {} \frac{\alpha \beta ^\alpha }{1-F_T(t_{j};\alpha , \beta )} \int _{t_{j}}^\infty \frac{u^{\alpha -1} \ln u}{(u^\alpha +\beta ^\alpha )^2} \,du \end{aligned}$$
(2.8)

and

$$\begin{aligned} B(t_{j}; \alpha , \beta )= & {} E\left[ \ln (Z_{jk}^\alpha +\beta ^\beta )|Z_{jk}>t_{j}\right] \nonumber \\= & {} \frac{\alpha \beta ^\alpha }{1-F_T(t_{j};\alpha , \beta )} \int _{t_{j}}^\infty \frac{ \ln (u^\alpha +\beta ^\alpha )}{(u^\alpha +\beta ^\alpha )^2} \,du. \end{aligned}$$
(2.9)

In M-step, we maximize the E-step. Let \((\alpha ^{(p)}, \beta ^{(p)})\) be an estimate of \((\alpha , \beta )\) at \(p\hbox {th}\) stage. The corresponding updated estimate \((\alpha ^{(p+1)}, \beta ^{(p+1)})\) can be obtained by maximizing the function given by

$$\begin{aligned} L_s(\alpha , \beta )= & {} n\ln (\alpha \beta ^\alpha ) +(\alpha -1)\left[ \sum _{j=1}^m \ln t_{j}+\sum _{j=1}^m U_j A(t_{j}; \alpha ^{(p)}, \beta ^{(p)})\right] \nonumber \\&-2\left[ \sum _{j=1}^m \ln (t_{j}^\alpha +\beta ^\alpha )+\sum _{j=1}^m U_j B(t_{j}; \alpha ^{(p)}, \beta ^{(p)})\right] . \end{aligned}$$
(2.10)

The likelihood equations of \(\alpha\) and \(\beta\) are respectively given by

$$\begin{aligned} n \left( \frac{1}{\alpha }+\ln \beta \right) +\sum _{j=1}^m A U_j-2 \sum _{j=1}^m \frac{\beta ^{\alpha } \ln \beta +t_{j}^{\alpha } \ln t_{j}}{\beta ^{\alpha }+t_{j}^{\alpha }}+\sum _{j=1}^m \ln t_{j}=0 \end{aligned}$$
(2.11)

and

$$\begin{aligned} n-2 \sum _{j=1}^m \frac{\beta ^{\alpha }}{\beta ^{\alpha }+t_j^{\alpha }}=0 \end{aligned}$$
(2.12)

with \(A=A(t_{j}; \alpha ^{(p)}, \beta ^{(p)})\). It is easy to see that the explicit forms of the solutions of (2.11) and (2.12) are hard to obtain. Therefore, we use Newton-Raphson iteration method which continues until \(|\alpha ^{(p+1)}-\alpha ^{(p)}|+|\beta ^{(p+1)}-\beta ^{(p)}|<\epsilon\), for some p, and a fixed small number of \(\epsilon\). Hereafter, we denote the MLEs of \(\alpha\) and \(\beta\) as \({\hat{\alpha }}\) and \({\hat{\beta }}\), respectively. Further, using invariance property of the MLE, the MLEs of r(t) and h(t) can be easily obtained. These are respectively

$$\begin{aligned} {\hat{r}}(t)=\frac{{\hat{\beta }}^{{\hat{\alpha }}}}{t^{{\hat{\alpha }}}+{\hat{\beta }}^{{\hat{\alpha }}}}\,\,\text{ and } \,\, {\hat{h}}(t)=\frac{{\hat{\alpha }} t^{{\hat{\alpha }}-1}}{t^{{\hat{\alpha }}}+{\hat{\beta }}^{{\hat{\alpha }}}} \end{aligned}$$
(2.13)

for time \(t\,(=t_{0})>0\).

3 Bayesian Estimation

In this section, we derive Bayes estimates of the unknown parameters \(\alpha\), \(\beta\), reliability function r(t) and the hazard function h(t) for the log-logistic distribution based on PT-II censored sample. The estimates are obtained with respect to five loss functions. These are (i) squared error loss function (SELF), (ii) weighted squared error loss function (WSELF), (iii) precautionary loss function (PLF), (iv) entropy loss function (ELF) and (v) LINEX loss function (LLF). Among these, the squared error and weighted squared error loss functions are symmetric in nature, and the precautionary, LINEX and entropy loss functions are asymmetric. The symmetric loss functions are not appropriate when overestimation or underestimation occur. In this case, the asymmetric loss functions can be taken for estimation. Note that the LINEX loss function is useful when overestimation is more serious than underestimation and viceversa. Let \(\psi\) be an estimator for the unknown parameter \(\phi\). The loss functions under study are presented in Table 1. Table 1 also provides the form of the Bayes estimates in terms of the mathematical expectations. The subscript on expectation (E) will refer to parameter values.

Table 1 Loss functions and corresponding Bayes estimates
Full size table

Note that the Bayes estimate of the parameter \(\phi\) under ELF reduces to the Bayes estimates with respect to the WSELF, SELF and PLF, respectively when \(c=1,-1\, \text{ and }\,-2\). To obtain the Bayes estimates, we consider independent gamma priors for \(\alpha\) and \(\beta\). The probability density functions of the gamma priors for \(\alpha\) and \(\beta\) are taken as

$$\begin{aligned} g_1(\alpha:\xi_1, \xi_2 )\propto \alpha ^{\xi _1-1}\exp \{-\alpha \xi _2\},\,\,\alpha>0,\,\, \xi _1,\xi _2>0 \end{aligned}$$
(3.1)

and

$$\begin{aligned} g_2(\beta: \xi_1, \xi_2 )\propto \beta ^{\xi _3-1}\exp \{-\beta \xi _4\},\,\,\beta>0,\,\, \xi _3,\xi _4>0, \end{aligned}$$
(3.2)

respectively. The joint probability density function of \(\alpha\) and \(\beta\) is

$$\begin{aligned} \pi ( \alpha ,\beta ) \propto \alpha ^{\xi _1-1} \beta ^{\xi _3-1} \exp \{- (\alpha \xi _2+\beta \xi _4)\},\, \alpha ,\beta>0,\,\, \xi _i>0,\, i=1,2,3,4. \end{aligned}$$
(3.3)

The posterior distribution of \(\alpha\), \(\beta\) given \({\underline{T}}={\underline{t}}\) is obtained as

$$\begin{aligned} \Pi (\alpha , \beta |{\underline{t}})= & {} \frac{1}{C}\alpha ^{m+\xi _1-1} \beta ^{m\alpha +\xi _3-1}\exp \{-(\alpha \xi _2+\beta \xi _4)\}\prod _{i=1}^{m} \Lambda (\alpha ,\beta ,U_{i},t_{i}),\,\alpha ,\beta >0, \end{aligned}$$
(3.4)

where \(\Lambda (\alpha ,\beta ,U_{i},t_{i})=(t_i^{\alpha -1} \beta ^{\alpha U_i})/((t_i^{\alpha }+\beta ^\alpha )^{2+U_i}),\,i=1,\ldots ,m\) and

$$\begin{aligned} C= & {} \int _{\alpha =0}^{\infty }\int _{\beta =0}^{\infty } \alpha ^{m+\xi _1-1} \beta ^{m\alpha +\xi _3-1}\exp \{-(\alpha \xi _2+\beta \xi _4)\}\prod _{i=1}^{m} \Lambda (\alpha ,\beta ,U_{i},t_{i}) d\alpha d\beta . \end{aligned}$$
(3.5)

Now, we are ready to propose the forms of the Bayes estimates of the unknown parameters, reliability and hazard functions. First, we discuss the Bayes estimates for the unknown model parameters \(\alpha\) and \(\beta\).

3.1 Bayes Estimates of \(\alpha\) and \(\beta\)

In this subsection, we present Bayes estimates of the unknown parameters \(\alpha\) and \(\beta\) with respect to various loss functions presented in Table 1. Utilizing the posterior probability density function given by (3.4), from Table 1, the Bayes estimates of \(\alpha\) with respect to the ELF and LLF can be obtained. These are respectively given by

$$\begin{aligned} {\hat{\alpha }}^{EN}_B =\left[ \frac{1}{C}\int _{\alpha =0}^{\infty } \int _{\beta =0}^{\infty } \alpha ^{m+\xi _1-c-1} \beta ^{m\alpha +\xi _3-1}\exp \{-(\alpha \xi _2+\beta \xi _4)\}\prod _{i=1}^{m}\Lambda (\alpha ,\beta ,U_{i},t_{i}) d\alpha d\beta \right] ^{-\frac{1}{c}} \end{aligned}$$

and

$$\begin{aligned}&{\hat{\alpha }}^{LL}_B=-\frac{1}{d}\ln \left[ \frac{1}{C} \int _{\alpha =0}^{\infty }\int _{\beta =0}^{\infty } \alpha ^{m+\xi _1-1} \beta ^{m\alpha +\xi _3-1}\right. \nonumber \\&\quad \left. \times\exp \{-(\alpha (d + \xi _2) +\beta \xi _4)\} \prod _{i=1}^{m}\Lambda (\alpha ,\beta ,U_{i},t_{i}) d\alpha d\beta \right] . \end{aligned}$$
(3.6)

Further, the Bayes estimates of the parameter \(\beta\) with respect to the above mentioned five loss functions can be deduced similarly. These expressions are skipped for the sake of brevity.

3.2 Bayes Estimates of r(t) and h(t)

In this subsection, we introduce Bayes estimates of the reliability and hazard functions. The expressions of the estimates can be obtained similar to the case as in the previous subsection. The respective Bayes estimates of r(t) under ELF and LLE are obtained as

$$\begin{aligned}&{\hat{r}}(t)^{EN}_B=\left[ \frac{1}{C}\int _{\alpha =0}^{\infty } \int _{\beta =0}^{\infty } r(t)^{-c} \alpha ^{m+\xi _1-1} \beta ^{m\alpha +\xi _3-1}\right. \\&\quad \left. \times \exp \{-(\alpha \xi _2+\beta \xi _4)\}\prod _{i=1}^{m} \Lambda (\alpha ,\beta ,U_{i},t_{i}) d\alpha d\beta \right] ^{-\frac{1}{c}} \end{aligned}$$

and

$$\begin{aligned}&{\hat{r}}(t)^{LL}_B = -\frac{1}{d}\ln \left[ \frac{1}{C}\int _{\alpha =0}^{\infty } \int _{\beta =0}^{\infty } \alpha ^{m+\xi _1-1} \beta ^{m\alpha +\xi _3-1}\right. \nonumber \\&\quad \left. \times \exp \{-(d r(t)+\alpha \xi _2+\beta \xi _4)\} \prod _{i=1}^{m} \Lambda (\alpha ,\beta ,U_{i},t_{i}) d\alpha d\beta \right] . \end{aligned}$$
(3.7)

The Bayes estimates of h(t) with respect to these loss functions can be obtained similarly. It is worth pointing that the Bayes estimates in Sects. 3.1 and 3.2 are difficult to get in explicit forms. Thus, one needs to adopt some computation techniques. Various approaches have been discussed in the literature (see [13, 27, 43]). The Lindley’s approximation and importance sampling methods are illustrated in the next section.

4 Computing Methods

In this section, we use two useful methods to compute the Bayes estimates of the unknown parameters as well as the reliability characteristics. First, we discuss Lindley’s approximation method.

4.1 Lindley’s Approximation Method

Here, we focus on the Lindley’s method for the evaluation of Bayes estimates obtained in Sects. 3.1 and 3.2. This method was developed by Lindley [27]. Below, we provide a brief illustration on this approximation method. Note that using this approach, one can approximate the ratio of two integrals of the form

$$\begin{aligned} \vartheta _{BL}({\underline{t}})=\frac{\int _{0}^{\infty }\int _{0}^{\infty } {\vartheta }(\eta _1,\eta _2)\exp \{l(\eta _1,\eta _2|{\underline{t}})+p(\eta _1,\eta _2)\}d\eta _1 d\eta _2}{\int _{0}^{\infty }\int _{0}^{\infty } \exp \{l(\eta _1,\eta _2|{\underline{t}})+p(\eta _1,\eta _2)\}d\eta _1 d\eta _2}. \end{aligned}$$
(4.1)

In (4.1), \(l(\eta _1,\eta _2|{\underline{t}})\) is the log-likelihood function and \(p(\eta _1,\eta _2)\) is the logarithm of the joint prior distribution of the unknown parameters, say \(\eta _1\) and \(\eta _2\). For simplicity of the presentation, we use l instead of \(l(\eta _1,\eta _2|{\underline{t}})\) and p instead of \(p(\eta _1, \eta _2)\). Applying Lindley’s approximation method, (4.1) can be approximated as

$$\begin{aligned} \vartheta _{BL}( {\underline{t}})={\vartheta }({\eta _1},{\eta _2})+ \frac{1}{2}\Big (D+l_{30}E_{12}+l_{03}E_{21}+l_{21}F_{12}+l_{12}F_{21}+ 2p_{1}D_{12}+2p_{2}D_{21}\Big ), \end{aligned}$$
(4.2)

where \(D=\sum _{i=1}^{2}\sum _{j=1}^{2}u_{ij}\delta _{ij}\), \(u_{ij}=\frac{\partial ^2 {\vartheta }}{\partial \eta _i \partial \eta _j}\), \(l_{ij}=\frac{\partial ^{i+j}l}{\partial \eta _1^i\partial \eta _2^j};\,i,j=0,1,2,3;\, i+j=3\), \(E_{ij}=(u_{i}\delta _{ii}+u_{j}\delta _{ij})\delta _{ii}\), \(F_{ij}=3u_i\delta _{ii}\delta _{ij}+u_j(\delta _{ii}\delta _{jj}+2\delta ^2_{ij})\), \(u_i=\frac{\partial {\vartheta }}{\partial \eta _i}\), \(p_i=\frac{\partial p}{\partial \eta _i}\), \(p=\ln \pi (\eta _1,\eta _2)\), \(D_{ij}=u_{i}\delta _{ii}+u_{j}\delta _{ji}\) and \(\delta _{ij}\) is the \((i,j)\hbox {th}\) element of the matrix \([-\frac{\partial ^{2}l}{\partial \eta ^{i}_{1}\partial \eta ^{j}_{2}}]^{-1}\), where \(i,j=1,2\). Note that the above terms are evaluated at the MLEs of \(\eta _1\) and \(\eta _2\). The desired partial derivatives are presented in appendix.

4.1.1 Bayes Estimates of \(\alpha\) and \(\beta\)

To obtain Bayes estimates of \(\alpha\) and \(\beta\) using Lindley’s approximation method with respect to various loss functions as in Table 1, we have to choose \(\vartheta (\alpha ,\beta )\) accordingly. First, consider the LINEX loss function. Under this loss function, \(\vartheta (\alpha ,\beta )=\exp \{-d\alpha \}\), and hence \(u_{1}=-d\exp \{-d\alpha \},\,u_{11}=d^2 \exp \{-d\alpha \},\,u_2=u_{12}=u_{21}=u_{22}=0\). Thus, from (4.2), the approximate Bayes estimate of \(\alpha\) is

$$\begin{aligned} {\hat{\alpha }}^{LL}_{BL}= & {} -d^{-1}\ln \big [\exp \{-d\alpha \} +0.5\big [d^2\exp \{-d\alpha \}\delta _{11}-d\exp \{-d\alpha \}I(\alpha ,\beta ) \big ] \big ]\Big |_{(\alpha ,\beta )=({\hat{\alpha }},{\hat{\beta }})}, \end{aligned}$$
(4.3)

where \(I(\alpha ,\beta )=l_{30}\delta _{11}^2 +l_{03}\delta _{21}\delta _{22}+3l_{21}\delta _{11}\delta _{12} +l_{12}(\delta _{11}\delta _{22}+2\delta _{21}^2)+2p_1\delta _{11}+2p_2\delta _{12}\). Further, For the entropy loss function, we have \(\vartheta (\alpha ,\beta )=\alpha ^{-c},u_{1}=-c\alpha ^{-(c+1)}, u_{11}=c(c+1)\alpha ^{-(c+2)}, u_2=u_{12}=u_{21}=u_{22}=0\). Similar to (4.3), the Bayes estimate of \(\alpha\) with respect to the entropy loss function is obtained as

$$\begin{aligned} {\hat{\alpha }}^{EN}_{BL}= & {} \big [\alpha ^{-c}+0.5[c(c+1)\alpha ^{-(c+2)} \delta _{11}-c I(\alpha ,\beta )\alpha ^{-(c+1)} ]]^{-\frac{1}{c}} \Big |_{(\alpha ,\beta )=({\hat{\alpha }},{\hat{\beta }})}. \end{aligned}$$
(4.4)

As discussed before, the Bayes estimates of \(\alpha\) with respect to the SELF, WSELF and PLF can be obtained from (4.4) for \(c=-1,1\,\text{ and } -2\), respectively. The Bayes estimates of the parameter \(\beta\) can be proposed similarly. These are omitted for the sake of conciseness.

4.1.2 Bayes Estimates of r(t) and h(t)

In this subsection, we derive Bayes estimates of r(t) and h(t) under the loss functions mentioned in Table 1. Similar to the previous subsection, the choice of \(\vartheta (\alpha ,\beta )\) in (4.1) gets modified for every loss functions. Now, from (4.2), the Bayes estimate of r(t) with respect to the LINEX loss function is

$$\begin{aligned} {\hat{r}}(t)^{LL}_{BL}= & {} -d^{-1} \ln [\exp \{-d r(t)\}+J(\alpha ,\beta )] \Big |_{(\alpha ,\beta )=({\hat{\alpha }},{\hat{\beta }})}, \end{aligned}$$
(4.5)

where

$$\begin{aligned} J(\alpha ,\beta )= & {} (1/2)[(u_{11} \delta _{11}+u_{22}\delta _{22}+2u_{12}\delta _{12}) +l_{30}(u_{1}\delta _{11}+u_{2}\delta _{12})\delta _{11} + l_{03}(u_{2}\delta _{22}+u_{1}\delta _{21}) \delta _{22}\\&+\,l_{21}(3u_{1}\delta _{11}\delta _{12} +u_{2}(\delta _{11}\delta _{22}+2\delta _{12}^2)) +l_{12}(3u_{2}\delta _{22}\delta _{21} +u_{1}(\delta _{22}\delta _{11}+2\delta _{21}^2))\\&+ 2p_{1}(u_{1}\delta _{11}+u_{2}\delta _{21})+2p_{2}(u_{2}\delta _{22}+u_{1}\delta _{12})]. \end{aligned}$$

The Bayes estimate of r(t) with respect to the entropy loss function is obtained as

$$\begin{aligned} {\hat{r}}(t)^{EN}_{BL}= & {} \big [r(t)^{-c}+J(\alpha ,\beta )\big ]^{-\frac{1}{c}}\Big |_{(\alpha ,\beta )=({\hat{\alpha }},{\hat{\beta }})}. \end{aligned}$$
(4.6)

Further, the Bayes estimates under SELF, WSELF and PLF can be obtained from (4.6) after substituting \(c=-1, 1\,\text{ and }\,-2\), respectively. The Bayes estimates of h(t) with respect to the five loss functions can be derived analogously. These are omitted to avoid repetitions.

4.2 Importance Sampling Method

We consider importance sampling method for the computation of Bayes estimates of the unknown parameters and the reliability characteristics of the log-logistic distribution. We recall that the random sample is PT-II censored. To apply this method, we need to rewrite the posterior density function of \(\alpha\) and \(\beta\) given by (3.4) as

$$\begin{aligned} \Pi (\alpha ,\beta | {\underline{t}})\propto & {} GA_\alpha \left( m+\xi _1,\xi _2-\sum _{i=1}^m \ln t_i\right) \times GA_{\beta |\alpha }\Big (m\alpha +\xi _3,\xi _4+m\Big ) \times \varrho (\alpha ,\beta ), \end{aligned}$$
(4.7)

where

$$\begin{aligned} \varrho (\alpha ,\beta )=\frac{(m+\xi _4)^{-(m\alpha +\xi _3)}\exp \{\beta m\}}{(\xi _2-\sum _{i=1}^m \ln t_i)^{m+\xi _1}} \prod _{i=1}^m \frac{\beta ^{\alpha U_i}}{t_i (t_i^\alpha +\beta ^\alpha )^{2+U_i}} \end{aligned}.$$
(4.8)

The following algorithm can be used to compute Bayes estimates of an arbitrary function of unknown parameters \(h(\alpha ,\beta ).\)

Algorithm-1

  • Step 1 Generate \(\alpha\) from \(GA_\alpha (m+\xi _1,\xi _2-\sum _{i=1}^m \ln t_i)\) (that is, from a Gamma distribution with shape parameter \((m+\xi _1)\) and scale parameter \((\xi _2-\sum _{i=1}^m \ln t_i)^{-1}\)).

  • Step 2 For a given \(\alpha\) as generated in Step 1, further, generate \(\beta\) from \(GA_{\beta |\alpha }(m\alpha +\xi _3,m+\xi _4)\) (that is, from a Gamma distribution with shape parameter \((m\alpha +\xi _3)\) and scale parameter \((m+\xi _4)^{-1}\)).

  • Step 3 Repeat Steps 1 and 2, M times to obtain \((\alpha _1, \beta _1)\), \((\alpha _2, \beta _2)\), ..., \((\alpha _M, \beta _M)\). In this paper, we take \(M=1000\).

The Bayes estimates of \(h(\alpha ,\beta )\) under the LLF and ELF are obtained as

$$\begin{aligned} {\hat{h}}^{LL}_{BI} =-\frac{1}{d}\ln \left[ \frac{\sum _{i=1}^M \exp \{-d h(\alpha _{i}, \beta _{i})\}\varrho (\alpha _i, \beta _i)}{\sum _{i=1}^M \varrho (\alpha _i, \beta _i)}\right] \end{aligned}$$
(4.9)

and

$$\begin{aligned} {\hat{h}}^{EN}_{BI} =\left[ \frac{\sum _{i=1}^M h(\alpha _i, \beta _i)^{-c} \varrho (\alpha _i, \beta _i)}{\sum _{i=1}^M \varrho (\alpha _i, \beta _i)}\right] ^{-\frac{1}{c}}. \end{aligned}$$
(4.10)

Substituting \(c=-1,1\,\text{ and }\,-2\) in (4.10), the respective Bayes estimates of \(h(\alpha ,\beta )\) with respect to SELF, WSELF and PLF can be obtained. We point out that to compute the Bayes estimates of \(\alpha , \beta , r(t)\) and h(t), one needs to substitute \(\alpha ,\beta , r(t)\) and h(t) in place of \(h(\alpha ,\beta )\), respectively in (4.9) and (4.10).

Remark 4.1

Here, we discuss how to evaluate the values of the hyper-parameters (i.e. \(\xi _i;\,i=1,2,3,4\)) under informative priors. The values of the hyper-parameters play very important role to obtain Bayes estimates. The first two hyper-parameter values \(\xi _1\) and \(\xi _2\) are obtained from gamma prior \(g_1(\alpha : \xi _1, \xi _2)\) of \(\alpha\) and the other two values \(\xi _3\) and \(\xi _4\) from other gamma prior \(g_2(\beta : \xi _3, \xi _4)\) of \(\beta\). We consider m samples from LL (\(\alpha , \beta\)). Then, obtain the associated MLEs of the parameters \(\alpha\) and \(\beta\). These are denoted by \({\hat{\alpha }}^j\) and \({\hat{\beta }}^j\) for \(j=1,2,\ldots ,m\) for each of these samples. Note that these hyper-parameter values can be evaluated based on the past data set (i.e. MLEs of parameters and number of samples m). At first, we calculate first two hyper-parameters \(\xi _1\) and \(\xi _2\). The mean and variance of gamma prior of \(\alpha\) i.e. \(\alpha ^{\xi _1-1}\exp \{-\xi _2\alpha \}\) are \(\frac{\xi _1}{\xi _2}\) and \(\frac{\xi _1}{\xi _2^2}\), respectively. The mean and variance of the MLEs of \(\alpha\) for m samples are \(\frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j\) and \(\frac{1}{m-1}\sum _{j=1}^{m}({\hat{\alpha }}^j-\frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j)^2\), respectively. Therefore, the mean and variance of these MLEs are equals to the mean and variance of gamma prior of \(\alpha\). Thus,

$$\begin{aligned} \frac{\xi _1}{\xi _2}=\frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j\,\,\text{ and }\,\,\frac{\xi _1}{\xi _2^2} =\frac{1}{m-1}\sum _{j=1}^{m}\left( {\hat{\alpha }}^j -\frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j\right) ^2. \end{aligned}$$

Solving these above equations, we get

$$\begin{aligned} \xi _1=\frac{\left( \frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j\right) ^2}{\frac{1}{m-1}\sum _{j=1}^{m}\left( {\hat{\alpha }}^j -\frac{1}{m}\sum _{j=1}^{m}{\hat{\alpha }}^j\right) ^2} \,\,\text{ and }\,\, \xi _2=\frac{\frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j}{\frac{1}{m-1}\sum _{j=1}^{m} \left( {\hat{\alpha }}^j-\frac{1}{m}\sum _{j=1}^{m} {\hat{\alpha }}^j\right) ^2}. \end{aligned}$$
(4.11)

Similarly, other hyper-parameters \(\xi _3\) and \(\xi _4\) are obtained from \(\xi _1\) and \(\xi _2\) replacing \(\beta\) in place of \(\alpha\) in (4.11), respectively. We may refer to Dey et al. [15], Singh et al. [41] and Dey et al. [16] in this direction.

5 Interval Estimation

In this section, we consider interval estimation of the unknown parameters, reliability and hazard functions of the log-logistic distribution when the random sample is PT-II censored. Five approaches are discussed. First, we develop observed Fisher information matrix. This is useful to get asymptotic confidence intervals.

5.1 Observed Fisher Information Matrix

In this subsection we evaluate observed Fisher information matrix. Louis [28] derived the Fisher information matrix using the missing information based on EM algorithm. According to Louis method, the observed information equals to the complete information minus the missing information. We have

$$\begin{aligned} I_T(\alpha , \beta )=I_W(\alpha , \beta )-I_{W|T}(\alpha , \beta ), \end{aligned}$$
(5.1)

where \(I_T(\alpha , \beta ), I_W(\alpha , \beta )\) and \(I_{W|T}(\alpha , \beta )\) are the observed, complete and missing information, respectively and T and W are the observed and complete data, respectively. The complete information matrix \(I_W(\alpha , \beta )\) is given as

$$\begin{aligned} I_W(\alpha , \beta )= -E\left( \begin{array}{cc} \frac{\partial ^2 \ell ^*}{\partial \alpha ^2}&{}\frac{\partial ^2 \ell ^*}{\partial \alpha \partial \beta }\\ \frac{\partial ^2 \ell ^*}{\partial \beta \partial \alpha }&{}\frac{\partial ^2 \ell ^*}{\partial \beta ^2}\\ \end{array} \right) =\left( \begin{array}{cc} a_{11}&{}a_{12}\\ a_{21}&{}a_{22}\\ \end{array} \right) _{|(\alpha , \beta )=({\hat{\alpha }}, {\hat{\beta }})}. \end{aligned}$$
(5.2)

Here, \(\ell ^*=\ell _c(W; \alpha , \beta )\) and \(a_{kl}=-E[\frac{\partial ^2 \ell ^* }{\partial \theta _k \partial \theta _l}]\) for \(k,l=1, 2\), where \(\theta _1=\alpha , \theta _2=\beta\). The missing information \(I_{W|T}(\alpha , \beta )\) is given as

$$\begin{aligned} I_{W|T}(\alpha , \beta )=\sum _{j=1}^m \Phi _j I^{j}_{W|X}(\alpha , \beta )=\left( \begin{array}{cc} b_{11}&{}b_{12}\\ b_{21}&{}b_{22}\\ \end{array} \right) _{|(\alpha , \beta )=({\hat{\alpha }}, {\hat{\beta }})}, \end{aligned}$$
(5.3)

where \(b_{kl}=-\sum _{j=1}^m R_j E_{Z_j|T_{j}}[\frac{\partial ^2 \ln f^* }{\partial \theta _k \partial \theta _l}]\), \(f^*=f_{Z_j|T_{j}}(z_j|t_{j}, \alpha , \beta )\) and \(I^{j}_{W|T}(\alpha , \beta )\) is the missing information at \(j\hbox {th}\) failure time \(x_{j:m:n}\) as

$$\begin{aligned} I^{j:m:n}_{W|T}(\alpha , \beta )= & {} -E_{Z_j|T_{j}}\left( \begin{array}{cc } \frac{\partial ^2 \ln f^*}{\partial \alpha ^2}&{}\frac{\partial ^2 \ln f^*}{\partial \alpha \partial \beta } \\ \frac{\partial ^2 \ln f^*}{\partial \beta \partial \alpha }&{}\frac{\partial ^2 \ln f^*}{\partial \beta ^2} \\ \end{array} \right) _{|(\alpha , \beta )=({\hat{\alpha }}, {\hat{\beta }})}. \end{aligned}$$
(5.4)

From the \(2\times 2\) order matrices given by (5.2) and (5.3), we compute the observed Fisher information matrix of \(\alpha\) and \(\beta\). The variance-covariance matrix can be obtained after inverting \(I_T({\hat{\alpha }}, {\hat{\beta }})\) given by (5.1). This is given by

$$\begin{aligned} {\hat{I}}_T^{-1}({\hat{\alpha }}, {\hat{\beta }})=\left( \begin{array}{cc} \text{ var }({\hat{\alpha }}) &{} \text{ cov }({\hat{\alpha }},{\hat{\beta }})\\ \text{ cov }({\hat{\alpha }},{\hat{\beta }}) &{} \text{ var }({\hat{\beta }})\\ \end{array} \right) . \end{aligned}$$
(5.5)

Further, by virtue of asymptotic normality of the maximum likelihood estimates, the asymptotic joint distribution of \({\hat{\alpha }}\) and \({\hat{\beta }}\) can be approximated with bivariate normal distribution as

$$\begin{aligned} \left( \begin{array}{c} {\hat{\alpha }} \\ {\hat{\beta }} \end{array} \right) \sim N\left[ \left( \begin{array}{c} \alpha \\ \beta \end{array} \right) ,\left( \begin{array}{cc} \text{ var }({\hat{\alpha }}) &{} \text{ cov }({\hat{\alpha }},{\hat{\beta }})\\ \text{ cov }({\hat{\alpha }},{\hat{\beta }}) &{} \text{ var }({\hat{\beta }})\\ \end{array} \right) \right] . \end{aligned}$$
(5.6)

Below, we obtain the distributions of \({\hat{r}}(t)\) and \({\hat{h}}(t)\) given by (1.4). In this purpose, delta method is useful (see [19]). Denote

$$\begin{aligned} {\hat{\xi }}'_{r(t)}=\left( \frac{\partial r(t)}{\partial \alpha },\frac{\partial r(t)}{\partial \beta }\right) _{|(\alpha ,\beta )=({\hat{\alpha }},{\hat{\beta }})}\,\,\text{ and }\,\,{\hat{\xi }}'_{h(t)}=\left( \frac{\partial h(t)}{\partial \alpha },\frac{\partial h(t)}{\partial \beta }\right) _{|(\alpha ,\beta )=({\hat{\alpha }},{\hat{\beta }})}. \end{aligned}$$

Then, using Delta method, the respective variances of \({\hat{r}}(t)\) and \({\hat{h}}(t)\) can be approximated by

$$\begin{aligned} {\widehat{Var}}({\hat{r}}(t))=\left[ {\hat{\xi }}'_{r(t)}{\hat{I}}_T^{-1} ({\hat{\alpha }},{\hat{\beta }}){\hat{\xi }}_{r(t)}\right] \,\,\text{ and }\,\, {\widehat{Var}}({\hat{h}}(t))=\left[ {\hat{\xi }}'_{h(t)}{\hat{I}}_T^{-1}({\hat{\alpha }},{\hat{\beta }}){\hat{\xi }}_{h(t)}\right] . \end{aligned}$$

From large sample theory, the respective asymptotic distributions of \({\hat{r}}(t)\) and \({\hat{h}}(t)\) can be obtained as

$$\begin{aligned} \frac{{\widehat{r}}(t)-r(t)}{\sqrt{{\widehat{Var}}({\hat{r}}(t))}}\sim N(0,1)\,\, \text{ and }\,\,\frac{{\hat{h}}(t)-h(t)}{\sqrt{{\widehat{Var}}({\hat{h}}(t))}}\sim N(0,1). \end{aligned}$$

5.2 Asymptotic Confidence Intervals

Here, we obtain confidence intervals using two techniques. These are discussed below. Exact distributions of the MLEs are difficult to derive. Thus, observed Fisher information matrix is useful in constructing the asymptotic confidence interval estimates.

5.2.1 Normal Approximation to the MLE

To obtain the confidence intervals based on this method, we compute the observed Fisher information matrix. It is given by (5.1). For simplicity of the presentation, we denote \(\eta _{\alpha }=Z_{\gamma /2}\sqrt{\text {var}({\hat{\alpha }})}\), \(\eta _{\beta }=Z_{\gamma /2}\sqrt{\text {var}({\hat{\beta }})}\), \(\eta _{r}^{*}=Z_{\gamma /2}\sqrt{\widehat{\text {var}}({\hat{r}}(t))}\) and \(\eta _{h}^{*}=Z_{\gamma /2}\sqrt{\widehat{\text {var}}({\hat{h}}(t))}\), where \(Z_{\gamma /2}\) is the percentile of the standard normal distribution with right-tail probability \(\gamma /2\). The \(100(1-\gamma )\%\) asymptotic confidence intervals for the unknown parameters \(\alpha\) and \(\beta\) are obtained as

$$\begin{aligned} \left( {\hat{\alpha }}- \eta _{\alpha },\,{\hat{\alpha }}+ \eta _{\alpha }\right) \,\,\text{ and }\,\,({\hat{\beta }}- \eta _{\beta },\,{\hat{\beta }}+ \eta _{\beta }), \end{aligned}$$

respectively. The \(100(1-\gamma )\%\) asymptotic confidence intervals of the reliability and hazard functions are respectively given by

$$\begin{aligned} \left( {\hat{r}}(t)- \eta _{r}^{*},\,{\hat{r}}(t)+ \eta _{r}^{*}\right) \,\,\text{ and }\,\, ({\hat{h}}(t)- \eta _{h}^{*},\,{\hat{h}}(t)+ \eta _{h}^{*}). \end{aligned}$$

We point out that this method has a drawback. Its performance is poor when the sample size is small. Sometimes, it produces negative lower bound. Meeker and Escobar [33] proposed another method which is based on the log-transformed MLE. This is presented below.

5.2.2 Normal Approximation to the Log-Transformed MLE

Denote \(\zeta _{\alpha }=Z_{\gamma /2}\sqrt{\delta _{11}(\ln {\hat{\alpha }})}\) and \(\zeta _{\beta }=Z_{\gamma /2}\sqrt{\delta _{11}(\ln {\hat{\beta }})}\). Here, \(\delta _{11}(\ln {\hat{\alpha }})\) and \(\delta _{22}(\ln {\hat{\beta }})\) are the estimated variances of \(\ln {\hat{\alpha }}\) and \(\ln {\hat{\beta }}\), respectively. The \(100(1-\gamma )\%\) asymptotic confidence intervals of the log-transformed MLEs of \(\alpha\) and \(\beta\) are obtained as

$$\begin{aligned} \left( \ln {\hat{\alpha }}- \zeta _{\alpha },\,\ln {\hat{\alpha }}+ \zeta _{\alpha }\right) \,\,\text{ and } \,\,(\ln {\hat{\beta }}- \zeta _{\beta },\,\ln {\hat{\beta }}+ \zeta _{\beta }). \end{aligned}$$

Thus, based on this approach, \(100(1-\gamma )\%\) confidence intervals for \(\alpha\) and \(\beta\) are given by

$$\begin{aligned} \left( {\hat{\alpha }}/\zeta _{\alpha }^*,\,{\hat{\alpha }}\times \zeta _{\alpha }^*\right) \,\,\text{ and }\,\, ({\hat{\beta }}/\zeta _{\beta }^*,\,{\hat{\beta }}\times \zeta _{\beta }^*), \end{aligned}$$

respectively, where \(\zeta _{\alpha }^*=\exp {\{ Z_{\gamma /2}\sqrt{\delta _{11}}/{\hat{\alpha }}\}}\) and \(\zeta _{\beta }^*=\exp {\{ Z_{\gamma /2}\sqrt{\delta _{22}}/{\hat{\beta }}\}}\). Using similar approach, the respective \(100(1-\gamma )\%\) confidence intervals for r(t) and h(t) are

$$\begin{aligned} \left( {\hat{r}}(t)/\lambda _{r},\,{\hat{r}}(t)\times \lambda _{r}\right) \,\,\text{ and }\,\, ({\hat{h}}(t)/\lambda _{h},\,{\hat{h}}(t)\times \lambda _{h}), \end{aligned}$$

respectively, where \(\lambda _{r}=\exp {\{ Z_{\gamma /2}\sqrt{{\widehat{Var}}({\hat{r}}(t))}/{\hat{r}}(t)\}}\) and \(\lambda _{h}=\exp {\{ Z_{\gamma /2}\sqrt{{\widehat{Var}}({\hat{h}}(t))}/{\hat{h}}(t)\}}\).

5.3 Parametric Bootstrap Confidence Intervals

For statistical inference, bootstrap is a resampling method. It is commonly used to estimate confidence intervals. However, it can also be used for estimating bias and variance of an estimator. The parametric bootstrap method is one of the latest development techniques for certain kind of statistical inference. In this subsection, we construct two bootstrap procedures such as the percentile bootstrap (see [17]) and bootstrap-t (see [20]) to propose confidence intervals of the unknown model parameters and the reliability and hazard functions.

5.3.1 Percentile Bootstrap

We compute interval estimates using percentile bootstrap method. Note that the confidence intervals based on the asymptotic normality property of the MLEs do not perform up to the desired level for small sample sizes. Below, we present algorithm to obtain percentile bootstrap (boot-p) confidence intervals.

Algorithm-2

  1. Step-1

    Based on the original dataset \(t_i,i=1,\ldots ,m\), we obtain \({\hat{\alpha }}\) and \({\hat{\beta }}\) from Equations (2.2) and (2.3) using the algorithm described in Balakrishnan and Sandhu [8].

  2. Step-2

    Based on \((U_1,\ldots ,U_m)\), we generate a bootstrap sample \(\varvec{t}^*=(t_{1}^*,\ldots ,t_{m}^*)\) from log-logistic distribution. Further, obtain \({\hat{\alpha }}^*\), \({\hat{\beta }}^*\), \({\hat{r}}(t)^*\) and \({\hat{h}}(t)^*\) based on the generated bootstrap sample. Denote \({\hat{\mu }}^*=({\hat{\alpha }}^*,{\hat{\beta }}^*, {\hat{r}}(t)^*,{\hat{h}}(t)^*)\) and \(\mu =(\alpha ,\beta , r(t), h(t))\).

  3. Step-3

    Repeat Step-2 for \(M=1000\) times to obtain \({\hat{\mu }}^*_1,\ldots ,{\hat{\mu }}^*_M\), where \({\hat{\mu }}_i^{*}=({\hat{\alpha }}^{*}_i, {\hat{\beta }}^{*}_i, {\hat{r}}(t)^*_i, {\hat{h}}(t)^*_i)\), \(i=1,\ldots ,M\).

  4. Step-4

    Arrange \({\hat{\mu }}^*_i\)’s in ascending order. We denote \({\hat{\mu }}^*_{(1)}\le \ldots \le {\hat{\mu }}^*_{(M)}\).

Thus, the \(100(1-\gamma )\%\) approximate bootstrap-p confidence intervals for \(\mu\) are given by \(({\hat{\mu }}_{\left( \frac{i\gamma }{2}\right) },\,{\hat{\mu }}_{\left( i \left( 1-\frac{\gamma }{2}\right) \right) }).\) Then, the percentile bootstrap confidence intervals of \(\mu\) at \(95\%\) level of confidence are \(({\hat{\mu }}_{(25)}, {\hat{\mu }}_{(975)})\).

5.3.2 Parametric Bootstrap-t

Another method known as parametric bootstrap-t was developed based on a studentized pivot. It requires an estimator of the variance of the MLEs of the unknown parameters \(\alpha ,\) \(\beta\), reliability function r(t) and hazard function h(t). Though the percentile bootstrap method is simple, the boot-t method is more accurate when sample size is small. To compute boot-t confidence intervals, the following algorithm can be adopted.

Algorithm-3

  1. Step-1

    Compute the MLEs \({\hat{\alpha }}\) and \({\hat{\beta }}\) from (2.2) and (2.3) using PT-II censored samples.

  2. Step-2

    Generate a bootstrap sample \(\varvec{t}^*=(t_{1}^*, \ldots ,t_{m}^*)\) based on a predefined censoring scheme from log-logistic distribution. We compute \({\hat{\alpha }}^*\), \({\hat{\beta }}^*\), \({\hat{r}}(t)^*\) and \({\hat{h}}(t)^*\) based on the bootstrap sample. Denote \({\hat{\mu }}^*=({\hat{\alpha }}^*,{\hat{\beta }}^*, {\hat{r}}(t)^*,{\hat{h}}(t)^*)\).

  3. Step-3

    Compute the variance-covariance matrix \({\hat{I}}_T^{* -1}({\hat{\alpha }}^*, {\hat{\beta }}^*)\). Denote a statistic for \(i=1,\ldots ,M\),

    $$\begin{aligned} T^*_{\mu _i}=\frac{{\hat{\mu }}_i^*-{\hat{\mu }}_i}{\sqrt{{\widehat{var}}({\hat{\mu }}_i^*)}}. \end{aligned}$$
  4. Step-4

    Repeat Step\(-1\) and Step\(-2\), M times to obtain \(T^*_{\mu _1}, \ldots ,T^*_{\mu _M}\). We assume \(M=1000\).

  5. Step-5

    Arrange the numbers \(T^*_{\mu _i}\), \(\,i=1,\ldots ,M\) in ascending order, which is denoted by \(T^*_{\mu _{(1)}}\le \ldots \le T^*_{\mu _{(M)}}\).

Now, the \(100(1-\gamma )\%\) approximate bootstrap-t confidence interval for the vector \(\mu\) is given by \(({\hat{T}}_{\mu _{(\frac{i \gamma }{2})}},\,{\hat{T}}_{\mu _{\left( i \left( 1-\frac{\gamma }{2}\right) \right) }}).\) When \(M=1000\), the approximate bootstrap-t confidence interval of \(\mu\) at \(95\%\) level of confidence is \(({\hat{T}}_{\mu _{(25)}}, {\hat{T}}_{\mu _{(975)}})\).

5.4 HPD Credible Intervals

In this subsection, we obtain HPD credible intervals for the unknown parameters, reliability and hazard functions of the log-logistic distribution. The sample is generated using importance sampling method. It is proposed by Chen and Shao [13]. First, we obtain HPD credible intervals for the unknown parameters \(\alpha\) and \(\beta\). Define

$$\begin{aligned} w_i=\frac{\varrho (\alpha ^{(i)},\beta ^{(i)})}{\sum _{i=1}^M \varrho (\alpha ^{(i)},\beta ^{(i)})},\,\,\,i=1,\ldots , M, \end{aligned}$$

where \(\alpha ^{(i)}\) and \(\beta ^{(i)}\) for \(i=1,\ldots ,M\) are the posterior samples generated from Step-1 and Step-2 of Algorithm 1 for \(\alpha\) and \(\beta\), respectively. Then, the pth quantile of \(\alpha\) can be estimated by

$$\begin{aligned}{\hat{\alpha }}^{(p)}= \left\{ \begin{array}{ll} \alpha _{(1)}, &{} p=0 \\ \alpha _{(i)}, &{} {\sum }_{j=1}^{i-1} w_j<p \le {\sum }_{j=1}^{i} w_j. \\ \end{array} \right. \end{aligned}$$

We obtain \(100(1-\gamma )\%\) confidence intervals for the parameter \(\alpha\) of the form

$$\begin{aligned} \left( {\hat{\alpha }}^{(\frac{j}{M})}, {\hat{\alpha }}^{\left( \frac{j+[M(1-\gamma )]}{M}\right) }\right) ,\,\, j=1,\ldots , M-[M(1-\gamma )], \end{aligned}$$

where [.] denotes the greatest integer function. We take the one interval with smallest width. Finally, the HPD credible interval of \(\alpha\) is that interval which has the shortest length. Similar to the above procedure, we can construct the HPD credible interval for \(\beta\). Note that the reliability and hazard functions are nonlinear. Thus, we can not obtain HPD credible intervals of r(t) and h(t) from HPD credible intervals of \(\alpha\) and \(\beta\). Next, we compute the HPD credible interval of r(t) from the importance sampling method. The same procedure is applicable of h(t). Define \(r_i=r(t;\alpha ^{(i)}, \beta ^{(i)})\), where \(\alpha ^{(i)}\) and \(\beta ^{(i)}\) for \(i=1,\ldots ,M\) are posterior samples generated from Step-1 and Step-2 of Algorithm 1, respectively. Let \(r_{(i)}\) be the ordered values of \(r_i\), \(i=1,\ldots ,M\). Then, the pth quantile of \(r(t;\alpha ,\beta )\) can be estimated by

$$\begin{aligned} {\hat{r}}^{(p)}= \left\{ \begin{array}{ll} r_{(1)}, &{} p=0 \\ r_{(i)}, &{} {\sum }_{j=1}^{i-1} w_j<p \le {\sum }_{j=1}^{i} w_j. \\ \end{array} \right. \end{aligned}$$

We obtain different \(100(1-\gamma )\%\) intervals for \(r(t;\alpha , \beta )\) of the form

$$\begin{aligned} \left( {\hat{r}}^{(\frac{j}{M})}, {\hat{r}}^{\left( \frac{j+[M(1-\gamma )]}{M}\right) }\right) ,\,\, j=1,\ldots , M-[M(1-\gamma )]. \end{aligned}$$

We choose the interval with smallest width, which is the HPD credible interval of the reliability function r(t).

6 Real Data Analysis

Here, we consider and analyze two real data sets. First data set represents survival times of 72 guinea pigs injected with different amount of tubercle. This data set was provided by Bjerkedal [12]. Recently, it has been used by Khorram and Meshkani Farahani [23] and Kharazmi et al. [22]. The first data set is given below.

Data set-1

12

15

22

24

24

32

32

33

34

38

38

43

44

48

52

53

54

54

55

56

57

58

58

59

60

60

60

60

61

62

63

65

65

67

68

70

70

72

73

75

76

76

81

83

84

85

87

91

95

96

98

99

109

110

121

127

129

131

143

146

146

175

175

211

233

258

258

263

297

341

341

376

The second data set represents average daily wind speeds (in meter/second) in November 2007 at Elanora Heights, a northeastern suburb of Sydney, Australia. This data set was provided by Best et al. [11]. Recently, it is used by Barot and Patel [9]. Below, we present the second data set.

Data set-2

0.5833

0.6667

0.6944

0.7222

0.7500

0.7778

0.8056

0.8056

0.8611

0.8889

0.9167

1.0000

1.0278

1.0278

1.1111

1.1111

1.1111

1.1667

1.1667

1.1944

1.2778

1.2778

1.3056

1.3333

1.3333

1.3611

1.4444

2.1111

2.1389

2.7778

      

For the purpose of goodness of fit test, four statistical models are considered: weighted exponential (WE), exponential (EXP), half-logistic (HL) and log-logistic (LL) distributions. Bayesian information criterion (\(\hbox {BIC}=k\ln n-2\ln L\)), second-order Akaike’s-information criterion (\(\hbox {AICc}=2k-2\ln L+2k(k+1)/(n-k-1))\), Akaike’s information criterion (\(\hbox {AIC}=2k-2\ln L)\), negative log-likelihood criterion and Kolmogorov-Smirnov (KS) statistic are used. Here, n, k and L are the number of observations, parameters and the maximum value of the log-likelihood function, respectively. Table 2 presents MLEs and the values of four test statistics. From Table 2, we observe that the log-logistic distribution fits well among all other distributions. Figure 3a, b show the histogram and the fitted probability density plots of four models for Data set-1 and Data set-2, respectively. The density plots are depicted using maximum likelihood method. From the graphs, we visualize that the LL distribution covers the maximum area of the data sets comparing to other distributions. Hence, this model can be used to make desired inference on unknown quantities of interest. Note that the scaled total time on test (TTT) plot is useful to detect the shape of the hazard rate function, see, for instance, Mudholkar et al. [35] and Mahmoudi et al. [29]. Let \(T_{(i)},\,i=1,\ldots ,n\) be the \(i\hbox {th}\) order statistic of the sample \((T_{1}, \ldots ,T_{n})\). Then, the scaled TTT transform is

$$\begin{aligned} \phi \left( \frac{v}{n}\right) =\frac{\sum _{i=1}^v T_{(i)} +(n-v)T_{(v)}}{\sum _{i=1}^n T_{(i)}}, \end{aligned}$$

where \(v=1,\ldots ,n\). It is known that the hazard rate function is increasing, decreasing, bathtub and unimodal when the graph of \((v/n, \phi (v/n))\) is concave, convex, convex followed by concave and concave followed by convex, respectively. The scaled TTT plots of the real data sets are presented in Fig. 4. This suggests that the hazard rate shapes of the real data sets are unimodal. We refer to Olson et al. [37], Shi et al. [39] optimization and Shi [38] for more details on data analysis.

Table 2 The MLEs, BIC, AICc, AIC, \(-\ln L\) and KS for the real data sets
Full size table

To obtain the desired estimates, we consider PT-II censored sample from two real data sets with failure sample sizes \(m=45\) and \(m=22\). This is presented in Table 3. For the purpose of computation of the estimates based on the real dataset, we adopt three different censoring schemes. These are given in Table 4.

Table 3 PT-II censored data for the real data sets
Full size table
Table 4 PT-II censoring scheme (CS) for the real data sets
Full size table
Fig. 3
figure 3

The histograms and the plots of the probability density functions of the fitted LL, WE, EXP, HL models for of the real data sets. Figure a represents for the real data set-1 and Figure b for the real data set-2

Full size image
Fig. 4
figure 4

The scaled TTT plot for the guinea pigs data and average daily wind speeds data sets. Figure a is for the guinea pigs data set and Figure b for the average daily wind speeds data set

Full size image

Figure 5 presents the plots of the density, reliability and hazard functions of the best fitted model (here Log-logistic) for different censoring schemes. The density functions of the LL distribution based on the estimated values of the model parameters are depicted in Fig. 5. Figure 6 represents the plots of the histogram and probability density functions of the LL distributions based on the real life data sets when parameters are estimated using MLE, Bayesian approach (via Lindley’e approximation and importance sampling methods). Here we consider the Bayes estimates with respect to the squared error loss function. The proper as well as the improper priors are considered. Figure 6a, b are for the real data set-1 and Fig. 6c, d for the real data set-2. All the figures are drawn in MATLAB software.

Fig. 5
figure 5

The plots of the density, reliability and hazard functions based on different censoring schemes (a, b, c Real data set-1, d, e, f) Real data set-2)

Full size image
Fig. 6
figure 6

The histogram of the real data sets and density plots based on proper and noninformative priors (a, b Real data set-1, c, d Real data set-2]

Full size image

Tables 5 and 6 present the estimated values of the model parameters and the reliability characteristics for two real data sets considered above. Table 5 represents for the guinea pigs data and Table 6 is for the wind speed data. In tables, Prior-I and Prior-II denote the proper and improper priors, respectively. The value of t is taken as 0.5, which is required for the estimation of r(t) and h(t). The values of the MLEs are presented in third column. Other columns are for the Bayes estimates. Corresponding to each estimand, we have two rows. For Bayes estimates, first row is for the estimates obtained using Lindley’s approximation and second row is for the importance sampling method. In Table 7, we provide \(95\%\) confidence intervals of \(\alpha , \beta , r(t)\) and h(t). Third column is for censoring schemes. The confidence intervals based on five different approaches are provided in \(4\hbox {th}\)-\(8\hbox {th}\) columns.

Table 5 Estimates for \(\alpha\), \(\beta\), r(t) and h(t) in data set-1
Full size table
Table 6 Estimates for \(\alpha\), \(\beta\), r(t) and h(t) in data set-2
Full size table
Table 7 \(95\%\) confidence interval estimates of \(\alpha\), \(\beta\), r(t) and h(t)
Full size table

7 Simulation Results

In this section, we carry out a detailed simulation study to observe the performance of the estimates for the unknown parameters, reliability and hazard functions. For specific total sample sizes (n), failure sample sizes (m) and censoring schemes, we generate PT-II censored samples from the LL distribution. To generate PT-II censored sample, we use the algorithm proposed by Balakrishnan and Sandhu [8]. Note that the simulation is performed in R-3.5.1 software for 1000 sets of random observations. We consider the values of n as 15, 25 and that of m as 10, 15 and 25. The true values of \(\alpha\) and \(\beta\) are taken to be 0.75 and 0.25, respectively. For the study of approximate Bayes estimates, we consider proper (prior-I) as well as noninformative (prior-II) priors. In case of the proper priors, for \(m=10, 15\) and 25, we get the values of hyper-parameters as \((\xi _1, \xi _2, \xi _3, \xi _4)=(0.11098, 0.01267, 0.11003, 0.03262),\) (0.19343, 0.03465, 0.19156, 0.09580) and (0.42555, 0.13541, 0.41248, 0.37348), respectively. For the noninformative priors, we take \(\xi _{1}=\xi _{2}=\xi _{3}=\xi _{4}=0\). The bias and mean squared errors (MSEs) of the estimates are computed using the following formula:

$$\begin{aligned} \text {bias}=\frac{1}{M}\sum _{i=1}^{M}\left( {\hat{\theta }}^{(i)}_{l}-\theta _{l}\right) \,\,\text {and}\,\, MSE=\frac{1}{M}\sum _{i=1}^{M}\left( {\hat{\theta }}^{(i)}_{l}-\theta _{l}\right) ^{2}, \end{aligned}$$

where \(l=1,2,3\) and 4. Here, \(\theta _{1}=\alpha ,\theta _{2}=\beta ,\theta _{3}=r(t)\) and \(\theta _{4}=h(t)\). For the reliability and hazard functions, \(t=0.5\) is taken. Further, for computing the Bayes estimates with respect to the LINEX and entropy loss functions, we assume \(p=0.0005\) and \(q=0.5\), respectively. For computation purpose, seven schemes with various values of n and m are taken (see Table 8). We present the bias and MSEs of the proposed estimates of the unknown parameters, reliability and hazard functions in Tables 9, 10 and 11.

Table 8 PT-II censoring scheme (CS)
Full size table

Tables 12 and 13 provide the average length of \(95\%\) confidence interval estimates. In Tables 9, 10 and 11, we have thirteen columns. Second and third columns are respectively for the censoring schemes and MLEs. Fourth to eighth and ninth to thirteen columns are for the Bayes estimates with respect to the proper and noninformative priors, respectively. Further, each scheme has four rows. The absolute bias of the estimates are allocated to the first and third rows. Second and fourth rows are for the MSEs. For the case of Bayes estimates, first and second rows are due to the Lindley’s approximation technique. The third and fourth rows are for the importance sampling method. In Tables 12 and 13, each scheme has a single row. The following observations are pointed out from the simulation study.

  1. (i)

    We provide the estimates for \(\alpha\) and \(\beta\) in Tables 9 and 10. Here, we observe that the Bayes estimates with respect to the proper as well as noninformative priors perform better than the MLEs in terms of the absolute bias and MSE. Among the five Bayes estimates, the one corresponding to the precautionary loss function has superior performance than others in terms of both absolute bias and MSE. The Bayes estimates with respect to the noninformative priors outperforms that with respect to the proper priors. It is observed that Lindley’e approximation technique gives better result than that of the importance sampling technique. The absolute bias and MSE decrease when m increases for fixed n. As expected, the absolute bias and MSE of the Bayes estimates under SELF and LLF are very close when p is small.

  2. (ii)

    Tables 10 and 11 represent the estimates for the reliability and hazard functions. The value of t, say 0.5 is taken. For \(t=0.5\), the true value of r(t) is 0.37288. The respective true value of h(t) is 0.94067 when \(t=0.5\). Similar pattern to the estimates of the parameters \(\alpha\) and \(\beta\) as in (i) is observed for r(t) and h(t). These are skipped for the sake of brevity.

  3. (iii)

    Table 12 provides the average lengths of the \(95\%\) confidence intervals of the unknown model parameters \(\alpha\) and \(\beta\). Among the asymptotic intervals, estimates obtained via normal approximation to the MLE (NA) performs better than the normal approximation to the log-transformed MLE (NL). From boot type intervals, Boot-t provides better confidence interval estimates than Boot-p method. Considering all the five methods together, it is observed that the HPD method outperforms others. Further, the average lengths of the confidence intervals decrease when effective sample size increases.

  4. (iv)

    In Table 13, we present the average lengths of the \(95\%\) confidence intervals for r(t) and h(t). Similar behaviour to the interval estimates of \(\alpha\) and \(\beta\) is also observed for that of r(t) and h(t).

Table 9 Bias and MSEs of the estimates for \(\alpha\) and \(\beta\)
Full size table
Table 10 Bias and MSEs of the estimates for \(\beta\) and r(t) at \(t=0.5\)
Full size table
Table 11 Bias and MSEs of the estimates for r(t) and h(t) at \(t=0.5\)
Full size table
Table 12 Average lengths of \(95\%\) confidence interval estimates of \(\alpha\) and \(\beta\)
Full size table
Table 13 Average lengths of \(95\%\) confidence interval estimates of r(t) and h(t) at \(t=0.5\)
Full size table

8 Concluding Remarks

In this paper, we studied estimation of the unknown parameters, reliability and hazard functions of a log-logistic distribution. The inference is proposed based on the progressive type-II censored sample. We derived various point estimates. In particular, the maximum likelihood estimates, Bayes estimates are obtained. To compute MLEs, EM algorithm has been used. For Bayesian estimation, we considered five loss functions. Few of them are symmetric and others are asymmetric in nature, which fits some real life situations well. Bayes estimates are difficult to produce in closed form. So, we used two approximation techniques: Lindley’s approximation and importance sampling methods. One advantage of the importance sampling method is that it can be used to derive credible interval estimates of the unknown quantities. Further, we introduced various interval estimates. In this purpose, five techniques such as two asymptotic methods, two boot type methods and highest posterior density method are used. Two real life data sets are taken and analysed. Based on the data sets, we proposed the estimates of the parameters, reliability and hazard functions. For the purpose of visual analysis, we have also plotted various graphs for the real data sets. A massive simulation study is performed to compute the proposed point and interval estimates. The estimates are presented in various tables for different censoring schemes. From the tables, various useful observations are made.