1 Introduction

The Fréchet distribution was introduced by a French mathematician Maurice Fréchet in 1927. Since then, various extreme value events (skewed data) have been modeled by this distribution. For several applications of Fréchet distribution, we refer to Kotz and Nadarajah (2000). Note that the Fréchet distribution is a particular case of the generalized extreme value distribution. It is dubbed as type-II extreme value distribution (or inverse Weibull distribution) in the literature. Sometimes, it is required to expand families of distributions by introducing new parameter(s) for better description of the data. A way to achieve this goal is by taking power of the cumulative distribution function (CDF), or its difference from 1. That is, \(G^{\alpha }\), which is known as Lehmann type-I distribution, or \(1-(1-G)^{\alpha }\), known as Lemann type-II distribution, where G is the baseline distribution. Nadarajah and Kotz (2003) introduced exponentiated Fréchet distribution with CDF

$$\begin{aligned} F(x;\alpha ,\lambda ,\sigma )=1-\left[ 1-\exp \left\{ -\left( \frac{\sigma }{x}\right) ^{\lambda } \right\} \right] ^{\alpha },~x>0,\,\sigma ,\lambda ,\alpha >0. \end{aligned}$$
(1.1)

Here, \(\sigma\) is known as the scale parameter, \(\lambda\) and \(\alpha\) are the shape parameters. The CDF given in (1.1) was constructed by taking the form \(1-(1-G)^{\alpha }\). Note that when \(\alpha =1\), the generalized Fréchet distribution reduces to the usual Fréchet distribution. Inverse generalized exponential distribution is obtained for \(\lambda =1\) (see Abouammoh and Alshingiti 2009). This distribution is right skewed with unique mode. Henceforth, we denote \(X\sim GF(\alpha ,\lambda ,\sigma )\) if X has the distribution function given by (1.1). The probability density function (PDF) of \(GF(\alpha ,\lambda ,\sigma )\) distribution is given by

$$\begin{aligned} f(x;\alpha ,\lambda ,\sigma )=\alpha \lambda \sigma ^{\lambda }\left[ 1-\exp \left\{ -\left( \frac{\sigma }{x}\right) ^{\lambda } \right\} \right] ^{\alpha -1}x^{-(\lambda +1)} \exp \left\{ -\left( \frac{\sigma }{x}\right) ^{\lambda } \right\} , \,x>0,\,\sigma ,\lambda ,\alpha >0. \end{aligned}$$
(1.2)

It can be observed that thicker tails are associated with small values of \(\alpha\) when other parameters are fixed. Further, more peaked distributions are obtained by larger values of \(\lambda\). The tail thickness of the distribution is determined by the product \(\alpha \lambda\). Thus, the generalized Fréchet distribution with CDF (1.1) is much more flexible than the usual Fréchet distribution. For example, in actuarial related studies, usually, a large loss generates a long-right tail distribution. In such cases, generalized Fréchet distribution is useful for modeling them (see Panjer 2006; Gündüz and Genç 2016).

Nadarajah and Kotz (2003) discussed maximum likelihood estimation for this distribution. Abd-Elfattah and Omima (2009) considered the problem of estimating parameters of a generalized Fréchet distribution based on the complete sample when \(\lambda\) is known. They obtained maximum likelihood estimates (MLEs) for \(\sigma\) and \(\alpha\). Mubarak (2011a) studied the problem of estimation of Fréchet distribution based on the record values and obtained various estimates for the unknown parameters. Mubarak (2011b) considered Fréchet distribution associated with scale, shape and location parameters and obtained MLEs based on progressive type-II censored data with binomial removals. Soliman et al. (2014) proposed various estimates of the unknown parameters for lifetime performance index of a two parameter exponentiated Fréchet distribution on the progressive first-failure-censored observations. Soliman et al. (2015) derived maximum likelihood and Bayes estimates for the parameters and some lifetime parameters (reliability and hazard rate functions) of a two parameter exponentiated Fréchet model based on the progressive type-II censored data. They computed approximate Bayes estimates using balanced squared and balanced linex loss functions.

In many practical situations, the Bayesian prediction problem plays a very important role under known prior information in statistics. It can manipulate the past data to acquire future observation for the same population. The main concern relating to the informative sample is the prediction of Bayes for unknown observable that is predicting the future sample from the current sample. It is useful for a real-life practical field such as bio-medical treatments, industrial experiments, and economic data, etc. For some more references in recent years where the problem prediction of censored or future observation based on Bayesian framework under progressive type-II censoring, we refer to Kayal et al. (2017), Singh et al. (2017), Dey et al. (2018) and Bdair et al. (2019). To the best of our knowledge, nobody has considered estimation and prediction for a generalized Fréchet distribution with CDF given in (1.1) based on the progressive type-II censored sample. In this paper, we study this problem. Below, we provide brief description on the progressive type-II censored sample.

The data are often censored in reliability and life testing experiments. The most popular censoring schemes are type-I and type-II. However, for these schemes, the main drawback is that we can not remove live items while an experiment is going on. As mentioned above, in this paper, we consider a generalization of the type-II censoring scheme, where the live items can be removed during the experiment. This is known as the progressive type-II censoring scheme. Under this scheme, we assume that n items are placed on a life testing experiment and \(m(<n)\) are completely observed until failure. When the first failure occurs at random time \(X_{1:m:n}\), \(R_1\) randomly chosen items are removed from \(n-1\) surviving items. At the second failure time \(X_{2:m:n}\), \(R_2\) items are removed randomly from \(n-R_1-2\) remaining items. We continue this process till the mth failure. Denote \(X_{m:m:n}\) as the mth failure time. The set of observed lifetimes \(X_{1:m:n},X_{2:m:n},\ldots ,X_{m:m:n}\) is known as the progressive type-II censored sample with scheme \((R_1,R_2,\ldots ,R_m)\). Note that when \(R_1=R_2=\cdots =R_{m-1}=0\) and \(R_{m}=n-m\), the progressive type-II censored scheme reduces to the type-II censoring scheme, and when \(R_1=R_2=\cdots =R_m=0\), it becomes complete sampling scheme. For relevant detail on this sampling scheme, we refer to Balakrishnan and Aggarwala (2000), Balakrishnan (2007) and Balakrishnan and Cramer (2014).

The objective of this paper is to obtain point and interval estimates of the model parameters and the lifetime parameters (reliability and hazard rate functions) of a \(GF(\alpha ,\lambda ,\sigma )\) distribution based on the progressive type-II censored sample. The reliability and hazard rate functions at time \(t>0\) are given by

$$\begin{aligned} r(t;\alpha ,\lambda ,\sigma )=\left[ 1-\exp \left\{ -\left( \frac{\sigma }{t}\right) ^{\lambda }\right\} \right] ^{\alpha } \end{aligned}$$
(1.3)

and

$$\begin{aligned} h(t;\alpha ,\lambda ,\sigma )=\frac{\alpha \lambda \sigma ^\lambda t^{-(\lambda +1)} \exp \left\{ -\left( \frac{\sigma }{t}\right) ^\lambda \right\} }{\left[ 1-\exp \left\{ -\left( \frac{\sigma }{t}\right) ^\lambda \right\} \right] }, \end{aligned}$$
(1.4)

respectively, where \(\alpha ,\lambda ,\sigma >0\). In particular, we obtain MLEs of \(\alpha ,\lambda ,\sigma ,r(t;\alpha ,\lambda ,\sigma )\) and \(h(t;\alpha ,\lambda ,\sigma )\). For convenience, denote \(r(t)\equiv r(t;\alpha ,\lambda ,\sigma )\) and \(h(t)\equiv h(t;\alpha ,\lambda ,\sigma )\). We also derive Bayes estimates with respect to various balanced loss functions. We obtain confidence intervals using normal and log-normal approximations of the MLEs. Note that various authors have considered estimation of parameters and their functions based on progressive type-II censored sample for different lifetime distributions. Few of these are Ahmed (2014, 2015), Dey and Dey (2014), Rastogi and Tripathi (2014a, b), Singh et al. (2015), Dey et al. (2016, 2017), Seo and Kang (2016), Lee and Cho (2017), Chaudhary and Tomer (2018), Kumar et al. (2018) and Maiti and Kayal (2019).

The paper is arranged as follows. In Sect. 2, we obtain MLEs of the unknown parameters, and the reliability and hazard rate functions. The asymptotic confidence intervals are calculated in Sect. 3. In Sect. 4, we compute Bayes estimates with respect to various balanced loss functions such as balanced squared error, balanced linex and balanced entropy loss functions. Note that it is difficult to obtain the Bayes estimates in closed form. In Sect. 5, importance sampling method is employed to obtain approximate Bayes estimates. Section 6 is devoted for Bayesian prediction. A simulation study is carried out in Sect. 7 to compare the estimates based on their average values and mean squared errors. Further, real life dataset is considered and analyzed for illustrating all the inferential methods developed in Sect. 8. Concluding remarks are added in Sect. 9.

2 Maximum likelihood estimation

In this section, we derive MLEs for the model parameters \(\alpha ,\lambda ,\sigma\), reliability function r(t) and hazard rate function h(t) of a \(GF(\alpha ,\lambda ,\sigma )\) distribution based on the progressive type-II censored data. Denote \(\varvec{X}=(X_{1:m:n},X_{2:m:n},\ldots ,X_{m:m:n})\) the progressive type-II censored sample of size m from a sample of size n drawn from \(GF(\alpha ,\lambda ,\sigma )\) distribution with CDF and PDF given in (1.1) and (1.2), respectively. For convenience, henceforth, we denote \(X_i=X_{i:m:n},\,i=1,2,\ldots ,m.\) The likelihood function is given by

$$\begin{aligned} L(\alpha ,\lambda ,\sigma |\varvec{x})=C \alpha ^{m}\lambda ^{m}\sigma ^{m\lambda }\prod _{i=1}^{m} x_{i}^{-(\lambda +1)}(1-\vartheta (\lambda ,\sigma ;x_{i})) \left[ \vartheta (\lambda ,\sigma ;x_{i})\right] ^{\alpha (R_i +1)-1}, \end{aligned}$$
(2.1)

where \(x_{i}=x_{i:m:n}\), \(\vartheta (\lambda ,\sigma ;x_{i})=1-\exp \{-\left( \sigma /x_{i}\right) ^{\lambda }\}\), \(\varvec{x}=(x_1,x_2,\ldots ,x_m)\) and \(C =n(n-R_1-1)(n-R_1-R_2-2)\ldots (n-\sum _{i=1}^{m-1}(R_i+1))\). On differentiating the log-likelihood function \((\ln L(.)=\ell (.))\) with respect to the parameters partially, and then equating to zero, we obtain the normal equations as

$$\begin{aligned}&\frac{m}{\alpha }+\sum _{i=1}^{m}(1+R_i)\ln \vartheta (\lambda ,\sigma ;x_{i})=0, \end{aligned}$$
(2.2)
$$\begin{aligned}&m\left( \frac{1}{\lambda }+\ln \sigma \right) -\sum _{i=1}^{m}\ln x_i +\sum _{i=1}^{m} \xi (\lambda ,\sigma ;x_{i})\ln \left( \frac{\sigma }{x_i}\right) \left( -1+\alpha (1+R_i)\right) \left( \frac{\sigma }{x_i}\right) ^\lambda -\sum _{i=1}^{m}\left( \frac{\sigma }{x_i}\right) ^\lambda \ln \left( \frac{\sigma }{x_i}\right) =0 \end{aligned}$$
(2.3)

and

$$\begin{aligned} \frac{m}{\sigma }+\sum _{i=1}^m \frac{1}{x_i}\left( \alpha (R_i+1)-1\right) \xi (\lambda ,\sigma ;x_{i}) \left( \frac{\sigma }{x_i}\right) ^{\lambda -1}-\sum _{i=1}^m \frac{ (\frac{\sigma }{x_i})^{\lambda -1}}{x_i}=0, \end{aligned}$$
(2.4)

where \(\xi (\lambda ,\sigma ;x_{i})=\exp \{-\left( \sigma /x_{i}\right) ^{\lambda }\}/ (1-\exp \{-\left( \sigma /x_{i}\right) ^{\lambda }\})\). The solutions of this system of non-linear equations give the MLEs of \(\alpha ,\lambda\) and \(\sigma\). It is easy to notice that the closed-form expressions of the MLEs of \(\alpha ,\lambda\) and \(\sigma\) do not exist. We need to adopt numerical iterative technique in order to get approximate solutions for \(\alpha ,\lambda\) and \(\sigma\). In this purpose, we employ Newton–Raphson iteration method. Denote the MLEs of \(\alpha ,\lambda\) and \(\sigma\) by \({\hat{\alpha }},{\hat{\lambda }}\) and \({\hat{\sigma }}\), respectively. Further, using invariant property, the MLEs of r(t) and h(t) at \(t=t_0\) are respectively obtained as

$$\begin{aligned} {\hat{r}}=\left[ \vartheta ({\hat{\lambda }},{\hat{\sigma }} ;t_0)\right] ^{{\hat{\alpha }}}\,\,\text{ and }\,\, {\hat{h}}={\hat{\alpha }}{\hat{\lambda }} {\hat{\sigma }}^{{\hat{\lambda }}} \xi ({\hat{\lambda }},{\hat{\sigma }} ;t_0)/t_{0}^{({\hat{\lambda }}+1)}. \end{aligned}$$
(2.5)

3 Interval estimation

In this section, we compute approximate confidence intervals for three parameters \(\alpha ,\lambda ,\sigma\), and two lifetime parameters r(t) and h(t). To evaluate asymptotic confidence intervals, the usual large sample approximation is used. Here, the maximum likelihood estimators can be treated as approximately multivariate normal. We use two approaches: (i) normal approximation (NA) of the MLE and (ii) normal approximation of the log-transformed (NL) MLE. To obtain the asymptotic confidence intervals of \(\alpha ,\lambda ,\sigma\), it is required to compute observed Fisher information matrix \((\hat{\mathcal {I}})\) of the MLEs. Denote \(\ell =\ln L\). Then,

$$\begin{aligned} \hat{\mathcal {I}}=\left( \begin{array}{ccc} -\frac{\partial ^2 \ell }{\partial \alpha ^2} &\quad -\frac{\partial ^2 \ell }{\partial \alpha \partial \lambda } &\quad -\frac{\partial ^2 \ell }{\partial \alpha \partial \sigma } \\ -\frac{\partial ^2 \ell }{\partial \lambda \partial \alpha } &\quad - \frac{\partial ^2 \ell }{\partial \lambda ^2} &\quad - \frac{\partial ^2 \ell }{\partial \lambda \partial \sigma }\\ -\frac{\partial ^2 \ell }{\partial \sigma \partial \alpha } &\quad - \frac{\partial ^2 \ell }{\partial \sigma \partial \lambda } &\quad-\frac{\partial ^2 \ell }{\partial \sigma ^2}\\ \end{array} \right)\left| \right. _{(\alpha ,\lambda , \sigma )=({\hat{\alpha }},{\hat{\lambda }}, {\hat{\sigma }})}, \end{aligned}$$
(3.1)

where the second order partial derivatives are given in Eqs. (10.1)–(10.5). Further, to obtain the asymptotic variance covariance matrix \(({\hat{M}})\) for the MLEs of \(\alpha ,\lambda\) and \(\sigma\), we need to compute the inverse of \(\hat{\mathcal {I}}\), which is given by

$$\begin{aligned} {\hat{M}}=\left( \begin{array}{ccc} \text {var}({\hat{\alpha }}) &\quad \text {cov}({\hat{\alpha }},{\hat{\lambda }})&\quad \text {cov} ({\hat{\alpha }},{\hat{\sigma }}) \\ \text {cov}({\hat{\alpha }}, {\hat{\lambda }}) &\quad \text {var}({\hat{\lambda }})&\quad \text {cov} ({\hat{\lambda }},{\hat{\sigma }})\\ \text {cov} ({\hat{\alpha }}, {\hat{\sigma }}) &\quad \text {cov} ({\hat{\lambda }}, {\hat{\sigma }}) &\quad \text {var} ({\hat{\sigma }}) \end{array} \right) =\left( \begin{array}{ccc} \tau _{11} &\quad \tau _{12}&\quad\tau _{13} \\ \tau _{21} &\quad \tau _{22}&\quad \tau _{23}\\ \tau _{31} &\quad \tau _{32}&\quad \tau _{33}\\ \end{array} \right) ,\,\text{ say, } \end{aligned}$$
(3.2)

that is, \(\tau _{ij}\) is the (i, j)th element of \({\hat{M}}\); \(i,j=1,2,3\).

3.1 Confidence intervals for \(\alpha ,\lambda\) and \(\sigma\)

In this section, we present confidence intervals for the unknown model parameters based on NA and NL methods. First, consider NA method.

3.1.1 Normal approximation of the MLE

In this subsection, we derive confidence intervals of the parameters \(\alpha ,\lambda\) and \(\sigma\) using asymptotic normality property of the MLEs. From large-sample theory of the MLEs, the sampling distribution of \(({\hat{\alpha }},{\hat{\lambda }},{\hat{\sigma }})\) can be approximately distributed as \(N((\alpha ,\lambda ,\sigma ),{\hat{M}})\). Thus, \(100(1-\gamma )\%\) approximate confidence intervals for \(\alpha ,\lambda\) and \(\sigma\) are obtained as

$$\begin{aligned} \left( {\hat{\alpha }}\pm Z_{\gamma /2}\sqrt{\tau _{11}}\right) ,\, \left( {\hat{\lambda }}\pm Z_{\gamma /2}\sqrt{\tau _{22}}\right) \,\text{ and }\,\left( {\hat{\sigma }}\pm Z_{\gamma /2}\sqrt{\tau _{33}}\right) , \end{aligned}$$

respectively, where \(Z_{\gamma /2}\) is the upper \((\gamma /2)\)th percentile of the standard normal distribution.

3.1.2 Normal approximation of the log-transformed MLE

Since the parameters \(\alpha ,\lambda\) and \(\sigma\) are positive valued, it is also possible to use logarithmic transformation to compute approximate confidence intervals for these parameters. We refer to Meeker and Escobar (1998) in this direction. They pointed out that the confidence interval obtained using NL method has better coverage probability than that obtained using NA method as in Sect. 3.1.1. The \(100(1-\gamma )\%\) normal approximate confidence intervals for log-transformed MLE are respectively

$$\begin{aligned} \left( \ln {\hat{\alpha }}\pm Z_{\gamma /2}\sqrt{\tau _{11}\ln {\hat{\alpha }}}\right) ,\,\left( \ln {\hat{\lambda }}\pm Z_{\gamma /2}\sqrt{\tau _{22} \ln {\hat{\lambda }}}\right) \,\text{ and }\, \left( \ln {\hat{\sigma }}\pm Z_{\gamma /2}\sqrt{\tau _{33}\ln {\hat{\sigma }}}\right) , \end{aligned}$$

where \(\tau _{11}\ln {\hat{\alpha }}=var(\ln {\hat{\alpha }})\), \(\tau _{22}\ln {\hat{\lambda }}=var(\ln {\hat{\lambda }})\) and \(\tau _{33}\ln {\hat{\sigma }}=var(\ln {\hat{\sigma }})\). Thus, based on NL method, \(100(1-\gamma )\%\) confidence intervals for \(\alpha\), \(\lambda\) and \(\sigma\) are obtained as

$$\begin{aligned} \left( {\hat{\alpha }}\times \exp \left\{ \pm \left[ \frac{Z_{\gamma /2}\sqrt{\tau _{11}}}{{\hat{\alpha }}}\right] \right\} \right) , \left( {\hat{\lambda }}\times \exp \left\{ \pm \left[ \frac{Z_{\gamma /2}\sqrt{\tau _{22}}}{{\hat{\lambda }}}\right] \right\} \right) \,\text{ and }\,\left( {\hat{\sigma }}\times \exp \left\{ \pm \left[ \frac{Z_{\gamma /2}\sqrt{\tau _{33}}}{{\hat{\sigma }}}\right] \right\} \right) , \end{aligned}$$

respectively.

3.2 Confidence intervals for r(t) and h(t)

In the previous subsection, we obtain confidence intervals for \(\alpha ,\lambda\) and \(\sigma\). Here, we compute confidence intervals for the reliability characteristics r(t) and h(t) given in (1.3) and (1.4), respectively.

3.2.1 Normal approximation of the MLE

Using this approach, to obtain the approximate confidence intervals for r(t) and h(t), it is required to evaluate their variances. This can be obtained from the inverted observed Fisher information matrix. Here, we use delta method. One may refer to Greene (2000) for detail on delta method. Denote \(A^t\) as the transpose of A. Let

$$\begin{aligned} \Phi _{r}^{t}=\left( \frac{\partial r}{\partial \alpha },\frac{\partial r}{\partial \lambda }, \frac{\partial r}{\partial \sigma }\right) \,\text{ and }\,\Phi _{h}^{t}=\left( \frac{\partial h}{\partial \alpha },\frac{\partial h}{\partial \lambda }, \frac{\partial h}{\partial \sigma }\right) , \end{aligned}$$
(3.3)

where the first order partial derivatives are given in (10.6)–(10.9). Now, from delta method, the estimates of the variances of \({\hat{r}}\) and \({\hat{h}}\) can be obtained approximately as

$$\begin{aligned} {\widehat{var}}({\hat{r}})=\left( \Phi _{r}^{t} {\hat{M}} \Phi _{r}\right) \,\text{ and }\,{\widehat{var}}({\hat{h}})=\left( \Phi _{h}^{t} {\hat{M}} \Phi _{h}\right) , \end{aligned}$$

respectively, where the partial derivatives are computed at \(({\hat{\alpha }},{\hat{\lambda }},{\hat{\sigma }})\). Again, from the general asymptotic theory of the MLE, the sampling distribution of

$$\begin{aligned} \frac{{\hat{r}}-r}{\sqrt{{\widehat{var}}({\hat{r}})}}\quad \text{ and }\quad \frac{{\hat{h}}-h}{\sqrt{{\widehat{var}}({\hat{h}})}} \end{aligned}$$

can be approximated by a standard normal distribution. Hence, \(100(1-\gamma )\%\) approximate confidence intervals of r and h respectively are

$$\begin{aligned} \left( {\hat{r}}\pm Z_{\gamma /2}\sqrt{ {\widehat{var}}({\hat{r}})}\right) \quad \text{ and }\quad \left( {\hat{h}} \pm Z_{\gamma /2}\sqrt{ {\widehat{var}}({\hat{h}})}\right) . \end{aligned}$$

3.2.2 Normal approximation of the log-transformed MLE

In this subsection, we obtain confidence intervals for r(t) and h(t) using NL method. Note that the computation is similar to that discussed in Sect. 3.1.2, and thus the details are omitted. The approximate \(100(1-\gamma )\%\) confidence intervals for the reliability and hazard rate functions are obtained respectively as,

$$\begin{aligned} \left( {\hat{r}}\times \exp \left\{ \pm \left[ \frac{Z_{\gamma /2}\sqrt{{\widehat{var}}({\hat{r}})}}{{\hat{r}}}\right] \right\} \right) \,\text{ and }\, \left( {\hat{h}}\times \exp \left\{ \pm \left[ \frac{Z_{\gamma /2}\sqrt{{\widehat{var}}({\hat{h}})}}{{\hat{h}}}\right] \right\} \right) . \end{aligned}$$

4 Bayesian estimation

This section concerns Bayesian point estimates for three unknown parameters \(\alpha\), \(\lambda\) and \(\sigma\), the reliability and hazard rate functions r(t) and h(t) of the \(GF(\alpha ,\lambda ,\sigma )\) distribution. One of the motivations of taking balanced loss functions is due to its usefulness in decision making. In statistical decision theory, usually, the loss functions focus on the precision of estimation. But, another important criterion in this direction is “goodness of fit”. Zellner (1994) first introduced a balanced loss function (BLF) for the estimation of an unknown parameter \(\theta\) based on random vector \(\varvec{Y}=(Y_1,Y_2, \ldots , Y_n)\) as

$$\begin{aligned} \frac{\omega }{n}\sum _{i=1}^{n} (Y_i-\delta )^2+(1-\omega )(\delta -\theta )^2, \end{aligned}$$
(4.1)

where \(0\le \omega \le 1\). Note that this loss function was studied in the context of the general linear model to reflect both goodness of fit and precision of estimation. In the statistical inference, loss functions often reflect any of these two criteria, but not both. As an example, least square estimation reflects goodness of fit consideration. The linex loss function involves a sole emphasis on the precision of estimation. later, Jozani et al. (2006) proposed an extended class of balanced type loss functions of the form

$$\begin{aligned} L_{b}(\theta ,\delta )=\omega \eta ({\hat{\delta }},\delta )+(1-\omega )\eta (\theta ,\delta ), \end{aligned}$$
(4.2)

where \(\eta (\theta ,\delta )\) is an arbitrary loss function, \({\hat{\delta }}\) is a priori target estimate of \(\theta\) which can be obtained from the criterion of maximum likelihood, \(\delta\) is an estimate of \(\theta\) and \(\omega \in [0,1]\) is weight. The loss function given by (4.2) has been used by various authors. In the direction, we refer to Farsipour and Asgharzadeh (2004), Asgharzadeh and Farsipour (2008), Ahmadi et al. (2009), Jozani et al. (2012) and Barot and Patel (2017). Note that this loss function was used by Zellner (1986, 1988) to develop minimum expected loss estimates for the coefficients of structural econometric models. It is also remarked that for many years, the balanced loss functions have been the subject of many theoretical and applied studies. For example, Rodrigues and Zellner (1994) used this loss function on the estimation of time to failure, Wolfe and Godsill (2003) applied the BLF on spectral amplitude estimation in audio signal analysis. Further, one may argue that the loss function given by (4.2) provides a potentially useful tool for decision making because of the flexibility of the choices of \(\omega\) and \({\hat{\delta }}\). The BLF (4.2) is well suited to assist in setting credibility insurance premiums with the target choice \({\hat{\delta }}\) relating to a collective estimate of risk and with many instances where a squared error loss is not necessarily an appropriate choice (see Gómez-Déniz 2008). Various authors used a symmetric loss function due to its symmetrical nature in several estimation problems. It provides equal weight to over-estimation as well as to under-estimation. However, there are many situations, where the loss function is not of symmetrical nature. In such situations, an asymmetric loss function would be a better choice than a symmetric loss function. In this paper, we consider both balanced symmetric loss function and balanced asymmetric loss function for better insight in the Bayesian estimation and prediction problems. Especially, we consider balanced squared error loss (BSEL), balanced linex loss (BLL) and balanced entropy loss (BEL) functions, which are respectively given as

$$\begin{aligned} L_{bs}(\theta ,\delta )&= \omega (\delta -{\hat{\delta }})^2 +(1-\omega )(\delta -\theta )^2, \end{aligned}$$
(4.3)
$$\begin{aligned} L_{bl}(\theta ,\delta )&= \omega [\exp \{p(\delta -{\hat{\delta }})\} -p(\delta -{\hat{\delta }})-1]+ (1-\omega )[\exp \{p(\delta -\theta )\}-p(\delta -\theta )-1],\,p\ne 0 \end{aligned}$$
(4.4)
$$\begin{aligned} L_{be}(\theta ,\delta )&= \omega [(\delta /{\hat{\delta }})^q-q \ln (\delta /{\hat{\delta }})-1]+(1-\omega )[(\delta /\theta )^q-q \ln (\delta /\theta )-1],\,q\ne 0. \end{aligned}$$
(4.5)

The Bayes estimates of the unknown parameter \(\theta\) with respect to the BSEL, BLL and BEL functions given in (4.3)–(4.5) are respectively given by (see Jozani et al. 2012; Barot and Patel 2017)

$$\begin{aligned} {\hat{\theta }}_{bs}(\varvec{x})&= \omega {\hat{\delta }} (\varvec{x})+(1-\omega )E[\theta |\varvec{X}=\varvec{x}], \end{aligned}$$
(4.6)
$$\begin{aligned} {\hat{\theta }}_{bl}(\varvec{x})&= -p^{-1}\ln [\omega \exp \{-p{\hat{\delta }} (\varvec{x})\}+(1-\omega )E[\exp \{-p\theta \}|\varvec{X}=\varvec{x}]], \end{aligned}$$
(4.7)
$$\begin{aligned} {\hat{\theta }}_{be}(\varvec{x})&= [\omega {\hat{\delta }}^{-q} (\varvec{x})+(1-\omega )E[\theta ^{-q}|\varvec{X}=\varvec{x}]]^{-\frac{1}{q}}. \end{aligned}$$
(4.8)

When \(\omega =1\), the above estimators reduce to the MLE. To derive Bayes estimates, it is required to assign prior distributions to describe the uncertainty of all the unknown parameters of the model. Here, we assume that the model parameters \(\alpha ,\lambda\) and \(\sigma\) have independent gamma distributions with PDFs

$$\begin{aligned} \pi _1(\alpha ;a_1,b_1)&= \frac{b_1^{a_1}\alpha ^{a_1-1}e^{-\alpha b_1}}{\Gamma (a_1)}, \,\alpha>0,\,a_1,b_1 >0, \end{aligned}$$
(4.9)
$$\begin{aligned} \pi _2(\lambda ;a_2, b_2)&= \frac{b_2^{a_2}\lambda ^{a_2-1}e^{-\lambda b_2}}{\Gamma (a_2)}, \,\lambda>0,\,a_2, b_2 >0, \end{aligned}$$
(4.10)
$$\begin{aligned} \pi _3(\sigma ;a_3, b_3)&= \frac{b_3^{a_3} \sigma ^{a_3-1}e^{-\sigma b_3}}{\Gamma (a_3)}, \,\sigma>0,\,a_3, b_3 >0, \end{aligned}$$
(4.11)

respectively, where the hyper-parameters \(a_{i},b_{i},\,i=1,2,3\) are known. The joint prior distribution of \(\alpha\), \(\lambda\) and \(\sigma\) is given by

$$\begin{aligned} \pi (\alpha , \lambda , \sigma )=\alpha ^{a_1-1}\lambda ^{a_2-1}\sigma ^{a_3-1}e^{-\alpha b_1}e^{-\lambda b_2}e^{-\sigma b_3}, \alpha , \lambda , \sigma>0,\,a_i, b_i>0,\,i=1,2,3. \end{aligned}$$

After some simplification, the posterior distribution of \(\alpha\), \(\lambda\) and \(\sigma\) given \(\varvec{X}=\varvec{x}\) is

$$\begin{aligned} \Pi (\alpha , \lambda , \sigma |\varvec{X}=\varvec{x})&= k^{-1}\alpha ^{m+a_1-1}\lambda ^{m+a_2-1} \sigma ^{m\lambda +a_3-1}\prod _{i=1}^{m}e_{1}(x_{i}), \end{aligned}$$
(4.12)

where

$$\begin{aligned} k&= \int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } \alpha ^{m+a_1-1}\lambda ^{m+a_2-1} \sigma ^{m\lambda +a_3-1} \prod _{i=1}^{m} e_{1}(x_{i})\,d\alpha d\lambda d\sigma \end{aligned}$$
(4.13)

and

$$\begin{aligned} e_{1}(x_{i})\equiv e_{1}(\alpha ,\lambda ,\sigma ;x_{i})=x_{i}^{-(\lambda +1)} \exp \left\{ -\left( \left( \frac{\sigma }{x_{i}}\right) ^\lambda +\alpha b_1+\lambda b_2+\sigma b_3\right) \right\} \vartheta ^{\alpha (R_i+1)-1}(\lambda ,\sigma ;x_i). \end{aligned}$$
(4.14)

Now, we compute Bayes estimates of the model parameters \(\alpha ,\lambda ,\sigma\) and lifetime parameters r(t), h(t) with respect to the BSEL, BLL and BEL functions. From (4.6), (4.7) and (4.8), the Bayes estimates for \(\varvec{\theta }=(\alpha ,\lambda ,\sigma , r, h)\) are respectively obtained as

$$\begin{aligned} \hat{\varvec{\theta }}_{bs}&= \omega \hat{\varvec{\theta }} +(1-\omega )\hat{\varvec{\theta }}_{s}, \end{aligned}$$
(4.15)
$$\begin{aligned} \hat{\varvec{\theta }}_{bl}&= -\frac{1}{p} \ln \left[ \omega \exp \{-p\hat{\varvec{\theta }}\}+(1-\omega )\exp \{-p\hat{\varvec{\theta }}_{l}\}\right] ,\,p\ne 0 \end{aligned}$$
(4.16)

and

$$\begin{aligned} \hat{\varvec{\theta }}_{be}=\left[ \omega \hat{\varvec{\theta }}^{-q}+(1-\omega )\hat{\varvec{\theta }}_{e}^{-q} \right] ^{-\frac{1}{q}},\,q\ne 0, \end{aligned}$$
(4.17)

where \(0\le \omega \le 1\) and \(\hat{\varvec{\theta }}\) is the MLE for \(\varvec{\theta }\). Further, \(\hat{\varvec{\theta }}_{s}\), \(\hat{\varvec{\theta }}_{l}\) and \(\hat{\varvec{\theta }}_{e}\) in (4.15), (4.16) and (4.17) are the Bayes estimates of \(\varvec{\theta }\) with respect to the squared error loss function \(\eta (\varvec{\theta },\delta )=(\delta -\varvec{\theta })^2\), linex loss function \(\eta (\varvec{\theta },\delta )=\exp \{p(\delta -\varvec{\theta })\}-p(\delta -\varvec{\theta })-1\), \(p\ne 0\) and generalized entropy loss function \(\eta (\varvec{\theta },\delta )=(\delta /\varvec{\theta })^{q}-q \ln (\delta /\varvec{\theta })-1,\,q\ne 0\). For the sake of brevity, we omit the complete form of the Bayes estimators of \(\alpha ,\lambda ,\sigma , r(t)\) and h(t) with respect to these loss functions.

5 Importance sampling method

We propose to use the importance sampling technique. In the section, we consider another approximation technique, the importance sampling method to obtain the Bayes estimates for the parameters, reliability and hazard functions. We rewrite the joint posterior distribution of \(\alpha\), \(\lambda\) and \(\sigma\) is given by (4.12) as

$$\begin{aligned} \Pi (\alpha ,\lambda , \sigma |\varvec{x})&\propto G_{\alpha |\lambda ,\sigma }\left( m+a_1, b_1-\sum _{i=1}^m (1+R_i)\ln \vartheta (\lambda ,\sigma ;x_i)\right) G_\lambda \left( m+a_2, b+\sum _{i=1}^m \ln x_i\right) \nonumber \\&\quad \times G_{\sigma |\lambda } (m\lambda +a_3, b_3) S( \lambda ,\sigma ; x_i), \end{aligned}$$
(5.1)

where

$$\begin{aligned} S(\lambda , \sigma ; x_i) =\frac{\left( b_1-\sum _{i=1}^m (1+R_i)\ln \vartheta (\lambda , \sigma ; x_i)\right) ^{-(m+a_1)}}{b_3^{(m\lambda +a_3)}\left( b+\sum _{i=1}^m \ln x_i\right) ^{(m+a_2)}} \prod _{i=1}^m \frac{\xi (\lambda , \sigma ;x_i)}{x_i}. \end{aligned}$$

Now, the importance sampling technique has following steps for sample generation process.

  1. Step-1

    Generate \(\lambda\) from \(G_\lambda \left( m+a_2, b+\sum _{i=1}^m \ln x_i\right)\) (i.e. a Gamma distribution with shape parameter \((m+a_2)\) and rate parameter \((b+\sum _{i=1}^m \ln x_i)\)).

  2. Step-2

    For a given \(\lambda\) in Step 1, generate \(\sigma\) from \(G_{\sigma |\lambda } (m\lambda +a_3, b_3)\) (i.e. a Gamma distribution with shape parameter \((m\lambda +a_3)\) and rate parameter \(b_3\)).

  3. Step-3

    For a given \(\lambda\) in Step 1 and \(\sigma\) in Step 2, generate \(\alpha\) from \(G_{\alpha |\lambda ,\sigma }\left( m+a_1, b_1-\sum _{i=1}^m (1+R_i)\ln \vartheta (\lambda ,\sigma ;x_i)\right)\) (i.e. a Gamma distribution with shape parameter \((m+a_1)\) and rate parameter \((b_1-\sum _{i=1}^m (1+R_i)\ln \vartheta (\lambda ,\sigma ;x_i))\)).

  4. Step-4

    We repeat 1000 times to obtain \((\alpha _1, \lambda _1, \sigma _1)\), \((\alpha _2,\lambda _2, \sigma _2)\), ..., \((\alpha _{1000}, \lambda _{1000}, \sigma _{1000})\).

The Bayes estimates of a parametric function \(g(\alpha , \lambda , \sigma )\) under linex and entropy loss functions are given by, respectively

$$\begin{aligned} {\hat{g}}^{Im}_{l}(\alpha ,\lambda , \sigma )=-\frac{1}{p}\ln \left[ \frac{\sum _{i=1}^{1000} \exp \{-p g(\alpha _i, \lambda _i, \sigma _i)\}S(\lambda _i, \sigma _i;x_i)}{\sum _{i=1}^{1000} S(\lambda _i, \sigma _i;x_i)}\right] \end{aligned}$$
(5.2)

and

$$\begin{aligned} {\hat{g}}^{Im}_{e}(\alpha , \lambda , \sigma )=\left[ \frac{\sum _{i=1}^{1000} g(\alpha _i, \lambda _i, \sigma _i)^{-q} S(\lambda _i, \sigma _i;x_i)}{\sum _{i=1}^{1000} S(\lambda _i, \sigma _i;x_i)}\right] ^{-\frac{1}{q}}. \end{aligned}$$
(5.3)

We compute the Bayes estimates of \(\alpha , \lambda , \sigma , r(t)\) and h(t) after substituting \(\alpha , \lambda , \sigma , r(t)\) and h(t) in place of \(g(\alpha , \lambda , \sigma )\), respectively in Eqs. (5.2) and (5.3) under linex and entropy loss functions. When \(q=-1\), (5.3) reduces to the Bayes estimate with respect to squared error loss function. The details of this method have been omitted to maintain brevity. The respective Bayes estimates with respect to the BLL and BEL can be obtained after replacing the desisted Bayes estimates in (4.15)–(4.17). For some recent references in this direction, we may refer to Sultan et al. (2014), Kundu and Raqab (2015) and Chacko and Asha (2018).

6 Bayesian prediction

In the previous section, we obtain the Bayesian estimation for unknown parameters, reliability and hazard functions. Here, we discuss Bayesian prediction for the future observations based on progressive type-II censoring sample from GF distribution and also compute the corresponding prediction intervals. For various applications of prediction problem, we refer to the recent articles Singh and Tripathi (2015), Asgharzadeh et al. (2015) and Kayal et al. (2017). In this section, we have used two different prediction methods (one-sample and two-sample) for computing prediction estimates and prediction intervals of progressive censoring observations.

6.1 One-sample prediction

Suppose we have observed n number of total life testing units on experiments. Let an informative observed progressive censored sample \(y_i=(y_{i1}, y_{i2}, \ldots , y_{iR_i})\) represents ith failure times at censored \(x_i\). We wish to predict future observations \(y=(y_{ic}; i=1,2,\ldots ,m; c=1,2,\ldots ,R_i)\). Let \(\varvec{x}=(x_1,x_2,\ldots ,x_m)\) be the progressive type-II censored sample with censoring scheme \(R=(R_1,R_2,\ldots ,R_m)\) from a distribution whose CDF and PDF are respectively given by (1.1) and (1.2). We wish to predict future observation \(y=(y_{ic}; i=1,2,\ldots ,m; c=1,2,\ldots ,R_i)\) based on observed samples \((x_1,x_2,\ldots ,x_m)\). The conditional density and distribution functions of y given \(\varvec{x}\) can be written as

$$\begin{aligned} f_1(y|\varvec{x}, \alpha , \lambda , \sigma )&= c{R_i \atopwithdelims ()c}\sum _{k=0}^{c-1} (-1)^{c-k-1}{c-1 \atopwithdelims ()k}f(y)(1-F(y))^{R_i-k-1}(1-F(x_i))^{k-R_i}\nonumber \\&= \alpha \lambda \sigma ^\lambda c{R_i \atopwithdelims ()c}\sum _{k=0}^{c-1} (-1)^{c-k-1}{c-1 \atopwithdelims ()k}x^{-(\lambda +1)}\vartheta ^{\alpha (R_i-k)-1}(\lambda ,\sigma ;y) \nonumber \\&\quad \times (1-\vartheta (\lambda ,\sigma ;y))\vartheta ^{\alpha (k-R_i)}(\lambda ,\sigma ;x_{i}) \end{aligned}$$
(6.1)

and

$$\begin{aligned} F_1(y|\varvec{x}, \alpha , \lambda , \sigma )&= c{R_i \atopwithdelims ()c}\sum _{k=0}^{c-1} \frac{(-1)^{c-k-1}}{R_i-k}{ c-1 \atopwithdelims ()k}\left[ 1-(1-F(x_i))^{k-R_i}(1-F(y))^{R_i-k}\right] \nonumber \\&= c{R_i \atopwithdelims ()c}\sum _{k=0}^{c-1} \frac{(-1)^{c-k-1}}{R_i-k} {c-1 \atopwithdelims ()k} \left[ 1-\vartheta ^{k-R_i}(\lambda ,\sigma ;x_i) \vartheta ^{R_i-k}(\lambda , \sigma ;y)\right] . \end{aligned}$$
(6.2)

Notice that the posterior predictive density and distribution functions under the prior \(\pi (\alpha , \lambda , \sigma )\) are respectively given by

$$\begin{aligned} f_1^*(y|\varvec{x})=\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } f_1(y|\varvec{x},\alpha ,\lambda , \sigma )\Pi (\alpha , \lambda , \sigma |\varvec{x}) d\alpha d\lambda d\sigma \end{aligned}$$
(6.3)

and

$$\begin{aligned} F_1^*(y|\varvec{x})=\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } F_1(y|\varvec{x},\alpha ,\lambda , \sigma )\Pi (\alpha , \lambda , \sigma |\varvec{x}) d\alpha d\lambda d\sigma . \end{aligned}$$
(6.4)

The Bayesian predictive estimate of y under linex and entropy functions are given by

$$\begin{aligned} {\widehat{y}}_{l} &=-\frac{1}{p}\ln \left[ \int _{x_i}^\infty \exp \{-p y\} f_1^*(y|\varvec{x})dy\right] &=-\frac{1}{p}\ln \left[ E(P_1(\alpha , \lambda , \sigma )|\varvec{x})\right] \end{aligned}$$
(6.5)

and

$$\begin{aligned} {\widehat{y}}_{q}=\left[ \int _{x_i}^\infty y^{-q} f_1^*(y|\varvec{x})dz\right] ^{-\frac{1}{q}}&= \left[ E(P_2(\alpha , \lambda , \sigma )|\varvec{x})\right] ^{-\frac{1}{q}}, \end{aligned}$$
(6.6)

where

$$\begin{aligned} P_1(\alpha , \lambda , \sigma )&= \int _{x_i}^\infty \exp \{-py\}f_1(y|\varvec{x},\alpha ,\lambda , \sigma )dy\nonumber \\&= \alpha \lambda \sigma ^\lambda c{R_i \atopwithdelims ()c}x^{-(\lambda +1)} \sum _{k=0}^{c-1} (-1)^{c-k-1}{c-1 \atopwithdelims ()k} \vartheta ^{\alpha (k-R_i)}(\lambda , \sigma ;x_i)\nonumber \\&\quad \times \int _{x_i}^\infty \exp \left\{ -\left( p y+\left( \frac{\sigma }{y}\right) ^\lambda \right) \right\} \vartheta ^{\alpha (R_i-k)-1}(\lambda ,\sigma ;y)dy \end{aligned}$$
(6.7)

and

$$\begin{aligned} P_2(\alpha , \lambda , \sigma )&= \int _{x_i}^\infty y^{-q}f_1(y|\varvec{x},\alpha ,\lambda , \sigma )dy\nonumber \\&= \alpha \lambda \sigma ^\lambda c{R_i \atopwithdelims ()c}x^{-(\lambda +1)}\sum _{k=0}^{c-1} (-1)^{c-k-1}{c-1 \atopwithdelims ()k}\vartheta ^{\alpha (k-R_i)}(\lambda , \sigma ;x_i)\nonumber \\&\quad \times \int _{x_i}^\infty y^{-q}(1-\vartheta (\lambda , \sigma ;y))\vartheta ^{\alpha (R_i-k)-1}\nonumber \\&\quad (\lambda ,\sigma ;y)dy. \end{aligned}$$
(6.8)

Note that the above integrals cannot be determined analytically. Thus, one needs to use numerical technique in order to compute the predictive estimates. In this purpose, we use importance sampling methods as mentioned in Sect. 5. Equations (6.5) and (6.6) can be evaluated using importance sampling method as

$$\begin{aligned} {\widehat{y}}_{l}=-\frac{1}{p}\ln \left[ \frac{\sum _{i=1}^{1000}P_1(\alpha _i, \lambda _i, \sigma _i)S(\lambda _i, \sigma _i;x_i) }{\sum _{i=1}^{1000}S(\lambda _i, \sigma _i;x_i) }\right] \end{aligned}$$
(6.9)

and

$$\begin{aligned} {\widehat{y}}_{q}=\left[ \frac{\sum _{i=1}^{1000}P_2(\alpha _i, \lambda _i, \sigma _i)S(\lambda _i, \sigma _i;x_i) }{\sum _{i=1}^{1000}S(\lambda _i, \sigma _i;x_i) }\right] ^{-1/q} \end{aligned}$$
(6.10)

6.1.1 Bayesian prediction interval

The associated predictive survival function \(S_1(y|\varvec{x}, \alpha , \beta )\) is obtained as

$$\begin{aligned} \frac{P(y>t|\varvec{x},\alpha ,\lambda , \sigma )}{P(y>x_i|\varvec{x},\alpha ,\lambda , \sigma )}&= \frac{\int _{t}^\infty f_1(u|\varvec{x},\alpha , \lambda , \sigma )du}{\int _{x_i}^\infty f_1(u|\varvec{x},\alpha , \lambda , \sigma )du}. \end{aligned}$$

The associated posterior distribution function under the prior distribution \(\pi (\alpha , \lambda , \sigma )\) is given by

$$\begin{aligned} S_1^*(y|\varvec{x}, \alpha , \lambda , \sigma )=\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty } S_1(y|\varvec{x},\alpha ,\lambda , \sigma )\Pi (\alpha , \lambda , \sigma |\varvec{x}) d\alpha d\lambda d\sigma . \end{aligned}$$
(6.11)

Equation (6.11) can be evaluated using importance sampling method under squared error loss function as

$$\begin{aligned} S_1^*(y|\varvec{x},\alpha , \lambda , \sigma )=\frac{\sum _{i=1}^{1000} S_1(y|\varvec{x},\alpha _i, \lambda _i, \sigma _i) S(\lambda _i, \sigma _i;x_i)}{\sum _{i=1}^{1000} S(\lambda _i, \sigma _i;x_i)}. \end{aligned}$$
(6.12)

We obtain two sided \(100(1-\gamma )\%\) equal-tail symmetric predictive interval (L, U), where the lower bound L and the upper bound U can be computed by solving the following non-linear equations

$$\begin{aligned} S^*_1(L|\varvec{x})=1-\frac{\gamma }{2}\,\,\text{ and }\,\,S^*_1(U|\varvec{x})=\frac{\gamma }{2}. \end{aligned}$$
(6.13)

One may refer to Singh and Tripathi (2015) for the algorithm to obtain L and U.

6.2 Two-sample prediction

In this section, we evaluate Bayesian two-sample prediction estimation from future observation based on progressive type-II censoring sample. Two-sample prediction is general version of one-sample prediction. Let \(\varvec{x}=(x_1,x_2,\ldots ,x_m)\) be a progressive censoring sample. Suppose, two-sample prediction is use to predict the jth failure time from a failure sample of size M. A two-sample prediction problem involves the prediction and associated inference about the failure sample \(\varvec{z}=(z_1,z_2,\ldots ,z_M)\). The condition predictive density function of \(z_j\) can be written as

$$\begin{aligned} f(z_j| \alpha , \lambda , \sigma )&= j{M \atopwithdelims ()j} \sum _{k=0}^{j-1} (-1)^{j-k-1} {j-1 \atopwithdelims ()k}\left[ 1-F(z_j)\right] ^{M-k-1} f(z_j)\nonumber \\&= \alpha \lambda \sigma ^\lambda j{M \atopwithdelims ()j} x^{-(\lambda +1)}(1-\vartheta (\lambda , \sigma ;z_j))\sum _{k=0}^{j-1}(-1)^{j-k-1}{j-1 \atopwithdelims ()k} \vartheta ^{\alpha (M-k)-1}(\lambda , \sigma ;z_j). \end{aligned}$$
(6.14)

The two-sample posterior predictive density function is given by

$$\begin{aligned} f^*(z_j|\varvec{x})&= \int _{0}^{\infty }\int _{0}^\infty \int _{0}^\infty f(z_j|\alpha , \lambda , \sigma ) \Pi (\alpha , \lambda , \sigma |\varvec{x}) d\alpha d\lambda d\sigma . \end{aligned}$$

The Bayesian predictive estimate of \(z_j\) under linex and entropy loss functions using importance sampling method are obtained as

$$\begin{aligned} {\widehat{z}}_{j_{l}}&= - \frac{1}{p} \ln \left[ \int _{0}^\infty \exp \{-py\}f^*(z_j|\varvec{x}) dz_j\right] \nonumber \\&= - \frac{1}{p} \ln \left[ \frac{\sum _{i=1}^{1000}T_1(\alpha _i, \lambda _i, \sigma _i)S(\lambda _i, \sigma _i;x_i)}{\sum _{i=1}^{1000}S(\lambda _i, \sigma _i;x_i)}\right] \end{aligned}$$
(6.15)

and

$$\begin{aligned} {\widehat{z}}_{j_{e}}=\left[ \int _{0}^\infty z_j^{-q}f^*(z_j|\varvec{x})dz_j\right] ^{-1/q} = \left[ \frac{\sum _{i=1}^{1000}T_2(\alpha _i, \lambda _i, \sigma _i)S(\lambda _i, \sigma _i;x_i)}{\sum _{i=1}^{1000}S(\lambda _i, \sigma _i;x_i)}\right] ^{-1/q}, \end{aligned}$$
(6.16)

where

$$\begin{aligned} T_1(\alpha , \lambda , \sigma )&= \int _{0}^\infty \exp \{-p z_j\}f(z_j|\alpha , \lambda , \sigma )dz_j\nonumber \\&= \alpha \lambda \sigma ^\lambda j{M \atopwithdelims ()j} x^{-(\lambda +1)}\sum _{k=0}^{j-1}(-1)^{j-k-1} {j-1 \atopwithdelims ()k}\int _{0}^\infty \exp \left\{ -\left( p z_j+\left( \frac{\sigma }{z_j}\right) ^\lambda \right) \right\} \nonumber \\&\quad \times \vartheta ^{\alpha (M-k)-1}(\lambda , \sigma ;z_j)dz_j \end{aligned}$$
(6.17)

and

$$\begin{aligned} T_2(\alpha , \lambda , \sigma )&= \int _{0}^\infty z_j^{-q} f(z_j|\alpha , \lambda , \sigma )dz_j\nonumber \\&= \alpha \lambda \sigma ^\lambda j{M \atopwithdelims ()j} x^{-(\lambda +1)}\sum _{k=0}^{j-1}(-1)^{j-k-1} {j-1 \atopwithdelims ()k}\int _{0}^\infty z_j^{-q}(1-\vartheta (\lambda , \sigma ;z_j))\nonumber \\&\quad \times \vartheta ^{\alpha (M-k)-1}(\lambda , \sigma ;z_j)dz_j. \end{aligned}$$
(6.18)

The predictive survival function is given by

$$\begin{aligned} S_1^*(z_j|\varvec{x})=\int _{0}^{\infty }\int _{0}^\infty \int _{0}^\infty S_1(z_j|\varvec{x}, \alpha , \lambda , \sigma ) \Pi (\alpha , \lambda , \sigma |\varvec{x})d\alpha d\lambda d\sigma \end{aligned}$$
(6.19)

where

$$\begin{aligned} S_1(z_j|\varvec{x}, \alpha , \lambda , \sigma )=\frac{\int _{z_j}^\infty f_1(u|\varvec{x},\alpha , \lambda , \sigma )du}{\int _{x_i}^\infty f_1(u|\varvec{x},\alpha , \lambda , \sigma )du}, \end{aligned}$$

which can be approximated using importance sampling method. To obtain the two-sided \(100(1-\gamma )\%\) equal-tail symmetric prediction interval \((L_1,U_1)\) for \(z_j\), we can solve the following non-linear equations

$$\begin{aligned} S^*_1(L_1|\varvec{x})=1-\frac{\gamma }{2}\quad \text{ and }\quad S^*_1(U_1|\varvec{x})=\frac{\gamma }{2}. \end{aligned}$$
(6.20)

7 Numerical comparisons

In this section, we perform a Monte Carlo simulation study to compare the estimates developed in the previous sections. We obtain their average values and the mean squared error values using statistical software R. Based on the algorithm proposed by Balakrishnan and Sandhu (1995), we replicated 1000 progressive type-II censored samples of size m from a sample of size n drawn from a generalized Fréchet distribution with CDF given by (1.1). Note that \(n=30,40\); \(m=20,25,30,40\) and \(\omega =0,0.3,1\) are considered for the purpose of the numerical study. The true value of \((\alpha , \lambda , \sigma )\) is taken as (0.75, 3.5, 0.25). For three distinct values of \(\omega =0,0.3,1\), the Bayes estimates with respect to the BSEL, BLL and BEL functions are calculated. The values of p and q are considered as \(p=-0.5, 0.005, 1.0\) and \(q=-0.25, -0.05, 0.5\), respectively. All the Bayes estimates are evaluated with respect to the noninformative prior distributions with \(a_1=a_2=a_3=0\) and \(b_1=b_2=b_3=1\). We compute mean squared error (MSE) using the formula

$$\begin{aligned} MSE=\frac{1}{M'}\sum _{i=1}^{M'}({\hat{\theta }}_{k}^{(i)} -\theta _{k})^{2},\,k=1,2,3,4,5. \end{aligned}$$
(7.1)

Here, \(\theta _1=\alpha ,\theta _2=\lambda , \theta _3=\sigma , \theta _4=r(t)\), \(\theta _5=h(t)\) and \(M'=1000\). We consider the following censoring schemes (CS)

  • CS-I: \((R_1,R_2,\ldots ,R_m)=(n-m, 0^*(m-1))\)

  • CS-II: \((R_1,R_2,\ldots ,R_m)=(0^*\frac{m}{2}, (n-m), 0^*(\frac{m}{2}-1))\) if m is even, \((R_1,R_2,\ldots ,R_m)=(0^*\frac{m-1}{2}, (n-m), 0^*\frac{m-1}{2})\) if m is odd

  • CS-III: \((R_1,R_2,\ldots ,R_m)=(0^*(m-1),n-m)\)

  • CS-IV: \((R_1,R_2,\ldots ,R_m)=(0^*m)\) if \(m=n\),

where for example \((0^*3,2)\) denotes the censoring scheme (0, 0, 0, 2). The average values and MSE values of the MLEs and the Bayes estimates of \(\alpha ,\lambda ,\sigma ,r(t)\) and h(t) are tabulated in Tables 1 and 2, respectively. Note that the third columns of all the tables are for the MLEs (when \(\omega =1\)), fifth is for the Bayes estimates under BSEL function, sixth, seventh and eighth columns are for the Bayes estimates under BLL function, and ninth, tenth and eleventh columns are for the Bayes estimates with respect to BEL function. Further, each value of \(\omega\) (here \(\omega =0,0.3\)) corresponds to four rows. First and second rows respectively represent average values and the MSE values of the Bayes estimates obtained via importance sampling method. The following points are observed from the tabulated values.

  1. (i)

    Table 1 presents the simulated values of the average values and the MSE values of the MLEs and the Bayes estimates for \(\alpha\), \(\lambda\) and \(\sigma\) for various choices of n and m. The values are presented under four different sampling schemes described above. In general, in terms of the average values and MSE values, the proposed Bayes estimates perform better than the MLEs. However, among all the Bayes estimates, estimates obtained with respect to the BEL function are superior to others. When considering BLL function, \(p=1\) seems to be a reasonable choice among the other choices. For the case of BEL function, \(q=0.5\) is the best choice among the other choices considered in Table 1. It is noticed that when p is small, the average and MSE values of the Bayes estimates with respect to the BLL and BSEL functions are quiet close, as expected. Moreover, we notice that the MSE decreases when n and m increase.

  2. (ii)

    Similar to Table 1, we present estimated average values and the MSE values of the reliability function r(t) and hazard rate function h(t) based on various sampling schemes in Table 2. Note that for \((\alpha , \lambda , \sigma )=(0.75, 3.5, 0.25)\), r(t) = 0.156858 and \(h(t)=5.021398\) for \(t=0.5\). Similar pattern of the estimates developed for r(t) and h(t) is observed.

  3. (iii)

    We have tabulated 90% and 95% asymptotic confidence intervals and coverage probabilities for the parameters \(\alpha ,\lambda\) and \(\sigma\) in Table 3. Six rows are presented corresponding to each sampling scheme. First, third and fifth rows are for the confidence intervals of \(\alpha ,\lambda\) and \(\sigma\), respectively. Second, fourth and sixth rows are for the coverage probabilities of \(\alpha ,\lambda\) and \(\sigma\), respectively. These intervals and coverage probabilities are calculated using NA and NL methods for various choices of n, m and sampling schemes. In general, with the effective increase in sample size, the average lengths of confidence intervals and coverage probabilities tend to decrease. It is also observed that the average lengths of confidence intervals and coverage probabilities obtained by NL method are larger than the corresponding lengths by NA method. Among the coverage probabilities, estimates obtained via NL method perform better than NA method. The coverage probabilities lie below the nominal level of 0.90 and 0.95.

  4. (iv)

    Table 4 represents \(90\%\) and \(95\%\) asymptotic confidence intervals for the reliability and hazard rate functions. Here, each sampling scheme corresponds to four rows. First and second rows present the asymptotic confidence interval and coverage probabilities for the reliability function and the third and fourth rows present the confidence intervals and coverage probabilities for the hazard rate function. Here, we observe similar pattern as discussed in the previous point.

  5. (v)

    In Tables 5 and 6, we present one-sample and two-sample predictive estimates under Bayesian framework using Monte Carlo simulation. Here, we consider same true values of the parameters and hyper-parameters. In one-sample prediction, the values of c are taken as 1 and 2 at the stage of ith failure. Similarly, in two-sample prediction, the values of j are considered as 1 and 2. Further, we take the sample size \(M=m\).

    For computing the predictive estimates with respect to the BLL and BEL loss functions, we assume \(p=-0.5,0.005,1.0\) and \(q=-0.25,-0.05,0.5\), respectively. With respective to BLL and BEL, the predictive estimate values seems to be smaller at \(p=1.0\) and \(q=0.5\), respectively. It is observed that the predictive estimate values increase when the lifetime of higher order units increase under one-and two-sample cases. Also, we notice that the values of predictive estimates tend to decrease with the effective increase in sample size.

  6. (vi)

    Table 7 provides the \(90\%\) and \(95\%\) prediction intervals for one-sample and two-sample Bayes prediction. We observe that the \(90\%\) produces prediction intervals with shorter average length than \(95\%\). The average lengths of prediction intervals tend to decrease with the increase in effective sample size. The lengths of these intervals increase with c and j increase under one-and two-sample prediction, respectively.

Table 1 Average values and MSE values of estimates for the parameters \(\alpha\), \(\lambda\) and \(\sigma\)
Full size table
Table 2 Average values and MSE values of estimates for the functions reliability r(t) and hazard h(t)
Full size table
Table 3 Interval estimates and coverage probabilities of \(\alpha\), \(\lambda\) and \(\sigma\)
Full size table
Table 4 Interval estimates and coverage probabilities of r(t) and h(t)
Full size table
Table 5 One-sample predicted values for future observations
Full size table
Table 6 Two-sample predicted values for future observations
Full size table
Table 7 Prediction intervals for future observations
Full size table

8 Real data analysis

In this section, we consider real dataset to discuss the estimates obtained in this paper. The dataset presented below, represents the number of cycles to failure for 60 electrical appliances in a life test experiment (see Lawless 2011). Note that this dataset has been used by Seo et al. (2017) (see also Sarhan et al. 2012) for the study of robust Bayesian estimation of a two-parameter bathtub-shaped distribution.

0.014

0.034

0.059

0.061

0.069

0.080

0.123

0.142

0.165

0.210

0.381

0.464

0.479

0.556

0.574

0.839

0.917

0.969

0.991

1.064

1.088

1.091

1.174

1.270

1.275

1.355

1.397

1.477

1.578

1.649

1.702

1.893

1.932

2.001

2.161

2.292

2.326

2.337

2.628

2.785

2.811

2.886

2.993

3.122

3.248

3.715

3.790

3.857

3.912

4.100

4.106

4.116

4.315

4.510

4.580

5.267

5.299

5.583

6.065

9.701

We consider fitting of four reliability models such as exponential (Exp), Fréchet (FR), exponentiated exponential (Eexp) and generalized Fréchet (GF) distributions (see Table 8). To estimate the parameters of these distributions, maximum likelihood estimation is used. Now, for the purpose of the test the goodness of fit of the above models, we employ various test statistics such as (i) Kolmogorov–Smirnov statistic (K–S statistic), (ii) the negative log-likelihood criterion, (iii) Akaikes-information criterion (AIC), (iv) the associated second-order information criterion (AICc) and (v) Bayesian information criterion (BIC).

From the computed values presented in Table 8, it is noticed that the generalized Fréchet distribution fits the given dataset reasonably well since it has the smallest values of the statistics among the fitted models. Thus, based on a progressive type-II censored sample with total size \(n=60\) and the failure sample size \(m=50\) (see Table 9) drawn from the given dataset, we calculate the estimates developed above. Here, we have used various sampling schemes discussed in Sect. 7.

Table 8 Goodness of fit tests
Full size table
Table 9 Progressive type-II censoring data for real dataset
Full size table

Tables 10 and 11 represent the average values of the estimates for \(\alpha ,\lambda , \sigma\) and r(t), h(t), respectively. Third column of these tables represents the MLEs, fifth represents the Bayes estimates under BSEL function (denoted as BS); sixth, seventh and eighth columns represent the Bayes estimates with respect to BLL function (denoted as BL) and the last three columns represent the Bayes estimates with respect to the BEL function (denoted as BE). Further, in Table 10, each censoring scheme has three row values in the third column (MLE) and six row values in the columns corresponding to the Bayes estimates under importance sampling method. First, second and third row values in the third column represent the MLEs of \(\alpha ,\lambda\) and \(\sigma\), respectively. Fifth column onwards, first two row values correspond to the Bayes estimates for \(\alpha\), next two row values represent the Bayes estimates for \(\lambda\) and final two row values correspond to that for \(\sigma\). In Table 11, each censoring scheme corresponds to two rows in the third column (MLE), and four rows for the Bayes estimates of r(t) and h(t) functions. Furthermore, each value of \(\omega\) corresponds to two rows. In Tables 12 and 13, we present \(90\%\) and \(95\%\) asymptotic confidence intervals and coverage probabilities of \(\alpha ,\lambda ,\sigma\) and r(t), h(t), respectively. In Table 12, each scheme has six rows. First, third and fifth rows and second, four and six rows are for asymptotic confidence intervals and coverage probabilities of \(\alpha ,\lambda\) and \(\sigma\), respectively. Similarly, in Table 13, each scheme has four rows. First two rows represent confidence interval and coverage probabilities for r(t) and the next two rows represent that for h(t). In Table 14, we obtain one-sample prediction estimates of the lifetime of first two units at ith failure. The two-sample prediction estimates of the lifetime of first two units and size of sample \(M=5\) are tabulated in Table 15. Finally, we represent \(90\%\) and \(95\%\) prediction intervals of one-and two-sample prediction cases (Table 16).

Table 10 Estimates of \(\alpha\), \(\lambda\) and \(\sigma\) for the real dataset
Full size table
Table 11 Estimates of r(t) and h(t) for the real dataset
Full size table
Table 12 Interval estimates and coverage probabilities of \(\alpha\), \(\lambda\) and \(\sigma\) for real dataset
Full size table
Table 13 Interval estimates and coverage probabilities of r(t) and h(t) for real dataset
Full size table
Table 14 One-sample predicted values for future observations under real dataset
Full size table
Table 15 Two-sample predicted values for future observations under real dataset
Full size table
Table 16 Prediction intervals for future observations under real dataset
Full size table

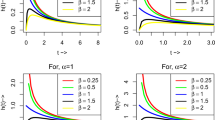
In Fig. 1, we present the histogram of the real dataset and fitted probability density function of four models such as exponential, Fréchet, exponentiated exponential and generalized Fréchet distributions. Here, we show the generalized Fréchet distribution covers the maximum area of the dataset comparing to other distributions. Figure 2a–c present estimated density, reliability and hazard function plots under four censoring schemes. In this case, the unknown model parameters are estimated using maximum likelihood estimation technique. Figure 3a represents the graphs of the estimated probability density functions where the parameters are estimated by maximum likelihood estimation and Bayesian estimation by importance sampling method under BSEL function. Figure 3b depicts the graphs of the density functions where parameters are estimated based on the Bayesian estimation under BLL function for \(p=-0.5,0.005\) and 1. In Fig. 3c, we plot the densities where parameters are estimated based on the Bayesian estimation under BEL function for \(q=-0.25,-0.05\) and 0.5. Similarly, Fig. 4 presents the graphs of the reliability and hazard rate functions for the given dataset. Here, we consider \(\omega =0.3\) while computing Bayes estimates with respect to balanced loss functions for the purpose of plotting the graphs. In Figs. 3 and 4, BS_Im denote for the Bayes estimates with respect to the squared error loss function using importance sampling method. Further, \(p=0.005\)_BL_Im (\(q=-0.05\)_BE_Im) represent Bayes estimates with respect to the BLL (BEL) function when \(p=0.005\) (\(q=-0.05\)).

Fig. 1
figure 1

The histogram of the real dataset and the plots of the probability density functions of the fitted Eexp, FR, Exp, GF models

Full size image
Fig. 2
figure 2

The plots of the a density, b reliability function and c hazard function based on different censoring schemes

Full size image
Fig. 3
figure 3

Estimated density plots based on real dataset presented in Sect. 8. a represents the density plots based on the MLE and the Bayes estimates with respect to the balanced squared error loss function, b presents the density plots based on the balanced linex loss function for different values of p, c we provide plots of the density functions using Bayes estimates under balanced entropy loss function for various values of q

Full size image
Fig. 4
figure 4

Estimated plots of the reliability (a–c) and hazard (d–f) functions based on real dataset

Full size image

9 Concluding remarks

In this paper, we established various methods for estimating the unknown parameters and reliability characteristics of the exponentiated Fréchet distribution based on progressive type-II censored sample. We applied Newton-Raphson method to compute the maximum likelihood estimates and the asymptotic confidence intervals. Further, Bayes estimates are obtained with respect to three balanced type loss functions. In this purpose, importance sampling method have been introduced. One-sample as well as two-sample Bayesian prediction for the Future observations based on progressive type-II censored sample have been considered. The prediction intervals are also computed. Monte-Carlo simulation is employed to proposed estimates. From the simulation study, it is noticed that the Bayesian estimation is more accurate than the maximum likelihood estimation.