Classical and Bayesian estimation in log-logistic distribution under random censoring

Abstract

This article deals with the classical and Bayesian estimation of the parameters of log-logistic distribution using random censorship model. The maximum likelihood estimators and the asymptotic confidence intervals based on observed Fisher information matrix of the parameters are derived. Bayes estimators of the parameters under generalized entropy loss function using independent gamma priors are obtained. For Bayesian computation, Tierney–Kadane’s approximation and Markov chain Monte Carlo (MCMC) methods are used. Also, the highest posterior credible intervals of the parameters based on MCMC method are constructed. A Monte Carlo simulation study is carried out to compare the behavior of various estimators developed in this article. Finally, a real data analysis is performed for illustration purposes.

1 Introduction

The log-logistic distribution (LLD) has probability density function (pdf) of the form

$$ f\left( {x;\,\alpha ,\,\lambda } \right)\, = \,\frac{{\alpha \,\lambda^{\alpha } \,x^{\alpha - 1} }}{{\left( {x^{\alpha } + \lambda^{\alpha } } \right)^{2} }},\,\,x > 0, $$

(1)

where, $\alpha > 0$ and $\lambda > 0$ are the shape and scale parameters, respectively. The survival and hazard functions, respectively, are given by

$$ S\left( {x;\,\alpha ,\,\lambda } \right)\, = \,\frac{{\lambda^{\alpha } }}{{\left( {x^{\alpha } + \lambda^{\alpha } } \right)}}\,,\,\,x > 0, $$

(2)

and

$$ h\left( {x;\,\alpha ,\,\lambda } \right)\, = \,\frac{{\alpha \,x^{\alpha - 1} }}{{\left( {x^{\alpha } + \lambda^{\alpha } } \right)}}\,,\,\,x > 0. $$

(3)

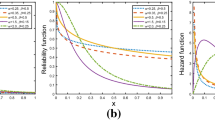
Figure 1 shows the plot of hazard function of LLD for different values of $\alpha$ with $\lambda = 1$. When $\alpha > 1$, the hazard increases from 0 to a peak at $x = \lambda \left( {\alpha - 1} \right)^{{{1 \mathord{\left/ {\vphantom {1 \alpha }} \right. \kern-0pt} \alpha }}}$ and then decreases, when $\alpha = 1$, the hazard starts from ${1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }$ and then decreases monotonically, when $\alpha < 1$, the hazard starts from infinity and then decreases. Thus, the LLD may be used to describe a first increasing and then decreasing hazard or monotonically decreasing hazard.

Fig. 1

Plot of the hazard function of LLD for different values of $\alpha$ with $\lambda = 1$

The LLD has been studied in literature by many authors like Shah and Dave (1963) wrote a note on log-logistic distribution, Kantam et al. (2001) considered acceptance sampling based on life tests using log-logistic model, Chen (2006) discussed the estimation of the shape parameter of LLD. Kuş and Kaya (2006) studied estimation of parameters of LLD based on progressive censoring. Kantam et al. (2006) discussed maximum likelihood estimation of the scale parameter when its shape parameter is known and reliability estimation for LLD. Abbas and Tang (2016) discussed objective Bayesian analysis for LLD. Al-Shomrani et al. (2016) studied LLD for survival data analysis using Markov Chain Monte Carlo (MCMC) methods. These studies suggest that LLD is a quite useful model in analyzing survival data.

In life testing experiments, the data are frequently censored. Censoring arises in a life testing experiment, when exact lifetimes are known only for a portion of test items and remainder of the lifetimes are known only to exceed certain values under a life test. There are several types of censoring schemes which are used in life testing experiments. In literature, the two most popular censoring schemes are conventional type I and type II censoring schemes. Recently, progressive and progressive first failure censoring have also been studied in detail in the literature. See for example, Kumar et al. (2015), Dube et al. (2016), Kumar et al. (2017). Another type of censoring called random censoring occurs when the item under study is lost or removed from the experiment before its failure.

Random censoring is a situation when an item under study is lost or removed randomly from the experiment before its failure. In other words, some subjects in the study have not experienced the event of interest at the end of the study. For example, in a clinical trial or a medical study, some patients may still be untreated and leave the course of treatment before its completion. In a social study, some subjects are lost for the follow-up in them idle of the survey. In reliability engineering, an electrical or electronic device such as bulb on test may break before its failure. In such cases, the exact survival time (or time to event of interest) of the subjects is unknown; therefore they are called randomly censored observations.

In this article, the classical and Bayesian estimation procedures in LLD under random censoring scheme are considered. Random censoring occurs when the subject under study is lost or removed from the experiment before its failure. Random censoring is an important censoring scheme in which the time of censoring is not fixed but taken as random. In survival analysis, we usually don’t have complete control on the experiment in hand, e.g. patients may enter a clinic for treatment from a certain disease at arbitrary points of time and leave before completion of treatment or die from a cause different from the one under consideration. As a result, the recorded survival times will include randomly censored data. Suppose failure times $X_{1} ,X_{2} , \ldots ,X_{n}$ are independent and identically distributed (iid) random variables with pdf $f_{X} \left( x \right),\,\,x > 0$ and survival function $S_{X} \left( x \right),\,x > 0\,.$ Associated with these failure times $T_{1} ,T_{2} , \ldots ,T_{n}$ are iid censoring times with pdf $f_{T} \left( t \right),\,\,t > 0$ and survival function $S_{T} \left( t \right),\,t > 0\,.$ Further, let $X_{i} 's$ and $T_{i} 's$ be mutually independent. We observe failure or censored time $Y_{i} = min\left( {X_{i} ,T_{i} } \right);\,\,\,i = 1,2, \ldots ,n,$ and the corresponding censor indicators $D_{i} = 1\,\,\left( 0 \right)$ if failure (censoring) occurs. This censoring scheme includes, as special cases, complete sample case when $T_{i} = \infty$ for all $i = 1,2, \ldots ,n,$ and Type I censoring when $T_{i} = t_{0}$ for all $i = 1,2, \ldots ,n,$ where, $t_{0}$ is the pre-fixed study period. Thus, the joint pdf of $Y$ and $D$ is given by

$$ f_{Y,D} \left( {y,d} \right) = \left\{ {f_{X} \left( y \right)S_{T} \left( y \right)} \right\}^{d} \left\{ {f_{T} \left( y \right)S_{X} \left( y \right)} \right\}^{1 - d} ;\,\,y > 0\,,\,\,d = 0,1 > 0\,. $$

(4)

The marginal distributions of $Y$ and $D$ are obtained as

$$ f_{Y} \left( y \right) = f_{X} \left( y \right)S_{T} \left( y \right) + f_{T} \left( y \right)S_{X} \left( y \right),\,\,y > 0\,, $$

$$ P\left[ {D = d} \right] = p^{d} \left( {1 - p} \right)^{1 - d} ,\,\,d = 0,1, respectively, $$

where, $p$ is the probability of observing a failure and is given by

$$ p = P\left[ {X \le T} \right] = \int\limits_{0}^{\infty } {S_{T} \left( y \right)f_{X} \left( y \right)dy} \,. $$

The statistical inference in different survival models under random censoring has been investigated by several authors like Gilbert (1962), Breslow and Crowley (1974), Koziol and Green (1976), Ghitany (2001), Saleem and Aslam (2009), Danish and Aslam (2013, 2014), Krishna et al. (2015), Garg et al. (2016), Ameraouia et al. (2016), Krishna and Goel (2017), etc. Now, let the failure time $X$ and censoring time $T$ follow $LLD\,\left( {\alpha ,\,\,\lambda } \right)$ and $LLD\,\left( {\alpha ,\,\theta } \right)$, respectively, the joint pdf of randomly censored variables $\left( {Y,\,D} \right)$ can be written as,

$$ f_{Y,D} \left( {y,d,\,\alpha ,\lambda ,\,\theta } \right) = \frac{{\alpha \lambda^{\alpha } \theta^{\alpha } y^{\alpha - 1} }}{{\left( {y^{\alpha } + \lambda^{\alpha } } \right)^{{\left( {1 + d} \right)}} \,\left( {y^{\alpha } + \theta^{\alpha } } \right)^{{\left( {2 - d} \right)}} }};\,\,y > 0\,,\,\,d = 0,1;\,\,\alpha ,\,\lambda ,\theta > 0. $$

(5)

and the probability of observing a failure is obtained as

$$ p = \alpha \lambda^{\alpha } \theta^{\alpha } \int\limits_{0}^{\infty } {\frac{{y^{\alpha - 1} }}{{\left( {y^{\alpha } + \theta^{\alpha } } \right)\left( {y^{\alpha } + \lambda^{\alpha } } \right)^{2} }}dy}. $$

The rest of the article is organized as follows: In Sect. 2, the maximum likelihood estimators, asymptotic confidence intervals and coverage probabilities of the unknown parameters are derived. Bayes estimators of the parameters using independent gamma priors under generalized entropy loss function are obtained in Sect. 3. For Bayesian computation, the Tierney–Kadaney’s and Gibbs sampling methods are considered. Also, the highest posterior density (HPD) credible intervals of the parameters are constructed. Sect. 4 deals with a Monte Carlo simulation study to compare the performance of the various estimation procedures developed in the previous sections. A real data example is provided for illustration purposes in Sect. 5. Finally, the concluding remarks on the article are appeared in Sect. 6.

2 Maximum likelihood estimation

In this section, we derive maximum likelihood estimators (MLEs) of the unknown parameters of LLD using randomly censored data. We also obtain asymptotic confidence intervals of the parameters based on observed Fisher information matrix. Let $\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{y} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{d} } \right) = \left( {y_{1} ,d_{1} } \right),\,\left( {y_{2} ,d_{2} } \right), \ldots ,\,\left( {y_{n} ,d_{n} } \right)$ be a randomly censored sample of size $n$ from model in (5), the likelihood function is given by

$$ L\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{y} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{d} ,\alpha ,\lambda ,\theta } \right) = \alpha^{n} \lambda^{n\alpha } \theta^{n\alpha } \prod\limits_{i = 1}^{n} {\frac{{y_{i}^{\alpha - 1} }}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{{\left( {1 + d_{i} } \right)}} \,\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{{\left( {2 - d_{i} } \right)}} }}} $$

(6)

Thus, the log-likelihood function becomes

$$ \begin{aligned} l\left( {\alpha ,\lambda ,\theta } \right) = n\ln \alpha + n\alpha \ln \lambda + n\alpha \ln \theta + \left( {\alpha - 1} \right)\sum\limits_{i = 1}^{n} {\ln y_{i} } \hfill \\ & \quad - \sum\limits_{i = 1}^{n} {\left( {1 + d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right) - \sum\limits_{i = 1}^{n} {\left( {2 - d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \theta^{\alpha } } \right) \hfill \\ \end{aligned} $$

(7)

On partially differentiating the log-likelihood function in (7) with respect to the parameters, we have following normal equations:

$$ \begin{aligned} \frac{{\partial l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \alpha } = \frac{n}{\alpha } + n\,\ln \lambda + n\,\ln \theta + \sum\limits_{i = 1}^{n} {\ln \,y_{i} } - \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)\,\left( {y_{i}^{\alpha } \ln y_{i} + \lambda^{\alpha } \ln \lambda } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)}}} - \hfill \\ \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)\,\left( {y_{i}^{\alpha } \ln y_{i} + \theta^{\alpha } \ln \theta } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)}}} = 0, \hfill \\ \end{aligned} $$

(8)

$$ \frac{{\partial l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \lambda } = \frac{n\alpha }{\lambda } - \alpha \lambda^{\alpha - 1} \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)}}} = 0, $$

(9)

$$ \frac{{\partial l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \theta } = \frac{n\alpha }{\theta } - \alpha \theta^{\alpha - 1} \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)}}} = 0\,. $$

(10)

The MLEs $\hat{\alpha }$, $\hat{\lambda }$ and $\hat{\theta }$ of the parameters $\alpha$, $\lambda$ and $\theta$, respectively, are the solutions of the non-linear Eqs. (8), (9) and (10). As theoretic solutions are not possible, we propose the use of a numerical iterative procedure such as Newton type method to solve Eqs. (8), (9) and (10). For the computation purpose, we have used a Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton method in this article.

2.1 Asymptotic confidence intervals

Since, the MLEs of the unknown parameters cannot be obtained in closed form, it is not easy to drive the exact distributions of the MLEs. Therefore, we obtain the asymptotic confidence intervals of the parameters based on observed Fisher information matrix. Let $\hat{\omega } = \left( {\hat{\alpha },\,\hat{\lambda },\,\hat{\theta }} \right)$ be the MLE of $\omega = \left( {\alpha ,\,\lambda ,\,\theta } \right)$. The observed Fisher information matrix is given by

$$ I\left( {\hat{\omega }} \right) = \left[ \begin{aligned} - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{{\partial \alpha^{2} }}\,\,\,\,\,\, - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{\partial \alpha \,\partial \lambda }\, - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{\partial \alpha \,\partial \theta } \hfill \\ - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{\partial \lambda \,\partial \alpha } - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{{\partial \lambda^{2} }}\,\, - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{\partial \lambda \,\partial \theta }\, \hfill \\ - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{\partial \theta \,\partial \alpha }\,\,\, - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{\partial \theta \,\partial \lambda } - \frac{{\partial^{2} l(\alpha ,\lambda ,\,\theta )}}{{\partial \theta^{2} \,}} \hfill \\ \end{aligned} \right]_{{\,\omega = \hat{\omega }}} $$

where,

$$ \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{{\partial \alpha^{2} }} = - \,\,\frac{n}{{\alpha^{2} }} - \lambda^{\alpha } \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)y_{i}^{\alpha } \,\left( {\ln y_{i} - \ln \lambda } \right)^{2} }}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{2} }}} - \theta^{\alpha } \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)y_{i}^{\alpha } \,\left( {\ln y_{i} - \ln \theta } \right)^{2} }}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{2} }}} , $$

$$ \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \alpha \,\partial \lambda } = \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \lambda \,\partial \alpha } = \frac{n}{\lambda } - \lambda^{\alpha - 1} \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)\left( {\alpha y_{i}^{\alpha } \left( {\ln \lambda - \ln y_{i} } \right) + y_{i}^{\alpha } + \lambda^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{2} }}} , $$

$$ \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \alpha \,\partial \theta } = \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \theta \,\partial \alpha } = \frac{n}{\theta } - \theta^{\alpha - 1} \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)\left( {\alpha y_{i}^{\alpha } \left( {\ln \theta - \ln y_{i} } \right) + y_{i}^{\alpha } + \theta^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{2} }}} , $$

$$ \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{{\partial \lambda^{2} }} = - \frac{n\alpha }{{\lambda^{2} }} - \alpha \lambda^{\alpha - 2} \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)\left( {\alpha y_{i}^{\alpha } - y_{i}^{\alpha } - \lambda^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{2} }}} , $$

$$ \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{{\partial \theta^{2} }} = - \frac{n\alpha }{{\theta^{2} }} - \alpha \theta^{\alpha - 2} \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)\left( {\alpha y_{i}^{\alpha } - y_{i}^{\alpha } - \theta^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{2} }}} , $$

$$ \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \lambda \,\partial \theta } = \frac{{\partial^{2} l\left( {\alpha ,\lambda ,\theta } \right)}}{\partial \theta \,\partial \lambda } = 0. $$

Thus, the observed variance–covariance matrix becomes $I^{ - 1} \left( {\hat{\omega }} \right)$. The asymptotic distribution of MLEs $\hat{\omega }$ is a trivariate normal distribution as $\hat{\omega } \sim N_{3} \left( {\omega ,\,I^{ - 1} \left( {\hat{\omega }} \right)} \right)$, see Lawless (2003). Consequently, two sided equal tail $100\left( {1 - \xi } \right)\%$ asymptotic confidence intervals for the parameters $\alpha ,$ $\lambda$ and $\theta$ are given by $\left( {\hat{\alpha } \pm z_{{\frac{\xi }{2}}} \sqrt {\hat{V}ar\left( {\hat{\alpha }} \right)} } \right)$, $\left( {\hat{\lambda } \pm z_{{\frac{\xi }{2}}} \sqrt {\hat{V}ar\left( {\hat{\lambda }} \right)} } \right)$ and $\left( {\hat{\theta } \pm z_{{\frac{\xi }{2}}} \sqrt {\hat{V}ar\left( {\hat{\theta }} \right)} } \right)$, respectively.

Here, $\hat{V}ar\left( {\hat{\alpha }} \right)$, $\hat{V}ar\left( {\hat{\lambda }} \right)$ and $\hat{V}ar\left( {\hat{\theta }} \right)$ are diagonal elements of the observed variance–covariance matrix $I^{ - 1} \left( {\hat{\omega }} \right)$ and $z_{{\frac{\xi }{2}}}$ is the upper $\left( {\frac{\xi }{2}} \right)^{th}$ percentile of the standard normal distribution. Also, the coverage probabilities (CPs) of the parameters are given by

$$ CP_{\alpha } = P\left[ {\left| {\frac{{\hat{\alpha } - \alpha }}{{\sqrt {\hat{V}ar\left( {\hat{\alpha }} \right)} }}} \right| \le z_{{\frac{\xi }{2}}} } \right],CP_{\lambda } = P\left[ {\left| {\frac{{\hat{\lambda } - \lambda }}{{\sqrt {\hat{V}ar\left( {\hat{\lambda }} \right)} }}} \right| \le z_{{\frac{\xi }{2}}} } \right]\,\,{\text{and}}\,\,CP_{\theta } = P\left[ {\left| {\frac{{\hat{\theta } - \theta }}{{\sqrt {\hat{V}ar\left( {\hat{\theta }} \right)} }}} \right| \le z_{{\frac{\xi }{2}}} } \right]\,\,. $$

3 Bayesian estimation

In this section, we discuss the Bayes estimators of the unknown parameters of the model in (5) under GELF using T–K approximation and MCMC methods. In order to select the best decision in decision theory, an appropriate loss function must be specified. The squared error loss function (SELF) is generally used for this purpose. The use of the SELF is well justified when over estimation and under estimation of equal magnitude has the same consequences. When the true loss is not symmetric with respect to over estimation and under estimation, asymmetric loss functions are used to represent the consequences of different errors. A general purpose loss function is GELF. The GELF was proposed by Calibria and Pulcini (1996). This loss function is a generalization of the entropy loss function and is given by

$$ L\left( {\theta ,\hat{\theta }} \right) \propto \left[ {\left( {\frac{{\hat{\theta }}}{\theta }} \right)^{q} - q\ln \left( {\frac{{\hat{\theta }}}{\theta }} \right) - 1} \right];\,\,\,\,\,\,\,\,q \ne 0, $$

where, $\hat{\theta }$ is the decision rule which estimates $\theta$. For $q > 0,$ a positive error has a more serious effect than a negative error and for $q < 0$, a negative error has a more serious effect than a positive error. Under GELF the Bayes estimator is given by

$$ \hat{\theta } = \left[ {E\left( {\left. {\theta^{ - q} } \right|data} \right)} \right]^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} . $$

(11)

It is important to note that for q = −1, 1, −2, the Bayes estimator given in (11) simplifies to the Bayes estimator under SELF, entropy loss function (ELF) and precautionary loss function (PLF), respectively. According to Arnold and Press (1983), there is no clear cut way how to choose prior. Now, we assume the following piecewise independent gamma priors for the parameters $\alpha ,\,\,\lambda \,\,{\text{and}}\,\,\theta$ as

$$ g_{1} \left( \alpha \right) \propto \alpha^{{a_{1} - 1}} \text{e}^{{ - b_{1} \alpha }} ,\,\,\alpha > 0,\,\,a_{1} ,\,b_{1} > 0, $$

$$ g_{2} \left( \lambda \right) \propto \lambda^{{a_{2} - 1}} \text{e}^{{ - b_{2} \lambda }} ,\,\,\lambda > 0,\,\,a_{2} ,\,b_{2} > 0, $$

and $g_{3} \left( \theta \right) \propto \theta^{{a_{3} - 1}} \text{e}^{{ - b_{3} \theta }} ,\,\,\theta > 0,\,\,a_{3} ,\,b_{3} > 0$, respectively.

Thus, the joint prior distribution of $\alpha ,\,\,\lambda \,\,{\text{and}}\,\,\theta$ can be written as

$$ g\left( {\alpha ,\lambda ,\theta } \right) \propto \alpha^{{a_{1} - 1}} \text{e}^{{ - b_{1} \alpha }} \lambda^{{a_{2} - 1}} \text{e}^{{ - b_{2} \lambda }} \theta^{{a_{3} - 1}} \text{e}^{{ - b_{3} \theta }} . $$

(12)

The assumption of independent gamma priors is reasonable. The class of the gamma prior distributions is quite flexible as it can model a variety of prior information. It is noted here that the non-informative priors on the shape and scale parameters are the special cases of independent gamma priors and can be achieved by approaching hyper-parameters to zero.

Now, using likelihood function in (6) and the joint prior distribution in (12), the joint posterior distribution of the parameters $\alpha ,$ $\lambda$ and $\theta$ is given by

$$ \begin{aligned} \pi \left( {\alpha ,\lambda ,\theta \left| {data} \right.} \right) \propto \alpha^{{n + a_{1} - 1}} \,\lambda^{{n\alpha + a_{2} - 1}} \,\theta^{{n\alpha + a_{3} - 1}} \,e^{{ - \alpha \left( {b_{1} - \sum\limits_{i = 1}^{n} {\ln y_{i} } } \right)}} \hfill \\ e^{{ - \sum\limits_{i = 1}^{n} {\left( {1 + d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)}} e^{{ - \sum\limits_{i = 1}^{n} {\left( {2 - d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)}} e^{{ - \left( {b_{2} \lambda + b_{3} \theta } \right)}} \hfill \\ \end{aligned} $$

(13)

Therefore, the posterior mean of $\phi \left( {\alpha ,\,\lambda ,\,\,\theta } \right)$, a function of $\alpha ,\,\,\lambda \,\,{\text{and}}\,\,\theta$ is given by

$$ E\left[ {\phi \left( {\alpha ,\,\lambda ,\,\theta } \right)|data} \right] = \frac{{\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\phi \left( {\alpha ,\,\lambda ,\,\theta } \right)L\left( {data|\alpha ,\,\lambda ,\,\theta } \right)g\left( {\alpha ,\,\lambda ,\,\theta } \right)d\alpha \,} } } d\lambda \,d\theta }}{{\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {L\left( {data|\alpha ,\,\lambda ,\,\theta } \right)g\left( {\alpha ,\,\lambda ,\,\theta } \right)d\alpha d\lambda d\theta } } } }} $$

(14)

The closed form solution of the ratio of integrals in Eq. (14) is not possible. Here, we use two different methods to get approximate solution of Eq. (14) namely, T–K approximation and MCMC methods.

3.1 Tierney–Kadane’s approximation Method

Tierney and Kadane (1986) proposed a method to approximate the posterior mean. According to this method the approximation of the posterior mean of $\phi \left( {\alpha ,\,\,\lambda ,\,\,\theta } \right)$ is given by

$$ E\left[ {\phi \left( {\alpha ,\lambda ,\theta } \right)|data} \right] = \frac{{\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {e^{{n\,\delta_{\phi }^{*} \left( {\alpha ,\lambda ,\theta } \right)}} d\alpha \,d\lambda \,d\theta } } } }}{{\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {e^{{n\,\delta \left( {\alpha ,\lambda ,\theta } \right)}} d\alpha \,d\lambda \,d\theta } } } }} \simeq \sqrt {\frac{{\left| {\sum_{\phi }^{*} } \right|}}{\left| \sum \right|}} \,e^{{n\left[ {\delta_{\phi }^{*} \left( {\hat{\alpha }_{{\delta^{*} }} ,\hat{\lambda }_{{\delta^{*} }} ,\hat{\theta }_{{\delta^{*} }} } \right) - \delta \left( {\hat{\alpha }_{\delta } ,\hat{\lambda }_{\delta } ,\hat{\theta }_{\delta } } \right)} \right]}} \,\,, $$

(15)

where, $\delta \left( {\alpha ,\lambda ,\theta } \right) = \frac{1}{n}\left[ {l\left( {\alpha ,\lambda ,\theta } \right) + \rho \left( {\alpha ,\lambda ,\theta } \right)} \right],$ and $\delta^{*} \left( {\alpha ,\lambda ,\theta } \right) = \delta \left( {\alpha ,\lambda ,\theta } \right)\, + \frac{1}{n}\ln \phi \left( {\alpha ,\lambda ,\theta } \right)\,\,,$ here, $l\left( {\alpha ,\lambda ,\theta } \right)$ is the log-likelihood function and $\rho \left( {\alpha ,\lambda ,\theta } \right) = \ln g\left( {\alpha ,\lambda ,\theta } \right)$. Also, $\left| {\sum_{\phi }^{*} } \right|$ and $\left| \sum \right|$ are the determinants of inverse of negative hessians of $\delta_{\phi }^{*} \left( {\alpha ,\lambda ,\theta } \right)$ and $\delta \left( {\alpha ,\lambda ,\theta } \right)$ at $\left( {\hat{\alpha }_{{\delta^{*} }} ,\hat{\lambda }_{{\delta^{*} }} ,\hat{\theta }_{{\delta^{*} }} } \right)$ and $\left( {\hat{\alpha }_{\delta } ,\hat{\lambda }_{\delta } ,\hat{\theta }_{\delta } } \right)$, respectively. $\left( {\hat{\alpha }_{\delta } ,\hat{\lambda }_{\delta } ,\hat{\theta }_{\delta } } \right)$ and $\left( {\hat{\alpha }_{{\delta^{*} }} ,\hat{\lambda }_{{\delta^{*} }} ,\hat{\theta }_{{\delta^{*} }} } \right)$ maximize $\delta \left( {\alpha ,\lambda ,\theta } \right)$ and $\delta^{*} \left( {\alpha ,\lambda ,\theta } \right)$, respectively. Next, we observe that

$$ \begin{aligned} \delta \left( {\alpha ,\lambda ,\theta } \right) = \frac{1}{n}\left[ {\left( {n + a_{1} - 1} \right)\ln \alpha + \left( {n\,\alpha + a_{2} - 1} \right)\ln \lambda + \left( {n\,\alpha + a_{3} - 1} \right)\ln \theta - \left( {\alpha - 1} \right)\sum\limits_{i = 1}^{n} {\ln y_{i} } } \right. \hfill \\ & \left. { - \sum\limits_{i = 1}^{n} {\left( {1 + d_{i} } \right)\ln \left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right) - } \sum\limits_{i = 1}^{n} {\left( {2 - d_{i} } \right)\ln \left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)} - b_{1} \alpha - b_{2} \lambda - b_{3} \theta } \right]\,\,. \hfill \\ \end{aligned} $$

Then, $\left( {\hat{\alpha }_{\delta } ,\hat{\lambda }_{\delta } ,\hat{\theta }_{\delta } } \right)$ are computed by solving the following non-linear equations

$$\begin{aligned} \frac{\partial \delta }{\partial \alpha } = \frac{{\left( {n + a_{1} - 1} \right)}}{\alpha } + n\ln \lambda + n\ln \theta + \sum\limits_{i = 1}^{n} {\ln y_{i} } \quad - \lambda \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)\left( {y_{i}^{\alpha } \ln y_{i} + \lambda^{\alpha } \ln \lambda } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)}}} \hfill \\ - \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)\left( {y_{i}^{\alpha } \ln y_{i} + \theta^{\alpha } \ln \theta } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)}}} - b_{1} = 0, \hfill \\ \end{aligned}$$

$$\frac{\partial \delta }{\partial \lambda } = \frac{{\left( {n\,\alpha + a_{2} - 1} \right)}}{\lambda } - \alpha \lambda^{\alpha - 1} \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)}}} - b_{2} = 0,$$

$$\frac{\partial \delta }{\partial \theta } = \frac{{\left( {n\,\alpha + a_{3} - 1} \right)}}{\theta } - \alpha \,\theta^{\alpha - 1} \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)}}} - b_{3} = 0.$$

Now, obtain $\left| \sum \right|$ from

$$\sum\nolimits^{ - 1} = \frac{1}{n}\left( {\begin{array}{*{20}c} {\delta_{\alpha \alpha } } & {\delta_{\alpha \lambda } } & {\delta_{\alpha \theta } } \\ {\delta_{\lambda \alpha } } & {\delta_{\lambda \lambda } } & {\delta_{\lambda \theta } } \\ {\delta_{\theta \alpha } } & {\delta_{\theta \lambda } } & {\delta_{\theta \theta } } \\ \end{array} } \right),$$

where,

$$ \delta_{\alpha \alpha } = - \frac{{\partial^{{^{2} }} \delta }}{{\partial \alpha^{2} }} = \,\,\frac{{\left( {n + a_{1} - 1} \right)}}{{\alpha^{2} }} + \lambda^{\alpha } \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)y_{i}^{\alpha } \,\left( {\ln y_{i} - \ln \lambda } \right)^{2} }}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{2} }}} + \theta^{\alpha } \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)y_{i}^{\alpha } \,\left( {\ln y_{i} - \ln \theta } \right)^{2} }}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{2} }}} , $$

$$ \delta_{\alpha \lambda } = \delta_{\lambda \alpha } = - \frac{{\partial^{{^{2} }} \delta }}{\partial \alpha \partial \lambda } = - \frac{n}{\lambda } + \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)\lambda^{\alpha - 1} \left( {\alpha y_{i}^{\alpha } \left( {\ln \lambda - \ln y_{i} } \right) + y_{i}^{\alpha } + \lambda^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{2} }}}, $$

$$ \delta_{\alpha \theta } = \delta_{\theta \alpha } = - \frac{{\partial^{{^{2} }} \delta }}{\partial \alpha \partial \theta } = - \frac{n}{\theta } + \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)\theta^{\alpha - 1} \left( {\alpha y_{i}^{\alpha } \left( {\ln \theta - \ln y_{i} } \right) + y_{i}^{\alpha } + \theta^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{2} }}} , $$

$$\delta_{\lambda \lambda } = - \frac{{\partial^{2} \delta }}{{\partial \lambda^{2} }} = \frac{{\left( {n\,\alpha + a_{2} - 1} \right)}}{{\lambda^{2} }} + \alpha \lambda^{\alpha - 2} \sum\limits_{i = 1}^{n} {\frac{{\left( {1 + d_{i} } \right)\left( {\alpha y_{i}^{\alpha } - y_{i}^{\alpha } - \lambda^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)^{2} }}},$$

$$ \delta_{\theta \theta } = - \frac{{\partial^{2} \delta }}{{\partial \theta^{2} }} = \frac{{\left( {n\,\alpha + a_{3} - 1} \right)}}{{\theta^{2} }} + \alpha \theta^{\alpha - 2} \sum\limits_{i = 1}^{n} {\frac{{\left( {2 - d_{i} } \right)\left( {\alpha y_{i}^{\alpha } - y_{i}^{\alpha } - \theta^{\alpha } } \right)}}{{\left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)^{2} }}}, $$

$$ \delta_{\lambda \theta } = \delta_{\theta \lambda } = - \frac{{\partial^{2} \delta }}{\partial \lambda \,\partial \theta } = 0. $$

In order to compute the Bayes estimator of $\alpha$ we take $\phi (\alpha ,\lambda ,\theta ) = \alpha^{ - q}$ and consequently $\delta_{\phi }^{*} \left( {\alpha ,\lambda ,\theta } \right)$ becomes

$$ \delta_{\alpha }^{*} \left( {\alpha ,\lambda ,\theta } \right) = \delta \left( {\alpha ,\lambda ,\theta } \right) - \frac{q}{n}\ln \alpha. $$

and then $\left( {\hat{\alpha }_{{\delta^{*} }} ,\,\,\hat{\lambda }_{{\delta^{*} }} ,\,\,\hat{\theta }_{{\delta^{*} }} } \right)$ are obtained as solutions of the following non-linear equations:

$$ \frac{{\partial \delta_{\alpha }^{*} }}{\partial \alpha } = \frac{\partial \delta }{\partial \alpha } - \frac{q}{n\alpha } = 0\,,\;\frac{{\partial \delta_{\alpha }^{*} }}{\partial \lambda } = \frac{\partial \delta }{\partial \lambda } = 0\,,\;\frac{{\partial \delta_{\alpha }^{*} }}{\partial \theta } = \frac{\partial \delta }{\partial \theta } = 0\,, $$

and obtain $\left| {\sum_{\alpha }^{*} } \right|$ from $\sum_{\alpha }^{* - 1} = \frac{1}{n}\left( {\begin{array}{*{20}c} {\delta_{\alpha \alpha }^{*} } & {\delta_{\alpha \lambda }^{*} } & {\delta_{\alpha \theta }^{*} } \\ {\delta_{\lambda \alpha }^{*} } & {\delta_{\lambda \lambda }^{*} } & {\delta_{\lambda \theta }^{*} } \\ {\delta_{\theta \alpha }^{*} } & {\delta_{\theta \lambda }^{*} } & {\delta_{\theta \theta }^{*} } \\ \end{array} } \right),$ where, $\delta_{\alpha \alpha }^{*} = - \frac{{\partial^{{^{2} }} \delta_{\alpha }^{*} }}{{\partial \alpha^{2} }} = - \frac{{\partial^{{^{2} }} \delta }}{{\partial \alpha^{2} }} - \frac{q}{{\alpha^{2} }},\,\delta_{\alpha \lambda }^{*} = \delta_{\alpha \lambda }^{{}} ,\delta_{\alpha \theta }^{*} = \delta_{\alpha \theta }^{{}} ,\;\delta_{\lambda \alpha }^{*} = \delta_{\lambda \alpha }^{{}} ,\;\delta_{\lambda \lambda }^{*} = \delta_{\lambda \lambda }^{{}} ,\;\delta_{\lambda \theta }^{*} = \delta_{\lambda \theta }^{{}} ,\;\delta_{\theta \alpha }^{*} = \delta_{\theta \alpha }^{{}} ,\;\delta_{\theta \lambda }^{*} = \delta_{\theta \lambda }^{{}} ,\;\delta_{\theta \theta }^{*} = \delta_{\theta \theta }^{{}}.$ Thus, the approximate Bayes estimator of $\alpha$ under GELF is given by

$$ \hat{\alpha }_{TK} = \left[ {\left. {\sqrt {\frac{{\left| {\sum_{\alpha }^{*} } \right|}}{\left| \sum \right|}} \,e^{{n\left[ {\delta_{\alpha }^{*} \left( {\hat{\alpha }_{{\delta^{*} }} ,\hat{\beta }_{{\delta^{*} }} ,\hat{\lambda }_{{\delta^{*} }} } \right) - \delta \left( {\hat{\alpha }_{\delta } ,\hat{\beta }_{\delta } ,\hat{\lambda }_{\delta } } \right)} \right]}} } \right]^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right. $$

Similarly, we can derive the approximate Bayes estimators of $\lambda \,\,\,{\text{and}}\,\,\theta$ as

$$ \hat{\lambda }_{TK} = \left[ {\left. {\sqrt {\frac{{\left| {\sum_{\lambda }^{*} } \right|}}{\left| \sum \right|}} \,e^{{n\left[ {\delta_{\lambda }^{*} \left( {\hat{\alpha }_{{\delta^{*} }} ,\hat{\beta }_{{\delta^{*} }} ,\hat{\lambda }_{{\delta^{*} }} } \right) - \delta \left( {\hat{\alpha }_{\delta } ,\hat{\beta }_{\delta } ,\hat{\lambda }_{\delta } } \right)} \right]}} } \right]} \right.^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} \,\,, $$

and $\hat{\theta }_{TK} = \left[ {\left. {\sqrt {\frac{{\left| {\sum_{\theta }^{*} } \right|}}{\left| \sum \right|}} \,e^{{n\left[ {\delta_{\theta }^{*} \left( {\hat{\alpha }_{{\delta^{*} }} ,\hat{\beta }_{{\delta^{*} }} ,\hat{\lambda }_{{\delta^{*} }} } \right) - \delta \left( {\hat{\alpha }_{\delta } ,\hat{\beta }_{\delta } ,\hat{\lambda }_{\delta } } \right)} \right]}} } \right]} \right.^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}$, respectively.

3.2 MCMC method

Here, we propose the use of MCMC method to draw sequences of samples from the full conditional distributions of the parameters, see Robert and Casella (2004). The Gibbs sampling method is a special case of MCMC method. The Gibbs sampler can be efficient when the full conditional distributions are easy to sample from, see Roberts and Smith (1993). The Metropolis–Hastings (M–H) algorithm can be used to obtain random samples from any arbitrarily complicated target distribution of any dimension that is known up to a normalizing constant. It was first developed by Metropolis et al. (1953) and later extended by Hastings (1970). For implementing the Gibbs algorithm, the full conditional posterior densities of the parameters $\alpha ,\,\,\lambda \,\,{\text{and}}\,\,\theta$ are given by

$$ \pi_{1} \left( {\lambda \left| {\alpha ,} \right.data} \right) = \lambda^{{n\alpha + a_{2} - 1}} e^{{ - \left( {b_{2} \lambda + \sum\limits_{i = 1}^{n} {\left( {1 + d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)} \right)}} $$

(16)

$$ \pi_{2} \left( {\left. \theta \right|\alpha ,data} \right) = \lambda^{{n\alpha + a_{3} - 1}} e^{{ - \left( {b_{3} \theta + \sum\limits_{i = 1}^{n} {\left( {2 - d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)} \right)}} $$

(17)

$$ \pi_{3} \left( {\left. \alpha \right|\beta ,\lambda ,data} \right) = \alpha^{{n + a_{1} - 1}} e^{{ - \alpha \left( {b_{1} - n\ln \lambda - n\ln \theta - \sum\limits_{i = 1}^{n} {\ln y_{i} } } \right)}} e^{{ - \sum\limits_{i = 1}^{n} {\left( {1 + d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \lambda^{\alpha } } \right)}} e^{{ - \sum\limits_{i = 1}^{n} {\left( {2 - d_{i} } \right)} \ln \left( {y_{i}^{\alpha } + \theta^{\alpha } } \right)}} $$

(18)

The posterior conditional distributions of $\alpha ,\,\,\lambda \,\,{\text{and}}\,\,\theta$ are not in well known form and therefore random numbers from these distributions can be generated by using M–H algorithm. Here, we consider multivariate normal distribution as proposal density. Therefore, the MCMC method has following steps for sample generation process:

Step 1

Start with an initial guess $\left( {\alpha^{\left( 0 \right)} ,\,\,\lambda^{\left( 0 \right)} ,\,\,\theta^{\left( 0 \right)} } \right).$

Step 2

Set $j = 1.$

Step 3

Using M–H algorithm, generate $\lambda^{\left( j \right)}$ from $\pi_{1} \left( {\lambda \left| {\alpha^{{\left( {j - 1} \right)}} ,\,\,} \right. data} \right)$.

Step 4

Using M–H algorithm, generate $\theta^{\left( j \right)}$ from $\pi_{2} \left( {\left. \theta \right|\alpha^{{\left( {j - 1} \right)}} ,\,\,data} \right)$.

Step 5

Using M–H algorithm, generate $\alpha^{\left( j \right)}$ from $\pi_{3} \left( {\left. \alpha \right|\beta^{{\left( {j - 1} \right)}} ,\lambda^{{\left( {j - 1} \right)}} ,\,\,data} \right)$.

Step 6

Set $j = j + 1.$

Step 7

Repeat steps 3-6, $M$ times and obtain MCMC sample as $\left( {\alpha^{\left( 1 \right)} ,\,\,\lambda^{\left( 1 \right)} ,\,\,\theta^{\left( 1 \right)} } \right),$ $\left( {\alpha^{\left( 2 \right)} ,\,\,\lambda^{\left( 2 \right)} ,\,\,\theta^{\left( 2 \right)} } \right), \ldots ,\;\left( {\alpha^{\left( M \right)} ,\,\,\lambda^{\left( M \right)} ,\,\,\theta^{\left( M \right)} } \right).$

Now, the Bayes estimates of $\alpha ,\,\,\lambda \,\,{\text{and}}\,\,\theta$ under GELF using MCMC method are, respectively, obtained as

$$ \begin{aligned} \hat{\alpha }_{MCMC} = \left[ {\frac{1}{{\left( {M - M_{0} } \right)}}\sum\limits_{{j = M_{0} + 1}}^{M} {\left( {\alpha^{\left( j \right)} } \right)^{ - q} } } \right]^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\;\hat{\lambda }_{MCMC} = \left[ {\frac{1}{{\left( {M - M_{0} } \right)}}\sum\limits_{{j = M_{0} + 1}}^{M} {\left( {\lambda^{\left( j \right)} } \right)^{ - q} } } \right]^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} \;{\text{and}} \hfill \\ \hat{\theta }_{MCMC} = \left[ {\frac{1}{{\left( {M - M_{0} } \right)}}\sum\limits_{{j = M_{0} + 1}}^{M} {\left( {\theta^{\left( j \right)} } \right)^{ - q} } } \right]^{{ - {1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} \,. \hfill \\ \end{aligned} $$

where, $M_{0}$ is the burn-in-period.

3.3 HPD credible intervals

Once we have desired posterior MCMC sample, the HPD credible interval for the parameter $\alpha$ can be constructed by using the algorithm proposed by Chen and Shao (1999). Let $\alpha_{\left( 1 \right)} < \alpha_{\left( 2 \right)} < \ldots < \alpha_{{\left( {M - M_{0} } \right)}}$ denote the ordered values of $\alpha^{{\left( {M_{0} + 1} \right)}} ,\alpha^{{\left( {M_{0} + 2} \right)}} , \ldots ,\alpha^{\left( M \right)}$, the $100 \times \left( {1 - \xi } \right)\% ,$ $0 < \xi < 1$, HPD credible interval for $\alpha$ is given by

$\left( {\alpha_{\left( j \right)} ,\alpha_{{\left( {j + \left[ {\left( {1 - \xi } \right)\left( {M - M_{0} } \right)} \right]} \right)}} } \right)$, where, $j$ is chosen such that

$$ \alpha_{{\left( {j + \left[ {\left( {1 - \xi } \right)\left( {M - M_{0} } \right)} \right]} \right)}} - \alpha_{\left( j \right)} = \mathop {\hbox{min} }\limits_{{1 \le i \le \xi \left( {M - M_{0} } \right)}} \left( {\alpha_{{\left( {i + \left[ {\left( {1 - \xi } \right)\left( {M - M_{0} } \right)} \right]} \right)}} - \alpha_{\left( i \right)} } \right),\,\,\,j = 1,2, \ldots ,\left( {M - M_{0} } \right), $$

here, $\left[ x \right]$ is the largest integer less than or equal to $x$. Similarly, we can construct the HPD credible intervals for the parameters $\lambda \,\,{\text{and}}\,\,\theta \,,$ respectively.

4 Monte Carlo simulation study

Here, a Monte Carlo simulation study is performed to compare various estimators developed in the previous sections. All the computations are performed using statistical software R. Five different sample sizes n = 25, 30, 40, 50 and 60 are considered in these simulations. Following combinations of the true values of the parameters $\left( {\alpha ,\,\,\lambda ,\,\,\theta } \right) = \left( {1.5,\,1,\,0.5} \right)$ and $\left( {1.5,\,0.5,\,1} \right)$ are taken so that the probability of failure become $0.3327$ and $0.6673$, respectively. In each case the ML and Bayes estimates of the unknown parameters are computed. For Bayesian estimators, TK approximation and MCMC methods are used. For Bayesian estimation, informative gamma priors under GELF with hyper-parameters $\left( {a_{1} ,\,\,b_{1} ,\,\,a_{2} ,\,\,b_{2} ,\,\,a_{3} ,\,\,b_{3} } \right) = \left( {3,\,\,2,\,2,\,2,\,\,2,\,4} \right)\,\,{\text{and}}\,\,\left( {3,\,2,\,2,\,4,\,2,\,2} \right)$ are used so that prior means are exactly equal to the true values of the parameters. All Bayes estimates of the unknown parameters are evaluated against three different values of $q = - 1,\,\,1,\,\, - 2$ in (11) so that Bayes estimates are computed under three different loss functions SELF, ELF and PLF, respectively. For MCMC method $M = 10,000$ with burn-in-period $M_{0} = 1,000$ is used. The $95\%$ asymptotic confidence intervals based on observed Fisher information matrix and HPD credible intervals based on MCMC method are computed. The whole process is simulated 1000 times and the average estimates (AE) and the corresponding mean squared error (MSE) are computed for different estimators. Also, the average length and the coverage probabilities of $95\%$ intervals are calculated. The results of the Monte Carlo simulation study are summarized in Tables 1, 2, 3, 4, 5, 6, 7, 8. From these results the following conclusions are made:

Table 1 Average estimate and MSE (in parenthesis) for $\alpha$ when $\alpha = 1.5,\,\,\lambda = 1,\,\,\theta = 0.5,\,p = 0.3327$

Table 2 Average estimate and MSE (in parenthesis) for $\lambda$ when $\alpha = 1.5,\,\,\lambda = 1,\,\,\theta = 0.5,\,p = 0.3327$

Table 3 Average estimate and MSE (in parenthesis) for $\theta$ when $\alpha = 1.5,\,\,\lambda = 1,\,\,\theta = 0.5$, $p = 0.3327$

Table 4 Average length and coverage probability (in parenthesis) of 95% asymptotic confidence and HPD credible intervals for $\alpha ,$ $\lambda$ and $\theta$ when $\alpha = 1.5,\,\,\lambda = 1,\,\,\theta = 0.5,\,p = 0.3327$

Table 5 Average estimate and MSE (in parenthesis) for $\alpha$ when $\alpha = 1.5,\,\,\lambda = 0.5,\,\,\theta = 1,\,\,p = 0.6673$

Table 6 Average estimate and MSE (in parenthesis) for $\lambda$ when $\alpha = 1.5,\,\,\lambda = 0.5,\,\,\theta = 1,\,\,p = 0.6673$

Table 7 Average estimate and MSE (in parenthesis) for $\theta$ when $\alpha = 1.5,\,\,\lambda = 0.5,\,\,\theta = 1,\,\,p = 0.6673$

Table 8 Average length and coverage probability (in parenthesis) of 95% asymptotic confidence and HPD credible intervals for $\alpha ,$ $\lambda$ and $\theta$ when $\alpha = 1.5,\,\,\lambda = 0.5,\,\,\theta = 1,\,\,p = 0.6673$

In general, as the sample size increases the bias, MSE of estimators and the average length of intervals decrease. In case of maximum likelihood estimation, as the value of the probability of failure increases, values of MSE and the bias decrease. The coverage probabilities attain their prescribed confidence levels in almost all cases. Bayes estimates are better than MLEs in terms of bias, MSE and average length as they include prior information. On average the HPD credible intervals are the shorter than the asymptotic confidence intervals. In case of Bayes estimation, TK approximation method is better than MCMC method in respect of both bias as well as MSE. In addition, the Bayes estimates obtained under entropy loss function perform quite better compared to other estimates for all cases. The coverage probabilities attain their prescribed nominal level in all cases.

Thus, we recommend the Bayes estimators when some prior information about parameters is available or using non-informative priors. In other cases ML estimators may be used for quick results.

5 Real data analysis

Here, we consider leukemia patients data set to demonstrate the usefulness of LLD in survival analysis. This data set consists remission times (in weeks) of a group of 30 patients with leukemia who received a similar treatment and has been taken from Lawless (2003, p. 139).

1, 1, 2, 4, 4, 6, 6, 6, 7, 8, 9, 9, 10, 12, 13, 14, 18, 19, 24, 26, 29, 31 + , 42, 45 + , 50 + , 57, 60, 71 + , 85 + , 91. The + sign denotes the censoring times.

We first use the scaled total time on test (TTT) transform of failure times to detect the shape of the hazard function, see, Mudholkar et al. (1996). The scaled TTT transform is given by $\phi \left( {{v \mathord{\left/ {\vphantom {v n}} \right. \kern-0pt} n}} \right) = {{\left[ {\sum\limits_{i = 1}^{v} {T_{\left( i \right)} } + \left( {n - v} \right)T_{\left( v \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{i = 1}^{v} {T_{\left( i \right)} } + \left( {n - v} \right)T_{\left( v \right)} } \right]} {\left( {\sum\limits_{i = 1}^{n} {T_{\left( i \right)} } } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{i = 1}^{n} {T_{\left( i \right)} } } \right)}}$, where, $T_{\left( i \right)} ,\,i = 1,2, \ldots ,\,n$ represent the $ith$ order statistic of the sample, and $v = 1,2, \ldots ,\,n$. The hazard function is increasing, decreasing and unimodal if the plot of $\left( {{v \mathord{\left/ {\vphantom {v n}} \right. \kern-0pt} n},\,\,\phi \left( {{v \mathord{\left/ {\vphantom {v n}} \right. \kern-0pt} n}} \right)} \right)$ is concave, convex, and concave followed by convex, respectively. The scaled TTT plot for leukemia patients data is shown in Fig. 2. This figure suggests a unimodal hazard shape of the leukemia patients data.

Fig. 2

Scaled TTT plot for leukemia patients data

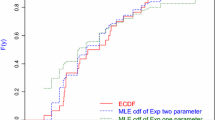
Now, we compare fitted LLD with some other well known survival distributions, namely, exponential, gamma, and Weibull for leukemia patients data. MLEs of the parameters of these distributions are obtained. These estimates, along with the data, are used to calculate the negative log likelihood function −lnL, the Akaike information criterion $\left( {AIC = 2 \times k - 2 \times {\text{lnL}}} \right)\,$, proposed by Akaike (1974) and Bayesian information criterion $\left( {BIC = k \times \ln (n) - 2 \times {\text{lnL}}} \right)$ proposed by Schwarz (1978), where k is the number of parameters in the reliability model, n is the number of observations in the given data set, L is the maximized value of the likelihood function for the estimated model and Kolmogorov–Smirnov (K–S) statistic with its p value. The best distribution corresponds to the lowest –lnL, AIC, BIC and K–S statistic and the highest p values. These −lnL, AIC, BIC and K–S statistics with p values are listed in Table 9. They indicate that LLD is the best choice among the competing distributions.

Table 9 Goodness-of-fit tests for the leukemia patients data

Also, we consider the Kaplan–Meier (KM) product limit estimator proposed by Kaplan and Meier (1958) for fitting the randomly censored data through the graphs. The KM estimator for the randomly censored data is given by

$$ \hat{S}\left( t \right) = \prod\limits_{{y_{i} \le t}}^{{}} {\left( {1 - \frac{1}{{n_{i} }}} \right)^{{d_{i} }} } , $$

where, $n_{i}$ = Number of items alive at time $y_{i}$ and $d_{i} = \left\{ \begin{array}{ll} 1\,\,\,\,\,\,{\text{if}}\,{\text{item}}\,{\text{failed/uncensored}} \hfill \\ 0\,\,\,\,\,\,{\text{if}}\,{\text{item}}\,{\text{is}}\,{\text{censored}} \hfill \\ \end{array} \right..$

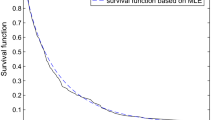
The graph of the KM estimator along with the estimates of survival functions for randomly censored exponential, gamma, Weibull and LL distributions are given in Fig. 3. From Fig. 3 we observe that the estimate of survival function for LLD is quite close to that proposed by K–M estimator. Thus, the KM estimator also supports the choice of LLD to represent the leukemia patients data.

Fig. 3

Estimates of survival functions of different competing survival models for leukemia patients data

Now, we obtain the ML and Bayes estimates of the unknown parameters of randomly censored LLD. The Bayes estimates are computed using non-informative priors under GELF as we do not have prior information about the parameters. The non-informative priors are obtained by taking hyper-parameters $a_{1} = b_{1} = a_{2} = b_{2} = a_{3} = b_{3} = 0$ in (12). The Bayes estimates of parameters are computed using T–K’s approximation and MCMC methods. For MCMC method, we use $M = 10,000$ with a burn-in period $M_{0} = 2,000$. Also, we check the convergence of generated samples of $\alpha$, $\lambda$ and $\theta$ for their stationary distributions using graphical diagnostic tools like trace plots, ACF plots and histograms. Figure 4 shows the trace plots, ACF plots and histograms with kernel density estimates for the parameters. The trace plots of the generated chains indicate a random scatter about the mean value (represented by solid line) and show the convergence of the chains for all parameters. ACF plots clearly show that chains are not at all autocorrelated, so the generated samples may be considered as independent samples from the target posterior distributions. The histograms with Gaussian kernel densities show that all the conditional marginal distributions of the parameters have almost symmetrical and unimodal figures. The vertical lines represent the mean values of the chains.

Fig. 4

The trace, ACF and histogram with Gaussian kernel density plots of the generated chains for the parameters

The ML, Bayes estimates and the 95% asymptotic confidence and HPD credible intervals of the parameters are presented in Table 10. Results of Table 10 indicate that the ML and Bayes estimates of parameters based on MCMC method under PLF are quite similar while based on other methods are quite different from each other. Also, it is interesting to observe that the HPD credible intervals obtained by using non-informative priors are smaller than the asymptotic confidence intervals for all the parameters.

Table 10 The ML and the Bayes estimates of the parameters using Tierney–Kadane’s (TK) and Gibbs sampling (GS) methods and the associated 95% asymptotic confidence and HPD credible intervals corresponding to the leukemia patients data

6 Concluding remarks

In this article we considered the classical and Bayesian estimation procedures in log-logistic distribution under random censoring. The maximum likelihood estimators and the asymptotic confidence intervals based on observed Fisher information matrix of the unknown parameters were derived. The Bayes estimates of the parameters under generalized entropy loss function were obtained using TK approximation and MCMC methods. The performance of these estimators was examined by a Monte Carlo simulation study, which indicated that MLEs can be obtained easily and quickly with satisfactory estimates. For more efficient estimators, Bayes estimation with available prior information or a convenient non-informative prior in the absence of prior information is recommended.