1 Introduction

Vibration energy harvesters (VEHs) have made significant advances in the past decade and have proven to be a promising potential technique to provide continuous energy from ambient vibrations [1,2,3,4,5,6], because of the urgent demand for portable or wireless electronics and long-life devices for potential applications. For improving broadband energy harvesting performance under low-level excitations, researchers have designed various nonlinear multi-stable VEHs with four or five stable equilibrium points, e.g., quad-stable or penta-stable VEHs, by adding the number of the external magnets of the cantilever beam on the basis of the magnetic bistable configuration [7,8,9,10]. Considering the inevitable random fluctuation of ambience vibrations, many researchers have studied stochastic mathematical models of the energy harvesting systems subject to noise excitations and have found that a suitable noise dosage has significant benefits for improving the energy harvesting performance [11,12,13,14]. For example, Jin et al. [14] discussed the effects of Gaussian white noise on the tri-stable VEH and concluded that a suitable noise dosage can induce stochastic resonance phenomenon and is rewarding to enhance the efficiency in power conversion.

Currently, mathematical models of the energy harvesting systems are generally constructed with ordinary differential equations (ODEs) or stochastic differential equations (SDEs) according to the fundamental governing laws of systems. However, in practical applications, it is sometimes difficult to model the SDEs precisely for strongly nonlinear multi-stable VEHs, especially for those subjected to additive and multiplicative white noises in a complex random environment, because of the existing challenges in quantifying the noise intensities, the nonlinear stiffness coefficients and the damping coefficient. To overcome this issue, we try to identify the SDEs models for VEHs with the observed data from the perspective of machine learning. To the authors’ knowledge, there is no work so far to model the SDEs from data for energy harvesting systems under noisy excitation.

One active area in current machine learning research is data-driven modeling, which focuses on models that create synthetic representative samples from massive datasets. In recent years, advances in machine learning and data science have led to some systems identification methods in modeling the complex nonlinear dynamical systems with the aid of massive datasets, e.g., sparse identification of nonlinear dynamics (SINDy) [15,16,17,18], network reconstruction techniques [19, 20], Kronecker product representation based on the least squares approximation [21], parameters estimation [22] and data-driven approximation of the Koopman generator (EDMD) [23]. All these methods are premised on the idea that even a nonlinear equation can be regarded as a linear combination of basis functions and then it leads to linear problems. They have been successfully applied in various fields, such as chemical [24], mechanical and electrical engineering [25], meteorology [26], finance [27], molecular and fluid dynamics [28]. A more detailed overview for different application is presented in [29]. One of these methods, the SINDy method, has recently been widely used in data-driven modeling of complex dynamical systems. It combines the ideas of sparse regression and compressed sensing to discover the drift term and the diffusion term of differential equations [16], and then, it is extended to identify parameters of a stochastic system by Kramers–Moyal formula. In what follows, we apply the method of SINDy to identify the SDEs from data for energy harvesting systems under noise excitation.

The purpose of this paper is to discover the general governing equation from observed data on system state time series for nonlinear multi-stable energy harvester under additive and multiplicative white noises. Motivated by this, we devise a sparse identification method to identify SDEs for VEHs in this paper. Based on the learned data-driven SDEs for VEHs, we can further explore the stochastic dynamical behaviors for enhancing energy harvesting performance. The remainder of this paper is organized as follows. In Sect. 2, the mathematical model for a general nonlinear multi-stable VEH under additive and multiplicative white noises is analyzed in detail. In Sect. 3, we devise a sparse identification method for identifying SDEs of VEHs under additive and multiplicative white noises from observed data on system state time series. Then, a penta-stable energy harvesting system is taken as an example to verify the feasibility and effectiveness of the devised sparse identification method for VEH in Sect. 4. Based on the learned data-driven SDE for the penta-stable VEH, the stochastic dynamics caused by noise intensities and nonlinear stiffness coefficients is simply discussed in Sect. 5. Finally, some conclusions are drawn in Sect. 6.

2 Multi-stable VEH under noise excitation

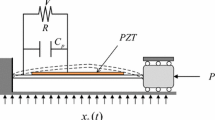
A general vibration energy harvester [1, 30, 31] is considered as shown in Fig. 1. Figure 1a shows the schematic diagram of a general energy harvester. And a case of basic framework of a multi-stable piezoelectric VEH is given in Fig. 1b. Regardless of the details of the employed power conversion mechanism, most energy harvesting systems rely on the oscillators to convert mechanical energy into electrical energy. By referring to literatures [32, 33], we consider a single-degree-of-freedom differential equation to describe the mechanical motion of the oscillator with respect to the nonlinear multi-stable VEH under noise excitation, i.e.,

$$ M\ddot{\overline{X}}(\overline{t}) + \overline{C}\dot{\overline{X}}(\overline{t}) + {{{\text{d}} \overline{U}(\overline{X})} \mathord{\left/ {\vphantom {{{\text{d}} \overline{U}(\overline{X})} {{\text{d}} \overline{X}}}} \right. \kern-\nulldelimiterspace} {{\text{d}} \overline{X}}} = - M\ddot{\overline{X}}_{b} , $$
(1)

where \(\overline{X}\) represents the displacement of the mass \(M\); \(\ddot{\overline{X}}_{b}\) denotes the base acceleration induced by the ambient noise excitation; \(\dot{\overline{X}}\) is the velocity of the mass \(M\); \(\overline{C}\) denotes the viscous damping coefficient; \(\overline{U}(\overline{X})\) denotes the multi-well potential function.

Fig. 1
figure 1

a Schematic diagram of a general VEH. b A multi-stable piezoelectric VEH

Full size image

The multi-well potential function for a general n-stable VEH can be expressed by a polynomial as

$$ \overline{U}(\overline{X}) = \frac{{\overline{k}_{1} }}{2}\overline{X}^{2} + \frac{{\overline{k}_{2} }}{3}\overline{X}^{3} + \cdots + \frac{{\overline{k}_{2n - 1} }}{2n}\overline{X}^{2n} = \sum\limits_{i = 1}^{2n - 1} {\frac{{\overline{k}_{i} }}{i + 1}} \overline{X}^{i + 1} , $$
(2)

where \(\overline{k}_{i}\) (\(i = 1,2, \cdots ,2n - 1\)) denote the stiffness coefficients which are mainly determined by the displacement and the distance of the magnets. Figure 2 shows some cases of mono-well, double-well, triple-well, quad-well and penta-well potentials.

Fig. 2
figure 2

Some cases of mono-well, double-well, triple-well, quad-well and penta-well potentials

Full size image

The following transformations are typically introduced to nondimensionalize Eq. (1)

$$ t = \omega_{0} \overline{t},X = \frac{{\overline{X}}}{l},X_{b} = \frac{{\overline{X}_{b} }}{l},\beta = \frac{{\overline{C}}}{{M\omega_{0} }},k_{i} = \frac{{\overline{k}_{i} l^{i - 1} }}{{M\omega_{0}^{2} }}, $$
(3)

where \(\omega_{0}\) denotes the natural frequency of the mechanical oscillator; \(l\) represents the length scale; \(X\) represents the dimensionless displacement; \(\ddot{X}_{b}\) denotes the dimensionless base acceleration induced by the ambient noise excitation; \(\beta\) denotes the dimensionless damping coefficient; \(k_{i}\) denotes the dimensionless stiffness coefficient.

Then, the dimensionless governing equation of the multi-stable VEH under noise excitation from Eq. (1) can be expressed as

$$ \ddot{X}(t) + \beta \dot{X}(t) + \sum\limits_{i = 1}^{2n - 1} {k_{i} X^{i} } = - \ddot{X}_{b} . $$
(4)

Due to the inevitability and universality of the ambient noise excitation for the nonlinear multi-stable VEH, the ambient noise excitation can be regarded as the uncorrelated additive and multiplicative white noises, i.e.,

$$ - \ddot{X}_{b} = \xi (t) + X\eta (t), $$
(5)

whose statistical properties can be given as follows

$$ \begin{array}{*{20}l} {\left\langle {\xi (t)} \right\rangle = 0,\left\langle {\eta (t)} \right\rangle = 0,} \\ {\left\langle {\xi (t)\xi (t^{\prime})} \right\rangle = 2D\delta (t - t^{\prime}),\left\langle {\eta (t)\eta (t^{\prime})} \right\rangle = 2Q\delta (t - t^{\prime}),} \\ \end{array} $$
(6)

where \(D\) and \(Q\) are the noise intensity of additive and multiplicative white noises, respectively.

Accordingly, Eq. (4) can be rewritten as the following \({\text{It}}\hat{o}\) stochastic differential equations (SDEs)

$$\begin{gathered} {\text{d}}X(t) = Y(t){\text{d}}t, \hfill \\ {\text{d}}Y(t) = \left( { - \beta Y(t) - \sum\limits_{{i = 1}}^{{2n - 1}} {k_{i} X^{i} (t)} } \right){\text{d}}t + \sqrt {2D + 2QX^{2} (t)} {\text{d}}B(t), \hfill \\ \end{gathered} $$
(7)

where \(B(t)\) denotes a scalar Brownian motion.

The drift term and the nonzero diffusion term are

$$ \begin{gathered} b_{1} (X,Y) = Y,\;\;b_{2} (X,Y) = - \beta Y - \sum\limits_{{i = 1}}^{{2n - 1}} {k_{i} X^{i} } , \hfill \\ a_{{22}} (X) = 2D + 2QX^{2} . \hfill \\ \end{gathered} $$
(8)

3 Sparse identification from data for VEHs

From the perspective of machine learning, by applying the least square method, the Stepwise Sparse Regressor (SSR) algorithm and the cross-validation method, a sparse identification method is devised to identify the SDEs of VEHs under noise excitation with the observed data of system state time series. According to the feature of Eq. (7), a dictionary of polynomial basis function is chosen to learn the unknown drift term \(b_{2} (X,Y)\) and the diffusion term \(a_{22} (X)\) in Eq. (8) from the system state time series.

Assume that \(N + 1\) data points of system state time series have been observed and have been dimensionless to \([x_{1} ,x_{2} , \cdots ,x_{N + 1} ]\) at \(t_{1} ,t_{2} , \cdots ,t_{N + 1}\). Then, the velocity of system can be computed as \(\left[ {y_{1} ,y_{2} , \cdots ,y_{N} } \right]\) by \(y_{i} (t) = {{(x_{i + 1} - x_{i} )} \mathord{\left/ {\vphantom {{(x_{i + 1} - x_{i} )} {(t_{i + 1} - t_{i} )}}} \right. \kern-\nulldelimiterspace} {(t_{i + 1} - t_{i} )}}\) (\(i = 1,2, \cdots ,N\)). To ensure the accuracy of the learning process, the time step \(\Delta t\) of the observed data should be as small as possible.

A pair of datasets containing \(N\) elements is organized as

$$ {\mathbf{X}} = [x_{1} ,x_{2} , \cdots ,x_{N} ], $$
(9)
$$ {\mathbf{Y}} = \left[ {y_{1} ,y_{2} , \cdots ,y_{N} } \right]. $$
(10)

For the identification of the drift term, according to its polynomial feature, a dictionary of polynomial basis function is constructed as

$$ {{\varvec{\Phi}}}(X,Y) = \left[ {\varphi_{1} (X,Y), \cdots ,\varphi_{K} (X,Y)} \right] = \left[ {1,X, \cdots ,X^{{K_{1} - 1}} ,Y,XY, \cdots ,X^{{K_{2} - 1}} Y} \right], $$
(11)

where \(K = K_{1} + K_{2}\).

Then, the drift term can be approximated as

$$ b_{2} \left( {X,Y} \right) \approx \sum\limits_{k = 1}^{K} {c_{k} \varphi_{k} \left( {X,Y} \right)} , $$
(12)

where \(c_{k}\) (\(k = 1,2 \cdots ,K\)) is the coefficients of the drift term need to be solved.

Based on the calculated data of system velocity in Eq. (10), the drift term can be estimated by the Kramers–Moyal formula [34]

$$ b_{2} (x_{i} ,y_{i} ) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{y_{i + 1} - y_{i} }}{\Delta t}. $$
(13)

Consequently, the coefficients \({\mathbf{c}}\) can be derived by

$$ {\mathbf{Ac}} = {\mathbf{B}}, $$
(14)

where

$$ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\varphi_{1} \left( {x_{1} ,y_{1} } \right)} & \cdots & {\varphi_{K} \left( {x_{1} ,y_{1} } \right)} \\ \vdots & \ddots & \vdots \\ {\varphi_{1} \left( {x_{N - 1} ,y_{N - 1} } \right)} & \cdots & {\varphi_{K} \left( {x_{N - 1} ,y_{N - 1} } \right)} \\ \end{array} } \right], $$
(15)
$$ {\mathbf{B}} = {{\left[ {y_{2} - y_{1} , \cdots ,y_{N} - y_{N - 1} } \right]} \mathord{\left/ {\vphantom {{\left[ {y_{2} - y_{1} , \cdots ,y_{N} - y_{N - 1} } \right]} {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}. $$
(16)

Similarly, for the identification of the diffusion term, the dictionary of polynomial basis function can be constructed as

$$ {{\varvec{\Psi}}}(X) = \left[ {\psi_{1} (X), \cdots ,\psi_{M} (X)} \right] = \left[ {1,X, \cdots ,X^{M} } \right]. $$
(17)

Then, the diffusion term can be approximated as

$$ a_{22} \left( X \right) \approx \sum\limits_{m = 1}^{M} {q_{m} \psi_{m} \left( X \right)} , $$
(18)

where \(q_{m}\) (\(m = 1,2 \cdots ,M\)) is the coefficients of the diffusion term that need to be solved.

Based on the calculated data of system velocity in Eq. (10), the diffusion term can be estimated by the Kramers–Moyal formula

$$ a_{22} (x_{i} ) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\left( {y_{i + 1} - y_{i} } \right)^{2} }}{\Delta t}. $$
(19)

Consequently, the coefficients \({\mathbf{q}}\) can be derived by

$$ {\hat{\mathbf{A}}\mathbf{q}} = {\hat{\mathbf{B}}}, $$
(20)

where

$$ {\hat{\mathbf{A}}} = \left[ {\begin{array}{*{20}c} {\psi_{1} \left( {x_{1} } \right)} & \cdots & {\psi_{M} \left( {x_{1} } \right)} \\ \vdots & \ddots & \vdots \\ {\psi_{1} \left( {x_{N - 1} } \right)} & \cdots & {\psi_{M} \left( {x_{N - 1} } \right)} \\ \end{array} } \right], $$
(21)
$$ {\hat{\mathbf{B}}} = {{\left[ {\left( {y_{2} - y_{1} } \right)^{2} , \cdots ,\left( {y_{N} - y_{N - 1} } \right)^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {y_{2} - y_{1} } \right)^{2} , \cdots ,\left( {y_{N} - y_{N - 1} } \right)^{2} } \right]} {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}. $$
(22)

The coefficients \({\mathbf{c}}\) and \({\mathbf{q}}\) can be obtained, respectively, by solving Eqs. (14) and Eq. (20), whereas Eqs. (14) and Eq. (20) may have no solutions since there may be more expressed equations than variables. Thus, it need to be solved in the least squares sense, i.e., \(\mathop {\arg \min }\limits_{{\mathbf{c}}} \left\| {{\mathbf{Ac}} - {\mathbf{B}}} \right\|_{2}^{2}\) and \(\mathop {\arg \min }\limits_{{\mathbf{q}}} \left\| {{\hat{\mathbf{A}}\mathbf{q}} - {\hat{\mathbf{B}}}} \right\|_{2}^{2}\). Thereby, the solution \({\mathbf{c}}\) of Eq. (14) and the solution \({\mathbf{q}}\) of Eq. (20) can be leaded as

$$ {\mathbf{c}} = \left( {{\mathbf{A}}^{T} {\mathbf{A}}} \right)^{ - 1} \left( {{\mathbf{A}}^{T} {\mathbf{B}}} \right), $$
(23)
$$ {\mathbf{q}} = \left( {{\hat{\mathbf{A}}}^{T} {\hat{\mathbf{A}}}} \right)^{ - 1} \left( {{\hat{\mathbf{A}}}^{T} {\hat{\mathbf{B}}}} \right). $$
(24)

Noting that here \({\mathbf{c}}\) and \({\mathbf{q}}\) are not yet the sparse solutions. For the goal of finding the least coefficients without loss of reliability representing the data among the large number of possibilities provided in the function dictionary, the sparsity of the coefficients \({\mathbf{c}}\) and \({\mathbf{q}}\) needs to be enforced.

Formally, the typical sparse solutions \({\tilde{\mathbf{c}}}\) and \({\tilde{\mathbf{q}}}\) can be achieved by minimizing

$$ {\tilde{\mathbf{c}}} = \mathop {\arg \min }\limits_{{\mathbf{c}}} \left( {\left\| {{\mathbf{Ac}} - {\mathbf{B}}} \right\|_{2}^{2} + \rho \left\| {\mathbf{c}} \right\|_{1} } \right), $$
(25)
$$ {\tilde{\mathbf{q}}} = \mathop {\arg \min }\limits_{{\mathbf{q}}} \left( {\left\| {{\hat{\mathbf{A}}\mathbf{q}} - {\hat{\mathbf{B}}}} \right\|_{2}^{2} + \rho \left\| {\mathbf{q}} \right\|_{1} } \right), $$
(26)

where \(\rho\) denotes a positive Lagrange multiplier used for controlling the weight of the sparsity constraint. Independently of the specific protocol, the solutions will have some coefficients equal to zero.

The simple and crude method is the iterative thresholding algorithm [16] proposed by Brunton et al. That is, for the solutions \({\mathbf{c}}\) and \({\mathbf{q}}\) in Eqs. (23) and (24), set the coefficients less than a predefined threshold value to zero and perform the least square regression on the remaining coefficients. Iterating this process until no coefficient is less than the threshold value. The threshold parameter is called as a sparsification knob that needs to be adjusted appropriately. However, the overfitting or underfitting may happen if an inappropriate threshold value is given in the above iterative thresholding algorithm.

In order to avoid the overfitting or underfitting regimes, we use the Stepwise Sparse Regressor (SSR) algorithm proposed in Ref. [18] to select solutions with the optimal sparsity. That is, set the only one coefficient with the smallest absolute value to zero in every iteration and use cross-validation to select the number of iterations. Finally, we achieve the optimal sparsity solutions \({\tilde{\mathbf{c}}}\) and \({\tilde{\mathbf{q}}}\).

The sparsity identification process is realized in MATLAB. The basic steps of identifying the drift item of the energy harvester are shown in Table 1. Similarly, its diffusion term can be identified.

Table 1 The algorithm for identifying the drift term \(b_{2} (X,Y)\) from data of system state time series
Full size table

Substituting the learned sparse solutions \({\tilde{\mathbf{c}}}\) and \({\tilde{\mathbf{q}}}\) into Eq. (12) and Eq. (18), the drift term \(b_{2} (X,Y)\) and the diffusion term \(a_{22} (X)\) can be obtained, including the damping coefficient, the stiffness coefficients and noise intensities. Thereby, the governing equation of VEH can be identified.

4 Data-driven identification for a penta-stable energy harvester

In order to verify the feasibility and effectiveness of the devised sparse identification method for the nonlinear multi-stable energy harvester under noise excitation, a strongly nonlinear penta-stable vibration energy harvester driven by additive and multiplicative white noises is considered with the simulated data from the original system.

The considered governing equation of motion can be expressed as

$$ \ddot{X} + \beta \dot{X} + k_{1} X + k_{3} X^{3} + k_{5} X^{5} + k_{7} X^{7} + k_{9} X^{9} = \xi (t) + X\eta (t), $$
(27)

where the noise intensities of the additive noise \(\xi (t)\) and the multiplicative noise \(\eta (t)\) are chosen as \(2D = 0.02\) and \(2Q = 0.01\), respectively. The damping coefficient is set as \(\beta = 0.1\) and the stiffness coefficients are set as \(k_{1} = 1\), \(k_{3} = - 7.7\), \(k_{5} = 16.3\), \(k_{7} = - 12.5\) and \(k_{9} = 3.1\) by reference to Refs. [9, 35].

According to the corresponding It \({\hat{\text{o}}}\) SDE form in Eq. (7), the drift term and the diffusion term of system (27) can be expressed as

$$ {\mathbf{b}}(X,Y) = [Y, - X + 7.7X^{3} - 16.3X^{5} + 12.5X^{7} - 3.1X^{9} - 0.1Y]^{T} , $$
(28)
$$ {\varvec{a}}(X) = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & {0.02 + 0.01X^{2} } \\ \end{array} } \right]. $$
(29)

Now we generate one hundred system state sample trajectories from the original system (27) as the observed data on system state time series \({\mathbf{X}}\) with the initial points distributed uniformly in \([ - 1.5,1.5]\) by using the following fourth-order Runge–Kutta algorithm [36]

$$ {\mathbf{Z}}_{n + 1} = {\mathbf{Z}}_{n} + \frac{\Delta t}{6}({\mathbf{K}}_{1} + 2{\mathbf{K}}_{2} + 2{\mathbf{K}}_{3} + {\mathbf{K}}_{4} ) + \sqrt {(2D + 2Q{\mathbf{Z}}_{n}^{2} (1))\Delta t} {\mathbf{W}}_{n} , $$
(30)

where \({\mathbf{Z}} = [X,Y]^{T}\),\(Y = \dot{X}\), \({\mathbf{W}} = [0,\zeta ]^{T}\), \({\mathbf{K}}_{1} = {\mathbf{b}}(t_{n} ,{\mathbf{Z}}_{n} )\), \({\mathbf{K}}_{2} = {\mathbf{b}}(t_{n} + {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 2}} \right. \kern-\nulldelimiterspace} 2},{\mathbf{Z}}_{n} + {{\Delta t{\mathbf{K}}_{1} } \mathord{\left/ {\vphantom {{\Delta t{\mathbf{K}}_{1} } 2}} \right. \kern-\nulldelimiterspace} 2})\), \({\mathbf{K}}_{3} = {\mathbf{b}}(t_{n} + {{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} 2}} \right. \kern-\nulldelimiterspace} 2},{\mathbf{Z}}_{n} + {{\Delta t{\mathbf{K}}_{2} } \mathord{\left/ {\vphantom {{\Delta t{\mathbf{K}}_{2} } 2}} \right. \kern-\nulldelimiterspace} 2})\), \({\mathbf{K}}_{4} = {\mathbf{b}}(t_{n} + \Delta t,{\mathbf{Z}}_{n} + \Delta t{\mathbf{K}}_{3} )\), \(\Delta t\) is the time step, \(\zeta\) is the standard normal distributed random variable. For each sample trajectory, the time step is set as \(\Delta t = 0.001\) and the series length is set as 105.

Thereby, for purpose of obtaining the damping coefficient, the stiffness coefficients of system and the noise intensities, by applying the devised sparse identification algorithm, what we need to learn from data of system state time series is \(b_{2} (X,Y) = - X - k_{3} X^{3} - k_{5} X^{5} - k_{7} X^{7} - k_{9} X^{9} - \beta Y\) and \(a_{22} (X) = 2D + 2QX^{2}\).

According to the characteristics of the penta-stable energy harvesting system, the orders of the polynomial basis functions \(\Phi (X,Y)\) and \(\Psi (X)\) in Eqs. (11) and (17) can be set as \(K = 14\) (where \(K_{1} = 11\), \(K_{2} = 3\)) and \(M = 4\), respectively. Then, based on the generated data \({\mathbf{X}}\) and the polynomial basis functions \(\Phi (X,Y)\) and \(\Psi (X)\), the matrices \({\mathbf{A}}\), \({\mathbf{B}}\), \({\hat{\mathbf{A}}}\) and \({\hat{\mathbf{B}}}\) can be calculated by Eqs. (15), (16), (21), (22). Accordingly, by performing the sparse identification algorithm devised in Table 1, the optimal sparsity solutions \({\tilde{\mathbf{c}}}\) and \({\tilde{\mathbf{q}}}\) can be learned as listed in Tables 2 and 3. One can find that the learned results are very close to the true values. Furthermore, the comparison between the true and the learned penta-stable potential is present in Fig. 3a. By using Monte Carlo method, the comparison in stationary probability density from the learned data-driven SDE and from the original system (27) is also present in Fig. 3b. These comparisons show that they are very well in agreement, which indicates that the above sparse identification method can be successfully applied to the parameter identification of a multi-stable vibration energy harvesting system under random excitation.

Table 2 Identified coefficients for the drift term \(b_{2} (X,Y)\)
Full size table
Table 3 Identified coefficients for the diffusion term \(a_{22} (X)\)
Full size table
Fig. 3
figure 3

a Comparison between the true and the learned penta-stable potential; b Comparison in stationary probability density from the learned data-driven SDE and from the original system (27)

Full size image

Furthermore, in order to show the consistency of the estimators of parameters (\(k_{1} ,k_{3} ,k_{5} ,k_{7} ,k_{9} ,\beta ,D,Q\)), the influences of the time step and the series length of data trajectory on the mean and standard deviation of the estimators are also discussed here. With reference to Refs. [37,38,39], whether the estimators converge to the true values of the parameters can be tested by checking the oscillations of estimators as data length increases: if the oscillations are small, the estimators are likely to converge. Table 4 shows the mean and standard deviation (in parentheses) of the estimators for three cases (\(\Delta t = 0.001\), \(N = 10^{5}\)), (\(\Delta t = 0.001\), \(N = 2*10^{5}\)) and (\(\Delta t = 0.002\), \(N = 10^{5}\)). It can be observed that the standard deviations of the estimators of all parameters decrease as data length N increases for fixed time step \(\Delta t = 0.001\). For fixed data length \(N = 10^{5}\), the estimators of \(2D\) and \(2Q\) have a very large deviation when \(\Delta t = 0.002\). It indicates that the larger time step will cause a larger deviation in learning the noise terms, whereas the standard deviations of the estimators of all stiffness and damping parameters decrease, due to the increasing trajectory length \(\Delta t \times N\). Thus, all the identified estimators, including the noise terms, can converge well to the true values of the parameters as the length of the data trajectory increases under a small time step.

Table 4 Consistency test. Mean and standard deviation (in parentheses) of the estimators of the parameters computed from 10 sets of the learned results with different time steps and data lengths
Full size table

5 Stochastic dynamics of data-driven energy harvesting system

In the practical application, VEHs will inevitably be interfered by the ambient noises. The interfered noise intensities from the environment where VEHs is located can be identified through implementing the devised sparse identification method from data generated by one instance of VEHs. Meanwhile, the damping coefficient and the stiffness coefficients of system can also be identified. Especially, the nonlinear form of potential can be determined, e.g., symmetrical double-well potential, asymmetrical double-well potential or asymmetrical triple-well potential and so on. Thereby, with the learned data-driven SDEs for VEHs, the stochastic dynamics of VEHs can be further explored for enhancing energy harvesting performance. In this section, based on the learned data-driven SDEs for VEHs, we will simply discuss the influences of noise intensities and nonlinear stiffness coefficients on the stationary probability density and the mean harvested power.

Since the multi-stability characteristic is an effective approach to reduce the potential barrier, a penta-stable VEH learned from data in Sect. 4 is considered here, i.e.,

$$ \ddot{X} + \beta \dot{X} + k_{1} X + k_{3} X^{3} + k_{5} X^{5} + k_{7} X^{7} + k_{9} X^{9} = \xi (t) + X\eta (t), $$
(31)

where the noise intensities of the additive noise \(\xi (t)\) and the multiplicative noise \(\eta (t)\) have been learned as \(2D = 0.0194\) and \(2Q = 0.0116\), which can be seen from Table 3. The damping coefficient has been learned as \(\beta = 0.1010\) and the stiffness coefficients have been learned as \(k_{1} = 0.9976\), \(k_{3} = - 7.7182\), \(k_{5} = 16.3409\), \(k_{7} = - 12.5293\), \(k_{9} = 3.1068\), which can be seen from Table 2. In the following study, the values of system parameters are fixed as above unless otherwise mentioned.

According to the \({\text{It}}\hat{o}\) SDE form of VEH in Eq. (7) coupled with \(Y = \dot{X}\), the corresponding Fokker–Planck equation of system (31) is given by

$$ \frac{\partial p}{{\partial t}} = - \frac{\partial }{\partial X}\left[ {Yp} \right] + \frac{\partial }{\partial Y}\left[ {\left( {\beta Y + k_{1} X + k_{3} X^{3} + k_{5} X^{5} + k_{7} X^{7} + k_{9} X^{9} } \right)p} \right] + \frac{{\partial^{2} }}{{\partial Y^{2} }}\left[ {(D + QX^{2} )p} \right], $$
(32)

where \(p = p(X,Y,t\left| {X_{0} ,Y_{0} ,t_{0} } \right.)\) denotes the joint probability density function of the system response. The initial condition is given by \(p(X,Y,t_{0} \left| {X_{0} ,Y_{0} ,t_{0} } \right.) = \delta (X - X_{0} )\delta (Y - Y_{0} )\).

When the Markov diffusion process reaches a stationary state, the stationary probability density is the limit of the transition probability density as time tends to infinity. That is, the stationary probability density can be derived by

$$ {{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}} = 0, $$
(33)

where \(p(X,Y)\) satisfies the following normalization condition

$$ \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {p(X,Y)} } {\text{d}} X{\text{d}} Y = 1. $$
(34)

It is difficult to solve the equation (33) because of the strongly nonlinear stiffness forms. Thus, the finite difference scheme is applied as

$$ \begin{array}{*{20}c} {\frac{{\partial p_{ij} }}{\partial X} = \frac{{p_{i + 1,j} - p_{i - 1,j} }}{\Delta X},} & {\frac{{\partial p_{ij} }}{\partial Y} = \frac{{p_{i,j + 1} - p_{i,j - 1} }}{\Delta Y},} & {\frac{{\partial^{2} p_{ij} }}{{\partial Y^{2} }} = \frac{{p_{i,j + 1} - 2p_{i,j} + p_{i,j - 1} }}{{\Delta Y^{2} }}.} \\ \end{array} $$
(35)

Accordingly, Eq. (33) can be discretized into the following linear equations

$$ [{\mathbf{K}}]\{ {\mathbf{p}}\} = 0, $$
(36)

where \({\mathbf{p}} = (p_{1,1} , \cdots ,p_{m,1} ,p_{1,2} , \cdots ,p_{m,m} )^{T}\) and \({\mathbf{K}}\) denotes the coefficient matrix.

In order to obtain the stationary probability density, the successive over relaxation (SOR) iteration method is applied here to solve Eq. (36) as follows

$$ p_{ij}^{(n + 1)} = p_{ij}^{(n)} + \alpha {{\left( { - \sum\limits_{k = 1}^{i - 1} {\sum\limits_{s = 1}^{j - 1} {K_{ks} p_{ks}^{(n + 1)} } - \sum\limits_{k = i}^{m} {\sum\limits_{s = j}^{m} {K_{ks} p_{ks}^{(n)} } } } } \right)} \mathord{\left/ {\vphantom {{\left( { - \sum\limits_{k = 1}^{i - 1} {\sum\limits_{s = 1}^{j - 1} {K_{ks} p_{ks}^{(n + 1)} } - \sum\limits_{k = i}^{m} {\sum\limits_{s = j}^{m} {K_{ks} p_{ks}^{(n)} } } } } \right)} {K_{ij} }}} \right. \kern-\nulldelimiterspace} {K_{ij} }}, $$
(37)

where the superscript \(n\) represents the n-th iteration. \(p_{ij} = p(X_{i} ,Y_{j} )\) in which \(i = 1,2, \cdots ,m\) and \(j = 1,2, \cdots ,m\). \(\alpha\) is the relaxation iteration factor and its value range is generally \((0,2)\) to ensure the convergence of Eq. (37). In the following study, we choose \(m = 50\) points evenly in the spatial domain \([ - 1.6,1.6] \times [ - 1.6,1.6]\) of \((X,Y)\), and the iteration error is set as \(10^{ - 5}\). The relaxation iteration factor \(\alpha\) is set as \(\alpha = 0.01\). Besides, in the actual iteration, the negative \(p_{ij}\) that may be generated in the iteration process is assigned to zero for purpose of ensuring the non-negativity of stationary probability density. And the normalization of Eq. (34) is performed every 10 iterations in order to ensure the convergence of iteration.

According to Refs. [2, 13, 40], the mean harvested power is proportional to the energy in velocity. For example, Daqaq [13] derived the expression of the mean power in the study of the response of a bistable inductive-type energy harvester and obtained the mean power as \(\left\langle P \right\rangle = \tilde{\alpha }\left\langle {\dot{x}^{2} } \right\rangle\), where \(\tilde{\alpha }\) denotes the electromechanical coupling coefficient. Thus, the mean harvested power \(E(P)\) can be assessed as

$$ E(P) \propto E(\dot{X}^{2} ) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {Y^{2} p(X,Y)} } {\text{d}}X{\text{d}} Y. $$
(38)

Figure 4 shows the variations of stationary response induced by noise excitations and nonlinear stiffness coefficients. The values of parameters are set as the learned results from Tables 2 and 3, unless otherwise mentioned. Comparison of Fig. 4a, b manifests that the larger noise intensities facilitate the transition of particles among potential wells. Comparison of Fig. 4a, c manifests that stiffness coefficients can cause the changes of topological structure of stationary probability density. The results indicate that both noise intensities and stiffness coefficients have the essential influences on stationary probability density of energy harvesting systems.

Fig. 4
figure 4

The variations of stationary probability density. a Data-driven SDE whose parameters are set as the learned result from Tables 2 and 3. b \(2D = 0.01\), \(2Q = 0.005\). c \(k_{3} = - 7.9\), \(k_{9} = 3.3\)

Full size image

The variations of the mean harvested power \(E(P)\) with the noise intensities and the strongly nonlinear stiffness coefficients are presented in Fig. 5a, b. It can be seen that \(E(P)\) increases monotonously with the increase in noise intensities \(D\) and \(Q\) of the additive and multiplicative white noises, whereas \(E(P)\) varies non-monotonously with the increase in strongly nonlinear stiffness coefficients \(k_{7}\) and \(k_{9}\), which indicates that there exist the optimal \(k_{7}\) and \(k_{9}\) that maximizes \(E(P)\). Besides, Fig. 5c shows the variations of the mean-square displacement \(E(X^{2} )\) with nonlinear stiffness coefficients. One can see that \(E(X^{2} )\) decreases monotonously as \(k_{7}\) and \(k_{9}\) increases. These results indicate that both noise intensities and stiffness coefficients play an important role in the mean harvested power and the mean-square displacement.

Fig. 5
figure 5

a The variations of the mean harvested power \(E(P)\) with noise intensities \(D\) and \(Q\); b The variations of \(E(P)\) with stiffness coefficients \(k_{7}\) and \(k_{9}\); c The variations of the mean-square displacement \(E(X^{2} )\) with stiffness coefficients \(k_{7}\) and \(k_{9}\)

Full size image

Thereby, based on the learned data-driven SDEs, the stochastic dynamics of energy harvesters can be further discussed by adjusting the system parameters appropriately, such as noise intensities and stiffness coefficients, for purpose of enhancing the energy harvesting performance and optimizing the miniaturization design.

6 Conclusions

From the perspective of machine learning, we devise a sparse identification method in this paper to discover the general governing equation for multi-stable vibration energy harvesters under additive and multiplicative white noises with the observed data on system state time series. With the observed data from energy harvesters, by implementing the devised sparse identification method, the drift term and the diffusion term (including noise intensity, damping coefficient and stiffness coefficients) can be learned, and then, the data-driven SDE can be identified. A penta-stable vibration energy harvester is taken as an example to verify the feasibility and effectiveness of the devised sparse identification method, which indicates that the method can be successfully applied to model the governing equation of a multi-stable vibration energy harvesting system under random excitation. Moreover, through the discussion of the consistency, all the identified estimators, including the noise terms, can converge well to the true values of the parameters as the length of the data trajectory increases under a small time step. With the learned penta-stable VEH, we simply discussed the influences of noise intensities and stiffness coefficients on the stochastic dynamics and energy harvesting performance of energy harvesters, which indicate that both noise intensities and stiffness coefficients play an important role in the stationary probability density and the mean harvested power. We will explore the stochastic dynamics of the penta-stable VEH in depth in the future for purpose of enhancing the harvested energy.

Thereby, based on the learned data-driven SDEs for energy harvesters, the stochastic dynamics, such as stochastic response, stochastic bifurcation, stochastic resonance and chaotic phenomenon, can be further explored by appropriately adjusting the system parameters to improve energy harvesting performance and optimize the miniaturization design. Especially, in the practical application, by implementing the proposed sparse identification method for SDEs of VEHs from data, the noise intensities and damping coefficient of the located environment can be identified easily.