Nonlinear dynamics of the rotating beam with time-varying speed under aerodynamic loads

Abstract

In this research, the bifurcation analysis is inspected for a rotatory pre-twisted beam which is subjected to the time varying angular velocity and aerodynamic forces. Aerodynamic loads are obtained by the Piston and Whitehead theories. It is assumed that a time-dependent periodic component is superposed on the angular velocity. The extended Hamilton's principle is utilized to derive the dynamic equations of motion in flapwise and chordwise directions. Then a combination of the Galerkin and multiple scales methods is established to obtain the modulation equations describing amplitude and phases of the interacting modes. Eigen value analysis is performed on the linear part of the equations and the possibility of 1:1 internal resonance condition is examined. The evolution of amplitudes is obtained versus the amplitude and frequency of the periodic angular velocity function. Primary and subharmonic resonance conditions are tuned between the angular velocity frequency and natural frequencies of the beam. Numerical simulations indicate that the nonlinear phenomena such as jump, saturation, and double jumping appear in nonlinear vibration of rotating beam with varying speed.

1 Introduction

The Blade is the main member of gas turbines. Distortion of the blades is caused by some parameters such as temperature gradient in blades, distribution of aerodynamic forces on the blades, and rubbing from the contact in the hub. These parameters lead to large amplitude vibrations and subsequent demolition of the blade. Thus, the dynamic response of the blades is essential for avoiding the large amplitude vibrations of blades. In what follows, some recent works related to the nonlinear vibration of blades are illustrated.

Turhan and Bulut [1] have derived the governing equations of a rotatory beam under harmonic excitation at the tip of beam and inertia loads. Primary, sub and super-harmonic resonances have been adjusted respectively when the frequency of the tip excitation force was very close to the one, triple and third of the lateral natural frequency of the beam. Amplitude and phases of the steady state solutions have been depicted for various spinning speed and hardening or softening response curves have been shown in simulations. Yonesian and Esmailzadeh [2] have obtained the vibration amplitude of the blade as a nonlinear expression of spinning speed and time, when the spinning speed gets larger or detracts as a linear function of time with a constant slope. In this work, the variation of amplitude has been investigated for positive and negative values of constant slope, different values of hub radius, and structural damping of the rotatory beam. Arvin and Bakhtiari-Nejad [3] have investigated the axial and transverse vibration of a rotatory beam. The stability investigation of the rotatory beam has been studied for internal resonance among the first axial and forth transverse modes. Wang and Zhang [4] have examined the stability boundaries of the rotatory blade. The spinning speed has been declared as a sinusoid function of time as well as a constant value of spinning speed. Bifurcation analysis has been performed in terms of amplitude and frequency of the sinusoid function. Yao et al. [5] have investigated the bifurcation diagram of the thin walled blade with an oscillating spin. The constant spinning speed has been varied with a harmonic function of time and frequency. Primary resonance condition was the nearness of the spinning frequency with the natural frequencies of the beam in flapwise and chordwise directions. Periodic, multi-periodic motions and chaos phenomenon have appeared for one to one internal resonance condition among two transverse modes. Stoykov and Ribeiro [6] have studied the nonlinear vibration of the rotatory Timoshenko beam under a periodic transversely force at the tip of the beam. Nonlinearity has arisen from the large deformation of the beam and inertia forces of the rotation. The equations have been solved by the finite element analysis and the influences of spinning speed and external excitation have been investigated.

Arvin and Bakhtiari-Nejad [7] have studied the lateral, axial and torsional vibration of the rotatory composite beam for various spinning speed. The number of layers in the composite beam, spinning speed and material properties of the beam were the main factors in producing the internal resonance condition between the modes. Stability of the modes has been investigated in this analysis. Vibration of the rotatory thin walled beam has been investigated in the torsional mode under the axial load and initial enforced torque by Sina and Haddadpour [8]. Fiber angles of the composite beam, inertia load, spinning speed and pre-twist of the beam have been affected on the vibrational characteristic of the beam.

Arvin and Lacarbonara [9] have analyzed the nonlinear frequencies and interaction between modes of the rotatory composite beam. Huang and Zhu [10] have utilized the method of harmonic balance to solve the nonlinear equations of rotatory beam. In this analysis, the weight of beam has been considered and the stability of the periodic responses has been determined using the Floquet Theory. The gravitational force emerged as the parametric excitation in linear terms and the external excitation in harmonic and nonlinear terms. Thomas et al. [11] showed that the jump phenomenon has been happened in frequency and forced responses of the rotatory beam under a force with sine function of time and frequency at the tip of beam by. When the frequency of tip force was near the natural frequency of the beam, hardening behavior has been presented in mode one for low spinning speed and softening behavior has been happened for high spinning speed. Moreover, softening behavior has been seen in any spinning speed for mode two. Arvin et al. [12] have studied the stability analysis of the rotatory beam with time varying spinning speed. The equations of motion in axial and lateral directions have been solved using the multiple scales method and the semi-analytic results have been collated with the obtained results by the differential quadrature method. Damping ratio and number of modes have changed the stability boundaries. Bekhoucha et al. [13] have plotted the steady state amplitudes of the hub-beam system as a function of spinning speed. Euler–Bernoulli and Timoshenko's theories have been considered in their analysis. Large deflection and small deformation have been assumed in deriving the equations of motion. The effects of spinning speed and shear deformation have been analyzed in diagrams.

Van der Male et al. [14] have investigated the dynamic response of the cantilevered rotatory blade under aerodynamic forces which were considered as the nonlinear function of wind oscillation, time derivatives of blade displacement, and time. The drag and lift forces have been explained in literature and numerical simulations demonstrated the importance of the considered forces on the nonlinear behavior of the simplified model of the blade. Kim and Chung [15] have selected the new variables for deriving the dynamic equations of the rotatory beam. The axial and lateral displacements of the beam have been obtained by integrating over time. Numerical simulations demonstrated that dynamic response of the model had a faster convergence rate and more accuracy than the previous models in the literature.

Zhang et al. [16] have determined the existence of Hopf bifurcation and quasi-periodic motion of the rotatory beam which has been investigated in previous work [5]. In this research, thin walled beam has been rotated with a harmonic function of time and has been subjected to the gas pressure as the external load. The thermal effect has been assessed in constitutive relations. Nearness of the natural frequencies of the beam to the frequency of the harmonic spinning speed function has been defined by two detuning parameters. Bifurcation analysis of the averaged equations describing the steady state responses has been analyzed using the center manifold and normal form theories. Tian et al. [17] have presented the effects of Coriolis and stretch terms on the vibrational characteristic of the rotatory extensional beam. For special beams with the low value of hub radius, the large value of slender ratio, and high spinning speed these mentioned effects have been observed in numerical simulations. Zhang et al. [18] have indicated the double jump and saturation phenomena in frequency and forced responses of the rotatory beam under gas excitation with high temperature. Distribution of gas pressure has been considered as the harmonic excitation. The frequency of the gas has been expressed near the natural frequencies in the flapwise and chordwise directions and the auto-parametric resonance condition has been imposed among two named directions. Steady state amplitudes of the beam versus the magnitude and frequency of the exciting pressure have been presented for various damping values.

Frequency-amplitude curves show the characteristic of forced vibration of the nonlinear systems. Depending on the nonlinearity, amplitudes have hardening or softening behavior which leads to a jump in frequency response curves. However, in the presence of internal resonance, amplitudes may have two jumps in frequency response curves and thus double jump phenomenon occurs. In double jump phenomenon, the steady state amplitudes bend to left and right directions and two jumps appear in amplitudes. Nayfeh et al. have found the double jump phenomenon in pitch and roll motions of a ship [19]. Other recent works related to the double jump phenomenon have been studied and explained in the literature [20,21,22,23].

Chen et al. have considered two modes for the lateral vibrations of pipe conveying fluid and internal resonance condition has obtained in the supercritical speed of flowing fluid [20]. Double jump has been presented in frequency response curves. Chen and Jiang have designed an electromagnetic energy harvester with a mass-spring system under primary and auto-parametric resonances [21] and the frequency responses have been presented the double jump phenomenon. Frequency responses show the double jump phenomenon. Karimpour and Eftekhari have attached a moving mass-spring system to the cantilevered beam [22]. The internal resonance condition has been constrained between the natural frequency of the moving mass and the natural frequencies of the beam. Double jump phenomenon has obtained in frequency responses.

Zhang et al. have modeled the blade as a composite plate and the blade has been excited by the subsonic airflow in the presence of two-to-one internal resonance condition between the bending and torsional modes [23]. Double jump and saturation have been represented in bifurcation diagrams.

Yao et al. investigated the nonlinear vibration of the rotatory thin-walled blade by considering the nonlinearity in deformation of the blade, time varying rotating speed and centrifugal and aerodynamic forces [24]. The averaged equations were obtained for the primary resonance and parametric resonance between the frequency of the transverse and lateral modes. The effects of periodic perturbation speed, nonlinearity and damping were shown in frequency response curves.

The combination of the extermum response surface method and the interval method was proposed by Bai et al. for probabilistic and non-probabilistic reliability analysis [25]. The computational efficiency of the method for the tuned and mistuned blisks was better than the Mont Carlo and the multilevel nested algorithm methods which were reported in literature.

The nonlinear equations of the rotatory composite plate with time varying speed were obtained by Yao et al. [26] in the presence of the centrifugal and the aerodynamic forces. The aerodynamic loads were applied on the blade by the first order Piston theory. Time varying speed was assumed as the constant value as well as the harmonic term. Three to one internal resonance condition between the first and second modes of transverse vibration was selected when the constant angular velocity was near the twice of the first natural frequency. Multi-periodic and chaotic behaviors were presented in numerical solutions.

Niu et al. studied the same problem by considering the functionally graded material for the composite cylindrical panel [27]. The natural frequencies were presented for different material and geometric parameters.

Bai et al. studied the vibration and reliability investigations of the mistuned bladed disk using the combination of the extremum response surface method and improved substructural component modal synthesis [28]. The dynamic probabilistic of the mistuned bladed disk was investigated and the new method could be established for the complex structures.

Zhang et al. investigated the free vibration characteristic of the rotating pre-twisted composite cylindrical panel reinforced by graphene coating layers [29]. The natural frequencies and the mode shapes of the tapered cantilever blade were obtained using the Chebyshev-Ritz method. The effectiveness of some parameters such as the graphene platelet geometry, graphene platelet weight fraction, taper ratio, length-to-radius ratio, pre-twist angle, presetting angle and rotating speed were presented in numerical simulations.

In this paper, the stability of fixed points of the rotatory beam with varying spinning speed is investigated under primary and 1:1 internal resonances. The variable operating speed of the rotatory beam is composed of constant value and periodic function of time. Based on the first order piston and Whitehead theories, the aerodynamic loads are dependent on the velocity of air flow, the time derivative of beam displacements, the twist angle of the beam, and Mach number. Hamilton's principle yields the governing equations of the rotatory beam in flapwise and chordwise directions. One-to one internal resonance condition appears between the transverse and lateral modes of the blade and the constant value of the spinning speed is equal to one and two times of the first natural frequency of the flapwise and chordwise directions. Double jump, jump, Hopf points (describing quasi-periodic or chaotic motions) and saturation are revealed in the internal and primary, sub-harmonic resonance conditions. To the best of our knowledge, double jump and saturation have not been reported in rotary blade with time varying spinning speed in the presence of 1–1 internal resonance and sub-harmonic external resonance. Moreover, the Whitehead theory is applied on the blade and unstable, saddle and Hopf points are shown in frequency response curves. The effect of amplitude and frequency of the periodic spinning function is studied on the stability of the beam amplitudes in resonance conditions.

2 Equation of motion for rotating blade

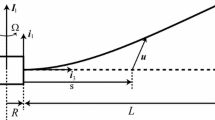
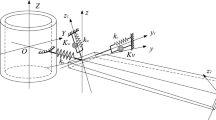
Figure 1a shows the pre-twisted cantilevered beam that rotates at a steady state speed $\Omega_{0}$ with a periodic function $A_{\Omega } \cos (\omega_{\Omega } t)$. The radius of the hub is $R_{0}$ and length of the cantilever beam is $L$. The cantilever beam is attached to the hub with a settling angle $\alpha$. $\beta (x)$ is the pre-twist angle of any cross section of the beam at position x with respect to the fixed end cross section with angle $\alpha$. As shown in Fig. 1b, the beam has a rectangular cross section with width $a$ and height $b$. The defined coordinates are: (1) inertial coordinate $XYZ$ at the Centre of the hub with unit vectors ${\mathbf{I}},{\mathbf{J}},{\mathbf{K}}$, (2) rotating coordinate $xyz$ is placed at the origin of the blade root with unit vectors ${\mathbf{i}},{\mathbf{j}},{\mathbf{k}}$ and (3) $x_{p} y_{p} z_{p}$ is placed at the arbitrary cross section of the beam with the principle axes of $y_{p} - z_{p}$. The considered assumptions are: (1) displacements of neutral axis in $y_{p} ,z_{p}$ directions are $v_{0} ,w_{0}$ and they are much larger than displacement in x direction or $u_{0}$. (2) In deriving equations, it is neglected from $u_{0}$ and derivatives of it. (3) Shear deformation and warping effects are neglected. (4) The beam model is Euler–Bernoulli and the material of the beam is isotropic. (5) The beam is subjected to the supersonic gas flow.

Fig. 1

A rotatory beam system with attached Cartesian coordinates

The relation between $x - y - z$ and $x^{p} - y^{p} - z^{p}$ are defined as

$$ \begin{aligned} x & = x^{p} , \\ y & = y^{p} \cos (\beta (x) + \alpha ) - z^{p} \sin (\beta (x) + \alpha ), \\ z & = y^{p} \sin (\beta (x) + \alpha ) + z^{p} \cos (\beta (x) + \alpha ), \\ \end{aligned} $$

(1)

where in Eq. (1), $\beta (x) = \beta_{0} x/L$ is the pre-twist of an arbitrary cross section at the position $x$ and $\beta_{0}$ is the pre-twist at the tip. The position vector of an arbitrary point on the deformed state of the beam is written as:

$$ {\mathbf{R(X,Y,Z,t)}} = (R_{0} + u + x){\mathbf{i}} + (y + v){\mathbf{j}} + (z + w){\mathbf{k}}, $$

(2)

where, the deformed and undeformed states of the beam are indicated by the generalized coordinates $u,v,w$ and $x,y,z$ respectively. The velocity vector of an arbitrary point can be obtained as:

$$ {\dot{\mathbf{R}}} = [\dot{u} - (y + v)\Omega (t)]{\mathbf{i}} + [\dot{v} + (R_{0} + x + u)\Omega (t)]{\mathbf{j}} + \dot{w}{\mathbf{k}}, $$

(3)

where, the dot defines the derivative with respect to time. The components of the displacement field of an Euler–Bernoulli beam can be written:

$$ u = u_{0} - z\partial w_{0} /\partial x - y\partial v_{0} /\partial x,\,\,v = v_{0} ,\,\,w = w_{0} , $$

(4)

where in Eq. (4), $u_{0} ,v_{0} ,w_{0}$ are the neutral axis translations along with the $x,y,z$ directions respectively. The displacement–strain relationships are obtained as:

$$ \begin{aligned} \varepsilon_{xx} & = \partial u/\partial x + 1/2((\partial v/\partial x)^{2} + (\partial w/\partial x)^{2} ),\,\,\varepsilon_{yy} = 1/2(\partial w/\partial x)^{2} , \\ \gamma_{xy} & = \,\gamma_{yz} = \gamma_{xz} = 0, \\ \end{aligned} $$

(5)

A Hamiltonian derivation of the dynamic equations of motion is rendered as:

$$ \int_{0}^{t} {(\delta T + \delta U - \delta W)dt = 0,} $$

(6)

where T and U are the total kinetic and potential energies respectively, $W$ is the work which is done by the external forces, $\delta$ is the variational operator and t is time. The kinetic and potential energies are obtained as:

$$ \begin{aligned} T & = 1/2\int_{0}^{l} {\rho A[(\partial v_{0} /\partial t)^{2} + (\partial w_{0} /\partial t)^{2} + \Omega^{2} (t)((R_{0} + x)^{2} + v_{0}^{2} \cos^{2} (\beta (x) + \alpha )} \\ & \quad + w_{0}^{2} \sin^{2} (\beta (x) + \alpha ) - 2v_{0} w_{0} \sin (\beta (x) + \alpha )\cos (\beta (x) + \alpha )) \\ & \quad + 2\Omega (t)((\partial v_{0} /\partial t)(R_{0} + x)\cos (\beta (x) + \alpha ) - (\partial w_{0} /\partial t)(R_{0} + x)\sin (\beta (x) + \alpha ))]dx, \\ \end{aligned} $$

(7)

$$ \begin{aligned} U_{1} & = (1/2)\int_{0}^{l} {F_{c} ((\partial v_{0} /\partial x)^{2} + (\partial w_{0} /\partial x)^{2} )d} x,\,\,F_{c} = \rho A\Omega^{2} (t)(R_{0} (L - x) + (1/2)(L^{2} - x^{2} )), \\ U_{2} & = (1/2)\int_{0}^{l} {\{ EA[(1/2)(\partial v_{0} /\partial x)^{2} (\partial w_{0} /\partial x)^{2} ) + (1/2)(\partial v_{0} /\partial x)^{4} + } (1/4)(\partial w_{0} /\partial x)^{4} ] \\ & \quad + EI_{z} (\partial^{2} v_{0} /\partial x^{2} )^{2} + EI_{y} (\partial^{2} w_{0} /\partial x^{2} )^{2} + 2EI_{yz} (\partial^{2} v_{0} /\partial x^{2} )(\partial^{2} w_{0} /\partial x^{2} )\} dx, \\ U & = U_{1} + U_{2} , \\ \end{aligned} $$

(8)

In Eqs. (7–8), $\rho$ is the beam density, $A$ is the cross-sectional area of the beam, E is the elasticity modulus, $I_{y} ,I_{z}$ are the moment inertia along y and z axes respectively and $I_{yz}$ is the product moment of inertia about y–z axes. The work done by the external loads is given by:

$$ W = \int_{0}^{L} {(p_{y} v_{0} + p_{z} w_{0} )} dx, $$

(9)

where $p_{y}$ and $p_{z}$ are the projections of the external forces on the y and z axes respectively which are caused by the gas pressure as [5]:

$$ p_{y} = a\Delta P_{{z^{p} }} \sin (\beta (x) + \alpha ) - b\Delta P_{{y^{p} }} \cos (\beta (x) + \alpha ), $$

(10)

$$ p_{z} = - a\Delta P_{{z^{p} }} \cos (\beta (x) + \alpha ) - b\Delta P_{{y^{p} }} \sin (\beta (x) + \alpha ), $$

(11)

In Eqs. (10–11), $\Delta P_{{z^{p} }}$ and $\Delta P_{{y^{p} }}$ are the pressures of the supersonic flow on the blade which are obtained from the first-order piston theory as follows [5]:

$$ \Delta P_{{z^{p} }} = C_{\infty } \rho_{\infty } ((\partial w^{p} /\partial t) + U_{{z^{p} }}^{t} (\partial w^{p} /\partial x)), $$

(12)

$$ \Delta P_{{y^{p} }} = C_{\infty } \rho_{\infty } ((\partial v^{p} /\partial t) + U_{{y^{p} }}^{t} (\partial v^{p} /\partial x)), $$

(13)

In Eqs. (12–13), $\rho_{\infty }$ is the density of air, $C_{\infty }$ is the speed of sound,$U_{{y^{p} }}^{t} ,U_{{z^{p} }}^{t}$ and $v^{p} ,w^{p}$ are respectively the fluid velocity components and the displacement components on the positive y^p and z^p directions. $v^{p} ,w^{p}$ are [5]:

$$ v^{p} = v_{0} \cos (\beta (x) + \alpha ) + w_{0} \sin (\beta (x) + \alpha ), $$

(14)

$$ w^{p} = - v_{0} \sin (\beta (x) + \alpha ) + w_{0} \cos (\beta (x) + \alpha ), $$

(15)

Substituting Eqs. (7–9) in to Eq. (6), and setting each of coefficients $\delta v_{0} (x,t),\delta w_{0} (x,t)$ equal to zero, the governing equations are obtained as:

$$ \begin{aligned} & \delta v_{0} : \\ & \quad EA[ - 3(v^{\prime}_{0} )^{2} v^{\prime\prime}_{0} - (1/2)(w^{\prime}_{0} )^{2} v^{\prime\prime}_{0} - v^{\prime}_{0} w^{\prime}_{0} w^{\prime\prime}_{0} ] + E(I_{z} v^{\prime\prime}_{0} )^{\prime\prime} + E(I_{yz} w^{\prime\prime}_{0} )^{\prime\prime} \\ & \quad + \rho A[\ddot{v}_{0} + \dot{\Omega }(R_{0} + x) - \Omega^{2} [((1/2)(L^{2} - x^{2} ) + R_{0} (L - x))v^{\prime\prime}_{0} - (R_{0} + x)v^{\prime}_{0} + v_{0} ]] - p_{y} = 0, \\ \end{aligned} $$

(16)

$$ \begin{aligned} & \delta w_{0} : \\ & \quad EA[ - 3(w^{\prime}_{0} )^{2} w^{\prime\prime}_{0} - (1/2)(v^{\prime}_{0} )^{2} w^{\prime\prime}_{0} - v^{\prime}_{0} w^{\prime}_{0} v^{\prime\prime}_{0} ] + E(I_{z} w^{\prime\prime}_{0} )^{\prime\prime} + E(I_{yz} v^{\prime\prime}_{0} )^{\prime\prime} \\ & \quad + \rho A[\ddot{w}_{0} - \Omega^{2} [((1/2)(L^{2} - x^{2} ) + R_{0} (L - x))w^{\prime\prime}_{0} - (R_{0} + x)w^{\prime}_{0} ]] - p_{z} = 0, \\ \end{aligned} $$

(17)

Boundary conditions are

at $x = 0$

$$ v_{0} = 0,w_{0} = 0,\,v^{\prime}_{0} = 0,w^{\prime}_{0} = 0, $$

(18)

at $x = L$

$$ \begin{aligned} & v_{0}^{\prime 3} + (1/2)v^{\prime}_{0} w_{0}^{\prime 2} + (1/A)(I_{y} v^{\prime\prime}_{0} - I_{yz} w^{\prime\prime}_{0} )^{\prime} = 0, \\ & w_{0}^{\prime 3} + (1/2)w^{\prime}_{0} v_{0}^{\prime 2} + (1/A)(I_{z} w^{\prime\prime}_{0} - I_{yz} v^{\prime\prime}_{0} )^{\prime} = 0,\quad v^{\prime\prime}_{0} = (I_{z} /I_{yz} )w^{\prime\prime}_{0} ,\,w^{\prime\prime}_{0} = (I_{y} /I_{yz} )v^{\prime\prime}_{0} , \\ \end{aligned} $$

(19)

The resultant equations are presented dimensionless by introducing the following parameters:

$$ \begin{array}{*{20}l} {\overline{x} = x/L} \hfill & {\overline{v}_{0} = v_{0} /L} \hfill & {\overline{w}_{0} = w_{0} /L} \hfill & {\overline{R}_{0} = R_{0} /L} \hfill & {\overline{a} = a/L} \hfill \\ {\overline{b} = b/L} \hfill & {\overline{I}_{y} = I_{y} /AL^{2} } \hfill & {\overline{I}_{z} = I_{z} /AL^{2} } \hfill & {\overline{I}_{yz} = I_{yz} /AL^{2} } \hfill & {\overline{P} = P\sqrt {\rho /E} } \hfill \\ {\overline{C}_{\infty } = C_{\infty } \sqrt {\rho /E} } \hfill & {\overline{\rho }_{\infty } = \rho_{\infty } (L^{2} /\rho A)} \hfill & {\overline{t} = t\sqrt {E/\rho L^{2} } } \hfill & {\overline{\Omega } = \Omega \sqrt {\rho L^{2} /E} } \hfill & {\dot{\overline{\Omega }} = \dot{\Omega }\rho L^{2} /E} \hfill \\ {\overline{M} = P/C_{\infty } ,} \hfill & {} \hfill & {} \hfill & {} \hfill & {} \hfill \\ \end{array} $$

(20)

The non-dimensional equations are obtained as:

$$ \begin{gathered} \ddot{v}_{0} - \Omega^{2} v_{0} - \Omega^{2} [((1/2)(1 - x^{2} ) + R_{0} (1 - x))v^{\prime\prime}_{0} - (R_{0} + x)v^{\prime}_{0} ] + (I_{z} v^{\prime\prime}_{0} )^{\prime\prime} + (I_{yz} w^{\prime\prime}_{0} )^{\prime\prime} \hfill \\ = 3(v^{\prime}_{0} )^{2} v^{\prime\prime}_{0} + (1/2)(w^{\prime}_{0} )^{2} v^{\prime\prime}_{0} + v^{\prime}_{0} w^{\prime}_{0} w^{\prime\prime}_{0} + \dot{\Omega }(R_{0} + x) + p_{y} , \hfill \\ \end{gathered} $$

(21)

$$ \begin{gathered} \ddot{w}_{0} - \Omega^{2} [((1/2)(1 - x^{2} ) + R_{0} (1 - x))w^{\prime\prime}_{0} - (R_{0} + x)w^{\prime}_{0} ] + (I_{z} w^{\prime\prime}_{0} )^{\prime\prime} + (I_{yz} v^{\prime\prime}_{0} )^{\prime\prime} \hfill \\ = 3(w^{\prime}_{0} )^{2} w^{\prime\prime}_{0} + (1/2)(v^{\prime}_{0} )^{2} w^{\prime\prime}_{0} + v^{\prime}_{0} w^{\prime}_{0} v^{\prime\prime}_{0} + p_{z} , \hfill \\ \end{gathered} $$

(22)

and non-dimensional boundary conditions are

at $x = 0$

$$ v_{0} = 0,w_{0} = 0,\,v^{\prime}_{0} = 0,w^{\prime}_{0} = 0, $$

(23)

at $x = 1$

$$ \begin{aligned} & v_{0}^{\prime 3} + (1/2)v^{\prime}_{0} w_{0}^{\prime 2} + (I_{y} v^{\prime\prime}_{0} - I_{yz} w^{\prime\prime}_{0} )^{\prime} = 0, \\ & w_{0}^{\prime 3} + (1/2)w^{\prime}_{0} v_{0}^{\prime 2} + (I_{z} w^{\prime\prime}_{0} - I_{yz} v^{\prime\prime}_{0} )^{\prime} = 0, \\ & v^{\prime\prime}_{0} = (I_{z} /I_{yz} )w^{\prime\prime}_{0} ,\,w^{\prime\prime}_{0} = (I_{y} /I_{yz} )v^{\prime\prime}_{0} , \\ \end{aligned} $$

(24)

In Eqs. (21–24), the bar sign is eliminated for simplicity.

3 Galerkin discretization

The Galerkin method is utilized to truncate Eqs. (21–22) by using the following approximation

$$ v_{0} (x,t) = p(t)H(x), $$

(25)

$$ w_{0} (x,t) = q(t)H(x), $$

(26)

where in the above equations $p(t),q(t)$ are the related time-dependent generalized coordinate variables and $H(x)$ is the shape function of the cantilevered beam which is given as:

$$ H(x) = \cosh (rx) - \cos (rx) - [(\cosh (r) + \cos (r))/(\sinh (r) + \sin (r))](\sinh (rx) - \sin (rx)), $$

(27)

where in Eq. (27), r is the root of

$$ \cosh (r)\cos (r) + 1 = 0, $$

(28)

Substituting Eqs. (25–26) in to Eqs. (21–22) and multiplying by $H(x)$ and integrating from 0 to 1, the following equations in the time domain are obtained:

$$ \begin{aligned} & [n_{5} ]\ddot{p}(t) + [n_{11} ]\dot{p}(t) + [n_{2} ]\dot{q}(t) + [n_{62} ]p^{3} (t) + [n_{61} ]q^{2} (t)p(t) \\ & \quad + [n_{13} + n_{17} - n_{10} \Omega_{0}^{2} ]p(t) + [n_{14} + n_{8} ]q(t) - 2[n_{10} ][\Omega_{0} ][A_{\Omega } ][p(t)][\cos (\omega_{\Omega } t)] \\ & \quad - [n_{10} ][A_{\Omega }^{2} ][p(t)][\cos^{2} (\omega_{\Omega } t)] = [n_{9} ][A_{\Omega } ][\omega_{\Omega } ][\sin (\omega_{\Omega } t)], \\ \end{aligned} $$

(29)

$$ \begin{aligned} & [n_{5} ]\ddot{q}(t) + [n_{21} ]\dot{q}(t) + [n_{2} ]\dot{p}(t) + [n_{62} ]q^{3} (t) + [n_{61} ]p^{2} (t)q(t) \\ & \quad + [n_{24} + n_{27} - n_{20} \Omega_{0}^{2} ]q(t) + [n_{23} + n_{8} ]p(t) - 2[n_{20} ][\Omega_{0} ][A_{\Omega } ][q(t)][\cos (\omega_{\Omega } t)] \\ & \quad - [n_{20} ][A_{\Omega }^{2} ][q(t)][\cos^{2} (\omega_{\Omega } t)] = 0, \\ \end{aligned} $$

(30)

where, the coefficients of Eqs. (29–30) are given in the Appendix 1. Dividing Eqs. (29) and (30) by n₅, the following equations are obtained as:

$$ \begin{aligned} & \ddot{p}(t) + [m_{12} ]\dot{p}(t) + [m_{13} ]\dot{q}(t) + [m_{52} ]p^{3} (t) + [m_{51} ]q^{2} (t)p(t) \\ & \quad + [\omega_{v}^{2} ]p(t) + [m_{11} ]q(t) - 2[m_{14} ][\Omega_{0} ][A_{\Omega } ][p(t)][\cos (\omega_{\Omega } t)] \\ & \quad - [m_{14} ][A_{\Omega }^{2} ][p(t)][\cos^{2} (\omega_{\Omega } t)] = [m_{16} ][A_{\Omega } ][\omega_{\Omega } ][\sin (\omega_{\Omega } t)], \\ \end{aligned} $$

(31)

$$ \begin{aligned} & \ddot{q}(t) + [m_{23} ]\dot{q}(t) + [m_{22} ]\dot{p}(t) + [m_{52} ]q^{3} (t) + [m_{51} ]p^{2} (t)q(t) \\ & \quad + [\omega_{w}^{2} ]q(t) + [m_{21} ]p(t) - 2[m_{24} ][\Omega_{0} ][A_{\Omega } ][q(t)][\cos (\omega_{\Omega } t)] \\ & \quad - [m_{24} ][A_{\Omega }^{2} ][q(t)][\cos^{2} (\omega_{\Omega } t)] = 0, \\ \end{aligned} $$

(32)

where, the coefficients in Eqs. (31–32) are defined in the Appendix 1.

4 Multiple scales method

Equations (31–32) can be changed to the Eqs. (34–35) by using the given assumption in (33):

$$ \begin{array}{*{20}l} {m_{11} \, \to \,\varepsilon m_{11} } \hfill & {m_{12} \, \to \,\varepsilon m_{12} } \hfill & {m_{13} \, \to \,\varepsilon m_{13} } \hfill \\ {m_{14} \, \to \,\varepsilon m_{14} } \hfill & {m_{51} \, \to \,\varepsilon m_{51} } \hfill & {m_{52} \, \to \,\varepsilon m_{52} } \hfill \\ {m_{16} \, \to \,\varepsilon m_{16} } \hfill & {m_{21} \, \to \,\varepsilon m_{21} } \hfill & {m_{22} \, \to \,\varepsilon m_{22} } \hfill \\ {m_{23} \, \to \,\varepsilon m_{23} } \hfill & {m_{24} \, \to \,\varepsilon m_{24} } \hfill & {} \hfill \\ \end{array} $$

(33)

$$ \begin{aligned} & \ddot{p}(t) + [\omega_{v}^{2} ]p(t) = - \varepsilon [m_{12} ][\dot{p}(t)] - \varepsilon [m_{13} ][\dot{q}(t)] - \varepsilon [m_{52} ][p^{3} (t)] - \varepsilon [m_{51} ][q^{2} (t)p(t)] \\ & \quad - \varepsilon [m_{11} ][q(t)] + 2\varepsilon [m_{14} ][\Omega_{0} ][A_{\Omega } ][p(t)]\cos (\omega_{\Omega } t) + \varepsilon [m_{14} ][A_{\Omega }^{2} ][p(t)]\cos^{2} (\omega_{\Omega } t) \\ & \quad + \varepsilon [m_{16} ][A_{\Omega }^{{}} ][\omega_{\Omega } ]\sin (\omega_{\Omega } t), \\ \end{aligned} $$

(34)

$$ \begin{aligned} & \ddot{q}(t) + [\omega_{w}^{2} ]q(t) = - \varepsilon [m_{22} ][\dot{p}(t)] - \varepsilon [m_{23} ][\dot{q}(t)] - \varepsilon [m_{52} ][q^{3} (t)] - \varepsilon [m_{51} ][p^{2} (t)q(t)] \\ & \varepsilon [m_{21} ][p(t)] + 2\varepsilon [m_{24} ][\Omega_{0} ][A_{\Omega } ][q(t)]\cos (\omega_{\Omega } t) + \varepsilon [m_{24} ][A_{\Omega }^{2} ][q(t)]\cos^{2} (\omega_{\Omega } t) \\ \end{aligned} $$

(35)

where $\varepsilon$ is a small perturbation parameter and $\omega_{v} ,\,\omega_{w}$ are defined in the Appendix 1. $p(t,\varepsilon ),\,q(t,\varepsilon )$ can be taken as a formal asymptotic expansion in terms of $\varepsilon$ as:

$$ p(t,\varepsilon ) = p_{0} (T_{0} ,T_{1} ) + \varepsilon p_{1} (T_{0} ,T_{1} ), $$

(36)

$$ q(t,\varepsilon ) = q_{0} (T_{0} ,T_{1} ) + \varepsilon q_{1} (T_{0} ,T_{1} ), $$

(37)

where $T_{0} = t,\,T_{1} = \varepsilon t$. Substituting Eqs. (36–37) in to (34–35) and using the derivatives $d/dt = D_{0} + \varepsilon D_{1} + \cdots ,\,\,d^{2} /dt^{2} = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \cdots$, the terms with equal orders of ε is balanced as:

Order $\varepsilon^{0} :$

$$ D_{0}^{2} p_{0} + [\omega_{v}^{2} ]p_{0} = 0, $$

(38)

$$ D_{0}^{2} q_{0} + [\omega_{w}^{2} ]q_{0} = 0, $$

(39)

Order $\varepsilon^{1} :$

$$ \begin{aligned} & D_{0}^{2} p_{1} + [\omega_{v}^{2} ]p_{1} = - 2D_{0} D_{1} p_{0} - [m_{12} ]D_{0} p_{0} - [m_{13} ]D_{0} q_{0} - [m_{11} ]q_{0} \\ & \quad + 2[m_{14} ][p_{0} ][\Omega_{0} ][A_{\Omega } ]\cos (\omega_{\Omega } t) + [m_{14} ][p_{0} ][A_{\Omega }^{2} ]\cos^{2} (\omega_{\Omega } t) - [m_{51} ]p_{0} q_{0}^{2} \\ & \quad - [m_{52} ]p_{0}^{3} + [m_{16} ][A_{\Omega } ][\omega_{\Omega } ]\sin (\omega_{\Omega } t), \\ \end{aligned} $$

(40)

$$ \begin{aligned} & D_{0}^{2} q_{1} + [\omega_{w}^{2} ]q_{1} = - 2D_{0} D_{1} q_{0} - [m_{22} ]D_{0} p_{0} - [m_{23} ]D_{0} q_{0} - [m_{21} ]p_{0} \\ & \quad + 2[m_{24} ][q_{0} ][\Omega_{0} ][A_{\Omega } ]\cos (\omega_{\Omega } t) + [m_{24} ][q_{0} ][A_{\Omega }^{2} ]\cos^{2} (\omega_{\Omega } t) - [m_{51} ]q_{0} p_{0}^{2} \\ & \quad - [m_{52} ]q_{0}^{3} , \\ \end{aligned} $$

(41)

The solutions of Eqs. (40–41) are in complex form as

$$ p_{0} = A_{1} (T_{1} )e^{{i\omega_{v} T_{0} }} + \overline{{A_{1} }} (T_{1} )e^{{ - i\omega_{v} T_{0} }} , $$

(42)

$$ q_{0} = A_{2} (T_{1} )e^{{i\omega_{w} T_{0} }} + \overline{{A_{2} }} (T_{1} )e^{{ - i\omega_{w} T_{0} }} , $$

(43)

where, $\overline{A}_{1} (T_{1} ),\,\overline{A}_{2} (T_{1} )$ are the complex conjugates of the $A_{1} (T_{1} ),\,A_{2} (T_{1} )$ respectively. Substituting Eqs. (42–43) in to the right hand of Eqs. (40–41), we get

$$ D_{0}^{2} p_{1} + [\omega_{v}^{2} ]p_{1} = RHp, $$

(44)

$$ D_{0}^{2} q_{1} + [\omega_{w}^{2} ]q_{1} = RHq, $$

(45)

where $RHp,RHq$ are respectively right hand of Eqs. (44) and (45) which are written in the Appendix 2.

5 Modulation equations

In this section, the modulation equations are derived for different cases of primary and internal resonances. After separating the secular terms, the modulation equations in the complex form are obtained and then are converted to the Cartesian form. The complex and Cartesian forms of the equations for the cases 1:6 are presented in the Appendix 2 as follows:

• Case1: $\omega_{\Omega } = \omega_{v} + \varepsilon \sigma$. Eqs. (B.3)–(B.9).

• Case2: $\omega_{\Omega } = \omega_{w} + \varepsilon \sigma$. Eqs. (B.10)–(B.16).

• Case 3: $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$. Eqs. (B.17)–(B.23).

• Case4: $\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma$. Eqs. (B.24)–(B.30).

• Case 5: $\omega_{\Omega } = \omega_{v} + \varepsilon \sigma$, $\omega_{w} = \omega_{v} + \varepsilon \delta /2$. Eqs. (B.31)–(B.37).

• Case 6: $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$, $\omega_{w} = \omega_{v} + \varepsilon \delta /2$. Eqs. (B.38)–(B.44).

In each case, $A_{1}$ and $A_{2}$ are defined and are substituted in modulation equations. Then real and imaginary parts are separated and equations are obtained in Cartesian form. The parameters $\sigma ,\delta$ are utilized for detuning external and internal resonances.

The fixed points of equations in each case are obtained from $p^{\prime}_{1} = q^{\prime}_{1} = p^{\prime}_{2} = q^{\prime}_{2} = 0.$ A pseudo-arc length continuation is applied to trace the branches of steady state responses. The fixed points lose the stability through the saddle-node, pitchfork or Hopf bifurcations.

6 Whitehead's theory

Whitehead's unsteady aerodynamic theory is used to derive the aerodynamic loading of the system [30]. The system of blades is considered as a two dimensional cascade and the effects of airfoil camber and thickness are neglected. The basic assumptions of the Whitehead's theory are

• 1. The airfoils vibrate in the bending and torsion modes with a constant phase angles between two adjacent blades and the amplitude of vibration are assumed to be small.

• 2. The flow is considered as subsonic, incompressible and inviscid.

The Lift and moment of the vibrating blades per unit length are derived as

$$ L(s) = - \pi \rho_{\infty } (a/2)^{3} \omega^{2} \sum\limits_{r = 0}^{N - 1} {[l_{hhr} \frac{{2h_{ar} }}{a} + l_{h\theta r} \theta_{ar} + l_{whr} ]} e^{{i(\omega t + \sigma_{r} s)}} $$

(46)

$$ M(s) = - \pi \rho_{\infty } (a/2)^{3} \omega^{2} \sum\limits_{r = 0}^{N - 1} {[l_{hhr} \frac{{2h_{ar} }}{a} + l_{h\theta r} \theta_{ar} + l_{whr} ]} e^{{i(\omega t + \sigma_{r} s)}} $$

(47)

where, $h_{ar} ,\theta_{ar}$ are the bending and torsional degrees of freedom of the blades in the rth mode. The coefficients $l_{hhr} ,l_{h\theta r} ,l_{whr} ,l_{\theta hr} ,l_{\theta \theta r} ,l_{w\theta r}$ are defined as

$$ \begin{aligned} l_{hhr} & = \frac{2i}{k}C_{Fq} , \\ l_{h\theta r} & = \frac{2}{{k^{2} }}(C_{F\theta } - i\lambda \eta C_{Fq} ), \\ l_{\theta hr} & = \frac{4i}{k}(C_{Mq} - \eta C_{Fq} ), \\ l_{\theta \theta r} & = \frac{4i}{{k^{2} }}(C_{M\theta } - \eta C_{Fq} - i\lambda \eta C_{Mq} + i\lambda \eta^{2} C_{Fq} ), \\ l_{whr} & = \frac{{ - 2w_{r} }}{{k^{2} P}}(e^{i\lambda \eta } C_{Fw} ), \\ l_{w\theta r} & = \frac{{ - 4w_{r} }}{{k^{2} P}}(e^{i\lambda \eta } C_{Mw} - \eta e^{i\lambda \eta } C_{Fw} ), \\ \lambda & = 2k,\quad \eta = \frac{1 + a}{2},\quad k = \frac{a\omega }{{2P}} \\ \end{aligned} $$

(48)

where, $\rho_{\infty }$ is the fluid density, $P$ is the free stream velocity relative to the blade and $w_{r}$ is the velocity induced by wakes. The coefficients $C_{Fq} ,C_{F\theta } ,C_{Mq} ,C_{M\theta } ,C_{Fw} ,C_{Mw}$ are evaluated by knowing the reduced frequency k, inter-blade phase angle $\sigma_{r}$ and the stagger angle $\alpha$. The coefficients $l_{whr} ,l_{w\theta r}$ are neglected which are used for the blades operating in the wakes. Since this work is focused on the bending vibration of the turbomachinery cascades, only the lift force is only considered in this analysis. The work done by the aerodynamic lift is evaluated and is substituted instead of the aerodynamic forces of Piston theory in Eqs. (21) and (22). The aerodynamic lift forces $L\sin (\alpha + \beta (x)), - L\cos (\alpha + \beta (x))$ are respectively added to the right hand of the Eqs. (21) and (22). By applying the Galekin method, the following equations are obtained

$$ \begin{gathered} \ddot{p}(t) + [m_{12} ]\dot{p}(t) + [m_{13} ]\dot{q}(t) + [m_{52} ]p^{3} (t) + [m_{51} ]q^{2} (t)p(t) + \hfill \\ [\omega_{v}^{2} ]p(t) + [m_{11} ]q(t) - 2[m_{14} ][\Omega_{0} ][A_{\Omega } ][p(t)][\cos (\omega_{\Omega } t)] - \hfill \\ [m_{14} ][A_{\Omega }^{2} ][p(t)][\cos^{2} (\omega_{\Omega } t)] - [m_{16} ][A_{\Omega } ][\omega_{\Omega } ][\sin (\omega_{\Omega } t)] - [m_{1L} ]e^{{i\omega_{L} t}} = 0, \hfill \\ \end{gathered} $$

(49)

$$ \begin{gathered} \ddot{q}(t) + [m_{23} ]\dot{q}(t) + [m_{22} ]\dot{p}(t) + [m_{52} ]q^{3} (t) + [m_{51} ]p^{2} (t)q(t) + \hfill \\ [\omega_{w}^{2} ]q(t) + [m_{21} ]p(t) - 2[m_{24} ][\Omega_{0} ][A_{\Omega } ][q(t)][\cos (\omega_{\Omega } t)] - \hfill \\ [m_{24} ][A_{\Omega }^{2} ][q(t)][\cos^{2} (\omega_{\Omega } t)] + [m_{2L} ]e^{{i\omega_{L} t}} = 0, \hfill \\ \end{gathered} $$

(50)

where, the coefficients of Eqs. (49) and (50) are given in the Appendix 2.

7 Numerical results

The steady state response of the rotatory beam with varying speed is investigated in this section. The Eqs. (B.31)–(B.37) in the Appendix 2 are obtained for primary and 1:1 internal resonances. The coefficients of these equations agree closely with the coefficients of modulation equations of thin-walled model [5] by ignoring thermal distribution in beam. The fixed points of the obtained equations for the thin-walled structure in Ref. [5] are plotted in Fig. 2. Fixed points lose the stability through a Hopf bifurcation at $A_{\Omega } = 2.7$. The results are in good agreement with numerical results in Ref. [5].

Fig. 2

Amplitude $x_{1}$ as a function of $A_{\Omega }$.(___) stable, (….) unstable with the real part of a complex conjugate pair of eigenvalues being positive, HF, Hopf bifurcation

The equilibrium points and their stability are presented in steady state responses. For this purpose, $p^{\prime}_{1} = q^{\prime}_{1} = p^{\prime}_{2} = q^{\prime}_{2} = 0$ in different cases and then the resulting equations are solved for $p_{1} ,q_{1} ,p_{2} ,q_{2}$ and specified values of $\sigma ,\delta$. The amplitudes $a_{1} ,a_{2}$ are evaluated from $a_{i} = (p_{i}^{2} + q_{i}^{2} )^{1/2} ,i = 1,2$. In all figures, the settling angle and pretwist angle at the tip of blade are equal to $\alpha = 10\deg ,\beta_{0} = 45\deg$ respectively. Moreover, in order to verify the frequency responses of the system under flapwise and chordewise excitations, the obtained amplitudes by the arc-length continuation method are authenticated by the Rang-kutta method.

Figure 3 shows the softening frequency response for $\omega_{\Omega } = \omega_{v} + \varepsilon \sigma ,\,A_{\Omega } = 0.05$.Mach numbers are 4,5 and amplitudes are almost the same and coincide together. As the frequency decreases, a jump phenomenon occurs at $\sigma = - 2$ and the amplitude is lessened from $a_{1} = 0.4176$ to zero as well.

Fig. 3

Variation of the response amplitude with the frequency detuning parameter $\sigma$.(___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Figure 4 shows the amplitude of rotatory beam versus $A_{\Omega }$ with the frequency of the excitation $\omega_{\Omega }$ held fixed ($\sigma = 1$). As $A_{\Omega }$ increases from -10 to -0.855, the stable amplitude $a_{1}$ decreases. Amplitudes $a_{1}$ and $a_{2}$ are zero from $A_{\Omega }$ equal -0.855 to 0.855. For further values of $A_{\Omega }$ from 0.855 to 10, stable branch of $a_{1}$ increases.

Fig. 4

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$.(___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Figures 5 and 6 show the amplitude of responses for sub-harmonic resonance case $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$ and $\alpha = 10\deg$, $\beta_{0} = 45\deg ,M = 5$. Figure 5 is plotted for $A_{\Omega } = 0.01$ and Fig. 6 is plotted for $\sigma = 0.$ In Fig. 5, the softening planar response is represented and the nonlinear inertia terms are dominant for $A_{\Omega } = 0.01$. As shown in Fig. 6, the amplitude $a_{2}$ is zero in the whole domain and $a_{1}$ is decreased for $A_{\Omega }$ from -0.1 to zero and is increased from zero to 0.1.

Fig. 5

Variation of the response amplitude with the frequency detuning parameter $\sigma$ for sub-harmonic resonance $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Fig. 6

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\,\sigma = 0.$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$

Figure 7 shows amplitude of responses versus the dimensionless parameter $A_{\Omega }$ for subharmonic resonance $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$ and detuning parameters $\sigma = 0.1,1.$ As seen in parts (a) and (b), $a_{2}$ is zero in whole domain and $a_{1}$ is zero for $\sigma = 0.1,1$ in the ranges $- 0.078 \le A_{\Omega } \le 0.078$ and $- 0.49 \le A_{\Omega } \le 0.49$ respectively. There are two points $PF_{1} ,PF_{2}$ with pitchfork bifurcations. For $A_{\Omega } \le PF_{1}$ and $A_{\Omega } \ge PF_{2}$, the amplitude of $a_{1}$ increases. Comparison of Figs. 6, 7 show that when the detuning parameter $\sigma$ increases the pitchfork bifurcations occur in a wider range of $A_{\Omega }$. Figure 8 shows the amplitude of responses versus $A_{\Omega }$ for sub-harmonic resonance case $\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma ,\,\sigma = 1,5.$ As seen in Fig. 8, the amplitude $a_{1}$ is zero in the whole domain. Two stable branches of $a_{2}$ increase for $A_{\Omega } \le PF_{1}$ or $A_{\Omega } \ge PF_{2}$. Figure 8 b presents $a_{2}$ is zero in $- 1.133 \le A_{\Omega } \le 1.133$ for $\,\sigma = 5$ and $- 0.391 \le A_{\Omega } \le 0.391$ for $\,\sigma = 1$ respectively.

Fig. 7

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\,\sigma = 0.1,1.$$\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$. (___) stable, (---) unstable with at least one eigenvalue being positive, PF, pitchfork bifurcation

Fig. 8

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\,\sigma = 1,5.$$(\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, PF, pitchfork bifurcation

Figure 9 is repeated for $\sigma = - 0.1$. As seen in this figure, supercritical and subcritical pitchfork bifurcations occur at $A_{\Omega } = - 0.0714,0.0714$ respectively. By increasing $A_{\Omega }$ from 0 to 0.15 and by decreasing $A_{\Omega }$ from 0.05 to -0.15 a jump phenomenon occurs at $A_{\Omega } = 0.00013$ and $a_{2}$ increases.

Fig. 9

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\,\sigma = - 0.1.$$(\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node, PF, pitchfork bifurcation

Figure 10 shows the amplitude versus $A_{\Omega }$ for $\omega_{\Omega } = \omega_{w} + \varepsilon \sigma ,\sigma = 1,5.$ amplitude of $a_{1}$ is zero in whole range of considered $A_{\Omega }$ and $a_{2}$ is zero $- 0.729 \le A_{\Omega } \le 0.729$,$\sigma = 1$ and $- 1.631 \le A_{\Omega } \le 1.631$, $\sigma = 5.$ For $A_{\Omega } \le PF_{1}$ as $A_{\Omega }$ decreases or for $A_{\Omega } \ge PF_{2}$ as $A_{\Omega }$ increases, the stable branch of $a_{2}$ increases.

Fig. 10

Variation of the response amplitude with the amplitude of periodic angular velocity $\Omega_{2}$ for $\,\sigma = 1,5.$$(\omega_{\Omega } = \omega_{w} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, PF, pitchfork bifurcation

Figures 11, 12, 13, 14, 15, 16, 17 show the amplitude of fixed points for $\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma$ or $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma$ and 1–1 internal resonance $\omega_{w} = \omega_{v} + \varepsilon \delta /2$. Figure 11 shows the amplitudes $a_{1} ,a_{2}$ versus $A_{\Omega }$ for detuning parameters $\sigma = 0.1,\delta = 0.$ it is noted that $a_{1} ,a_{2}$ are zero in a range of $- 0.045 \le A_{\Omega } \le 0.045$. Pitchfork bifurcations occur at $A_{\Omega } = - 0.045,0.045.$ Moreover, transfer of energy occur between two modes due to internal resonance.

Fig. 11

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\sigma = 0.1,\delta = 0.$ $(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive

Fig. 12

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\,\sigma = 0.1,\delta = 0.1.$$(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, PF, pitchfork bifurcation

Fig. 13

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\sigma = - 0.1,\delta = - 0.1.$$(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node, PF, pitchfork bifurcation

Fig. 14

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\sigma = 0,\delta = 0.1.$$(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\,\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node, PF, pitchfork bifurcation

Fig. 15

Variation of the response amplitude with the internal detuning parameter $\delta$ for $A_{\Omega } = 0.1,\sigma = 0.$.$(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Fig. 16

Variation of the response amplitude with the internal detuning parameter $\delta$ for $A_{\Omega } = 0.1,\sigma = 0.1.$$(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node, (….) unstable with the real part of a complex conjugate pair of eigenvalues being positive, HF, Hopf bifurcation

Fig. 17

Variation of the response amplitude with the internal detuning parameter $\delta$ for $A_{\Omega } = 0.1,\sigma = - 0.1.$ $(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Figure 12 shows the amplitude of response as a function of $A_{\Omega }$ for internal resonance $\omega_{w} = \omega_{v} + \varepsilon \delta /2$ and two cases of subharmonic resonances (1) $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\sigma = 0.1,\delta = 0.1$ and (2) $\,\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma ,\sigma = 0.1,\delta = 0.1.$ In two cases, since the internal resonance occurs, both amplitudes $a_{1} ,a_{2}$ are excited. The response undergoes the subcritical pitchfork bifurcations at $A_{\Omega } = - 0.00673,\,0.00673$. As $A_{\Omega }$ increases from -0.1 to 0.1, the amplitudes undergo a saddle-node bifurcation at $A_{\Omega } = 0.001$, resulting in a jump in to non-planar response. For further values of $A_{\Omega }$ up to 0.1, $a_{1}$ and $a_{2}$ amplitudes increase. As $A_{\Omega }$ decreases from 0.1 to -0.1, a jump occurs at $A_{\Omega } = 0.001$ and $a_{1} ,a_{2}$ amplitudes increase from zero to 0.015. For lower values of $A_{\Omega }$, amplitudes increase. The external and internal detuning parameters are changed to $\sigma = - 0.1$ and $\delta = - 0.1$ respectively and amplitudes are plotted versus $A_{\Omega }$ in Fig. 13. As shown, the amplitudes undergo the saddle-node bifurcations at $A_{\Omega } = - 0.1015$ ($SN_{1}$) and $A_{\Omega } = 0.1015$($SN_{2}$) resulting in jump phenomenon. Moreover, a jump occurs at $A_{\Omega } = 0.0003$ and $a_{1} ,a_{2}$ amplitudes jump to values 0.0508 and 0.0226 respectively. Pitchfork bifurcations occur at $A_{\Omega } = - 0.00645$ ($PF_{1}$) and $A_{\Omega } = 0.00645$($PF_{2}$).

Figure 14 indicates the amplitudes for the perfectly external detuning parameter $\sigma = 0$ and internal detuning parameter $\delta = 0.1$. Saddle-node bifurcations $SN_{1} ,SN_{2}$ occur at $A_{\Omega } = - 0.0840,0.0840$ respectively which is resulted in two peaks bending to the left and right respectively. The heights of two peaks are the same. Pitchfork bifurcations occur at $A_{\Omega } = - 0.0097,0.0097$. Curves jump downwards for increasing $A_{\Omega }$ at $\Omega_{2} = 0.0840$ and for decreasing $A_{\Omega }$ at $A_{\Omega } = - 0.0840$. By increasing $A_{\Omega }$, amplitudes jump upwards $A_{\Omega } = 0.0002$ from zero to values 0.0226, 0.0508 for $a_{1} ,a_{2}$ respectively. Also, by decreasing $A_{\Omega }$ from 0.1 to zero, the amplitudes jump downwards at $A_{\Omega } = 0.0002$.

Figure 15 presents the amplitude as a function of internal detuning parameter $\delta$ for 1–1 internal resonance and $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\,A_{\Omega } = 0.1,\sigma = 0,$ or $\omega_{\Omega } = 2\omega_{w} + \varepsilon \sigma ,A_{\Omega } = 0.1,\sigma = 0.$ as $\delta$ increases from -1 to 5, the nontrivial solution undergoes a saddle-node bifurcation at $\delta = 0.115$. By increasing $\delta$ from 0 to 0.218, amplitudes jump upwards at $\delta = 0.115$ and by decreasing $\delta$ from 0.2 to zero, amplitudes jump downwards at $\delta = 0.115$. There are three points ($\delta = 0.115,0.218,0.258$) with saddle node bifurcations. As $\delta$ exceeds the critical value $\delta = 0.258$, $a_{1}$ saturates and $a_{2}$ decreases.

Figure 16 is repeated for detuning parameter $\sigma = 0.1$. There are two points ($\delta = - 0.0508,0.207$) with saddle-node bifurcation and two points ($\delta = 0.207,0.230$) with Hopf bifurcations. Dynamic response between two points $HF_{1} ,HF_{2}$ may be periodic or chaotic. A single jump occurs at $SN_{2}$ resulting in a non-planar response. For $\delta \ge 0.207$, $a_{1}$ saturates and $a_{2}$ decreases. Figure 17 is plotted for $\sigma = - 0.1$ and fixed points lose stability through saddle-node bifurcations at $\delta = - 0.283, - 0.274, - 0.096$. A pitchfork bifurcation occurs at $\delta = - 0.298$ and by increasing $\delta$, the amplitudes jump downwards at $\delta = - 0.283, - 0.096$. Figure 18 shows the amplitudes versus $\delta$ for $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\,A_{\Omega } = 1,\sigma = 1.$ There is a saddle-node bifurcation at $\delta = - 0.178$. for $A_{\Omega } = 1,\sigma = 1$, the $a_{2}$ amplitude bends to the right and the nonlinearity type is hardening.

Fig. 18

Variation of the response amplitude with the internal detuning parameter $\delta$ for $A_{\Omega } = 1,\sigma = 1.$ $(\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma )$. (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Figure 19 shows the amplitude of response as a function of $A_{\Omega }$ for internal resonance $\omega_{w} = \omega_{v} + \varepsilon \delta /2$, $\omega_{L} = \omega_{v} + \varepsilon \sigma$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\sigma = - 0.1,\delta = - 0.02$ by Whitehead's theory. Saddle-node bifurcations $SN_{1} ,SN_{6}$ occur at $A_{\Omega } = - 0.0520,0.0520$ respectively which result in two peaks bending to the left and right respectively. The heights of two peaks are the same. As seen in Fig. 19, the other symmetric jumps are presented at $SN_{2} ,SN_{5}$ respectively for $A_{\Omega } = - 0.0320,0.0320.$ Moreover, two saddle-node bifurcations $SN_{3} ,SN_{4}$ occur at $A_{\Omega } = - 0.0127,0.008$ respectively and the amplitudes lose the stability through the Hopf bifurcation ($HF$) at $A_{\Omega } = 9.65 \times 10^{ - 3}$. In the range of $A_{\Omega } = 9.65 \times 10^{ - 3}$ to $A_{\Omega } = 6 \times 10^{ - 3}$ periodic, quasi-periodic or chaotic motions may be occurred.

Fig. 19

Variation of the response amplitude with the amplitude of periodic angular velocity $A_{\Omega }$ for $\omega_{w} = \omega_{v} + \varepsilon \delta /2$, $\omega_{L} = \omega_{v} + \varepsilon \sigma$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\sigma = - 0.1,\delta = - 0.02$. (Whitehead's theory) (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node, (….) unstable with the real part of a complex conjugate pair of eigenvalues being positive, HF, Hopf bifurcation

Figure 20 presents the amplitude as a function of internal detuning parameter $\delta$ for 1–1 internal resonance and $\omega_{L} = \omega_{v} + \varepsilon \sigma$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\,A_{\Omega } = 1,\sigma = - 0.02$ by Whitehead's theory. The fixed points lose stability through saddle-node bifurcations at $SN_{1} ,SN_{2} ,SN_{3}$ respectively for detuning parameters $\delta = - 0.283, - 0.283, - 0.283.$ Moreover, the $a_{2}$ amplitude bends to the right and the type of nonlinearity is hardening.

Fig. 20

Variation of the response amplitude with the internal detuning parameter $\delta$ for $\omega_{w} = \omega_{v} + \varepsilon \delta /2$, $\omega_{L} = \omega_{v} + \varepsilon \sigma$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\sigma = - 0.02,A_{\Omega } = 1$. (Whitehead's theory) (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

Figure 21 presents the amplitude as a function of internal detuning parameter $\sigma$ for 1–1 internal resonance and $\omega_{L} = \omega_{v} + \varepsilon \sigma$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\,A_{\Omega } = 0,\delta = - 2$ by Whitehead's theory. The $a_{2}$ amplitude bends to the left and the nonlinearity type is softening. Jumps occur at $SN_{1} ,SN_{2}$ for detuning parameters $\sigma = - 0.007, - 1.09$ respectively.

Fig. 21

Variation of the response amplitude with the detuning parameter $\sigma$ for $\omega_{w} = \omega_{v} + \varepsilon \delta /2$, $\omega_{L} = \omega_{v} + \varepsilon \sigma$ $\omega_{\Omega } = 2\omega_{v} + \varepsilon \sigma ,\delta = - 2,A_{\Omega } = 0$. (Whitehead's theory) (___) stable, (---) unstable with at least one eigenvalue being positive, SN, saddle-node

8 Conclusion

Nonlinear vibration of the rotatory Euler–Bernoulli beam with time-varying angular velocity is inquired under aerodynamic loads. Nonlinearity comes from varying speed, strain–displacement relation and aerodynamic forces. The equations describing the flexural and lateral motions of the pretwist, presetting rotatory beam are obtained and are transformed to the discrete ones by the Galerkin method. The multiple scales method is employed and the four dimensional ordinary averaged equations are obtained for internal and primary resonances. The obtained and concluded results are as follows:

• (1) In the subharmonic and 1:1 internal resonance case, when the pulsation amplitude of varying speed function is changed the double-jump phenomenon appears in bifurcation diagrams.

• (2) Bifurcation diagrams are plotted for $M = 5$. For other Mach numbers from 0 to 5, amplitudes are almost as same as amplitudes for Mach 5.

• (3) Saturation of directly excited mode occurs for 1:1 internal and subharmonic resonances.

• (4) Periodic, quasi-periodic or chaotic motions appear between Hopf bifurcation points of amplitudes in subharmonic and 1:1 internal resonances.

• (5) By increasing the external detuning parameter in primary and suharmonic resonances, amplitude of excited mode is zero for the wider range of $A_{\Omega }$.

• (6) Softening and hardening type nonlinearities appear in amplitudes.

Appendices

Appendix 1

$$ n_{5} = \int_{0}^{1} {H^{2} (x)dx} $$

(A.1)

$$ n_{2} = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } (a - b)[\sin (\alpha + \beta x)][\cos (\alpha + \beta x)]H^{2} (x)dx $$

(A.2)

$$ n_{61} = \int_{0}^{1} { - (3/2)} H(x)[H^{\prime}(x)]^{2} H^{\prime\prime}(x)dx $$

(A.3)

$$ n_{17} = \int_{0}^{1} {H(x)} [I_{z} H^{\prime\prime}(x)]^{\prime\prime}dx $$

(A.4)

$$ \begin{aligned} n_{14} & = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } \{ P(a[\sin^{2} (\alpha + \beta x)][\cos (\alpha + \beta x)] \\ & \quad - b[\cos^{2} (\alpha + \beta x)][\sin (\alpha + \beta x)]H(x)H^{\prime}(x) + P\beta_{0} [ - a\sin^{3} (\alpha + \beta x)] \\ & \quad - b[\cos^{3} (\alpha + \beta x)]H^{2} (x)\} dx \\ \end{aligned} $$

(A.5)

$$ n_{10} = \int_{0}^{1} {[H^{2} (x) + ((1 - x^{2} )/2 + R_{0} (1 - x))H(x)H^{\prime\prime}(x) - } (R_{0} + x)H(x)H^{\prime}(x)]dx, $$

(A.6)

$$ n_{21} = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } ( - a[\cos^{2} (\alpha + \beta x)] - b[\sin^{2} (\alpha + \beta x)]H^{2} (x)dx, $$

(A.7)

$$ n_{27} = \int_{0}^{1} {H(x)} (I_{y} H^{\prime\prime}(x))^{\prime\prime}dx, $$

(A.8)

$$ \begin{aligned} n_{23} & = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } \{ P[a\sin^{2} (\alpha + \beta x)][\cos (\alpha + \beta x)] \\ & \quad - b[\cos^{2} (\alpha + \beta x)][\sin (\alpha + \beta x)]H(x)H^{\prime}(x) + P\beta_{0} (a[\sin (\alpha + \beta x)][\cos^{2} (\alpha + \beta x)] \\ & \quad + b[\sin^{2} (\alpha + \beta x)][\cos (\alpha + \beta x)]H^{2} (x)\} dx, \\ \end{aligned} $$

(A.9)

$$ n_{11} = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } ( - a[\sin^{2} (\alpha + \beta x)] - b[\cos^{2} (\alpha + \beta x)]H^{2} (x)dx, $$

(A.10)

$$ n_{62} = \int_{0}^{1} { - 3H(x)} [H^{\prime}(x)]^{2} H^{\prime\prime}(x)dx, $$

(A.11)

$$ \begin{aligned} n_{23} & = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } \{ P[ - a\sin^{3} (\alpha + \beta x)] \\ & \quad - b[\cos^{3} (\alpha + \beta x)]H(x)H^{\prime}(x) + P\beta_{0} ( - a[\sin^{2} (\alpha + \beta x)][\cos (\alpha + \beta x)] \\ & \quad + b[\sin (\alpha + \beta x)][\cos^{2} (\alpha + \beta x)]H^{2} (x)\} dx, \\ \end{aligned} $$

(A.12)

$$ n_{8} = \int_{0}^{1} {H(x)} (I_{yz} H^{\prime\prime}(x))^{\prime\prime}dx, $$

(A.13)

$$ n_{9} = \int_{0}^{1} {(R_{0} + x)H(x)} dx, $$

(A.14)

$$ \begin{aligned} n_{24} & = \int_{0}^{1} { - C_{\infty } } \rho_{\infty } \{ P[ - a\sin (\alpha + \beta x)][\cos^{2} (\alpha + \beta x)] \\ & \quad - b[\sin^{2} (\alpha + \beta x)][\cos (\alpha + \beta x)]H(x)H^{\prime}(x) + P\beta_{0} (a[\sin^{2} (\alpha + \beta x)][\cos (\alpha + \beta x)] \\ & \quad - b[\sin (\alpha + \beta x)][\cos^{2} (\alpha + \beta x)]H^{2} (x)\} dx, \\ \end{aligned} $$

(A.15)

$$ n_{20} = \int_{0}^{1} {[((1 - x^{2} )/2 + R_{0} (1 - x))H(x)H^{\prime\prime}(x) - } (R_{0} + x)H(x)H^{\prime}(x)]dx, $$

(A.16)

$$ \begin{aligned} m_{11} & = (n_{14} + n_{8} )/n_{5} ,\quad m_{12} = (n_{11} )/n_{5} ,\quad m_{21} = (n_{23} + n_{8} )/n_{5} ,\quad m_{22} = m_{13} = (n_{2} )/n_{5} , \\ m_{23} & = (n_{21} )/n_{5} ,\quad m_{14} = (n_{10} )/n_{5} , \\ \end{aligned} $$

(A.17)

$$ \begin{aligned} m_{24} & = (n_{20} )/n_{5} ,\quad m_{16} = (n_{9} )/n_{5} ,\quad m_{51} = (n_{61} )/n_{5} ,\quad m_{52} = (n_{62} )/n_{5} , \\ \omega_{v}^{2} & = (n_{13} + n_{17} - n_{10} \Omega_{0}^{2} )/(n_{5} ),\quad \omega_{w}^{2} = (n_{24} + n_{27} - n_{20} \Omega_{0}^{2} )/(n_{5} ), \\ \end{aligned} $$

(A.18)

Appendix 2

The right hand of Eqs. (44) and (45) are given in Eqs. (B.1) and (B.2) as follows

$$ \begin{aligned} & RHp = - 2\left\{ {[\partial A_{1} /\partial T_{1} ][i\omega_{v} ]e^{{i\omega_{v} T_{0} }} + [\partial \overline{A}_{1} /\partial T_{1} ][ - i\omega_{v} ]e^{{ - i\omega_{v} T_{0} }} } \right\} \\ & \quad - [m_{12} ]\left\{ {A_{1} [i\omega_{v} ]e^{{i\omega_{v} T_{0} }} + \overline{A}_{1} [ - i\omega_{v} ]e^{{ - i\omega_{v} T_{0} }} } \right\} \\ & \quad - [m_{13} ]\left\{ {A_{2} [i\omega_{w} ]e^{{i\omega_{w} T_{0} }} + \overline{A}_{2} [ - i\omega_{w} ]e^{{ - i\omega_{w} T_{0} }} } \right\} - [m_{11} ]\left\{ {A_{2} e^{{i\omega_{w} T_{0} }} + \overline{A}_{2} e^{{ - i\omega_{w} T_{0} }} } \right\} \\ & \quad + [m_{14} ][\Omega_{0} ][A_{\Omega } ]\left\{ {A_{1} e^{{i(\omega_{v} + \omega_{\Omega } )T_{0} }} + \overline{A}_{1} e^{{i(\omega_{\Omega } - \omega_{v} )T_{0} }} + A_{1} e^{{i(\omega_{v} - \omega_{\Omega } )T_{0} }} + \overline{A}_{1} e^{{i( - \omega_{\Omega } - \omega_{v} )T_{0} }} } \right\} \\ & \quad + [m_{14} /4][A_{\Omega }^{2} ]\left\{ {A_{1} e^{{i(\omega_{v} + 2\omega_{\Omega } )T_{0} }} + \overline{A}_{1} e^{{ - i(2\omega_{\Omega } - \omega_{v} )T_{0} }} + A_{1} e^{{i(\omega_{v} - 2\omega_{\Omega } )T_{0} }} + \overline{A}_{1} e^{{i( - 2\omega_{\Omega } - \omega_{v} )T_{0} }} } \right. \\ & \quad \left. { + 2A_{1} e^{{i(\omega_{v} )T_{0} }} + 2\overline{A}_{1} e^{{ - i(\omega_{v} )T_{0} }} } \right\} - [m_{52} ]\left\{ {A_{1}^{3} e^{{3i\omega_{v} T_{0} }} + 3A_{1}^{2} \overline{A}_{1} e^{{i\omega_{v} T_{0} }} + 3A_{1} \overline{A}_{1}^{2} e^{{ - i\omega_{v} T_{0} }} + \overline{A}_{1}^{3} e^{{ - 3i\omega_{v} T_{0} }} } \right\} \\ & \quad + [m_{16} ][A_{\Omega }^{{}} ][\omega_{\Omega } ]\left\{ {[e^{{i\omega_{\Omega } T_{0} }} - e^{{ - i\omega_{\Omega } T_{0} }} ]/2} \right\}, \\ \end{aligned} $$

(B.1)

$$ \begin{aligned} & RHq = - 2\left\{ {[\partial A_{2} /\partial T_{1} ][i\omega_{w} ]e^{{i\omega_{w} T_{0} }} + [\partial \overline{A}_{2} /\partial T_{1} ][ - i\omega_{w} ]e^{{ - i\omega_{w} T_{0} }} } \right\} \\ & \quad - [m_{22} ]\left\{ {A_{1} [i\omega_{v} ]e^{{i\omega_{v} T_{0} }} + \overline{A}_{1} [ - i\omega_{v} ]e^{{ - i\omega_{v} T_{0} }} } \right\} \\ & \quad - [m_{23} ]\left\{ {A_{2} [i\omega_{w} ]e^{{i\omega_{w} T_{0} }} + \overline{A}_{2} [ - i\omega_{w} ]e^{{ - i\omega_{w} T_{0} }} \} - [m_{21} ]\{ A_{1} e^{{i\omega_{v} T_{0} }} + \overline{A}_{1} e^{{ - i\omega_{v} T_{0} }} } \right\} \\ & \quad + [m_{24} ][\Omega_{0} ][A_{\Omega } ]\left\{ {A_{2} e^{{i(\omega_{w} + \omega_{\Omega } )T_{0} }} + \overline{A}_{2} e^{{i(\omega_{\Omega } - \omega_{w} )T_{0} }} + A_{2} e^{{i(\omega_{w} - \omega_{\Omega } )T_{0} }} + \overline{A}_{2} e^{{i( - \omega_{\Omega } - \omega_{w} )T_{0} }} } \right\} \\ & \quad + [m_{24} /4][A_{\Omega }^{2} ]\left\{ {A_{2} e^{{i(\omega_{w} + 2\omega_{\Omega } )T_{0} }} + \overline{A}_{2} e^{{ - i(2\omega_{\Omega } - \omega_{w} )T_{0} }} + A_{2} e^{{i(\omega_{w} - 2\omega_{\Omega } )T_{0} }} + \overline{A}_{2} e^{{i( - 2\omega_{\Omega } - \omega_{w} )T_{0} }} } \right. \\ & \quad \left. { + 2A_{2} e^{{i(\omega_{w} )T_{0} }} + 2\overline{A}_{2} e^{{ - i(\omega_{w} )T_{0} }} } \right\} - [m_{52} ]\left\{ {A_{2}^{3} e^{{3i\omega_{w} T_{0} }} + 3A_{2}^{2} \overline{A}_{2} e^{{i\omega_{w} T_{0} }} + 3A_{2} \overline{A}_{2}^{2} e^{{ - i\omega_{w} T_{0} }} + \overline{A}_{2}^{3} e^{{ - 3i\omega_{w} T_{0} }} } \right\} \\ & \quad - [m_{51} ]\left\{ {A_{1}^{2} A_{2} e^{{i(\omega_{w} + 2\omega_{v} )T_{0} }} + \overline{A}_{1}^{2} A_{2} e^{{i(\omega_{w} - 2\omega_{v} )T_{0} }} + 2A_{1} \overline{A}_{1} A_{2} e^{{i(\omega_{w} )T_{0} }} + A_{1}^{2} \overline{A}_{2} e^{{i(2\omega_{v} - \omega_{w} )T_{0} }} } \right. \\ & \quad \left. { + \overline{A}_{1}^{2} \overline{A}_{2} e^{{i( - \omega_{w} - 2\omega_{v} )T_{0} }} + 2A_{1} \overline{A}_{1} \overline{A}_{2} e^{{ - i(\omega_{w} )T_{0} }} } \right\}, \\ \end{aligned} $$

(B.2)

The modulation equations for case 1:

$$ \begin{aligned} D_{1} A_{1} & = - [m_{12} /2][A_{1} ] + i[m_{51} /\omega_{v} ][A_{1} ][A_{2}^{2} ] + i[3m_{52} /2\omega_{v} ][A_{1}^{2} ][\overline{A}_{1} ] - [m_{16} /4\omega_{v} ][\omega_{\Omega } ][A_{\Omega } ][e^{{i\sigma T_{1} }} ] \\ & \quad - i[m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][A_{1} ] - i[m_{14} /8\omega_{v} ][A_{\Omega }^{2} ][\overline{A}_{1} ][e^{{2i\sigma T_{1} }} ], \\ \end{aligned} $$

(B.3)

$$ D_{1} A_{2} = - [m_{23} /2][A_{2} ] + i[m_{51} /\omega_{w} ][A_{1} ][\overline{A}_{1} ][A_{2}^{{}} ] + i[3m_{52} /2\omega_{v} ][A_{2}^{2} ][\overline{A}_{2} ] - i[m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][A_{2} ], $$

(B.4)

$$ A_{1} = (1/2)(p_{1} - iq_{1} )[e^{{i\sigma T_{1} }} ],A_{2} = (1/2)(p_{2} - iq_{2} ), $$

(B.5)

$$ \begin{aligned} p^{\prime}_{1} & = - [\sigma ][q_{1} ] - [m_{12} /2][p_{1} ] - [m_{16} /2\omega_{v} ][A_{\Omega } ][\varepsilon \sigma + \omega_{v} ] + [m_{51} /4\omega_{v} ][q_{1} ][p_{2}^{2} ] \\ & \quad + [m_{51} /4\omega_{v} ][q_{1} ][q_{2}^{2} ] - [m_{14} /8\omega_{v} ][A_{\Omega }^{2} ][q_{1} ] + [3m_{52} /8\omega_{v} ][p_{1}^{2} ][q_{1} ] + [3m_{52} /8\omega_{v} ][q_{1}^{3} ], \\ \end{aligned} $$

(B.6)

$$ \begin{aligned} q^{\prime}_{1} & = - [\sigma ][p_{1} ] - [m_{12} /2]q_{1} - [m_{51} /4\omega_{v} ]p_{1} p_{2}^{2} - [m_{51} /4\omega_{v} ]p_{1} q_{2}^{2} \\ & \quad + [3m_{14} /8\omega_{v} ][A_{\Omega }^{2} ]p_{1} - [3m_{52} /8\omega_{v} ]p_{1} q_{1}^{2} - [3m_{52} /8\omega_{v} ]p_{1}^{3} , \\ \end{aligned} $$

(B.7)

$$ \begin{aligned} p^{\prime}_{2} & = - [m_{23} /2]p_{2} - [m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][q_{2} ] + [m_{51} /4\omega_{w} ]q_{2} p_{1}^{2} \\ & \quad + [m_{51} /4\omega_{w} ]q_{2} q_{1}^{2} + [3m_{52} /8\omega_{w} ][p_{2}^{2} ][q_{2} ] + [3m_{52} /8\omega_{w} ]q_{2}^{3} , \\ \end{aligned} $$

(B.8)

$$ \begin{aligned} q^{\prime}_{2} & = - [m_{23} /2]q_{2} + [m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][p_{2} ] - [m_{51} /4\omega_{w} ]p_{2} p_{1}^{2} \\ & \quad - [m_{51} /4\omega_{w} ]p_{2} q_{1}^{2} - [3m_{52} /8\omega_{w} ][q_{2}^{2} ][p_{2} ] - [3m_{52} /8\omega_{w} ]p_{2}^{3} , \\ \end{aligned} $$

(B.9)

The modulation equations for case 2:

$$ D_{1} A_{1} = - [m_{12} /2]A_{1} + i[m_{51} /\omega_{v} ]A_{1} A_{2}^{{}} \overline{A}_{2} + i[3m_{52} /2\omega_{v} ]A_{1}^{2} \overline{A}_{1} - i[m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][A_{1} ], $$

(B.10)

$$ \begin{aligned} D_{1} A_{2} & = - [m_{23} /2]A_{2} + i[m_{51} /\omega_{w} ]A_{1} A_{2}^{{}} \overline{A}_{1} + i[3m_{52} /2\omega_{w} ]A_{2}^{2} \overline{A}_{2} - i[m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][A_{2} ] \\ & \quad - i[m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][\overline{A}_{2} ]e^{{2i\sigma T_{1} }} , \\ \end{aligned} $$

(B.11)

$$ A_{1} = (1/2)(p_{1} - iq_{1} ),A_{2} = (1/2)(p_{2} - iq_{2} )e^{{i\sigma T_{1} }} , $$

(B.12)

$$ \begin{aligned} p^{\prime}_{1} & = - [m_{12} /2]p_{1} - [m_{14} /4\omega_{w} ][A_{\Omega }^{2} ][q_{1} ] + [m_{51} /4\omega_{v} ]q_{1} p_{2}^{2} + [m_{51} /4\omega_{v} ]q_{1} q_{2}^{2} \\ & \quad + [3m_{52} /8\omega_{v} ]p_{1}^{2} q_{1} + + [3m_{52} /8\omega_{v} ]q_{1}^{3} , \\ \end{aligned} $$

(B.13)

$$ \begin{aligned} q^{\prime}_{1} & = - [m_{12} /2]q_{1} - [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ]p_{1} - [m_{51} /4\omega_{v} ]p_{1} p_{2}^{2} - [m_{51} /4\omega_{v} ]p_{1} q_{2}^{2} \\ & \quad - [3m_{52} /8\omega_{v} ]p_{1} q_{1}^{2} - [3m_{52} /8\omega_{v} ]p_{1}^{3} , \\ \end{aligned} $$

(B.14)

$$ \begin{aligned} p^{\prime}_{2} & = - [\sigma ][q_{2} ] - [m_{23} /2]p_{2} + [m_{51} /4\omega_{w} ][p_{1}^{2} ][q_{2} ] + [m_{51} /4\omega_{w} ][q_{1}^{2} ][q_{2} ] \\ & \quad - [m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][q_{2} ] + [3m_{52} /4\omega_{w} ]q_{2} p_{2}^{2} + [3m_{52} /8\omega_{w} ]q_{2}^{3} , \\ \end{aligned} $$

(B.15)

$$ \begin{aligned} q^{\prime}_{2} & = - [\sigma ][q_{2} ] - [m_{23} /2]q_{2} - [m_{51} /4\omega_{w} ]p_{2} p_{1}^{2} - [m_{51} /4\omega_{w} ]p_{2} q_{1}^{2} + [3m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][p_{2} ] \\ & \quad - [3m_{52} /8\omega_{w} ]p_{2} q_{2}^{2} - [3m_{52} /8\omega_{w} ]p_{2}^{3} , \\ \end{aligned} $$

(B.16)

The modulation equations for case 3:

$$ \begin{aligned} D_{1} A_{1} & = - [m_{12} /2]A_{1} + i[m_{51} /\omega_{v} ]A_{1} A_{2} \overline{A}_{2} - i[m_{14} /2\omega_{v} ][\Omega_{0} ][A_{\Omega } ]\overline{A}_{1} e^{{i\sigma T_{1} }} \\ & \quad + i[3m_{52} /2\omega_{v} ]A_{1}^{2} \overline{A}_{1} - i[m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][A_{1} ], \\ \end{aligned} $$

(B.17)

$$ D_{1} A_{2} = - [m_{23} /2]A_{2} + i[m_{51} /\omega_{w} ]A_{1} A_{2}^{{}} \overline{A}_{1} + i[3m_{52} /2\omega_{w} ]A_{2}^{2} \overline{A}_{2} - i[m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][A_{2} ], $$

(B.18)

$$ A_{1} = (1/2)(p_{1} - iq_{1} )e^{{i\sigma T_{1} }} ,A_{2} = (1/2)(p_{2} - iq_{2} ), $$

(B.19)

$$ \begin{aligned} p^{\prime}_{1} & = - [\sigma /2]q_{1} - [m_{12} /2]p_{1} + [m_{14} /2\omega_{v} ][\Omega_{0} ][A_{\Omega } ]q_{1} - [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][q_{1} ] \\ & \quad + [m_{51} /4\omega_{v} ]q_{1} p_{2}^{2} + [m_{51} /4\omega_{v} ]q_{1} q_{2}^{2} + [3m_{52} /8\omega_{v} ]p_{1}^{2} q_{1} + + [3m_{52} /8\omega_{v} ]q_{1}^{3} , \\ \end{aligned} $$

(B.20)

$$ \begin{aligned} q^{\prime}_{1} & = - [\sigma /2]p_{1} - [m_{12} /2]q_{1} + [m_{14} /2\omega_{v} ][\Omega_{0} ][A_{\Omega }^{{}} ]p_{1} + [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ]p_{1} - [m_{51} /4\omega_{v} ]p_{1} p_{2}^{2} \\ & \quad - [m_{51} /4\omega_{v} ]p_{1} q_{1}^{2} - [3m_{52} /8\omega_{v} ]p_{1}^{3} , \\ \end{aligned} $$

(B.21)

$$ \begin{aligned} p^{\prime}_{2} & = - [m_{23} /2]p_{2} - [m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][q_{2} ] + [m_{51} /4\omega_{w} ][p_{1}^{2} ][q_{2} ] \\ & \quad + [m_{51} /4\omega_{w} ][q_{1}^{2} ][q_{2} ] + [3m_{52} /4\omega_{w} ]q_{2} p_{2}^{2} + [3m_{52} /8\omega_{w} ]q_{2}^{3} , \\ \end{aligned} $$

(B.22)

$$ \begin{aligned} q^{\prime}_{2} & = - [m_{23} /2]q_{2} + [3m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][p_{2} ] - [m_{51} /4\omega_{w} ]p_{2} p_{1}^{2} - [m_{51} /4\omega_{w} ]p_{2} q_{1}^{2} + \\ & \quad - [3m_{52} /8\omega_{w} ]p_{2} q_{2}^{2} - [3m_{52} /8\omega_{w} ]p_{2}^{3} , \\ \end{aligned} $$

(B.23)

The modulation equations for case 4:

$$ D_{1} A_{1} = - [m_{12} /2]A_{1} + i[m_{51} /\omega_{v} ]A_{1} A_{2} \overline{A}_{2} + i[3m_{52} /2\omega_{v} ]A_{1}^{2} \overline{A}_{1} - i[m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][A_{1} ], $$

(B.24)

$$ \begin{aligned} D_{1} A_{2} & = - [m_{23} /2]A_{2} + i[m_{51} /\omega_{w} ]A_{1} A_{2}^{{}} \overline{A}_{1} + i[3m_{52} /2\omega_{w} ]A_{2}^{2} \overline{A}_{2} \\ & \quad - i[m_{24} /2\omega_{w} ][\Omega_{0} ][A_{\Omega }^{{}} ][\overline{A}_{2} ]e^{{i\sigma T_{1} }} - i[m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][A_{2} ], \\ \end{aligned} $$

(B.25)

$$ A_{1} = (1/2)(p_{1} - iq_{1} ),A_{2} = (1/2)(p_{2} - iq_{2} )e^{{(i\sigma T_{1} /2)}} , $$

(B.26)

$$ \begin{aligned} p^{\prime}_{1} & = - [m_{12} /2]p_{1} + [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][q_{1} ] + [m_{51} /4\omega_{v} ]q_{1} p_{2}^{2} + [m_{51} /4\omega_{v} ]q_{1} q_{2}^{2} \\ & \quad + [3m_{52} /8\omega_{v} ]p_{1}^{2} q_{1} + [3m_{52} /8\omega_{v} ]q_{1}^{3} , \\ \end{aligned} $$

(B.27)

$$ \begin{aligned} q^{\prime}_{1} & = - [m_{12} /2]q_{1} + + [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ]p_{1} - [m_{51} /4\omega_{v} ]p_{1} q_{2}^{2} - [m_{51} /4\omega_{v} ]p_{1} q_{2}^{2} \\ & \quad - [3m_{52} /8\omega_{v} ]p_{1}^{3} - [3m_{52} /8\omega_{v} ]p_{1} q_{1}^{2} , \\ \end{aligned} $$

(B.28)

$$ \begin{aligned} p^{\prime}_{2} & = - [\sigma /2]q_{2} - [m_{23} /2]p_{2} - [m_{24} /2\omega_{w} ][\Omega_{0} ][A_{\Omega } ][q_{2} ] - [m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][q_{2} ] \\ & \quad + [m_{51} /4\omega_{w} ][p_{1}^{2} ][q_{2} ] + [m_{51} /4\omega_{w} ][q_{1}^{2} ][q_{2} ] + [3m_{52} /8\omega_{w} ]q_{2}^{3} , \\ \end{aligned} $$

(B.29)

$$ \begin{aligned} q^{\prime}_{2} & = [\sigma /2]p_{2} - [m_{23} /2]q_{2} + [m_{24} /2\omega_{w} ][\Omega_{0} ][A_{\Omega } ]p_{2} + [m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][p_{2} ] \\ & \quad - [m_{51} /4\omega_{w} ]p_{2} p_{1}^{2} - [m_{51} /4\omega_{w} ]p_{2} q_{1}^{2} - [3m_{52} /8\omega_{w} ]p_{2} q_{2}^{2} - [3m_{52} /8\omega_{w} ]p_{2}^{3} , \\ \end{aligned} $$

(B.30)

The modulation equations for case 5:

$$ \begin{aligned} D_{1} A_{1} & = - [m_{12} /2]A_{1} - [m_{13} \omega_{w} /2\omega_{v} ]A_{2} e^{{i(\delta T_{1} /2)}} + i[m_{51} /\omega_{v} ]A_{1} A_{2} \overline{A}_{2} \\ & \quad + i[m_{11} /2\omega_{v} ]A_{2} e^{{i(\delta T_{1} /2)}} + i[m_{51} /2\omega_{v} ]\overline{A}_{1} A_{2}^{2} e^{{i(\delta T_{1} /2)}} + i[3m_{52} /2\omega_{v} ]A_{1}^{2} \overline{A}_{1} \\ & \quad - i[m_{16} /4\omega_{v} ][A_{\Omega }^{{}} ][\omega_{\Omega } ]e^{{i(\sigma T_{1} )}} - i[m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][A_{1} ] - i[m_{14} /8\omega_{v} ][A_{\Omega }^{2} ][\overline{A}_{1} ]e^{{i(2\sigma T_{1} )}} , \\ \end{aligned} $$

(B.31)

$$ \begin{aligned} D_{1} A_{2} & = - [m_{23} /2]A_{2} - [m_{22} \omega_{v} /2\omega_{w} ]A_{1} e^{{ - i(\delta T_{1} /2)}} + i[m_{51} /\omega_{w} ]A_{1} A_{2}^{{}} \overline{A}_{1} \\ & \quad + i[m_{21} /2\omega_{w} ]A_{1} e^{{ - i(\delta T_{1} /2)}} + i[m_{51} /2\omega_{w} ]A_{1}^{2} \overline{A}_{2} e^{{ - i(\delta T_{1} )}} + i[3m_{52} /2\omega_{w} ]A_{2}^{2} \overline{A}_{2} \\ & \quad + - i[m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][A_{2} ] - i[m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][\overline{A}_{2} ]e^{{i(2\sigma T_{1} )}} e^{{ - i(\delta T_{1} )}} , \\ \end{aligned} $$

(B.32)

$$ A_{1} = (1/2)(p_{1} - iq_{1} )e^{{(i\sigma T_{1} )}} ,A_{2} = (1/2)(p_{2} - iq_{2} )e^{{(i[\sigma - \delta /2]T_{1} )}} , $$

(B.33)

$$ \begin{aligned} p^{\prime}_{1} & = - [\sigma ][q_{1} ] - [m_{12} /2]p_{1} - [m_{16} (\varepsilon \sigma + \omega_{v} )/2\omega_{v} ][A_{\Omega } ] - [m_{13} (\varepsilon \delta /2 + \omega_{v} )/2\omega_{v} ]p_{2} \\ & \quad + [m_{11} /2\omega_{v} ]q_{2} + [m_{51} /4\omega_{v} ]p_{1} p_{2} q_{2} - [m_{14} /8\omega_{v} ][A_{\Omega }^{2} ][q_{1} ] + [3m_{52} /8\omega_{v} ]p_{1}^{2} q_{1} \\ & \quad + [m_{51} /8\omega_{v} ]q_{1} p_{2}^{2} + [3m_{52} /8\omega_{v} ]q_{2}^{2} q_{1} + [3m_{52} /8\omega_{v} ]q_{1}^{3} , \\ \end{aligned} $$

(B.34)

$$ \begin{aligned} q^{\prime}_{1} & = - [\sigma ][q_{1} ] - [m_{12} /2]q_{1} - [m_{13} /2\omega_{v} ]p_{2} - [m_{13} (\varepsilon \delta /2 + \omega_{v} )/2\omega_{v} ]q_{2} \\ & \quad - [m_{51} /4\omega_{v} ]p_{2} q_{1} q_{2} + [3m_{14} /8\omega_{v} ][A_{\Omega }^{2} ][p_{1} ] - [3m_{52} /8\omega_{v} ]p_{1} q_{1}^{2} \\ & \quad - [3m_{51} /8\omega_{v} ]p_{1} p_{2}^{2} - [m_{51} /8\omega_{v} ]p_{1} q_{2}^{2} - [3m_{52} /8\omega_{v} ]p_{1}^{3} , \\ \end{aligned} $$

(B.35)

$$ \begin{aligned} p^{\prime}_{2} & = - [\sigma ][q_{2} ] + [\delta /2]q_{2} - [m_{23} /2]p_{2} - [m_{22} (\omega_{w} - \varepsilon \delta /2)/2\omega_{w} ]p_{1} + [m_{21} /2\omega_{w} ][q_{1} ] \\ & \quad + [m_{51} /4\omega_{w} ][p_{1} ][q_{1} ][p_{2} ] - [m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][q_{2} ] + [m_{51} /8\omega_{w} ][p_{1}^{2} ][q_{2} ] + \\ & \quad + [3m_{51} /8\omega_{w} ]q_{2} q_{1}^{2} + [3m_{52} /8\omega_{w} ][p_{2}^{2} ][q_{2} ] + [3m_{52} /8\omega_{w} ]q_{2}^{3} , \\ \end{aligned} $$

(B.36)

$$ \begin{aligned} q^{\prime}_{2} & = [\sigma ][p_{2} ] - [\delta /2][p_{2} ] - [m_{23} /2][q_{2} ] - [m_{21} /2\omega_{w} ][p_{1} ] - - [m_{22} (\omega_{w} - \varepsilon \delta /2)/2\omega_{w} ]q_{1} \\ & \quad - [m_{51} /4\omega_{w} ][p_{1} ][q_{1} ][q_{2} ] + [3m_{24} /8\omega_{w} ][A_{\Omega }^{2} ][p_{2} ] - [3m_{51} /8\omega_{w} ]p_{2} p_{1}^{2} - [m_{51} /8\omega_{w} ]p_{2} q_{1}^{2} - \\ & \quad - [3m_{52} /8\omega_{w} ]p_{2} q_{2}^{2} - [3m_{52} /8\omega_{w} ]p_{2}^{3} , \\ \end{aligned} $$

(B.37)

The modulation equations for case 6:

$$ \begin{aligned} D_{1} A_{1} & = - [m_{12} /2][A_{1} ] - [m_{13} \omega_{w} /2\omega_{v} ]A_{2} e^{{i(\delta T_{1} /2)}} + i[m_{51} /\omega_{v} ]A_{1} A_{2} \overline{A}_{2} \\ & \quad + i[m_{11} /2\omega_{v} ]A_{2} e^{{i(\delta T_{1} /2)}} + i[m_{51} /2\omega_{v} ]\overline{A}_{1} A_{2}^{2} e^{{i(\delta T_{1} )}} + i[3m_{52} /2\omega_{v} ]A_{1}^{2} \overline{A}_{1} \\ & \quad - i[m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][A_{1} ] - i[m_{14} /2\omega_{v} ][A_{\Omega }^{{}} ][\Omega_{0} ][\overline{A}_{1} ]e^{{i(\sigma T_{1} )}} , \\ \end{aligned} $$

(B.38)

$$ \begin{aligned} D_{1} A_{2} & = - [m_{23} /2]A_{2} - [m_{22} \omega_{v} /2\omega_{w} ]A_{1} e^{{ - i(\delta T_{1} /2)}} + i[m_{51} /\omega_{w} ]A_{1} A_{2}^{{}} \overline{A}_{1} \\ & \quad + i[m_{21} /2\omega_{w} ]A_{1} e^{{ - i(\delta T_{1} /2)}} + i[m_{51} /2\omega_{w} ]A_{1}^{2} \overline{A}_{2} e^{{i(\delta T_{1} )}} + i[3m_{52} /2\omega_{w} ]A_{2}^{2} \overline{A}_{2} + \\ & \quad - i[m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][A_{2} ] - i[m_{24} /2\omega_{w} ][\Omega_{0} ][A_{\Omega }^{{}} ][\overline{A}_{2} ]e^{{i(\sigma T_{1} )}} e^{{ - i(\delta T_{1} )}} , \\ \end{aligned} $$

(B.39)

$$ A_{1} = (1/2)(p_{1} - iq_{1} )e^{{(i\sigma T_{1} )}} ,A_{2} = (1/2)(p_{2} - iq_{2} )e^{{i[(\sigma - \delta )/2]T_{1} )}} , $$

(B.40)

$$ \begin{aligned} p^{\prime}_{1} & = - [\sigma /2][q_{1} ] - [m_{12} /2]p_{1} + [m_{14} /2\omega_{v} ][\Omega_{0} ][A_{\Omega } ][q_{1} ] - [m_{13} (\varepsilon \delta /2 + \omega_{v} )/2\omega_{v} ]p_{2} \\ & \quad + [m_{11} /2\omega_{v} ][q_{2} ] - [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][q_{1} ] + [m_{51} /4\omega_{v} ]p_{1} p_{2} q_{2} + [3m_{52} /8\omega_{v} ]p_{1}^{2} q_{1} \\ & \quad + [m_{51} /8\omega_{v} ]q_{1} p_{2}^{2} + [3m_{52} /8\omega_{v} ]q_{2}^{2} q_{1} + [3m_{52} /8\omega_{v} ]q_{1}^{3} , \\ \end{aligned} $$

(B.41)

$$ \begin{aligned} q^{\prime}_{1} & = - [\sigma /2][p_{1} ] - [m_{12} /2]q_{1} + [m_{14} /2\omega_{v} ][\Omega_{0} ][A_{\Omega } ]p_{1} - [m_{11} /2\omega_{v} ][p_{2} ] \\ & \quad - [m_{13} (\varepsilon \delta + \omega_{v} )/2\omega_{v} ]q_{2} + [m_{14} /4\omega_{v} ][A_{\Omega }^{2} ][p_{1} ] - [m_{51} /4\omega_{v} ]p_{2} q_{1} q_{2} - [3m_{52} /8\omega_{v} ]p_{1} q_{1}^{2} \\ & \quad - [3m_{51} /8\omega_{v} ]p_{1} p_{2}^{2} - [m_{51} /8\omega_{v} ]p_{1} q_{2}^{2} - [3m_{52} /8\omega_{v} ]p_{1}^{3} , \\ \end{aligned} $$

(B.42)

$$ \begin{aligned} p^{\prime}_{2} & = - [\sigma ][q_{2} ] + [\delta /2]q_{2} - [m_{23} /2]p_{2} - [m_{22} (\omega_{w} - \varepsilon \delta /2)/2\omega_{w} ]p_{1} + [m_{21} /2\omega_{w} ][q_{1} ] \\ & \quad + [m_{24} /2\omega_{w} ][\Omega_{0} ][A_{\Omega }^{{}} ][q_{2} ] - [m_{24} /2\omega_{w} ][A_{\Omega }^{2} ][q_{2} ] + [m_{51} /4\omega_{w} ][p_{1} ][q_{1} ][p_{2} ] \\ & \quad + [m_{51} /8\omega_{w} ][p_{1}^{2} ][q_{2} ] + [3m_{51} /8\omega_{w} ]q_{2} q_{1}^{2} + [3m_{52} /8\omega_{w} ][p_{2}^{2} ][q_{2} ] + [3m_{52} /8\omega_{w} ]q_{2}^{3} , \\ \end{aligned} $$

(B.43)

$$ \begin{aligned} q^{\prime}_{2} & = [\sigma /2][p_{2} ] - [\delta /2][p_{2} ] - [m_{23} /2][q_{2} ] - [m_{21} /2\omega_{w} ][p_{1} ] - [m_{22} (\omega_{w} - \varepsilon \delta /2)/2\omega_{w} ]q_{1} \\ & \quad + [m_{24} /2\omega_{w} ][\Omega_{0} ][A_{\Omega } ]p_{2} + [m_{24} /4\omega_{w} ][A_{\Omega }^{2} ][p_{2} ] - [m_{51} /4\omega_{w} ][p_{1} ][q_{1} ][q_{2} ] \\ & \quad - [3m_{51} /8\omega_{w} ]p_{2} p_{1}^{2} - [m_{51} /8\omega_{w} ]p_{2} q_{1}^{2} - [3m_{52} /8\omega_{w} ]p_{2} q_{2}^{2} - [3m_{52} /8\omega_{w} ]p_{2}^{3} , \\ \end{aligned} $$

(B.44)

The coefficients of Eqs. (49) and (50) are

$$ \begin{aligned} m_{12} & = 0,\quad m_{13} = 0,\quad \omega_{v}^{2} = (n_{13} + n_{17} - n_{10} \Omega_{0}^{2} )/n_{5} n_{13} = 0, \\ m_{11} & = (n_{14} + n_{8} )/n_{5} ,\quad n_{14} = 0, \\ m_{23} & = 0,\quad \omega_{w}^{2} = (n_{24} + n_{27} - n_{20} \Omega_{0}^{2} )/n_{5} ,\quad n_{24} = 0, \\ m_{21} & = (n_{23} + n_{8} )/n_{5} ,\quad n_{23} = 0, \\ m_{1L} & = n_{1L} /n_{5} ,\quad m_{2L} = n_{2L} /n_{5} , \\ n_{1L} & = C_{1} \int\limits_{0}^{1} {H(x)\sin (\alpha + \beta (x))dx,} \quad n_{2L} = C_{1} \int\limits_{0}^{1} {H(x)\cos (\alpha + \beta (x))dx,} \\ C_{1} = & - \pi \overline{\rho }_{\infty } (kM\overline{C}_{\infty } )(l_{hhr} ),\quad \omega_{L} = (2kM\overline{C}_{\infty } /\overline{a}), \\ \end{aligned} $$

(B.45)