Response Analysis of a Rotating Tapered Beam

Abstract

The vibration characteristics of a rotating tapered beam under the excitation of wake flows are considered. The governing equation of the beam is obtained and discretized to a set of ordinary differential equations by using the Galerkin’s method. The coupled vibrations for the first two modes of the beam are investigated. The effects of system parameters such as the taper ratio, the non-dimensional frequency ratio and radius on the first two natural frequencies of the vibrations are studied. Moreover, the vibration responses and stabilities of the coupled system are studied under the 1:1 primary resonance. And the relations between the amplitude of the vibration for the first mode and the parameters including the detuning parameter, the non-dimensional frequency ratio as well as the damping coefficient are investigated for different taper ratios.

Supported by National Natural Science Foundation of China (No.11702111) and the Natural Science Foundation of Shandong Province (No. ZR2017QA005).

1 Introduction

The vibrations of tapered beams have attracted much interest of many researchers for the significant applications such as wind turbines, helicopter rotors and compressors of aero-engine, etc. Especially, the tapered structures are widely used in rotating machines to save weight or to reduce stresses. The static and dynamic characteristics of the tapered beams with various working conditions were investigated. Lee et al. studied the elastica of cantilevered beams of variable cross sections subjected to combined loading by using the numerical and experimental methods [1]. The vibrations of a tapered cantilever (Euler-Bernoulli) beam carrying a moving mass were investigated in [2, 3], and the mode shapes of the free tapered beam as well as the effect the tapering, the magnitude and velocity of the mass on the tip deflections of the beam were studied. The effect of taper ratio on parametric stability of a rotating tapered beam was investigated by Bulut [4]. The dynamic stiffness method was developed to investigate the free vibration of a rotating tapered Rayleigh beam by Banerjee and Jackson [5]. The modal analysis of rotating axially functionally graded tapered Euler-Bernoulli beams with various boundary conditions was carried out by Fang and Zhou [6]. The free vibrations and effects of various taper ratios on the natural frequencies of a tapered beam were investigated by using the transfer-matrix method [7]. Yao and Zhang [8] studied the reliability and sensitivity of an axially moving beam with simply supported boundary conditions. In [9] the nonlinear bending and torsional vibrations of tapered beams made of axially functionally graded (AFG) material were analyzed numerically. The adomian modified decomposition method (AMDM) was employed by Desmond and Martin [10] for the free transverse vibration analysis of the rotating non-uniform tapered Euler-Bernoulli beams with several boundary conditions, rotation speeds, and beam lengths. The out-of-rotation plane bending vibrations of a rotating tapered beam with periodically varying speed were considered in [10]. Mazanoglu and Guler studied the flap-wise and chord-wise vibrations of AFG tapered beams rotating around a hub, and the effects of taper ratio, hub radius, angular velocity and non-homogeneity on the thin beams with several classical boundary conditions were investigated as well [11].

Owing to the complex working circumstance, the free vibrations of the tapered beam and the system parameter effects such as the tapered ratio, rotating speed on either the natural frequencies or responses were the main points investigated in the articles. Herein, the vibrations of the rotating cantilever beam under the excitation of wake flows are investigated. A number of articles have investigated the influence of the wake flows on the vibrations of the beams. However, there is no uniform model to represent the characteristics of the wake-flows. While the effect of the wake-flows was modeled as the a series of harmonic forces in some articles. The impact vibration characteristics of a shrouded blade with asymmetric gaps under wake flow excitations were studied [12], where the wake-flow aerodynamic excitation acting on the blade was assumed as a periodic force. Ma et al. studied the vibration characteristics of rotating shrouded blades with impacts [13], in which the aerodynamic load owing to the fluid force was assumed as a harmonic force. The flow velocity was assumed harmonically vary along the pipe rather than with time in [14] when investigate dynamics and stability of fluid-conveying corrugated pipes. Moreover, the effect of the wake-flows was represented by the time-varying oscillation, such as the van der Pol oscillator, etc. In order to analyse the characteristics of the rotating tapered beam, the effect of the wake-flow on the structure is represented by the harmonic force as well.

In this paper, an Euler-Bernoulli tapered beam attached to a rotating rigid disk is considered, where the excitation owing to the wake flows is assumed as a harmonic force. And the integro-partial differential equation is obtained and discretized by the Galerkin’s method to a set of ordinary differential equations. Then the theoretical analysis about the coupling vibrations of first two modes is carried out by using the multiple scale method. Moreover, the effects of system parameters including the taper ratio, the non-dimensional frequency ratio, the non-dimensional radius on the natural frequencies of the first two modes are investigated. The vibration responses under the 1:1 primary resonance of the first two modes are studied by using the averaged equations. Furthermore, with different taper ratios, the relations between the amplitude for the vibration of the first mode and different system parameters are studied by using the direct integration method.

2 Modeling

2.1 Modeling of a Rotating Tapered Beam

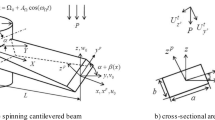
The model of the rotating tapered beam is assumed as a continuous straight cantilever beam based on the Euler-Bernoulli formulation in the centrifugal force field as shown in Fig. 1, where $\varOmega , \bar{r}, \rho , l, c, A(x), EI(x)$ denote the rotating speed, the radius of the rotating disk, mass density, length of the beam, the viscous damping coefficient, the area of the beam cross-section and the bending rigidity, respectively. Assume the beam has the constant breadth, and the height varying from $x=0$ to $x=l$ linearly, then one have that $A(x)=A_0(1-k\displaystyle \frac{x}{l}), I(x)=I_0(1-k\frac{x}{l})^3$, where k denotes the taper ratio and $k\in (0, 1)$, $A_0, I_0$ are the area of the cross-section and the area moment of the inertia at $x=0$, respectively.

Fig. 1.

The rotating beam with taper ratio.

The governing equation of motion of the beam can be obtained by considering the equilibrium of forces and moments acting on the differential segment of the beam with a length of dx as follows,

$$\begin{aligned} \begin{array}{l} \left[ {\displaystyle \frac{{\partial ^2 }}{{\partial x^2 }}\left( {EI(x)\displaystyle \frac{{\partial ^2 w(x,t)}}{{\partial x^2 }}} \right) } \right] dx - \left[ {\displaystyle \frac{\partial }{{\partial x}}\left( {F_{cent} \displaystyle \frac{{\partial w(x,t)}}{{\partial x}}} \right) } \right] dx + \rho A(x)\displaystyle \frac{{\partial ^2 w(x,t)}}{{\partial t^2 }}dx\\ {} +\, c\displaystyle \frac{{\partial w(x,t)}}{{\partial t}}dx = \tilde{F}dx, \end{array} \end{aligned}$$

(1)

where

$$\begin{aligned} F_{cent} = \int _x^l {f_{cent} } (\xi ,t)d\xi = \int _x^l {\rho \varOmega ^2\,A(\xi )} (\bar{r} + \xi )d\xi , \end{aligned}$$

(2)

and $f_{cent} (x,t) = \rho \varOmega ^2 A(x)(\bar{r} + x)$ is the distributed load owing to the centrifugal force. $\tilde{F}$ denotes the aerodynamic force induced by the wake flows which is complex from the point view of the fluid characteristics. However, it could be seen as a periodic force due to the rotating of the beam as studied in [12] and [13]. Where the wake-flow aerodynamic excitation acting on the blade is assumed as a sum of a series of harmonic forces, reads $\tilde{F}=F_0+F_1 \cos (n\varOmega t)+F_2 \cos (2n\varOmega t)+\cdots +F_m \cos (mn\varOmega t)$. The frequency of the excitation is n times of the rotating speed of the blade, where n is the number of obstacles in the front of the rotor-beam. $F_0$ is a constant, and $F_m$ ($m = 1, 2, 3,\cdots$) is the amplitude of the mth harmonic component. In this study, the first harmonic component of the wake-flow force is adopted, that is $\tilde{F}=F_1 \cos (n\varOmega t)$.

Introducing $y=w/l, v=x/l, \bar{\xi }=\xi /l, r=\bar{r}/l, \tau =\varOmega t$, Eq. (1) becomes

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{{\partial ^2 y(v,\tau )}}{{\partial \tau ^2 }} + \frac{\eta }{{1 - kv}}\frac{{\partial y(v,\tau )}}{{\partial \tau }} + \omega ^2 (1 - kv)^2 \frac{{\partial ^4 y(v,\tau )}}{{\partial v^4 }} - 6\omega ^2 (1 - kv)k\frac{{\partial ^3 y(v,\tau )}}{{\partial v^3 }} \\ +\, 6\omega ^2 k^2 \displaystyle \frac{{\partial ^2 y(v,\tau )}}{{\partial v^2 }} - \frac{1}{{1 - kv}}\left( {\int _v^1 {(1 - k\bar{\xi })( r + \bar{\xi })} d\bar{\xi }} \right) \frac{{\partial ^2 y(v,\tau )}}{{\partial v^2 }} + ( r + v)\frac{{\partial y(v,\tau )}}{{\partial v}} \!= \!\bar{F} \cos (n\tau ), \end{array} \end{aligned}$$

(3)

where $\bar{F}= \displaystyle \frac{F_1}{{\rho A_0 l\varOmega ^2 (1 - kv)}}$, $\omega = \displaystyle \frac{{\omega _0 }}{\varOmega }$, $\omega _0 = \sqrt{\displaystyle \frac{{EI_0 }}{{\rho A_0 l^4 }}}$, $\eta = \displaystyle \frac{c}{{\rho A_0 \varOmega }}$.

The boundary conditions are assumed as that of a cantilever beam, $y(0) = y'(0) = y''(1) = y'''(1) = 0$.

2.2 The Galerkin Discretization for the Governing Equation

Discretization of the partial differential equation (3) into the finite-dimensional system is done according to the study in [15, 16]. Assuming the dimensionless transverse response is expanded as $y(\tau ,v) = \sum \limits _{j = 1}^n {y_j (\tau )\tilde{y}_j (v)}$, where $\tilde{y}_j (v)$ is assumed as the set of eigenfunctions of an Euler-Bernoulli beam, that is

$$\begin{aligned} \tilde{y}_j (v) = \cosh \lambda _j v - \cos \lambda _j v - \frac{{\cosh \lambda _j + \cos \lambda _j }}{{\sinh \lambda _j + \sin \lambda _j }}(\sinh \lambda _j v - \sin \lambda _j v) \end{aligned}$$

(4)

and $\lambda _j (j=1,2\cdots )$ are the roots of the transcendental equation $1 + \cos \lambda \cosh \lambda = 0$.

The differential equations of the tapered rotating beam are obtained by using the Galerkin’s discretization, reads

$$\begin{aligned} \begin{array}{l} \displaystyle \frac{{d^2 y_j (\tau )}}{{d\tau ^2 }} + \eta \sum \limits _{i = 1}^n {A_{ij} \displaystyle \frac{{dy_j (\tau )}}{{d\tau }}} + \omega ^2 \sum \limits _{i = 1}^n {B_{ij} y_j (\tau )} - 6\omega ^2 k\sum \limits _{i = 1}^n {C_{ij} y_j (\tau )} + 6\omega ^2 k^2 \sum \limits _{i = 1}^n {D_{ij} y_j (\tau )} \\ - \sum \limits _{i = 1}^n {E_{ij} } y_j (\tau ) + r\sum \limits _{i = 1}^n {M_{ij} y_j (\tau )} + \sum \limits _{i = 1}^n {N_{ij} } y_j (\tau ) = F a_j \cos (n\tau ), (j=1,2,\ldots )\\ \end{array} \end{aligned}$$

(5)

where $A_{ij} = \displaystyle \int _0^1 {\displaystyle \frac{{\tilde{y}_i (v)\tilde{y}_j (v)}}{{1 - kv}}dv}$, $B_{ij} = \displaystyle \int _0^1 {(1 - kv)^2 \displaystyle \frac{{\partial ^4 \tilde{y}_i (v)}}{{\partial v^4 }}\tilde{y}_j (v)dv}$,

$C_{ij} = \displaystyle \int _0^1 {(1 - kv)\displaystyle \frac{{\partial ^3 \tilde{y}_i (v)}}{{\partial v^3 }}\tilde{y}_j (v)dv}$, $D_{ij} = \displaystyle \int _0^1 {\displaystyle \frac{{\partial ^2 \tilde{y}_i (v)}}{{\partial v^2 }}\tilde{y}_j (v)dv}$,

$E_{ij} \mathrm{{\, = }}\displaystyle \int _0^1 {\left( {\displaystyle \frac{1}{{1 - kv}}\left( { r(1 - v) + \displaystyle \frac{{1 - k r}}{2}(1 - v)^2 - \displaystyle \frac{k}{3}(1 - v)^3 } \right) } \right) \displaystyle \frac{{\partial ^2 \tilde{y}_i (v)}}{{\partial v^2 }}\tilde{y}_j (v)dv}$,

$M_{ij} = \displaystyle \int _0^1 {\displaystyle \frac{{\partial \tilde{y}_i (v)}}{{\partial v}}\tilde{y}_j (v)dv}$, $N_{ij} = \displaystyle \int _0^1 {v\displaystyle \frac{{\partial \tilde{y}_i (v)}}{{\partial v}}\tilde{y}_j (v)dv}$, $a_j = \displaystyle \int _0^1 {\displaystyle \frac{1}{{(1 - kv)}}\tilde{y}_j (v)dv}$, $F= \displaystyle \frac{F_1}{{\rho A_0 l\varOmega ^2}}$.

To investigate the effects of system parameters on the natural frequencies as well as vibration characteristics of the beam, the vibrations for the first two modes are investigated in the following,

$$\begin{aligned} \begin{array}{l} \ddot{y}_1 (\tau ) + \eta A_{11} \dot{y}_1 (\tau ) + \eta A_{21} \dot{y}_2 (\tau ) + ( {\omega ^2 B_{11} - 6\omega ^2 kC_{11} + 6\omega ^2 k^2 D_{11} - E_{11} + rM_{11} + N_{11} } )y_1 (\tau ) \\ +\, ( {\omega ^2 B_{21} - 6\omega ^2 kC_{21} + 6\omega ^2 k^2 D_{21} - E_{21} + rM_{21} + N_{21} } )y_2 (\tau ) = F a_1 \cos (n\tau ), \\ \end{array} \end{aligned}$$

(6)

$$\begin{aligned} \begin{array}{l} \ddot{y}_2 (\tau ) + \eta A_{12} \dot{y}_1 (\tau ) + \eta A_{22} \dot{y}_2 (\tau ) + \left( {\omega ^2 B_{12} - 6\omega ^2 kC_{12} + 6\omega ^2 k^2 D_{12} - E_{12} + rM_{12} + N_{12} } \right) y_1 (\tau ) \\ + \left( {\omega ^2 B_{22} - 6\omega ^2 kC_{22} + 6\omega ^2 k^2 D_{22} - E_{22} + rM_{22} + N_{22} } \right) y_2 (\tau ) = F a_2 \cos (n\tau ). \\ \end{array} \end{aligned}$$

(7)

3 The 1:1 Primary Resonance

3.1 Effects of System Parameters on the First Two Natural Frequencies

The multiple scale method [16] is often utilized to understand the qualitative characteristics of the system which presents the resonant conditions. Introducing the scaling parameters $\eta \rightarrow \varepsilon \eta , F \rightarrow \varepsilon F$ into Eqs. (6) and (7), one can obtain

$$\begin{aligned} \ddot{y}_1 (\tau ) + K_1 (\omega )y_1 (\tau ) + K_2 (\omega )y_2 (\tau ) = \varepsilon Fa_1 \cos (n\tau ) - \varepsilon \eta A_{11} \dot{y}_1 (\tau ) - \varepsilon \eta A_{21} \dot{y}_2 (\tau ), \end{aligned}$$

(8)

$$\begin{aligned} \ddot{y}_2 (\tau ) + K_3 (\omega )y_2 (\tau ) + K_4 (\omega )y_1 (\tau ) = \varepsilon Fa_2 \cos (n\tau ) - \varepsilon \eta A_{22} \dot{y}_2 (\tau ) - \varepsilon \eta A_{12} \dot{y}_1 (\tau ), \end{aligned}$$

(9)

where

$$\begin{array}{l} K_1 = \omega ^2 B_{11} - 6\omega ^2 kC_{11} + 6\omega ^2 k^2 D_{11} - E_{11} + rM_{11} + N_{11}, \\ K_2 = \omega ^2 B_{21} - 6\omega ^2 kC_{21} + 6\omega ^2 k^2 D_{21} - E_{21} + rM_{21} + N_{21}, \\ K_3 = \omega ^2 B_{22} - 6\omega ^2 kC_{22} + 6\omega ^2 k^2 D_{22} - E_{22} + rM_{22} + N_{22}, \\ K_4 = \omega ^2 B_{12} - 6\omega ^2 kC_{12} + 6\omega ^2 k^2 D_{12} - E_{12} + rM_{12} + N_{12}. \\ \end{array}$$

Assume the approximate form of the solutions as follows,

$$\begin{aligned} \begin{array}{l} y_1 (\varepsilon ,\tau ) = y_{10} (T_0 ,T_1 ) + \varepsilon y_{11} (T_0 ,T_1 ) + \cdots , \\ y_2 (\varepsilon ,\tau ) = y_{20} (T_0 ,T_1 ) + \varepsilon y_{21} (T_0 ,T_1 ) + \cdots . \\ \end{array} \end{aligned}$$

(10)

Substituting the solutions (10) into Eqs. (8) and (9) and equating coefficient of like powers of $\varepsilon$, one can obtain that

Order $\varepsilon ^0$,

$$\begin{aligned} D_0^2 y_{10} + K_1 y_{10} + K_2 y_{20} = 0, \end{aligned}$$

(11)

$$\begin{aligned} D_0^2 y_{20} + K_3 y_{20} + K_4 y_{10} = 0. \end{aligned}$$

(12)

Order $\varepsilon ^1$,

$$\begin{aligned} D_0^2 y_{11} + K_1 y_{11} + K_2 y_{21} = \frac{1}{2}F a_1 e^{{\mathop {\mathrm {i}}\nolimits } n\tau } - \eta A_{11} D_0 y_{10} - \eta A_{21} D_0 y_{20} - 2D_0 D_1 y_{10} + c.c., \end{aligned}$$

(13)

$$\begin{aligned} D_0^2 y_{21} + K_3 y_{21} + K_4 y_{11} = \frac{1}{2}F a_2 e^{in\tau } - \eta A_{22} D_0 y_{20} - \eta A_{12} D_0 y_{10} - 2D_0 D_1 y_{20} + c.c., \end{aligned}$$

(14)

where $\displaystyle \frac{d}{{d t }} = D_0 + \varepsilon D_1 + \varepsilon ^2 D_2 + \cdots$, $\displaystyle \frac{d^2}{{d t ^2 }} = D_0^2 + 2\varepsilon D_0 D_1 + \cdots$, and $D_n = \displaystyle \frac{\partial }{{\partial T_n }}$.

The general solutions of Eqs. (11) and (12) can be obtained in the complex form

$$\begin{aligned} \begin{array}{l} y_{10} = \bar{Y}_1 (T_1 )e^{i\omega _1 T_0 } + \bar{Y}_2 (T_1 )e^{i\omega _2 T_0 } + c.c.,\\ y_{20} = \phi _1 \bar{Y}_1 (T_1 )e^{i\omega _1 T_0 } + \phi _2 \bar{Y}_2 (T_1 )e^{i\omega _2 T_0 } + c.c., \\ \end{array} \end{aligned}$$

(15)

where $\omega _1$ and $\omega _2$ are the natural frequencies of the coupled system (11) and (12), yielding $\omega _{1,2} = \displaystyle \sqrt{\frac{{K_1 + K_3 \mp \sqrt{(K_1 + K_3 )^2 - 4(K_1 K_3 - K_2 K_4 )} }}{2}}$. And $\phi _i = \displaystyle \frac{{\omega _i^2 - K_1 }}{{K_2 }} = \displaystyle \frac{{K_4 }}{{\omega _i^2 - K_3 }},$ (i = 1, 2) are the mode coefficients, c.c. stands for the complex conjugate of the proceeding terms.

As shown in the expressions, the natural frequencies $\omega _1$ and $\omega _2$ of vibrations of the first two modes are determined by three parameters, that is, the taper ratio k, the non-dimensional frequency ratio $\omega$ as well as the non-dimensional radius r. Hence, the effects of system parameters on the natural frequencies $\omega _1$ and $\omega _2$ are studied by using the numerical methods as shown in Fig. (2) to Fig.(7).

As can be seen from Fig. 2, when $\omega$ is fixed at 1, for $r=0.6$ and $r=1.0$, the frequency $\omega _1$ of the first mode is increasing while the frequency $\omega _2$ of the second mode is decreasing firstly and then increases as the taper ratio k increases. Meanwhile, for $r=1.5$ and $r=2.0$, both the frequencies $\omega _1$ and $\omega _2$ of the first and second modes increase as k increases.

Fig. 2.

The relations between natural frequencies $\omega _1$ and $\omega _2$ for vibrations of the first two modes with respect to the taper ratio k for $r=0.6, 1.0, 1.5, 2.0$ respectively.

Figure 3 shows that when r is fixed at 1, and for $\omega =0.08$, both the frequencies $\omega _1$ and $\omega _2$ of the first and second modes increase as k increases. While for $\omega =0.10$ and 0.12, the first natural frequency $\omega _1$ increases firstly and then decreases with the taper ratio k increases. On the other hand, the second natural frequency $\omega _2$ decreases firstly and then increases with the taper ratio k increases.

One can see from Fig. 4 that both the frequencies $\omega _1$ and $\omega _2$ of the first and second modes increase as r increases when the taper ratio $k=0.0, 0.5, 0.9$, respectively, and the parameter $\omega$ is fixed at 0.1. Moreover, for a fixed r, the first natural frequency $\omega _1$ increases while the second natural frequency $\omega _2$ decreases as k increases.

Fig. 3.

The relations between natural frequencies $\omega _1$ and $\omega _2$ for vibrations of the first two modes with respect to the taper ratio k for $\omega =0.08, 0.10, 0.12$ respectively.

Fig. 4.

The relations between natural frequencies $\omega _1$ and $\omega _2$ for vibrations of the first two modes with respect to r for $k=0.0, 0.5, 0.9$ respectively.

Figure 5 shows that when k is fixed at 0.5, both the first two natural frequencies $\omega _1$ and $\omega _2$ increase as the non-dimensional radius r increases for $\omega =0.8, 1.0, 1.2$ respectively.

One can see from Fig. 6 that when r is fixed at 2, both the first two natural frequencies $\omega _1$ and $\omega _2$ increase as the non-dimensional frequency ratio $\omega$ increases for $k=0.0, 0.5, 0.9$ respectively. Figure 7 shows that when k is fixed at 0.5, both the first two natural frequencies $\omega _1$ and $\omega _2$ increase as the non-dimensional frequency ratio $\omega$ increases for $r=0.6, 1.0, 1.5, 2.0$ respectively.

The results indicates that the effect of the taper ratio on the natural frequencies is complicated and several cases are existing. Moreover, increasing the radius of the hub and decreasing the rotating speed can increase the first two natural frequencies of the beam.

Fig. 5.

The relations between natural frequencies $\omega _1$ and $\omega _2$ for vibrations of the first two modes with respect to r for $\omega =0.8, 1.0, 1.2$ respectively.

Fig. 6.

The relations between natural frequencies $\omega _1$ and $\omega _2$ for vibrations of the first two modes with respect to $\omega$ for $k=0.0, 0.5, 0.9$ respectively.

Fig. 7.

The relations between natural frequencies $\omega _1$ and $\omega _2$ for vibrations of the first two modes with respect to $\omega$ for $r=0.6, 1.0, 1.5, 2.0$ respectively.

3.2 The Vibration Response Analysis for the Coupled System

The research in [17, 18] showed that the dynamic systems can present rich vibration characteristics when the resonance occurs. To investigate the effects of the system parameters on the responses of the system, the 1:1 primary resonance is studied and the relation between the frequency of the fluid force as well as the first natural frequency is assumed as $n:\omega _1\approx 1:1,{} {} {} {} n = \omega _1 - \varepsilon \sigma$, where $\sigma$ denotes the detuning parameter. Substitute (15) into Eqs. (13) and (14) and consider the resonance conditions yielding

$$\begin{aligned} \begin{array}{l} D_0^2 y_{11} + K_1 y_{11} + K_2 y_{21} = \displaystyle \frac{1}{2}F a_1 e^{{\mathop {\mathrm {i}}\nolimits } (\omega _1 - \varepsilon \sigma )\tau } - i\eta A_{11} (\omega _1 \bar{Y}_1 e^{i\omega _1 T_0 } + \omega _2 \bar{Y}_2 e^{i\omega _2 T_0 } ) \\ -\, i\eta A_{21} (\omega _1 \phi _1 \bar{Y}_1 e^{i\omega _1 T_0 } + \omega _2 \phi _2 \bar{Y}_2 e^{i\omega _2 T_0 } ) - 2i(\omega _1 e^{i\omega _1 T_0 } D_1 \bar{Y}_1 + \omega _2 e^{i\omega _2 T_0 } D_1 \bar{Y}_2 ) + c.c., \\ \end{array} \end{aligned}$$

(16)

$$\begin{aligned} \begin{array}{l} D_0^2 y_{21} + K_3 y_{21} + K_4 y_{11} = \displaystyle \frac{1}{2}F a_2 e^{i(\omega _1 - \varepsilon \sigma )\tau } - i\eta A_{22} (\omega _1 \phi _1 \bar{Y}_1 e^{i\omega _1 T_0 } + \omega _2 \phi _2 \bar{Y}_2 e^{i\omega _2 T_0 } ) \\ -\, i\eta A_{12} (\omega _1 \bar{Y}_1 e^{i\omega _1 T_0 } + \omega _2 \bar{Y}_2 e^{i\omega _2 T_0 }) - 2i(\omega _1 \phi _1 e^{i\omega _1 T_0 } D_1 \bar{Y}_1 + \omega _2 \phi _2 e^{i\omega _2 T_0 } D_1 \bar{Y}_2 ) + c.c. \\ \end{array} \end{aligned}$$

(17)

Letting

$$\begin{array}{l} P_1 = \displaystyle \frac{1}{2}F a_1 e^{ - i\sigma T_1 } - i\eta A_{11} \omega _1 \bar{Y}_1 - i\eta A_{21} \omega _1 \phi _1 \bar{Y}_1 - 2i\omega _1 D_1 \bar{Y}_1, \\ Q_1 = - i\eta A_{11} \omega _2 \bar{Y}_2 - i\eta A_{21} \omega _2 \phi _2 \bar{Y}_2 - 2i\omega _2 D_1 \bar{Y}_2, \\ P_2 = \displaystyle \frac{1}{2}F a_2 e^{ - i\sigma T_1 } - i\eta A_{22} \omega _1 \phi _1 \bar{Y}_1 - i\eta A_{12} \omega _1 \bar{Y}_1 - 2i\omega _1 \phi _1 D_1 \bar{Y}_1 , \\ Q_2 = - i\eta A_{22} \omega _2 \phi _2 \bar{Y}_2 - i\eta A_{12} \omega _2 \bar{Y}_2 - 2i\omega _2 \phi _2 D_1 \bar{Y}_2 , \\ \\ \end{array}$$

the solvability conditions can be obtained as

$$\begin{aligned} \left| \begin{array}{l} K_1 - \omega _1^2 {} P_1 {} \\ K_4 {} P_2 {} \\ \end{array} \right| = \left| \begin{array}{l} K_1 - \omega _2^2 {} Q_1 {}\\ K_4 {} Q_2 {} \\ \end{array} \right| = 0. \end{aligned}$$

(18)

The derivatives of amplitudes $\bar{Y}_1$ and $\bar{Y}_2$ with respect to $T_1$ can be obtained by Eq. (18), that is

$$\begin{aligned} D_1 \bar{Y}_1 = \frac{1}{{2[\phi _1 (K_1 - \omega _1^2 {} ) - K_4 ]\omega _1 }}\left\{ \begin{array}{l} \frac{1}{2}iF e^{ - i\sigma T_1 } [K_4 a_1 - a_2 (K_1 - \omega _1^2 {} )] \\ + \eta \omega _1 [K_4 (A_{11} + A_{21} \phi _1 ) - (K_1 - \omega _1^2 {} )(A_{22} \phi _1 + A_{12} )]\bar{Y}_1 \\ \end{array} \right\} , \end{aligned}$$

(19)

$$\begin{aligned} D_1 \bar{Y}_2 = \frac{{K_4 {} (A_{11} + A_{21} \phi _2 ) + (\omega _2^2 - K_1 {} ){} {} (A_{22} \phi _2 + A_{12} )}}{{2\phi _2 (K_1 - \omega _2^2 {} ) - 2K_4 }}\eta \bar{Y}_2. \end{aligned}$$

(20)

Assuming the functions $\bar{Y}_1$ and $\bar{Y}_2$ are expressed in the polar co-ordinates, which reads

$$\begin{aligned} \bar{Y}_1(T_1) = \displaystyle \frac{{Y_1(T_1)}}{2}e^{i\theta _1(T_1) }, \bar{Y}_2(T_1) = \displaystyle \frac{{Y_2(T_1) }}{2}e^{i\theta _2(T_1) }, \end{aligned}$$

(21)

where $Y_j, \theta _j (j=1, 2)$ represent the amplitudes and phase angles of the responses, respectively. The first-order averaged equations can be obtained after separating the real and imaginary parts by substituting (21) into Eqs. (19) and (20), that is

$$\begin{aligned} Y_1 ' = \frac{1}{{2[\phi _1 (K_1 - \omega _1^2 {} ) - K_4 ]\omega _1 }}\left\{ \begin{array}{l} F [K_4 a_1 - a_2 (K_1 - \omega _1^2 {} )]\sin \varphi + \\ \eta \omega _1 [K_4 (A_{11} + A_{21} \phi _1 ) - (K_1 - \omega _1^2 {} )(A_{22} \phi _1 + A_{12} )]Y_1 \\ \end{array} \right\} , \end{aligned}$$

(22)

$$\begin{aligned} \theta _1 ' = \frac{{F [K_4 a_1 - a_2 (K_1 - \omega _1^2 {} )]}}{{2[\phi _1 (K_1 - \omega _1^2 {} ) - K_4 ]\omega _1 Y_1 }}\cos (\sigma T_1 + \theta _1 ), \end{aligned}$$

(23)

$$\begin{aligned} Y_2 ' = \frac{{K_4 {} (A_{11} + A_{21} \phi _2 ) + (\omega _2^2 - K_1 {} ){} {} (A_{22} \phi _2 + A_{12} )}}{{2\phi _2 (K_1 - \omega _2^2 {} ) - 2K_4 }}\eta Y_2, \end{aligned}$$

(24)

$$\begin{aligned} \theta '_2= 0, \end{aligned}$$

(25)

where $(')$ denotes the derivatives with respect to $T_1$ and $\varphi =\sigma {T_1}+\theta _1$.

The averaged Eqs. (24) and (25) show that the vibration of the second mode for the rotating beam is periodic. Hence the response of the vibration for the first mode is studied in the following. The equilibrium solutions of Eqs. (22) and (23) correspond to periodic motions of the coupled system. The steady-state solutions for the system (22) and (23) are obtained by the direct numerical method when assuming $Y'_1=0, \varphi '=0$ and

$$\begin{aligned} \varphi ' = \frac{{F [K_4 a_1 - a_2 (K_1 - \omega _1^2 {} )]}}{{2[\phi _1 (K_1 - \omega _1^2 {} ) - K_4 ]\omega _1 \bar{Y}_1 }}\cos \varphi + \sigma . \end{aligned}$$

(26)

Fig. 8.

Bifurcation curves: (a) the amplitude $Y_1$ of the response for the first mode vibration with respect to the detunig parameter $\sigma$ for $\omega =0.5,1,2$ respectively; (b) the amplitude $Y_1$ of the response for the first mode vibration with respect to the frequency ratio $\omega$ for $\eta =0.001, 0.01$ respectively; (c) the amplitude $Y_1$ of the response for the first mode vibration with respect to the damping $\eta$ for $F=0.001, 0.01$ respectively. The other parameters are fixed at $k=0, r=2$.

As can be seen from Fig. 8(a) to Fig. 10(a), when the non-dimensional frequency ratio $\omega$ is fixed, the amplitude $Y_1$ for the vibration of the first mode increases with the detuning parameter $\sigma$ increases firstly until $\sigma =0$, then the amplitude $Y_1$ decreases as $\sigma$ increases. While Fig. 8(b) to Fig. 10(b) show that the amplitude $Y_1$ decreases as $\omega$ increases for a fixed $\eta$, which has a good agreement with that of shown in Fig. 8(a) to Fig. 10(a).

Fig. 9.

Bifurcation curves: (a) the amplitude $Y_1$ of the response for the first mode vibration with respect to the detunig parameter $\sigma$ for $\omega =0.5,1,2$ respectively; (b) the amplitude $Y_1$ of the response for the first mode vibration with respect to the frequency ratio $\omega$ for $\eta =0.001, 0.01$ respectively; (c) The amplitude $Y_1$ of the response for the first mode vibration with respect to the damping $\eta$ for $F=0.001, 0.01$ respectively. The other parameters are fixed at $k=0.5, r=2$.

Fig. 10.

Bifurcation curves: (a) the amplitude $Y_1$ of the response for the first mode vibration with respect to the detunig parameter $\sigma$ for $\omega =0.5,1,2$ respectively; (b) the amplitude $Y_1$ of the response for the first mode vibration with respect to the frequency ratio $\omega$ for $\eta =0.001, 0.01$ respectively; (c) the amplitude $Y_1$ of the response for the first mode vibration with respect to the damping $\eta$ for $F=0.001, 0.01$ respectively. The other parameters are fixed at $k=0.9, r=2$.

Moreover Fig. (8)(c) to (10)(c) show that the amplitude $Y_1$ increases as $\eta$ increases firstly until $\eta =0$, then the amplitude decreases as $\eta$ increases. Especially, the Hopf bifurcation (H) occurs when $\eta =0$. Meanwhile, the amplitude $Y_1$ increases when F is increasing. In addition, Fig. 8 to Fig. 10 show that the response characteristics of the vibration for the first mode are kept when the taper ratio k are chosen as 0.0, 0.5, 0.9 respectively. And the results indicated that the design of tapered beam is very useful in engineering.

4 Conclusions

The vibrations of a rotating tapered beam under the excitation of wake flows have been investigated, where the rotating blade was modeled as a cantilever beam and the effect of wake flows was represented as a periodic force. The coupled equations of the first two modes of the beam were obtained by the Galerkin discretization. The 1:1 primary resonance for the coupled system were studied by using the multiple scale method. Effects of the system parameters including the taper ratio k, the non-dimensional frequency ratio $\omega$ as well as the non-dimensional radius r on the first two natural frequencies were studied. The results indicates that for a constant taper ratio k, increasing the radius of the disk or decreasing the rotating speed could increase the first two natural frequencies; while for the effects of the taper ratio, there exist several cases: (a) for the certain value $\omega$ and r, increasing the taper ratio k, the first frequency of the coupled system increases while the second natural frequency decreases firstly and then increases; (b) for the certain value $\omega$ and r, both the natural frequencies increases according to the increasing the taper ratio k; (c) for the certain value $\omega$ and r, increasing the taper ratio k, the first natural frequency increases firstly then decreases and the second natural frequency decreases firstly then increases. The varying trends of the two natural frequencies are opposite to each other.

Moreover, the averaged equations were derived and the relation curves were computed. Effects of the system parameters including the dutuning parameter $\sigma$, the taper ratio k, the damping coefficient $\eta$, the non-dimensional frequency ratio $\omega$ on the responses were investigated. And the results indicate that increasing the rotating speed of the beam or the damping coefficient can suppress the vibration for the first mode. While increasing the amplitude of the air flow force could excite the large-amplitude vibration of the first mode. Meanwhile, the system displays the similar vibration characteristics for different taper ratio.