1 Introduction

Electronic circuits exhibiting chaotic behaviour have attracted wide attention because they provide excellent platform for practical implementation of chaotic oscillators (see for example Ref. [1–17] and references therein). Among the several chaotic circuits, the Van der–Pol Duffing oscillator is a very prominent and important classical model circuit that has been extensively studied in the context of several specific problems ranging from global bifurcation structures, control and synchronization (see for example Ref. [5–9, 18]).

The Van der Pol–Duffing oscillator can be used as a model in physics, engineering, electronics, biology, neurology and many other disciplines  [19, 20]. King et al.  [8, 9] proposed a schematic circuit of Van der-Pol Duffing oscillator which is equivalent to Chua’s autonomous circuit but with a cubic nonlinear element  [2] and can be described by the following set of autonomous dimensionless differential equations:

$$\begin{aligned} \dot{x} = -m\big (x^{3}-\alpha x- y+\mu _{of}\big ), \ \dot{y} = x - y - z, \ \dot{z} = \beta y\nonumber \\ \end{aligned}$$
(1)

where the overdots stands for the differentiation with respect to normalized time \(\tau \); \(x, ~y\) and \(z\) corresponds to the re-scaled form of the voltages across \(C_{1}\), \(C_{2}\) and the current through \(L\) respectively (1). \(\alpha , \beta ~\text{ and } ~\mu \) are the parameters of the system. System (1) exhibits rich dynamical behaviours including a double-scroll chaos for the system parameters: \(\alpha = 0.35\), \(\beta = 300\), \(\mu _{of}= 0\), and \(m=100\) [8, 9].

In 2005 and 2007, Fotsin et al. [5–7] proposed a modified Van der Pol-Duffing oscillator (MVDPD) circuit by adding a series resistance of the inductor \(R_{L}\), thus yielding the dimensionless equation:

$$\begin{aligned} \dot{x} = -m\big (x^{3}-\alpha x- y + \mu _{of}\big ), \ \dot{y} = x - y - z, \ \dot{z} = \beta y - \gamma z \end{aligned}$$
(2)

where the additional parameter, \(\gamma \) is associated with the effect of the resistance of the inductor on the system dynamics. With \(\gamma = 0.2\), system (2) exhibits the same double-scroll attractor similar to system (1) and when \(\mu _{of} \ne 0\), a one scroll chaotic attractor was found [5]. Recently, Matouk and Agiza [21] introduced another modification by adding to the Van der Pol– Duffing oscillator circuit described by the autonomous system (1) a resistor in parallel with the inductor, giving rise to a new system which takes the form:

$$\begin{aligned} \dot{x} = -m(x^{3}-\alpha x- y), \ \dot{y} = x - \mu y - z, \ \dot{z} = \beta y. \end{aligned}$$
(3)

The modified circuit by Matouk and Agiza [21] has some advantages in that all the dynamics of the oscillator are displayed in a small range by varying the new systems parameter, \(\mu \) arising from the parallel resistance. Furthermore, a complete description of the regions in the parameter space for which multiple small periodic solutions arise through the Hopf bifurcations at the equilibria in system (3) was recently analyzed in detail by Braga et al. [22]. Very recently, a similar work was done for the Chua’s circuit by Prebianca et al. [14].

All of the above Van der Pol–Duffing oscillator circuit models deal with self-oscillatory (i. e. autonomous) systems. In this paper, we investigate the dynamics of a nonautonomous unified Van der Pol– Duffing oscillator (UVDP) circuit by introducing a changeable electrical power source (acting as subject to a periodic driving force) [10]. We examine the combined effects of the series and parallel resistances as shown in Fig. 1, as well as the periodic driving. Systems with periodic forcing are often used for practical applications, in areas such as communications. Much effort has also been keenly devoted to understanding the dynamics of nonautonomous oscillators driven from equilibrium by a variety of external forcing because deterministic influences often arise in practice as in cellular dynamics, blood circulation, and brain dynamics [23, 24]. The model we investigate exhibit more complex and richer dynamics as the amplitude and frequency of the forcing is varied. Besides various chaotic and periodic orbits, our system also show chaos-hyperchaos transitions, coexisting attractors, as well as Hopf bifurcations in which quasiperiodic orbits are born. We first present in Sect. 2, the unified and periodically forced Van der Pol–Duffing oscillator (UVDP) and discuss its basic dynamical properties. Sections 3 and 4 are devoted to the local and global bifurcation structures and chaotic behaviour respectively; while Sect. 5 concludes the paper.

2 Description of the model

2.1 Driven Van der Pol–Duffing oscillator circuit

The periodically driven Van der Pol–Duffing oscillator considered here can be modeled by the circuit shown in Fig. 1, in which a series resistance \(R\) is added to the \(C_{2}\) branch of the circuit, while another resistance \(R_p\) is placed parallel to it. In addition, a periodic signal generator \(G\), acting as periodic driving force is connected to the left end of the circuit as shown. By applying Kirchhoff’s laws to the various branches of the circuit of Fig. 1, and noting that the \(i(v)\) characteristics of the nonlinear resistor (N) is approximated by the cubic polynomial \(i(V_1) = aV_1+bV_1^{3}\), \((a < 0, ~ b > 0)\) [21], we obtain the following set of equations:

Fig. 1
figure 1

Driven Van der Pol–Duffing oscillator circuit

Full size image
$$\begin{aligned} \frac{dV_{1}}{dt}&= -\frac{1}{C_1}\left( \frac{1}{R}+a \right) V_{1}+\frac{V_{2}}{RC_{1}}-\frac{b}{C_{1}}V_{1}^{3}, \nonumber \\ \frac{dV_{2}}{dt}&= \frac{V_{1}}{RC_{2}}-\frac{\mu V_{2}}{RC_{2}}-\frac{i_{L}}{C_{2}}+\frac{i_G}{C_{2}}\sin \omega t,\nonumber \\ \frac{di_{L}}{dt}&= \frac{V_{2}}{L}-\frac{R_{L}}{L}i_{L}. \end{aligned}$$
(4)

Making appropriate rescaling of Eq. (4) by setting \(x=V_{1}\sqrt{bR}\), \(y=V_{2}\sqrt{bR}\), \(z=i_{L}\sqrt{bR^{3}}\), \(\tau = \frac{t}{RC_2}\),

\(m=\frac{C_2}{C_1}\), \(\alpha = -(1+aR)\), \(\beta = \frac{R^{2}C_2}{L}\), \(\gamma = \frac{R_{L}RC_2}{L}\),

\(a_0 = R(\sqrt{bR})I_G\), \(\Omega = \frac{\omega }{R C_2}\) and \(\mu = \frac{R+R_p}{R_p}\),

we obtain the following dimensionless equation:

$$\begin{aligned} \dot{x}&= -m(x^{3}-\alpha x- y), \nonumber \\ \dot{y}&= x - \mu y - z + a_0\sin \omega \tau ,\nonumber \\ \dot{z}&= \beta y - \gamma z. \end{aligned}$$
(5)

System (5) is a three-dimensional nonautonomous system; where the new parameters \(\omega \) and \(a_0\) are the frequency and amplitude of the periodic driving force, respectively. Thus, our model system (5) has four Lyapunov exponents, allowing for hyperchaotic behaviour, i.e. with the possibility of having two positive Lyapunov exponents along with one zero and one negative. Beginning with the pioneering work of R\(\ddot{o}\)ssler [25], the study of hyperchaos has witnessed tremendous research interest in the last three decades, in the fields of nonlinear circuits [10, 25–27], secure communications [28–30], nonlinear optics [31], control and synchronization [24, 32, 33], to mention a few. Due to its great potential in technological applications, the generation of hyperchaos from nonlinear systems has recently become one focal topic for research [10, 24, 34, 35]. Our goal here is to investigate the effect of \(\omega \) and \(a_0\) on the dynamics of (5) and show that under periodic driving, the modified Van der Pol–Duffing oscillator would exhibit richer dynamical complexities, including the existence of hyperchaos.

2.2 Equilibria and their stability

To examine the stability of system (5), we first obtain the fixed points by solving the general equation \(F(\dot{u} )=0\), where \(F\) is the nullcline and \(u\) is the vector space containing \(x\), \(y\) and \(z\). It appears that for \(\alpha (\mu \gamma +\beta )+\gamma < 0,\) we have only one fixed point \(S_0{(0,0,0)}\) and, for \(\alpha (\mu \gamma +\beta )+\gamma > 0,\) we have three fixed points, namely \(S_{1}(-p,-\gamma q,-\beta q)\), \(S_{0}(0,0,0)\) and \(S_{2}(p,\gamma q,\beta q)\) where

$$\begin{aligned} p = \sqrt{\frac{\alpha (\mu \gamma +\beta )+\gamma }{\mu \gamma +\beta }}; \ \ q = \sqrt{\frac{\alpha (\mu \gamma +\beta )+\gamma }{(\mu \gamma +\beta )^3}}. \end{aligned}$$
(6)

In both cases, by considering the Jacobian matrix of one of these equilibria and calculating their eigenvalues, we can investigate the stability of the equilibrium point based on the roots of the characteristic equation

$$\begin{aligned} S^{3}+b_{0}S^{2}+b_{1}S+b_{2}=0 \end{aligned}$$
(7)

where \(b_{0}=\mu +\gamma -m\big (3x_{0}^{2}-\alpha \big )\), \(b_{1}=\mu \gamma +\beta +m\big (3x_{0}^{2}-\alpha \big )\big (\mu +\gamma \big )-m\), and \(b_{2}=-m\big (3x_{0}^{2}-\alpha \big )\big (\mu \gamma +\beta \big )+m\gamma \).

We know that the fixed points are stable if the real parts of the roots of the characteristics equation are all negative. Otherwise, the fixed points are unstable. Using Routh-Hurwitz criterion [36], for the sign of the real part of the roots, we obtain that the real parts of the roots are negative if and only if all the other coefficients \(b_{0},~b_{1} ~\text{ and } ~b_{2}\) are positive and all the determinants \(\Delta _{1}=b_{0}b_{2}-b_{1} ~\text{ and } ~\Delta _{2}=b_{2}(b_{0}b_{2}-b_{1})\) also positive. Before analyzing the stability status of each point, it is important to consider the practical process of modeling system 4 (see Sect. 2.1). It is clear that only \(\alpha \) can take on negative or positive values. The other parameters are always positive. Focussing on the fixed point \(S_0\), the analysis leads us to the conclusion that for \(0 < \alpha < \frac{\mu +\gamma }{m}\) this fixed point is always stable. The other fixed points \(S_1\) and \(S_2\) can be stable or unstable depending on the choice of space parameter of the system. Therefore the stability condition should be checked according to the criteria defined above before any use is made of the system.

3 Local bifurcations and attractors

The numerical results that follows were performed using the standard fourth order Runge-Kutta routine with step-size \(h=2\pi /(N\omega )\), where \(N=100\) is an integer. The Lyapunov exponents were computed using the Wolf et al.’s algorithm [37] which requires the linearized version of Eq. (5) for small variations from the trajectory in tangent space and the Graham Smith’s orthonormalization procedure allows us to compute the complete spectrum from maximal to minimal. For clarity and brevity, we will present only the first two exponents, namely \(\lambda _1\) and \(\lambda _2\) which determine exclusively the system’s behaviours; while the full spectra would be considered in analyzing the global bifurcation in parameter phase space. Unless otherwise stated, the following parameters were fixed: \(\alpha = 0.35\), \(\beta = 300\), and \(m=100\); while the other parameters, namely \(\mu \), \(\gamma \), \(a_0\) and \(\omega \) were varied for the different cases considered. In the absence of the forcing we obtain the Fotsin and Woafo model when \(\mu = 1.0\), and \(\gamma = 0.2\) [6, 7]; whereas, when \(\mu > 1.0\) and \(\gamma = 0\) we have the Matouk and Agiza model [21].

We begin by considering the case for \(\mu =1.0\) and \(\gamma = 0.2\). We set \(\omega = 10\) and display in Fig. 2 the bifurcation diagram as function of the driving amplitude \(a_0\) (upper panel (a)) and the corresponding maximal (\(\lambda _1\)) and second (\(\lambda _2\)) Lyapunov exponents in the same range of \(a_0\) (lower panel (b)). Clearly, we observe four distinct regimes corresponding to different transitions, and denoted by I, II, III and IV. Notice that when \(a_0=0\), a double-scroll chaotic attractor exist [6, 7] for the chosen parameters. However, when \(a_0\) increases gradually, the chaotic attractor loses it stability and undergoes a variety of bifurcations from regions (I) to (IV) which is terminated in a controlled systems of period-1 orbit. In particular, regimes I and III show several interesting dynamical transitions including the existence of hyperchaotic solution which we will describe below.

Fig. 2
figure 2

Bifurcation diagram of the local maximum of \(x\) and the corresponding Lyapunov exponents as function of the driving amplitude, \(a_0\). \(\alpha = 0.35\), \(\beta = 300\), \(m=100\), \(\gamma = 0.2\), \(\mu = 1.0\), and \(\omega = 10\). In b, solid line denotes the first Lyapunov exponents, while dotted line denotes the second Lyapunov exponents

Full size image

In Fig. 3, we display a zoom of the Lyapunov exponents corresponding to region I of Fig. 2. The first (maximal) Lyapunov exponent, \(\lambda _1\) is positive for \(a_0 \le 1.8\) and drops to zero at \(a_0 \approx 1.8\). The second Lyapunov exponent \(\lambda _2\) oscillates marginally around zero for \(a_0 < 0.5\), positive for \(0.5 \le a_0 \le 1.57\) and for \(a_0 > 1.57\), drops to negative. Obviously, the system has two positive Lyapunov exponents in the amplitude interval \(0.4 \le a_0 \le 1.6\), indicating instability in two directions and signalling hyperchaotic state [25]; one positive and one negative Lyapunov exponents for \(1.6 \le a_0 \le 1.8\) (chaos); and one zero and one negative Lyapunov exponents for \(1.8 \le a_0 \le 7.8\) –a signature of quasiperiodicity. The existence of hyperchaotic behaviour implies that the system exhibits anomalous instability. Thus, a change in \(a_0\) to a value within this regime switches the system from chaos \(\rightarrow \) hyperchaos \(\rightarrow \) chaos \(\rightarrow \) quasiperiodicity (a limit cycle) for the same orbit as the system transits from region I to region II.

Fig. 3
figure 3

Zoom of the Lyapunov exponents as function of the driving amplitude, for region I in Fig. 2 for the same set of parameters

Full size image

Apparently, the chaos-hyperchaos transition at \(a_0 \approx 0.4\) is accompanied by the so-called attractor splitting (or reverse attractor merging) crises earlier reported by Grebogi et al.  [38, 39] and well classified by Ott  [40]. Here, the double-scroll chaotic attractor, corresponding to the unforced system, and shown in Fig. 4(a) breaks up into two branches, which eventually merge as \(a_0\) further increases during the hyperchaos-chaos transition, forming another structurally different chaotic attractor. The \(a_0\) range for which two branches of chaotic band exist in the bifurcation structure corresponds to the hyperchaotic regime. Our detailed numerical simulations show that the hyperchaotic behaviour in the forced system arises due to attractor splitting crises, though the branching point depends on the value of \(\omega \). Furthermore, we observed that the chaos-quasiperiodic transition is accompanied by boundary crisis at \(a_0 > a^c_0 \approx 1.762\) in which a chaotic attractor collides with an unstable periodic orbit on its basin boundary [38–41]; and consequently replaced by a chaotic transient, wherein the orbit spends a very long time in the neighbourhood of the non-attracting chaotic set before leaving; and thereafter moves on to the stable quasi-periodic state that governs its long-time motion. Figure 5 shows a typical chaotic transient motion for \(a_0 = 1.77\). During the initial phase (\(t \le 580\)), the motion appears very irregular and quite indistinguishable from motion on a chaotic attractor and for \(t \ge 580\), the system is in a stable quasiperiodic motion. Inside this narrow parameter window, attractors may co-exist and the length of time during which the orbit spends in the initial chaotic phase depends on the value \(a_0\) as well as the initial conditions. For instance, for \(a_0 = 1.78\), the initial transient phase is longer, \(t \approx 950\).

Fig. 4
figure 4

Attractors for different \(a_0\) and for the parameters \(\alpha = 0.35\), \(\beta = 300\), \(m=100\), \(\gamma = 0.2\), \(\mu = 1.0\), and \(\omega = 10\). a Phase portrait of a double-scroll chaos for \(a_0=0\), b phase portrait of a hyperchaotic attractor for \(a_0 = 1.51\), c Poincaré section \(a_0 = 1.72\) and d Poincaré section for \(a_0 = 1.51\) depicting attractor splitting in the hyperchaotic state

Full size image
Fig. 5
figure 5

Time Series of a transient chaos for \(a_0 = 1.77\). Other parameters are: \(\alpha = 0.35\), \(\beta = 300\), \(m=100\), \(\gamma = 0.2\), \(\mu = 1.0\), and \(\omega = 10\). The initial phase is \(t \le 580\)

Full size image

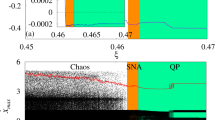
With increasing \(a_0\), a different scenario is observed. Figure 6 shows the enlarged portion of Fig. 2 in the regime III. Here, we find multiple transitions beginning with a sudden loss of stability by the limit cycle in the broad range of the driving amplitude, namely \(1.8 \le a_0 \le 7.8\) (region II) and the appearance of alternating periodic orbits, first a period-10 attractor (shown in Fig. 7(a) for \(a_0 = 7.836\) together with a limit cycle at \(a_0=7.5\)), followed by various orbits of higher periodicity (typically \(n > 10\), where \(n\) is the period of the orbit) spanning the entire regime \(7.8 \le a_0 \le 9.5\). This sequence is however terminated with the emergence of a chaotic band in the range \(9.13 \le a_0 \le 9.58\) where \(\lambda _1\) is typically positive. A typical chaotic attractor in this band for \(a_0 = 9.45\) is shown in Fig. 7(b). Following the chaotic band, a period-17 orbit (see Fig. 7(c)) born in the large window loses its stability in a bifurcation at \(a_0 \approx 9.92\) with the birth of a strange nonchaotic attractor of quasiperiodic orbits exemplified by the orbits in Fig. 7(d) for \(a_0 = 9.95\). Notice that the strange nonchaotic attractor in Fig. 7(d) has structural resemblance with the chaotic attractor in Fig. 7(b). However, the attractor in Fig. 7(b) has one positive Lyapunov exponent (\(\lambda _1 = 0.212\)) and one negative (\(\lambda _2 = -0.706 \)), whereas \(\lambda _1 = 0\), and\(\lambda _2 = -0.479\) for the attractor in Fig. 7(d). As \(a_0\) increases further pass \(a_0 \approx 10.05\), we find that the region \(10.1 \le a_0 \le 10.35\) is dominated by quasiperiodic orbits of invariant curve, which undergoes Hopf bifurcation to a period-1 orbit. Deformation and lost of smoothness of the invariant curve takes place around \(a_0 \approx 10.0\) before its final destruction as \(a_0\) decreased–giving rise to the strange nonchaotic attractor.

Fig. 6
figure 6

Enlarged bifurcation diagram of the local maximum of \(x\) and the corresponding Lyapunov exponents as function of the driving amplitude, for region III in Fig. 2 for the same set of parameters. (Color figure online)

Full size image
Fig. 7
figure 7

Poincaré sections showing various attractors during the transitions from regions II to IV of Fig. 2 for the same set of parameters and for increasing \(a_0\). a Limit cycle (closed dotted curve) for \(a_0=7.5\) together with period-10 orbit (open points) for \(a_0 = 7.836\) (Note that there are two repeated overlapping points), b new chaotic attractor for \(a_0 = 9.45\), c period-17 orbit for \(a_0 = 9.745\) and d strange non-chaotic attractor for \(a_0 = 9.95\)

Full size image

4 Global bifurcation structure

In the previous section, we examined the local bifurcations with \(a_0\) being the bifurcation parameter. The bifurcations may also be investigated using \(\omega \) as the bifurcation parameter. However, a global view of this system can conveniently be captured by simultaneously scanning a wide range of the forcing parameters, i.e. bifurcations in \(a_0 - \omega \) parameter space plane. Here, we employ the Lyapunov spectrum formed by all the Lyapunov exponents \(\lambda _n (i=1,2,3,4)\) as a tool for constructing the dynamical system parameter space diagram. The nature of the attractor can be characterized by the values of these four Lyapunov exponents. The system is considered hyperchaotic (HC), if \(\lambda _{1,2} > 0, \lambda _{3,4} \le 0\), chaotic (CH) if \(\lambda _1 > 0, \lambda _{2,3,4} \le 0\), quasi-periodic oscillation on a torus \(T^2\) or limit cycle (QP), if \(\lambda _1 = 0, \lambda _{2,3,4} \le 0\); and periodic orbit or a fixed point (PO) when \(\lambda _{i} < 0 (i=1,2,3,4)\). Keeping the above characteristic properties, and with the aid of GramSchmidt orthonormalization, we computed all the Lyapunov exponents by applying the Wolf et al.’s algorithm [37] as done previously. We remark that due to the non-exact computation of the exponents, we consider an exponent null if its value is within the interval \(-0.0005 \le {\lambda } \le 0\).

Fig. 8
figure 8

Two Parameter space diagram obtained from the Lyapunov spectra, indicating the behavior of the driven Van der Pol–Duffing circuit for \(\alpha = 0.35\), \(\beta = 300\), \(m=100\), \(\gamma = 0.2\), and \(\mu = 1.0\), showing different regions of hyperchaos (dotted blue), chaos (dotted red), quasiperiodic (dotted green) and periodic (elsewhere—white) orbits. In a \(\mu = 1.0\) and b \(\mu = 1.5\). (Color figure online)

Full size image

Shown in Fig. 8 are typical two-parameter space plots showing clearly different regions of hyperchaos (HC), chaos (CH), quasiperiodic (QP) orbits and periodic orbits (PO). For \(\mu = 1.0\) on the left panel, both hyperchaotic and chaotic orbits can show up by making appropriate choice of the external forcing parameters. In the low frequency regime, \(\omega < 3\), the dynamics are largely dominated by HC and CH orbits for nearly all forcing amplitudes, \(a_0\). As the frequency increases pass \(\omega \approx 3.0\), QP and PO orbits begin to appear, dominating a wide range of the parameter space. For \(\omega = 10\), we find that HC orbits lies within the low amplitude regime, typical \(a_0 < 2.0\); while higher values of \(a_0\) will drive the system to QP states.

For further increase in \(\omega \) up-to \(\omega \approx 17.0\), we observe phase locking at \(\omega = \omega _0 \approx 17.0\), where the harmonic force locks with oscillations of the system—the consequence being stabilization to periodic state. The periodic state is a stable stationary solution in the parameter space (i.e. mode locking regions) where the frequency of the oscillator coincides with the forcing frequency. This region, called synchronization region, or resonance (or Arnold) tongue occurs when a self-excited oscillation interacts with a driving force, resulting in an adjustment of the oscillation [42, 43].

Finally, it would be significant to examine the effects of the parallel resistance, \(R_p\) in Fig. 1 denoted by the dimensionless quantity, \(\mu \) in Eqs. 4 and 5. In Fig. 8(b), we illustrate the effect of \(\mu \) on the global dynamics of the driven oscillator. We find that for \(\mu =1.5\), chaotic (CH) and hyperchaotic (HC) regions are replaced by periodic orbits—Implying that the parallel resistance could act as a simple control input in the system. The parameter space is largely dominated by periodic orbits with some visible regions of chaos and hyperchaos behaviour.

5 Conclusions

In this paper, we have reported on the influence of an external periodic signal on the familiar double-scroll chaotic attractor of the autonomous Van der–Pol Duffing oscillator circuit by introducing to the circuit a periodic signal source. As the external forcing parameters are varied, new dynamical behaviors emerge, including hyperchaos arising from attractor splitting, quasiperiodicity, strange-nonchaotic attractors and periodic orbits of higher periodicity. The regimes of existence of different dynamical behaviors in two-parameter space of the driving force were identified with the aid of two parameter bifurcation diagram computed using complete spectra of the Lyapunov exponents. By comparison, we find that the modified model presented by Fotsin et al. [5–7] show more complex behavior when periodically driven than the Matouk model [21, 44]. For instance, in a wide range of \(\omega - a_0\) parameter space, adjusting the value of the parallel resistance \(R_p\) in the circuit of Fig. 1, denoted by the dimensionless parameter \(\mu \), in Eq. 5, drives the system to periodic states—implying that variation in \(R_p\) would initiate chaos control in the systems. Thus, chaotic behaviour could be conveniently tamed in practical experiment, whereby \(R_p\) act as a simple limiter. This is very important for practical applications where chaos is undesirable. On the other hand, when \(R_p\) is absent, that is \(\mu =1\), the system would be more complex in the presence of the driving signal, presenting also chaos and hyperchaos in larger parameter space. In communication systems where security is important, such high complexities are significant for secure communication applications.