1 Introduction

A chaotic system is a nonlinear deterministic system that displays complex, noisy like and unpredictable behavior. The sensitive dependence on initial conditions and the system parameters variation are prominent characteristics of chaotic behavior. Chaotic systems synchronization has been interesting research fields since the pioneering work of Pecora and Carroll [1], which were simultaneously reported in 1990. Chaos synchronization has many potential applications particularly in secure communication, engineering, laser physics, chemical reactor process, biomedical, power converters, information processing, etc. which have further increased the interest of research community.

In most of the chaos synchronization approaches, the master-slave or drive response formalism has been used. If a particular chaotic system is called the master or drive system and another chaotic system is called the slave or response system, then the idea of synchronization is to use the output of the master system to control the slave system so that the output of the slave system tracks the output of the master system asymptotically. In recent years, many interesting chaotic systems are observed and simulated in circuits. These chaotic and/or hyperchaotic systems show different dynamical properties. So far, various types of synchronization phenomenon have been found such as functional synchronization [2], complete synchronization [3], observer based synchronization [4], phase synchronization [5], generalized synchronization [6], anti-synchronization [7–9], distributed synchronization [10], robust synchronization [11], and projective synchronization [12, 13]. Transition of synchronization [14–18] induced in the chaotic systems has been explored extensively. The networks as reported by Wang et al. [17, 18] can give good clues to understand the mechanism of information encoding and wave propagation among neurons. Chaos control and synchronization have been extensively investigated during last two decade [19, 20] and still have attracted increasing attention in recent years. Since chaotic attractors were found by Lorenz in 1963, many chaotic systems have been constructed, such as the Chen system [21–24], Lu system [23–25], T-system [26], Lorenz system [27], etc.

Control and synchronization of chaotic/hyperchaotic systems have been explored extensively using linear and nonlinear control techniques [7, 28]. It is very critical to estimate unknown parameters in the system by using adaptive synchronization [29–31] and Lyapunov stability theory within the study and control of chaos, hyperchaos, patterns formation and transition of spatiotemporal pattern within the networks of chaotic oscillators.

Along with that, hyperchaotic systems are paid more and more attention due to presence of more than one positive Lyapunov exponent, which improves the security in communication applications by generating more complex dynamics clearly [32]. Many conventional or novel control methods have been applied to synchronize two identical hyperchaotic (or chaotic) systems [33]. Chaotic synchronization of hyperchaotic systems with single control variable is more simple, efficient, and easy to implement in practical applications than the proposed control schemes in the past research works.

In this paper, the proposed approach targets the problem of designing control scheme to stabilize, complete synchronize and adaptive synchronize hyperchaotic Lu systems. For this purpose, sliding mode control scheme is utilized along with Lyapunov stability theory to design the suitable control structure. A PI switching surface is proposed to simplify the task of assigning the performance of closed-loop error system in sliding mode. The proposed controller guarantees the occurrence of sliding motion and achieves synchronization of hyperchaotic Lu systems in master-slave configuration. The adaptive synchronization problem of the four-dimensional Lu system was recently proposed by Elabbasy et al. [34] with uncertain parameters. This concept is extended by Chi-Ching Yang [35] applying the single control input to the Hyperchaotic Lu systems and four dimensional (4D) Lorenz-Stenflo chaotic systems [36]. However, the approach presented in this paper differs from the work already reported in the literature in the sense that here, stabilisation and synchronization are achieved by using sliding mode technique based single control input. The proposed controller along with adaptation laws for uncertain parameters ensures convergence of estimates of system parameters to their true value. The Numerical simulations are presented for the Hyperchaotic Lu system to show the efficacy of proposed strategy.

This paper is organized as follows: In Sect. 2.1, description of hyperchaotic Lu system is given. In Sect. 2.2, switching function and stabilizing controller design is proposed. In Sect. 3.1, describe the synchronization of two 4D hyperchaotic Lu systems. In Sect.  3.2, design of the switching function and sliding mode controller for synchronization problem is proposed. In Sect. 3.3, describe the adaptive synchronization with uncertain parameters. In Sect. 3.4, design of the switching function and sliding mode controller for synchronization problem for uncertain parameters is proposed. Numerical simulation results are given in Sect. 4, to show the effectiveness of the proposed controller and switching function. Finally, conclusion is presented in Sect. 5.

2 Design of single input stabilizing controller

In the present section, dynamics of hyperchaotic Lu system is described and then PI switching function based SMC strategy is developed to stabilize the hyperchaotic Lu system.

2.1 The hyperchaotic Lu system description

In 2006, Elabbasy et al. [34] presented the 4D hyperchaotic Lu dynamical system, based on the 3D Lu system [23] by adding the state feedback. The differential equations of 4D hyperchaotic Lu systems are described by

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{1}=a(x_{2}-x_{1})\\ \dot{x}_{2}=cx_{2}-x_{1}x_{3}+x_{4}\\ \dot{x}_{3}=x_{1}x_{2}-bx_{3}\\ \dot{x}_{4}=x_{3}-dx_{4}\\ \end{array}\right. } \end{aligned}$$
(1)

where \({{x}_{1},{x}_{2},{x}_{3},{x}_{4}}\) are state variables and \({a,b,c,d}\) are positive system parameters. The 4D hyperchaotic Lu system demonstrates a hyperchaotic attractors at the parameter values. \({a=15,b=5,c=10,d=1}\). The projections of attractors are shown in Fig. 1.

Fig. 1
figure 1

The phase portraits of hyperchaotic Lu system (1): a–d 3D phase portraits for different states

Full size image

2.2 Switching function and stabilizing controller design

Let the dynamics of controlled hyperchaotic Lu system be defined as

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{1}=a(x_{2}-x_{1})\\ \dot{x}_{2}=cx_{2}-x_{1}x_{3}+x_{4}+u\\ \dot{x}_{3}=x_{1}x_{2}-bx_{3}\\ \dot{x}_{4}=x_{3}-dx_{4}\\ \end{array}\right. } \end{aligned}$$
(2)

where \({u}\) is the control input to be designed for stabilizing the system in (2).

The SMC technique to achieve stabilization of a pair of 4D hyperchaotic Lu systems involves two major steps: (1) Select an appropriate switching function which can guarantee the stability of the equivalent dynamics in the sliding mode such that the system dynamics converges to zero. (2) Establish a SMC law which guarantees the existence of sliding mode \({s(t)=0}\).

For ensuring the asymptotical stability of the sliding mode, the PI switching function \({s(t)}\) is defined as follows:

$$\begin{aligned} s(t)=x_{2}+\int _{0}^{t}\{(k_1-c)x_{2}+\lambda ax_{1}+x_{1}x_{3}\} d\tau \end{aligned}$$
(3)

where \({k_1}\) is a positive constant specified by designer. According to the works presented in [20], when the system operates in the sliding mode \({s(t)=0}\), the following equations hold:

$$\begin{aligned} \dot{s}(t)=\dot{x}_{2}+(k_1-c)x_{2}+\lambda ax_{1}+x_{1}x_{3} \end{aligned}$$
(4)

and

$$\begin{aligned} \dot{x}_{2}=-(k_1-c)x_{2}-\lambda ax_{1}-x_{1}x_{3} \end{aligned}$$
(5)

Therefore, from (5) the following equivalent sliding mode dynamics can be obtained:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{1}=a(x_{2}-x_{1})\\ \dot{x}_{2}=-(k_1-c)x_{2}-\lambda ax_{1}-x_{1}x_{3}\\ \dot{x}_{3}=x_{1}x_{2}-bx_{3}\\ \dot{x}_{4}=x_{3}-dx_{4}\\ \end{array}\right. } \end{aligned}$$
(6)

For the system (2) with the control input \({u}\) appropriately designed and selecting positive constant \({\lambda >0}\), zero equilibrium point \({(x_1=x_2=x_3=x_4=0)}\) of the system (6) can be ensured to be globally asymptotically stable(GAS).

To establish the stability of the sliding mode dynamics (6) based on Lyapunov stability theory, let the Lyapunov function be selected as:

$$\begin{aligned} V_{1}(t)=0.5\left( \lambda x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}\right) , \quad \lambda >0 \end{aligned}$$
(7)

The derivative of (7) with respect to time, results in following equation while using (6):

$$\begin{aligned} \dot{V_{1}}(t)= & {} \lambda x_{1}\dot{x}_{1}+x_{2}\dot{x}_{2}+x_{3}\dot{x}_{3}+x_{4}\dot{x}_{4}\nonumber \\= & {} \lambda x_{1}[a(x_{2}-x_{1})]+x_{2}[-(k_1-c)x_{2}-\lambda ax_{1}\nonumber \\&-\,x_{1}x_{3}]+x_{3}[x_{1}x_{2}-bx_{3}]+x_{4}[x_{3}-dx_{4}]\nonumber \\= & {} -\lambda ax_{1}^{2}-(k_1-c)x_{2}^{2}-bx_{3}^{2}-dx_{4}^{2}+x_{3}x_{4}\nonumber \\= & {} -\lambda ax_{1}^{2}-(k_1-c)x_{2}^{2}-bx_{3}^{2}-dx_{4}^{2}+|x_{3}||x_{4}|\nonumber \\= & {} -\mathbf {X}^{T}P_{1}\mathbf {X} \end{aligned}$$
(8)

where \({\mathbf {X}=[|x_1|,|x_2|,|x_3|,|x_4|]^{T}}\) is absolute state vector. The matrix \({P_1}\) is real symmetric and can be expressed as

$$\begin{aligned} P_{1}=\begin{bmatrix} \lambda a&\quad 0&\quad 0&\quad 0 \\ 0&\quad (k_1-c)&\quad 0&\quad 0 \\ 0&\quad 0&\quad b&\quad -\frac{1}{2} \\ 0&\quad 0&\quad -\frac{1}{2}&\quad d \end{bmatrix} \end{aligned}$$
(9)

From the Lyapunov theorem of stability, it is simple to point out that zero equilibrium point \((x_{1}=x_{2}=x_{3}=x_{4}=0)\) of the system is GAS if the real symmetric matrix \({P_1}\) is positive definite. By using the Sylvesters theorem [37], it is clear that with \({\lambda >0}\) and \({k_{1}>c}\), real symmetric matrix \({P_1}\) being positive definite and the state system being GAS.

To ensure the occurrence of the sliding motion, following control law is proposed:

$$\begin{aligned} u=-\lambda ax_{1}-k_{1}x_{2}-x_{4}-\eta ~sgn(s) \end{aligned}$$
(10)

where \({\eta }\) is a positive constant specified by designer.

In the following, the proposed controller \({u}\) will be proved to be able to ensure the existence of the sliding motion and achieving stabilization.

Property: The signum function of a real number \({s}\) is defined as follows [37]: \({sgn(s):\mathbb {R}\rightarrow \{-1,0,1\}}\). The signum function exhibits the property that \(s~sgn(s)=|s|\). This simple result will be exploited often in the analysis.

Theorem

(Sylvesters theorem) [37] Assuming that \({M}\) is \({n\times n}\) square and symmetric matrix, a necessary and sufficient condition for \({M}\) to be positive definite is that all its leading principal minors should be strictly positive.

Theorem

(Lyapunov theorem of stability) [38] Let \(\mathbf {x=0}\) be an equilibrium point for the autonomous system \({\dot{\mathbf {x}}}=f (\mathbf {x})\) where \(f :D\rightarrow \mathbb {R}^n\) is a local Lipschitz map from a domain \(D\subset \mathbb {R}^n\) and is continuously differentiable function such that

$$\begin{aligned}&{\mathbf {V(0)}=0}\,and\,V{(\mathbf {x})>0, ~~\forall ~~\mathbf {x}\ne 0} \\&||\mathbf {x}||\rightarrow \infty \Rightarrow V(\mathbf {x})\rightarrow \infty \\&\dot{V}(\mathbf {x})<0, \quad \quad \forall \mathbf {x}\ne 0 \end{aligned}$$

Then, the equilibrium point \(\mathbf {x=0}\) is globally asymptotically stable.

Theorem 1

Consider the state dynamics (2), if the system is controlled by \({u}\) in (10), then the system trajectories converge to sliding surface \({s(t)=0}\) and \(lim_{t\rightarrow \infty }\) \(||x_{i}(t)||=0\), for \((i=1,2,3,4)\).

Proof

Consider the new Lyapunov function candidate as

$$\begin{aligned} V_{2}(t)=0.5s^{2}(t) \end{aligned}$$
(11)

Taking the time derivative of (11) and using (2) and (4), one can get

$$\begin{aligned} \dot{V_{2}}(t)= & {} s(t)\dot{s}(t)\nonumber \\= & {} s\left[ \dot{x}_{2}+(k_1-c)x_{2}+\lambda ax_{1}+x_{1}x_{3}\right] \nonumber \\= & {} s\left[ cx_{2}\!-\!x_{1}x_{3}\!+\!x_{4}\!+\!u\!+\!(k_1\!-\!c)x_{2}\!+\!\lambda ax_{1}\!+\!x_{1}x_{3}\right] \nonumber \\= & {} s\left[ \lambda ax_{1}+k_{1}x_{2}+x_{4}+u(t)\right] \end{aligned}$$
(12)

Using the control function \({u}\) as given in (10), one can get

$$\begin{aligned} \dot{V}_{2}\le -\eta |s| \end{aligned}$$
(13)

One can show derivative \(\dot{V_{2}}(t)=s(t)\dot{s}(t)<0\) when \(s(t)\ne 0\). Thus according to Lyapunov stability theory, \({s(t)}\) always converges to switching surface \({s(t)=0}\), Furthermore, since the state dynamics in the sliding manifold is GAS according to (8), it clearly shows that the state dynamics converges to zero asymptotically. i.e. \(lim_{t\rightarrow \infty }||x_{i}(t)||=0\), for \({(i=1,2,3,4)}\). \(\square \)

3 Design of single input synchronization controller

In this section, the results presented in previous section are extended to address synchronization problem of systems based on SMC.

3.1 Synchronization of two 4D hyperchaotic Lu system

The master system is defined as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{m1}=a(x_{m2}-x_{m1})\\ \dot{x}_{m2}=cx_{m2}-x_{m1}x_{m3}+x_{m4}\\ \dot{x}_{m3}=x_{m1}x_{m2}-bx_{m3}\\ \dot{x}_{m4}=x_{m3}-dx_{m4}\\ \end{array}\right. } \end{aligned}$$
(14)

For the system in (14), slave system can be defined as

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{s1}=a(x_{s2}-x_{s1})\\ \dot{x}_{s2}=cx_{s2}-x_{s1}x_{s3}+x_{s4}+u\\ \dot{x}_{s3}=x_{s1}x_{s2}-bx_{s3}\\ \dot{x}_{s4}=x_{s3}-dx_{s4}\\ \end{array}\right. } \end{aligned}$$
(15)

where \({u}\) is a control input in slave system (15). Now define the error vector \(\mathbf {e}(t)=[e_{1}(t)~e_{2}(t)~e_{3}(t)~e_{4}(t)]^{T}\) as:

$$\begin{aligned} e_i (t)=x_{si}(t)-x_{mi}(t)\quad for \, (i=1,2,3,4) \end{aligned}$$
(16)

which implies

$$\begin{aligned} \dot{e}_{i}(t)=\dot{x}_{si}(t)-\dot{x}_{mi}(t)\quad for\, (i=1,2,3,4) \end{aligned}$$
(17)

It results in following error dynamics:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{e}_{1}=a(e_{2}-e_{1})\\ \dot{e}_{2}=ce_{2}+e_{4}-x_{s1}e_{3}-x_{s3}e_{1}+e_{1}e_{3}+u\\ \dot{e}_{3}=x_{s2}e_{1}+x_{s1}e_{2}-e_{1}e_{2}-be_{3}\\ \dot{e}_{4}=e_{3}-de_{4}\\ \end{array}\right. } \end{aligned}$$
(18)

For two hyperchaotic systems without control (i.e. \(u=0\)), the trajectories of the systems will quickly separate from each other and become extraneous with the initial conditions, \((x_{m1}(0),x_{m2}(0),x_{m3}(0),x_{m4}(0))\ne (x_{s1}(0),x_{s2}(0), x_{s3}(0),x_{s4}(0))\).

Therefore to synchronize the master and slave hyperchaotic system defined in (14) and (15), one need to design a SMC such that the resulting error vector satisfies

$$\begin{aligned} lim_{t\rightarrow \infty }||e(t)||=lim_{t\rightarrow \infty }||[e_{1}(t)~e_{2}(t)~e_{3}(t)~e_{4}(t)]||\rightarrow 0 \end{aligned}$$
(19)

Analysis of switching function is similar to as described in Sect. 2.2 and further, analysis of controller is discussed in this section. For ensuring the asymptotical stability of the sliding mode \({s(t)=0}\), the PI switching surface \({s(t)}\) is defined as follows:

$$\begin{aligned} s(t)=e_{2}+\int _{0}^{t}\{(k_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3}\} d\tau \end{aligned}$$
(20)

where \({k_{2}}\) is a positive parameter specified by designer suitably. When the system operates in the sliding mode \({s(t)=0}\), the following equation holds:

$$\begin{aligned} \dot{s}(t)=\dot{e}_{2}+(k_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3} \end{aligned}$$
(21)

It further implies that

$$\begin{aligned} \dot{e}_{2}=-(k_2-c)e_{2}-\lambda ae_{1}-x_{s1}e_{3}+e_{1}e_{3} \end{aligned}$$
(22)

Therefore, from (22) the following equivalent sliding mode dynamics can be obtained:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{e}_{1}=a(e_{2}-e_{1})\\ \dot{e}_{2}=-(k_2-c)e_{2}-\lambda ae_{1}-x_{s1}e_{3}+e_{1}e_{3}\\ \dot{e}_{3}=x_{s2}e_{1}+x_{s1}e_{2}-e_{1}e_{2}-be_{3}\\ \dot{e}_{4}=e_{3}-de_{4}\\ \end{array}\right. } \end{aligned}$$
(23)

Further, the hyperchaotic systems (14) and (15) can be synchronized effectively by the proposed single controller as per following theorem.

3.2 Design of switching function and controller

Theorem 2

For the systems (14) and (15) with corresponding error dynamical system (18), suppose that \({B_2}\) is the upper bounds of absolute values of state variable \({x_{s2}}\) if the system (15), then for the positive constant \(\lambda >dB_{2}^2/[a(4bd-1)]>0\), if the following control law is applied to the system (15):

$$\begin{aligned} u(t)=-(\lambda a-x_{s3})e_{1}-k_{2}e_{2}-e_{4}-\eta sgn(s) \end{aligned}$$
(24)

Then both the systems get synchronized, asymptotically.

Proof

To establish the stability of the sliding mode dynamics based on Lyapunov stability theory, Lyapunov function is selected as:

$$\begin{aligned} V_{3}(t)=0.5\left( \lambda e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+e_{4}^{2}\right) \quad \lambda >0 \end{aligned}$$
(25)

Therefore, taking the derivative of (25) with respect to time will result in following equation while using (23):

$$\begin{aligned} \dot{V}_{3}(t)= & {} \lambda e_{1}\dot{e}_{1}+e_{2}\dot{e}_{2}+e_{3}\dot{e}_{3}+e_{4}\dot{e}_{4}\nonumber \\= & {} \lambda e_{1}[a(e_{2}-e_{1})]+e_{2}[-(k_2-c)e_{2}-\lambda ae_{1}\nonumber \\&\,-\,x_{s1}e_{3}+e_{1}e_{3}]+e_{3}[x_{s2}e_{1}+x_{s1}e_{2}-e_{1}e_{2}-be_{3}]\nonumber \\&+\,e_{4}[e_{3}-de_{4}]\nonumber \\= & {} -\lambda ae_{1}^{2}-(k_{2}-c)e_{2}^{2}-be_{3}^{2}-de_{4}^{2}+x_{s2}e_{1}e_{3}+e_{3}e_{4}\nonumber \\< & {} -\lambda ae_{1}^{2}-(k_{2}-c)e_{2}^{2}-be_{3}^{2}-de_{4}^{2}+B_{2}|e_{1}||e_{3}|\nonumber \\&\,+\,|e_{3}||e_{4}|\nonumber \\= & {} -\mathbf {E}^{T}P_{2}\mathbf {E} \end{aligned}$$
(26)

where \({0\le |x_{s2}|<B_{2}, \mathbf {E}=[|e_1|,|e_2|,|e_3|,|e_4|]^{T}}\) is the absolute state error vector. The magnitude matrix \({P_2}\) is real symmetric and can be expressed as

$$\begin{aligned} P_{2}=\begin{bmatrix} \lambda a&\quad 0&\quad -\frac{B_{2}}{2}&\quad 0 \\ 0&\quad (k_2-c)&\quad 0&\quad 0 \\ -\frac{B_{2}}{2}&\quad 0&\quad b&\quad -\frac{1}{2} \\ 0&\quad 0&\quad -\frac{1}{2}&\quad d \end{bmatrix} \end{aligned}$$
(27)

From the Lyapunov theorem of stability, it can be shown that zero equilibrium point \((e_1=e_2=e_3=e_4=0)\) of the error dynamical system is GAS if the real symmetric matrix \({P_{2}}\) is positive definite. By using the Sylvesters theorem, \({k_{2}}\) should be such that \({k_{2}>c>0}\) condition is satisfied and following conditions should hold for the real symmetric matrix \({P_{2}}\) to be positive definite.

$$\begin{aligned} \lambda >min\left[ \left( \frac{B_{2}^{2}}{4ab},\frac{dB_{2}^{2}}{a(4bd-1)}\right) \right] =\frac{dB_{2}^{2}}{a(4bd-1)} \end{aligned}$$
(28)

is satisfied for \({d=1}\). Satisfying the above conditions would ensure the GAS of error dynamics in (23). This completes the proof of Theorem 2.

There is a single-input control law to show the globally asymptotically(GA) synchronization to occur between system (14) and system (15). \(\square \)

Theorem 3

Consider the error dynamics (23), if the system is controlled by \({u(t)}\) in (24), then the system trajectories converge to switching function \({s(t)=0}\) and \(lim_{t\rightarrow \infty } ||e_i (t)||=0\), for \((i=1,2,3,4)\).

Proof

Consider the new Lyapunov function candidate as

$$\begin{aligned} V_{4}(t)=0.5s^{2}(t) \end{aligned}$$
(29)

Therefore, taking the derivative of (29) with respect to time and using (21) and (23), one can get

$$\begin{aligned} \dot{V_{4}}(t)= & {} s(t)\dot{s}(t)\nonumber \\= & {} s[\dot{e}_{2}+(k_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3}]\nonumber \\= & {} s[ce_{2}+e_{4}-x_{s1}e_{3}-x_{s3}e_{1}+e_{1}e_{3}+(k_2-c)e_{2}\nonumber \\&\,+\,\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3}]\nonumber \\= & {} s[(\lambda a-x_{s3})e_{1}+k_{2}e_{2}+e_{4}+u(t)] \end{aligned}$$
(30)

Using the control function \({u}\) as given in (24), the above expression reduces to

$$\begin{aligned} \dot{V}_{4}(t)\le -\eta |s| \end{aligned}$$
(31)

Thus according to Lyapunov stability theory, \({s(t)}\) always converges to switching function \({s(t)=0}\), Furthermore, since the error dynamics in the sliding manifold is asymptotically stable according to (26), it clearly shows that the error dynamic converges to zero asymptotically. i.e. \(lim_{t\rightarrow \infty }||e_i (t)||=0\), for \((i=1,2,3,4)\). \(\square \)

3.3 Adaptive synchronization with uncertain parameters

In practical situation, some or all of the system parameters cannot be exactly known in anticipating of synchronization applications. The effect of parameter uncertainties will destroy the synchronization and even break it. Therefore, one is invited to study the hyperchaotic synchronization problem in the presence of uncertain system parameters. In this section, the adaptive control methodology based on the aforementioned feedback control laws is applied to synchronize two nearly identical 4D hyperchaotic Lu systems in spite of the difference in initial conditions. In the following, let the system (14) be the master system and parameters \({a,b,c,d}\) be known. The slave system is defined by

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{x}_{s1}=a_{r}(x_{s2}-x_{s1})\\ \dot{x}_{s2}=c_{r}x_{s2}-x_{s1}x_{s3}+x_{s4}+u\\ \dot{x}_{s3}=x_{s1}x_{s2}-b_{r}x_{s3}\\ \dot{x}_{s4}=x_{s3}-d_{r}x_{s4}\\ \end{array}\right. } \end{aligned}$$
(32)

where the parameters of \({a_{r},b_{r},c_{r},d_{r}}\) in the slave system (32) are uncertain which need to be estimated and controller \({u}\) to be designed, accordingly. The aim of this section is to determine the controller for achieving synchronization between the system (14) and (32). For this purpose, the error dynamical system between system (14) and system (32) can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{e}_{1}=a(e_{2}-e_{1})+e_{a}(x_{s2}-x_{s1})\\ \dot{e}_{2}=ce_{2}-x_{s3}e_{1}-x_{s1}e_{3}+e_{1}e_{3}+e_{4}+e_{c}x_{s2}+u\\ \dot{e}_{3}=x_{s2}e_{1}+x_{s1}e_{2}-be_{3}-e_{1}e_{2}-e_{b}x_{s3}\\ \dot{e}_{4}=e_{3}-de_{4}-e_{d}x_{s4}\\ \end{array}\right. } \end{aligned}$$
(33)

where \({e_{a}=a_{r}-a ,e_{b}=b_{r}-b ,e_{c}=c_{r}-c ,e_{d}=d_{r}-d}\) are defined to be the parametric errors between the parameter estimates and their true values. Here, \({a_{r}, b_{r}, c_{r}, d_{r}}\) are the estimates and \({a, b, c, d}\) are the true parameters of hyperchaotic Lu system.

3.4 Design of switching function and controller with uncertain parameters

Analysis of switching function is again similar to as described in Sect 2.2. For ensuring the asymptotical stability of the sliding mode \({s(t)=0}\), the PI switching function \({s(t)}\) is defined as follows:

$$\begin{aligned} s(t)=e_{2}+\int _{0}^{t}\left\{ (\tilde{k}_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3}\right\} d\tau \end{aligned}$$
(34)

where \({\tilde{k}_{2}}\) is an estimated positive constant specified by designer. When the system operates in the sliding mode \({s(t)=0}\), the following equation holds:

$$\begin{aligned} \dot{s}(t)=\dot{e}_{2}+(\tilde{k}_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3} \end{aligned}$$
(35)

and

$$\begin{aligned} \dot{e}_{2}=-(\tilde{k}_{2}-c)e_{2}-\lambda ae_{1}-x_{s1}e_{3}+e_{1}e_{3} \end{aligned}$$
(36)

Therefore, from (36) the following equivalent sliding mode error dynamics can be obtained:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{e}_{1}=a(e_{2}-e_{1})+e_{a}(x_{s2}-x_{s1})\\ \dot{e}_{2}=-(\tilde{k}_2-c)e_{2}-\lambda ae_{1}-x_{s1}e_{3}+e_{1}e_{3}\\ \dot{e}_{3}=x_{s2}e_{1}+x_{s1}e_{2}-be_{3}-e_{1}e_{2}-e_{b}x_{s3}\\ \dot{e}_{4}=e_{3}-de_{4}-e_{d}x_{s4}\\ \end{array}\right. } \end{aligned}$$
(37)

Theorem 4

Consider the error dynamical system (33) with the uncertain parameters \({a_{r},b_{r},c_{r},d_{r}}\) are controlled, if the adaptive controller is applied for the slave system (32).

To ensure the occurrence of the sliding motion, following control law is proposed:

$$\begin{aligned} u(t)=-e_{c}x_{s2}+(x_{s3}-\lambda a)e_{1}-\tilde{k}_{2}e_{2}-\eta ~sgn(s) \end{aligned}$$
(38)

where \({\tilde{k}_{2}}\) is the estimated feedback gain updated according to the following adaptation algorithm:

$$\begin{aligned} \tilde{k}_{2}(t)=\beta _{1}e_{2}^{2}, \quad \tilde{k}_{2}(0)=0 \end{aligned}$$
(39)

where \(\beta _{1}\) is a positive gain determining the adaptation process. Further, the adaptive update laws of system parameters \({a_{r},b_{r},c_{r},d_{r}}\) are suggested to be as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll}\dot{e}_{a}=-\beta _{2}e_{a}-\lambda e_{1}(x_{s2}-x_{s1})\\ \dot{e}_{b}=-\beta _{3}e_{b}+e_{3}x_{s3}\\ \dot{e}_{c}=-\beta _{4}e_{c}-e_{2}x_{s2}\\ \dot{e}_{d}=-\beta _{5}e_{d}e_{3}+e_{4}x_{s4}\\ \end{array}\right. } \end{aligned}$$
(40)

where \({\beta _{2}>0,\beta _{3}>0,\beta _{4}>0,\beta _{5}>0}\) are positive gains determining the estimated process of the system parameters and \({e_{a}(0),e_{b}(0),e_{c}(0),e_{d}(0)}\) are specified. Then, the zero equilibrium point of the error dynamical system (33) is GAS, and thus the two systems (14) and (32) are GA synchronized.

Proof

Consider the new positive Lyapunov function:

$$\begin{aligned} V_{5}(t)=V_{3}(t)\!+\!0.5\left( e_{a}^{2}\!+\!e_{b}^{2}\!+\!e_{c}^{2}\!+\!e_{d}^{2}\right) \!+\!\frac{1}{2\beta _{1}}\left( \tilde{k_{2}}\!-\!k_{2}\right) ^{2}\!\ge \! 0\nonumber \\ \end{aligned}$$
(41)

where \({V_3 (t)}\) is the positive Lyapunov function defined in (26). The constant \({k_2}\) is positive, and it will be determined later. Taking the time derivative of (41) along system (33), the adaptive controller in (38) associated with (39), and the adaptive update laws of system parameters in (40), it follows that

$$\begin{aligned} \dot{V}_{5}(t)= & {} \dot{V}_{3}(t)\!+\!e_{a}\dot{e}_{a}\!+\!e_{b}\dot{e}_{b}\!+\!e_{c}\dot{e}_{c}\!+\!e_{d}\dot{e}_{d} \!+\!\frac{1}{\beta _{1}}(k_{2}\!-\!k_{2})\dot{\tilde{k}}_{2}\nonumber \\= & {} -\lambda ae_{1}^{2}-(k_2-c)e_{2}^{2}-be_{3}^{3}-de_{4}^{2}+x_{s2}e_{1}e_{3}\nonumber \\&\,+\,e_{3}e_{4}-\beta _{2}e_{a}^{2}-\beta _{3}e_{b}^{2}-\beta _{4}e_{c}^{2}-\beta _{5}e_{d}^{2}\nonumber \\< & {} -\mathbf {E}^{T}P_{2}\mathbf {E}-\mathbf {E}_{p}^{T}D\mathbf {E}_{p} \end{aligned}$$
(42)

where \(\mathbf {E}\), the absolute error vector is defined in (26) and \({\mathbf {E}_{p}=[|e_{a}|\quad |e_{b}|\quad |e_{c}|\quad |e_{d}|]^{T}}\) is the absolute system parameter error vector. The matrix \({P_{2}}\) and \({D}\) are real symmetric and diagonal, respectively. The diagonal matrix \({D}\) can be expressed by

$$\begin{aligned} D=\begin{bmatrix} \beta _{2}&\quad 0&\quad 0&\quad 0 \\ 0&\quad \beta _{3}&\quad 0&\quad 0 \\ 0&\quad 0&\quad \beta _{4}&\quad 0 \\ 0&\quad 0&\quad 0&\quad \beta _{5} \end{bmatrix} \end{aligned}$$
(43)

It is easy to show that the zero equilibrium point of the error dynamical system (33) is GAS if \({k_{2}>c>0}\). The \({\dot{V}_{5}(t)}\) is negative definite. It means that \({V_{5}(t)}\) is a positive and decreasing function and it follows that the equivalent point \((e_1=e_2=e_3=e_4=0,\tilde{k}_{2}=k_2,e_a=e_b=e_c=e_d=0)\) is GAS. Then systems (14) and (32) with the uncertain parameters \({a_r,b_r,c_r,d_r}\) can be synchronized by applying the adaptive controller in (38) associated with (39) and the adaptive update laws of system parameters in (31), and this completes the proof of Theorem 4. \(\square \)

Theorem 5

Consider the error dynamics (33), if the system is controlled by u(t) in (38), then the system trajectories converge to switching function \({s(t)=0}\) and error dynamics converges to zero asymptotically.

Proof

Consider the new Lyapunov function candidate as

$$\begin{aligned} V_{6}(t)=0.5s^{2}(t) \end{aligned}$$
(44)

Therefore, taking the derivative of (44) with respect to time and using (33), one can get

$$\begin{aligned} \dot{V_{6}}(t)= & {} s(t)\dot{s}(t)\nonumber \\= & {} s(t)[\dot{e}_{2}+(\tilde{k}_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3}]\nonumber \\= & {} s(t)[ce_{2}+e_{4}-x_{s1}e_{3}-x_{s3}e_{1}+e_{1}e_{3}+x_{s2}e_{c}\nonumber \\&+\,u+(\tilde{k}_2-c)e_{2}+\lambda ae_{1}+x_{s1}e_{3}-e_{1}e_{3}]\nonumber \\= & {} s(t)[(\lambda a-x_{s3})e_{1}+\tilde{k}_{2}e_{2}+e_{4}+e_{c}x_{s2}+u] \end{aligned}$$
(45)

Using the control function \({u}\) as given in (38), one can get

$$\begin{aligned} \dot{V}_{6}(t)\le -\eta |s| \end{aligned}$$
(46)

So according to Lyapunov stability theory, \({s(t)}\) always converges to switching function \({s(t)=0}\), Furthermore, since the error dynamics in the sliding manifold is GA according to (42), it clearly shows that the state of the error dynamic system converges to a desired target network within a finite time. i.e. \(lim_{t\rightarrow \infty }||e_i (t)||=0\), for \((i=1,2,3,4)\). \(\square \)

4 Numerical simulations

Numerical simulations are presented here to verify the effectiveness of the method proposed, for synchronization of hyperchaotic systems in uncertain environment. The fourth-order Runge-Kutta method is used to solve the nonlinear system with time step size 0.1. In the simulations, the system parameters are chosen as \(a=15,b=5,c=10,d=1\) and \({\eta >0}\) have to be selected suitably in all the cases. Assume the initial condition for states as \(x_{1}(0)=0.1,x_{2}(0)=0.1,x_{3}(0)=0.1,x_{4}(0)=0.1\). The constant \({\lambda =1.5}\) is selected as suitably in stabilization case. Positive parameter of stabilization is selected as \({k_{1}>c}\). Operation of without controller is shown in Fig. 1a–d three dimensional phase portraits for different states. In this case stabilization is considered. Figure 2 represents the variation of states of system with time. Fig. 3a represents the variation of switching function \({s}\). Fig. 3b represents the variation of control input \({u}\) with time.

Fig. 2
figure 2

Variation of states of system with time [controller (10)]

Full size image
Fig. 3
figure 3

Response of hyperchaotic Lu system [with stabilization controller (10)]: a variation of switching function s and b variation control input u with time

Full size image

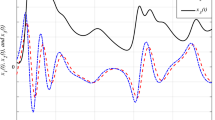
In next part of simulation, synchronization operation is achieved using controller given in (24). In this case, the initial conditions are set as \(x_{m1}(0)=0.1,\) \(x_{m2}(0)=0.1,x_{m3}(0)=0.1,x_{m4}(0)=0.1\), and \(x_{s1}(0)\!=\!-9.9,x_{s2}(0)\!=\!-4.9,x_{s3}(0)=5.1,x_{s4}(0)=10.1\), respectively. Figure 4a–d represents the time response of the states trajectories of master and slave system (14) and (15) with controller in (24). Figure 5 represents the time response of synchronization errors between master and slave system (14) and (15). For the control law, the constant is selected as \({\lambda =1.5}\) which induces the lower bound of the feedback gain. Figure 6a gives the variation of switching function \({s}\) with time. Figure 6b gives the variation of control input \({u}\) with time.

Fig. 4
figure 4

Response of the hyperchaotic Lu system (with synchronization): a–d variation of states trajectories of master (solid line) and slave (dash line) systems (14) and (15) with controller in (24)

Full size image
Fig. 5
figure 5

Synchronization error between states of master and slave systems in (14) and (15)

Full size image
Fig. 6
figure 6

Response of synchronization: a variation of switching function s and b variation of control input u with time

Full size image

In next part of simulation, for the same parameter settings, synchronization operation is achieved using controller given in (38). In this case, one of the parameter of the system is taken as uncertain. The initial condition for the states of master and slave hyperchaotic Lu system are taken as that of previous case. In addition, the initial conditions of the adaptive update laws of system parameters are \(e_{a}(0)= e_{b}(0)= e_{c}(0)=e_{d}(0)=5\). Value of \({B_{2}}\), the upper bounds of the absolute value of state variables \({x_{s2}}\) of system (15), can be chosen as \({B_{2}=20}\). The other positive constants of adaptation are chosen as \(\beta _{1}=100,\beta _{2}=3,\beta _{3}=0.5,\beta _{4}=1.75,\beta _{5}=2\). Figure 7 represents the time response of synchronization error between master and slave system for the case of uncertain. Figure 8a represents the variation of switching function \({s}\) with time. Figure 8b represents the variation of control input \({u}\) with time. Figure 9a represents the convergence behavior of estimates of uncertain parameters. The values of estimated uncertain parameters are \(a_{r}=14.9952,b_{r}=4.9429,c_{r}=10.0007,d_{r}=-0.2541\). Figure 9b represents the convergence behavior of adaptive feedback gain with time. Simulations justify the synchronization of the two hyperchaotic Lu systems in uncertain environment with proposed controller. It gives the estimate of uncertain parameter which converges to true value with time and value of adaptive feedback gain \({49.8036}\), which is shown in Fig. 9b.

Fig. 7
figure 7

The time response of synchronization error between master and slave systems in uncertain case

Full size image
Fig. 8
figure 8

Response of hyperchaotic Lu system (with uncertain synchronization): a variation of switching function s and b variation of control input u with time

Full size image
Fig. 9
figure 9

Response of hyperchaotic Lu system (with uncertain synchronization): a convergence behavior of estimates of uncertain parameters and b convergence behavior of adaptive feedback gain(49.8036) with time

Full size image

5 Conclusions

In this paper, PI switching function based SMC scheme is presented to investigate the stabilization, complete synchronization and adaptive synchronization of 4D hyperchaotic Lu systems. A SMC has been proposed to guarantee the occurrence of the sliding motion. It has been shown that by proper choice of the control parameters the master and slave systems is synchronized in master-slave configuration. This paper has examined the single control input scheme for synchronization of two identical 4D hyperchaotic Lu systems. Meanwhile, the designed adaptive controller and the adaptive update laws of the system parameters ensure a GAS complete synchronization and adaptive synchronization between two nearly identical 4D hyperchaotic Lu systems. The proposed methodology ensures convergence of estimates of system parameters to their true value as well. Finally, effectiveness of the proposed approach is validated through numerical simulations.