Probabilistic solution of the vibratory energy harvester excited by Gaussian white noise

Abstract

This paper aims to investigate the statistical characteristics of strongly nonlinear vibratory energy harvesters under Gaussian white noise excitation. The high-dimensional Fokker–Planck–Kolmogorov (FPK) equation of the coupled electromechanical system is reduced to a low-dimensional equation by using the state-space-split method. The conditional moment given by the equivalent linearization method is employed to decouple the FPK equations of coupled system, and then obtained an equivalent nonlinear uncoupled subsystem. The exact stationary solution of the reduced FPK equation of the subsystem is established. The mean output power is derived by the second order conditional moment from the associated approximate probability density function of mechanical subsystem. The procedure is applied to mono- and bi-stable energy harvesters. Effectiveness of the probability density function of the proposed approach is examined via comparison with equivalent linearization method and Monte Carlo simulation. The effects of the system parameters on the mean-square displacement and the mean output power are discussed. The approximate analytical outcomes are qualitatively and quantitatively supported by the numerical simulations.

1 Introduction

Scavenging otherwise wasted mechanical energy to support low power consumption electronics has recently appeared as an important technology which continues to grow at rapidly [1, 2]. Therefore, vibration-based energy harvesting has been extensively investigated in recent years. There are several prominent and comprehensive review papers, especially Sodano [3], Anton and Sodano [4], Tang et al. [5], Pellegrini et al. [6], Harne and Wang [7] and Daqaq et al. [8], introducing the state of the art in different time phases of investigations related to vibratory energy harvesters. Vibratory energy harvesters are extensible power generators which can be divided into four kinds based on electromechanical transduction mechanism, namely electromagnetic, piezoelectric, electrostatic, or magnetostrictive. The study of vibratory energy harvesters has become a hot topic, won widely development in theories and experiments, and included a series of results [9,10,11,12].

Noises are a very common feature in most real-world circumstances. Many practical problems in engineering science are described as randomness. The investigation on the stochastic response of vibratory energy harvester under random excitation has been an interesting topic. Cottone et al. [13] observed numerically and experimentally that the bistable oscillators can outperform the linear ones under Gaussian white noise excitation. Adhikari et al. [14] derived the mean power of a linear energy harvester subjected to random base excitation with and without an inductor. Litak et al. [15] reported that the bistable piezomagnetoelastic energy harvester exhibits a stochastic resonance phenomenon. Gammaitoni et al. [16] considered numerically that noise activated bistable and monstable energy harvesters can enhanced the performances in terms of averaged root-mean-square voltage. Daqaq [17] demonstrated that the nonlinearity of monostable harvester does not enhance power over the linear system under Gaussian white noise and colored noise excitations, respectively. He also [18] derived an approximate expression for the mean power under exponentially correlated noise and demonstrated the existence of an optimal potential shape maximizing the output power. Green et al. [19] reported Duffing-type nonlinearities can reduce the output power than the linear system via equivalent linearization method. Ali et al. [20] established a closed-form approximate power expression of the bistable piezomagnetoelastic energy harvester under random excitation and validated against the Monte Carlo numerical simulation results. Masana and Daqaq [21] investigated the influence of stiffness nonlinearities on the transduction of buckling piezoelectric beam under band-limited noise by experiment. Daqaq [22] applied the method of moment differential equations of FPK equation to calculate response statistics and demonstrated that the energy harvesters time constant ratio plays a critical role in characterizing the performance of nonlinear harvesters in a random environment. Martens et al. [23] studied the stationary response of magnetopiezoelectric energy harvester under stochastic excitation by using the Galerkin method. He and Daqaq [24, 25] employed the statistical linearization techniques and finite element method of the FPK equation to investigate how the shape of the potential energy function influences the mean steady-state approximate output power. Jiang and Chen [26] employed the method of moment differential equations of Itô equation to investigate the response moments of piezoelectric energy harvester. Xu et al. [27] introduced the stochastic averaging of energy envelope for Duffing-type vibration energy harvesters, and discussed the effects of the system parameters on the mean square output voltage and power. Kumar et al. [28] used the finite element method to solve the FPK equation of the associated bistable energy harvester, and analyzed the effects of the system parameters on the mean square output voltage and power. Jin et al. [29] introduced the generalized harmonic transformation to decouple the electromechanical equations, and applied the equivalent nonlinearization technique to derive a semi-analytical solution of the corresponding nonlinear vibration energy harvesters subjected to Gaussian white noise excitation. De Paula et al. [30] shown bistable energy harvester have a better performance than linear and monostable systems when the beam oscillates around two stable equilibrium configuration. Yue et al. [31] applied the generalized cell mapping method to compute the transient and stationary probability density functions of piezomagnetoelastic energy harvester system subjected to harmonic and Poisson white noise excitations. Jiang and Chen employed standard stochastic averaging method [32] and the generalized stochastic averaging method [33] to decopled the electromechanical system, and computed the exact stationary solution of the reduced FPK equation. Liu et al. [34] investigated the chaotic behavior of the vibration energy harvester with fractional-order potential energy. Xiao and Jin [35] considered the harvesting performance of piezoelectric energy harvester under correlated multiplicative and additive white noise.

The FPK equation provides a powerful tool for treating the statistical characteristics of nonlinear stochastic system. To solve the FPK equation is the most effective method to obtain the evolutive properties of the system response. The FPK equation of the coupled electromechanical system is a three-dimensional nonlinear partial differential equation. Its exact solution is difficult to calculate, even for exact stationary probability densities. Therefore some approximate methods for solving the FPK equation of the coupled electromechanical system have been reported which include the statistical linearization techniques [14, 17,18,19], the moment differential equations method [22, 26], the Galerkin method [23], the finite element method [24, 25, 28], the stochastic averaging of energy envelope [27, 32, 33], the equivalent nonlinearization technique [29] and the cell mapping method [31]. Recently, Er [36] first proposed the SSS method as a scheme to reduce the high-dimensional FPK equation and demonstrated it is an effective method for Gaussian white noise [37] and Poisson impulses excitations [38, 39]. From the above analysis, the PDF solution of coupled electromechanical nonlinear systems under stochastic excitation is less investigated. To address the lack of research in the aspect, the present work applies the SSS method to compute and study the statistical characteristics of vibratory energy harvesters.

The paper is organized as follows. Section 2 proposes the FPK equation of vibratory energy harvester. In Sect. 3, the procedure for solving the FPK equation of the coupled electromechanical equations by SSS method is presented, and derived the PDF of decoupled mechanical subsystem. Simultaneously, computed the output power via second order conditional moment scheme. Section 4 applies the SSS method to monostable vibration energy harvesters, discusses the effects of the system parameters on the mean-square displacement and the mean power. Section 5 employ the SSS method to bistable vibration energy harvesters, proposes the effects of the system parameters on the mean-square displacement and the mean power. Finally, some concluding remarks are made in Sect. 6.

2 Problem formulation

The coupled electromechanical equations of piezoelectric energy harvesters under Gaussian white noise excitation can be given as [22]

$$\begin{aligned}&m\ddot{x} + c\dot{x} + \frac{{dU(x)}}{{dx}} + \theta v = -\,m{\ddot{x}_b} \end{aligned}$$

(1)

$$\begin{aligned}&{C_p}\dot{v} + {v / R} = \theta \dot{x} \end{aligned}$$

(2)

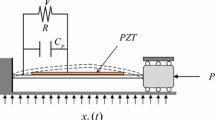
where x represents the displacement of mass m, v is the voltage collected via the resistive R, c is the viscous damping coefficient, $\theta$ is the electromechanical coupling coefficient, $C_p$ is the capacitance of the circuit, ${\ddot{x}_b}$ is the base acceleration. The physical model of piezoelectric energy harvesters as shown in Fig. 1. The potential of the mechanical system can be written as

$$\begin{aligned} U(x) = \frac{1}{2}{k_1}(1 - r){x^2} + \sum \limits _{i = 2}^n {\frac{1}{i+1}} {k_i}{x^{i+1}} \end{aligned}$$

(3)

where $k_1$ and $k_i$ are the linear and nonlinear stiffness coefficients, respectively, and n being a positive integer.

Fig. 1

The physical model of piezoelectric energy harvesters [21]

The non-dimensional electromechanical coupling equations can be derived via the non-dimensional transformations [22] as the following general form

$$\begin{aligned}&\ddot{X} + 2\zeta \dot{X} + g(X) + \kappa Y = \xi (t) \end{aligned}$$

(4)

$$\begin{aligned}&\dot{Y} + \alpha Y = \dot{X} \end{aligned}$$

(5)

where $g(X) = (1 - r)X + {\delta _i}{X^i}(i = 2,3, \ldots ,n)$, $\zeta$ represents the damping ratio, $\kappa$ denotes the electromechanical coupling coefficient, $\alpha$ is the time constant ratio, and $\xi (t) = -\,\ddot{x}_{\mathrm{b}}$ is the base acceleration. $\xi (t)$ is Gaussian white noise with zero mean and autocorrelation function

$$\begin{aligned} E\left[ {\xi (t)\xi (t + \tau )} \right] = 2D\delta (\tau ) \end{aligned}$$

(6)

in which $E[\cdot ]$ denotes the expected value, D is the intensity of the excitation, and $\delta \left( \cdot \right)$ is the Dirac function.

The FPK equation corresponding to Eqs. (4) and (5) is

$$\begin{aligned}&\frac{{\partial p(\mathbf x ,t)}}{{\partial t}} + \frac{{\partial [{f_1}p(\mathbf x ,t)]}}{{\partial {x_1}}} + \frac{{\partial [{f_2}p(\mathbf x ,t)]}}{{\partial {x_2}}} + \frac{{\partial [{f_3}p(\mathbf x ,t)]}}{{\partial {x_3}}}\nonumber \\&\quad - \,D\frac{{{\partial ^2}p(\mathbf x ,t)}}{{\partial x_2^2}} = 0 \end{aligned}$$

(7)

where $\mathbf x =[{x_1},{x_2},{x_3}] = [X,\dot{X},Y]$, ${f_1} = {x_2}, {f_2} = - \left( {2\zeta {x_2} + g({x_1}) + \kappa {x_3}} \right) , {f_3} = - \alpha {x_3} + {x_2}.$ For the stationary case, the FPK equation (7) is reduced to the following form

$$\begin{aligned} \frac{{\partial [{f_1}p(\mathbf x )]}}{{\partial {x_1}}} + \frac{{\partial [{f_2}p(\mathbf x )]}}{{\partial {x_2}}} + \frac{{\partial [{f_3}p(\mathbf x )]}}{{\partial {x_3}}} - D\frac{{{\partial ^2}p(\mathbf x )}}{{\partial x_2^2}} = 0\nonumber \\ \end{aligned}$$

(8)

It is assumed that the solution $p(\mathbf x ,t)$ in Eq. (7) or the solution $p(\mathbf x )$ in (8) satisfies the following boundary conditions

$$\begin{aligned}&\mathop {\lim }\limits _{{x_i} \rightarrow \infty } {f_j}(\mathbf x )p(\mathbf x ,t) = 0 \quad and\nonumber \\&\mathop {\lim }\limits _{{x_i} \rightarrow \infty } \frac{{\partial p(\mathbf x ,t)}}{{\partial {x_i}}} = 0 \quad (i,j = 1,2,3). \end{aligned}$$

(9)

3 State space split method

Er [36] first pioneered the SSS method as a scheme to reduce the high-dimensional FPK equation. The SSS method has been applied to the solution of the high-dimensional FPK equation of the nonlinear system under Gaussian white noise [37] and Poisson impulses excitations [38, 39].

According to the SSS method, separate the state vector $\mathbf x$ of energy harvesting system (4) and (5) into two parts $\mathbf{x _1} =\{{x_1, x_2}\}\in {R^{{2}}}$ and $\mathbf{x _2} =\{x_3\} \in {R}$, and $\mathbf x = \left\{ {\mathbf{x _1},\mathbf{x _2}} \right\} \in {R^{{3}}} = {R^{{2}}} \times {R}$. $\mathbf{x _1}$ is the state space of the mechanical subsystem, and $\mathbf{x _2}$ represents the electric circuit system. $\mathbf{x _1}$ contains the response whose PDF is to be obtained, whereas $\mathbf{x _2}$ contains the response which is to be approximately replaced by some functions of $\mathbf{x _1}$ via the SSS method.

Denote the stationary PDF of $\mathbf{x }$ as $p_1(\mathbf{x _1})$. In order to obtain the $p_1(\mathbf{x _1})$, integrating Eq. (8) over the circuit interval ${R_3}$ gives

$$\begin{aligned}&\int _{R_3} {\frac{{\partial [{f_1}p(\mathbf x )]}}{{\partial {x_1}}}} d{x_3} + \int _{R_3} {\frac{{\partial [{f_2}p(\mathbf x )]}}{{\partial {x_2}}}} d{x_3} \nonumber \\&\quad + \,\int _{R_3} {\frac{{\partial [{f_3}p(\mathbf x )]}}{{\partial {x_3}}}} d{x_3} - D\int _{R_3} {\frac{{{\partial ^2}p(\mathbf x )}}{{\partial x_2^2}}} d{x_3} = 0 \end{aligned}$$

(10)

In addition, the PDF of $\mathbf x _1$ can be derived by integrating $p(\mathbf x )$ over ${R_3}$ as follows:

$$\begin{aligned} \int _{R_3} {p({x_1},{x_2},{x_3})d} {x_3} = p({x_1},{x_2}) \end{aligned}$$

(11)

The electromechanical coupling equations in the second term of Eq. (10) is reformulated as

$$\begin{aligned} {f_2} = f_2^I({x_1},{x_2}) + f_2^{II}({x_1},{x_2},{x_3}) \end{aligned}$$

(12)

where $f_2^I({x_1},{x_2}) = - \left[ {2\zeta {x_2} + g({x_1})} \right] , f_2^{II}({x_1},{x_2},{x_3}) = -\,\kappa {x_3}$.

Substituting Eq. (12) into (10), by using the boundary condition (9) and the relationship (11), integrating Eq. (10) gives

$$\begin{aligned}&{x_2}\frac{{\partial p({x_1},{x_2})}}{{\partial {x_1}}} - \frac{\partial }{{\partial {x_2}}}\left[ (2\zeta {x_2} + g({x_1}))p({x_1},{x_2}) \right. \nonumber \\&\quad \left. +\, \int _{R_3} {\kappa {x_3}p({x_1},{x_2},{x_3})d{x_3}} \right] - \,D\frac{{{\partial ^2}p({x_1},{x_2})}}{{\partial x_2^2}} = 0\nonumber \\ \end{aligned}$$

(13)

Correspondingly, ${p({x_1},{x_2},{x_3})}$ can be further expressed by the conditional PDF as

$$\begin{aligned} p({x_1},{x_2},{x_3}) = p({x_1},{x_2})q({x_3}\left| {{x_1},{x_2})} \right. \end{aligned}$$

(14)

where $q({x_3}\left| {{x_1},{x_2})} \right.$ is the conditional PDF of voltage ${x_3}$ for given the mechanical subsystem ${x_1}$ and ${x_2}$.

Substituting Eq. (14) into (13), Eq. (13) is reformulated as

(15)

The conditional PDF $q({x_3}\left| {{x_1},{x_2})} \right.$ is unknown and it can be approximated by the result given by the equivalent linearization method for Gaussian white noise. Equation (15) is further formulated as

(16)

where $\overline{q} ({x_3}\left| {{x_1},{x_2})} \right.$ is the conditional PDF given by the equivalent linearization method. Correspondingly, the exact stationary PDF $p ({x_1},{x_2})$ is replaced by its approximation ${\overline{p} ({x_1},{x_2})}$.

Denote

$$\begin{aligned} {\overline{f} _2}= & {} -\,2\zeta {x_2} - g({x_1}) - \int _{R_3} {\kappa {x_3}\bar{q}({x_3}\left| {{x_1},{x_2})} \right. d{x_3}} \nonumber \\= & {} -\,2\zeta {x_2} - g({x_1}) - \kappa E[{x_3}\left| {{x_1},{x_2}} \right. ]\nonumber \\= & {} -\,2\zeta {x_2} - g({x_1}) - \kappa \left[ E[{x_3}] + {\rho _{{x_3},{x_1}}}\frac{{{\sigma _{{x_3}}}}}{{{\sigma _{{x_1}}}}}\left( {{x_1} - E[{x_1}]} \right) \right. \nonumber \\&+\,\left. {\rho _{{x_3},{x_2}}}\frac{{{\sigma _{{x_3}}}}}{{{\sigma _{{x_2}}}}}\left( {{x_2} - E[{x_2}]} \right) \right] \end{aligned}$$

(17)

where ${\rho _{( \cdot )}}\$ is the correlation coefficient of $( \cdot )$ of the equivalent linearization system, and ${\sigma _{( \cdot )}}\$ is the standard deviation of $( \cdot )$ of the equivalent linearization system.

Finally, the high-dimensional FPK equation of the coupled electromechanical harvesting system can be approximated by a low-dimensional FPK equation of the mechanical subsystem as follows:

$$\begin{aligned} \frac{{\partial [{x_2}\overline{p} ({x_1},{x_2})]}}{{\partial {x_1}}} + \frac{{\partial [{{\overline{f} }_2}\overline{p} ({x_1},{x_2})]}}{{\partial {x_2}}} - D\frac{{{\partial ^2}\overline{p} ({x_1},{x_2})}}{{\partial x_2^2}} = 0\nonumber \\ \end{aligned}$$

(18)

The exact stationary solution of the low-dimensional FPK equation (18) of the mechanical subsystem can be given by

$$\begin{aligned} \overline{p} ({x_1},{x_2}) = C\exp \left[ {\frac{{ - \overline{\zeta }}}{{2D}}\left( {x_2^2 + \overline{k} x_1^2 + \frac{2}{i + 1}{\delta _i}x_1^{i + 1}} \right) } \right] \nonumber \\ \end{aligned}$$

(19)

in which C is a normalized constant, $\overline{\zeta }= 2\zeta + \kappa {{{\sigma _{{x_2}{x_3}}}} / {\sigma _{{x_2}}^2}},\overline{k} = 1 - r + \kappa {{{\sigma _{{x_1}{x_3}}}} / {\sigma _{{x_1}}^2}}$, and $\sigma _{{x_i}{x_j}}(i\ne j)$ is the covariance of ${x_i}$ and ${x_j}$.

The non-dimensional output power can be expressed as

$$\begin{aligned} P= & {} \alpha \kappa E[x_3^2] = \alpha \kappa \int _{{R^3}} {x_3^2p({x_1},{x_2},{x_3})d{x_1}d{x_2}d{x_3}} \nonumber \\\approx & {} \alpha \kappa \int _{{R^3}} {x_3^2\overline{p}({x_1},{x_2})q({x_3}\left| {{x_1},{x_2})} \right. d{x_1}d{x_2}d{x_3}} \nonumber \\\approx & {} \alpha \kappa \int _{{R^2}} {\overline{p}({x_1},{x_2})} E[x_3^2\left| {{x_1},{x_2}} \right. ]d{x_1}d{x_2}. \end{aligned}$$

(20)

In addition, the second order conditional moment can be given by [37]

$$\begin{aligned} E[x_3^2\left| {{x_1},{x_2}} \right. ] = {\left( {E[{x_3}\left| {{x_1},{x_2}} \right. ]} \right) ^2} + {\sigma ^2}({x_3}\left| {{x_1},{x_2}} \right. ) \end{aligned}$$

(21)

in which the conditional mean can be written as

$$\begin{aligned} E[{x_3}\left| {{x_1},{x_2}} \right. ]= & {} E[{x_3}]+ \frac{{{\sigma _{{x_1}{x_3}}}}}{{ \sigma _{{x_1}}^2}}\left( {{x_1} - E[{x_1}]} \right) \nonumber \\&+ \,\frac{{{\sigma _{{x_2}{x_3}}}}}{{ \sigma _{{x_2}}^2}}\left( {{x_2} - E[{x_2}]} \right) \end{aligned}$$

(22)

and the conditional variance is expressed as

$$\begin{aligned} {\sigma ^2}({x_3}\left| {{x_1},{x_2}} \right. ) = \left( {1 - \frac{{\sigma _{{x_1}{x_3}}^2}}{{\sigma _{{x_1}}^2\sigma _{{x_3}}^2}} - \frac{{\sigma _{{x_1}{x_3}}^2}}{{ \sigma _{{x_1}}^2\sigma _{{x_3}}^2}}} \right) \sigma _{{x_3}}^2 \end{aligned}$$

(23)

.

Fig. 2

Comparison of PDFs and logarithmic PDFs for monostable energy harvester

4 Application to monostable energy harvester

The monostable energy harvester is an important model of nonlinear vibration energy harvester and has been the focal field of many research studies in recent years [1,2,3,4, 8]. The physical model can be realized by a clampedCclamped axially loaded piezoelectric beam which can operate in the pre-buckling configurations as shown in Fig. 1. However, the analysis on the probabilistic solutions of high-dimensional FPK equation has been a challenge. Therefore, the coupled FPK equation of energy harvesters has received less attention. Some methods were extended for obtaining the approximate probabilistic solutions of monostable energy harvesting systems under the small excitation intensity. Here, we consider the probabilistic solutions for coupled FPK equation of monostable energy harvesters subjected to lager excitation intensity.

Fig. 3

Variations of the mean-square displacement and the mean output power with the excitation intensity for monostable energy harvester

Fig. 4

Variations of the mean-square displacement and the mean output power with the nonlinearity coefficient for monostable energy harvester

Fig. 5

Variations of the mean-square displacement and the mean output power with the coupling coefficient for monostable energy harvester

Fig. 6

Variations of the mean-square displacement and the mean output power with the coupling coefficient for monostable energy harvester

The non-dimensional electromechanical coupling equations can be expressed as

$$\begin{aligned}&\ddot{X} + 2\zeta \dot{X} + X + \delta {X^3} + \kappa Y = \xi (t) \end{aligned}$$

(24)

$$\begin{aligned}&\dot{Y} + \alpha Y = \dot{X} \end{aligned}$$

(25)

The system parameters are selected by the previous studies [22, 29] with the nonlinear stiffness coefficient $\delta =0.5$, the time constant ratio $\alpha =0.05$, the electromechanical coupling coefficient $\kappa =0.5625$, the damping ratio $\zeta =0.01$ and the excitation intensity $2D = 0.4$. The stationary PDFs obtained from the SSS method, equivalent linearization (EQL) method, and Monte Carlo simulation (MCS) methods are compared in order to check the effectiveness of the SSS method in analyzing the strongly nonlinear monostable energy harvesting systems under Gaussian white noise excitations.

Figure 2 shows a comparison on the obtained PDF and logarithmic PDFs solutions of the mechanical subsystem $x_1$ and $x_2$ from the SSS method, EQL method, and MCS methods. It is seen that the PDFs and the tails of the PDFs of displacement $x_1$ calculated from SSS method are close to MCS while the PDFs from EQL method deviate from simulation result, especially in the tail regions. For the PDFs and the logarithmic PDFs of velocity $x_2$, the results from SSS method and EQL method are close to MCS.

Fig. 7

Comparison of PDFs and logarithmic PDFs for bistable energy harvester

As already mentioned the importance of the mean output power E[P] for energy harvesting and the mean-square displacement $E [x_1^2]$ for the miniaturization of the harvesting devices [22, 29, 32, 33], the mean-square displacement and the mean output power are calculated in the following discussion.

Fig. 8

Variations of the mean-square displacement and the mean output power with the excitation intensity for bistable energy harvester

Fig. 9

Variations of the mean-square displacement and the mean output power with the nonlinearity coefficient for bistable energy harvester

The influences of the excitation intensity D, the nonlinear coefficient $\delta$, the electromechanical coupling coefficient $\kappa$ and the time constant ratio $\alpha$ are shown in Figs. 3, 4, 5 and 6, in which the solid lines represent the analytical results from SSS method and red dotted circles are MCS numerical results based on Eqs. (24) and (25). The mean-square displacement and mean output power increase with the excitation intensity D, decrease as the nonlinear coefficient $\delta$ increases. Figure 5 shows that the mean output power increases while the mean-square displacement decreases as the electromechanical coupling coefficient $\kappa$ increases. Figure 6 demonstrates that there exists an optimal time constant ratio $\alpha$ to observe the maximal output power, and the mean-square displacement corresponding to the optimal time constant ratio closes to the minimum. According to previous studies [22, 29, 33], the time constant ratio $\alpha$ represents the load resistance. Thus, the occurrence of the optimal time constant ratio means that there exists an optimal load resistance which can generate maximal power. The consistency of the analytical solutions and the MCS results verifies the accuracy of the SSS method.

5 Application to bistable energy harvester

The bistable energy harvester has been investigated as a possible device to improve the performance of energy harvesters in harmonic and random excitations [5,6,7,8,9, 13, 20, 26]. The bistable mechanism has two stable static equilibria station separated by an unstable saddle which can generate large amplitude voltages over a wide range of frequencies under sufficient external excitation. Since the bistable is a strongly nonlinear oscillator and the corresponding FPK is multidimensional partial differential equation with varying coefficients. Thus, obtaining its exact solution is not a simple problem. As a result, some researchers proposed the statistical linearization method [20], Galerkin method [23] and finite element method [25, 28] to approximate the response statistics of the bistable system. In addition, some studies presented the Monte Carlo numerical simulation [13,14,15, 26] to calculate the response of the system. As of today, there are less analytical methods to address the statistics characteristics of bistable harvesters. Therefore, the SSS method was applied to investigate the probabilistic solutions for the coupled FPK equation of bistable energy harvesters subjected to Gaussian white noise.

Fig. 10

Variations of the mean-square displacement and the mean output power with the coupling coefficient for bistable energy harvester

Fig. 11

Variations of the mean-square displacement and the mean output power with the coupling coefficient for bistable energy harvester

The non-dimensional electromechanical coupling equations can be written as

$$\begin{aligned}&\ddot{X} + 2\zeta \dot{X} - X + \delta {X^3} + \kappa Y = \xi (t) \end{aligned}$$

(26)

$$\begin{aligned}&\dot{Y} + \alpha Y = \dot{X}. \end{aligned}$$

(27)

The system parameters are the same as Sect. 4. The physical model can be realized by a clampedCclamped axially loaded piezoelectric beam which can operate in the post-buckling configurations as shown in Fig. 1. The stationary PDFs obtained from the SSS method, EQL method, and MCS method are compared in Fig. 7. It is found that the results from SSS method of bistable energy harvester agree very well with the ones from MCS simulation. In addition, the stationary PDFs of displacement obtained from the SSS method essentially has two peaks which are symmetrical and bimodal, and the response may switch from one stable static equilibria station to another which is consistent with the corresponding potential energy function. However, the stationary PDFs of displacement from EQL method only has one peak. From the comparison, it is seen that the qualitative behaviors of the SSS method and the EQL method are different, and the effectiveness of the SSS method is observed by the MCS method in analyzing the nonlinear bistable energy harvesting systems under Gaussian white noise excitations.

The effects of the system parameters of bistable energy harvester on the mean-square displacement and the mean output power are discussed in the following, in which the solid lines represent the analytical results from SSS method and red dotted circles are MCS numerical results based on Eqs. (26) and (27). Figure 8 describes the variations of the excitation intensity D on the mean-square displacement and the mean output power. Both the response amplitude increase with the excitation intensity. Figure 9 shows that the mean-square displacement and the mean output power decrease quickly as the nonlinear coefficient $\delta$ increases, the change trend becomes flat along with the increase of $\delta$. Figure 10 shows that the mean output power increases while the mean-square displacement decreases as the electromechanical coupling coefficient $\kappa$ increases. Figure 11 implicates that there exists an optimal time constant ratio $\alpha$ to observe the maximal output power, while the mean-square displacement increases as time constant ratio increases, which is a little different from the monostable energy harvester. From the Figs. 8, 9, 10 and 11, it concludes that the analytical solutions given by the SSS method matched well with the MCS results.

6 Conclusions

This paper investigates the statistical responses of strongly nonlinear vibratory energy harvesters under Gaussian white noise excitation. The FPK equation of the coupled electromechanical system is reduced to a low-dimensional equation via the SSS method. The conditional moment is adopted to decouple the FPK equations of coupled system, and then obtained an equivalent nonlinear uncoupled subsystem. The exact stationary PDF of the reduced FPK equation is established for the mechanical subsystem. The mean output power is computed by the second order conditional moment from the associated approximate PDF of mechanical subsystem. The procedure is employed to mono- and bi-stable energy harvesters, the PDFs given by the SSS approach are compared with those given by EQL method and Monte Carlo simulation. The effects of the system parameters on the mean-square displacement and the mean output power are calculated. The approximate analytical outcomes are qualitatively and quantitatively supported by the numerical simulations.

It should be pointed out that the SSS method is not only suitable for the strongly nonlinear monostable energy harvester, but also suitable for the bistable energy harvesting systems. It is found that the stationary PDFs of displacement for bistable energy harvester obtained from the SSS method essentially has two peaks which is consistent with the corresponding potential energy function. From the comparison, it is seen that the qualitative behaviors of the SSS method and the EQL method are completely different. The stationary PDFs of displacement from the SSS method are bimodal, while the results from EQL method only are monomodal, and the effectiveness of the SSS method is observed by the MCS method.