1 Introduction

The theory of micro-continuum explains the complexities lying in the microstructures and discusses the microscopic motion and long-range material interactions. Eringen [1] was perhaps the first who introduced the theory of micromorphic bodies. Eringen [2] also generalized the theory of micropolar elastic materials to develop the theory of microstretch elastic solids. The material points in the microstretch bodies have seven degrees of freedom and can independently stretch and contract along with translations and rotations.

The thermoelastic theory studies the consequences of the disturbances occurred due to thermal, stress and strain fields on an elastic body. Biot [3] presented an unified treatment of thermoelasticity by employing and further developing the method of irreversible thermodynamics using two vector fields, displacement and an entropy flowfield to describe the state of the materials. Lord and Shulman [4] and Green and Lindsay [5] generalized the theory of thermoelasticity that allows finite velocity of transmission for the thermal waves. They introduce one and two thermal relaxation times, respectively, to discuss the thermal character in the continuum body. The theory of thermo-microstretch elastic solid was developed by Eringen [6] to induce the consequences of heat conduction in the microstretch theory and established the uniqueness theorem for the mixed initial boundary value problem. De Cicco and Nappa [7] verified finite velocities for thermal waves in the linearized theory of thermo-microstretch elastic solids. Ciarletta and Scalia [8] studied the spatial and temporal response of thermoelastodynamic phenomenon on microstretch continuum materials.

Sherief et al. [9] proved the variation theorem and uniqueness of the governing equations for the generalized thermoelastic diffusion materials. Aouadi [10] derived the equations of generalized thermoelastic diffusion, based on the Lord–Shulman theory and established the uniqueness and reciprocity theorem using Laplace transformation. Aouadi [11] inferred the field equations for thermoelastic diffusion plates considering three distinct heat and diffusion transmission laws. Khurana and Tomar [12] established the existence of three longitudinal and two transverse frequency dependent waves in non-local microstretch solid. Goyal et al. [13] investigated the inhomogeneous nature of Rayleigh waves with the aid of its secular equations in a swelling porous medium. Kumar [14] presented the characteristics of harmonic waves traveling through thermo-microstretch diffusion medium and obtained the amplitude/energy ratios of the reflected and refracted waves. Kumar et al. [15] developed the dispersion relations for Rayleigh waves through microstretch thermoelastic diffusion medium under a liquid layer with negligible viscosity. Singh et al. [16] derived the reflection and refraction coefficients in microstretch thermoelastic diffusion half-spaces subject to three distinct thermoelastic theories. Royer and Dieulesaint [17] summarized the theories related to the propagation of elastic waves in different materials, wave equations and their solutions, energy flow and reflection/refraction phenomena. Some important problems in thermoelastic materials are Singh [18], Zorammuana and Singh [19], Singh and Lianngenga [20], Lotfy and Othman [21], Singh and Tochhawng [22], Kumar and Kansal [23], Abo-Dahab et al. [24], Kumar et al.[25, 26], Singh and Yadav [27].

Lamb [28] examined surface waves in an isotropic elastic plate where the wave moves parallel to the medial plane. Zhu and Wu [29] obtained the dispersion equations of Lamb waves of a plate bordered with viscous liquid layer/a half-space of viscous liquid on both sides and evaluated the numerical solutions of dispersion equations. Conry et al. [30] solved the problem of low frequency Rayleigh-Lamb waves and detected the defects/cracks in a centrally embedded aluminum plate. Tomar [31] simulated the frequency equation of Rayleigh-Lamb wave propagation in a plate of micropolar elastic material with voids of finite thickness for velocity and attenuated curves. Lianngenga and Singh [32] studied the problem of symmetric and anti-symmetric vibrations in micropolar thermoelastic plate with voids and obtained the dispersive frequency equations for different surface waves propagating in the plate. We have observed interesting problems of Lamb waves in Sharma and Pal [33], Kumar et al. [34], Kumar and Pratap [35, 36], Sharma and Thakur [37], Sharma and Othman [38], Sharma and Kumar [39], Apostol [40], Ezzin et al. [41], Sharma and Kumar [42] and Goldstein and Kuznetsov [43].

The problems of Lamb wave are frequently used in civil engineering, architectures, navigation, chemical pipes, aerospace engineering, etc. The interest of researchers in such studies are increasing due to its ability to completely understand the structure of plates and shells, which are using in multi-sensors to detect the damages in metallic structures [44], and it is used in health monitoring devices [45, 46]. Our study of Lamb wave in microstretch thermoelastic diffusion plates may give new light to explore the skull and the human brain with better ultrasound imaging system [47, 48]. This investigation may provide to the researchers with an appropriate data to construct new medical and engineering devices. We will compare the results of Lamb wave propagating through a microstretch thermoelastic diffusion plate for the three thermoelastic theories, i.e., GL, LS and CT theories. The secular equations for symmetric and anti-symmetric Lamb wave modes will be derived for stress-free thermally insulated/impermeable and isothermal/isoconcentrated conditions.

2 Governing equations

The equations of motion for linearly isotropic and homogeneous microstretch thermoelastic diffusion media in the absence of body forces and heat sources are given by [2, 9]:

$$\begin{aligned}{} & {} (\lambda +2\mu +\kappa )\nabla (\nabla \cdot \textbf{u})-(\mu +\kappa )\nabla \times \nabla \times \textbf{u}+\kappa \nabla \times \varvec{\phi } \nonumber \\ {}{} & {} \quad + \lambda _0\nabla \varphi ^* -\beta _1(1 + \tau _1\frac{\partial }{\partial t}) \nabla T - \beta _2(1 + \tau ^1\frac{\partial }{\partial t})\nabla C\nonumber \\ {}{} & {} \quad =\rho \frac{\partial ^2 \textbf{u}}{\partial t^{2}}, \end{aligned}$$
(1)
$$\begin{aligned}{} & {} (\alpha +\beta +\gamma )\nabla (\nabla \cdot \varvec{\phi })-\gamma \nabla \times \nabla \times \varvec{\phi }+\kappa \nabla \times \textbf{u}-2\kappa \varvec{\phi }\nonumber \\ {}{} & {} \quad =\rho j\frac{\partial ^2 \varvec{\phi }}{\partial t^2}, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \alpha _0 \nabla ^2 \varphi ^*+\nu _1\left(1 + \tau _1\frac{\partial }{\partial t}\right) T + \nu _2\left(1 + \tau ^1\frac{\partial }{\partial t}\right) C-\lambda _1 \varphi ^*-\lambda _0\nabla \cdot \textbf{u}\nonumber \\ {}{} & {} \quad =\frac{\rho j_0}{2}\frac{\partial ^2 \varphi ^*}{\partial t^2}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \beta _1 T_0\left(1 + \varepsilon \tau _0\frac{\partial }{\partial t}\right) \nabla \cdot \frac{\partial \textbf{u}}{\partial t}+\nu _1 T_0\left(1 + \varepsilon \tau _0\frac{\partial }{\partial t}\right)\frac{\partial \varphi ^*}{\partial t}\nonumber \\ {}{} & {} \quad + \rho C^*\left(1 + \tau _0\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial t}+ aT_0\left(1 + \gamma _1 \frac{\partial }{\partial t}\right)\frac{\partial C}{\partial t}=K^*\nabla ^2 T, \end{aligned}$$
(4)
$$\begin{aligned}{} & {} d\beta _2 \nabla ^2 \left(\nabla \cdot \textbf{u}\right)+d\nu _2\nabla ^2 \varphi ^*+da\left(1+\tau _1\frac{\partial }{\partial t}\right)\nabla ^2 T\nonumber \\ {}{} & {} \quad +\left(1 + \varepsilon \tau ^0\frac{\partial }{\partial t}\right)\frac{\partial C}{\partial t}-db\left(1 + \tau ^1\frac{\partial }{\partial t}\right)\nabla ^2 C=0. \end{aligned}$$
(5)

The constitutive relations for the linearly isotropic and homogeneous microstretch thermoelastic diffusion solid are given as:

$$\begin{aligned}&t_{ij} = \lambda u_{i,i}\delta _{ij} + 2\mu e_{ij} + \kappa (u_{j,i}-e_{ijk}\phi _k)+\lambda _0\delta _{ij}\varphi ^* - \beta _1\left(1 + \tau _1\frac{\partial }{\partial t}\right) T\delta _{ij}\nonumber \\ {}{} & {} \quad - \beta _2\left(1 + \tau ^1\frac{\partial }{\partial t}\right)C\delta _{ij}, \end{aligned}$$
(6)
$$\begin{aligned}&m_{ij} = \alpha \phi _{i,i}\delta _{ij} + \beta \phi _{i,j} + \gamma \phi _{j,i} + b_0e_{kji}\varphi _{,k}^*, ~~~\lambda _i^* \nonumber \\ {}{} & {} \quad = \alpha _0\varphi _{,i}^* + b_0e_{ijk}\phi _{j,k}, ~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(7)

Here, \(\beta _1 = (3\lambda +2\mu +\kappa )\alpha _{t1},~ \beta _2=(3\lambda +2\mu +\kappa )\alpha _{c1}, ~\nu _1=(3\lambda +2\mu +\kappa )\alpha _{t2}\), \(\nu _2=(3\lambda +2\mu +\kappa )\alpha _{c2}\) and all the parameters are defined in the Table 1 as nomenclature. The relaxation times are taken in such a way that they satisfy \(\tau ^1\ge \tau ^0\ge 0\) and \(\tau _1\ge \tau _0\ge 0\).

Table 1 Nomenclature
Full size table

3 Problem formulation and solution

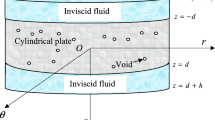
A plate of 2D thick microstretch thermoelastic diffusion with initial uniform temperature, \(T_0\) , is considered for the present model. The Cartesian co-ordinate system is taken in such a way that the \(x_3\)-axis lies normal to the plate, the \(x_1-x_2\) plane concurs with the middle surface and all three axes intersect at the center of the plate. The plate has free surfaces at \(x_3=\pm D\). Figure 1 provides the outlook geometry of the problem. Take \(\textbf{u}=(u_1,0,u_3)\) and \(\varvec{\phi }=(0,\phi _2,0)\) for the two-dimensional problem. We introduce the potentials \(\Omega\) and \(\Omega '\) for \(\textbf{u}\) so that

$$\begin{aligned} u_1= \frac{\partial \Omega }{\partial x_1}-\frac{\partial \Omega '}{\partial x_3},~~~~~~u_3=\frac{\partial \Omega }{\partial x_3}+\frac{\partial \Omega '}{\partial x_1}. \end{aligned}$$
(8)

Inserting Eq. (8) into (1–5), we get the following sets of equations

$$\begin{aligned}{} & {} (\lambda +2\mu +\kappa )\nabla ^2\Omega + \lambda _0\varphi ^* -\beta _1\left(1+\tau _1\frac{\partial }{\partial t}\right)T\nonumber \\ {}{} & {} \quad -\beta _2\left(1+\tau ^1\frac{\partial }{\partial t}\right)C = \rho \frac{\partial ^2 \Omega }{\partial t^2}, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} -\lambda _0\nabla ^2\Omega +(\alpha _0\nabla ^2-\lambda _1)\varphi ^*+\nu _1\left(1 + \tau _1\frac{\partial }{\partial t}\right)T+\nu _2\left(1+\tau ^1\frac{\partial }{\partial t}\right)C \nonumber \\ {}{} & {} \quad = \frac{\rho j_0}{2}\frac{\partial ^2\varphi ^*}{\partial t^2}, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \beta _1 T_0\left(1+\varepsilon \tau _0\frac{\partial }{\partial t}\right)\nabla ^2\frac{\partial \Omega }{\partial t}+\nu _1 T_0\left(1+\varepsilon \tau _0\frac{\partial }{\partial t}\right)\frac{\partial \varphi ^*}{\partial t}\nonumber \\ {}{} & {} \quad +\rho C^*\left(1+\tau _0\frac{\partial }{\partial t}\right)\frac{\partial T}{\partial t}\nonumber \\ {}{} & {} \quad -K^*\nabla ^2 T+aT_0\left(1+\gamma _1 \frac{\partial }{\partial t}\right)\frac{\partial C}{\partial t}=0, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} d\beta _2\nabla ^4\Omega +d\nu _2\nabla ^2\varphi ^*+d a\left(1+\tau _1\frac{\partial }{\partial t}\right)\nabla ^2T+\left(1+\varepsilon \tau ^0\frac{\partial }{\partial t}\right)\frac{\partial C}{\partial t}\nonumber \\ {}{} & {} \quad -db\left(1+\tau ^1\frac{\partial }{\partial t}\right)\nabla ^2C=0, \end{aligned}$$
(12)
$$\begin{aligned}{} & {} (\mu +\kappa )\nabla ^2\Omega '+\kappa \phi _2 \nonumber \\ {}{} & {} \quad = \rho \frac{\partial ^2\Omega '}{\partial t^2}, ~~~~ -\kappa \nabla ^2\Omega '+(\gamma \nabla ^2-2\kappa )\phi _2 = \rho j\frac{\partial ^2\phi _2}{\partial t^2}. \end{aligned}$$
(13)

Equations (9–12) show four coupled longitudinal waves in \(\Omega ,~\varphi ^*,~T\) and C, while Eq. (13) gives two coupled shear waves in \(\Omega '\) and \(\phi _2\).

Fig. 1
figure 1

Geometry of the problem

Full size image

For the plane waves propagating along \(x_1\)-axis, the following form of solution is taken as:

$$\begin{aligned}{} & {} \left\{ \Omega ,T,\varphi ^{*},C,\Omega ',\phi _2\right\} (x_1,x_3,t)\nonumber \\ {}{} & {} \quad = \left\{ \overline{\Omega },\overline{T},\overline{\varphi ^{*}},\overline{C},{\overline{\Omega }'},{\overline{\phi }_2}\right\} (x_3) e^{\imath k\left( x_1-vt\right) }, \end{aligned}$$
(14)

where \(\overline{\Omega },~\overline{\varphi ^{*}},~\overline{C},~\overline{T},~{\overline{\Omega }'}\) and \({\overline{\phi }_2}\) are the functions of \(x_3\), \(\omega (=kv)\) is the angular frequency, k is the wavenumber and v is the phase velocity.

Inserting Eq. (14) into Eqs. (9–13), we obtain the following solution:

$$\begin{aligned}{} & {} \lbrace \Omega ,T,\varphi ^{*},C\rbrace (x_1,x_3,t)\nonumber \\ {}{} & {} \quad =\sum \limits _{i=1}^{4} \lbrace 1,\gamma _{1i},\gamma _{2i},\gamma _{3i}\rbrace [A_i\cosh (m_i x_3)+B_i\sinh (m_i x_3)]e^{\left\{ \imath k\left( x_1-vt\right) \right\} }, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \lbrace \Omega ',\phi _2\rbrace (x_1,x_3,t) \nonumber \\ {}{} & {} \quad =\sum \limits _{i=5}^{6}\lbrace 1,\gamma _{4i}\rbrace [A_i\sinh (m_i x_3)+B_i\cosh (m_i x_3)] e^{\left\{ \imath k\left( x_1-vt\right) \right\} }, \end{aligned}$$
(16)

where \(A_i\) and \(B_i\) are the unknown amplitudes, \(m_i\) for \(i=1, 2, 3, 4\) and \(i=5, 6\) are, respectively, solutions of the following equations

$$\begin{aligned}{} & {} A(m^2-k^2)^4+B(m^2-k^2)^3+C(m^2-k^2)^2+E(m^2-k^2)-F=0, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} L(m^2-k^2)^2+M(m^2-k^2)-N=0, \end{aligned}$$
(18)

where the coefficients A,  B,  C,  E,  F,  L,  M and N are given in Annexure-I. The coupling parameters \(\gamma _{1i},~\gamma _{2i},~\gamma _{3i}\) and \(\gamma _{4i}\) are written as:

$$\begin{aligned} \gamma _{ri}= & {} \frac{P_{ri}}{P_i}, ~~~ (r=1, 2, 3;~ i=1,2,3,4) ~~~\text{ and }\nonumber \\ \gamma _{4i}= & {} \frac{c_{21}^2(m_i^2-k^2)}{c_{22}^2(m_i^2-k^2)-c_{23}^2}, ~~~(i=5, 6) \end{aligned}$$
(19)

where the expressions of \(P_{ri}\) and \(P_i\) are given in Annexure-II.

4 Boundary conditions

We consider two types of thermal and diffusion boundary conditions for the stress-free plate. At \(x_3=\pm D\), these conditions can be written as:

$$\begin{aligned}{} & {} t_{x_3x_3}=0,~~t_{x_3x_1}=0,~~m_{x_3x_2}=0,~~\lambda ^*_{x_3}=0,~~\frac{\partial T}{\partial x_3}+h_1T=0, \nonumber \\ {}{} & {} \quad \frac{\partial C}{\partial x_3}+h_2C=0, \end{aligned}$$
(20)

where \(h_1,h_2\rightarrow 0\) stands for thermally insulated and impermeable boundary, while \(h_1,h_2\rightarrow \infty\) stands for isothermal and isoconcentrated boundary.

Using Eqs. (6) and (7) into (20), we have

$$\begin{aligned}{} & {} (\lambda +2\mu +\kappa )\frac{\partial ^2 \Omega }{\partial x_3^2}+(2\mu +\kappa )\frac{\partial ^2 \Omega '}{\partial x_1\partial x_3} +\lambda \frac{\partial ^2 \Omega }{\partial x_1^2}\nonumber \\ {}{} & {} \quad +\lambda _0\varphi ^* -\beta _1\left(1+\tau _1\frac{\partial }{\partial t}\right)T-\beta _2\left(1+\tau ^1\frac{\partial }{\partial t}\right)C=0, \end{aligned}$$
(21)
$$\begin{aligned}{} & {} (2\mu +\kappa )\frac{\partial ^2 \Omega }{\partial x_1 \partial x_3}-(\mu +\kappa )\frac{\partial ^2 \Omega '}{\partial x_3^2}+\mu \frac{\partial ^2 \Omega '}{\partial x_1^2}-\kappa \phi _2=0, \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \gamma \frac{\partial \phi _2}{\partial x_3}+b_0\frac{\partial \varphi ^*}{\partial x_1}=0,~~\alpha _0 \frac{\partial \varphi ^*}{\partial x_3}-b_0\frac{\partial \phi _2}{\partial x_1}=0. \end{aligned}$$
(23)

Using Eqs. (15) and (16) into the boundary conditions, we get

$$\begin{aligned}{} & {} \sum \limits _{i=1}^{6}a_{1i}[A_i\cosh (m_iD)\pm B_i\sinh (m_iD)]=0,\nonumber \\ {}{} & {} \sum \limits _{i=1}^{6}a_{2i}[A_i\sinh (m_iD)\pm B_i\cosh (m_iD)]=0, \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \sum \limits _{i=1}^{6}a_{3i}[A_i\cosh (m_iD)\pm B_i\sinh (m_iD)]=0,\nonumber \\ {}{} & {} \sum \limits _{i=1}^{6}a_{4i}[A_i\sinh (m_iD)\pm B_i\cosh (m_iD)]=0, \end{aligned}$$
(25)

(for thermally insulated and impermeable boundary)

$$\begin{aligned}{} & {} \sum \limits _{i=1}^{6}a_{5i}[A_i\sinh (m_iD)\pm B_i\cosh (m_iD)]=0,\nonumber \\ {}{} & {} \sum \limits _{i=1}^{6}a_{6i}[A_i\sinh (m_iD)\pm B_i\cosh (m_iD)]=0, \end{aligned}$$
(26)

(for isothermal and isoconcentrated boundary)

$$\begin{aligned}{} & {} \sum \limits _{i=1}^{6}a_{7i}[A_i\cosh (m_iD)\pm B_i\sinh (m_iD)]=0,\nonumber \\ {}{} & {} \sum \limits _{i=1}^{6}a_{8i}[A_i\cosh (m_iD)\pm B_i\sinh (m_iD)]=0. \end{aligned}$$
(27)

where the nonzero \(a_{ji}\) are given by:

$$\begin{aligned}a_{1i}= & {} (\lambda +2\mu +\kappa )m_i^2-\lambda k^2+\lambda _0\gamma _{2i}-\beta _1(1-\imath \tau _1\omega )\gamma _{1i}\\ {}{} & {} \quad -\beta _2(1-\imath \tau ^1 \omega )\gamma _{3i},~~a_{2i}=(\kappa +2\mu )\imath km_i, \\ a_{3i}= & {} \imath b_0 k\gamma _{2i},~~a_{4i}=\alpha _0m_i\gamma _{2i},~~a_{5i}=\gamma _{1i}m_i,~~a_{6i} =\gamma _{3i}m_i,~~a_{7i}=\gamma _{1i},\\ {}{} & {} \quad a_{8i}=\gamma _{3i},~~i=1, 2, 3, 4\\ a_{1i}= & {} (\kappa +2\mu )\imath km_i,~~a_{2i}=-[(\mu +\kappa )m_i^2+\mu k^2+\kappa \gamma _{4i}],\\ {}{} & {} \quad a_{3i}=\gamma m_i\gamma _{4i}, ~a_{4i}=-\imath b_0 k\gamma _{4i},~~ i = 5, 6. \end{aligned}$$

5 Secular equation

5.1 For thermally insulated and impermeable boundary

We separate \(A_i\) and \(B_i\) in Eqs. (24–26) by adding and subtracting two suitable equations of the system and obtain the following two set of equations as

$$\begin{aligned}{} & {} \begin{pmatrix} a_{11}C_{h1} &{} a_{12}C_{h2} &{} a_{13}C_{h3} &{} a_{14}C_{h4} &{} a_{15}C_{h5} &{} a_{16}C_{h6}\\ a_{21}S_{h1} &{} a_{22}S_{h2} &{} a_{23}S_{h3} &{} a_{24}S_{h4} &{} a_{25}S_{h5} &{} a_{26}S_{h6}\\ a_{31}C_{h1} &{} a_{32}C_{h2} &{} a_{33}C_{h3} &{} a_{34}C_{h4} &{} a_{35}C_{h5} &{} a_{36}C_{h6}\\ a_{41}S_{h1} &{} a_{42}S_{h2} &{} a_{43}S_{h3} &{} a_{44}S_{h4} &{} a_{45}S_{h5} &{} a_{46}S_{h6}\\ a_{51}S_{h1} &{} a_{52}S_{h2} &{} a_{53}S_{h3} &{} a_{54}S_{h4} &{} 0 &{} 0\\ a_{61}S_{h1} &{} a_{62}S_{h2} &{} a_{63}S_{h3} &{} a_{64}S_{h4} &{} 0 &{} 0\\ \end{pmatrix} \begin{pmatrix} A_1\\ A_2\\ A_3\\ A_4\\ A_5\\ A_6 \end{pmatrix} =0, \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \begin{pmatrix} a_{11}S_{h1} &{} a_{12}S_{h2} &{} a_{13}S_{h3} &{} a_{14}S_{h4} &{} a_{15}S_{h5} &{} a_{16}S_{h6}\\ a_{21}C_{h1} &{} a_{22}C_{h2} &{} a_{23}C_{h3} &{} a_{24}C_{h4} &{} a_{25}C_{h5} &{} a_{26}C_{h6}\\ a_{31}S_{h1} &{} a_{32}S_{h2} &{} a_{33}S_{h3} &{} a_{34}S_{h4} &{} a_{35}S_{h5} &{} a_{36}S_{h6}\\ a_{41}C_{h1} &{} a_{42}C_{h2} &{} a_{43}C_{h3} &{} a_{44}C_{h4} &{} a_{45}C_{h5} &{} a_{46}C_{h6}\\ a_{51}C_{h1} &{} a_{52}C_{h2} &{} a_{53}C_{h3} &{} a_{54}C_{h4} &{} 0 &{} 0\\ a_{61}C_{h1} &{} a_{62}C_{h2} &{} a_{63}C_{h3} &{} a_{64}C_{h4} &{} 0 &{} 0\\ \end{pmatrix} \begin{pmatrix} B_1\\ B_2\\ B_3\\ B_4\\ B_5\\ B_6 \end{pmatrix} =0, \end{aligned}$$
(29)

where \(C_{hi}=\cosh (m_iD), ~S_{hi}=\sinh (m_iD)\).

The non-trivial solution of Eqs. (28) and (29) gives the secular equations for the symmetric and anti-symmetric modes of vibrations, respectively, as

$$\begin{aligned} a_{1231}a'_{3456}c_{t12}+a_{1133}a'_{2456}c_{t13}+a_{1431}a'_{2356}c_{t14} +a_{1135}a'_{2346}c_{t15}+a_{1631}a'_{2345}c_{t16}~~~~~~~~~~~\nonumber \\ +a_{1332}a'_{1456}c_{t23}+a_{1234}a'_{1356}c_{t24}+a_{1532}a'_{1346}c_{t25} +a_{1236}a'_{1345}c_{t26}+a_{1433}a'_{1256}c_{t34}~~\nonumber \\ +a_{1335}a'_{1246}c_{t35}+a_{1633}a'_{1245}c_{t36}+a_{1534}a'_{1236}c_{t45} +a_{1436}a'_{1235}c_{t46}+a_{1635}a'_{1234}c_{t56}=0,~~~ \end{aligned}$$
(30)

and

$$\begin{aligned} a_{1231}a'_{3456}t_{12}+a_{1133}a'_{2456}t_{13}+a_{1431}a'_{2356}t_{14} +a_{1135}a'_{2346}t_{15}+a_{1631}a'_{2345}t_{16}~~~~~~~~~~~~~~~~\nonumber \\ +a_{1332}a'_{1456}t_{23}+a_{1234}a'_{1356}t_{24}+a_{1532}a'_{1346}t_{25} +a_{1236}a'_{1345}t_{26}+a_{1433}a'_{1256}t_{34}~~~\nonumber \\ +a_{1335}a'_{1246}t_{35}+a_{1633}a'_{1245}t_{36}+a_{1534}a'_{1236}t_{45}+a_{1436}a'_{1235}t_{46}+a_{1635}a'_{1234}t_{56}=0,~~~~~~~ \end{aligned}$$
(31)

where

$$\begin{aligned} a_{ijkl}= & {} a_{ij}a_{kl}-a_{il}a_{kj}, ~~c_{tij}=\coth (m_iD)\coth (m_jD), ~~ t_{ij}= \tanh (m_iD)\tanh (m_jD),\\ a'_{pqrs}= & {} \begin{vmatrix} a_{2p}&a_{2q}&a_{2r}&a_{2s}\\ a_{4p}&a_{4q}&a_{4r}&a_{4s}\\ a_{5p}&a_{5q}&a_{5r}&a_{5s}\\ a_{6p}&a_{6q}&a_{6r}&a_{6s} \end{vmatrix} \text{ for }~ i,j,k,l,p,q,r,s=1(1)6 ~\text{ and } \text{ for }~ s, r\ge 5,~ a_{jr}=a_{js}=0, ~j=5,6. \end{aligned}$$

5.2 For isothermal and isoconcentrated boundary

Using Eqs. (24), (25) and (27), we obtain the following two set of equations as

$$\begin{aligned}{} & {} \begin{pmatrix} a_{11}C_{h1} &{} a_{12}C_{h2} &{} a_{13}C_{h3} &{} a_{14}C_{h4} &{} a_{15}C_{h5} &{} a_{16}C_{h6}\\ a_{21}S_{h1} &{} a_{22}S_{h2} &{} a_{23}S_{h3} &{} a_{24}S_{h4} &{} a_{25}S_{h5} &{} a_{26}S_{h6}\\ a_{31}C_{h1} &{} a_{32}C_{h2} &{} a_{33}C_{h3} &{} a_{34}C_{h4} &{} a_{35}C_{h5} &{} a_{36}C_{h6}\\ a_{41}S_{h1} &{} a_{42}S_{h2} &{} a_{43}S_{h3} &{} a_{44}S_{h4} &{} a_{45}S_{h5} &{} a_{46}S_{h6}\\ a_{71}C_{h1} &{} a_{72}C_{h2} &{} a_{73}C_{h3} &{} a_{74}C_{h4} &{} 0 &{} 0\\ a_{81}C_{h1} &{} a_{82}C_{h2} &{} a_{83}C_{h3} &{} a_{84}C_{h4} &{} 0 &{} 0\\ \end{pmatrix} \begin{pmatrix} A_1\\ A_2\\ A_3\\ A_4\\ A_5\\ A_6 \end{pmatrix} =0, \end{aligned}$$
(32)
$$\begin{aligned}{} & {} \begin{pmatrix} a_{11}S_{h1} &{} a_{12}S_{h2} &{} a_{13}S_{h3} &{} a_{14}S_{h4} &{} a_{15}S_{h5} &{} a_{16}S_{h6}\\ a_{21}C_{h1} &{} a_{22}C_{h2} &{} a_{23}C_{h3} &{} a_{24}C_{h4} &{} a_{25}C_{h5} &{} a_{26}C_{h6}\\ a_{31}S_{h1} &{} a_{32}S_{h2} &{} a_{33}S_{h3} &{} a_{34}S_{h4} &{} a_{35}S_{h5} &{} a_{36}S_{h6}\\ a_{41}C_{h1} &{} a_{42}C_{h2} &{} a_{43}C_{h3} &{} a_{44}C_{h4} &{} a_{45}C_{h5} &{} a_{46}C_{h6}\\ a_{71}S_{h1} &{} a_{72}S_{h2} &{} a_{73}S_{h3} &{} a_{74}S_{h4} &{} 0 &{} 0\\ a_{81}S_{h1} &{} a_{82}S_{h2} &{} a_{83}S_{h3} &{} a_{84}S_{h4} &{} 0 &{} 0\\ \end{pmatrix} \begin{pmatrix} B_1\\ B_2\\ B_3\\ B_4\\ B_5\\ B_6 \end{pmatrix} =0, \end{aligned}$$
(33)

The non-trivial solution of Eqs. (32) and (33) gives the secular equation for the symmetric and anti-symmetric modes of vibrations, respectively, as

$$\begin{aligned}{} & {} a_{2241}a''_{3456}t_{12}+a_{2143}a''_{2456}t_{13}+a_{2441}a''_{2356}t_{14} +a_{2145}a''_{2346}t_{15}+a_{2641}a''_{2345}t_{16}~~~~~~~~~~~~~~\nonumber \\{} & {} +a_{2342}a''_{1456}t_{23}+a_{2244}a''_{1356}t_{24}+a_{2542}a''_{1346}t_{25} +a_{2246}a''_{1345}t_{26}+a_{2443}a''_{1256}t_{34}~~~\nonumber \\{} & {} +a_{2345}a''_{1246}t_{35}+a_{2643}a''_{1245}t_{36}+a_{2544}a''_{1236}t_{45} +a_{2446}a''_{1235}t_{46}+a_{2645}a''_{1234}t_{56}=0,~~~~~ \end{aligned}$$
(34)

and

$$\begin{aligned}{} & {} a_{2241}a''_{3456}c_{t12}+a_{2143}a''_{2456}c_{t13}+a_{2441}a''_{2356}c_{t14}+a_{2145}a''_{2346}c_{t15} +a_{2641}a''_{2345}c_{t16}~~~~~~~~~~\nonumber \\{} & {} +a_{2342}a''_{1456}c_{t23}+a_{2244}a''_{1356}c_{t24} +a_{2542}a''_{1346}c_{t25}+a_{2246}a''_{1345}c_{t26}+a_{2443}a''_{1256}c_{t34}~\nonumber \\{} & {} +a_{2345}a''_{1246}c_{t35}+a_{2643}a''_{1245}c_{t36} +a_{2544}a''_{1236}c_{t45}+a_{2446}a''_{1235}c_{t46}+a_{2645}a''_{1234}c_{t56}=0,~ \end{aligned}$$
(35)

where

$$\begin{aligned} a''_{pqrs}= \begin{vmatrix} a_{1p}&a_{1q}&a_{1r}&a_{1s}\\ a_{3p}&a_{3q}&a_{3r}&a_{3s}\\ a_{7p}&a_{7q}&a_{7r}&a_{7s}\\ a_{8p}&a_{8q}&a_{8r}&a_{8s} \end{vmatrix} ~ \text{ for }~ p, q, r, s =1(1)6~ \text{ and } \text{ for }~ s, r\ge 5,~ a_{jr}=a_{js}=0,~j=7,8. \end{aligned}$$

These secular equations are transcendental by nature and contain complete information about the phase velocity, wavenumber and attenuation of the surface waves. Since the wavenumbers are complex quantities, these waves are attenuated.

6 Limiting cases

6.1 Symmetric vibration

We obtain the secular equation for plate wave when the wavelength is longer compared to the thickness 2D. The quantity kD is small, and hence, \(m_iD\) is also small as long as the velocity of the surface wave is finite. In such case, \(\tanh x\rightarrow x\). Equations (30) and (34), respectively, reduce to

$$\begin{aligned}{} & {} a_{1231}a'_{3456}m_{3456}+a_{1133}a'_{2456}m_{2456}+a_{1431}a'_{2356}m_{2356} +a_{1135}a'_{2346}m_{2346}+a_{1631}a'_{2345}m_{2345}+~~\nonumber \\{} & {} a_{1332}a'_{1456}m_{1456} +a_{1234}a'_{1356}m_{1356}+a_{1532}a'_{1346} m_{1346} +a_{1236}a'_{1345}m_{1345}+a_{1433}a'_{1256}m_{1256}+~~~\nonumber \\{} & {} a_{1335}a'_{1246}m_{1246}+a_{1633}a'_{1245}m_{1245} +a_{1534}a'_{1236}m_{1236}+a_{1436}a'_{1235}m_{1235}+a_{1635}a'_{1234}m_{1234}=0, \end{aligned}$$
(36)

and

$$\begin{aligned}{} & {} a_{2241}a''_{3456}m_{12}+a_{2143}a''_{2456}m_{13}+a_{2441}a''_{2356}m_{14} +a_{2145}a''_{2346}m_{15}+a_{2641}a''_{2345}m_{16}+~~~~~~~~~~~\nonumber \\{} & {} a_{2342}a''_{1456}m_{23}+a_{2244}a''_{1356}m_{24}+a_{2542}a''_{1346}m_{25} +a_{2246}a''_{1345}m_{26}+a_{2443}a''_{1256}m_{34}~~~\nonumber \\{} & {} +a_{2345}a''_{1246}m_{35}+a_{2643}a''_{1245}m_{36}+a_{2544}a''_{1236}m_{45} +a_{2446}a''_{1235}m_{46}+a_{2645}a''_{1234}m_{56}=0,~~~~~~ \end{aligned}$$
(37)

where \(m_{ijkl}=m_im_jm_km_l\), \(m_{ij}=m_im_j\) for \(i,j,k,l=1,2,3,4,5,6\).

For short wavelengths and finite real velocity so that \(m_i\) is real, the quantity kD is very large and \(\tanh x\rightarrow 1\). In this case, Eqs. (30) and (34), respectively, reduce to

$$\begin{aligned}{} & {} a_{1231}a'_{3456}+a_{1133}a'_{2456}+a_{1431}a'_{2356}+a_{1135}a'_{2346}+a_{1631}a'_{2345}+~\nonumber \\{} & {} a_{1332}a'_{1456}+ a_{1234}a'_{1356}+a_{1532}a'_{1346} +a_{1236}a'_{1345}+a_{1433}a'_{1256}+~\nonumber \\ {}{} & {} a_{1335}a'_{1246}+a_{1633}a'_{1245} +a_{1534}a'_{1236}+a_{1436}a'_{1235}+a_{1635}a'_{1234}=0, \end{aligned}$$
(38)

and

$$\begin{aligned}{} & {} a_{2241}a''_{3456}+a_{2143}a''_{2456}+a_{2441}a''_{2356}+a_{2145}a''_{2346}+a_{2641}a''_{2345}+~\nonumber \\{} & {} a_{2342}a''_{1456}+a_{2244}a''_{1356}+a_{2542}a''_{1346} +a_{2246}a''_{1345}+a_{2443}a''_{1256} +\nonumber \\ {}{} & {} a_{2345}a''_{1246}+a_{2643}a''_{1245}+a_{2544}a''_{1236}+a_{2446}a''_{1235}+a_{2645}a''_{1234}=0. \end{aligned}$$
(39)

These equations present the secular equations for Rayleigh waves in microstretch thermoelastic diffusion materials, and these results exactly match with Kumar et al. [34] for the relevant problem.

6.2 Anti-symmetric vibration

If we consider longer wavelength compared to the thickness of the plate with real \(m_r\), then \(\tanh x\rightarrow x-\frac{x^3}{3}\). Equations(31) and (35) reduce, respectively, to

$$\begin{aligned}{} & {} a_{1231}a'_{3456}r_{12}m_{12}+a_{1133}a'_{2456}r_{13}m_{13}+a_{1431}a'_{2356}r_{14}m_{14} +a_{1135}a'_{2346}r_{15}m_{15}~~~~~~~~\nonumber \\{} & {} +a_{1631}a'_{2345}r_{16}m_{16}+a_{1332}a'_{1456}r_{23}m_{23}+a_{1234}a'_{1356}r_{24}m_{24} +a_{1532}a'_{1346}r_{25}m_{25}~\nonumber \\{} & {} +a_{1236}a'_{1345}r_{26}m_{26}+a_{1433}a'_{1256}r_{34}m_{34}+a_{1335}a'_{1246}r_{35}m_{35} +a_{1633}a'_{1245}r_{36}m_{36}~~~~~~~\nonumber \\{} & {} +a_{1534}a'_{1236}r_{45}m_{45}+a_{1436}a'_{1235}r_{46}m_{46}+a_{1635}a'_{1234}r_{56}m_{56}=0, \end{aligned}$$
(40)

and

$$\begin{aligned}{} & {} a_{2241}a''_{3456}r_{3456}m_{3456}+a_{2143}a''_{2456}r_{2456}m_{2456}+a_{2441}a''_{2356}r_{2356}m_{2356} +a_{2145}a''_{2346}r_{2346}m_{2346}~~~~\nonumber \\ {}{} & {} +a_{2641}a''_{2345}r_{2345}m_{2345} +a_{2342} a''_{1456}r_{1456}m_{1456}+a_{2244}a''_{1356}r_{1356}m_{1356}+a_{2542}a''_{1346}r_{1346}m_{1346}~~\nonumber \\{} & {} +a_{2246}a''_{1345}r_{1345}m_{1345}+a_{2443}a''_{1256}r_{1256}m_{1256} +a_{2345}a''_{1246}r_{1246}m_{1246} +a_{2643}a''_{1245}r_{1245}m_{1245}~~\nonumber \\{} & {} +a_{2544}a''_{1236}r_{1236}m_{1236}+a_{2446}a''_{1235}r_{1235}m_{1235} +a_{2645}a''_{1234}r_{1234}m_{1234} =0, \end{aligned}$$
(41)

where \(r_i=1-\frac{m_i^2D^2}{3}\), \(r_{ij}=r_ir_j,~ r_{ijkl}=r_ir_jr_kr_l\) for \(i,j,k,l=1,2,3,4,5,6\).

Equations (40) and (41) give the secular equations for the flexural waves in microstretch thermoelastic diffusion plate.

7 Special cases

Case (i) In the absence of diffusion effect, the problem reduces to Lamb wave propagation in microstretch thermoelastic plate. Under this condition, \(d,~a,~\alpha _{c1},~\alpha _{c2},~b,~\tau ^1\) and \(\tau ^0\) vanish. Consequently, \(\gamma _{14}=\gamma _{24}=\gamma _{34} =0\). The secular equations (30, 31, 34 and 35) for both symmetric and anti-symmetric cases reduce, respectively, to

$$\begin{aligned}{} & {} a_{1132}a'_{356}c_{t12}+a_{1331}a'_{256}c_{t13}+a_{1135}a'_{236}c_{t15}+a_{1631}a'_{235}c_{t16}+a_{1233}a'_{156}c_{t23}+\nonumber \\{} & {} a_{1532}a'_{136}c_{t25}+a_{1236}a'_{135}c_{t26}+a_{1335}a'_{126}c_{t35}+a_{1633}a'_{125}c_{t36}+a_{1536}a'_{123}c_{t56}=0, \end{aligned}$$
(42)
$$\begin{aligned}{} & {} a_{1132}a'_{356}t_{12}+a_{1331}a'_{256}t_{13}+a_{1135}a'_{236}t_{15}+a_{1631}a'_{235}t_{16}+a_{1233}a'_{156}t_{23}+~~~\nonumber \\{} & {} a_{1532}a'_{136}t_{25}+a_{1236}a'_{135}t_{26}+a_{1335}a'_{126}t_{35}+a_{1633}a'_{125}t_{36}+a_{1536}a'_{123}t_{56}=0, \end{aligned}$$
(43)
$$\begin{aligned}{} & {} a_{2142}a''_{356}t_{12}+a_{2341}a''_{256}t_{13}+a_{2145}a''_{236}t_{15}+a_{2641}a''_{235}t_{16}+a_{2243}a''_{156}t_{23}+\nonumber \\{} & {} a_{2542}a''_{136}t_{25}+a_{2246}a''_{135}t_{26}+a_{2345}a''_{126}t_{35}+a_{2643}a''_{125}t_{36}+a_{2546}a''_{123}t_{56}=0, \end{aligned}$$
(44)

and

$$\begin{aligned}{} & {} a_{2142}a''_{356}c_{t12}+a_{2341}a''_{256}c_{t13}+a_{2145}a''_{236}c_{t15}+a_{2641}a''_{235}c_{t16}+a_{2243}a''_{156}c_{t23}+\nonumber \\{} & {} a_{2542}a''_{136}c_{t25}+a_{2246}a''_{135}c_{t26}+a_{2345}a''_{126}c_{t35}+a_{2643}a''_{125}c_{t36}+a_{2546}a''_{123}c_{t56}=0, \end{aligned}$$
(45)

where

$$\begin{aligned}a'_{pqr}= & {} \begin{vmatrix} a_{2p}&a_{2q}&a_{2r}\\ a_{4p}&a_{4q}&a_{4r}\\ a_{5p}&a_{5q}&a_{5r} \end{vmatrix} ~\text{ and } ~a''_{pqr}= \begin{vmatrix} a_{1p}&a_{1q}&a_{1r}\\ a_{3p}&a_{3q}&a_{3r}\\ a_{7p}&a_{7q}&a_{7r} \end{vmatrix} \text{ for }~ p, q, r=1,2,4,5,6;\\ a_{jq}= & {} a_{jr}=0 ~~\text{ for } ~j=5, 6, 7, 8,~\text{ and }~ q,r\ge 5. \end{aligned}$$

These expressions match with the results of Kumar and Pratap [36].

Case (ii) If we neglect the microstretch, thermal and diffusion effects, the present study reduces to the propagation of Lamb wave in micropolar elastic plate. In this case, \(\lambda _0,~\alpha _0,~\lambda _1,~b_0,~j_0,~d,~a,\) \(\alpha _{c1},~\alpha _{c2},~b,~\tau ^1,~\tau ^0,~\tau _1,~\tau _0,~K^*,~a,~\alpha _{t1},~\alpha _{t2}\) and \(C^*\) vanish. Consequently, \(\gamma _{12}=\gamma _{22}=\gamma _{32}=\gamma _{13}=\gamma _{23}=\gamma _{33}=\gamma _{14}=\gamma _{24}=\gamma _{34}=0\). Equations (30 and 34) reduce to

$$\begin{aligned} a_{11}(a_{25}a_{36}c_{t6}-a_{26}a_{35}c_{t5})c_{t1}+a_{1635}a_{21}c_{t56}=0. \end{aligned}$$
(46)

Similarly, Equations (31 and 35) transform to

$$\begin{aligned} a_{11}(a_{25}a_{36}t_6-a_{26}a_{35}t_5)t_1+a_{1635}a_{21}t_{56}=0, \end{aligned}$$
(47)

where \(c_{ti}=\coth {(m_iD)},~\text{ and }~t_i=\tanh {(m_iD)}\).

These results are similar to those of Kumar and Pratap [35].

Case (iii) If the micropolar and diffusion effects are neglected, then the problem reduces to the propagation of Lamb wave in a thermoelastic plate. In this case, the parameters \(\lambda _0,~\alpha _0,\) \(\lambda _1,~b_0,~j_0,\) \(j,~\alpha ,~\beta ,~\gamma ,\) \(\kappa ,~\beta _2,~\nu _2,~a,~\tau ^0,~\tau ^1,~b\) and d vanish, and consequently, \(\gamma _{13}=\gamma _{23}=\gamma _{33}=\gamma _{45}=\gamma _{14}=\gamma _{24}=\gamma _{34}=0\). Equations (30, 31, 34 and 35), respectively, reduce to

$$\begin{aligned}{} & {} a_{12}a_{25}a_{51}c_{t2}-a_{11}a_{25}a_{52}c_{t1}+a_{15}a_{2152}c_{t5}=0, \end{aligned}$$
(48)
$$\begin{aligned}{} & {} a_{12}a_{25}a_{51}t_{2}-a_{11}a_{25}a_{52}t_{1}+a_{15}a_{2152}t_{5}=0,\end{aligned}$$
(49)
$$\begin{aligned}{} & {} a_{21}a_{15}a_{72}t_1-a_{22}a_{15}a_{71}t_2+a_{25}a_{1172}t_5=0,~~ \end{aligned}$$
(50)

and

$$\begin{aligned} a_{21}a_{15}a_{72}c_{t1}-a_{22}a_{15}a_{71}c_{t2}+a_{25}a_{1172}c_{t5}=0. \end{aligned}$$
(51)

These equations match with a particular case of Kumar and Pratap [36].

Case (iv) In the absence of micropolar, diffusion and thermal effects, the problem reduces to Lamb wave propagation of isotropic elastic solid. In this case, all the parameters except \(\lambda\), \(\mu\) and \(\rho\) vanish, and consequently, all the coupling parameters vanish. The secular equations (30, 31, 34 and 35) reduce to

$$\begin{aligned} \left[ \frac{t_5}{t_1}\right] ^{\pm 1}=\frac{4k^2m_1m_2\mu }{(\lambda m_1^2+2\mu m_1^2+\lambda k^2)(m_2^2+ k^2)}, \end{aligned}$$
(52)

where \(+1\) corresponds to symmetric vibration modes and \(-1\) corresponds to anti-symmetric vibration modes. These are well-known secular equations of Rayleigh–Lamb waves in classical elasticity [28].

8 Numerical computations

We develop a program in MATLAB to compute the phase velocity and attenuation of the Lamb wave. Aluminum epoxy has wide use from electrical conduits to airplane parts, to household goods and beyond. Hence, the study of Lamb wave in the aluminum epoxy medium can be used for quick inspection of the structures built using aluminum epoxy. The following relevant parameters of aluminum epoxy [12] and thermal and diffusion parameters [14] are taken as Table 2.

Table 2 Numerical values of parameters
Full size table

Equations (17 and 18) are of the form \(G\left( m,k\right) =0\) and are solved for ‘m’ using the roots function of MATLAB at a fixed value of phase velocity corresponding to the longitudinal wave. These roots are taken as \(m_i\) and used in solving the secular equations. The secular equations (30, 31, 34 and 35) are solved numerically by the iteration method using ’for loop’ programming for wavenumbers of symmetric and anti-symmetric vibrations. We have observed from Eqs. (30, 31, 34 and 35) that there exist three modes in the solution of secular equations for the symmetric and anti-symmetric vibrations in the microstretch thermoelastic diffusion plate. One of these modes is the counterpart of the classical Lamb wave and the other two modes arise due to the presence of thermo-diffusion and microstretch effects. The phase velocity and attenuation for the surface waves are defined as [13]

$$\begin{aligned} v_i=\frac{\omega }{Re\left( k_i\right) }, ~~~~~~~\mid A_i\mid =-Im\left( k_i\right) , ~~~\left( i=1,2,3,4,5,6\right) . \end{aligned}$$

The velocity curves and attenuation for symmetric and anti-symmetric vibration with angular frequency \((\omega )\) are plotted in Figs. 2, 3, 4, 5, 6, 7, 8 and 9, and a comparison for the three thermoelastic theories has been shown. We choose the following suitable values for different thermoelastic theories:

for \(G-L\) theory: \(\tau _0=0.001s,~\tau ^0=0.003s,~\tau _1=0.009s,~\tau ^1=0.005s,\)   \(\varepsilon =0, ~\gamma _1=0.003s.\)

for \(L-S\) theory: \(\tau _1=\tau ^1=0,~\tau _0=0.001s,~\tau ^0=0.003s,~ \varepsilon =1,~ \gamma _1=0.001s.\)

for CT theory: \(\tau _1=\tau ^1=\tau _0=\tau ^0=0,~\gamma _1=0.002s\).

Figures 2 and 3 present the velocities of three modes of symmetric and anti-symmetric vibrations for thermally insulated and impermeable plate. The velocity curves corresponding to mode-1 for both symmetric and anti-symmetric vibration in Figs. 2a and 3a, respectively, ascend with the increasing \(\omega\). The velocity corresponding to mode-2 diminishes for symmetric vibrations and enlarges for anti-symmetric vibrations as the impact of \(\omega\) surges. The velocity curves represented by mode-3 for both symmetric and anti-symmetric cases in Figs. 2c and 3c lessen with \(\omega\). Figures 4 and 5 represent the attenuation of the three modes of symmetric and anti-symmetric vibrations for thermally insulated and impermeable plate. The attenuation curves for mode-1 corresponding to anti-symmetric vibration in Fig. 5a and mode-3 corresponding to symmetric vibration in Fig. 4c escalate, while the attenuation curves in Figures 4b, 5b and c decrease with \(\omega\). The attenuation corresponding to mode-1 for symmetric vibration shoots up to \(-0.5955~ ms^{-1}\) at \(\omega =1.5~ s^{-1}\) and then declines up to a certain angular frequency which increases thereafter.

Figures 6 and 7, respectively, depict the velocity of symmetric and anti-symmetric vibration for an isothermal and isoconcentrated plate. Positive effects of \(\omega\) are noticed on the mode-1 velocity curves for both symmetric and anti-symmetric vibrations in Figs. 6a and 7a, while the mode-2 corresponding to anti-symmetric vibrations in Fig. 7b ascends with \(\omega\). The mode-2 velocity curve for symmetric case shoots up from \(1581.0039~ ms^{-1}\) to \(1675.5786~ ms^{-1}\) at \(\omega =0.4~ s^{-1}\) and sets off to a gentle descending path. The mode-3 curve for symmetric vibrations falls steeply to \(1687.9793~ ms^{-1}\) at \(\omega =0.8~s^{-1}\) and then declines gently thereafter, while the velocity curve of same mode for anti-symmetric vibration in Fig. 7c inclines for certain angular frequency and then decreases. Figures 8 and 9 represent the attenuations of symmetric and anti-symmetric vibration, respectively, for an isothermal and isoconcentrated plate. The attenuation curve represented by mode-1 of symmetric vibration elevates from \(-0.055713 m^{-1}\) at \(\omega =0.2 s^{-1}\) to \(-0.045635 m^{-1}\) at \(\omega =1.3 s^{-1}\) and then descends to ascend thereafter. The mode-2 attenuation for symmetric and mode-2 and mode-3 for anti-symmetric vibration decrease and mode-1 attenuation for anti-symmetric vibration and mode-3 for symmetric vibration increase with \(\omega\).

For both thermally insulated/impermeable and isothermal/isoconcentrated plates, the mode-1 velocity curve for symmetric vibration is the lowest in \(G-L\) theory and same values for the other two theories, while the velocity of same mode for anti-symmetric vibration attains the highest value in the \(G-L\) theory followed by \(L-S\) and CT theories. The mode-3 velocity curve for symmetric vibration in Fig. 2c is highest under \(G-L\) theory followed by CT and \(L-S\) theories. The mode-2 and mode-3 velocity curves for symmetric vibrations in the isothermal/isoconcentrated plate coincide for all the three theories. In both the plates, the mode-2 and mode-3 velocity curves for anti-symmetric vibration acquire the highest value under the \(L-S\) theory followed by CT and \(G-L\) theories. The mode-1 attenuation curve for symmetric vibration and mode-2 and mode-3 for anti-symmetric vibration are highest under the \(G-L\) theory followed by \(L-S\) and CT theories. In the thermally insulated/impermeable and isothermal/isoconcentrated plates, the mode-2 and mode-3 attenuation curves for symmetric vibration coincide for all three theories, while the mode-1 for anti-symmetric vibration attains the highest value under \(G-L\) theory and coincide for the other two theories.

Fig. 2
figure 2

Dispersion of symmetric vibrations for thermally insulated and impermeable plate

Full size image
Fig. 3
figure 3

Dispersion of anti-symmetric vibrations for thermally insulated and impermeable plate

Full size image
Fig. 4
figure 4

Attenuation of symmetric vibrations for thermally insulated and impermeable plate

Full size image
Fig. 5
figure 5

Attenuation of anti-symmetric vibrations for thermally insulated and impermeable plate

Full size image
Fig. 6
figure 6

Dispersion of symmetric vibrations for isothermal and isoconcentrated plate

Full size image
Fig. 7
figure 7

Dispersion of anti-symmetric vibrations for isothermal and isoconcentrated plate

Full size image
Fig. 8
figure 8

Attenuation of symmetric vibrations for isothermal and isoconcentrated plate

Full size image
Fig. 9
figure 9

Attenuation of anti-symmetric vibrations for isothermal and isoconcentrated plate

Full size image

9 Conclusions

The propagation of Lamb wave subject to thermally insulated/impermeable and isothermal /isoconcentrated boundary conditions in a homogeneous microstretch thermoelastic diffusion plate has been investigated. We have obtained the secular equations for symmetric and anti-symmetric vibrations in the plate. The velocity curves and attenuation of the surface waves are computed numerically for a model, and results are depicted graphically. We summarize with the following remarks:

  1. (i)

    The secular equations explicate the behavior of different modes of the symmetric and anti-symmetric vibrations of Lamb wave. The secular equations corresponding to the plate waves and Rayleigh are obtained as a limiting case by considering longer and shorter wavelength, respectively.

  2. (ii)

    Three modes of solution exist for the secular equation of symmetric and anti-symmetric vibrations, plate, flexural and Rayleigh waves. The phase velocity and the attenuation coefficients for all three modes depend on angular frequency, thermal, diffusion, microstretch, micropolar and Lamé parameters. The velocity of the corresponding Lamb wave increases from the first to the third mode of symmetric vibration.

  3. (iii)

    In both thermally insulated/impermeable and isothermal/isoconcentrated plates, the velocity curves corresponding to mode-2 and mode-3 for anti-symmetric vibration attain the highest values under the L-S theory and followed by CT and G-L theories. The attenuations corresponding to mode-2 and mode-3 for symmetric vibration coincide for all three theories, while the attenuation of mode-1 for anti-symmetric vibration attains the highest value under G-L theory and the same results for other two theories.