Introduction

Biot [3] proposed the concept of coupled thermoelasticity which though removed the one drawback of classical uncoupled thermoelasticity but could not fix the paradox of infinite velocity of thermal waves. Therefore, to eliminate this paradox, Lord and Shulman [19], and Green and Lindsay [9] proposed the theories of generalized thermoelasticity.

The circular-crested waves emanate from a point source which produces waves propagating in a pattern of concentric circles. Lamb waves are guided elastodynamic waves propagating in plates which are employed for sensors, nondestructive evaluation, and material characterization. Knowledge of dispersion characteristics is the basis of these applications. The cylindrical panels and plates are frequently used as structural components. Therefore, their vibrational characteristics are helpful to design such components. Thick composite cylindrical plates and shells can be used in applications concerning offshore, aerospace, submarine structures, civil engineering structures, pressure vessels, chemical pipes as well as automotive suspension components. These structures can be easily exposed to various temperature fields in different environments.

The theory of multi-modal waves in the solid plate has been established by Lamb [16], and in his honor, these waves are called, after his name, Lamb waves. Wu and Zhu [34] derived the frequency equation for the elastic waves in the solid plate framed with the non-viscous layers of liquid. Such type of commonality of the solid–liquid interface while studying wave propagation can also be seen in those of Pathania and Dhiman [23, 24], Pathania and Joshi [26], as well as Kumar and Kumar [15]. Eisenberger and Jabareen [6] found the exact axisymmetric vibration frequencies of circular and annular variable thickness plates and employed the exact element method to find the solutions. The study of generalized elasto-thermal straight/circular-crested waves in the isotropic homogeneous solid plate joined by the non-viscous fluid layers has been carried out by Sharma and Pathania [29, 30]. The study about the circular-crested waves can also be found in the work of Sharma and Singh [31], Kaur [12], Kumar and Kansal [14], Zhou et al. [36], and Pathania et al. [22].

Cowin and Nunziato [5] proposed the linear theory of elasto-porous materials. Some problems of technological interest such as static pure bending of an isotropic, homogeneous, poroelastic beam have been studied by Cowin and Nunziato [5], in which they proved that the stress distribution across the beam is not linear as opposed to the classical elasticity solution due to the void-volume variation. Ieşan [11] carried forward the work of Cowin and Nunziato [5] by considering the temperature effect in an isotropic homogeneous elasto-porous material. Tomar [33] obtained the frequency equation for the flexural and longitudinal modes of waves in a micropolar elasto-porous plate. The waves in the solid plate have also been studied by Li et al. [18], Gilbert et al. [7], Hawwa [10], and Pathania and Dhiman [25]. Youssef [35] derived the governing equations describing the behavior of a thermo-poroelastic medium using the generalized thermoelasticity model with one relaxation time. Singh and Pal [32] studied the waves in the thermo-poroelastic semi-infinite material underlying another different thermo-poroelastic semi-infinite material using the LS generalization.

Biswas and Sarkar [4] studied plane wave propagation in a thermoelastic medium with vacuous cavities in the context of the dual-phase-lag model of generalized thermoelasticity. The equations of generalized thermoelasticity with voids, gravity, and micro-temperatures have been derived by Othman and Abd-Elaziz [21] using the coupled and generalized thermoelasticity models. Khan et al. [13] studied the magneto-thermoelastic waves in an electrically conducting rotating monoclinic system. Lan et al. [17] studied the effects of homojunction on the transmitted and reflected waves at the interface between two elasto-thermal semiconductor half-spaces. Using a new heat conduction model including fractional operators without non-singular kernels, Abouelregal [1] carried out a comparative study of a thermoelastic problem for an infinite rigid cylinder with thermal properties. Using the Generalized Ohm’s law and Moore–Gibson–Thompson thermoelastic model, Moaaz et al. [20] analyzed the transversely isotropic annular circular cylinder plunged in the magnetic field. Using the MGT thermoelastic model, Abouelregal and Alesemi [2] investigated the mechanical and thermal waves in anisotropic, viscoelastic, fiber-reinforced, magnetic solid with temperature-dependent properties.

The proposed work is the extension of the work due to Sharma and Pathania [30] by considering the additional influencing factor voids in the solid plate. Void volume fraction has been taken as an independent kinematic variable. The inclusion of a new variable requires additional microforces to provide proper equilibrium of the micropore volume. The voids affect the density of the material and thereby the waves propagating through them. Therefore, the results are comparatively more accurate by taking into account the presence of vacuous cavities rather than neglecting it. In order to develop the micro equilibrium of the void-volume, a new micromechanics theory involving the balance of equilibrated force is introduced. It would be inadequate to leave out the void-volume fraction field which also contributes to the coupled system of waves in the poro-thermoelastic material. The literature review indicates that the current model has not been discussed so far to the best of the authors’ span of knowledge. To fill this research gap, in the present paper, crested thermo-poroelastic Lamb-type waves in the isotropic homogeneous plate sandwich-packed by the layers of liquid without viscosity have been investigated using the Lord–Shulman (LS) and Green–Lindsay (GL) models. The frequency equation and its particular cases have been derived along with the amplitude of displacements, volume fraction field change, and temperature change. Apart from that, some results such as thick plate waves, long-wavelength waves, etc. have also been discussed. It has been found that there exists a coupled system of three longitudinal, and one decoupled shear vertical wave in the solid plate. In addition, one dilatational wave in each fluid layer occurs. Computational work has also been carried out and manifested by plotting the various graphs which prove the theoretical findings.

Mathematical Formulation of the Problem

Physical Model

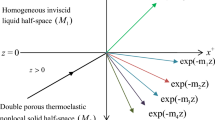
As shown in Fig. 1, the model under consideration comprises a cylindrical layer of inviscid fluid on top and bottom of the thermo-poroelastic isotropic homogeneous cylindrical plate. The thickness of the plate and liquid layer is \(2d\) and \(h\), respectively. Initially, a uniform temperature \(T_{0}\) has been maintained in the whole system. On the middle surface of the plate, the origin \(O\) of the cylindrical system of coordinates \(\left( {r,\,\,\theta ,\,\,z} \right)\) is situated. The \(rz -\) plane has been chosen to coincide with the middle surface and the \(z -\)axis has been taken along the normal direction to this plane i.e., along with the thickness. The interfaces \(z = \pm d\) are subjected to various boundary conditions. The plane of incidence has been described by \(rz -\) plane and the solutions have been assumed explicitly independent of \(\theta -\)coordinate.

Fig. 1
figure 1

Cylindrical coordinates on a liquid-loaded plate of thickness 2d extended infinitely in the radial direction

Full size image

Governing Differential Equations

The behavior of inviscid fluid layers is governed by the Navier–Stokes equation. Governing equations for a thermo-poroelastic plate have been modeled by introducing the Lord–Shulman and Green–Lindsay models.

Inviscid Fluid

Following Sharma and Pathania [30], equations of motion for each inviscid layer can be written as

$$K_{L} \left( {u_{{L_{q} ,rr}} + \frac{{u_{{L_{q} ,r}} }}{r} - \frac{{u_{{L_{q} }} }}{{r^{2} }} + w_{{L_{q} ,rz}} } \right) = \rho_{L} \ddot{u}_{{L_{q} }} ;\,\,q = 1 - 2,$$
(1)
$$K_{L} \left( {u_{{L_{q} ,rz}} + \frac{{u_{{L_{q} ,z}} }}{r} + w_{{L_{q} ,zz}} } \right) = \rho_{L} \ddot{w}_{{L_{q} }} ;\,\,q = 1 - 2.$$
(2)

where

$$q = \left\{ \begin{gathered} 1\,;z \in \left[ {d,\,d + h} \right] \hfill \\ 2;z \in \left[ { - d,\, - d - h} \right] \hfill \\ \end{gathered} \right..$$

Here, \(\left( {u_{{L_{q} }} ,\,0,\,w_{{L_{q} }} \,} \right);\,\,q = 1 - 2\) is the liquid displacement vector; the superposed dot and subscript “,” are for the partial derivative w.r.t. the time and space coordinate, respectively. \(\rho_{L}\) is the mass density and \(K_{L}\) is the liquid’s bulk modulus.

Thermo-Poroelastic Solid

In the absence of equilibrated forces, external heat sources, and body forces, the governing equations, following Sharma and Pathania [30] and Pathania and Dhiman [23], for the solid thermo-poroelastic plate are

$$\left( {\lambda + 2\mu } \right)\left( {u_{,rr} + \frac{{u_{,r} }}{r} - \frac{u}{{r^{2} }}} \right) + \mu u_{,zz} + \left( {\lambda + \mu } \right)w_{,rz} + b\phi_{,r} - \beta \left( {T + t_{2} \delta_{2k} \dot{T}} \right)_{,r} = \rho \ddot{u},$$
(3)
$$\left( {\lambda + \mu } \right)\left( {u_{,rz} + \frac{{u_{,z} }}{r}} \right) + \mu \left( {w_{,rr} + \frac{{w_{,r} }}{r}} \right) + \left( {\lambda + 2\mu } \right)w_{,zz} + b\phi_{,z} - \beta \left( {T + t_{2} \delta_{2k} \dot{T}} \right)_{,z} = \rho \ddot{w},$$
(4)
$$- b\left( {u_{,r} + \frac{u}{r} + w_{,z} } \right) + \alpha^{ * } \left( {\phi_{,rr} + \frac{{\phi_{,r} }}{r} + \phi_{,zz} } \right) - \xi_{1} \phi - \xi_{2} \dot{\phi } + m^{ * } T = \rho \chi \mathop \phi \limits^{..},$$
(5)
$$- T_{0} \left[ {\beta \left\{ {\left( {\dot{u}_{,r} + \frac{{\dot{u}}}{r} + \dot{w}_{,z} } \right) + t_{1} \delta_{1k} \left( {\ddot{u}_{,r} + \frac{{\ddot{u}}}{r} + \ddot{w}_{,z} } \right)} \right\} + m^{ * } \left( {\dot{\phi } + t_{1} \delta_{1k} \ddot{\phi }} \right)} \right] + K\left( {T_{,rr} + \frac{{T_{,r} }}{r} + T_{,zz} } \right) = \rho C_{e} \left( {\dot{T} + t_{1} \ddot{T}} \right),$$
(6)

where the vector \(\left( {u,0,w} \right)\) represents the displacement for the solid material; \(T\) denotes the change in temperature; \(\mu\) and \(\lambda\) are Lame’s parameters; \(K,\,\,\rho ,\) and \(C_{e}\) represent, respectively, the thermal conductivity, mass density, and the specific heat at constant strain; \(\phi\) is the variation in the field due to the void-volume fraction; \(\beta = \left( {2\mu + 3\lambda } \right)\alpha_{T}\) is the thermal coefficient where \(\alpha_{T}\) is the thermal expansion coefficient; \(\alpha^{ * } ,\,\,b,\,\,\xi_{1}\), and \(\xi_{2}\) are material constants due to the vacuous cavities; \(m^{ * }\) is the thermo-porous parameter; \(\chi\) denotes the equilibrated inertia; \(t_{1}\) and \(t_{2}\) are the thermal relaxation times.

Dimensionless Basic Equations

The basic governing Eqs. (1)–(6) for the liquid and solid mediums, using non-dimensional quantities

$$\overline{t} = \omega^{ * } t,\,\,\overline{t}_{1} = \omega^{ * } t_{1} ,\,\,\overline{t}_{2} = \omega^{ * } t_{2} ,\,\,\,\overline{T} = \frac{T}{{T_{0} }},\,\,\overline{c} = \frac{c}{{c_{1}^{ * } }},\,\,\overline{u}_{{L_{q} }} = \frac{{\rho \omega^{ * } c_{1}^{ * } u_{{L_{q} }} }}{{\beta T_{0} }},\,\,\overline{w}_{{L_{q} }} = \frac{{\rho \omega^{ * } c_{1}^{ * } w_{{L_{q} }} }}{{\beta T_{0} }};\,\,q = 1 - 2,\,$$
$$\overline{u} = \frac{{\rho \omega^{ * } c_{1}^{ * } u}}{{\beta T_{0} }},\,\,\overline{w} = \frac{{\rho \omega^{ * } c_{1}^{ * } w}}{{\beta T_{0} }},\,\,\overline{r} = \frac{{\omega^{ * } r}}{{c_{1}^{ * } }},\,\,\overline{z} = \frac{{\omega^{ * } z}}{{c_{1}^{ * } }}\,,\,\,\overline{\omega } = \frac{\omega }{{\omega^{ * } }},\,\,\overline{\xi } = \frac{{\xi c_{1}^{ * } }}{{\omega^{ * } }},\,\,\overline{\phi } = \frac{{\omega^{ * 2} \chi \phi }}{{c_{1}^{ * 2} }},$$
(7)

after omitting bars, have been obtained as

$$u_{{L_{q} ,rr}} + \frac{{u_{{L_{q} ,r}} }}{r} - \frac{{u_{{L_{q} }} }}{{r^{2} }} + w_{{L_{q} ,rz}} = \frac{1}{{\delta_{L}^{2} }}\ddot{u}_{{L_{q} }} ;\,\,q = 1 - 2,$$
(8)
$$u_{{L_{q} ,rz}} + \frac{{u_{{L_{q} ,z}} }}{r} + w_{{L_{q} ,zz}} = \frac{1}{{\delta_{L}^{2} }}\ddot{w}_{{L_{q} }} ;\,\,q = 1 - 2,$$
(9)
$$\left( {u_{,rr} + \frac{{u_{,r} }}{r} - \frac{u}{{r^{2} }}} \right) + \left( {1 - \delta^{2} } \right)w_{,rz} + \delta^{2} u_{,zz} + a_{1} \phi_{,r} - \left( {T + t_{2} \delta_{2k} \dot{T}} \right)_{,r} = \ddot{u},$$
(10)
$$\left( {1 - \delta^{2} } \right)\left( {u_{,rz} + \frac{{u_{,z} }}{r}} \right) + \delta^{2} \left( {w_{,rr} + \frac{{w_{,r} }}{r}} \right) + w_{,zz} + a_{1} \phi_{,z} - \left( {T + t_{2} \delta_{2k} \dot{T}} \right)_{,z} = \ddot{w},$$
(11)
$$- a_{2} \left( {u_{,r} + \frac{u}{r} + w_{,z} } \right) + \phi_{,rr} + \frac{{\phi_{,r} }}{r} + \phi_{,zz} - a_{3} \left( {\phi + \overline{{\xi^{*} }} \dot{\phi }} \right) + a_{4} T = \frac{{\ddot{\phi }}}{{\delta_{1}^{2} }},$$
(12)
$$- \varepsilon_{T} \left( {\dot{u}_{,r} + \frac{{\dot{u}}}{r} + \dot{w}_{,z} + t_{1} \delta_{1k} \left( {\ddot{u}_{,r} + \frac{{\ddot{u}}}{r} + \ddot{w}_{,z} } \right)} \right) - a_{5} \left( {\mathop \phi \limits^{.} + t_{1} \delta_{1k} \ddot{\phi }} \right) + T_{,rr} + \frac{{T_{,r} }}{r} + T_{,zz} = \mathop T\limits^{.} + t_{1} \ddot{T},$$
(13)

where

$$a_{1} = \,\frac{{bc_{1}^{ * 2} }}{{\beta T_{0} \chi \omega^{ * 2} }},\,\,a_{2} = \frac{{b\chi \beta T_{0} }}{{\alpha^{ * } \rho c_{1}^{ * 2} }},\,\,\,a_{3} = \frac{{\xi_{1} c_{1}^{ * 2} }}{{\alpha^{ * } \omega^{ * 2} }},\,\,\,a_{4} = \frac{{m^{ * } T_{0} \chi }}{{\alpha^{ * } }}\,,\,\,a_{5} = \frac{{m^{ * } c_{1}^{ * 4} }}{{K\chi \omega^{ * 3} }},$$
$$\delta = \frac{{c_{2}^{ * } }}{{c_{1}^{ * } }}\,,\,\,\delta_{1} = \frac{{c_{3}^{ * } }}{{c_{1}^{ * } }},\,\,\delta_{L} = \frac{{c_{L}^{ * } }}{{c_{1}^{ * } }},\,\,c_{1}^{ * } = \sqrt {\frac{\lambda + 2\mu }{\rho }} ,\,\,c_{2}^{ * } = \sqrt {\frac{\mu }{\rho }} ,\,\,c_{3}^{ * } = \sqrt {\frac{{\alpha^{ * } }}{\rho \chi }} ,\,\,c_{L}^{ * } = \sqrt {\frac{{K_{L} }}{{\rho_{L} }}} ,$$
$$\overline{{\xi^{*} }} = \frac{{\xi_{2} \omega^{ * } }}{{\xi_{1} }},\,\,\omega^{ * } = \frac{{C_{e} \left( {\lambda + 2\mu } \right)}}{K},\,\,\varepsilon_{T} = \frac{{\beta^{2} T_{0} }}{{\rho C_{e} \left( {\lambda + 2\mu } \right)}}.$$
(14)

Here, \(\omega^{ * }\) denotes the characteristic frequency of the solid plate; \(c_{1}^{ * }\), \(c_{2}^{ * }\) and \(c_{3}^{ * }\) are the velocities of the dilatational wave, shear wave, and the wave due to void-volume fractional field variation, respectively, in the thermo-poroelastic solid plate. \(c_{L}^{ * }\) and \(\varepsilon_{T}\) are, respectively, the velocity of the dilational wave in the fluid and the thermomechanical coupling constant for the solid medium. \(a_{q} ;\,\,q = 1 - 5\) and \(\overline{{\xi^{*} }}\) are the poro-thermoelastic coupling parameters that are obtained after the non-dimensionalization of Eqs. (3)–(6). \(\delta\), \(\delta_{1}\) and \(\delta_{L}\) are the velocity ratios of \(c_{2}^{ * }\), \(c_{3}^{ * }\) and \(c_{L}^{ * }\) to \(c_{1}^{ * }\).

Helmholtz Decomposition Principle

Using the Helmholtz decomposition principle, the solid and liquid displacements can be decomposed as

$$u_{{L_{q} }} = G_{{L_{q} ,r}} ,\,\,\,w_{{L_{q} }} = G_{{L_{q} ,z}} ;\,\,q = 1 - 2\,,$$
(15)
$$u = G_{,r} + \psi_{,z} ,\,w = G_{,z} - \psi_{,r} - \frac{\psi }{r},$$
(16)

where \(\psi\) is the negative of the \(\theta -\)component of the vector potential \(\vec{\psi } = \left( {0,\, - \psi ,\,0} \right)\), similarly, \(G_{{L_{q} }}\) and \(G\) are the scalar potentials. Since inviscid fluid does not support the transversal motion, therefore, vector potentials have not been considered in Eq. (15).

Using Eqs. (15) and (16), Eqs. (8)–(13) can be written as

$$\nabla^{2} G_{{L_{q} }} - \frac{1}{{\delta_{L}^{2} }}\ddot{G}_{{L_{q} }} = 0;\,\,q = 1 - \,2,$$
(17)
$$\nabla^{2} \psi - \frac{\psi }{{r^{2} }} - \frac{{\ddot{\psi }}}{{\delta^{2} }} = 0,$$
(18)
$$\nabla^{2} G - \ddot{G} + a_{1} \phi - T - t_{2} \delta_{2k} \dot{T} = 0\,,$$
(19)
$$- a_{2} \nabla^{2} G + \nabla^{2} \phi - a_{3} \left( {\phi + \overline{{\xi^{*} }} \dot{\phi }} \right) - \frac{{\ddot{\phi }}}{{\delta_{1}^{2} }} + a_{4} T = 0,$$
(20)
$$- \varepsilon_{T} \nabla^{2} \left( {\dot{G} + t_{1} \delta_{1k} \ddot{G}} \right) - a_{5} \left( {\dot{\phi } + t_{1} \delta_{1k} \ddot{\phi }} \right) + \nabla^{2} T - \dot{T} - t_{1} \ddot{T} = 0\,\,,$$
(21)

where \(\nabla^{2} = \frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{\partial }{r\partial r} + \frac{{\partial^{2} }}{{\partial z^{2} }}\) is the Laplacian operator in \(rz -\)plane.

Solution of the Problem

Normal mode analysis has become one of the standard techniques to obtain solutions to governing equations for wave propagation. This method provides the solutions accurately without any assumed restrictions on displacements, void-volume fraction field variation, temperature change, and stress distributions. In order to study the characteristics of waves, following Sharma and Pathania [30], the solutions have been chosen as

$$\left\{ {G_{{L_{q} }} ,\,G,\,\phi ,\,T} \right\} = \left\{ {\overline{{G_{{L_{q} }} }} \left( z \right),\,\overline{G} \left( z \right),\overline{\phi } \left( z \right),\overline{T} \left( z \right)} \right\}J_{0} \left( {\xi r} \right)e^{ - \iota \omega t},$$
(22)
$$\psi = \overline{\psi }\left( z \right)J_{1} \left( {\xi r} \right)e^{ - \iota \omega t},$$
(23)

where \(\overline{{G_{{L_{q} }} }} \left( z \right);\,\,q = 1 - 2\), \(\overline{G} \left( z \right),\,\overline{\phi } \left( z \right),\,\overline{T} \left( z \right),\,\overline{\psi } \left( z \right)\) represent the waves’ amplitudes and \(\omega = \xi c\) is the non-dimensional angular frequency with \(\xi\) and \(c\) as the non-dimensional wavenumber and phase velocity, \(J_{0} \left( {\xi r} \right)\) and \(J_{1} \left( {\xi r} \right)\) are the Bessel functions of order zero and one, respectively. Solving the partial differential equations [Eqs. (17)–(21)] using the assumed solutions (22) and (23) for \(G_{{L_{q} }} \left( z \right);\,\,q = 1 - 2\), \(G,\,\,\phi ,\,\,T\) and \(\psi\) gives

$$G_{{L_{1} }} = A_{5} \sin m_{5} \left[ {z - d - h} \right]J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} \,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for}}\,\,z \in \left[ {d,\,\,d + h} \right],$$
(24)
$$G_{{L_{2} }} = A_{6} \sin m_{5} \left[ {z + d + h} \right]J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} \,\,\,\,\,\,\,{\text{for}}\,\,z \in \left[ { - d - h,\,\, - d} \right],$$
(25)

which represent the standing wave solutions for the bottom and upper layers, respectively:

$$\left. \begin{gathered} G = \sum\limits_{q = 1}^{3} {\left( {A_{q} \sin m_{q} z + B_{q} \cos m_{q} z} \right)} J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} \hfill \\ \phi = \sum\limits_{q = 1}^{3} {W_{q} } \left( {A_{q} \sin m_{q} z + B_{q} \cos m_{q} z} \right)J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} \hfill \\ T = \sum\limits_{q = 1}^{3} {S_{q} } \left( {A_{q} \sin m_{q} z + B_{q} \cos m_{q} z} \right)J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} \hfill \\ \psi = \left( {A_{4} \sin m_{4} z + B_{4} \cos m_{4} z} \right)\,J_{1} \left( {\xi r} \right)e^{ - \iota \omega t} \hfill \\ \end{gathered} \right\}{\text{for}}\,\,z \in \left[ { - d,\,\,d} \right],$$
(26)

where the unknowns \(A_{q} ;\,\,q = 1 - 6\) and \(B_{q} ;\,\,q = 1 - 4\) represent the amplitudes of waves. \(W_{q} ;\,\,q = 1 - 3\) and \(S_{q} ;\,\,q = 1 - 3\) are the amplitude ratios.

Characteristic Equation and Its Solution


Here, \(m_{q}^{2} ;\,\,q = 1 - 5\) are the roots of the equation

$$\prod\limits_{q = 1}^{5} {m^{2} - m_{q}^{2} } = 0,$$
(27)

which signifies the characteristic equation, the roots can be organized as

$$m_{q}^{2} = \xi^{2} \left( {1 - \lambda_{q}^{2} c^{2} } \right);\,\,q = 1 - 5.$$
(28)

Equations (24)–(26) indicate that the characteristic roots \(m_{q}^{2} ;\,\,q = 1 - 3\) are coupled which corresponds to the coupled system of waves comprised of thermal waves, elastic waves, and volume fraction field waves while the characteristic roots \(m_{4,\,5}^{2}\) are uncoupled roots representing three decoupled mechanical waves, one in solid and one in each liquid layer, these uncoupled roots \(m_{4,\,5}^{2}\) can be obtained by introducing

$$\lambda_{4}^{2} = \frac{1}{{\delta^{2} }},\,\,\lambda_{5}^{2} = \frac{1}{{\delta_{L}^{2} }},$$
(29)

in Eq. (28) for the appropriate values of \(q\).

In addition, the unknowns \(\lambda_{q}^{2} ;\,\,q = 1 - 3\) are the roots of the equation

$$\eta^{3} - L\eta^{2} + M\eta - N = 0,$$
(30)

with

$$L = \kappa + \,\gamma + \frac{{a_{3} }}{{\omega^{2} }}\frac{{\varepsilon_{\phi } \varepsilon_{b}^{2} }}{{\varepsilon_{T} }},$$
$$M = \tau_{1} + \kappa \gamma - \frac{{a_{3} \varepsilon_{\phi } }}{{\omega^{2} }}\left[ {\tau^{\prime}_{1} \left\{ {1 - \varepsilon_{b} \left( {1 - \iota \omega \tau_{2} } \right)} \right\} - \frac{{\tau_{1} \varepsilon_{b}^{2} }}{{\varepsilon_{T} }}} \right],$$
$$N = \tau_{1} \left( {\gamma - \frac{{a_{3} \varepsilon_{\phi } }}{{\omega^{2} }}} \right),$$
(31)

where

$$\varepsilon_{\phi } = \frac{{a_{4} a_{5} }}{{a_{3} }},\,\,\,\varepsilon_{b} = \frac{{a_{2} }}{{a_{4} }},\,\,\,\varepsilon_{T} = \frac{{a_{2} a_{5} }}{{a_{1} a_{4} }},\,\,\,\overline{{\xi_{0} }} = 1 - \iota \omega \overline{{\xi^{*} }} ,\,\,\tau_{1} = t_{1} + \tau ,\,\,\tau^{\prime}_{1} = t_{1} \delta_{1k} + \tau ,\,\,\tau_{2} = t_{2} \delta_{2k} + \tau ;\,\,\tau = \iota \omega^{ - 1} ,$$
$$\kappa = 1 + \tau_{1} - \iota \omega \tau^{\prime}_{1} \tau_{2} \varepsilon_{T} ,\,\,\,\gamma = \frac{1}{{\delta_{1}^{2} }} - \frac{{a_{3} \overline{{\xi_{0} }} }}{{\omega^{2} }}.$$

Here, \(\varepsilon_{\phi }\) is the porothermal coupling parameter while \(\varepsilon_{b}\) denotes the poroelastic coupling parameter. \(\tau_{1}\), \(\tau^{\prime}_{1}\) and \(\tau_{2}\) are the time parameters. \(\overline{{\xi_{0} }}\), \(\kappa\) and \(\gamma\) are coupling parameters.

Amplitude Ratios

The amplitude ratios explore the effect of various interacting fields on the waves and are obtained as

$$W_{q} = \frac{{a_{4} \left[ {\lambda_{q}^{2} \left( {1 + \iota \omega \tau_{2} \varepsilon_{b} } \right) - 1} \right]}}{{\iota \omega \tau_{2} \left( {\lambda_{q}^{2} - \gamma } \right) + \frac{{a_{3} }}{{\omega^{2} }}\frac{{\varepsilon_{\phi } \varepsilon_{b} }}{{\varepsilon_{T} }}}},\,$$
$$S_{q} = \iota \omega^{ - 1} \tau_{2}^{ - 1} \left[ {a_{1} W_{q} + \omega^{2} \left( {1 - \lambda_{q}^{2} } \right)} \right]\,;\,\,q = 1 - 3.$$
(32)

Special Cases of the Roots and Amplitude Ratios

(i) In the case of elasticity with voids, \(m^{*} = 0 = \beta \Rightarrow \varepsilon_{T} = 0 = \varepsilon_{\phi }\), therefore, Eqs. (31) and (32) give

$$\lambda_{1}^{2} + \lambda_{2}^{2} = 1 + \gamma + \frac{{a_{3} }}{{\omega^{2} }}\frac{{\varepsilon_{\phi } \varepsilon_{b}^{2} }}{{\varepsilon_{T} }},\,\lambda_{1}^{2} \lambda_{2}^{2} = \gamma {\text{ and }}\lambda_{3}^{2} = \tau_{1},$$
(33)
$$W_{q} = \left\{ \begin{gathered} \frac{{\omega^{2} \left( {\lambda_{q}^{2} - 1} \right)}}{{a_{1} }}\,;\,\,\,q = 1 - 2 \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,;\,\,q = 3 \hfill \\ \end{gathered} \right.,\,\,S_{q} = \left\{ \begin{gathered} 0;\,\,\,q = 1 - 2 \hfill \\ 1;\,\,\,\,q = 3 \hfill \\ \end{gathered} \right..$$
(34)

(ii) In the absence of voids, \(m^{*} = 0 = b\) so that \(\varepsilon_{\phi } = 0 = \varepsilon_{b}\), therefore, from (31) and (32), one gets

$$\lambda_{1}^{2} + \lambda_{3}^{2} = \kappa ,\,\,\lambda_{1}^{2} \lambda_{3}^{2} = \tau_{1} {\text{ and }}\lambda_{2}^{2} = \gamma ,\,$$
(35)
$$W_{q} = \left\{ \begin{gathered} 0\,;\,\,\,q = 1,3 \hfill \\ 1\,;\,\,q = 2 \hfill \\ \end{gathered} \right.,\,\,S_{q} = \left\{ \begin{gathered} \iota \omega \tau_{2}^{ - 1} \left( {1 - \lambda_{q}^{2} } \right);\,\,\,q = 1,3 \hfill \\ 0\,;\,\,q = 2 \hfill \\ \end{gathered} \right..$$
(36)

(iii) Further, for the elastic case, \(m^{*} = 0 = \beta = b \Rightarrow \varepsilon_{T} = 0 = \varepsilon_{\phi } = \varepsilon_{b}\), Eqs. (35) and (36) reduce to

$$\lambda_{1}^{2} = 1{\text{ and }}\lambda_{2}^{2} = \gamma ,\,\,\lambda_{3}^{2} = \tau_{1},$$
(37)
$$W_{q} = \left\{ \begin{gathered} 0\,;\,\,\,q = 1,3 \hfill \\ 1\,;\,\,\,q = 2 \hfill \\ \end{gathered} \right.,\,\,S_{q} = \left\{ \begin{gathered} 0\,;\,\,\,q = 1,2 \hfill \\ 1;\,\,\,q = 3 \hfill \\ \end{gathered} \right..$$
(38)

Interface Conditions

The boundary conditions for the current problem at each solid–liquid smooth interface \(z = \pm d\) of the thermo-poroelastic solid plate and inviscid liquid layers have been considered as

Normal Stress-Free Condition

The equilibrium of the total normal stress at the liquid–solid interface is given by (cf. Sharma and Pathania [30]

$$\ddot{G} - 2\delta^{2} \left( {G_{,rr} + \psi_{,rz} + \frac{{G_{,r} + \psi_{,z} }}{r}} \right) = \frac{{\rho_{L} }}{\rho }\ddot{G}_{{L_{q} }} ;\,\,q = 1 - 2.$$
(39)

Shear Stress-Free Condition

The equilibrium of the shear stress at the liquid–solid interface is given by (cf. Sharma and Pathania [30]

$$2G_{,rz} + \psi_{,zz} - \psi_{,rr} - \frac{{\psi_{,r} }}{r} + \frac{\psi }{{r^{2} }} = 0.$$
(40)

No-Slip Condition


Here, the liquid is inviscid which becomes the cause of slippage between the thermo-poroelastic solid and the fluid medium. Therefore, to maintain the no slippage condition intact at the liquid–solid junction \(z = \pm d\), the \(z -\)component of displacement of the liquid and solid is equal (cf. Qiu et al. [27]), i.e.,

$$G_{,z} - \psi_{,r} - \frac{\psi }{r} = G_{{L_{q} ,z}} ;\,\,q = 1 - 2.$$
(41)

Equilibrated Stress-Free Condition

The boundary condition due to voids resembles that of classical elasticity. The boundary condition on the self-equilibrated stress vector is taken to have a vanishing normal component (cf. Sadd [28]), which results in

$$\phi_{,z} = 0.$$
(42)

Adiabatic and Isothermal Interface Condition

The solid–liquid interface \(z = \pm d\) has been assumed adiabatic and isothermal (cf. Sharma and Pathania [30], i.e.,

$$T_{,z} + HT = 0.$$
(43)

Here, \(H\) is the coefficient of heat transfer which represents the isothermal and adiabatic solid–liquid interface when \(H \to \infty\) and \(H \to 0\), respectively.

Frequency Equation

Using the solutions (24)–(26) in the boundary conditions (39)–(43), the system of ten linear homogeneous equations in ten unknowns \(A_{q} ;\,\,q = 1 - 6\) and \(B_{q} ;\,q = 1 - 4\) have been obtained in stiffness matrix form as

$$M\left[ {A_{1} \,\,B_{1} \,\,A_{2} \,\,B_{2} \,\,A_{3} \,\,B_{3} \,\,A_{4} \,\,B_{4} \,\,A_{5} \,\,A_{6} } \right]^{tr} = 0,$$
(44)

where “tr” represents the transpose of the row vector. The determinant of the coefficient matrix of these equations is zero to obtain the non-zero solution for \(A_{q} ;\,q = 1 - 6\) and \(B_{q} ;\) \(q = 1 - 4.\) Mathematically,

$$\left| M \right| = 0.$$
(45)

Equation (45) is the frequency equation for waves in the thermo-poroelastic isotropic homogeneous solid plate sandwich-packed by layers of non-viscous liquid. It is also known as the secular equation because it reveals complete information regarding the waves’ characteristics. After doing a rigorous mathematical workout, Eq. (45) becomes

$$\begin{gathered} \left[ {\frac{{T_{1} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} }}{{m_{2} }}\left( {\frac{{W_{3} S_{1} - W_{1} S_{3} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right)\left[ {\frac{{T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} }}{{m_{3} }}\left( {\frac{{W_{1} S_{2} - W_{2} S_{1} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right)\left[ {\frac{{T_{3} }}{{T_{4} }}} \right]^{ \pm 1} + \left( {\frac{{\rho_{L} \omega^{2} \left( {m_{4}^{2} + \xi^{2} } \right)m_{1} }}{{\rho m_{5} \delta^{2} \left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}\frac{{T_{5} }}{{\left[ {T_{4} } \right]^{ \pm 1} }}} \right. \hfill \\ \left. { + \frac{{4\xi^{2} m_{1} m_{4} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}} \right)\left( {1 + \frac{{W_{3} S_{1} - W_{1} S_{3} }}{{W_{2} S_{3} - W_{3} S_{2} }} + \frac{{W_{1} S_{2} - W_{2} S_{1} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right) + \frac{{4\xi^{2} m_{4} S_{1} \left( {W_{3} - W_{2} } \right)H\left[ {T_{4} } \right]^{ \pm 1} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} \left( {W_{2} S_{3} - W_{3} S_{2} } \right)}} \hfill \\ \left[ {\frac{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} W_{3} \left( {S_{1} - S_{2} } \right)}}{{4\xi^{2} m_{2} m_{4} \left[ {T_{4} } \right]^{ \pm 1} S_{1} \left( {W_{3} - W_{2} } \right)}}\left( {\left[ {\frac{{T_{1} T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} W_{1} \left( {S_{2} - S_{3} } \right)}}{{m_{3} W_{3} \left( {S_{1} - S_{2} } \right)}}\left[ {\frac{{T_{2} T_{3} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{2} W_{2} \left( {S_{3} - S_{1} } \right)}}{{m_{3} W_{3} \left( {S_{1} - S_{2} } \right)}}\left[ {\frac{{T_{1} T_{3} }}{{T_{4} }}} \right]^{ \pm 1} } \right)} \right. \hfill \\ \left. { + \left( {1 + \frac{{\left( {m_{4}^{2} + \xi^{2} } \right)\omega^{2} \rho_{L} }}{{4\xi^{2} \rho \delta^{2} m_{4} m_{5} }}\frac{{T_{5} }}{{\left[ {T_{4} } \right]^{ \pm 1} }}} \right)\left( {\left[ {\frac{{T_{1} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} \left( {W_{1} - W_{3} } \right)S_{2} }}{{m_{2} \left( {W_{3} - W_{2} } \right)S_{1} }}\left[ {\frac{{T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} \left( {W_{2} - W_{1} } \right)S_{3} }}{{m_{3} \left( {W_{3} - W_{2} } \right)S_{1} }}\left[ {\frac{{T_{3} }}{{T_{4} }}} \right]^{ \pm 1} } \right)} \right]= 0, \hfill \\ \end{gathered}$$
(46)

where \(T_{q} = \tan m_{q} d\,;\,\,q = 1 - 4\,\) and \(T_{5} = \tan m_{5} h.\) Equation (46) satisfies the condition \(m_{5} \ne 0\) and \(m_{5} h \ne \left( {2n - 1} \right){\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}\), \(n \in N\), set of natural numbers. Here, the superscript \(+ 1\) and \(- 1\) represent flexural and longitudinal modes, respectively. The frequency Eq. (46) for the Rayleigh–Lamb-type equation resembles the same obtained by Pathania and Dhiman [23] for the longitudinal and flexural modes of thermo-poroelastic waves in the infinite rectangular plate sandwich-packed by non-viscous liquid layers. Therefore, it proves that the Rayleigh–Lamb-type frequency equation also governs circularly crested thermo-poroelastic waves in the cylindrical isotropic homogeneous plate sandwich-packed by layers of non-viscous liquid layers. Though the relationship between frequency and wavenumber holds good whether the system chosen would be rectangular or cylindrical. In the case of circularly crested waves, the displacements and stresses vary according to Bessel functions rather than trigonometric functions. For very large values of \(r\),

$$J_{0} \left( \Xi \right) \to \frac{\sin \left( \Xi \right) + \cos \left( \Xi \right)}{{\sqrt {\pi \Xi } }},$$
$$J_{1} \left( \Xi \right) \to \frac{\sin \left( \Xi \right) - \cos \left( \Xi \right)}{{\sqrt {\pi \Xi } }};\,\,\Xi = \xi r.$$

Therefore, the motion becomes periodic at a comparatively larger distance from the origin which comes within four to five zeros of the Bessel function. The circularly crested waves approach straight crested waves for the large values of \(r\). This result agrees with Sharma and Singh [31] and Graff [8]. As, for the large value of the radius, the curved periphery of the circle looks as if it is flat if its small portion is taken into consideration as Earth seems flat from the Earth itself although it is spherical when seen from space.

Special Cases

Upon varying some of the functional parameters of the frequency equation such as the width of the layer, voids, and temperature, we infer its various forms which have been discussed below.

Leaky Waves

The propagation of leaky Lamb waves has been used as an effective tool for nondestructive evaluation (NDE) of the structure of the solid body. Owing to the characteristics such as long-range inspection, multimode, and dispersion, Leaky Lamb waves can provide ample information about the defects or material properties as compared to the conventional bulk wave methods. These have aroused extensive theoretical and experimental studies of Leaky Lamb waves in the past decades. If the width of the liquid layer approaches infinity i.e., if \(h \to \infty ,\) then some part of the energy in the plate leaks into the semi-infinite liquid. These waves are termed leaky Lamb waves. In this case, \(T_{5} \to - \iota\), therefore, Eq. (46) becomes

$$\begin{gathered} \left[ {\frac{{T_{1} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} }}{{m_{2} }}\left( {\frac{{W_{3} S_{1} - W_{1} S_{3} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right)\left[ {\frac{{T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} }}{{m_{3} }}\left( {\frac{{W_{1} S_{2} - W_{2} S_{1} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right)\left[ {\frac{{T_{3} }}{{T_{4} }}} \right]^{ \pm 1} - \left( {\frac{{\iota \rho_{L} \omega^{2} \left( {m_{4}^{2} + \xi^{2} } \right)m_{1} }}{{\rho m_{5} \delta^{2} \left( {m_{4}^{2} - \xi^{2} } \right)^{2} \left[ {T_{4} } \right]^{ \pm 1} }}} \right. \hfill \\ \left. { - \frac{{4\xi^{2} m_{1} m_{4} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}} \right)\left( {1 + \frac{{W_{3} S_{1} - W_{1} S_{3} }}{{W_{2} S_{3} - W_{3} S_{2} }} + \frac{{W_{1} S_{2} - W_{2} S_{1} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right) + \frac{{4\xi^{2} m_{4} S_{1} \left( {W_{3} - W_{2} } \right)H\left[ {T_{4} } \right]^{ \pm 1} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} \left( {W_{2} S_{3} - W_{3} S_{2} } \right)}} \hfill \\ \left[ {\frac{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} W_{3} \left( {S_{1} - S_{2} } \right)}}{{4\xi^{2} m_{2} m_{4} \left[ {T_{4} } \right]^{ \pm 1} S_{1} \left( {W_{3} - W_{2} } \right)}}} \right.\left( {\left[ {\frac{{T_{1} T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} W_{1} \left( {S_{2} - S_{3} } \right)}}{{m_{3} W_{3} \left( {S_{1} - S_{2} } \right)}}\left[ {\frac{{T_{2} T_{3} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{2} W_{2} \left( {S_{3} - S_{1} } \right)}}{{m_{3} W_{3} \left( {S_{1} - S_{2} } \right)}}\left[ {\frac{{T_{1} T_{3} }}{{T_{4} }}} \right]^{ \pm 1} } \right) \hfill \\ \left. { + \left( {1 - \frac{{\iota \left( {m_{4}^{2} + \xi^{2} } \right)\omega^{2} \rho_{L} }}{{4\xi^{2} \rho \delta^{2} m_{4} m_{5} \left[ {T_{4} } \right]^{ \pm 1} }}} \right)\left( {\left[ {\frac{{T_{1} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} \left( {W_{1} - W_{3} } \right)S_{2} }}{{m_{2} \left( {W_{3} - W_{2} } \right)S_{1} }}\left[ {\frac{{T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} \left( {W_{2} - W_{1} } \right)S_{3} }}{{m_{3} \left( {W_{3} - W_{2} } \right)S_{1} }}\left[ {\frac{{T_{3} }}{{T_{4} }}} \right]^{ \pm 1} } \right)} \right] = 0. \hfill \\ \end{gathered}$$
(47)

Isothermal Case

For the isothermal case \(\left( {H \to \infty } \right)\), Eq. (46) becomes

$$\begin{gathered} \left[ {\frac{{T_{1} }}{{T_{4} }}} \right]^{ \pm 1} + \left( {\frac{{m_{3} W_{3} S_{1} \left[ {T_{1} } \right]^{ \pm 1} - m_{1} W_{1} S_{3} \left[ {T_{3} } \right]^{ \pm 1} }}{{m_{2} W_{2} S_{3} \left[ {T_{3} } \right]^{ \pm 1} - m_{3} W_{3} S_{2} \left[ {T_{2} } \right]^{ \pm 1} }}} \right)\left[ {\frac{{T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \left( {\frac{{m_{1} W_{1} S_{2} \left[ {T_{2} } \right]^{ \pm 1} - m_{2} W_{2} S_{1} \left[ {T_{1} } \right]^{ \pm 1} }}{{m_{2} W_{2} S_{3} \left[ {T_{3} } \right]^{ \pm 1} - m_{3} W_{3} S_{2} \left[ {T_{2} } \right]^{ \pm 1} }}} \right)\left[ {\frac{{T_{3} }}{{T_{4} }}} \right]^{ \pm 1} \hfill \\ + \left( {\frac{{\left( {m_{4}^{2} + \xi^{2} } \right)\omega^{2} \rho_{L} m_{1} }}{{\rho \delta^{2} m_{5} \left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}\frac{{T_{5} }}{{\left[ {T_{4} } \right]^{ \pm 1} }} + \frac{{4\xi^{2} m_{1} m_{4} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}} \right)\left( {1 + \frac{{m_{2} \left( {m_{3} W_{3} S_{1} \left[ {T_{1} } \right]^{ \pm 1} - m_{1} W_{1} S_{3} \left[ {T_{3} } \right]^{ \pm 1} } \right)}}{{m_{1} \left( {m_{2} W_{2} S_{3} \left[ {T_{3} } \right]^{ \pm 1} - m_{3} W_{3} S_{2} \left[ {T_{2} } \right]^{ \pm 1} } \right)}}} \right. \hfill \\ \left. { + \frac{{m_{3} \left( {m_{1} W_{1} S_{2} \left[ {T_{2} } \right]^{ \pm 1} - m_{2} W_{2} S_{1} \left[ {T_{1} } \right]^{ \pm 1} } \right)}}{{m_{1} \left( {m_{2} W_{2} S_{3} \left[ {T_{3} } \right]^{ \pm 1} - m_{3} W_{3} S_{2} \left[ {T_{2} } \right]^{ \pm 1} } \right)}}} \right) = 0. \hfill \\ \end{gathered}$$
(48)

Adiabatic Case

For thermally shielded case \(\left( {H \to 0} \right)\), Eq. (46) reduces to

$$\begin{gathered} \left[ {\frac{{T_{1} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} }}{{m_{2} }}\left( {\frac{{W_{3} S_{1} - W_{1} S_{3} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right)\left[ {\frac{{T_{2} }}{{T_{4} }}} \right]^{ \pm 1} + \frac{{m_{1} }}{{m_{3} }}\left( {\frac{{W_{1} S_{2} - W_{2} S_{1} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right)\left[ {\frac{{T_{3} }}{{T_{4} }}} \right]^{ \pm 1} + \left( {\frac{{\rho_{L} \omega^{2} \left( {m_{4}^{2} + \xi^{2} } \right)m_{1} }}{{\rho m_{5} \delta^{2} \left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}\frac{{T_{5} }}{{\left[ {T_{4} } \right]^{ \pm 1} }}} \right. \hfill \\ \left. { + \frac{{4\xi^{2} m_{1} m_{4} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}} \right)\left( {1 + \frac{{W_{3} S_{1} - W_{1} S_{3} }}{{W_{2} S_{3} - W_{3} S_{2} }} + \frac{{W_{1} S_{2} - W_{2} S_{1} }}{{W_{2} S_{3} - W_{3} S_{2} }}} \right) = 0. \hfill \\ \end{gathered}$$
(49)

Different Regions of the Secular Equation

It is quite obvious that the secular Eq. (46) is the function of its characteristic roots \(m_{q} ;\,\,q = 1 - 4\), therefore, secular equation changes as and when characteristic roots alter.

Equation (46) can be represented in the plane \(\left( {\omega ,\,\,\xi } \right)\) which defines a curve known as a dispersion curve. The nature of \(m_{q} \,;\,\,q = 1 - \,4\) decides that the curve can be separated into three regions (cf. Figure 2) which are described below.

Fig. 2
figure 2

Division of \(\omega - \xi\) plane into three regions

Full size image

Region I

The secular Eq. (46) falls in the region I if the roots \(m_{q} ;\,\,q = 1 - 4\) are replaced with \(\iota m^{\prime}_{q} ;\)

\(q = 1 - 4\) in the secular Eq. (46).

Region II

The secular Eq. (46) lies in region II if the roots \(m_{q} ;\,\,q = 1 - 3\) are replaced with \(\iota m^{\prime}_{q} ;\,q = 1 - 3\), leaving \(m_{4}\) unchanged, in the secular Eq. (46).

Region III

Equation (46) represents the frequency equation for region III in the case of the thermally shielded and isothermal surface.

Thin Plate Waves

As the title implies, in this case \(2d \ll \xi^{ - 1}\), i.e., the thickness of the plate is very small as compared with the wavelength of the thermo-poroelastic waves in the solid plate cladded with non-viscous liquid layers. For this region, these are also termed waves of long wavelengths. In this section, thin plate results have been discussed for regions I and II.

Thin Plate Waves for the Region I


Here, the thermally insulated case of the secular equation for the region I has been considered for the flexural mode of waves. In the secular equation for region I, hyperbolic tangent functions have been expanded up to the first two terms of the series and one obtains

$$\left( {m_{4}^{\prime 2} - \xi^{2} } \right)^{2} + \frac{4}{3}d^{2} \xi^{2} m_{4}^{\prime 2} - \frac{1}{3}d^{2} \left( {m_{4}^{\prime 2} + \xi^{2} } \right)^{2} \frac{P}{F} - \frac{{\rho_{L} \omega^{2} \left( {m_{4}^{\prime 2} - \xi^{2} } \right)T_{5} }}{{\rho m_{5} \delta^{2} d}} = 0,$$
(50)

where

$$F = S^{\prime}_{1} \left( {W^{\prime}_{3} - W^{\prime}_{2} } \right) + S^{\prime}_{2} \left( {W^{\prime}_{1} - W^{\prime}_{3} } \right) + S^{\prime}_{3} \left( {W^{\prime}_{2} - W^{\prime}_{1} } \right),$$
$$P = S_{1}^{\prime } \left( {m_{2}^{\prime 2} W_{3}^{\prime } - m_{3}^{\prime 2} W_{2}^{\prime } } \right) + S_{2}^{\prime } \left( {m_{3}^{\prime 2} W_{1}^{\prime } - m_{1}^{\prime 2} W_{3}^{\prime } } \right) + S_{3}^{\prime } \left( {m_{1}^{\prime 2} W_{2}^{\prime } - m_{2}^{\prime 2} W_{1}^{\prime } } \right).$$

In the absence of voids, Eq. (50), using relations (35) and (36), becomes

$$\left( {m_{4}^{\prime 2} - \xi^{2} } \right)^{2} + \frac{4}{3}d^{2} \xi^{2} m_{4}^{\prime 2} - \frac{1}{3}d^{2} \alpha^{2} \left( {m_{4}^{\prime 2} + \xi^{2} } \right)^{2} - \frac{{\rho_{L} \omega^{2} \left( {m_{4}^{\prime 2} - \xi^{2} } \right)T_{5} }}{{\rho m_{5} \delta^{2} d}} = 0,$$
(51)

which is analogous to that of Sharma and Pathania [30] and Pathania and Dhiman [23].

Upon neglecting the effect of liquid \(\left( {\rho_{L} \to 0} \right)\), Eq. (51) shrinks to

$$\left( {m_{4}^{\prime 2} - \xi^{2} } \right)^{2} + \frac{4}{3}d^{2} \xi^{2} m_{4}^{\prime 2} - \frac{1}{3}d^{2} \alpha^{2} \left( {m_{4}^{\prime 2} + \xi^{2} } \right)^{2} = 0,$$
(52)

which matches that of Kaur [12] and Pathania and Dhiman [23].

Thin Plate Waves for Region II

The secular equation for region II has been considered for the insulated and longitudinal wave mode case and the tangent hyperbolic and circular tangent functions except \(T_{5}\) have been expanded up to only the first order, therefore, the resulting frequency equation is

$$\begin{gathered} m_{1}^{\prime 2} S^{\prime}_{1} \left( {m_{3}^{\prime 2} W^{\prime}_{3} - m_{2}^{\prime 2} W^{\prime}_{2} } \right) + m_{2}^{\prime 2} S^{\prime}_{2} \left( {m_{1}^{\prime 2} W^{\prime}_{1} - m_{3}^{\prime 2} W^{\prime}_{3} } \right) + m_{3}^{\prime 2} S^{\prime}_{3} \left( {m_{2}^{\prime 2} W^{\prime}_{2} - m_{1}^{\prime 2} W^{\prime}_{1} } \right) \hfill \\ - \left( {4 + \frac{{\rho_{L} c^{2} d\left( {m_{4}^{2} + \xi^{2} } \right)T_{5} }}{{\rho m_{5} \delta^{2} }}} \right)\,\frac{{\xi^{2} m_{1}^{\prime 2} m_{2}^{\prime 2} m_{3}^{\prime 2} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}F = 0. \hfill \\ \end{gathered}$$
(53)

In the absence of voids i.e., for the elasto-thermal plate with liquid, using relations (35) and (36), Eq. (53) reduces to

$$m_{1}^{\prime 2} + m_{3}^{\prime 2} - \left[ {\alpha^{2} + \left( {4 + \frac{{\rho_{L} c^{2} d\left( {m_{4}^{2} + \xi^{2} } \right)T_{5} }}{{\rho m_{5} \delta^{2} }}} \right)\frac{{\xi^{2} m_{1}^{\prime 2} m_{3}^{\prime 2} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}} \right] = 0,$$
(54)

which matches with Sharma and Pathania [30].

Neglecting the inviscid fluid, i.e., only for the elasto-thermal plate, Eq. (54) reduces to

$$m_{1}^{\prime 2} + m_{3}^{\prime 2} - \left( {\alpha^{2} + \frac{{4\xi^{2} m_{1}^{\prime 2} m_{3}^{\prime 2} }}{{\left( {m_{4}^{2} - \xi^{2} } \right)^{2} }}} \right) = 0.$$
(55)

Equation (55) matches with Sharma and Pathania [30] and Kaur [12].

Thick Plate Waves

If the wavelength of waves approaches to zero i.e., if \(\xi^{ - 1} \to 0,\) then the information regarding the asymptotic behavior of the solution can be achievable. In this case, the region I contains the characteristic roots of the secular equation. Hence, the secular equation for region I has been considered for a thermally insulated case. For \(\xi \to \infty ,\)\(\tanh m^{\prime}_{q} d\, \to 1;\,\,q = 1 - 4\) and \(\,\tan m_{5} h \to - \iota\). Hence, the secular equation for region I for the asymptotic behavior reduces to

$$\begin{gathered} \left( {\alpha_{4}^{2} + 1} \right)^{2} \left[ {S^{\prime}_{1} \alpha^{\prime}_{1} \left( {W^{\prime}_{3} \alpha^{\prime}_{3} - W^{\prime}_{2} \alpha^{\prime}_{2} } \right) + S^{\prime}_{2} \alpha^{\prime}_{2} \left( {W^{\prime}_{1} \alpha^{\prime}_{1} - W^{\prime}_{3} \alpha^{\prime}_{3} } \right) + S^{\prime}_{3} \alpha^{\prime}_{3} \left( {W^{\prime}_{2} \alpha^{\prime}_{2} - W^{\prime}_{1} \alpha^{\prime}_{1} } \right)} \right] \hfill \\ = \left( {4\alpha^{\prime}_{4} \pm \frac{{\iota \rho_{L} c^{4} }}{{\alpha_{5} \rho \delta^{4} }}} \right)\alpha^{\prime}_{1} \alpha^{\prime}_{2} \alpha^{\prime}_{3} F, \hfill \\ \end{gathered}$$
(56)

where

$$\alpha^{\prime}_{q} = \sqrt {\lambda_{q}^{2} c^{2} - 1} ;\,\,j = 1 - 4,\,\,\alpha_{q} = \sqrt {1 - \lambda_{q}^{2} c^{2} } ;\,\,q = 4 - \,5.$$

For the elasto-thermal plate with voids, ignoring the inviscid fluid, Eq. (56) reduces to

$$\begin{gathered} \left( {\alpha_{4}^{2} + 1} \right)^{2} \left[ {S^{\prime}_{1} \alpha^{\prime}_{1} \left( {W^{\prime}_{3} \alpha^{\prime}_{3} - W^{\prime}_{2} \alpha^{\prime}_{2} } \right) + S^{\prime}_{2} \alpha^{\prime}_{2} \left( {W^{\prime}_{1} \alpha^{\prime}_{1} - W^{\prime}_{3} \alpha^{\prime}_{3} } \right) + S^{\prime}_{3} \alpha^{\prime}_{3} \left( {W^{\prime}_{2} \alpha^{\prime}_{2} - W^{\prime}_{1} \alpha^{\prime}_{1} } \right)} \right] \hfill \\ = 4\alpha^{\prime}_{1} \alpha^{\prime}_{2} \alpha^{\prime}_{3} \alpha^{\prime}_{4} F, \hfill \\ \end{gathered}$$
(57)

which agrees with that of Kaur [12].

For the elasto-thermal plate with liquid, ignoring the voids, using relations (35) and (36), Eq. (56) becomes

$$\left( {\alpha_{4}^{2} + 1} \right)^{2} \left[ {\alpha_{0}^{\prime 2} + \alpha_{1}^{\prime 2} + \alpha^{\prime}_{3} \left( {\alpha^{\prime}_{1} + \alpha^{\prime}_{3} } \right)} \right] = \left( {4\alpha^{\prime}_{4} \pm \frac{{\iota \rho_{L} c^{4} }}{{\rho \delta^{4} \alpha_{5} }}} \right)\alpha^{\prime}_{1} \alpha^{\prime}_{3} \left( {\alpha^{\prime}_{1} + \alpha^{\prime}_{3} } \right),$$
(58)

where \(\alpha_{0}^{\prime 2} = 1 - c^{2}\).

Furthermore, for the elasto-thermal plate, ignoring both liquid and voids, Eq. (56) cuts down to

$$\left( {\alpha_{4}^{2} + 1} \right)^{2} \left[ {\alpha_{0}^{\prime 2} + \alpha_{1}^{\prime 2} + \alpha^{\prime}_{3} \left( {\alpha^{\prime}_{1} + \alpha^{\prime}_{3} } \right)} \right] = 4\left( {\alpha^{\prime}_{1} + \alpha^{\prime}_{3} } \right)\alpha^{\prime}_{1} \alpha^{\prime}_{3} \alpha^{\prime}_{4}.$$
(59)

Equations (58) and (59) are also discussed by Sharma and Pathania [30] and Pathania and Dhiman [23].

Derivation of Amplitudes of Displacements, Temperature, and Volume Fraction Field Variation

In thin-walled structures such as plates and shells, upper and bottom surfaces guide the wave propagation producing transverse horizontal (TH) waves in the \(r\theta -\)plane and Lamb waves in the \(rz -\)plane. The displacement pattern of Lamb-type waves can be seen in two forms named symmetric (longitudinal) and antisymmetric (flexural) modes (cf. Figure 3).

Fig. 3
figure 3

Displacement of Lamb wave modes

Full size image

With the aid of Eqs. (16) and (26), one gets the amplitudes of the \(r -\) and \(z -\)components of the change in the position, void-volume fractional field, and the temperature as

$$u_{sy} = \left[ {\iota \xi \left( {\cos m_{1} z + L_{1} \cos m_{2} z + M_{1} \cos m_{3} z} \right) + N_{1} m_{4} \cos m_{4} z} \right]B_{1} J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(60)
$$w_{asy} = - \left[ {m_{1} \sin m_{1} z + L_{1} m_{2} \sin m_{2} z + M_{1} m_{3} \sin m_{3} z + \iota \xi N_{1} \sin m_{4} z} \right]B_{1} J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(61)
$$\phi_{sy} = \left[ {W_{1} \cos m_{1} z + L_{1} W_{2} \cos m_{2} z + M_{1} W_{3} \cos m_{3} z} \right]B_{1} J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(62)
$$T_{sy} = \left[ {S_{1} \cos m_{1} z + L_{1} S_{2} \cos m_{2} z + M_{1} S_{3} \cos m_{3} z} \right]B_{1} J_{0} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(63)
$$u_{asy} = \left[ {\iota \xi \left( {\sin m_{1} z + L_{1}^{ * } \sin m_{2} z + M_{1}^{ * } \sin m_{3} z} \right) - N_{1}^{ * } m_{4} \sin m_{4} z} \right]A_{1} J_{1} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(64)
$$w_{sy} = \left[ {m_{1} \cos m_{1} z + L_{1}^{ * } m_{2} \cos m_{2} z + M_{1}^{ * } m_{3} \cos m_{3} z - \iota \xi N_{1}^{ * } \cos m_{4} z} \right]\,A_{1} J_{1} \left( {\xi r} \right)e^{ - \iota \omega t},$$
(65)
$$\phi_{asy} = \left[ {W_{1} \sin m_{1} z + L_{1}^{ * } W_{2} \sin m_{2} z + M_{1}^{ * } W_{3} \sin m_{3} z} \right]A_{1} J_{1} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(66)
$$T_{asy} = \left[ {S_{1} \sin m_{1} z + L_{1}^{ * } S_{2} \sin m_{2} z + M_{1}^{ * } S_{3} \sin m_{3} z} \right]A_{1} J_{1} \left( {\xi r} \right)e^{ - \iota \omega t} .$$
(67)

Similarly, using Eqs. (15) and (24), amplitudes of displacements for the bottom liquid layer are given by

$$u_{{L_{1} }} = \iota \xi O_{1}^{ * } \sin m_{5} \left[ {z - d - h} \right]A_{1} J_{1} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(68)
$$w_{{L_{1} }} = m_{5} O_{1}^{ * } \cos m_{5} \left[ {z - d - h} \right]A_{1} J_{1} \left( {\xi r} \right)e^{ - \iota \omega t} ,$$
(69)

where

$$L_{1} = \frac{{s_{4} \left( {m_{3} c_{1} s_{3} W_{3} - m_{1} c_{3} s_{1} W_{1} } \right) + q^{ * } m_{1} m_{3} m_{4} c_{4} s_{1} s_{3} \left( {W_{3} - W_{1} } \right)}}{{s_{4} \left( {m_{2} c_{3} s_{2} W_{2} - m_{3} c_{2} s_{3} W_{3} } \right) + q^{ * } m_{2} m_{3} m_{4} c_{4} s_{2} s_{3} \left( {W_{2} - W_{3} } \right)}},$$
$$M_{1} = \frac{{s_{4} \left( {m_{1} c_{2} s_{1} W_{1} - m_{2} c_{1} s_{2} W_{2} } \right) + q^{ * } m_{1} m_{2} m_{4} c_{4} s_{1} s_{2} \left( {W_{1} - W_{2} } \right)}}{{s_{4} \left( {m_{2} c_{3} s_{2} W_{2} - m_{3} c_{2} s_{3} W_{3} } \right) + q^{ * } m_{2} m_{3} m_{4} c_{4} s_{2} s_{3} \left( {W_{2} - W_{3} } \right)}},$$
$$N_{1} = \frac{{2\xi \left[ {m_{1} m_{3} c_{2} s_{1} s_{3} \left( {W_{1} - W_{3} } \right) + m_{1} m_{2} c_{3} s_{1} s_{2} \left( {W_{2} - W_{1} } \right) + m_{2} m_{3} c_{1} s_{2} s_{3} \left( {W_{3} - W_{2} } \right)} \right]}}{{\lambda_{4}^{2} \omega^{2} \,\left[ {s_{4} \left( {m_{2} c_{3} s_{2} W_{2} - m_{3} c_{2} s_{3} W_{3} } \right) + q^{ * } m_{2} m_{3} m_{4} c_{4} s_{2} s_{3} \left( {W_{2} - W_{3} } \right)} \right]}},$$
$$L_{1}^{ * } = \frac{{\left( {p^{ * } c_{4} s_{5} + q^{ * } m_{4} m_{5} c_{5} s_{4} } \right)m_{1} m_{3} c_{1} c_{3} \left( {W_{1} - W_{3} } \right) + m_{5} c_{4} c_{5} \left( {m_{1} c_{1} s_{3} W_{1} - m_{3} c_{3} s_{1} W_{3} } \right)}}{{\left( {p^{ * } c_{4} s_{5} + q^{ * } m_{4} m_{5} c_{5} s_{4} } \right)m_{2} m_{3} c_{2} c_{3} \left( {W_{3} - W_{2} } \right) + m_{5} c_{4} c_{5} \left( {m_{3} c_{3} s_{2} W_{3} - m_{2} c_{2} s_{3} W_{2} } \right)}},$$
$$M_{1}^{ * } = \frac{{\left( {p^{ * } c_{4} s_{5} + q^{ * } m_{4} m_{5} c_{5} s_{4} } \right)m_{1} m_{2} c_{1} c_{2} \left( {W_{2} - W_{1} } \right) + m_{5} c_{4} c_{5} \left( {m_{2} c_{2} s_{1} W_{2} - m_{1} c_{1} s_{2} W_{1} } \right)}}{{\left( {p^{ * } c_{4} s_{5} + q^{ * } m_{4} m_{5} c_{5} s_{4} } \right)m_{2} m_{3} c_{2} c_{3} \left( {W_{3} - W_{2} } \right) + m_{5} c_{4} c_{5} \left( {m_{3} c_{3} s_{2} W_{3} - m_{2} c_{2} s_{3} W_{2} } \right)}},$$
$$N_{1}^{ * } = \frac{{2\xi m_{5} c_{5} }}{{\lambda_{4}^{2} \omega^{2} \,}}\frac{{\left[ {m_{2} m_{3} c_{2} c_{3} s_{1} \left( {W_{3} - W_{2} } \right) + m_{1} m_{3} c_{1} c_{3} s_{2} \left( {W_{1} - W_{3} } \right) + m_{1} m_{2} c_{1} c_{2} s_{3} \left( {W_{2} - W_{1} } \right)} \right]}}{{\left( {p^{ * } c_{4} s_{5} + q^{ * } m_{4} m_{5} c_{5} s_{4} } \right)m_{2} m_{3} c_{2} c_{3} \left( {W_{3} - W_{2} } \right) + m_{5} c_{4} c_{5} \left( {m_{3} c_{3} s_{2} W_{3} - m_{2} c_{2} s_{3} W_{2} } \right)}},$$
$$O_{1}^{ * } = - c_{4} \frac{{\left[ {m_{1} m_{2} c_{1} c_{2} s_{3} \left( {W_{1} - W_{2} } \right) + m_{2} m_{3} c_{2} c_{3} s_{1} \left( {W_{2} - W_{3} } \right) + m_{1} m_{3} c_{1} c_{3} s_{2} \left( {W_{3} - W_{1} } \right)} \right]}}{{\left( {p^{ * } c_{4} s_{5} + q^{ * } m_{4} m_{5} c_{5} s_{4} } \right)m_{2} m_{3} c_{2} c_{3} \left( {W_{3} - W_{2} } \right) + m_{5} c_{4} c_{5} \left( {m_{3} c_{3} s_{2} W_{3} - m_{2} c_{2} s_{3} W_{2} } \right)}}.$$

Here,

$$s_{i} = \sin m_{i} d,\,\,\,c_{i} = \cos m_{i} d;\,\,i = 1 - 4,\,\,\,s_{5} = \sin m_{5} h,\,\,\,c_{5} = \cos m_{5} h,$$
$$\,p^{ * } = \frac{{\rho_{L} }}{{\rho \omega^{2} }}\left( {\,2\xi^{2} - \lambda_{4}^{2} \omega^{2} } \right),\,\,q^{ * } = \frac{{4\xi^{2} }}{{\lambda_{4}^{4} \omega^{4} }}.$$

In addition, in the absence of liquid, displacements given by relations (60)–(67) are the same as obtained by Kaur [12].

Solution of the Secular Equation

The frequency Eq. (46) for Rayleigh–Lamb waves gives information about the behavioral pattern of the waves, for instance, phase velocity, attenuation coefficient, etc., which can be known after working on the frequency equation. To solve this frequency equation, the following relation has been considered.

$$c^{ - 1} = V^{ - 1} + \iota \omega^{ - 1} Q,$$
(70)

which gives \(\xi = R + \iota Q;\,R = {\omega \mathord{\left/ {\vphantom {\omega V}} \right. \kern-0pt} V},\,Q \in R\), a set of real numbers. Here \(Q\) and \(V\) represent, respectively, the coefficient of attenuation and waves’ speed. For the existence of waves, the real part of phase velocity \(c\) must be non-negative i.e., \({\text{Re}} \left( c \right) \ge 0\), where “\({\text{Re}}\)” denotes the real part. For the undamped time-harmonic wave waves, the imaginary part of the phase velocity \(c\) must be zero i.e., \({\text{Im}} \left( c \right) = 0\), where “\({\text{Im}}\)” denotes the imaginary part. Also, for the damped waves, the imaginary part of the phase velocity \(c\) must be negative i.e., \({\text{Im}} \left( c \right) < 0\). Five real roots of the secular Eq. (46) correspond to the propagation speeds of the elastic longitudinal waves, elastic shear waves, void-volume fraction variation waves (V-mode), and thermal waves for the solid medium as well as one compressional wave for each liquid layer. A program in MatLab software has been written to solve the Eq. (30) and the secular Eq. (46) to find the phase velocity, attenuation coefficient, etc. with the aid of the functional iteration method, and the which yields

$$V = \frac{1}{{{\text{Re}} \left( \xi \right)}},\,\,Q = \omega {\text{Im}} \left( \xi \right).$$
(71)

Specific Damping Capacity

In a stress cycle of the specimen, while strain is maximal, the rate at which energy dissipates in a system is named as a specific loss or specific damping capacity and can be measured for a stress cycle without any assumptions being made related to the nature of internal friction. The specific loss for the sinusoidal plane wave of small amplitude is given by

$$SL = \left| {\frac{\Delta W}{W}} \right| = 4\pi \left| {\frac{{{\text{Im}} (\xi )}}{{{\text{Re}} \left( \xi \right)}}} \right| = 4\pi \left| {\frac{VQ}{\omega }} \right|.$$
(72)

Penetration Depth

The penetration depth of the surface waves is typically taken to be the depth at which the amplitude of the wave is attenuated to \(e^{ - 1}\) of its value at the surface. The characteristic penetration depth is about \(0.4\lambda^{ * }\) for the Rayleigh waves with wavelength \(\lambda^{ * }\). The main point of difference between Rayleigh waves and Lamb waves is that Rayleigh waves penetrate only up to one full wavelength while Lamb waves penetrate and affect entire plate thickness. The penetration depth is given by

$$PD = \frac{1}{{\left| {{\text{Im}} (\xi )} \right|}} = \frac{1}{\left| Q \right|},$$
(73)

where \({\text{Re}} \left( \xi \right)\) and \({\text{Im}} \left( \xi \right)\) represent the real and imaginary part of the \(\xi\).

Numerical Study

For the numerical findings, the solid plate has been supposed to be made up of magnesium crystal and the bordered layers have been supposed to be of water. The values of relevant parameters, following Pathania and Dhiman [23] are

$$\rho = 1.74 \times 10^{3} Kgm^{ - 3} ,\,\,\rho_{L} = 1000Kgm^{ - 3} ,\,\,\lambda = 2.17 \times 10^{10} Nm^{ - 2} ,\,\,\lambda_{L} = 2140Nm^{ - 2} ,$$
$$\,\,\mu = 1.639 \times 10^{10} Nm^{ - 2} ,\,T_{0} = 298K,\,\,K = 1.7 \times 10^{2} Wm^{ - 1} K^{ - 1} ,\,\,C_{e} = 1.04 \times 10^{3} JKg^{ - 1} K^{ - 1} ,\,$$
$$\,\,\alpha^{ * } = 3.688 \times 10^{ - 5} N,\,\beta = 2.68 \times 10^{6} Nm^{ - 2} K^{ - 1} ,\,\,m^{ * } = 2.0 \times 10^{6} Nm^{ - 2} K^{ - 1} ,\,\,\chi = 1.753 \times 10^{ - 15} m^{2} ,$$
$$\,\xi_{1} = 1.475 \times 10^{10} Nm^{ - 2} ,\,\,\xi_{2} = 1.475 \times 10^{10} Nsm^{ - 2} ,\,\,b = 1.13849 \times 10^{10} Nm^{ - 2} ,\,\,\,\omega^{*} = 3.33 \times 10^{11} s^{ - 1} .$$

For the longitudinal and flexural families of the wave for the different modes’ values n, the effect of wavenumber on the phase velocity has been depicted in Fig. 4. For the fundamental longitudinal mode, the phase velocity of Lamb-type waves is dispersionless and attains its value close to thermo-poroelastic Rayleigh wave velocity. Phase velocity for the fundamental flexural mode \(\left( {A_{0} } \right)\) has a small value for a low wavenumber value but as the wavenumber value increases, it first increases gradually and then eventually becomes steady and approaches the Rayleigh wave velocity at higher values of wavenumber.

Fig. 4
figure 4

Effect of wavenumber on the phase velocity

Full size image

Each optical mode (n > 0) is dispersive and at a small value of wave number, the phase velocity is high which follows with a decline in its value up to the arrival of steady-state as the wavenumber increases. This approaches Rayleigh wave velocity because, at such a steady state, the vibrational energy primarily travels through the liquid–solid interface rather than the interior of the plate. A similar type of result has also been obtained by Sharma and Pathania [30], Kaur [12], and Pathania and Dhiman [23].

Figure 5 presents the effect of wavenumber on the coefficient of attenuation for the flexural modes. The coefficient of attenuation has a negligible value for the fundamental mode (n = 0). For the optical modes (n > 0), the attenuation coefficient attains zero value for the small value of the wavenumber which increases as the wavenumber increases and then decreases after reaching its saturation point, then, it repeats this trend taking different magnitude values of wavenumber. The attenuation coefficient becomes large at some fixed wavenumbers because of the easy dispersion of waves due to the existence of voids present in the material. For n = 1, it attains the largest peak value. The combined effect of voids, thermal parameters, and liquid results in the suppression of sinusoidal behavior with a significant decrease in the magnitude of profile deviations in this range of wavenumbers. Similar trends have been obtained for the longitudinal mode.

Fig. 5
figure 5

Effect of wavenumber on the attenuation coefficient

Full size image

In Fig. 6, the effect of wavenumber on the variation of the specific loss has been presented for the flexural modes. Specific loss has a negligible magnitude value for the fundamental mode (n = 0). For the optical modes (n > 0), the specific loss for the flexural mode attains the large values for the insignificant values of the wavenumber and when the wavenumber takes higher values, it decreases and keeps on decreasing up to a fixed point and then, it begins to increase. Again, as the wavenumber value increases, specific loss decreases but with reduced magnitudes, and like this, alternative increase and decrease repeat. It is observed that there is a negligible effect of voids, thermal parameters, and liquid on the specific loss factor at high wavenumbers. Similar trends have been obtained for the longitudinal mode.

Fig. 6
figure 6

Effect of wavenumber on the specific loss

Full size image

For different values of n, Fig. 7 depicts the effect of the wavenumber on the penetration depth for the flexural modes. It has been noted that for the small values of the wavenumber, the magnitude of penetration depth is small for each mode, which increases with the increase in the wavenumber up to a certain value and then decreases with a further increase in the wavenumber. On further increase in the value of wavenumber, this trend repeats with varying magnitude values of penetration depth. For n = 0, penetration depth attains the maximum value. Similar trends have been obtained for the longitudinal mode.

Fig. 7
figure 7

Effect of wavenumber on the penetration depth

Full size image

For the optical and acoustical modes, Fig. 8 shows the effect of \(h\), i.e., the layer width on the phase velocity for the longitudinal and flexural family of waves. From the behavior of curves for optical modes, it has been observed that the volume of inviscid fluid affects the phase velocity for optical modes i.e., phase velocity for optical modes decreases with the increase in the value of layer width. The damping effect becomes more and more prominent as the layer width increases.

Fig. 8
figure 8

Variation of the phase velocity with the layer width

Full size image

In Fig. 9, the relation between the coefficient of attenuation and layer width has been presented for the longitudinal and flexural family of wave modes. For each mode, the magnitude of the coefficient of attenuation is small if the width of the layer is small as it raises, the coefficient of attenuation also increases until it reaches its peak point and then decreases gradually up to a certain value on a further increase of the values of layer width in the considered range from 0 to 9.

Fig. 9
figure 9

Variation of coefficient of attenuation with the layer width

Full size image

Figure 10 describes the effect of layer width on the specific loss for the longitudinal and flexural wave modes. Specific loss has a negligible magnitude value for the fundamental mode (n = 0). For the optical modes (n > 0), the specific loss is comparatively high for the small value of layer width, which declines at a slow pace as the layer width increases from 0 to 9. In this case, the specific loss decreases with the increase in the value of layer width. Therefore, for more volume of an inviscid fluid, the specific loss must be small.

Fig. 10
figure 10

Variation of the specific loss with the layer width

Full size image

For h = 0.25, 0.50, 0.75, and 1, Fig. 11 presents the effect of the plate thickness on the \(r -\)component of solid displacement for the longitudinal mode. The minimum value of \(u_{sy}\) exists at the plate surface while the maximum one is at the center. It is shown that the displacement is in direct relation with the layer width because the amplitude of the radial component of displacement increases parallelly when the layer width value shifts from 0.25 to 1. The attributes of \(\phi_{sy} ,\,w_{asy} \,\,\) and \(T_{sy}\) have been found similar to the \(u_{sy}\) but with different magnitude values.

Fig. 11
figure 11

Variation of the solid displacement \(u_{sy}\) with the plate thickness

Full size image

For h = 0.25, 0.50, 0.75, and 1, Fig. 12 has been portrayed showing the graph between the \(r -\)component of the solid displacement for the flexural mode and the plate thickness. On the horizontal line going through the origin \(O\) (see Fig. 1), \(u_{sy}\) is zero while at \(z = \pm d\), while it is very large. The behavior of \(w_{sy} ,\,\,\phi_{asy}\) and \(T_{asy}\) has been found similar to the \(u_{asy}\) but with different magnitude values. Here, contrary to the longitudinal case, the amplitude of displacement attains the maximum value at the liquid–solid interface, and at the center, it reduces to zero. From Figs. 11 and 12, it can be inferred that the magnitude values for the flexural mode have been dominated by those for the longitudinal mode. Similar results have been obtained by Sharma and Pathania [30] and Pathania and Dhiman [23].

Fig. 12
figure 12

Variation of the solid displacement \(u_{asy}\) with the plate thickness

Full size image

Figure 13 exhibits the impact of plate thickness on the radial component of liquid displacement \(\left( {u_{{L_{1} }} } \right)\) for the varying widths of the liquid layer. For \(h = 0.25\), the magnitude of liquid displacement \(u_{{L_{1} }}\) is almost negligible. As the layer width increases from 0.25 to 1, the corresponding increase in the liquid displacement \(u_{{L_{1} }}\) has been observed from the curved lines plotted in Fig. 13.

Fig. 13
figure 13

Variation of the liquid displacement \(u_{{L_{1} }}\) with the plate thickness

Full size image

For h = 0.25, 0.50, 0.75, and 1, the impact of plate thickness value on the \(z -\)component of liquid displacement has been portrayed in Fig. 14 by two-dimensional curves. It has been observed that the \(w_{{L_{1} }}\) has a comparatively lower magnitude for h = 0.25 than the \(w_{{L_{1} }}\) for other values of h, the layer width. Like \(u_{{L_{1} }}\), the amplitude of displacement \(w_{{L_{1} }}\) is proportional to the magnitude value of layer depth.

Fig. 14
figure 14

Variation of the liquid displacement \(w_{{L_{1} }}\) with the plate thickness

Full size image

Summary and Conclusions

In this contribution, circularly crested thermo-poroelastic waves in a thermally conducting, isotropic homogeneous, cylindrical solid plate sandwich-packed by layers of non-viscous fluid using the LS and GL theories have been studied. The frequency equation for Rayleigh–Lamb waves has been obtained for the longitudinal and flexural modes. The special cases of the frequency equation have also been obtained. Some observations/results obtained from the analytical and numerical study have been reported as

  1. (1)

    The transverse horizontal waves (TH-mode) propagate only in the horizontal plane of the plate because their polarization is not modified by eventual reflections and refractions. It is worth noting that these waves travel without being dispersed and attenuated because it remains unaffected by the voids and thermal variation.

  2. (2)

    The guided normal Lamb waves appear in a plate of thickness \(2d\) comparable to the wavelength \(\xi^{ - 1}\), due to the existing coupling between the mechanical longitudinal waves (L-mode), transverse vertical waves (TV-mode), void-volume fraction field motion (V-mode), and thermal waves (T-mode) components.

  3. (3)

    In addition to the waves in the solid plate, one mechanical wave in each liquid layer also exists. Since the shear stresses do not exist in the inviscid liquid, therefore, these waves are dilatational (sound waves) in nature.

  4. (4)

    In thick plate results (\(2d > > > > \xi^{ - 1}\)) in the absence of liquid (\(\rho_{L} \to 0\)), the frequency equation reduces to the same for wave propagation in the thermo-poroelastic semi-infinite solid i.e., Rayleigh waves (cf. Figure 4).

  5. (5)

    For the optical modes, the phase velocity and the specific loss decrease with the increase in either the layer width or wavenumber value. For the fundamental longitudinal modes (n = 0), the phase speed is the function of neither wavenumber nor layer width which means phase velocity curves are non-dispersive in such a case.

  6. (6)

    For the symmetric mode, solid displacement is maximum at the center of the plate whereas the same attains the largest value at the solid–liquid interface for the antisymmetric mode.

The Lamb waves have been used in nondestructive evaluation (NDE) techniques for damage identification in materials. Abundant information regarding damage is encoded in the Lamb waves scattered by that damage, and this paper provides ample information about the behavioral pattern of Lamb wave motion through the homogeneous isotropic thermoelastic plate with voids bordered with inviscid liquid on both sides. The advantage of the present study is that Lamb waves can also be used for nondestructive testing (NDT), sensors, and material characterization.