Robust control with a novel 6-DOF dynamic model of indoor bridge crane for suppressing vertical vibration

Abstract

A new six-degree-of-freedom dynamic model is established to more completely characterize the physical features of a bridge crane. Previous works on this type of crane control system have focused primarily on trajectory tracking and anti-sway of the cargo, but the problem of vertical vibration attenuation is rarely studied. Although this type of vibration has a much smaller amplitude than the other two horizontal vibrations, it has severe negative impacts on system durability due to fatigue failure, energy consumption level, and operational efficiency. In this study, a robust integral sliding mode control algorithm is designed based on Lyapunov and Barbalat criteria to ensure the convergence of the tracking errors to the origin. Consequently, not only does the control law minimize the vertical vibration of cargo, but also it guarantees the conventional working requirements even when the system is influenced by external disturbances. The suitability of the proposed dynamic model and the effectiveness of the control algorithms are investigated by numerical simulations based on the system parameters of a real-work crane. On the one hand, the similarity of physical characteristics of the built model with the actual model can confirm the correctness of the model qualitatively and, on the other hand, through simulation of the system driven by the proposed controller and the traditional PID controller (whose characteristics are quite similar to that of the crane driver) tracking the given reference trajectory. With the influence of noise, the efficiency and feasibility of the whole work can be clearly realized. Therefore, the development of the model-based controller can be a premise for application in industrial crane platforms, especially for systems with high technical requirements.

1 Introduction

Bridge cranes, including overhead cranes [1, 2] and gantry cranes [3, 4], are lifting and handling equipment with three translational directions of cargo movements. Unlike rotary cranes [5,6,7,8,9], bridge cranes are normally harnessed in static working location because of their good stability and high reliability. Controlling such an under-actuated crane is a wide topic that has attracted numerous researchers in recent decades [10]; most of whom have focused on anti-sway and tracking cargo positions [11]. To date, we have not found research addressing how to reduce the vertical oscillation of cargo. This fluctuation, which is derived from the elastic properties of the cable, steel structure, and hoisting equipment, causes a small amplitude but very high wasted energy and jerk forces. Because the angle of the major force (the tension force in the cable) is very close to vertical orientation, this motion shortens the steel construction life, lessens the crane’s productivity, and increases the level of consumed energy. Moreover, horizontal vibrations are relatively easy to suspend using a small external force, such as one applied by auxiliary workers, whereas vertical vibrations can only interfere with the hoist or self-extinguish due to the enormous difference between the cable tension force and the horizontal force.

Actual crane systems undergo many external disturbances, including the impacts of wind and railway connection points, which change the friction coefficient. Furthermore, inaccuracies in the measurement and estimation of the system parameters significantly affect the control quality. Many methods have been proposed and successfully applied to control the under-actuated crane systems, such as proportional–integral–derivative (PID) control, input shaping [12], feedback linearization [2, 13], double-loop control [3, 14], and combined nonlinear controls [15, 16]. So-called sliding mode control [17,18,19] based on Lyapunov stability theory [20,21,22] has been developed and evaluated in numerous studies [11, 23, 24] and has various applications [25] because of its robustness and short finite-time convergence. These advantageous properties make it a high-potential candidate to control bridge cranes.

This study discusses a new control problem of bridge cranes, suppressing the vertical vibration. To this end, we have developed a novel dynamic model with six degrees of freedom (DOF), including three main movements and three unexpected motions of cargo. On the basis of established mathematical dynamics, a proper integral sliding mode controller (ISMC), which satisfies the working conditions while overcoming the disturbances’ influences, is desired to control the system. Numerical simulations are given in Sects. 2 and 3 to investigate the accuracy of the dynamic model and the feasibility of the controller.

The fundamental contributions of this work are:

• 1. This study provides the analyses of the effects of the cargo's vertical vibrations based on the operational characteristics of a real overhead crane. Subsequently, an approach to minimizing this type of oscillation by adopting robust nonlinear control is proposed.

• 2. Unlike previous crane researches which only dealt with up to 5-DOF dynamic models, a new 6-DOF model for complete crane dynamics is used to handle the mentioned control issue.

• 3. Applying stable and robust SMC not only guarantees cargo position tracking conditions, but also minimizes unwanted fluctuations. We hope this study can provide a fundamental idea for further research into more effective controllers and approaches in the future for this type of crane.

2 Nonlinear 6-DOF dynamic model

2.1 System description

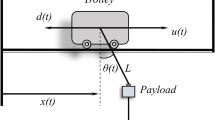
The physical model of an under-actuated indoor bridge crane is illustrated in Fig. 1. The novel system has six-DOF corresponding to six generalized coordinates, specifically the trolley position along the girder x(t), the angle of the hoist drum,$\varphi \left( t \right)$, the displacement of the bridge along the rail y(t) in the global frame Ox₀y₀z₀, the swing motions of the cargo in the O_xz and O_yz planes, and the vertical oscillation. Here, the first three generalized coordinates, x(t), y(t), and $\varphi \left( t \right)$ are considered as actuated states, and the last three, $\theta$_x(t), $\theta$_y(t), and $\theta$(t), are un-actuated.

Fig. 1

Physical model of a bridge crane

In a real crane system, the vertical displacement of the cargo is mainly decided by the rotation angle of the hoist drum. But, there exists vertically fluctuating oscillation caused by the elasticity and deformation of the cables, rails, joints or bearings, and bridge frames. This oscillation is much smaller than other vibrations, but its impact on the energy consumption and life span of the system is significant, especially during the lifting process and when the two horizontal sways have large amplitudes. By proposing a new generalized coordinate, $\delta$(t), which represents the vertical fluctuation of the cargo, this study develops a dynamic model-based control law that minimizes the mentioned oscillation as well as inherits the characteristics of controllers of the previous researches [1, 2].

The actuated movements generate the precise position of the cargo inside the working space; in contrast, the un-actuated motions are undesired. The major objectives of control are to satisfy the tracking conditions and shorten the phase and amplitude of oscillations. The system consists of three masses: the cargo, the trolley with hoist, and the bridge, which are denoted as m_c, m_t, and m_b, respectively. Depending on the particular working conditions and type of handled cargo, the carrying equipment is adjusted and its mass can be significant. In these cases, both the masses of the cargo and the lifting equipment are related to m_c. Here, $\Delta \delta$ denotes the initial elongation, and k_e refers to the equivalent elastic coefficient. $J_{d}$, and $r_{d}$ represent the moment of inertia and radius of the payload-hoisting drum. The damping coefficients $b_{m} ,\,b_{b} ,\,b_{t}$, and $b_{r}$ represent the friction forces associated with movements of the hoisting mechanism, bridge, trolley, and the friction inside wire rope, respectively. $\tau_{1}$, $\tau_{2}$, and $\tau_{3}$ are active control inputs generated by the trolley, bridge moving, and payload-lifting mechanisms, respectively.

2.2 Dynamic modeling

In the scope of this research, the investigated moving range of cargo in an indoor bridge crane is small compared with the crane’s whole operating range. Thus, the dynamic model is established with the following assumptions:

• The movement of cargo in the y-direction (along the cable drum) caused by lifting the load is ignored.

• The ratio transmission of the cable pulley is 1.

• The deformation and horizontal vibration of the steel structure are much less than those in the vertical direction, and the equivalent elastic coefficient, $k_{e}$, is considered to be unchanged.

• The cargo is considered to be a mass point, and the rotational motions around its axes are ignored.

The kinetic energy of the system, which considers the motions of the cargo in the working space, is computed as:

$$T = T_{c} + T_{t} + T_{b} + T_{r} ,$$

(1)

where $T_{t} = 0.5m_{t} \dot{x}^{2}$ and $T_{b} = 0.5m_{b} \dot{y}^{2}$ are the kinetic energies of the trolley and the entire bridge crane (including trolley). $T_{r} = 0.5J_{d} \dot{\varphi }^{2}$ is the kinetic energy of the rotary motion of the payload-hoisting drum. The kinetic energy $T_{c}$ of the cargo is given as:

$$T_{c} = T_{cx} + T_{cy} + T_{cz} ,$$

(2)

where $T_{cx}$, $T_{cy}$, and $T_{cz}$ are, respectively, the kinetic energy corresponding to the motions in x, y, and z directions that are computed as

$$T_{cx} = \frac{{m_{c} }}{2}\left( {\dot{x} + \left( \begin{gathered} \left( {\dot{\delta } + r_{d} (\dot{\varphi } + \dot{\theta }_{x} )} \right)\sin \theta_{x} \hfill \\ + \left( {\delta + \Delta \delta + r_{d} \theta_{x} + r_{d} \varphi } \right) \hfill \\ \times \dot{\theta }_{x} \cos \theta_{x} - r_{d} \dot{\theta }_{x} \sin \theta_{x} \hfill \\ \end{gathered} \right)} \right)^{2} ,$$

$$T_{cy} = \frac{{m_{c} }}{2}\left( {\begin{array}{*{20}l} {\dot{y} + \left( {\dot{\delta } + r_{d} (\dot{\varphi } + \dot{\theta }_{x} )} \right)\cos \theta_{x} \sin \theta_{y} } \hfill \\ { + \left( {\delta + \Delta \delta + r_{d} \theta_{x} + r_{d} \varphi } \right)} \hfill \\ { \times \left( {\dot{\theta }_{y} \cos \theta_{x} \cos \theta_{y} - \dot{\theta }_{x} \sin \theta_{x} \sin \theta_{y} } \right) + } \hfill \\ \end{array} } \right)^{2} ,$$

$$T_{cz} = \frac{{m_{c} }}{2}\left( {\begin{array}{*{20}l} {\left( {\delta + \Delta \delta + r_{d} \theta_{x} + r_{d} \varphi } \right)\left( {\dot{\theta }_{x} \sin \theta_{x} \cos \theta_{y} } \right)} \hfill \\ { + r_{d} \dot{\theta }_{x} \cos \theta_{x} - \cos \theta_{x} \cos \theta_{y} \left( {\dot{\delta } + r_{d} (\dot{\varphi } + \dot{\theta }_{x} )} \right)} \hfill \\ { + \left( {r_{d} \theta_{x} + \delta + \Delta \delta + r_{d} \varphi } \right)\dot{\theta }_{y} \cos \theta_{x} \sin \theta_{y} } \hfill \\ \end{array} } \right)^{2} .$$

It is noted that in case the cargo was hung directly on the hoist drum, the length of the rope is not a fixed constant but it changes a small amount, $r_{d} \theta_{x}$, depending on the swing angle in xOz plane even when $\varphi$ is a constant. At the same time, this change also makes the cargo move up and down a distance, $r_{d} \cos \theta_{y} \sin \theta_{x}$. Therefore, potential energy is given as:

$$\begin{aligned} \Pi & = r_{d} m_{c} g\cos \theta_{y} \sin \theta_{x} + \frac{1}{2}k_{e} \left( \delta \right)^{2} \\ & \quad - m_{c} g(r_{d} \varphi + r_{d} \theta_{x} + \delta + \Delta \delta )\cos \theta_{x} \cos \theta_{y} . \\ \end{aligned}$$

(3)

The expenditure energy is formulated as:

$$\Phi = \frac{1}{2}b_{m} \dot{\varphi }^{2} + \frac{1}{2}b_{r} \dot{\delta }^{2} + \frac{1}{2}b_{t} \dot{x}^{2} + \frac{1}{2}b_{b} \dot{y}^{2} .$$

(4)

The physical features of the indoor bridge crane are characterized for full-state variables ${{\varvec{\upchi}}}_{s} = \left[ {\begin{array}{*{20}c} x & y & \varphi & {\theta_{x} } & {\theta_{y} } & \delta \\ \end{array} } \right]^{T}$. The calculations are based on the Euler–Lagrange equation:

$$\frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{\chi }_{i} }}} \right) - \frac{\partial T}{{\partial \chi_{i} }} = - \frac{\partial \Pi }{{\partial \chi_{i} }} - \frac{\partial \Phi }{{\partial \dot{\chi }_{i} }} + Q_{i} \,\,\,\,\,\,\left( {i = \left\{ {1,2, \ldots ,6} \right\}} \right),$$

(5)

where $Q_{i}$ is the force corresponding to the generalized coordinates $\chi_{i}$.

The system dynamics are provided in matrix form as:

$${\mathbf{M(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{s} {\mathbf{ + B\dot{\chi }}}_{s} {\mathbf{ + C(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\chi }}_{s} {\mathbf{ + G(\chi }}_{s} {\mathbf{) = U}},$$

(6)

where ${\dot{\mathbf{\chi }}}_{s}$ and ${\mathbf{\ddot{\chi }}}_{s}$ are the first-order and second-order time derivatives of the system states, respectively; the input vector ${\mathbf{U}} = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{s} } & 0 & 0 & 0 \\ \end{array} } \right]^{T}$ with ${\mathbf{U}}_{s} = \left[ {\begin{array}{*{20}c} {\tau_{1} } & {\tau_{2} } & {\tau_{3} } \\ \end{array} } \right]^{T}$; the mass matrix ${\mathbf{M(\chi }}_{s} {\mathbf{)}} = {\mathbf{M}}^{T} {\mathbf{(\chi }}_{s} {\mathbf{)}}$ is positive definite (PD); ${\mathbf{C(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$ represents a Coriolis and centrifugal matrix; ${\mathbf{B}}$ is a damping coefficient matrix; and ${\mathbf{G(\chi }}_{s} {\mathbf{)}}$ denotes a gravity vector. The equations representing these matrices are provided as:

$${\mathbf{M(\chi }}_{s} {\mathbf{) = }}\left[ {\begin{array}{*{20}l} {m_{11} } \hfill & 0 \hfill & {m_{13} } \hfill & {m_{14} } \hfill & 0 \hfill & {m_{16} } \hfill \\ 0 \hfill & {m_{22} } \hfill & {m_{23} } \hfill & {m_{24} } \hfill & {m_{25} } \hfill & {m_{26} } \hfill \\ {m_{31} } \hfill & {m_{32} } \hfill & {m_{33} } \hfill & {m_{34} } \hfill & {m_{35} } \hfill & {m_{36} } \hfill \\ {m_{41} } \hfill & {m_{42} } \hfill & {m_{43} } \hfill & {m_{44} } \hfill & {m_{45} } \hfill & {m_{46} } \hfill \\ 0 \hfill & {m_{52} } \hfill & {m_{53} } \hfill & {m_{54} } \hfill & {m_{55} } \hfill & {m_{56} } \hfill \\ {m_{61} } \hfill & {m_{62} } \hfill & {m_{63} } \hfill & {m_{64} } \hfill & {m_{65} } \hfill & {m_{66} } \hfill \\ \end{array} } \right],$$

$${\mathbf{B}} = \left[ {\begin{array}{*{20}l} {b_{11} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {b_{22} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {b_{33} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {b_{44} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right].$$

$${\mathbf{C(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{) = }}\left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {c_{13} } \hfill & 0 \hfill & {c_{15} } \hfill & {c_{16} } \hfill \\ 0 \hfill & 0 \hfill & {c_{23} } \hfill & {c_{24} } \hfill & {c_{25} } \hfill & {c_{26} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {c_{34} } \hfill & {c_{35} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {c_{43} } \hfill & {c_{44} } \hfill & {c_{45} } \hfill & {c_{46} } \hfill \\ 0 \hfill & 0 \hfill & {c_{53} } \hfill & {c_{54} } \hfill & {c_{55} } \hfill & {c_{56} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {c_{64} } \hfill & {c_{65} } \hfill & 0 \hfill \\ \end{array} } \right],\quad {\mathbf{G(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ {g_{3} } \hfill \\ {g_{4} } \hfill \\ {g_{5} } \hfill \\ {g_{6} } \hfill \\ \end{array} } \right],$$

The elements of ${\mathbf{M(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{C(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, ${\mathbf{B}}$, and ${\mathbf{G(\chi }}_{s} {\mathbf{)}}$ are provided in the “Appendix”.

2.3 Dynamic simulations

In this study, both the dynamic characteristics and the efficiency of the controller are investigated through simulations in Simulink, a MATLAB-based graphical programming environment for modeling, simulating, and analyzing multidomain dynamical systems. Understandably, they can allow control of the system in the real-time, complex, or frequency domains. On the other hand, they can also connect to the workspace, MATLAB 3D simulation, even allow control of realistic robot models.

The primary interface of Simulink is a graphical block diagramming tool and a customizable set of block libraries. Simulink offers tight integration with the rest of the MATLAB environment and can either drive MATLAB or be scripted from such an environment. The differential equations in Simulink are solved by numerical methods, such as Runge–Kutta, Bogacki–Shampine, and backward Euler. Simulink can also easily extract graphs for simulations of dynamic systems in real time by connecting signal channels with output windows (Scope).

From Simulink, the data can be easily collected to the workspace directly for processing and analyzing. Additionally, Simulink also provides numerous available libraries or blocks for data processing.

In this section, numerical simulations are implemented to investigate the physical and dynamical characteristics of the entire system, which experiences different external forces. Through observing the variation of physical parameters under the influence of different conditions, it is possible to conclude with relative accuracy the reliability and accuracy of the qualitative dynamics model. This is important because it is directly related to the validation of the controller designed in the following Section. To end this, a practical indoor bridge crane, a 5-ton R&M QX modular double-girder crane from Ace Industries, Inc, was utilized. The system parameters are provided as: $m_{c}$ = 5,000 kg, $m_{b}$ = 2,316.5 kg, $m_{t}$ = 371.9 kg, $r_{d}$ = 0.31 m, $J_{d}$ = 180 kg m², $b_{t}$ = 310 Nm/s, $b_{b}$ = 350 Nm/s, $b_{m}$ = 170 Nm/s, $b_{r}$ = 260 Nm/s, $g$ = 9.81 m/s², $k_{e}$ = 300,000 N/m, and $\Delta \delta$ = 0.01 m.

The dynamical simulations were carried out in two cases to characterize the crane features, as illustrated in Figs. 2, 3, 4, 5 and 6.

Fig. 2

Actuated states with initial values of angles and axial vibration

Fig. 3

Oscillations with initial values of angles and axial vibration

Fig. 4

The pulse input forces given to the system

Fig. 5

Actuated states with the pulses of actuated forces

Fig. 6

Oscillations with the pulses of actuated forces

In the first case, the kinematic properties of the system with the influences of the initial values of the cable angle and the vertical vibration of cargo are simulated in Figs. 2 and 4.

The initial values of the state variables are selected from their working ranges, such as the working spans and the lifting height. For the first case of simulation, these values are chosen as $x = 5\,(m)$, $y = 7\,(m)$, $\varphi = 5\,(rad)$,$\theta_{x} = 7^{ \circ }$, $\theta_{y} = 5^{ \circ }$, $\delta$ = $5 \times 10^{ - 3}$ m (Fig. 3). This simulates the case where the cargo is pulled vertically in two vertical planes (Oxz, Oyz), and the cable is stretched from its equilibrium position (similar to the case where the motors of all mechanisms have just stopped moving). The purpose of this process is to investigate the effects of deflection angles and cable extensions on crane motion.

The initial un-actuated states cause the vibrations (Fig. 3) and variations in the actuated state variables (Fig. 2). The trolley moved from the position of 2.5–2.75 m in a period of 15 s because the cargo was much heavier than the mass of the trolley. The energy of the gravity potential was largely transformed into kinetic energy for movement of the trolley, and the vibration of the cargo, $\theta_{x}$, occurred for a short period of approximately 5 s (Fig. 3a). The swing of the cargo $\theta_{y}$ occurred for 8 s (Fig. 3c) and resulted in oscillation of the bridge displacement around the position of 7 m (Fig. 2c).

With the effects of the two swings and the elasticity of the cable, the complicated vertical vibration is illustrated in Fig. 3e.

In the second case, Fig. 4 describes the pulses of the force inputs, which affected the crane, and the system response is depicted in Figs. 5 and 6. All initial values of the un-actuated states were set to zero, with the pulses of the input exciting forces, playing almost the same role as the forces $\tau_{1} ,\tau_{2} ,\tau_{3}$ acting on the actuated part of the system, given in the period from 4 to 6 s (Fig. 4). The trolley and bridge were moved from the positions of 5 m and 7 m to 7 m and 7.8 m, respectively. The pulses generated the vibration of the cargo $\theta_{y}$, until the end of the survey time (Fig. 6c). Meanwhile, the angle $\theta_{x}$ was both deflected and made to vibrate due to complex motions, as shown in Fig. 6a. The vertical vibration is illustrated in Fig. 6e.

The vertical vibrations of the cargo appeared in both simulation cases, but the phase and amplitude of this vibration were much larger when the hoisting mechanism suddenly started.

3 Controller development

3.1 Nonlinear controller design

To design an integrated controller that satisfies the overall tracking conditions, the system dynamic was divided into actuated and un-actuated parts by decoupling as follows:

$$\begin{aligned} & {\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{a} {\mathbf{ + M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{u} {\mathbf{ + B}}_{11} {\dot{\mathbf{\chi }}}_{a} \\ & \quad {\mathbf{ + C}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{a} {\mathbf{ + C}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} {\mathbf{ + G}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{) = U}}_{s} , \\ \end{aligned}$$

(7)

$$\begin{aligned} & {\mathbf{M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{a} {\mathbf{ + M}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{u} {\mathbf{ + B}}_{22} {\dot{\mathbf{\chi }}}_{u} \\ & \quad {\mathbf{ + C}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{a} {\mathbf{ + C}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} {\mathbf{ + G}}_{2} {\mathbf{(\chi }}_{s} {\mathbf{) = }}0, \\ \end{aligned}$$

(8)

where ${{\varvec{\upchi}}}_{a} = \left[ {\begin{array}{*{20}c} x & y & \varphi \\ \end{array} } \right]^{T}$ is the actuated state vector; ${{\varvec{\upchi}}}_{u} = \left[ {\begin{array}{*{20}c} {\theta_{x} } & {\theta_{y} } & \delta \\ \end{array} } \right]^{T}$ is the un-actuated state; and the block matrices $\,{\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{M}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{B}}_{11}$, ${\mathbf{B}}_{22}$, ${\mathbf{C}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, ${\mathbf{C}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, ${\mathbf{C}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, ${\mathbf{C}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, ${\mathbf{G}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{)}}$, and ${\mathbf{G}}_{2} {\mathbf{(\chi }}_{s} {\mathbf{)}}$ are given as: $\,{\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}l} {m_{11} } \hfill & 0 \hfill & {m_{13} } \hfill \\ 0 \hfill & {m_{22} } \hfill & {m_{23} } \hfill \\ {m_{31} } \hfill & {m_{32} } \hfill & {m_{33} } \hfill \\ \end{array} } \right],\,{\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}l} {m_{14} } \hfill & 0 \hfill & {m_{16} } \hfill \\ {m_{24} } \hfill & {m_{25} } \hfill & {m_{26} } \hfill \\ {m_{34} } \hfill & {m_{35} } \hfill & {m_{36} } \hfill \\ \end{array} } \right],\,$

$${\mathbf{M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}l} {m_{41} } \hfill & {m_{42} } \hfill & {m_{43} } \hfill \\ 0 \hfill & {m_{52} } \hfill & {m_{53} } \hfill \\ {m_{61} } \hfill & {m_{62} } \hfill & {m_{63} } \hfill \\ \end{array} } \right],\,\,{\mathbf{M}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}l} {m_{44} } \hfill & {m_{45} } \hfill & {m_{46} } \hfill \\ {m_{54} } \hfill & {m_{55} } \hfill & {m_{56} } \hfill \\ {m_{64} } \hfill & {m_{65} } \hfill & {m_{66} } \hfill \\ \end{array} } \right],$$

$${\mathbf{B}}_{11} = \left[ {\begin{array}{*{20}l} {b_{11} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {b_{22} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {b_{33} } \hfill \\ \end{array} } \right],\;{\mathbf{B}}_{22} = \left[ {\begin{array}{*{20}l} {b_{44} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]$$

$${\mathbf{C}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{) = }}\left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {c_{13} } \hfill \\ 0 \hfill & 0 \hfill & {c_{23} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\quad {\mathbf{C}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{) = }}\left[ {\begin{array}{*{20}l} 0 \hfill & {c_{15} } \hfill & {c_{16} } \hfill \\ {c_{24} } \hfill & {c_{25} } \hfill & {c_{26} } \hfill \\ {c_{34} } \hfill & {c_{35} } \hfill & 0 \hfill \\ \end{array} } \right],$$

$${\mathbf{C}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{) = }}\left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {c_{43} } \hfill \\ 0 \hfill & 0 \hfill & {c_{53} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right],\;{\mathbf{C}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{) = }}\left[ {\begin{array}{*{20}l} {c_{44} } \hfill & {c_{45} } \hfill & {c_{46} } \hfill \\ {c_{54} } \hfill & {c_{55} } \hfill & {c_{56} } \hfill \\ {c_{64} } \hfill & {c_{65} } \hfill & 0 \hfill \\ \end{array} } \right],$$

$${\mathbf{G}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}c} 0 & 0 & {g_{3} } \\ \end{array} } \right]^{T} ,\quad {\mathbf{G}}_{2} {\mathbf{(\chi }}_{s} {\mathbf{)}} = \left[ {\begin{array}{*{20}c} {g_{4} } & {g_{5} } & {g_{3} } \\ \end{array} } \right]^{T} .$$

The integral sliding surface ${{\varvec{\upzeta}}}_{s} \left( t \right) = \left[ {\begin{array}{*{20}c} {\zeta_{\alpha } \left( t \right)} & {\zeta_{\beta } \left( t \right)} & {\zeta_{\gamma } \left( t \right)} \\ \end{array} } \right]^{T}$ is defined as:

$${{\varvec{\upzeta}}}_{s} \left( t \right) = {\mathbf{\dot{\tilde{\chi }}}}_{a} + {{\varvec{\upmu}}}_{1} {\tilde{\mathbf{\chi }}}_{a} + {{\varvec{\upmu}}}_{2} \int\limits_{0}^{\tau } {{\tilde{\mathbf{\chi }}}_{a} } {\text{d}}t + {{\varvec{\upmu}}}_{3} {\tilde{\mathbf{\chi }}}_{u} + {{\varvec{\upmu}}}_{4} \int\limits_{0}^{\tau } {{\tilde{\mathbf{\chi }}}_{u} } {\text{d}}t,$$

(9)

where the matrices of the controller coefficients are: ${{\varvec{\upmu}}}_{1} = {\text{diag}}\left( {\mu_{1a} ,\,\mu_{1b} ,\,\mu_{1c} } \right),$${{\varvec{\upmu}}}_{2} = {\text{diag}}\left( {\mu_{2a} ,\,\mu_{2b} ,\,\mu_{2c} } \right),$${{\varvec{\upmu}}}_{3} = {\text{diag}}\left( {\mu_{3a} ,\,\mu_{3b} ,\,\mu_{3c} } \right),$ ${{\varvec{\upmu}}}_{4} = {\text{diag}}\left( {\mu_{4a} ,\,\mu_{4b} ,\,\mu_{4c} } \right)$ and $\mu_{ia} ,\,\mu_{ib} ,\,\mu_{ic} > 0\,\,\left( {i = \left\{ {1,\,2,\,3,\,4} \right\}} \right)$. ${\tilde{\mathbf{\chi }}}_{a} = {{\varvec{\upchi}}}_{a} - {{\varvec{\upchi}}}_{at}$ and ${\tilde{\mathbf{\chi }}}_{u} = {{\varvec{\upchi}}}_{u} - {{\varvec{\upchi}}}_{ut}$ are the tracking error vectors, with the target value vectors ${{\varvec{\upchi}}}_{at}$, ${{\varvec{\upchi}}}_{ut}$ being ${{\varvec{\upchi}}}_{at} = \left[ {\begin{array}{*{20}c} {x_{t} } & {y_{t} } & {\varphi_{t} } \\ \end{array} } \right]^{T}$ and ${{\varvec{\upchi}}}_{ut} = \left[ {\begin{array}{*{20}c} {\theta_{xt} } & {\theta_{yt} } & {\delta_{t} } \\ \end{array} } \right]^{T}$. Here, $x_{t} ,y_{t} ,\varphi_{t} ,\theta_{xt} ,\theta_{yt} ,\delta_{t}$ are the reference values of these corresponding state variables, and the states of vibration should converge to zero.

Lemma 1

The control law is designed as follows (10) will satisfy the sliding condition, and the integral second-order sliding surface is asymptotically stable since ${{\varvec{\uplambda}}} = {\text{diag}}\left( {\lambda_{a} ,\,\lambda_{b} ,\,\lambda_{c} } \right)$ is PD. Here, $\lambda_{a} ,\,\lambda_{b} ,\,\lambda_{c}$ belonging to the diagonal matrix ${{\varvec{\uplambda}}}$ are the controller coefficients. Here, the control signal is computed as.

$${\mathbf{U}}_{s} = \left\{ {\begin{array}{*{20}l} { - {\mathbf{\lambda sgn}}({{\varvec{\upzeta}}}_{s} ) + {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)\ddot{\chi }}}_{at} - {\mathbf{G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}} \hfill \\ { - {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)\mu }}_{1} \int\limits_{0}^{\tau } {\left( {{{\varvec{\upmu}}}_{2} {\tilde{\mathbf{\chi }}}_{a} + {{\varvec{\upmu}}}_{4} {\tilde{\mathbf{\chi }}}_{u} } \right)} {\text{d}}t} \hfill \\ { - {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)}}\left( {2{{\varvec{\upmu}}}_{1} + {{\varvec{\upmu}}}_{2} + {{\varvec{\upmu}}}_{1}^{T} {{\varvec{\upmu}}}_{1} } \right){\tilde{\mathbf{\chi }}}_{a} } \hfill \\ { - {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)}}\left( {{{\varvec{\upmu}}}_{3} + {{\varvec{\upmu}}}_{4} + {{\varvec{\upmu}}}_{1} {{\varvec{\upmu}}}_{3} } \right){\tilde{\mathbf{\chi }}}_{u} + {\mathbf{C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)\dot{\chi }}}_{a} } \hfill \\ \end{array} } \right\},$$

(10)

The matrices ${\mathbf{M}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{C}}_{2\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, and ${\mathbf{G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}$ in control law (10) are formulated as follows:

$${\mathbf{M}}_{\Sigma } \left( {{{\varvec{\upchi}}}_{s} } \right) = {\mathbf{M}}_{11} \left( {{{\varvec{\upchi}}}_{s} } \right) - {\mathbf{M}}_{12} \left( {{{\varvec{\upchi}}}_{s} } \right){\mathbf{M}}_{22}^{ - 1} \left( {{{\varvec{\upchi}}}_{s} } \right){\mathbf{M}}_{21} \left( {{{\varvec{\upchi}}}_{s} } \right)$$

(11)

$$\begin{aligned} {\mathbf{C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} & = {\mathbf{ + B}}_{11} {\mathbf{ + C}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}} \\ & \quad - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)C}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}, \\ \end{aligned}$$

(12)

$$\begin{aligned} {\mathbf{C}}_{2\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}} & = {\mathbf{ + C}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}} - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)B}}_{22} \\ & \quad - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)C}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}, \\ \end{aligned}$$

(13)

$${\mathbf{G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} = {\mathbf{ + G}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{)}} - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)G}}_{2} {\mathbf{(\chi }}_{s} {\mathbf{)}}.$$

(14)

The vector of sign function ${\mathbf{sgn}}({{\varvec{\upzeta}}}_{s} )$ is defined as:

$${\mathbf{sgn}}({{\varvec{\upzeta}}}_{s} ) = \left[ {\begin{array}{*{20}c} {{\text{sgn}} \left( {\zeta_{\alpha } \left( t \right)} \right)} & {{\text{sgn}} \left( {\zeta_{\beta } \left( t \right)} \right)} & {{\text{sgn}} \left( {\zeta_{\gamma } \left( t \right)} \right)} \\ \end{array} } \right]^{T} .$$

(15)

and

$${\text{sgn}} \left( {\zeta \left( t \right)} \right) = \left\{ {\begin{array}{*{20}l} { + 1} \hfill & {{\text{if}}\,\,\zeta \left( t \right) > 0} \hfill \\ 0 \hfill & {{\text{if}}\,\,\zeta \left( t \right) = 0} \hfill \\ { - 1} \hfill & {{\text{if}}\,\,\zeta \left( t \right) < 0} \hfill \\ \end{array} } \right..$$

(16)

This controller is designed based on some approaches taken in some previous studies such as [26,27,28].

Proof

The Lyapunov candidate function is chosen as follows:

$$\Upsilon \left( t \right) = 0.5{{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\upzeta}}}_{s} \left( t \right).$$

(17)

Differentiating this function with respect to time yields:

$$\dot{\Upsilon }\left( t \right) = {\dot{\mathbf{\zeta }}}_{s}^{T} \left( t \right){{\varvec{\upzeta}}}_{s} \left( t \right).$$

(18)

From the decoupled Eqs. (7) and (8), the mathematical model is inferred as follows:

$${\mathbf{\ddot{\chi }}}_{u} = - {\mathbf{M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}}\left[ \begin{gathered} {\mathbf{M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{a} + {\mathbf{B}}_{22} {\dot{\mathbf{\chi }}}_{u} + {\mathbf{G}}_{2} {\mathbf{(\chi }}_{s} {\mathbf{)}} \hfill \\ + {\mathbf{C}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{a} + {\mathbf{C}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} \hfill \\ \end{gathered} \right],$$

(19)

$$\left\{ {\begin{array}{*{20}l} {\left( {{\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)}} - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)}}} \right){\mathbf{\ddot{\chi }}}_{a} } \hfill \\ { - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}}\left[ {{\mathbf{B}}_{22} + {\mathbf{C}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}} \right]{\dot{\mathbf{\chi }}}_{u} } \hfill \\ { - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}}\left[ {{\mathbf{C}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{a} + {\mathbf{G}}_{2} {\mathbf{(\chi }}_{s} {\mathbf{)}}} \right]} \hfill \\ {{\mathbf{ + B}}_{11} {\dot{\mathbf{\chi }}}_{a} {\mathbf{ + C}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{a} {\mathbf{ + C}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} {\mathbf{ + G}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{)}}} \hfill \\ \end{array} } \right\}{\mathbf{ = U}}_{s} .$$

(20)

Given that the block symmetric matrix ${\mathbf{M}}_{22} {\mathbf{(\chi }}_{s} {\mathbf{)}}$ is PD, the matrix of the component $\left[ {{\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)}} - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)}}} \right]$ is computed as:

$${\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)}} - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)}} = diag\left( {m_{t} ,\,m_{b} ,\,J_{d} } \right).$$

(21)

Set: ${\mathbf{M}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} = {\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)}} - {\mathbf{M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{22}^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)M}}_{21} {\mathbf{(\chi }}_{s} {\mathbf{)}}$.

The masses $m_{t}$, $m_{b}$ and the initial $J_{d}$ are positive, then this diagonal matrix ${\mathbf{M}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} = {\mathbf{M}}_{\Sigma }^{T} {\mathbf{(\chi }}_{s} {\mathbf{)}}$ is PD. Consequently, the second-order time derivatives of the actuated state vectors are computed as:

$$\begin{aligned} {\mathbf{\ddot{\chi }}}_{a} & {\mathbf{ = }} - {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)\dot{\chi }}}_{a} - {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)C}}_{2\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} \\ & \quad + {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} + {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)U}}_{s} \,, \\ \end{aligned}$$

(22)

where ${\mathbf{C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}$, ${\mathbf{C}}_{2\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)}}$, and ${\mathbf{G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}$ are provided as Eqs. (12), (13), and (14), respectively.

From Eqs. (9), (18), (19), (10), and (22), it is calculated that:

$$\dot{\Upsilon }\left( t \right) = \left( { - {{\varvec{\uplambda}}}{\text{sign}}\left( {{{\varvec{\upzeta}}}_{s} \left( t \right)} \right)} \right)^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)\zeta }}_{s} \left( t \right) - {{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\upmu}}}_{1} {{\varvec{\upzeta}}}_{s} \left( t \right).$$

(23)

The sign of function $\dot{\Upsilon }\left( t \right)$ is similar to the function:

$$\dot{\Upsilon }^{*} \left( t \right) = - {{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\uplambda}}}^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)\zeta }}_{s} \left( t \right) - {{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\upmu}}}_{1} {{\varvec{\upzeta}}}_{s} \left( t \right).$$

(24)

The controller coefficient matrix is PD $\left( {{{\varvec{\uplambda}}}^{T} \succ 0} \right)$ because ${{\varvec{\uplambda}}} \succ 0$, and ${\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{s} {\mathbf{)}} \succ 0$. The matrix ${{\varvec{\uplambda}}}^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}}$ is PD $\left( {{{\varvec{\uplambda}}}^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}} \succ 0} \right)$. Then the quadratic functions ${{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\uplambda}}}^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)\zeta }}_{s} \left( t \right)$ and $\,{{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\upmu}}}_{1} {{\varvec{\upzeta}}}_{s} \left( t \right)$ are always positive or equal to zero, and the first-order derivative function $\dot{\Upsilon }^{*} \left( t \right)$ is always non-positive $\left( {\dot{\Upsilon }^{*} \left( t \right) \le 0} \right)$ and $\left( {\dot{\Upsilon }\left( t \right) \le 0} \right)$ since $t \to \infty$. This is based on the fact that ${{\varvec{\upmu}}}_{1}$ is PD. Consequently, $\left( {\Upsilon \left( t \right) \le \Upsilon \left( 0 \right)} \right)$; thus, the sliding surfaces belonging to vector ${{\varvec{\upzeta}}}_{s} \left( t \right)$ are bounded and $\zeta_{\alpha }^{2} \left( t \right),\zeta_{\beta }^{2} \left( t \right),\zeta_{\gamma }^{2} \left( t \right)$ decrease as $t \to \infty$. In this case, the sliding mode surfaces $\zeta_{\alpha }^{{}} \left( t \right),\zeta_{\beta }^{{}} \left( t \right),\zeta_{\gamma }^{{}} \left( t \right)$ are stable in the Lyapunov sense. On the basis of Barbalat’s Lemma [29], the functions $\zeta_{\alpha }^{{}} \left( t \right),\zeta_{\beta }^{{}} \left( t \right),\zeta_{\gamma }^{{}} \left( t \right)$ approach zero $\left( {\zeta_{\alpha }^{{}} \left( t \right) \to 0,\,\zeta_{\beta }^{{}} \left( t \right) \to 0,\,\zeta_{\gamma }^{{}} \left( t \right) \to 0} \right)$. Eventually, the state variables, ${{\varvec{\upchi}}}_{s}$, will be consolidated to their reference values when $t \to \infty$.

This is the end of the proof of Lemma 1□

For an indoor bridge crane, the external disturbances and the internal uncertainties are considered as a composite disturbance, which mostly affects the actuated part and causes inaccuracy in the control process with the increase of vibrations. The time-varying function of the disturbances, ${{\varvec{\updelta}}}_{\alpha } \left( t \right) = \left[ {\begin{array}{*{20}c} {\delta_{\alpha 1} \left( t \right)} & {\delta_{\alpha 2} \left( t \right)} & {\delta_{\alpha 3} \left( t \right)} \\ \end{array} } \right]^{T}$, which directly affect the system, is as follows:

$$\begin{aligned} & {\mathbf{M}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{a} {\mathbf{ + M}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{)\ddot{\chi }}}_{u} {\mathbf{ + B}}_{11} {\dot{\mathbf{\chi }}}_{a} \\ & \quad {\mathbf{ + C}}_{11} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{a} {\mathbf{ + C}}_{12} {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} {\mathbf{ + \tilde{G}}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{) = U}}_{s} , \\ \end{aligned}$$

(25)

where ${\tilde{\mathbf{G}}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{)}} = {\mathbf{G}}_{1} {\mathbf{(\chi }}_{s} {\mathbf{)}} + {{\varvec{\updelta}}}_{\alpha } \left( t \right)$.

Lemma 2

If the time-varying composite function ${{\varvec{\updelta}}}_{\alpha } \left( t \right)$ is bounded $\left| {{{\varvec{\updelta}}}_{\alpha } \left( t \right)} \right| \le {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta } }}_{\alpha } = \left[ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 1} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 2} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 3} } \\ \end{array} } \right]^{T}$, the robustness of the designed controller overcomes the disturbance’s influences. Eventually, the sliding surface is asymptotically stable [26,27,28] and the tracking errors and the un-actuated variables converge to zero.

Proof

On the basis of Eqs. (10), (18), (22), and (25), it is computed that:

$$\dot{\Upsilon }\left( t \right) = \left[ {\begin{array}{*{20}l} { - {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}}\,\left[ {{\mathbf{C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)\dot{\chi }}}_{a} + {\mathbf{C}}_{2\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} - {\mathbf{G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}} \right]} \hfill \\ { + \left\{ {\begin{array}{*{20}l} { - {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)}}\left( {{{\varvec{\upmu}}}_{3} {\mathbf{\dot{\tilde{\chi }}}}_{u} + 2{{\varvec{\upmu}}}_{1} {\mathbf{\dot{\tilde{\chi }}}}_{a} } \right) - {\tilde{\mathbf{G}}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} - {{\varvec{\uplambda}}}sign({{\varvec{\upzeta}}}_{s} )} \hfill \\ { - {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)}}\left[ {\left( {{{\varvec{\upmu}}}_{4} + {{\varvec{\upmu}}}_{1} {{\varvec{\upmu}}}_{3} } \right){\tilde{\mathbf{\chi }}}_{u} + \left( {{{\varvec{\upmu}}}_{2} + {{\varvec{\upmu}}}_{1}^{T} {{\varvec{\upmu}}}_{1} } \right){\tilde{\mathbf{\chi }}}_{a} } \right]} \hfill \\ { + {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)\ddot{\chi }}}_{at} + {\mathbf{C}}_{1\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)\dot{\chi }}}_{a} + {\mathbf{C}}_{2\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{,\dot{\chi }}}_{s} {\mathbf{)\dot{\chi }}}_{u} } \hfill \\ { - {\mathbf{M}}_{\Sigma }^{{}} {\mathbf{(\chi }}_{nl} {\mathbf{)}}\int\limits_{0}^{\tau } {\left( {{{\varvec{\upmu}}}_{1} {{\varvec{\upmu}}}_{2} {\tilde{\mathbf{\chi }}}_{a} + {{\varvec{\upmu}}}_{1} {{\varvec{\upmu}}}_{4} {\tilde{\mathbf{\chi }}}_{u} } \right)} dt} \hfill \\ \end{array} } \right\}} \hfill \\ { \times {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)}} + {{\varvec{\upmu}}}_{1} {\mathbf{\dot{\tilde{\chi }}}}_{a} + {{\varvec{\upmu}}}_{2} {\tilde{\mathbf{\chi }}}_{a} + {{\varvec{\upmu}}}_{3} {\mathbf{\dot{\tilde{\chi }}}}_{u} + {{\varvec{\upmu}}}_{4} {\tilde{\mathbf{\chi }}}_{u} - {\mathbf{\ddot{\chi }}}_{at} } \hfill \\ \end{array} } \right].$$

(26)

and

$$\dot{\Upsilon }\left( t \right) = \left( \begin{gathered} \left( { - {{\varvec{\uplambda}}}_{2} sign\left( {{{\varvec{\upzeta}}}_{s} \left( t \right)} \right)} \right)^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)\zeta }}_{s} \left( t \right) - {{\varvec{\upzeta}}}_{s}^{T} \left( t \right){{\varvec{\upmu}}}_{1} {{\varvec{\upzeta}}}_{s} \left( t \right) \hfill \\ - \left( {{\mathbf{G}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}} - {\tilde{\mathbf{G}}}_{\Sigma } {\mathbf{(\chi }}_{s} {\mathbf{)}}} \right)^{T} {\mathbf{M}}_{\Sigma }^{ - 1} {\mathbf{(\chi }}_{s} {\mathbf{)\zeta }}_{s} \left( t \right) \hfill \\ \end{gathered} \right),$$

(27)

From the calculations in Lemma 1, it is derived that:

$$\dot{\Upsilon }\left( t \right) \le \left( \begin{gathered} - \left( {\left( {\lambda_{a} {\text{sgn}} \left( {\zeta_{\alpha } \left( t \right)} \right) - \delta_{\alpha 1} } \right)\frac{{\zeta_{\alpha } \left( t \right)}}{{m_{t} }}} \right) \hfill \\ - \left( {\left( {\lambda_{b} {\text{sgn}} \left( {\zeta_{\beta } \left( t \right)} \right) - \delta_{\alpha 2} } \right)\frac{{\zeta_{\beta } \left( t \right)}}{{m_{b} }}} \right) \hfill \\ - \left( {\left( {\lambda_{c} {\text{sgn}} \left( {\zeta_{\gamma } \left( t \right)} \right) - \delta_{\alpha 3} } \right)\frac{{\zeta_{\gamma } \left( t \right)}}{{J_{d} }}} \right) \hfill \\ \end{gathered} \right),$$

(28)

because

$$\dot{\Upsilon }\left( t \right) \le \left( { - \left[ {\begin{array}{*{20}c} {\lambda_{a} } & 0 & 0 \\ 0 & {\lambda_{b} } & 0 \\ 0 & 0 & {\lambda_{c} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{sgn}} \left( {\zeta_{\alpha } \left( t \right)} \right)} \\ {{\text{sgn}} \left( {\zeta_{\beta } \left( t \right)} \right)} \\ {{\text{sgn}} \left( {\zeta_{\gamma } \left( t \right)} \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\delta_{\alpha 1} } \\ {\delta_{\alpha 2} } \\ {\delta_{\alpha 3} } \\ \end{array} } \right]} \right)^{T} \times {\mathbf{\rm N}}_{A} ,$$

(29)

where ${\mathbf{\rm N}}_{A} = \left[ {\begin{array}{*{20}c} {\frac{1}{{m_{t} }}} & 0 & 0 \\ 0 & {\frac{1}{{m_{b} }}} & 0 \\ 0 & 0 & {\frac{1}{{J_{d} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\zeta_{\alpha } \left( t \right)} \\ {\zeta_{\beta } \left( t \right)} \\ {\zeta_{\gamma } \left( t \right)} \\ \end{array} } \right].$

If the controller coefficients are selected which satisfy the conditions:$\lambda_{a} > \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 1}$, $\lambda_{b} > \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 2}$, $\lambda_{c} > \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 3}$, it is ensured that the time derivative of the Lyapunov function is non-positive $\left( {\dot{\Upsilon }\left( t \right) \le 0} \right)$ since $t \to \infty$. This is based on the fact that:

$$\left\{ \begin{gathered} - \left( {\left( {\lambda_{a} {\text{sgn}} \left( {\zeta_{\alpha } \left( t \right)} \right) - \delta_{\alpha 1} } \right)\frac{{\zeta_{\alpha } \left( t \right)}}{{m_{t} }}} \right) \le - \left( {\lambda_{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 1} } \right)\frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} \hfill \\ - \left( {\left( {\lambda_{b} {\text{sgn}} \left( {\zeta_{\beta } \left( t \right)} \right) - \delta_{\alpha 2} } \right)\frac{{\zeta_{\beta } \left( t \right)}}{{m_{b} }}} \right) \le - \left( {\lambda_{b} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 2} } \right)\frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} \hfill \\ - \left( {\left( {\lambda_{c} {\text{sgn}} \left( {\zeta_{\gamma } \left( t \right)} \right) - \delta_{\alpha 3} } \right)\frac{{\zeta_{\gamma } \left( t \right)}}{{J_{d} }}} \right) \le - \left( {\lambda_{c} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 3} } \right)\frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }} \hfill \\ \end{gathered} \right.,$$

(30)

and

$$\dot{\Upsilon }\left( t \right) \le \left( {\begin{array}{*{20}l} { - \left( {\lambda_{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 1} } \right)\frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} - } \hfill \\ {\left( {\lambda_{b} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 2} } \right)\frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} - \left( {\lambda_{c} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 3} } \right)\frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \hfill \\ \end{array} } \right).$$

(31)

Set $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} = \lambda_{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 1}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} = \lambda_{b} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 2}$, and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} = \lambda_{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\delta }_{\alpha 3}$ then

$$\dot{\Upsilon }\left( t \right) \le \left\{ { - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \right\} \le 0.$$

(32)

Integrating this equation produces

$$\int\limits_{0}^{t} {\dot{\Upsilon }\left( t \right)} {\text{d}}t \le \int\limits_{0}^{t} {\left\{ { - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \right\}} {\text{d}}t.$$

(33)

It can then be inferred that

$$\mathop {\lim }\limits_{t \to \infty } \int\limits_{0}^{t} {\left\{ { + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \right\}{\text{d}}t} < \infty ,$$

(34)

and

$$\left\{ {\begin{array}{*{20}l} {\mathop {\lim }\limits_{t \to \infty } \int\limits_{0}^{t} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }}{\text{d}}t} < \infty ,\,\,\mathop {\lim }\limits_{t \to \infty } \int\limits_{0}^{t} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }}{\text{d}}t} < \infty ,} \hfill \\ {\mathop {\lim }\limits_{t \to \infty } \int\limits_{0}^{t} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}{\text{d}}t} < \infty ,} \hfill \\ \end{array} } \right.$$

(35)

Because

$$\begin{aligned} \Upsilon \left( 0 \right) & \ge \Upsilon \left( t \right) + \int\limits_{0}^{t} {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \right\}{\text{d}}t} \\ & \ge \int\limits_{0}^{t} {\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \right\}{\text{d}}t} , \\ \end{aligned}$$

(36)

it is clear that $\zeta_{\alpha } \left( t \right) \in L_{1}$, $\zeta_{\beta } \left( t \right) \in L_{1}$, and $\zeta_{\gamma } \left( t \right) \in L_{1}$ with $m_{t} > 0$, $m_{b} > 0$, and $J_{d} > 0$.

Furthermore,

$$\begin{aligned} \Upsilon_{f} \left( t \right) & \le \Upsilon_{f} \left( 0 \right) - \int\limits_{0}^{t} {\left\{ { + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a1} \frac{{\left| {\zeta_{\alpha } \left( t \right)} \right|}}{{m_{t} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{b2} \frac{{\left| {\zeta_{\beta } \left( t \right)} \right|}}{{m_{b} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{a3} \frac{{\left| {\zeta_{\gamma } \left( t \right)} \right|}}{{J_{d} }}} \right\}{\text{d}}t} \\ & \le \Upsilon_{f} \left( 0 \right) \le \infty , \\ \end{aligned}$$

(37)

and, $\Upsilon_{f} \left( t \right) \in L_{\infty }$.

On the other hand,$\dot{\Upsilon }\left( t \right) = {\dot{\mathbf{\zeta }}}_{s}^{T} \left( t \right){{\varvec{\upzeta}}}_{s} \left( t \right) \le 0$. Then, $\dot{\zeta }_{\alpha } \left( t \right) \in L_{\infty }$, $\dot{\zeta }_{\beta } \left( t \right) \in L_{\infty }$, and $\dot{\zeta }_{\gamma } \left( t \right) \in L_{\infty }$.

According to the above evidences, it is clear that the function $\zeta_{\alpha } \left( t \right)$, $\zeta_{\beta } \left( t \right)$, and $\zeta_{\gamma } \left( t \right)$ are asymptotically stable based on Barbalat’s Lemma [29]. The functions $\zeta_{\alpha } \left( t \right)$, $\zeta_{\beta } \left( t \right)$, and $\zeta_{\gamma } \left( t \right)$ approach zero as the time approaches infinity, that is the $\mathop {\lim }\limits_{t \to \infty } \zeta_{\alpha } (t) = 0$, $\mathop {\lim }\limits_{t \to \infty } \zeta_{\beta } (t) = 0$, $\mathop {\lim }\limits_{t \to \infty } \zeta_{\gamma } (t) = 0$. Consequently, all of the tracking conditions are satisfied.

This ends the proof of Lemma 2.□

3.2 Numerical implementation and analysis

In this section, numerical simulations are performed for the controller in two cases of interference effects at different times, specifically when the cargo is being moved or stationary. Here, the simulations for the proposed controller are compared with traditional PID control, which is similar to the system controlled by the workers through joystick, to see the efficiency. The performance of the controller is investigated and illustrated in Figs. 7, 8, 9, 10, 11 and 12. In the figures, the state variables of the ISMC and PID controls are shown in the continuous violet line and the dashed green line, respectively.

Fig. 7

The pulse input given to the system (Case 1)

Fig. 8

Actuated states controlled by ISMC (Case 1)

Fig. 9

Suppressing vibrations by ISMC (Case 1)

Fig. 10

The pulse input given to the system (Case 2)

Fig. 11

Actuated states controlled by ISMC (Case 2)

Fig. 12

Suppressing vibrations by ISMC (Case 2)

In Figs. 8 and 9, the system is controlled by the given controller designed in Lemma 1. With the horizontal movement distance being 3 m and the desired angle of the hoisting drum being 12 rad, the cargo can reach its target position within 12 s (Fig. 8). All of the tracking conditions are satisfied. The movement velocities are in the working range of the actual crane before converging to zero. Moreover, the angles of the swings $\theta_{x} ,\,\theta_{y}$ are directly reduced in a short time and are limited to an amplitude of approximately 1° (Fig. 9), which can be compared with the swing angles with PID control.

The vertical vibration associated with the lifting action of the crane exists in only one phase before being directly stopped. After the state variables have converged to the reference values, the system undergoes the effects of the disturbance, as given in Fig. 7. The disturbances cause the deflections of the cargo position and also the swing angles. However, all the state values are recovered to their reference points via the robustness of the ISMC in about 3 s (Fig. 8). This number represents superiority with PID control with the recovery time being in the range from 8 to 10 s.

In the second case, the designed ISMC controlled the system under the influences of the disturbances, as shown in Fig. 10. All of the system states were forced to their reference values in Fig. 11, despite the composite disturbance impacts on the system in the period from 4 to 6 s. The tracking conditions were satisfied by the robust control law, with the target points of the trolley, bridge, and hoisting cable being 11 m, 12 m, and 13 rad, respectively. Afterward, the achieved velocities were consolidated to zero. Three residual oscillations were reduced during the operation of the mechanism and suspended when the cargo reached its target point.

During operation, the crane is affected by many factors such as uncertainties as well as disturbances, such as movement through rail joints, sudden changes in frictional conditions, alignment, Inaccuracies, or impact loads in the mechanisms. All of them are considered as variable external pulse forces acting on the mechanisms, as shown in Figs. 7, 10.

Apparently, although the pulse of disturbances (Figs. 7 and 10) in both cases of controlling were higher than the values in the dynamical simulation (Fig. 5), the amplitudes and time periods of the three residual vibrations are significantly shortened (Figs. 9, 12). The swing angles and vertical vibrations were limited despite the operations of the mechanisms and the effect of disturbances while the ISMC was focusing on ensuring the tracking position of the cargo.

It can be clearly observed that in all simulation cases, the SMC controller exhibits shorter convergence times of actuated variables and smaller control errors. Moreover, all horizontal oscillations and vertical fluctuation are actively quenched within a short period of time. Also, the deviation from the desired trajectory of the cargo, trolley, and bridge are smaller when subjected to external disturbances under the controlling of robust ISMC. In short, the control quality of the system is greatly improved with an ISMC controlled system when compared to a PID controller or manual control. This can serve as a premise and foundation for the application of this idea and solution to crane systems in practice.

4 Conclusion

In this study, a new problem in bridge crane control, suspending the vertical vibration of cargo, is discussed. A novel 6-DOF mathematical model, which illustrates the highly nonlinear dynamical behavior of such cranes, is established. On the basis of the dynamics, a robust integral sliding mode controller (ISMC) for an under-actuated crane is appropriately developed. Not only does the controller accurately drive the cargo to its reference displacement, but it also limits the undesired states of vibrations during the movements and forces them to zero at the target point of the cargo. The technical properties of this novel dynamic model with the designed ISMC controller are investigated by numerical simulations. Through results, it can be clearly seen the ISMC's effectiveness and significant superiority in control quality compared to traditional PID or manual control, especially the ability to suppress oscillations. This has great significance in improving efficiency and reducing energy consumption when operating the crane. Therefore, the concept and the constructed algorithm may have promising potential for application in industrial crane systems.

Appendix

The elements of the mass matrix ${\mathbf{M}}\left( {{{\varvec{\upchi}}}_{s} } \right)$ are given as:

$$m_{11} = m_{c} + m_{t} ,\,\,\,m_{13} = m_{31} = m_{c} r_{d} S\theta_{x} ,\,\,$$

$$m_{14} = m_{41} = m_{c} C\theta_{x} (\delta + \Delta \delta + r_{d} \theta_{x} + \varphi r_{d} ),$$

$$m_{16} = m_{61} = m_{c} S\theta_{x} ,\,\,m_{22} = m_{b} + m_{c} ,\,\,$$

$$m_{23} = m_{32} = m_{c} r_{d} S\theta_{y} C\theta_{x} ,m_{26} = m_{62} = m_{c} S\theta_{y} C\theta_{x} ,$$

$$m_{24} = m_{42} = - m_{c} \left( {\left( {\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} } \right)S\theta_{x} S\theta_{y} - r_{d} C\theta_{x} S\theta_{y} } \right),$$

$$m_{25} = m_{52} = m_{c} (\delta + r_{d} \varphi + r_{d} \theta_{x} + \Delta \delta )C\theta_{x} C\theta_{y} ,\,\,$$

$$m_{34} = m_{43} = \frac{1}{2}(\delta + \Delta \delta + r_{d} \varphi )(1 - C^{2} \theta_{y} )m_{c} r_{d} S2\theta_{x} ,$$

$$m_{33} = J_{d} + 2m_{c} r_{d}^{2} - m_{c} r_{d}^{2} C^{2} \theta_{x} - m_{c} r_{d}^{2} C^{2} \theta_{y} + m_{c} r_{d}^{2} C^{2} \theta_{x} C^{2} \theta_{y} ,$$

$$m_{35} = m_{53} = \frac{1}{2}(\delta + \Delta \delta + r_{d} \varphi )(1 - C^{2} \theta_{x} )m_{c} r_{d} S2\theta_{y} ,$$

$$m_{36} = m_{63} = 2m_{c} r_{d} - m_{c} r_{d} C^{2} \theta_{x} - m_{c} r_{d} C^{2} \theta_{y} + m_{c} r_{d} C^{2} \theta_{x} C^{2} \theta_{y} ,$$

$$m_{44} = m_{c} (C^{2} \theta_{x} + C^{2} \theta_{y} - C^{2} \theta_{x} C^{2} \theta_{y} )(r_{d} \varphi + \delta + \Delta \delta )^{2} ,$$

$$\begin{aligned} m_{45} & = m_{54} = \left( {r_{d}^{2} \varphi^{2} + \delta^{2} + \Delta \delta^{2} + 2r_{d} \varphi \delta + 2\delta \Delta \delta + 2r_{d} \varphi \Delta \delta } \right) \\ & \quad \times m_{c} C\theta_{x} C\theta_{y} S\theta_{x} S\theta_{y} , \\ \end{aligned}$$

$$m_{46} = m_{64} = \frac{1}{2}(\delta + \Delta \delta + r_{d} \varphi )(1 - C^{2} \theta_{y} )m_{c} S2\theta_{x} ,$$

$$m_{55} = m_{c} (C^{2} \theta_{x} + C^{2} \theta_{y} - C^{2} \theta_{x} C^{2} \theta_{y} )(r_{d} \varphi + \delta + \Delta \delta )^{2} ,$$

$$m_{56} = m_{65} = \frac{1}{2}\left( {\delta + \Delta \delta + \varphi r_{d} } \right)\left( {1 - \cos^{2} \theta_{x} } \right)m_{c} S2\theta_{y} ,m_{66} = m_{c} .$$

Each element of the matrix ${\mathbf{C}}\left( {{{\varvec{\upchi}}}_{s} ,{\dot{\mathbf{\chi }}}_{s} } \right)$ is given as:

$$c_{13} = m_{c} r_{d} \dot{\theta }_{x} C\theta_{x} ,c_{26} = m_{c} \left( {\dot{\theta }_{y} C\theta_{x} C\theta_{y} - \dot{\theta }_{x} S\theta_{x} S\theta_{y} } \right),\,c_{33} = 0,$$

$$c_{14} = m_{c} \left( {C\theta_{x} \left( {\dot{\delta } + r_{d} \dot{\theta }_{x} + r_{d} \dot{\varphi }} \right) - (\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} )\dot{\theta }_{x} S\theta_{x} } \right),$$

$$c_{15} = 0,\,\,c_{16} = m_{c} \dot{\theta }_{x} C\theta_{x} ,\,\,c_{23} = m_{c} r_{d} \dot{\theta }_{y} C\theta_{y} ,$$

$$c_{24} = m_{c} \left( \begin{gathered} \left( {\dot{\delta } + 2r_{d} \dot{\theta }_{x} + r_{d} \dot{\varphi }} \right)S\theta_{x} S\theta_{y} - 2r_{d} \dot{\theta }_{y} C\theta_{x} C\theta_{y} \hfill \\ + (\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} )(\dot{\theta }_{x} + \dot{\theta }_{y} )C\theta_{x} S\theta_{y} \hfill \\ \end{gathered} \right),$$

$$c_{25} = m_{c} (C\theta_{y} \left( {\dot{\delta } + r_{d} \dot{\varphi } + r_{d} \dot{\theta }_{x} } \right) - S\theta_{y} \dot{\theta }_{y} (\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} ),$$

$$\begin{aligned} c_{45} & = (\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} )\{ (\delta + \Delta \delta + r_{d} \varphi )m_{c} \dot{\theta }_{x} S2\theta_{y} C^{2} \theta_{x} \\ & \quad + (\delta + \Delta \delta + r_{d} \varphi )m_{c} \dot{\theta }_{y} S2\theta_{x} C^{2} \theta_{y} - \dot{\theta }_{x} (\delta + \Delta \delta )m_{c} S2\theta_{y} \\ & \quad + \frac{1}{2}(\dot{\delta } + r_{d} \dot{\varphi })m_{c} S2\theta_{x} S2\theta_{y} \} - m_{c} r_{d} \varphi \dot{\theta }_{x} S2\theta_{y} , \\ \end{aligned}$$

$$\begin{aligned} c_{54} & = \frac{1}{2}m_{c} (r_{d} \varphi + \delta + \Delta \delta + r_{d} \theta_{x} )(2\delta \dot{\theta }_{x} C\theta_{y} S\theta_{y} C^{2} \theta_{x} \\ & \quad - \dot{\theta }_{y} \Delta \delta S(2\theta_{x} ) - \delta \dot{\theta }_{y} S(2\theta_{x} ) - r_{d} \varphi \dot{\theta }_{y} S(2\theta_{x} ) \\ & \quad + 2\delta \dot{\theta }_{y} C\theta_{x} S\theta_{x} C^{2} \theta_{y} + 2\Delta \delta \dot{\theta }_{x} C\theta_{y} S\theta_{y} C^{2} \theta_{x} \\ & \quad + 2\Delta \delta \dot{\theta }_{y} C\theta_{x} S\theta_{x} C^{2} \theta_{y} + 2r_{d} \dot{\varphi }C\theta_{x} S\theta_{y} C\theta_{y} S\theta_{x} ) \\ & \quad + 2\dot{\delta }C\theta_{y} S\theta_{y} C\theta_{x} S\theta_{x} + 2r_{d} \varphi \dot{\theta }_{x} C\theta_{y} S\theta_{y} C^{2} \theta_{x} \\ & \quad + 2r_{d} \varphi \dot{\theta }_{y} C\theta_{x} S\theta_{x} C^{2} \theta_{y} , \\ \end{aligned}$$

$$\begin{aligned} c_{35} & = \frac{1}{2}m_{c} r_{d}^{2} \dot{\varphi }S2\theta_{y} + \frac{1}{2}m_{c} r_{d} \dot{\delta }S2\theta_{y} + m_{c} r_{d}^{2} \varphi \dot{\theta }_{y} C^{2} \theta_{y} \\ & \quad - m_{c} r_{d} \delta \dot{\theta }_{y} - m_{c} r_{d} \Delta \delta \dot{\theta }_{y} + m_{c} r_{d} \Delta \delta \dot{\theta }_{y} C^{2} \theta_{y} + m_{c} r_{d} \delta \dot{\theta }_{y} C^{2} \theta_{y} \\ & \quad - m_{c} r_{d} \delta \dot{\theta }_{y} C^{2} \theta_{y} C^{2} \theta_{x} - m_{c} r_{d} \Delta \delta \dot{\theta }_{y} C^{2} \theta_{y} C^{2} \theta_{y} - m_{c} r_{d}^{2} \varphi \dot{\theta }_{y} \\ & \quad - m_{c} r_{d} \dot{\delta }S\theta_{y} \cos \theta_{y} C^{2} \theta_{x} - m_{c} r_{d}^{2} \varphi \dot{\theta }_{y} C^{2} \theta_{y} C^{2} \theta_{x} \\ & \quad - m_{c} r_{d}^{2} \dot{\varphi }S\theta_{y} C\theta_{y} C^{2} \theta_{x} + m_{c} r_{d}^{2} \varphi \dot{\theta }_{x} C\theta_{y} S\theta_{y} C\theta_{x} S\theta_{x} \\ & \quad + m_{c} r_{d} \delta \dot{\theta }_{x} C\theta_{y} S\theta_{y} C\theta_{x} S\theta_{x} + m_{c} r_{d} \Delta \delta \dot{\theta }_{x} C\theta_{x} S\theta_{y} C\theta_{y} S\theta_{x} , \\ \end{aligned}$$

$$\begin{aligned} c_{44} & = m_{c} (r_{d} \varphi + \delta + \Delta \delta )(2\dot{\delta }C^{2} \theta_{y} + 2\dot{\delta }C^{2} \theta_{x} - \delta \dot{\theta }_{x} S2\theta_{y} ) \\ & \quad + 2r_{d} \varphi \dot{\theta }_{x} C\theta_{x} S\theta_{x} C^{2} \theta_{y} - r_{d} \varphi \dot{\theta }_{x} S(2\theta_{x} ) - \delta \dot{\theta }_{y} S(2\theta_{y} ) \\ & \quad + 2r_{d} \dot{\varphi }C^{2} \theta_{y} + 2\Delta \delta \dot{\theta }_{y} C\theta_{y} S\theta_{y} C^{2} \theta_{x} - r_{d} \varphi \dot{\theta }_{y} S(2\theta_{y} ) \\ & \quad - \Delta \delta \dot{\theta }_{y} S(2\theta_{y} ) + 2\delta \dot{\theta }_{y} C\theta_{y} S\theta_{y} C^{2} \theta + 2r_{d} \dot{\varphi }C^{2} \theta_{x} \\ & \quad - 2\dot{\delta }C^{2} \theta_{x} C^{2} \theta_{y} - 2r_{d} \dot{\varphi }C^{2} \theta_{x} C^{2} \theta_{y} + 2r_{d} \varphi \dot{\theta }_{y} C\theta_{y} S\theta_{y} C^{2} \theta_{x} ) \\ & \quad + 2\delta \dot{\theta }_{x} C\theta_{x} S\theta_{x} C^{2} \theta_{yx} + 2\delta \dot{\theta }_{x} C\theta_{x} S\theta_{x} C^{2} \theta_{y} - \Delta \delta \dot{\theta }_{x} S(2\theta_{x} ), \\ \end{aligned}$$

$$c_{46} = m_{c} \left( {\begin{array}{*{20}l} {(\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} )(\dot{\theta }_{x} C^{2} \theta_{x} + \dot{\theta }_{x} C^{2} \theta_{y} )} \hfill \\ { - \dot{\theta }_{x} \cos^{2} \theta_{x} + \dot{\theta }_{y} C\theta_{x} S\theta_{y} C\theta_{y} S\theta_{x} } \hfill \\ \end{array} } \right),$$

$$c_{53} = m_{c} r_{d} \left( {\begin{array}{*{20}l} {\delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} )(\dot{\theta }_{y} C^{2} \theta_{y} + \dot{\theta }_{y} C^{2} \theta_{x} } \hfill \\ { - \dot{\theta }_{y} C^{2} \theta_{y} + \dot{\theta }_{x} C\theta_{y} S\theta_{x} S\theta_{x} S\theta_{y} } \hfill \\ \end{array} } \right),$$

$$\begin{aligned} c_{34} & = \frac{1}{2}\left( {\dot{\delta } + r_{d} \dot{\varphi }} \right)\left( {1 - C^{2} \theta_{y} } \right)m_{c} r_{d} S2\theta_{x} @ - \left( {\delta + \Delta \delta + r_{d} \varphi } \right)m_{c} r_{d} \dot{\theta }_{x} \\ & \quad + \left( {\delta + \Delta \delta + r_{d} \varphi } \right)\left( {1 - C^{2} \theta_{y} } \right)m_{c} r_{d} \dot{\theta }_{x} C^{2} \theta_{x} \\ & \quad + \left( {\delta + \Delta \delta + r_{d} \varphi } \right)m_{c} r_{d} \dot{\theta }_{y} C\theta_{x} C\theta_{x} C\theta_{y} S\theta_{y} , \\ \end{aligned}$$

$$\begin{aligned} c_{43} & = + m_{c} r_{d}^{2} \varphi \dot{\theta }_{x} C^{2} \theta_{y} + m_{c} r_{d} \delta \dot{\theta }_{x} C^{2} \theta_{x} C^{2} \theta_{y} + m_{c} r_{d} \delta \dot{\theta }_{x} \\ & \quad - m_{c} r_{d} \delta \dot{\theta }_{x} C^{2} \theta_{x} C^{2} \theta_{y} - m_{c} r_{d} \Delta \delta \dot{\theta }_{x} C^{2} \theta_{x} \\ & \quad - m_{c} r_{d}^{2} \varphi \dot{\theta }_{x} C^{2} \theta_{x} C^{2} \theta_{y} + m_{c} r_{d}^{2} \varphi \dot{\theta }_{x} C^{2} \theta_{x} + m_{c} r_{d} \Delta \delta \dot{\theta }_{y} C^{2} \theta_{y} \\ & \quad - m_{c} r_{d}^{2} \varphi \dot{\theta }_{y} C\theta_{x} S\theta_{y} C\theta_{y} S\theta_{x} C^{2} \theta_{y} m_{c} r_{d} \Delta \delta \dot{\theta }_{x} C^{2} \theta_{x} \\ & \quad + m_{c} r_{d} \delta \dot{\theta }_{y} C\theta_{x} S\theta_{y} C\theta_{y} S\theta_{x} + m_{c} r_{d} \Delta \delta \dot{\theta }_{y} C\theta_{x} S\theta_{y} C\theta_{y} S\theta_{x} , \\ \end{aligned}$$

$$\begin{aligned} c_{55} & = \frac{1}{2}m_{c} (r_{d} \varphi + \delta + \Delta \delta + r_{d} \theta_{x} )(2\dot{\delta }C^{2} \theta_{x} + 2\dot{\delta }C^{2} \theta_{y} \\ & \quad - \delta \dot{\theta }_{x} S(2\theta_{x} ) - \dot{\theta }_{y} S(2\theta_{y} ) + 2r_{d} \dot{\varphi }C^{2} \theta_{x} + 2r_{d} \dot{\varphi }C^{2} \theta_{y} \\ & \quad - \Delta \delta \dot{\theta }_{x} S(2\theta_{x} ) - \Delta \delta \dot{\theta }_{y} S(2\theta_{y} ) - 2\dot{\delta }C^{2} \theta_{x} C^{2} \theta_{y} \\ & \quad - 2r_{d} \dot{\varphi }C^{2} \theta_{x} C^{2} \theta_{y} - r_{d} \varphi \dot{\theta }_{x} S(2\theta_{x} ) - r_{d} \varphi \dot{\theta }_{y} S(2\theta_{y} ) \\ & \quad + 2r_{d} \varphi \dot{\theta }_{x} C\theta_{x} S\theta_{x} C^{2} \theta_{y} + 2\delta \dot{\theta }_{y} C\theta_{y} S\theta_{y} C^{2} \theta_{x} \\ & \quad + 2\delta \dot{\theta }_{x} C\theta_{x} S\theta_{x} C^{2} \theta_{y} + 2\Delta \delta \dot{\theta }_{y} C\theta_{y} S\theta_{y} C^{2} \theta_{x} \\ & \quad + 2\dot{\theta }_{x} C\theta_{x} S\theta_{x} C^{2} \theta_{y} + 2r_{d} \varphi \dot{\theta }_{y} C\theta_{y} S\theta_{y} C^{2} \theta_{x} ), \\ \end{aligned}$$

$$c_{56} = m_{c} \left( \begin{gathered} \delta + \Delta \delta + r_{d} \varphi + r_{d} \theta_{x} )(\dot{\theta }_{y} C^{2} \theta_{x} + \dot{\theta }_{y} C^{2} \theta_{y} \hfill \\ - \dot{\theta }_{y} C^{2} \theta_{x} C^{2} \theta_{y} + \dot{\theta }_{x} C\theta_{x} C\theta_{y} C\theta_{y} S\theta_{x} \hfill \\ \end{gathered} \right),\,\,\,\,\,$$

$$c_{65} = - \frac{1}{2}m_{c} \left( {\begin{array}{*{20}l} {(2\delta \dot{\theta }_{y} + 2\Delta \delta \dot{\theta }_{y} - \dot{\delta }S(2\theta_{y} ) - 2\delta \dot{\theta }_{y} C^{2} \theta_{y} } \hfill \\ { + 2\dot{\delta }C\theta_{y} S\theta_{y} \cos^{2} \theta_{x} + 2\delta \theta_{y} C^{2} \theta_{y} C^{2} \theta_{x} } \hfill \\ { - 2r_{d} \varphi \dot{\theta }_{y} C^{2} \theta_{y} + 2r_{d} \varphi \dot{\theta }_{y} S^{2} \theta_{y} C^{2} \theta_{x} } \hfill \\ { + 2r_{d} \dot{\varphi }C\theta_{y} S\theta_{y} C^{2} \theta_{x} - 2\Delta \delta \dot{\theta }_{x} C\theta_{x} S\theta_{x} C\theta_{y} S\theta_{y} } \hfill \\ { - 2\delta \dot{\theta }_{x} C\theta_{y} S\theta_{y} C\theta_{x} S\theta_{x} - r_{d} \dot{\varphi }\dot{\theta }_{y} - 2\Delta \delta \dot{\theta }_{y} C^{2} \theta_{y} } \hfill \\ { - 2r_{d} \varphi \dot{\theta }_{x} C\theta_{x} S\theta_{x} C\theta_{y} S\theta_{y} ) + 2\Delta \delta \theta_{y} C^{2} \theta_{y} C^{2} \theta_{x} } \hfill \\ \end{array} } \right),$$

where $C\chi = \cos \left( \chi \right)$, $S\chi = \sin \left( \chi \right)$.

The elements of the damping matrix ${\mathbf{B}}$ are given as:

$$b_{11} = b_{t} ,b_{22} = b_{b} ,b_{33} = b_{m} ,b_{44} = b_{r}$$

The components of the gravity vector, ${\mathbf{G}}\left( {{{\varvec{\upchi}}}_{s} } \right)$, are computed as:

$$g_{3} = - m_{c} r_{d} gC\theta_{x} C\theta_{y} ,\,g_{6} = \left( {k_{e} + \Delta \delta } \right)\delta - m_{c} gC\theta_{x} C\theta_{y} ,$$

$$\begin{aligned} g_{4} & = m_{c} g\delta C\theta_{y} S\theta_{x} + m_{c} g\Delta \delta C\theta_{y} S\theta_{x} \\ & \quad + m_{c} gr_{d} \varphi C\theta_{y} S\theta_{x} + m_{c} gr_{d} \theta_{x} C\theta_{y} S\theta_{x} , \\ \end{aligned}$$