Aggregated Hierarchical Sliding Mode Control for Vibration Suppression of an Excavator on an Elastic Foundation

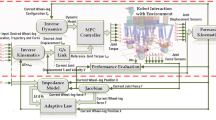
Abstract

Crawler excavators are important, utilitarian machines in construction industries. Special features of the chain and chassis allow them to operate and move on unstable ground. The shock motions of the links, which coincide with the changes of the forces impacting the foundation, create vibrations within the entire system. The highest level of vibrations appears when the boom moves, as it holds the robotic excavator's entire actuator with large mass and moment of inertia. These undesired fluctuations cause system instability, driver discomfort, reduced operating efficiency, and increased energy consumption. In this study, a hierarchical sliding mode control focusing on boom movement is designed based on the system dynamic model. This controller allows the boom to move precisely with a slight fluctuation angle of the main body, even while the other links are moving using a parameter estimator. Maintaining stable boom movements significantly simplifies arm and bucket control. The effectiveness of the entire work is investigated by numerical simulation and implementation results on a small-scale hydraulic excavator.

1 Introduction

The hydraulic excavator [1] is a machine used to excavate soil and has been widely used in industries for a long period. Based on the chassis structure, a crawler excavator and wheel excavator are available based on the working environment. Here, the crawler excavator moves on a chain wheel system, which allows the machine to function on unstable soil; meanwhile, the wheel excavator moves on wheels and is normally exploited for plain ground operations.

A working feature present in both versions of the excavator is strong oscillation (in the lifting plane) of the entire system, which is derived from the elasticity of the ground for a crawler excavator and that of the tires of a wheel excavator. These unexpected oscillations are responsible for instability, increased energy consumption, decrease in operating productivity, and discomfort for the excavator operator. However, these fluctuations will be much larger and more complicated for the crawler crane depending on the characteristics of the ground and working terrain. There have been numerous methods, mainly focused on finishing dampers, which have been used for a long period. In terms of robotics and control, this study proposes an approach based on the construction of an under-actuated dynamic system [2,3,4] and application of a non-linear controller to suspend oscillation and precisely control link displacement.

The sliding mode control (SMC) controller [5] is a classical and well-known non-linear controller widely used for its robustness [6, 7] and short convergence time with variable versions [8,9,10] and variable structures [11,12,13] The structure of hierarchical sliding mode control (HSMC) is a well-known and specialized application for single input multiple output systems. It takes advantage of sliding-mode algorithm flexibly for each specific system and is a suitable candidate for the mathematical model of the designed system. In this study, a controller based on the construction of an under-actuated dynamic system is built to quench oscillation. In particular, a robust IHSMC to accurately control the boom position (the main source of oscillation for the whole system), and to limit the oscillation of the main body is designed. By using an additional system parameter estimator, the controller can accurately control the position of the boom in both cases, whether or not the other link is moving. The error or inaccuracy in parameter estimation and the inertial loading of the links are overcome by the robustness of the integral sliding mode algorithm. The controller ensures a stable boom without any movement of the main body, which allows easy control of the arm and bucket with a proportional − integral − derivative (PID) controller. This approach simplifies and reduces the calculation volume for the controller but still ensures control quality. The effectiveness and feasibility of the controller are shown through not only simulation but also experiment.

The major contribution and originality of this study are: A control scheme utilized the fundamentals of hierarchical sliding mode is designed and applied to an under-actuated excavator system on the elastic foundation. Not only does the control law reduce the vibration of the overall system when the boom moving, but it also allows the other links to move simultaneously with tiny angular vibrations by using a parameter estimator. In this case, the controller can combine with other simple controllers such as PID for tracking control while ensuring the stable movement of the entire system.

The paper is organized in the following structure: after the introduction, the description and build process of the full dynamic system are noted in Sect. 2. The IHSMC controller was then established to control the vibration quenching by simplifying the built-in dynamic model described in Sect. 3. Finally, the results of simulation and experiment are discussed in Sect. 4, and summary, analysis, and conclusions are provided in Sect. 5.

2 System Dynamic

2.1 System Description and Kinematic Model

The under-actuated robotic excavator with an elastic foundation is illustrated in Fig. 1.

Fig. 1

The crawler excavator model and its coordinate systems

The oscillations of the links and counter move around a virtual axis that passes through the origin O and is perpendicular to the working plane. The damping coefficients and equivalent stiffness ($b_{m}$ and $k_{eq}$) of the angular vibration are calculated from the coefficients $k_{g}$ and $b_{g}$, respectively. The coordinate frames $R_{0} \left( {O_{0} x_{0} y_{0} } \right)$, $R_{1} \left( {O_{1} x_{1} y_{1} } \right)$, $R_{2} \left( {O_{2} x_{2} y_{2} } \right)$, $R_{3} \left( {O_{3} x_{3} y_{3} } \right)$, and $R_{4} \left( {O_{4} x_{4} y_{4} } \right)$ are selected, as shown in Fig. 1. The set of rotational generalized coordinates is denoted by $\alpha \left( t \right),\beta \left( t \right),\gamma \left( t \right)$, and $\theta \left( t \right)$, which represent the angles of the main body, boom, arm, and bucket, respectively. The angle of the body is expressed as $\alpha \left( t \right) = \alpha_{0} + \delta \left( t \right)$, where $\alpha_{0}$ is the fixed angle between $O_{0} O_{2}$; and the line through the underside of the chain, $\delta \left( t \right) = \delta_{\alpha 0} + \delta_{\alpha } \left( t \right)$, is the angle between the main body and the horizontal flat, while $\delta_{\alpha 0}$ is the initial angle.

The matrices representing the link positions in $\left( {R_{0} } \right)$ are provided by the transformation matrices, as follows:

$${\mathbf{C}}_{4} = \left[ {\begin{array}{*{20}c} {C_{\alpha \beta \gamma \theta } } & \quad { - S_{\alpha \beta \gamma \theta } } & \quad 0 & \quad {a_{3} C_{\alpha \beta \gamma } + a_{2} C_{\alpha \beta } + a_{1} C_{\alpha } } \\ {S_{\alpha \beta \gamma \theta } } & \quad {C_{\alpha \beta \gamma \theta } } & \quad 0 & \quad {a_{3} S_{\alpha \beta \gamma } + a_{2} S_{\alpha \beta } + a_{1} S_{\alpha } } \\ 0 & \quad 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \\ \end{array} } \right],$$

(1)

$${\mathbf{C}}_{3} = \left[ {\begin{array}{*{20}c} {C_{\alpha \beta \gamma } } & \quad { - S_{\alpha \beta \gamma } } & \quad 0 & \quad {a_{2} C_{\alpha \beta } + a_{1} C_{\alpha } } \\ {S_{\alpha \beta \gamma } } & \quad {C_{\alpha \beta \gamma } } & \quad 0 & \quad {a_{2} S_{\alpha \beta } + a_{1} S_{\alpha } } \\ 0 & \quad 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \\ \end{array} } \right],$$

(2)

$${\mathbf{C}}_{2} = \left[ {\begin{array}{*{20}c} {C_{\alpha \beta } } & \quad { - S_{\alpha \beta } } & \quad 0 & \quad {a_{1} C_{\alpha } } \\ {S_{\alpha \beta } } & \quad {C_{\alpha \beta } } & \quad 0 & \quad {a_{1} S_{\alpha } } \\ 0 & \quad 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \\ \end{array} } \right],$$

(3)

$${\mathbf{C}}_{1} = \left[ {\begin{array}{*{20}c} {C_{\alpha } } & \quad { - S_{\alpha } } & \quad 0 & \quad 0 \\ {S_{\alpha } } & \quad {C_{\alpha } } & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 1 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 1 \\ \end{array} } \right],$$

(4)

where $S_{\alpha } = \sin \alpha$, $C_{\alpha } = \cos \alpha$, $S_{\alpha \beta } = \sin (\alpha + \beta )$ and $C_{\alpha \beta } = \cos (\alpha + \beta )$,$a_{i}$ denotes the length of the ith link ($a_{1} = O_{1} O_{2} = O_{0} O_{2}$, $a_{2} = O_{2} O_{3}$, $a_{3} = O_{3} O_{4}$, $a_{4} = O_{4} E$).

The displacement of the last point E in $\left( {R_{0} } \right)$ is

$${}^{h}{\mathbf{r}}_{E}^{(0)} = {\mathbf{C}}_{3} {}^{h}{\mathbf{u}}_{E}^{(3)} ,$$

(5)

where the transformation matrix ${\mathbf{C}}_{3} {}^{h}$ is given by

$${\mathbf{C}}_{3} {}^{h} = \left[ {\begin{array}{*{20}c} {C_{\alpha \beta \gamma \theta } } & { - S_{\alpha \beta \gamma \theta } } & 0 & {a_{3} C_{\alpha \beta \gamma } + a_{2} C_{\alpha \beta } + a_{1} C_{\alpha } } \\ {S_{\alpha \beta \gamma \theta } } & {C_{\alpha \beta \gamma \theta } } & 0 & {a_{3} S_{\alpha \beta \gamma } + a_{2} S_{\alpha \beta } + a_{1} S_{\alpha } } \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right],$$

(6)

and the vector $^{h} {\mathbf{u}}_{E}^{(3)}$ is

$$^{h} {\mathbf{u}}_{E}^{(3)} = \left[ {\begin{array}{*{20}c} {a_{4} } & 0 & 0 & 1 \\ \end{array} } \right]^{T} .$$

(7)

The angular velocity of the ith link is inferred from the matrix to be

$${\tilde{\mathbf{\omega }}}_{i}^{(0)} = {\dot{\mathbf{A}}}_{i} {\mathbf{A}}_{i}^{T} ,$$

(8)

where ${\mathbf{A}}_{i}^{{}}$ is the rotary transformation matrix extracted from ${\mathbf{C}}_{i}^{{}}$.

Thus, we have

$${\tilde{\mathbf{\omega }}}_{4}^{(0)} = {\dot{\mathbf{A}}}_{4} {\mathbf{A}}_{4}^{T} = \left[ {\begin{array}{*{20}c} 0 & { - \left( {\dot{\alpha } + \dot{\beta } + \dot{\gamma } + \dot{\theta }} \right)} & 0 \\ {\left( {\dot{\alpha } + \dot{\beta } + \dot{\gamma } + \dot{\theta }} \right)} & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right].$$

(9)

The angular velocity of the bucket is given as

$${{\varvec{\upomega}}}_{4}^{(0)} = \left[ {\begin{array}{*{20}c} {{}^{{R_{o} }}\omega_{{x_{o} }}^{4} } \\ {{}^{{R_{o} }}\omega_{{y_{o} }}^{4} } \\ {{}^{{R_{o} }}\omega_{{z_{o} }}^{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma } + \dot{\theta }} \\ \end{array} } \right].$$

(10)

Similarly, the angular velocities of the arm and boom are

$${{\varvec{\upomega}}}_{3}^{(0)} = \left[ {\begin{array}{*{20}c} {{}^{{R_{o} }}\omega_{{x_{o} }}^{3} } \\ {{}^{{R_{o} }}\omega_{{y_{o} }}^{3} } \\ {{}^{{R_{o} }}\omega_{{z_{o} }}^{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma }} \\ \end{array} } \right],$$

(11)

$${{\varvec{\upomega}}}_{2}^{(0)} = \left[ {\begin{array}{*{20}c} {{}^{{R_{o} }}\omega_{{x_{o} }}^{2} } \\ {{}^{{R_{o} }}\omega_{{y_{o} }}^{2} } \\ {{}^{{R_{o} }}\omega_{{z_{o} }}^{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\dot{\delta }_{\alpha } + \dot{\beta }} \\ \end{array} } \right].$$

(12)

The angular velocity of the body is

$${{\varvec{\upomega}}}_{1}^{(0)} = \left[ {\begin{array}{*{20}c} {{}^{{R_{o} }}\omega_{{x_{o} }}^{1} } \\ {{}^{{R_{o} }}\omega_{{y_{o} }}^{1} } \\ {{}^{{R_{o} }}\omega_{{z_{o} }}^{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\dot{\delta }_{\alpha } } \\ \end{array} } \right].$$

(13)

2.2 Dynamic Model of the Entire System

The kinetic energy of the system is formulated in general form as

$$T = \frac{1}{2}{\dot{\mathbf{\varsigma }}}_{S}^{T} \left( {\sum\limits_{i = 1}^{p} {m_{i} {\mathbf{J}}_{Ti}^{T} {\mathbf{J}}_{Ti}^{{}} } + \sum\limits_{i = 1}^{p} {{\mathbf{J}}_{Ri}^{T} {\mathbf{A}}_{i} {\mathbf{I}}_{i} {\mathbf{A}}_{i}^{T} {\mathbf{J}}_{Ri}^{T} } } \right){\mathbf{\varsigma }}_{S} ,$$

(14)

where ${\mathbf{J}}_{Ti}^{{}}$ and ${\mathbf{J}}_{Ri}^{{}}$ are the Jacobian matrices for translation and rotation of the $i^{th}$ link, respectively; $p = 4$ is the number of links; $m_{i}$ and ${\mathbf{I}}_{i}$ are the masses and moment of inertia of the links, respectively; and ${\mathbf{\varsigma }}_{s} \left( t \right) = \left[ {\begin{array}{*{20}c} {\delta_{\alpha } \left( t \right)} & {\beta \left( t \right)} & {\gamma \left( t \right)} & {\theta \left( t \right)} \\ \end{array} } \right]^{T} \in \Re^{4 \times 1}$ is the state vector of the system. The matrix ${\mathbf{J}}_{Ri}^{{}}$ is basically calculated from the angular velocity of the links. The matrix ${\mathbf{J}}_{Ti}^{{}}$ of the links is given in the Appendix.

The kinetic and potential energy of the system are provided as

$$\begin{aligned} T& = \frac{1}{2}I_{3z} \left( {\dot{\beta } + \dot{\delta }_{\alpha } + \dot{\gamma }} \right)^{2} + \frac{1}{2}I_{1z} \dot{\delta }_{\alpha }^{2} \\ & \quad + \frac{1}{2}\left( {I_{4z} \left( {\dot{\beta } + \dot{\delta }_{\alpha } + \dot{\gamma } + \dot{\theta }} \right)} \right)^{2} + \frac{1}{2}I_{2z} \left( {\dot{\beta } + \dot{\delta }_{\alpha } } \right)^{2} \\ & \quad + \frac{1}{2}m_{1} a_{c1}^{2} \dot{\delta }_{\alpha }^{2} \cos^{2} \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right) \\ & \quad + \frac{1}{2}m_{1} a_{c1}^{2} \dot{\delta }_{\alpha }^{2} \sin^{2} \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right). \\ & \quad + \frac{1}{2}m_{4} \left( \begin{gathered} a_{2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta }} \right) \hfill \\ + \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right)\dot{\delta }_{\alpha } \hfill \\ + a_{3} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma } \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma }} \right) \hfill \\ + a_{c3} \cos \left( \begin{gathered} \alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} \hfill \\ + \beta + \gamma + \theta - \varphi_{4} \hfill \\ \end{gathered} \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma } + \dot{\theta }} \right) \hfill \\ \end{gathered} \right)^{2} \\ & \quad + \frac{1}{2}m_{2} \left( \begin{gathered} a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha 0} + \delta_{\alpha } + \beta - \varphi_{2} } \right)\left( {\dot{\beta } + \dot{\delta }_{\alpha } } \right) \hfill \\ + a_{1} \cos \left( {\alpha_{0} + \delta_{\alpha 0} + \alpha } \right)\dot{\delta }_{\alpha } \hfill \\ \end{gathered} \right)^{2} \\ & \quad + \frac{1}{2}m_{2} \left( \begin{gathered} a_{c2} \sin \left( {\alpha_{0} + \delta_{\alpha 0} + \delta_{\alpha } + \beta - \varphi_{2} } \right)\left( {\dot{\beta } + \dot{\delta }_{\alpha } } \right) \hfill \\ + a_{1} \sin \left( {\alpha_{0} + \delta_{\alpha 0} + \alpha } \right)\dot{\delta }_{\alpha } \hfill \\ \end{gathered} \right)^{2} \\ & \quad + \frac{1}{2}m_{4} \left( \begin{gathered} a_{2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta }} \right) \hfill \\ + \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right)\dot{\delta }_{\alpha } \hfill \\ + a_{3} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma } \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma }} \right) \hfill \\ + a_{c3} \sin \left( \begin{gathered} \alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma \hfill \\ + \theta - \varphi_{4} \hfill \\ \end{gathered} \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma } + \dot{\theta }} \right) \hfill \\ \end{gathered} \right)^{2} \\ & \quad + \frac{1}{2}m_{3} \left( \begin{gathered} a_{2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta }} \right) \hfill \\ + \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right)\dot{\delta }_{\alpha } \hfill \\ + a_{c3} \cos \left( \begin{gathered} \alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} \hfill \\ + \beta + \gamma - \varphi_{3} \hfill \\ \end{gathered} \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma }} \right) \hfill \\ \end{gathered} \right)^{2} \\ & \quad + \frac{1}{2}m_{3} \left( \begin{gathered} a_{2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta }} \right) \hfill \\ + \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right)\dot{\delta }_{\alpha } \hfill \\ + a_{c3} \sin \left( \begin{gathered} \alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} \hfill \\ + \beta + \gamma - \varphi_{3} \hfill \\ \end{gathered} \right)\left( {\dot{\delta }_{\alpha } + \dot{\beta } + \dot{\gamma }} \right) \hfill \\ \end{gathered} \right)^{2} , \\ \end{aligned}$$

(15)

where $\varphi_{1} = \widehat{{C_{1} O_{1} O_{2} }}$, $\varphi_{2} = \widehat{{C_{2} O_{2} x_{2} }}$, $\varphi_{3} = \widehat{{C_{3} O_{3} x_{3} }}$, $\varphi_{4} = \widehat{{C_{4} O_{4} x_{4} }}$. Here, $C_{1}$, $C_{2}$, $C_{3}$, and $C_{4}$ are respectively the centers of masses of the main body, boom, arm, and bucket.

The potential energy is calculated as

$$\Pi = \left( \begin{gathered} m_{1} a_{C1} \sin \left( {\alpha + \varphi_{1} } \right) + m_{2} \left( {a_{1} \sin \alpha + a_{C2} \sin \left( {\alpha + \beta - \varphi_{2} } \right)} \right) \hfill \\ + m_{4} \left( \begin{gathered} a_{1} \sin \alpha + a_{2} \sin \left( {\alpha + \beta } \right) \hfill \\ + a_{3} \sin \left( {\alpha + \beta + \gamma } \right) \hfill \\ + a_{C4} \sin \left( {\alpha + \beta + \gamma + \theta - \varphi_{4} } \right) \hfill \\ \end{gathered} \right) + \frac{1}{2}k_{eq} \left( {\delta_{\alpha } } \right)^{2} + \hfill \\ m_{3} \left( {a_{1} \sin \alpha + a_{2} \sin \left( {\alpha + \beta } \right) + a_{C3} \sin \left( {\alpha + \beta + \gamma - \varphi_{3} } \right)} \right) \hfill \\ \end{gathered} \right).$$

(16)

The equations illustrating the dynamic features of the system can be computed by applying the principle and Lagrange’s equation.

3 Controller Design

3.1 Dynamic Model for Boom Control

On the basis of practical working conditions, the vibration derived from the movement of the boom is much larger than that of other links. Consequently, the controller is designed to concentrate on the accurate motion of the boom while reducing the vibration of the body.

In this case, the overall excavator can be considered as a two-link system encompassing the main body and a synthesis link of the boom, arm, and bucket. Here, the synthesis link’s position is controlled through precise control of the boom angle $\beta \left( t \right)$.

The angular velocities of the synthesis link and the body are

$${\mathbf{\omega^{\prime}}}_{2}^{(0)} = {{\varvec{\upomega}}}_{2}^{(0)} ,$$

(17)

$${\mathbf{\omega^{\prime}}}_{1}^{(0)} = {{\varvec{\upomega}}}_{1}^{(0)} .$$

(18)

The translating velocities of the links’ centers in the global frame are

$${\mathbf{v}}^{\prime}_{C1} = \left[ {\begin{array}{*{20}c} {a_{C1} C_{{\alpha \varphi_{1} }} } & {a_{C1} S_{{\alpha \varphi_{1} }} } & 0 \\ \end{array} } \right]^{T} ,$$

(19)

$${\mathbf{v}}^{\prime}_{C2} = \left[ {\begin{array}{*{20}c} {a_{1} C_{\alpha } + a^{\prime}_{C2} C_{{\varphi ^{\prime}_{2} }} } & {a_{1} S_{\alpha } - a^{\prime}_{C2} S_{{\varphi ^{\prime}_{2} }} } & 0 \\ \end{array} } \right]^{T} .$$

(20)

The kinetic energy of the system is formulated as

$$T^{\prime} = \frac{1}{2}{\dot{\mathbf{\chi }}}_{S}^{T} \left( {\sum\limits_{i^{\prime} = 1}^{q} {m_{i^{\prime}} {\mathbf{J}}_{Ti^{\prime}}^{T} {\mathbf{J}}_{Ti^{\prime}} } + \sum\limits_{i^{\prime} = 1}^{q} {{\mathbf{J}}_{Ri^{\prime}}^{T} {\mathbf{A}}_{i^{\prime}} {\mathbf{I}}_{i^{\prime}} {\mathbf{A}}_{i^{\prime}}^{T} {\mathbf{J}}_{Ri^{\prime}}^{T} } } \right){{\varvec{\upchi}}}_{S} ,$$

(21)

where ${\mathbf{J}}_{Ti^{\prime}}^{{}}$ and ${\mathbf{J}}_{Ri^{\prime}}^{{}}$ are the Jacobian matrices for translation and rotation of the iʹth link, respectively; $q = 2$ is the number of links; $m_{i^{\prime}}$ and ${\mathbf{I}}_{i^{\prime}}$ are the masses and moment of inertia of the links, respectively; and ${{\varvec{\upchi}}}_{s} \left( t \right) = \left[ {\begin{array}{*{20}c} {\delta_{\alpha } \left( t \right)} & {\beta \left( t \right)} \\ \end{array} } \right]^{T} \in \Re^{2 \times 1}$ is the vector of state variables of the system. Consequently, the kinetic energy of the system is computed as

$$\begin{aligned} T^{\prime} & = + \frac{1}{2}m_{1} a_{c1}^{2} \dot{\delta }_{\alpha }^{2} \cos^{2} \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right) + \frac{1}{2}I_{1z} \dot{\delta }_{\alpha }^{2} \\ & \quad + \frac{1}{2}m_{1} a_{c1}^{2} \dot{\delta }_{\alpha }^{2} \sin^{2} \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right)\frac{1}{2} + I_{2z} \left( {\dot{\beta } + \dot{\delta }_{\alpha } } \right)^{2} \\ & \quad + \frac{1}{2}m_{2} \left( \begin{gathered} a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha 0} + \delta_{\alpha } + \beta - \varphi_{2} } \right)\left( {\dot{\beta } + \dot{\delta }_{\alpha } } \right) \hfill \\ + a_{1} \cos \left( {\alpha_{0} + \delta_{\alpha 0} + \alpha } \right)\dot{\delta }_{\alpha } \hfill \\ \end{gathered} \right)^{2} \\ & \quad + \frac{1}{2}m_{2} \left( \begin{gathered} a_{c2} \sin \left( {\alpha_{0} + \delta_{\alpha 0} + \delta_{\alpha } + \beta - \varphi_{2} } \right)\left( {\dot{\beta } + \dot{\delta }_{\alpha } } \right) \hfill \\ + a_{1} \sin \left( {\alpha_{0} + \delta_{\alpha 0} + \alpha } \right)\dot{\delta }_{\alpha } \hfill \\ \end{gathered} \right)^{2} . \\ \end{aligned}$$

(22)

The potential energy is provided as

$$\Pi ^{\prime} = \left( \begin{gathered} m_{1} a_{C1} \sin \left( {\alpha + \varphi_{1} } \right) + \frac{1}{2}k_{eq} \left( {\delta_{\alpha } } \right)^{2} \hfill \\ +\, m_{\Sigma 2} \left( {a_{1} \sin \alpha + a_{C2} \sin \left( {\alpha + \beta - \varphi ^{\prime}_{2} } \right)} \right) \hfill \\ \end{gathered} \right).$$

(23)

The system dynamic can be computed and given in matrix form as follows:

$${\mathbf{M(\chi }}_{S} {\mathbf{)\ddot{\chi }}}_{S} + {\mathbf{B\dot{\chi }}}_{S} + {\mathbf{C(\chi }}_{S} {\mathbf{,\dot{\chi }}}_{S} {\mathbf{)\dot{\chi }}}_{S} + {\mathbf{G(\chi }}_{S} {\mathbf{)}} = {{\varvec{\Psi}}}_{f} ,$$

(24)

where

$${\mathbf{M(\chi }}_{S} {\mathbf{)}} = \left[ {\begin{array}{*{20}c} {m_{11} } & {m_{12} } \\ {m_{21} } & {m_{22} } \\ \end{array} } \right],$$

$$\begin{aligned} & {\mathbf{C}}({{\varvec{\upchi}}}_{S} ,{\dot{\mathbf{\chi }}}_{S} ) = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } \\ {c_{21} } & 0 \\ \end{array} } \right], \\ & {\mathbf{B}} = \left[ {\begin{array}{*{20}c} {b_{1} } & 0 \\ 0 & {b_{2} } \\ \end{array} } \right],{\mathbf{G}}({{\varvec{\upchi}}}_{S} ) = \left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ \end{array} } \right],{{\varvec{\Psi}}}_{f} = \left[ {\begin{array}{*{20}c} 0 & {\Psi_{bo} } \\ \end{array} } \right]^{T} . \\ \end{aligned}$$

The coefficients of the mass matrix ${\mathbf{M(\chi }}_{S} {\mathbf{)}}$ are provided as

$$\begin{aligned} {\mathbf{M(\chi }}_{S} {\mathbf{)}} & = \left[ {\begin{array}{*{20}c} {m_{11} } & {m_{12} } \\ {m_{21} } & {m_{22} } \\ \end{array} } \right], \\ m_{11} & = \left( \begin{gathered} m_{\Sigma 2} a_{1}^{2} + 2m_{\Sigma 2} \cos \left( {\beta - \varphi_{2} } \right)a_{1} a_{c2} \hfill \\ + m_{1} a_{1}^{2} + m_{\Sigma 2} a_{c2}^{2} + I_{1z} + I_{\Sigma 2z} \hfill \\ \end{gathered} \right), \\ m_{12} & = m_{21} = m_{\Sigma 2} a_{c2}^{2} + 2m_{\Sigma 2} \cos \left( {\beta - \varphi_{2} } \right)a_{1} a_{c2} + I_{\Sigma 2z} , \\ m_{22} & = m_{\Sigma 2} a_{c2}^{2} + I_{\Sigma 2z} ,m_{\Sigma 2} = m_{2} + m_{3} + m_{4} , \\ \end{aligned}$$

Here, the equivalent moment of inertia $I_{\Sigma 2z}$ is

$$\begin{aligned} I_{\Sigma 2z} & = I_{2cz} + m_{2} a_{c2}^{2} + I_{3cz} \\ & \quad + \,m_{3} \left( {a_{2}^{2} + a_{c3}^{2} - 2a_{2} a_{c3} \cos \left( {\gamma - \pi + \varphi_{3} } \right)} \right) + I_{4cz} \\ & \quad +\, m_{4} \left( \begin{gathered} a_{2}^{2} + a_{3}^{2} - 2a_{2} a_{3} \cos \left( {2\pi - \gamma } \right) + a_{c4}^{2} \hfill \\ - \frac{{a_{4} }}{{a_{3} }} \cdot \left( {a_{2}^{2} + a_{3}^{2} - 2a_{2} a_{3} \cos \left( {2\pi - \gamma } \right) + a_{3}^{2} - a_{2}^{2} } \right) \hfill \\ \end{gathered} \right)s. \\ \end{aligned}$$

(25)

Based on the dynamic model established from previous system, the size parameters $a^{\prime}_{C2} ,\,\,\varphi ^{\prime}_{2}$ can be calculated as follows:

$$a^{\prime}_{C2} = \left\| {{\mathbf{R}}_{m} } \right\|,$$

(26)

$$\varphi ^{\prime}_{2} = \beta + \alpha - 2\pi - arctag\left( {\frac{{{\mathbf{R}}_{m2} }}{{{\mathbf{R}}_{m1} }}} \right),$$

(27)

where

$${\mathbf{R}}_{m} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{m1} } & {{\mathbf{R}}_{m2} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\frac{{\Omega_{1} + \Omega_{2} }}{{m_{\Sigma 2} }}} & {\frac{{\Omega_{3} + \Omega_{4} }}{{m_{\Sigma 2} }}} \\ \end{array} } \right]^{T} ,$$

(28)

with

$$\begin{aligned} \Omega_{1} & = \left( \begin{gathered} m_{2} a_{C2} \cos \left( {\alpha + \beta - \varphi_{2} } \right) + \hfill \\ m_{3} \left( {a_{2} \cos \left( {\alpha + \beta } \right) + a_{C3} \cos \left( {\alpha + \beta + \gamma - \varphi_{3} } \right)} \right) \hfill \\ \end{gathered} \right), \\ \Omega_{2} & = \left( {m_{4} \left( \begin{gathered} a_{2} \cos \left( {\alpha + \beta } \right) + a_{3} \cos \left( {\alpha + \beta + \gamma } \right) \hfill \\ + a_{C4} \cos \left( {\alpha + \beta + \gamma + \theta - \varphi_{4} } \right) \hfill \\ \end{gathered} \right)} \right), \\ \Omega_{3} & = \left( \begin{gathered} m_{2} a_{C2} \sin \left( {\alpha + \beta - \varphi_{2} } \right) + \hfill \\ m_{3} \left( {a_{2} \sin \left( {\alpha + \beta } \right) + a_{C3} \sin \left( {\alpha + \beta + \gamma - \varphi_{3} } \right)} \right) \hfill \\ \end{gathered} \right), \\ \Omega_{4} & = \left( {m_{4} \left( \begin{gathered} a_{2} \sin \left( {\alpha + \beta } \right) + a_{3} \sin \left( {\alpha + \beta + \gamma } \right) \hfill \\ + a_{C4} \sin \left( {\alpha + \beta + \gamma + \theta - \varphi_{4} } \right) \hfill \\ \end{gathered} \right)} \right). \\ \end{aligned}$$

The system of Eqs. (20)–(23) is using to estimate the physical parameters of the equivalent link, which is used for the HSMC.

The matrix of Coriolis and centrifugal coefficients $\,{\mathbf{C(\chi }}_{S} {\mathbf{,\dot{\chi }}}_{S} {\mathbf{)}}$ involves

$$\begin{aligned} c_{11} & = - a_{1} a_{c2} m_{\sum 2} \sin \left( {\beta - \varphi ^{\prime}_{2} } \right)\dot{\beta }, \\ c_{12} & = - a_{1} a_{c2} m_{\sum 2} \sin \left( {\beta - \varphi ^{\prime}_{2} } \right)\dot{\beta } - a_{1} a_{c2} m_{\sum 2} \sin \left( {\beta - \varphi ^{\prime}_{2} } \right)\dot{\delta }_{\alpha } , \\ c_{21} & = a_{1} a_{c2} m_{\sum 2} \sin \left( {\beta - \varphi ^{\prime}_{2} } \right)\dot{\delta }_{\alpha } . \\ \end{aligned}$$

The components of damping matrix ${\mathbf{B}}$ are

$$b_{1} = b_{m} ,\,b_{2} = b_{bo} .$$

The components of gravity vector ${\mathbf{G(\chi }}_{S} {\mathbf{)}}$ are given as

$$\begin{aligned} g_{1} & = \delta_{\alpha } k_{eq} + \delta_{\alpha 0} k_{eq} + a_{1} gm_{\Sigma 2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} } \right) \\ & \quad +\, a_{c2} gm_{\Sigma 2} \cos \left( {\alpha_{0} + \beta + \delta_{\alpha } + \delta_{\alpha 0} - \varphi ^{\prime}_{2} } \right) \\ & \quad +\, a_{c1} gm_{1} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} - \varphi_{1} } \right), \\ g_{2} & = a_{c2} gm_{\Sigma 2} \cos \left( {\alpha_{0} + \beta + \delta_{\alpha } + \delta_{\alpha 0} - \varphi ^{\prime}_{2} } \right). \\ \end{aligned}$$

3.2 Hierarchical Sliding Mode

The structure of HSMC with a parameter estimator is illustrated in Fig. 2.

Fig. 2

_{Control schematics of the proposed algorithm}

With setting the system states as $\chi_{1} = \delta_{\alpha }$ and $\chi_{2} = \beta$, the dynamic model can be re-written as

$$\left( \begin{gathered} m_{11} {\mathbf{(\chi }}_{S} {\mathbf{)}}\ddot{\chi }_{S1} {\mathbf{ + }}m_{12} {\mathbf{(\chi }}_{S} {\mathbf{)}}\ddot{\chi }_{S2} {\mathbf{ + }}b_{11} \dot{\chi }_{S1} {\mathbf{ + }}b_{12} \dot{\chi }_{S2} \hfill \\ {\mathbf{ + }}\,c_{11} {\mathbf{(\chi }}_{S} {\mathbf{,\dot{\chi }}}_{S} {\mathbf{)}}\dot{\chi }_{S1} {\mathbf{ + }}c_{12} {\mathbf{(\chi }}_{S} {\mathbf{,\dot{\chi }}}_{S} {\mathbf{)}}\dot{\chi }_{S2} {\mathbf{ + }}g_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}} \hfill \\ \end{gathered} \right){\mathbf{ = }}0,$$

(29)

$$\left( \begin{gathered} m_{21} {\mathbf{(\chi }}_{S} {\mathbf{)}}\ddot{\chi }_{S1} {\mathbf{ + }}m_{22} {\mathbf{(\chi }}_{S} {\mathbf{)}}\ddot{\chi }_{S2} {\mathbf{ + }}b_{21} \dot{\chi }_{S1} {\mathbf{ + }}b_{22} \dot{\chi }_{S2} \hfill \\ {\mathbf{ + }}\,c_{21} {\mathbf{(\chi }}_{S} {\mathbf{,\dot{\chi }}}_{S} {\mathbf{)}}\dot{\chi }_{S1} {\mathbf{ + }}c_{22} {\mathbf{(\chi }}_{S} {\mathbf{,\dot{\chi }}}_{S} {\mathbf{)}}\dot{\chi }_{S2} {\mathbf{ + }}c_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}} \hfill \\ \end{gathered} \right){\mathbf{ = }}\Psi_{bo} ,$$

(30)

Using state space representations, the dynamic model can be re-written as

$$\begin{gathered} \dot{\chi }_{S1} = \chi_{S2} ,\,\,\dot{\chi }_{S2} = \Theta_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}} + \Gamma_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}}\Psi_{bo} , \hfill \\ \dot{\chi }_{S3} = \chi_{S4} ,\,\,\dot{\chi }_{S4} = \Theta_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}} + \Gamma_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}}\Psi_{bo} , \hfill \\ \end{gathered}$$

(31)

where

$$\begin{aligned} \Theta_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}} & = \left( {m_{11} m_{12} - m_{12} m_{21} } \right)^{ - 1} \left( \begin{gathered} m_{12} \left( {g_{2} + b_{2} \dot{\chi }_{S1} + c_{21} \dot{\chi }_{S1} } \right) \hfill \\ - m_{22} \left( \begin{gathered} g_{1} + b_{1} \dot{\chi }_{S1} \hfill \\ + c_{11} \dot{\chi }_{S1} + c_{12} \dot{\chi }_{S2} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right), \\ \Gamma_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}} & = - m_{12} \left( {m_{11} m_{12} - m_{12} m_{21} } \right)^{ - 1} , \\ \Theta_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}} & = \left( {m_{11} m_{12} - m_{12} m_{21} } \right)^{ - 1} \left( \begin{gathered} - m_{11} \left( {g_{2} + b_{2} \dot{\chi }_{S2} + c_{21} \dot{\chi }_{S1} } \right) \hfill \\ + m_{21} \left( \begin{gathered} g_{1} + b_{1} \dot{\chi }_{S1} \hfill \\ + c_{11} \dot{\chi }_{S1} + c_{12} \dot{\chi }_{S2} \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered} \right), \\ \Gamma_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}} & = m_{11} \left( {m_{11} m_{12} - m_{12} m_{21} } \right)^{ - 1} . \\ \end{aligned}$$

The sliding mode surfaces are defined to control the body and the composite actuator as

$$\begin{aligned} \zeta_{1} & = \left( {\chi_{S2} - \chi_{S2T} } \right) + \lambda_{a1} \left( {\chi_{S1} - \chi_{S1T} } \right) + \lambda_{a2} \int\limits_{0}^{t} {\left( {\chi_{S1} - \chi_{S1T} } \right)} d\tau \\ & = \varsigma_{2} + \lambda_{a1} \varsigma_{1} + \lambda_{a2} \int\limits_{0}^{t} {\varsigma_{1} } d\tau = \left( {\chi_{S2} - \chi_{S2T} } \right) + \lambda_{a1} \varsigma_{1} + \lambda_{a2} \int\limits_{0}^{t} {\varsigma_{1} } d\tau , \\ \end{aligned}$$

(32)

$$\begin{aligned} \zeta_{2} & = \left( {\chi_{S4} - \chi_{S4T} } \right) + \lambda_{u1} \left( {\chi_{S3} - \chi_{S3T} } \right) + \lambda_{u2} \int\limits_{0}^{t} {\left( {\chi_{S3} - \chi_{S3T} } \right)} d\tau \\ & = \varsigma_{4} + \lambda_{u1} \varsigma_{3} + \lambda_{u2} \int\limits_{0}^{t} {\varsigma_{3} } d\tau = \left( {\dot{\chi }_{S4} - \dot{\chi }_{S4T} } \right) + \lambda_{u1} \varsigma_{3} + \lambda_{u2} \int\limits_{0}^{t} {\varsigma_{3} } d\tau , \\ \end{aligned}$$

(33)

where $\lambda_{a1} ,\,\lambda_{a2} ,\,\lambda_{u1} ,\,\lambda_{u2}$ are controller parameters. $\varsigma_{1} = \chi_{S1} - \chi_{S1T} ,$ $\varsigma_{2} = \chi_{S2} - \chi_{S2T} ,$ $\varsigma_{3} = \chi_{S3} - \chi_{S3T} ,$ and $\varsigma_{4} = \chi_{S4} - \chi_{S4T}$ are the tracking errors.

Differentiating with respect to time yields

$$\dot{\zeta }_{1} = \left( {\dot{\chi }_{S2} - \dot{\chi }_{S2T} } \right) + \lambda_{a1} \dot{\varsigma }_{1} + \lambda_{a2} \varsigma_{1} ,$$

(34)

$$\dot{\zeta }_{2} = \left( {\dot{\chi }_{S4} - \dot{\chi }_{S4T} } \right) + \lambda_{u1} \dot{\varsigma }_{3} + \lambda_{u2} \varsigma_{3} ,$$

(35)

To satisfy the tracking conditions, the first-order derivative of sliding manifolds $\dot{\zeta }_{i} = 0$. Consequently, the equivalent controls of sub-systemsare calculated as

$$\Psi_{eq1} = \Gamma_{1}^{ - 1} {\mathbf{(\chi }}_{S} {\mathbf{)}}\left( {\dot{\chi }_{S2T} - \lambda_{a1} \dot{\varsigma }_{1} - \lambda_{a2} \varsigma_{1} - \Theta_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}}} \right),$$

(36)

$$\Psi_{eq2} = \Gamma_{1}^{ - 1} {\mathbf{(\chi }}_{S} {\mathbf{)}}\left( {\dot{\chi }_{S4T} - \lambda_{u1} \dot{\varsigma }_{3} - \lambda_{u2} \varsigma_{3} - \Theta_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}}} \right),$$

(37)

The hierarchical structure of the sliding mode surfaces is designed as noted in Fig. 3. It can be observed clearly that the control mechanism consists of two layer: the first layer receives all the state variables to synthesis with their desired values and generate the first layer sliding surfaces; the second layer receive the output of the first layer which designs for both under-actuated or actuated parts of the dynamic model to design the overall controller for the entire system.

Fig. 3

_{Hierarchical structure of agrregrated sliding mode surfaces}

The first layer sliding mode surface (SMS) is designed for the actuator system $S_{1} = \zeta_{2}$. The second layer SMS is constructed by utilizing $S_{1}$ with SMS $\zeta_{1}$ of the main body as

$$S_{2} = \vartheta S_{1} + \zeta_{1} ,$$

(38)

where $\vartheta$ is a controller parameter.

For the first layer surface, the Lyapunov candidate function is chosen as

$$\Upsilon_{1} \left( t \right) = S_{1}^{T} S_{1} .$$

(39)

The controller for the sub-system of the boom is designed as

$$\Psi_{bo2} = \Psi_{eq2} + \Psi_{sw2} ,$$

(40)

where $\Psi_{sw2}$ is the switch control law of the first layer SMC.

Differentiate $\Upsilon_{1} \left( t \right)$ with respect to time and let $\dot{S}_{1} = - \omega_{f1} S_{1} - \omega_{f2} {\text{sgn}} \left( {S_{1} } \right)$. Here, $\omega_{f1} ,\,\,\omega_{f2}$ are the controller gains in the first layer.

Then, the control law (35) can be re-written as

$$\Psi_{bo2} = \Psi_{eq2} + \Gamma_{2}^{ - 1} {\mathbf{(\chi }}_{S} {\mathbf{)}}\dot{S}_{1} .$$

(41)

The second order controller is designed as

$$\Psi_{bo1} = \Psi_{bo2} + \Psi_{eq1} + \Psi_{sw1} ,$$

(42)

where $\Psi_{sw1}$ is the switch control law of the second layer controller.

The candidate Lyapunov function for this layer is selected as

$$\Upsilon_{2} \left( t \right) = \frac{1}{2}S_{2}^{T} S_{2} .$$

(43)

Differentiating $\Upsilon_{1} \left( t \right)$ with respect to time, we have,

$\dot{S}_{2} = - \omega_{s1} S_{2} - \omega_{s2} {\text{sgn}} \left( {S_{2} } \right)$, where $\omega_{s1} ,\,\,\omega_{s2}$ are the controller gains in the second layer.

The entire aggregated hierarchical SMC is constructed as

$$\Psi_{bo} = \left( \begin{gathered} - \omega_{s1} {\text{sgn}} \left( {S_{2} } \right) + \Gamma_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}}\Psi_{eq1} \hfill \\ - \omega_{s2} S_{2} + \vartheta \Gamma_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}}\Psi_{eq2} \hfill \\ \end{gathered} \right) \times \left( \begin{gathered} \Gamma_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}} \hfill \\ + \vartheta \Gamma_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}} \hfill \\ \end{gathered} \right)^{ - 1} .$$

(44)

3.3 Stability Analysis

The analysis of the closed-loop system stability is implemented by investigating the convergence of the composite sliding surface $S_{2} \left( t \right)$ and its sliding manifold components $S_{1} \left( t \right)$, $\zeta_{1} \left( t \right)$ to the origin. The asymptotical stability of these surfaces are provided as follows.

From the Lyapunov function (38) for the dynamic model (26), it is inferred that

$$\int\limits_{0}^{t} {\dot{\Upsilon }_{2} \left( t \right)d\tau } = \int\limits_{0}^{t} {\left( { - \omega_{s1} S_{2}^{2} - \omega_{s2} \left| {S_{2} } \right|} \right)d\tau } .$$

(45)

Then,

$$\Upsilon_{2} \left( t \right) - \Upsilon_{2} \left( 0 \right) = \int\limits_{0}^{t} {\left( { - \omega_{s1} S_{2}^{2} - \omega_{s2} \left| {S_{2} } \right|} \right)d\tau } ,$$

(46)

$$\begin{aligned} \Upsilon_{2} \left( 0 \right) & = \Upsilon_{2} \left( t \right) + \int\limits_{0}^{t} {\left( {\omega_{s1} S_{2}^{2} + \omega_{s2} \left| {S_{2} } \right|} \right)d\tau } \\ & \ge \int\limits_{0}^{t} {\left( {\omega_{s1} S_{2}^{2} + \omega_{s2} \left| {S_{2} } \right|} \right)d\tau } . \\ \end{aligned}$$

(47)

The actual system is affected by various disturbances caused by motion of the arm and the bucket, changes in lifting loads, and inaccuracies in the estimation of system parameters. They can be denoted by the bounded composite functions $\xi_{1} \left( t \right) \le \left| {\xi_{1} \left( t \right)} \right| \le \hat{\xi }_{1} \left( t \right)$, $\xi_{2} \left( t \right) \le \left| {\xi_{2} \left( t \right)} \right| \le \hat{\xi }_{2} \left( t \right)$.

For the system affected by such disturbances, the dynamic model becomes

$$\begin{aligned} & \dot{\chi }_{S1} = \chi_{S2} ,\dot{\chi }_{S2} = \Theta_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}} + \Gamma_{1} {\mathbf{(\chi }}_{S} {\mathbf{)}}\Psi_{bo} + \xi_{1} \left( t \right), \\ & \dot{\chi }_{S3} = \chi_{S4} ,\dot{\chi }_{S4} = \Theta_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}} + \Gamma_{2} {\mathbf{(\chi }}_{S} {\mathbf{)}}\Psi_{bo} + \xi_{2} \left( t \right), \\ \end{aligned}$$

(48)

The first-order derivative of the Lyapunov function is calculated as

$$\dot{\Upsilon }_{2} = S_{2} \dot{S}_{2} = S_{2} \left\{ \begin{gathered} - \omega_{s1} {\text{sgn}} \left( {S_{2} } \right) - \omega_{s2} S_{2} \hfill \\ + \vartheta \xi_{1} \left( t \right) + \xi_{2} \left( t \right) \hfill \\ \end{gathered} \right\}$$

(49)

It is obvious that

$$\dot{\Upsilon }_{2} \left( t \right) \le - \omega_{s1} S_{2}^{2} - \hat{\omega }_{s2} \left| {S_{2} } \right|,$$

(50)

where $\hat{\omega }_{s2} = \omega_{s2} - \vartheta {\kern 1pt} \hat{\xi }_{1} \left( t \right) - \hat{\xi }_{2} \left( t \right)$ is a positive number with $\omega_{s2} \ge \vartheta {\kern 1pt} \hat{\xi }_{1} \left( t \right) - \hat{\xi }_{2} \left( t \right)$. Because $\dot{\Upsilon }_{2} \le - \omega_{s1} S_{2}^{2} - \left| {S_{2} } \right|\left( {\omega_{s2} - \vartheta {\kern 1pt} \hat{\xi }_{1} \left( t \right) - \hat{\xi }_{2} \left( t \right)} \right)$, we have

$$\int\limits_{0}^{t} {\dot{\Upsilon }_{2} \left( t \right)d\tau } \le \int\limits_{0}^{t} {\left( { - \omega_{s1} S_{2}^{2} - \hat{\omega }_{s2} \left| {S_{2} } \right|} \right)d\tau } ,$$

(51)

and

$$\begin{aligned} \Upsilon_{2} \left( 0 \right) & \ge \Upsilon_{2} \left( t \right) + \int\limits_{0}^{t} {\left( {\omega_{s1} S_{2}^{2} + \hat{\omega }_{s2} \left| {S_{2} } \right|} \right)d\tau } \\ & \ge \int\limits_{0}^{t} {\left( {\omega_{s1} S_{2}^{2} + \hat{\omega }_{s2} \left| {S_{2} } \right|} \right)d\tau } . \\ \end{aligned}$$

(52)

In both cases, we have

$$\mathop {\lim }\limits_{t \to \infty } \int\limits_{0}^{t} {\left( {\omega_{s1} S_{2}^{2} + \hat{\omega }_{s2} \left| {S_{2} } \right|} \right)d\tau } \le \Upsilon_{2} \left( 0 \right) \le \infty ,$$

(53)

$$\mathop {\lim }\limits_{t \to \infty } \int\limits_{0}^{t} {\left( {\omega_{s1} S_{2}^{2} + \omega_{s2} \left| {S_{2} } \right|} \right)d\tau } \le \Upsilon_{2} \left( 0 \right) \le \infty .$$

(54)

Similarly,$\mathop {\lim }\limits_{t \to \infty } S_{1} \to 0$. On the basis of Barbalat’s lemma, it is inferred that $+ \omega_{s1} S_{2}^{2} + \hat{\omega }_{s2} \left| {S_{2} } \right| \to 0$,$+ \omega_{s1} S_{2}^{2} + \omega_{s2} \left| {S_{2} } \right| \to 0$,$+ \omega_{f1} S_{1}^{2} + \omega_{f2} \left| {S_{1} } \right| \to 0$, $\mathop {\lim }\limits_{t \to \infty } S_{2} = 0,$ and $\mathop {\lim }\limits_{t \to \infty } S_{2} = 0$ since $t \to \infty$, and $S_{1}$, $S_{2}$ are asymptotically stable.

In addition,

$$\mathop {\lim }\limits_{t \to \infty } S_{2} = \mathop {\lim }\limits_{t \to \infty } \left( {\vartheta S_{1} + \zeta_{1} } \right) = \vartheta \mathop {\lim }\limits_{t \to \infty } S_{1} + \mathop {\lim }\limits_{t \to \infty } \zeta_{1} = \mathop {\lim }\limits_{t \to \infty } \zeta_{1} .$$

From the previous proof, $\mathop {\lim }\limits_{t \to \infty } \zeta_{1} = \mathop {\lim }\limits_{t \to \infty } S_{2} = 0$. Therefore, the sliding surface of the overall subsystem satisfies the asymptotic stability conditions, and all of the state variables are converged to their desired values.

4 Simulation and Experiment Results

In this section, the simulations and experiments are explained in a general case. Here, the controller focuses on controlling the boom motion and reducing the vibration of the main body while the arm and bucket are driven.

4.1 Experimental Platform and System Parameters

The experimental platform of a small-scale excavator is given in Fig. 4.

Fig. 4

_{The small-scale experimental excavator system on an elastic foundation}

The system parameters are primarily obtained by direct measurement and reference of machine documentation, and a small number of them are estimated by data analysis. The values of these parameters are provided bellows.

$m_{1} = 25$ kg, $m_{2} = 3$ kg, $m_{3} = 1,2$ kg, $m_{4} = 0.9$ kg, $I_{1z} = 5$ kg m², $I_{2z} = 0.5$ kg m², $I_{3z} = 0.15$ kg m², $I_{4z} = 0.1$ kg m², $b_{1} = 200$ Nms/rad, $b_{2} = 30$ Nms/rad, $b_{3} = 20$ Nms/rad, $K_{eq} = 500$ Nm/rad, $g = 9.81$ m/s², $a_{1} = 16 \times 10^{ - 2}$ m, $a_{2} = 48 \times 10^{ - 2}$ m, $a_{3} = 16 \times 10^{ - 2}$ m, $a_{4} = 14 \times 10^{ - 2}$ m, $a_{c1} = 14 \times 10^{ - 2}$ m, $a_{c2} = 23.3 \times 10^{ - 2}$ m, $a_{c3} = 6.3 \times 10^{ - 2}$ m, $a_{c1} = 6.4 \times 10^{ - 2}$ m, $\varphi_{1} = 24 \times \pi /180$ rad, $\varphi_{1} = 24 \times \pi /180$ rad, $\varphi_{2} = 24 \times \pi /180$ rad $\varphi_{3} = 18 \times \pi /180$ rad, $\varphi_{4} = 59 \times \pi /180$ rad, $\alpha_{0} = 82 \times \pi /180$ rad.

4.2 Numerical Simulation

Figures 5 and 6 show the boom angle and the boom angular velocity of the excavator system controlled by the IHSMC which controls the boom angle from 290 to 300 degrees within 3 s, respectively. The convergence time for driving the boom to its reference values is 1.5 (s) for lifting and 0.75 (s) for lowering. In this case, the amplitude of the body’s vibration is limited, with the maximum value being 1 degree, as shown in Fig. 7, and the number of cycles to oscillate is one (the red solid line). Meanwhile, the numbers of joystick control are nearly two degrees and five cycles (the green dashed line). The differences are much more significant when investigating the body angular velocity, as shown in Fig. 8.

Fig. 5

Boom position control

Fig. 6

Boom angular velocity

Fig. 7

Body angle

Fig. 8

Body angular velocity

The control performances are satisfied with the motion of the other links and the impact of the composite disturbance given to the system during the period from 3.25 to 3.75 (s), as shown in Fig. 9. The IHSMC maintains the stability of the boom as a foundation on which the arm and bucket reside. Eventually, these links can be controlled accurately by a non-dynamic PID controller, as shown in Figs. 10, 11 and 12, 13.

Fig. 9

Composite disturbance

Fig. 10

Bucket position control

Fig. 11

Bucket angular velocity

Fig. 12

_{Arm position control}

Fig. 13

Arm angular velocity

4.3 Implementation Results

The results of experimentation are illustrated in Figs. 14, 15, 16, 17, 18, 19, 20, 21. The period for the boom to reach to its target value at 320 degrees is approximately 2 (s), as shown in Fig. 14. The vibration amplitude is limited to a value around 0.1 degree. In Fig. 16, the tiny vibrations of the main body (the amplitude is less than 0.1 degree) appear primarily when the boom starts and stops moving and reach zero at the desired value of the boom. The number of cycles and the oscillation phase of the body and boom coincide in the period from 3.8 (s) to 5 (s), which indicates that the vibration of the boom primarily affects the body. Consequently, the idea of quenching the vibration based on boom control is reasonable.

Fig. 14

_{Boom position control}

Fig. 15

Boom angular velocity

Fig. 16

Body angle

Fig. 17

Body angular velocity

Fig. 18

Bucket position control

Fig. 19

Bucket angular velocity

Fig. 20

Arm position control

Fig. 21

Arm angular velocity

The IHSMC not only ensures stable and accurate movement of the main body and boom, but also makes it easier to control other links when all of them are placed on the boom. Here, arm and boom are controlled by a simple PID controller, with the results shown in Figs. 18 and 20, respectively.

Remark

To apply the proposed controller to a real system, several issues arise as follows. One main issue is that the small-scale experimental excavator uses low-power directional electro-hydraulic servo valves, but a real excavator is usually controlled by the operator’s joystick operation. Therefore, to apply the proposed control law to a real excavator, the valve system must be adjusted. Moreover, it is more challenging to determine the system parameters, and the uncertainty is higher for real excavator systems. If the level of uncertainty is not so severe, the robust feature of the sliding mode algorithm can maintain control stability and accuracy. In severe uncertainty, the combination of the designed controller and an adaptive algorithm is more effective for real systems. The last issue is that the small experimental excavator model uses a brushless direct-current (BLDC) motor to drive a gear pump that supplies hydraulic pressure to the entire system, but a real excavator is actually powered by a high-performance internal combustion engine. This difference in mechanical properties is also an issue that requires attention when controlling a real system.

5 Conclusion

To address the problem of suspension of the excavator's vibration, this study proposes an integral hierarchical sliding mode control law, which is established to primarily control the boom and the main body accurately and stably. This control scheme is based on the real working condition that the oscillations are mostly derived from the motions of the boom while the excavator operates on an elastic foundation. The asymptotical stabilities of the sliding surfaces in the first and second layers guarantee the tracking conditions and suspending vibration. The composite disturbance impacting the system is overcome by the robust properties of the sliding algorithm. By using a parameter estimator, the designed control law can be employed coinciding with the operations of the arm and the bucket, which can be effortlessly controlled by a simple PID controller without any significant vibration. The effectiveness of the entire work is demonstrated by the experimental and the implemented results.

Appendix

The Jacobian matrix for translation of the ith link is given as follows:

$${\mathbf{J}}_{T1} = \left[ {\begin{array}{*{20}c} {J_{T1(11)} } & 0 & 0 & 0 \\ {J_{T1(21)} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\,\,{\mathbf{J}}_{T4} = \left[ {\begin{array}{*{20}c} {J_{T4(11)} } & {J_{T4(12)} } & {J_{T4(13)} } & {J_{T4(14)} } \\ {J_{T4(21)} } & {J_{T4(22)} } & {J_{T4(23)} } & {J_{T4(24)} } \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],$$

$${\mathbf{J}}_{T2} = \left[ {\begin{array}{*{20}c} {J_{T2(11)} } & 0 & 0 & {J_{T2(14)} } \\ {J_{T2(21)} } & 0 & 0 & {J_{T2(24)} } \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],{\mathbf{J}}_{T3} = \left[ {\begin{array}{*{20}c} {J_{T3(11)} } & {J_{T3(12)} } & 0 & {J_{T3(14)} } \\ {J_{T3(21)} } & {J_{T3(22)} } & 0 & {J_{T3(24)} } \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\,$$

where

$$\begin{aligned} J_{T1(11)} & = - a_{c1} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right),J_{T1(21)} = a_{c1} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \varphi_{1} } \right), \\ J_{T2(11)} & = - a_{c2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta - \varphi_{2} } \right), \\ J_{T2(21)} & = a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta - \varphi_{2} } \right), \\ J_{T2(14)} & = - a_{c2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta - \varphi_{2} } \right) - a_{1} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} } \right), \\ J_{T2(24)} & = a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta - \varphi_{2} } \right) - a_{1} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} } \right), \\ J_{T3(11)} & = - a_{c3} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma - \varphi_{3} } \right) - a_{2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right), \\ J_{T3(12)} & = - a_{c3} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma - \varphi_{3} } \right), \\ J_{T3(14)} & = - a_{c3} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma - \varphi_{3} } \right) \\ & \quad - a_{2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right) - a_{1} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} } \right), \\ J_{T3(21)} & = a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma - \varphi_{3} } \right) + a_{2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right), \\ J_{T3(22)} & = a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma - \varphi_{3} } \right), \\ J_{T3(24)} & = a_{c2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma - \varphi_{3} } \right) \\ & \quad + a_{2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right) - a_{1} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} } \right), \\ J_{T4(11)} & = - a_{c4} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma + \theta - \varphi_{4} } \right) \\ & \quad - a_{2} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right) - a_{3} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma } \right), \\ J_{T4(12)} & = - a_{c4} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma + \theta - \varphi_{4} } \right) \\ & \quad - a_{3} \sin \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma } \right), \\ J_{T4(22)} & = + a_{c4} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma + \theta - \varphi_{4} } \right) \\ & \quad + a_{3} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma } \right), \\ J_{T4(23)} & = + a_{c4} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma + \theta - \varphi_{4} } \right), \\ J_{T4(24)} & = + a_{3} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma } \right) + a_{2} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta } \right) \\ & \quad + a_{1} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} } \right) + a_{c4} \cos \left( {\alpha_{0} + \delta_{\alpha } + \delta_{\alpha 0} + \beta + \gamma + \theta - \varphi_{4} } \right). \\ \end{aligned}$$