1 Introduction

Friction-induced instability has been known as the root cause of undesired oscillations and noises in many engineering applications such as pad/pin–disk coupling in automotive industry [1,2,3,4], machining processes [5,6,7,8] and wheel–rail interactions [9,10,11]. Numerous researches have been conducted experimentally and theoretically to study the response of the systems oscillating due to the frictional contact; see [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] for further details. The common underlying mechanisms of friction generated instability in mechanical systems with various conditions have also been comprehensively reviewed in [27,28,29].

Nonlinearity in systems with frictional interface can arise due to the different mechanisms such as inertial nonlinearity, geometric nonlinearity, material nonlinearity, contact stiffness nonlinearity and nonlinearity due to the planar effects of friction [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Understanding the dynamics of oscillators with planar friction effects has been a canonical problem of interest for scientists over the past decades; see [45,46,47] and the references therein for further details. Using a ball-on-plate-type sliding system, Oberst and Lai investigated nonlinear in-plane friction coupling in their system [48]. Furthermore, they showed that the variation of the plate angle can cause instabilities in the structure. Similar findings about the role of the plate angle (also termed as the yaw angle misalignment (YAM)) on the motion stability of minimal models were reported in [49, 50].

Such structures may represent complex nonlinear phenomena such as modal interactions under various designs, loads and environmental conditions [51,52,53,54]. This means the energy used to excite a primary mode may be channeled to another mode (secondary mode) by means of a nonlinear coupling between the modes with commensurate or nearly commensurate linear natural frequencies [55]. Nonetheless and to our knowledge, the precise role of parameters associated with the planar friction (i.e., friction coefficient, periodically modulated normal force, plate angle and plate velocity) on modal interactions has received less attention from nonlinear dynamics perspective [56,57,58]. Therefore, the present problem is introduced to address this scientific issue. The system is a simple two-DOF linear structure integrated with a geometrically nonlinear elastic attachment [59]. Periodically modulated normal force, which is perpendicular to the in-plane modes, is exerted on the structure. In essence, the addition of the external attachment and friction forces introduces nonlinearities in the structure while imposing the two-to-one internal resonance between the modes. The objective of this paper is to investigate the stability of the aforementioned system and conduct a comprehensive parametric study to understand the role of various parameters on the nonlinear response of the system.

This paper is structured as follows. In Sect. 2, physical realization and mathematical modeling of a nonlinear two-DOF system in contact with the rigid plate are established. Then, nonlinear response and bifurcation characteristics of the aforementioned system are computed using AUTO software [60] in Sect. 3. A comprehensive parametric study is conducted to show the effect of the various parameters on the nonlinear response of the system in Sect. 4. Finally, Sect. 5 recapitulates the main findings of the paper.

Fig. 1
figure 1

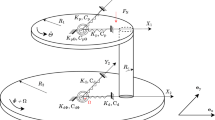
a A minimal two-DOF structure, \(c_i=4\pi \zeta _i m_if_i\), and \(f_i\) is the natural frequency of the structure without the external spring; b structure under the periodic normal force (perpendicular to the x-y plane) and in contact with the sliding rigid plate; c the deformed structure in contact with the sliding rigid plate; d side view of the model under the exerted normal force (N) and always in contact with the sufficiently large sliding rigid plate. Note that the vertical and horizontal modes have almost the same natural frequencies (\(f_1\approx f_2\)) without the external attachment. The external attachment and friction forces introduce nonlinearities [49, 59] and impose 2:1 internal resonance in the structure (\(f_{1a}\approx 2 f_2\)) . Note that x and y are the horizontal axis and the vertical axis, respectively. \(\alpha\) is the angle of misalignment or plate angle, \(\phi\) is the angle of the relative velocity (\({V_{rel}}\)) with respect to the x axis, \(V_d\) is the velocity of the rigid moving plate, and \(\theta\) is the angle of the deformed geometry. It can be understood that \(\sin (\phi )=\frac{V_d \sin (\alpha )-\dot{y}}{V_{rel}}\) and \(\cos (\phi )=\frac{V_d \cos (\alpha )-\dot{x}}{V_{rel}}\)

Full size image

2 Description of the mechanical model

Inspired by [49, 59, 61], a minimal two-DOF model in contact with a sufficiently large rigid moving plate (\(V_d\)) and under a periodically modulated normal force (\(N=N_s+N_d \cos (2\pi f t)\)) is considered, as sketched in Fig. 1. It must be noted that \(0<N_d<N_s\) (i.e., dynamic normal force amplitude (\(N_d\)) is less than the static normal force amplitude (\(N_s\))); thus, the structure is constrained to only oscillate in x-y plane. The Coulomb friction force (\(F_f=\mu ~N\)) aligned with the relative velocity (\(V_{rel}\)) is assumed in this study. The external attachment (\(k_{ext}=1000~N/m\)) with an initial length (L) and the planar friction force impose a two-to-one ratio between the vertical (\(f_{1a}\)) and the horizontal (\(f_2\)) natural frequencies of the structure, \(f_{1a} \approx 2f_{2}\). In this study, frequency range of investigation (f) for the normal force is around the vicinity of the vertical mode. The linear modal parameters of the structure (damping ratio coefficient\((\zeta )\), stiffness(k), natural frequency (\(f_n\))) without the addition of the external attachment are assumed as \(k_1=317.98~\mathrm {N/m}, \zeta _{1}=0.006, f_{1}=6.12~\mathrm {Hz}, k_2=362.58~\mathrm {N/m}, \zeta _{2}=0.0057, f_{2}=6.59~\mathrm {Hz}\). Indices one and two denote the vertical and the horizontal directions, respectively. After the attachment of the external spring to the structure, the vertical linear natural frequency becomes \(f_{1a}=12.46~\mathrm {Hz}\) (i.e., approximately twice the horizontal natural frequency). Note that these values were chosen as representative examples without loss of generality of the problem.

Linear modal stiffness and linear modal damping cause the linear restoring/dissipative forces (\(f_{l_x}\),\(f_{l_y}\)). As shown in Fig. 1, the external elastic attachment imposes length-dependent nonlinear restoring forces (\(f_{Nl_x}\),\(f_{Nl_y}\)) in the deformed configuration due to its length variation (\(\varDelta {L}\)). Considering the angle of deformed geometry (\(\theta\)) and the angle of the relative velocity with respect to the x axis (\(\phi\)), the restoring, dissipative and friction forces (\(f_{f_x}\),\(f_{f_y}\)) are mathematically expressed as:

$$\begin{aligned} f_{l_y}=\, & {} k_1y+ c_1\dot{y},~f_{Nl_y}\nonumber \\=\, & {} k_{ext}({\sqrt{(L+{y})^2+{x}^2}}-L)\sin \theta ,~f_{f_y}=F_f\sin \phi \end{aligned}$$
(1)
$$\begin{aligned} f_{l_x}= \,& {} k_2x+ c_2\dot{x},~f_{Nl_x}\nonumber \\=\, & {} k_{ext}({\sqrt{(L+{y})^2+{x}^2}}-L)\cos \theta ,f_{f_x}=\,F_f\cos \phi \end{aligned}$$
(2)

where

$$\begin{aligned} \sin \theta=\, & {} \frac{L+y}{\sqrt{(L+{y})^2+{x}^2}},~~~\cos \theta =\, \frac{x}{\sqrt{(L+{y})^2+{x}^2}} \nonumber \\ \sin \phi=\, & {} \frac{V_d \sin (\alpha )-\dot{y}}{V_{rel}}, ~~~~~~\cos (\phi )=\,\frac{V_d \cos (\alpha )-\dot{x}}{V_{rel}} \end{aligned}$$
(3)

Having defined the forces applied to the structure, the governing equations of motion are written based on the Newton’s law of motion as:

$$\begin{aligned} m_1\ddot{{y}}+ f_{l_y}+ f_{Nl_y}=\, & {} f_{f_y} \end{aligned}$$
(4)
$$\begin{aligned} m_2\ddot{{x}}+ f_{l_x}+ f_{Nl_x}=\, & {} f_{f_x} \end{aligned}$$
(5)

Finally, the governing differential equations (DEs) of such model are expressed as:

$$\begin{aligned}&\ddot{\tilde{y}}+ 2\zeta _{1}\omega _{1}\dot{\tilde{y}}+ \omega _{1}^2\tilde{y}\nonumber \\&\quad + \frac{k_{ext}(1+\tilde{y})}{m_{1}}(1-\frac{1}{\sqrt{(1+\tilde{y})^2+\tilde{x}^2}})= \frac{F_f}{m_{1}L} \sin \phi \end{aligned}$$
(6)
$$\begin{aligned}&\ddot{\tilde{x}}+ 2\zeta _{2}\omega _{2}\dot{\tilde{x}}+ \omega _{2}^2\tilde{x}\nonumber \\&\quad + \frac{k_{ext}\tilde{x}}{m_{2}}(1-\frac{1}{\sqrt{(1+\tilde{y})^2+\tilde{x}^2}})=\frac{F_f}{m_{2}L} \cos \phi \end{aligned}$$
(7)

where \(\tilde{y}=y/L\) (dimensionless vertical displacement), \(\tilde{x}=x/L\) (dimensionless horizontal displacement), \(\omega _i=\sqrt{k_i/m_i}, \zeta _i=c_i/(2\omega _i m_i)\); \(c_i\) and \(m_i, i =1, 2\) are the damping coefficients and masses, respectively; \(F_f= \mu ~(N_s+N_d \cos (2\pi f t))\), t is time; and \(\mu\) is the Coulomb friction coefficient.

Equations (6) and (7) are solved numerically for zero initial conditions and then the bifurcation characteristics of the system is studied using AUTO software. Considering \(V_{rel}= \sqrt{(V_d^2+(\dot{x}^2+\dot{y}^2)-2V_d~(\dot{x}\cos {\alpha }+\dot{y}\sin {\alpha }))}\), velocity-dependent friction models [18] could also be assumed to study the stick–slip response of the system. This issue will be investigated in the future studies. This paper considers the effect of modal interaction in the regions where stick-slip behavior does not exist (i.e., relatively large values for \(V_d\))[49]. Therefore, it is reasonable to consider Coulomb friction model in the aforementioned structure.

Fig. 2
figure 2

a Auto-calculated force–response curves with \(f=12.5~\mathrm {Hz}\) and \(f=12.2~\mathrm {Hz}\) for the dimensionless vertical displacement (\(\tilde{y}=\frac{y}{L}\)). The dashed lines represent the unstable motion due to the denoted bifurcations; b force–response curves with \(f=12.5~\mathrm {Hz}\) and \(f=12.2~\mathrm {Hz}\) for the dimensionless horizontal displacement (\(\tilde{x}=\frac{x}{L}\)); c fast Fourier transform (FFT) of \(\tilde{y}\) for \(f=12.2~\mathrm {Hz}\) and \(N_d=0.05~\mathrm {N}\);d FFT of \(\tilde{x}\) for \(f=12.2~\mathrm {Hz}\) and \(N_d=0.05~\mathrm {N}\);e FFT of \(\tilde{y}\) for \(f=12.2~Hz\) and \(N_d=0.15~N\); f FFT of \(\tilde{x}\) for \(f=12.2~Hz\) and \(N_d=0.15~N\). L is 5\(~\mathrm {mm}\) in all the above simulations. Parameters are \(\alpha = \frac{\pi }{3}\), \(V_d= 0.6~\mathrm {m/s}\), \(N_s=1~N\), \(\mu =0.5\)

Full size image
Fig. 3
figure 3

a Auto-calculated vertical frequency responses; b horizontal frequency responses; the dashed lines and dotted lines denote the unstable solutions due to the saddle-node bifurcation and Hopf bifurcation, respectively. Response is not periodic after the occurrence of the Hopf bifurcation (amplitude–phase-modulated response). Note that frequency response curves are calculated by fixing \(N_d\) and sweeping f (the horizontal axis). Note that L is 5\(~\mathrm {mm}\), \(\alpha = \frac{\pi }{3}\), \(V_d= 0.6~\mathrm {m/s}\), \(N_s=1~N\), \(\mu =0.5\)

Full size image
Fig. 4
figure 4

\(V_d\) effects on a force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless vertical displacement (\(\tilde{y}=\frac{y}{L}\)) and b force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless horizontal displacement (\(\tilde{x}=\frac{x}{L}\)). Other parameters are \(\alpha =\frac{\pi }{3}\), \(\mu =0.5\), \(N_s=1~N\), \(L= 5~\mathrm {mm}\)

Full size image
Fig. 5
figure 5

\(N_s\) effects on a force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless vertical displacement (\(\tilde{y}=\frac{y}{L}\)) and b force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless horizontal displacement (\(\tilde{x}=\frac{x}{L}\)). Other parameters are \(\alpha =\frac{\pi }{3}\), \(\mu =0.5\), \(V_d=1~\mathrm {m/s}\), \(L= 5~\mathrm {mm}\)

Full size image
Fig. 6
figure 6

\(\mu\) effects on a force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless vertical displacement (\(\tilde{y}=\frac{y}{L}\)) and b force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless horizontal displacement (\(\tilde{x}=\frac{x}{L}\)). Other parameters are \(\alpha =\frac{\pi }{3}\), \(N_s=1~N\), \(V_d=1~\mathrm {m/s}\), \(L= 5~\mathrm {mm}\)

Full size image
Fig. 7
figure 7

\(\alpha\) effects on a force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless vertical displacement (\(\tilde{y}=\frac{y}{L}\)) and b force–response curves with \(f=12.5~\mathrm {Hz}\) and for the dimensionless horizontal displacement (\(\tilde{x}=\frac{x}{L}\)). Other parameters are \(N_s=~1~N\), \(\mu =0.5\), \(V_d=1~\mathrm {m/s}\), \(L= 5~\mathrm {mm}\)

Full size image

3 Numerical bifurcation analysis

AUTO can be used to study the bifurcation characteristics of the dynamical systems with a periodic force. In that regard, the first step is to rescale time as \(t\rightarrow t/T\) and write the equations of motion in the state space with displacements and velocities as the state variables. Note that T is the period of the solution. Then, the non-autonomous system should be converted to the autonomous one by either of two methods: (i) time is introduced as a new added state and (ii) the harmonic forcing term is replaced by an autonomous dynamical system with a stable periodic orbit. The latter is used to calculate the bifurcation diagrams; see Chapter 7 in [62] for further details. Force–response curves [51] (Figs. 2a and   b) are calculated by fixing the normal force excitation frequency (f) and increasing the dynamic part of the normal force excitation amplitude (\(N_d\)). Given a fixed nonzero number for the static part of the normal force (\(N_s\)), when the \(N_d\) has a certain amplitude with a frequency close to the twice the horizontal natural frequency (\(f \approx 2f_2\)), horizontal response loses its stability, period-doubling (PD) bifurcation, leading to the formation of a periodic limit cycle with a frequency of \(\frac{f}{2}\) (Fig. 2c–f). The criticality (sub-critical vs super-critical) of the PD bifurcation is controlled by f for a constant set of parameters as shown in Fig. 2. Further increase in the excitation amplitude (\(N_d\)) may lead to an amplitude–phase-modulated response in the structure. The occurrence of the Hopf bifurcation is also governed by the parameters such as in-plane angular misalignment (\(\alpha\)) and the plate constant velocity (\(V_d\)). This will be investigated comprehensively in the next section.

Frequency–response curves show the effect of normal force excitation frequency (f) while the dynamic normal force amplitude (\(N_d\)) remains constant. Internal resonance property is manifest through the frequency splitting of the vertical response in Fig. 3a [51]. Moreover, it is observed that there is an interval (bandwidth) for the normal force frequency over which the horizontal mode is activated by showing a softening behavior in Fig. 3b. The width of the interval depends on \(N_d\). It is understood that increasing \(N_d\) provides a wider bandwidth for the horizontal mode activation. Furthermore, frequency–response curves show the existence of Hopf bifurcation, which causes an amplitude–phase-modulated response, for a range of normal force frequencies in Fig. 3. In fact, the 2:1 internal resonance between the in-plane modes are superficially similar to Froude oscillations of a ship and other previously reported mechanical structures in the literature [51, 52].

To conclude this section, the horizontal mode activation occurs because of the presence of 2:1 internal resonance (2:1 ratio between the natural frequencies) and friction forces with a time-periodic normal force with an excitation frequency close to the twice the horizontal natural frequency.

4 Parametric study

This section examines the role of the dynamic normal force amplitude (\(N_d\)), static normal force amplitude (\(N_s\)), in-plane angular misalignment or YAM (\(\alpha\)), friction coefficient (\(\mu\)) and the plate velocity (\(V_d\)). While the two-to-one internal resonance property is retained, this parametric study demonstrates practical ways to alter the required threshold for the PD bifurcation and the elimination of the subsequent Hopf bifurcation in the structure response. As discussed earlier, there is a threshold for \(N_d\) above which the horizontal mode is activated . While other parameters remain the same, force–response curves for different values of the plate velocity (\(V_d\)) are shown in Fig. 4. It is understood that increasing \(V_d\) leads to a lower required threshold (\(N_d\)) for the (super-critical) PD bifurcation. Furthermore, lower values of \(V_d\) eliminate the occurrence of the Hopf bifurcation in the system response. Figure 5 depicts the effect of the static normal force (\(N_s\)) while the other parameters are the same. It can be seen that the lower values of \(N_s\) reduce the thresholds for the PD bifurcation and the subsequent Hopf bifurcation alongside reducing the vibration level of the structure. It can be seen that the required threshold for the PD bifurcation and the subsequent Hopf bifurcation grows by decreasing the value of the friction coefficient (\(\mu\)) while other parameters are unchanged (Fig. 6). force–response curves for different values of the plate angle (\(\alpha\)) are illustrated in Fig. 7. It can be seen that the in-plane angular misalignment alters the required threshold of PD bifurcation. Furthermore, the Hopf bifurcation can be eliminated due to the YAM angle (\(\alpha\)). Similar to the earlier works [49], It can be understood that the YAM angle, the rigid plate velocity and the friction coefficient provide a damping effect to reduce the vibration level of the structure. This parametric study showed a trade-off between the vibration level of the structure and the occurrence of the potential bifurcations.

To sum up, the parameters such as in-plane angular misalignment (\(\alpha\)), friction coefficient (\(\mu\)) and initial plate velocity (\(V_d\)) act as threshold force tuning parameters. These findings can be useful for design improvement of the vibration mitigation structures and problems which involve frictional contacts such as disc brake squeal [27, 49].

5 Conclusions

The nonlinear dynamics of a two-DOF internally resonant sliding system in contact with a rigid plate is investigated in this work. The structure, subjected to a harmonic normal load, shows period-doubling (PD) and Hopf bifurcations when the dynamic normal force amplitude is increased at a frequency close to the twice the horizontal natural frequency. Comprehensive numerical calculations reveal that (a) the required threshold for the occurrence of the PD bifurcation can be altered by the system parameters and (b) Hopf bifurcation can be eliminated by properly choosing the plate angle and plate velocity. These can be attributed to the fact that the total damping of the structure can be altered by the generated friction forces due to the different configurations for the rigid plate. The results presented in this work may provide some insights in the design improvement of the current vibration mitigation structures and systems with frictional contacts such as pad–brake coupling in automotive industries.

The future plan of this work is to build a test rig of the model presented in this study. Furthermore, the practicality of tuning the nonlinearities by changing the parameters such as in-plane angular misalignment, friction coefficient and plate velocity will be studied experimentally. Exploring the dynamics of the system in the regions where stick–slip behavior occurs under certain conditions will also be discussed in future works.