Bifurcation for Non-smooth Dynamical Systems via Reduction Methods

Abstract

Due to the presence of discontinuities, non-smooth dynamical systems (PWS) present a wide variety of bifurcations, which cannot be explained by the classical theory, for instance, transition from sticking to sliding due to friction and sudden loss of stability as typically observed in mechanics. These phenomena are due to interactions between the boundaries and the phase trajectories that cross them from one region to another. In the present work, we review the concept of invariant sets given as cone-like objects which has turned out as an appropriate generalization of the notion of center manifolds. The existence of invariant cones containing a segment of sliding orbits and stability properties of those cones are also investigated. Based on these results we present new bifurcation phenomena in a class of 3D-PWS concerning sliding modes. Further we show that the dynamics within the sliding motion area is described by a simple one-dimensional equation. We illustrate various forms of bifurcation, stick-slip motion, and the reduction procedure by a six-dimensional brake system given by three coupled oscillators.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Non-smooth dynamical systems occur as models in many applications related to science, engineering, economics, and control theory. Typically non-smooth effects are due to dry friction or impacts in mechanics, switches in electrical systems, control of pacemakers through external state-dependent impulses, etc.

A large class of such situations can be modelled by systems of ordinary differential equations defined on adjacent components of the phase space together with additional rules for the transition from one component to another.

A typical situation can be written in the form

$$\displaystyle{ \dot{\xi }= f_{i}(\xi ),(\xi \in \mathcal{M}_{i})(i = 1,\ldots,n), }$$

where the phase space ${\mathbb{R}}^{n}$ is separated into disjoint and open sets $\mathcal{M}_{i}$ such that ${\mathbb{R}}^{n} =\bigcup _{ i}^{n}\bar{\mathcal{M}}_{i}$.

The transition rules can be formulated as

$$\displaystyle{ \xi (t_{+}^{{\ast}}) = R(\xi (t_{ -}^{{\ast}})), }$$

when the trajectory $\xi (t) \in \mathcal{M}_{j}(t <{t}^{{\ast}})$ reaches the boundary $\partial \mathcal{M}_{j}$ of $\mathcal{M}_{j}$ at the time t ^∗.

Typical constellations for transition are

• Direct crossing from $\mathcal{M}_{j}$ to some $\mathcal{M}_{i}$

• Sliding in $\partial \mathcal{M}_{j}$ for some time

• Jumps due to impacts

Of course, the class of non-smooth systems allows more general types of equations such as algebraic components (related to DAE), PDE, or even mixed forms usually called hybrid systems.

Here we will restrict our attention to systems described by ODE.

The fundamental theory for such systems as far as an appropriate notion of the term “solution” as well as fundamental properties like existence and uniqueness are concerned have already been laid by Filippov [8, 9]. Qualitative properties have been less studied. More than half a century ago investigations concerning the dynamics and bifurcations for non-smooth systems raised a rather new topic developed during the past decades. An excellent recent review is given in [5].

First investigations had been stimulated by experiments exploring phenomena related to dry friction or impacts. As an idealized experimental set up to analyze such phenomena friction and impact oscillators [1, 5] in various forms have been designed which can easily be modeled by differential equations. Since experimental results show similar effects concerning for example bifurcation as were known for smooth systems, it was suggested to analyze the corresponding mathematical systems systematically and to develop appropriate tools known from classical bifurcation theory.

Questions of particular interest were related to a characterization of solutions with regard to stability, to various mechanisms of bifurcation especially to the generation of periodic orbits, to qualify systems by characteristic numbers such as Lyapunov exponents, or to establish procedures like the center manifold approach to reduce higher dimensional systems to an equivalent lower dimensional system carrying the essential dynamics.

As all these methods crucially depend on an approximation by linearization, differentiability is needed which by definition does not hold for non-smooth systems.

Hence, new approaches had to be developed. According to the degree of nonsmoothness the systems can be divided into various classes. The simplest situation is given by continuous but not differentiable systems. In that case solutions are (absolutely) continuous going along with a direct crossing from one component to another.

Discontinuous systems allow a great variety of phenomena due to an abrupt change of the corresponding vector fields, for example sliding motion, if all vector fields of the adjacent components are directed toward the boundary. The solution is then forced to remain within the boundary leading to a sliding motion which is governed by the Filippov extension [8, 9].

A particular case is given by impact systems; due to impacts the trajectory in phase space is no longer continuous but involves jumps. For mechanical systems jumps typically occur in the velocity component. As an illustrative example we refer to the motion of bells where the interaction of the coupled system of bell and clapper and the influence of impacts can be analyzed [12, 15].

Lyapunov exponents are frequently used to characterize stable resp. chaotic motion. Since the classical definition depends on properties of the linearized flow, existence for non-smooth system is not obvious. Various investigations have shown that they can be defined properly for non-smooth systems as well and that they provide a reliable tool to describe the dynamics, see [11] for a review.

Standard bifurcation theory as well is built up on linearization techniques such as the Lyapunov–Schmidt procedure or a center manifold approach.

The change of stationary solutions to periodic motion is a frequent situation in practical applications. The corresponding mathematical result in the form of Hopf-bifurcation relies on properties of the linearized system such as the crossing of a pair of complex eigenvalues through the imaginary axis. These analytical criteria do not work for non-smooth systems since there is no linearization.

The corresponding geometric analog though suggests a suitable approach. At the bifurcation point there is a switch in the basic system from a stable focus to an unstable focus via a center. This feature exists for appropriate piecewise linear systems as well and can be used to trigger the bifurcation of periodic orbits in the form of some kind of generalized Hopf-bifurcation. This approach has been carried out first for planar systems [22–24] using a simple Poincaré map. The idea to split a piecewise nonlinear system into a piecewise linear system (PWLS) and remaining terms of higher order first used for planar systems serves as an useful approach for higher dimensional systems as well. A successful technique to analyze the dynamics of high dimensional systems is based on reduction to lower dimensional systems which contain the essential dynamics. Usually, this is done by the construction of invariant manifolds. The center manifold approach is known as a well-established procedure for such a reduction.

There are various ways to construct invariant manifolds, which are usually defined as solution of an appropriate fixed point problem in function spaces. It is common to these approaches that they are based on properties of the linearized problem, and hence differentiality is required.

Since that situation is typically not given for non-smooth systems, new methods have to be developed.

The key idea which we pursue is based on the splitting of the piecewise smooth system into a piecewise linear part and nonlinear perturbations of higher order.

For piecewise linear systems it is easy to set up a Poincaré map, to study its properties, and to define invariant sets, typically given as invariant cones.

It can then be shown that these invariant sets remain under small perturbation in the way that they are deformed to cone like surfaces. These invariant surfaces can be seen as generalization of center manifolds for piecewise smooth systems, and they can be used to reduce investigation of the bifurcation and stability. We note that such cones have already been detected in the analysis of continuous piecewise linear systems [3, 4]. Our analysis is based on the fact that the Poincaré map for the PWLS can be split into a sum of two operators representing different differentiality properties crucial for the analysis.

The motion on the cones can easily been used to illustrate the fact well known in control theory that the combination of stable systems may lead to instability. This corresponds to the situation that the cone itself is attractive, but the dynamics on the cone is unstable. In [16] Marsden and Scheurle presented a general approach to construct invariant manifolds for smooth systems by a method based on deformations of the linear part. It would be an interesting project to investigate if that approach could be carried over with piecewise linear systems used as a base.

For 3D continuous piecewise smooth systems with two zones a normal form has been derived [3, 4]. In the case of discontinuous systems this is more complicated. Preliminary results have been obtained by Weiss [18].

In addition, discontinuous piecewise linear systems exhibit a more complicated behavior, such as sliding or constellations with multiple attractive invariant cones.

Within the sliding area the dimension is reduced anyway. For piecewise linear smooth system the dimension can be further reduced due to the special homogeneous form of the Filippov extension. This reduction allows a simplified analysis of the sliding motion dynamics; in particular for three-dimensional systems the situation turns out to be simple, since the sliding motion can be split into components separated by invariant manifolds.

The dynamics within the sliding area may as well lead to further bifurcations; various situations will be illustrated by examples. For higher dimensional systems the situation is more complicated.

The concept of generalized invariant “manifold” carries over to the case that sliding is involved. The proof is obvious if the flow in the sliding area is linear which holds under certain conditions. The general results need some extra care, which will be carried out elsewhere [20].

2 General Setting

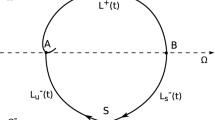
To describe the results we use a simplified setting of a piecewise smooth system (PWS) in ${\mathbb{R}}^{n}$ given in two half-spaces separated by a hyperplane $\mathcal{M}:=\{\xi \in {\mathbb{R}}^{n}\vert \;h(\xi ) = 0\}$, Fig. 5.1:

$$\displaystyle\begin{array}{rcl} \dot{\xi }& =& \left \{\begin{array}{cc} f_{+}(\xi ),&\xi \in \mathbb{R}_{+}^{n}, \\ f_{-}(\xi ),&\xi \in \mathbb{R}_{-}^{n},\\ \end{array} \right.{}\end{array}$$

(5.1)

where $f_{\pm }: {\mathbb{R}}^{n} \rightarrow {\mathbb{R}}^{n}$ are sufficiently smooth functions and ${\mathbb{R}}^{n}$ is split into two regions $\mathbb{R}_{+}^{n}$ and $\mathbb{R}_{-}^{n}$ by the separation manifold $\mathcal{M}$ such that ${\mathbb{R}}^{n} = \mathbb{R}_{+}^{n} \cup \mathcal{M}\cup \mathbb{R}_{-}^{n}$. The regions $\mathbb{R}_{+}^{n}$ and $\mathbb{R}_{-}^{n}$ are defined as

$$\displaystyle{ \begin{array}{cl} \mathbb{R}_{+}^{n} =\{\xi \in {\mathbb{R}}^{n}\vert h(\xi )> 0\}, \\ \mathbb{R}_{-}^{n} =\{\xi \in {\mathbb{R}}^{n}\vert h(\xi ) <0\}. \end{array} }$$

On the separating hyperplane $\mathcal{M}$ we need additional rules describing the interaction:

• (a) Direct transversal crossing.

  Fig. 5.1

  

  Two half-spaces separated by a hyperplane

  Let $\rho (\xi ) = {n}^{\!\mathrm{T}}(\xi )f_{ +}(\xi ){n}^{\!\mathrm{T}}(\xi )f_{ -}(\xi )$, (the normal vector n(ξ) perpendicular to the manifold $\mathcal{M}$ is given by $n(\xi ) = \frac{\nabla h(\xi )} {\|\nabla h(\xi )\|_{2}}$). Then, the direct crossing set is defined as ${\mathcal{M}}^{c} =\{\xi \in \mathcal{M}\vert \rho (\xi )> 0\}$. Further, the direct crossing set can be partitioned into two subsets: $\mathcal{M}_{-}^{c} =\{\xi \in {\mathcal{M}}^{c}\;\vert \;{n}^{\!\mathrm{T}}(\xi )f_{ +}(\xi ) <0\}$ and $\mathcal{M}_{+}^{c} =\{\xi \in {\mathcal{M}}^{c}\;\vert \;{n}^{\!\mathrm{T}}(\xi )f_{ +}(\xi )> 0\}$, Fig. 5.2a.

Fig. 5.2

Schematic illustration dynamics at a switching manifold. (a) Transversal crossing; (b) sliding mode

A simple system showing direct crossing is given by the continuous but piecewise smooth linear system.

Example 5.1 ([4]). 

Set $h(\xi ) = e_{1}^{\!\mathrm{T}}\xi$, $f_{\pm }(\xi ) = {A}^{\pm }\xi$, ${A}^{\pm } = \left (\begin{array}{ccc} {t}^{\pm } &- 1&0 \\ {m}^{\pm }& 0 &1 \\ {d}^{\pm } & 0 &0\\ \end{array} \right )$,

here both matrices satisfy the continuity relation ${A}^{+} - {A}^{-} = ({A}^{+} - {A}^{-})e_{1}e_{1}^{\!\mathrm{T}}$. Hence, all trajectories of this system approaching the hyperplane $\mathcal{M}$ cross it immediately and for such initial condition, there is a unique absolutely continuous solution.

• (b) Sliding on $\mathcal{M}$.

  The sliding mode set is defined as ${\mathcal{M}}^{s} =\{\xi \in \mathcal{M}\;\vert \;\rho (\xi ) \leq 0\}$. This set is further classified as attracting $\mathcal{M}_{-}^{s}$ or repulsive $\mathcal{M}_{+}^{s}$

  $$\displaystyle{ \begin{array}{cl} \mathcal{M}_{-}^{s} =\{\xi \in {\mathcal{M}}^{s}\;\vert \;{n}^{\!\mathrm{T}}(\xi )f_{ +}(\xi ) <0\}, \\ \mathcal{M}_{+}^{s} =\{\xi \in {\mathcal{M}}^{s}\;\vert \;{n}^{\!\mathrm{T}}(\xi )f_{ +}(\xi )> 0\}.\end{array} }$$

  If $\xi \in \mathcal{M}_{-}^{s}$, then the vector field of both systems at ξ points toward ${\mathcal{M}}^{s}$, hence the flow cannot leave ${\mathcal{M}}^{s}$ at ξ; $\mathcal{M}_{-}^{s}$ is called attractive sliding area.

  If $\xi \in \mathcal{M}_{+}^{s}$, then both vector fields are directed away from ${\mathcal{M}}^{s}$ at ξ; hence the flow in forward time is not uniquely defined at ξ and $\mathcal{M}_{+}^{s}$ is called repulsive, Fig. 5.2b. The flow in ${\mathcal{M}}^{s}$ itself is governed by Filippov’s extension:

  $$\displaystyle{ \dot{\xi }= \frac{{n}^{\!\mathrm{T}}(\xi )f_{ -}(\xi ) \cdot f_{+}(\xi ) - {n}^{\!\mathrm{T}}(\xi )f_{ +}(\xi ) \cdot f_{-}(\xi )} {{n}^{\!\mathrm{T}}(\xi )(f_{-}(\xi ) - f_{+}(\xi ))}. }$$

  (5.2)

Example 5.2 ([7]). 

Set: $h(\xi ) =\xi _{2} - 0.2$ and

$$\displaystyle{ f_{+}(\xi ) = \left (\begin{array}{c} \xi _{2} \\ -\xi _{1} - \frac{1} {0.8+\xi _{2}}\\ \end{array} \right ),\quad f_{-}(\xi ) = \left (\begin{array}{c} \xi _{2} \\ -\xi _{1} + \frac{1} {1.2-\xi _{2}}\\ \end{array} \right ). }$$

We can define the sliding region as: ${\mathcal{M}}^{s} =\{\xi \in \mathcal{M},(\xi _{1} + 1)(\xi _{1} - 1) <0\}$ which is attractive, i.e., ${\mathcal{M}}^{s} = \mathcal{M}_{-}^{s}$ where $\mathcal{M}_{-}^{s} =\{\xi \in {\mathcal{M}}^{s},\xi _{1} \in (-1,1)\}$. Therefore using the sliding vector field (5.2), we obtain F _s as:

$$\displaystyle{ F_{s} = \left (\begin{array}{c} 0.2\\ 0\\ \end{array} \right ). }$$

Thus, the sliding flow in ξ ₁ grows linearly within $\mathcal{M}_{-}^{s}$ until it reaches the boundary of sliding at ξ ₁ = 1. In Fig. 5.3, we show the periodic orbit containing a segment of sliding motion.

• (c) Jumps in phase space

  Fig. 5.3

  

  Periodic orbit comprising a sliding segment

  Impacts at a specific time ${t}^{i}\;(i = 1,2,\ldots )$ will cause a jump in phase space due to an impact rule

  $$\displaystyle{ \xi (t_{+}^{i}) = R(\xi (t_{ -}^{i})), }$$

  where t ₋ and t ₊ are the instants of time immediately before and after an impact.

Usually Newton’s impact rule is used and formulated as reflection of the velocity at the impact point together with some damping. Typical examples are given by impact oscillators.

Example 5.3 (Impact Pendulum [2]). 

The dynamics of the impact pendulum (Fig. 5.4) between impacting is described by the equations:

$$\displaystyle\begin{array}{rcl} \ddot{\phi }(t) +\sin \phi (t) = g(t),\;\;\;-\hat{\phi } <\phi (t),& & {}\\ \left.\begin{array}{c} \phi (t_{+}) =\phi (t_{-}) \\ \dot{\phi }(t_{+}) = -r\dot{\phi }(t_{-})\\ \end{array} \right \},\mathrm{if}\;\phi (t) = -\hat{\phi }&&{}\\ \end{array}$$

where r ∈ (0, 1] denotes some factor reflecting damping.

Example 5.4 (Bells as Impacting System). 

Bells are a nice example for impacting systems with state-dependent impacts. Following Veltmann’s analysis [17] with regard to the large Emperor’s bell in the Cathedral of Cologne the system of bell and clapper can be modelled as a (forced) double pendulum.

While Veltmann has derived this system to understand the curious behavior why the Cathedral of Cologne did not ring when installed in 1887, the system of bell and clapper provides an example of an impacting system showing typical behavior such as multiple impacts eventually leading to grazing. Following [12, 15] the non-dimensionalized equations of motion for a model of an impacting-contact model of a bell and clapper takes the form

$$\displaystyle{ \mathbf{M}(\Phi )\ddot{\Phi } + \mathbf{B}(\Phi )\dot{{\Phi }}^{2} + \mathbf{C}\dot{\Phi } + \mathbf{D}(\Phi ) = \mathbf{F}(\tau ), }$$

(5.3)

with impact events

$$\displaystyle{ \dot{\varphi }_{2}(\tau _{+}) -\dot{\varphi }_{1}(\tau _{+}) =\mu \big (\dot{\varphi }_{2}(\tau _{-}) -\dot{\varphi }_{1}(\tau _{-})\big),\mathrm{when}\;\varphi _{2} =\varphi _{1} \pm \frac{\psi } {2} }$$

(5.4)

where $\Phi = {[\varphi _{1},\varphi _{2}]}^{\!\mathrm{T}}$ represent the angular displacement of the motion of bell and the clapper, ψ is the maximum angular displacement of the clapper, $\dot{\varphi }_{1,2}(\tau _{-})$ and $\dot{\varphi }_{1,2}(\tau _{+})$ are the velocities immediately before and after impact, respectively, $\mathbf{C}$ is a constant damping coefficient and

Fig. 5.4

Schematic illustration of impact

$$\displaystyle{ \mathbf{M}(\Phi ) = \left (\begin{array}{cc} \alpha &\varepsilon \cos (\varphi _{1} -\varphi _{2}) \\ \varepsilon \cos (\varphi _{1} -\varphi _{2})& 1\\ \end{array} \right ),\;\;\mathbf{B}(\Phi ) = \left (\begin{array}{cc} 0 &\varepsilon \sin (\varphi _{1} -\varphi _{2}) \\ -\varepsilon \sin (\varphi _{1} -\varphi _{2})& 0\\ \end{array} \right ), }$$

$$\displaystyle{ \mathbf{D}(\Phi ) = \left (\begin{array}{c} \gamma \sin (\varphi _{1}) \\ \sin (\varphi _{2})\\ \end{array} \right ),\quad \mathbf{F}(\tau ) = \left (\begin{array}{c} \hat{\psi }\cos (\omega _{0}\tau ) \\ 0\\ \end{array} \right ),\dot{{\Phi }}^{2} = {(\dot{\varphi _{ 1}^{2}},\dot{\varphi _{ 1}^{2}})}^{T}. }$$

Here, $\alpha,\varepsilon$, $\hat{\psi }$, and γ are constant parameters.

System (5.3) and (5.4) can be written as 5D-PWS

$$\displaystyle{ \frac{d} {\mathit{dt}}\mathrm{Z} = f(\mathrm{Z}(\tau )),\quad \mathrm{Z} = [\varphi _{1},\varphi _{2},\dot{\varphi }_{1},\dot{\varphi }_{2},\omega _{0}\tau ] }$$

Multiple impact and grazing bifurcation behavior is shown in Fig. 5.5.

Fig. 5.5

Quasiperiodic solution associated with grazing bifurcations and multiple impact (chattering) [figures produced in cooperation with P. Piiroinen and J. Mason]

3 Concept of Generalized Center Manifolds

For smooth systems $\dot{\xi }= f(\xi ),\xi \in {\mathbb{R}}^{n}$ the center manifold approach can be used to determine the dynamics near a special solution $\bar{\xi }$ by reducing the system to a smaller system, which can be employed to investigate bifurcation, stability, and the dependence on critical parameters.

As an essential tool for the analysis linearization techniques are used. Since such properties are not at hand for non-smooth systems near a special solution, new methods have to be developed.

Following [25], we assume that $\bar{\xi }= 0 \in \mathcal{M}$ is a stationary solution of our system which will be written as:

$$\displaystyle{ \begin{array}{cc} \dot{\xi } = f_{\pm }(\xi,\lambda ) =\underbrace{\mathop{ {A}^{\pm }(\lambda )\xi }}\limits _{basic\;linear\;term} +\underbrace{\mathop{ {g}^{\pm }(\xi,\lambda ),}}\limits _{nonlinear\;term}\;\lambda \in \mathbb{R},\;\pm e_{1}^{\!\mathrm{T}}\xi> 0,\end{array} }$$

(5.5)

where A ^± are constant (parameters dependent) matrices and g ^± denote smooth functions of higher order terms.

We first review the situation for planar piecewise smooth system to investigate mechanisms leading to the generation of periodic orbits. The standard procedure for smooth system is given by Hopf-bifurcation triggered by the crossing of exactly one pair of eigenvalues through the imaginary axis. For a piecewise smooth system the notion of eigenvalues is not at hand, but it turned out that instead of this analytical criterium the geometric correspondent remains available. Geometrically Hopf-bifurcation occurs, when the stationary solution changes from a stable focus to an unstable focus via a center. It turns out that this situation carries over to non-smooth systems. The formal procedure relies on the construction of a Poincaré map for the two-dimensional piecewise linear system $\dot{\xi }= {A}^{\pm }(\lambda )\xi$ of the form

$$\displaystyle{ P(\xi _{2},\lambda ) = {e}^{\pi b(\lambda )}\xi _{ 2},\quad b(\lambda ) {=\alpha }^{+}(\lambda ){/\omega }^{+}(\lambda ) {+\alpha }^{-}(\lambda ){/\omega }^{-}(\lambda ). }$$

We consider the following assumptions:

(H1):

$f_{\pm }(\xi,\lambda )$ are ${\mathbf{C}}^{k}$-smooth (k ≥ 2) for $(\xi,\lambda ) \in \mathbb{R}_{2}^{\pm }\times \mathbb{R}$.

(H2):

f _±(0, λ) ≡ 0 for $\lambda \in \mathbb{R}$.

(H3):

The spectrum of ${A}^{\pm }(\lambda )$ consists of a pair of complex conjugate eigenvalues ${\alpha }^{\pm }(\lambda ) \pm {i\omega }^{\pm }(\lambda )$, $\omega (\lambda )> 0$ for $\lambda \in \mathbb{R}$.

(H4):

a ₁₂ ^± > 0 or a ₁₂ ^± < 0.

(H5):

transversality condition, b(0) = 0, $\frac{\mathit{db}} {d\lambda } (0)\neq 0$.

Under the previous assumptions, the main result is given in the following theorem.

Theorem 5.1 ( [25]). 

Suppose that (H1) − (H5) hold, then there bifurcates a continuous branch of periodic orbits for the planar PWS (5.5) from the origin at λ = 0.

Example 5.5 (Brake System for a Bike [25]). 

The mathematical model is a system of two differential equations:

$$\displaystyle{ \begin{array}{cc} m\ddot{x} + d_{1}\dot{x} + c_{1}x {=\sigma }^{+}(x,\dot{x},\lambda ),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{if}\;\;x> 0 \\ m\ddot{x} + (d_{1} + d_{2})\dot{x} + (c_{1} + c_{2})x {=\sigma }^{-}(x,\dot{x},\lambda ),\;\text{if}\;\;x <0\end{array} }$$

(5.6)

where the mass rests on a smooth surface and is connected to the walls by springs c _j and dampers d _j , j = 1, 2, σ ^± representing external force and λ is a free parameter. Set x = u, $\dot{x} =\mathrm{ v}$, and m = 1; without loss of generality [25], we assume that the system (5.6) is of the following form

$$\displaystyle{ \left (\begin{array}{c} \mathrm{\dot{u}}\\ \mathrm{\dot{v} }\\ \end{array} \right ) = \left (\begin{array}{c} \mathrm{v} \\ (\mathrm{b_{1}^{\pm }\lambda - b_{0}^{\pm }})\mathrm{v} - {a}^{\pm }\mathrm{u} {-\beta }^{\pm }\mathrm{{u}^{3}}\\ \end{array} \right ). }$$

(5.7)

Note that the origin is always an equilibrium point, hence the eigenvalues corresponding to the linearization of (5.7) at the origin are given by ${\alpha }^{\pm }(\lambda ) \pm {i\omega }^{\pm }(\lambda ) = -\frac{1} {2}(b_{0}^{\pm }- b_{ 1}^{\pm }\lambda ) \pm i\frac{1} {2}\big{(4{a}^{\pm }- {(b_{ 0}^{\pm }- b_{ 1}^{\pm }\lambda )}^{2}\big)}^{1/2}$.

The assumption (H1)–(H5) hold if $b_{0}^{-} = -{({a}^{-}/{a}^{+})}^{1/2}b_{0}^{+}$. Therefore, generalized Hopf-bifurcation occurs as the parameter λ crosses 0.

We assume that the transition at $\mathcal{M}$ is determined by the vector field of (5.1), i.e., here we first consider either direct transition or sliding but no jumps in phase space.

As an interesting example for systems of the form we use the following brake system suggested by K. Popp (1998, private communication), consisting of three coupled oscillators connected by friction forces. To capture realistic friction behavior we have slightly extended the system by allowing a general friction characteristic μ ₂.

Example 5.6 (Brake System). 

A brake pad 1 on a rigid frame acts on a brake disc 2. Between brake pad and brake disc there is a relative displacement with constant velocity v > 0, Fig. 5.6; for that reason friction forces depend only on the normal force and the kinematic friction μ ₁. The coefficients of the linear viscous dampers are represented by d ₁, d ₂ and spring constants are denoted by c ₁, c ₂. Therefore, the brake pad is equipped with three mechanical degrees of freedom:

• Vertical movement x ₁

• Horizontal movement x ₂

• Rotation ϕ

The pad is supported via a friction contact with velocity depending friction force R(ν _rel ) by the frame where R is of the form $R(\nu _{\mathit{rel}}) = F_{n} \cdot \mu _{2}(\nu _{\mathit{rel}})$. As friction characteristic we take

$$ \displaystyle\begin{array}{rcl} \mu _{2}(\nu ) = sgn(\nu )\big[\alpha _{1} + \frac{\beta _{1}} {1 +\gamma _{1}\vert \nu \vert } +\delta { _{1}\nu }^{2}\big].& & {}\\ \end{array} $$

Fig. 5.6

Three-degree-of-freedom brake system model

Note that the simple Coulomb friction characteristic is included for $\beta _{1} =\delta _{1} = 0$, but for δ ₁ > 0 care is taken to incorporate the fact that friction increases for large value of the relative velocity.

The equations of motion are given as:

$$\displaystyle\begin{array}{rcl} \begin{array}{cl} m\ddot{x}_{1} & = -(d_{1} + d_{2})\dot{x}_{1} + \frac{b} {2}(d_{2} - d_{1})\dot{\phi } - (c_{1} + c_{2})x_{1} + \frac{b} {2}(c_{2} - c_{1})\phi \\ &\;\;\;\;\;\;\; - sgn(\dot{x}_{1} - a\dot{\phi })c_{3}x_{2}\big[\alpha _{1} + \frac{\beta _{1}} {1+\gamma _{1}\vert (\dot{x}_{1}-a\dot{\phi })\vert } +\delta _{1}{(\dot{x}_{1} - a\dot{\phi })}^{2}\big] \end{array} & &{}\end{array}$$

(5.8a)

$$\displaystyle\begin{array}{rcl} \begin{array}{cl} m\ddot{x}_{2} & = (d_{1} + d_{2})\mu _{1}\dot{x}_{1} + \frac{\mu _{1}b} {2} (d_{1} - d_{2})\dot{\phi } + (c_{1} + c_{2})\mu _{1}x_{1} - c_{3}x_{2} \\ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{\mu _{1}b} {2} (c_{1} - c_{2})\phi,\end{array} & &{}\end{array}$$

(5.8b)

$$\displaystyle\begin{array}{rcl} \begin{array}{cl} \mathbf{j}\ddot{\phi }& =\big (\frac{b} {2}(d_{2} - d_{1}) + (d_{1} + d_{2})h\mu _{1}\big)\dot{x}_{1} -\big (\frac{{b}^{2}} {4} (d_{1} + d_{2}) + \frac{\mathit{bh}\mu _{1}} {2} (d_{2} - d_{1})\big)\dot{\phi } \\ &\;\;\;\;\;\; -\big (\frac{b} {2}(c_{1} - c_{2}) - (c_{1} + c_{2})h\mu _{1}\big)x_{1} + c_{3}sx_{2} -\big (\frac{{b}^{2}} {4} (c_{1} + c_{2}) + \frac{\mathit{bh}\mu _{1}} {2} (c_{2} - c_{1})\big)\phi \\ &\;\;\;\;\;\; + sgn(\dot{x}_{1} - a\dot{\phi })c_{3}ax_{2}\big[\alpha _{1} + \frac{\beta _{1}} {1+\gamma _{1}\vert (\dot{x}_{1}-a\dot{\phi })\vert } +\delta _{1}{(\dot{x}_{1} - a\dot{\phi })}^{2}\big]. \end{array} & &{}\end{array}$$

(5.8c)

3.1 Brake Model as PWS

System (5.8) contains six unknown variables $(x_{1},\dot{x}_{1},x_{2},\dot{x}_{2},\phi,\dot{\phi })$ and 13 parameters. Non-smooth components enter just in two ways by the term $sgn(\dot{x}_{1} - a\dot{\phi })$. It is clear that an exact analytic solution is unavailable. Our approach to such a problem is to view it as a non-smooth system. We first carry out the following transformation and scaling of t described as:

$$\displaystyle\begin{array}{rcl} z_{1}:= x_{1},\;\;z_{2}:= x_{2},\;\;z_{3}:= x_{1} - a\phi,\;\;z_{4}:=\mu _{1}\dot{x}_{1},\;\;z_{5}:=\dot{ x}_{2},\;\;z_{6}:=\dot{ x}_{1} - a\dot{\phi },\;\;t \rightarrow ma\mu _{1}t,& & {}\\ \end{array}$$

where a, m, μ ₁ > 0, which has no effect on the solution behavior of the model system.

To be specific, we rewrite (5.8) by using the above transformation as an equivalent six-dimensional system as follows:

$$\displaystyle{ \dot{z} = \left \{\begin{array}{@{}l@{\quad }l@{}} {A}^{+}z + {g}^{+}(z),\quad &z_{ 6}> 0, \\ {A}^{-}z + {g}^{-}(z),\quad &z_{6} <0, \end{array} \right. }$$

(5.9)

with the simple form of the matrices

$$\displaystyle{{ A}^{\pm } = \left (\begin{array}{cccccc} 0 & 0 & 0 &a_{14} & 0 & 0 \\ 0 & 0 & 0 & 0 &a_{25} & 0 \\ 0 & 0 & 0 & 0 & 0 &a_{25} \\ a_{41} & \mp \alpha &a_{43} & a_{44} & a_{45} & a_{46} \\ a_{51} & a_{52} & a_{53} & a_{54} & 0 &a_{56} \\ a_{61} & \mp \beta &a_{63} & a_{64} & a_{65} & a_{66}\\ \end{array} \right ),{g}^{\pm } = \mp \left (\begin{array}{c} 0\\ 0 \\ 0 \\ c_{3}a\mu _{1}^{2}z_{2}(\tilde{\epsilon }z_{6} +\tilde{\tilde{\epsilon }} z_{6}^{2})+\ldots \\ 0 \\ - ac_{3}\mu _{1}(1 + \frac{{\mathit{ma}}^{2}} {\mathbf{j}} )z_{2}(\tilde{\epsilon }z_{6} +\tilde{\tilde{\epsilon }} z_{6}^{2})+\ldots \\ \end{array} \right ) }$$

(5.10)

where

a ₁₄ = ma, $a_{25} = \mathit{ma}\mu _{1},$ $a_{41} = a\mu _{1}^{2}(c_{1} + c_{2}) -\frac{b\mu _{1}^{2}(c_{ 2}-c_{1})} {2},$ $\alpha = \mathit{ac}_{3}\mu _{1}^{2}\mu _{2}^{0},$ $a_{43} = -\frac{b\mu _{1}^{2}(c_{ 2}-c_{1})} {2},$ $a_{44} = -a\mu _{1}(d_{1} + d_{2}) + \frac{b\mu _{1}(d_{2}-d_{1})} {2}$, $a_{46} = -\frac{b\mu _{1}^{2}} {2} (d_{2} - d_{1})$, $a_{51} = a\mu _{1}^{2}(c_{1} + c_{2}) + \frac{b\mu _{1}^{2}(c_{ 2}-c_{1})} {2}$, $a_{52} = -ac_{3}\mu _{1}$, $a_{53} = \frac{-b\mu _{1}^{2}(c_{ 2}-c_{1})} {2}$, $a_{54} = a\mu _{1}(d_{1} + d_{2}) + \frac{b\mu _{1}(d_{1}-d_{2})} {2}$, $a_{56} = -\frac{b\mu _{1}^{2}} {2} (d_{1} - d_{2})$, $a_{61} = \frac{b\mu _{1}} {2} (c_{2}-c_{1})-a\mu _{1}(c_{1}+c_{2})+ \frac{{\mathit{ma}}^{2}\mu _{ 1}} {\mathbf{j}} (\frac{b} {2}(c_{1}-c_{2})-(c_{1}+c_{2})h\mu _{1})+ \frac{\mathit{ma}\mu _{1}} {\mathbf{j}} (\frac{{b}^{2}} {4} (c_{1}+c_{2})+ \frac{\mathit{bh}\mu _{1}} {2} (c_{2}-c_{1}))$, $\beta = \mp (ac_{3}\mu _{1}\mu _{2}^{0} + \frac{{a}^{3}c_{ 3}m\mu _{1}\mu _{2}^{0}} {\mathbf{j}} ) -\frac{{a}^{2}c_{ 3}\mathit{sm}\mu _{1}} {\mathbf{j}}$, $a_{63} = \frac{b\mu _{1}} {2} (c_{1} - c_{2}) -\frac{\mathit{ma}\mu _{1}} {\mathbf{j}} (\frac{{b}^{2}} {4} (c_{1} + c_{2}) + \frac{\mathit{bh}\mu _{1}} {2} (c_{2} - c_{1}))$, $a_{64} = -a(d_{1} +d_{2})-\frac{{\mathit{ma}}^{2}} {\mathbf{j}} (\frac{b} {2}(d_{2} -d_{1})+(d_{1} +d_{2})h\mu _{1})+ \frac{\mathit{ma}} {\mathbf{j}} (\frac{{b}^{2}} {4} (d_{1} +d_{2})+ \frac{\mathit{bh}\mu _{1}} {2} (d_{2} -d_{1}))$, $a_{65} = \frac{b\mu _{1}} {2} (d_{2} - d_{1}),a_{66} = -\frac{b\mu _{1}} {2} (d_{2} - d_{1}) -\frac{\mathit{ma}\mu _{1}} {\mathbf{j}} (\frac{{b}^{2}} {4} (d_{1} + d_{2}) + \frac{\mathit{bh}\mu _{1}} {2} (d_{2} - d_{1}))$, $\mu _{2}^{0} =\alpha _{1} +\beta _{1}$, $\tilde{\epsilon }= -\alpha _{1}\gamma _{1}$, $\tilde{\tilde{\epsilon }}= 2(\delta _{1} +\alpha _{1} +\gamma _{ 1}^{2})$.

For PWS it is necessary to know the direction of the flow of the vector field when the trajectory reaches $\mathcal{M}$. We will discuss the vector field on $\mathcal{M}$ in two main cases, namely direct crossing through $\mathcal{M}$ or sliding motion on $\mathcal{M}$ where the sliding surface is particularly important with regard to the friction coefficient.

3.2 Detecting Crossing and Sliding Regions

In this section we demonstrate the existence of a crossing and sliding mode from the point of view of a Filippov system. Let $\Upsilon (z) = a_{61}z_{1} + a_{63}z_{3} + a_{64}z_{4} + a_{65}z_{5}$. The direct crossing in ${\mathcal{M}}^{c}$ for z ₆ = 0 occurs if both quantities $[{n}^{\!\mathrm{T}}(z)f_{ \pm }(z)]$ have the same sign. Therefore, the crossing region ${\mathcal{M}}^{c}:=\{ z \in \mathcal{M}\vert \Upsilon {(z)}^{2} - {(\beta z_{2})}^{2}> 0\}$ is divided into two main regions, namely

$$\displaystyle{ \begin{array}{c} \mathcal{M}_{+}^{c}:=\{ z \in {\mathcal{M}}^{c}\vert \Upsilon (z)>\beta z_{2}\}, \\ \mathcal{M}_{-}^{c}:=\{ z \in {\mathcal{M}}^{c}\vert \Upsilon (z) <\beta z_{2}\}. \end{array} }$$

In a similar way, we can define the sliding mode region as ${\mathcal{M}}^{s}:=\{ z \in \mathcal{M}\vert \Upsilon {(z)}^{2} - {(\beta z_{2})}^{2} \leq 0\}$ which is divided into two main regions, namely

$$\displaystyle{ \begin{array}{c} \mathcal{M}_{-}^{s}:=\{ z \in {\mathcal{M}}^{s}\vert \Upsilon (z) <\beta z_{2}\}, \\ \mathcal{M}_{+}^{s}:=\{ z \in {\mathcal{M}}^{s}\vert \Upsilon (z)>\beta z_{2}\}, \end{array} }$$

where we use the notation $\mathcal{M}_{-}^{s}$ to represent the attractive sliding motion and $\mathcal{M}_{+}^{s}$ to represent repulsive sliding motion.

4 Piecewise Smooth Linear System

PWLS are extensively used to model many physical phenomena such as mechanical devices [6] or electronic circuits [21]. We consider the n-dimensional piecewise smooth linear system:

$$\displaystyle{ \dot{\xi }= \left \{\begin{array}{@{}l@{\quad }l@{}} {A}^{+}\xi,\quad &h(\xi )> 0, \\ {A}^{-}\xi,\quad &h(\xi ) <0, \end{array} \right. }$$

(5.11)

where $\xi \in {\mathbb{R}}^{n}$ and A ^± are n ×n real matrices. For that setting the stationary solution is always located within the separating manifold. We are interested to investigate the dynamical behavior in a neighborhood of the stationary solution and in particular to study the generation of periodic orbits. Other questions concern stability and the possibility to reduce the system to a lower dimensional one.

4.1 Concepts of Invariant Cones

PWLS can be classified in two classes depending on the degree of smoothness properties of the associated vector field, namely continuous PWLS (non-sliding flow) and discontinuous PWLS (sliding flow).

To analyze the dynamical behavior of n-dimensional PWLS (5.11), we assume that both matrices have at least a pair of complex conjugated eigenvalues introducing rotations in the system. For initial values $\xi \in \mathcal{M}$ for which ${n}^{\!\mathrm{T}}(\xi ){A}^{\pm }\xi$ have both negative sign and for which ${e}^{t_{-}(\xi ){A}^{-} }\xi$ reaches $\mathcal{M}$ again for the first time t ₋(ξ) at η, we define the Poincaré map $P_{-}(\xi ):= {e}^{t_{-}(\xi ){A}^{-} }\xi$ and similarly $P_{+}(\eta ):= {e}^{t_{+}(\eta ){A}^{+} }\eta$.

If both P ₋ and P ₊ are well defined so that $P_{+}(P_{-}(\xi ))$ exists, we can study the behavior of the combined map $P_{+} \circ P_{-}$. If there exists $\tilde{\xi }\in \mathcal{M}$ such that

$$\displaystyle{ P(\tilde{\xi }) =\mu _{c}\tilde{\xi }, }$$

for some μ _c  > 0, then the same holds for the half-ray $\{\lambda \tilde{\xi }\;\vert \lambda> 0\}$.

In that way an invariant cone is generated by the flow of (5.11).

The “eigenvalue” parameter μ _c determines the dynamics on the cone; if μ _c  < 1 resp. μ _c  > 1 the flow on the cone spirals in resp. out; for μ _c  = 1 the cone is foliated by periodic orbits of (5.11), Fig. 5.7. The “eigenvalue” μ _c of P is an eigenvalue of the linear operator DP evaluated at $\tilde{\xi }$ as well.

Fig. 5.7

Different dynamics on cones, μ _c  < 1, μ _c  = 1 and μ _c  > 1, respectively

Attractivity of the invariant cone is determined by the remaining (n − 2) eigenvalues of $\mathit{DP}(\tilde{\xi })$.

Theorem 5.2 ( [13]). 

If there exists $\bar{\xi }\in \mathcal{M}_{-}^{c}$ and μ _c > 0 such that

$$\displaystyle{ P(\tilde{\xi }) =\mu _{c}\tilde{\xi }, }$$

then $\tilde{\xi }$ generates an invariant cone under the flow of (5.11) due to $P(\lambda \tilde{\xi }) =\lambda P(\tilde{\xi }) =\lambda \mu _{c}\tilde{\xi }$ ; moreover,

• (i) If μ _c > 1, then the stationary solution 0 is unstable.

• (ii) If μ _c = 1, then the cone consists of periodic orbits.

• (iii) If μ _c < 1, then the stability of 0 depends on the stability of P with respect to the complimentary directions.

The existence of an invariant cone for 3D problems has been studied in detail in [10, 14]; further a general nonlinear determining system to compute the generating vector $\tilde{\xi }$ has been set up in [13].

For homogenous and continuous 3D-PWLS with two zones existence of invariant cones and their bifurcations have already been studied in [3, 4]. There also, an example is given demonstrating that the combination of two stable systems may be unstable; an effect already known in control theory.

This nevertheless surprising result can systematically be explained in our setting by the existence of an invariant attractive cone with the property that the motion on the cone is unstable, i.e., μ _c  > 1.

In general coexistence of several attractive cones is possible; a result which does not hold for continuous PWLS.

Example 5.7 (Existence of Multiple Invariant Cones). 

Set

$$\displaystyle{ \begin{array}{c} {A}^{-} = \left (\begin{array}{ccc} {\lambda }^{-}&- 1&0 \\ 1&{ \lambda }^{-} &0 \\ 0& 0 &{\mu }^{-} \end{array} \right ),\quad {A}^{+} = \left (\begin{array}{ccc} {2\lambda }^{+} & - 1&{ \mu }^{+} \\ {\lambda }^{+2} + 1& 0 & {-\lambda }^{+2} + {2\lambda {}^{+}\mu }^{+} - 1 \\ 0 & 0 &{ \mu }^{+} \end{array} \right ). \end{array} }$$

The ⊖ -system possesses an invariant plane ξ ₃ = 0 with constant return time $t_{-}(\xi ) =\pi$. For the ⊕ -system the line $\xi _{3} ={ \frac{1} {\mu }^{+}} \xi _{2}$ determines the boundary of the sliding motion area in the $(\xi _{2},\xi _{3})$-plane.

Note that vanishing or appearing of a sliding area is based on one parameter μ ⁺.

Here, we assume that the starting point $\xi \in \mathcal{M}_{+}^{c}$ hence ξ ₂ < 0, and the Poincaré map $P = P_{-}\circ P_{+}(\xi )$ mapping ($\xi _{2},\xi _{3}$) into itself (i.e., $P(\xi ): \mathcal{M}_{+}^{c} \rightarrow \mathcal{M}_{+}^{c}$ ) is given by

$$\displaystyle{ \begin{array}{c} P(\xi ) =\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \\ F\left (\begin{array}{cc} {\lambda }^{+}\sin (t_{ +}) -\cos (t_{+})&\sin (t_{+})(1 {-\lambda }^{+2}) + {2\lambda }^{+}\big(\cos (t_{ +}) - {e}^{{(\mu }^{+}{-\lambda }^{+})t_{ +}}\big)\\ \\ 0 & {e}^{{(\mu }^{+}{-\lambda }^{+})t_{ +}+\pi {(\mu }^{-}{-\lambda }^{-}) }\\ \end{array} \right )\left (\begin{array}{c} \xi _{2}\\ \xi _{ 3}\\ \end{array} \right ), \end{array} }$$

where $F = {e}^{{\lambda }^{+}t_{ +}{+\pi \lambda }^{-} }$ and the return time t ₊(ξ) depends on ξ in a nonlinear linear way, and it is determined by the smallest positive solution of the following equation

$$\displaystyle{ -\sin (t_{+})\xi _{2} + {(\lambda }^{+}\sin (t_{ +}) -\cos (t_{+}) + {e}^{t_{+}{(\mu }^{+}{-\lambda }^{+}) })\xi _{3} = 0. }$$

(5.12)

Lemma 5.1 ( [10]). 

If $\xi \in \mathcal{M}_{\pm }^{c}$ and ${\lambda }^{+} = {-\lambda }^{-}$ , then the present system has, at least, two invariant cones with periodic orbits. One of them can be asymptotically stable and the other unstable or both can be unstable foci; but there is also the situation where both invariant cones are asymptotically stable.

Proof.

Set $\xi \in \mathcal{M}_{+}^{c}$ and ${\lambda }^{+} = {-\lambda }^{-}$. Since an invariant cone consisting of periodic orbits requires that either $\mu _{c_{1}} = {e}^{{\lambda }^{-}(\pi -t_{ +})}{(\lambda }^{+}\sin (t_{+}) -\cos (t_{+}))$ or $\mu _{c_{2}} = {e}^{{\mu }^{+}t_{ +}{+\pi \mu }^{-} }$ equals 1 we get

• (i) $\mu _{c_{1}} = 1$, and $t_{+} =\pi$ by direct analysis of the fixed point equation P(ξ) = ξ which requires $-{2\lambda }^{+}(1 + {e}^{{(\mu }^{+}{-\lambda }^{+})\pi })\xi _{3} = 0$, hence ξ ₃ = 0. In this case we obtain a flat cone given as the invariant plane which is attractive if ${\mu }^{+} <{-\mu }^{-}$ or repulsive if ${\mu }^{+}> {-\mu }^{-}$.

• (ii) $\mu _{c_{2}} = 1$, hence $t_{+} = -\frac{{\mu }^{-}\pi } {{\mu }^{+}}$. The corresponding eigenvector is calculated as

  $$\displaystyle{ \tilde{\xi }= \left (\begin{array}{c} - 1 \\ - \frac{1+{e}^{{\lambda }^{+}t_{+}{+\pi \lambda }^{-} }\big{(\lambda }^{+}\sin (t_{ +})-\cos (t_{+})\big)} {{e}^{{\lambda }^{+}t_{+}{+\pi \lambda }^{-} }\big(\sin (t_{+})(1{-\lambda }^{+2})+{2\lambda }^{+}(\cos (t_{+})-{e}^{{(\mu }^{+}{-\lambda }^{+})t_{+}})\big)}\\ \end{array} \right ) }$$

  To prove the existence of the function $t_{+}(\xi ) \in (0,\pi )$, without loss of generality, we set $\xi \in \partial \mathcal{M}_{+}^{s}$ ($\partial \mathcal{M}_{+}^{s}$ refer to the boundary between sliding and crossing areas), then the existence of a solution for Eq. (5.12) requires ${(\mu }^{+} {-\lambda }^{+}) <1$.

  The corresponding cone is attractive, resp. repulsive if $\mu _{c_{1}} <1$ resp. $\mu _{c_{1}}> 1$.

Figure 5.8 shows an example to illustrate the situation of two attractive invariant cones for the special choice of parameters. □ 

Example 5.8 (Existence of an Invariant Cone for the Linear Brake System Without Sliding Motion [10]). 

For the simple Coulomb friction characteristic included by $\beta _{1} =\delta _{1} = 0$, the nonlinear brake system (5.8) reduces to a linear form. To simplify, we set the parameters $c:= c_{1} = c_{2}$ and $d:= d_{1} = d_{2}$. In Fig. 5.9, we fix all parameters values as in Table 5.1 and choose the friction coefficient smaller than the static one (i.e., $\mu _{2}^{0} \ll \mu _{1})$. The main reason for choosing μ ₂ ⁰ is that this choice rapidly restores the spring to a more relaxed length. Note that a change of this parameter μ ₂ ⁰ changes the control parameters $\alpha,\;\beta$ (i.e., the friction force). The parameter $\beta$ in turn causes the existence of sliding and crossing regions.

Figure 5.9 shows an invariant cone, a 4-periodic orbit and solution components at d = 0 and μ ₂ ⁰ = 0. 00014 which is quite small.

Fig. 5.8

Two attractive invariant cones, ${\lambda }^{+} = {-\lambda }^{-} = 0.6,\;\;$ ${\mu }^{+} = -1.13,\;\;$ ${\mu }^{-} = 0.4266$, where $t_{+} =\pi$ for the flat cone and $t_{+} = 1.1306$ for the other

Fig. 5.9

Invariant cones and solution components for linear brake system without sliding motion

Table 5.1 Parameters are presented in K. Popp (1998, private communication)

5 PWLS with Sliding

Example 5.6 indicates that sliding motion occurs. Following Filippov the motion within $\mathcal{M}$ is determined by (5.2). For a piecewise linear system (5.11) this reduces to

$$\displaystyle{ \dot{\xi }= \frac{{n}^{\!\mathrm{T}}(\xi ){A}^{-}\xi \cdot {A}^{+}\xi - {n}^{\!\mathrm{T}}(\xi ){A}^{+}\xi \cdot {A}^{-}\xi } {{n}^{\!\mathrm{T}}(\xi )({A}^{-}\xi - {A}^{+}\xi )} }$$

(5.13)

In general this is a nonlinear system. Due to the homogeneity special features hold.

• (a) If ξ(t) is a solution, then λ ξ(t) as well for λ ≥ 0.

• (b) Half-rays are mapped into half-rays, with constant time of evaluation from one half-ray to another, hence if some trajectory leaves $\mathcal{M}$ a half-ray does at the same time.

  Further, if there are stationary solutions in $\mathcal{M}$, i.e., $F_{s}(\bar{\xi }) = 0$, then there is a half-ray of stationary solution.

For an initial position in $\mathcal{M}_{-}^{s}$ or if the flow of a subsystem of (5.11) arrives at the sliding region $\mathcal{M}_{-}^{s}$, the sliding motion can be observed along the discontinuity surface in phase space. Let ${\varphi }^{s}(t_{s}(\xi ),\xi )$ in ${\mathbf{C}}^{k},\;k \geq 1$, denote the sliding flow generated by solution of (5.13), and let t _s be the time spent in the $\mathcal{M}_{-}^{s}$ region.

Then we define the sliding map as

$$\displaystyle{ \begin{array}{c} P_{s}: \mathcal{M}_{-}^{s} \rightarrow \mathcal{M}_{-}^{s}, \\ \;\;\xi \rightarrow P_{s}(\xi ) {=\varphi }^{s}(t_{s},\xi ).\end{array} }$$

The existence of an invariant cone passing through the sliding region depends on the existence of an “eigenvector” $\bar{\xi }\not\in \mathcal{M}_{+}^{s}$ of the nonlinear eigenvalue problem $P(\tilde{\xi }) =\mu _{c}\tilde{\xi }$ where P is the required composition of one or both of (P ₋, P ₊) and P _s .

Example 5.9 (Existence of Invariant Cone for the Linear Brake System with Sliding Motion). 

For the special choice that the initial friction coefficient μ ₂ ⁰ is equal to the static $\mu _{2}^{0} =\mu _{1} = 0.4$, the complex behavior of the brake system is revealed to multiple periodic orbits including sliding. In Fig. 5.10 we show a 4-periodic orbit where a transition phase slip motions with small length appear. Stationary solutions and invariant manifolds within $\mathcal{M}$ may strongly influence the flow in $\mathcal{M}$; in particular they can prevent trajectories to leave $\mathcal{M}$ so that the long time motion might be restricted to $\mathcal{M}$. For that reason it is worth while to investigate the flow in $\mathcal{M}$. Due to special properties the system can be reduced to a lower dimensional system or even to a linear system under additional hypotheses.

In the following we assume without restriction that n = e ₁.

Fig. 5.10

Invariant cones and solution components, existence of 4-sliding periodic orbit when $\alpha \neq 0,\beta \neq 0$

Using a suitable transformation T we can simplify system (5.13).

Assume that T leaves $\mathcal{M}$ invariant, i.e., $Te_{1} = e_{1}$ and set Tη: = ξ. Then

$$\displaystyle{ \dot{\eta }= \frac{1} {e_{1}^{\!\mathrm{T}}({A}^{-}- {A}^{+})T\eta }\big[(e_{1}^{\!\mathrm{T} }{A}^{-}T\eta ){T}^{-1}{A}^{+}T\eta - (e_{ 1}^{\!\mathrm{T} }{A}^{+}T\eta ){T}^{-1}{A}^{-}T\eta \big]. }$$

Further we can arrange that for $\eta \in \mathcal{M}$

$$\displaystyle{ e_{1}^{\!\mathrm{T} }({A}^{-}- {A}^{+})T\eta =\eta _{ j}, }$$

for some $j \in \{ 2,\ldots,n\}$; we assume without restriction that j = n. Then

$$\displaystyle{ \dot{\eta }= \frac{1} {\eta _{n}}\big[(e_{1}^{\!\mathrm{T} }{A}^{-}T\eta ){T}^{-1}{A}^{+}T\eta - (e_{ 1}^{\!\mathrm{T} }{A}^{+}T\eta ){T}^{-1}{A}^{-}T\eta \big]. }$$

Define slopes $s_{i} =\eta _{i}/\eta _{n},(i = 1,\ldots,n)$. Then for $\eta \in \mathcal{M}$: $\dot{s}_{1} = 0$ and $\dot{s}_{n} = 0$; for $i \in \{ 2,\ldots,n - 1\}$ we obtain

$$\displaystyle{ \dot{s_{i}} =\big [\dot{\eta _{i}}\eta _{n} -\eta _{i}\dot{\eta }_{n}\big]/\eta _{n}^{2}. }$$

By using the differential equations of $\dot{\eta }$, we obtain a reduced system for the slopes describing the motion in $\mathcal{M}$.

Lemma 5.2.

The flow in $\mathcal{M}$ is governed by the evolution of the slopes $s_{i},(i = 2,\ldots,n - 1)$ :

$$\displaystyle{ \begin{array}{l} \dot{s_{i}} = e_{1}^{\!\mathrm{T}}{A}^{-}\mathit{Tse}_{ i}^{\!\mathrm{T}}{T}^{-1}{A}^{+}\mathit{Ts} - e_{ 1}^{\!\mathrm{T}}{A}^{+}\mathit{Tse}_{ i}^{\!\mathrm{T}}{T}^{-1}{A}^{-}\mathit{Ts}\qquad \\ - s_{i}\big[e_{1}^{\!\mathrm{T}}{A}^{-}\mathit{Tse}_{ n}^{\!\mathrm{T}}{T}^{-1}{A}^{+}\mathit{Ts} - e_{ 1}^{\!\mathrm{T}}{A}^{+}\mathit{Tse}_{ n}^{\!\mathrm{T}}{T}^{-1}{A}^{-}\mathit{Ts}\big].\end{array} }$$

(5.14)

Remark 5.1.

Since the right-hand side of (5.14) consists of quadratic resp. cubic (polynomial) forms statements can be drawn concerning for example the number of stationary lines.

As a special situation consider n = 3. Then

$$\displaystyle\begin{array}{rcl} & & \dot{s}_{1} = 0, {}\\ & & \qquad \qquad \dot{s}_{2} = e_{1}^{\!\mathrm{T} }{A}^{-}\mathit{Tse}_{ 2}^{\!\mathrm{T} }{T}^{-1}{A}^{+}\mathit{Ts} - e_{ 1}^{\!\mathrm{T} }{A}^{+}\mathit{Tse}_{ 2}^{\!\mathrm{T} }{T}^{-1}{A}^{-}\mathit{Ts}\qquad {}\\ & & \qquad \qquad \qquad \qquad \qquad - s_{2}\big[e_{1}^{\!\mathrm{T} }{A}^{-}\mathit{Tse}_{ 3}^{\!\mathrm{T} }{T}^{-1}{A}^{+}\mathit{Ts} - e_{ 1}^{\!\mathrm{T} }{A}^{+}\mathit{Tse}_{ 3}^{\!\mathrm{T} }{T}^{-1}{A}^{-}\mathit{Ts}\big] = g(s_{ 2}). {}\\ & & \dot{s}_{3} = 0.\qquad {}\\ \end{array}$$

Since g(s ₂) is either a quadratic resp. cubic polynomial in s ₂, the number of possible stationary solutions is limited to at most 2 resp. 3; in a similar way stability can be obtained via the derivative of g.

Example 5.10.

As a simple example to illustrate possible features resulting of sliding motion we consider a situation where ${A}^{+},{A}^{-}$ are chosen such that T = I and h(x) = ξ ₁. We take

$$\displaystyle\begin{array}{rcl}{ A}^{+} = \left (\begin{array}{ccc} {\lambda }^{+} & - 1& 0 \\ 1 &{ \lambda }^{+} & a_{23}^{+} \\ 0 & 0 &{ \mu }^{+}\\ \end{array} \right ),\;\;{A}^{-} = \left (\begin{array}{ccc} { \lambda }^{-} & - 1 & 1 \\ a_{21}^{-}& 0 &a_{23}^{-} \\ 0 &a_{32}^{-}&{ \mu }^{-}\\ \end{array} \right ).& & {}\\ \end{array}$$

Then, for $\mathcal{M} =\{\xi \in {\mathbb{R}}^{3}\;\vert \;\xi _{1} = 0\}$ the attractive sliding motion area is given by

$$\displaystyle\begin{array}{rcl} \mathcal{M}_{-}^{s} =\{\xi \in {\mathbb{R}}^{3}\;\vert \;\xi _{ 1} = 0,\xi _{3} \geq \xi _{2} \geq 0\}.& & {}\\ \end{array}$$

In Fig. 5.11 we show $\mathcal{M}_{-}^{s}$ is bounded by the half-rays G ₁ and G ₂.

The sliding motion dynamics is governed for $s_{1} = 0,\;s_{3} = 1$ by:

$$\displaystyle\begin{array}{rcl} \dot{s}_{2} = -a_{32}^{-}s_{ 2}^{3} + {(\mu }^{+} {-\mu }^{-}{-\lambda }^{+})s_{ 2}^{2} + {(\lambda }^{+} {-\mu }^{+} + a_{ 23}^{-}- a_{ 23}^{+})s_{ 2} + a_{23}^{+} =: \mathbf{g}(s_{ 2}),& & {}\\ \end{array}$$

($0 \leq s_{2} \leq 1$).

Fig. 5.11

Schematic illustration location of attractive sliding region $\mathcal{M}_{-}^{s}$ consists of stationary solution (pseudo-equilibrium line)

Remark 5.2.

• (i) For the 3-dimensional system the dynamics within the sliding motion area is described by a simple equation $\dot{s}_{2} = \mathbf{g}(s_{2})$.

  Since g is a polynomial of degree 3 there are at most 3 stationary solutions.

  The degree of g is equal to 3 if a ₃₂ ⁻≠0. In case $a_{32}^{-} = 0$ there are at most 2 zeros of g. The flow on the boundary of the sliding motion area is determined by $\dot{s}_{2} = \mathbf{g}(s_{2})$ for s ₂ = 0 resp. s ₂ = 1, hence by

  $$\displaystyle\begin{array}{rcl} \mathbf{g}(0) = a_{23}^{+},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;& & {}\\ \mathbf{g}(1) = a_{23}^{+} - a_{ 32}^{-}{-\mu }^{-}.& & {}\\ \end{array}$$

  If a ₂₃ ⁺ > 0 then the flow enters $\mathcal{M}_{-}^{s}$ through G ₁, if a ₂₃ ⁺ < 0 the flow leaves $\mathcal{M}_{-}^{s}$ through G ₁, and if $a_{23}^{+} = 0$ then G ₁ is invariant. In a similar way the flow on G ₂ can be characterized by $\mathbf{g}(1) = a_{23}^{+} - a_{32}^{-}{-\mu }^{-}$.

• (ii) If 0 ≤ a ₂₃ ⁺ and $a_{23}^{+}> a_{32}^{-} {+\mu }^{-}$, then the flow enters $\mathcal{M}_{-}^{s}$ through G ₁ and leaves it through G ₂ and there are either no zero of g in [0, 1] or one stable and one unstable one.

• (iii) If $0 \leq a_{23}^{+} <a_{32}^{-} {+\mu }^{-}$, then the flow enters $\mathcal{M}_{-}^{s}$ through G ₁ and G ₂, and there is exactly one stable zero of g in [0, 1].

• (iv) Stationary solutions of $\dot{s}_{2} = \mathbf{g}(s_{2})$ correspond to invariant lines for the system $\dot{\xi }= F_{s}(\xi )$ which can be a stable, unstable, or a center manifold separating the planar phase space.

  In higher dimensional systems those lines do not separate the phase space; so it is interesting to investigate if separating manifolds can be used to structure $\mathcal{M}_{-}^{s}$ in dimensions greater than 3.

• (v) If the line G ₁ is mapped back to $\mathcal{M}_{-}^{s}$ by the flow of the system than it depends on the structure in $\mathcal{M}_{-}^{s}$ and the location of the return if the flow remains in $\mathcal{M}_{-}^{s}$ for all times or if an invariant closed cone will be generated. Invariant lines in $\mathcal{M}_{-}^{s}$ will serve as separatrix and lead to bifurcation. Using the classification in (ii) and (iii) together with properties of P ₊ and P ₋, parameters can be chosen appropriately.

  Illustrative examples are shown in Fig. 5.12.

• (vi) The relationship

  $$\displaystyle{ ({A}^{+}-{A}^{-})\left (\begin{array}{c|c} 0 & 0 \\\hline 0&\mathit{I}\\ \end{array} \right ) = x\;{y}^{\!\mathrm{T} }, }$$

  for suitable vectors x and y which leads to a linear flow in $\mathcal{M}_{-}^{s}$ holds if ${\lambda }^{+} = 0$ and a ₃₂ ⁻, x and y can be chosen as $y_{1} = y_{2} = 0$, y ₃ = 1, $x_{1} = -1,x_{2} = a_{23}^{+} - a_{23}^{-}$.

In special situations such as for the brake system the sliding motion is governed by a linear equation:

Fig. 5.12

Bifurcation of invariant cone involving sliding depending on the location of the return map, the cone is closed (consists of periodic orbits, see (i)) or destroyed with solution remaining in $\mathcal{M}_{-}^{s}$ (see (ii))

$$\displaystyle{ \dot{z} = \left (\begin{array}{c} a_{14}z_{4} \\ a_{25}z_{5} \\ 0 \\ (a_{41} -\frac{\alpha }{\beta }a_{61})z_{1} + (a_{43} -\frac{\alpha }{\beta }a_{63})z_{3} + (a_{44} -\frac{\alpha }{\beta }a_{64})z_{4} + (a_{45} -\frac{\alpha }{\beta }a_{65})z_{5} \\ a_{51}z_{1} + a_{52}z_{2} + a_{53}z_{3} + a_{54}z_{4}\\ \end{array} \right ). }$$

This simplification holds under conditions which are described in [20]:

Theorem 5.3.

Assume that Te ₁ = e ₁ and that for suitable vectors x,y the relation

$$\displaystyle\begin{array}{rcl} ({A}^{+} - {A}^{-})T[I - e_{ 1}e_{1}^{\!\mathrm{T} }] = x{y}^{\!\mathrm{T} },& & {}\\ \end{array}$$

holds. Then the flow within $\mathcal{M}$ is described by the linear system

$$\displaystyle\begin{array}{rcl} \dot{\eta }= {T}^{-1}{A}^{+}T\eta - \frac{1} {e_{1}^{\!\mathrm{T}}x}e_{1}^{\!\mathrm{T} }{A}^{+}T\eta {T}^{-1}x.& & {}\\ \end{array}$$

Proof.

Using

$$\displaystyle\begin{array}{rcl} \dot{\xi }& =& \frac{1} {e_{1}^{\!\mathrm{T}}[{A}^{-}- {A}^{+}]\xi }\big[(e_{1}^{\!\mathrm{T} }{A}^{-}\xi ){A}^{+}\xi - (e_{ 1}^{\!\mathrm{T} }{A}^{+}\xi ){A}^{-}\xi \big]\qquad {}\\ & =& \frac{1} {e_{1}^{\!\mathrm{T}}[{A}^{-}- {A}^{+}]\xi }\big[(e_{1}^{\!\mathrm{T} }{A}^{-}\xi ){A}^{+}\xi - (e_{ 1}^{\!\mathrm{T} }{A}^{+}\xi ){A}^{+}\xi + (e_{ 1}^{\!\mathrm{T} }{A}^{+}\xi ){A}^{+}\xi {}\\ & & -(e_{1}^{\!\mathrm{T} }{A}^{+}\xi ){A}^{-}\xi \big] {}\\ & =& {A}^{+}\xi + \frac{(e_{1}^{\!\mathrm{T}}{A}^{+}\xi )} {e_{1}^{\!\mathrm{T}}[{A}^{-}- {A}^{+}]\xi }[{A}^{+} - {A}^{-}]\xi \qquad {}\\ \end{array}$$

and

$$\displaystyle\begin{array}{rcl} & & \dot{\eta }= {T}^{-1}{A}^{+}T\eta - \frac{(e_{1}^{\!\mathrm{T}}{A}^{+}T\eta )} {e_{1}^{\!\mathrm{T}}[{A}^{-}- {A}^{+}]T\eta }{T}^{-1}[{A}^{+} - {A}^{-}]T\eta {}\\ & & \qquad \qquad \qquad \qquad = {T}^{-1}{A}^{+}T\eta -\frac{(e_{1}^{\!\mathrm{T}}{A}^{+}T\eta )} {e_{1}^{\!\mathrm{T}}x{y}^{\!\mathrm{T}}\eta } {T}^{-1}x{y}^{\!\mathrm{T} }\eta {}\\ & & \qquad \qquad \qquad \qquad \qquad = {T}^{-1}{A}^{+}T\eta -\frac{(e_{1}^{\!\mathrm{T}}{A}^{+}T\eta )} {e_{1}^{\!\mathrm{T}}x} {T}^{-1}x. {}\\ \end{array}$$

 □ 

6 Nonlinear Piecewise Smooth Systems (PWNS)

Recently [19], the existence of cone-like invariant manifolds as an extension to nonlinear perturbations of certain n-dimensional non-smooth systems under appropriate conditions in the case without sliding motion carrying the essential dynamics of the full system has been proved. To see this we introduce the following hypotheses:

• (a) We assume

  $$\displaystyle\begin{array}{rcl} \begin{array}{c} \dot{\xi } = f_{\pm }(\xi ) =\underbrace{\mathop{ {A}^{\pm }\xi }}\limits _{basic\;linear\;term} +\underbrace{\mathop{ {g}^{\pm }(\xi ),}}\limits _{nonlinear\;term}\;\; \pm e_{1}^{\!\mathrm{T}}\xi> 0,\xi \in {\mathbb{R}}^{n},\end{array} & & {}\end{array}$$

  (5.15)

  with constant matrices A ^± and nonlinear ${C}^{k}$-parts ${g}^{\pm }(\xi ) = o(\|\xi \|)$, $k \geq 1$.

• (b) Direct transition between $\mathbb{R}_{-}^{n}$ and $\mathbb{R}_{+}^{n}$ through $\mathcal{M}$, hence, without loss of generality, $\xi \in \mathcal{M}_{-}^{c}$.

• (c) Existence of μ _c  > 0 and $\bar{\xi }$ such that $P(\bar{\xi }) =\mu _{c}\bar{\xi }$ for linear PWS.

• (d) The attractivity condition is satisfied, i.e., the remaining (n-2) eigenvalues of $\lambda _{-},\ldots,\lambda _{n-2}$ of DP satisfy $\vert \lambda _{j}\vert <\min \{ 1,\mu _{c}\},(j = 1,\ldots,n - 2).$

Theorem 5.4 ( [19]). 

Under the previous hypotheses on the corresponding PWLS and $g_{\pm }$ , there exists a sufficiently small $\delta$ and a ${C}^{1}$ -function $H: [0,\delta ) \rightarrow \mathcal{M}$ satisfying $H(0) = 0$ and $\frac{\partial } {\partial u}H(0) =\bar{\xi }$ such that

$$\displaystyle\begin{array}{rcl} & & \{H(u)\mid 0 \leq u <\delta \} {}\\ \end{array}$$

is locally invariant and attractive under the Poincaré map of system (1). For $k = 2$ the function $H$ is ${C}^{k}$ in case of $\mu _{c} \geq 1$ and ${C}^{\min (k,j)}$ in case of $\mu _{c} <1$ and $\alpha <\mu _{ c}^{j}$ .

Example 5.11 (Class of 3D-PWNS). 

Set:

$$\displaystyle{ \begin{array}{cc} {A}^{\pm } = {(\mathbf{S_{\pm }})}^{-1}A_{N}^{\pm }\mathbf{S_{\pm }},A_{N}^{\pm } = \left (\begin{array}{ccc} { \lambda }^{\pm } &{-\omega }^{\pm }&0 \\ {-\omega }^{\pm }&{ \lambda }^{\pm } &0 \\ 0 & 0 &{\mu }^{\pm }\\ \end{array} \right ),{(S_{-})}^{-1} = \left (\begin{array}{ccc} 1&\frac{-\alpha (\alpha +1)} {2} &-\alpha \\ -\delta & 1 &0 \\ 0& -\delta &1 \end{array} \right ), \\ {(S_{+})}^{-1} = I,{g}^{+}(\xi ) =\rho _{+}\left (\begin{array}{c} 0\\ 0 \\ \xi _{1}^{2} +\xi _{ 2}^{2}\\ \end{array} \right ),\ {g}^{-}(\xi ) =\rho _{-}\left (\begin{array}{c} \xi _{3}^{2} \\ 0\\ 0\\ \end{array} \right ).\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{array} }$$

Attractivity of the cone is guaranteed if $\vert \mu _{1}\vert <\min \{ 1,\mu _{c}\}$ and the invariant “eigenvector” $\bar{\xi }$ satisfying $P(\bar{\xi }) =\mu _{c}\bar{\xi }$ in PWLS is chosen as $\bar{\xi }= {(\bar{y},\bar{z})}^{\!\mathrm{T}} = {(1,m)}^{\!\mathrm{T}}$ with m as slope of the invariant line.

If $\alpha =\rho _{-} = 0$, system (5.15) has an invariant curve given by

$$\displaystyle{ H(y) = \mathit{my} + \frac{b_{2}} {\mu _{c}^{2} -\mu _{1}}{y}^{2}+\ldots, }$$

where $b_{2} = \frac{\rho _{+}\mu _{c}\big({e}^{{2\lambda }^{+}\pi {/\omega }^{+}}-{e}^{{\mu }^{+}\pi {/\omega }^{+}}\big)} {{2\lambda }^{+}{-\mu }^{+}}$.

Figure 5.13 shows that an invariant cone is generated by H(y) with parameters set as ω ^± = 1. 0, ${\lambda }^{+} = {-\lambda }^{-} = 1.0$, ${\mu }^{+} = 0.02$, $\rho _{+} = 12.3$, t _± = π.

Figure 5.14 (left) shows another situation, where the system (5.15) has two invariant curves, hence there are two attractive invariant cones. A periodic orbit on the manifold generated by Hopf-bifurcation is shown in Fig. 5.14 (right). The simulation is done with parameters set at ${\lambda }^{+} = -0.5{,\lambda }^{-} = 0.5{,\mu }^{+} = 0.2,\alpha = 0.5,$ $t_{+} =\pi {,\omega }^{+} {=\omega }^{-} = 1.0,\rho _{-} = -0.01,\rho _{+} = 0.1$ and bifurcation parameter ${\mu }^{-}$ close to $\mu _{0}^{-}:= {-\mu }^{+}t_{+}/t_{-}(\bar{\xi }) \approx -1.0604$, where $t_{-}(\bar{\xi }) \approx 0.5928$.

Fig. 5.13

An attractive cone generated by invariant curve H(y) of PWNS

Fig. 5.14

Two generalized center manifolds of PWNS (${\rho }^{-} = -0.01{,\rho }^{+} = 0.1$) for ${\mu }^{-} =\mu _{ 0}^{-}$ (left), stable periodic orbit of PWNS for ${\mu }^{-} = -1.06>\mu _{ 0}^{-}$ (right)

Extension of these results to situations involving sliding motion are given in [20].