The complicated bifurcation of an archetypal self-excited SD oscillator with dry friction

Abstract

In this paper, we investigate the local and global bifurcation behaviors of an archetypal self-excited smooth and discontinuous oscillator driven by moving belt friction. The belt friction is described in the sense of Stribeck characteristic to formulate the mathematical model of the proposed system. For such a friction characteristic, the complicated bifurcation behaviors of the system are discussed. The bifurcation of the multiple sliding segments for this self-excited system is exhibited by analytically exploring the collision of tangent points. The Hopf bifurcation of this self-excited system with viscous damping is analyzed by making the examination of the eigenvalues at the steady state and discussing the stability of the limit cycles. The bifurcation diagrams and the corresponding phase portraits are depicted to demonstrate the complicated dynamical behaviors of double tangency bifurcation, the bifurcation of sliding homoclinic orbit to a saddle, subcritical Hopf bifurcation and grazing bifurcation for this system.

1 Introduction

Bifurcation theory is presently not a new but the well-known and carefully inspected branch of dynamics being still under deep considerations. It is characterized by a qualitative change in the structural behavior while a system parameter value passes through any critical points. Bifurcations in smooth systems are well understood in theoretical classification theorems [1, 2] and engineering applications [3], but little is known about bifurcations in discontinuous systems. Filippov systems [4] form a very important subclass of discontinuous systems which can be described by a set of first order ordinary differential equations with a discontinuous right-hand side. As mentioned in [5], there is no general agreement on what a bifurcation could be in Filippov systems. In the earlier research, the study was restricted to bifurcations of Filippov systems not allowing for sliding [6,7,8] which greatly simplified the analysis and gave a incomplete classification. Later, the bifurcation of sliding cycles was deficiently treated [4]. Actually, the contributions on sliding bifurcations of limit cycles in Filippov systems refer to the mechanical systems with dry friction [9,10,11,12,13,14,15,16,17]. The geometrical criterion for defining and classifying sliding bifurcation is developed, and the explicit topological normal forms for all codim 1 local sliding bifurcation were derived in [18]. Very little is known on bifurcation behaviors of the nonlinear friction system characterized by geometric nonlinearities.

In fact, there are many nonlinear friction systems characterized by geometric nonlinearities of elastic large deformation or large displacement in practical mechanical engineering, i.e., the geometric nonlinear vibration induced by friction between the brake disk and pad in a brake system [19, 20], the moving tectonic plates in an earthquake fault moving across each other [21, 22], and the ice stream and moving subglacial bed of Whillans Ice Stream (WIS) [23] capable of stick–slip motion.

In this paper, a self-excited smooth and discontinuous (SD) oscillator proposed in [24] is a geometrical nonlinear friction system, based upon the well-known geometrical mode of SD oscillator [25,26,27] and classical moving belt. The SD oscillator can be smooth and discontinuous depending on the value of the smoothness parameter $\alpha$. The smooth dynamics appears if $\alpha >0$, while the discontinuous dynamics behavior occurs when $\alpha =0$. Note, in this case of $\alpha =0$, this system has become physically unrealistic because the distance between the rigid supports has become zero, and the model corresponds to an oscillating mass supported by two parallel vertical springs. The self-excited SD oscillator is characterized by the multiple stick zones, hyperbolic structure transition and friction-induced asymmetry phenomena. Under perturbation, the multiple stick–slip periodic motion and multiple stick–slip chaos for this system are demonstrated. At present, the research on the bifurcation theory of the geometrical nonlinear friction system is very insufficient. Therefore, it is necessary to investigate the bifurcation behaviors of a nonlinear friction system with geometric nonlinearity for gaining a deeper understanding of nonlinear friction-induced vibration in mechanical engineering.

The motivation of this paper is to investigate the local and global bifurcation behaviors of an archetypal self-excited SD oscillator with geometrical nonlinearity in the sense of Stribeck friction characteristic. This paper examines the sliding motion of the self-excited SD oscillator including the tangent points, sliding homoclinic orbits, fixed points, limit cycles and their stability. The bifurcation behavior of this system can be analyzed by the bifurcation theory. The analysis is based on the theoretical bifurcation analysis and phase plane plots to better exhibit the bifurcation behaviors of this self-excited system. Through these investigations of self-excited SD oscillator, we can get insight into the mechanism of the geometric nonlinear friction dynamics in mechanical engineering and geography.

This paper is organized as follows. In Sect. 2, some basic theoretical backgrounds of Filippov system are introduced, including switch control function and tangent points. In Sect. 3, the description of the self-excited SD oscillator with Stribeck friction characteristic and motion equation is presented. In Sect. 4, the dynamical behavior analysis of this system without viscous damping is performed. In Sect. 5, the analytical investigations on stability and bifurcation due to the Stribeck friction characteristic in the self-excited SD oscillator with viscous damping are investigated. Finally, some remarks of this paper are concluded.

2 Preliminaries

Our analysis is based on a generic Filippov system of the form

$$\begin{aligned} {{\varvec{x}}}=\left\{ \begin{array}{ll} f^{(1)}({{\varvec{x}}}),\qquad {{\varvec{x}}} \in S_1, \\ f^{(2)}({{\varvec{x}}}),\qquad {{\varvec{x}}} \in S_2. \end{array} \right. \end{aligned}$$

(1)

where ${{\varvec{x}}}\in \mathbf{R }^n$, and $f^{(i)}: \mathbf{R }^n \rightarrow \mathbf{R }^n, i=1,2$, are smooth functions.

Moreover, the discontinuity boundary $\mathrm {\Sigma }$ separating the two regions is described as

$$\begin{aligned} \mathrm {\Sigma }=\{{{\varvec{x}}} \in \mathbf{R }^n: H({{\varvec{x}}})=0\}, \end{aligned}$$

(2)

where H is a smooth scalar function with nonvanishing gradient $H_{{\varvec{x}}}({{\varvec{x}}})=\partial H({{\varvec{x}}})/\partial {{\varvec{x}}}$ on the discontinuity boundary $\mathrm {\Sigma }$, and

$$\begin{aligned} \begin{array}{ll} S_1=\{{{\varvec{x}}}\in \mathbf{R }^n: H({{\varvec{x}}})<0 \}, \\ S_2=\{{{\varvec{x}}}\in \mathbf{R }^n: H({{\varvec{x}}})>0 \}. \end{array} \end{aligned}$$

(3)

Fig. 1

a Visible and b invisible tangent point. The thick orbit is a sliding orbit

Fig. 2

a Dynamical model of the self-excited SD oscillator on moving belt. b Stribeck friction characteristic with exponential description

The boundary $\mathrm {\Sigma }$ is either closed or goes to infinity in both directions and $f^{(1)} \not \equiv f^{(2)}$ on $\mathrm {\Sigma }$.

It is possible to construct the desired general solutions of Eq. (1) by concatenating standard solutions in $S_{1,2}$ and sliding solutions on $\mathrm {\Sigma }$ obtained with the well-known Filippov convex method [4]. Let

$$\begin{aligned} \sigma ({{\varvec{x}}})=\langle H_{{\varvec{x}}}({{\varvec{x}}}), f^{(1)}\rangle \langle H_{{\varvec{x}}}({{\varvec{x}}}), f^{(2)}\rangle , \end{aligned}$$

(4)

be the definition of switch control function in which $\langle \cdot ,\cdot \rangle$ denotes the standard scalar product in $\mathbf{R }^n$.

The crossing set $\mathrm {\Sigma }_c \subset \mathrm {\Sigma }$ is defined as

$$\begin{aligned} \mathrm {\Sigma }_c=\{{{\varvec{x}}}\in \mathrm {\Sigma }: \sigma ({{\varvec{x}}})>0 \}, \end{aligned}$$

(5)

which is the set of all points ${{\varvec{x}}}\in \mathrm {\Sigma }$, where at these points the orbit of system (1) crosses the boundary $\mathrm {\Sigma }$, i.e., the orbit reaching ${{\varvec{x}}}$ from $S_i$ concatenates with the orbit entering $S_j$, $i\ne j$, from ${{\varvec{x}}}$.

The sliding set $\mathrm {\Sigma }_s$ is the complement to $\mathrm {\Sigma }_c$ in $\mathrm {\Sigma }$:

$$\begin{aligned} \mathrm {\Sigma }_s=\{{{\varvec{x}}}\in \mathrm {\Sigma }: \sigma ({{\varvec{x}}})\le 0 \}, \end{aligned}$$

(6)

where at these points ${{\varvec{x}}}\in \mathrm {\Sigma }_s$, the orbit of system (1) which reaches ${{\varvec{x}}}$ does not leave $\mathrm {\Sigma }$. and will therefore have to move along $\mathrm {\Sigma }$.

The crossing set is open, while the sliding set is the union of closed sliding segments and isolated sliding points. In general, the orbit of system (1) crosses $\mathrm {\Sigma }$ at points ${{\varvec{x}}}\in \mathrm {\Sigma }_c$, while it slides on $\mathrm {\Sigma }$ when points ${{\varvec{x}}}\in \mathrm {\Sigma }_s$.

Notice that, a sliding segment is delimited either by a boundary equilibrium ${{\varvec{x}}}_B$, or by a point ${{\varvec{x}}}_T$(called tangent point) in which one of the vectors $f^{(i)}({{\varvec{x}}}_T)$ is tangent to $\mathrm {\Sigma }$ and both of them are nonzero. Therefore, the following definition of the tangent points ${{\varvec{x}}}\in \mathrm {\Sigma }_s$ holds:

$$\begin{aligned} \langle H_{{\varvec{x}}}({{\varvec{x}}}_T), f^{(i)}({{\varvec{x}}}_T) \rangle =0, \quad i=1,2. \end{aligned}$$

(7)

We say that this tangent point is visible if the orbit of $\dot{{{\varvec{x}}}}=f^{(1)}({{\varvec{x}}})$ starting from ${{\varvec{x}}}_T$ belongs to $S_1$ for sufficiently small $|t|\ne 0$. In other hand, the same point is invisible if the mentioned orbit belongs to $S_2$ (as in Fig.1).

3 The governing equation

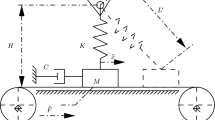
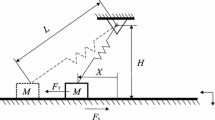
The system analyzed in this paper is composed by a mass M, supported by a moving belt, connected to a dashpot with damping coefficient C and a fixed support by a inclined linear spring of stiffness coefficient K, which is capable of resisting both tension and compression, as shown in Fig. 2a. The contact surface between the mass and belt is rough so that the belt exerts a friction force on the mass. The mass vibrates under the influence of dry friction $F_S$ existing in the contact zone created by the mass’s surface and the outer belt’s surface. The belt moves with a constant velocity $V_0$. We assume a non-deformable moving belt being under action of normal force from total force of the gravity $N=Mg$ and spring force in the contact zone, and the mass is secured to move in the horizontal direction without leaving the belt. The position of the mass over the belt is represented by X.

The equation of motion for this mass-spring on the moving belt is given by

$$\begin{aligned} M{\ddot{X}}+C{\dot{X}}+KX\Big (1-\displaystyle \frac{L}{\sqrt{X^{2}+H^2}}\Big )+F_S=0, \end{aligned}$$

(8)

where L is the original length of the spring, H is the distance between fixed point and belt, and the friction force $F_S$ between the mass and belt is described as

$$\begin{aligned} F_S= & {} \mu (V_\mathrm{{rel}})\Big [Mg-KH\Big (1-\displaystyle \frac{L}{\sqrt{X^{2}+H^2}}\Big )\Big ]\nonumber \\&\times \text {sgn}({\dot{X}}-V_0), \end{aligned}$$

(9)

where $\mu (V_\mathrm{{rel}})$ is the friction coefficient depending on the relative velocity $V_\mathrm{{rel}}={\dot{X}}-V_0$ between the mass and belt in an exponential description with a Stribeck friction characteristic [28, 29], as

$$\begin{aligned} \mu (v_\mathrm{{rel}})=\mu _k+\varDelta \mu \text {e}^{-a|V_\mathrm{{rel}}|}, \end{aligned}$$

(10)

where $\mu _k$ represents the kinetic friction coefficient when the relative velocity $V_\mathrm{{rel}}$ goes to infinity, $\mu _0$ is the static friction coefficient, $\varDelta \mu =\mu _0-\mu _k$ and a denotes a slope parameter (see Fig. 2b).

Without loss of generality, the non-dimensional variables and parameters are introduced as follows:

$$\begin{aligned} x= & {} \displaystyle \frac{X}{L}, \quad \omega _{0}^{2}=\displaystyle \frac{K}{M},\quad c=\displaystyle \frac{C}{M\omega _0},\quad \alpha =\displaystyle \frac{H}{L},\quad \nonumber \\ g_1= & {} \displaystyle \frac{g}{L\omega _0^2},\quad v_0=\displaystyle \frac{V_0}{L\omega _0^2}\quad \tau =\omega _0t. \end{aligned}$$

(11)

Then, substituting Eq. (11) into Eq. (8), the non-dimensional equation of motion for this system is obtained as follows

$$\begin{aligned}&{\ddot{x}}+c{\dot{x}}+x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\nonumber \\&\quad = -\mu (v_\mathrm{{rel}})\Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]\text {sgn}({\dot{x}}-v_0),\nonumber \\ \end{aligned}$$

(12)

where the dot denotes the derivative with respect to $\tau$.

Equation (12) describes the dynamics of the self-excited vibration that occurs during the dry friction between contacting surfaces of mass and the movable belt.

Changing in Eq. (12) the state variable $\dot{x}=y$, we get the following generic planar Filippov system

$$\begin{aligned} \dot{{{\varvec{x}}}}= & {} f({{\varvec{x}}})\nonumber \\= & {} \left\{ \begin{array}{ll} \left[ y,-cy-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\right. \\ \left. +\,\, \mu (v_\mathrm{{rel}})\Big [g_{1}-\alpha \Big ( 1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ] \right] \quad \text {for}\ y < v_0, \\ \left[ y,-cy-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\right. \\ \left. -\,\, \mu (v_\mathrm{{rel}})\Big [g_{1}-\alpha \Big (1- \displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]\right] \quad \text {for} \ y > v_0, \end{array} \right. \nonumber \\ \end{aligned}$$

(13)

where ${{\varvec{x}}}=[x,y]^T$ and $f=[f^{(1)},f^{(2)}]^T$.

4 The system with no viscous damping

Prior to further discussions, we investigate the dynamical behavior of system (12) with no viscous damping. The equation of motion for the system can be easily obtained from Eq. (13) by assuming $c=0$

$$\begin{aligned} \dot{{{\varvec{x}}}}= & {} f({{\varvec{x}}})\nonumber \\= & {} \left\{ \begin{array}{ll} \left[ y,-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\right. \\ \left. +\,\, \mu (v_\mathrm{{rel}})\Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2} +\alpha ^2}}\Big )\Big ] \right] \quad \text {for}\ y < v_0, \\ \left[ y,-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\right. \\ \left. -\, \mu (v_\mathrm{{rel}})\Big [g_{1}-\alpha \Big (1- \displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]\right] \quad \text {for} \ y > v_0, \end{array} \right. \nonumber \\ \end{aligned}$$

(14)

where ${{\varvec{x}}}=[x,y]^T$ and $f=[f^{(1)},f^{(2)}]^T$.

4.1 Bifurcation of tangent points

In this subsection, bifurcations of stick zones and corresponding tangent points of this Filippov system are considered. According to the Filippov’s theory, the switch control function $\sigma (x)$ given in Eq. (4) have now the form

$$\begin{aligned} \sigma ({{\varvec{x}}})=f^{(1)}_{II}(x)f^{(2)}_{II}(x), \end{aligned}$$

(15)

where $f^{(1)}_{II}$ and $f^{(2)}_{II}$ are the second components of $f^{(1)}$ and $f^{(2)}$ of Eq. (14).

Assume that ${{\varvec{x}}}_v=[x,v_0]^{T}$ and the switch control function $\sigma (x)$ on the boundary will be as follows

$$\begin{aligned} \sigma ({{\varvec{x}}}_v)= & {} x^2\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )^2\nonumber \\&-\,\, \mu _{0}^2\Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]^2. \end{aligned}$$

(16)

If there exists a derivative of function $\sigma ({{\varvec{x}}}_v)$, it is possible to find critical points of the function by means of the conditions

$$\begin{aligned} \left\{ \begin{array}{ll} D_{\sigma _0}=\displaystyle \frac{\partial \sigma ({{\varvec{x}}}_{v_0})}{\partial {{\varvec{x}}}_{v}}=0, \\ \sigma ({{\varvec{x}}}_{v_0})=0, \end{array} \right. \end{aligned}$$

(17)

then we obtain a set of roots of conditions (17)

$$\begin{aligned} {{\varvec{x}}}_{v_0}^{(i)}= & {} \Big \{0, \pm \sqrt{1-\alpha ^2}, \pm \Big [\displaystyle \frac{1}{2}\mu _0(g_1-\alpha )\nonumber \\&-\displaystyle \frac{1}{2}\sqrt{{\varUpsilon }_1(\mu _0)+\varDelta (\mu _0)}\Big ] \Big \}, \qquad i=1,\ldots ,5. \nonumber \\ \end{aligned}$$

(18)

Substituting ${{\varvec{x}}}_{v_0}^{(i)}$ given by Eq. (18) into Eq. (16) and then solving it with respect to $\mu _0$ and $\alpha$, we get the following boundary conditions

$$\begin{aligned} {\mathscr {H}}={\mathscr {H}}_1\cup {\mathscr {H}}_2, \end{aligned}$$

(19)

where

$$\begin{aligned} {\mathscr {H}}_1= & {} \{(\alpha , \mu _0)| 2{\varUpsilon }_1(\alpha , \mu _0)-\varDelta (\alpha , \mu _0)\nonumber \\&-{\varUpsilon }_2(\alpha , \mu _0)=0, 0<\alpha <1, \mu _0>0 \}, \end{aligned}$$

(20)

$$\begin{aligned} {\mathscr {H}}_2= & {} \{(\alpha , \mu _0)| \mu _0=0,\alpha \ge 0 \}, \end{aligned}$$

(21)

$$\begin{aligned} {\varUpsilon }_1(\mu _0)= & {} \displaystyle \frac{1}{3}(\mu _0\alpha -\mu _0 g_1)^2-\displaystyle \frac{2}{3}(\alpha ^2-1),\\ {\varUpsilon }_2(\mu _0)= & {} \displaystyle \frac{8(\mu _0 g_1-\mu _0\alpha )^3-16\mu _0\alpha (\alpha ^2-g_1\alpha -1)+8(\mu _0\alpha -\mu _0 g_1)[(\mu _0\alpha -\mu _0 g_1)^2+\alpha ^2-1]}{4\sqrt{{\varUpsilon }_1+\varDelta }}, \end{aligned}$$

$$\begin{aligned} \varDelta (\mu _0)= & {} \displaystyle \frac{\root 3 \of {2}\varDelta _1(\mu _0)}{3\root 3 \of {\varDelta _2(\mu _0)+\sqrt{-4{\varDelta }_1^3(\mu _0)+\varDelta _2^2(\mu _0)}}}\\&+\displaystyle \frac{\root 3 \of {{\varDelta }_2(\mu _0) +\sqrt{-4\varDelta _1^3(\mu _0)+{\varDelta }_2^2(\mu _0)}}}{3\root 3 \of {2}},\\ \varDelta _1(\mu _0)= & {} 12\mu _0^2\alpha ^2[(g_1-\alpha )^2-1]\\&-12(\mu _0\alpha -\mu _0 g_1)(\mu _0\alpha ^3-\mu _0\alpha ^2g_1-\mu _0\alpha )\\&+[(\mu _0\alpha -\mu _0 g_1)^2+\alpha ^2-1]^2,\\ \varDelta _2(\mu _0)= & {} 108\mu _0^2\alpha ^2(\mu _0\alpha -\mu _0 g_1)^2[(\alpha -g_1)^2-1]\\&-72\mu _0^2\alpha ^2[(\alpha -g_1)^2-1][(\mu _0\alpha -\mu _0 g_1)^2\\&+\alpha ^2-1] -36(\mu _0\alpha -\mu _0 g_1)(\mu _0\alpha ^{3}\\&-\mu _0\alpha ^2g_1-\mu _0\alpha )[(\mu _0\alpha -\mu _0 g_1)^2+\alpha ^2-1]\\&+108(\mu _0\alpha ^3-\mu _0\alpha ^2g_1-\mu _0\alpha )^2 \\&+2[(\mu _0\alpha -\mu _0 g_1)^2+\alpha ^2-1]^3. \end{aligned}$$

Fig. 3

Two-parameter bifurcation diagram of the boundary conditions for system (14) when $g_1=2$. The curves labeled as ${\mathscr {H}}_1$ corresponds to double tangency bifurcation curve, ${\mathscr {H}}_2$ represents that system (14) becomes the SD oscillator when $\mu _0=0$

Fig. 4

a Tangent points (circles) on the intersection of function $\sigma (x)$ with the axis x for $\mu _0=0$ (dash line) and $\mu _0=\mu _0^{(2)}$ (thick line). b Bifurcations of tangent points at changes of the parameter $\mu _0$ from 0 to 0.2 for system (14)

Fig. 5

Double tangency bifurcation of the closing of two “crossing windows” for system (14) with the parameters: $g_1=2$, $\alpha =0.4$, $v_0=0.1$, ${\varDelta }\mu =0.02$, $a=2$. a $\mu _0=0.1$. b $\mu _0=\mu _0^{(2)}=0.1331$. c $\mu _0=0.14$. The stick zones are marked with the green lines. The signs “$*$” invisible tangent points, “” visible tangent points, and “$\emptyset$” double tangent points. (Color figure online)

Figure 3 shows the two-parameter bifurcation diagram of the boundary conditions marked by ${\mathscr {H}}_1$ and ${\mathscr {H}}_2$ for system (14) by assuming $g_1=2$. The curve labeled as ${\mathscr {H}}_1$ corresponds to double tangency bifurcation [18] curve, as well as the bifurcation curve of the sliding segments in this Filippov system. Collision of tangent points in this system happens when the parameters $\alpha$ and $\mu _0$ are taken values in the curve ${\mathscr {H}}_1$. The curve marked with ${\mathscr {H}}_2$ represents that system (14) becomes the SD oscillator when $\mu _0=0$, and furthermore, it is discontinuous for $\alpha =0$, $\mu _0=0$.

In order to vividly describe the bifurcation of tangent points, we get the set of boundary values $\mu _0^{(i)}=\{0,0.1331\}$ for $i=1,2$ assuming the following parameters in Eq. (16): $g_1=2$, $\alpha =0.4$, and the function $\sigma (x)$ are shown in Fig. 4a when the parameter $\mu _0$ takes different value.

The set of values $\{\mu _0^{(i)}\}$ places the switch control function $\sigma (x)$ of the stick zone as a tangential to the abscissa of the plane $\{\sigma (x),x\}$, as shown in Fig. 4a. It is worth noticing that for $\mu _0=0$ marked in Fig. 4a by a dashed line, the sliding segments vanish and degenerate to the three tangent points, and no stick exists. Another scenario is regarded to the graph marked in Fig. 4a by a thick line for $\mu _0=\mu _0^{(2)}$ that is tangent from below to the abscissa. Three sliding segments merge into one large sliding segment and the collisions of tangent points happen. The stick zone in this case is wide and extends from left to right branch of graph in the plane $\{\sigma (x),x\}$. It confirms that the location of a stick zone depends on the parameters of this particular dynamical system, since the values of $\mu _0$ are determined by the parameters $g_1$, $\alpha$.

The control function introduced in Eq. (15) multiplies the two terms $f^{(1)}_{II}$ and $f^{(2)}_{II}$ which can be used to find tangent points of $f^{(1)}$ and $f^{(2)}$ in the discontinuity zone. Bifurcations of tangent points at changes of control parameter $\mu _0$ are presented in Fig. 4b.

Figure 5 shows the behavior of double tangency bifurcation of system (14) for the variation of parameter $\mu _0$. In all of the following phase portraits, the parameters of the system will be fixed $g_1=2$, $\alpha =0.4$ and $a=2$, the cusps correspond to a sign change of the relative velocity, the short horizontal parts marked with green lines in the phase portraits correspond to the sticking zones, and the sign “$\otimes$” represents the unstable fixed point of the system.

When $\mu _0<\mu _0^{(2)}$, there are three stable sliding segments separated by two “crossing windows” between the visible and invisible points, marked with and $*$, respectively, as shown in Fig. 5a. The sliding motions starting on the left sliding segment terminate at a visible tangent point and end up in the left stable stick–slip limit cycle. The sliding trajectories starting on the middle sliding segment terminate at a visible tangent point, and continue along a standard orbit which reaches the right sliding segment, finally terminate at a visible tangent point and end up in the right stable stick–slip limit cycle. These tangent points collide at $\mu _0=\mu _0^{(2)}$ forming two double tangent points marked with the sign $\emptyset$, as depicted in Fig. 5b, and the “crossing windows” close. The sliding trajectories originating on the left sliding segment will enter into the right stick–slip limit cycle after through two double tangent points and the left limit cycle disappears. In Fig. 5c, there is an uninterrupted sliding orbit ending in the right stick–slip limit cycle, and one large sliding segment remains.

In the following study, we will focus on the case of taking the values of parameters $\alpha$ and $\mu _0$ below the curve ${\mathscr {H}}_1$ in Fig. 3.

4.2 The effect of belt velocity

For a more general view, once the other parameters of system (14) have been chosen, the steady-state motion of the system depends only upon the driving velocity $v_0$.

If we assume for example in Eq. (14), $g_1=2$, $\alpha =0.4$, $\mu _0=0.1$, $\varDelta \mu =0.02$, $a=2$, it is possible to detect five qualitatively different steady-state motions. If $0<v_0<v_1=0.2204$, a pair of asymmetric stick–slip limit cycles coexist and the orbits of motion are presented in Fig. 6a, and the sticking of their motions exists in two different stick regions.

Fig. 6

Variation of the belt velocity $v_0$ in system (14) for $g_1=2$, $\alpha =0.4$, $\mu _0=0.1$, ${\varDelta }\mu =0.02$ and $a=2$. a Coexisting stick–slip limit cycles for $0<v_0<v_1=0.2204$. b Coexistence of a homoclinic orbit and a stick–slip limit cycle for $v_0=v_1$. A bifurcation of a sliding homoclinic orbit to a saddle happens. c Only a stick–slip limit cycle for $v_1<v_0<v_2=0.84638$. d A large sliding homoclinic orbit for $v_0=v_2$. The bifurcation of a sliding homoclinic orbit to a saddle happens again. e A large stick–slip limit cycle for $v_0>v_2$. (Color figure online)

With the increase of the driving velocity $v_0$, the radiuses of two limit cycles become larger up to the value $v_0=v_1$, the left limit cycle collides with a saddle point, a left sliding homoclinic orbit appears in Fig. 6b, and system (14) undergoes a bifurcation of a sliding homoclinic orbit to a saddle [18]. If $v_1< v_0<v_2=0.84638$, the left homoclinic orbit disappears and the right stick–slip limit cycle remains and grows, as depicted in Fig. 6c. As the belt velocity $v_0$ increases, the saddle point has a right homoclinic orbit containing a sliding segment at $v_0=v_2$ in Fig. 6d, and system (14) undergoes a bifurcation of a sliding homoclinic orbit to a saddle again. When $v_0\ge v_2$, the right homoclinic orbit disappears and a large stick–slip limit cycle appears which encompasses all the left and right limit cycles mentioned above, as shown in Fig. 6e. The critical values 0.2204 and 0.84638 have been computed numerically.

The following study concentrates on the cases of small driving velocity, and therefore, in the remainder the driving velocity $v_0$ will be less than $v_1$.

5 Hopf bifurcation

To consider the influence of the damping $(c\ne 0)$, the theoretical and numerical analysis is carried out to further investigate the dynamical behaviors of system (13). A Hopf bifurcation is a local bifurcation in which a fixed point of the system changes its stability as a parameter is varied. It is clear that the fixed points can only occur when the mass of this system is continuously slipping; therefore, we firstly have to find all the fixed points of system (13) and discuss their stability.

5.1 Fixed points and their stability

In this subsection, the focus will be on the fixed points of system (13). Since there is no fixed point in the system for $y>v_0>0$, we only analyze the fixed point by assuming $y<v_0$, then system (13) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{x}}=y, \\ {\dot{y}}=-c{\dot{x}}-x\Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\\ \qquad +\,\,\mu (v_{rel})\Big [g_{1}-\alpha \Big (1-\displaystyle \frac{1}{\sqrt{x^{2}+\alpha ^2}}\Big )\Big ]. \end{array} \right. \end{aligned}$$

(22)

After some calculations the fixed points of system (22) are $(x_1,0)$, $(x_2,0)$ and $(x_3,0)$, where

$$\begin{aligned} x_1= & {} \displaystyle \frac{1}{2}\mu (v_0)(g_1-\alpha )-\displaystyle \frac{1}{2}\sqrt{{\varUpsilon }_1(\mu (v_0))+\varDelta (\mu (v_0))}\nonumber \\&+\displaystyle \frac{1}{2}\sqrt{2{\varUpsilon }_1(\mu (v_0))-\varDelta (\mu (v_0))-{\varUpsilon }_2(\mu (v_0))},\nonumber \\ x_2= & {} \displaystyle \frac{1}{2}\mu (v_0)(g_1-\alpha )+\displaystyle \frac{1}{2}\sqrt{{\varUpsilon }_1(\mu (v_0))+\varDelta (\mu (v_0))}\nonumber \\&+\displaystyle \frac{1}{2}\sqrt{2{\varUpsilon }_1(\mu (v_0))-\varDelta (\mu (v_0))+{\varUpsilon }_2(\mu (v_0))},\nonumber \\ x_3= & {} \displaystyle \frac{1}{2}\mu (v_0)(g_1-\alpha )-\displaystyle \frac{1}{2}\sqrt{{\varUpsilon }_1(\mu (v_0))+\varDelta (\mu (v_0))}\nonumber \\&-\displaystyle \frac{1}{2}\sqrt{2{\varUpsilon }_1(\mu (v_0))-\varDelta (\mu (v_0))-{\varUpsilon }_2(\mu (v_0))},\nonumber \\ \end{aligned}$$

(23)

and $\mu (v_{0})=\mu _k+{\varDelta }\mu \text {e}^{-av_{0}}$.

The associated Jacobian matrix of system (22) at $(x_s,0)_{s=1,2,3}$ can be derived as

$$\begin{aligned} J\begin{pmatrix} x\\ y \end{pmatrix}_{(x_s,0)}=\begin{pmatrix} 0 &{} 1 \\ {\varPsi }(x_s) &{} {\varPhi }(x_s)-c \end{pmatrix}, \end{aligned}$$

(24)

where

$$\begin{aligned} {\varPsi }(x)= & {} -1+\displaystyle \frac{1}{\sqrt{x^2+\alpha ^2}}-\displaystyle \frac{x^2}{(x^2+\alpha ^2)^{3/2}}\\&-\displaystyle \frac{x\alpha \mu (v_0)}{(x^2+\alpha ^2)^{3/2}},\\ {\varPhi }(x)= & {} \varDelta \mu a\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{x^2+\alpha ^2}}\Big )\text {e}^{-av_0}. \end{aligned}$$

The characteristic equation of matrix (24) can be obtained and written as

$$\begin{aligned} \lambda ^2-\lambda [{\varPhi }(x_s)-c]-{\varPsi }(x_s)=0, \end{aligned}$$

(25)

from which we can get

$$\begin{aligned} \lambda _{1,2}|_{(x_s,0)}=\displaystyle \frac{{\varPhi }(x_s)-c\pm \sqrt{({\varPhi }(x_s)-c)^2+4{\varPsi }(x_s)}}{2}. \nonumber \\ \end{aligned}$$

(26)

Assuming the set of parameters, $g_1=2$, $\alpha =0.4$, $\mu _k=0.08$, $\varDelta \mu =0.02$, $a=2$, $v_0=0.2$, and substituting $x_s$ obtained in Eq. (23) into the ${\varPhi }(x_s)$ and ${\varPsi }(x_s)$ lead to

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varPhi }(x_s)>0, s=1,2,3, \\ {\varPsi }(x_1)>0, {\varPsi }(x_{2,3})<0. \end{array}\right. } \end{aligned}$$

(27)

For the fixed point $(x_1,0)$, no matter what value c is, relation (27) shows that the two eigenvalues are real and one is positive, another is negative. Thus the fixed point $(x_1,0)$ is a saddle point.

For the fixed points $(x_s,0)$, $s=2,3$, if c is large, relations (27) show that the two eigenvalues are real and negative; consequently, the fixed points are stable. As c decreases, when ${\varPhi }(x_s)-c$ is slightly large than 0, the two eigenvalues are complex-conjugate and their real parts change sigh at a critical value

$$\begin{aligned} c=c_s={\varPhi }(x_s). \end{aligned}$$

(28)

In that case, $\lambda _{1,2}|_{(x_s,0)}=\pm \text {i}\sqrt{-{\varPsi }(x_s)}$, $s=2,3$, the system undergo a Hopf bifurcation and a limit cycle branching from the fixed point $(x_s,0)$, $s=2,3$, is born.

5.2 Analytical approximative solution for periodic motion

In order to examine the limit cycle, the approximative solutions of periodic motions for the self-excited SD oscillator are sought by applying the averaging method. By introducing the coordinate transformation $z=x-x_s$, $s=2,3$, system (22) can be rewritten in the so-called standard form such that $z=0$ corresponds to the steady state

$$\begin{aligned} {\ddot{z}}+z=\varepsilon f(z,{\dot{z}}), \end{aligned}$$

(29)

where

$$\begin{aligned} \varepsilon f(z,{\dot{z}})= & {} -c{\dot{z}}+\displaystyle \frac{z+x_s}{\sqrt{(z+x_s)^2+\alpha ^2}}+\Big (\mu _k+{\varDelta }\mu \text {e}^{a({\dot{z}}-v_0)}\Big )\\&\times \Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(z+x_s)^2+\alpha ^2}}\Big )-x_s. \end{aligned}$$

Letting $z=A \cos \theta$, ${\dot{z}}=-\sin \theta$ and $\theta =\tau +{\varTheta }(\tau )$, Eq. (29) can be transformed into a new coordinates in the form of slowly varying amplitude and phase

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{A}}=-f(A \cos \theta ,-A\sin \theta )\sin \theta , \\ {\dot{{\varTheta }}}=-\displaystyle \frac{1}{A}f(A \cos \theta ,-A\sin \theta )\cos \theta . \end{array} \right. \end{aligned}$$

(30)

Averaging Eq. (30) over one period $[0, 2\pi ]$ yields the averaged equation

$$\begin{aligned} \left\{ \begin{array}{ll} {\dot{A}}=-\frac{1}{2} Ac-\frac{1}{2\pi }\int _{0}^{2\pi }\Big ({\varDelta }\mu \text {e}^{-av_0}\text {e}^{-aA\sin \theta }\Big )\\ \qquad \quad \Big (g_1-\alpha +\frac{\alpha }{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin \theta \text {d}\theta , \\ {\dot{{\varTheta }}}=-\frac{1}{2\pi A}\int _{0}^{2\pi }\frac{A \cos \theta +x_s+\alpha (\mu _k+{\varDelta }\mu \text {e}^{-av_0}\text {e}^{-aA\sin \theta })}{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\\ \qquad \quad \cos \theta \text {d}\theta . \end{array} \right. \nonumber \\ \end{aligned}$$

(31)

Since the amplitude of the limit cycle is determined by solving the amplitude equation for A, the first equation of Eq. (31) is investigated for solutions of stationary amplitudes with ${\dot{A}}=0$ and rewritten as following

$$\begin{aligned} 0= & {} -\displaystyle \frac{1}{2} Ac-\displaystyle \frac{1}{2\pi }\int _{0}^{2\pi }\Big (\varDelta \mu \text {e}^{-av_0}\text {e}^{-aA\sin \theta }\Big )\nonumber \\&\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin \theta \text {d}\theta . \nonumber \\ \end{aligned}$$

(32)

Looking at Eq. (32), it is obvious that

$$\begin{aligned} A_1=0 \end{aligned}$$

(33)

is always a solution of stationary amplitude. Separating this solution from Eq. (32) yields

$$\begin{aligned} 0= & {} -\displaystyle \frac{1}{2}c-\displaystyle \frac{1}{2\pi A}\int _{0}^{2\pi }\Big ({\varDelta }\mu e^{-av_0}\text {e}^{-aA\sin \theta }\Big )\nonumber \\&\times \Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin \theta \text {d}\theta \nonumber \\= & {} -\displaystyle \frac{1}{2}c-\displaystyle \frac{1}{2\pi A}\int _{0}^{2\pi } {\varDelta }\mu \text {e}^{-av_0}\sum _{n=0}^{+\infty }\displaystyle \frac{(-aA\sin \theta )^n}{n!}\nonumber \\&\times \Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin \theta \text {d}\theta \nonumber \\= & {} -\displaystyle \frac{1}{2}c+{\varDelta }\mu \text {e}^{-av_0}\sum _{k=1}^{+\infty }\displaystyle \frac{a^{2k-1}A^{2k-2}}{(2k-1)!}\nonumber \\&\times \left<\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin ^{2k}\theta \right>,\nonumber \\ \end{aligned}$$

(34)

where $\langle f(\theta )\rangle =\displaystyle \frac{1}{2\pi }\int _{0}^{2\pi }f(\theta ) \text {d}\theta$ denotes averaging the function $f(\theta )$ over a period $[0,2\pi ]$.

The amplitude $A_2$ of this limit cycle should satisfies the response equation in the following

$$\begin{aligned} \displaystyle \frac{1}{2}c= & {} \varDelta \mu \text {e}^{-av_0}\displaystyle \sum _{k=1}^{+\infty }\displaystyle \frac{a^{2k-1}A_2^{2k-2}}{(2k-1)!}\nonumber \\&\left<\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A_2\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin ^{2k}\theta \right>\nonumber \\= & {} \displaystyle \frac{1}{2}{\varDelta }\mu a \text {e}^{-av_0}\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{x_s^2+\alpha ^2}}\Big )\nonumber \\&+\varDelta \mu \text {e}^{-av_0}\sum _{k=2}^{+\infty }\displaystyle \frac{a^{2k-1}A_2^{2k-2}}{(2k-1)!}\nonumber \\&\times \left<\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A_2\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin ^{2k}\theta \right>\nonumber \\= & {} \displaystyle \frac{1}{2}{\varPhi }(x_s)+\varDelta \mu \text {e}^{-av_0}\displaystyle \sum _{k=2}^{+\infty }\displaystyle \frac{a^{2k-1}A_2^{2k-2}}{(2k-1)!}\nonumber \\&\times \left<\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A_2\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin ^{2k}\theta \right>.\nonumber \\ \end{aligned}$$

(35)

Regarding Eq. (35), since ${\varDelta }\mu$, $\text {e}^{-av_0}$ and the quantities of the sum are positive, the existence of a limit cycle with a real amplitude $A_2$ should satisfy the condition

$$\begin{aligned} A_2\in \mathbf{R }^+ \Leftrightarrow c- {\varPhi }(x_s)>0. \end{aligned}$$

(36)

In addition, differential equation (22) holds for ${\dot{x}}<v_0$ where in the entire half plane of motion for this system below the stick line ${\dot{x}}=v_0$. The presented investigation of dynamical behavior for the examined system will be valid as long as the trajectories do not touch the stick line, since this would cause them to be trapped by the stick–slip limit cycle. With this, the amplitude of the limit cycle in the sense of Eq. (35) has to fulfill the condition

$$\begin{aligned} A_2<v_0. \end{aligned}$$

(37)

5.3 Stability of the limit cycles

To study the stability of limit cycles given by Eqs. (33) and (35), the analytical method developed in [29] is applied in this system. We examine the first derivative of the first equation of Eq. (31) with respect to A as following

$$\begin{aligned} \displaystyle \frac{\mathrm{d}{\dot{A}}}{\mathrm{d}A}= & {} -\displaystyle \frac{1}{2}c+\displaystyle \frac{1}{2}{\varPhi }(x_s) +{\varDelta }\mu \text {e}^{-av_0}\displaystyle \sum _{k=2}^{+\infty }\displaystyle \frac{a^{2k-1}A^{2k-2}}{(2k-2)!}\nonumber \\&\times \left<\Big (g_1-\alpha +\displaystyle \frac{\alpha }{\sqrt{(A\cos \theta +x_s)^2+\alpha ^2}}\Big )\sin ^{2k}\theta \right>\nonumber \\&+\,\,{\varDelta }\mu \text {e}^{-av_0}\displaystyle \sum _{k=1}^{+\infty }\displaystyle \frac{a^{2k-1}A^{2k-1}}{(2k-1)!}\nonumber \\&\times \left<\displaystyle \frac{\alpha \cos \theta (A\cos \theta +x_s)}{\sqrt{\big [(A\cos \theta +x_s)^2+\alpha ^2\big ]^3}}\sin ^{2k}\theta \right>, \end{aligned}$$

(38)

from which the evaluation at the fixed point $A_1=0$ yields

$$\begin{aligned} \displaystyle \frac{\mathrm{d}{\dot{A}}}{\mathrm{d}A}\bigg |_{A=A_1}=-\displaystyle \frac{1}{2}\big (c-{\varPhi }(x_s)\big ). \end{aligned}$$

(39)

As qualitatively outlined in Fig. 7, two cases can be given

• (I) If $c<{\varPhi }(x_s)$, then $\displaystyle \frac{\mathrm{d}{\dot{A}}}{\mathrm{d}A}\bigg |_{A=A_1}>0$: the steady-state fixed point is unstable. The existence of the limit cycle is not fulfilled according to the condition (36); therefore, there is only a unstable fixed point. The curve (I) in Fig. 7 describes this behavior qualitatively.

• (II) If $c>{\varPhi }(x_s)$, then $\displaystyle \frac{\mathrm{d}{\dot{A}}}{\mathrm{d}A}\bigg |_{A=A_1}<0$: the steady-state fixed point is stable. Simultaneously condition (36) is fulfilled. Therefore, there is a limit cycle coexisting to the stable fixed point, and the instability of the limit cycle can easily be seen from Fig. 7, since small perturbations will be amplified. These behaviors are qualitatively presented in curve (II) in Fig. 7. But the amplitude $A_2$ of the unstable limit cycle has to satisfy the condition (37) to avoid being swallowed by the stick–slip limit cycle.

Fig. 7

Qualitative sketch of the amplitude growth behavior for system parameters $g_1=2$, $\alpha =0.4$, $v_0=0.2$, $a=2$, ${\varDelta }\mu =0.02$. (I) $c=0.05$. (II) $c=0.0522$

Therefore, behavior of the Hopf bifurcation (i.e., unstable fixed point $\rightleftarrows$ stable fixed point $+$ unstable limit cycle) in this system is indeed a subcritical Hopf bifurcation. The formal proof of the Hopf bifurcation can be found in “Appendix”.

5.4 Bifurcation diagram

The bifurcation diagram of the damped self-excited SD oscillator is shown in Fig. 8 which demonstrates the variation of the maximum velocity $y_{max}^{(x_s)}$ $(s=2,3)$ of the steady-state motions for varying viscous damping c with respect to the points $(x_2,0)$ and $(x_3,0)$. The system undergoes two subcritical Hopf bifurcations at the critical bifurcation values $c=c_1$ and $c=c_3$.

Fig. 8

Bifurcation diagram of the damped self-excited SD oscillator for $g_1=2$, $v_0=0.2$, $\alpha =0.4$, $\mu _0=0.1$, ${\varDelta }\mu =0.02$, $a=2$. (Color figure online)

With the increasing of the damping coefficient c, the amplitude of the unstable limit cycle also increases. When the maximum value of the velocity of the unstable motions reaches the value $y_{max}^{(x_s)}=v_0$, two critical values for the damping coefficient $c_2$ and $c_4$ are defined, as shown in Fig. 8. In this case the stable stick–slip limit cycles and unstable limit cycles coincide at a discontinuous fold bifurcation [30, 31].

The dynamical behavior of this damped self-excited system with the increasing of viscous damping coefficient c is presented in Fig. 9, where the signs “$\bullet$” and “$\otimes$” denote the stable and unstable fixed points of the system, respectively.

Fig. 9

The behavior of the steady-state for this system as variation of the damped coefficient c for $g_1=2$, $\alpha =0.4$, $v_0=2$, $a=2$, $\mu _0=0.1$ and ${\varDelta }\mu =0.02$. (Color figure online)

• in the range $0<c<c_1$, a pair of asymmetric stable stick–slip limit cycles coexist, as shown in Fig. 9a. Trajectories starting from the points external to the limit cycles are attracted to them. Especially, the unstable manifolds of the saddle point $(x_1,0)$ finally end up in two stick–slip limit cycles after passing through one or two stick regions. The stable manifolds of the saddle point $(x_1,0)$ are the boundary of basin of attractions for the two limit cycles. Trajectories generated from the internal points are repelled by the unstable fixed points $(x_2,0)$ and $(x_3,0)$, and they start to tend to the stick–slip limit cycles.

• in the range $c_1<c<c_2$, there are a pair of asymmetric stable stick–slip limit cycles coexisting to a unstable limit cycle, as shown in Fig. 9b. The system undergoes a subcritical Hopf bifurcation when c increases from $c<c_1$ and passes the borderline $c=c_1={\varPhi }(x_2)$. The fixed point $(x_2,0)$ changes from an unstable one to an asymptotically stable one, an unstable limit cycle bifurcates from it, and simultaneously, the fixed point $(x_3,0)$ is unstable yet. It is easily seen in Fig. 8 that the amplitude of the unstable limit cycle becomes larger when the damping coefficient c increases.

• for $c=c_2$ the coexistence of a stable stick–slip limit cycle and a semi-stable limit cycle is presented in Fig. 9c. The stick–slip limit cycle repelled by the unstable fixed point $(x_3,0)$ is still stable, but for the stable fixed point $(x_2,0)$ the stable stick–slip limit cycle and the unstable limit cycle coincide. The system undergoes a grazing bifurcation at $c=c_2$ where the semi-stable limit cycle is tangent to the line $y=v_0$ in the phase plane, and it is an attracting motion for the external initial conditions, and a repelling motion for the internal points. The stable manifolds of the saddle point $(x_1,0)$ are the boundary of basin of attractions for the two limit cycles yet.

• in the range of $c_2<c<c_3$ there is only a stable stick–slip limit cycle, as shown in Fig. 9d, which is still respelled by the unstable fixed point $(x_3,0)$. Especially, one of unstable manifolds of the saddle point $(x_1,0)$ finally ends up in a stick–slip limit cycle, and another is attracted toward the stable fixed point $(x_2,0)$. The stable manifolds of the saddle point $(x_1,0)$ are the boundary of basin of attractions for the stick–slip limit cycle and fixed point $(x_2,0)$.

• in the range of $c_3<c<c_4$ the stick–slip limit cycle is still stable, but the fixed point $(x_3,0)$ is asymptotically stable separated by an unstable limit cycle in the left-hand half phase plane $(x,{\dot{x}})$, as shown in Fig. 9e. The unstable limit cycle defines the area of attraction of the stable fixed point $(x_3,0)$. There is only a stable fixed point $(x_2,0)$ in the right-hand half phase plane, and neighbored trajectories move toward it.

• for $c=c_4$ there is only a semi-stable limit cycle repelled by the stable fixed point $(x_3,0)$, as presented in Fig. 9f, the stable stick–slip limit cycle and the unstable limit cycle coincide. The system undergoes a grazing bifurcation again at $c=c_4$ where the semi-stable limit cycle is tangent to the line $y=v_0$ in the phase plane. Trajectories generated from the neighbored points external to the limit cycle are attracted them. The fixed point $(x_2,0)$ is still stable.

• in the range of $c>c_4$ the limit cycle disappears and only two stable fixed points $(x_2,0)$ and $(x_3,0)$ remain, as shown in Fig. 9e. The stable manifolds of the saddle point $(x_1,0)$ are the separatrix curve to separate the basin of attractions of two fixed points $(x_2,0)$ and $(x_3,0)$.

The bifurcation diagram Fig. 8 and the motions of Fig. 9 are characterized by the following parameters: $g_1=2$, $\alpha =0.4$, $v_0=2$, $a=2$, $\mu _0=0.1$, ${\varDelta }\mu =0.02$. From Eq. (23), Three fixed points is exactly located at $(x_1,0)=(0.184423,0)$, $(x_2,0)=(1.1228,0)$ and $(x_3,0)=(-0.655524,0)$, where the fixed point $(x_1,0)$ is always a saddle point, the fixed point $(x_2,0)$ is unstable for values of the viscous damping smaller than $c=c_1={\varPhi }(x_2)=0.0519$ and stable for large values. Simultaneously the fixed point $(x_3,0)$ is unstable for values of the damping smaller than $c=c_3={\varPhi }(x_3)=0.0569$ and stable for large values. Numerical computations are carried out for two critical values of viscous damping at $c_2=0.05301$ and $c_4=0.05865$.

6 Summary and conclusion

In this paper, the local and global bifurcations due to the Stribeck friction characteristic of an archetypal self-excited smooth and discontinuous oscillator have been investigated. It has been found that this system can admit the complicated bifurcation behaviors such as the double tangency bifurcation and the bifurcation of sliding homoclinic orbit to a saddle, which are governed by the hyperbolic structure associated with the stationary state, depending on the value of parameters $\alpha$, $\mu _0$ and $v_0$. It has also been shown that the system with the presence of viscous damping can undergo a subcritical Hopf bifurcation from an unstable fixed point to an unstable limit cycle after making a local examination of the eigenvalues at the steady state. Formal investigation in normal form of Hopf bifurcation has been discussed. Phase portraits have been depicted for the better understanding the bifurcation behaviors of the system.

The self-excited SD oscillator presented in this paper is being actively studied in two main directions. Firstly, further research is required to completely understand the full bifurcation structure of this self-excited system, which can be an important friction system with geometric nonlinearity arising in mechanical engineering. The second pursued direction is to focus on the experimental research to measure the related friction characteristic for this oscillator. We are currently working in these directions.

Appendix

In this appendix, we will focus our attention on the formal investigation of the subcritical Hopf bifurcation of Sect. 5. The theorem of Hopf bifurcation [2] is precisely introduced here.

Consider the a system

$$\begin{aligned} \dot{{{\varvec{x}}}}=f_\varepsilon ({{\varvec{x}}}), \end{aligned}$$

(40)

where ${{\varvec{x}}}\in \mathbf{R }^n$, $\varepsilon$ is a bifurcation parameter. The system has an equilibrium ${{\varvec{x}}}_0$ for the parameter value $\varepsilon _0$. The system undergoes a Hopf bifurcation, if the following properties are satisfied:

• $D_{{{\varvec{x}}}}f_{\varepsilon _0}({{\varvec{x}}}_0)$ has a simple pair of pure imaginary eigenvalues ($\lambda _{\varepsilon _0}$, ${\bar{\lambda }}_{\varepsilon _0}$) and no other eigenvalues with zero real parts.

• The derivative of the real part of the eigenvalues with respect to the parameter $\varepsilon$ evaluated at $\varepsilon _0$ has to be different to zero:

  $$\begin{aligned} \displaystyle \frac{\text {d}}{\text {d}\varepsilon }(\text {Re} \lambda (\varepsilon ))\big |_{\varepsilon =\varepsilon _0}=d\ne 0. \end{aligned}$$

  (41)

If the first Lyapunov value $L_1$ [32] at the bifurcation parameter value $\varepsilon _0$ is different to zero:

$$\begin{aligned} l=L_1(\varepsilon _0)\ne 0, \end{aligned}$$

(42)

then there is a surface of periodic solutions in the center manifold which has quadratic tangency with the eigenspace of ($\lambda _{\varepsilon _0}$, ${\bar{\lambda }}_{\varepsilon _0}$) agreeing to second order with the paraboloid $\varepsilon =-(l/d)(x^2+y^2)$. Moreover, the sign of l actually determines the type of the Hopf bifurcation, which is supercritical if $l<0$ and subcritical if $l>0$.

For a two dimensional system of the form

$$\begin{aligned} \begin{pmatrix} {\dot{x}}\\ {\dot{y}} \end{pmatrix} =\begin{pmatrix} 0 &{} -\omega \\ \omega &{} 0 \end{pmatrix} \begin{pmatrix} {x}\\ {y} \end{pmatrix} +\begin{pmatrix} f(x,y)\\ g(x,y) \end{pmatrix} \end{aligned}$$

(43)

with $f(\mathbf{{0}})=g(\mathbf{{0}})=0$ and $Df(\mathbf{{0}})=Dg(\mathbf{{0}})=0$, the normal form calculation for the parameter l given by (42) yields

$$\begin{aligned} l= & {} \displaystyle \frac{1}{16}\big (f_{xxx}+f_{xyy}+g_{xxy}+g_{yyy}\big )\nonumber \\&+\displaystyle \frac{1}{16\omega }\big [f_{xy}(f_{xx}+f_{yy})-g_{xy}(g_{xx}+g_{yy})\nonumber \\&-f_{xx}g_{xx}+f_{yy}g_{yy}\big ], \end{aligned}$$

(44)

where all partial derivatives are evaluated at the bifurcation point, i.e., $(x,y)=(0,0)$.

To investigate the Hopf bifurcation occurring in the system (22), the eigenvalues $\lambda _{1,2}$ obtained in (26) are of the form

$$\begin{aligned} \lambda _{1,2}^{{{{\varvec{x}}}}_s}=\displaystyle \frac{{\varPhi }(x_s)-c}{2}\pm \sqrt{\frac{\big ({\varPhi }(x_s)-c\big )^2}{4}+{\varPsi }(x_s)}, \end{aligned}$$

(45)

where $\lambda _{1,2}^{{{{\varvec{x}}}}_s}$, $s=2,3$, represent the eigenvalues of the fixed point ${{\varvec{x}}}_s=(x_s,0)$ obtained in (23) for the examined system. We know that ${\varPsi }(x_s)<0$ from the conditions (27) for $s=2,3$. Assuming the bifurcation parameter $\varepsilon ={\varPhi }(x_s)-c$ and $P_s=-{\varPsi }(x_s)>0$, the eigenvalues take the form

$$\begin{aligned} \lambda _{1,2}^{{{{\varvec{x}}}}_s}=\displaystyle \frac{\varepsilon }{2}+\sqrt{\big (\displaystyle \frac{\varepsilon }{2}\big )^2-P_s}. \end{aligned}$$

(46)

For the bifurcation value $\varepsilon =\varepsilon _0=0$, the eigenvalues at the fixed point are purely imaginary and there exist no other eigenvalues. The derivative of the real part of the eigenvalues with respect to $\varepsilon$ evaluated at $\varepsilon _0$ yields

$$\begin{aligned} \displaystyle \frac{\text {d}}{\text {d}\varepsilon }(\text {Re} \lambda _{1,2}^{{{\varvec{x}}}_s})\big |_{\varepsilon =\varepsilon _0}=\displaystyle \frac{1}{2}\ne 0. \end{aligned}$$

(47)

Therefore, two conditions of the Hopf bifurcation theorem are fulfilled and the Hopf bifurcation occurs. For investigating whether the Hopf bifurcation is supercritical or subcritical, system (22) will be transformed to the standard form. Under a coordinate transformation

$$\begin{aligned}&\begin{pmatrix} z\\ y \end{pmatrix} =\begin{pmatrix} 0 &{} \displaystyle \frac{1}{\sqrt{P_s}} \\ 1 &{} 0 \end{pmatrix} \begin{pmatrix} {\xi }\\ {\eta } \end{pmatrix},\nonumber \\&\begin{pmatrix} {\xi }\\ {\eta } \end{pmatrix} =\begin{pmatrix} 0 &{} 1 \\ \sqrt{P_s} &{} 0 \end{pmatrix} \begin{pmatrix} z \\ y \end{pmatrix}, \end{aligned}$$

(48)

we obtain the system in standard form:

$$\begin{aligned} \begin{pmatrix} {\dot{\xi }}\\ {\dot{\eta }} \end{pmatrix} =\begin{pmatrix} 0 &{} -\sqrt{P_s} \\ \sqrt{P_s} &{} 0 \end{pmatrix} \begin{pmatrix} \xi \\ \eta \end{pmatrix} +\begin{pmatrix} f(\xi , \eta )\\ g(\xi , \eta ) \end{pmatrix}, \end{aligned}$$

(49)

where

$$\begin{aligned} f(\xi ,\eta )= & {} -c\xi +\big (\sqrt{P_s}-\displaystyle \frac{1}{\sqrt{P_s}}\big )\eta \\&+\displaystyle \frac{\frac{1}{\sqrt{P_s}}\eta +x_s}{\sqrt{(\frac{1}{\sqrt{P_s}}\eta +x_s)^2+\alpha ^2}}\\&+\Big (\mu _k+{\varDelta }\mu \text {e}^{a(\xi -v_0)}\Big )\\&\times \Big (g_1-\alpha +\frac{\alpha }{\sqrt{(\frac{1}{\sqrt{P_s}}\eta +x_s)^2+\alpha ^2}}\Big )-x_s,\\ g(\xi ,\eta )= & {} 0. \end{aligned}$$

To undergo the Hopf bifurcation, expression $\varepsilon _0={\varPhi }(x_s)-c=0$ has to be fulfilled. At the origin of the space $(\xi ,\eta )$, which is the fixed point (0, 0) of system (22), $f(0,0)=0$ and $Df(0,0)=0$. Therefore, relation (44) can be applied in order to computer the parameter

$$\begin{aligned} l_{{{\varvec{x}}}_s}= & {} \displaystyle \frac{1}{16}\big (f_{\xi ,\xi ,\xi }+f_{\xi ,\eta ,\eta }\big )\nonumber \\&+\frac{1}{16\sqrt{P_s}}\Big [f_{\xi ,\eta }(f_{\xi ,\xi }+f_{\eta ,\eta })\Big ]\nonumber \\= & {} \displaystyle \frac{1}{16}{\varDelta }\mu a^3 \text {e}^{-a v_0}\Big (g_1-\alpha + \frac{\alpha }{\sqrt{x_s^2+\alpha ^2}}\Big )\nonumber \\&\times \Big (1- \frac{{\varDelta }\mu \alpha x_s \text {e}^{-a v_0}}{P_s(x_s^2+\alpha ^2)^{3/2}}\Big )+\frac{{\varDelta }\mu a \alpha \text {e}^{-a v_0}}{16P_s^2(x_s^2+\alpha ^2)^{5/2}}\nonumber \\&\times \Big (2 x_s^2-\alpha ^2+\frac{\alpha }{\sqrt{x_s^2+\alpha ^2}}\Big ). \end{aligned}$$

(50)

For the values of the parameters mentioned in Sect. 5, we can numerically get $l_{{{\varvec{x}}}_2}=0.01373>0$ and $l_{{{\varvec{x}}}_3}=0.02089>0$. Therefore the two Hopf bifurcations occurring in this system is subcritical. According to the 3.4.2 of [2], the limit cycles generated at the Hopf bifurcations are unstable.