1 Introduction

1.1 Research significance of composite leaf springs with a main spring and an auxiliary spring

A leaf spring is a reliable elastic component in the suspension of automobile. Its weight accounts for 10–20% of the un-sprung weight of the automobile [1]. Composite leaf springs are a category of leaf springs that are fabricated by fiber reinforced plastic. At least a 50% reduction in suspension weight can be obtained by replacing a steel leaf spring with a composite leaf spring of the same function [2, 3]. The other important characteristics of glass/carbon fiber reinforced composites which make them excellent for leaf springs are [4]: superior fatigue strength, “fail-safe” capabilities, excellent corrosion resistance and higher natural frequency, etc. Therefore, the design method and performance investigation of composite leaf springs are the research hotspots in the application field of composite structures. Joint reliability [5, 6], structure design [7,8,9,10,11,12,13,14,15], ply design [16], stiffness calculation [17], optimization [18,19,20,21], performance investigation [22,23,24,25,26,27,28,29,30,31,32,33] and structural health monitoring [34,35,36,37,38] of composite mono leaf springs have been studied comprehensively and systematically.

However, there are great differences in the requirements of suspension stiffness in some working conditions of automobile such as only the driver on the automobile, all the passengers plus the driver and the luggage on the automobile. But the stiffness of composite mono leaf spring is not adjustable after curing. So it can only achieve a moderate suspension performance after a compromise. Therefore, the composite leaf spring with a main spring and an auxiliary spring, which can provide two levels of stiffness and take into account the lightweight and performance of automobiles at the same time, is the most suitable type for application at present. Eye-end design [39], fatigue life prediction [40, 41] and dynamic performance investigation [42] of composite leaf spring with a main spring and an auxiliary spring have been studied by several scholars. However, the design theory of composite leaf spring with a main spring and an auxiliary spring is still underdeveloped.

1.2 Research significance of determining the stiffness of composite leaf springs with a main spring and an auxiliary spring

Stiffness is the core performance parameter of composite leaf springs with a main spring and an auxiliary spring, which directly determines the stiffness of the suspension and further affects the handling stability and comfort of the automobile. Therefore, there is an ideal stiffness for the spring installed on a specific automobile and the ideal stiffness is decided by matching design based on the performance of the automobile. In order to make the actual stiffness of the spring close to the ideal stiffness, it is necessary to calculate the stiffness of the spring accurately and modify the design scheme of the spring by adjusting the relevant parameters with the highest stiffness sensitivity. Compared with the composite mono leaf spring, the composite stiffness of the composite leaf spring with a main spring and an auxiliary spring, which is the key characteristic that distinguishes it from the composite mono leaf spring, is much more difficult to calculate.

Fortunately, the theoretical model for the stiffness of multiple leaf springs has already been proposed by several scholars. The theoretical calculation method for multiple leaf springs, which is based on common curvature method, was proposed by Liu [43]. However, the proposed calculation method does not consider the detail features of the leaf spring, leading to a relatively large error between the test stiffness and the theoretical stiffness. Then, an efficient method for calculating the nonlinear stiffness of a progressive multi-leaf spring is developed by Kim et al [44]. In their calculation method, the main and the auxiliary spring are modelled as multi-leaf cantilever beams, which are then integrated as one by connecting the models for each side of the progressive multi-leaf spring at the center bolt. However, the modeling process of this method is tedious and the method requires too many parameters, which is not suitable for engineering application. Liu et al. [45] put forward an efficient method based on integral formula of isotropic materials for calculating the composite stiffness of steel leaf springs with dual springs system, and the accuracy of the calculation method is verified by the rig test and FEA analysis. However, this method is based on the integral formula of isotropic materials and is not suitable for composite materials with anisotropy.

1.3 Introduction of innovation points

In this paper, a theoretical model used for determining the stiffness of composite leaf springs with a main spring and an auxiliary spring was established and verified. The advantages of the theoretical model are as shown:

  • The model takes into account the detail features of the spring and the anisotropy of composite material.

  • The model is suitable for programming calculation. Therefore, the model has high computational efficiency and accuracy.

Finally, the design parameters that influence its stiffness were analyzed to provide a guide for the stiffness matching and optimization of this kind of composite leaf springs.

2 Structure design

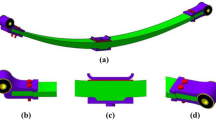
To design a leaf spring with low noise and high reliability, it is essential to have low friction between the leaves. Parabolic leaf springs are better than flat leaf springs because they only make contact at their end points so that the friction between the leaves is minimal. And this kind of leaf spring also has the characteristic of “equal stress beam,” which has the highest material utilization rate. Therefore, the design scheme of the composite leaf spring with a main spring and an auxiliary spring is shown in Fig. 1.

Fig. 1
figure 1

Structure of a composite leaf spring with a main spring and an auxiliary spring

Full size image

The main spring and the auxiliary spring are made from fiber reinforced resin matrix composites. And they are fixed with a center bolt. Although the structure leads to the spring body to be drilled, and the interlaminar shear strength of composite laminates is relatively weak, this structure can reliably transmit the load between the two leaf springs. In addition, the center segment of the spring assembly is fixed by the bolts of the suspension. Therefore, there is almost no deformation in this segment. In addition, targeted reinforcement such as placing local enhancement layer can be carried out in the lamination design to ensure the reliability of this segment. This paper devoted to solving the problem of stiffness calculation, so the design of reinforcement layer scheme in the drilling area is not discussed.

A steel plate and a plastic plate are fixed to the central sections of the assembly to prevent any direct contact among the bolts of the suspension and the two leaf springs. At the same time, the plastic plate can also provide a gap for the two leaf springs, as shown in region B. The gap can avoid the clamping of sediment and rocks that may threaten the reliability of the spring assembly. In addition, a nylon pad is fixed to each end of the auxiliary spring so that the main spring and the auxiliary spring can achieve a low friction contact. The main spring is connected to the frame of the automobile through a steel joint fixed by two joint bolts. Because the tensile modulus of steel is much higher than that of the resin matrix composite material, the chamfering of the steel joint (region A) is carried out to prevent the cutting effect of the steel joint edges on the spring body during the deformation of the spring.

3 Establishment of the theoretical model

To calculate the stiffness of a composite leaf spring with a main spring and an auxiliary spring, the stiffness of composite mono leaf spring should be calculated first. A composite mono leaf spring is essentially a composite laminated plate, and the theoretical model of composite mono leaf springs has been established by Qian [17] based on the mechanics of composite material, and the anisotropy of composite materials has been considered in this model. In the theoretical model, the bending stiffness of an arbitrary cross section of composite leaf spring is:

$$ K = \frac{b}{3}\left[ {\sum\limits_{{k_{1} = 1}}^{{n_{1} }} {E_{x}^{{(k_{1} ),t}} \left( {z_{{k_{1} }}^{3} - z_{{k_{1} - 1}}^{3} } \right)} + \sum\limits_{{k_{2} = 1}}^{{n_{2} }} {E_{x}^{{(k_{2} ),c}} \left( {z_{{k_{2} }}^{3} - z_{{k_{2} - 1}}^{3} } \right)} } \right] $$
(1)

where b is the width of the cross section, n1 is the number of layers in the tensile region of the cross section, n2 is the number of layers in the compressed region of the cross section, \( z_{{k_{i} }} \) is the distance from the ki layer to the geometric neutral layer of the cross section. And \( E_{x}^{{(k_{1} ),t}} \) is the elastic modulus along the x axis of the k1 layer in the tensile region of cross section, \( E_{x}^{{(k_{2} ),c}} \) is the elastic modulus along the x axis of the k2 layer in the compressed region of the cross section. \( E_{x}^{{(k_{1} ),t}} \) and \( E_{x}^{{(k_{2} ),c}} \) can be obtained by formulas (2):

$$ \begin{array}{*{20}l} {E_{x} = \frac{{\sigma_{x} }}{{\varepsilon_{x}^{(x)} }} = \frac{1}{{\bar{S}_{11} }},} \hfill & {\mu_{x} = - \frac{{\varepsilon_{y}^{(x)} }}{{\varepsilon_{x}^{(x)} }} = - \frac{{\bar{S}_{21} }}{{\bar{S}_{11} }},} \hfill & {\eta_{xy,x} = \frac{{\gamma_{xy}^{(x)} }}{{\varepsilon_{x}^{(x)} }} = \frac{{\bar{S}_{61} }}{{\bar{S}_{11} }}} \hfill \\ {E_{y} = \frac{{\sigma_{y} }}{{\varepsilon_{y}^{(y)} }} = \frac{1}{{\bar{S}_{22} }},} \hfill & {\mu_{y} = - \frac{{\varepsilon_{x}^{(y)} }}{{\varepsilon_{y}^{(y)} }} = - \frac{{\bar{S}_{12} }}{{\bar{S}_{22} }},} \hfill & {\eta_{xy,y} = \frac{{\gamma_{xy}^{(y)} }}{{\varepsilon_{y}^{(y)} }} = \frac{{\bar{S}_{62} }}{{\bar{S}_{22} }}} \hfill \\ {G_{xy} = \frac{{\tau_{xy} }}{{\gamma_{xy}^{(xy)} }} = \frac{1}{{\bar{S}_{66} }},} \hfill & {\eta_{x,xy} = \frac{{\varepsilon_{x}^{(xy)} }}{{\gamma_{xy}^{(xy)} }} = \frac{{\bar{S}_{16} }}{{\bar{S}_{66} }},} \hfill & {\eta_{y,xy} = \frac{{\varepsilon_{y}^{(xy)} }}{{\gamma_{xy}^{(xy)} }} = \frac{{\bar{S}_{26} }}{{\bar{S}_{66} }}} \hfill \\ \end{array} $$
(2)

where Ex and Ey are the moduli of x- and y-axes, respectively. \( \mu_{x} \) and \( \mu_{y} \) are the Poisson coupling coefficients. \( \eta_{x,xy} \) and \( \eta_{y,xy} \) are the shear-to-tension coupling coefficients. \( \eta_{xy,x} \) and \( \eta_{xy,y} \) are the tension-to-shear coupling coefficients. And in formulas (2),

$$ \begin{aligned} \bar{S}_{11} & = U_{1S} + U_{2S} \cos 2\theta + U_{3S} \cos 4\theta \\ \bar{S}_{22} & = U_{1S} - U_{2S} \cos 2\theta + U_{3S} \cos 4\theta \\ \bar{S}_{12} & = U_{4S} - U_{3S} \cos 4\theta \\ \bar{S}_{66} & = 2\left( {U_{1S} - U_{4S} } \right) - 4U_{3S} \cos 4\theta \\ \bar{S}_{16} & = U_{2S} \sin 2\theta + 2U_{3S} \sin 4\theta \\ \bar{S}_{26} & = U_{2S} \sin 2\theta - 2U_{3S} \sin 4\theta \\ U_{1S} & = \frac{1}{8}\left( {3S_{11} + 3S_{22} + 2S_{12} + S_{66} } \right) \\ U_{2S} & = \frac{1}{2}\left( {S_{11} - S_{22} } \right) \\ U_{3S} & = \frac{1}{8}\left( {S_{11} + S_{22} - 2S_{12} - S_{66} } \right) \\ U_{4S} & = \frac{1}{8}\left( {S_{11} + S_{22} + 6S_{12} - S_{66} } \right) \\ S_{11} & = \frac{1}{{E_{1} }},\quad S_{22} = \frac{1}{{E_{2} }},\quad S_{66} = \frac{1}{{G_{12} }},\quad S_{12} = - \frac{{\upsilon_{2} }}{{E_{2} }},\quad S_{21} = - \frac{{\upsilon_{1} }}{{E_{1} }}, \\ S_{16} & = S_{61} = S_{26} = S_{62} = 0 \\ \end{aligned} $$
(3)

where

$$ \begin{aligned} S_{11} & = \frac{1}{{E_{1} }},\quad S_{22} = \frac{1}{{E_{2} }},\quad S_{66} = \frac{1}{{G_{12} }},\quad S_{12} = - \frac{{\upsilon_{2} }}{{E_{2} }},\quad S_{21} = - \frac{{\upsilon_{1} }}{{E_{1} }}, \\ S_{16} & = S_{61} = S_{26} = S_{62} = 0 \\ \end{aligned} $$
(4)

In formulas (4), E1 is the longitudinal elastic modulus (GPa); E2 is the transverse elastic modulus (GPa); G12 is the in-plane shear elastic modulus (GPa); \( \upsilon_{1} \) is the longitudinal Poisson’s ratio;\( \upsilon_{2} \) is the transverse Poisson’s ratio.

In the theoretical model proposed in this paper, the calculation program for the bending stiffness of the cross section of composite leaf spring written based on formulas (1) to (4) will be called. Therefore, how to calculate the composite stiffness of the assembly when the main spring and the auxiliary spring are working together becomes an important problem to be solved in the next step.

3.1 Introduction of finite difference method

According to the material mechanics, the differential equations of the isotropic beam with bending deformation are:

$$ \frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }} = \frac{M (x)}{EI (x)},\theta (x) = {\text{d}}f/{\text{d}}x $$
(5)

where f, \( M (x) \), \( I (x) \) and \( \theta (x) \) is, respectively, the deflection, bending moment, moment of inertia and rotation angle of the beam at location x. E is the elastic modulus of the isotropic material, which is also a variable whose value depends on the type of composite material selected. Similarly, for a composite leaf spring, the differential equations of its bending deformation are:

$$ \frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }} = \frac{M (x)}{{K_{x} }},\theta (x) = {\text{d}}f/{\text{d}}x $$
(6)

where \( K_{x} \) is the bending stiffness of the cross section of composite leaf spring at location x. According to formula (6), in order to determine the deflection and the rotation angle of location x, two integrals need be taken, but the integrated term in this case cannot be integrated. For this reason, many methods have been proposed to approximate the integral results, including the finite difference method.

According to the finite difference theory, the following relationships exist between the segment elements in a deformed leaf spring:

$$ \left( {\frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }}} \right)_{i} = \frac{{f_{i - 1} - 2f_{i} + f_{i + 1} }}{{a^{2} }},\left( {\frac{{{\text{d}}f}}{{{\text{d}}x}}} \right)_{i} = \frac{{f_{i - 1} - f_{i + 1} }}{2a} $$
(7)

where i is the serial number of cross sections, and a is the difference spacing. Then, the finite difference equations of a composite leaf spring with bending deformation are:

$$ f_{i - 1} - 2f_{i} + f_{i + 1} = a^{2} \frac{{M(x)_{i} }}{{K_{i} }} $$
(8)
$$ \theta_{i} = \frac{{f_{i - 1} - f_{i + 1} }}{2a} $$
(9)

where fi and \( \theta_{i} \) are, respectively, the deflection and rotation angle of the cross sections with serial number i. If the composite leaf spring is divided into (n + 1) segments, then there are a total of (n + 1) cross sections in the composite leaf spring including the fixed end cross section with a serial number of 0. Then, a set of equations consisting of (n + 1) equations can be obtained from formula (8):

$$ \left\{ {\begin{array}{*{20}l} {f_{ - 1} - 2f_{0} + f_{1} = a^{2} \frac{{M_{0} }}{{K_{0} }}} \hfill \\ {f_{0} - 2f_{1} + f_{2} = a^{2} \frac{{M_{1} }}{{K_{1} }}} \hfill \\ {f_{1} - 2f_{2} + f_{3} = a^{2} \frac{{M_{2} }}{{K_{2} }}} \hfill \\ \ldots \hfill \\ {f_{n - 1} - 2f_{n} + f_{n + 1} = a^{2} \frac{{M_{n} }}{{K_{n} }}} \hfill \\ \end{array} } \right. $$
(10)

Since there is no deflection and rotation angle at the fixed end, so

$$ f_{ - 1} = f_{1} ,f_{0} = 0 $$
(11)

Thus, \( f_{1} \) can be determined by the first equation of the system equation, then \( f_{2} \) can be determined by \( f_{1} \) and \( f_{0} \), and so on. Finally, the deflection of the cross section i can be expressed as

$$ f_{i} = a^{2} \left( {\frac{{iM_{0} }}{{2K_{0} }} + \sum\limits_{j = 1}^{i - 1} {\frac{{jM_{i - j} }}{{K_{i - j} }}} } \right)\quad (i = 2,3, \ldots ,n,n + 1) $$
(12)

Then, \( f_{n - 1} \) and \( f_{n + 1} \) can be obtained from formula (12), and \( \theta_{n} \) can be obtained by substituting them into formula (9).

It is important to emphasize that the finite difference method is not only suitable for the calculation of the deflection of the leaf spring with any section shape, but also suitable for programming.

3.2 Theoretical model of composite leaf spring with a main spring and an auxiliary spring

Taking the rear half of the main and auxiliary composite leaf spring as an example, the structure and related parameters of the spring are shown in Fig. 2. The width of the spring can be of arbitrary value. The assembly is subjected to a vertical load at the center of the joint (point O). The main spring and the auxiliary spring contact at point D of the main spring, and the acting force and reaction force are \( F_{D} \) and \( F^{\prime}_{D} \), respectively. The AB segment is fixed by the bolts of the suspension, so its deflection and rotation angle are ignored, and the cross section BG is regarded as the fixed end of the main and auxiliary spring.

Fig. 2
figure 2

Structure and related parameters of the rear half of the main and auxiliary composite leaf spring

Full size image

3.2.1 Calculation theory for the deflection of point O and cross section D when the main spring is only subjected to the external force \( F_{O} \)

Assuming that the main spring is only subjected to the force \( F_{O} \). Then, the segment BE of the main spring is divided into (m + 1) segments to form a total of (m + 1) cross sections. Assuming that the length of each segment is a, thus

$$ a = \frac{{L_{\text{r}} - S_{\text{r}} - l_{1} }}{m + 1} $$
(13)

Then, a set of equations consisting of (m + 1) equations can be obtained for the segment BE

$$ \left\{ {\begin{array}{*{20}l} {f_{ - 1} - 2f_{0} + f_{1} = a^{2} \frac{{M_{0} }}{{K_{0} }}} \hfill \\ {f_{0} - 2f_{1} + f_{2} = a^{2} \frac{{M_{1} }}{{K_{1} }}} \hfill \\ {f_{1} - 2f_{2} + f_{3} = a^{2} \frac{{M_{2} }}{{K_{2} }}} \hfill \\ \ldots \hfill \\ {f_{m - 1} - 2f_{m} + f_{m + 1} = a^{2} \frac{{M_{m} }}{{K_{m} }}} \hfill \\ \end{array} } \right. $$
(14)

where

$$ M_{i} = - F_{O} x = - F_{O} (L_{\text{r}} - S_{\text{r}} - ia)\quad (i = 0,1,2, \ldots ,m) $$
(15)

Similarly, the deflection of the cross section i can be expressed as

$$ f_{i} = a^{2} \left( {\frac{{iM_{0} }}{{2K_{0} }} + \sum\limits_{j = 1}^{i - 1} {\frac{{jM_{i - j} }}{{K_{i - j} }}} } \right)\quad (i = 2,3, \ldots ,m,m + 1) $$
(16)

Then, the deflection and the rotation angle of cross section E are

$$ f_{E} = - a^{2} F_{O} \left\{ {\frac{{(m + 1)(L_{\text{r}} - S_{\text{r}} )}}{{2K_{0} }} + \sum\limits_{j = 1}^{m} {\frac{{j[L_{\text{r}} - S_{\text{r}} - (m + 1 - j)a]}}{{K_{m + 1 - j} }}} } \right\} $$
(17)
$$ \begin{aligned} \theta_{E} &= \frac{{aF_{O} }}{2}\left\{ {\frac{{L_{\text{r}} - S_{\text{r}} }}{{K_{0} }} + \sum\limits_{j = 1}^{m} {\frac{{j[L_{\text{r}} - S_{\text{r}} - (m + 1 - j)a]}}{{K_{m + 1 - j} }}}}\right.\\&\quad\left.{{ - \sum\limits_{j = 1}^{m - 2} {\frac{{j[L_{\text{r}} - S_{\text{r}} - (m - 1 - j)a]}}{{K_{m - 1 - j} }}} } } \right\} \end{aligned} $$
(18)

So when the main spring is only subjected to the external force \( F_{O} \), the deflection of the point O is

$$ f_{O} = f_{O1} + f_{E} + f_{E\theta } = f_{E} + \theta_{E} \times l_{1} $$
(19)

where \( f_{O1} \) is the deflection of the point O when the point O is subjected to the load \( F_{O} \) and the cross section E is fixed at the same time. Because segment EO is covered by metal joints, so it is regarded as a rigid body, thus \( f_{O1} {=} 0 \). And \( f_{E\theta } \) is the deflection of point O caused by the rotation angle of the cross section E.

As m tends to infinity, the deflection of cross section D can be regarded as the deflection of the nearest cross section of the main spring. According to the formula below

$$ S_{\text{r}} + ia = L_{\text{r}} - l_{1} - l_{2} $$
(20)

when

$$ i = \frac{{L_{\text{r}} - l_{1} - l_{2} - S_{\text{r}} }}{a} $$
(21)

the deflection of cross section D is approximately equal to the deflection of cross section i1, which is obtained by rounding the value of i. Therefore, when the main spring is only subjected to the external force \( F_{O} \), the deflection of cross section D is

$$ f_{D} = - F_{O} a^{2} \left\{ {\frac{{i_{1} (L_{\text{r}} - S{}_{\text{r}})}}{{2K_{0} }} + \sum\limits_{j = 1}^{{i_{1} - 1}} {\frac{{j[L_{\text{r}} - S{}_{\text{r}} - (i_{1} - j)a]}}{{K_{{i_{1} - j}} }}} } \right\} $$
(22)

3.2.2 Calculation theory for the deflection of cross section D when the main spring is only subjected to the internal force \( F_{D} \)

Assuming that the main spring is only subjected to the force \( F_{D} \). Then, the segment BD of the main spring is divided into (p + 1) segments to form a total of (p + 1) cross sections. Assuming that the length of each segment is a, thus

$$ a' = \frac{{L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} }}{p + 1} $$
(23)

Then, a set of equations consisting of (p + 1) equations can be obtained for the segment BD

$$ \left\{ {\begin{array}{*{20}l} {f_{ - 1}^{'} - 2f_{0}^{'} + f_{1}^{'} = a^{'2} \frac{{M_{0}^{'} }}{{K_{0}^{'} }}} \hfill \\ {f_{0}^{'} - 2f_{1}^{'} + f_{2}^{'} = a^{'2} \frac{{M_{1}^{'} }}{{K_{1}^{'} }}} \hfill \\ {f_{1}^{'} - 2f_{2}^{'} + f_{3}^{'} = a^{'2} \frac{{M_{2}^{'} }}{{K_{2}^{'} }}} \hfill \\ \ldots \hfill \\ {f_{p - 1}^{'} - 2f_{p}^{'} + f_{p + 1}^{'} = a^{'2} \frac{{M_{p}^{'} }}{{K_{p}^{'} }}} \hfill \\ \end{array} } \right. $$
(24)

where

$$ M_{i}^{'} = F_{D} (L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} - ia')\quad (i = 0,1,2, \ldots ,p) $$
(25)

Similarly, the deflection and the rotation angle of cross section D can be expressed as

$$ \begin{aligned} f_{D}^{\prime} &= a^{\prime 2} F_{D} \left\{ {\frac{{(p + 1)(L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} )}}{{2K^{\prime}_{0} }}}\right.\\&\quad\left.{ + \sum\limits_{j = 1}^{p} {\frac{{j[L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} - (p + 1 - j)a^{\prime}}}{{K_{p + 1 - j}^{\prime} }}} } \right\} \end{aligned} $$
(26)
$$ \begin{aligned} \theta_{D}^{\prime} &= \frac{{a^{\prime}F_{D} }}{2}\left\{ {\sum\limits_{j = 1}^{p - 2} {\frac{{j[L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} - (p - 1 - j)a^{\prime}]}}{{K_{p - 1 - j}^{\prime} }}}}\right.\\&\quad\left.{{ - \sum\limits_{j = 1}^{p} {\frac{{j[L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} - (p + 1 - j)a^{\prime}]}}{{K_{p + 1 - j}^{\prime} }} }}}\right.\\&\quad\left.{{{- \frac{{L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} }}{{K_{0}^{\prime} }}} } } \right\} \end{aligned} $$
(27)

There is no external concentrated load in the segment DO, and its own gravity can be ignored. Therefore, when the main spring is only subjected to the internal force \( F_{D} \), the deflection of point O is:

$$ f_{O}^{'} = f_{D}^{'} + f_{D\theta }^{'} = f_{D}^{'} + \theta_{D}^{'} \times (l_{1} + l_{2} ) $$
(28)

where \( f_{D\theta }^{'} \) is the deflection of point O caused by the rotation angle of the cross section D.

3.2.3 Calculation theory for the deflection of cross section I when the auxiliary spring is only subjected to the internal force \( F_{D}^{'} \)

Assuming that the auxiliary spring is only subjected to the force \( F_{D}^{'} \). Then, the segment GI (I is the symmetric center of the nylon pad of the auxiliary spring) of the auxiliary spring is divided into (q + 1) segments to form a total of (q + 1) cross sections. Assuming that the length of each segment is \( a^{\prime\prime} \), thus

$$ a^{\prime\prime} = \frac{{L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} }}{q + 1} $$
(29)

Then, a set of equations consisting of (q + 1) equations can be obtained for the segment GI

$$ \left\{ {\begin{array}{*{20}l} {f_{ - 1}^{''} - 2f_{0}^{''} + f_{1}^{''} = a^{''2} \frac{{M_{0}^{''} }}{{K_{0}^{''} }}} \hfill \\ {f_{0}^{''} - 2f_{1}^{''} + f_{2}^{''} = a^{''2} \frac{{M_{1}^{''} }}{{K_{1}^{''} }}} \hfill \\ {f_{1}^{''} - 2f_{2}^{''} + f_{3}^{''} = a^{''2} \frac{{M_{2}^{''} }}{{K_{2}^{''} }}} \hfill \\ \ldots \hfill \\ {f_{q - 1}^{''} - 2f_{q}^{''} + f_{q + 1}^{''} = a^{''2} \frac{{M_{q}^{''} }}{{K_{q}^{'} }}} \hfill \\ \end{array} } \right. $$
(30)

where

$$ M_{i}^{''} = - F_{D}^{'} x' = - F_{D} (L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} - ia'')\quad (i = 0,1,2, \ldots ,q) $$
(31)

Similarly, when the auxiliary spring is only subjected to the force \( F^{\prime}_{D} \), the deflection of the cross section I can be expressed as

$$ \begin{aligned} f_{I}& = - a^{\prime\prime 2} F_{D} \left\{ {\frac{{(q + 1)(L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} )}}{{2K_{0}^{\prime\prime} }} }\right.\\&\quad\left.{+ \sum\limits_{j = 1}^{q} {\frac{{j[L_{\text{r}} - S_{\text{r}} - l_{1} - l_{2} - (q + 1 - j)a^{\prime\prime}]}}{{K_{q + 1 - j}^{\prime\prime} }}} } \right\} \end{aligned} $$
(32)

3.2.4 Determination of the internal force \( F_{D} \)

In fact, when the main spring and the auxiliary spring are working together, the deflection of the cross section D of the main spring is caused by the combined action from \( F_{D} \) and \( F_{O} \). Thus, the actually deflection of the cross section D is

$$ f_{D}^{''} = f_{D} + f_{D}^{'} $$
(33)

The main spring and the auxiliary spring have the same deflection at the contact point D, so we can obtain

$$ f_{D}^{''} = f_{I} $$
(34)

In formula (34), geometric parameters and \( F_{O} \) are known quantities. And m, p and q are the numbers of cross sections taken in the calculation theory. The larger the value is, the higher the calculation accuracy will be. \( K_{i} \), \( K_{i}^{'} \) and \( K_{i}^{''} \) are, respectively, the bending stiffness of each cross sections of the spring body in each calculation program, the relevant calculation theory has been established by Qian [17]. When the parameters of the main and auxiliary composite leaf spring are known, these bending stiffness values are also known quantities. Then, the internal force \( F_{D} \) can be obtained through formula (34).

3.2.5 Determination of the composite stiffness of the main and auxiliary composite leaf spring

In fact, when the main spring and the auxiliary spring are working together, the deflection of the point O of the main spring is caused by the combined action from \( F_{D} \) and \( F_{O} \). Thus, the actually deflection of the point O is

$$ f_{O}^{''} = f_{O} + f_{O}^{'} = (f_{E} + \theta_{E} \times l_{1} ) + [f_{D}^{'} + \theta_{D}^{'} \times (l_{1} + l_{2} )] $$
(35)

In formula (35), \( f_{E} \) and \( \theta_{E} \) is unrelated with \( F_{D} \), while \( f_{D}^{'} \) and \( \theta_{D}^{'} \) is related with \( F_{D} \). The deflection value of \( f_{O}^{''} \) can be obtained by substituting the value of \( F_{D} \) obtained by formula (34) into formula (35). Then, the composite stiffness of the rear half of the main and auxiliary composite leaf spring is

$$ K_{\text{r}} = \frac{{F_{O} }}{{f_{O}^{''} }} $$
(36)

Similarly, the composite stiffness of the front half of the main and auxiliary composite leaf spring can be calculated through the theory mentioned above. Finally, the composite stiffness of the main and auxiliary composite leaf spring [2] is

$$ K = (K_{\text{f}} + K_{\text{r}} )\frac{{\delta (1 + \lambda )^{2} }}{{(1 + \delta )(1 + \delta \lambda^{2} )}} $$
(37)

where

$$ \delta = \frac{{K_{\text{f}} }}{{K_{\text{r}} }},\quad \lambda = \frac{{L_{\text{f}} }}{{L_{\text{r}} }} $$
(38)

In formula (38), \( L_{\text{f}} \) and \( L_{\text{r}} \) are, respectively, the length of the front half and the rear half of the spring assembly in flat status.

4 Verification of the correctness of the theoretical model

4.1 Material selection

In order to make the theoretical model universal, the specific information of materials is not given in the previous derivation. Therefore, in the following examples, material information needs to be materialized. The resin used to make composite leaf spring mainly include epoxy resin and polyurethane. Although both of their mechanical properties can meet the requirements of composite leaf springs, polyurethane has better toughness, impact strength and wetting ability than epoxy resin. Therefore, polyurethane is selected as the matrix material of the main and auxiliary composite leaf spring. As E-glass fiber has the highest cost performance, E-glass fiber is selected as the fiber reinforcement material. In addition, 40Cr steel is selected as the manufacturing material of the metal parts, and nylon is selected as the material of the plastic plate.

The sample of E-glass fiber/polyurethane laminate was prepared, and its mechanical properties were tested. The mechanical properties of E-glass fiber/polyurethane laminates are shown in Table 1. In the following examples, all the ply orientations are consistent with the longitudinal direction of the spring.

Table 1 Mechanical properties of E-glass/polyurethane
Full size table

4.2 Validation of the theoretical model of composite mono leaf spring and the finite element simulation method

In order to verify the correctness of the theoretical model of composite mono leaf spring, finite element simulation and rig stiffness test of the composite mono leaf spring are carried out, respectively, as shown in Fig. 3. In the FEA model, C3D8I element is selected to discretize the composite mono leaf spring because the calculation accuracy of this kind of element is higher when the element has small deformation. However, the computational accuracy of the C3D8I element will be reduced when the element has a large deformation. Therefore, in order to ensure the quality of the mesh, the hexadecimal mesh is used for meshing. Standard analysis module of Abaqus software was selected to perform the simulation task. Stacking sequence of the composite mono leaf spring was defined in the composite layup manager dialog box of the Property module of Abaqus software, where the stacking direction was defined by discrete method. In the Interaction module of Abaqus software, binding constraints are defined between layers. Coupling constraints are defined among reference points and regions such as joints and middle part of the spring body that will influence the freedom degree of the model. The sliding formulation of contact between layers is set as finite sliding, in which the tangential behavior is set as penalty, and the normal behavior is set as “hard” contact. The load and boundary conditions of the FEA model are defined in the Load module. The load is applied to the reference point coupled with the middle part of the spring body, and the load is the same as the load gradually applied to the sample in the rig stiffness test of the composite mono leaf spring (18500 N). The freedom degree constraint of the model is realized by constraining the freedom degree of the reference points that coupled with the middle part of the spring body and the freedom degree of the two reference points that coupled with the two joints, respectively.

Fig. 3
figure 3

Finite element simulation and rig stiffness test of the composite mono leaf spring [2]

Full size image

According to the relevant research results, the comparison among the stiffness values obtained by theoretical model, finite element simulation and rig test are shown in Table 2. According to Table 2, the error is less than 2%, which meets the requirements of engineering applications. So the theoretical model and the finite element simulation method for calculating the stiffness of composite mono leaf spring are correct and credible.

Table 2 Comparison among the stiffness values obtained by the theoretical model, finite element simulation and bench test [17]
Full size table

4.3 Validation of the correctness of the calculation method of composite stiffness of leaf springs

The calculation theory for calculating the composite stiffness of leaf springs with variable stiffness, which has the same train of thought with the theoretical model of main and auxiliary composite leaf spring proposed in this paper, has been verified by the rig test and finite element simulation. The variable stiffness is also achieved by using main-auxiliary spring system. The experimental apparatus for measuring the stiffness of the main-auxiliary spring is shown in Fig. 4. In the rig test, the load is gradually increased to 24,500 N from 0 N and then reloaded to 0 N.

Fig. 4
figure 4

Rig test for measuring the stiffness of the main-auxiliary spring [43]

Full size image

According to the relevant research results, the comparison among the stiffness values obtained by theoretical model, finite element simulation and rig test are shown in Table 3.

Table 3 Comparison among the stiffness values obtained by the theoretical model, finite element simulation and rig test [43]
Full size table

According to Table 3, the error is less than 5%, which also meets the requirements of engineering applications. So the theoretical model and the finite element simulation method for calculating the composite stiffness of leaf springs with variable stiffness are correct and credible.

4.4 Validation of the correctness of the theoretical model of composite leaf spring with a main spring and an auxiliary spring

On the basis of the verification works mentioned above, the same finite element method (FEM) was used to establish the finite element model of a composite leaf spring with a main spring and an auxiliary spring, as shown in Fig. 5. And a MATLAB program was written using MATLAB software according to the theoretical model.

Fig. 5
figure 5

Finite element model of a main and auxiliary parabolic composite leaf spring

Full size image

The geometric parameters of the composite leaf spring are shown in Tables 4 and 5, and the material parameters used in the finite element simulation of the composite mono leaf spring are also used in the finite element model. The laying angle of the main and auxiliary composite leaf spring is all 0°. It should be noted that in the theoretical model, the ply orientation is also a variable. Here, 0° is selected as a typical example to verify the correctness of the theoretical model.

Table 4 Geometric parameters of the main parabolic composite leaf spring
Full size table
Table 5 Geometric parameters of the auxiliary parabolic composite leaf spring
Full size table

The stress distribution state under the maximum dynamic load (28,500 N) and the stiffness curve of the main and auxiliary composite leaf spring obtained by finite element simulation are, respectively, shown in Figs. 6 and 7. According to Fig. 6, the load transfer between the main spring and the auxiliary spring is effective, and the spring body is in a normal deformation state. The maximum tensile stress of the assembly is 504.28 MPa, and the maximum compressive stress is 41.85 MPa, both of which are less than the strength limit of the composite material. According to Fig. 7, the stiffness values of the assembly is 75.36 N/mm and 134.02 N/mm, respectively, when only the main spring is working or both the main and the auxiliary spring are working.

Fig. 6
figure 6

Stress distribution state under the maximum dynamic load (28,500 N) of the main and auxiliary composite leaf spring

Full size image
Fig. 7
figure 7

F–S curve of the main and auxiliary composite leaf spring

Full size image

The stiffness values of the main and auxiliary composite leaf spring was also calculated by using the MATLAB program, which was written based on the theoretical model. The comparison between the stiffness values obtained by the theoretical model and finite element simulation is shown in Table 6. According to Table 6, the error is less than 4%, which also meets the requirements of engineering applications. Thus, the correctness and the precision of the theoretical model of main and auxiliary composite leaf springs are verified.

Table 6 Comparison between the stiffness values obtained by the theoretical model and finite element simulation
Full size table

5 Analysis of design parameters that influence the stiffness of composite leaf spring with a main spring and an auxiliary spring

Take a composite leaf spring with a main parabolic spring and an auxiliary parabolic spring as an example. Its length and arc height are determined by the installation environment. The shape of the spring body should be maintained in parabola shape invariant to ensure the “equal stress beam” characteristics considering material utilization. The thickness of the center segment and the spring body are determined by the target stiffness. According to related research results, the influence law of four key design parameters on the stiffness of a composite mono leaf spring was investigated. Those four key design parameters are layer width, number of the layer (corresponding to the thickness of the spring body), the angle of layer and the layer thickness. As the thickness of a single layer is determined by the manufacturing process, it is no need to study it again. For a composite leaf spring with a main parabolic spring and an auxiliary parabolic spring, besides those four design parameters, there are other design parameters that affect its stiffness characteristics, including the tensile modulus of the material E and the contact position of the main spring. The influence law of these design parameters on the stiffness of the composite leaf spring, which are obtained by adjusting the corresponding parameter in the model and then be calculated by the MATLAB program, is shown in Fig. 8, 9, 10, 11, 12 and 13.

Fig. 8
figure 8

Influence of the layer width (B) on the stiffness of the composite leaf spring

Full size image
Fig. 9
figure 9

Influence of the thickness increment of the main spring (Δhm) on the stiffness of the composite leaf spring

Full size image
Fig. 10
figure 10

Influence of the thickness increment of the auxiliary spring (Δha) on the stiffness of the composite leaf spring

Full size image
Fig. 11
figure 11

Influence of the angle of layer (θ°) on the stiffness of the composite leaf spring

Full size image
Fig. 12
figure 12

Influence of the tensile modulus of the material (E) on the stiffness of the composite leaf spring

Full size image
Fig. 13
figure 13

Influence of the position of the contact point (ΔS), namely the offset distance between the new contact point of the spring and the existing contact position D, on the stiffness of the composite leaf spring

Full size image

Therefore, increasing the layer width, the number of layers in the main spring or the auxiliary spring and the tensile modulus of the material can all increase the stiffness of the composite leaf spring approximate linearly. Increasing the angle of layer changes the stiffness of the composite leaf spring nonlinearly starting from 0°, a minimum section of stiffness exists between 45° and 55°. And the composite leaf spring obtain a maximum stiffness when the angle of layer is 0°. According to Fig. 13, the stiffness of the composite leaf spring changes approximately linearly with the change of the position of the contact point, and the further the contact point from the center of the spring assembly, the higher the composite stiffness of the composite leaf spring.

Because changing the layer width is limited by the installation environment, and the number of layers is mainly determined by the target stiffness. So from the point of saving material to reduce the cost, ply orientation of 0° and the material with the highest tensile modulus should be selected, and the contact point should keep away from the center of the spring assembly as far as possible.

6 Conclusions

A theoretical model used for determining the stiffness of composite leaf springs with a main spring and an auxiliary spring was established and verified in this paper. And the design parameters that influence its stiffness were analyzed. The research conclusions are as follows:

  • Compared with the finite element method, the theoretical model established in this paper can rapidly and accurately calculate the stiffness of composite leaf springs with a main spring and an auxiliary spring, providing the possibility for optimizing the design of this kind of composite leaf springs. Therefore, the development cycle of composite leaf springs with a main spring and an auxiliary spring is shortened significantly.

  • The theoretical model is established based on finite difference method with general applicability and the calculation task of the bending stiffness of each cross section is modularized. Therefore, the theoretical model provides a new thought of numerical calculation for the stiffness calculation problem of composite elastic structures with arbitrary cross-sectional shape or complex material consisting.

  • The thickness of the spring body is a significant factor influencing the stiffness of composite leaf springs with a main spring and an auxiliary spring. The change in the width of the composite leaf spring can be used for linear adjustment of the stiffness.

  • In order to improve the material utilization rate of composite leaf springs with a main spring and an auxiliary spring, ply orientation of 0° and the material with the highest tensile modulus should be selected, and the contact point should keep away from the center of the spring assembly as far as possible.

Based on the above conclusions, the theory for determining the stiffness of composite leaf springs with a main spring and an auxiliary spring can be further understood. In the following studies, the optimization design of composite leaf springs with a main spring and an auxiliary spring should be further carried out to obtain the optimal structural design scheme and laminate design scheme based on the theoretical model established in this paper, so as to finally optimize its comprehensive performance.