1 Introduction

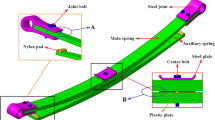
Weight reduction of automobile is an important method to achieve energy saving, decrease environmental pollution and improve driving range. Helical spring is an elastic component widely used in automobile suspension. For the purpose of saving energy and improving the performance of vibration isolation system, advanced springs with lightweight effect and high performance have been widely used for today’s automobiles and mechanical systems [1,2,3]. The replacement of steel helical springs with composite helical springs can bring at least 40% weight reduction. In addition, due to its outstanding properties such as high specific strength, more elastic strain energy storage capacity, no rusting, corrosion resistance and the numerous possibilities of function integration, fiber-reinforced composites have gradually replaced steels or traditional steels and become the key materials for advanced springs recently [4,5,6]. The typical structure and installation environment of steel helical spring and composite helical spring are shown in Fig. 1.

Fig. 1
figure 1

Typical structures of steel helical spring and composite helical spring

Full size image

Composite helical spring with nonlinear stiffness (NS-CHS) is a kind of advanced composite helical spring because nonlinear stiffness characteristics is introduced to make the spring have the optimal stiffness value under different typical working conditions (such as no-load and full-load conditions). The nonlinear stiffness studied in this paper means when the automobile has not yet reaches the full-load state, the stiffness of the spring is no-load stiffness. Similarly, when the automobile reaches the full-load state due to excessive passengers or goods, the helical spring will show the full-load stiffness. Therefore, NS-CHS does not have the function of active stiffness control, but has the function of passive stiffness control under two typical working conditions of automobile, namely no load and full load. Compared with air suspension with active stiffness control function, NS-CHS can not only achieve a certain control effect of nonlinear stiffness, but also achieve a far lower cost, simpler structure and no energy consumption. As a result, NS-CHS is a balance between performance and cost. The replacement of steel helical springs with NS-CHS can not only achieve the advantages of composite helical spring with constant stiffness, but also can greatly improve the dynamic performance of the automobile and passenger driving comfort. Therefore, NS-CHS has obvious performance advantages and bright application prospects.

At present, many scholars have made research on composite helical spring with constant stiffness. In terms of feasibility, Budan and Manjunatha[7] have demonstrated the feasibility of making helical springs from composite materials by, respectively, making three helical spring samples with carbon fiber composite material (CFRP), glass fiber composite material (GFRP) and carbon fiber/glass fiber (CF/GF) mixed composite material. Oh and Choi[8] studied the design parameters for application of composite helical spring in a passenger automobile. Sequeira A A et al. [9] used finite element method to prove that the weight of CFRP helical spring could be reduced by about 80% on the premise of the same strength and stiffness as the steel spring. In terms of structure and performance matching design, Chang Hsuan Chiu et al. [10] have found that adding rubber spindle to the spring wire or wrapping a braided film tightly around the outermost part of the spring wire can improve the mechanical properties of composite helical springs such as stiffness. Choi et al.[11] established a numerical method for optimizing the design nonlinears of composite coil springs. Zhiyuan Xiong et al. [12] deduced the equivalent stiffness calculation formula of composite helical spring and analyzed the influencing factors of spring stiffness. In terms of optimization design, Djomseu et al. [13] obtained the final optimization results by modifying the nonlinears and the cyclic process of finite element simulation. Zebdi O et al. [14] adopted a multi-objective optimization algorithm to coordinate the two contradictory objectives of minimum spring mass and maximum spring stiffness, and compared the effects of three different fiber-reinforced materials, namely carbon, Kevlar and glass, on the performance of composite helical spring. In terms of manufacturing processes, Ying Miao[15] selected the VARI process to fabricate composite helical springs and explored the influence of wrapping method and twisting method to form fiber reinforcement on the performance of composite helical spring. Zhong Jilun[16] derived the calculation formula for the stiffness of composite helical spring with constant stiffness and analyzed the influence of molding parameters on the performance of the spring.

At the same time, many scholars have studied the steel helical spring with nonlinear stiffness. Vondracek H and Nadorfr G[17] designed a steel helical spring with nonlinear stiffness and proved that the spring can improve the dynamic performance of the automobile without changing the spatial structure of the suspension through experimental results. Watanabe K and Kunoh T[18] conducted a theoretical study on the stress distribution of a steel helical spring with nonlinear stiffness, and verified the theoretical calculation results through finite element method. Ramezani A and Shahriari S[19] established the mechanical equation of steel helical spring with nonlinear stiffness by using discretization theory method, then they analyzed its stiffness characteristics and predicted the fatigue life of the spring. Qi Hongzhong et al. [20] used the secondary development module of UG software to establish the geometric model of the steel helical spring with changing helical diameter and wire diameter. Holanda S A et al. [21] studied the helical spring made of shape memory alloy and found that the spring can ensure the vibration frequency of the suspension within a certain range. Some scholars also analyzed the advantages of various structural types of spring with nonlinear stiffness and verified the feasibility of nonlinear stiffness steel helical springs through loading tests [22, 23]. Diao Zengxiang[24] analyzed the nonlinear screw diameter and equal inner diameter compression screw spring, and established a set of complete design calculation method, which provided reference for the research and the nonlinear stiffness screw spring. Shi PC[25] proposed an optimal design method for two-segment cylindrical helical springs with unequal pitches by combining the design theory and method of helical springs and using VC +  + 6.0 programming language. Zhou Beiyue [26] obtained the nonlinear stiffness characteristic curve of screw spring based on ANSYS analysis of nonlinear diameter, equal diameter compression screw spring.

Therefore, although there are many researches on the composite helical spring with constant stiffness and the steel helical spring with nonlinear stiffness, the research on composite helical spring with nonlinear stiffness is still very scarce. This paper integrates the mechanics of composite materials and the design theory of helical spring and finally puts forward a theoretical model used for stiffness matching design and structure optimization of NS-CHS, especially establishes the stiffness calculation model for nonlinear stiffness characteristic for the first time. The correctness of the model was verified by the results obtained by theoretical calculation, finite element simulation and bench test. This paper also systematically studied the key problems that need to be solved in the design process of NS-CHS and put forward a complete design method include structural design, stiffness matching design, layer design, optimization, FEA modeling and manufacturing process of NS-CHS. Those models and methods can provide theoretical and methodological support for the application of NS-CHS in automobiles.

2 Material selection

Considering the cost, process operability and mechanical properties, E-glass fiber/epoxy unidirectional prepreg is selected to fabricate the composite helical spring with nonlinear stiffness. The mechanical properties of the corresponding laminates are shown in Table 1. All the glass fiber parameters in this table are measured experimentally.

Table 1 Mechanical properties of E-glass fiber/epoxy unidirectional prepreg
Full size table

In the table, E1 and E2 are the longitudinal and transverse elastic modulus of unidirectional glass fiber composites, respectively, and G12 is the longitudinal shear modulus. v12, v13, v23 represent the Poisson’s ratio in each direction, and \(\rho\) is the density of the material. XT, XC, YT, YC, S12 are the basic strength values of glass fiber unidirectional cloth composites.

The stiffness of the top spring seat and the bottom spring seat is much greater than that of the spring itself, the two spring seats are treated as a rigid body during subsequent calculations and simulations.

3 Structure design

Compared with the composite helical spring with constant stiffness, the structure of composite helical spring with nonlinear stiffness is more complex and diversified. Different types of spring structures can be designed according to different nonlinear stiffness principles, as shown in Fig. 2.

Fig. 2
figure 2

Typical structures of helical spring with nonlinear stiffness

Full size image

The stiffness of the helical spring is generally controlled by changing the number of effective coils that involved in deformation. There are three methods to change the number of effective coils. The first method is changing the number of self-contact pairs between the effective coils, such as type (b), (c) and (g). The second method is changing the contact area between the effective coils and the spring seat, such as type (a), (d), (e) and (h). Type (a) is a symmetrical structure, the middle part contains equal helical diameter structure, the helical diameter of the upper and lower ends gradually decreases from the middle to the two ends; in type (b), the helical diameter increases gradually from the middle to both ends; in type (c), the helical diameter of the bottom end is the largest and gradually decreases to the top; in type (d), the lower half part has equal helical diameter, and the helical diameter of the upper half gradually reduced; the difference between type (e) and type (a) is that the middle part of type (a) contains an equal helical diameter part, while type (e) does not; type (f) is a combined spring composed of two springs; type (g) is an equal helical diameter spring with varying pitch at both ends; type (h) is on the basis of type (a); the difference between them is that the diameter of the spring wire changes in type (h), while type (a) has constant diameter of the spring wire.

The last method is combined application of helical springs with different constant stiffness, such as type (f). For composite helical spring, the first method will produce compression stress concentration and impact load between the self-contact pairs, and compression stress or impact load will seriously threaten the reliability of composite spring. The second method can reduce the impact load and contact stress between the effective coil and the spring seat by arranging a rubber cushion on the spring seat, which is beneficial to spring reliability and the comfort of automobile. The last method will not only greatly increase the weight of the spring, but also lead to new problems of installation and dynamic deformation interference. Therefore, changing the contact area between the effective coils and the spring seat is a more reasonable approach. In this structure type, the whole deformation state of composite helical spring can be further coordinated by adjusting the diameter of spring wire, the diameter of coils and the pitch of the spring, so as to achieve the purpose of nonlinear stiffness.

Therefore, the optimal structure can be selected from type (a), (d), (e) and (h). In type (a), the diameter of the middle part is obviously larger than the diameter of the end parts, this structural feature will greatly increase the difficulty of demolding during the fabrication of the spring. In type (d), the upper structure and the lower structure of the spring are not symmetrical, this structural feature will force carmakers to change the structure of the spring seat, and it may also cause deformation instability. In type (e), the middle part is combined by helicals with gradually helical diameters; this structural feature will also greatly increase the difficulty of mold manufacturing. Therefore, type (h) is the relatively ideal structure type. The spring wire diameter of this structure is nonlinear, so it has the best lightweight effect, but it also increases the difficulty of ply design.

Figure 3 shows a structural diagram of type (h), which is composed of a constant diameter part and two nonlinear diameter parts. In Fig. 4 d1 and d2 are the minimum diameter and the maximum diameter of the spring wire, respectively; D1 and D2 are the minimum helical diameter and the maximum helical diameter, respectively. The effective helical number of the constant diameter part and the nonlinear diameter part is, respectively, represented by N and N1. In the constant diameter part, the diameter of the spring wire, the diameter of the helical and the pitch of the spring are constant.

Fig. 3
figure 3

Structural diagram of composite helical spring with nonlinear stiffness

Full size image
Fig. 4
figure 4

Cross section structure of NS-CHS

Full size image

4 Ply design

The considered cross-sectional ply structure of the spring wire is shown in Fig. 4. The cross section of the spring wire is divided into two parts. The inner part is a polyurethane rod and the outer part is a composite layer formed by winding E-glass fiber/epoxy unidirectional prepreg. The force form of the spring wire is mainly torsional deformation. As the ply angle increases from 0° to 45°, the stiffness and strength of the composite suspension spring increase. When the ply angle is 45°, the stiffness and strength of the spring reach the maximum [16]. So, the angle between the E-glass fiber/epoxy unidirectional prepreg and the axis of the spring wire is set to 45°. It should be noted that, although the overall braided sleeve on the outside of the spring wire has a certain effect on the impact resistance and fatigue reliability of the composite helical spring, the strength of the braid sleeve is much lower than that of the unidirectional cloth. Therefore, its strength is still not enough, and the introduction of braiding sleeve will also significantly increases the cost and manufacturing difficulty of composite helical spring.

The overall ply diagram of the NS-CHS is shown in Fig. 5. The E-glass fiber/epoxy unidirectional prepreg is cut into a step-like shape as shown in Fig. 5, and the prepreg is then wrapped around the polyurethane core shaft to obtain the integral preformation body of the spring wire. The shape of glass fiber is mainly determined by the middle diameter of the spring structure and the thickness of each layer of fiber. The stepped shape can ensure the continuity of glass fiber prepreg. The specific size is determined by the structure of the nonlinear middle diameter and nonlinear diameter part of the spring.

Fig. 5
figure 5

Overall ply diagram of NS-CHS

Full size image

5 Establishment of the stiffness calculation model

5.1 Establishment of the stiffness calculation model for constant stiffness characteristic

Consider the spring wire shown in Fig. 6.

Fig. 6
figure 6

A diagram of the cross-sectional curve coordinate system

Full size image

The length of the spring wire is denoted by L; its diameter is denoted by D. It is assumed that D <  < L and no dimensional restrictions on the wall thickness h are imposed, distinguishing this treatment from a thin-walled theory. For the convenience of analysis, the Cartesian coordinate system (x, y, z) and the curvilinear coordinate system (x, s, n) are established in the present analysis. The radius of the spring wire is denoted by r. The curve coordinate system is established by taking the circle at the radius of r/2 on the section of the spring wire. The axis s points to the circular tangent direction, which is agreed to be positive to when point to counterclockwise. The axis n points to the circle radius direction, which is agreed to be positive when point to the outer surface of the spring wire.

According to the research result of Kim C, etc.[27], the cross-sectional displacement function of thick hollow composite beams under general loadings is

$$ \begin{gathered} u_{x} (x,s,n) = u_{0} (x) - r_{y} \{ \phi_{y} (x) + \frac{{4r_{y}^{2} }}{{3D^{2} }}[v_{0} (x)^{\prime} - \phi_{y} (x)]\} - r_{{\text{z}}} \{ \phi_{z} (x) + \frac{{4r_{s}^{2} }}{{3d^{2} }}[w_{0} (x)^{\prime} - \phi_{z} (x)]\} \hfill \\ u_{s} (x,s,n) = v_{0} (x)\frac{{{\text{d}}\overline{y} (s)}}{{{\text{d}}s}} + w_{0} (x)\frac{{{\text{d}}\overline{z} (s)}}{{{\text{d}}s}} + \theta (x)[r_{n} (s) + n] \hfill \\ u_{n} (x,s,n) = v_{0} (x)\frac{{{\text{d}}\overline{z} (s)}}{{{\text{d}}s}} - w_{0} (x)\frac{{{\text{d}}\overline{y} (s)}}{{{\text{d}}s}} \hfill \\ \end{gathered} $$
(1)

where ux(x, s, n), us(x, s, n) and un (x, s, n)are the elastic displacement of the spring wire along the axial direction, the tangential and the radius directions of the curve coordinate system, respectively. u0(x), v0(x) and w0(x) are the rigid body displacement of the spring wire along the three axial direction of the Cartesian coordinate system, respectively. The apostrophe “'” represents a derivative with respect to x.\(\theta (x)\), \(\phi_{y} (x)\) and \(\phi_{z} (x)\) are the rotation angle of the spring wire around x, z and y axes, respectively. The equations \(y = \overline{y}(s)\) and \(z = \overline{z}(s)\) define the closed mid-line contour in the cross section, and the prime denotes differentiation with respect to x, and

$$ r_{n} (s) = r/2 $$
(2)

The functions ry and rz denote the y and z components of the position vector r, respectively, and can be expressed as

$$ r_{y} = (\frac{r}{2} + n)\cos \alpha ,r_{{\text{z}}} = (\frac{r}{2} + n)\sin \alpha $$
(3)

Because the elasticity modulus of the polyurethane rod is obviously lower than that of composite layer, the stiffness contribution of polyurethane core is ignored. The constitutive relationship of any composite layer in the curvilinear coordinate system can be represented as:

$$ \left( {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{ss} } \\ {\sigma_{nn} } \\ {\tau_{sn} } \\ {\tau_{nx} } \\ {\tau_{xs} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {\overline{{Q_{11} }} } & {\overline{{Q_{12} }} } & {\overline{{Q_{13} }} } & 0 & 0 & {\overline{{Q_{16} }} } \\ {\overline{{Q_{12} }} } & {\overline{{Q_{22} }} } & {\overline{{Q_{23} }} } & 0 & 0 & {\overline{{Q_{26} }} } \\ {\overline{{Q_{13} }} } & {\overline{{Q_{23} }} } & {\overline{{Q_{33} }} } & 0 & 0 & {\overline{{Q_{36} }} } \\ 0 & 0 & 0 & {\overline{{Q_{44} }} } & {\overline{{Q_{45} }} } & 0 \\ 0 & 0 & 0 & {\overline{{Q_{45} }} } & {\overline{{Q_{55} }} } & 0 \\ {\overline{{Q_{16} }} } & {\overline{{Q_{26} }} } & {\overline{{Q_{36} }} } & 0 & 0 & {\overline{{Q_{66} }} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{ss} } \\ {\varepsilon_{nn} } \\ {\gamma_{sn} } \\ {\gamma_{nx} } \\ {\gamma_{sx} } \\ \end{array} } \right) $$
(4)

where \(\overline{Q}_{ij}\) denotes the stiffness conversion factors. According to the assumptions of Kim C, etc.[27] 28, the stress components at any point of the cross section of the spring wire after bearing load are \(\sigma_{xx} ,\tau_{xs} ,\tau_{nx}\); then formula (4) can be simplified as

$$ \left( {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\tau_{xs} } \\ {\tau_{nx} } \\ \end{array} } \right) = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{33} } \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\gamma_{xs} } \\ {\gamma_{nx} } \\ \end{array} } \right){ = }\left[ C \right]\left( {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\gamma_{xs} } \\ {\gamma_{nx} } \\ \end{array} } \right) $$
(5)
$$ \begin{gathered} C_{11} = \overline{Q}_{11} { + }\frac{{2\overline{Q}_{12} \overline{Q}_{13} \overline{Q}_{23} { - }\overline{Q}_{12}^{2} \overline{Q}_{33} { - }\overline{Q}_{13}^{2} \overline{Q}_{22} }}{{\overline{Q}_{22} \overline{Q}_{33} { - }\overline{Q}_{23}^{2} }},C_{12} = \overline{Q}_{16} { + }\frac{{\overline{Q}_{12} \overline{Q}_{23} \overline{Q}_{36} { - }\overline{Q}_{12} \overline{Q}_{26} \overline{Q}_{33} { + }\overline{Q}_{13} \overline{Q}_{23} \overline{Q}_{26} { - }\overline{Q}_{13} \overline{Q}_{22} \overline{Q}_{36} }}{{\overline{Q}_{22} \overline{Q}_{33} { - }\overline{Q}_{23}^{2} }} \hfill \\ C_{22} = \overline{Q}_{66} { + }\frac{{2\overline{Q}_{23} \overline{Q}_{26} \overline{Q}_{36} { - }\overline{Q}_{26}^{2} \overline{Q}_{33} { - }\overline{Q}_{36}^{2} \overline{Q}_{22} }}{{\overline{Q}_{22} \overline{Q}_{33} { - }\overline{Q}_{23}^{2} }},C_{33} = \overline{Q}_{55} { - }\frac{{\overline{Q}_{45}^{2} }}{{\overline{Q}_{44} }} \hfill \\ \end{gathered} $$

where

$$ \varepsilon_{xx} = \frac{{\partial u_{x} }}{\partial x},\gamma_{xs} = \frac{{\partial u_{x} }}{\partial s} + \frac{{\partial u_{s} }}{\partial x},\gamma_{nx} = \frac{{\partial u_{x} }}{\partial n} + \frac{{\partial u_{n} }}{\partial x} $$
(6)

Substituting formula (1) into formula (6) can obtain

$$ \begin{gathered} \left[ \varepsilon \right] = [H]\{ u^{*}\} \hfill \\ \{ u^{*}\} = [\begin{array}{*{20}c} {u_{0} ^{\prime}(x)} & {\theta ^{\prime}(x)} & {w_{0} ^{\prime}(x) - \phi_{z} (x)} & {\phi_{y} ^{\prime}(x)} \\ \end{array} ] \hfill \\ \end{gathered} $$
(7)

where \(\left[ \varepsilon \right]\) is a strain matrix consists of three nonlinears, namely \(\varepsilon_{xx}\),\(\gamma_{xs}\) and \(\gamma_{nx}\), and \(\left[ H \right]\) is conversion coefficient matrix.

According to the related theory in mechanics of materials, when the helical angle is small, the related forces caused by the helical angle can be ignored[29]. In stiffness calculation problems, shear forces can also be ignored. Therefore, the torque acting on the cross section of spring wire can be expressed as [28]

$$ T(x) = \int_{0}^{2\pi } {\int_{ - h/2}^{h/2} {\varepsilon_{xx} \cdot [r_{y} (\tau_{xs} \frac{{{\text{d}}\overline{z}({\text{s}})}}{{{\text{d}}s}} - \tau_{nx} \frac{{{\text{d}}\overline{y}({\text{s}})}}{{{\text{d}}s}}) - r_{{\text{z}}} (\tau_{xs} \frac{{{\text{d}}\overline{z}({\text{s}})}}{{{\text{d}}s}} + \tau_{nx} \frac{{{\text{d}}\overline{y}({\text{s}})}}{{{\text{d}}s}})]} } \cdot (\frac{r}{{2}} + n){\text{d}}n{\text{d}}s $$
(8)

where T(x) is the torque along the x axis.

The stress in formula (8) can be expressed by displacement nonlinear and written in matrix form, and the governing equation can be expressed as follows:

$$ \begin{gathered} \{ T\} = \left[ {\begin{array}{*{20}c} 0 & {T(x)} & 0 & 0 \\ \end{array} } \right]{ = }[K]\left\{ {u*} \right\} \hfill \\ [K] = \left[ {\begin{array}{*{20}c} {K_{11} } & {K_{12} } & 0 & 0 \\ {K_{21} } & {K_{22} } & 0 & 0 \\ 0 & 0 & {K_{33} } & {K_{34} } \\ 0 & 0 & {K_{43} } & {K_{44} } \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(9)

where the stiffness matrix [K] can be obtained by integration:

$$ [K] = \int\limits_{0}^{2\pi } {\int_{{r_{{{\text{inner}}}} }}^{{r_{{{\text{outer}}}} }} {[H]^{T} } [C][H]} {\text{d}}n{\text{d}}s $$
(10)

In formula (10),\(r_{{{\text{inner}}}}\) and \(r_{{{\text{outer}}}}\) represent the inner torus radius and the outer torus radius of the composite layer, respectively.

According to the principle of energy conservation, the work done by the external force on the spring is equal to the spring's elastic potential energy. Assuming that the spring is subjected to the vertical downward load P, the corresponding deformation of the spring is f, and the effective distance of the spring is L, then

$$ P \cdot f = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\int\limits_{{r_{{{\text{inner}}}} }}^{{r_{{{\text{outer}}}} }} {\{ \varepsilon \}^{T} } } } [\sigma ]{\text{d}}n{\text{d}}s{\text{d}}x = \int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\int\limits_{{r_{{{\text{inner}}}} }}^{{r_{{{\text{outer}}}} }} {\{ \varepsilon \}^{T} } } } [C]\{ \varepsilon \} {\text{d}}n{\text{d}}s{\text{d}}x{ = }\int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\int\limits_{{r_{{{\text{inner}}}} }}^{{r_{{{\text{outer}}}} }} {\{ u*\}^{T} } } } [H]^{T} [C][H]\{ u*\} {\text{d}}n{\text{d}}s{\text{d}}x $$
(11)

According to the relevant research results [26], \(\{ u*\}\) is independent of the nonlinear x in the effective deformation part of the helical spring. Therefore, simultaneous formulas (9),(10) to (11) can obtain

$$ P \cdot f = \{ u*\} ^{T} \cdot K \cdot \{ u*\} \cdot L = \{ u*\} ^{T} \cdot \{ T\} \cdot L $$
(12)

Because \(T(x) = PD/2\), assume that \([J] = [K]^{ - 1}\),then \(\{ u*\}\) can be expressed as:

$$ \{ u*\} = \left[ K \right]^{{ - 1}} \{ T\} = \left[ J \right]\{ T\} {\text{ = }}\left[ {\begin{array}{*{20}c} 0 & {J_{{22}} P\frac{D}{2}} & 0 & 0 \\ \end{array} } \right] $$
(13)

where

$$ [J] = [K]^{ - 1} = \left[ {\begin{array}{*{20}c} {\frac{{K_{22} }}{{K_{11} \cdot K_{22} - K_{12} \cdot K_{21} }}} & {\frac{{ - K_{12} }}{{K_{11} \cdot K_{22} - K_{12} \cdot K_{21} }}} & 0 & 0 \\ {\frac{{ - K_{21} }}{{K_{11} \cdot K_{22} - K_{12} \cdot K_{21} }}} & {\frac{{K_{11} }}{{K_{11} \cdot K_{22} - K_{12} \cdot K_{21} }}} & 0 & 0 \\ 0 & 0 & {\frac{{K_{44} }}{{K_{33} \cdot K_{44} - K_{34} \cdot K_{43} }}} & {\frac{{ - K_{34} }}{{K_{33} \cdot K_{44} - K_{34} \cdot K_{43} }}} \\ 0 & 0 & {\frac{{ - K_{43} }}{{K_{33} \cdot K_{44} - K_{34} \cdot K_{43} }}} & {\frac{{K_{33} }}{{K_{33} \cdot K_{44} - K_{34} \cdot K_{43} }}} \\ \end{array} } \right] $$
$$ \begin{gathered} J_{22} = \frac{{K_{11} }}{{K_{11} \cdot K_{22} - K_{12} \cdot K_{21} }} \hfill \\ \frac{1}{{J_{22} }} = K_{22} - \frac{{K_{12} K_{21} }}{{K{}_{11}}} \hfill \\ K_{11} = \pi \overline{{Q_{11} }}^{{}} (r_{{{\text{outer}}}}^{2} - r_{{{\text{inner}}}}^{2} ) \hfill \\ K_{12} = K_{21} = \frac{{1}}{{2}}\pi \overline{{Q_{16} }}^{{}} (r_{{{\text{outer}}}}^{3} - r_{{{\text{inner}}}}^{3} ) \hfill \\ K_{22} = \frac{1}{2}\pi \overline{{Q_{66} }}^{{}} (r_{{{\text{outer}}}}^{4} - r_{{{\text{inner}}}}^{4} ) \hfill \\ \end{gathered} $$
(14)

The effective wire length of the constant diameter part can be expressed as \(L = \pi DN\). The stiffness of the spring can be obtained by combining formula (12–14):

$$ P \cdot f{\text{ }} = \{ u^{*} \} ^{T} \cdot \{ T\} \cdot L = \left[ {\begin{array}{*{20}c} 0 \\ {J_{{22}} P\frac{D}{2}} \\ 0 \\ 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 & {P\frac{D}{2}} & 0 & 0 \\ \end{array} } \right] \cdot L{\text{ }} = J_{{22}} \cdot P^{2} \cdot \left( {\frac{D}{2}} \right)^{2} \cdot \pi \cdot D \cdot N{\text{ }} $$

and

$$ f = 2\pi \cdot J_{22} \cdot P \cdot \left( \frac{D}{2} \right)^{3} \cdot N $$

Therefore, the stiffness of calculation formula for constant stiffness characteristic is

$$ k = \frac{P}{f} = \frac{1}{{2\pi J_{22} \left( \frac{D}{2} \right)^{3} N}} = \frac{4}{{\pi J_{22} ND^{3} }} $$
(15)

5.2 Establishment of the stiffness calculation model for nonlinear stiffness characteristic

The stiffness of nonlinear diameter part of the spring can be calculated by approximate numerical calculation method, i.e., discrete method. Its basic idea is to discrete the nonlinear diameter part into finite units. When the quantity of finite units is large enough, each finite units can be considered to be a spring wire with constant diameter and constant stiffness, and its stiffness expression can be established by using the calculation theory of chapter 5.1.

In the nonlinear diameter part of the spring, the helical diameter gradually increases from D1 to D2, and the diameter of the spring wire gradually increases from d1 to d2, and r1 = d1/2, r2 = d2/2. If the nonlinear diameter part is divided into an amount of segments, and the effective helical number of each segment is n, then the total number of segments is N1/n. When N1/n is large enough, the helical diameter and the spring wire diameter of segment i(\(1 \le i \le {\text{N}}_{1} /n\))can be approximately expressed as

$$ d_{i} = d_{1} + \left( {\frac{i}{{N_{1} /n}}} \right) \times \left( {d_{2} - d_{1} } \right)r_{i} = r_{1} + \left( {\frac{i}{{N_{1} /n}}} \right) \times \left( {r_{2} - r_{1} } \right) $$
(16)

By substituting N = 0.01 into formula (15) for the stiffness of the composite helical spring, the stiffness of segment i (\(1 \le i \le {\text{N}}_{1} /n\)) can be expressed as

$$ K_{i} = \frac{1}{{2\pi J_{22i} \left( {\frac{{d_{i} }}{2}} \right)^{3} N}} = \frac{4}{{\pi J_{22i} Nd_{i}^{3} }} = \frac{400}{{\pi J_{22i} d_{i}^{3} }} $$
(17)

where

$$ \begin{gathered} \frac{1}{{J_{22i} }} = K_{22i} - \frac{{K_{12i} K_{21i} }}{{K{}_{11i}}} \hfill \\ K_{11i} = \pi \overline{{Q_{11} }}^{i} (r_{i}^{2} - r_{3}^{2} ) \hfill \\ K_{12i} = K_{21i} = \frac{{1}}{{2}}\pi \overline{{Q_{16} }}^{i} (r_{i}^{3} - r_{3}^{3} ) \hfill \\ K_{22i} = \frac{1}{2}\pi \overline{{Q_{66} }}^{i} (r_{i}^{4} - r_{3}^{4} ) \hfill \\ r_{3} { = }d_{3} {/2} \hfill \\ \end{gathered} $$
(18)

When segments with different stiffness are connected in series, the calculation expression of the nonlinear diameter part is

$$ \frac{1}{{K_{{\text{V}}} }} = \sum\limits_{i = 1}^{{N_{1} /n}} {\frac{1}{{K_{i} }}} $$
(19)

Therefore, the overall stiffness of the composite helical spring with nonlinear stiffness under no load is

$$ \frac{1}{{K_{{\text{O}}} }} = \frac{1}{{K_{{\text{C}}} }} + \frac{2}{{K_{{\text{V}}} }} $$
(20)

In formula (19), KC is the stiffness of the constant diameter part that has constant stiffness characteristic.

$$ K_{{\text{C}}} = \frac{1}{{2\pi J_{22} \left( {\frac{{d_{2} }}{2}} \right)^{3} N}} = \frac{4}{{\pi J_{22} Nd_{2}^{3} }} $$
(21)

When the spring is fully loaded, the nonlinear diameter part is completely pressed on the spring seat. Therefore, the stiffness of the spring under full load is the stiffness of the constant diameter part, namely

$$ K_{{\text{F}}} = K_{{\text{C}}} $$
(22)

The no-load stiffness \(K_{{\text{O}}}\) and full-load stiffness \(K_{{\text{F}}}\) are the stiffness characteristics of the spring under different range loads. According to the automobile suspension design theory, the optimal stiffness of no-load and full-load working conditions is calculated by

$$ f = \frac{1}{2\pi }\sqrt{\frac{k}{m}} $$
(23)

where f is the offset frequency of automobile suspension, k is the stiffness of the suspension, m is the sprung mass. For a certain automobile, m is a definite value in no-load and full-load working conditions, and f is also a definite design value in no-load and full-load working conditions; they are all known parameters. Therefore, the optimal stiffness according to the working conditions can be calculated by formula (23) for a certain automobile. For no-load working condition, the optimal stiffness is Ko, and for full-load working condition, the optimal stiffness is KF. Under the external load, the stiffness of the composite helical spring can be adjusted automatically by changing the contact state between spring wire and spring seat caused by deformation.

5.3 Analysis for the key influencing factors of stiffness

As the ply angle increases from 0° to 45°, the stiffness and strength of the composite helical spring increase. When the ply angle is 45°, the stiffness and strength of the spring reach the maximum [16]. Therefore, the ply angle of composite material is not considered as a factor affecting the spring stiffness. The geometrical parameters of the composite material are related to the structural dimensions of the spring: the number of layers is determined by the corresponding spring wire diameter and the thickness of the composite prepreg (the thickness of each layer is known); the layer dimensions are determined by the shape of the variable diameter part of the spring.

MATLAB software was used to write the corresponding stiffness calculation program according to the calculation theory mentioned above. Due to the limitation of the installation and the structure of the spring seat, the height and the D1 are not considered as the design nonlinears of the stiffness matching design. In order to study the sensitivity of key influencing factors to the stiffness of the spring, several groups of data were selected within the value range of each influencing factor for theoretical calculation, and the relationships among the stiffness and the key influencing factors are shown in Fig. 7. The work conditions of the composite helical spring with nonlinear stiffness include two cases, namely no load (before the stiffness changes) and full load (after the stiffness changes).

Fig. 7
figure 7

The relationships among the stiffness of composite helical spring with nonlinear stiffness and the key influencing factors

Full size image

According to Fig. 7 (a) and (c), the no-load stiffness and full-load stiffness of the spring decrease rapidly with the increase of the helical diameter or the effective helical number of the constant diameter part. However, increasing the effective helical number will greatly increase the risk of collision between adjacent spring wires, so it is not appropriate to adjust the effective helical number too much. According to Fig. 7 (b), the no-load stiffness of the spring decreases gently with the increase of the effective helical number of the nonlinear diameter part. According to Fig. 7 (d), the no-load stiffness and full-load stiffness of the spring increase rapidly with the increase of the radius of the constant diameter part. Therefore, adjusting the helical diameter and the radius of the constant diameter part is more efficient to achieve stiffness matching design.

6 Establishment of the strength calculation model

Strength is another important performance parameter of composite helical spring with nonlinear stiffness. For a helical spring with circular cross section made of isotropic material under compression force, the total stress on the cross section of the spring wire is synthesized by two sub-stress vectors. One is the shear stress \(\tau_{1}\) caused by the shear force Q due to the compression force P, and the other is the shear stress \(\tau_{2}\) caused by the torque T of the spring wire. Because \(D_{2} \gg d_{2}\), \(\tau_{1} \ll \tau_{2}\).Therefore, only \(\tau_{2}\) shall be considered. According to the rod twist theory, the shear stress \(\tau_{2}\) on any cross section is proportional to the distance to the center of the cross section, so the outermost layer has the greatest shear stress \(\tau_{2\max }\).

The coordinate transformation relation of stress component of unidirectional laminated plate is

$$ \left[ {\begin{array}{*{20}c} {\sigma_{{1}} } \\ {\sigma_{2} } \\ {\tau_{{{12}}} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & {\sin^{2} \theta } & {2\sin \theta \cos \theta } \\ {\sin^{2} \theta } & {\cos^{2} \theta } & { - 2\sin \theta \cos \theta } \\ { - \sin \theta \cos \theta } & {\sin \theta \cos \theta } & {\cos^{2} \theta - \sin^{2} \theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\tau_{xy} } \\ \end{array} } \right] $$
(24)

where \(\sigma_{{1}}\), \(\sigma_{2}\) and \(\tau_{{{12}}}\) are, respectively, the normal stress along the fiber direction of the outermost layer, the normal stress perpendicular to the fiber direction of the outermost layer and the corresponding in-plane shear stress.

When \(\sigma_{x} { = }0\), \(\sigma_{y} { = }0\) and \(\theta { = 45}^{ \circ }\), formula (24) can be simplified to[30]

$$ \left[ {\begin{array}{*{20}c} {\sigma_{{1}} } \\ {\sigma_{{2}} } \\ {\tau_{{{12}}} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\tau_{{x{\text{y}}}} } \\ { - \tau_{xy} } \\ 0 \\ \end{array} } \right] $$
(25)

Substitute the positive axial stress of the outermost layer \(\sigma_{1}\), \(\sigma_{2}\) and \(\tau_{12}\) into the Tsai–Wu tensor criterion

$$ (F_{11} \sigma_{1}^{2} + 2F_{12} \sigma_{1} \sigma_{2} + F_{22} \sigma_{2}^{2} + F_{66} \tau_{12}^{2} )R^{2} + (F_{1} \sigma_{1} + F_{2} \sigma_{2} )R{ = }1 $$
(26)

namely

$$ R = \frac{{ - B \pm \sqrt {B^{2} { + }4A} }}{2A} $$
$$ A = F_{11} \sigma_{1}^{2} + 2F_{12} \sigma_{1} \sigma_{2} + F_{22} \sigma_{2}^{2} + F_{66} \tau_{12}^{2} $$
$$ \;B = F_{1} \sigma_{1} + F_{2} \sigma_{2} $$

where \(F_{i}\) and \(F_{ij}\) are the strength parameters of the stress space. If R = 1, it means that the layer is just damaged. The higher R is, the greater the safety margin of the single layer will be, and vice versa.

7 Multi-objective optimization

After completing the material selection, structure design and ply design, many structural dimension parameters have important influence on the stiffness, strength and mass of NS-CHS, forming a complex multivariate and multi-objective causal relationship. At the same time, due to the installation size, loading performance requirements and process feasibility limits, there are internal correlation and competitive relations among the spring performance objectives. Therefore, how to balance the performance parameters to optimize the overall performance of the spring is the key problem in the design of NS-CHS.

7.1 Introduction of genetic algorithm

Genetic algorithm is a global random search algorithm developed according to the principle of "natural selection, survival of the fittest" in nature. It carries out continuous iterative operations through selection, crossover, mutation and other genetic operations, and finally approximates the optimal solution or suboptimal solution of the problem. Compared with the traditional optimization search algorithm, genetic algorithm breaks through the limitation of domain search, obtains the global optimal solution more easily, and reduces the dependence on human–computer interaction in the search process, which has the characteristics of strong robustness. For the optimization problem of NS-CHS, it is convenient to encode the design nonlinears of nonlinears into the genes required by genetic algorithm by means of real-number coding, and then optimize the complete design parameters of NS-CHS through the calculation system of genetic algorithm. Therefore, genetic algorithm is selected to optimize the performance of the NS-CHS.

7.2 Design nonlinears selection

There are five main structural design parameters that affect the performance of the spring, i.e., the effective helical number of the constant diameter part N, the minimum helical diameter D1, the maximum helical diameter D2, the minimum diameter of the spring wire d1, and the maximum diameter of the spring wire d2, as shown in Fig. 3. Therefore, the design nonlinear is set to X = [N, D1, D2, d1, d2]. In addition, considering the engineering application, the values of all design nonlinears are greater than 0, and the values of all design nonlinears are rounded into an integer.

7.3 Constraint conditions

7.3.1 Constraint of installation space

In order to avoid the motion interference between the spring and other parts of the suspension in the process of deformation, the outer diameter of the spring D must be limited within a certain range, and the corresponding constraint is

$$ D = D_{2} + d_{2} \le 70 $$
(27)

The height constraint is reflected in the subsequent stability constraint. In addition, the end ring of the nonlinear diameter part shall be consistent with the spring seat, and no motion interference shall occur when the nonlinear diameter part is completely pressed on the spring seat. The inner diameter of the spring seat is 56 mm, and the shortest transverse distance between the end ring and the adjacent ring is about two fifths of the reduced diameter. Therefore, the corresponding constraint is

$$ D_{1} { - }d_{1} { = 28}, D_{1} { + }d_{1} < D_{2} - \frac{{2(D_{2} - D_{1} )}}{5} $$
(28)

7.3.2 Structural characteristic constraint

The helical diameter and spring wire diameter of the nonlinear diameter part shall have a decreasing trend. Therefore, the corresponding constraint is

$$ d_{2} > d_{1}, D_{2} > D_{1} $$
(29)

7.3.3 Winding ratio constraint

The winding ratio is related to the internal and external stress difference of the helical spring and the utilization rate of the material, so a reasonable range needs to be set. Referring to the relevant standards for steel helical springs, the corresponding constraint is

$$ 4 \le D_{1} /d_{1} \le 7,4 \le D_{2} /d_{2} \le 7 $$
(30)

As the ply angle increases from 0° to 45°, the stiffness and strength of the composite suspension spring increase. When the ply angle is 45°, the spring stiffness and strength of the composite suspension reach the maximum. Moreover, the number of fiber layers is determined by the diameter of the spring wire, this paper does not consider the number of layers and layer angle nonlinears as optimization objectives.

7.3.4 Stability constraint

The spring should meet stability requirements to avoid lateral bending. Referring to the relevant standards for steel helical springs, when the one end of helical spring is fixed and the other end can be rotated freely, the stability constraint is

$$ 1{ + }0.5N{ + }1.5d_{1} /D_{1} \le 3.7 $$
(31)

7.3.5 Stiffness constraint

The NS-CHS needs to meet two different stiffness requirements under no-load and full-load conditions. For the spring studied in this paper, the no-load stiffness k1 is 11 N/mm, and the full-load stiffness k2 is 18 N/mm.

7.4 Fitness function

For the helical spring, the key performance parameters are stiffness, strength and mass when considering the matching design of the structure dimensions. Generally, the strength should be as high as possible and the weight should be as small as possible under the premise that the stiffness meets the design requirements. Therefore, the fitness function is

$$ F = \omega_{{1}} F_{1} + \omega_{{2}} F_{2} + \omega_{{3}} F_{3} $$
(32)

where \( \omega_{i} i{ = }1,2,3\) denote the weight coefficients of each sub-objective, F1 is the sub-objective of stiffness, F2 is the sub-objective of stress, F3 is the sub-objective of weight, and

$$ \begin{aligned} F_{1} & = \left| {k_{1} - 11} \right| + \left| {k_{2} - 18} \right| \\ F_{2} & = \tau _{{\max }} = \frac{{8PD_{2} }}{{\pi d_{2}^{3} - d_{3}^{3} }} \\ F_{3} & = m_{1} + 2m_{2} + m_{3} \\ m_{1} & = \pi ^{2} \rho D_{2} N(r_{2}^{2} - r_{3}^{2} ) \\ m_{2} & = 0.5 \times \pi ^{2} \rho \left\{ {\sum\limits_{{j = 1}}^{{50}} {(D_{2} - \frac{{D_{2} - D_{1} }}{{50}}j)\left[ {(r_{2} - \frac{{r_{2} - r_{1} }}{{50}}j)^{2} - r_{3}^{2} } \right]} } \right\} \\ m_{3} & = \pi ^{2} \rho D_{1} \times 1.5 \times (r_{1}^{2} - r_{3}^{2} ) \\ r_{1} & = \frac{{d_{1} }}{2},r_{2} = \frac{{d_{2} }}{2},r_{3} = \frac{{d_{3} }}{2} \\ \end{aligned} $$
(33)

Fitness function is used to evaluate the individual adaptability of the population in genetic algorithm, and the smaller the value of the target function, the stronger the adaptability of the individual. According to the importance of performance parameters, the priority of each sub-objective is sorted as \(F_{1} > F_{2} > F_{3}\).Therefore, the weight coefficients are arranged as \(\omega_{1} > \omega_{2} > \omega_{3}\).

7.5 Analysis of optimization results

After the establishment of the multi-objective optimization model, the basic parameters such as composite material parameters and geometric parameters were first processed, and the genotype string structure data of the genetic space was obtained by encoding the initial geometric parameters. Then 150 initial individuals, which form the initial population, are randomly generated, and the calculation program of the stiffness, strength and weight of NS-CHS was called. The adaptability of each individual in the population is evaluated according to the fitness function, and the adaptability of the individual is sorted. The first 1% of the most adaptable individuals were retained in the next generation of populations and 80% of the remaining individuals were cross-operated, while the rest are mutated to produce other individuals in the next generation of populations. And so on, evolution is considered over when it stops for 50 generations. The distribution state of Pareto solution calculated by genetic algorithm is shown in Fig. 8.

Fig. 8
figure 8

The distribution state of Pareto solution calculated by genetic algorithm

Full size image

The optimal solution is shown in the green sphere in Fig. 7. The performance parameters before and after optimization are shown in Table 2, and the corresponding structural dimension parameters are shown in Table 3. According to Table 2, the weight and maximum stress of the spring are significantly reduced under the premise of small adjustment of stiffness, so the optimization effect is significant.

Table 2 Performance parameters of NS-CHS before and after optimization
Full size table
Table 3 Structural dimension parameters of NS-CHS before and after optimization
Full size table

8 Finite element analysis

8.1 Statics simulation

In order to predict the rationality of the design scheme, the stiffness and stress distribution of the design scheme are simulated by finite element method. The three-dimensional geometric model established by Catia software is imported into Hypermesh software, and meshed by hexagonal solid elements. The C3D8I element with high simulation accuracy in large deformation problem was selected as the element type. The finite element model with meshing completed is shown in Fig. 9 (A). The model was then imported into Abaqus software to set the ply of the spring, including the ply information and material parameters, etc., and the finite element model after material parameter setting is completed is shown in Fig. 9 (B). The state of the local coordinate system of composite helical spring is shown in Fig. 9 (C). The model realizes the support, constraint and loading of the spring through the two spring seats.

Fig. 9
figure 9

The finite element model under different modeling stage

Full size image

The stiffness curve of NS-CHS and the stress nephogram of NS-CHS with free state (a), critical nonlinear stiffness state (b) and full-load state (c) obtained by FEM are shown in Fig. 10. According to Fig. 10, the designed spring deforms normally in the compression process without any abnormal phenomena such as lateral bending and deformation instability. The maximum tensile stress is 637 MPa and the maximum compressive stress is 32 MPa, both of which are far lower than the strength limit of the material. By linear fitting of the stiffness curve in Fig. 10, the no-load stiffness of the spring is 13.2 N/mm, and the full-load stiffness is 20.2 N/mm. Considering the modeling simulation error and the moderate simplification of the theoretical calculation model, the simulation error is within the acceptable range, so the subsequent sample manufacture can be carried out.

Fig. 10
figure 10

Stress nephogram under each key deformation stage and stiffness curve of NS-CHS

Full size image

8.2 Modal simulation

In the process of automobile driving, the composite helical spring will be excited by the vibration of the road and the engine. Accurately predict the modal of the composite helical spring at the early stage of spring development, and make the natural frequency of the composite helical spring avoid the frequency range of external excitation, finally avoid the resonance of the coupling between the composite helical spring and the external excitation, which is of great significance to ensure the fatigue life of the composite spring and the NVH performance of the automobile.

Fiber-reinforced resin matrix composite is a typical nonlinear material with anisotropy and viscoelasticity, which obviously has a certain influence on the actual mode of composite helical spring. However, in modal analysis, the nonlinear characteristics of materials will be ignored, even if the nonlinear element is specified, it will also be treated as a linear element. Therefore, the anisotropy of composites can only be considered in the finite element modeling process, which is different from the actual mechanical properties of resin matrix composites. However, if the modal prediction results are acceptable, this simplification can be considered reasonable.

The established finite element model is submitted to the solver of ABAQUS for calculation. After the calculation is completed, the post-processing module of ABAQUS is used to post-process the calculation results, and the modal prediction results are shown in Fig. 11.

Fig. 11
figure 11

Modal shapes of NS-CHS

Full size image

Modal frequencies of NS-CHS are shown in Table 4.

Table 4 Modal frequencies
Full size table

9 Verification for the correctness of the theoretical model

9.1 Manufacturing process of NS-CHS

In order to manufacture the test sample of NS-CHS at low cost, the inner mold was made by gypsum and the sample was made by vanishing mold process. The main process is shown in Fig. 12. After the completion of mold clamping, pressure is applied to the spring wire through the mechanical mechanism of the mold, and the whole mold is heated through an oven. The curing temperature curve is shown in Fig. 13. After the solidification is completed, the gypsum core mold was smashed to get the NS-CHS sample.

Fig. 12
figure 12

Main manufacturing process of NS-CHS

Full size image
Fig. 13
figure 13

During temperature curve of NS-CHS sample

Full size image

9.2 Test for stiffness performance

In order to test the nonlinear stiffness characteristics of the sample and verify the correctness of the calculation model, three qualified composite helical spring samples with nonlinear stiffness were prepared and tested in quasi-static form during the test, the dynamic mechanical properties of the spring were not studied, the quasi-static compression experiments of the composite helical spring with nonlinear stiffness were carried out at the rate of 2 mm/min by using MTS test bench. The data of the three samples were measured and averaged, and the MTS test bench was trained three times before the stiffness was measured in the formal experiment. Three cycles were set in the test process. Finally, the load displacement curve of the sample measured in the test is shown in Fig. 14. Subjecting to the limitations of manufacturing process, the performance of the sample is not up to the level of industrial applications, but there is no problem with stiffness verification. When the test was loaded to the vicinity of 1125 N, the spring emitted intensive acoustic emission signals. In order to ensure the integrity of the sample, the test is unloaded and stopped. According to the stiffness curve measured by the test, the no-load stiffness of the sample is 11.2 N/mm, and the full-load stiffness is 18.9 N/mm.

Fig. 14
figure 14

Test photograph and the stiffness curve measured by the test

Full size image

The stiffness characteristic curve of the nonlinear stiffness composite helical spring measured by the test is divided into two sections under full-load and no-load conditions, and then they are fitted by polynomial, respectively, and simple functions are fitted to make it easier to identify the stiffness difference more intuitively.

When the deformation of the spring reaches 44.5 mm, the effective circle of the spring is merged with the base pressure, and the number of effective circles changes. At this time, the working state of the spring changes from no-load state to full-load state, and the stiffness changes from no-load stiffness to full-load stiffness. Corresponding data of the average value of load and deformation obtained in the compression test were fitted by polynomial with MATLAB software, and the functional relationship between load F and displacement S was obtained as follows.

$$ F = \left\{ {\begin{array}{*{20}c} {11.2S - 6.45,0 < S < 44.5} \\ {{18}{\text{.9}}S - 44.93,44.5 < S < 79} \\ \end{array} } \right. $$
(34)

In the formula, F unit is N and S unit is mm. The corresponding no-load stiffness and full-load stiffness can be obtained by derivation of the function.

The stiffness results obtained from theoretical calculation, finite element simulation and bench test are shown in Table 5

Table 5 Stiffness results obtained from theoretical calculation model, FEM model and bench test
Full size table

In general, the simulation value is slightly larger than the experimental value, because the FEM model usually considered the material to be perfect, but the actual situation is that the material is always defective for various reasons. In addition, the theoretical calculation model is also moderately simplified and some forces are neglected, and due to the influence of sample quality and test error, the test results themselves will inevitably have a certain error. According to Table 5, the maximum error obtained from theoretical calculation model, FEM model and bench test is 15.2% for no-load stiffness and 9.1% for full-load stiffness. Therefore, the calculation model is correct and can provide theoretical support for the design of NS-CHS.

9.3 Performance comparison with steel spring

In order to highlight the advantages of NS-CHS, the performance of NS-CHS is compared with steel spring. Because the steel helical spring used in suspension does not have the performance of variable stiffness, the stiffness of the steel spring is equal to the full-load stiffness of NS-CHS and it also has the same interface size. The performance comparison is shown in the following table.

According to Table 6, although the maximum stress value increases in NS-CHS, it is still within the maximum stress range that the composite material can withstand. At the same time, the weight decrease of NS-CHS is 69.4%.

Table 6 Performance comparison
Full size table

The finite element model of steel helical spring is established and submitted to ABAQUS solver for calculation. The modal prediction results are shown in Fig. 15.

Fig. 15
figure 15

Modal shapes of steel helical spring

Full size image

Modal frequencies of steel helical spring are shown in Table 7. Comparing Table 3 with Table 6, modal frequencies of NS-CHS are much higher than steel helical spring. Therefore, NS-CHS is much less likely to resonate under external excitation.

Table 7 Modal frequencies
Full size table

10 Conclusion

A theoretical model used for stiffness matching design and structure optimization of composite helical spring with nonlinear stiffness was established and verified in this paper. The parameters that influence its stiffness, the stiffness simulation method and the manufacturing process of composite helical spring with nonlinear stiffness were also studied. The research conclusions are as follows:

  1. (1)

    Considering the service environment, the characteristics of composite materials and the fabricate feasibility of the spring, type (h),which is composed of a constant diameter part and two nonlinear diameter parts, is the relatively ideal structure type.

  2. (2)

    The helical diameter and the radius of the constant diameter part of the spring is a significant factor influencing the stiffness of NS-CHS. Therefore, adjusting the helical diameter and the radius of the constant diameter part is more efficient to achieve stiffness matching design.

  3. (3)

    In terms of weight reduction effect, this mass of the NS-CHS is 98.0 g, which is 69.4% less than that of steel helical spring, and modal frequencies of NS-CHS are much higher than steel helical spring.

This paper also studied the key problems that need to be solved in the design process of NS-CHS, including ply design, performance simulation and manufacturing process. These research results lay a theoretical foundation for the application of composite helical spring with nonlinear stiffness in automobiles.