Carreau nanofluid heat and mass transfer flow through wedge with slip conditions and nonlinear thermal radiation

Abstract

In the present study, we have perceived the impact of nonlinear thermal radiation on heat transfer analysis of Carreau nanofluid flow through wedge by considering slip conditions into account. The extremely nonlinear partial differential equations are transformed into nonlinear ordinary differential equations by using suitable similarity variables, and these equations together with boundary conditions are solved by using the most extensively validated finite element method. The impact of various pertinent parameters, such as Weissenberg number, wedge angle parameter, radiation parameter, temperature ratio parameter, Prandtl number, thermophoresis parameter, Brownian motion parameter, constant velocity ratio parameter, suction parameter, temperature slip parameter, Lewis number, power law index parameter, concentration slip parameter, chemical reaction parameter and magnetic parameter, on velocity, temperature and concentration profiles is calculated and is revealed through graphs. The values of Nusselt number, Sherwood number and skin friction coefficient are also calculated and shown in tables. It is noticed that there is a remarkable intensification in the values of Nusselt number, Sherwood number and skin friction coefficient as the values of Weissenberg number rise. The temperature and concentration distributions both intensify with rising values of temperature slip parameter (ξ).

1 Introduction

In many manufacturing and industrial processes such as paper fabrication, generation of power, chemical practices, glass fiber and polymer extrusion processes, higher heat transfer proficiency is a core requisite. The better heat transfer efficiency may be accomplished by suspending the nanoscale solid particles in common heat transfer fluids which change the thermophysical properties of these fluids and enhanced the heat transfer rate remarkably. Several authors [1,2,3,4,5,6] have perceived significant natural convection heat transfer enhancement in their experimental and numerical studies over different geometries by taking various nanoparticals like, copper, single- and multi-walled carbon nanotubes, etc., into account.

Most of the fluids applied in manufacturing industries are non-Newtonian in nature. There is nonlinear association between shear rate and shear stress in such fluids. Tooth paste, molten polymers, animal blood, pulps, etc., are the examples of these types of fluids. The corrected equation of this type of Carreau fluid which is associated with momentum equation is given by $\mu \left( {\dot{\gamma }} \right) = \mu_{\infty } + \left( {\mu_{0} - \mu_{\infty } } \right)\left( {1 + \varGamma^{2} \left( {\dot{\gamma }} \right)^{2} } \right)^{{\frac{n - 1}{2}}}$, where μ_∞ is the infinite shear stress viscosity, μ₀ is the zero shear stress viscosity and n and Γ are the material parameters. Hashim et al. [7] perceived the sway of zero mass flux condition on Buongiorno’s model Carreau nanofluid flow over a stretching sheet and noticed deterioration in the rate of heat transfer with enhancing values of thermophoretic parameter. Hayat et al. [8] presented homotopy analysis method to discover the impact of Biot number on three-dimensional Carreau nanofluid flows over stretchable linear surface and identified depreciation in the temperature and concentration of the Carreau nanofluid with rising values of Weissenberg number. Khan et al. [9] deliberated a comparison between numerical solutions of homotopy analysis method and bvp4c on MHD three-dimensional Carreau nanofluids over a stretching sheet with the impact of nanoparticle mass flux condition on the surface of the wall. Irfan et al. [10] identified a nominal impact on the rate of heat transfer with higher values of Brownian motion parameter, in their study on three-dimensional Carreau nanofluid flow over bidirectional stretching sheet with variable viscosity, heat source/sink and zero mass flux condition. The heat and mass transfer characteristics of Carreau nanofluid over stretching surface with the impact of magnetic field, zero mass flux condition on the surface of the wall and thermal radiation are discussed by [11,12,13,14].

In recent times, nanofluid flows past wedge-shaped geometries have gained much consideration because of its extensive range of applications in engineering and science, such as magnetohydrodynamics, crude oil extraction, heat exchangers, aerodynamics and geothermal systems. Virtually, these types of nanofluid flows happen in ground water pollution, aerodynamics, retrieval of oil, packed bed reactors, geothermal industries, etc. Motivating from the above applications, Singh et al. [15] studied the impact of suction/injection on unsteady boundary layer, heat and mass transfer flow over a vertical wedge. In this study, finite difference technique is implemented to find the numerical solution of the resulting nonlinear ordinary differential equations. Chamkha et al. [16] observed elevation in the values of Sherwood number as the values of wedge angle parameter rise in their numerical study on Buongiorno’s model nanofluid flow over a vertical wedge by taking thermophoresis and Brownian motion parameter into account. Khan et al. [17] perceived the influence of thermophoresis and Brownian motion on nanofluid flow over a stretching/shrinking wedge and noticed significant improvement in non-dimensional heat and mass transfer rate with intensified values of both thermophoresis and Brownian motion. Ganapathi Rao et al. [18] studied unsteady flow over a vertical plate by taking heat generation or absorption and chemical reaction into account and recognized in the rates of heat and mass transfer with up surging values of non-uniform slot suction; however, reverse trend is detected in the case of slot injection. Srinivasacharya et al. [19] deliberated Au–water and Ag–water nanofluid flow over a wedge and concluded enhancement in the temperature and concentration of the both nanofluids with growing values of nanoparticle volume fraction parameter. Ellahi et al. [20] analyzed the effect of aggregation on heat transfer flow over a porous wedge filled with Al₂O₃-based nanofluid and implemented homotopy analysis method to solve the resulting equations. Ahmad et al. [21] detected significant deterioration in the surface temperature with improving values of magnetic parameter in their study on Carreau nanofluid flow over a wedge with Newtonian heating. Kasmani et al. [22] studied heat and mass transfer flow over a moving wedge by taking Soret and Dufour effects into consideration and perceived notable enhancement in the rate of heat transfer with enhancing values of Soret number. Roy et al. [23] discussed the effect of radiation and heat generation or absorption on unsteady micropolar fluid flow over a wedge and identified marginal enhancement in the Nusselt number with improving values of magnetic parameter. Liu et al. [24] noticed intensification in the velocity and temperature of nanofluid with rising values of both suction/injection parameter and thermophoresis parameter. El-Dawy et al. [25] presented unsteady CuO–water-based nanofluid flow over shrinking/stretching wedge saturated by porous media with solar radiation. Shanmugapriya et al. [26] discussed Cu–water nanofluid flow over a moving wedge and perceived deterioration in temperature distributions with higher values of radiation parameter. Jiang et al. [27] studied the impact of dual Doppler effect on wedge-type photonic crystal which is investigated in this analysis and used finite difference algorithm to solve the proposed model. Abdul Gaffar et al. [28] perceived Buongiorno’s model nanofluid flow over a wedge with magnetic field and pressure gradient. Khan et al. [29] presented the nanofluid flow over a wedge with chemical reaction and slip effects and noticed deterioration in the nanofluid temperature and rate of heat transfer with heightening values of temperature slip parameter. Ali et al. [30] observed intensification in Nusselt number values with higher values of velocity ratio parameter in their study over wedge geometry. Das et al. [31] studied the sway of variable viscosity and temperature on Buongiorno’s model nanofluid flow over wedge and detected that as the values of above parameters rise, the fluid temperature elevates significantly. Hassan et al. [32] noticed substantial enhancement in the heat transfer rate of the base fluid as the size of the added nanoparticle diminishes. Hashim et al. [33] analyzed Carreau nanofluid flow over a wedge and noticed that the rate of heat transfer of the fluid elevates with elevating values of temperature ratio parameter. Tlili et al. [34] deliberated MHD boundary layer flow, heat and mass transfer characteristics of Buongiorno’s model nanofluid flow over a wedge with Navier slip and Biot number. Sheremet et al. [35] presented Buongiorno’s model nanofluid flow over right-angled trapezoidal porous cavity. Eid et al. [36] deliberated the impact of chemical reaction and heat generation on two-phase nanofluid flow over a stretching sheet. Sheremet et al. [37] deliberated the impact of Brownian diffusion and thermophoresis on free convection in a partially heated wavy porous cavity. Bondareva et al. [38] perceived heat line visualization of natural convection in a thick-walled open cavity filled with a nanofluid. Khan et al. [39] presented impact of nonlinear thermal radiation and gyrotactic microorganisms on the Magneto-Burgers nanofluid. Eid et al. [40,41,42,43,44,45] discussed the heat transfer analysis of non-Newtonian nanofluid flow over stretching sheet by considering different effects into consideration. Irfan et al. [46] perceived thermal and solutal stratifications in flow of Oldroyd-B nanofluid with variable conductivity. Taseer et al. [47] presented significance of Darcy–Forchheimer nanofluid flow through porous medium filled with carbon nanotubes. Wakif et al. [48] discussed unsteady MHD couette Cu–water-based nanofluid flow in the presence of thermal radiation using single- and two-phase models. Al-Hossainy et al. [49] presented structural, DFT, optical dispersion characteristics of novel [DPPA-Zn-MR(Cl)(H₂O)] nanostructured thin films. Irfan et al. [50, 51] deliberated heat transfer characteristics of Carreau/Oldroyd-B nanofluid flow by taking heat sink/source and nonlinear radiative heat flux into account.

After careful observation of the literature, we found that no studies have been reported yet to discuss Buongiorno’s model nanofluid heat and mass transfer characteristics over a wedge by taking slip effects into consideration. Hence, we made an attempt to discuss the above problem in this paper. The problem is modeled by taking thermophoresis and Brownian motion into account.

2 Mathematical analysis of the problem

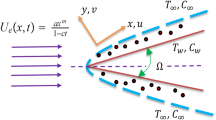
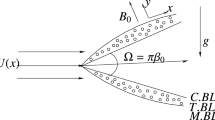
We contemplate a steady, incompressible, MHD laminar boundary layer, two-dimensional flow of viscous nanofluid of density ρ_nf with moving velocity u_w and free stream velocity U over a wedge with inclined angle $\varOmega = \gamma \varPi$. Choose the positive x-coordinate which is measured along the surface of the wedge while y-axis is perpendicular to the surface of the wedge plotted in Fig. 1. In this problem, we considered the boundary layer flow under the velocity, temperature and concentration slip conditions. A fluid magnetic field of strength $B_{0}$ is applied along the y-direction with $B_{0}$ constant. It is predicated that with constant temperature and nanoparticle volume fraction taken as T_w and C_w on the wedge surface ambient temperature and nanoparticle volume fraction are $T_{\infty }$ and C_∞. The governing partial equations for continuity, momentum, thermal energy and solutal of nanoparticles can be exemplified as follows [7]:

Fig. 1

Geometry of the problem

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(1)

$$\begin{aligned} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} &= u_{e} \frac{{{\text{d}}u_{e} }}{{{\text{d}}x}} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}\left( {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right)^{{\frac{n - 1}{2}}}\\ &\quad + \nu \left( {n - 1} \right)\varGamma^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left( {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right)^{{\frac{n - 3}{2}}} \\ &\quad- \frac{{\sigma_{\text{nf}} }}{{\rho_{\text{nf}} }}B_{0}^{2} \left( {u - u_{e} } \right) \end{aligned}$$

(2)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{k}{{\rho_{cp} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \left[ {D_{\text{B}} \frac{\partial T}{\partial y}\frac{\partial C}{\partial y} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] - \frac{1}{{\rho_{cp} }}\frac{{\partial q_{\rm r} }}{\partial y}$$

(3)

$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - K_{\rm r} \left( {C - C_{\infty } } \right)$$

(4)

The related boundary conditions are:

$$\begin{aligned} & u = L\frac{\partial u}{\partial y},\quad v = v_{\text{w}} ,\quad w = 0,\quad T = T_{\text{w}} + k_{1} \frac{\partial T}{\partial z},\quad \\&C = C_{\text{w}} + k_{2} \frac{\partial C}{\partial z} ,\quad {\text{at}}\,y = 0 \end{aligned}$$

(5)

$$u \to u_{e} = b x^{m} , \quad T \to T_{\infty } ,\quad C \to C_{\infty } ,\quad {\text{at}}\,y \to \infty$$

(6)

The stream function ψ can be demarcated as follows:

$$u = \frac{\partial \psi }{\partial y}, \quad v = - \frac{\partial \psi }{\partial x}$$

(7)

The subsequent similarity transformations are presented to streamline the mathematical study of the problem:

$$\begin{aligned}&\psi = {\left( {\frac{{2\nu b}}{{m + 1}}} \right)^{1/2}}{x^{\frac{{m + 1}}{2}}}f\left( \eta \right),\quad \eta = \sqrt {\frac{{b\left( {m + 1} \right)}}{{2\nu }}} {x^{\frac{{m - 1}}{2}}}y,\quad \\&\theta \left( \eta \right) = \frac{{T - {T_\infty }}}{{{T_{\text{w}}} - {T_\infty }}},\quad S\left( \eta \right) = \frac{{C - {C_\infty }}}{{{C_{\text{w}}} - {C_\infty }}}\end{aligned}$$

(8)

By using Rosseland approximation for radiation, the radiative heat flux q_r is defined as:

$$q_{\rm r} = - \frac{{4\sigma^{*} }}{{3K^{*} }}\frac{{\partial T^{4} }}{\partial z} = - \frac{{16\sigma^{*} T^{3} }}{{3K^{*} }}\frac{\partial T}{\partial z}$$

(9)

The non-dimensional temperature $\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}$ can be simplified as:

$$T = T_{\infty } \left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta } \right)$$

(10)

where $\theta_{\text{w}} = \frac{{T_{\text{w}} }}{{T_{\infty } }}$ is the temperature parameter.

$$\begin{aligned} & f^{\prime\prime\prime}\left[ {1 + We^{2} f^{{{\prime \prime }2}} } \right]^{{\frac{n - 3}{2}}} \left( {1 + n We^{2} f^{{{\prime \prime }2}} } \right) \\&\quad+ f f^{\prime\prime} + \gamma \left[ {1 - f^{{{\prime }2}} } \right] - M\left( {f^{\prime} - 1} \right) = 0 \end{aligned}$$

(11)

$$\begin{aligned} & \theta^{\prime\prime} + Pr f \theta^{\prime} + PrN_{\text{t}} \theta^{\prime 2} + PrN_{\text{b}} \theta^{\prime}\phi^{\prime} + \frac{4}{3 R}\left[ {1 + \theta \left( {\theta_{\text{w}} - 1} \right)} \right]^{3} \theta^{\prime\prime}\\ &\quad + \frac{4}{R}\left[ {1 + \theta \left( {\theta_{\text{w}} - 1} \right)} \right]^{2} \left( {\theta_{\text{w}} - 1} \right)\theta^{\prime 2} = 0, \end{aligned}$$

(12)

$$S^{\prime\prime} + Le f S^{\prime} + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\theta^{\prime\prime} - C_{1} S = 0$$

(13)

The associate transformed conditions are:

$$\begin{aligned} & f\left( 0 \right) = V_{0} , \quad f^{\prime}\left( 0 \right) = \lambda f^{{{\prime \prime }}} \left( 0 \right), \quad \theta \left( 0 \right) = 1 + \xi \theta^{\prime}\left( 0 \right),\quad \\&S\left( 0 \right) = 1 + \beta S^{\prime}\left( 0 \right) \end{aligned}$$

(14)

$$f^{\prime}\left( \infty \right) \to 1,\quad \theta \left( \infty \right) \to 0,\quad S\left( \infty \right) \to 0$$

(15)

The associated non-dimensional parameters are defined as:

$$\begin{aligned} & Pr = \frac{{\mu_{cf} }}{k},\quad N_{\text{t}} = \frac{{\rho_{cp} D_{T} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{T_{\infty } \nu \rho_{cf} }}, \\ & N_{\text{b}} = \frac{{\rho_{cp} D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}}{{\nu \rho_{cf} }},\quad \theta_{\rm w} = \frac{{T_{\text{w}} }}{{T_{\infty } }},\quad Le = \frac{\nu }{{D_{B} }}, \\ & C_{1} = \frac{{2\nu k_{\rm r} }}{{D_{\text{B}} b\left( {m + 1} \right)x^{m - 1} }},\quad M = \frac{{\sigma B_{0}^{2} }}{{2\omega_{1} \rho_{\text{f}} }},\quad R = \frac{{16T_{\infty }^{3} \sigma^{*} }}{{3K^{*} k_{\text{f}} }}, \\ & \gamma = \frac{2m}{m + 1},\quad We = \left( {\frac{{b^{3} \varGamma^{2} \left( {m + 1} \right)x^{3m - 1} }}{2\nu }} \right)^{1/2} \\ \end{aligned}$$

(16)

The another object of this problem is to calculate skin friction coefficient (C_fx), Nusselt number (Nu_x) and Sherwood number (Sh_x) given as:

$$C_{{{\text{f}}x}} = \frac{{\tau_{\text{w}} }}{{\rho u_{\text{e}}^{2} /2}},\quad Nu_{x} = \frac{{xq_{\text{w}} }}{{k\left( {T_{\text{w}} - T_{\infty } } \right)}},\quad Sh_{x} = \frac{{xJ_{\text{w}} }}{{D_{m} \left( {C_{\text{w}} - C_{\infty } } \right)}}$$

where

$$\begin{aligned} &\tau_{\rm w} = \mu_{0} \frac{\partial u}{\partial y}\left[ {\left( {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} } \right]_{y = 0} , \quad \\&q_{\rm w} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} + \left( {q_{\rm r} } \right)_{y = 0} ,\quad J_{\rm w} = - D_{m} \left( {\frac{\partial C}{\partial y}} \right)_{y = 0} \end{aligned}$$

(17)

Using the similarity variables, the above equations take the form:

$$\begin{aligned} Re^{ - 1/2} C_{{{\text{f}}x}} & = \frac{2}{{\sqrt {2 - \beta } }}f^{\prime \prime } \left( 0 \right)\left[ {1 + We^{2} (f^{\prime \prime } \left( 0 \right))^{2} } \right]^{{\frac{n - 1}{2}}} \\ Re^{ - 1/2} Nu_{x} & = - \frac{2}{{\sqrt {2 - \beta } }}\theta^{\prime } \left( 0 \right)\left[ {1 + \frac{4}{{3N_{R} }}[1 + \left( {\theta_{\rm w} - 1} \right)\left( {\theta \left( 0 \right)} \right)^{3} } \right] \\ Re^{ - 1/2} Sh_{x} & = - \frac{2}{{\sqrt {2 - \beta } }}S^{\prime } \left( 0 \right), \\ \end{aligned}$$

where $Re = \frac{{x u_{\text{e}} }}{\nu }$ is the Reynolds number.

3 Numerical method of solution

3.1 The finite element method

The finite element method (FEM) is such a powerful method for solving ordinary differential equations and partial differential equations. The basic idea of this method is dividing the whole domain into smaller elements of finite dimensions called finite elements. This method is such a good numerical method in modern engineering analysis, and it can be applied for solving integral equations including heat transfer, fluid mechanics, chemical processing, electrical systems and many other fields. The steps involved in the finite element method [52,53,54,55] are as follows:

• (i) Finite element discretization

The whole domain is divided into a finite number of subdomains, which is called the discretization of the domain. Each subdomain is called an element. The collection of elements is called the finite element mesh.

• (ii) Generation of the element equations

  • a. From the mesh, a typical element is isolated and the variational formulation of the given problem over the typical element is constructed.

  • b. An approximate solution of the variational problem is assumed, and the element equations are made by substituting this solution in the above system.

  • c. The element matrix, which is called stiffness matrix, is constructed by using the element interpolation functions.

• (iii) Assembly of element equations

The algebraic equations so obtained are assembled by imposing the inter element continuity conditions. This yields a large number of algebraic equations known as the global finite element model, which governs the whole domain.

• (iv) Imposition of boundary conditions

The essential and natural boundary conditions are imposed on the assembled equations.

• (v) Solution of assembled equations

The assembled equations so obtained can be solved by any of the numerical techniques, namely the Gauss elimination method, LU decomposition method, etc. An important consideration is that of the shape functions which are employed to approximate actual functions.

For the solution of system of nonlinear ordinary differential Eqs. (11)–(13) together with boundary conditions (14)–(15), first we assume that:

$$\frac{{{\text{d}}f}}{{{\text{d}}\eta }} = h$$

(18)

Equations (11)–(13) then reduce to:

$$\begin{aligned} & h^{\prime\prime}\left[ {1 + We^{2} (h^{\prime} )^{2} } \right]^{{\frac{n - 3}{2}}} \left( {1 + nWe^{2} (h^{\prime} )^{2} } \right) \\ & \quad + f h^{\prime} + \gamma \left[ {1 - h^{2} } \right] + M\left( {1 - h} \right) = 0 \end{aligned}$$

(19)

$$\begin{aligned} & \theta^{\prime\prime} + Pr f \theta^{\prime} + PrN_{\text{t}} \theta^{\prime 2} + PrN_{\text{b}} \theta^{\prime}\phi^{\prime} + \frac{4}{3 R}\left[ {1 + \theta \left( {\theta_{\text{w}} - 1} \right)} \right]^{3} \theta^{\prime\prime} \\ &\quad+ \frac{4}{R}\left[ {1 + \theta \left( {\theta_{\text{w}} - 1} \right)} \right]^{2} \theta^{\prime\prime}\left( {\theta_{\text{w}} - 1} \right)\theta^{\prime 2} = 0 \end{aligned}$$

(20)

$$\phi^{\prime\prime} + Lef \phi^{\prime} + \frac{{N_{\text{b}} }}{{N_{\text{t}} }}\theta^{\prime\prime} - C_{1} \phi = 0$$

(21)

The boundary conditions take the form:

$$\eta = 0, \quad f = V_{0} , \quad h = \lambda h', \quad \theta = 1 + \xi \theta^{\prime},\quad \phi = 1 + \beta \phi^{'}$$

(22)

$$\eta \to \infty ,\quad h = 1,\quad \theta = 0,\quad \phi = 0.$$

(23)

3.2 Variational formulation

The variational form associated with Eqs. (18)–(21) over a typical linear element $\left( {\eta_{e} , \eta_{e + 1} } \right)$ is given by:

$$\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{1} \left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }} - h} \right){\text{d}}\eta = 0$$

(24)

$$\begin{aligned} & \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{2} \left( {h^{\prime\prime}\left[ {1 + We^{2} (h^{\prime} )^{2} } \right]^{{\frac{n - 3}{2}}} \left( {1 + nWe^{2} (h^{\prime} )^{2} } \right) }\right.\\&\quad +\left.{ f h^{\prime} + \gamma \left[ {1 - h^{2} } \right] + M\left( {1 - h} \right)} \vphantom{\left[ {1 + We^{2} (h^{\prime} )^{2} } \right]^{{\frac{n - 3}{2}}} }\right){\text{d}}\eta = 0 \end{aligned}$$

(25)

$$\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{3} \left( {\phi^{\prime\prime} + Lef \phi^{\prime} + \frac{{N_{\text{b}} }}{{N_{\text{t}} }}\theta^{\prime\prime} - C_{1} \phi } \right){\text{d}}\eta = 0$$

(26)

where w₁, w₂, and $w_{3}$ are arbitrary test functions and may be viewed as the variations in $f, h, \theta ,$ and ϕ, respectively.

3.3 Finite element formulation

The finite element model may be obtained from the above equations by substituting finite element approximations of the form:

$$f = \mathop \sum \limits_{j = 1}^{2} f_{j} \psi_{j} ,\quad h = \mathop \sum \limits_{j = 1}^{2} h_{j} \psi_{j} ,\quad \theta = \mathop \sum \limits_{j = 1}^{2} \theta_{j} \psi_{j} ,\quad \phi = \mathop \sum \limits_{j = 1}^{2} \phi_{j} \psi_{j} ,$$

(27)

with

$$w_{1} = w_{2} = w_{3} = \psi_{i} ,\quad \left( {i = 1,2,3} \right),$$

where ψ_i are the shape functions for a typical element $\left( {\eta_{e} , \eta_{e + 1} } \right)$ and are defined as:

$$\begin{aligned} \psi_{1}^{e} & = \frac{{\left( {\eta_{e + 1} + \eta_{e} - 2 \eta } \right) \left( {\eta_{e + 1} - \eta } \right)}}{{(\eta_{e + 1} - \eta_{e} )^{2} }},\quad \psi_{2}^{e} = \frac{{4\left( {\eta - \eta_{e} } \right)\left( {\eta_{e + 1} - \eta } \right)}}{{(\eta_{e + 1} - \eta_{e} )^{2} }} \\ \psi_{3}^{e} & = \frac{{\left( {\eta_{e + 1} + \eta_{e} - 2 \eta } \right) \left( {\eta - \eta_{e} } \right)}}{{(\eta_{e + 1} - \eta_{e} )^{2} }},\quad \eta_{e} \le \eta \le \eta_{e + 1} . \\ \end{aligned}$$

(28)

The finite element model of the equations thus formed is given by:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left[ {K^{11} } \right] } & {\left[ {K^{12} } \right] \left[ {K^{13} } \right]} & {\left[ {K^{14} } \right]} \\ {\left[ {K^{21} } \right] } & {\left[ {K^{22} } \right] \left[ {K^{23} } \right]} & {\left[ {K^{24} } \right]} \\ {\left[ {K^{31} } \right]} & {\left[ {K^{32} } \right] \left[ {K^{33} } \right]} & {\left[ {K^{34} } \right]} \\ \end{array} } \\ {\left[ {K^{41} } \right] \left[ {K^{42} } \right] \left[ {K^{43} } \right] \left[ {K^{44} } \right] } \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} f \\ h \\ \theta \\ \end{array} } \\ \phi \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left\{ {r^{1} } \right\}} \\ {\left\{ {r^{2} } \right\}} \\ {\left\{ {r^{3} } \right\}} \\ \end{array} } \\ {\left\{ {r^{4} } \right\}} \\ \end{array} } \right]$$

where [K^mn] and [r^m] (m, n = 1, 2, 3, 4) are defined as:

$$\begin{aligned} K_{ij}^{11} & = \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta ,\quad K_{ij}^{12} = - \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta ,\quad K_{ij}^{13} = K_{ij}^{14} = 0. \\ K_{ij}^{21} & = 0, \\ K_{ij}^{22} & = \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \left[ {1 + We^{2} \left( {\frac{{\partial \psi_{i} }}{\partial \eta }} \right)^{2} } \right]^{{\frac{n - 3}{2}}} \left( {1 + nWe^{2} \left( {\frac{{\partial \psi_{i} }}{\partial \eta }} \right)^{2} } \right)\frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + \bar{f}_{1} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ & \quad + \bar{f}_{2} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{2} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - \frac{1 }{2}\gamma \bar{h}_{1} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \psi_{j} {\text{d}}\eta - \frac{1}{2}\gamma \bar{h}_{2} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta - M\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta . \\ K_{ij}^{23} & = 0,\quad K_{ij}^{24} = 0,\quad K_{ij}^{31} = 0,\quad K_{ij}^{32} = 0, \\ K_{ij}^{33} & = \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + Pr\bar{f}_{1} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + Pr\bar{f}_{2} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j } \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ & \quad + Pr\bar{\theta }_{1} N_{\rm t}\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{1} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + Pr\bar{\theta }_{2} N_{\rm t}\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{2} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + Pr\bar{\phi } _{1} N_{\rm b}\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ & \quad + Pr\bar{\phi } _{2} N_{\rm b}\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{2} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + \frac{4}{3 R}\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \left[ {1 + \psi_{i} \left( {\theta_{\rm w} - 1} \right)} \right]^{3} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ & \quad + \frac{4}{R}\bar{\theta }_{1} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \left( {\left[ {1 + \psi_{i} \left( {\theta_{\rm w} - 1} \right)} \right]^{2} \left( {\theta_{\rm w} - 1} \right)} \right)\frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ & \quad + \frac{4}{R}\bar{\theta }_{2} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \left( {\left[ {1 + \psi_{i} \left( {\theta_{\rm w} - 1} \right)} \right]^{2} \left( {\theta_{\rm w} - 1} \right)} \right)\frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ K_{ij}^{34} & = 0. \\ K_{ij}^{41} & = 0,\quad K_{ij}^{42} = 0, \quad K_{ij}^{43} = \frac{N_{\rm t}}{N_{\rm b}}\mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\rm d}\eta \\ K_{ij}^{44} & = \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + Le \bar{f}_{1} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta + Le \bar{f}_{2} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{2} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - C_{1} \mathop \int \nolimits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i } \psi_{j} {\text{d}}\eta \\ r_{i}^{2} & = 0,\quad r_{i}^{2} = - \left( {\psi_{i} \frac{{{\text{d}}\psi_{i} }}{{{\text{d}}\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} ,\quad r_{i}^{3} = - \left( {\psi_{i} \frac{{{\text{d}}\psi_{i} }}{{{\text{d}}\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} ,\quad r_{i}^{4} = - \left( {\psi_{i} \frac{{{\text{d}}\psi_{i} }}{{{\text{d}}\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} \\ \end{aligned}$$

4 Results and discussion

Carreau nanofluid flow, heat and mass transfer characteristics past a moving wedge by considering magnetic field, slip conditions and nonlinear thermal radiation are analyzed numerically in this analysis. The results are displayed graphically and in the tabulated form. Graphs represent the physical significance of the problem for the velocity, temperature and concentration profiles for various parameters and are represented in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 and 26. In the estimation of results, in Table 1, we made a comparison and found excellent agreement with the existing work.

Fig. 2

Effect of (M) on f′

Fig. 3

Effect of (M) on θ

Fig. 4

Effect of (M) on S

Fig. 5

Effect of (We) on f′

Fig. 6

Effect of (Le) on S

Fig. 7

Effect of (Pr) on θ

Fig. 8

Effect of (Pr) on S

Fig. 9

Effect of (θ_w) on θ

Fig. 10

Effect of (θ_w) on S

Fig. 11

Effect of (N_b) on S

Fig. 12

Effect of (N_t) on S

Fig. 13

Effect of (n) on f′

Fig. 14

Effect of (n) on θ

Fig. 15

Effect of (n) on S

Fig. 16

Effect of (β) on S

Fig. 17

Effect of (C₁) on S

Fig. 18

Effect of (R) on θ

Fig. 19

Effect of (R) on S

Fig. 20

Effect of (γ) on f′

Fig. 21

Effect of (ξ) on θ

Fig. 22

Effect of (ξ) on S

Fig. 23

Effect of (λ) on f′

Fig. 24

Effect of (V₀) on f′

Fig. 25

Effect of (V₀) on θ

Fig. 26

Effect of (V₀) on S

Table 1 Comparison of Nu₁ with Kuo [56] for various values of m

The impact of magnetic parameter (M) on velocity, temperature and concentration profiles is illustrated in Figs. 2, 3 and 4. With the higher values of (M), the velocity distributions of the Carreau nanofluid intensify in the fluid region and are shown in Fig. 2. From Figs. 3 and 4, we witnessed that the thickness of thermal boundary layer as well as solutal boundary layer of the Carreau nanofluid deteriorates with a higher value of M. This is because of the Lorentz force produced by the magnetic field in the fluid region.

It can see from Fig. 5 that higher values of Weissenberg number (We) cause enhancement in the velocity profiles of Carreau nanofluid. A significant reduction in the concentration boundary layer thickness is noticed in Fig. 6 with the boosting values of Lewis number (Le). The disparity of temperature profiles for diverse higher values of Prandtl number (Pr) is represented in Fig. 7 and perceived debasing nature in the temperature of the fluid along the wedge. The concentration boundary layer thickness upsurges with heightening values of (Pr) as shown in Fig. 8.

Figures 9 and 10 illustrate the temperature and concentration profiles of the Carreau nanofluid for varying values of temperature ratio parameter θ_w. The temperature profiles escalate as the values of θ_w rise; however, concentration boundary layer thickness deteriorated with the rising values of θ_w. The influence of Brownian motion parameter (N_b) on concentration boundary layer thickness is shown in Fig. 11. With rising values of (N_b), the concentration profiles of the Carreau nanofluid diminish in the fluid region. Figure 12 indicates the sway of thermophoresis parameter (N_t) on concentration distributions and noticed intensification in the thickness of solutal boundary layer.

Figures 13, 14 and 15 signify the impact of power law index parameter $(n)$ on hydrodynamic, thermal and solutal boundary layers of the Carreau nanofluid. With the strengthening values of power law index (n), the velocity profiles change its behavior and go on decreasing (Fig. 13). Nevertheless, the thickness of thermal and concentration boundary layers enlarges with the augmenting values of (n) as shown in Figs. 14 and 15. As the values of concentration slip parameter (β) rise, the Carreau nanofluid concentration deteriorates in the boundary layer region (Fig. 16). Furthermore, concentration boundary layer thickness also decelerates as the values of chemical reaction parameter C₁ rise and is depicted in Fig. 17.

Figures 18 and 19 elucidate the temperature and concentration profiles for diverse values of radiation parameter (R). It is clear from Fig. 18 that with higher values of (R), temperature distributions of the Carreau nanofluid diminish; however, concentration profiles heighten with higher values of (R) in the fluid region and are depicted in Fig. 19. It is perceived from Fig. 20 that the velocity profiles elevate as the values of Wedge angle parameter $\left( \gamma \right)$ rise.

The temperature and concentration distributions both intensify with rising values of temperature slip parameter $\left( \xi \right)$. This is because of the fact that as the values of $\left( \xi \right)$ rise, the thickness of both thermal and solutal boundary layers amplifies and is shown in Figs. 21 and 22. It is noticed from Fig. 23 that the velocity profiles of the Carreau nanofluid heighten with the enlarging values of velocity slip parameter (λ). The reason for this behavior is that with the greater values of (λ) the stretching velocity is conveyed to the fluid, which causes the elevation in the velocity profiles.

We observe that the suction parameter (V₀) has an alteration for the velocity, temperature and concentration profiles, respectively. Velocity profiles have a greater change for increasing values of suction parameter (V₀), and temperature and concentration boundary layer thickness profiles abate for better values of suction parameter (V₀) is depicted in Figs. 24, 25 and 26.

Table 2 reveals the values of skin friction coefficient, Nusselt number and Sherwood number for different variations in $M$, We, γ, V₀, λ and ξ. The values of skin friction coefficient at wedge intensify with rising values of (M); furthermore, the values of Nusselt number as well as Sherwood number also heighten with the improving values of (M). As the values of (We) elevate, the values of skin friction coefficient escalate at wedge; furthermore, it elevates the values of both Nusselt number and Sherwood number in the Carreau nanofluids. The non-dimensional rate of change of velocity upsurges as (γ) values rise. With the elevating values of (γ), the Nusselt number values escalate and Sherwood number values also heighten. We have noticed that as the values of suction parameter (V₀) rise, the values of skin friction coefficient, Nusselt number and Sherwood number augment in the Carreau nanofluid. Deterioration in the values of non-dimensional rates of velocity, nevertheless, elevation in the values of non-dimensional rates of temperature and concentration is perceived at wedge with rising values of (λ). We have identified deterioration in the values of both C_f and Nu_x; nevertheless, the values of Sh_x intensify with higher values of temperature slip parameter (ξ).

Table 2 Numerical values of skin friction coefficient, Nusselt number, Sherwood number for various values of parameters

The values of skin friction coefficient, Nusselt and Sherwood number in Carreau nanofluid over the wedge for different variations in $R$, θ_w, N_b, N_t, β are shown in Table 3. The values of non-dimensional rates of velocity upsurge in Carreau nanofluids as the values of (R) rise. The Nusselt number values at wedge intensify; however, Sherwood number values worsen in the fluid region with the improving values of (R). As the values of θ_w rise, the values of C_f and Nu_x diminish in the fluid region. Nevertheless, the values of Sherwood number upsurge as the values of θ_w rise. We have detected from this table that with amplifying values of (N_b) the non-dimensional rates of velocity and temperature diminish; nevertheless, the values of Sherwood number intensify with cumulative values of (N_b). An intensification in the rates velocity (C_f) is perceived; however, deterioration in the rate of temperature (Nu_x) and rates of concentration (Sh_x) is detected as the values of (N_t) rise. With rising values of $C_{1}$, the non-dimensional rates’ velocity diminishes; however, heat and mass transfer rates elevate in fluid region. The values of C_f and Nu_x heighten, whereas Sh_x values diminish with higher values of concentration slip parameter (β).

Table 3 Numerical values of skin friction coefficient, Nusselt number, Sherwood number for various values of parameters

5 Conclusion

The impact of slip effects on heat and mass transfer characteristics of Buongiorno’s mathematical chemically reacting Carreau nanofluid flow over a wedge is analyzed in this analysis. Finite element method is adopted to solve the reduced nonlinear ordinary differential equations which represent momentum, temperature and concentration of the Carreau nanofluid. The significant outcomes of the present analysis are summarized as follows:

• 1. The Carreau nanofluid hydrodynamic boundary layer thickness is elevated with higher values of wedge angle parameter (γ).

• 2. Temperature of the Carreau nanofluid intensifies as the values of (ξ) rise.

• 3. With the improving values of (λ), the velocity scatterings of the nanofluid escalate in the fluid region.

• 4. The values of non-dimensional rates of concentration upsurge as (N_b) values amplify.

• 5. Nusselt number values deteriorate significantly as the values of nonlinear thermal radiation parameter (θ_w) rise.