1 Introduction

Given the growing interests of boundary layer flow of fluid in a wide range of physical problems, the boundary layer theory plays a significant role in disseminating knowledge. One such application is the two-dimensional incompressible and steady laminar flow passing over a wedge. Falkner and Skan [1] have reported such a type of flow over a static wedge. This type of flow has many applications in aerodynamics, nuclear reactors, solar power collectors, etc. Literature has witnessed a good number of studies for the flow across a wedge. The pioneering works of Na [2], Rajagopal et al [3], Lin and Lin [4], Hsu et al [5], Kuo [6] are praiseworthy.

The heating and cooling effect of the fluid plays a vital role in power and transportation industries. Adequate cooling is necessary for nuclear reactor high energy devices. Due to reduced heat transfer characteristics, standard coolants like water and ethylene glycol have low heat transfer capacities. However, metals are good conductors, even have high thermal conductivity. It is possible to prepare a medium by mixing water and metal such that the medium will behave like a fluid and has high thermal conductivity. Nanofluids are such fluids which contain small volumetric quantities of particles of nanometre size. These particles are known as nanoparticles. These fluids are engineered colloidal suspension of nanoparticles in a base fluid.

When nanoparticles (1–100 nm) such as oxides of alumina, silica, titania, copper, etc. are mixed with base fluids like water and organic liquids such as ethanol and ethylene glycol, nanofluids are formed. The size of nanoparticles is relatively similar to the size of the base fluid molecules to build a very stable suspension for an extended period. Steps are taken to make a volumetric fraction of the nanoparticles below \(5\%\). Experimental evidence concluded an abnormal increase in thermal conductivity relative to the base fluid [7, 8]. However, Das et al [9] found that the thermal conductivity of the nanofluid largely increases with temperature compared to pure liquids. A similar correlation has also been established for the viscosity of nanofluids.

Researchers like Pak and Cho [10], Xuan and Roetzel [11] and Xuan and Li [12] proposed that enhancement in heat transfer due to convection is because of the dispersal of nanoparticles in a nanofluid. Moreover, it has been suggested that the absolute velocity of nanoparticles results from the addition of base fluid velocity and relative velocity. Seven slip mechanisms can produce a relative velocity. Out of the seven types of slip mechanisms, only Brownian motion and thermophoresis are necessary [12,13,14,15]. Based on this mechanism, Buongiorno [16] developed a two-component four-equation non-homogeneous equilibrium model to explain mass and heat transfer in fluids containing nanosized particles. He also pointed out that the transfer of energy due to dispersion is minimal. To explain the abnormal increase in heat transfer coefficient within the boundary layer, Buongiorno considered the contribution of temperature gradient and thermophoresis.

Time-dependent free and forced convection boundary layer flow along with a symmetric wedge has been reported by Hossain et al [17]. Magnetohydrodynamics laminar convection flow past a wedge moving in a nanofluid has been studied by Khan et al [18]. MHD decelerating flow over a wedge was discussed by Ashwini and Eswara [19]. The effect of variable magnetic field on the electrically conducting flow together with heat and mass transfer characteristics for a fixed wedge in a nanofluid has been investigated by Srinivasacharya [20] without considering Brownian motion and thermophoresis. Sheikholeslami et al [21] discussed nanofluid flow and heat transfer between two horizontal plates in a rotating system. MHD stretched nanofluid flow with power-law velocity and chemical reaction has been reviewed by Hayat et al [22]. Patil et al [23] reported the influence of MHD nanofluid flow on wall heating or cooling. The thermal energy model was established by Qureshi et al [24] for unsteady MHD nanofluid flow through porous disks with heat and mass transfer aspects in the presence of spherical Au-metallic nanoparticles.

The effect of heat source or sink as an explicit function of the local temperature in the boundary layer has been studied by several researchers [25,26,27]. Transport processes controlled by buoyancy forces’ combined action due to heat and mass transfer are observed in nuclear reactors, safety and combustion systems, etc. These processes are associated with the chemical reaction. Their other applications include solidifying binary alloys and crystal with dissolved materials or particulate water inflows. The presence of a foreign mass in water causes some chemical reactions. Foreign mass moving in fluid over the surface is responsible for the chemical reaction in many processes involved in chemical engineering [28].

Motivated by the aforementioned studies and their useful applications, the variable magnetic field problem on mixed convection boundary layer flow over a fixed wedge has been studied with temperature-dependent heat source. The model incorporates the Brownian motion and thermophoresis with Rosseland diffusion approximation, magnetic field and chemical reaction. This aspect of the nanofluid flow over the wedge has not been discussed earlier. This effect is more pronounced when momentum transport and energy transport equations are coupled. The dimensionless governing equations are converted into non-similar form and then numerically solved. The salient features of new results are analysed and depicted graphically. The present study may have useful applications in many thermal engineering processes such as geothermal systems, crude oil extractions, groundwater pollution, thermal insulation, heat exchangers, storage of nuclear waste etc.

2 Mathematical formulation

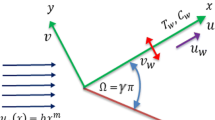
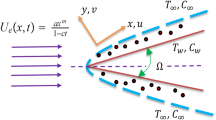
Electrically conducting steady boundary layer nanofluid flow embedded in a free stream moving with a velocity U over a wedge is considered. The effects of the variable magnetic field and thermal radiation are incorporated into the model.

Fig. 1
figure 1

Geometry of the flow model.

Full size image

The x-axis is parallel to the wedge surface and the y-axis is normal to the surface of the wedge (see figure 1). The surface of the wedge is maintained at variable temperature \(T_{w}(x)\) and variable nanoparticle volume fraction \(C_{w}(x)\). Ambient values of temperature and nanoparticle volume fraction are taken to be \(T_{\infty }\) and \(C_{\infty }\), respectively. T and C indicate temperature and nanoparticle volume fraction at any arbitrary reference point in the medium, respectively. A variable magnetic field B(x) is applied normal to the wedge surface. In terrestrial applications, specifically in low velocity, free convection flows, the Reynolds number is assumed to be small. Therefore, the induced magnetic field is negligible compared to the applied field. The effects of Brownian motion and thermophoresis are included for the nanofluid based on the Buongiorno model [16]. The model also consists of the effects of thermal radiation and chemical reaction.

Under the approximation of Boussinesq and Rosseland diffusion, the governing equations can be written as

$$\begin{aligned}&\frac{\partial u}{\partial x}+ \frac{\partial v}{\partial y} =0 \end{aligned}$$
(1)
$$\begin{aligned}&u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y} = U(x)\frac{\mathrm {d}U}{\mathrm {d}x} {+} \nu \frac{\partial ^2 u}{\partial y^2} {+}\frac{\sigma B^{2}(x)}{\rho }(U(x)-u) \nonumber \\&+ g\beta (T-T_{\infty }) \sin (\Omega /2)\nonumber \\&+g\beta ^{*}(C-C_{\infty })\sin (\Omega /2) \nonumber \\&+\frac{\nu }{k}\left( U(x)-u\right) \end{aligned}$$
(2)
$$\begin{aligned}&u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y} = \alpha \frac{\partial ^2 T}{\partial y^2} +\frac{\nu }{c_{p}}\left( \frac{ \partial u}{\partial y}\right) ^2\; \nonumber \\&+\tau \left( D_{\mathrm {B}}\frac{\partial C}{\partial y}\frac{\partial {T}}{\partial y}+ \frac{D_\mathrm{T}}{T_{\infty }}\left( \frac{\partial T}{\partial y}\right) ^2\right) \nonumber \\&-\frac{1}{\rho c_{p}}\frac{\partial q_{r}}{\partial y} + \frac{Q_{0}}{\rho c_{p}}(T_{\infty }-T), \end{aligned}$$
(3)
$$\begin{aligned}&u \frac{\partial C}{\partial x}+v \frac{\partial C}{\partial y} = D_\mathrm{B} \frac{\partial ^2 C}{\partial y^2} \nonumber \\&+\frac{D_\mathrm{T}}{T_{\infty }} \left( \frac{ \partial ^2 T}{\partial y^2}\right) -k_{r}(C-C_{\infty }), \end{aligned}$$
(4)

where u and v are velocity components along x- and y-directions respectively, \(\nu \) is the kinematic viscosity of the nanofluid, \(\alpha \) is the thermal diffusivity of the nanofluid, \(\tau =(\rho c_{p})_{p}/(\rho c_{p})_{nf}\) is the ratio of heat capacity of the nanoparticle to the heat capacity of the nanofluid. Brownian motion is described by Brownian diffusion coefficient, \(D_{\mathrm {B}} = k_{\mathrm {B}}T/(3\pi \mu d_{p})\) which is given by the Einstein–Stokes equation [13]. Here \(k_{\mathrm {B}}\) is the Boltzmann constant, \(\mu \) is the nanofluid viscosity, \(d_{p}\) is the nanoparticle diameter. \(D_\mathrm{T}=\bar{\beta } \mu C/\rho \) stands for the thermal diffusion coefficient and \(\bar{\beta } =0.26k_{f}/(2k_{f}+k_{p})\) is the thermophoretic coefficient. \(k_{f}\) and \(k_{\rho }\) denote the thermal conductivity of the fluid and the nanoparticles respectively.

In the present study, the surface of the wedge is assumed to be impermeable. Therefore, there will be no flow normal to the surface. The boundary conditions for the present problem are

$$\begin{aligned}&u=0, v=0, T=T_{w}(x), C =C_{w}(x)\quad \text {at}\quad y=0 \nonumber \\\end{aligned}$$
(5)
$$\begin{aligned}&u\rightarrow U(x), T \rightarrow T_{\infty }, C \rightarrow C_{\infty } \quad \text {as}\quad y \rightarrow \infty . \end{aligned}$$
(6)

In the end, we shall estimate the skin friction coefficient \(C_{f}\), local heat transfer coefficient (Nusselt number) \(Nu_{x}\) and local mass transfer coefficient (Sherwood number) \(Sh_{x}\), which are defined as

$$\begin{aligned}&C_{f} = \frac{\mu }{\rho U^{2}(x)}\left( \frac{\partial u}{\partial y}\right) _{y=0}, \end{aligned}$$
(7)
$$\begin{aligned}&Nu_{x} = \frac{x q_{w}}{k (T_{w}(x)-T_{\infty })}, \end{aligned}$$
(8)

where \(q_{w}\) is the surface heat flux, i.e.,

$$\begin{aligned} q_{w}= & {} - k\left( \frac{\partial T}{\partial y}\right) _{y=0} + \left( q_{r}\right) _{y=0} \nonumber \\= & {} -\left( k+\frac{16\sigma ^{*}T_{w}^{3}}{3k^{*}}\right) \left( \frac{\partial T}{\partial y}\right) _{y=0} \end{aligned}$$
(9)

and

$$\begin{aligned} Sh_{x} = - \frac{x}{(C_{w}(x)-C_{\infty })}\left( \frac{\partial C}{\partial y}\right) _{y=0}. \end{aligned}$$
(10)

3 Method of solution

Let us find similarity solution for this problem. We consider that the free stream velocity U(x) is of the form \(U(x)=U_{0}x^{m}\), where \(U_{0}\) is a constant and m is the Falkner–Skan power law parameter with \(0\le m \le 1\), \(m=\beta _{0}/(2-\beta _{0})\) (\(0\le \beta _{0} \le 1\)). Here \(\beta _{0}\) is the Hartree pressure gradient that corresponds to \(\beta _{0} = \Omega /\pi \) for the total wedge angle \(\Omega \), \(\beta _{0}=0\) corresponds to the horizontal wall case and \(\beta _{0}=1\) corresponds to the vertical wall case. The magnetic field B(x) is regarded as \(B(x)=B_{0}x^{({m-1})/{2}}\).

Equation (1) implies a stream function \(\phi (x, y)\) such that

$$\begin{aligned} u = \frac{\partial \phi }{\partial y} \quad \text {and}\quad v = -\frac{\partial \phi }{\partial x}. \end{aligned}$$
(11)

The similarity variables considered in this problem are

$$\begin{aligned}&\phi = \left( \nu U_{0} x^{m+1}\right) ^{1/2} F(\eta ), \quad \eta = \left( \frac{U_{0} x^{m+1}}{\nu }\right) ^{1/2} \frac{y}{x}, \nonumber \\&\theta (\eta ) = \frac{T-T_{\infty }}{T_{w}(x)-T_{\infty }},\quad \psi (\eta ) = \frac{C-C_{\infty }}{C_{w}(x)-C_{\infty }}, \end{aligned}$$
(12)

with \(T_{w}(x)-T_{\infty } = x\Delta T\) and \(C_{w}(x)-C_{\infty } = x\Delta C\).

Using similarity transformation, eq. (2) reduces to

$$\begin{aligned}&F^{'''} -\left( m F{'^2} -\frac{m+1}{2} F F{''} -m\right) \nonumber \\&+ \left( M+k_{1}\right) (1-F{'}) \nonumber \\&+ \lambda _{T} \theta \,\sin (\Omega /2) + \lambda _{M} \psi \,\sin (\Omega /2) =0. \end{aligned}$$
(13)

The net radiative heat flux for optically thick media is given by Rosseland approximation

$$\begin{aligned} q_{r}= -\frac{4}{3k^{*}} \nabla e_{b}, \end{aligned}$$
(14)

where \(k^{*}\) is the Rosseland mean absorption coefficient and \(e_{b}\) is the emission power of the black body. Emission power in terms of absolute temperature T is given by Stefan–Boltzmann law, \(e_{b}=\sigma ^{*}T^{4}\), where \(\sigma ^{*}\) is Stefan–Boltzmann constant. The symbol \(\nabla \) is denoted as a nabla operator. The value of the Stefan–Boltzmann constant was calculated by using Planck’s quantum theory [29] and found to be \(8\pi ^{5}k_{\mathrm {B}}^{4}/15c^{3}h^{3}\). Here \(k_{\mathrm {B}}\) stands for the Boltzmann constant, h is the Planck’s constant and c is the speed of light in vacuum. Physically, Stefan–Boltzmann constant implies that when an electron of charge e is accelerated through \(3.543\times 10^{11}\,\)eV of energy per unit area per second, it produces a change in the temperature of \(1\,\)K.

Thus, the radiative heat flux \(q_{r}\) is given by

$$\begin{aligned} q_{r} = - \frac{4 \sigma ^{*}}{3 k^{*}} \frac{\partial T^{4}}{\partial y}. \end{aligned}$$
(15)

The temperature difference within the flow is assumed to be sufficiently small, so that \(T^{4}\) can be expressed as a linear function of free stream temperature of the flow. This can be accomplished by expanding \(T^{4}\) in a Taylor’s series about \(T_{\infty }\), and neglecting higher-order terms, we have

$$\begin{aligned} T^{4}\sim & {} T_{\infty }^{4} + 4 T_{\infty }^{3}(T-T_{\infty }) \\&+ 6 T_{\infty }^{2}(T-T_{\infty })^2 + \cdots \end{aligned}$$
$$\begin{aligned} T^{4} \sim 4T_{\infty }^{3}T - 3T_{\infty }^{4} \end{aligned}$$
(16)

and using eqs (15) and (16), we have

$$\begin{aligned} \frac{\partial q_{r}}{\partial y} = \frac{-16 \sigma ^{*} T_{\infty }^{3}}{3 k^{*}}\frac{\partial ^2 T}{\partial y^2}. \end{aligned}$$
(17)

Now, the simplest form of the temperature-dependent heat source and sink term consistent with the thermal boundary layer reads as

$$\begin{aligned} \left( \frac{Q_{0}}{\rho c_{p}}\right) (T_{\infty }-T), \end{aligned}$$
(18)

where \(Q_{0}\) is a constant which may take either positive or negative values. When the wall temperature \(T_{w}\) exceeds free stream temperature \(T_{\infty }\), then eq. (18) represents heat source when \(Q_{0}<0\) and heat sink when \(Q_{0}>0\). When \(T_{w}< T_{\infty }\), eq. (18) represents heat source for \(Q_{0}>0\) and heat sink for \(Q_{0}<0\). Equations (3) and (4), with the help of similarity transformation, reduce to

$$\begin{aligned}&Pr\left( F{'}\theta -\left( \frac{m+1}{2}\right) F\theta {'}\right) = \theta {''} + \frac{4}{3N_{r}}\theta {''}\nonumber \\&\quad + Pr Ec (F{''})^2 \nonumber \\&\quad +PrN_{b} \theta {'} \psi {'} + PrN_{t}\theta {'^2} -Pr\delta \theta \end{aligned}$$
(19)
$$\begin{aligned}&\psi {''} + \frac{N_{t}}{N_{b}}\theta {''} = LePr\left( F{'}\psi -\frac{m+1}{2}\psi {'}F\right) \nonumber \\&+ \lambda _{1}\;Re_{x} Le \, Pr \psi , \end{aligned}$$
(20)

where prime denotes differentiation with respect to \(\eta \). The non-dimensional quantities are

$$\begin{aligned}&\lambda _{T} = \frac{g \beta x(T_{w}(x)-T_{\infty })}{U_{0}^2 x^{2m}}= \frac{Gr_{x}}{Re_{x}^2}\\&\quad (\text {thermal convective parameter})\\&\lambda _{M} = \frac{g \beta ^{*} x(C_{w}(x)-C_{\infty })}{U_{0}^2 x^{2m}}= \frac{Gm_{x}}{Re_{x}^2}\\&\quad (\text {mass convection parameter}) \end{aligned}$$

where

$$\begin{aligned}&Gr_{x} = \frac{g \beta x^3 (T_{w}(x)-T_{\infty })}{\nu ^2} \\&Gm_{x} = \frac{g \beta ^{*} x^3 (C_{w}(x)-C_{\infty })}{\nu ^2} \end{aligned}$$

and

$$\begin{aligned}&Re_{x} = \frac{U_{0}x^{m+1}}{\nu }.\\&M = \frac{\sigma B_{0}^2}{\rho U_{0}}\quad (\text {Magnetic parameter})\\&\lambda _{1}=\frac{k_{r}\nu }{U^2} \quad (\text {Chemical reaction parameter})\\&LePr = \frac{\nu }{D_{B}}, \quad Ec = \frac{U^2}{c_{p}(T_{w}(x)-T_{\infty })},\\&\delta = \frac{Q_{0}x}{\rho c_{p} U}, \quad k_{1}= \frac{\nu x^{1-m}}{kU_{0}}, \quad Nr = \frac{kk^{*}}{4\sigma ^{*}T_{\infty }^{3}}\\&N_{b} = \frac{\tau D_\mathrm{B}(C_{w}(x)-C_{\infty })}{\nu }, \\&N_{t} = \frac{\tau D_\mathrm{T}(T_{w}(x)-T_{\infty })}{\nu T_{\infty }}. \end{aligned}$$

Here \(\lambda _{T}\) represents the ratio of buoyancy forces to inertia forces. Therefore, this parameter plays a vital role in establishing the dominant region of free and forced convection. The free convection is dominant when \(\lambda _{T} \gg 1\), and when \(\lambda _{T}=1\), the free and forced convection are of comparable magnitude, and forced convection dominates when \(\lambda _{T}\ll 1\).

The boundary conditions (eqs (5) and (6)) in terms of F, \(\theta \) and \(\psi \) are At \(\eta =0\):

$$\begin{aligned} F(0)=0,\quad F{'}(0)=0,\quad \theta (0)=1,\quad \psi (0)=1 \end{aligned}$$
(21)

and when \(\eta \rightarrow \infty \):

$$\begin{aligned} F{'}\rightarrow 1, \;\theta \rightarrow 0,\; \psi \rightarrow 0. \end{aligned}$$
(22)

Hence, the non-dimensional skin friction coefficient, local heat transfer coefficient and mass transfer coefficient derived from eqs (7), (8) and (10) respectively are

$$\begin{aligned}&\bar{C_{f}} = C_{f}(R_{ex})^{1/2} = F{''}(0), \end{aligned}$$
(23)
$$\begin{aligned}&\overline{Nu_{x}}= Nu_{x}(R_{ex})^{-1/2} = -\left( \frac{3N_{r}+4}{3N_{r}}\right) \theta ^{\prime }(0), \end{aligned}$$
(24)
$$\begin{aligned}&\overline{Sh_{x}} = Sh_{x}(R_{ex})^{-1/2} = -\psi {'}(0), \end{aligned}$$
(25)

where \(Re_{x}\) is the local Reynolds number, i.e., \(Re_{x}=U_{0}x^{m+1}/\nu \).

4 Result and discussions

The fourth-order Runge–Kutta method in association with the shooting technique is employed to solve the boundary value problem of nonlinear ordinary differential equations to obtain numerical solutions. The source of error may surge in the numerical scheme due to boundary conditions at infinity. The numerical domain is finite; therefore, we have considered the length of the computational domain sufficiently large to have boundary conditions at the far end and to avoid error. The grid of size \(\Delta \eta = 6/300\) is considered to achieve accuracy of order \(O(10^{-6})\). The parameter values used throughout this discussion, unless otherwise stated, are \(M=2\), \(k_{1}=0.5\), \(\lambda _{T}=0.2\), \(\lambda _{M}=0.2\), \(\Omega =30^{\circ }\), \(Pr=1\), \(Nr=1\), \(Ec=0.3\), \(N_{b}=0.2\), \(N_{t}=0.2\), \(\delta =0.2\), \(Le=1\), \(\lambda _{1}=0.3\) and \(Re_{x}=0.5\).

4.1 Validation

To verify the accuracy of the numerical results obtained in this analysis, we first validate our results under a simplified assumption with previously published works. We consider the fluid to be pure water for reference and measure skin friction by neglecting porosity, diffusion, heat source, radiation, Brownian motion, thermophoretic, thermal and mass convective and chemical reaction effects in the problem, i.e., \(k_{1}=Ec=\delta =Nr=N_{b}=\lambda _{T}=\lambda _{M}=\lambda _{1}=0\). We compared the simulated results with the results of Ariel [30] and Srinivasacharya et al [20] and found that they are in excellent agreement as shown in table 1, thus validating the scheme implementation.

Table 1 Skin friction coefficients \(F{''}(0)\), for different values of magnetic parameter M with \(m=1\), \(Pr=1\) and \(Le=0.24\).
Full size table

4.2 The Falkner–Skan parameter

The skin friction coefficient \(\bar{C_{f}}\), heat transfer coefficient (\(\overline{Nu_{x}}\)) and mass transfer coefficient (\(\overline{Sh_{x}}\)) are tabulated in table 2 for different values of pressure gradient m. Increasing value of pressure gradient from \(m=0\) to \(m=1\), physically, we are moving from fluid flow over flat plate (\(m=0\)) case to stagnation point flow (\(m=1\)). Obviously, the skin friction coefficient, rate of heat transfer and mass transfer rate increase from flat plate case to stagnation point flow.

Table 2 Skin friction coefficients \(F{''}(0)\), heat transfer coefficients \(\overline{Nu_{x}}\) and mass transfer coefficients \(\overline{Sh_{x}}\) for different values of Falkner–Skan power law parameter m.
Full size table

The velocity profiles \(F{'}(\eta )\) for different values of m are depicted in figure 2 with increasing pressure gradient (\(m>0\)). It shows that the nanofluid flow is accelerated. The laminar boundary layer can withstand very small retardation of flow before separation takes place. For accelerated flow (\(m>0\)), i.e., increasing pressure gradient, the thickness of temperature and concentration profiles decrease (figure 3).

Fig. 2
figure 2

Velocity profiles for different values of Falkner–Skan coefficient m.

Full size image
Fig. 3
figure 3

Effect of Falkner–Skan coefficient. (a) Temperature profiles and (b) concentration profiles.

Full size image

4.3 Magnetic field

Effect of magnetic parameter on the velocity of the conducting nanofluid over a wedge is exhibited in figure 4. It is observed that the velocity of the conducting nanofluid over the wedge increases with increasing magnetic field strength. Physically, this is due to the Lorentz force, which is the combined effect of electric and magnetic fields. This Lorentz force acts in such a way which accelerates the flow with increase in M. The combined effect of the increase of electrical conductivity and decrease of nanofluid density in the convective wedge surface is responsible for this phenomenon.

Fig. 4
figure 4

Velocity profiles for different values of magnetic parameter M.

Full size image

4.4 Brownian motion

The effect of Brownian motion on temperature and concentration profiles is depicted in figure 5. It is observed that the Brownian motion parameter \(N_{b}\) increases the temperature of the fluid but decreases volume fraction. The increase in thermal conductivity for small particles (1–5 nm) is due to their high Brownian velocity and relatively higher particle diffusivity. Particle size \(d\, \ge \) 10 nm exhibits high repulsion and low random diffusion. Therefore, an increase in thermal conductivity is not solely due to the Brownian motion. An increase in the Brownian motion parameter \(N_{b}\) increases the diffusion of nanoparticles due to Brownian effects and consequently decreases the concentration profiles.

Fig. 5
figure 5

Effect of Brownian motion parameter \(N_{b}\). (a) Temperature profiles and (b) concentration profiles.

Full size image
Fig. 6
figure 6

Effect of thermophoresis parameter \(N_{t}\). (a) Temperature profiles and (b) concentration profiles.

Full size image

4.5 Thermophoretic parameter

The influence of thermophoretic parameter \(N_{t}\) on dimensionless temperature and dimensionless concentration for fixed values of other parameters are shown in figure 6. We observed that both dimensionless temperature and volume fraction increase due to the thermophoretic parameter \(N_{t}\). This increase in profiles is due to the temperature gradient’s thermophoretic force, which induces high-velocity flow away from the surface. In this way, hot fluid moves away from the surface, and consequently, as \(N_{t}\) increases, the temperature within the boundary layer increases. The high-velocity nanofluid flow associated with the thermophoretic force induces an increase in the thickness of the concentration boundary layer. The concentration profiles decrease for all values of \(N_{t}\) up to \(\eta =0.5\). As the thermophoretic force becomes stronger (\(N_{t}=2.0\)), the concentration of nanofluid adjacent to the wedge surface exceeds that on the wedge surface.

4.6 Viscous dissipation parameter

The effect of viscous dissipation parameter Ec on temperature and concentration profiles are presented in the left and right panels of figure 7. The kinetic energy of the fluid can transform to potential energy by doing work against viscous fluid stress. This relationship is defined by the Eckert number (Ec). It is observed that temperature increases with an increase of Ec. Temperature attains maximum value on the surface and falls rapidly near the surface and slowly decreases away from the surface. Physically, it means that the thermal boundary layer becomes thicker with a considerable value of Eckert number. The concentration profiles fall rapidly near the wedge’s body and then slowly away from the surface. Concentration profile corresponding to \(Ec=3\) decreases at a faster rate than \(Ec=0\) up to \(\eta =1.5\) and then increases above \(Ec=0\).

Fig. 7
figure 7

Effect of Eckert number Ec. (a) Temperature profiles and (b) concentration profiles.

Full size image
Fig. 8
figure 8

Effect of heat source parameter \(\delta \). (a) Temperature profiles and (b) concentration profiles.

Full size image

4.7 Temperature-dependent heat source

Let us interpret the heat transfer result physically. We have considered the positive and negative values of \(\delta \) separately. For positive \(\delta \) (\(Q_{0}>0\)), according to eq.  (3) there is a heat source in the boundary layer when \(T_{w}<T_{\infty }\) and a heat sink when \(T_{w}>T_{\infty }\). These correspond respectively, to recombination and dissociation in the boundary layer. When \(T_{w}<T_{\infty }\), there is heat transfer from the fluid to the wall, even in the absence of a heat source. The presence of a heat source (\(\delta >0\)) will further increase the heat flow to the wall. When \(\delta \) is negative, (\(-Q_{0}\)), eq. (3) indicates a heat source for \(T_{w}>T_{\infty }\) and a heat sink for \(T_{w}<T_{\infty }\). These correspond respectively to combustion and endothermic chemical reactions. When \(T_{w}>T_{\infty }\), the presence of a heat source (\(\delta >0\)) creates a layer of hot fluid adjacent to the surface. Therefore, heat transfer from the wall diminishes. Further increasing negative values of \( \delta \), the hot fluid layer’s temperature exceeds that of the surface. Thus, heat will flow from the fluid into the surface when \(T_{w}>T_{\infty }\). When \(T_{w}<T_{\infty }\) (cooled wall), the presence of heat sink (\(\delta <0\)) blankets the surface with a layer of cool fluid, thus decreasing heat flow into the surface. Further decreasing the value of \(\delta \), the cool fluid layer’s temperature may be lower than that of the wall. This phenomenon leads to heat flow from the wall even though \(T_{w}<T_{\infty }\).

The effect of temperature-dependent heat source is depicted in the left panel of figure 8 for temperature profiles, and the concentration profiles are shown in the right panel of figure 8. The maximum value of temperature is unity on the wall and decreases to zero in the free stream. (i) When \(T_{w}>T_{\infty }\), with \(\delta >0\) indicates a heat sink. The effect is visible in the figure by a rapid drop of temperature as heat flowing from the surface is absorbed. (ii) When \(T_{w}>T_{\infty }\) with \(\delta <0\), the heat source causes a rise in temperature in the entire boundary layer. The concentration profiles (right panel of figure 8) steadily rises up to the wedge length \(\eta =2\) (non-dimensional) near the wedge surface and then decreases away from the wedge with an increase in temperature-dependent heat source parameter value.

4.8 Thermal and mass convective parameters

Figures 9 and 10 exhibit dimensionless velocity, temperature and concentration distribution for different values of thermal convective parameter \(\lambda _{T}\). The momentum boundary layer follows the boundary condition due to a moving wedge. An increase in thermal convective or thermal buoyancy parameter tends to accelerate the flow near the wedge surface strongly and nanofluid flow attains a constant velocity away from the wedge surface. By increasing thermal convection parameter \(\lambda _{T}\), more heat transfer occurs along the surface of the wedge and dimensionless temperature decreases. So also the thickness of the thermal boundary layer decreases (left panel of figure 10). Similar finding has been observed for the concentration profiles (right panel of figure 10).

Fig. 9
figure 9

Velocity profiles for different values of \(\lambda _{T}\).

Full size image
Fig. 10
figure 10

Effect of thermal convective parameter \(\lambda _{T}\). (a) Temperature profiles and (b) concentration profiles.

Full size image

The dimensionless velocity distribution for different mass convective parameter values is shown in figure 11. The mass convective parameter serves to increase the velocity distribution near the wedge surface. Therefore, increasing species buoyancy force only adds momentum and increases velocity boundary layer thickness.

Far away from the surface, velocity attains a constant value for different values of species buoyancy force. Nanoparticle concentration decreases by increasing species buoyancy force. Therefore, concentration boundary layer thickness lowered with increasing mass convective parameter (right panel of figure 12). Similar findings have been observed for temperature profiles (left panel of figure 12) concerning \(\lambda _{M}\).

Fig. 11
figure 11

Velocity profiles for different values of \(\lambda _{M}\).

Full size image
Fig. 12
figure 12

Effect of thermophoresis parameter \(\lambda _{M}\). (a) Temperature profiles and (b) concentration profiles.

Full size image

The calculated values of local Nusselt number and local Sherwood number as a function of \(N_{b}\) and \(N_{t}\) are given in table 3. It is observed that large Brownian motion is associated with a low heat transfer rate and high Sherwood number. However, the increase in thermophoretic parameter corresponds to a decrease in both the Nusselt number and Sherwood number.

4.9 Radiation parameter

The characteristic features of radiation parameter \(N_{r}\) are presented in figure 13. The decrease in temperature and the thermal boundary layer is observed with an increase in thermal radiation parameter \(N_{r}\), as shown in figure 13. The radiation effect decreases the rate of energy transport to the fluid. Hence, the temperature of fluid decreases, which is in agreement with eq. (19). The heat transfer rate increases as the thermal radiation parameter \(N_{r}\) increases. The result is due to the extra term that contributes to the flow (eq. (9), [31]).

Table 3 Heat and mass transfer rate for different values of \(N_{b}\) and \(N_{t}\).
Full size table
Fig. 13
figure 13

Effect of thermal radiation parameter on temperature profiles.

Full size image

The temperature profiles for different values of radiation parameter \(N_{r}\) are shown in figure 13. The fluid temperature decreases with increasing \(N_{r}\). This suggests that heat energy flowing into the liquid diminishes. That means most of the heat energy is radiated away from the surface. As the temperature of the fluid gradually decreases, more heat energy is radiated away from the surface. This is in accordance with figure 14, where the heat transfer rate increases with increasing \(N_{r}\). For \(N_{r}=0\), Nusselt number is contributed by pure conduction. A gradual increase in Nusselt number is observed with increasing \(N_{r}\).

Fig. 14
figure 14

Nusselt number vs. radiation parameter.

Full size image

4.10 Permeability parameter

Figure 15 illustrates the effect of permeability parameter (\(k_{1}\)) on velocity profiles. When \(k_{1}=0\) the permeability (k) tends to infinity, and the term representing the effect of porous medium is absent in eq. (2) and its dimensional counterpart eq. (13). This equation represents the momentum equation without the porous medium. It can be seen from this results that when \(k_{1}\) increases (i.e., in the presence of porous medium), the velocity of the nanofluid on the porous surface increases. Subsequently, the boundary layer thickness decreases. However, nanofluid flow away from the surface maintains a steady value. The boundary layer thickness tends to zero for a higher value of \(k_{1}\).

Fig. 15
figure 15

Effect of permeability parameter on velocity profiles.

Full size image

4.11 Chemical reaction parameter

Chemical reaction effect has been illustrated in figure 16. The reaction can be termed homogeneous or heterogeneous depending on whether it occurs on an interface or a single-phase volume reaction. For a first-order reaction, the rate of reaction is directly proportional to concentration. The destructive chemical reaction enhances the mass transfer rate resulting in a decrease in nanoparticle concentration. For destructive reaction, the diffusion species is destroyed in the flow and \(\lambda _{1}>0\). The last term in the mass-diffusive equation (4) becomes positive and it contributes to the reduction in concentration. Otherwise, the last terms of eq. (4) becomes negative for \(\lambda _{1}<0\). This corresponds to a generative reaction and an increase in concentration. The destructive chemical reaction enhances the mass transfer rate resulting in a decrease in nanoparticle concentration. The generative chemical reaction decreases the mass transfer rate which increases the corresponding nanoparticle concentration.

Fig. 16
figure 16

Effect of chemical reaction parameter on concentration profiles.

Full size image

5 Conclusion

The effects of thermal radiation, Brownian motion parameter, thermophoretic parameter, magnetic parameter, thermal convection parameter, mass convection parameter, chemical reaction parameter and temperature-dependent heat source parameter on the mixed convection MHD nanofluid flow over the moving wedge have been investigated. The numerical solution to the problem has been found out after reducing the governing boundary value equations to nonlinear ones. The effects of governing factors on the flow, heat and mass transfer properties have been analysed and depicted graphically. It has been observed that

  • Surface shear stress coefficient, rate of heat transfer and rate of mass transfer show increasing tendency with the Falkner–Skan coefficient. This situation corresponds to the nanofluid flow along with a flat plate (\(m=0\)) to stagnation point flow (\(m=1\)). Velocity also increases in this limit.

  • Magnetic field has an enhanced effect on the velocity of the conducting nanofluid. Viscous drag force is unimportant for larger magnetic parameters.

  • Increase in Brownian motion corresponds to higher temperature and lower concentration.

  • Thermophoretic force generated by the temperature gradient increases both temperature and volume fractions.

  • Work done against the viscous fluid is utilised for converting kinetic energy into thermal energy for which temperature increases and concentration decreases with an increase in Eckert number.

  • Due to the source of heat a layer of hot fluid nearer to the surface is created which reduces the heat transfer from the wall.

  • Destructive reaction (\(\lambda _{1}>0\)) corresponds to reduction in concentration and generative reaction (\(\lambda _{1}<0\)) implies an increase in concentration.

  • An increase in radiation parameter \(N_{r}\) decreases temperature profiles. However, an increase in the radiation parameter increases the heat transfer rate.

The present work can be applied to non-Newtonian fluid flow over a porous wedge by considering the impacts of physical phenomena such as position and concentration-dependent diffusivity. Again, a comparative analysis can be done for different theoretical models of nanofluids. In view of engineering applications, this will be an informative and fruitful discussion.