Non-linear radiation and chemical reaction effects on slip flow of Williamson nanofluid due to a static/moving wedge: a revised model

Abstract

In the present study, heat and mass transfer characteristics of unsteady, two-dimensional stagnation-point flow of Williamson nanofluid along a static/moving wedge in the presence of velocity slip and chemical reaction effects are investigated. The Rosseland approximation is adopted for thermal radiation effects and Buongiorno model is used for incorporating the effects of Brownian diffusion and thermophoresis. The wall of wedge is heated by the convection current from hotter fluid and revised model is also considered in this study. The governing boundary-layer equations are altered into a coupled non-linear ordinary differential equations using suitable transformations and then tackled numerically employing Runge–Kutta–Fehberg method with shooting technique. The effects of intricate physical parameters on the dimensionless velocity, temperature, nanoparticle concentration profiles as well as skin friction coefficient and local Nusselt number are explored graphically and discussed in detail. Verification of present code is achieved via benchmarking with previously published results, and generally, very excellent agreement is revealed. Our study reveals that the intensifying values of temperature ratio parameter enhances the nanofluid temperature and thermal boundary-layer thickness. The rate of heat transfer is seen to be higher with the growth of Prandtl number and Biot number. Moreover, the nanoparticle concentration is decreased as the Brownian motion and Schmidt number increasing.

Introduction

Nanofluids are designed by scattering a little amount of nano-sized particles usually under 100 nm, which are consistently and steadily suspended into traditional fluids such as ethylene glycol, oil, water, lubricants, bio-fluids, and polymer solutions. During the recent decades, researchers are prompted to discover alternate sources for energy due to fossil fuel deficiency. It is already proven that the addition of nanoparticles in working fluid can improve the performance of solar systems significantly, and can make them more efficient. Nanofluids also play a key role in cooling and heating processes. Recently, the flow of nanofluids is of great interest in various areas of science, designing and innovation, chemical and nuclear industries, and bio-mechanics. Choi (1995) was the first who introduced the innovative procedure to enhance the heat transfer of nanofluids using the mixture of nanoparticles and base liquids. Later on, Boungiorno (2006) declared the main reasons of improvement of heat transfer of nanofluids and found that the impact of Brownian motion and thermophoresis diffusion are prime factor for heat transfer enhancement. On the behalf of this novel idea, Nield and Kuznetsov (2009) and Kuznetsov and Nield (2010) have investigated the double diffusive free convective flow of nanofluids generated by a flat surface. The thermal conductivity and diffusivity of nanofluids are significantly a function of nanoparticle concentration. These investigations have achieved the effective thermal properties in terms of volume fraction of nanoparticles or concentration. In this regard, Khan and Pop (2010) discussed the boundary-layer flow of nanofluid and heat transport features towards stretched surfaces in the presence of Brownian motion and thermophoresis parameter. Their study indicate that rate of heat and mass transfer at the surface are strongly depend on the influences on the Brownian motion, thermophoretic and Lewis number. Mabood et al. (2015) numerically investigated the electrically conducting water-based nanofluid flow induced by a non-linear stretching sheet. They have found that thermal boundary-layer thickness grows with Brownian motion parameter. In another article, Mabood and Mastroberardino (2015) investigated the combined effects of viscous dissipation and second-order slip on MHD flow of water-based nanofluid past a stretching sheet. They revealed that local Nusselt number rises with an increment in viscous dissipation. Furthermore, Ahmad et al. (2016) examined the bidirectional flow of MHD nanofluid over an exponentially stretched surface. They showed that temperature exponent parameter is the main factor to upgrade the heat transfer rate at the surface. Bai et al. (2016) employed homotopy analysis method (HAM) to explore the effects of electrically conducting Maxwell nanofluids along a stretched sheet by incorporating Brownian motion diffusion. The found that rate of heat transfer is a decreasing function of thermophoresis parameter. In addition, Ibrahim (2017) numerically investigated the melting heat transfer in stagnation-point flow of nanofluid induced by a stretched surface. They pointed out that wall shear stress decreases with the larger values of magnetic parameter. Reddy et al. (2017) utilized spectral quasi-linearization method (SQLM) to elaborate the mechanisms of heat transfer of Williamson nanofluid past a stretching sheet with variable thickness and variable thermal conductivity. Their outcomes show that velocity of the fluid reduces for rising values of wall thickness parameter. Moreover, Eid and Mahny (2017) have studied the effects of heat source/sink on non-Newtonian nanofluid flow of two-phase model past a porous wall, wherein they reported that Lorentz forces decrease the rate of heat and mass transfer. Very recently, Gupta et al. (2018) examined the characteristics of Brownian motion and thermophoresis diffusion in non-Newtonian fluid past an inclined surface with thermal radiation and chemical reaction. Their investigation reveals that velocity of the fluid slows down with augmented magnetic field parameter.

Thermal radiation assumes very critical part in the surface heat transfer when convection heat transfer is very small. It has applications in assembling enterprises, gas turbines, air ship, rockets, satellites, space vehicles, space innovation, and procedure relating high temperature. In the perspective of aforementioned applications, Pal (2013) studied the unsteady boundary-layer flow of viscous fluid along a continuously stretching surface by incorporating the thermal radiation effects. They have illustrated that thermal boundary-layer thickness decreases with unsteadiness parameter. Jonnadula et al. (2015) employed Keller box method to investigate the characteristics of electrically conducting fluid over a permeable sheet in the presence of thermal radiation. They reported that skin friction coefficient reduces with uplifting mass transfer parameter. After that, Dogonchi and Ganji (2016) examined the thermal radiation effect on buoyancy flow due to a stretching sheet. Their results show that temperature of the fluid decreases with radiation parameter. Pal and Saha (2016) investigated the aspects of non-linear radiation and variable viscosity in a thin-liquid film induced by a time-dependent stretching sheet. They found that local Sherwood number is an increasing function of thermal radiation parameter. The effects of non-linear thermal radiation on flow and heat transfer of Sisko nanofluid along a non-linear stretched surface are investigated by Prasannakumara et al. (2017). Their study reveals that Sisko fluid parameter reduces the velocity profile. Khan et al. (2017) obtained the dual solutions of slip flow of nanofluid over a shrinked surface with thermal radiation. Moreover, Sreedevi et al. (2017) examined the heat transfer flow of nanofluid past a linear and non-linear stretching surface under the influence of chemical reaction and thermal radiation. Very recently, Soomro et al. (2018) studied the non-linear radiation and heat generation/absorption effects on stagnation-point flow past a moving surface. They used finite-difference approach and revealed that thermal radiation parameter rises the rate of heat transfer.

In the recent years, the investigation of magnetohydrodynamic (MHD) has increased impressive consideration because of its useful applications in various innovations, including MHD control generators, cooling of atomic reactors, and construction of heat exchangers, installation of nuclear accelerators, blood flow estimation procedures, and on the execution of a few different frameworks utilizing electrically conducting liquids. On the other hand, magnetic nanofluids have both the magnetic and fluid properties. In view of these applications, Ishak et al. (2006) presented the results for MHD flow of micropolar fluid along a wedge with variable magnetic field. Their study reveals that skin friction coefficient is an increasing function of wedge angle parameter. Latterly, Su et al. (2012) have studied MHD mixed convective flow past a permeable stretching wedge with Ohmic heating. Khan et al. (2014) discussed the combine effects of heat generation, chemical reaction, and thermal radiation on magneto-hydrodynamics flow over a wedge-shaped body. Their results show that thermal conductivity increases the fluid temperature. Furthermore, Nagendramma et al. (2015) investigated the unsteady flow of viscous fluid induced by a stretching wedge in the presence of transverse magnetic field. They showed that unsteadiness parameter declines the thermal boundary-layer thickness. Melting heat transfer mechanisms' MHD Falkner–Skan wedge flow of second-grade nanofluid is presented by Hayat et al. (2016). They noticed that wedge angle parameter rises the temperature of the fluid. In addition, Raju and Sandeep (2017) addressed the MHD flow of Casson fluid past a moving wedge in the presence of convective boundary conditions. They observed that Casson parameter rises the heat transfer rate. Ullah et al. (2017) numerically investigated the electrically conducting flow of Casson fluid along non-isothermal moving wedge with viscous dissipation. Their results show that in case of assisting, flow velocity of the fluid increases with higher Eckert number. In another article, Ullah et al. (2018). Unsteady MHD flow generated by a moving wedge in a nanofluid is studied by Alam et al. (2017). They reported that magnitude of the velocity rises with stronger magnetic parameter. In another investigation, Ali et al. (2017) obtained the similarity solution of MHD flow over a wedge in the presence of Buongiorno’s model. They found that thermophoresis parameter and Lewis number reduce the nanoparticle concentration profile. Moreover, Hsiao (Hsiao 2016a, b, 2017a, b) discussed the characteristics of heat transfer in MHD flow of electrically conducting fluids.

To the best of author’s knowledge, the investigation of transient MHD flow through a moving wedge in the presence of non-linear radiation, chemical reaction, and heat source/sink parameter has remained unexplored. Therefore, this phenomenon is discussed in this article. The novelty of the present study includes the following aspects:

• 1) Consideration of Falkner–Skan flow of a Williamson fluid past a static and moving wedge, the flow is subjected to classical Blasius problem.

• 2) Inclusion of thermal radiation is justified, since the flow and heat transport processes occur using this effect plays a significant role in industrial processes and space technology involving high operating temperatures so as to obtain high thermal efficiency.

• 3) Inclusion of chemical reaction term in the mass transport equation which is vital, since the fluids may be chemically reactive. It plays a vital role in the design of chemical processing equipment, processing of food, and cooling towers on the flow of heat and/or mass transfer over different surfaces.

To explore the problem of unsteady chemically reactive Williamson nanofluid flow induced by a wedge-shaped geometry with velocity slip, convective boundary conditions, and revised model, following steps have been carried out:

• (a) To solve the governing Williamson flow model including time-dependent momentum, energy, and concentration equations using significant numerical technique known as Runge–Kutta–Fehlberg method (RKF-45).

• (b) In addition, to investigate the flow field distribution such as velocity, temperature, and concentration across the boundary layer. Further investigation on system parameters effect of skin friction and local Nusselt number.

Mathematical model of flow

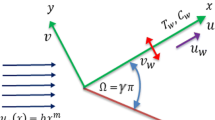
Consider unsteady, incompressible and MHD stagnation-point flow of a non-Newtonian nanofluids past a static/moving wedge. The nanofluid flow behavior is investigated in the presence of heat and mass transfer features by considering magnetic field effects. In this model of nanofluid, we incorporate the effects of thermophoresis and Brownian motion. It is assumed that stretching wedge has the velocity ${U_w}(x,t) = {\textstyle{{b{x^m}} \over {1 - ct}}}$ as well as the free stream velocity ${U_e}(x,t) = {\textstyle{{a{x^m}} \over {1 - ct}}},$ where $a$, $b$, $c$ , and $m$ are positive constants with $0 \le m \le 1$. Here, ${U_w}(x,t) > 0$ corresponds to a stretching wedge surface velocity and ${U_w}(x,t) < 0$ compares to a contracting wedge surface velocity. The wedge angle is assumed to be $\varOmega = \beta \pi$, where $\beta = \tfrac{2m}{m + 1}$ is related to the pressure gradient. An external time-dependent magnetic field $B(t) = \tfrac{{B_{0} }}{{\left( {1 - ct} \right)^{1/2} }}$ is applied normal to the wedge surface (see Fig. 1). It is also considered that the surface temperature ${T_w}(x,t)$ and concentration ${C_w}(x,t)$ at the surface of wedge are considered to be higher than the ambient temperature $T_{\infty } (T_{w} > T_{\infty } )$ and ambient concentration $C_{\infty } (C_{w} > C_{\infty } ),$ respectively.

Fig. 1

Physical sketch of the flow model

With the above assumptions and using boundary-layer approximations, the governing equations for the Williamson fluid flow are given by:

Continuity equation:

$$\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}x}} + \frac{{{\mathbf{\partial }}v}}{{{\mathbf{\partial }}y}} = 0.$$

(1)

Momentum equation:

$$\begin{array}{ccccc}\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = & \frac{{\partial {U_e}}}{\partial t} + {U_e}\frac{{\partial {U_e}}}{\partial x} + \nu \frac{{{\partial^2}u}}{{\partial {y^2}}}\left[ {{\beta^* } + (1 - {\beta^* }){{\left( {1 - \varGamma \frac{\partial u}{\partial y}} \right)}^{ - 1}}} \right]\\ & + \nu \varGamma \left( {\frac{\partial u}{\partial y}} \right)\left( {\frac{{{\partial^2}u}}{{\partial {y^2}}}} \right)\left[ {(1 - {\beta^* }){{\left( {1 - \varGamma \frac{\partial u}{\partial y}} \right)}^{ - 2}}} \right] - \frac{{\sigma {B^2}\left( t \right)}}{\rho }\left( {u - {U_e}} \right).\end{array}$$

(2)

Energy equation:

$$\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{m} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \left[ {D_{B} \frac{{{\mathbf{\partial }}C}}{{{\mathbf{\partial }}y}}\frac{{{\mathbf{\partial }}T}}{{{\mathbf{\partial }}y}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] + \frac{{16\sigma^{ * } }}{{3k^{ * } \rho c_{p} }}\frac{\partial }{\partial y}\left( {T^{3} \frac{{{\mathbf{\partial }}T}}{{{\mathbf{\partial }}y}}} \right).$$

(3)

Concentration equation:

$$\frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{B} \frac{{{\mathbf{\partial }}^{2} C}}{{{\mathbf{\partial }}y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - k_{c} \left( {C - C_{\infty } } \right).$$

(4)

With boundary conditions:

$$\begin{array}{ccccc}u = & {U_w} + {U_{\rm slip}},{\rm{ }}v = 0,{\rm{ }} - k\frac{\partial T}{\partial y} = {h_f}({T_w} - T),{\rm{ }}{D_B}\frac{\partial C}{\partial y} + \frac{D_T}{T_\infty }\frac{\partial T}{\partial y} = 0{\rm{ at }}y = 0,\\u \to & {U_e},{\rm{ }}T \to {T_\infty },{\rm{ }}C \to {C_\infty }{\rm{ as }}y \to \infty .\end{array}$$

(5)

The partial slip velocity $U_{\text{slip}}$ for Williamson fluid model in the problem can be defined as:

$$U_{\text{slip}} = l\frac{\partial u}{\partial y}\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \varGamma \frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}y}}} \right)^{ - 1} } \right],$$

(6)

where $l$ represents the slip length having dimension of length.

To convert the PDEs into ODEs, we introduce the following local similar transformations:

$$\eta = y{\left( {\frac{{(m + 1){U_e}}}{2\nu x}} \right)^{0.5}},{\rm{ }}\psi (x,y,t) = {\left( {\frac{{2\nu x{U_e}}}{m + 1}} \right)^{0.5}}f(\eta ),{\rm{ }}{\theta_w} = \frac{T_w}{T_\infty },{\rm{ }}\theta (\eta ) = \frac{{T - {T_\infty }}}{{{T_w} - {T_\infty }}},{\rm{ }}\phi (\eta ) = \frac{{C - {C_\infty }}}{C_\infty },$$

(7)

where $\psi$ indicates the stream function that satisfies the equation of continuity with:

$$\left( {u,v} \right) = \left( {\frac{\partial \psi }{\partial y}, - \frac{\partial \psi }{\partial x}} \right).$$

(8)

Thus, the transformed non-linear momentum, energy, and concentration equations can be written as:

$$\begin{array}{*{20}c} {\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - Wef^{\prime\prime}} \right)^{ - 2} } \right]f^{\prime\prime\prime} + ff^{\prime\prime} + \beta \left\{ {1 - (f^{\prime})^{2} } \right\}} \\ { - A\left\{ {f^{\prime} + \tfrac{\eta }{2}f^{\prime\prime} - 1} \right\} - M\left\{ {1 - f^{\prime}} \right\} = 0,} \\ \end{array}$$

(9)

$$\theta^{\prime\prime} + \mathop {\Pr }\limits f\theta^{\prime} - \mathop {\Pr }\limits \frac{A}{2}\eta \theta^{\prime} + \mathop {\Pr }\limits {N}_{\rm b}\theta^{\prime}\phi^{{^{\prime } }} + \mathop {\Pr }\limits {N}_{\rm T}\left( {\theta^{\prime}} \right)^{2} + \frac{4}{{3N_{R} }}\frac{d}{d\eta }\left[ {\left( {1 + \left( {\theta_{w} - 1} \right)\theta } \right)^{3} \theta^{\prime}} \right] - \mathop {\Pr }\limits Q\theta = 0,$$

(10)

$$\phi^{\prime\prime} + {\rm Sc}f\phi^{\prime} - {\rm Sc}\frac{A}{2}\eta \phi^{\prime} + \frac{{N}_{\rm T}}{{N}_{\rm b}}\theta^{\prime\prime} - {\rm Sc}\gamma_{1} \phi = 0,$$

(11)

and the boundary conditions become:

$$\begin{aligned} f(0) = & 0,f^{\prime}(0) = \lambda + \delta f^{\prime\prime}(0)\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - Wef^{\prime\prime}(0)} \right)^{ - 1} } \right], \\ \theta^{{^{\prime } }} (0) = & - \gamma \left\{ {1 - \theta (0)} \right\}, \, {N}_{\rm b}\phi^{\prime}(0) + {N}_{\rm T}\theta^{{^{\prime } }} (0) = 0, \\ \end{aligned}$$

(12)

$$f^{\prime}(\infty ) \to 1, \, \theta (\infty ) \to 0, \, \phi (\infty ) \to 0.$$

In the above equations, prime denotes differentiation with respect to $\eta$ and $We\left( { = \sqrt {\tfrac{{\varGamma^{2} (m + 1)U_{e}^{3} }}{2\nu x}} } \right)$ is the local Weissenberg number, $\Pr \left( { = \tfrac{\nu }{{\alpha_{m} }}} \right)$ the Prandtl number, $A\left( { = \tfrac{c}{{\left( {m + 1} \right)ax^{m - 1} }}} \right)$ the unsteadiness parameter, $\beta \left( { = \tfrac{2m}{m + 1}} \right)$ the wedge angle parameter, $\lambda \left( { = \tfrac{{_{b} }}{a}} \right)$ the velocity ratio parameter, $M\left( { = \tfrac{{\rho B_{0}^{2} }}{{\rho ax^{m - 1} }}} \right)^{1/2}$ the magnetic field parameter, ${\text{Sc}}\left( { = \tfrac{\nu }{{D_{B} }}} \right)$ the Schmidt number, ${{{N}_{\rm T}}}\left( { = \tfrac{{\tau D_{T} (T_{w} - T_{\infty } )}}{{\alpha_{m} T_{\infty } }}} \right)$ the thermophoresis parameter, ${{{N}_{\rm b}}}\left( { = \tfrac{{\tau D_{B} C_{\infty } }}{{\alpha_{m} }}} \right)$ the Brownian motion parameter, $\theta_{w} \left( { = \tfrac{{T_{w} }}{{T_{\infty } }}} \right)$ the temperature ratio parameter, $N_{\text{R}} \left( { = \tfrac{{kk^{ * } }}{{4\sigma^{ * } T_{\infty }^{3} }}} \right)$ the radiation parameter, $Q\left( { = \tfrac{2Qx}{{\rho C_{p} (m + 1)U_{e} }}} \right)$ the heat generation/absorption parameter, $\delta \left( { = l\sqrt {\tfrac{{(m + 1)U_{e} }}{2\nu x}} } \right)$ the velocity slip parameter, $\gamma_{\begin{aligned} 1 \hfill \\ \end{aligned} } \left( { = \tfrac{{2k_{r} \nu }}{{(m + 1)U_{e}^{2} }}} \right)$ the chemical reaction parameter, and $\gamma \left( { = \tfrac{{h_{f} }}{k}xRe^{ - 1/2} } \right)$ the generalized Biot number.

The local skin friction coefficient $C_{fx} ,$ and the local Nusselt number ${\text{Nu}}_{x}$ are the quantities of physical interest which are defined as:

$$C_{fx} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} }}, \, Nu_{x} = \frac{{xq_{w} }}{{k(T_{w} - T_{\infty } )}},$$

(13)

where $\tau_{w}$ and $q_{w}$ denote the wall shear stress and wall heat flux, respectively, which are defined as:

$$\tau_{w} = \mu_{0} \frac{\partial u}{\partial y}\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \varGamma \frac{\partial u}{\partial y}} \right)^{ - 1} } \right], \, q_{w} = \left. { - k\left( {\frac{\partial T}{\partial y}} \right)} \right|_{y = 0} + \left. {q_{r} } \right|_{y = 0} .$$

(14)

In view of Eqs. (7), (13), and (14), we obtain the following dimensionless form:

$$\begin{aligned}\left( {2 - \beta } \right)^{1/2} Re^{1/2} C_{fx} = & f^{\prime\prime}(0)[\beta^{ * } + (1 - \beta^{ * } )\left\{ {1 - Wef^{\prime\prime}(0)} \right\}^{ - 1} ], \end{aligned}$$

(15)

$$\begin{aligned} \left( {2 - \beta } \right)^{1/2} Re^{ - 1/2} Nu_{x} = & - \theta^{\prime}(0)\left[ {1 + \frac{4}{{3N_{R} }}\left\{ {1 + \left( {\theta_{w} - 1} \right)\theta (0)} \right\}^{3} } \right],\end{aligned}$$

(16)

where $Re$ $\left( { = \tfrac{{xU_{e} }}{\nu }} \right)$ represents the local Reynolds number.

Description of numerical approach

The system of non-linear ordinary differential Eqs. (9)–(11) with the associated boundary conditions (12) is solved numerically using Runge–Kutta–Fehlberg method with shooting technique. It is known that the boundary value problem cannot be tackled on an infinite interval and it would be impractical to solve it for even a very large finite interval. To do this, the set of coupled non-linear ordinary differential equations subjected to the boundary conditions have been discretized to a system of seven simultaneous equations of first order by introducing new dependent variables:

$$f = X_{1} , \, f^{\prime} = X_{2} , \, f^{\prime\prime} = X_{3} , \, \theta = X_{4} , \, \theta^{\prime} = X_{5} , \, \phi = X_{6} , \, \phi^{\prime} = X_{7} .$$

$$\left( {\begin{array}{*{20}l} {X_{1}^{\prime } } \hfill \\ {X_{2}^{\prime } } \hfill \\ {X_{3}^{\prime } } \hfill \\ {X_{4}^{\prime } } \hfill \\ {X_{5}^{\prime } } \hfill \\ {X_{6}^{\prime } } \hfill \\ {X_{7}^{\prime } } \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {X_{2} } \hfill \\ {X_{3} } \hfill \\ {\tfrac{{ - X_{1} X_{3} - \beta (1 - X_{2}^{2} ) + A(X_{2} + \tfrac{\eta }{2}X_{3} - 1) + M^{2} \left( {1 - X_{2} } \right)}}{{\left[ {\beta ^{*} + (1 - \beta ^{*} )\left( {1 - WeX_{3} } \right)^{{ - 2}} } \right]}}} \hfill \\ {X_{5} } \hfill \\ {\tfrac{{ - \Pr X_{1} X_{5} + \Pr A\tfrac{\eta }{2}X_{5} - \Pr \left( {N_{{\text{b}}} X_{5} X_{7} + N_{{\text{T}}} X_{5}^{2} } \right) - \tfrac{4}{{N_{{\text{R}}} }}\left[ {\left( {\theta _{r} - 1} \right)\left\{ {1 + \left( {\theta _{r} - 1} \right)X_{4}^{2} } \right\}} \right]X_{5}^{2} + \Pr QX_{4} }}{{\left[ {1 + \tfrac{4}{{3NR}}\left[ {\left\{ {1 + \left( {\theta _{r} - 1} \right)X_{4} } \right\}^{3} } \right]} \right]}}} \hfill \\ {X_{7} } \hfill \\ { - {\text{Sc}}X_{1} X_{7} + {\text{Sc}}A\tfrac{\eta }{2}X_{7} + \tfrac{{N_{{\text{T}}} }}{{N_{{\text{b}}} }}X_{5}^{\prime } + {\text{Sc}}\gamma _{1} X_{6} } \hfill \\ \end{array} } \right)$$

(17)

and initial conditions:

$$\left( {\begin{array}{*{20}l} {X_{1} \left( 0 \right)} \hfill \\ {X_{2} \left( 0 \right)} \hfill \\ {X_{2} \left( \infty \right)} \hfill \\ {X_{5} \left( 0 \right)} \hfill \\ {X_{4} \left( \infty \right)} \hfill \\ {N_{{\text{T}}} X_{5} \left( 0 \right) + N_{{\text{b}}} X_{7} \left( 0 \right)} \hfill \\ {X_{6} \left( \infty \right)} \hfill \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} 0 \hfill \\ {\lambda + \delta X_{3} \left( 0 \right)\left[ {\beta ^{*} + (1 - \beta ^{*} )\left( {1 - WeX_{3} (0)} \right)^{{ - 2}} } \right]} \hfill \\ 1 \hfill \\ { - \gamma \left( {1 - X_{4} (0)} \right)} \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right).$$

(18)

For the current problem, we took the step size $\Delta \eta = 0.001$ and $\eta_{\infty } = 6$ accuracy within a tolerance level of $10^{ - 6}$.

Interpretation of results

The numerical computations for the non-linear ordinary differential Eqs. (9)–(11) subject to boundary conditions (12) are obtained through RKF fourth–fifth order of integration process. To explore the results, the numerical results are carried out for changed values of dimensionless governing parameters on the flow, heat and mass transfer of unsteady Williamson fluid flow past a wedge-shaped geometry. For numerical computations, we fix the non-dimensional quantities as ${\text{We}} = 1.0;$ $\beta^{ * } = 0.1;$ $\beta = 1.0;$ $\Pr = 5.0;$ ${\text{Sc}} = 2.0;$ $M = 1.0;$ ${{{N}_{\rm T}}} = 0.1;$ ${{{N}_{\rm b}}} = 0.1;$ $A = 0.02;$ ${\text{Nr}} = 0.1;$ ${\text{Tw}} = 1.3;$ $Q = 1.0;$ $\gamma = 0.7;$ $\delta = 0.2;$ $\lambda = 0.2;$ $\gamma_{1} = 1.0.$. These values are preserved as common in the whole analysis excluding the different values that are presented in the graphs.

Table 1 compares the values of local Nusselt number $Re^{ - 1/2} {\text{Nu}}_{x}$ for selected values of the Prandtl number and the wedge angle parameter with those obtained by White (2006), observed in close agreement. Additionally, Table 2 presents the numerical outcomes of local Nusselt number of varying values of the influential parameters. 

Table 1 Comparison results of $(2 - \beta )^{1/2 \, } Re^{ - 1/2} Nu$ for different values of $\Pr$ and $\beta$ when $\gamma = Nr = 10^{6} ,$ $\theta_{w} = 1.7,$ and $\beta^{ * } = We = \lambda = A = {N}_{\rm T} = {N}_{\rm b} = {\rm Sc} = \delta = \eta = 0$

Table 2 Numerical values of $(2 - \beta )^{1/2 \, } Re^{ - 1/2} Nu$ for distinct values of $A,$ $\beta ,$ $N_{R} ,$ $\theta_{w} ,$ $\gamma ,$ $\delta ,$ ${N}_{\rm b},$ ${N}_{\rm T},$ and ${\rm Sc}$ when $\beta^{ * } = 0.2,$ $We = 0.5,$ $\lambda = 0.1,$ and $\Pr = 5.0$

The main objective of this section is to investigate the effects of governing flow parameters on dimensionless velocity $f^{\prime}(\eta )$, temperature $\theta (\eta ),$ nanoparticle concentration $\phi \left( \eta \right)$, reduced skin friction coefficient $Re^{1/2} C_{fx},$ and local Nusselt number $Re^{ - 1/2} {\text{Nu}}_{x}$.

Figure 2 illustrates the impact of magnetic field parameter on velocity profiles $f^{\prime}(\eta )$ in both cases for static and moving wedge. It is clear that rising values of magnetic parameter $M$ develop the velocity profiles, but in case of stagnation-point flow, we get an opposite behavior. From this figure, it can be seen that higher values of magnetic parameter increases the velocity of the fluid for both the Falkner–Skan and Blasius flow cases. Physically, the drag force which is also known as Lorentz force has a tendency to resist the movement of the fluid occurs due to the applied transverse magnetic field, and leads for diminishing the velocity of the fluid.

Fig. 2

Effects of $M$ on velocity profile

The impact of wedge angle parameter $\beta$ on velocity profile $f^{\prime}(\eta )$ is portrayed in Fig. 3 for both moving and static wedge cases. This figure illustrates that velocity profile increases by uplifting the values of wedge angle for both cases. It can also be observed that velocity of the fluid is larger in case of Falkner–Skan flow i.e., moving wedge when compared to Blasius flow i.e., static wedge. It is necessary to mention here that $\lambda$ is the constant moving wedge parameter with $\lambda > 0$ and $\lambda < 0$ relates to a moving wedge with the same and reverse directions to the free stream velocity, respectively. It is important to note that wedge angle parameter $\beta$ is the Hartree pressure gradient parameter which is denoted by $\beta = \tfrac{\varOmega }{\pi }$ with the total wedge angle $\varOmega .$ On the analysis of White (2017), $\beta > 0$ indicates that pressure gradient is favorable or negative than the direction of the flow will be accelerating along the surface. It is also note that $\beta < 0$ shows that pressure gradient is adverse then the flow will be decelerating. Furthermore, $\beta = 0(m = 0)$ corresponds to boundary-layer flow past a horizontal flat surface and $\beta = 1(m = 1)$ relates to boundary-layer flow near the stagnation point of a vertical flat surface.

Fig. 3

Effects of $\beta$ on velocity profile

Figure 4 displays to investigate the impact of velocity slip parameter $\delta$ on velocity profiles $f^{\prime}(\eta )$ both moving and static wedge cases. From this plot, one can observed that velocity of the fluid grows for higher estimations of static and moving wedge. It is obvious that velocity slip parameter has significant effect on the solution. We get the no-slip condition for the case $\delta = 0.$. It is also observed that when slip occurs (for non-zero values of $\delta ),$ velocity of the fluid increases because under the slip condition; the pulling of the stretching wedge can be only partly transmitted to the fluid.

Fig. 4

Effects of $\delta$ on velocity profile

Figure 5 depicts to analyze the impact of temperature ratio parameter $T_{\text{w}}$ on temperature profile $\theta (\eta )$ . On the evidence of this picture, it is illustrated that rising values of $T_{\text{w}}$ corresponds to stronger wall temperate as compared to ambient fluid. The fluid temperature uplifting in this case. It is also observed that higher values of $T_{\text{w}}$ enhances the thermal boundary-layer thickness.

Fig. 5

Effects of $T_{w}$ on temperature profile

The variation of temperature profile $\theta (\eta )$ for varying values of radiation parameter $N_{\text{R}}$ is shown in Fig. 6. From this figure, it is observed that large values of $N_{\text{R}}$ give more heat to the fluid which causes to increase the temperature as well as thermal boundary-layer thickness. It is due to the fact that an increase in the thermal radiation parameter yields an increase in the interaction in the thermal boundary layer. Furthermore, the higher values of radiation parameter produce a large amount of heating to the nanofluid which rises the nanofluid temperature profile and thermal boundary-layer thickness. In view of this fact, the impact of radiation parameter becomes more prominent as $N_{\text{R}} \to \infty$ and the radiation effects can be ignored when $N_{\text{R}} = 0.$

Fig. 6

Effects of $N_{R}$ on temperature profile

To analyze the influence of Biot number $\gamma$ on temperature profile $\theta (\eta )$, Fig. 7 is plotted. On the behalf of this figure, one can predict temperature and thermal boundary-layer thickness increases. Mathematically, it can be deduced that for $\gamma = 0,$ the wedge’s surface is purely isolated. However, due to the large internal resistance of the wedge surface, the convective heat transfer does not occur from the wedge surface to the colder fluid which lies far away from the wedge.

Fig. 7

Effects of $\gamma$ on temperature profile

The impact of thermophoresis parameter $N_{\text{t}}$ is displayed in Fig. 8. From this figure, we can observe that temperature profiles $\theta (\eta )$ reduce due to greater impact of $N_{\text{t}}$ . It happens on the grounds that the bigger estimations of $N_{t}$ delivers the addition in the thermophoresis force which tend to move the nanoparticles from hot surface to the colder surface. Accordingly, the heat transfer rate boosts in the boundary-layer region for nanoparticles.

Fig. 8

Effects of $N_{t}$ on temperature profile

Figure 9 demonstrates the effect of heat generation/absorption parameter $Q$ on dimensionless temperature profile. For $Q = 0$, there is no heat generation/absorption parameter. It is evident from this figure as $Q$ rises, the temperature of the fluid and associated boundary-layer thickness enhanced significantly.

Fig. 9

Effects of $Q$ on temperature profile

The effect of Biot number $\gamma$ on dimensionless concentration profile is illustrated in Fig. 10. For physical point of view, the ratio of internal thermal resistance of a solid to the boundary-layer thermal resistance is known as Biot number. One can observed that as Biot number increases, the nanoparticle concentration is increased significantly.

Fig. 10

Effects of $\gamma$ on concentration profile

Figure 11 exhibits the dimensionless concentration profile for distinct values of thermophoresis parameter $N_{\text{t}}$ . From this figure, one can reveal that higher values of $N_{\text{t}}$ increase the concentration profile. It happens, because the stronger values of $N_{\text{t}}$ relates to enhancement of the thermophoresis force in the boundary-layer region which in results enhanced the nanoparticle concentration.

Fig. 11

Effects of $N_{t}$ on concentration profile

Figure 12 portrays the dimensionless concentration profile for varying values of Brownian motion parameter $N_{\text{b}}$ . It has been observed that an increases of $N_{\text{b}}$, the thermophoresis force is declined in the thermal boundary layer, in result concentration of boundary-layer thickness decreases. Consequently, the concentration profile of the nanoparticles is reduced with growth of $N_{\text{b}}$. This reduction is due to the nanoparticle of the high thermal conductivity being driven away from hotter wedge to the quiescent nanofluid.

Fig. 12

Effects of $N_{b}$ on concentration profile

The impact of chemical reaction parameter $\gamma_{1}$ on nanoparticle concentration profile is displayed in Fig. 13. On can explore that concentration profile increases with the growing effect of chemical reaction closer to the wedge surface, while reverse pattern is observed far away from the wedge surface. Physically, the rate of intermolecular mass transfer rises with chemical reaction which results in the volumetric increment in nanoparticles.

Fig. 13

Effects of $\gamma_{1}$ on concentration profile

Figure 14 represents the influence of Schmidt number ${\text{Sc}}$ on nanoparticle concentration profile. From this sketch, we observe that concentration profile of nanoparticles reduces by uplifting the value of Schmidt number. In physical point of view, Schmidt number is defined as the ratio of viscous diffusion rate to molecular mass diffusivity for augmenting ${\text{Sc}}$ caused a reduction in mass diffusion rate in the system which resulted in a decline greatly in nanoparticle concentration profile.

Fig. 14

Effects of ${\rm Sc}$ on concentration profile

Figure 15 presents the variation of skin friction coefficient for varying values of velocity slip parameter $\delta$ for the case $\left( {\beta = 0} \right)$ flow over a horizontal flat sheet and $\left( {\beta = 1} \right)$ flow past a vertical flat sheet against magnetic field parameter $M.$ This graph shows that for higher values of slip parameter, wall shear stress declines for both cases $\left( {\beta = 0{\text{ and }}\beta = 1} \right).$ It can be also observed that the effects of boundary-layer flow past a vertical flat sheet are more significant as compared to flow past a horizontal flat sheet.

Fig. 15

Variation of skin friction for various $\delta ,\beta ,M$

Figure 16 exhibits the influence of local Nusselt number for various values of Biot number $\gamma$ for both cases $\left( {\beta = 0{\text{ and }}\beta = 1} \right)$ against Prandtl number $\Pr$. This figure shows that heat transfer rate is higher for increasing values of Biot number and Prandtl number.

Fig. 16

Variation of Nusselt number for various $\gamma ,\beta ,\Pr$

Conclusions

The numerical solutions for unsteady MHD slip flow of Williamson nanofluid past a moving wedge with non-linear thermal radiation, heat generation/absorption, chemical reaction, and new mass flux condition are analyzed, and the following concluding remarks have been observed.

• Velocity profiles increases with the increase in magnetic parameter.

• Temperature profile increases with radiation parameter.

• Solutal concentration increases with Biot number and thermophoresis parameter, and it decreases with an increase in Brownian motion, Schmidt number, and chemical reaction parameter.

• Skin friction coefficient is reduced with increasing values of velocity slip parameter.

• The rate of heat transfer increases with increasing Biot number.