1 Introduction

The mechanical behaviors of conveying fluid carbon nanotubes need to be investigated in the presence of different external effects due to the wide range of their applications in various engineering components such as nanocontainers for gas storage [1] and drug delivery devices [2]. These kinds of researches conduct engineers to more accurate designs, and in recent years scholars have studied various aspects of this field. Here some of them are reviewed. Tang and Yang [3] conducted a study on post-buckling and nonlinear vibration of functionally graded pipes with internal fluid flow. They analyzed the influences of flow velocity, fluid density and the initial stress on the responses. In some experimental researches [4,5,6] which is the most reliable method, it was shown that in submicron scales, mechanical properties are size dependent, and consequently, classical theories cannot be used. Molecular dynamic simulation is a useful numerical method to predict nanostructures behavior, but it is often time-consuming. Therefore, non-classical theories are employed to consider the size effects and they can be calibrated by molecular dynamic simulation [7,8,9] to achieve more accurate responses. In addition, this material can be used in electrical devices such as those mentioned in Refs [10,11,12]. Nonlocal elasticity theory expresses the stress field at a reference point that is assumed to be dependent on the strains at all points in the body, not only at the reference point [13]. Many vibrational studies [14,15,16,17,18] have paid attention to nonlocal effects using nonlocal elasticity theory. Lee et al. [19] employed nonlocal elasticity theory to analyze the effects of flow velocity on the vibration frequency and mode shapes of the single-walled carbon nanotube conveying fluid flow. Their results showed that increasing the nonlocal parameter reduces the real component of frequency, and this behavior is more obvious in lower flow velocities and higher modes. Arani et al. [20, 21] developed cylindrical shell model to investigate the nonlinear and nonlocal vibration of embedded double-walled carbon and boron nitride nanotubes conveying fluid. They demonstrated that the critical flow velocity of proposed models is inversely related to the nonlocal parameter, so that an increase in the parameter reduces the critical flow velocity. Bahaadini and hosseini [22] worked on the free vibration and flutter instability of viscoelastic cantilever carbon nanotubes conveying fluid flow using nonlocal elasticity theory and slip boundary condition. Tang and Yang [23] employed the Euler–Bernoulli beam and Eringen’s theory to develop a model of conveying fluid nanotubes made of functionally graded materials along the both axial and radical directions. They proved this kind of materials distribution can dramatically change the natural frequency and structural stability of system. Wang et al. [24] studied the variations of natural frequency for cantilevered CNTs conveying fluid in the presence of magnetic field. They showed an increase in magnetic field makes the system stiffer so that critical flow velocity increases; moreover, in case the magnetic field parameter is greater than flow velocity, the CNT system becomes stable. Askari and Esmailzadeh [25] proposed a nonlocal Euler–Bernoulli beam model to examine vibration primary resonance and linear natural frequency of a CNT conveying fluid flow. Zhang et al. [26] studied the nonlocal and surface effects on longitudinal wave propagation of a piezoelectric nanoplate. Based on their result, increasing the wave number and scale coefficient can enhance the dispersion degree. Zhang et al. [27] considered the quantum effect in the study of fluid induced vibration of a nonlocal Euler–Bernoulli beam as a single-walled carbon nanotube. They showed that the root of mean-squared amplitude of the vibration estimated by quantum theory is lower than those of the law of energy equipartition. Some studies paid attention to pulsating fluid flow. Azrar et al. [28] analyzed the effects of fluid pulsation, nonlocal parameter and viscoelastic carbon nanotube parameters on dynamics instability of a SWCNT with internal fluid flow. Mirfazal et al. [29] modeled a double-walled carbon nanotube using higher-order sinusoidal shear order deformation shell theory and investigated the influence of pulsating flow on the dynamic behavior of system.

Although nonlocal elasticity theory is a size-dependent continuum mechanics theory which is appropriate to predict the vibrational behavior of nanostructures, the strain gradient theory and modified couple stress theory seem to have a better agreement with experimental reports [30]. Researches have widely paid attention to the effects of various parameters on the buckling and vibration characteristics of submicron shells based on the strain gradient theory [31,32,33,34,35] and the modified couple stress theory [36,37,38,39,40]. Here it is worth referencing some recent studies on static and dynamic analysis of carbon nanotubes conveying fluid flow in the framework of these theories. Zeighampour and Beni [41] conducted a study on the vibration analysis of double-walled carbon nanotubes conveying fluid using the modified couple stress theory (MCST) and Donnell’s shell model. Ansari et al. [42] studied the vibration behavior and instability of cylindrical microshells made of functionally graded (FG) materials and containing flowing fluid. They showed that increasing the value of material property gradient index of FGM microshell enhances the natural frequency and the critical flow velocity. Tang et al. [43] developed a nonlinear model for three-dimensional vibration of curved microtubes conveying fluid with clamped–clamped boundary conditions based on the modified couple stress theory. They considered the in-plane and out-of-plane bending motions, the axial motion and the twist angle of microtube in their model. Safarpour and Ghadiri [44] studied the critical velocity of viscous fluid flow and the free vibration analysis of a spinning single-walled carbon nanotube. Hu et al. [45] presented a nonlinear theoretical model to explore the possible size-dependent nonlinear responses based on the modified couple stress theory for cantilevered micropipes conveying fluid. Guo et al. [46] studied three-dimensional nonlinear vibration of cantilever micropipes conveying fluid. They proved increasing the material length scale enlarges the region of mass ratio for stable planar periodic motion. Yang et al. [47] analyzed nonlinear free vibration of a microtube conveying microfluid via modified couple stress theory. In this work, geometric nonlinearity due to midplane stretching was accounted.

According to Mindlin’s strain gradient theory, Sotudeh and Afrahim [48] studied the small-scale nonlinear vibration of micropipes conveying fluid. They proved material length scale and FG power index have significant influences on the fundamental natural frequency and fluid critical velocity. Ghorbanpour et al. [49] conducted a study on dynamic instability of a double-walled carbon nanotube with internal pulsating fluid flow based on sinusoidal shear deformation beam theory. They employed strain gradient and Gurtin–Morduch elasticity theories to capture the effects of size and surface, respectively. Ansari et al. [50] worked on the thermo mechanical vibration and instability of the functionally graded nanoshells in the presence of inner fluid flow. They [51] also considered the surface effect in the nonlinear vibration of conveying fluid nanoscale pipes. Ghazavi et al. [52] applied the second gradient theory on Euler–Bernoulli beam model to study nonlinear vibration of conveying fluid nanotubes for the first time. They indicated that considering the hardening effects, nonlinear instabilities are obtained more precisely. Li et al. [53] derived Timoshenko and Euler–Bernoulli beam models for microtubes conveying fluid flow using the nonlocal strain gradient theory (NSGT) in which both nonlocal and material length-scale effects are considered. Mohammadi et al. [54] developed FSDT cylindrical shell model based on NSGT for analyzing vibration behavior of CNTs. Mahinzare et al. [55] investigated the effects of size-dependent parameters of NSGT on critical flow velocity in CNTs with internal water flow. They indicated nonlocal parameter shrinks the stability region, whereas material length scale extends this region. In addition, current nanostructure can be used in smart systems [56, 57]. There are some cases in engineering designs that expose cylindrical shells to axial forces, so some researchers have paid attention to this condition. In an analytical study, Sheng and Wang [58] investigated the nonlinear vibration of cylindrical shell under the axial loads in a thermal environment. Jansen and Rolfes [59] studied the nonlinear vibration of laminated cylindrical shells subjected to static axial loads under different boundary conditions. Sofiyev [60] employed the shear deformation theory to analyze the vibration and stability of a conical FG shell subjected to compressive axial force. Liang and Su [61] developed a frequency–amplitude plane to obtain the stability regions for a single-walled carbon nanotube conveying pulsating fluid flow under tensile force. In this study, it was shown that axial tensile force significantly changes the natural frequency.

According to the above literature, some scientific papers studied the effects of fluid flow or axial external force on the dynamic instability of microbeams, microshells and other micronanostructures, separately. But there is no research on the vibration analysis of CNTs considering the effects of both viscous fluid flow and distributed axial load in one cylindrical nanoshell model; therefore, in this paper for the first time, an investigation is made on the dynamic stability analysis of a viscoelastic double-walled carbon nanotube conveying viscous fluid flow and subjected to distributed axial force in the framework of FSDT and modified couple stress theory. Using the Hamilton’s principle and GDQ solution method, critical values of axial force and flow velocity are determined; moreover, the effects of some factors such as the effect of flow velocity, axial load, mode number, length-to-radius ratio, radius-to-thickness ratio, visco-Pasternak foundation and boundary conditions are investigated on the critical pressure and natural frequency of the viscoelastic DWCNT with inner viscous fluid flow subjected to axial force.

2 Formulation

2.1 Governing equations of motion and corresponding boundary conditions

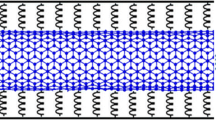
Figure 1 presents a schematic of DWCNT conveying viscous fluid subjected to the mechanical loading. Moreover, this figure demonstrates the effect of the visco-Pasternak foundation between the two walls and the surroundings of this structure. L, R and h denote the length, radius and the thickness of the DWCNT, respectively. In this study, the DWCNT is modeled as two cylindrical viscoelastic shells. According to the FSDT, the displacement field of each cylindrical shell along the three directions of x, θ, z is as follows:

$$\begin{aligned} U(x,\theta ,z,t) & = u(x,\theta ,t) + z\psi_{x} (x,\theta ,t)\,\,\,\,\, \\ V(x,\theta ,z,t) & = v(x,\theta ,t) + z\psi_{\theta } (x,\theta ,t) \\ W(x,\theta ,z,t) & = w(x,\theta ,t) \\ \end{aligned}$$
(1)

where u(x,θ,t), v(x,θ,t) and w(x,θ,t) represent the displacements in axial, circumferential and radial directions, respectively. \(\psi_{\theta }\) (x,θ,t) and ψx(x,θ,t) are the rotations about the circumferential and axial directions. In addition, strain tensor is expressed as:

Fig. 1
figure 1

A viscoelastic DWCNT conveying viscous fluid flow subjected to distributed axial force

Full size image
$$\begin{aligned} \varepsilon_{ij} & = \frac{1}{2}(\varLambda_{i,j} + \varLambda_{j,i} ),\,\,\,\,\,\,\,\,\,\,\, \\ \chi_{ij}^{s} & = \frac{1}{2}(\varphi_{i,j} + \varphi_{j,i} ),\,\,\,\,\,\, \\ m_{ij}^{s} & = 2l^{2} \mu (\hat{z})\chi_{ij}^{s} . \\ \end{aligned}$$
(2)

In Eq. (2) \({\text{u}}_{\text{i}}\) and \(\emptyset_{\text{i}}\) represent the components of displacement vector and infinitesimal rotation vector, respectively. Furthermore, \(l\) is the parameter which denotes the additional and independent material length-scale parameter which relates to the symmetric rotation gradients. The stress–strain equations in plane stress cases are written as follows for the elastic isotropic moderately thick cylindrical shell model:

$$\,\left\{ \begin{aligned} \sigma_{xx} \hfill \\ \sigma_{\theta \theta } \hfill \\ \sigma_{x\theta } \hfill \\ \sigma_{\theta z} \hfill \\ \sigma_{xz} \hfill \\ \end{aligned} \right\} = \left[ {\begin{array}{*{20}c} {\frac{E}{{1 - \nu^{2} }}} & {\frac{E\nu }{{1 - \nu^{2} }}} & 0 & 0 & 0 \\ {\frac{E\nu }{{1 - \nu^{2} }}} & {\frac{E}{{1 - \nu^{2} }}} & 0 & 0 & 0 \\ 0 & 0 & {\frac{E}{2(1 + \nu )}} & 0 & 0 \\ 0 & 0 & 0 & {\frac{E}{2(1 + \nu )}} & 0 \\ 0 & 0 & 0 & 0 & {\frac{E}{2(1 + \nu )}} \\ \end{array} } \right]\left\{ \begin{aligned} \varepsilon_{xx} \hfill \\ \varepsilon_{\theta \theta } \hfill \\ 2\varepsilon_{x\theta } \hfill \\ 2\varepsilon_{\theta z} \hfill \\ 2\varepsilon_{xz} \hfill \\ \end{aligned} \right\}$$
(3)

The principle of minimum potential energy is used in order to derive the equations of motion and the associated boundary conditions:

$$\int_{{t_{1} }}^{{t_{2} }} {(\delta T - \delta U + \delta W){\text{d}}t = 0}$$
(4)

where U and T are strain and kinetic energies, respectively. W is the work done by the external forces acting on the wall. The strain energy of a cylindrical shell includes classical strain energy U1 and non-classical strain U2. Therefore, the variation of strain energy would be written as follows:

$$\delta U = \delta U_{1} + \delta U_{2}$$
(5)

where

$$\begin{aligned} \delta U_{1} = \frac{1}{2}\iiint\limits_{V} {(\sigma_{ij} \delta \varepsilon_{ij} )}{\text{d}}V = \iint\limits_{A} {\left\{ {\begin{array}{*{20}l} {\left( {N_{xx} \frac{\partial }{\partial x}\delta u + M_{xx} \frac{\partial }{\partial x}\delta \psi_{x} } \right) + N_{\theta \theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta v + \frac{\delta w}{R}} \right)} \hfill \\ { + M_{\theta \theta } \frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{\theta } + Q_{xz} \left( {\delta \psi_{x} + \frac{\partial }{\partial x}\delta w} \right)} \hfill \\ { + N_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta u + \frac{\partial }{\partial x}\delta v} \right) + M_{x\theta } \left( {\frac{1}{R}\frac{\partial }{\partial \theta }\delta \psi_{x} + \frac{\partial }{\partial x}\delta \psi_{\theta } } \right)} \hfill \\ { + Q_{z\theta } \left( {\delta \psi_{\theta } + \frac{1}{R}\frac{\partial }{\partial \theta }\delta w - \frac{\delta v}{R}} \right)} \hfill \\ \end{array} } \right\}}R{\text{d}}x{\text{d}}\theta \hfill \\ \delta U_{2} = \frac{1}{2}\iiint\limits_{V} {(m_{ij}^{s} \delta \chi_{ij}^{s} )}{\text{d}}V = \iint\limits_{A} {\left\{ \begin{aligned} \hfill \\ \begin{array}{*{20}l} {\left( { - \frac{{Y_{\theta \theta } }}{{2R^{2} }} + \frac{{Y_{zz} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta u - \left( {\frac{{Y_{\theta z} }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta u - \left( {\frac{{Y_{zx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta u} \hfill \\ { + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2R}} \right)\frac{\partial }{\partial x}\delta v + \left( {\frac{{Y_{xz} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta v - \left( {\frac{{Y_{\theta x} }}{{2R^{2} }}} \right)()\frac{\partial }{\partial \theta }\delta v} \hfill \\ { + \left( {\frac{{Y_{\theta z} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta v + \left( {\frac{{Y_{xz} }}{{2R^{2} }}} \right)\delta v + \left( {\frac{{Y_{\theta z} }}{2R}} \right)\frac{\partial }{\partial x}\delta w - \left( {\frac{{Y_{\theta x} }}{2}} \right)\frac{{\partial^{2} }}{{\partial x^{2} }}\delta w} \hfill \\ { - \left( {\frac{{Y_{zx} }}{{2R^{2} }}} \right)\frac{\partial }{\partial \theta }\delta w + \left( {\frac{{Y_{x\theta } }}{{2R^{2} }}} \right)\frac{{\partial^{2} }}{{\partial \theta^{2} }}\delta w + \left( { - \frac{{Y_{\theta \theta } }}{2R} + \frac{{Y_{xx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta w} \hfill \\ { + \left( {\frac{{Y_{x\theta } }}{2}} \right)\frac{\partial }{\partial x}\delta \psi_{x} + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2R}} \right)\frac{\partial }{\partial \theta }\delta \psi_{x} - \left( {\frac{{T_{zx} }}{2R}} \right)\frac{{\partial^{2} }}{\partial \theta \,\partial x}\delta \psi_{x} } \hfill \\ { - \left( {\frac{{Y_{z\theta } }}{2R}} \right)\delta \psi_{x} - \left( {\frac{{Y_{x\theta } }}{2R}} \right)\frac{\partial }{\partial \theta }\delta \psi_{\theta } + \left( {\frac{{Y_{\theta \theta } }}{2R} - \frac{{Y_{xx} }}{2} + \frac{{Y_{zz} }}{2}} \right)\frac{\partial }{\partial x}\delta \psi_{\theta } } \hfill \\ { + \left( {\frac{{T_{z\theta } }}{2R}} \right)\frac{{\partial^{2} \delta \psi_{\theta } }}{\partial \theta \,\partial x} - \left( {\frac{{T_{z\theta } }}{{2R^{2} }}} \right)\frac{{\partial^{2} \delta \psi_{x} }}{{\partial \theta^{2} \,}} + \left( {\frac{{T_{xz} }}{2}} \right)\frac{{\partial^{2} \delta \psi_{\theta } }}{{\partial x^{2} }} - \frac{{Y_{xz} }}{2R}\delta \psi_{\theta } } \hfill \\ \end{array} \hfill \\ \end{aligned} \right\}}R{\text{d}}x{\text{d}}\theta \hfill \\ \end{aligned}$$
(6)

where classical and non-classical force and momentum are defined as below:

$$\begin{aligned} (N_{xx} ,N_{\theta \theta } ,N_{x\theta } ) & = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } ){\text{d}}z,} \\ (M_{xx} ,M_{\theta \theta } ,M_{x\theta } ) & = \int_{ - h/2}^{h/2} {(\sigma_{xx} ,\sigma_{\theta \theta } ,\sigma_{x\theta } )z{\text{d}}z} , \\ (Q_{xz} ,Q_{z\theta } ) & = \int_{ - h/2}^{h/2} {k_{s} (\sigma_{xz} ,\sigma_{z\theta } ){\text{d}}z} , \\ (Y_{xx} ,Y_{\theta \theta } ,Y_{zz} ,Y_{x\theta } ,Y_{xz} ,Y_{z\theta } ) & = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } ){\text{d}}z,} \\ (T_{xx} ,T_{\theta \theta } ,T_{zz} ,T_{x\theta } ,T_{xz} ,T_{z\theta } ) & = \int_{ - h/2}^{h/2} {(m_{xx} ,m_{\theta \theta } ,m_{zz} ,m_{x\theta } ,m_{xz} ,m_{z\theta } )z{\text{d}}z} \\ \end{aligned}$$
(7)

Furthermore, the kinetic energy of a DWCNT can be expressed as:

$$\delta T = \int\limits_{Z} {\iint\limits_{A} {\rho \left\{ {\begin{array}{*{20}l} {\left( {\frac{\partial u}{\partial t} + z\frac{{\partial \psi_{x} }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta u + z\frac{\partial }{\partial t}\delta \psi_{x} } \right)} \hfill \\ { + \left( {\frac{\partial v}{\partial t} + z\frac{{\partial \psi_{\theta } }}{\partial t}} \right)\left( {\frac{\partial }{\partial t}\delta v + z\frac{\partial }{\partial t}\delta \psi_{\theta } } \right) + \left( {\frac{\partial w}{\partial t}} \right)\delta w} \hfill \\ \end{array} } \right\}}} R\,{\text{d}}z\,{\text{d}}x\,{\text{d}}\theta$$
(8)

The first variation of the corresponding work to the external mechanical loading is [62]:

$$\delta W_{1} = \iint\limits_{A} {\left[ {(\bar{F})\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x} + (\bar{F})\frac{\partial v}{\partial x}\frac{\partial \delta v}{\partial x}} \right]}R{\text{d}}x{\text{d}}\theta$$
(9)

where \(\bar{F} = F/2\pi R\) is the force per length unit of the shell circumference and the axial stress is uniformly distributed along the thickness. Figure 2 shows a schematic of the DWCNT under axial loading.

Fig. 2
figure 2

Geometry and coordinates of the DWCNT under axial loading

Full size image

Consider the fluid flow in a CNTRC cylindrical shell in which the flow is assumed to be axially symmetric, Newtonian and laminar [63]. By the well-known Navier–Stokes equation, the basic momentum governing equation of the flow is simplified as:

$$\rho_{b} \frac{{{\text{d}}V_{R} }}{{{\text{d}}t}} = - \frac{\partial P}{\partial R} + \frac{1}{R}\frac{{\partial \tau_{R\theta } }}{\partial \theta } - \frac{{\tau_{\theta \theta } }}{R} + \frac{{\partial \tau_{Rx} }}{\partial x}$$
(10)

In Eq. (10), P and \(\rho_{b}\) are pressure and mass density of the fluid, respectively. The fluid force acting on the SWCNT can be calculated from Eq. (10). Since the acceleration and the velocity of the SWCNT and fluid at the contact point are equal [63], there are below relations:

$$v_{R} = \frac{{{\text{d}}w}}{{{\text{d}}t}},\,\,\,\,\,\,\,\,\,\,\,\,\frac{\text{d}}{{{\text{d}}t}} = \frac{\partial }{\partial t} + v_{x} \frac{\partial }{\partial x}$$
(11)

where \(v_{x}\) is the mean flow velocity. In Eq. (11), shear stress (\(\tau\)) depends on the viscosity (\(\mu\)) which can be obtained as below:

$$\tau_{R\theta } = \frac{\mu }{R}\frac{{\partial V_{R} }}{\partial \theta },\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tau_{\theta \theta } = 2\mu \frac{{V_{R} }}{R},\,\,\,\,\,\,\,\,\,\,\,\,\tau_{Rx} = \mu \frac{{\partial V_{R} }}{\partial x}$$
(12)

Finally, using Eqs. (11) and (12) and combining them with Eq. (10), the pressure of fluid (\(\frac{\partial P}{\partial R}\)) will be obtained. The fluid flow work can be written as:

$$\delta W_{2} = \int_{0}^{2\pi } {\int_{0}^{L} {\frac{\partial P}{\partial R}} } R{\text{d}}x{\text{d}}\theta$$
(13)

The axial fluid velocity in the above relation can be written as:

$$v_{x} = v_{ave,slip} = VCF \times v_{ave,noslip}$$
(14)

where the modified dimensionless coefficient VCF may be defined as [64]:

$$VCF = (1 + aK_{n} ) \times \left[ {1 + 4\left( {\left( {\frac{{2 - \sigma_{v} }}{{\sigma_{v} }}} \right)\left( {\frac{{k_{n} }}{{1 + k_{n} }}} \right)} \right)} \right]$$
(15)

where the slip of flow from inner SWCNT is considered through the Knudsen number (\(k_{n}\)). Practically, it is supposed to be \(\sigma_{v}\) = 0.7; in addition, other parameters are:

$$a = a_{0} \frac{2}{\pi }(\tan^{ - 1} (a1k_{n}^{B} )),\quad a_{0} = \frac{64}{3\pi }\left( {1 - \frac{4}{b}} \right)^{ - 1} ,\quad \mu = \mu_{0} (1 + ak_{n} )^{ - 1}$$
(16)

In Eq. (16), \(\mu\) and \(\mu_{0}\) are fluid viscosity and bulk viscosity, respectively. The work done by Pasternak foundation, as the surrounding medium acting on the DWCNT, can be expressed as [41]:

$$\begin{aligned} \delta W_{3} & = \left\{ {K_{\text{w}} w + K_{\text{p}} \nabla^{2} w} \right\}\delta w\,R\,{\text{d}}V, \\ \nabla^{2} & = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} }}{{\partial \theta^{2} }} \\ \end{aligned}$$
(17)

in which KW and Kp are the Winkler and Pasternak coefficients, respectively. The energy dissipated by the dampers acting on DWCNT by the surrounding medium can be expressed as [41]:

$$\dot{\delta }D = \iiint\limits_{V} {\left\{ {C_{d} \frac{\partial w}{\partial t}\frac{\partial }{\partial t}\dot{\delta }w} \right\}R\,}{\text{d}}V$$
(18)

in which Cd is the damping constant. Now equations of motion and boundary conditions can be obtained by substituting Eqs. (6), (8), (9), (13), (17) and (18) into (4) and integrating by parts.

For inner nanotube:

$$\begin{aligned} & \delta u_{1} :\frac{{\partial N^{1}_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N^{1}_{x\theta } }}{\partial \theta } + \frac{1}{{2R^{2} }}\left( { - \frac{{\partial Y^{1}_{\theta \theta } }}{\partial \theta } + \frac{{\partial Y^{1}_{zz} }}{\partial \theta }} \right) + \frac{1}{2R}\frac{{\partial^{2} Y^{1}_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y^{1}_{\theta z} }}{{\partial \theta^{2} }} \\ & \quad = I^{1}_{0} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + I^{1}_{1} \frac{{\partial^{2} \psi_{1x} }}{{\partial t^{2} }} \\ & \delta v_{1} :\frac{{\partial N^{1}_{x\theta } }}{\partial x} + \frac{1}{R}\frac{\partial }{\partial \theta }N^{1}_{\theta \theta } + \frac{{Q^{1}_{z\theta } }}{R} + \frac{1}{2}\left\{ {\begin{array}{*{20}l} {\frac{1}{R}\frac{\partial }{\partial x}( - Y^{1}_{xx} + Y^{1}_{\theta \theta } )} \hfill \\ { - \frac{1}{{R^{2} }}\frac{{\partial Y^{1}_{\theta x} }}{\partial \theta } - \frac{{\partial^{2} Y^{1}_{xz} }}{{\partial x^{2} }} - \frac{{Y^{1}_{xz} }}{{R^{2} }} - \frac{1}{R}\frac{{\partial^{2} Y^{1}_{z\theta } }}{\partial \theta \,\partial x}} \hfill \\ \end{array} } \right\} \\ & \quad = \,I^{1}_{0} \left[ {\frac{{\partial^{2} v_{1} }}{{\partial t^{2} }}\,\,} \right] + I^{1}_{1} \left\{ {\frac{{\partial^{2} \psi_{1\theta } }}{{\partial t^{2} }}} \right\} \\ & \delta w_{1} :\frac{{\partial Q^{1}_{xz} }}{\partial x} + \frac{1}{R}\frac{{\partial Q^{1}_{z\theta } }}{\partial \theta } - \frac{{N^{1}_{\theta \theta } }}{R} - \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y^{1}_{\theta x} }}{{\partial \theta^{2} }} - \frac{1}{{2R^{2} }}\frac{{\partial Y^{1}_{zx} }}{\partial \theta } + \frac{1}{2R}\frac{{\partial Y^{1}_{\theta z} }}{\partial x} + \frac{{\partial^{2} Y^{1}_{x\theta } }}{{2\partial x^{2} }} \\ & \quad - \frac{1}{2R}\frac{{\partial^{2} }}{\partial \theta \,\partial x}(Y^{1}_{xx} - Y^{1}_{\theta \theta } ) - \varsigma_{1} v_{{_{x} }}^{2} \frac{{\partial^{2} w_{1} }}{{\,\partial x^{2} }} - \varsigma_{2} v_{x} \frac{{\partial w_{1} }}{\,\partial x} + \varsigma_{3} v_{x} \frac{{\partial^{3} w_{1} }}{{\,\partial x^{3} }} - K_{1} (w_{1} - w_{2} ) + \bar{F}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) \\ & \quad + K_{1p} \nabla^{2} (w_{1} - w_{2} ) - C_{1d} \left( {\frac{{\partial w_{1} }}{\partial t} - \frac{{\partial w_{2} }}{\partial t}} \right) = I^{1}_{0} \left( {\frac{{\partial^{2} w_{1} }}{{\partial t^{2} }}} \right) + \varsigma_{4} \frac{{\partial^{2} w_{1} }}{{\partial t^{2} }} - \varsigma_{5} v_{x} \frac{{\partial^{2} w_{1} }}{\,\partial x\partial t} - \varsigma_{6} \frac{{\partial w_{1} }}{\,\partial t} + \varsigma_{7} \frac{{\partial^{3} w_{1} }}{{\,\partial t\partial x^{2} }} \\ & \delta \psi_{1x} :\frac{{\partial M^{1}_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial M^{1}_{\theta \theta } }}{\partial \theta } - Q^{1}_{xz} + \frac{1}{2}\frac{{\partial Y^{1}_{\theta x} }}{\partial x} - \frac{1}{2R}\frac{\partial }{\partial \theta \,}(Y^{1}_{zz} - Y^{1}_{\theta \theta } ) + \frac{{Y^{1}_{zz} }}{R} + \frac{1}{2R}\frac{{\partial^{2} T^{1}_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} T^{1}_{\theta z} }}{{\partial \theta^{2} }} \\ & \quad = I^{1}_{1} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + I^{1}_{2} \frac{{\partial^{2} \psi_{1x} }}{{\partial t^{2} }} \\ & \delta \psi_{1\theta } :\frac{1}{R}\frac{{\partial M^{1}_{\theta \theta } }}{\partial \theta } + \frac{{\partial M^{1}_{x\theta } }}{\partial x} - Q^{1}_{z\theta } + \frac{1}{2}\frac{\partial }{\partial x}\left( {Y^{1}_{zz} - Y^{1}_{xx} + \frac{{T^{1}_{\theta \theta } }}{R}} \right) - \frac{1}{2}\frac{{\partial Y^{1}_{\theta x} }}{\partial \theta } + \frac{{Y^{1}_{xz} }}{2R} - \frac{1}{2R}\frac{{\partial^{2} T^{1}_{\theta z} }}{\partial \theta \,\partial x} - \frac{1}{2}\frac{{\partial^{2} T^{1}_{zx} }}{{\,\partial x^{2} }} \\ & \quad = I^{1}_{1} \left( {\frac{{\partial^{2} v_{1} }}{{\partial t^{2} }}} \right) + I^{1}_{2} \left( {\frac{{\partial^{2} \psi_{1\theta } }}{{\partial t^{2} }}} \right)\, \\ \end{aligned}$$
(19)

For outer nanotube:

$$\begin{aligned} & \delta u_{2} :\frac{{\partial N^{2}_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N^{2}_{x\theta } }}{\partial \theta } + \frac{1}{{2R^{2} }}\left( { - \frac{{\partial Y^{2}_{\theta \theta } }}{\partial \theta } + \frac{{\partial Y^{2}_{zz} }}{\partial \theta }} \right) + \frac{1}{2R}\frac{{\partial^{2} Y^{2}_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y^{2}_{\theta z} }}{{\partial \theta^{2} }} \\ & \quad = I^{2}_{0} \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + I^{2}_{1} \frac{{\partial^{2} \psi_{2x} }}{{\partial t^{2} }} \\ & \delta v_{2} :\frac{{\partial N^{2}_{x\theta } }}{\partial x} + \frac{1}{R}\frac{\partial }{\partial \theta }N^{2}_{\theta \theta } + \frac{{Q^{2}_{z\theta } }}{R} + \frac{1}{2}\left\{ {\begin{array}{*{20}l} {\frac{1}{R}\frac{\partial }{\partial x}( - Y^{2}_{xx} + Y^{2}_{\theta \theta } )} \hfill \\ { - \frac{1}{{R^{2} }}\frac{{\partial Y^{2}_{\theta x} }}{\partial \theta } - \frac{{\partial^{2} Y^{2}_{xz} }}{{\partial x^{2} }} - \frac{{Y^{2}_{xz} }}{{R^{2} }} - \frac{1}{R}\frac{{\partial^{2} Y^{2}_{z\theta } }}{\partial \theta \,\partial x}} \hfill \\ \end{array} } \right\} \\ & \quad = \,I^{2}_{0} \left[ {\frac{{\partial^{2} v_{2} }}{{\partial t^{2} }}} \right] + I^{2}_{1} \left\{ {\frac{{\partial^{2} \psi_{2\theta } }}{{\partial t^{2} }}} \right\} \\ & \delta w_{2} :\frac{{\partial Q^{2}_{xz} }}{\partial x} + \frac{1}{R}\frac{{\partial Q^{2}_{z\theta } }}{\partial \theta } - \frac{{N^{2}_{\theta \theta } }}{R} - \frac{1}{{2R^{2} }}\frac{{\partial^{2} Y^{2}_{\theta x} }}{{\partial \theta^{2} }} - \frac{1}{{2R^{2} }}\frac{{\partial Y^{2}_{zx} }}{\partial \theta } + \frac{1}{2R}\frac{{\partial Y^{2}_{\theta z} }}{\partial x} + \frac{{\partial^{2} Y^{2}_{x\theta } }}{{2\partial x^{2} }} + \bar{F}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial x^{2} }}} \right) \\ & \quad - \frac{1}{2R}\frac{{\partial^{2} }}{\partial \theta \,\partial x}(Y^{2}_{xx} - Y^{2}_{\theta \theta } ) - K_{1} (w_{2} - w_{1} ) + K_{1p} \nabla^{2} (w_{2} - w_{1} ) - C_{1d} \left( {\frac{{\partial w_{2} }}{\partial t} - \frac{{\partial w_{1} }}{\partial t}} \right) - K_{2} (w_{2} ) \\ & \quad + K_{2p} \nabla^{2} (w_{2} ) - C_{2d} \left( {\frac{{\partial w_{2} }}{\partial t}} \right) = I^{2}_{0} \left( {\frac{{\partial^{2} w_{2} }}{{\partial t^{2} }}} \right) \\ & \delta \psi_{2x} :\frac{{\partial M^{2}_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial M^{2}_{\theta \theta } }}{\partial \theta } - Q^{2}_{xz} + \frac{1}{2}\frac{{\partial Y^{2}_{\theta x} }}{\partial x} - \frac{1}{2R}\frac{\partial }{\partial \theta \,}(Y^{2}_{zz} - Y^{2}_{\theta \theta } ) + \frac{{Y^{2}_{zz} }}{R} + \frac{1}{2R}\frac{{\partial^{2} T^{2}_{zx} }}{\partial \theta \,\partial x} + \frac{1}{{2R^{2} }}\frac{{\partial^{2} T^{2}_{\theta z} }}{{\partial \theta^{2} }} \\ & \quad = I^{2}_{1} \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + I^{2}_{2} \frac{{\partial^{2} \psi_{2x} }}{{\partial t^{2} }} \\ & \delta \psi_{2\theta } :\frac{1}{R}\frac{{\partial M^{2}_{\theta \theta } }}{\partial \theta } + \frac{{\partial M^{2}_{x\theta } }}{\partial x} - Q^{2}_{z\theta } + \frac{1}{2}\frac{\partial }{\partial x}(Y^{2}_{zz} - Y^{2}_{xx} + \frac{{T^{2}_{\theta \theta } }}{R}) - \frac{1}{2}\frac{{\partial Y^{2}_{\theta x} }}{\partial \theta } + \frac{{Y^{2}_{xz} }}{2R} - \frac{1}{2R}\frac{{\partial^{2} T^{2}_{\theta z} }}{\partial \theta \,\partial x} - \frac{1}{2}\frac{{\partial^{2} T^{2}_{zx} }}{{\,\partial x^{2} }} \\ & \quad = I^{2}_{1} \left( {\frac{{\partial^{2} v_{2} }}{{\partial t^{2} }}} \right) + I^{2}_{2} \left( {\frac{{\partial^{2} \psi_{2\theta } }}{{\partial t^{2} }}} \right)\, \\ \end{aligned}$$
(20)

Also, associated boundary conditions for each nanotube are as below:

$$\begin{aligned} \delta u & = 0\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\left( {N_{xx} + \frac{1}{4R}\frac{{\partial Y_{xz} }}{\partial \theta }} \right)n_{x} + \left( {N_{x\theta } - \frac{{Y_{\theta \theta } - Y_{zz} }}{2R} + \frac{1}{4}\frac{{\partial Y_{xz} }}{\partial x} + \frac{1}{2R}\frac{{\partial Y_{\theta z} }}{\partial \theta }} \right)n_{\theta } = 0, \\ \delta v & = 0\,\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\left( {N_{x\theta } + \frac{{Y_{\theta \theta } - Y_{xx} }}{2R} - \frac{1}{2}\frac{{\partial Y_{xz} }}{\partial x} - \frac{1}{4R}\frac{{\partial Y_{\theta z} }}{\partial \theta }} \right)n_{x} + \left( {N_{\theta \theta } - \frac{1}{4R}\frac{{\partial Y_{\theta z} }}{\partial x} - \frac{{Y_{\theta x} }}{2R}} \right)n_{\theta } = 0, \\ \delta w & = 0\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\,\left( {Q_{xz} + \frac{{Y_{z\theta } }}{2R} + \frac{1}{2}\frac{{\partial Y_{x\theta } }}{\partial x} + \frac{1}{4R}\frac{{\partial (Y_{\theta \theta } - Y_{xx} )}}{\partial \theta }} \right)n_{x} + \left( {Q_{\theta z} - \frac{{Y_{zx} }}{2R} - \frac{1}{2R}\frac{{\partial Y_{x\theta } }}{\partial \theta } + \frac{1}{4}\frac{{\partial (Y_{\theta \theta } - Y_{xx} )}}{\partial x}} \right)n_{\theta } = 0, \\ \delta \psi_{x} & = 0\,\,\,\,\,or\,\,\,\,\,\,\,\,\left( {M_{xx} + \frac{1}{4R}\frac{{\partial T_{xz} }}{\partial \theta } + \frac{{Y_{x\theta } }}{2}} \right)n_{x} + \left( {M_{\theta x} + \frac{1}{4}\frac{{\partial T_{xz} }}{\partial x} + \frac{1}{2R}\frac{{\partial T_{\theta z} }}{\partial \theta } + \frac{{(Y_{\theta \theta } - Y_{zz} )}}{2}} \right)n_{\theta } = 0, \\ \delta \psi_{\theta } & = 0\,\,\,\,\,\,or\,\,\,\,\,\,\,\left( {M_{x\theta } - \frac{{(Y_{xx} - Y_{zz} )}}{2} - \frac{1}{4R}\frac{{\partial T_{\theta z} }}{\partial \theta } - \frac{1}{2}\frac{{\partial T_{xz} }}{\partial x} + \frac{{T_{\theta \theta } }}{2R}} \right)n_{x} + \left( {M_{\theta \theta } - \frac{{Y_{x\theta } }}{2} - \frac{1}{4}\frac{{\partial T_{\theta z} }}{\partial x}} \right)n_{\theta } = 0, \\ \end{aligned}$$
(21)

For example:

The clamped boundary conditions at x = 0, L:

$$u = v = w = \psi_{x} = \psi_{\theta } = 0$$
(22)

The simply supported boundary conditions at x = 0, L:

$$\begin{aligned} & v = w = \psi_{\theta } = 0, \\ & \left( {N_{xx} + \frac{1}{4R}\frac{{\partial Y_{xz} }}{\partial \theta }} \right) = 0,\,\,\,\,\left( {M_{xx} + \frac{1}{4R}\frac{{\partial T_{xz} }}{\partial \theta } + \frac{{Y_{x\theta } }}{2}} \right) = 0. \\ \end{aligned}$$
(23)

The free boundary conditions at x = 0, L:

$$\begin{aligned} \left( {N_{xx} + \frac{1}{4R}\frac{{\partial Y_{xz} }}{\partial \theta }} \right) & = 0,\,\,\,\,\left( {M_{xx} + \frac{1}{4R}\frac{{\partial T_{xz} }}{\partial \theta } + \frac{{Y_{x\theta } }}{2}} \right) = 0, \\ \left( {N_{x\theta } + \frac{{Y_{\theta \theta } - Y_{xx} }}{2R} - \frac{1}{2}\frac{{\partial Y_{xz} }}{\partial x} - \frac{1}{4R}\frac{{\partial Y_{\theta z} }}{\partial \theta }} \right) & = 0,\,\,\,\left( {Q_{xz} + \frac{{Y_{z\theta } }}{2R} + \frac{1}{2}\frac{{\partial Y_{x\theta } }}{\partial x} + \frac{1}{4R}\frac{{\partial (Y_{\theta \theta } - Y_{xx} )}}{\partial \theta }} \right) = 0, \\ \left( {M_{x\theta } - \frac{{(Y_{xx} - Y_{zz} )}}{2} - \frac{1}{4R}\frac{{\partial T_{\theta z} }}{\partial \theta } - \frac{1}{2}\frac{{\partial T_{xz} }}{\partial x} + \frac{{T_{\theta \theta } }}{2R}} \right) & = 0 \\ \end{aligned}$$
(24)

3 Solution method

Differential quadrature method (DQM) was presented by Bellman et al. [65, 66] in 1970s. In this method, the precision of results depends on the numbers of grid points. In the preliminary version, the weighting coefficients were established using an algebraic equation which limited the utilization of large numbers of grid points. Shu [67] introduced a new method using an explicit formula for the weighting coefficients with infinite number of grid points which is known as GDQ. Shu and Richards [68] employed a new domain decomposition technique that can be applied in multi-domain problems. In this article, GDQ method is used in order to solve the governing equations under different boundary conditions.

According to this method, the approximate r-th derivative of f(x) is obtained by discretizing rule in the form of the linear sum of the function values as follows [68]:

$$\left. {\frac{{\partial^{r} f(x)}}{{\partial x^{r} }}} \right|_{{x = x_{p} }} = \sum\limits_{j = 1}^{n} {C_{ij}^{(r)} f(x_{i} )}$$
(25)

where n represents the number of distributed points along the x-axis and “Cij” is the weighting coefficient calculated as below for the first-order derivative.

$$\begin{array}{*{20}l} {C_{ij}^{\left( 1 \right)} = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}} \hfill & {i,j = 1,2, \ldots ,n\,\,\,\,{\text{and}}\,\,\,\,i \ne j} \hfill \\ {C_{ij}^{\left( 1 \right)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( 1 \right)} } } \hfill & {i = j} \hfill \\ \end{array}$$
(26)

where

$$M\left( {x_{i} } \right) = \prod\limits_{j = 1,j \ne i}^{n} {\left( {x_{i} - x_{j} } \right)}$$
(27)

In addition, the weighting coefficients for higher-order derivatives are determined by the following relations:

$$\begin{array}{*{20}l} {C_{ij}^{\left( r \right)} = r\left[ {C_{ij}^{{\left( {r - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {r - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]} \hfill & {i,j = 1,2, \ldots ,n,i \ne j\,\,\,{\text{and}}\,\,\,2 \le r \le n - 1} \hfill \\ {C_{ii}^{\left( r \right)} = - \sum\limits_{j = 1,i \ne j}^{n} {C_{ij}^{\left( r \right)} } } \hfill & {i,j = 1,2, \ldots ,n\,\,\,{\text{and}}\,\,\,1 \le r \le n - 1} \hfill \\ \end{array}$$
(28)

For the free vibration of cylindrical shell analysis based on the first shear deformation theory, displacement field can be defined as follows due to the geometrical periodicity along \(\theta\) direction

$$\left\{ \begin{aligned} u(x,\theta ,t) \hfill \\ v(x,\theta ,t) \hfill \\ w(x,\theta ,t) \hfill \\ \psi_{x} (x,\theta ,t) \hfill \\ \psi_{\theta } (x,\theta ,t) \hfill \\ \end{aligned} \right\} = \sum\limits_{n = 1}^{\infty } {\left\{ {\begin{array}{*{20}l} {\bar{U}(x)\,\cos \,(n\theta )e^{i\omega t} } \hfill \\ {\bar{V}(x)\,\,\sin \,(n\theta )e^{i\omega t} } \hfill \\ {\bar{W}(x)\,\cos \,(n\theta )e^{i\omega t} } \hfill \\ {\bar{\varPsi }_{x\,} (x)\,\cos \,(n\theta )e^{i\omega t} } \hfill \\ {\bar{\varPsi }_{\theta } (x)\,\sin \,(n\theta )e^{i\omega t} } \hfill \\ \end{array} } \right\}}$$
(29)

Substituting Eqs. (29) into governing equations, the following equation is achieved:

$$\left( {[M]\{ \omega^{2} \} + [C]\{ \omega \} + [K]} \right)\left( \begin{aligned} \beta_{\text{b}} \hfill \\ \beta_{\text{d}} \hfill \\ \end{aligned} \right) = 0$$
(30)

Then GDQ is applied to the equations of motion and the boundary conditions to obtain the mass matrix [M], damping matrix [C] and stiffness matrix [K]. d and b indexes donate domain and boundary, respectively, and \(\beta\) shows the mode shape. A proper way for solving Eq. (30) is to rewrite it as follows:

$$\left\{ {\dot{Z}} \right\} = \left\{ A \right\}\left\{ Z \right\}$$
(31)

in which state vector Z and state matrix [A] are defined as:

$$Z = \left\{ \begin{aligned} d_{d} \hfill \\ \dot{d}_{d} \hfill \\ \end{aligned} \right\}\;{\text{and}}\;\left[ A \right] = \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {\left[ I \right]} \\ { - \left[ {M^{ - 1} K} \right]} & { - \left[ {M^{ - 1} C} \right]} \\ \end{array} } \right]$$
(32)

In Eq. (32), [0] and [I] are the zero and unit (identity) matrices, respectively. Eventually, the natural frequency and its mode shape are obtained.

4 Results and discussion

4.1 Validation

The obtained results of present study need to be validated by the reports of previous researches. Therefore, in this section the first three natural frequencies of simply supported one-layer homogeneous isotropic nanoshell are compared with ref [69]. These results are presented in Table 1. The comparison suggests that for both classical (l = 0) and modified couple stress (l = h) theories, achieved responses by generalized differential quadrature method (GDQM) are verified by those of [69]. As another validation in Table 2, the first dimensionless natural frequencies of the single-walled carbon nanotube with different thicknesses reported by [70] are compared with obtained responses of GDQM and Navier analytical method in the present research. As can be seen, numerical and analytical responses are in good accordance with ref [70].

Table 1 The comparison of the first three dimensionless natural frequencies of simply supported one-layer homogeneous isotropic nanoshells with different thicknesses. (L = 11.6 nm, L/R = 5, = KW = 0)
Full size table
Table 2 The comparison of the first dimensionless natural frequencies of single-walled carbon nanotube with different thicknesses (L = 11.6 nm, L/R = 5, KW = l=0 and n = 1)
Full size table

4.2 Convergence

In all figures and tables, \(K_{\text{w}} i \cdot o\), \(K_{\text{p}} i \cdot o\) and \(C_{\text{d}} i \cdot o\) are Winkler, Pasternak and damping coefficients of the inner and outer surfaces of DWCNT, respectively. In addition, Li, Lo, Ri, Ro, hi and ho are the inner and outer lengths, radiuses and thicknesses of cylindrical shell, respectively. Table 3 shows the natural frequency variations versus the number of grid points for a double-walled carbon nanotube. This table indicates that N = 19 is enough for getting the convergent results; therefore, more grid points are not required. Table 1 also shows that an increase in the fluid flow velocity and axial load reduces the natural frequency in clamped–clamped and simply supported boundary conditions.

Table 3 The effect of number of grid points on evaluating convergence of the natural frequency(GHz) of DWCNT with respect to boundary conditions (BCs) where \(L_{i}\)/\(R_{i}\) = 10, \(L_{o}\)/\(R_{o}\) = 12.5, \(h_{i}\) = \(R_{i}\)/10, \(h_{o}\) = \(R_{o}\)/10, \(l_{i}\) = \(R_{i}\)/3, \(l_{o}\) = \(R_{o}\)/3, \(K_{w} i.o\) = 1e10, \(K_{p} i.o\) = 10, \(C_{d} i.o\) = 100
Full size table

4.3 Parametric results

Table 4 provides some information on the effect of circumferential wave numbers, length-to-radius ratio and fluid flow velocity on natural frequency of a double-walled carbon nanotube conveying fluid under different boundary conditions. Increasing the modes of frequency leads to a considerable increase in natural frequency in both boundary conditions. This table also shows that an increase in the length-to-radius ratio is accompanied by decreasing the natural frequency due to a decrease in the rigidity of nanotube. Fluid flow velocity is the last parameter but not the least one which is investigated in Table 2, and results show its increase causes a decrease in the natural frequency in all modes, length-to-radius ratio and boundary conditions.

Table 4 The variations of first three natural frequencies versus flow velocity and length-to-radius ratio of a conveying fluid DWCNT where \(h_{i}\) = \(R_{i}\)/10, \(h_{o}\) = \(R_{o}\)/10, \(l_{i}\) = \(R_{i}\)/3, \(l_{o}\) = \(R_{o}\)/3, \(K_{\text{w}} i,o\) = 1e10, \(K_{\text{p}} i,o\) = 10, \(C_{d} i,o\) = 100 and \(F\) = 1.75(N)
Full size table

Table 5 shows the influences of circumferential wave numbers, radius-to-thickness and axial load on the natural frequency of a double-walled carbon nanotube conveying fluid. As can be seen, the effect of the circumferential wave numbers is similar to the previous table and frequency increases significantly in the second and third modes. Another result achieved from Table 3 is that an increase in the radius-to-thickness leads to a decrease in natural frequency under the different axial loads and boundary conditions. In addition, increasing the axial load reduces the frequency especially in the first mode.

Table 5 The variations of first three natural frequencies versus the axial load and radius-to-thickness of a conveying fluid DWCNT where \(L_{i}\)/\(R_{i}\) = 10, \(L_{o}\)/\(R_{o}\) = 12.5, \(l_{i}\) = \(R_{i}\)/3, \(l_{o}\) = \(R_{o}\)/3, \(K_{w} i,o\) = 1e10, \(K_{p} i,o\) = 10, \(C_{d} i,o\) = 100 and v = 100 m/s
Full size table

4.4 The effect of material length scale on the critical flow velocity and axial load

Figures 3 and 4 illustrate the effect of length-scale parameter on the natural frequency of a double-walled carbon nanotube conveying fluid. As can be seen, increasing the axial load natural frequency tends to decrease and eventually in a specific amount of load, known as the critical axial load, frequency drops to zero, and the buckling phenomenon occurs. These figures also show that an increase in the material length scale enhances the natural frequency and critical buckling load. Figure 5 shows the effect of length-scale parameter on the natural frequency and critical flow velocity (the velocity in which frequency becomes zero) of a double-walled carbon. This figure expresses that an increase in the length-scale parameter also enhances the critical flow velocity and stability region.

Fig. 3
figure 3

The variations of natural frequency versus the axial load of a conveying fluid DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(K_{\text{p}} i \cdot o\) = 10, \(C_{\text{d}} i \cdot o\) = 100, v = 100 and simply supported boundary conditions in different length scales

Full size image
Fig. 4
figure 4

The variations of natural frequency versus the axial load of a conveying fluid DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(K_{\text{p}} i \cdot o\) = 10, \(C_{\text{d}} i \cdot o\) = 100, v = 100 and clamped–clamped boundary conditions in different length scales

Full size image
Fig. 5
figure 5

The effect of material length scale on the critical flow velocity of a DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(K_{\text{p}} i \cdot o\) = 10, \(C_{\text{d}} i \cdot o\) = 100, F = 1 under different boundary conditions

Full size image

4.5 The effect of Winkler foundation on the critical flow velocity and axial load

Figures 6, 7 and 8 illustrate the effect of Winkler foundation on the critical flow velocity and critical axial load of a double-walled carbon nanotube conveying fluid. These figures show that an increase in the Winkler foundation constant is coupled with an increase in the critical axial load and critical flow velocity. Figures 6 and 7 show that the influence of Winkler foundation on the critical axial load increase is stronger, when the constants of foundation are smaller. Another notable point is related to boundary conditions, natural frequencies, critical flow velocities and critical axial loads which are greater under the clamped–clamped boundary conditions because its rigidity is greater than simply supported.

Fig. 6
figure 6

The variations of natural frequency versus the axial load of a conveying fluid DWCNT where \(K_{\text{p}} i \cdot o\) = 10, \(C_{\text{d}} i \cdot o\) = 100, v = 100 m/s under simply supported boundary conditions, with the different constants of Winkler foundation

Full size image
Fig. 7
figure 7

The variations of natural frequency versus the axial load of a conveying fluid DWCNT where \(K_{\text{p}} i \cdot o\) = 10, \(C_{\text{d}} i \cdot o\) = 100, v = 100, under clamped–clamped boundary conditions, with the different constants of Winkler foundation

Full size image
Fig. 8
figure 8

The effect of Winkler foundation on the critical flow velocity of a DWCNT where \(K_{\text{p}} i \cdot 10\) = 10, \(C_{\text{d}} i \cdot o\) = 100, P = 0.5, and under different boundary conditions

Full size image

4.6 The effect of Pasternak foundation on the critical flow velocity and axial load

Figures 9, 10 and 11 demonstrate the influence of Pasternak foundation on the critical flow velocity and critical axial load of a double-walled carbon nanotube conveying fluid. As can be seen in Figs. 9 and 10, an increase in the constant of Pasternak foundation increases the natural frequency and critical axial load. In simply supported boundary conditions, this increase is significantly stronger than clamped–clamped. Figure 11 shows that a similar trend occurs about the critical flow velocity, but the effect of foundation constants is more obvious in smaller constants, while the different foundation constants have almost equal effects on the critical axial load.

Fig. 9
figure 9

The variations of natural frequency versus axial load of a conveying fluid DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(C_{\text{d}} i \cdot o\) = 100, v = 100, under simply supported boundary conditions, with the different constants of Pasternak foundation

Full size image
Fig. 10
figure 10

The variations of natural frequency versus axial load of a conveying fluid DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(C_{\text{d}} i \cdot o\) = 100, v = 100 m/s, under clamped–clamped boundary conditions, with different constants of Pasternak foundation

Full size image
Fig. 11
figure 11

The effect of Pasternak foundation on the critical flow velocity of a DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(C_{\text{d}} i \cdot o\) = 100, F = 1, under different boundary conditions

Full size image

4.7 The effect of dampers on the critical flow velocity and axial load

Figures 12, 13 and 14 demonstrate the effect of dampers on the critical flow velocity and critical axial load of a double-walled carbon nanotube conveying fluid. It can be concluded from Figs. 12 and 13 that an increase in the dampers constant reduces the natural frequencies and critical axial loads, but decreasing the critical axial loads is more intense in the greater constants of dampers. Figure 14 shows that increasing the dampers constant leads the stability region to shrink and the natural frequency to decrease. These effects are more obvious in simply supported boundary conditions.

Fig. 12
figure 12

The variations of natural frequency versus axial load of a conveying fluid DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(K_{\text{p}} i \cdot o\) = 10, v = 100, under simply supported boundary conditions, with the different constants of dampers

Full size image
Fig. 13
figure 13

The variations of natural frequency versus the axial load of a conveying fluid DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(K_{\text{p}} i \cdot o\) = 10, v = 100, under clamped–clamped boundary conditions, with the different constants of dampers

Full size image
Fig. 14
figure 14

The effect of dampers on the critical flow velocity of a DWCNT where \(K_{\text{w}} i \cdot o\) = 1e10, \(K_{\text{p}} i \cdot o\) = 10, v = 0.5, and under different boundary conditions

Full size image

5 Conclusion

This paper investigates the influences of fluid flow velocity and distributed axial load on the dynamic stability and buckling analysis of a viscoelastic double-walled carbon nanotube conveying viscous fluid. These effects are considered in one cylindrical shell model simultaneously for the first time. The nanotube is modeled as two orthotropic moderately thick cylindrical shells. The effects of small size and structural damping are considered based on the modified couple stress and Kelvin–Voigt theories. The elastic medium between the inner and outer layers of double-walled nanotube is simulated using visco-Pasternak foundation. The viscous fluid and its related forces are applied to formulation by modified Navier–Stokes relation, considering the slip boundary condition and Knudsen number. Finally, according to Hamilton’s principle, the governing equations of motion and boundary conditions are derived and solved via both Navier and GDQM methods. The results show that the velocity of the viscous fluid flow, axial load, mode number, length-to-radius ratio, radius-to-thickness ratio, visco-Pasternak foundation and boundary conditions play an important role on the critical pressure and natural frequency of the viscoelastic DWCNT conveying viscous fluid flow and subjected to axial force.