1 Introduction

Nanotechnology is one of the most important and development frontiers in the modern science. It was originally used to define any work done on the molecular scale, or one billionth of a meter (nm or 10−9 m). Carbon nanotubes (CNTs) with nano scale dimension have been well-known over the past 15 years. It was first discovered by Iijima (1991), when he was studying the synthesis of fullerenes using electric arc discharge technique. Some unrivaled properties of CNTs are, chemical and thermal stability, extremely high tensile strength and elasticity, and high conductivity. And some amazingly characteristics of CNTs are, a SWCNT can be up to 100 times stronger than steel with the same weight, the Young’s Modulus of SWCNT is up to 1TPa, which is 5 times greater than steel (230 GPa) while the density is only 1.3 g/cm3 and the thermal conductivity (2,000 W/m K) is five times greater than that of copper (400 W/m K) (Terrones 2003). These over mentioned properties has made CNTs one of the best candidate materials for uses in various industrial applications, in stance, sensors, actuators, fluid storage, composite materials, coatings and films, microelectronics, biotechnology, battery, solar cell and water filter (Lim et al. 2010).

At nanometer length scale, the properties of a material such as its melting point, its electronic and optical properties will change. Sometimes, the classical theory cannot describe some phenomena of the material at atomic level. However, the change of these properties offers new opportunities for technological and commercial development and applications. There are two types of theories applied to calculate the stress in materials, one of them supposes that the stress at a defined point depends on the strain at the same point so it is named local elasticity theory but another one is assumes that the stress at a point is a function of strains at all points in the continuum therefore it is called nonlocal elasticity theory. Hitherto some different nonlocal elasticity theories are defined such as, Eringen, couple stress, modified couple stress and strain gradient. The Eringen’s nonlocal elasticity theory which was initiated by Eringen (1983), has been widely utilized to study the mechanical manners in the micron and nano scale structures. Strain gradient theory was proposed by Mindlin (1965) and improved by Lam et al. (2003). This theory includes three additional material length scale parameters for linear elastic isotropic materials. The MSGT has been used by many researchers in order to analyze size-dependent structures. For instance, Akgöz and Civalek (2013a, b) studied free vibration analysis of axially functionally graded tapered Bernoulli–Euler microbeams based on the modified couple stress theory. Ghorbanpour Arani et al. (2012) investigated nonlocal wave propagation in an embedded double-walled boron nitride nanotubes (DWBNNT) conveying fluid via strain gradient theory. Akgöz and Civalek (2013a, b) presented a size-dependent shear deformation beam model based on the strain gradient elasticity theory. Bending and vibration of functionally graded sinusoidal micro beams based on the strain gradient elasticity theory were carried out by Lei et al. (2013a). Analysis of micro-sized beams for various boundary conditions based on the strain gradient elasticity theory was investigated by Akgöz and Civalek (2012). They demonstrated that the bending values obtained by these higher-order elasticity theories have a significant difference with those calculated by the classical elasticity theory.

For the time being, the mechanical behaviors of beams are being studied by applying various beam theories. Euler–Bernoulli theory (EBT) which applied for slender beams is one of these theories but this is utilized in situation that the shear deformation effect is negligible. However, effects of shear deformation and rotary inertia become more prominent and cannot be ignored for moderately thick beams and vibration responses on higher modes. For achieving the higher accuracy in dynamic behaviors of beam structures, several higher-order shear deformation theories are such as parabolic (third-order) beam theory of Levinson (1981) and Reddy (1984), trigonometric beam theory of Touratier (1991), hyperbolic beam theory of Soldatos (1992), exponential beam theory of Karama et al. (2003), and a general exponential beam theory of Aydogdu (2009). Li et al. (2014) performed the comparison of various shear deformation theories for free vibration of laminated composite beams with general lay-ups. Thai and Vo (2012) carried out the a nonlocal SSDBT with application to bending, buckling, and vibration of nano beams.

Dynamic behavior of nano-tubes conveying fluid is one of the great important problem with the most applications in targeted drug delivery systems. Hence, there are many remarkable investigations on the vibration and dynamic behaviors of nano-tubes conveying fluid. Khodami Maraghi et al. (2013) presented the nonlocal vibration and instability of embedded DWBNNT conveying viscose fluid. They indicated that increasing flow velocity decreases system stability. Wang (2011) carried out a modified nonlocal beam model for vibration and stability of nanotubes conveying fluid. Kiani (2013) studied the effects of small-scale parameter, inclination angle, speed and density of the fluid flow on the maximum dynamic amplitude factors of longitudinal and transverse displacements. Recently, it is shown by Kaviani and Mirdamadi (2013) that considering the small-size effects of the flow field on the dynamic characteristics of CNTs conveying fluid is essential. They investigated wave propagation analysis of CNTs conveying fluid including slip boundary condition and strain/inertial gradient theory. Mirramezani et al. (2013) showed that based on their result, they could have developed an innovative model for one dimensional coupled vibrations of CNTs conveying fluid using slip velocity of the fluid flow on the CNT walls as well as utilizing size-dependent continuum theories to consider the size effects of nano-flow and nano-structure. However, it should be noted that all of the research mentioned above, have considered constant flow velocity. Actually, in many NEMS/MEMS, the flow inside the pipes and tubes becomes pulsative type due to power systems and alternative pressurized devices. Hence, dynamic analysis of CNTs conveying pulsating fluid is very significant and essential. The stability analysis of a SWCNT conveying pulsating and viscous fluid with nonlocal effect was investigated by Liang and Su (2013). They showed that decrease of nonlocal parameter and increase of viscous parameter both increases the fundamental frequency and critical flow velocity. Ghorbanpour Arani et al. (2014b) carried out the nonlocal surface piezoelasticity theory for dynamic stability of DWBNNTs conveying viscose fluid based on different theories. In this study DIR of EBT, Timoshenko beam theory (TBT) and cylindrical shell theory are compared to each other. Nonlinear dynamic instability of DWCNT under periodic excitation is reported by Fu et al. (2009) based on EBB theory. Results show that DWCNT can be considered as single column when the vdW forces are sufficiently strong, also the area of DIR could be reduced by stiffness medium and increment of the aspect ratio of nanotubes. Ghorbanpour Arani et al. (2013) presented the nonlocal TBT for dynamic stability of DWBNNTs conveying nano-flow.

In macro structures, the surface free energy can be neglected in comparison with the bulk energy while in nano scale structures, the surface stress should be taken into account due to the high surface to volume ratio. Malekzadeh and Shojaee (2013) presented the surface and nonlocal effects on the nonlinear free vibration of non-uniform nano beams. They found that increase of the amplitude ratio causes reduction of the surface effects. Gheshlaghi and Hasheminejad (2011) investigated the surface effects on nonlinear free vibration of nano beams.

In some applications of nano-engineering, the investigation on dynamic characteristic of CNTs under magnetic field as a parametric controller is useful. Ghorbanpour Arani et al. (2014a) presented that the magnetic field is fundamentally an effective factor on increasing resonance frequency leading to stability of system. Wang et al. (2010) carried out the influences of longitudinal magnetic field on wave propagation in CNTs embedded in elastic matrix. The results obtained show that wave propagation in CNTs embedded in elastic matrix under longitudinal magnetic field appears in critical frequencies at which the velocity of wave propagation drops dramatically. Kiani (2014) investigated the vibration and instability of a SWCNT in a three-dimensional magnetic field. The obtained results reveal that the critical transverse magnetic field increases with the longitudinally induced magnetic field. Further, its value decreases as the effect of the small-scale parameter increases. He studied the effects of the longitudinal and transvers magnetic fields on the longitudinal and flexural frequencies.

Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and quickly return to their original state once the stress is removed. Lei et al. (2013c) presented the Dynamic characteristics of damped viscoelastic nonlocal EBT. Ghorbanpour Arani and Amir (2013) studied the electro-thermal vibration of visco-elastically coupled BNNT systems conveying fluid embedded on elastic foundation via strain gradient theory. Vibration of nonlocal Kelvin–Voigt viscoelastic damped Timoshenko beams is carried out by Lei et al. (2013b).

However, to date, no report has been found in the literature on dynamic stability of viscoelastic DWCNTs conveying pulsating fluid based on surface sinusoidal strain gradient theory. Motivated by these considerations, in order to improve optimum design of nanostructures, we aim to present a realistic model for dynamic instability of DWCNTs resting on visco-Pasternak medium by considering the viscoelastic property of the nanotubes. DWCNTs are placed in 2D magnetic field and modeled by SSDBT as well as strain gradient theory. Visco- DWCNTs are conveying pulsating fluid in which the effect of slip boundary condition is considered using Knudsen number correct factor. The Gurtin–Murdoch elasticity theory is applied for incorporation the surface stress effects. DQM is used in order to calculate the DIR of visco-DWCNTs induced by pulsating fluid. To confirm the validity of the present research, the results are compared with those reported in the literature. The effects of the nonlocal parameter, magnetic field, visco-Pasternak foundation, Knudsen number, surface stress and fluid velocity on the dynamic instability of visco-DWCNTs are elucidated.

2 Strain gradient elasticity theory

Unlike the modified couple stress theory of Yang et al. (2002) the strain gradient elasticity theory proposed by Lam et al. (2003) introduces additional dilatation gradient tensor and the deviatoric stretch gradient tensor in addition to the symmetric rotation gradient tensor. The strain energy U in a deformed isotropic linear elastic material occupying region Ω is given by Lei et al. (2013a), Ghorbanpour Arani et al. (2012):

$$U = \frac{1}{2}\int_{\Omega } {\left( {\sigma_{ij} \varepsilon_{ij} + p_{i} \gamma_{i} + \tau_{ijk}^{(1)} \eta_{ijk}^{(1)} + m_{ij} \chi_{ij} } \right)dV,}$$
(1)

where ε ij , γ i , \(\eta_{ijk}^{(1)}\), \(\chi_{ij}\) represent the strain, the dilatation gradient, the deviatoric stretch gradient and the symmetric rotation gradient tensors, respectively, which are defined by:

$$\varepsilon_{ij} = \frac{1}{2}\left( {\frac{{\partial u_{j} }}{{\partial x_{i} }} + \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right),$$
(2)
$$\gamma_{i} = \frac{{\partial \varepsilon_{mm} }}{{\partial x_{i} }},$$
(3)
$$\eta_{ijk}^{(1)} = \frac{1}{3}\left( {\frac{{\partial \varepsilon_{jk} }}{{\partial x_{i} }} + \frac{{\partial \varepsilon_{ki} }}{{\partial x_{j} }} + \frac{{\partial \varepsilon_{ij} }}{{\partial x_{k} }}} \right) \,-\, \frac{1}{15}\left[ {\delta_{ij} \left( {\frac{{\partial \varepsilon_{mm} }}{{\partial x_{k} }} + 2\frac{{\partial \varepsilon_{mk} }}{{\partial x_{m} }}} \right)\,+\,\delta_{jk} \left( {\frac{{\partial \varepsilon_{mm} }}{{\partial x_{i} }} + 2\frac{{\partial \varepsilon_{mi} }}{{\partial x_{m} }}} \right)} \right. +\,\left. {\delta_{ki} \left( {\frac{{\partial \varepsilon_{mm} }}{{\partial x_{j} }} + 2\frac{{\partial \varepsilon_{mj} }}{{\partial x_{m} }}} \right)} \right],$$
(4)
$$\chi_{ij} = \frac{1}{2}\left( {e_{ipq} \frac{{\partial \varepsilon_{qj} }}{{\partial x_{p} }} + e_{jpq} \frac{{\partial \varepsilon_{qi} }}{{\partial x_{p} }}} \right),$$
(5)

where u i , δ ij and e ijk are the displacement vector, the knocker delta and the alternate tensor, respectively. The classical stress tensor, σ ij , the higher-order stresses, p i , \(\tau_{ijk}^{(1)}\) and m ij are given by:

$$\sigma_{ij} = E\delta_{ij} \varepsilon_{mm} + 2G\left( {\varepsilon_{ij} - \frac{1}{3}\varepsilon_{mm} \delta_{ij} } \right),$$
(6)
$${\text{p}}_{i} = 2l_{0}^{2} G\gamma_{i},$$
(7)
$$\tau_{ijk}^{(1)} = 2l_{1}^{2} G\eta_{ijk}^{(1)},$$
(8)
$$m_{ij} = 2l_{2}^{2} G\chi_{ij},$$
(9)

where E and G are the bulk modulus and the shear modulus, respectively, (l 0, l 1, l 2) are independent material length scale parameters.

2.1 Surface effect theory

In nano structure such as nanotubes and nano plates, the ratio of surface to volume is high, therefore the surface effect should be considered. The classical constitutive relation of the surface can be calculated as given by Gurtin and Murdoch (1975, 1978). Hence the classical stress tensor related to the surface, σ s, the higher-order stresses of surface, \({\text{p}}_{i}^{s}\), \(\tau_{ijk}^{s(1)}\) and \(m_{ij}^{s}\) can be expressed as Malekzadeh and Shojaee (2013):

$$\sigma^{s} = \tau_{s} + E_{s} \varepsilon_{x}^{s},$$
(10)
$${\text{p}}_{i}^{s} = 2l_{0}^{2} G_{s} \gamma_{i}^{s},$$
(11)
$$\tau_{ijk}^{s(1)} = 2l_{1}^{2} G_{s} \eta_{ijk}^{s(1)},$$
(12)
$$m_{ij}^{s} = 2l_{2}^{2} G_{s} \chi_{ij}^{s},$$
(13)

where τ s , E s and G s , the residual surface tension in the axial direction, the surface elastic modulus and surface shear modulus.

2.2 Viscoelastic SSDBT

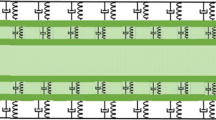
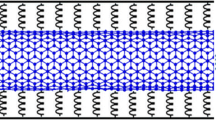
A schematic of visco-DWCNT conveying pulsating fluid embedded in visco Pasternak foundation under 2D magnetic field is shown in Fig. 1. The displacement fields of DWCNTs based on SSDBT can be described as Simsek and Reddy (2013):

$$u_{x} (x,z,t) = u(x,t) - z\frac{\partial w(x,t)}{\partial x} + \Phi (z)\varphi (x,t),$$
(14a)
$$u_{y} (x,z,t) = 0,$$
(14b)
$$u_{z} (x,z,t) = w(x,t),$$
(14c)
$$\varphi (x,t) = \frac{\partial w(x,t)}{\partial x} - \phi (x,t),$$
(14d)
$$\Phi (z) = \frac{h}{\pi }\sin \left( {\frac{\pi z}{h}} \right),$$
(14e)

where u and w are the axial and the transverse displacement of any point on the neutral axis, t denotes time φ and ϕ are the transverse shear strain of any point on the neutral axis and the total bending rotation of the cross-sections at any point on the neutral axis. \(\Phi (z)\) is a function of z, that characterizes the transverse shear and stress distribution along the thickness of the beam.

Fig. 1
figure 1

a Schematic of DWCNT conveying pulsating fluid embedded in visco Pasternak foundation under 2D magnetic field. b Cross section of the nanotube

Full size image

All materials exhibit some viscoelastic response. According to Kelvin–Voigt (Lei et al. 2013b) at real life, nano structure mechanical properties depend on the time variation. This model represents, as the stress is released, the material gradually relaxes to its undeformed state. By considering this model, Young’s modulus, E, shear modulus, G, Young’s modulus of surface, E s and shear modulus of surface, G s , are as follows:

$$E^{*} = E\left( {1 + g\frac{\partial }{\partial t}} \right),$$
(15a)
$$E_{s}^{*} = E_{s} \left( {1 + g\frac{\partial }{\partial t}} \right),$$
(15b)
$$G^{*} = G\left( {1 + g\frac{\partial }{\partial t}} \right),$$
(15c)
$$G_{s}^{*} = G_{s} \left( {1 + g\frac{\partial }{\partial t}} \right).$$
(15d)

3 Formulation

The energy method is applied to derive equations of motion, in this study. Total potential energy \(\Pi\), is given by:

$$\Pi = U_{s} - (K + W),$$
(16)

U s , K and W indicate total strain energy, total kinetic energy and the total external work in DWCNTs system.

Hamilton’s principle is used to derive the motion equations of embedded DWCNTs conveying pulsating viscose fluid as follows:

$$\int\limits_{{t_{0} }}^{{t_{1} }} {\left[ {\delta U_{s} - \left( {\delta K_{nanotube} + \delta W_{fluid} + \delta W_{lorentz} +\,\delta W_{visco - pasternak} + \delta W_{vdw} } \right)} \right]} = 0.$$
(17)

3.1 Strain gradient theory and surface effect

The total strain energy is come to result by combining the strain gradient theory and the surface effect theory as follows:

$$\begin{aligned} {\text{U}}_{\text{s}} = {\text{U}}_{\text{s}}^{\text{b}} + {\text{U}}_{\text{s}}^{\text{s}} = & \frac{1}{2}\int_{\Omega } {\left( {\sigma_{ij} \varepsilon_{ij} + p_{i} \gamma_{i} + \tau_{ijk}^{(1)} \eta_{ijk}^{(1)} + m_{ij} \chi_{ij} } \right)dAdx} \\ & + \frac{1}{2}\int_{\Omega } {\left( {\sigma_{ij}^{s} \varepsilon_{ij}^{s} + p_{i}^{s} \gamma_{i}^{s} \tau_{ijk}^{s(1)} \eta_{ijk}^{s(1)} + m_{ij}^{s} \chi_{ij}^{s} } \right)} dSdx, \\ \end{aligned}$$
(18)

Here \({\text{U}}_{\text{s}}^{\text{b}}\) is the strain energy of bulk and \({\text{U}}_{\text{s}}^{\text{s}}\) is the strain energy of surface. Total strain energy is came into result step by step as follows.

By substituting Eq. (14) into Eq. (2), the strain is

$$\left( {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{x}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & { - 1} & 1 & { - 1} \\ 1 & { - 1} & 1 & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{\partial u}{\partial x}} \\ {z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{h}{\pi }\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{\partial \phi }{\partial x}\,f^{(\sin )} } \\ \end{array} } \right),$$
(19a)
$$\left( {\begin{array}{*{20}c} {\varepsilon_{xz} } \\ {\varepsilon_{xz}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \frac{1}{2} & { - \frac{1}{2}} \\ 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{\partial w}{\partial x}f^{{({ \cos })}} } \\ {\phi f^{{({ \cos })}} } \\ \end{array} } \right),$$
(19b)

where

$$f^{(\sin )} = \sin \left( {\frac{\pi z}{h}} \right),\,f^{{({ \cos })}} = \cos \left( {\frac{\pi z}{h}} \right).$$
(19c)

And from Eqs. (19) and (3), it results that

$$\left( {\begin{array}{*{20}c} {\gamma_{x} } \\ {\gamma_{x}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 1 & { - 1} & 1 & { - 1} \\ 1 & { - 1} & 1 & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ \end{array} } \right),$$
(20a)
$$\left( {\begin{array}{*{20}c} {\gamma_{z} } \\ {\gamma_{z}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - 1} & 1 & { - 1} \\ { - 1} & 1 & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right),$$
(20b)
$$\gamma_{y} = \gamma_{y}^{s} = 0.$$
(20c)

By applying Eqs. (19) and (4) gives

$$\left( {\begin{array}{*{20}c} {\eta_{111}^{(1)} } \\ {\eta_{111}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \frac{2}{5} & { - \frac{2}{5}} & \frac{2}{5} & { - \frac{2}{5}} & \frac{1}{5} & { - \frac{1}{5}} \\ \frac{2}{5} & { - \frac{2}{5}} & \frac{2}{5} & { - \frac{2}{5}} & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right),$$
(21a)
$$\left( {\begin{array}{*{20}c} {\eta_{113}^{(1)} } \\ {\eta_{113}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{131}^{(1)} } \\ {\eta_{131}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{311}^{(1)} } \\ {\eta_{311}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \frac{4}{15}} & \frac{8}{15} & { - \frac{8}{15}} \\ { - \frac{4}{15}} & \frac{4}{15} & { - \frac{4}{15}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right),$$
(21b)
$$\left( {\begin{array}{*{20}c} {\eta_{122}^{(1)} } \\ {\eta_{122}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{221}^{(1)} } \\ {\eta_{221}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {\eta_{212}^{(1)} } \\ {\eta_{212}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & \frac{1}{15} & { - \frac{1}{15}} \\ { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right),$$
(21c)
$$\left( {\begin{array}{*{20}c} {\eta_{133}^{(1)} } \\ {\eta_{133}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{331}^{(1)} } \\ {\eta_{331}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{313}^{(1)} } \\ {\eta_{313}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & { - \frac{4}{15}} & \frac{4}{15} \\ { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right),$$
(21d)
$$\left( {\begin{array}{*{20}c} {\eta_{223}^{(1)} } \\ {\eta_{223}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} {\eta_{232}^{(1)} } \\ {\eta_{232}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{322}^{(1)} } \\ {\eta_{322}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}l} \frac{1}{15} & { - \frac{2}{15}} & \frac{2}{15} \\ \frac{1}{15} & { - \frac{1}{15}} & \frac{1}{15} \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right),$$
(21e)
$$\left( {\begin{array}{*{20}c} {\eta_{333}^{(1)} } \\ {\eta_{333}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{333}^{(1)} } \\ {\eta_{333}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\eta_{333}^{(1)} } \\ {\eta_{333}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} \frac{1}{5} & { - \frac{2}{5}} & \frac{2}{5} \\ \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right).$$
(21f)

And by substituting Eq. (19) into Eq. (5) gives the non-zero symmetric rotation gradient tensor as

$$\left( {\begin{array}{*{20}c} {\chi_{xy} } \\ {\chi_{xy}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\chi_{yx} } \\ {\chi_{yx}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \frac{1}{2}} & \frac{1}{4} & { - \frac{1}{4}} \\ { - \frac{1}{2}} & \frac{1}{2} & { - \frac{1}{2}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right),$$
(22a)
$$\left( {\begin{array}{*{20}c} {\chi _{{yz}} } \\ {\chi _{{yz}}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\chi _{{zy}} } \\ {\chi _{{zy}}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} { - \frac{1}{4}} & { + \frac{1}{4}} \\ 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{\pi }{h}\frac{{\partial w}}{{\partial x}}{\mkern 1mu} f^{{(\sin )}} } \\ {\frac{\pi }{h}\phi {\mkern 1mu} f^{{(\sin )}} } \\ \end{array} } \right). $$
(22b)

By using Eqs. (19), (10), (6) and (15) the stresses are

$$\left( {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{x}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {E^{*} } & {E_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & { - 1} & 1 & { - 1} \\ 1 & { - 1} & 1 & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{\partial u}{\partial x}} \\ {z\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{h}{\pi }\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{\partial \phi }{\partial x}\,f^{(\sin )} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} 0 \\ {\tau_{s} } \\ \end{array} } \right),$$
(23a)
$$\left( {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{xz}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & { - 1} \\ 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{\partial w}{\partial x}\,f^{{({ \cos })}} } \\ {\phi\,f^{{({ \cos })}} } \\ \end{array} } \right).$$
(23b)

By considering Eq. (15) and substituting Eq. (20) into Eq. (11) and (7)

$$\left( {\begin{array}{*{20}c} {p_{x} } \\ {P_{x}^{s} } \\ \end{array} } \right) = 2l_{0}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} 1 & { - 1} & 1 & { - 1} \\ 1 & { - 1} & 1 & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ \end{array} } \right),$$
(24a)
$$\left( {\begin{array}{*{20}c} {p_{z} } \\ {P_{z}^{s} } \\ \end{array} } \right) = 2l_{0}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - 1} & 1 & { - 1} \\ { - 1} & 1 & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right).$$
(24b)

From Eqs. (21), (12), (8) and (15), the non-zero higher-order \(\tau_{ijk}^{(1)}\), \(\tau_{ijk}^{s(1)}\) are

$$\left( {\begin{array}{*{20}c} {\tau_{111}^{(1)} } \\ {\tau_{111}^{s(1)} } \\ \end{array} } \right) = 2l_{1}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \frac{2}{5} & { - \frac{2}{5}} & \frac{2}{5} & { - \frac{2}{5}} & \frac{1}{5} & { - \frac{1}{5}} \\ \frac{2}{5} & { - \frac{2}{5}} & \frac{2}{5} & { - \frac{2}{5}} & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right),$$
(25a)
$$\left( {\begin{array}{*{20}c} {\tau_{113}^{(1)} } \\ {\tau_{113}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{131}^{(1)} } \\ {\tau_{131}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{311}^{(1)} } \\ {\tau_{311}^{s(1)} } \\ \end{array} } \right) = 2l_{1}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \frac{4}{15}} & \frac{8}{15} & { - \frac{8}{15}} \\ { - \frac{4}{15}} & \frac{4}{15} & { - \frac{4}{15}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}f^{{({ \cos })}} } \\ \end{array} } \right),$$
(25b)
$$\left( {\begin{array}{*{20}c} {\tau_{122}^{(1)} } \\ {\tau_{122}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{221}^{(1)} } \\ {\tau_{221}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{212}^{(1)} } \\ {\tau_{212}^{s(1)} } \\ \end{array} } \right) = 2l_{1}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & \frac{1}{15} & { - \frac{1}{15}} \\ { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right),$$
(25c)
$$\left( {\begin{array}{*{20}c} {\tau_{133}^{(1)} } \\ {\tau_{133}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{331}^{(1)} } \\ {\tau_{331}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{313}^{(1)} } \\ {\tau_{313}^{s(1)} } \\ \end{array} } \right) = 2l_{1}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & { - \frac{4}{15}} & \frac{4}{15} \\ { - \frac{1}{5}} & \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \\ {z\frac{{\partial^{3} w}}{{\partial x^{3} }}} \\ {\frac{h}{\pi }\frac{{\partial^{3} w}}{{\partial x^{3} }}\,f^{(\sin )} } \\ {\frac{h}{\pi }\frac{{\partial^{2} \phi }}{{\partial x^{2} }}\,f^{(\sin )} } \\ {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right),$$
(25d)
$$\left( {\begin{array}{*{20}c} {\tau_{223}^{(1)} } \\ {\tau_{223}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{232}^{(1)} } \\ {\tau_{232}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{322}^{(1)} } \\ {\tau_{322}^{s(1)} } \\ \end{array} } \right) = 2l_{1}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \frac{1}{15} & { - \frac{2}{15}} & \frac{2}{15} \\ \frac{1}{15} & { - \frac{1}{15}} & \frac{1}{15} \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right),$$
(25e)
$$\left( {\begin{array}{*{20}c} {\tau_{333}^{(1)} } \\ {\tau_{333}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{333}^{(1)} } \\ {\tau_{333}^{s(1)} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\tau_{333}^{(1)} } \\ {\tau_{333}^{s(1)} } \\ \end{array} } \right) = 2l_{1}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} \frac{1}{5} & { - \frac{2}{5}} & \frac{2}{5} \\ \frac{1}{5} & { - \frac{1}{5}} & \frac{1}{5} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right).$$
(25f)

By utilizing Eq. (15) and inserting Eq. (22) into (13) and (9) the higher-order stresses \(m_{ij}\), \(m_{ij}^{s}\) are

$$\left( {\begin{array}{*{20}c} {m_{xy} } \\ {m_{xy}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {m_{yx} } \\ {m_{yx}^{s} } \\ \end{array} } \right) = 2l_{2}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \frac{1}{2}} & \frac{1}{4} & { - \frac{1}{4}} \\ { - \frac{1}{2}} & \frac{1}{2} & { - \frac{1}{2}} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\,f^{{({ \cos })}} } \\ {\frac{\partial \phi }{\partial x}\,f^{{({ \cos })}} } \\ \end{array} } \right),$$
(26a)
$$\left( {\begin{array}{*{20}c} {m_{yz} } \\ {m_{yz}^{s} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {m_{zy} } \\ {m_{zy}^{s} } \\ \end{array} } \right) = 2l_{2}^{2} \left( {\begin{array}{*{20}c} {G^{*} } & {G_{s}^{*} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} { - \frac{1}{4}} & { + \frac{1}{4}} \\ 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {\frac{\pi }{h}\frac{\partial w}{\partial x}\,f^{(\sin )} } \\ {\frac{\pi }{h}\phi\,f^{(\sin )} } \\ \end{array} } \right).$$
(26b)

Substituting Eqs. (19)–(26) into Eq. (18) for each layer, leads to

$$\begin{aligned} {\text{U}}_{\text{s}} =&\frac{1}{2}\int_{0}^{L} {\left\{ {B1{\mkern 1mu} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}\,+\,B2{\mkern 1mu} \left( {\frac{{\partial w_{i} }}{\partial x}} \right)^{2}\,+\,B3_{i} \left( {\frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}} \right)^{2}\,+\,B4{\mkern 1mu} \left( {\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}} \right)^{2}\,+\,B5{\mkern 1mu} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}\frac{{\partial w_{i} }}{\partial x}\,+\,B6{\mkern 1mu} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }}\frac{{\partial w_{i} }}{\partial x}} \right.} \\ &\,+\,B7{\mkern 1mu} \frac{{\partial u_{i} }}{\partial x}\frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}\,+\,B8{\mkern 1mu} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}\frac{{\partial^{2} u_{i} }}{{\partial x^{2} }}\,+\,B9{\mkern 1mu} \phi_{i} \frac{{\partial w_{i} }}{\partial x}\,+\,B10{\mkern 1mu} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}\frac{{\partial \phi_{i} }}{\partial x}\,+\, B11{\mkern 1mu} \phi_{i} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}\,+\,B12{\mkern 1mu} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} \\ &\,+\, B13_{i} \frac{{\partial u_{i} }}{\partial x}\,+\,B14_{i} \left( {\frac{{\partial u_{i} }}{\partial x}} \right)^{2}\,+\,B15_{i} \left( {\frac{{\partial^{2} u_{i} }}{{\partial x^{2} }}} \right)^{2} \,+\,B16{\mkern 1mu} \frac{{\partial \phi_{i} }}{\partial x}\frac{{\partial u_{i} }}{\partial x} \,+\,B17{\mkern 1mu} \phi_{i} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }}\,+\,B18{\mkern 1mu} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }}\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} \\ &\,+\,B19{\mkern 1mu} \left( {\phi_{i} } \right)^{2}\,+\, b20{\mkern 1mu} \frac{{\partial \phi_{i} }}{\partial x}\,+\,B21{\mkern 1mu} \left( {\frac{{\partial \phi_{i} }}{\partial x}} \right)^{2}\,+\,B22{\mkern 1mu} \left( {\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }}} \right)^{2} \left. { \,+\,B23{\mkern 1mu} \phi_{i} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }}\,+\,B24{\mkern 1mu} \frac{{\partial w_{i} }}{\partial x}\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }}} \right\}dx{ ,} \\ \end{aligned}$$
(27)

Subscript i denotes the number of nanotube where i = 1, 2 demonstrate inner and outer nanotubes, and B ij are defined in Appendix 1.

The total kinetic energy of nanotubes can be expressed as:

$$k_{tube} = \frac{1}{2}\rho_{t} \int\limits_{0}^{L} {\left\{ {\int\limits_{{A_{i} }} {\left[ {\left( {\frac{{\partial u_{xi} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial u_{zi} }}{\partial t}} \right)^{2} } \right]} dA_{i} } \right\}} dx.$$
(28)

3.2 Virtual work of pulsating nano-flow

The well-known Navier–Stokes equations are stated as follows Mirramezani et al. (2013):

$$\rho \frac{{D\overrightarrow {V} }}{Dt} = - \nabla \overrightarrow {P} + \mu \nabla^{2} \overrightarrow {V} + \overrightarrow {F}_{body},$$
(29)

where \(\frac{D}{Dt}\) is the material or total derivative and \(\overrightarrow {V}\) is the flow velocity, \(\overrightarrow {P}\) and μ are, respectively, the pressure and the viscosity of the flowing fluid, \(\rho\) is the mass density of the internal fluid, and \(\overrightarrow {F}_{body}\) represents body forces.

According to the reference (Mirramezani et al. 2013), the viscosity parameter could not appear in the fluid–structure interaction (FSI) equation. So the force exerted due to the fluid flow on the nanotube can be obtained as follows:

$$F_{f} = A_{f} \frac{{\partial p_{r} }}{\partial r} - \mu_{0} A_{f} \left[ {\frac{{\partial^{3} W}}{{\partial x^{2} \partial t}} + V_{f} \frac{{\partial^{3} W}}{{\partial x^{3} }}} \right] = - \rho A_{f} \left[ {\frac{{\partial^{2} W}}{{\partial t^{2} }} + 2V_{f} \frac{{\partial^{2} W}}{\partial x\partial t} + V_{f}^{2} \frac{{\partial^{2} W}}{{\partial x^{2} }}} \right],$$
(30)

where F f is the exerted force by fluid to the nanotube. A f , \(\rho\), V f and μ denote the cross sectional area of the internal fluid, the fluid density, the velocity of the fluid flow in the longitudinal direction on the CNT wall and the viscosity of the flowing fluid, respectively.

For CNTs conveying fluid, the \(Kn\) may be larger than 10-2; consequently, the assumption of no-slip boundary condition is not true and the fluid slip velocity should be modified. The slip velocity is presented as follows Mirramezani et al. (2013):

$$V_{avg,slip} = \frac{\gamma }{1 + \gamma }V_{avg,(no - slip)},$$
(31a)

where

$$\gamma = 4\left( {\frac{{2 - \sigma_{v} }}{{\sigma_{v} }}} \right)\left( {\frac{Kn}{1 + Kn}} \right),$$
(31b)

Here \(\sigma_{v}\) is tangential moment accommodation coefficient and is considered to be 0.7 for most practical purpose.

The case of pulsating internal flow is assumed harmonically fluctuating, as follows Liang and Su (2013):

$$V_{f} = V_{avg,(no - slip)} = V_{0} (1 + \alpha \,{ \cos }(\omega t)),$$
(32)

where V 0 is the mean flow velocity, α is the amplitude of the harmonic fluctuation (assumed small) and ω its frequency.

The total virtual work of pulsating nano-flow is

$$W_{f} = \int_{0}^{l} {F_{f} w_{1} dx} = \int_{0}^{l} {\left\{ { - \rho A_{f} \left[ {\frac{{\partial^{2} w_{1} }}{{\partial t^{2} }}\,+\, 2U_{f} \frac{{\partial^{2} w_{1} }}{\partial x\partial t}\,+\, U_{f}^{2} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }}} \right]} \right\}w_{1} \, dx}.$$
(33)

It is noticed that \(U_{f} = \frac{\gamma }{1 + \gamma } \times V_{f}\) in the governing equations.

3.3 Maxwell’s equation

Maxwell’s equation are given by Wang et al. (2010):

$$\overrightarrow {J} = \nabla \times \overrightarrow {h},$$
(34a)
$$\nabla \times e = - \eta \left( {\frac{\partial h}{\partial t}} \right),$$
(34b)
$$\nabla \cdot \overrightarrow {h} = 0,$$
(34c)
$$e = - \eta \left( {\frac{\partial D}{\partial t} \times \overrightarrow {H} } \right),$$
(34d)
$$\overrightarrow {h} = \nabla \times (\overrightarrow {D} \times \overrightarrow {H} ),$$
(34e)

where, \(\overrightarrow {J}\), e, η and h represent the current density, strength vectors of electric field, the magnetic field permeability and disturbing vectors of magnetic field respectively. \(\overrightarrow {D} = (u_{x} ,u_{y} ,u_{z} )\) is the displacement vector and magnetic field vector is:

$$\overrightarrow {H} = \left( {\begin{array}{*{20}c} {H_{x} } \\ 0 \\ {H_{z} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {H\,{ \cos }(\theta )} \\ 0 \\ {H\,{ \sin }(\theta )} \\ \end{array} } \right).$$
(35)

By using Eq. (34) \(\overrightarrow {h}\) and\(\overrightarrow {J}\) are describe:

$$\begin{aligned} \overrightarrow {h} & = \nabla \times \left( {D \times \overrightarrow {H} } \right) \\ & { = }\left( {\begin{array}{*{20}l} { - H_{z} \frac{{\partial w_{i} }}{\partial x} + H_{z} \cos \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial w_{i} }}{\partial x} - H_{z} \cos \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\phi_{i} } \\ 0 \\ {H_{x} \frac{{\partial w_{i} }}{\partial x} - H_{z} \frac{{\partial u_{i} }}{\partial x} + H_{z} z\frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} - H_{z} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}\,+\,H_{z} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial \phi_{i} }}{\partial x}} \\ \end{array} } \right), \\ \end{aligned}$$
(36)
$$\begin{aligned} \overrightarrow {J} = & \nabla \times \overrightarrow {h} = \left( { - H_{z} \frac{\pi }{h}\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right){\mkern 1mu} \frac{{\partial w_{i} }}{\partial x}\,+\,H_{z} \frac{\pi }{h}\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right){\mkern 1mu} \phi_{i}\,-\, H_{x} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}\,+\,H_{z} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }}\,-\,H_{z} z\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}} \right. \\ & \left. { + H_{z} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }}\,-\,H_{z} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }}} \right){j}. \\ \end{aligned}$$
(37)

The Lorentz force in three directions is:

$$f = \left( {f_{x} ,f_{y} ,f_{z} } \right) = \eta \left( {\overrightarrow {J} \times \overrightarrow {H} } \right).$$
(38)

Introducing Eq. (37) to Eq. (38) and utilizing Eq. (35), the Lorentzian forces are obtained as:

$$f_{x} = - {\mkern 1mu} \eta {\mkern 1mu} H_{z}^{2} \frac{\pi }{h}{\mkern 1mu} \sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial w_{i} }}{\partial x} + \eta {\mkern 1mu} H_{z}^{2} \frac{\pi }{h}{\mkern 1mu} \sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right){\mkern 1mu} \phi_{i} - \eta {\mkern 1mu} H_{z} H_{x} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} + \eta {\mkern 1mu} H_{z}^{2} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }} - \eta {\mkern 1mu} H_{z}^{2} z\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} + \eta {\mkern 1mu} H_{z}^{2} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} - \eta {\mkern 1mu} H_{z}^{2} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }},$$
(39a)
$$f_{y} = 0,$$
(39b)
$$\begin{aligned} f_{z} = & \eta {\mkern 1mu} H_{x} H_{z} \frac{\pi }{h}{\mkern 1mu} \sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial w_{i} }}{\partial x} - \eta {\mkern 1mu} H_{x} H_{z} \frac{\pi }{h}{\mkern 1mu} \sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right){\mkern 1mu} \phi_{i} + \eta {\mkern 1mu} H_{x}^{2} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} - \eta {\mkern 1mu} H_{x} H_{z} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }} \\ \, & + \eta {\mkern 1mu} H_{x} H_{z} z\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} - \eta {\mkern 1mu} H_{x} H_{z} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} + \eta {\mkern 1mu} H_{x} H_{z} \frac{h}{\pi }\sin \left( {\frac{{\pi {\mkern 1mu} z}}{h}} \right)\frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }}. \\ \end{aligned}$$
(39c)

The resultant Lorentz’s forces, \(R = (R_{x} ,R_{y} ,R_{z} )\), and the corresponding bending moments, \(M = (M_{x} ,M_{y} ,M_{z} )\), as follows Kiani (2014):

$$\begin{aligned} R_{x} = & \int_{{A_{i} }} {f_{x} } \, dA_{i} = - {\mkern 1mu} \eta {\mkern 1mu} H_{z}^{2} \frac{\pi }{h}{\mkern 1mu} p_{0} \frac{{\partial w_{i} }}{\partial x} + \eta {\mkern 1mu} H_{z}^{2} \frac{\pi }{h}{\mkern 1mu} {\mkern 1mu} p_{0} \phi_{i} - \eta {\mkern 1mu} H_{z} H_{x} A_{i} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} + \eta {\mkern 1mu} H_{z}^{2} A_{i} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }} \\ & + \eta {\mkern 1mu} H_{z}^{2} \frac{h}{\pi }p_{0} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} - \eta {\mkern 1mu} H_{z}^{2} \frac{h}{\pi }p_{0} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }}, \\ \end{aligned}$$
(40a)
$$R_{y} = \int_{{A_{i} }} {f_{y} } \, dA_{i} = 0,$$
(40b)
$$R_{z} = \int_{{A_{i} }} {f_{z} } \, dA_{i} = \eta {\mkern 1mu} H_{x} H_{z} \frac{\pi }{h}{\mkern 1mu} p_{0} \frac{{\partial w_{i} }}{\partial x} - \eta {\mkern 1mu} H_{x} H_{z} \frac{\pi }{h}{\mkern 1mu} p_{0} {\mkern 1mu} \phi_{i} + \eta {\mkern 1mu} H_{x}^{2} A_{i} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }} - \eta {\mkern 1mu} H_{x} H_{z} A_{i} \frac{{\partial^{2} u_{i} }}{{\partial x^{2} }} - \eta {\mkern 1mu} H_{x} H_{z} \frac{h}{\pi }p_{0} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} + \eta {\mkern 1mu} H_{x} H_{z} \frac{h}{\pi }p_{0} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }},$$
(40c)
$$M_{x} = M_{z} = 0,$$
(40d)
$$M_{y} = \int_{{A_{i} }} {z \, f_{x} } \, dA_{i} = - \eta {\mkern 1mu} H_{z}^{2} p_{1} \frac{\pi }{h}{\mkern 1mu} \frac{\partial }{\partial x}w_{i} + \eta {\mkern 1mu} H_{z}^{2} p_{1} \frac{\pi }{h}{\mkern 1mu} \phi_{i} - I\eta {\mkern 1mu} H_{z}^{2} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} + \eta {\mkern 1mu} H_{z}^{2} \frac{h}{\pi }p_{1} \frac{{\partial^{3} w_{i} }}{{\partial x^{3} }} - \eta {\mkern 1mu} H_{z}^{2} \frac{h}{\pi }p_{1} \frac{{\partial^{2} \phi_{i} }}{{\partial x^{2} }} \,$$
(40e)

Eventually, Lorentz work is written as Kiani (2014):

$$W_{lorentz} = \int\limits_{0}^{L} {(R_{x} u_{i} + R_{z} w_{i} } + M_{y,x} w_{i} )dx.$$
(41)

3.4 Visco-Pasternak foundation and vdW interaction

The external work due to visco-Pasternak foundation and vdW forces are written as:

$$\begin{aligned} W_{visco - pasternak,vdw} = & \int\limits_{0}^{L} {C_{v} \frac{{R_{1} }}{{R_{2} }}(w_{2} - w_{1} )w_{1} dx} + \int\limits_{0}^{L} {C_{v} (w_{1} - w_{2} )w_{2} dx} + \int\limits_{0}^{L} {( - K_{w} w_{2} + G_{P} \nabla^{2} w_{2} )w_{2} dx} \\ & \, + \int\limits_{0}^{L} {C_{d} \frac{{\partial w_{2} }}{\partial t}} dx, \\ \end{aligned}$$
(42)

where K w , C d , C v and G P Winkler’s spring modulus, damper, vdW interaction coefficient and Pasternak’s shear modulus of elastic medium, respectively.

According to Hamilton’s principle (i.e. Eq. (17)), the motion equations are obtained as follows:

$$\delta u_{1}\!\!: { } B_{6} {\mkern 1mu} \frac{{\partial^{3} w_{1} }}{{\partial x^{3} }} - B_{7} {\mkern 1mu} \frac{{\partial^{3} w_{1} }}{{\partial x^{3} }} + B_{17} {\mkern 1mu} \frac{{\partial^{2} \phi_{1} }}{{\partial x^{2} }} + B_{8} {\mkern 1mu} \frac{{\partial^{5} w_{1} }}{{\partial x^{5} }} - B_{16} {\mkern 1mu} \frac{{\partial^{2} \phi_{1} }}{{\partial x^{2} }} + B_{18} {\mkern 1mu} \frac{{\partial^{4} \phi_{1} }}{{\partial x^{4} }} - 2{\mkern 1mu} B_{{14_{1} }} \frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} + 2{\mkern 1mu} B_{{15_{1} }} \frac{{\partial^{4} u_{1} }}{{\partial x^{4} }} + \rho_{t} A_{1} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} + \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{3} w_{1} }}{{\partial x\partial t^{2} }} - \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{2} \phi_{1} }}{{\partial t^{2} }} - R_{x} ,$$
(43)
$$\begin{aligned} \delta w_{1}\!\!: { } & - B_{9} {\mkern 1mu} \frac{{\partial \phi_{1} }}{\partial x} - 2{\mkern 1mu} B_{4} {\mkern 1mu} \frac{{\partial^{6} w_{1} }}{{\partial x^{6} }} - B_{11} {\mkern 1mu} \frac{{\partial^{3} \phi_{1} }}{{\partial x^{3} }} - B_{8} {\mkern 1mu} \frac{{\partial^{5} u_{1} }}{{\partial x^{5} }} + B_{10} {\mkern 1mu} \frac{{\partial^{3} \phi_{1} }}{{\partial x^{3} }} - 2{\mkern 1mu} B_{{2{\mkern 1mu} }} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} - B_{12} {\mkern 1mu} \frac{{\partial^{5} \phi_{1} }}{{\partial x^{5} }} - B_{24} {\mkern 1mu} \frac{{\partial^{3} \phi_{1} }}{{\partial x^{3} }} \\ & - B_{6} {\mkern 1mu} \frac{{\partial^{3} u_{1} }}{{\partial x^{3} }} + B_{7} {\mkern 1mu} \frac{{\partial^{3} u_{1} }}{{\partial x^{3} }} - 2{\mkern 1mu} B_{5} {\mkern 1mu} \frac{{\partial^{4} w_{1} }}{{\partial x^{4} }} + 2{\mkern 1mu} B_{{3_{1} }} \frac{{\partial^{4} w_{1} }}{{\partial x^{4} }} - \frac{{\rho_{t} hP_{1} }}{\pi }\frac{{\partial^{3} \phi_{1} }}{{\partial x\partial t^{2} }} - \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{4} w_{1} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{3} \phi_{1} }}{{\partial x\partial t^{2} }} \\ & - I\rho_{t} \frac{{\partial^{4} w_{1} }}{{\partial x^{2} \partial t^{2} }} + \rho_{t} A_{1} \frac{{\partial^{2} w_{1} }}{{\partial t^{2} }} - \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{3} u_{1} }}{{\partial x\partial t^{2} }} + 2{\mkern 1mu} \frac{{\rho_{t} hP_{1} }}{\pi }\frac{{\partial^{4} w_{1} }}{{\partial x^{2} \partial t^{2} }} - 2{\mkern 1mu} \tau_{s} \left( {h + b} \right)\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} - R_{z} - M_{y,x} \\ \, & - \frac{{c_{v} R_{1} }}{{R_{2} }}\left( {w_{2} - w_{1} } \right) + \rho {\mkern 1mu} A_{f} \frac{{\partial^{2} w_{1} }}{{\partial t^{2} }} + 2{\mkern 1mu} \rho {\mkern 1mu} A_{f} U_{f} \frac{{\partial^{2} w_{1} }}{\partial x\partial t} + \rho {\mkern 1mu} A_{f} U_{f}^{2} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }}{ ,} \\ \end{aligned}$$
(44)
$$\begin{aligned} \delta \phi_{1}\!\!: & - B_{10} {\mkern 1mu} \frac{{\partial^{3} w_{1} }}{{\partial x^{3} }} + B_{12} {\mkern 1mu} \frac{{\partial^{5} w_{1} }}{{\partial x^{5} }} + B_{{18{\mkern 1mu} }} \frac{{\partial^{4} u_{1} }}{{\partial x^{4} }} + 2{\mkern 1mu} B_{22} {\mkern 1mu} \frac{{\partial^{4} \phi_{1} }}{{\partial x^{4} }} + B_{9} {\mkern 1mu} \frac{{\partial w_{1} }}{\partial x} + B_{24} {\mkern 1mu} \frac{{\partial^{3} w_{1} }}{{\partial x^{3} }} + B_{17} {\mkern 1mu} \frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} \\ & + B_{{11{\mkern 1mu} }} \frac{{\partial^{3} w_{1} }}{{\partial x^{3} }} + 2{\mkern 1mu} B_{19} {\mkern 1mu} \phi_{1} + 2{\mkern 1mu} B_{23} {\mkern 1mu} \frac{{\partial^{2} \phi_{1} }}{{\partial x^{2} }} - 2{\mkern 1mu} B_{21} {\mkern 1mu} \frac{{\partial^{2} \phi_{1} }}{{\partial x^{2} }} - B_{16} {\mkern 1mu} \frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} - \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} \\ & + \frac{{\rho_{t} hP_{1} }}{\pi }\frac{{\partial^{3} w_{1} }}{{\partial x\partial t^{2} }} - \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{3} w_{1} }}{{\partial x\partial t^{2} }} + \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{2} \phi_{1} }}{{\partial t^{2} }}, \\ \end{aligned}$$
(45)
$$\delta u_{2}\!\!: { } B_{{6{\mkern 1mu} }} \frac{{\partial^{3} w_{2} }}{{\partial x^{3} }} - B_{7} {\mkern 1mu} \frac{{\partial^{3} w_{2} }}{{\partial x^{3} }} + B_{{17{\mkern 1mu} }} \frac{{\partial^{2} \phi_{2} }}{{\partial x^{2} }} + B_{8} {\mkern 1mu} \frac{{\partial^{5} w_{2} }}{{\partial x^{5} }} - B_{{16{\mkern 1mu} }} \frac{{\partial^{2} \phi_{2} }}{{\partial x^{2} }} + B_{18} {\mkern 1mu} \frac{{\partial^{4} \phi_{2} }}{{\partial x^{4} }} - 2{\mkern 1mu} B_{{14_{2} }} \frac{{\partial^{2} u_{2} }}{{\partial x^{2} }} + 2{\mkern 1mu} B_{{15_{2} }} \frac{{\partial^{4} u_{2} }}{{\partial x^{4} }} + \rho_{t} A_{2} \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} + \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{3} w_{2} }}{{\partial x\partial t^{2} }} - \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{2} \phi_{2} }}{{\partial t^{2} }} - R_{x},$$
(46)
$$\begin{aligned} \delta w_{2}\!\!: & - B_{9} {\mkern 1mu} \frac{{\partial \phi_{2} }}{\partial x} - 2{\mkern 1mu} B_{4} \frac{{\partial^{6} w_{2} }}{{\partial x^{6} }} - B_{11} {\mkern 1mu} \frac{{\partial^{3} \phi_{2} }}{{\partial x^{3} }} - B_{8} {\mkern 1mu} \frac{{\partial^{5} u_{2} }}{{\partial x^{5} }} + B_{10} {\mkern 1mu} \frac{{\partial^{3} \phi_{2} }}{{\partial x^{3} }} - 2{\mkern 1mu} B_{2} {\mkern 1mu} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} - B_{12} {\mkern 1mu} \frac{{\partial^{5} \phi_{2} }}{{\partial x^{5} }} - B_{24} {\mkern 1mu} \frac{{\partial^{3} \phi_{2} }}{{\partial x^{3} }} \\ & - B_{{6{\mkern 1mu} }} \frac{{\partial^{3} u_{2} }}{{\partial x^{3} }} + B_{7} {\mkern 1mu} \frac{{\partial^{3} u_{2} }}{{\partial x^{3} }} - 2{\mkern 1mu} B_{5} {\mkern 1mu} \frac{{\partial^{4} w_{2} }}{{\partial x^{4} }} + 2{\mkern 1mu} B_{{3_{2} }} \frac{{\partial^{4} w_{2} }}{{\partial x^{4} }} - \frac{{\rho_{t} hP_{1} }}{\pi }\frac{{\partial^{3} \phi_{2} }}{{\partial x\partial t^{2} }} - \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{4} w_{2} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{3} \phi_{2} }}{{\partial x\partial t^{2} }} \\ & - I\rho_{t} \frac{{\partial^{4} w_{2} }}{{\partial x^{2} \partial t^{2} }} + \rho_{t} A_{2} \frac{{\partial^{2} w_{2} }}{{\partial t^{2} }} - \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{3} u_{2} }}{{\partial x\partial t^{2} }} + 2{\mkern 1mu} \frac{{\rho_{t} hP_{1} }}{\pi }\frac{{\partial^{4} w_{2} }}{{\partial x^{2} \partial t^{2} }} - 2{\mkern 1mu} \tau_{s} \left( {h + b} \right)\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} - R_{z} - M_{y,x} \\ & - c_{v} \left( {w_{1} - w_{2} } \right) - G_{p} \nabla^{2} {\mkern 1mu} w_{2} + K_{w} w_{2} + c_{d} \frac{{\partial w_{2} }}{\partial t}, \\ \end{aligned}$$
(47)
$$\begin{aligned} \delta \phi_{2}\!\! : \, & - B_{{10{\mkern 1mu} }} \frac{{\partial^{3} w_{2} }}{{\partial x^{3} }} + B_{12} {\mkern 1mu} \frac{{\partial^{5} w_{2} }}{{\partial x^{5} }} + B_{18} {\mkern 1mu} \frac{{\partial^{4} u_{2} }}{{\partial x^{4} }} + 2{\mkern 1mu} B_{22} {\mkern 1mu} \frac{{\partial^{4} \phi_{2} }}{{\partial x^{4} }} + B_{9} {\mkern 1mu} \frac{{\partial w_{2} }}{\partial x} + B_{24} {\mkern 1mu} \frac{{\partial^{3} w_{2} }}{{\partial x^{3} }} + B_{17} {\mkern 1mu} \frac{{\partial^{2} u_{2} }}{{\partial x^{2} }} \\ & + B_{{11{\mkern 1mu} }} \frac{{\partial^{3} w_{2} }}{{\partial x^{3} }} + 2{\mkern 1mu} B_{19} {\mkern 1mu} \phi_{2} + 2{\mkern 1mu} B_{23} {\mkern 1mu} \frac{{\partial^{2} \phi_{2} }}{{\partial x^{2} }} - 2{\mkern 1mu} B_{{21{\mkern 1mu} }} \frac{{\partial^{2} \phi_{2} }}{{\partial x^{2} }} - B_{16} {\mkern 1mu} \frac{{\partial^{2} u_{2} }}{{\partial x^{2} }} - \frac{{\rho_{t} hP_{0} }}{\pi }\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} \\ & + \frac{{\rho_{t} hP_{1} }}{\pi }\frac{{\partial^{3} w_{2} }}{{\partial x\partial t^{2} }} - \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{3} w_{2} }}{{\partial x\partial t^{2} }} + \frac{{\rho_{t} h^{2} L}}{{\pi^{2} }}\frac{{\partial^{2} \phi_{2} }}{{\partial t^{2} }}. \\ \end{aligned}$$
(48)

Boundary conditions at x = 0and \(x = L\) read (Lei et al. 2013a):

$$\begin{aligned} \frac{{\partial^{2} \delta w_{i} }}{{\partial x^{2} }} & = 0,\,\frac{{\partial \delta w_{i} }}{\partial x} = 0,\,\delta w_{i} = 0, \\ \frac{{\partial \delta \phi_{i} }}{\partial x} & = 0,\,\delta \phi_{i} = 0, \\ \frac{{\partial \delta u_{i} }}{\partial x} & = 0,\,\delta u_{i} = 0. \\ \end{aligned}$$
(49)

3.5 Solution procedure

3.5.1 DQM

DQM is employed in this section which in essence approximates the partial derivative of a function, with respect to a spatial variable at a given discrete point, as a weighted linear sum of the function values at all discrete points chosen in the solution domain of the spatial variable (Khodami Maraghi et al. 2013). Let F be a function representing \(u_{1} ,u_{2}\), \(w_{1} ,w_{2}\) and \(\varphi_{1} ,\varphi_{2}\) with respect to variable x in the domain of (\(0 < x < L\)) having N x grid points along these variable. The nth-order partial derivative of F(x) with respect to x may be expressed discretely as

$$\frac{{d^{n} F(x_{i} )}}{{dx^{n} }} = \sum\limits_{k = 1}^{{N_{x} }} {A_{ik}^{(n)} F(x_{k} )} \quad n = 1, \ldots ,N_{x} - 1,$$
(50)

where \(A_{ik}^{(n)}\) is the weighting coefficient, whose recursive formula are described in Khodami Maraghi et al. (2013). The Chebyshev–Gauss–Lobatto polynomials (Civalek 2004, 2006) was used to determine the unequally spaced position of the grid points as follows

$$x_{i} = \frac{L}{2}\left[ {1 - \cos \left( {\frac{2i - 1}{{N_{x} - 1}}} \right)\pi } \right],$$
(51)

Combining all the motion equations along with the corresponding boundary conditions using DQM and rewritten them in matrix form yields

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {\left[ 0 \right]_{14 \times 14} } & {\left[ 0 \right]_{{14 \times \left( {6N_{x} - 14} \right)}} } \\ {\left[ {M_{db} } \right]_{{\left( {6N_{x} - 14} \right) \times 14}} } & {\left[ {M_{dd} } \right]_{{\left( {6N_{x} - 14} \right) \times \left( {6N_{x} - 14} \right)}} } \\ \end{array} } \right]_{{6N_{x} \times 6N_{x} }} \left\{ \begin{gathered} \left\{ { \, \ddot{{Y}}_{b} } \right\} \hfill \\ \left\{ { \,{\ddot{Y}}_{d} } \right\} \hfill \\ \end{gathered} \right\} \\ & \; + \left( \begin{gathered} \left[ {\begin{array}{*{20}c} {\left[ 0 \right]_{14 \times 14} } & {\left[ 0 \right]_{{14 \times \left( {6N_{x} - 14} \right)}} } \\ {\left[ {C_{db} } \right]_{{\left( {6N_{x} - 14} \right) \times 14}} } & {\left[ {C_{dd} } \right]_{{\left( {6N_{x} - 14} \right) \times \left( {6N_{x} - 14} \right)}} } \\ \end{array} } \right] \hfill \\ + \left( {V_{0} + V_{0} \alpha \,{ \cos }(\omega t)} \right)\left[ {\begin{array}{*{20}c} {\left[ 0 \right]_{14 \times 14} } & {\left[ 0 \right]_{{14 \times \left( {6N_{x} - 14} \right)}} } \\ {\left[ {C_{db} } \right]_{{\left( {6N_{x} - 14} \right) \times 14}}^{f} } & {\left[ {C_{dd} } \right]_{{\left( {6N_{x} - 14} \right) \times \left( {6N_{x} - 14} \right)}}^{f} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right)_{{6N_{x} \times 6N_{x} }} \,\,\left\{ \begin{gathered} \left\{\!{ \, \dot{Y}_{b} } \right\} \hfill \\ \left\{ { \, \dot{Y}_{d} }\! \right\} \hfill \\ \end{gathered} \right\} \\ & \; + \left( \begin{gathered} \left[ {\begin{array}{*{20}c} {\left[ {K_{bb} } \right]_{14 \times 14} } & {\left[ {K_{bd} } \right]_{{14 \times \left( {6N_{x} - 14} \right)}} } \\ {\left[ {K_{db} } \right]_{{\left( {6N_{x} - 14} \right) \times 14}} } & {\left[ {K_{dd} } \right]_{{\left( {6N_{x} - 14} \right) \times \left( {6N_{x} - 14} \right)}} } \\ \end{array} } \right] \hfill \\ + \left( {V_{0} + V_{0} \alpha \,{ \cos }(\omega t)} \right)^{2} \left[ {\begin{array}{*{20}c} {\left[ {K_{bb} } \right]_{14 \times 14}^{f} } & {\left[ {K_{bd} } \right]_{{14 \times \left( {6N_{x} - 14} \right)}}^{f} } \\ {\left[ {K_{db} } \right]_{{\left( {6N_{x} - 14} \right) \times 14}}^{f} } & {\left[ {K_{dd} } \right]_{{\left( {6N_{x} - 14} \right) \times \left( {6N_{x} - 14} \right)}}^{f} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right)_{{6N_{x} \times 6N_{x} }} \,\,\left\{ \begin{gathered} \left\{\!{Y_{b} } \right\}_{14 \times 1} \hfill \\ \left\{ {Y_{d} } \right\}_{{\left( {6N_{x} - 14} \right) \times 1}} \hfill \\ \end{gathered}\!\right\} = 0, \\ \end{aligned}$$
(52)

where [M], [C] and [K] are the mass, damping and stiffness matrixes, respectively; [C f] and [K f] are the respectively, damping and stiffness matrixes related to pulsating fluid; \(\left\{ Y \right\}\) is the displacement vector (i.e. \(\left\{ Y \right\} = \left\{ {u_{i} ,v_{i} ,w_{i} } \right\}\,\,\,i = 1,2\)); subscript b and d represent boundary and domain points.

3.6 Bolotin method

In order to determinate the DIR of visco-DWCNTs, the method suggested by Bolotin (1964) is applied. Hence, the components of \(\left\{ d \right\}\) can be written in the Fourier series with period 2T as

$$ \left\{ d \right\} = \sum\limits_{k = 1,3, \ldots }^{\infty } {\left[ {\left\{ a \right\}_{k} \sin \frac{k\omega t}{2} + \left\{ b \right\}_{k} \cos \frac{k\omega t}{2}} \right] \, ,} $$
(53)

According to this method, the first instability region is usually the most important in studies of structures. It is due to the fact that the first DIR is wider that other DIRs and structural damping in higher regions becomes neutralize (Lanhe et al. 2007). Substituting Eq. (53) into Eq. (52) and setting the coefficients of each sine and cosine as well as the sum of the constant terms to zero, yields

$$\left|{\left( {\left[ K \right] + \left( {1 \pm \alpha + \frac{{\alpha^{2} }}{2}} \right)\left[ K \right]^{f} } \right) + \left( { \pm \left[ C \right]\frac{\omega }{2} + \left( {\frac{\alpha \omega }{4} \pm \frac{\omega }{2}} \right)\left[ C \right]^{f} } \right)\,\, - \left[ M \right]\frac{{\omega^{2} }}{4}} \right|\,\, = 0,$$
(54)

Solving the above equation based on eigenvalue problem, the variation of ω with respect to α can be plotted as DIR.

4 Results and discussion

Based on DQM and Bolotin method, the effects of nonlocal parameter, magnetic field, visco-Pasternak foundation, Knudsen number, surface stress and fluid velocity on the DIR of visco-DWCNTs are investigated. The material properties of the DWCNTs related to bulk are: Young’s modulus of \({\text{E}} = 1\,\,\,{\text{Tpa}}\), Poisson’s ratio of \(\upsilon = 0.27\), density of ρ = 2,300 kg/m3 and thickness of h = 0.34 mm (Lei et al. 2012). Generally, the surface material properties can be calculated by atomic simulations. However, the material properties of the DWCNTs related to surface are: surface Young’s modulus of, E s  = 35.3 N/m and residual surface stress of, τ s  = 0.31 N/m (Lei et al. 2012).

4.1 Convergence of DQM

The convergence and accuracy of the DQM in evaluating the DIR of the visco-DWCNTs are shown in Table 1 for two cases of with and without considering surface effects. The results are prepared for different values of the DQM grid points. Fast rate of convergence of the DQM is quite evident. As can be seen, eleven grid points can yield accurate results.

Table 1 Convergence behavior and accuracy of the DQM for DIR of DWCNTs
Full size table

4.2 Validation

To the best of the authors’ knowledge no published literature is available for visco-DWCNTs pulsating fluid embedded in a visco-Pasternak foundation based on surface sinusoidal strain gradient theory. Since, no reference to such a work is found to-date in the literature, its validation is not possible. However, in an attempt to validate this work as far as possible, a simplified analysis of this paper is carried out without considering the surface effect, pulsating fluid, visco-Pasternak foundation and viscoelastic property of DWCNTs. Present results are compared with the work of Akgöz and Civalek (2013a, b) who studied nonlocal vibration analysis of microbeams based on SSDBT and strain gradient theory. Considering the material properties the same as Ref. (Akgöz and Civalek 2013a, b) and dimensionless frequency as \(\bar{\omega } = \omega L^{2} \sqrt {m_{0} /EI}\), the results are shown in Table 2. It is evident that the present results are in a good agreement with those obtained results by Ref. (Akgöz and Civalek 2013a, b). It should be noted that setting \(\Phi (z) = 0\) and \(\Phi (z) = z\) yields the EBT and TBT, respectively. It is also concluded that the frequency of SSDBT is higher than EBT and TBT. In addition, one can see that excellent agreement exist between the results of the DQM in the present paper with exact solution in Ref. (Akgöz and Civalek 2013a, b).

Table 2 Validation of present work with Ref. [16] for non-dimensional fundamental frequency of firs mode
Full size table

4.3 The effect of different parameters on DIR

Figure 2 represents the effect of different nonlocal theories including classical, modified couple stress and strain gradient on the dimensionless pulsation frequency (i.e. \(\Omega = \omega L\sqrt {\rho_{t} /E}\)) versus the dimensionless pulsation amplitude. Comparing classical theory with two non-classical theories, it can be concluded that the DIR predicted by the strain gradient theory is higher than the classical and modified couple stress theories. This is because the strain gradient theory expresses the three additional dilatation gradient tensor, the deviatoric stretch gradient tensor and the rotation gradient tensor.

Fig. 2
figure 2

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different nonlocal theories

Full size image

Figure 3 illustrates the effect of Knudsen number on the dimensionless pulsation frequency with respect to the dimensionless pulsation amplitude. It is came to know by enhancing Knudsen number, DIR and the dimensionless pulsation frequency shift to left and decrease. It is because that, when the Knudsen number increases, the mean free path of liquid molecules increases and results in lower stiffness.

Fig. 3
figure 3

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different values of Knudsen number

Full size image

Figure 4 depicts variations of the dimensionless pulsation frequency as a function of the dimensionless pulsation amplitude by varying the type of DWCNT surrounding foundation. Four different elastic medium are considered namely as visco-Pasternak, Pasternak, visco-Winkler and Winkler mediums. As can be seen considering elastic foundation increases the magnitude of dimensionless pulsation frequency and subsequently, DIR shifts to right. It is due to the fact that putting DWCNT in an elastic medium makes the system more stable and stiffer. It is also concluded that the DIR of Pasternak or visco-Pasternak model is higher than Winkler or visco-Winkler one. It is because Pasternak model considers not only the normal stresses but also the transverse shear deformation and continuity among the spring elements. Furthermore, the DIR predicted by visco-Pasternak and visco-Winkler mediums is lower than Pasternak and Winkler models, respectively.

Fig. 4
figure 4

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different elastic medium

Full size image

The effects of the vdW force on the dimensionless pulsation frequency with respect to the dimensionless pulsation amplitude are shown in Fig. 5. Stiffness of tube increases by considering vdW force so the dimensionless pulsation frequency increases.

Fig. 5
figure 5

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for vdW effect

Full size image

Figure 6 demonstrates variations of the dimensionless pulsation frequency versus the dimensionless pulsation amplitude for different magnitude of longitudinal magnetic field intensity. It can be observed that increment of magnetic field intensity makes the system more stable, hence the DIR and dimensionless pulsation frequency shift to right and increases. In addition, the longitudinal magnetic field has little influence on DIR when its magnitude is very small.

Fig. 6
figure 6

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different values of magnetic field

Full size image

In order to show the magnetic field angle effects, Fig. 7 is plotted where the dimensionless pulsation frequency is a function of the dimensionless pulsation amplitude. It is shown that when the magnetic field angle is zero (i.e. longitudinal magnetic field) the dimensionless pulsation frequency and DIR are maximum. With increasing magnetic field angle, the dimensionless pulsation frequency and DIR decrease and in magnetic field angle of \(\pi /2\) (i.e. lateral magnetic field), those become minimum.

Fig. 7
figure 7

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different values of magnetic field angle

Full size image

Figure 8 illustrates the surface stress effect on the dimensionless pulsation frequency with respect to the dimensionless pulsation amplitude. This figure shows that the surface stress effect is remarkable so that with ignoring this effect the DIR and the dimensionless pulsation frequency are not inaccurate. This is due to the fact that considering surface stress increases the stability of the DWCNT.

Fig. 8
figure 8

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different values of surface effect parameters

Full size image

Figure 9 shows the dimensionless pulsation frequency with respect to the dimensionless pulsation amplitude for different values of fluid velocities. Increasing the fluid velocity through the inner nanotube frequency decreases the dimensionless pulsation frequency. Furthermore, shifting the DIRs is obvious in higher flow velocities. Flowing fluid through the DWCNT exerts compressive axial load and for higher velocities the magnitude of this load increases, so increasing the flow velocity results in frequency and DIR decreasing.

Fig. 9
figure 9

Dimensionless pulsation amplitude versus dimensionless pulsation frequency for different values of fluid velocity

Full size image

5 Conclusion

Dynamic response of DWCNTs have applications in designing many NEMS/MEMS devices such as sensors, actuators, fluid storage, solar cell and biomechanic. Pulsating fluid induced dynamic instability of DWCNTs considering structural damping, surface stress effect and viscoelastic foundation was the main contributions of the present paper. The DWCNTs were subjected to 2D magnetic field and simulated by sinusoidal strain gradient theory. Bolotin method in conjunction with DQM were used for calculating the DIR of the visco-DWCNT The Chebyshev–Gauss–Lobatto polynomials was used to determine the unequally spaced position of the grid points. The effects of nonlocal parameter, magnetic field, visco-Pasternak foundation, Knudsen number, surface stress and fluid velocity on the DIR of the visco-DWCNT were discussed. Results depict that the imposed magnetic field was an effective controlling parameter for dynamic instability of visco-DWCNTs. The DIR predicted by the strain gradient theory was higher than the classical and modified couple stress theories. It was shown that when the magnetic field angle is zero (i.e. longitudinal magnetic field) the dimensionless pulsation frequency and DIR are maximum. Furthermore, considering surface stress increases the stability of the DWCNT. The results of this study were in good agreement with those reported by Ref. (Akgöz and Civalek 2013a, b). The results presented in this work can be useful for the study and design of the next generation of nano/micro structures that make use of the nonlocal dynamic instability of visco-CNTs embedded in visco-Pasternak medium.