1 Introduction

In order to analyze a real-world phenomenon, it is also necessary to deal with uncertain factors. In this situation, the theory of fuzzy sets may be one of the best non-statistical approach, which leads us to investigate theory of fuzzy fractional calculus. Several scientists in their earliest works introduced fuzzy fractional calculus as an uncertain fractional calculus to consider fractional-order systems with uncertain initial values or uncertain relationships between parameters. The basic concept as a Riemann–Liouville fractional integral, Riemann–Liouville H-differentiability, Caputo type fractional derivative based on Hukuhara and generalized Hukuhara difference and strongly generalized differentiability are defined in fuzzy fractional calculus (see, e.g., Agarwal et al. 2010; Allahviranloo et al. 2014; Armand and Mohammadi 2014; Arshad and Lupulescu 2011; Mazandarani and Vahidian Kamyad 2013; Mazandarani and Najariyan 2014; Salahshour et al. 2012). Fuzzy theory of fractional differential equations and integro-differential equations is a new and important branch of fuzzy mathematics. The topic of fuzzy fractional integro-differential equations (FFIDEs) has gained the attention of researchers in recent times because it is considered a powerful tool by which to present vague parameters and to handle with their dynamical systems in natural fuzzy environments (Long 2018a, b; Long et al. 2017, 2018). Indeed, it has a great significance in the fuzzy analysis theory and its applications in fuzzy control models, artificial intelligence, quantum optics, measure theory, and atmosphere (Alaroud et al. 2019; Son et al. 2020a, b). In Alikhani and Bahrami (2013), Allahviranloo (2020), Armand and Gouyandeh (2015), Balasubramaniam and Muralisankar (2001), the existence and uniqueness theorems for a fuzzy fractional integro-differential equation by considering the type of differentiability of solutions were proved. Most FFIDEs problems cannot be solved analytically, and hence, finding good approximate solutions using numerical methods will be very valuable. Recently, numerous scholars have devoted their interest to studying and investigating solutions to FFIDEs utilizing different numerical and semi-analytical techniques; these solutions include the Fuzzy Laplace transforms technique (Priyadhasini et al. 2016), two-dimensional Legendre wavelet technique (Shabestari et al. 2018a), Bernoulli wavelet method (Shabestari et al. 2018b) Adomian decomposition technique (Padmapriya et al. 2017), variational iteration technique (Matinfar et al. 2013), and the fractional residual power series technique (Alaroud et al. 2019).

In this paper, we consider the fuzzy Fredholm nonlinear fractional integro-differential equations of the second kind

$$\begin{aligned} \left\{ \begin{array}{ll} (_{gH}D_{*,0}^{\alpha }y)(t)=f(t)+ \int _{0}^{1}\kappa (t,s)G(y(s))\mathrm{d}s, \\ \\ y(0)=\tilde{y} _{0} \in \mathbb{R}_\mathcal{F} \end{array} \right. \end{aligned}$$
(1)

where \(\mathbb{R}_\mathcal{F}\) be the set of all fuzzy numbers on \(\mathbb{R}\), \(0<\alpha \le 1\), \( G:\mathbb{R}_{\mathcal{F}} \rightarrow \mathbb{R}_{\mathcal{F}} \), \(f:[0,1]\rightarrow \mathbb{R}_\mathcal{F}\) is a given continuous fuzzy-number-valued function, and \( \kappa (t,s):[0,1]\times [0,1]\rightarrow \mathbb{R}\) is a positive ordinary kernel function, and the operator \(_{gH}D^{\alpha }_{*,0}\) denotes the fuzzy Caputo type fractional generalized derivative of order \(\alpha \). The main goal of this paper is to extend an accurate numerical method for approximating the solution of Eq. (1). The proposed method is based on matrix formulation of spectral method as Tau method (Canuto et al. 2006) to approximating the solution of Eq. (1). It is known that the singular behavior of solution of fractional differential and/or integral equations makes the direct application of the spectral methods with standard orthogonal polynomials such as Legendre, Chebyshev, and Jacobi with poor convergence rates. Therefore, the rate of convergence of the numerical solutions will not be acceptable. To overcome this problem, we employ a new basis functions by replacing \( t\rightarrow t^{\alpha }\) in the standard Jacobi polynomials, which is called fractional-order Jacobi polynomials (see Bhrawy and Zaky 2015 for more detail). The simplicity of implementation proposed method and good approximation is addressed by some theorems and numerical examples.

The paper is organized as follows: Some basic properties of fuzzy calculus and fuzzy fractional calculus are given in Sect. 2. Section 3 discusses the existence and uniqueness of solution for Eq. (1). In Sect. 4, shift fractional Jacobi polynomials approximation and operational matrix for fractional integral have been derived. Section 5 is dedicated to propose a technique in order to apply the shifted Jacobi fractional operational matrices for solving the nonlinear fuzzy fractional Fredholm integro-differential equations. In Sect. 6, we discuss about error bound and convergence analysis of proposed method. Section 7 contains some numerical examples which confirm the applicability and efficiency of the proposed method. Section 7 states the conclusion of this paper.

2 Preliminaries

In the current section, the essential notations, definitions and the basic results relating to fuzzy calculus and fuzzy fractional calculus are presented.

Definition 1

(Dubois and Prade 1987) A fuzzy number is a function \(v:=\mathbb{R}\rightarrow [0,1]\) which satisfies the following properties:

  • v is upper semi-continuous function.

  • v is normal, that is, \(\exists t_{0}\) in \(\mathbb{R}\) for which \(v(t_{0})=1\).

  • v is fuzzy convex, that is,

    $$v(\lambda t+(1-\lambda )s)\ge \mathrm{min}\lbrace v(t),v(s)\rbrace $$

    for all \(t,s \in \mathbb{R}\), \(\lambda \in [0,1]\).

  • supp \(v:=\lbrace t \in \mathbb{R} \vert v(t)>0 \rbrace \) is the support of v, and its closure, i.e., \(cl(\mathrm{supp} \ v)\) is compact.

The r-level set of a fuzzy number v denoted by \([v]^r \) is defined as

$$\begin{aligned} {[}v]^r:=\lbrace t \in \mathbb{R} \vert v(t)\ge r \rbrace =[\underline{v}^{r},\overline{v}^{r}], \ \ \ 0<r\le 1 \end{aligned}$$
(2)

where \(\underline{v}^{r}:=\underline{v}(r)\) and \(\overline{v}^{r}:=\overline{v}(r)\) are bounded left-continuous, non-decreasing and non-increasing function in (0, 1], respectively, and \(v(0)=cl(\mathrm{supp}\ v)\). For \(u,v \in \mathbb{R}_\mathcal{F}, \lambda \in \mathbb{R}\), the addition and scalar multiplication are defined in terms of r-level sets, as follows:

  • \([u+v]^r=[u]^r+[v]^r=[\underline{u}^{r}+\underline{v}^{r},\overline{u}^{r}+\overline{v}^{r}]\),

  • \([\lambda u]^{r}=\lambda \cdot [u]^{r}=\left\{ \begin{array}{ll} \left[ \lambda \underline{u}^{r}, \lambda \overline{u}^{r}\right] , & \quad \lambda \ge 0, \\ \left[ \lambda \overline{u}^{r},\lambda \underline{u}^{r}\right] , & \quad \lambda <0. \end{array} \right. \)

The Hausdorff distance between two fuzzy numbers \(u,v \in \mathbb{R}_{\mathcal{F}}\) is defined by \(D:\mathbb{R}_{\mathcal{F}} \times \mathbb{R}_{\mathcal{F}}\rightarrow \mathbb{R}^{+}\),

$$\begin{aligned} D(u,v)=\underset{r \in [0,1]}{sup}\max \lbrace \vert \underline{u}^{r}-\underline{v}^{r}\vert , \vert \overline{u}^{r}-\overline{v}^{r} \vert \rbrace . \end{aligned}$$

It is easy to see that D is a metric in \(\mathbb{R}_{\mathcal{F}}\) and has the following properties (Wu and Gong 2001)

  1. 1.

    \(D(u+v,w+v)=D(u,w)\), \(\forall u,v,w \in \mathbb{R}_{\mathcal{F}}\),

  2. 2.

    \(D(ku,kv)=\vert k \vert D(u,v)\), \(\forall u,v \in \mathbb{R}_{\mathcal{F}} \quad \forall k \in \mathbb{R},\)

  3. 3.

    \(D(u+v,w+e)\le D(u,w)+D(v,e),\ \ \forall u,v,w,e \in \mathbb{R}_{\mathcal{F}}\)

  4. 4.

    \((\mathbb{R}_{\mathcal{F}},D)\) is a complete metric space.

Definition 2

(Bede and Gal 2005) Let \(u,v \in \mathbb{R}_\mathcal{F}\). If there exists \(w \in \mathbb{R}_\mathcal{F}\) such that \(u=v+w\), then w is called the Hukuhara difference of u and v, and it is denoted by \(u\ominus v\).

Definition 3

(Bede and Stefanini 2013) The generalized Hukuhara difference of two fuzzy number \(u,v\in \mathbb{R}_{\mathcal{F}}\) (gH-difference) is \(w\in \mathbb{R}_{\mathcal{F}}\) , which is defined as follows;

$$\begin{aligned} u\ominus _{gH}v=w \Leftrightarrow \left\{ \begin{array}{ll} \ \ \ \ ~ (i) & u=v+w \\ or \ \ (ii) & v=u+(-1)w. \end{array} \right. \end{aligned}$$

Definition 4

(Congxin and Cong 1997) A fuzzy-valued function \(f:[a,b] \rightarrow \mathbb{R}_{\mathcal{F}}\) is said to be continuous at \(t_0\in [a,b]\) if for each \(\varepsilon >0\) there is \(\delta >0\) such that \(D\left( f\left( t\right) ,f\left( t_0 \right) \right) <\varepsilon \) whenever \(\left| t-t_0\right| <\delta \). If f is continuous for each \(t\in [a,b]\) then we say that f is fuzzy continuous on [a, b].

On the set

$$\begin{aligned} C_{\mathcal{F}}[a,b]=\left\{ f:[a,b]\rightarrow \mathbb{R}_{\mathcal{F}}|f\, \mathrm{is\,continuous} \right\} {.}\end{aligned}$$

Definition 5

(Bica and Popescu 2014) Let \(f,g \in C_\mathcal{F}[a,b]\), the uniform distance between f and g is defined by

$$\begin{aligned} D^{*}(f,g)=\underset{t\in [a,b]}{sup}D(f(t),g(t)) \end{aligned}$$

\(\left( C_{\mathcal{F}}[a,b],D^*\right) \) is a complete metric space and we can derive corresponding properties of metric D for metric \(D^*\). (see Bica and Popescu 2014).

Definition 6

(Bede and Stefanini 2013)(gH-differentiable) Let \(f:(a,b)\rightarrow \mathbb{R}_{\mathcal{F}}\) and \(t_{0}\in (a,b)\). The generalized Hukuhara differentiable for f at \(t_{0}\) is defined as follows: If there exists an element \( f'_{gH}(t_{0})\in \mathbb{R}_{\mathcal{F}}\), such that

$$\begin{aligned} f'_{gH}(t_{0})=\lim _{h\rightarrow 0}\frac{f(t_{0}+h)\ominus _{gH} f(t_{0})}{h}. \end{aligned}$$
(3)

Definition 7

(Congxin and Ming 1992) The fuzzy-valued function \(f:[a,b]\rightarrow \mathbb{R}_{\mathcal{F}}\) is fuzzy Riemann integrable in \(\mathbf{I}\) if for any \( \epsilon >0 \), there exists \( \delta >0 \) such that for any division \(P=\lbrace [u,v];\xi \rbrace \) with the norms \(\varDelta (P)< \delta \), we have

$$\begin{aligned} D\left( \sum _{p}^{*}(v-u)f(\xi ), \mathbf{I}\right) <\epsilon , \end{aligned}$$

where \( \sum _{p}^{*} \) denotes the fuzzy summation. We choose to write

$$\begin{aligned} \mathbf{I}:=\int _{a}^{b}f(t)\mathrm{d}t. \end{aligned}$$

Note that, for the fuzzy Riemann integrable function \(f:[a,b]\rightarrow \mathbb{R}_{\mathcal{F}}\) where \( [f(t)]^{r}=\left[ \underline{f}^{r}(t),\overline{f}^{r}(t)\right] \), we have

$$\begin{aligned} \int _{a}^{b}[f(t)]^{r}\mathrm{d}t=\left[ \int _{a}^{b}\underline{f}^{r}(s)\mathrm{d}s,\int _{a}^{b}\overline{f}^{r}(s)\mathrm{d}s\right] \end{aligned}$$
(4)

for all \(r \in [0,1]\).

Throughout this paper, we denote the space of all integrable fuzzy-valued functions on the bounded interval [a, b] by \(L_{\mathcal{F}}[a,b]\), the space of fuzzy-valued functions that are absolutely continuous by \(A_{\mathcal{F}}[a,b]\) .

Definition 8

(Salahshour et al. 2012) Let \( f\in L_{\mathcal{F}}[a,b] \). The fuzzy Riemann–Liouville integral of fuzzy-valued function f is defined as follows:

$$\begin{aligned} I_{*,a}^q f (t):= \frac{1}{\varGamma (q)} \int _{a}^{t}{\frac{f(s)\mathrm{d}s}{(t-s)^{1-q}} },~~~~a<s<t, \end{aligned}$$
(5)

where \( 0<q\le 1. \)

Lemma 1

(Salahshour et al. 2012) Let \( f\in L_{\mathcal{F}}[a,b] \) and

$$\begin{aligned} {[}f(t)]^{r}=\left[ \underline{f}^{r}(t),\overline{f}^{r}(t)\right] , \end{aligned}$$

then the parametric form of the fuzzy Riemann–Liouville integral of f can be expressed by

$$\begin{aligned} {[}I_{*,a}^q f(t)]^r=\left[ I_{a}^q \underline{f}^{r}(t), I_{a}^q \overline{f}^{r} (t)\right] ,\quad 0<q\le 1 \end{aligned}$$

where

$$\begin{aligned} I_{a}^q g(t):= \frac{1}{\varGamma (q)} \int _{a}^{t}{\frac{g(s)\mathrm{d}s}{(t-s)^{1-q}} },~~~~a<s<t, \end{aligned}$$

for a real function \( g:[a,b]\rightarrow \mathbb{R} \).

Definition 9

(Shabestari et al. 2018a; Allahviranloo et al. 2014) Let \(f\in A_{\mathcal{F}}[a,b]\) and \(q \in \mathbb{R}^{+}\). The Caputo fractional gH-derivative of f is defined by

$$\begin{aligned} _{gH}D_{*,a}^{q}f(t):=\frac{1}{\varGamma (\lceil q\rceil - q)} \int _{a}^{t}(t-s)^{\lceil q\rceil - q-1} f^{\lceil q\rceil }_{gH}(s)\mathrm{d}s. \end{aligned}$$
(6)

Definition 10

(Shabestari et al. 2018a; Allahviranloo et al. 2014) Let \(f\in A_{\mathcal{F}}(a,b)\) that is Caputo fractional gH-differentiable at \(t_{0}\in (a,b)\). We say that f is \(^{cf}[(i)-gH]\)-differentiable at \(t_{0}\) if

$$\begin{aligned} {[}_{gH}D_{*,a}^qf)(t_0)]^r=[(D_{a}^{q}\underline{f}^{r})(t_0), (D_{a}^{q}\overline{f}^{r})(t_0)], \end{aligned}$$

and that f is \(^{cf}[(ii)-gH]\)-differentiable, if

$$\begin{aligned} {[}_{gH}D_{*,a}^{q}f)(t_0)]^{r}=[(D_{a}^{q}\overline{f}^{r}) (t_0),(D_{a}^{q}\underline{f}^{r})(t_0)], \end{aligned}$$

where

$$\begin{aligned}&D_{a}^{q}g(t):=\frac{1}{\varGamma (m - q)} \int _{a}^{t}(t-s)^{m -q-1} g^{(m)}(s)\mathrm{d}s, \\&m-1< q \le m, ~m\in \mathbb{N}, \end{aligned}$$

for a real function \( g:[a,b]\rightarrow \mathbb{R} \).

Lemma 2

(Shabestari et al. 2018a; Allahviranloo et al. 2014) Let \(0<q \le 1\) and \(f\in A_{\mathcal{F}}[a,b]\). Then,

$$\begin{aligned} I_{*,a}^{q}(_{gH}D_{*,a}^{\alpha }f)(t)=f(t)\ominus _{gH}f(a). \end{aligned}$$
(7)

3 Existence and uniqueness

In this section, we prove the existence and uniqueness of solutions for Eq. (1) under Caputo gH-differentiability. We are going to utilize the ideas presented in Shabestari et al. (2018a).

Theorem 1

Assume that real function \( \kappa (t,s) \) be continuous and positive on \( 0\le t,s\le 1 \), \( f\in C_{\mathcal{F}}[0,1] \) and \(G:\mathbb{R}_ {\mathcal{F}} \rightarrow \mathbb{R}_\mathcal{F}\) in Eq. (1) satisfies in Lipschitz condition

$$\begin{aligned} D(G(u),G(v)) \le L\cdot D(u,v),\ \ \forall u,v\in \mathbb{R}_\mathcal{F}, \end{aligned}$$

with constant \(L>0\). If \(\frac{L\gamma _{0}}{\varGamma (1+\alpha )} < 1\) such that \( \gamma _{0}:=\underset{t,s \in [0,1]}{\max \vert \kappa (t,s) \vert } \). Then, Eq. (1) has a unique solution on the interval [0, 1].

Proof

From Lemma 2, the fuzzy integro-differential equation (1) is equivalent to

$$\begin{aligned} y(t)\ominus _{gH}y(0)=I_{*,0}^{\alpha }f(t)+I_{*,0}^{\alpha } \int _{0}^{1}\kappa (t,s)G(y(s))\mathrm{d}s, \end{aligned}$$

and from Lemma 3.2 in Shabestari et al. (2018a), we have

$$\begin{aligned} y(t)=y(0)+I_{*,0}^{\alpha }f(t)+I_{*,0}^{\alpha } \int _{0}^{1}\kappa (t,s)G(y(s))\mathrm{d}s \end{aligned}$$
(8)

when y(t) be \(^{cf}[(i)-gH]\)-differentiable and

$$\begin{aligned} y(t)=y(0)\ominus (-1)\left( I_{*,0}^{\alpha }f(t)+I_{*,0}^{\alpha } \int _{0}^{1}\kappa (t,s)G(y(s))\mathrm{d}s \right) \end{aligned}$$
(9)

for y(t) be \(^{cf}[(ii)-gH]\)-differentiable.

First, consider the case \(^{cf}[(i)-gH]\)-differentiable of y(t). The operator \(F:C_{\mathcal{F}}[a,b]\rightarrow C_{\mathcal{F}}[a,b]\), defined as

$$\begin{aligned} Fy(t)= y(0)+\widehat{f}(t)+\frac{1}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}(My)(s)\mathrm{d}s, \end{aligned}$$
(10)

transform Eq. (8) into a fixed point problem \(y(t)=Fy(t),\) where

$$\begin{aligned} \widehat{f}(t)=I_{*,0}^{\alpha } f(t),\ \ \ My(t)= \int _{0}^{1}\kappa (t,s)G(y(s))\mathrm{d}s. \end{aligned}$$

Let \( \lbrace y_{n}\rbrace \) be a sequence in \(C_{\mathcal{F}}[0,1]\) which \( y_{n}\rightarrow y\) for \(n\rightarrow \infty \). Then,

$$\begin{aligned}&D(Fy_{n},Fy) \\&=\frac{1}{\varGamma (\alpha )}D(\int _{0}^{t}(t-s)^{\alpha -1} (My_{n})(s)\mathrm{d}s,\int _{0}^{t}(t-s)^{\alpha -1}(My)(s)\mathrm{d}s) \\&\le \frac{1}{\varGamma (\alpha )}\left( \int _{0}^{t}(t-s)^{\alpha -1}D\left( My_{n}(s),My(s)\right) \mathrm{d}s\right) \\&\le \frac{1}{\varGamma (\alpha )} D^{*}(My_{n},My)\int _{0}^{t}(t-s)^{\alpha -1}\mathrm{d}s \\&= \frac{t^{\alpha }}{\varGamma (1+\alpha )} D^{*}(My_{n},My). \end{aligned}$$
(11)

Since the operator M is continuous [0, 1], (see Theorem 5 in Ezzati and Ziari 2013) we obtain

$$\begin{aligned} D(Fy_{n},Fy)\le \left( \frac{t^{\alpha }}{\varGamma (1+\alpha )} D^{*}(My_{n},My)\right) \rightarrow 0,\ \ n\rightarrow \infty . \end{aligned}$$

Thus, F is a fuzzy continuous operator. Also, for every \(y_{1}, y_{2}\in C_\mathcal{F}[0,1]\), we have

$$\begin{aligned}&D\left( My_{1}(s),My_{2}(s)\right) \\ &\quad =D\left( \int _{0}^{1}\kappa (t,s)G(y_{1}(s))\mathrm{d}s, \int _{0}^{1}\kappa (t,s)G(y_{2}(s))\mathrm{d}s \right) \\ &\quad \le \int _{0}^{1}|\kappa (t,s)|D\left( G(y_{1}(s)),G(y_{2}(s))\right) \mathrm{d}s \\ & \quad \le L\gamma _{0} D^{*}(y_{1},y_{2}). \end{aligned}$$
(12)

From (12), we have

$$\begin{aligned}&D(Fy_{1},Fy_{2}) \\&\le \frac{1}{\varGamma (\alpha )}\left( \int _{0}^{t}(t-s)^{\alpha -1}D\left( My_{1}(s),My_{2}(s)\right) \mathrm{d}s\right) \\ &\quad \le \frac{L\gamma _{0} D^{*}(y_{1},y_{2})}{\varGamma (\alpha )} \int _{0}^{t}(t-s)^{\alpha -1}\mathrm{d}s \\ &\quad \le \frac{L\gamma _{0}}{\varGamma (1+\alpha )} D^{*}(y_{1},y_{2}). \end{aligned}$$
(13)

Thus, if \(\frac{L\gamma _{0}}{\varGamma (1+\alpha )} < 1\), the operator F is a contraction on the Banach space \((C_\mathcal {F}[0,1],D^*)\). Consequently, the Banach fixed point principle implies that F has unique fixed point which is \(^{cf}[(i)-gH]\)-differentiable solution of Eq. (8). The proof for the case \(^{cf}[(ii)-gH]\)-differentiable will be obtained in similar manner and hence is omitted. \(\square \)

4 Shifted fractional-order Jacobi functions

The Jacobi polynomials, denoted by \( J_{n}^{(a,b)}(t),\ a,b >-1 \), are the eigenfunctions of the singular Sturm–Liouville problem (see Canuto et al. 2006 for more detail)

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( (1-t)^{a+1}(1+t)^{b+1}\frac{\mathrm{d}}{\mathrm{d}t}f(t)\right) +\gamma (1-t)^{a}(1+t)^{b}f(t)=0, \ \end{aligned}$$
(14)

where \(t\in [-1,1]\) and corresponding eigenvalues are \( \gamma _{n}^{(a,b)}=n(n+a+b+1) \), and satisfy the following orthogonality:

$$\begin{aligned} \int _{-1}^{1}J_{i}^{(a,b)}(t)J_{j}^{(a,b)}(t)\omega ^{(a,b)}(t)\mathrm{d}t=\lambda _{j}^{(a,b)}\delta _{i,j} \end{aligned}$$
(15)

where \(\omega ^{(a,b)}(t)=(1-t)^{a}(1+t)^{b}\) is the Jacobi weight function and

$$\begin{aligned} \lambda _{i}^{(a,b)}=\frac{2^{a+b+1}\varGamma (i+a+1)\varGamma (i+b+1)}{(2i+a+b+1)i!\varGamma (i+a+b+1)} \end{aligned}$$

is the normalization factor and \( \delta _{i,j} \) is the Kronecker delta function. The three-term recursion formula is given by

$$\begin{aligned}&J_{0}^{(a,b)}(t)=1, \ \ \ \ J_{1}^{(a,b)}(t)=\frac{a+b+2}{2}t+\frac{a-b}{2}, \end{aligned}$$
(16)
$$\begin{aligned}&J_{n+1}^{(a,b)}(t)=(\gamma _{n}^{(a,b)}t-\theta _{n}^{(a,b)}) J_{n}^{(a,b)}(t)-\vartheta _{n}^{(a,b)}J_{n-1}^{(a,b)}(t),\ \ \ \end{aligned}$$
(17)

for \(n=1,2,\ldots \), where

$$\begin{aligned} \gamma _{n}^{(a,b)} &= \frac{(2n+a+b+1)(2n+a+b+2)}{2(n+1)(n+a+b+1)},\\ \theta _{n}^{(a,b)}&= \frac{(b^{2}-a^{2})(2n+a+b+1)}{2(n+1)(n+a+b+1)(2n+a+b)}, \\ \vartheta _{n}^{(a,b)}&= \frac{(n+a)(n+b)(2n+a+b+2)}{(n+1)(n+a+b+1)(2n+a+b)}. \end{aligned}$$

The shifted Jacobi polynomials are defined on [0, 1] as

$$\begin{aligned} \widehat{J}_{n}^{(a,b)}(t)=J_{n}^{(a,b)}(2t-1), \end{aligned}$$

with weight function \(\widehat{\omega } ^{(a,b)}(t)=(1-t)^{a}t^{b}\). The orthogonality condition of the shifted Jacobi polynomials is as follows:

$$\begin{aligned} \int _{0}^{1}\widehat{J}_{i}^{(a,b)}(t)\widehat{J}_{j}^{(a,b)}(t)\widehat{\omega }^{(a,b)}(t)\mathrm{d}t=\widehat{\lambda }_{j}^{(a,b)}\delta _{i,j} \end{aligned}$$
(18)

where \( \widehat{\lambda }_{j}^{(a,b)}=\frac{\lambda _{j}^{(a,b)}}{2^{a+b+1}} \). Moreover, the analytic form of the shifted Jacobi polynomials on [0, 1] is given by

$$\begin{aligned} \widehat{J}_{n}^{(a,b)}(t)=\sum _{i=0}^{n}\frac{(-1)^{n-i}\varGamma (n+b+1)\varGamma (n+a+b+1+i)}{i!(n-i)!)\varGamma (i+b+1)\varGamma (n+a+b+1)}t^{i},\ \end{aligned}$$
(19)

for \(n=0,1,\ldots \). The shifted fractional Jacobi functions (SFJFs) of order \(\nu \) on [0,1] are given by replace \(t\rightarrow t^\nu \) in (19) as follows (Bhrawy and Zaky 2015):

$$\begin{aligned} \widehat{J}_{n}^{(a,b,\nu )}(t)=\sum _{i=0}^{n}\frac{(-1)^{n-i}\varGamma (n+b+1)\varGamma (n+a+b+1+i)}{i!(n-i)!)\varGamma (i+b+1)\varGamma (n+a+b+1)}t^{i\nu }. \end{aligned}$$
(20)

These new fractional polynomial basis form a complete space \( L^{2}_{{\chi } ^{(a,b,\nu )}}[0,1] \) with the following weighted inner product condition

$$\begin{aligned} {<}\widehat{J}_{i}^{(a,b,\nu )}(t),\widehat{J}_{j}^{(a,b,\nu )}(t)>_{\chi ^{a,b,\nu }(t)}=\widehat{\lambda }_{j}^{(a,b)}\delta _{i,j}, \end{aligned}$$
(21)

where \(\chi ^{a,b,\nu }(t)=\nu (1-t^{\nu })^{a}t^{\nu b+\nu -1}\).

4.1 Function approximation

We define

$$\begin{aligned} \mathbf{P}_{N,\nu }=span\lbrace \widehat{J}_{n}^{(a,b,\nu )}(t):~0\le n \le N\rbrace , \end{aligned}$$

as the finite-dimensional fractional-polynomial space. By the orthogonality (21), any \( u\in L^{2}_{{\chi } ^{(a,b,\nu )}}[0,1] \) can be expanded in terms of SFJFs as (Bhrawy and Zaky 2015)

$$\begin{aligned} u(t)=\sum _{i=0}^{\infty }{u_{i}}\widehat{J}_{i}^{(a,b,\nu )}(t) , \end{aligned}$$
(22)
$$\begin{aligned} u_{i}=\big ( \widehat{\lambda }_{j}^{(a,b)}\big )^{-1}\int _{0}^{1}{u(x)\widehat{J}_{i}^{(a,b,\nu )}(t)\chi ^{a,b,\nu }(t)\mathrm{d}t } \end{aligned}$$
(23)

and they hold the Parseval identity:

$$\begin{aligned} \Vert u\Vert _{\chi ^{a,b,\nu }(t)}^2=\sum _{i=0}^{\infty }{\widehat{\lambda }_{i}^{(a,b)} |u_i|^2 }. \end{aligned}$$

Consider the \( u\in L^{2}_{{\chi } ^{(a,b,\nu )}}[0,1] \)-orthogonal projection upon \( \mathbf{P}_{N,\nu } \), defined by

$$\begin{aligned} \left( u- u_N,v\right) _{{\chi } ^{(a,b,\nu )}}=0,~~~~\forall v\in \mathbf{P}_{N,\nu } \end{aligned}$$

By definition, we have

$$\begin{aligned} u_N(t)=\sum _{i=0}^{N}u_i\widehat{J}_{i}^{(a,b,\nu )}(t) ={\mathbf{U}}^T\mathbf{\Phi }(t). \end{aligned}$$
(24)

where

$$\begin{aligned} \mathbf{U}&= [u_{0},u_{1},u_{2},\ldots ,u_{N}]^{T}, \\ \mathbf{\Phi }(t)&= [\widehat{J}_{0}^{(a,b,\nu )}(t), \widehat{J}_{1}^{(a,b,\nu )}(t),\ldots ,\widehat{J}_{N}^{(a,b,\nu )}(t)]^{T}=\varvec{\Omega } \mathbf{X}(t), \end{aligned}$$
(25)

and

$$\begin{aligned} \mathbf{X}(t)=[1,t^{\nu },t^{2\nu },\ldots ,t^{N\nu }]^{T}, \end{aligned}$$

where \(\varvec{\Omega }=[\phi _{i,j}]_{(N+1)\times (N+1)}\) is the lower triangular matrix and is defined as follows:

$$\begin{aligned} \phi _{i,j}=\left\{ \begin{array}{l} \frac{(-1)^{i-j}\varGamma (i+b)\varGamma (i+j+a+b-1)}{(j-1)!(i-j)!\varGamma (j+b)\varGamma (i+a+b)},~~j\le i \\ \\ 0,~~i<j \end{array} \right. \end{aligned}$$

for \( i,j=1,\ldots ,N+1 \).

Similarly, we can approximate \(\kappa (t,s)\) by SFJFs as follows:

$$\begin{aligned}&\kappa (t,s)\simeq \sum _{i=0}^{N}\sum _{j=0}^{N}k_{i,j}\widehat{J}_{i}^{(a,b,\nu )}(t) \widehat{J}_{j}^{(a,b,\nu )}(s)=\mathbf{\Phi }^{T}(t)\mathbf{K}\mathbf{\Phi }(s), \end{aligned}$$
(26)

the coefficients \(k_{i,j}\) can be calculated by

$$\begin{aligned} k_{i,j}=\frac{1}{\widehat{\lambda }_{i}^{(a,b)} \widehat{\lambda }_{j}^{(a,b)}}&\int _{0}^{1}\int _{0}^{1}\kappa (t,s)\widehat{J}_{i}^{(a,b,\nu )}(t) \widehat{J}_{j}^{(a,b,\nu )}(s) \\&\chi ^{a,b,\nu }(t)\chi ^{a,b,\nu }(s)\mathrm{d}t\mathrm{d}s. \end{aligned}$$
(27)

Lemma 3

(Kamali and Saeedi 2018) If \(u_{N}(t)\in \mathbf{P}_{N,\nu }\) is the best approximation of smooth function u(t), then

$$\begin{aligned} \Vert u-u_{N}\Vert _{\infty } \le \frac{C}{2^{2N+1}(N+1)!}, \end{aligned}$$
(28)

that, \(C=\underset{t \in [0,1]}{\mathop {\max }} \vert {\frac{d^{N+1}u(t)}{d t^{N+1}}} \vert \).

Lemma 4

(Bhrawy and Zaky 2016) If \( U=[u_{0},u_{1},\ldots ,u_{N}]^{T}\), then

$$\begin{aligned} \mathbf{\Phi }(t)\mathbf{\Phi }^{T}(t)U \simeq \widehat{U}\mathbf{\Phi }(t), \end{aligned}$$
(29)

with

$$\begin{aligned} \widehat{U}=[\widehat{u}_{i,j}]_{i,j=0}^{N},\ \ \ \widehat{u}_{i,j}=\sum _{l=0}^{N}u_{l}\mu _{i,l,j}. \end{aligned}$$
(30)

and \( \mu _{i,l,j} \) will be defined throughout the proof.

Proof

Form left side of (29), we have

$$\begin{aligned} \mathbf{\Phi }(t)\mathbf{\Phi }^{T}(t)U=\left( \begin{array}{c} \sum _{j=0}^{N}u_{j}\widehat{J}_{0}^{(a,b,\nu )}(t)\widehat{J}_{j}^{(a,b,\nu )}(t) \\ \sum _{j=0}^{N}u_{j}\widehat{J}_{1}^{(a,b,\nu )}(t)\widehat{J}_{j}^{(a,b,\nu )}(t) \\ \vdots \\ \sum _{j=0}^{N}u_{j}\widehat{J}_{N}^{(a,b,\nu )}(t)\widehat{J}_{j}^{(a,b,\nu )}(t)\\ \end{array} \right) . \end{aligned}$$
(31)

Approximating

$$\begin{aligned} \widehat{J}_{i}^{(a,b,\nu )}(t)\widehat{J}_{j}^{(a,b,\nu )}(t)\simeq \sum _{k=0}^{N}\mu _{i,j,k}\widehat{J}_{k}^{(a,b,\nu )}(t) \end{aligned}$$

for \(i,j=0,\ldots ,N\), we have

$$\begin{aligned} \sum _{j=0}^{N}u_{j}\widehat{J}_{i}^{(a,b,\nu )}(t)&\widehat{J}_{j}^{(a,b,\nu )}(t) \\&\simeq \sum _{j=0}^{N}u_{j}\left( \sum _{k=0}^{N}\mu _{i,j,k}\widehat{J}_{k}^{(a,b,\nu )}(t)\right) \\&=\sum _{k=0}^{N}\left( \sum _{j=0}^{N}u_{j}\mu _{i,j,k}\right) \widehat{J}_{k}^{(a,b,\nu )}(t) \\&=\sum _{k=0}^{N}\widehat{u}_{i,k}\widehat{J}_{k}^{(a,b,\nu )}(t). \end{aligned}$$
(32)

Inserting (32) into (31) leads to the desired result. \(\square \)

4.2 Operational matrix of the fractional-order integration

Theorem 2

(Bhrawy and Zaky 2016) Let \( \mathbf{\Phi }(t)\) be fractional Jacobi polynomials vector defined in (25). Then, for \( \alpha >0 \)

$$\begin{aligned} I_{0}^{\alpha }\mathbf{\Phi }(t)\simeq \mathbf{P}_\alpha \mathbf{\Phi }(t), \end{aligned}$$

where \(\mathbf{P}_\alpha =\varvec{\Omega }\mathbf{D}\mathbf{E}\) and

$$\begin{aligned} \mathbf{D}=diag[\frac{\varGamma (1)}{\varGamma (\alpha +1)},\frac{\varGamma (\nu +1)}{\varGamma (\alpha +\nu +1)},\ldots ,\frac{\varGamma (n\nu +1)}{\varGamma (n\nu +\alpha +1)}]. \end{aligned}$$

and \( \mathbf{E} \) will be defined throughout the proof.

Proof

Since \( I^{\alpha }_0t^\nu =\frac{\varGamma (\nu +1)}{\varGamma (\alpha +\nu +1)}t^{\nu +\alpha } \), we have

$$\begin{aligned} I_{0}^{\alpha }\mathbf{\Phi }(t)=I_{0}^{\alpha }\varvec{\Omega }\mathbf{X}(t)&=\varvec{\Omega }I_{0}^{\alpha }\mathbf{X}(t) \\&=\varvec{\Omega }[I_{0}^{\alpha }1,I_{0}^{\alpha }t^\nu , I_{0}^{\alpha }t^{2\nu },\ldots ,I_{0}^{\alpha }t^{n\nu }]^{T} \\&=\varvec{\Omega }\mathbf{D}[t^{\alpha },t^{\nu +\alpha },\ldots ,t^{n\nu +\alpha }]^{T}. \end{aligned}$$
(33)

By approximating \(t^{i\nu +\alpha }\) by \(n+1\) terms of fractional Jacobi polynomials, we get that

$$\begin{aligned} t^{i\nu +\alpha }\simeq \sum _{j=0}^{n}\xi _{i,j}\widehat{J}_{j}^{(a,b,\nu )}(t), \end{aligned}$$
(34)

where \(\xi _{i,j}\) is given from (21) as follows:

$$\begin{aligned} \xi _{i,j}=\frac{1}{\widehat{\lambda }_{j}^{(a,b)}}\int _{0}^{1}t^{i\nu +\alpha }\widehat{J}_{j}^{(a,b,\nu )}(t)\chi ^{a,b,\nu }(t)\mathrm{d}t. \end{aligned}$$
(35)

Therefore, by setting \( \mathbf{E}=[\xi _{i,j}]_{i,j=0}^{n}\), the desired result can be obtain. \(\square \)

Lemma 5

Let \(u\in C[0,1]\) and \( \kappa (t,s) \) be a continuous function on \( 0\le t,s\le 1 \), operator \(L:C[0,1]\rightarrow C[0,1]\), defined as

$$\begin{aligned} Lu(t)=I^{\alpha }_{0}\left( \int _{0}^{1}\kappa (t,s)u^n(s)\mathrm{d}s\right) , \end{aligned}$$

then,

$$\begin{aligned} Lu(t)\simeq \mathbf{\Phi }^{T}(t){\mathbf{P}}_{\alpha }^{T}\mathbf{K}\mathbf{\Psi }(U^{n})^{T}U \end{aligned}$$
(36)

where the matrix \( {\mathbf{P}}_{\alpha }^{T} \) and \( \mathbf{K} \) are defined above.

Proof

Let \(u(t)\simeq U^{T}\mathbf{\Phi }(t)\), where \(U=[u_{0},\ldots ,u_{N}]^{T}\). From Lemma 4, \(u^n(t)\simeq U^{T}\ {\widehat{U}}^{n-1} \mathbf{\Phi }(t)\). By substituting matrix representation (26) and using Theorem 2 we obtain

$$\begin{aligned}&(Lu)(t) \\&= \frac{1}{\varGamma (\alpha )}\int _{0}^{t}\int _{0}^{1}(t-s)^{\alpha -1}\kappa (s,x)u^n(x)\mathrm{d}x\mathrm{d}s \\&\simeq \underbrace{\frac{1}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}\mathbf{\Phi }^{T}(s)\mathrm{d}s}_{\mathbf{\Phi }^{T}(t){\mathbf{P}}_{\alpha }^{T}} \mathbf{K}\underbrace{\int _{0}^{1}\mathbf{\Phi }(x)\mathbf{\Phi }^{T}(x)\mathrm{d}x}_{\mathbf{\Psi }}({\widehat{U}}^{n-1})^{T}U \\&=\mathbf{\Phi }^{T}(t){\mathbf{P}}_{\alpha }^{T}\mathbf{K}\mathbf{\Psi }({\widehat{U}}^{n-1})^{T}U, \end{aligned}$$
(37)

which completes the proof. \(\square \)

5 Numerical method

Consider the following fuzzy Fredholm nonlinear fractional integro-differential equation, under the conditions of Theorem 1,

$$\begin{aligned} \left\{ \begin{array}{ll} (_{gH}D_{*,0}^{\alpha }y)(t)=f(t)+ \int _{0}^{1}\kappa (t,s)y^n(s)\mathrm{d}s, \\ \\ y(0)=\tilde{y} _{0}\in \mathbb{R}_\mathcal {F}. \end{array} \right. \end{aligned}$$
(38)

Applying \(I_{*,0}^\alpha \) on both sides of Eq. (38). To find the numerical solution of the initial value problem (38), we will the following expressions:

Case 1.

Let assume that y(s) is \(^{cf}[(i)-gH]\)-differentiable and \( \left[ y^n(s)\right] ^r=\left[ \left( \underline{y}^{r}(s)\right) ^n,\left( \overline{y}^{r}(s)\right) ^n \right] \). It means that \(y^n(s)\) is a fuzzy number-valued function. So by Eq. (8), we have the following fractional integro-differential equations system:

$$\begin{aligned} \tilde{\mathbf{Y}}(t,r)=\tilde{\mathbf{Y}}(0,r)+I_{0}^{\alpha }\tilde{\mathbf{F}}(t,r)+I_{0}^{\alpha } \int _{0}^{1}\kappa (t,s){\tilde{\mathbf{Y}}^n(s,r)}(s)\mathrm{d}s \end{aligned}$$
(39)

where \( \tilde{\mathbf{Y}}(t,r)=\left( \begin{array}{c} \underline{y}^{r}(t) \\ \overline{y}^{r}(t) \\ \end{array} \right) ,\tilde{\mathbf{Y}}^n(t,r)=\left( \begin{array}{c} \left( \underline{y}^{r}(t)\right) ^n \\ \left( \overline{y}^{r}(t)\right) ^n \\ \end{array} \right) \) and \(\tilde{\mathbf{F}}(t,r)=\left( \begin{array}{c} \underline{f}^{r}(t) \\ \overline{f}^{r}(t) \\ \end{array} \right) \).

It is clear that

$$\begin{aligned} \begin{array}{c} \underline{y}^{r}(t)= \underline{y}^{r}_0+I^{\alpha }_{0} \underline{f}^{r}(t) + I^{\alpha }_{0} \int _{0}^{1}\kappa (t,s) \left( \underline{y}^{r}(s)\right) ^n\mathrm{d}s \\ \overline{y}^{r}(t)= \overline{y}^{r}_0+I^{\alpha }_{0} \overline{f}^{r}(t) + I^{\alpha }_{0} \int _{0}^{1}\kappa (t,s) \left( \overline{y}^{r}(s)\right) ^n\mathrm{d}s \end{array} \end{aligned}$$
(40)

Now, we explain the propose method to solve Eqs. (40). In order to apply SFJFs in (40), from Theorem 2, we can write

$$\begin{aligned} \begin{array}{c} I^{\alpha }_{0}\underline{f}^{r}(t) \simeq I^{\alpha }_{0} \underline{\mathbf{F}}_{r}^{T}\mathbf{\Phi }(t)= \underline{\mathbf{F}}_{r}^{T}I^{\alpha }_{0}\mathbf{\Phi }(t)=\underline{\mathbf{F}}_{r}^{T} \mathbf{P} \mathbf{\Phi }(t),\\ I^{\alpha }_{0}\overline{f}^{r}(t) \simeq I^{\alpha }_{0} \overline{\mathbf{F}}_{r}^{T}\mathbf{\Phi }(t)= \overline{\mathbf{F}}_{r}^{T}I^{\alpha }_{0}\mathbf{\Phi }(t)=\overline{\mathbf{F}}_{r}^{T} \mathbf{P} \mathbf{\Phi }(t), \end{array} \end{aligned}$$
(41)

and for fuzzy initial condition \(y_{0}\) we can write

$$\begin{aligned}&\underline{y}^{r}_{0} \simeq \underline{\mathbf{Y}}^{T}_{0,r}\mathbf{\Phi }(t)\ \ , \overline{y}^{r}_{0} \simeq \overline{\mathbf{Y}}^{T}_{0,r}\mathbf{\Phi }(t). \end{aligned}$$
(42)

Also, the unknown functions \( \underline{y}^{r}(t),~ \overline{y}^{r}(t) \) are approximated by SFJFs as follows:

$$\begin{aligned} \underline{y}^{r}(t)\simeq \mathbf{\Phi }^{T}(t)\underline{\mathbf{Y}}_{r}~~,\overline{y}^{r}(t)\simeq \mathbf{\Phi }^{T}(t)\overline{\mathbf{Y}}_r \end{aligned}$$
(43)

where \( \underline{\mathbf{Y}}_{r}=[\underline{y}^{r}_{0},\underline{y}^{r}_{1},\ldots ,\underline{y}^{r}_{N}]^{T} \), and \( \overline{\mathbf{Y}}_{r}=[\overline{y}^{r}_{0},\overline{y}^{r}_{1},\ldots ,\overline{y}^{r}_{N}]^{T} \).

By inserting matrix relations (36) and (41)–(43) in (40) , we get

$$\begin{aligned} \mathbf{\Phi }^{T}(t)\underline{\mathbf{Y}}_{r}&= \mathbf{\Phi }^{T}(t)\underline{\mathbf{Y}}_{0,r}+\mathbf{\Phi }^{T}(t){\mathbf{P}}^{T}\underline{\mathbf{F}}^{r} \\ &\quad + \mathbf{\Phi }^{T}(t){\mathbf{P}}^{T}\mathbf{K}\mathbf{\Psi }(\underline{{\widehat{Y}}}^{n-1})^{T}\underline{\mathbf{Y}}_{r}+\underline{\mathbf{R}}_{r}(t), \\ \mathbf{\Phi }^{T}(t)\overline{\mathbf{Y}}_{r}&=\mathbf{\Phi }^{T}(t)\overline{\mathbf{Y}}_{0,r} +\mathbf{\Phi }^{T}(t){\mathbf{P}}^{T}\overline{\mathbf{F}}^{r} \\ &\quad +\mathbf{\Phi }^{T}(t){\mathbf{P}}^{T}\mathbf{K}\mathbf{\Psi }(\overline{{\widehat{Y}}}^{n-1})^{T}\overline{\mathbf{Y}}_{r}+\overline{\mathbf{R}}_{r}(t). \end{aligned}$$
(44)

in which the terms \(\underline{\mathbf{R}}_{r}(t), \overline{\mathbf{R}}_{r}(t)\) are “residual function”. Now, based on spectral Tau method, we must have

$$\begin{aligned} {<}\underline{\mathbf{R}}_{r}(t),\widehat{J}_{i}^{(a,b,\nu )}(t)>_{\chi ^{(a,b,\nu )}}=<\overline{\mathbf{R}}_{r}(t),\widehat{J}_{i}^{(a,b,\nu )}(t)>_{\chi ^{(a,b,\nu )}}=0, \end{aligned}$$
(45)

for \(i=0,\ldots ,N\), where \(r\in [0,1]\). Then, a simple rearrangement of Eqs. (44) yields

$$\begin{aligned}&\underline{\mathbf{Y}}_{r}- \underline{\mathbf{Y}}_{0,r}-{\mathbf{P}}^{T}\underline{\mathbf{F}}^{r}-{\mathbf{P}}^{T}\mathbf{K}\mathbf{\Psi }((\underline{{\widehat{Y}}}^{n-1})^{T}\underline{\mathbf{Y}}_{r}=0, \\&\overline{\mathbf{Y}}_{r} -\overline{\mathbf{Y}}_{0,r} -{\mathbf{P}}^{T}\overline{\mathbf{F}}^{r}-{\mathbf{P}}^{T}\mathbf{K}\mathbf{\Psi }(\overline{{\widehat{Y}}}^{n-1})^{T}\overline{\mathbf{Y}}_{r}=0. \end{aligned}$$
(46)

with unknown vectors \(\underline{\mathbf{Y}}_{r}\) and \(\overline{\mathbf{Y}}_{r}\) (see Ahmadian et al. 2013; Canuto et al. 2006 for more detail). By solving this system of equations, the approximate solution \(y^{r}_{N}(t)\) will be obtained for \(r\in [0,1]\).

Case 2.

Let assume that y(t) is \(^{cf}[(i)-gH]\)-differentiable and \( \left[ y^n(t)\right] ^r=\left[ \left( \underline{y}^{r}(t)\right) ^n,\left( \overline{y}^{r}(t)\right) ^n \right] \), so by Eq. (9), we have the following fractional integro-differential equations system:

$$\begin{aligned} \tilde{\mathbf{Y}}(t,r)&=\tilde{\mathbf{Y}}(0,r)\\& \ominus (-1)\left( I_{0}^{\alpha }\tilde{\mathbf{F}}(t,r)+I_{0}^{\alpha } \int _{0}^{1}\kappa (t,s){\tilde{\mathbf{Y}}^n(s,r)}(s)\mathrm{d}s\right) \end{aligned}$$
(47)

Using definition of Hukuhara difference, system (47) can be written as follows:

$$\begin{aligned} \begin{array}{c} \underline{y}^{r}(t)= \underline{y}^{r}_0+I^{\alpha }_{0} \overline{f}^{r}(t) + I^{\alpha }_{0} \int _{0}^{1}\kappa (t,s) \left( \overline{y}^{r}(s)\right) ^n\mathrm{d}s \\ \overline{y}^{r}(t)= \overline{y}^{r}_0+I^{\alpha }_{0} \underline{f}^{r}(t) + I^{\alpha }_{0} \int _{0}^{1}\kappa (t,s) \left( \underline{y}^{r}(s)\right) ^n\mathrm{d}s \end{array} \end{aligned}$$
(48)

Similarly as the Case 1, we obtain

$$\begin{aligned}&\underline{\mathbf{Y}}_{r}=\underline{\mathbf{Y}}_{0,r}+{\mathbf{P}}^{T}\overline{\mathbf{F}}^{r}+{\mathbf{P}}^{T}\mathbf{K}\mathbf{\Psi }(\overline{{\widehat{Y}}}^{n-1})^{T}\overline{\mathbf{Y}}_{r}, \\&\overline{\mathbf{Y}}_{r} =\overline{\mathbf{Y}}_{0,r} +{\mathbf{P}}^{T}\underline{\mathbf{F}}^{r}+{\mathbf{P}}^{T}\mathbf{K}\mathbf{\Psi }(\underline{{\widehat{Y}}}^{n-1})^{T}\underline{\mathbf{Y}}_{r}. \end{aligned}$$
(49)

6 Error analysis

Assume that the fuzzy function \( y_N(t) \) is the approximate solution of Eq. (1) which obtained by means of SFJFs, then

$$\begin{aligned} {[}y_{N}(t)]^r&=[\underline{y}^{r}_{N}(t),\overline{y}^{r}_{N}(t)]=\left[ \mathbf{\Phi }^{T}(t)\underline{\mathbf{Y}}_{r},\mathbf{\Phi }^{T}(t)\overline{\mathbf{Y}}_{r}\right] \\&=\left[ \sum _{i=0}^{N}{\underline{y}^r_i}\widehat{J}_{i}^{(a,b,\nu )}(t), \sum _{i=0}^{N}{\overline{y}^r_i}\widehat{J}_{i}^{(a,b,\nu )}(t)\right] \\&=\left[ \sum _{i\in \mathbf{J}^+}\underline{y}^{r}_{i}\widehat{J}_{i}^{(a,b,\nu )}(t)+\sum _{i\in \mathbf{J}^-}\underline{y}^{r}_{i}\widehat{J}_{i}^{(a,b,\nu )}(t),\right. \\&\left. \sum _{i\in \mathbf{J}^+}\overline{y}^{r}_{i}\widehat{J}_{i}^{(a,b,\nu )}(t)+\sum _{i\in \mathbf{J}^-}\overline{y}^{r}_{i}\widehat{J}_{i}^{(a,b,\nu )}(t)\right] \end{aligned}$$

for all \( t\in [0,1] \), where

$$\begin{aligned} \mathbf{J}^-=\left\{ i=0,\ldots ,N|\widehat{J}_{i}^{(a,b,\nu )}(t)<0,~~ t\in [0,1] \right\} \\ \mathbf{J}^+=\left\{ i=0,\ldots ,N|\widehat{J}_{i}^{(a,b,\nu )}(t)\ge 0,~~ t\in [0,1] \right\} . \end{aligned}$$

Therefore

$$\begin{aligned} {[}y_{N}(t)]^{r}&=\sum _{i\in \mathbf{J}^-}\widehat{J}_{i}^{(a,b,\nu )}(t)[\overline{y}^{r}_{i},\underline{y}^{r}_{i}]+\sum _{i\in \mathbf{J}^+}\widehat{J}_{i}^{(a,b,\nu )}(t)[\underline{y}^{r}_{i},\overline{y}^{r}_{i}] \\&=\sum _{i=0}^N [x_i]^r \widehat{J}_{i}^{(a,b,\nu )}(t), \end{aligned}$$

that is \( y_N(t)=\mathbf{\Phi }^{T}(t) \tilde{\mathbf{X}}_N \), where \(\tilde{\mathbf{X}}_N=\left[ x_0,x_1,\ldots ,x_N \right] \) is a fuzzy vector, such that \( [{x}_i]^r=[\underline{x}_i^r,\overline{x}_i^r] \) and

$$\begin{aligned} \underline{x}_{i}^r&=\left\{ \begin{array}{l} \underline{y}_{i}^r,~~\widehat{J}_{i}^{(a,b,\nu )}(t)\ge 0\\ \overline{y}_{i}^r,~~\widehat{J}_{i}^{(a,b,\nu )}(t)<0 \end{array} \right. ,\\ ~~\overline{x}_{i}^r&=\left\{ \begin{array}{l} \overline{y}_{i}^r,~~\widehat{J}_{i}^{(a,b,\nu )}(t)\ge 0\\ \underline{y}_{i}^r,~~\widehat{J}_{i}^{(a,b,\nu )}(t)<0 \end{array} \right. \end{aligned}$$

Now, based on shift fractional-order Jacobi polynomials approximation, we obtain the error bound for (22).

Theorem 3

The error bound for the fuzzy Jacobi approximation \(y_{N}(t)=\mathbf{\Phi }^{T}(t) \tilde{\mathbf{X}}_N \) of fuzzy-valued function \(y:[0,1]\rightarrow \mathbb{R}_{\mathcal {F}} \) in (22) is presented as follows:

$$\begin{aligned} D^{*}(y,y_{N}) \le \frac{C}{2^{2N+1}(N+1)!} \end{aligned}$$

Proof

From Definition 5 and Lemma 3 we can get

$$\begin{aligned} D^{*}&(y,y_{N}) \\&=\underset{t\in [0,1]}{sup}D(y(t),y_{N}(t)) \\&=\underset{t\in [0,1]}{sup}\underset{r \in [0,1]}{sup}\max \lbrace \vert \underline{y}^{r}(t)-\underline{y}^{r}_{N}(t)\vert , \vert \overline{y}^{r}(t)-\overline{y}^{r}_{N}(t) \vert \rbrace \\&=\underset{r \in [0,1]}{sup}\max \lbrace \Vert \underline{y}^{r}(t)-\underline{y}^{r}_{N}(t)\Vert _{\infty }, \Vert \overline{y}^{r}(t)-\overline{y}^{r}_{N}(t) \Vert _{\infty }\rbrace \\&=\underset{r \in [0,1]}{sup}\max \lbrace \frac{\underline{C}_{r}}{2^{2N+1}(N+1)!}, \frac{\overline{C}_{r}}{2^{2N+1}(N+1)!}\rbrace \\&\le \frac{C}{2^{2N+1}(N+1)!} \end{aligned}$$
(50)

that \(C=\max \lbrace \underline{C}_{r}, \overline{C}_{r}\rbrace \), which completes the proof. \(\square \)

The obtained error bound shows the convergence of approximation solution \(y_{N}\) to the y(t) as \(N\rightarrow \infty \).

7 Numerical examples

In this section, we solve some examples in order to show the accuracy of the proposed method. All of them were computed with Maple 16 with Digits = 40.

Example 1

Consider the fractional integro-differential equation,

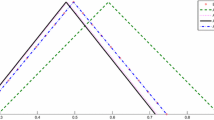
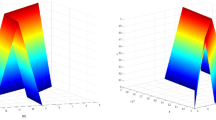
$$\begin{aligned} \left\{ \begin{array}{ll} (_{gH}D_{*,0}^{1/2}y)(t)=\frac{[r+1,5-3r]}{15\sqrt{\pi }}(48t^{\frac{5}{2}}-\sqrt{\pi }t)+ \int _{0}^{1}\frac{st}{3}y(s)\mathrm{d}s,\\ \\ y(0)=\tilde{0}. \end{array} \right. \end{aligned}$$
(51)

where the exact solution is \(y(t)=t^{3}[r+1,5-3r]\). Let \(N=6\), \(a=b=0\), and the absolute errors of our method with Jacobi polynomial (\(\nu =1/2\)) are presented in Table 1. In Figs. 1, 2, 3 and 4 we plot the absolute error functions for \(\nu =1\) and \(\nu =1/2,\) respectively. This comparison shows the accuracy of proposed method when using the fractional Jacobi polynomials.

Table 1 Numerical results for Example 1
Full size table
Fig. 1
figure 1

Plot of absolute error for \(\underline{y}^{r}(t)\) for \(\nu =1/2\)

Full size image
Fig. 2
figure 2

Plot of absolute error for \(\overline{y}(t,r)\) for \(\nu =1/2\)

Full size image
Fig. 3
figure 3

Plot of absolute error for \(\underline{y}^{r}(t)\) for \(\nu =1\)

Full size image
Fig. 4
figure 4

Plot of absolute error for \(\overline{y}(t,r)\) for \(\nu =1\)

Full size image

Example 2

Consider the fuzzy fractional integro-differential equation,

$$\begin{aligned} \left\{ \begin{array}{ll} (_{gH}D_{*,0}^{1/3}y)(t)=f(t)- \frac{1}{20}\int _{0}^{1}(t+s)y(s)\mathrm{d}s,\ \ \ \\ \\ y(0)=\tilde{0}. \end{array} \right. \end{aligned}$$
(52)

where the function f(t) is chosen such that the exact solution is \(y(t)=\sin (t^{2/3})[2+3r,8-3r]\). Let \(N=5\), \(a=-b=1/2\), and the absolute error for \(\nu =1,1/2,1/3\) is shown in Tables 2, 3. From these tables we can conclude that the approximate solution is in good agreement with the exact solution for fractional value of \(\nu \).

Table 2 Absolute error of \(\underline{y}^{r}(t)\) in Example 2
Full size table
Table 3 Absolute error of \(\overline{y}^{r}(t)\) in Example 2
Full size table

Example 3

Consider the fuzzy fractional integro-differential equation,

$$\begin{aligned} \left\{ \begin{array}{ll} (_{gH}D_{*,0}^{1/2}y)(t)= \frac{2\sqrt{t}}{\sqrt{\pi }}[1+2r,8-5r] \\ - \frac{1}{45}[(1+2r)^{2},(8-5r)^{2}] + \frac{1}{15}\int _{0}^{1}y^{2}(s)\mathrm{d}s,\ \ \ \\ \\ y(0)=\tilde{0}. \end{array} \right. \end{aligned}$$

with the exact solution is \(y(t)=t[1+2r,8-5r]\). Let \(N=5\), \(a=b=1/2\), and the numerical results for different values of \(\nu \) are shown in Tables 4, 5. Obviously, the accuracy of our method is very high, while only a few terms of fractional Jacobi polynomials are needed.

Table 4 Absolute error of \(\underline{y}^{r}(t)\) in Example 3
Full size table
Table 5 Absolute error of \(\overline{y}^{r}(t)\) in Example 3
Full size table

8 Conclusion

In this paper, we extend a spectral method with fractional Jacobi polynomials for solving a fuzzy nonlinear integro-differential equation. The proposed method is more accurate than those obtained by standard Jacobi polynomials. This method is easy to implement and yields satisfactory results only a few number of bases. In addition, numerical results have been presented to show the accuracy of the proposed method. As a further work, we develop this method for system of fuzzy nonlinear integro-differential equation.