Differential Transform Method: A Tool for Solving Fuzzy Differential Equations

Abstract

In this work we use a decomposition method which is called differential transform method (DTM) to obtain the numerical or analytical solutions of fuzzy differential equations. The DTM has been applied to many nonlinear differential equations of integer order as well as fractional orders. Here by considering strongly generalized differentiable of fuzzy differential equations we obtain all possible solution of given equations by DTM. Two examples are presented to show the capacity of this method.

Introduction

During last few decades fuzzy differential equations (FDEs) has a tremendous use in science and engineering. The concept of the fuzzy calculus was introduced by Chang and Zadeh [7] and then Dubois and Prade followed up it [10]. Other methods have been studied by Goetschel and Voxman [11], and Puri and Ralescu [20]. Concept of the FDEs applied in the fuzzy dynamical problems by Kandel and Byatt [16, 17]. The Cauchy problem and FDE were rigorously discussed by He and Yi [12], Kaleva [14, 15], Kloeden [18], Menda [19], Seikkala [21], and by other researchers (see [3,4,5,6, 8, 9, 13]). Allahviranloo et al. used numerical methods to solve FDEs [1, 2].

In this work, the differential transform method (DTM) is used to obtain analytical and approximate solution of FDEs. The paper is arranged as follows.

In “Differential Transformation Method” section, we give a brief review of the differential transform method for solving FDEs. Then the mentioned method is applied to two examples in “Numerical Examples” section. Finally, some conclusions are summarized in “Conclusion” section.

Differential Transformation Method

Definition 2.1

Let x(t, r) in the time domain T is strongly generalized differentiable of order n then if x is (i)-differentiable,

$$\begin{aligned} \overline{\vartheta }(t,n,r)= & {} \dfrac{d^{n}(~ \overline{x}(t,r) ~)}{dt^{n}} \qquad \forall t\in T ,\\ \overline{\mathcal {X}}_{i}(n,r)= & {} \overline{\vartheta }(t_{i},n,r)=\dfrac{d^{n}(~\overline{x}(t,r)~) }{dt^{n}}] _{t=t_{i}}\qquad \forall n\in N ,\\ \underline{\vartheta }(t,n,r)= & {} \dfrac{d^{n}(~\underline{x}(t,r)~)}{dt^{n}} \qquad \forall t\in T ,\\ \underline{\mathcal {X}}_{i}(n,r)= & {} \underline{\vartheta }(t_{i},n,r)=\dfrac{d^{n}(~\underline{x}(t,r)~)}{dt^{n}}] _{t=t_{i}}\qquad \forall n\in N , \end{aligned}$$

and if x is (ii)-differentiable,

$$\begin{aligned} \overline{\vartheta }(t,n,r)= & {} \dfrac{d^{n}(~ \underline{x}(t,r) )}{dt^{n}} \qquad \forall t\in T,\\ \overline{\mathcal {X}}_{i}(n,r)= & {} \underline{\vartheta }(t_{i},n,r)=\dfrac{d^{n}(~\overline{x}(t,r)~)}{dt^{n}}] _{t=t_{i}}\qquad n~\text { is~ odd},\\ \underline{\vartheta }(t,n,r)= & {} \dfrac{d^{n}(~\overline{x}(t,r)~)}{dt^{n}} \qquad \forall t\in T ,\\ \underline{\mathcal {X}}_{i}(n,r)= & {} \overline{\vartheta }(t_{i},n,r)=\dfrac{d^{n}(~\underline{x}(t,r)~)}{dt^{n}}] _{t=t_{i}}~~~~n \text {~is ~odd} , \end{aligned}$$

Here $~\overline{\mathcal {X}}(n,r) \,\, and \,\, \underline{\mathcal {X}}(n, r)~$ are named the upper and the lower spectrum of  x(t, r) respectively in the domain N at $t = t_{i}$ . So, for (i)-differentiable x, we can write x(t, r) as

$$\begin{aligned} \underline{x}(t,r)= & {} \sum _{n=0}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!}~\underline{\mathcal {X}}(t,r) ,\\ \overline{x}(t,r)= & {} \sum _{n=0}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!}~\overline{\mathcal {X}}(t,r) , \end{aligned}$$

or for (ii)-differentiable f, we can represent x(t, r) as

$$\begin{aligned} \underline{x}(t,r)= & {} \sum _{n=1,odd}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!}~\overline{\mathcal {X}}(t,r) +\sum _{n=0,even}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!}~\underline{\mathcal {X}}(t,r)~ ,\\ \overline{x}(t,r)= & {} \sum _{n=1,odd}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!}~\underline{\mathcal {X}}(t,r) +\sum _{n=0,even}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!}~\overline{\mathcal {X}}(t,r). \end{aligned}$$

The inverse transform of X(n) can be obtained as above set of equations. If X(n) is described as

$$\begin{aligned} \underline{\mathcal {X}}(n,r)= & {} M(n)\left[ ~\dfrac{d^{n}(\underline{p(t)~x(t,r)})}{dt^{n}}~\right] _{t=0} ,~~~~n=0,1,2,\ldots ,\infty ~~~~~\\ \overline{\mathcal {X}}(n,r)= & {} M(n)\left[ ~\dfrac{d^{n}(\overline{q(t)~x(t,r)})}{dt^{n}}~\right] _{t=0},~~~~n=0,1,2,\ldots ,\infty ~~~~~ \end{aligned}$$

or

$$\begin{aligned} \underline{\mathcal {X}}(n,r)= & {} M(n)\left[ ~\dfrac{d^{n}(\overline{p(t)~x(t,r)})}{dt^{n}}~\right] _{t=0} ,~~~~n=0,1,2,\ldots ,\infty ~~~~~\\ \overline{\mathcal {X}}(n,r)= & {} M(n)\left[ ~\dfrac{d^{n}(\underline{p(t)~x(t,r)})}{dt^{n}}~\right] _{t=0},~~~~n=0,1,2,\ldots ,\infty ~~~~~ \end{aligned}$$

Then the function x(t, r) can be written as

$$\begin{aligned} \underline{x}(t,r)= & {} \dfrac{1}{p(t)}~\sum _{n=0}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!} ~\dfrac{\underline{\mathcal {X}}(n,r)}{M(n)},\\ \overline{x}(t,r)= & {} \dfrac{1}{p(t)}~\sum _{n=0}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!} ~\dfrac{\overline{\mathcal {X}}(n,r)}{M(n)} , \end{aligned}$$

or

$$\begin{aligned} \underline{x}(t,r)= & {} \dfrac{1}{p(t)}~\left( ~\sum _{n=1,odd}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!} ~\dfrac{\overline{\mathcal {X}}(n,r)}{M(n)}~+\sum _{n=0,even}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!} ~\dfrac{\underline{\mathcal {X}}(n,r)}{M(n)}~\right) ,\\ \overline{x}(t,r)= & {} \dfrac{1}{p(t)}~\left( ~\sum _{n=1,0dd}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!} ~\dfrac{\underline{\mathcal {X}}(n,r)}{M(n)}~+\sum _{n=0,even}^{\infty }~\dfrac{(t-t_{i})^{n}}{n!} ~\dfrac{\overline{\mathcal {X}}(n,r)}{M(n)}~\right) , \end{aligned}$$

where $p(t) > 0$ and $M(n) > 0$. Here p(t) is considered as a kernel corresponding to x(t, r) and M(n) is known the weighting factor. In this article, we apply the $p(t) = 1$ and $M(n)=\dfrac{H^{n}}{n!}$, Here H is the time horizon of interest. If f is (i)-differentiable, then

$$\begin{aligned}&\underline{\mathcal {X}}(n,r)=\dfrac{H^{n}}{n!}~\dfrac{d^{n}(~\underline{x}(t,r))}{dt^{n}}, \\&\overline{\mathcal {X}}(n,r)=\dfrac{H^{n}}{n!}~\dfrac{d^{n}(~\overline{x}(t,r)) }{dt^{n}}, \end{aligned}$$

If f is (ii)-differentiable, then

$$\begin{aligned} \underline{\mathcal {X}}(n,r)= & {} \dfrac{H^{n}}{n!}~\dfrac{d^{n}(~\overline{x}(t,r))}{dt^{n}}, ~~~~~n~ is~ odd\\ \overline{\mathcal {X}}(n,r)= & {} \dfrac{H^{n}}{n!}~\dfrac{d^{n}(~\underline{x}(t,r)) }{dt^{n}}, ~~~~~n~ is~ odd \end{aligned}$$

If n is even, then $\vartheta$ is considered as in the first form (i). Using the DTM, a differential equation can be transformed into an algebraic equation in the domain n. Also x(t, r) can be shown as the finite-term Taylor series plus a remainder, as

$$\begin{aligned} \underline{x}(t,r)= & {} \dfrac{1}{p(t)}~\sum _{n=0}^{n}~\dfrac{(t-t_{0})^{n}}{n!} ~\dfrac{\underline{\mathcal {X}}(n,r)}{M(n)}~+R_{n+1}(t)\\= & {} \sum _{n=0}^{n}~\left( \dfrac{t-t_{0}}{H}\right) ^{n} ~\underline{\mathcal {X}}(n,r)+R_{n+1}(t).\\ \overline{x}(t,r)= & {} \dfrac{1}{p(t)}~\sum _{n=0}^{n}~\dfrac{(t-t_{0})^{n}}{n!} ~\dfrac{\overline{\mathcal {X}}(n,r)}{M(n)}~+R_{n+1}(t)\\= & {} \sum _{n=0}^{n}~\left( \dfrac{t-t_{0}}{H}\right) ^{n} ~\overline{\mathcal {X}}(n,r)+R_{n+1}(t). \end{aligned}$$

or

$$\begin{aligned} \underline{x}(t,r)= & {} \dfrac{1}{p(t)}~\left( ~\sum _{n=1,odd}^{n}~\dfrac{(t-t_{0})^{n}}{n!} ~\dfrac{\overline{\mathcal {X}}(n,r)}{M(n)}~+\sum _{n=0,even}^{n}~\dfrac{(t-t_{0})^{n}}{n!} ~\dfrac{\underline{\mathcal {X}}(n,r)}{M(n)}~\right) ~+R_{n+1}(t)\\= & {} ~\sum _{n=1,odd}^{n}~\left( \dfrac{t-t_{0}}{H}\right) ^{n} \overline{\mathcal {X}}(n,r)+\sum _{n=0,even}^{n}~\left( \dfrac{t-t_{0}}{H}\right) ^{n} \underline{\mathcal {X}}(n,r)+R_{n+1}(t).\\ \overline{x}(t,r)= & {} \dfrac{1}{p(t)}~\left( ~\sum _{n=1,0dd}^{n}~\dfrac{(t-t_{0})^{n}}{n!} ~\dfrac{\underline{\mathcal {X}}(n,r)}{M(n)}~+\sum _{n=0,even}^{n}~\dfrac{(t-t_{0})^{n}}{n!} ~\dfrac{\overline{\mathcal {X}}(n,r)}{M(n)}~\right) ~+R_{n+1}(t)\\= & {} ~\sum _{n=1,odd}^{n}~\left( \dfrac{t-t_{0}}{H}\right) ^{n} \underline{\mathcal {X}}(n,r)+\sum _{n=0,even}^{n}\left( \dfrac{t-t_{0}}{H}\right) ^{n} \overline{\mathcal {X}}(n,r)+R_{n+1}(t). \end{aligned}$$

Definition 2.2

The transformation of the nth derivative and the inverse transformation of a function can be defined as follows, respectively.

$$\begin{aligned} F(n)= & {} \dfrac{1}{n!}~\left[ \dfrac{d^{n}}{dx^{n}}~f(x)\right] _{x=x_{0}}\\ f(x)= & {} \sum _{n=0}^{\infty }~F(n)~(x-x_{0})^{n} . \end{aligned}$$

From definition (2.1), it can be easily shown that the transformation function has basic mathematical operations as Table 1.

Table 1 Functional forms and differential transforms

Numerical Examples

In this section, we solve few examples by the DTM.

Example 3.1

Consider the following second-order nonlinear FDE

$$\begin{aligned}&y''-y+4y^{3}-3y^{5}=0,\qquad x\in [0,1] \nonumber \\&\widetilde{y}(0)=\left( \dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{2}}{4}r , 3\dfrac{\sqrt{2}}{4}-\dfrac{\sqrt{2}}{4}r \right) ,\quad \widetilde{y}'(0)=\left( \dfrac{\sqrt{2}}{4}r , \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{4}r\right) , \end{aligned}$$

(1)

To use the DTM, first we rewrite Eq. (1) in the following form:

$$\begin{aligned}&(n+1)(n+2)~Y(n+2)=\mathcal {Y}(n)-4\sum _{n_{2}=0}^{n}\sum _{n_{1}=0}^{n_{2}}\mathcal {Y}(n_{1})\mathcal {Y}(n_{2}-n_{1})\mathcal {Y}(n-n_{2})\\&\quad +3\sum _{n_{4}=0}^{n}\sum _{n_{3}=0}^{n_{4}}\sum _{n_{2}=0}^{n_{3}}\sum _{n_{1}=0}^{n_{2}}\mathcal {Y}(n_{1})\mathcal {Y}(n_{2}-n_{1})\mathcal {Y}(n_{3}-n_{2})\mathcal {Y}(n_{4}-n_{3})\mathcal {Y}(n-n_{4}). \end{aligned}$$

The related initial conditions should be also transformed as follows:

$$\begin{aligned} \mathcal {Y}(0,r)= & {} \left( \dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{2}}{4}r ,\dfrac{3\sqrt{2}}{4}-\dfrac{\sqrt{2}}{4}r \right) ,\nonumber \\ \mathcal {Y}(1,r)= & {} \left( \dfrac{\sqrt{2}}{4}r , \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{4}r\right) ,\quad r=0,1,2,\ldots \end{aligned}$$

(2)

with substituting Eq. (2) into (2) and by recursive method, we have:

$$\begin{aligned} \underline{\mathcal {Y}}(0,r)&=\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{2}}{4}r, \\ \underline{\mathcal {Y}}(1,r)&=\dfrac{\sqrt{2}}{4}r,\\ \underline{\mathcal {Y}}(2,r)&= \dfrac{1}{512}(35\sqrt{2}-17\sqrt{2}r-66\sqrt{2}r^{2}-2\sqrt{2}r^{3}+15\sqrt{2}r^{4}+3\sqrt{2}r^{5}), \\ \underline{\mathcal {Y}}(3,r)&=\dfrac{1}{1536}(-17\sqrt{2}r-132\sqrt{2}r^{2}-6\sqrt{2}r^{3}+60\sqrt{2}r^{4}+15\sqrt{2}r^{5}),\\&\vdots \end{aligned}$$

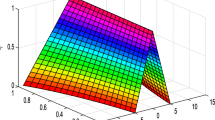
Some solutions with $r = 0,0.05,0.1,\ldots ,0.95,1$ and $x=1$ are shown in the Table 2.

Table 2 Solutions with $r = 0,0.05,\ldots ,1$ and $x=1$

Figure 1 is given to illustrate obtained solutions in the Table 2.

Fig. 1

Obtained solutions in the Table 2

and

$$\begin{aligned} \overline{\mathcal {Y}}(0,r)&=\dfrac{3\sqrt{2}}{4}-\dfrac{\sqrt{2}}{4}r, \\ \overline{\mathcal {Y}}(1,r)&=\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{4}r,\\ \overline{\mathcal {Y}}(2,r)&=\dfrac{1}{512}(57\sqrt{2}-415\sqrt{2}r+522\sqrt{2}r^{2}-238\sqrt{2}r^{3}+45\sqrt{2}r^{4}-3\sqrt{2}r^{5}), \\ \overline{\mathcal {Y}}(3,r)&=\dfrac{1}{1536}(830\sqrt{2}-2503\sqrt{2}r+2472\sqrt{2}r^{2}-1074\sqrt{2}r^{3}+210\sqrt{2}r^{4}-15\sqrt{2}r^{5}), \\&\vdots \end{aligned}$$

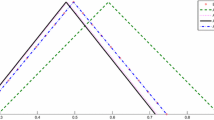
Some solutions with $r = 0,0.05,0.1,\ldots ,0.95,1$ and $x=1$ are shown in the Table 3.

Table 3 Solutions for $r = 0,0.05,\ldots ,1$ and $x=1$

Figure 2 is given to illustrate obtained solutions in the Table 3.

Fig. 2

Obtained solutions in the Table 3

Example 3.2

Consider the second-order nonlinear FDE

$$\begin{aligned}&y''-y+3y^{5}=0,\qquad x\in [0,1] \nonumber \\&\widetilde{y}(0)=(r , 2-r ),\qquad \widetilde{y}'(0)=(-1+r , 1-r), \end{aligned}$$

(3)

To apply the DTM, first we rewrite Eq. (3) in the following form:

$$\begin{aligned} (n+1)(n+2)~\mathcal {Y}(n+2)= & {} \mathcal {Y}(n)-3\sum _{n_{4}=0}^{n}\sum _{n_{3}=0}^{n_{4}} \sum _{n_{2}=0}^{n_{3}} \sum _{n_{1}=0}^{n_{2}}\mathcal {Y}(n_{1})\mathcal {Y}(n_{2}-n_{1})\mathcal {Y}(n_{3}-n_{2})\nonumber \\&\mathcal {Y}(n_{4}-n_{3})\mathcal {Y}(n-n_{4}). \end{aligned}$$

(4)

The related initial conditions should be also transformed as follows:

$$\begin{aligned} \mathcal {Y}(0,r)= & {} (r , 2-r ),\nonumber \\ \mathcal {Y}(1,r)= & {} (-1+r , 1-r),~~~~~~~~~~r=0,1,2,\ldots \end{aligned}$$

(5)

with substituting Eq. (5) into (4) and by recursive method, we have:

$$\begin{aligned} \underline{\mathcal {Y}}(0,r)=&r, \\ \underline{\mathcal {Y}}(1,r)=&-1+r,\\ \underline{\mathcal {Y}}(2,r)=&\dfrac{1}{2}(r-3r^{5}), \\ \underline{\mathcal {Y}}(3,r)=&\dfrac{1}{6}(-1+r-15(-1+r)r^{4}),\\&\vdots \\ \end{aligned}$$

Some solutions with $r = 0,0.05,0.1,\ldots ,0.95,1$ and $x=1$ are shown in the Table 4. Figure 3 is given to illustrate obtained solutions in the Table 4.

Table 4 Solutions with $r = 0,0.05,\ldots ,1$ and $x=1$

Fig. 3

Obtained solutions in the Table 4

and

$$\begin{aligned} \overline{\mathcal {Y}}(0,r)&=2-r, \\ \overline{\mathcal {Y}}(1,r)&=1-r,\\ \overline{\mathcal {Y}}(2,r)&=\dfrac{1}{2}(2-3(2-r)^{5}-r), \\ \overline{\mathcal {Y}}(3,r)&=\dfrac{1}{6}(-239+719r-840r^{2}+480r^{3}-135r^{4}+15r^{5}),\\ {}&\vdots \\ \end{aligned}$$

Some solutions with $r = 0,0.05,0.1,\ldots ,0.95,1$ and $x=1$ are shown in the Table 5.

Figure 4 is given to illustrate obtained solutions in the Table 5.

Table 5 Solutions with r = 0, 0.05, $\ldots ,$ 1, and $\hbox {x}=1$

Fig. 4

Obtained solutions in the Table 5

Conclusion

In this paper, the differential transform method has been utilized to obtain solution of nonlinear fuzzy differential equations with initial conditions. It has shown that the DTM is a useful mathematical method for solving nonlinear FDEs. Two examples were used to illustrate the efficiency of this technique.