Unveiling the dynamics of canard cycles and global behaviour in a singularly perturbed predator–prey system with Allee effect in predator

Abstract

In this article, we have considered a planar slow–fast modified Leslie–Gower predator–prey model with a weak Allee effect in the predator, based on the natural assumption that the prey reproduces far more quickly than the predator. We present a thorough mathematical analysis demonstrating the existence of homoclinic orbits, heteroclinic orbits, singular Hopf bifurcation, canard limit cycles, relaxation oscillations, birth of canard explosion by combining the normal form theory of slow–fast systems, Fenichel’s theorem and blow-up technique near non-hyperbolic point. We have obtained very rich dynamical phenomena of the model, including the saddle-node, Hopf, transcritical bifurcation, generalized Hopf, cusp point, homoclinic orbit, heteroclinic orbit, and Bogdanov–Takens bifurcations. Moreover, we have investigated the global stability of the unique positive equilibrium, as well as bistability, which shows that the system can display either “prey extinction”, “stable coexistence”, or “oscillating coexistence” depending on the initial population size and values of the system parameters. The theoretical findings are verified by numerical simulations.

1 Introduction

Singularly perturbed systems of ordinary differential equations may be used to predict the evolution of a wide range of physical and applied systems with multiple timescales. Such a system can be written in the standard form as follows:

$$\begin{aligned} \dot{x}&= F\left( x, y,\mu , \epsilon \right) , \end{aligned}$$

(1a)

$$\begin{aligned} \dot{y}&= \epsilon G\left( x, y, \mu , \epsilon \right) , \end{aligned}$$

(1b)

where $(x,y) \in \mathbb {R}^m\times \mathbb {R}^n$ such that x, y are the fast and the slow variables respectively, $\mu \in \mathbb {R}^k$ are system parameters, $m,n,k\ge 1$, F and G are the sufficiently smooth functions, $0 < \epsilon \ll 1$ is the singular perturbation parameter, and the over dot $(~ \dot{}~ )$ stands for (fast) time derivative $\frac{d}{dt}$. A powerful mathematical framework for studying slow–fast systems (1) is known as Geometric Singular Perturbation Theory (GSPT). GSPT encompasses a wide variety of geometric methods for doing so, namely, Fenichel theory (Fenichel 1979), blow-up method (Dumortier et al. 1996; Krupa and Szmolyan 2001a, c), slow-fast normal form theory (Arnold 1994). For $\epsilon \rightarrow 0$, the limiting subsystem obtained from (1) is a fast subsystem (or layered system) $\dot{x} = F\left( x, y,\mu , 0\right)$ where the slow variable y acting as a parameter. By rescaling time from t to $\tau =t/\epsilon$, the fast to the slow timescale in (1), an equivalent system to (1) is obtained which yields a differential-algebraic equation (called the slow subsystem associated with (1)) for the singular limit $\epsilon \rightarrow 0$. The slow subsystem is a dynamical system on the set $M_0 = \{(x, y) \in \mathbb {R}^m \times \mathbb {R}^n: F(x, y, \mu , 0) = 0\}$. This is also the set of equilibria of the fast subsystem, with y acting as a parameter. We refer to $M_0$ as a critical manifold if it is a submanifold. Normal hyperbolicity is a crucial property that manifolds $M_0$ may have. A point $p\in M_0$ is an equilibrium point of the fast subsystem. If all the eigenvalues of the $m\times m$ matrix $(D_xF)(p)$ have non-zero real parts, then we say that $M_0$ is normally hyperbolic at the point $p\in M_0$. When all the eigenvalues of the $m\times m$ matrix $(D_xF)(p,\mu , 0)$ have negative real parts for $p\in S\subset M$, then we say that $S\subset M$ is attracting, and when all the eigenvalues have positive real parts, then we say that S is repelling. When $M_0$ is a normally hyperbolic critical manifold, Fenichel’s theorems is applied as a regular perturbation corresponding to the singular system near $M_0$, and it says that $M_0$ is perturbed to the invariant slow manifolds $M_\epsilon$ which is at a distance $\mathcal {O}(\epsilon )$ away from $M_0$. What this means is that as $\epsilon$ approaches zero, the flow on the (locally) invariant manifold $M_\epsilon$ converges to the slow subsystem on the critical manifold $M_0$.

Fig. 1

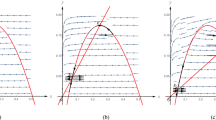
The critical manifold $M_0=S_0^a\cup N\cup S_0^r$ (shown by blue curve) where $S_0^a$ and $S_0^r$ are the attracting and repelling submanifolds, respectively, and the normally non-hyperbolic point is $Q (x_m,y_m)\in N$ (shown by blue dot). The double arrows represent fast flow, and the single arrows represent slow flow. a The slow manifolds $S_\epsilon ^a$ and $S_\epsilon ^r$ near the jump point Q are represented by the red curve. b The slow manifolds $S_\epsilon ^a$ and $S_\epsilon ^r$ (shown by red curve) near the canard point Q (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

In the non-normally hyperbolic domain, however, Fenichel–Tikhonov theory fails. Suppose, $M_0=S_0^a\cup N\cup S_0^r$, where $S_0^a$ and $S_0^r$ are the attracting and repelling branches of $M_0$ and N is a non-normally hyperbolic point or submanifold. Away from the non-normally hyperbolic singularity, Fenichel’s theorem shows that, for $0<\epsilon \ll 1$, $S_0^a$ and $S_0^r$ are smoothly perturbed to invariant manifolds $S_\epsilon ^a$ and $S_\epsilon ^r$ respectively. For instance, in the most typical scenario, the non-hyperbolic singularities $Q\in N$ are jump points, canard points (Krupa and Szmolyan 2001a; Kuehn 2015), etc. In the case $Q\in N$, the blow-up method, introduced by Dumortier et al. (1996) and developed by Krupa and Szmolyan (2001a, 2001c) is commonly used to investigate the dynamics of the slow–fast system (1) where the non-hyperbolic singularities $Q\in N$ are de-singularized by using this blow-up method. Such desigularization enables one to explore the dynamics in the non-normally hyperbolic domain using classical approaches such as regular perturbation and centre manifold theory for the study of dynamical systems. The scenario of loss of normal hyperbolicity is effectively significant as it is associated with the dynamical properties like relaxation oscillations, canards, heteroclinic orbits, homoclinic orbits, etc (Kuehn 2015; Krupa and Szmolyan 2001a, c; Zhao and Shen 2022; Kuehn 2010; Atabaigi 2021; Zhao and Shen 2022; Wang and Zhang 2019; Saha et al. 2021). A generic fold point $Q\in M_0$ is referred to as a jump point if a candidate orbit follows first the attracting branch $S_0^a$ closely, reaches the vicinity of the fold point Q, and then follows the direction of the fast flow abruptly away from Q, as shown in Fig. 1a. A canard point is a fold point Q for which $G(Q,\mu ,0)=0$ for some $\mu$. In this case, it could happen that the attracting slow manifold $S_\epsilon ^a$ will remain close to the repelling slow manifold $S_\epsilon ^r$ for a time of $\mathcal {O}(1)$ (see Fig. 1b). Such solutions are known as canards. There is a possibility that there are specific values of $\mu (\epsilon )$ for which the attracting slow manifold $S_\epsilon ^a$ connects to the repelling slow manifold $S_\epsilon ^r$. The term “maximal canard”is used to describe such solutions (Krupa and Szmolyan 2001c). Another well-known occurrence in this setting is relaxation oscillations, when solutions approach a fold point slowly but then abruptly jump from the fold point to another stable branch of $M_0$, then follow the slow dynamics again until a new fold point is reached, and so on, and finally forming periodic orbits (Krupa and Szmolyan 2001c; Zhao and Shen 2022; Kuehn 2015). A quick shift upon change of a control parameter from a small amplitude limit cycle via canard cycles to a large amplitude relaxation oscillation may occur for the system (1) within an exponentially narrow range $\mathcal {O}(e^{-1/\epsilon })$ of the control parameter. It is referred to as canard explosion.

In this article, under the natural assumption that the prey reproduces considerably quicker than the predator, the primary emphasis is on planar slow-fast predator–prey systems with two time scales of the type (1) where $m=n=1$. A significant amount of research has been put into investigating the canard phenomena and the existence of relaxation oscillations of planar slow-fast predator–prey systems. The following are just a few instances, by no means exhaustive, where this kind of investigation has been done. Rinaldi and Muratori (1992) first investigated the presence of relaxation oscillation in a slow-fast predator–prey system. Additionally, they examined the periodic population fluctuations in a three-species model operating within a slow-fast framework, accounting for both one and multiple timescale parameters. Hek (2010) applied the Fenichel’s theory to biology. Using asymptotic expansion techniques, Kooi and Poggiale (2018) demonstrated how to locate a canard solution at the turning point in the Rosenzweig–MacArthur model on two time scales. In Ambrosio et al. (2018), authors considered a slow-fast predator–prey model of modified Leslie-Gower type with two time scales. By using the blow-up method, they were able to clearly display the behaviour close to the fold point and demonstrated that the limit-cycle experiences the canard phenomena while crossing the folded node. The dynamics of a slow-fast predator–prey model were investigated in Atabaigi (2021), where the predator is a generalist predator that feeds on both the focal prey and the functional response is Holling type III. Using tools like the theory of normal forms for slow–fast systems, the theory of geometric singular perturbations, and the blow-up method, the author explored the existence of relaxation oscillations and canard limit cycles bifurcating from singular homoclinic cycles. In the article (Banasiak et al. 2019), the authors explored the delayed exchange of stability in singularly perturbed nonautonomous equations with backward bifurcations in quasi-steady manifolds and applied the analysis to describe canard solutions in predator–prey models.

The Allee effect has been the subject of several publications on predator–prey system (Courchamp et al. 2008; Terry 2015; Zhou et al. 2005; Rahmi et al. 2021; Feng and Kang 2015; Hadjiavgousti and Ichtiaroglou 2008; Pal and Saha 2015; González-Olivares and Rojas-Palma 2011). Most studies among them have considered the Allee impact of the prey population growth. Many observations, however, suggest that the Allee effect is also evident in the population of predators, for instance, Seabirds and the African wild dog (Lycaon pictus) (Courchamp et al. 2008). There has been little research on the impact of the Allee effect on predator populations (Terry 2015; Zhou et al. 2005; Rahmi et al. 2021; Feng and Kang 2015). To the best of our knowledge, there is almost no literature pertaining to geometric singular perturbation analysis of predator–prey models in which the growth of the predator population is subject to the influence of a weak Allee effect. By the term $\Phi (v)=\frac{v}{n+v}$, often known as the weak Allee effect function with n as the Allee effect constant, we introduce an Allee effect into the predator equation. $\Phi (v)$ measures the probability that a female predator will come into contact with at least one male and mate with him during the reproductive stage. This Allee effect function reduces the predator’s per capita growth rate from s to $\frac{sv}{n+v}$. The Beddington–DeAngelis functional response $\Psi (u,v)=\frac{mv}{a+bu+cv}$ is comparable to the well-known Holling type II functional response $\Psi (u,v)=\frac{mv}{a+bu}$, with the addition of an additional factor cv in the denominator. Here, $u = u(t)$ and $v = v(t)$ respectively denote the prey and predator population densities, m denotes the maximum per capita consumption rate of a predator, both a and b are prey saturation constants, c is the predator interference. The factor cv reflects the mutual interference between predators. In situations with low population densities, the Beddington–DeAngelis functional response is the preferred option due to its ability to circumvent the controversial issue associated with the ratio-dependent functional response $\Psi (u,v)=\frac{mv}{bu+cv}$.

In Yu (2014), the author examined the modified Leslie–Gower model with the Beddington-DeAngelis functional response, delving into aspects of system permanence, as well as local and global stability. In a separate study conducted by Vera-Damián et al. (2019), the same model was considered, focusing on the investigation of limit cycle, Bogdanov–Takens bifurcations, and homoclinic bifurcations. Recognizing the significance of the Allee effect in the predator population, as elucidated above, our motivation in this present investigation was to extend the model by introducing an Allee effect in the predator population. The model is presented as follows:

$$\begin{aligned} \frac{du}{dT}&=ru\left( 1- \frac{u}{K}\right) -\frac{muv}{a + bu +cv}, \end{aligned}$$

(2a)

$$\begin{aligned} \frac{dv}{dT}&=sv\left( \frac{v}{n+v}-\frac{v}{d+hu}\right) , \end{aligned}$$

(2b)

subjected to initial conditions $u(0)\ge 0$, $v(0)\ge 0$, parameters $(r, K, m, n, a, b, c, s, d, h)\in \textrm{Int }~\mathbb {R}_+^{10}$ such that $u = u(t)$ and $v = v(t)$ respectively denote the prey and predator population densities at time $t > 0$. The Allee effect is considered in predator population because the predator population is more prone than their prey (Terry 2015). Here, r is the intrinsic per capita growth rate of prey, K is the environmental carrying capacity, h measures of the food quality, d is the amount of alternative food available for predators, and the meaning of other parameters are already mentioned above.

Non-dimensionalizing the system (2) by using the following rescaling transformations:

$$\begin{aligned} t = rT,~~ x = \frac{u}{K}, ~~y = \frac{cv}{bK}, \end{aligned}$$

(3)

we have

$$\begin{aligned} \frac{dx}{dt}&=x\left( 1-x\right) -\frac{\alpha xy}{\beta +x+ y}=f(x,y,\mu ), \end{aligned}$$

(4a)

$$\begin{aligned} \frac{dy}{dt}&=\epsilon y\left( \frac{y}{y+\gamma }-\frac{y}{\delta + \theta x}\right) =\epsilon g(x,y,\mu ), \end{aligned}$$

(4b)

where x, y are the new dimensionless variables, $\mu =(\alpha , \beta , \gamma , \delta , \theta )$ with $\alpha =\frac{m}{rc},\beta =\frac{a}{bk}$, $\gamma =\frac{nc}{bK}$, $\delta =\frac{cd}{bK}$, $\theta =\frac{ch}{b}$ and $\epsilon =\frac{s}{r}$. The parameters are positive with $0<\epsilon \ll 1$.

From model (2), in the absence of the prey u, the growth of the predator is governed by the model $\frac{dv}{dT}=sv\left( \frac{v}{n+v}-\frac{v}{d}\right)$, indicating the per capita growth rate is increasing at small densities of the predator for $d - n > 0$. This implies that this model demonstrates the weak Allee effect only when $d - n > 0$, which corresponds to $\delta >\gamma$ in the dimensionless system described by equation (4). In cases where this condition is not met, no Allee effect occurs.

The remaining part of this article is organized as follows. In Sect. 2, we present some basics results for the system (4). The slow-fast system is analysed in Sect. 3. The existence of the singular Hopf bifurcation and canard cycles are investigated in Sect. 4. In Sect. 5, we also provide thorough proof of the existence of heteroclinic and homoclinic orbits. In Sect. 6, we prove the existence of relaxation oscillation and the bistability phenomenon. The main theoretical predictions are verified using numerical simulations in appropriate sections. Finally, some brief conclusions of our findings are presented in Sect. 7.

2 Basic results

In this section, we discuss some basic results, including the invariance, boundedness, existence of equilibria and their nature, and bifurcation scenario for the system (4).

Lemma 1

The first quadrant $\mathbb {R}^2_+=\{(x,y)\in \mathbb {R}^2|x\ge 0, y\ge 0\}$ is invariant under the flow generated by the system (4).

Lemma 2

All the solutions of the model system (4) initiated from the interior of $\mathbb {R}^2_+$ are bounded.

The system (4) has three equilibria on the co-ordinate axes, namely, the trivial equilibrium $E_0(0,0)$ and the boundary equilibria $E_{1b}(1,0)$, $E_{2b}(0,\delta -\gamma )$ where $E_{2b}$ exists if $\delta >\gamma$. We have the following results on the nature of the equilibria on the coordinate axes.

Lemma 3

• (i) The trivial equilibrium $E_0(0,0)$ is either a saddle node or a non-hyperbolic saddle.

• (ii) The boundary equilibrium $E_{1b}(1,0)$ is either a saddle node or a stable node.

• (iii) The boundary equilibrium $E_{2b}(0, \delta -\gamma )$ which exists provided $\delta >\gamma$ is a hyperbolic saddle if $\alpha \le 1$. For $\alpha >1$, $E_{2b}$ is a hyperbolic stable node if $\delta >\gamma +\frac{\beta }{\alpha -1}$, a hyperbolic saddle if $\delta <\gamma +\frac{\beta }{\alpha -1}$, and either a saddle node or a stable node if $\delta =\gamma +\frac{\beta }{\alpha -1}$.

Proof

• (i) The Jacobian matrix of the system (4) at an arbitrary point (x, y) is given by

  $$\begin{aligned} J=\left[ \begin{array}{cc} f_x &{} f_y\\ \epsilon g_x &{} \epsilon g_y\end{array}\right] , \end{aligned}$$

  where

  $$\begin{aligned} f_x&=1-2x-\frac{\alpha y(\beta +y)}{(\beta +x+y)^2},\,\,\, f_y=-\frac{\alpha x(\beta +x)}{(\beta +x+y)^2},\\ g_x&= \frac{\theta y^2}{(\delta +\theta x)^2},\,\, \,\,g_y=y\left( \frac{y+2\gamma }{(y+\gamma )^2}-\frac{2}{\delta +\theta x}\right) . \end{aligned}$$

  Correspondingly, we see that the Jacobian matrix $J_{E_0}$ at the trivial equilibrium $E_0(0,0)$ has eigenvalues $\lambda _1=1$ and $\lambda _2=0$. The flow on the centre manifold near $E_0$ is given by

  $$\begin{aligned} \frac{dy}{dt}=\frac{\epsilon }{\delta \gamma }(\delta -\gamma )y^2-\frac{\epsilon }{\gamma ^2}y^3+\mathcal {O}(y^4). \end{aligned}$$

  (5)

  Now, if $\delta \ne \gamma$, then it follows that the equilibrium $E_0$ is a saddle node, a neighbourhood of which consists of two hyperbolic sectors and one parabolic sector. For $\delta =\gamma$, the equilibrium $E_0$ is a non-hyperbolic saddle.

• (ii) The Jacobian matrix $J_{E_{1b}}$ at $E_{1b}(1,0)$ is given by

  $$\begin{aligned} J_{E_{1b}}=\left[ \begin{array}{cc} -1 &{} -\frac{\alpha }{\beta +1}\\ 0 &{} 0\end{array}\right] , \end{aligned}$$

  with eigenvalues $\lambda _1=-1$ and $\lambda _2=0$. We now translate the equilibrium $E_{1b}$ to the origin by means of the translation $(u,v)=(x-1, y)$ and write the system (4) in a neighbourhood of $E_{1b}$ in the following form

  $$\begin{aligned} \frac{du}{dt}&=-u-\frac{\alpha }{\beta +1}v+g_{20}u^2+g_{11}{uv}+g_{02}{v^2}+\mathcal {O}(\left\Vert u,v\right\Vert ^3), \end{aligned}$$

  (6a)
  $$\begin{aligned} \frac{dv}{dt}&=h_{02}v^2+\mathcal {O}(\left\Vert u, v\right\Vert ^3), \end{aligned}$$

  (6b)

  where $g_{20}=-1$, $g_{11}=-\frac{\alpha \beta }{(\beta +1)^2}$, $g_{02}=\frac{\alpha }{(\beta +1)^2}$ and $h_{02}=\frac{\epsilon (\delta +\theta -\gamma )}{\gamma (\delta +\theta )}$. Subsequently, the following transformation,

  $$\begin{aligned} \begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} 1 &{} -\frac{\alpha }{\beta +1} \\ 0 &{} 1 \end{bmatrix} \begin{bmatrix} X \\ Y \end{bmatrix}, \end{aligned}$$

  transforms the system (6) in a neighbourhood of the origin into

  $$\begin{aligned} \frac{dX}{dt}&=-X+p_{20}X^2+p_{11}XY+p_{02}Y^2+\mathcal {O}(\left\Vert X,Y\right\Vert ^3), \end{aligned}$$

  (7a)
  $$\begin{aligned} \frac{dY}{dt}&=q_{02}Y^2+\mathcal {O}(\left\Vert X, Y\right\Vert ^3), \end{aligned}$$

  (7b)

  where $p_{20}=-1$, $p_{11}=\left( \frac{2\alpha }{\beta +1}-\frac{\alpha \beta }{(\beta +1)^2}\right)$, $p_{02}=\left( \frac{\alpha }{(\beta +1)^2}+\frac{\alpha ^2\beta }{(\beta +1)^3}+\frac{\alpha \epsilon (\delta +\theta -\gamma )}{\gamma (\beta +1)(\delta +\theta )}\right.$ $\left. -\frac{\alpha ^2}{(\beta +1)^2}\right)$ and $q_{02}=\frac{\epsilon (\delta +\theta -\gamma )}{\gamma (\delta +\theta )}$. The flow of (7) on the centre manifold near the origin is given by

  $$\begin{aligned} \frac{dY}{dt}&=q_{02}Y^2+\mathcal {O}(Y^3). \end{aligned}$$

  (8)

  Hence, if $q_{02}\ne 0$ then the boundary equilibrium $E_{1b}(1,0)$ is a saddle node. For $q_{02}<0$, all the trajectories in the parabolic sector asymptotically tend to $E_{1b}$, and correspondingly, $E_{1b}$ is an attracting saddle node. But, for $q_{02}>0$, $E_{1b}$ is a repelling saddle node. Now, if $q_{02}=0$ (i.e., if $\delta +\theta =\gamma$) then keeping the higher order terms, the flow of (7) on the centre manifold near the origin is given by

  $$\begin{aligned} \frac{dY}{dt}&=q_{03}Y^3+\mathcal {O}(Y^4), \end{aligned}$$

  (9)

  where $q_{03}=-\frac{\epsilon }{\gamma ^2}\left( 1+\frac{\alpha \theta }{\beta +1}\right) <0$, and consequently, $E_{1b}$ is a stable node.

• (iii) The boundary equilibrium $E_{2b}(0, \delta -\gamma )$ exists provided $\delta >\gamma$ and the Jacobian matrix at $E_{2b}$ is given by

  $$\begin{aligned} J_{E_{2b}}=\left[ \begin{array}{cc} 1-\frac{\alpha (\delta -\gamma )}{\beta +\delta -\gamma } &{} 0\\ \frac{\theta \epsilon }{\delta ^2}(\delta -\gamma )^2 &{} -\frac{\epsilon }{\delta ^2}(\delta -\gamma )^2\end{array}\right] , \end{aligned}$$

  with eigenvalues $\lambda _1=1-\frac{\alpha (\delta -\gamma )}{\beta +\delta -\gamma }$ and $\lambda _2=-\frac{\epsilon }{\delta ^2}(\delta -\gamma )^2<0$. For $\alpha \le 1$, we have $\lambda _1>0$ and, correspondingly, the equilibrium $E_{2b}$ is a hyperbolic saddle. We now assume $\alpha >1$ and investigate the nature of the boundary equilibrium $E_{2b}$. We observe that $\lambda _1<0 (\lambda _1>0)$ if $\delta >\gamma +\frac{\beta }{\alpha -1} \left( \delta <\gamma +\frac{\beta }{\alpha -1}\right)$ and consequently, the equilibrium $E_{2b}$ is a stable node (hyperbolic saddle). Now, for $\delta =\gamma +\frac{\beta }{\alpha -1}$, the Jacobian matrix $J_{2b}$ has eigenvalues $\lambda _1=0$ and $\lambda _2=-\frac{\beta ^2\epsilon }{(\gamma (\alpha -1)+\beta )^2}$. Shifting the equilibrium $E_{2b}$ to the origin by the translation $(u,v)=(x, y-(\delta -\gamma ))$ and using the transformation

  $$\begin{aligned} \begin{bmatrix} u\\ v \end{bmatrix} = \begin{bmatrix} 1 &{} 0 \\ \theta &{} 1 \end{bmatrix} \begin{bmatrix} X \\ Y \end{bmatrix}, \end{aligned}$$

  we write the system (4) as

  $$\begin{aligned} \frac{dX}{dt}&=p_{20}'X^2+p_{11}'XY+\mathcal {O}(\left\Vert X,Y\right\Vert ^3) \end{aligned}$$

  (10a)
  $$\begin{aligned} \frac{dY}{dt}&=-\frac{\beta ^2\epsilon }{(\beta +\gamma (\alpha -1))^2}Y+q_{20}'X^2+q_{11}'XY+q_{02}'Y^2+\mathcal {O}(\left\Vert X, Y\right\Vert ^3), \end{aligned}$$

  (10b)

  where

  $$\begin{aligned} p_{20}'&=\frac{1}{\alpha \beta }\left( (\alpha -1)(1-\theta (\alpha -1))-\alpha \beta \right) ,\,\,\, p_{11}'=-\frac{(\alpha -1)^2}{\alpha \beta },\\ q_{20}'&=-\theta p_{20}',\,\,\, q_{11}'=-\frac{2\beta \theta \gamma \epsilon (\alpha -1)^2}{(\beta +\gamma (\alpha -1))^3}-\theta p_{11}',\,\,\, q_{02}'=-\frac{\beta \epsilon (\alpha -1)(\beta +2\gamma (\alpha -1))}{(\beta +\gamma (\alpha -1))^3}. \end{aligned}$$

  The flow of (10) on the centre manifold near the origin is given by

  $$\begin{aligned} \frac{dX}{dt}=p_{20}'X^2+\mathcal {O}(X^3). \end{aligned}$$

  (11)

  Now, if $p_{20}'\ne 0$ then $E_{2b}$ is a saddle node, a small neighbourhood of which consists of two hyperbolic sectors and one parabolic sector. Now, for $p_{20}'<0$, the parabolic sector is in $\mathbb {R}^2_+$ and all trajectories in this parabolic sector asymptotically tend to the equilibrium $E_{2b}$, classifying the equilibrium $E_{2b}$ as an attracting saddle node. But, for $p_{20}'>0$, the two hyperbolic sectors are in $\mathbb {R}^2_+$ and consequently, $E_{2b}$ is a repelling saddle node. For $p_{20}'=0$, the flow on the centre manifold is given by

  $$\begin{aligned} \frac{dX}{dt}=p_{30}'X^3+\mathcal {O}(X^4), \end{aligned}$$

  (12)

  where $p_{30}'=-\frac{(\alpha -1)^2}{\alpha ^2\beta ^2}<0$ and hence, in this case, the equilibrium $E_{2b}$ is a stable node.

$\square$

The interior equilibria are the points of intersection of the non-trivial prey and predator nullclines (see Fig. 2) given by

$$\begin{aligned} f_1(x,y)&=1-x-\frac{\alpha y}{\beta +x+y}=0,\\ g_1(x,y)&=\frac{1}{y+\gamma }-\frac{1}{\delta +\theta x}=0. \end{aligned}$$

Denoting,

$$\begin{aligned} D&=(\alpha \theta +\delta -\gamma +\beta -\theta -1)^2-4(1+\theta )\left( \alpha (\delta -\gamma )-(\delta -\gamma )-\beta \right) , \end{aligned}$$

we consider the following parametric regions

$$\begin{aligned} R_1&=\left\{ \mu \Bigg |D>0,\, \alpha>\frac{1}{1-\beta }, \beta<1, \delta >\gamma +\frac{\beta }{\alpha -1},\theta (\alpha -1)+\beta +\delta -\gamma <1\right\} , \end{aligned}$$

(13a)

$$\begin{aligned} R_2&=\left\{ \mu \Bigg |D=0,\,\alpha>\frac{1}{1-\beta }, \beta<1, \delta >\gamma +\frac{\beta }{\alpha -1}, \theta (\alpha -1)+\beta +\delta -\gamma <1\right\} ,\end{aligned}$$

(13b)

$$\begin{aligned} R_3&=\left\{ \mu \Bigg |\alpha >\frac{1}{1-\beta }, \beta<1, \{0\le \gamma -\delta<\theta \}\cup \{\gamma<\delta <\gamma +\frac{\beta }{\alpha -1}\}\right\} ,\end{aligned}$$

(13c)

$$\begin{aligned} R_4&=\left\{ \mu \Bigg |\{D<0\}\cup \{\gamma \ge \delta +\theta \}\cup \{D>0,\alpha>\frac{1}{1-\beta },\beta <1, \delta>\gamma +\frac{\beta }{\alpha -1},\right. \nonumber \\&(\delta -\gamma )+\theta (\alpha -1)>1-\beta \} \biggl \}. \end{aligned}$$

(13d)

We now state the following results on the existence and local stability of the interior equilibria of the system (4).

Lemma 4

• (i) If $\mu \in R_1$, then there exist two interior equilibrium points $E_{1*}(x_{1*}, y_{1*})$ and $E_{2*}(x_{2*}, y_{2*})$, where

  $$\begin{aligned} x_{1*}&= \frac{\theta +1-\alpha \theta -\beta +\gamma -\delta -\sqrt{D}}{2(1+\theta )},\,\, y_{1*}=\delta -\gamma +\theta x_{1*},\\ x_{2*}&=\frac{\theta +1-\alpha \theta -\beta +\gamma -\delta +\sqrt{D}}{2(1+\theta )},\,\, y_{2*}=\delta -\gamma +\theta x_{2*}. \end{aligned}$$

  The equilibrium $E_{1*}$ is a hyperbolic saddle and $E_{2*}$ is a locally stable equilibrium point if $x_{2*}\ge x_m$, where $x_m$ is the abscissa of the local maximum of the non-trivial prey nullcline. For $x_{2*}<x_m$, the equilibrium $E_{2*}$ will be either stable or unstable, depending on whether ${\text{ t }race}\, (J_{E_{2*}})< {\text{ o }r} >0$.

• (ii) If $\mu \in R_2$ then there exists only one interior equilibrium point $\bar{E}(\bar{x}, \bar{y})$, where

  $$\begin{aligned} \bar{x}&=\frac{\theta +1-\alpha \theta -\beta +\gamma -\delta }{2(1+\theta )},\,\, \bar{y}=\delta -\gamma +\theta \bar{x}. \end{aligned}$$

  In this case, the non-trivial predator nullcline touches the non-trivial prey nullcline tangentially at the point $\bar{E}$. The equilibrium $\bar{E}$ is a saddle node provided ${\text{ t }race}\, (J_{\bar{E}})\ne 0$.

• (iii) If $\mu \in R_3$ then there exists only one interior equilibrium point $E_{*}(x_{*}, y_{*})$, where

  $$\begin{aligned} x_{*}&=\frac{\theta +1-\alpha \theta -\beta +\gamma -\delta +\sqrt{D}}{2(1+\theta )},\,\, y_{*}=\delta -\gamma +\theta x_{*}. \end{aligned}$$

  The equilibrium $E_*$ is stable if $x_*\ge x_m$ and for $x_*<x_m$, it will be either stable or unstable depending on whether ${\text{ t }race}\, (J_{E_{*}})< {\text{ o }r} >0$.

• (iv) If $\mu \in R_4$ then the system (4) has no interior equilibrium in $\mathbb {R}^2_+$.

Proof

• (i) For $\mu \in R_1$, one can easily verify that the non-trivial prey nullcline has a local maximum at $Q(x_m, y_m)$ in $\mathbb {R}^2_+$, where $x_m=1-\alpha +\sqrt{\alpha \left( \alpha -1-\beta \right) }$, $y_m=\frac{(\beta +x_m)(1-x_m)}{\alpha +x_m-1}$ and the non-trivial predator nullcline is a straight line passing through the boundary equilibrium $E_{2b}(0, \delta -\gamma )$. For $\mu \in R_1$, the non-trivial predator nullcline intersects the non-trivial prey nullcline at the points $E_{1*}(x_{1*}, y_{1*})$ and $E_{2*}(x_{2*}, y_{2*})$ in $\mathbb {R}^2_+$ such that $x_{1*}<x_m$. The Jacobian matrix $J_E$ of the system (4) at an interior equilibrium E(x, y) is given by,

  $$\begin{aligned} J_E = \left[ \begin{array}{cc} xf_{1x} &{} xf_{1y}\\ \epsilon y^2 g_{1x}&{} \epsilon y^2 g_{1y}\end{array} \right] _E. \end{aligned}$$

  where

  $$\begin{aligned} f_{1x}&=-1+\frac{\alpha y}{(\beta +x+y)^2},\,\,\, f_{1y}=-\frac{\alpha (\beta +x)}{(\beta +x+y)^2},\\ g_{1x}&= \frac{\theta }{(\delta +\theta x)^2},\,\, \,\,g_{1y}=-\frac{1}{(y+\gamma )^2}. \end{aligned}$$

  Fig. 2

  

  In this representation, the relative positions of the nullclines are shown as solid lines. The x and y axes represent the densities of prey and predator species, respectively. Non-trivial prey nullcline is shown by the blue curve, whereas non-trivial predator nullclines are shown by straight lines for the variable $\delta$. The equilibria are shown by solid red circles. The two non-hyperbolic points P and Q are shown by the solid blue circles. For the given parameter values of $\alpha =1.5, \beta =0.0207, \gamma =0.3, \theta =0.3$ and variable $\delta$, the figure shows that the number of interior equilibrium points ranges from 0 to 2. Different relative positions of predator nullclines are shown in different colours for various values of $\delta$: black for $\delta =0.55$ ($\mu \in R_4$, no interior equilibrium), cyan for $\delta =0.49576955$ ($\mu \in R_2$, unique interior equilibrium), red for $\delta =0.41$ ($\mu \in R_1$, two interior equilibrium), green for $\delta =0.32$ ($\mu \in R_3$, unique interior equilibrium) (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

  Now, from the geometry of the non-trivial prey and predator nullclines (see Fig. 2) it follows that the slope of the tangent line to the non-trivial prey nullcline at $E_{1*}$ is greater than the slope of the non-trivial predator nullcline at $E_{1*}$, i.e., $-\frac{f_{1x}}{f_{1y}}\bigg \vert _{E_{1*}}>-\frac{g_{1x}}{g_{1y}}\bigg \vert _{E_{1*}}>0$ and hence, $\textrm{det}\, (J_{E_{1*}})<0$. Consequently, the equilibrium $E_{1*}$ is a hyperbolic saddle. The equilibrium $E_{2*}$ may lie to the left or right of Q (local maximum of the prey nullcline) or it may coincide with Q. We first assume that $E_{2*}$ lies to the right of Q i.e., $x_{2*}>x_m$. Then the slope of the tangent line to the predator nullcline at $E_{2*}$, given by $-\frac{g_{1x}}{g_{1y}}\bigg \vert _{E_{2*}}$ is positive and greater than the slope of the tangent line to the prey nullcline at $E_{2*}$, given by $-\frac{f_{1x}}{f_{1y}}\bigg \vert _{E_{2*}}<0$. We also observe that the non-trivial prey nullcline decreases strictly for $x>x_m$. Hence, we have that $\textrm{trace}\,(J_{E_{2*}})<0$, and $\textrm{det}\,(J_{E_{2*}})>0$. Therefore, $E_{2*}$ is locally stable. Similarly, if $E_{2*}$ coincides with Q i.e., $x_{2*}=x_m$, then $f_{1x}\bigg \vert _{E_{2*}=Q} = 0$. Consequently, we have $\textrm{trace}\,(J_{E_{2*}})<0$, and $\textrm{det}\,(J_{E_{2*}})>0$. Hence, $E_{2*}$ is a locally stable equilibrium point. Let the coexistence equilibrium $E_{2*}$ lie to the left of Q i.e., $x_{2*}<x_m$. Then following the nature of nullclines (see Fig. 2) and the fact that the non-trivial prey nullcline increases strictly in $0<x<x_m$, we have that the slope of the tangent line to the non-trivial predator nullcline at $E_{2*}$ is greater than the slope of the non-trivial prey nullcline at $E_{2*}$ i.e., $\textrm{det}\,(J_{E_{2*}})>0$. Thus, $E_{2*}$ is a locally stable equilibrium if $\textrm{trace}\,(J_{E_{2*}}) < 0$ and an unstable equilibrium if $\textrm{trace}\,(J_{E_{2*}}) > 0$.

• (ii) For $\mu \in R_2$, the non-trivial prey and predator nullclines intersect tangentially at the point $\bar{E}(\bar{x}, \bar{y})$ in $\mathbb {R}^2_+$. Therefore, at $\bar{E}(\bar{x}, \bar{y})$, we have $-\frac{f_{1x}}{f_{1y}}=-\frac{g_{1x}}{g_{1y}}$ and consequently, $\textrm{det}\, (J_{\bar{E}})=0$. Hence, by deriving the flow on the centre manifold, one can show that the equilibrium $\bar{E}$ is a saddle node provided $\textrm{trace}\, (J_{\bar{E}})\ne 0$. Now, if $\textrm{trace}\, (J_{\bar{E}})= 0$ then the centre manifold is two-dimensional and the local behaviour of the equilibrium $\bar{E}$ can be investigated by reducing the flow on the centre manifold. It has been shown numerically (see Fig. 3) for a particular choice of parameters that $\bar{E}$ corresponding to the Bogdanov-Takens (BT) point is a cusp of codimension two.

• (iii) The non-trivial prey nullcline cuts the y-axis at the point $P(0, \frac{\beta }{\alpha -1})$. For $\mu \in R_3$ the intersection point of the non-trivial predator nullcline cuts the y-axis at a point which lies below the point P (see Fig. 2) and correspondingly, the non-trivial nullclines intersect only at one point $E_*(x_*, y_*)$ in $\mathbb {R}^2_+$. The stability results of the equilibrium $E_*$ will be the same as that of $E_{2*}$ which we have already discussed.

• (iii) For $\mu \in R_4$, one can readily check that the non-trivial nullclines have no intersection in $\mathbb {R}^2_+$ and consequently, in this case, the system (4) has no interior equilibrium.

$\square$

2.1 Bifurcation scenario

The non-trivial prey and predator nullclines intersect the positive y-axis at the point $P(0, \frac{\beta }{\alpha -1})$ and $E_2(0, \delta -\gamma )$ and consequently, based on the nature of the non-trivial nullclines we have that if $E_{2b}$ lies below the point P then there always exists a unique interior equilibrium point $E_{*}$, if $E_{2b}$ lies above the point P then under certain parametric conditions (as mentioned in Lemma 4) there may exist zero, one or two interior equilibrium points. Thus, we see that varying the control parameter $\delta$ it follows that for $\delta =\delta _{TC}=\gamma +\frac{\beta }{\alpha -1}$, the model system (4) undergoes a transcritical bifurcation as one interior equilibrium bifurcates from $E_2(0,\delta -\gamma )$ as $\delta$ passes through $\delta =\delta _{TC}$. Assuming the parametric conditions $\alpha>\frac{1}{1-\beta }, \beta<1, \delta >\gamma +\frac{\beta }{\alpha -1},\theta (\alpha -1)+\frac{\alpha \beta }{\alpha -1}<1$, we have that for $D>0$, there exist two interior equilibrium points $E_{1*}$ and $E_{2*}$ where $E_{1*}$ is a hyperbolic saddle point; for $D=0 (\theta =\theta _{SN})$, the two equilibrium points $E_{1*}, E_{2*}$ coalesce at the degenerated saddle node equilibrium point $\bar{E}(\bar{x},\bar{y})$ and for $D<0$ there exists no equilibrium point. Thus, we have saddle node bifurcation of equilibria, i.e., the model system (4) undergoes a saddle node bifurcation as $\theta$ passes through $\theta =\theta _{SN}$. For $(\delta , \theta )=(\delta _{TC}, \theta _{SN})$, the model system (4) undergoes a saddle-node-transcritical bifurcation topologically equivalent to co-dimension 2 cusp bifurcation as $(\delta , \theta )$ passes through $(\delta , \theta )=(\delta _{TC}, \theta _{SN})$. Now, it may also happen that varying $\delta$, there may take place Hopf bifurcation around $E_{2*}$ (or $E_*$) for $\delta =\delta _H$ and will be studied in the next section in the realm of slow-fast analysis. We also have that for $D=0$, Trace  $J(\bar{E})=0 \left( (\delta , \theta )=(\delta _{H}, \theta _{SN})\right)$, the equilibrium $\bar{E}$ is a cusp of codimension-2 and thus, varying the parameter $(\delta , \theta )$ in a neighbourhood of the Bogdanov-Takens (BT) point $(\delta , \theta )=(\delta _{H}, \theta _{SN})$, codimension-2 BT bifurcation (SN bifurcation of equilibria, emergence of a periodic orbit through Hopf bifurcation, saddle homoclinic bifurcation etc.) will be observed. Following (Kuznetsov et al. 1998) one can explicitly compute the normal forms of the various bifurcations mentioned here and verify the results analytically. But, as the article aims to investigate the dynamics of a slow-fast system in the realm of GSPT and blow-up technique, we present in Fig. 3 the two-parameter bifurcation diagram for the various bifurcation results.

Fig. 3

Two-parameter bifurcation diagram in $\delta -\theta$ parameter plane. The Hopf (H) bifurcation curve (cyan) intersects at the Generalized Hopf (GH) bifurcation point located at $(\delta _{GH}, \theta _{GH})=(0.361212, 0.638870)$ in the region $R_1$ with the limit point of cycles (LPC) bifurcation curve (green). The thick black curve represents the saddle-node (SN) bifurcation curve, and the thick blue line is the transcritical bifurcation curve (TC). The TC and SN curves intersect tangentially at a cusp point (CP). The broken blue line is the equation $\delta =\gamma$ determines the existence of boundary equilibrium point $E_{2b}$. The horizontal red line represents the equation $\theta (\alpha -1)+\frac{\alpha \beta }{\alpha -1}=1$. The SN and H curves approach each other and eventually collide at a Bogdanov–Takens (BT) point located at $(\delta _{BT}, \theta _{BT})=(0.581662, 0.005247)$ when $\delta$ increases. The areas $R_3$, $R_1$, and $R_4$ correspond to the pink, olive green, and green regions, respectively, whereas the region $R_2$ is on the black SN curve. There also exists a homoclinic curve originating from the BT point, but not shown here as its range of existence is very narrow. The other parameter values are $\alpha =1.5$, $\beta =0.0207$ $\gamma =0.3$ and $\epsilon =0.01$ (for the interpretation of the colour references in this figure caption, the reader is referred to the web version of this article)

3 Slow–fast analysis

With the time scaling $\tau = \epsilon t$, $0<\epsilon \ll 1$ the system (4) transforms to the following topologically equivalent system:

$$\begin{aligned} \epsilon \frac{dx}{d\tau }&=x(1-x)-\frac{\alpha xy}{\beta +x+y}, \end{aligned}$$

(14a)

$$\begin{aligned} \frac{dy}{d\tau }&=y\left( \frac{y}{y+\gamma }-\frac{y}{\delta +\theta x}\right) . \end{aligned}$$

(14b)

The model system (4) or (14) is a standard form of slow–fast system with t as the fast timescale and $\tau$ as the slow timescale, respectively. The variables x and y are referred to as fast and slow variables, respectively. In the singular limit $\epsilon \rightarrow 0$, the systems (4) and (14) transform to the following fast and slow subsystems.

$$\begin{aligned} \frac{dx}{dt}&=x(1-x)-\frac{\alpha xy}{\beta +x+y}, \end{aligned}$$

(15a)

$$\begin{aligned} \frac{dy}{dt}&=0, \end{aligned}$$

(15b)

and

$$\begin{aligned} 0&=x(1-x)-\frac{\alpha xy}{\beta +x+y}, \end{aligned}$$

(16a)

$$\begin{aligned} \frac{dy}{d\tau }&=y\left( \frac{y}{y+\gamma }-\frac{y}{\delta +\theta x}\right) . \end{aligned}$$

(16b)

The slow flow corresponding to the slow subsystem (16) is constrained on the critical set $M_0$ given by

$$\begin{aligned} M_0&=\left\{ \left( x,y\right) \in \mathbb {R}^2_+ \,\big |\, f(x,y)=0\right\} . \end{aligned}$$

The critical set $M_0$ consists of two kinds of critical manifolds given by

$$\begin{aligned} M_{10}&=\left\{ \left( x,y\right) \in \mathbb {R}^2_+ \,\big |\, x=0\right\} , \end{aligned}$$

(17a)

$$\begin{aligned} M_{20}&=\left\{ \left( x,y\right) \in \mathbb {R}^2_+ \,\Bigg |\, y =\phi (x)= \frac{ (1-x)(\beta + x)}{\alpha +x-1}, \alpha >\frac{1}{1-\beta }, \beta <1\right\} . \end{aligned}$$

(17b)

We now have the following basic result on the nature of the function $\phi (x)$:

Lemma 5

• (i) The function $\phi (x)$ strictly decreases when $1<\alpha \le \beta +1$.

• (ii) The function $\phi (x)$ has a local maximum at $x_m=1-\alpha +\sqrt{\alpha \left( \alpha -1-\beta \right) }$ in $\mathbb {R}^2_+$ if $\alpha >\frac{1}{1-\beta }$, $\beta <1$.

Henceforth, we will be assuming throughout the article the parametric condition that $\alpha >\frac{1}{1-\beta },\,\beta <1$, to ensure that the critical manifold $M_{20}$ is of parabolic shape, increases in $0<x<x_m$ and decreases in $x_m<x<1$. The critical manifold $M_{20}$ looses its normal hyperbolicity at $P\left( 0, \frac{\beta }{\alpha -1}\right)$ and $Q(x_m, y_m)$ (maximum point), $y_m=\phi (x_m)$. Consequently, it consists of two branches $S_0^r$ and $S_0^a$ where $S_0^r$ is the branch from P to Q and is hyperbolic repelling; $S_0^a$ is the branch from Q to R(1, 0), and is hyperbolic attracting. Thus,

$$\begin{aligned} S_0^r&=M_{20}\cap \left\{ (x,y)\in \mathbb {R}^2_+ \,\big |\, 0<x<x_m\right\} , \end{aligned}$$

(18)

$$\begin{aligned} S_0^a&=M_{20} \cap \left\{ (x,y)\in \mathbb {R}^2_+ \,\big |\, x_m<x< 1\right\} . \end{aligned}$$

(19)

Similarly, the normally hyperbolic repelling and attracting parts of the critical manifold $M_{10}$, denoted by $S_0^{r+}$ and $S_0^{a+}$ are given by

$$\begin{aligned} S_0^{r+}&=M_{10}\cap \left\{ (x,y)\in \mathbb {R}^2_+ \,\Bigg |\, 0<y<\frac{\beta }{\alpha -1}\right\} , \end{aligned}$$

(20)

$$\begin{aligned} S_0^{a+}&=M_{10} \cap \left\{ (x,y)\in \mathbb {R}^2_+ \,\Bigg |\, y>\frac{\beta }{\alpha -1}\right\} . \end{aligned}$$

(21)

The slow flow that evolves on the critical manifold $M_{20}$ is given by,

$$\begin{aligned} \frac{dx}{d\tau }&=\frac{\phi ^2(x)\left( (1+\theta )x^2+(\alpha \theta +\delta -\gamma +\beta -\theta -1)x+\alpha (\delta -\gamma )-(\delta -\gamma )-\beta \right) }{\phi '(x)(\delta +\theta x)(-x^2+x(1+\gamma -\beta )+(\alpha \gamma +\beta -\gamma )}, \end{aligned}$$

(22)

and is not defined at the point Q. The point Q is known as the fold point because it corresponds to a fold bifurcation for (15) considering y as a parameter. Now, for $0<\epsilon \ll 1$, Fenichel’s theorem tells us that $S_0^{r}$ and $S_0^a$ can be perturbed to $S_{\epsilon }^{r}$ and $S_{\epsilon }^a$ which are within $\mathcal {O}(\epsilon )$ distance from $S_0^{r}$ and $S_0^a$ (Fig. 4).

Fig. 4

The dynamics of the fast and slow subsystems (15) and (16), respectively, are illustrated. Two possible interior equilibrium positions are represented by solid red circles, and the non-hyperbolic points on the slow-manifold $M_{20}$ (blue curve) are shown by solid blue circles: the generic transcritical point $P(0,\beta /(\alpha -1) )$ and the generic fold point $Q(x_m, y_m)$. The normally hyperbolic attracting branch $S_0^a$ (from Q to the point R(1, 0) for $x_m< x< 1$) and repelling branch $S_0^r$ (from P to Q for $0<x<x_m$) of the critical manifold $M_{20}$ are illustrated. The manifold $M_{10}$ is along the positive y-axis. The red arrows (horizontal) indicate fast flow, and the blue arrows on $M_{20}$ indicate slow flow (for the interpretation of the colour references in this figure caption, the reader is referred to the web version of this article)

4 Singular Hopf bifurcation and canard cycles

Here, we assume $\mu \in R_1\cup R_3$ so that the existence of the interior equilibrium $E_{2*}$ ($E_{2*}=E_*$ for $\mu \in R_3$) is ensured. It also follows that for $\delta =\delta _*$, the interior equilibrium $E_{2*}$ coincides with the fold point $Q(x_m, y_m)$, where $\delta _*$ is given by

$$\begin{aligned} \delta _*=\left( \theta +2\right) \left( \alpha -\sqrt{\alpha \left( \alpha -1-\beta \right) }-1\right) +\gamma -\beta +1. \end{aligned}$$

We also observe that

$$\begin{aligned} \left. f(x,y)\right| _{(x_m,y_m,\delta _*)}&=0,\,\,\,\, \left. g(x,y)\right| _{(x_m,y_m,\delta _*)}=0,\\ \left. \frac{\partial f(x,y)}{\partial x}\right| _{(x_m,y_m,\delta _*)}&=0,\,\,\,\,\left. \frac{\partial f(x,y)}{\partial y}\right| _{(x_m,y_m,\delta _*)}=-\frac{\alpha x_m(\beta +x_m)}{(\beta +x_m+y_m)^2}<0,\\ \left. \frac{\partial g(x,y)}{\partial x}\right| _{(x_m,y_m,\delta _*)}&=\frac{\theta y_m^2}{(\delta _*+\theta x_m)^2},\,\,\,\,\left. \frac{\partial g(x,y)}{\partial \delta }\right| _{(x_m,y_m,\delta _*)}=\frac{y_m^2}{(\delta _*+\theta x_m)^2}=\frac{y_m^2}{(\gamma +y_m)^2}. \end{aligned}$$

Further, we assume that

$$\begin{aligned} \left. \frac{\partial ^2f}{\partial x^2}\right| _{(x_m,y_m,\delta _*)}&=2\left( \frac{\alpha y_m(\beta +y_m)}{(\beta +x_m+y_m)^3}-1\right) \ne 0. \end{aligned}$$

(23)

Consequently, we have the following

$$\begin{aligned} f(x_m,y_m,\delta _*)=0,\,\,g(x_m,y_m,\delta _*)=0,\,\,\text {and}\,\frac{\partial f}{\partial x}(x_m,y_m,\delta _*)=0, \end{aligned}$$

(24)

and

$$\begin{aligned} \frac{\partial f}{\partial y}(x_m,y_m,\delta _*)\ne 0,\,\,\frac{\partial ^2 f}{\partial x^2}(x_m,y_m,\delta _*)\ne 0,\,\,\frac{\partial g}{\partial x}(x_m,y_m,\delta _*)\ne 0 \,\,\, \frac{\partial g}{\partial \delta }(x_m,y_m,\delta _*)\ne 0. \end{aligned}$$

(25)

With the above assumption, the fold point Q is now the non-degenerate canard point or the singular contact point of the system. Using the transformation $X=x-x_m$, $Y=y-y_m$ and $\lambda =\delta -\delta _*$, the system (4) transforms to the following form

$$\begin{aligned} \frac{dX}{dt}&=Y\left( a_{01}+a_{11}X+\mathcal {O}(X^2, XY, Y^2)\right) +X^2\left( \frac{a_{20}}{2}+\frac{a_{30}}{6}X+\mathcal {O}(X^2, Y^2)\right) , \end{aligned}$$

(26a)

$$\begin{aligned} \frac{dY}{dt}&=\epsilon \left[ X\left( b_{10}+\frac{b_{20}}{2}X+b_{11}Y +\mathcal {O}(X^2, XY, Y^2)\right) +\lambda \left( \frac{y_m^2}{(y_m+\gamma )^2}+\mathcal {O}(X,Y,\lambda )\right) \right. \nonumber \\&\left. +Y\left( b_{01}+\frac{b_{02}}{2}Y+\mathcal {O}(X^2, XY, Y^2)\right) \right] , \end{aligned}$$

(26b)

where $\displaystyle a_{ij}=\left. \frac{\partial ^{i+j}f}{\partial u^i\partial v^j}\right| _{(u_m,v_m,\delta _*)}$ and $\displaystyle b_{ij}=\left. \frac{\partial ^{i+j}g}{\partial u^i\partial v^j}\right| _{(u_m,v_m,\delta _*)}$ i.e.,

$$\begin{aligned} \begin{aligned}&a_{01}=-\frac{\alpha x_m(\beta +x_m)}{(\beta +x_m+y_m)^2},\,\, a_{20}=2\left( \frac{\alpha y_m(\beta +y_m)}{(\beta +x_m+y_m)^3}-1\right) ,\\&a_{11}=-\frac{\alpha }{(\beta +x_m+y_m)^3}\left( \beta (\beta +x_m+y_m)+2x_my_m)\right) , \,\,a_{30}=-\frac{6\alpha y_m(\beta +y_m)}{(\beta +x_m+y_m)^4},\\&b_{10}=\frac{\theta y_m^2}{(\gamma +y_m)^2},\,\,b_{01}=-\frac{y_m^2}{(\gamma +y_m)^2}, \,\,b_{20}=-\frac{2\theta ^2 y_m^2}{(\gamma +y_m)^3},\\&b_{02}=-\frac{2y_m(2\gamma +y_m)}{(\gamma +y_m)^3},\,\, b_{11}=\frac{2\theta y_m}{(\gamma +y_m)^2}. \end{aligned} \end{aligned}$$

In order to use the theory as developed in Krupa and Szmolyan (2001c), we use the following re-scaling

$$\begin{aligned} X=aX',\,\,Y=bY',\,\,\, t=ct' \end{aligned}$$

where

$$\begin{aligned} a=-\frac{2b_{10}a_{01}}{a_{20}}\sqrt{-\frac{1}{a_{01}b_{10}}},\,\,b=\frac{2b_{10}}{a_{20}},\,\,\, c=\sqrt{-\frac{1}{a_{01}b_{10}}}. \end{aligned}$$

The system (26) is then topologically equivalent to the following canonical form

$$\begin{aligned} \frac{dX'}{dt'}&=-Y'h_1(X',Y')+X'^2 h_2(X', Y')+\epsilon h_3(X', Y'), \end{aligned}$$

(27a)

$$\begin{aligned} \frac{dY'}{dt'}&=\epsilon \left[ X'h_4(X',Y')-\lambda ' h_5(X',Y',\lambda ')+Y'h_6(X',Y')\right] , \end{aligned}$$

(27b)

where

$$\begin{aligned} h_1(X', Y')&=1-bca_{11}X'+\mathcal {O}(X'^2, X'Y', Y'^2),\\ h_2(X', Y')&=1+\frac{a^2c}{6}a_{30}X'+\mathcal {O}(X'^2, Y'^2),\\ h_3(X',Y')&=0,\,\,\, h_4(X', Y')=1+\frac{a^2c}{2b}b_{20}X'+acb_{11}Y'+\mathcal {O}(X'^2, X'Y', Y'^2),\\ h_5(X',Y',\lambda ')&=1+\mathcal {O}(X', Y', \lambda '),\\ h_6(X', Y')&=cb_{01}+\frac{bc}{2}b_{02}Y'+\mathcal {O}(X'^2, Y'^2), \lambda '=-\frac{c\lambda }{b}\frac{y_m^2}{(y_m+\gamma )^2}. \end{aligned}$$

Now, by the formulae (3.12) and (3.13) of Krupa and Szmolyan (2001c) we have

$$\begin{aligned} a_1&=\frac{\partial h_3}{\partial X'}(0,0)=0, \end{aligned}$$

(28a)

$$\begin{aligned} a_2&=\frac{\partial h_1}{\partial X'}(0,0)=-bca_{11},\end{aligned}$$

(28b)

$$\begin{aligned} a_3&=\frac{\partial h_2}{\partial X'}(0,0)=\frac{a^2c}{6}a_{30},\end{aligned}$$

(28c)

$$\begin{aligned} a_4&=\frac{\partial h_4}{\partial X'}(0,0)=\frac{a^2c}{2b}b_{20},\end{aligned}$$

(28d)

$$\begin{aligned} a_5&=h_6(0,0)=cb_{01}, \end{aligned}$$

(28e)

$$\begin{aligned} \text {and~} A&=-a_2+3a_3-2a_4-2a_5=bca_{11}+\frac{a^2c}{2}a_{30}-\frac{a^2c}{b}b_{20}-2cb_{01}. \end{aligned}$$

(29)

Hence, following the formulae (3.15) and (3.16) of Krupa and Szmolyan (2001c) the expansions of singular Hopf bifurcation and maximal canard curves are given by

$$\begin{aligned} \lambda _H'(\sqrt{\epsilon })&=-\frac{a_1+a_5}{2}\epsilon +\mathcal {O}(\epsilon ^{3/2}),\\ \lambda _c'(\sqrt{\epsilon })&=-\left( \frac{a_1+a_5}{2}+\frac{A}{8}\right) \epsilon +\mathcal {O}(\epsilon ^{3/2}). \end{aligned}$$

In terms of original parameters, the singular Hopf and maximal canard curves can be written as

$$\begin{aligned} \delta _H(\sqrt{\epsilon })&=\delta _*+\frac{bb_{01}(y_m+\gamma )^2}{2y_m^2}\epsilon +\mathcal {O}(\epsilon ^{3/2}), \end{aligned}$$

(30)

$$\begin{aligned} \delta _c(\sqrt{\epsilon })&=\delta _*+\frac{b(y_m+\gamma )^2}{4y_m^2}\left( b_{01}+\frac{b}{2}a_{11}+\frac{a^2}{4}a_{30}-\frac{a^2}{2b}b_{20}\right) \epsilon +\mathcal {O}(\epsilon ^{3/2}). \end{aligned}$$

(31)

We assume $\mu _*= (\alpha , \beta , \gamma , \delta _*, \theta )$ so that for $\mu =\mu _*$, we have $\delta =\delta _*$. Assuming $\mu _*\in R_1\cup R_3$ and the condition (23), we define a continuous family $\Gamma (s)$ of singular canard cycles for the vector field $V_{0,\mu _*}$ passing through the canard point Q and consisting of a part of fast flow $y=s$ and parts of the attracting and repelling manifolds $S_{0}^a$ and $S_0^r$ as shown in Fig. 5, where $s\in (0, s_*)$ with

$$\begin{aligned} s_*=\left\{ \begin{array}{c} y_m-y_{1*},\,\,\,\, \mu _*\in R_1\\ y_m-\frac{\beta }{\alpha -1},\,\,\,\,\mu _*\in R_3\end{array}\right. \end{aligned}$$

(32)

Assuming that $x_l(s)<x_r(s)$ are the two distinct roots of $\phi (x)=y_m-s$, we can parametrize the family of canard cycles $\Gamma (s)$ for $s\in (0, s_*)$ as follows.

$$\begin{aligned} \Gamma (s)=\left\{ (x, \phi (x)): x\in [x_l(s), x_r(s)]\right\} \cup \left\{ (x, y_m-s): x\in [x_l(s), x_r(s)]\right\} . \end{aligned}$$

The slow–fast cycle $\Gamma (s)$ as defined here is known as the canard slow-fast cycle without a head. Similarly, assuming $\mu _*\in R_3$ and the condition (23), we define a continuous family of canard slow–fast cycles with a head $\bar{\Gamma }(s)$ for the vector field $V_{0,\mu _*}$ passing through the canard point Q as follows (see Fig. 5).

$$\begin{aligned} \bar{\Gamma }(s)&=\left\{ (x, y_m-s): x\in [0, x_l(s)]\right\} \cup \left\{ (0, y_m-s): y\in [y', y_m-s]\right\} \cup \left\{ (x, y'): x\in [0, x']\right\} \\&\cup \left\{ (x, \phi (x)): x\in [x_l(s), x']\right\} , \end{aligned}$$

where $s\in \left( \frac{\beta }{\alpha -1}, \frac{2\beta }{\alpha -1}\right)$, $x'=\phi ^{-1}(y')$ and $y'$ is defined by (34) in Lemma 6.

Fig. 5

Slow–fast cycles without head through the canard point $Q(x_m, y_m)$ (black curve) of system (4) when a $\mu _*\in R_1$, b $\mu _*\in R_3$. c Slow–fast cycle with head through the canard point $Q(x_m, y_m)$ (black curve) of system (4)

We now state the following results based on Theorems (3.3) and (3.5) of Krupa and Szmolyan (2001c).

Theorem 1

Assume $0<\epsilon \ll 1$, $\mu _*\in R_1\cup R_3$ and the condition (23) hold. Then $\exists$ $\epsilon _0>0$ and $\delta _0>0$ such that for $0<\epsilon <\epsilon _0$ and $|\delta -\delta _*|<\delta _0$, the system (4) has an equilibrium point $Q_2$ in a neighbourhood of the fold point Q which converges to Q as $(\epsilon , \delta )\rightarrow (0,\delta _*)$. The system (4) undergoes a singular Hopf bifurcation at $\delta =\delta _H(\sqrt{\epsilon })$, where $\delta _H(\sqrt{\epsilon })$ is defined in (30). The Hopf bifurcation is non-degenerate when $A\ne 0$. It is supercritical if $A<0$ and sub-critical if $A>0$ where A is given by (29).

Theorem 2

Assume $0<\epsilon \ll 1$, $\mu _*\in R_1\cup R_3$, $K>0$ a constant and the condition (23) hold. Then for every $s\in (0, s_*) (s\in \left( \frac{\beta }{\alpha -1}, \frac{2\beta }{\alpha -1}\right) )$, the system (4) has a smooth family of canard cycles $s\rightarrow (\delta (s,\sqrt{\epsilon }), \Gamma (s,\sqrt{\epsilon })(\bar{\Gamma }(s,\sqrt{\epsilon }))$ bifurcating from the singular canard cycle $\Gamma (s)(\bar{\Gamma }(s))$ where $\delta (s, \sqrt{\epsilon })$ satisfies

$$\begin{aligned} |\delta (s, \sqrt{\epsilon })-\delta _c(\sqrt{\epsilon })|\le e^{-\frac{1}{\epsilon ^K}}, \end{aligned}$$

and $\delta _c(\sqrt{\epsilon })$ is given by (31). Moreover, $\Gamma (s,\sqrt{\epsilon })(\bar{\Gamma }(s,\sqrt{\epsilon }))$ approaches to $\Gamma (s)(\bar{\Gamma }(s))$ in the Hausdorff distance as $\epsilon \rightarrow 0$.

The phenomenon is manifested as follows: for $\mu _*\in R_1\cup R_3$ a supercritical singular Hopf bifurcation produces a small limit cycle, which quickly expands for the increase of the value of $\delta$ (see Fig. 6a). The shape of the cycle distorted during this expansion, and finally a large amplitude stable oscillation is formed. This finding indicates that the instantaneous change from small to big cycles happens over an exponentially small parameter interval of $\delta$. This event is called a "canard explosion" (see Fig. 6b).

Fig. 6

a For the case of $\mu \in R_1$, canard cycles and the birth of a homoclinic orbit at the canard point are illustrated. For four distinct values of $\delta$, namely $\delta =0.416$ (magenta), 0.0.4149 (cyan), 0.41483 (green), and 0.41481573598 (black), four unstable periodic orbits are shown, with the amplitude of the orbits increasing with decreasing $\delta$. The figure evidently depicts the formation of a homoclinic orbit (black periodic orbit) via canard point for $\delta =0.41481573598$, whereby the homoclinic orbit connects the saddle equilibrium point $E_{1*}$. The other parameter values are $\alpha =1.5, \beta =0.0207, \gamma =0.3, \theta =0.51, \epsilon =0.1$. b For $\mu \in R_3$, the existence of the stable canard cycles and canard explosion phenomenon are seen in the diagram with small $\epsilon >0$. For various values of $\delta$, such as 0.247 (cyan), 0.24746 (green), 0.24747 (black), the stable periodic orbits (canard cycles) that arose through a supercritical singular Hopf bifurcation are displayed. When the bifurcation parameter $\delta$ is raised exponentially very small parameter interval from 0.24746 (the green small amplitude cycle) to 0.24747 (the black large amplitude canard cycle with a head), the figure shows that the amplitude of the orbit dramatically increases (canard explosion). The other parameter values are $\alpha =1.5, \beta =0.0207, \gamma =0.3, \theta =0.975,$ and $\epsilon =0.01$ (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

For $0<\epsilon \ll 1$, and $\mu \in R_3$, Fig. 7a depicts a simplified representation of the $\delta -\epsilon$ parametric plane that separates it into five distinct regions based on the locations of the threshold curves $\delta =\delta _H(\sqrt{\epsilon })$ (blue line), $\delta =\delta (s,\sqrt{\epsilon })$ (dashed black line), $\delta =\delta _c(\sqrt{\epsilon })$ (red line), and $\delta =\delta _r(\sqrt{\epsilon })$ (dashed black line). In domain , when $\delta <\delta _H$, there exists no periodic orbit. After crossing the singular Hopf bifurcation threshold $\delta =\delta _H$ with the increase of $\delta$ and $0<\epsilon \ll 1$ fixed, as one moves from domain into domain , the small-amplitude ($\mathcal {O}(\epsilon )$) stable periodic orbit develop for $\delta _H\sqrt{\epsilon }<\delta (s,\sqrt{\epsilon })$. The periodic orbit transforms into a canard cycle with or without a head when $\delta$ approaches the dashed line $\delta =\delta (s,\sqrt{\epsilon })$. The size of the canard cycle increases on increasing $\delta$. Along the curve $\delta =\delta _r(\sqrt{\epsilon })$, the family of canard cycles ends at a stable relaxation oscillation (existence of relaxation oscillation has been shown in Sect. 6) surrounding an unstable interior equilibrium point. The beginning and the end of the canard explosion are shown by the two black dashed lines $\delta =\delta (s,\sqrt{\epsilon })$ and $\delta =\delta _r(\sqrt{\epsilon })$ for sufficiently small $\epsilon$. Canard explosion describes the sudden change from a small canard cycle to a bigger relaxation oscillation within a limited range of the parameter $\delta$. In Fig. 7b, a numerical example is provided to better demonstrate this approach. It is clear from this numerical illustration that the amplitude of the periodic solution (the vertical axis) evolves more rapidly from small-amplitude canard cycles to large-amplitude relaxation oscillations when the governing parameter $\delta$ increases within an exponentially small range.

Fig. 7

a Schematic diagram depicting the singular Hopf bifurcation curve (blue), the maximum canard curve (red), and the relaxation oscillation cycle (dashed black curve). b A bifurcation diagram corresponding to the supercritical singular Hopf bifurcation for system (4) depicting the change in the amplitude of the canard cycles with respect to the variation of $\delta$ for fixed parameter values $\alpha =1.5$, $\beta =0.0207$, $\gamma =0.3$, $\epsilon =0.01$. Here $\delta _c=0.2475079340$ (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

Following the singular Hopf bifurcation, it follows that the Hopf-bifurcation threshold given by (30) depends on $\epsilon$ and by computing the asymptotic expansion of the first Lyapunov coefficient in the blow-up coordinates (Kuehn 2010), one can observe that the leading order term i.e., A in the expansion of the first Lyapunov coefficient determines the criticality of the singular Hopf bifurcation with respect to $\epsilon \rightarrow 0$. Thus, the criticality of the singular Hopf bifurcation will be changed if A changes its sign, i.e., the singular Hopf bifurcation will be degenerate if $A=0$. Using MATCONT, we uncover the occurrence of the codimension two generalized Hopf (GH) bifurcations. For the parameter values $\alpha =1.5$, $\beta =0.0207$ $\gamma =0.3$ and $\epsilon =0.01$, the generalized Hopf bifurcation (GH) point located at $(\delta _{GH}, \theta _{GH})=(0.361212, 0.638870)$ in the region $R_1$ (see Fig. 3), at which the critical point (0.347909, 0.283481) has a pair of purely imaginary eigenvalues, $A=-2.2\times 10^{-8}$ i.e., A is very near to zero and the leading order term of the second Lyapunov coefficient is positive. Consequently, the system undergoes a generalized Hopf bifurcation and the generalized Hopf bifurcation threshold is given by $(\delta _{GH}, \theta _{GH})=(0.361212 0.638870)$. Referring to the Fig. 3, the GH bifurcation occurs at the transition between supercritical ($H^-$) and sub-critical ($H^+$) Hopf bifurcations, the Hopf curve $H^+$ below the GH point is sub-critical whereas the Hopf curve above the GH is supercritical. The existence of a Limit Point of Cycles (LPC) curve has been detected emanating from the GH point propagates outward from the GH point towards the $H^-$ curve with a very close in distance with $H^-$ (see Fig. 3). It is to be mentioned that in the region $R_1$ bounded by the LPC curve and the Hopf curve $H^{-}$, there exists two canard cycles (unstable and stable canard cycles). The unstable and the stable canard cycles collide and disappear via a saddle node bifurcation of limit cycles on the LPC curve. It has been shown in Lemma 3 that for the system parameters belonging to the region $R_1$ the prey-free equilibrium $E_{2b}$ is a hyperbolic stable node and correspondingly, when we have the existence of two canard cycles (stable and unstable) emerging due to the generalized Hopf bifurcation, the system exhibits a bi-stability phenomenon i.e., the system can either approach to “prey extinction", or “oscillating coexistence" depending on the initial population size.

5 Heteroclinic and homoclinic orbits

In this section, we aim to show the existence of heteroclinic and homoclinic orbits for the system (4) under various parametric conditions.

Proposition 1

Assume $0<\epsilon \ll 1$, $\mu \in R_1$ and $x_{2*}>x_m$. Then we have the following results. There exists one heteroclinic orbit connecting each pair of the equilibria $(E_0, E_{1b})$, $(E_0, E_{1*})$, $(E_{1b}, E_{2*})$, $(E_{1*}, E_{2b})$, $(E_{1*}, E_{2*})$ and infinitely many heteroclinic orbits connecting the pair of equilibria $(E_0, E_{2b})$, $(E_0, E_{2*})$. Moreover, the system (4) has no canard cycle and relaxation oscillation.

Proof

For $\mu \in R_1$, the equilibria $E_0, E_{1b}$ are saddle nodes, $E_{1*}$ is a hyperbolic saddle, $E_{2b}$ is a stable node and $E_{2*}$ is a stable equilibrium point. $E_0$ and $E_{1b}$ being saddle node equilibria, a neighbourhood of them consists of two hyperbolic and one parabolic sectors. Every trajectory starting in $\mathbb {R}_+^2$ and in a neighbourhood of $E_0$ moves away from $E_0$ whereas, for $E_{1b}$, two hyperbolic sectors are separated by the two stable separatrices and an unstable separatrix. It also follows by Fenichel’s theorem that for $0<\epsilon \ll 1$, the normally hyperbolic manifolds $S_0^r, S_0^a$ perturb to $S_{\epsilon }^{r}$ and $S_{\epsilon }^a$ which are within $\mathcal {O}(\epsilon )$ distance from $S_0^{r}$ and $S_0^a$ and the same scenario for the normally hyperbolic manifolds $S_0^{r+}$ and $S_0^{a+}$. The x and y axes are invariant under the flow and accordingly, the unstable orbit for $E_0$ along the positive x-axis gets connected to $E_{1b}$ forming a heteroclinic connection joining $E_0$ and $E_{1b}$.

$E_{1*}$ being a saddle equilibrium, the $\alpha$-limit set of one of its stable separatrix will be $E_0$ and hence, it forms a heteroclinic connection joining $E_0$ and $E_{1*}$. For $0<\epsilon \ll 1$, the unstable separatrix of $E_{1b}$ follows $S_{\epsilon }^a$ slowly and gets attracted to $E_{2*}$ forming a heteroclinic orbit joining $E_{1b}$ and $E_{2*}$. One unstable separatrix of $E_{1*}$ is first attracted to the slow manifold $S_{\epsilon }^a$ in a fast timescale and then follows it slowly and, finally, gets attracted to the stable equilibrium $E_{2*}$, forming a heteroclinic connection joining $E_{1*}$ and $E_{2*}$. Another unstable separatrix of $E_{1*}$ is first attracted to the slow manifold $S_\epsilon ^{a+}$ in a fast speed and then follows it in slow speed and finally gets attracted to the stable node $E_{2b}$, forming a heteroclinic orbit joining $E_{1*}$ and $E_{2b}$.

For the trajectories starting in the region bounded by the heteroclinic orbits joining the pair of equilibria $(E_0, E_{1b})$, $(E_0, E_{1*})$ and $(E_{1*}, E_{2*})$ the $\alpha$-limit set is $E_0$ and $\omega$-limit set is $E_{2*}$ as because all such trajectories will first get attracted to $S_{\epsilon }^a$ following approximately layers of the fast subsystem (15) and then follow $S_\epsilon ^a$ in slow time and finally, attracted to the stable equilibrium $E_{2*}$. Hence, we have infinitely many heteroclinic orbits joining $E_0$ and $E_{2*}$. Similarly, all the trajectories starting in the region bounded by the heteroclinic orbits joining the pair of equilibria $(E_0, E_{1*})$ and $(E_0, E_{2b})$ have $E_0$ as their $\alpha$-limit set and $E_{2b}$ as their $\omega$-limit set and consequently, there exist infinitely many heteroclinic orbits joining $E_0$ and $E_{2b}$.

Under the parametric conditions as mentioned, the system has no canard point and no slow-fast cycle. Consequently, the system has no canard cycle and relaxation oscillation.$\square$

Fig. 8

Numerical illustration for the existence of heteroclinic orbits for $\mu \in R_1$, $x_{2*}>x_m$, and $0<\epsilon \ll 1$. a Each set of equilibrium points $(E_0, E_{1b})$, $(E_0, E_{1*})$, $(E_{1b}, E_{2*})$, $(E_{1*}, E_{2b})$, and $(E_{1*}, E_{2*})$ is connected by a single heteroclinic orbit presented by solid magenta, solid green, dashed yellow, solid cyan, and solid black curve respectively. b Both green and cyan curves are the heteroclinic orbits connecting the equilibrium points $E_0$ and $E_{2b}$, and the two black curves are the heteroclinic orbits connecting the equilibria $E_0$ and $E_{2*}$. The parameter values are $\alpha =1.5, \beta =0.0207, \gamma =0.3, \delta =0.41, \theta =0.3, \epsilon =0.1$ (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

For a geometrical description of the proof of proposition 1, see Fig. 8.

Proposition 2

Assume $0<\epsilon \ll 1$, $\mu \in R_1$, $x_{2*}=x_m$, and the condition (23) holds. Then the system (4) has a unique homoclinic orbit connecting to the saddle equilibrium $E_{1*}$ if and only if $\delta =\delta _c(\sqrt{\epsilon })$, where $\delta _c(\sqrt{\epsilon })$ is given by (31). Furthermore, if this is the case then there exists infinitely many heteroclinic orbits connecting $E_0$ and $E_{2b}$, one heteroclinic orbit connecting each pair of the equilibria $(E_{1b}, E_{2b}), (E_0, E_{1*}), (E_0, E_{1b})$ and $(E_{1*}, E_{2b})$.

Proof

Under the said conditions $E_{1*}$ is a saddle, $E_{2*}$ is a canard point and the system (4) undergoes a singular Hopf bifurcation for $\delta =\delta _H(\sqrt{\epsilon })$. As in the Theorem 1, by the Fenichel’s theorem $S_0^r$ and $S_0^a$ perturb to the slow manifolds $S_\epsilon ^r$ and $S_\epsilon ^a$ respectively. One of the stable separatrices of $E_{1*}$, say, $W^s$ exactly follows, $S_\epsilon ^r$ and the other stable separatrix of $E_{1*}$ has $E_0$ as its $\alpha$-limit set. Consequently, we have a heteroclinic orbit connecting $E_0$ and $E_{1*}$. For $0<\epsilon \ll 1$, one of the unstable separatrices of $E_{1*}$, say $W^u$ first follows a layer of the fast subsystem (15) and then gets attracted to the slow manifold $S_{\epsilon }^a$ and finally, it reaches near the canard point Q and by Theorem 3.2 in Krupa and Szmolyan (2001c) the slow manifolds $S_\epsilon ^r$ and $S_\epsilon ^a$ get connected for $\delta =\delta _c(\sqrt{\epsilon })$ given by (31). This shows that for $\delta = \delta _c(\sqrt{\epsilon })$ given by (31), $W^s$ and $W^u$ get connected and form a homoclinic orbit homoclinic to $E_{1*}$.

Now, one of the unstable separatrices of $E_{1b}$ follows exactly $S_\epsilon ^a$ and reaches in a neighbourhood of $S_\epsilon ^{a+}$ passing the canard point Q and finally, gets attracted to the stable node $E_{2b}$. Hence, we have a heteroclinic connection joining $E_{1b}$ and $E_{2b}$. Similarly, the other unstable separatrix of $E_{1*}$ follows a layer of the fast subsystem (15) until it reaches in a neighbourhood of $S_\epsilon ^{a+}$ and finally, gets attracted to the stable node $E_{2b}$ forming a heteroclinic orbit joining $E_{1*}$ and $E_{2b}$.

Finally, following the same reason as in Proposition 1, all the trajectories initiating in $\mathbb {R}^2_+$ and in a neighbourhood of $E_0$ except the heteroclinic connections joining $E_0$ and $E_{1b}$ along the x-axis and $E_0$ and $E_{1*}$ along the stable manifold of $E_{1*}$ have $E_{2b}$ as their $\omega$-limit set and $E_0$ as $\alpha$-limit set. Hence, we have infinitely many heteroclinic orbits joining $E_0$ and $E_{2b}$.$\square$

Fig. 9

Numerical illustration for the existence of heteroclinic orbits for $\mu \in R_1$, $x_{2*}=x_m$, and $0<\epsilon \ll 1$. a Each set of equilibrium points $(E_{1b}, E_{2b})$, $(E_0, E_{1*})$, and $(E_0, E_{1b})$ is connected by a single heteroclinic orbit presented by solid black, solid green, and solid cyan curve respectively. The dashed magenta curve is the homoclinic orbit connecting the equilibrium point $E_{1*}$ to itself. b Both cyan curves are the heteroclinic orbits connecting the equilibrium points $E_0$ and $E_{2b}$. The black curve is the unique heteroclinic orbit connecting the equilibria $E_{1*}$ and $E_{2b}$. The parameter values are $\alpha =1.5, \beta =0.0207, \gamma =0.3, \delta =0.41481573598, \theta =0.51, \epsilon =0.1$ (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

For a geometrical description of the proof of proposition 2, see Fig. 9.

Proposition 3

Assume $0<\epsilon \ll 1$, $\mu \in R_2$. Then the system (4) has one heteroclinic orbit connecting each pair of equilibria $(E_0, E_{1b}), (E_0, \bar{E}), (E_{1b}, E_{2b})$ and infinitely many heteroclinic orbits joining the pair of equilibria $(E_0, E_{2b})$ and $(\bar{E}, E_{2b})$. Furthermore, the system has neither a canard cycle nor a relaxation oscillation.

Proof

Under the said condition the interior equilibria $E_{1*}$ and $E_{2*}$ get merged to the single equilibrium $\bar{E}$ which is saddle node in nature and a neighbourhood of $\bar{E}$ consists of two hyperbolic and one parabolic sectors (infinitely many centre manifolds and one unstable manifold). For $0<\epsilon \ll 1$, any orbit in the parabolic sector follows a layer of the fast subsystem (15) until it arrives in a neighbourhood of $S_\epsilon ^a$ or $S_\epsilon ^{a+}$. Now, if the orbit reaches a neighbourhood of $S_\epsilon ^{a+}$, it will then be attracted to the stable node, $E_{2b}$ forming a heteroclinic orbit connecting $\bar{E}$ and $E_{2b}$. Else, the orbit reaches in the vicinity of $S_\epsilon ^a$, and following it passes the fold point by Theorem (2.1) of Krupa and Szmolyan (2001c). The orbit then arrives in a $\mathcal {O}(\epsilon )$ neighbourhood of $S_\epsilon ^{a+}$ following a layer of the fast subsystem (15) and finally, gets attracted to the stable node, $E_{2b}$ forming a heteroclinic connection joining $\bar{E}$ and $E_{2b}$. This phenomenon is true for all the orbits emanating from the parabolic sector of the saddle node $\bar{E}$. Hence, we have infinitely many heteroclinic orbits joining $\bar{E}$ and $E_{2b}$.

For $0<\epsilon \ll 1$, the unique stable branch of the infinitely many centre manifolds of $\bar{E}$ exactly follows $S_\epsilon ^r$ and has $E_0$ as its $\alpha$-limit set. Therefore, the system (4) has a heteroclinic orbit connecting $E_0$ and $\bar{E}$. Proceeding in the same way as in the Proposition 3, we have the existence of one heteroclinic orbit joining the pair of the equilibria $(E_0, E_{1b})$ and $(E_{1b}, E_{2b})$.

Finally, all the trajectories initiating in $\mathbb {R}^2_+$ and in a neighbourhood of $E_0$ except the heteroclinic connections joining $E_0$ and $E_{1b}$ along the x-axis and $E_0$ and $\bar{E}$ along the unique stable branch of the centre manifolds of $\bar{E}$ have $E_{2b}$ as their $\omega$-limit set and $E_0$ as $\alpha$-limit set. Consequently, we have infinitely many heteroclinic orbits joining $E_0$ and $E_{2b}$.

Under the said condition, the system has no canard point and no slow-fast cycle. Consequently, the system has no canard cycle and relaxation oscillation. $\square$

For a geometrical description of the proof of proposition 3, see Fig. 10.

Fig. 10

Numerical illustration for the existence of heteroclinic orbits for $\mu \in R_2$, and $0<\epsilon \ll 1$. a Each set of equilibrium points $(E_{0}, E_{1b})$, $(E_0, \bar{E})$, and $(E_{1b}, E_{2b})$ is connected by a single heteroclinic orbit presented by solid cyan, dashed black, and solid green curve respectively. b Both the magenta and black curves are the heteroclinic orbits connecting the equilibrium points $\bar{E}$ and $E_{2b}$. The cyan and green curves are the heteroclinic orbits connecting the equilibrium points $E_0$ and $E_{2b}$. The parameter values are $\alpha =1.5, \beta =0.0207, \gamma =0.3, \delta =0.49576955, \theta =0.3, \epsilon =0.1$ (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

Proposition 4

Assume $0<\epsilon \ll 1$, $\mu \in R_3$ and $x_*>x_m$. Then the system (4) has a heteroclinic orbit connecting each pair of the equilibria $(E_0, E_{1b})$, $(E_0, E_{2b})$, $(E_{1b}, E_*)$, $(E_{2b}, E_*)$ provided $E_{2b}$ exists and infinitely many heteroclitic orbits connecting $E_0$ and $E_*$. Moreover, if this is the case, then the interior equilibrium $E_*(x_*, y_*)$ is globally stable in the interior of $\mathbb {R}^2_+$.

Proof

For $0<\epsilon \ll 1$, the equilibrium $E_{2b}$ is a saddle whereas the unique interior equilibrium $E_*$ on the normally hyperbolic attracting manifold $S_0^a$ is a stable singularity. The stable manifold of $E_{2b}$ is exactly the critical manifold $M_{10}$ along the y-axis and as y-axis is invariant, there exists a heteroclinic connection between $E_0$ and $E_{2b}$. One of the unstable separatrices of $E_{2b}$ arrived in a neighbourhood of the slow manifold $S_\epsilon ^a$ following a layer of the fast subsystem (15) in fast time and finally, following the slow manifold $S_\epsilon ^a$ gets attracted to the stable singularity $E_*$. Hence, there exists a heteroclinic connection joining $E_{2b}$ and $E_*$. Proceeding as in the previous propositions, there also exists a heteroclinic connection joining the equilibria $E_0$ and $E_{1b}$; $E_{1b}$ and $E_*$. Finally, all infinitely many centre manifolds in the parabolic sector of $E_0$ in $\mathbb {R}^2_+$ have $E_{*}$ as their $\omega$-limit set and $E_0$ as $\alpha$-limit set. This shows that there exist infinitely many heteroclinic orbits connecting the singularities $E_0$ and $E_*$.

One of the unstable separatrices of $E_{2b}$ first follows a layer of the fast subsystem (15) and reaches a neighbourhood of $S_\epsilon ^a$, and following $S_\epsilon ^a$ it gets attracted to the stable singularity $E_*$. From the geometry of the $S^a_0,$ it follows that $E_*$ is locally asymptotically stable. To claim that $E_*$ is globally stable, we need to show that there does not exist any periodic orbit in the interior of $\mathbb {R}^2_+$. We consider a vertical line $x=x_m$ which divides the interior of $\mathbb {R}^2_+$ into two domains $D_1$ and $D_2$, where

$$\begin{aligned} D_1=\{(x,y):0<x\le x_m, y>0\}\,\,\text {and}\,\, D_2=\{(x,y):x>x_m, y>0\}. \end{aligned}$$

In the domain $D_2$, we define the Dulac function $H:D_2\rightarrow \mathbb {R}$ by $H(x,y)=\frac{\beta +x+y}{x(\alpha +x-1)y^2}$. Now, as in $D_2$, the critical manifold $M_{20}$ decreases, we have

$$\begin{aligned} \frac{\partial (fH)}{\partial x} +\epsilon \frac{\partial (gH)}{\partial y}= \frac{1}{y^2}\phi '(x)-\frac{(\beta +x+y)}{x(\alpha +x-1)(y+\gamma )^2}<0,\,\, \forall \,\,(x,y)\in D_2. \end{aligned}$$

Hence, by the Dulac criterion, the system (4) has no periodic orbit which entirely lies in $D_2$. Consequently, it follows that $E_{*}$ is the only $\omega$-limit point of every trajectory starting in $D_2$. For $0<\epsilon \ll 1$, we consider tracking of trajectories which start in $D_1$. This will suffice our claim if we can show that $E_*$ is the only $\omega$-limit point of the two trajectories $\Gamma _1$ and $\Gamma _2$ which start above and below the critical manifold $M_{20}$ but in $D_1$. The trajectory $\Gamma _1$ which starts in $D_1$ but above $M_{20}$ arrives in the vicinity of $S_\epsilon ^{a+}$ as $S_\epsilon ^{a+}$ is hyperbolic attracting and passes the fold point P. Now, as the fold point P is also a jump point, the trajectory $\Gamma _1$ then moves away from the normally hyperbolic repelling manifold $S_\epsilon ^{r+}$ following a fast layer of the subsystem (15) and reaches a $\mathcal {O}(\epsilon )$ neighbourhood of $S_\epsilon ^{a}$ which lies in the region $D_2$. Finally, the trajectory gets attracted to $E_*$ following $S_\epsilon ^{a}$, i.e., $E_*$ is the $\omega$-limit point of the trajectory $\Gamma _1$. Similarly, the trajectory $\Gamma _2$ starting below $M_{20}$ but in $D_1$ arrives in the vicinity of $S_\epsilon ^{a}$ following a fast layer of the subsystem (15) and gets attracted to $E_*$ following $S_\epsilon ^{a}$. Thus, any trajectory starting in $D_1$ or $D_2$ converges to $E_*$ showing that $E_*$ is globally stable for $0<\epsilon \ll 1$. $\square$

Fig. 11

Numerical illustration for the existence of heteroclinic orbits for $\mu \in R_3$, $x_{*}>x_m$ and $0<\epsilon \ll 1$. a Each set of equilibrium points $(E_{0}, E_{1b})$, $(E_0, E_{2b})$ and $(E_{2b}, E_{*})$ is connected by a single heteroclinic orbit presented by solid cyan, black and green curve respectively. b The equilibrium point $(E_{1b}, E_{*})$ is connected by a unique heteroclinic orbit presented by broken green. $E_*$ is globally asymptotically stable, and there does not exist any periodic orbit in the first quadrant. c Then the system (4) has infinitely many heteroclitic orbits (using black curves, we only present two here) connecting $E_{0}$ and $E_*$. The parameter values are $\alpha =1.5, \beta =0.0207, \gamma =0.3, \delta =0.32, \theta =0.3, \epsilon =0.1$ (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

For a geometrical description of the proof of proposition 4, see Fig. 11.

Proposition 5

Assume $0<\epsilon \ll 1$, $\mu \in R_3$ and $x_*<x_m$. Then the system (4) has a unique stable relaxation oscillation.

Proof

The proof has been shown in the next section with the help of entry-exit function. $\square$

6 Relaxation oscillation

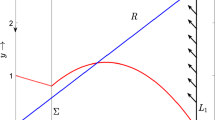
Here, our target is to show the existence of relaxation oscillation for the system (4) for $0<\epsilon \ll 1$ whenever $\mu \in R_3$ and $x_{*}<x_m$ with the help of entry-exit function. A relaxation oscillation for the system (4) is a periodic orbit $\Gamma _\epsilon$ which converges to a piece-wise smooth singular closed orbit $\Gamma _0$ consisting of slow fast segments as $\epsilon \rightarrow 0$ in the Hausdorff distance.

We know that the critical manifold $M_{10}$ i.e., the y-axis is normally hyperbolic attracting for $y>\frac{\beta }{\alpha -1}$ and normally hyperbolic repelling for $y<\frac{\beta }{\alpha -1}$. We consider the system (4) and observe that for $\epsilon =0$, the y- axis consists of equilibria, attracting for $y>\frac{\beta }{\alpha -1}$ and repelling for $y<\frac{\beta }{\alpha -1}$. For $\epsilon >0$, very small, a trajectory starting at $(x_0,y_0)$, $x_0>0$, very small, $y_0>\frac{\beta }{\alpha -1}$ gets attracted towards the y-axis and then drifts downward and when crosses the line $y=\frac{\beta }{\alpha -1}$ gets repelled from the y-axis. Thus, for $\epsilon >0$, very small, the trajectory re-intersects the line $x=x_0$ at $(x_0, p_\epsilon (y_0))$ such that $\displaystyle \lim _{\epsilon \rightarrow 0}p_\epsilon (y_0)=p_0(y_0)$, where $p_0(y_0)$ is determined by

$$\begin{aligned} \int _{y_0}^{p_{0}(y_0)}\frac{1-\frac{\alpha y}{\beta }}{y^2\left( \frac{1}{y+\gamma }-\frac{1}{\delta }\right) }dy=0. \end{aligned}$$

(33)

The function $y_0\rightarrow {p_0(y_0)}$ is referred to as an entry-exit function.

Lemma 6

If $\gamma -\delta \ge 0$ or $\gamma -\delta < 0$ then there exists a unique $y'$, where $0<y'<\frac{\beta }{\alpha -1}$ or $\delta -\gamma<y'<\frac{\beta }{\alpha -1}$ such that

$$\begin{aligned} J(y')=\int _{y'}^{y_m} \frac{1-\frac{\alpha y}{\beta +y}}{y^2\left( \frac{1}{y+\gamma }-\frac{1}{\delta }\right) }dy=0. \end{aligned}$$

(34)

Proof

We have,

$$\begin{aligned} J(y)&=\int _{y}^{y_m} \frac{1-\frac{\alpha y}{\beta +y}}{y^2\left( \frac{1}{y+\gamma }-\frac{1}{\delta }\right) }dy\\&= -\delta \int _y^{y_m}\frac{(\beta +(1-\alpha ) y)(y+\gamma )}{y^2(\beta +y)(y+\gamma -\delta )}dy\\&=-\delta \left[ \frac{\alpha \gamma (\delta -\gamma )-\beta \delta }{\beta (\gamma -\delta )^2}\int _y^{y_m}\frac{1}{y}dy+\frac{\gamma }{\gamma -\delta }\int _y^{y_m}\frac{1}{y^2}dy+\frac{\alpha (\beta -\gamma )}{\beta (\beta -\gamma +\delta )}\int _y^{y_m}\frac{1}{\beta +y}dy\right. \\&\left. +\frac{\delta (\alpha -1)(\gamma -\delta )+\beta \delta )}{(\beta -\gamma +\delta )(\gamma -\delta )^2}\int _y^{y_m}\frac{1}{y+\gamma -\delta }dy\right] \\&\rightarrow -\infty \,\, \textrm{as}\,\, y\rightarrow 0^+, \, \gamma -\delta \ge 0\,\,\textrm{or}\,\,\textrm{as}\,\, y\rightarrow (\delta -\gamma )^+,\, \gamma -\delta <0. \end{aligned}$$

Further,

$$\begin{aligned} J'(y)=\frac{\delta (\beta -(\alpha -1) y)(y+\gamma )}{y^2(\beta +y)(y+\gamma -\delta )}>0, \end{aligned}$$

$\mathrm{either \,\,for}\,\,0<y<\frac{\beta }{\alpha -1},\,\gamma -\delta \ge 0\,\, \mathrm{or\,\, for }\,\,\delta -\gamma<y<\frac{\beta }{\alpha -1},\, \gamma -\delta <0$. Hence, J(y) increases strictly for $0<y<\frac{\beta }{\alpha -1}$, $\gamma -\delta \ge 0$ or for $\delta -\gamma<y<\frac{\beta }{\alpha -1}$, $\gamma -\delta <0$.

We also have,

$$\begin{aligned} J\left( \frac{\beta }{\alpha -1}\right) = -\delta \int _{\frac{\beta }{\alpha -1}}^{y_m}\frac{(\beta -(\alpha -1) y)(y+\gamma )}{y^2(\beta +y)(y+\gamma -\delta )}dy>0. \end{aligned}$$

Thus, it follows that there exists a unique $y'$ where $0<y'<\frac{\beta }{\alpha -1}$, $\gamma -\delta \ge 0$ or $\delta -\gamma<y'<\frac{\beta }{\alpha -1}$, $\gamma -\delta <0$ such that $J(y')=0$. $\square$

The critical manifolds $M_{10}$ and $M_{20}$ lose its normal hyperbolicity at $P(0,\frac{\beta }{\alpha -1})$ and $Q(x_m, y_m)$. The point $Q(x_m,y_m)$ is a generic fold point for the system (4) and also a jump point as at this point the fast flow (15) is moved away from the critical manifold $M_{20}$ and gets attracted toward $S_0^{a+}$, the attracting branch of the critical manifold $M_{10}$. For the point P, we have

$$\begin{aligned}&\left. \frac{\partial f}{\partial x}\right| _{P}= 0 =\left. \frac{\partial f}{\partial y}\right| _{P}, ~~\left. \frac{\partial ^2 f}{\partial x^2}\right| _{P}=2\frac{\alpha (1-\beta )-1}{\alpha \beta }>0, \\&\quad \left. g\right| _P=\frac{\beta ^2}{(\alpha -1)^2}\left( \frac{(\delta -\gamma )(\alpha -1)-\beta }{ \delta (\beta +\gamma (\alpha -1))}\right) <0, \end{aligned}$$

and

$$\begin{aligned} \textrm{det} \left[ \begin{array}{cc} \frac{\partial ^2 f}{\partial x^2} &{}\frac{\partial ^2 f}{\partial x\partial y} \\ \frac{\partial ^2 f}{\partial x \partial y} &{}\frac{\partial ^2 f}{\partial y^2}\end{array} \right] _{P} =-\frac{(\alpha -1)^4}{\alpha ^2\beta ^2}<0, \end{aligned}$$

and hence, P is a generic transcritical point for the system (4). The point P is also a jump point, as at this point the fast flow (15) is moved away from the critical manifold $M_{10}$.

We now consider a singular slow-fast cycle $\Gamma _0$ with the following trajectory: starting at the point $S(0, y_m)$, we follow the slow flow (16) down the y-axis until we reach $T(0,y')$; then we follow the fast flow (15) to intersect the attracting branch $S_0^{a}$ at $T'(x', y')$; next we follow the slow flow (16) along $S_0^{a}$ until we reach point Q and finally we follow the fast flow (15) to the left of Q until returning to the starting point, $S(0, y_m)$. Consequently, we have a singular orbit $\Gamma _0$ consisting of slow and fast segments for which T, Q are jump points and $T', S$ are drop points as at these points, the fast flow is moved toward the critical manifolds.

Theorem 3

Let $\mu \in R_3$, $x_{*}<x_m$ and N be a tubular neighbourhood of $\Gamma _0$. Then for each fixed $0 < \epsilon \ll 1$, the system (4) has a unique relaxation oscillation $\Gamma _\epsilon \subset N$ which is strictly attracting with characteristic multiplier bounded by $-K/\epsilon$ for some constant $K > 0$. Moreover, the cycle $\Gamma _\epsilon$ converges to $\Gamma _0$ in the Hausdorff distance as $\epsilon \rightarrow 0$.

Proof

Conditions stated in the theorem ensure that the system (4) has a unique interior equilibrium $E_*(x_*,y_*)$ and the equilibrium lies to the left of the generic fold point Q. For $\epsilon >0$ very small, following the Fenichel’s theorem $S_0^a$, $S_0^{a+}$, perturb to nearby slow manifolds $S_\epsilon ^{a}$ and $S_\epsilon ^{a+}$ and by Theorem (2.1) of Krupa and Szmolyan (2001a), the slow manifolds $S_\epsilon ^a$ can be continued beyond the generic fold point Q and by Theorem (2.1) of Krupa and Szmolyan (2001b), the slow manifold $S_\epsilon ^{a+}$ can be continued beyond the generic transcritical point P. The slow manifold $S_\epsilon ^a$ (resp. $S_\epsilon ^{a+}$) lies close to $S_0^a$ (resp. $S_0^{a+}$) until it arrives at the vicinity of the generic fold point Q (resp. generic transcritical point P).

We consider a small vertical section $\Delta =\{(x_0, y)|y\in [y_m-\epsilon _0, y_m+\epsilon _0]\}$, $0<\epsilon _0\ll 1$ We know that for every point $(0,y_0)$, $y_0\in [y_m-\epsilon _0, y_m+\epsilon _0]$ we can define $p_0(y_0)$ such that $0<p_0(y_0)<\frac{\beta }{\alpha -1}$ for $\gamma -\delta \ge 0$ or $\delta -\gamma<p_0(y_0)<\frac{\beta }{\alpha -1}$ for $\gamma -\delta <0$ by the result derived in Lemma 6.

We now follow tracking two trajectories $\Gamma _\epsilon ^{1,2}$ starting on $\Delta$ at the points $(x_0, y^{1,2})$. For $0 < \epsilon \ll 1$, it follows by Fenichel’s theorem that $\Gamma _\epsilon ^{1,2}$ get attracted toward the slow manifold $S_\epsilon ^{a+}$ exponentially with a rate $\mathcal {O}(e^{-1/\epsilon })$ and move downward slowly. Then by Theorem (2.1) of Krupa and Szmolyan (2001a) $\Gamma _\epsilon ^{1,2}$ passes by the generic transcritical point P contracting exponentially toward each other and leave the repelling branch $S_0^{r+}$ of the critical manifold $M_{10}$ at the points $(0, p_0(y^{1,2}))$ and then jump horizontally to $(x_0, p_\epsilon (y^{1,2}))$ where $\displaystyle \lim _{\epsilon \rightarrow 0}p_\epsilon (y^{1,2})= p_0(y^{1,2})$. The trajectories then follow two layers of the fast flow (15) and get attracted towards the slow manifold $S_\epsilon ^a$ and pass the generic fold point Q contracting exponentially and thus, finally return to $\Delta$.

Tracking the forward trajectories, we thus have a return map $\Pi : \Delta \rightarrow \Delta$ inducted by the flow of (4) for $0 < \epsilon \ll 1$. The return map $\Pi$ is a contraction map as the trajectories contract toward each other with rate $\mathcal {O}(e^{-1/\epsilon })$ and by the contraction mapping theorem $\Pi$ has a unique fixed point which is stable. This fixed point is the desired limit cycle $\Gamma _\epsilon$ which exists in a tubular neighbourhood of the singular slow-fast cycle $\Gamma _0$ and as the contraction is exponential, the characteristic multiplier of $\Gamma _\epsilon$ is bounded above by $-K/\epsilon$ for some $K>0$. Again applying Fenichel’s theorem, Theorem (2.1) of Krupa and Szmolyan (2001b) and Theorem (2.1) of Krupa and Szmolyan (2001a), we conclude that the periodic orbit $\Gamma _\epsilon$ converges to the singular orbit $\Gamma _0$ as $\epsilon \rightarrow 0$ in the Hausdorff distance.$\square$

For a geometrical description of the proof of theorem 3, see Fig. 12.

Fig. 12

a Representation of the singular orbit $\Gamma _0$ (green) and a relaxation oscillation orbit $\Gamma _\epsilon$ (black) for the system (4) with $0<\epsilon \ll 1$ for $x_{*}<x_m$. The blue curve and red line, respectively, represent the non-trivial prey and predator nullclines. The two non-hyperbolic points P and Q, shown by the solid blue circles, are the generic transcritical and generic fold points, respectively. The trajectory of $\Gamma _0$ is as follows: (i) it travels from $S(0,y_m)$ to $T(0,y')$ along the y-axis downward following the slow-flow (16); (ii) it travels from $T(0,y')$ to $T'(x',y')$ parallel to x-axis following a layer of the fast subsystem (15); (iii) it travels from $T'$ to Q along the attracting branch $S_0^a$ following the slow-flow (16) and (iv) finally, travels from Q to S following the fast-flow (15). According to the Fenichel’s theorem, the submanifolds $S_0^{r}$ and $S_0^a$ could be perturbed to $S_{\epsilon }^{r}$ and $S_{\epsilon }^a$ for, $0<\epsilon \ll 1$ respectively. These submanifolds are located within $\mathcal {O}(\epsilon )$ distance from $S_0^{r}$ and $S_0^a$, respectively. The vertical section $\Delta$ is defined in the text. b A numerical illustration of a relaxation oscillation (thick black periodic orbit) for the system (4) encompassing the unique interior equilibrium point obtained for the parameter values $\alpha =1.5, \beta =0.0207, \gamma =0.3,\delta =0.31,$ $\theta =1.25$ and $\epsilon =0.005$. Slow flow is represented by black arrows, whereas fast flow is shown by red arrows (for interpretation of the references to colour in this figure caption, the reader is referred to the web version of this article)

6.1 Bi-stability

A phenomenon of bi-stability will occur for the system (4) whenever $\mu \in R_1$ and $x_{2*}>x_m$. Under these parametric restrictions, both the equilibria $E_2(0,\delta -\gamma )$ and $E_{2*}$ are stable, whereas the equilibrium $E_{1*}$ is a hyperbolic saddle. Thus, we have the basins of attraction for the equilibria $E_{2*}$ and $E_2$ separated by the stable and unstable separatrices of the saddle equilibrium $E_{1*}$. Geometrically, this signifies that if initially, the prey species lie to the left of the stable separatrix of $E_{1*}$, then in the long run the prey species will die out otherwise both the species will coexist.

A common phenomenon for the model system (4) is that the generalist predator species have the choice of an alternate food source when their preferred prey is absent. This observation is reflected in the model system when $\mu \in R_4$, as in this case, there is no interior equilibrium for the system (4) but the boundary equilibrium point $E_{2b}(0,\delta -\gamma )$ is a stable singularity. Thus, for $\mu \in R_4$, the prey species will die out in the long run, whereas the predator species will exist (Fig. 13).

Fig. 13

The bistability scenario is shown in the phase portrait of the system (4) for $\mu \in R_1$ and $x_{2*}>x_m$. Non-trivial prey and predator nullclines are shown by the solid blue and red curves, respectively. The stable and unstable manifolds of the saddle equilibrium point $E_{1*}$ are shown by green and magenta curves, respectively. The phase portrait depicts that the system has two basins of attraction of $E_{2b}(0,\delta -\gamma )$ and $E_{2*}$ separated by the stable manifold (magenta) of the saddle equilibrium point $E_{1*}$. The parameter values used are given by $\alpha =1.5, \beta =0.0207, \gamma =0.3, \delta =0.41$, $\theta =0.3$ and $\epsilon =0.1$ (for the interpretation of the colour references in this figure caption, the reader is referred to the web version of this article)

7 Conclusion

In this work, we focus on the investigation of the dynamics of a planar slow-fast modified Leslie-Gower predator–prey model with a weak Allee effect in the predator, based on the natural assumption that the prey reproduces far more quickly than the predator. The Allee effect and its significance in population growth and decline have been extensively discussed in the empirical and scientific literature. In this article, the Allee effect is incorporated in the predator population due to the fact that the Allee effect has a significant impact on dynamics, especially boosting population decline and population extinction (Boukal et al. 2007). Predators may experience the Allee effect for a variety of reasons, including poor sperm quality, a paucity of suitable mates, poor fertilization rate, or even cooperative breeding (Courchamp et al. 2008; Berec et al. 2007). Here, we are assuming that the Allee effect exists exclusively in predators whose predation behaviour is governed by the Beddington-DeAngelis functional response. Furthermore, the predator population is assumed to be a generalist predator, meaning that if the preferred prey is not readily accessible, the predator population might switch to consuming some additional food. We emphasize that our model offers a more realistic representation due to the considerations mentioned above. Notably, the model in references (Yu 2014; Vera-Damián et al. 2019) is a specific instance achieved by setting the parameter $n = 0$ in our model (4). In contrast to Yu (2014); Vera-Damián et al. (2019), the system (4) is a singularly perturbed system, which is shown to provide a more realistic description of ecological dynamics compared to the models presented in references (Yu 2014; Vera-Damián et al. 2019). For instance, the singular Hopf bifurcation, canard limit cycles, relaxation oscillations, and the emergence of canard explosion are not possible in Yu (2014) and Vera-Damián et al. (2019).

We have applied Fenichel’s theorems for normally hyperbolic critical manifold, and used the blow-up method to fully understand the geometry of the manifolds and how they cross at non-hyperbolic places. The parameter space has been divided into four regions $R_1, R_2, R_3$ and $R_4$ (see Fig. 3) and the dynamical analysis of the system is performed in these regions.

It has been observed that the canard point Q, which exists on the parabolic critical curve $M_{20}$, serves as an organizing centre for complicated dynamics, as in a neighbourhood of the canard point, we have detected various rich phenomena including canard cycles due to singular Hopf bifurcation, the birth of canard explosions (transition from a small amplitude canard cycle to a large amplitude relaxation oscillation for $\mu \in R_3$), relaxation oscillation, homoclinic orbits and heteroclinic orbits. The occurrence of relaxation oscillations is demonstrated by the entry-exit function. In order to demonstrate the existence of homoclinic orbits, homoclinic to the hyperbolic saddle $E_{1*}$ and enclosing the canard point; heteroclinic orbits (unique or infinitely many) connecting various equilibria, we present a thorough mathematical study. This exhibits the long-term behaviour of the system. Each of the above results is verified numerically for the choice of parameter values in various regions.

The presence of relaxation oscillation and the inception of canard explosion are particularly relevant to this discussion, as they have important ecological implications. The thorough mathematical results in this regard are also presented in previous sections. The large amplitude relaxation oscillation, when $0 < \epsilon \ll 1$, exists in the region $R_3$ and has a shape consisting of two segments parallel to the x-axis, one segment parallel to the y-axis, and a curved segment similar to the attracting branch $S_0^a$ of the slow manifold $M_{20}$ (see Fig. 12b). From a biological perspective, the presence of the relaxation oscillation is an indication of the possibility of prey and predator living together. A prey breakout happens in a very short amount of time if the density of predators drops to a level that is lower than the lowest value on the critical curve. Once the density of the prey reaches a level that is enough to sustain the reproduction of the predators, the density of the predators will continue to gradually increase over an extended period of time until it reaches a density that is higher than the maximum value of the critical curve. The number of potential prey is thus decreasing noticeably over a shorter period of time. When there is less food available (prey), the number of predators steadily drops over a shorter period of time. After some time has passed, the reduced prey population density leads the number of predators to fall as well. This ensures that the cycle will continue, allowing populations of both prey and predator to coexist. The canard explosion is a very surprising and interesting phenomenon, which occurs in an exponentially small range of the parameter $\delta$. The change from a small amplitude canard cycle to a large amplitude relaxation oscillation takes place as a result of a sequence of canard cycles that occur very near to the canard point, follow the repelling slow manifold, and then jump to one of the attracting slow manifolds. From a biological point of view, this canard explosion might be seen as an early warning sign of a forthcoming regime shift as a result of an exponentially small change of parameter $\delta$.

The important part of the conclusion is that we have obtained various co-dimension 1 and 2 bifurcation structures of the slow-fast model, including the saddle-node, Hopf, transcritical bifurcation, generalized Hopf, cusp point, homoclinic, heteroclinic and Bogdanov–Takens bifurcations and used bifurcation diagrams to support the outcomes of the bifurcation. The boundary curves that divide the parametric space into different domains in the two-parameter bifurcation diagram are called bifurcation curves (see Fig. 3). A qualitative change in the system has been observed and reflected through the bifurcation analysis as we shift from one region to the other through the parameter variations. The following scenarios show that bi-stability exists when the parameters are in the region $R_1$:

• 1. The co-existing equilibrium $E_{2*}$ lies right to the fold point Q. In such a case, the basins of attraction for the co-existing equilibrium $E_{2*}$ and the prey-free equilibrium $E_{2b}$ are separated by the stable and unstable separatrices of the hyperbolic saddle $E_{1*}$. Thus, we have the stable coexistence of both the interior equilibria and the prey-free equilibrium, in spite of having an Allee effect in the predator.

• 2. We also have coexistence of stable oscillation around the canard point and the prey free equilibrium point $E_{2b}$, and these phenomena have been realized in a neighbourhood of the GH point when the parameters belong to the region $R_1$ bounded by the Hopf curve and LPC curve.

From a biological point of view, such bi-stability indicates that the system exhibits either ‘prey extinction’, ‘stable coexistence of the populations’, or ‘oscillating coexistence of the populations as a result of the appearance of the LPC curve emerging from the GH point’ depending on the initial population size and values of system parameters. Moreover, the global stability of the unique positive equilibrium point $E_*$ for $\mu \in R_3$, $x_*>x_m$, $0<\epsilon \ll 1$ is investigated.

At the end of this study, we would like to bring attention to the fact that a further interesting and challenging work of determining cyclicity by using slow divergence integral of various limit periodic sets like the canard slow-fast cycles with or without the head, canard point when $A=0$ etc will be performed in near future.